Abstract
The refractive index gradient of the eye lens is controlled by the concentration and distribution of its component crystallin proteins, which are highly enriched in polarizable amino acids. The current understanding of the refractive index increment (dn/dc) of proteins is described using an additive model wherein the refractivity and specific volume of each amino acid type contributes according to abundance in the primary sequence. Here we present experimental measurements of dn/dc for crystallins from the human lens and those of aquatic animals under uniform solvent conditions. In all cases, the measured values are much higher than those predicted from primary sequence alone, suggesting that structural factors also contribute to protein refractive index.
1. Introduction
In organisms with camera-type eyes, the transparent, refractive medium that focuses light on the retina is made up of densely packed crystallin proteins [1]. This specialized tissue is a crowded molecular environment; the protein concentration ranges from 400 mg·mL−1 in the human lens to nearly 700 mg·mL−1 in some aquatic species [2, 3, 4]. In terrestrial organisms, much of the refractive power is provided by the air/water interface at the cornea. In aquatic animals, the lens alone is responsible for refraction; hence their higher protein concentration and, on average, greater refractivity of the proteins themselves. Vertebrates share two conserved lens protein classes, the α-crystallins, which are small heat shock proteins [5], and the structural βγ-crystallins, which are primarily β-sheet proteins with a characteristic two-domain double Greek key fold [6]. In addition to these crystallin superfamilies, there are a variety of taxon-specific crystallins. For example, the S-crystallins of cephalopods are thought to have evolved from the enzyme glutathione S-transferase [7, 8, 9]. The ∊ crystallin of crocodiles and some birds is identical to lactate dehydrogenase; in the duck lens, it retains its catalytic activity even at very high concentrations [10]. The box jelly Tripedalia cystophora has three lens proteins; the J1- and J3-crystallins show similarity to ADP-ribosylglycohydrolases and vertebrate saposins, respectively, whereas J2-crystallin has no apparent sequence homologs [11]. All of these proteins have in common their high stability and solubility, consistent with the necessity for lens proteins to last the lifetime of the organism. The current model of lens protein evolution is that an abundant, soluble protein is recruited to the lens, followed by gene duplication and further selection for stability and aggregation resistance, as well as the refractive index [1, 12].
The refractive index (n) describes how much the path of light is bent when traversing the boundary between one isotropic medium and another. It is defined as , where c is the speed of light in vacuum and υ is the phase velocity of light in the material of interest. For molecules in solution, an important quantity is the refractive index increment, dn/dc [13], in which c refers to solute concentration. dn/dc values are required for data analysis when performing analytical ultracentrifugation, using a refractometer to detect analytes in size-exclusion chromatography [14], and characterizing protein oligomerization via multi-angle light scattering [15]. In many cases, the approximate average value of 0.185 mL·g−1 is used for all proteins [16]. Depending on the application, this approximation may be sufficient, but in the crystallins of the eye lens, dn/dc is generally higher than for proteins not selected for this function. A better approximation is to use the weighted average dn/dc predicted based on the amino acid composition of the protein of interest. Zhao and coworkers developed a dn/dc calculator based on the model that protein refractive index is fully explained by the amino acid composition [3]. Using this model, Mahendiran et al. investigated the effects of protein structure and primary sequence to refractive index increment. This study found that the predicted dn/dc values for βγ crystallins are much higher than for non-lens proteins with similar Greek key domain structures, a feature attributed to the higher fraction of polarizable amino acids such as arginine and methionine in the crystallins relative to other proteins [17].
Experimental measurements of dn/dc have been performed for well-characterized proteins such as bovine serum albumin (BSA) [16] and hen egg white lysozyme (HEWL) [18]. Measurements of dn/dc for bovine α-, β, and γ-crystallins have enabled rationalization of the refractive index gradient in the mammalian lens [19]. Recent experiments have shown that protein refractive index also depends on environmental factors such as solvent dielectric, ionic strength, and temperature [20]. Here we report the measured dn/dc values of several vertebrate and invertebrate crystallins. Contrary to the prevailing model, we find that for the lens crystallins the measured dn/dc values are much higher than those predicted using amino acid composition alone.
2. Methods
Protein sample preparation and dn/dc measurements
Lyophilized lysozyme from hen egg egg white (Cat. No. 195303) was purchased from MP Biomedicals (Solon, OH). Lysozyme was dissolved 10 mM sodium phosphate buffer, 100 mM sodium chloride, 0.05% sodium azide at pH 6.9 for a final concentration of 50 mg·mL−1. Human γS-crystallin [21] and Ciona intestinalis-βγ-crystallin [22] were expressed and purified as previously described. Plasmids containing the cDNA sequences fo6r Dissotichus mawsoni γS1, γS2 γM8b-, γM8c-, γM8d-, and J2-crystallin were purchased from Blue Heron (Bothell, WA). All but J2-crystallin oligonucleotides were purchased from Integrated DNA Technologies (Coralville, IA); the J2-crystallin primer was purchased from Sigma-Aldrich (St. Louis, MO). The crystallin genes were amplified with primers containing flanking restriction sites for NcoI and XhoI, an N-terminal 6× His tag, and a TEV cleavage sequence (ENLYFQG) except γS1 and γS2, which lacked an N-terminal 6× His tag, and a TEV cleavage sequence. The polymerase chain reaction product was cloned into a pET28a(+) vector, purchased from Novagen (Darmstadt, Germany). The toothfish crystallins were overexpressed in Rosetta (DE3) Escherichia coli using the Studier autoinduction protocol at 25°C for 24 hours. J2-crystallin was overexpressed in Rosetta (DE3) E. coli using standard IPTG-induced overexpression protocols at 25 °C for 18 hours. Cells were lysed by sonication and cell debris was removed by centrifugation. His-tagged crystallins were purified on an Ni-IDA column purchased from Bio-Rad (Hercules, CA) and cleaved by a His-tagged TEV protease (produced in-house). The TEV protease and His-tag were removed by a second application to an Ni-NTA column. Untagged γS1 and γS2 were dialyzed in 10 mM Tris, 0.05% sodium azide, pH 8 then purified by anion exchange on an UNOsphere Q column purchased from Bio-Rad (Hercules, CA) using a 1 M sodium chloride gradient. The final purification step for all crystallins was application to a HiLoad 16/600 Superdex 75 PG gel filtration column from GE (Pittsburgh, PA) using 10 mM sodium phosphate buffer, 100 mM sodium chloride, 0.05% sodium azide at pH 6.9. Samples for dn/dc measurements were prepared by serial dilution from a starting concentration of 50 mg·mL−1, measured using UV absorbance measurements at 280 nm using the extinction coefficients given in Table 1.
Table 1.
Calculated vs. measured dn/dc values
| Protein | Organism | Calculated dn/dc (mL·g−1) |
Measured dn/dc (mL·g−1) |
Standard Deviations Between Calculated and Measured dn/dc | Extinction coefficient (mL·g−1) |
|---|---|---|---|---|---|
| lysozyme | G. gallus | 0.1963 | 0.1970 ± 0.0010 | 0.189 | 2.64 |
| γS | H. sapiens | 0.1985 | 0.2073 ± 0.0014 | 2.38 | 1.94 |
| βγ | C. intestinalis | 0.1917 | 0.1985 ± 0.0012 | 1.84 | 1.54 |
| γM8b | D. mawsoni | 0.2003 | 0.2158 ± 0.0015 | 4.19 | 1.06 |
| γM8c | D. mawsoni | 0.2003 | 0.2061 ± 0.0014 | 1.57 | 0.957 |
| γM8d | D. mawsoni | 0.1995 | 0.2041 ± 0.0014 | 1.24 | 1.03 |
| γS1 | D. mawsoni | 0.2020 | 0.2183 ± 0.0014 | 4.41 | 2.15 |
| γS2 | D. mawsoni | 0.2002 | 0.2168 ± 0.0014 | 4.49 | 2.31 |
| J2 | T. cystophora | 0.1920 | 0.2037 ± 0.0012 | 3.16 | 0.283 |
Refractive index increments were measured following the batch-mode technique using an Optilab rEX refractive index detector (Wyatt Technology, Santa Barbara, CA) configured with a 685 nm fiber-optic laser diode source. The instrument measures differential refraction using a flow cell where the light path first passes through the sample containing the analyte then through a reference sample. Any difference in refraction between the two solutions results in beam deflection that is detected by an array of photodiodes. The most common sources of experimental error in this type of measurement are caused by temperature fluctuations or inaccuracies in the sample concentration.
Refractive index calculations
The method used here to calculate protein refractive index increment (dn/dc) is adapted from the work of McMeekin and coworkers [23, 24]. This treatment also forms the basis of the dn/dc calculator published by Zhao and colleagues [3, 25].
Protein refractivity (RP) per gram is calculated from the weight percentages of each amino acid (indexed i) applying the same method used to calculate protein partial specific volume (). Empirical values for refractivity [24] (Ri) and specific volume () of the individual amino acids [26] are summed, as in (1) and (2), respectively.
| (1) |
| (2) |
The refractive index of the protein follows from a rearrangement of the Lorentz-Lorenz equation (3), which is itself an expanded Gladstone-Dale expression [27], yielding (4).
| (3) |
| (4) |
Assuming volume additivity, the refractive index of protein (np) in solution can be calculated from the Wiener equation (from Heller et. al.[28], eq. 7, eq. 17) such that (5) becomes (6) when the sample is sufficiently dilute nsolution→nsolvent.
| (5) |
| (6) |
Corrections for the wavelength (7) and temperature (8) were implemented by Zhao et al. based on work by Perlmann and Longsworth [29].
| (7) |
| (8) |
In this implementation, an R script was written to compute predictions of protein (dn/dc) from multiple amino-acid sequence inputs. All calculations were run using nsolvent = 1.3340, T = 25°C, and λ = 589.3 nm (corresponding to the wavelength used to measure the amino acid dn/dc values by McMeekin and coworkers).
Molecular Modeling and Calculation of Solvent Accessible Surface Area
Three-dimensional structural models were obtained for each protein in order investigate potential sources of the deviation from the additive model of dn/dc. Experimentally determined structures were used where they were available: structural models for hen egg white lysozyme (PDB ID: 4WG1 and 4WG7) [30], human γS-crystallin (PDB ID: 2M3T) [31], and Ciona intestinalis βγ-crystallin (PDB ID: 2BV2 [32]) were downloaded from the Protein Data Bank (PDB) [33]. For the proteins that lack empirical structures, models were calculated using the Robetta server [34], which predicts three-dimensional structure from a primary sequence input. Robetta uses comparative modeling based on solved PDB structures of similar sequence fragments, followed by all-atom refinement. J2-crystallin was omitted from the structure calculations because it has no known sequence homologs, reducing our confidence in this type of comparative modeling in its case. Solvent accessible surface areas (SASA) were computed in UCSF Chimera [35] using the MSMS package with default settings [36]. This package calculates SASA using a rolling sphere of radius 1.4 Å to approximate a water molecule.
π-Pair Refractive Index Correction
The 3D models described above were also used to generate a correction factor to the dn/dc calculations accounting for short-range interactions between pairs of highly polarizable residues, focally tryptophan, phenylalanine, tyrosine, histidine, and arginine. These highly polarizable residues all contain π-bonding systems, thus we refer to this term as the π-pair correction. We estimated the polarizability contribution of each residue to be its dn/dc difference from alanine , as this takes into account only contributions from the side chain beyond the β-carbon. The refractive index correction factor for a given protein (CF) was determined based on the distance (d) between the polarizable side chain centroids of residues (i, j) as follows.
| (9) |
Upper bound distance cuto s for π-π and cation-π interactions were taken as 7 Å and 6 Å respectively, where any interaction with arginine considered to be cation-π and all others treated as π-π. Unscaled correction factors were fit to residuals using a multiple linear regression yielding best fits of δπ−π = 0.11 and δcation−π = −0.08.
Results and Discussion
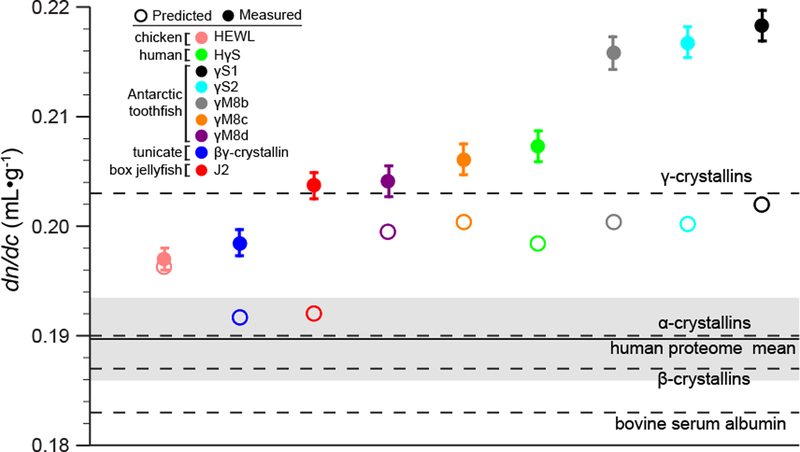
The proteins investigated here include human γS-crystallin, γM8b-, γM8c-, γM8d-, γS1-, and γS2-crystallins from the Antarctic toothfish (Dissotichus mawsoni), J2-crystallin from the box jellyfish (Tripedalia cystophora), and βγ-crystallin from the tunicate Ciona intestinalis, as well as hen egg white lysozyme (HEWL) as a non-lens control protein. The results are shown in Figure 1. Comparisons to the calculated dn/dc values are summarized in Table 1 and Figure 2. Figure 2 shows the predicted (open circle) and measured (filled circle) dn/dc values for each protein in our set. Predictions were performed using the methodology of Zhao and coworkers as described above [3]. In comparison, predicted dn/dc values were also calculated for all known proteins in the the human proteome, comprising 70,940 human proteome sequences gathered from the Uniprot database (organism 9606 and proteome up000005640). The distribution of predicted dn/dc values for the human proteome is approximated well by a Gaussian with an average dn/dc of 0.1897 mL·g −1 and a standard deviation of 0.0037 mL·g−1. This range provides a benchmark against which to compare the predicted and measured values for the lens proteins.
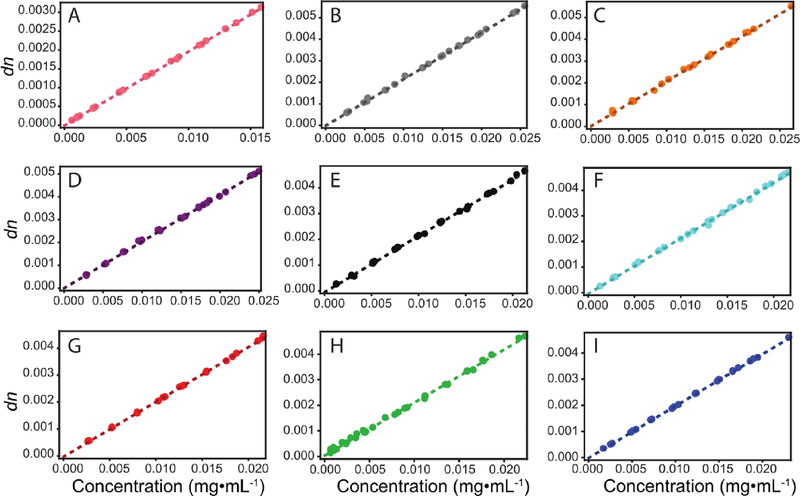
Figure 1.
Experimentally determined dn/dc values for lens proteins from different organisms. A. HEWL (control), B. γM8b-crystallin, C. γM8c-crystallin, D. γM8dcrystallin, E. γS1-crystallin, F. γS2-crystallin, G. J2-crystallin, H. human γS-crystallin, I. tunicate βγ-crystallin. Hen egg white lysozyme was measured as a control protein that has not been selected for high refractivity.
Figure 2.
Measured dn/dc values compared to predicted. The dn/dc of HEWL, human γS-crystallin, toothfish γS1-, γS2-, γM8b-, γM8c-, and γM8d-crystallins, box jelly J2-crystallin and tunicate βγ-crystallin were measured and compared to their predicted values, represented by filled and open circles respectively. The solid line represents the mean dn/dc of the human proteome, with the shaded region representing one standard deviation from the mean. The dashed lines indicate the literature dn/dc values for bovine serum albumin [39], and α-, β, and γ-crystallin fractions from bovine eye lens [19].
For lysozyme, which has not been subject to selective pressure for refractivity, the measured value agrees with that calculated based on its amino acid composition, as well as with a previously measured literature value [37]. In contrast, all of the eye lens proteins investigated here have a dn/dc of 0.20 mL·g−1 or higher. This average value is more than 2.5 standard deviations higher than the standard value of 0.185 mL·g−1 often cited as the mean for all proteins. Furthermore, for all the lens proteins, the measured dn/dc values are much higher than the predictions (between 1–4 standard deviations), indicating that amino acid composition alone is not sufficient to explain the high refractivity of lens proteins.
Although all the crystallin proteins exhibit a difference between the predicted and measured dn/dc, the largest discrepancies are observed for the γS1-, γS2-, and γM8bcrystallins from the Antarctic toothfish, D. mawsoni. The discrepancy for J2-crystallin from the box jelly is nearly as large, while those for human γS-crystallin and toothfish γM8b- and γM8c-crystallin are more moderate. The differences among dn/dc values for the toothfish proteins are particularly interesting in light of the fact that D. mawsoni has at least has thirteen γ-crystallin paralogs [38]. This diversity may be necessary to balance the competing requirements for lens function in the Antarctic habitat of this fish: maintaining a high refractive index while also resisting freezing and cold cataract formation at −2 °C. Taken together, these results raise the question of which other features of lens proteins have evolved to increase refractivity beyond selection for a large fraction of highly polarizable amino acid residues.
In order to discover the molecular basis for the deviation from the predicted values, it is necessary to examine the assumptions made in this treatment of refractive index. In particular, the Gladstone-Dale relation assumes straightforward volume additivity and isotropic polarizability [40]. In this treatment, the refractive volume of one protein molecule in nm3 is given by R(Mm)/NA, and the refractivity of one protein molecule is given by , where Mm is the molecular mass, NA is Avogadro’s number and α is the average polarizability. The fact that α is a second-rank tensor is ignored because the sample in question is an isotropic solution where all orientations of these small globular proteins are assumed to be equally represented in the ensemble. The deviation of our measured dn/dc data from the additive model could be explained if the assumption that the protein partial specific volume is equal to the sum of that for its component amino acids is incorrect, or if the anisotropic polarizability of the individual amino acids (or small groups of them) is not negligible in the context of a folded protein.
Volume additivity could play a major role in principle, as the effective volume of an amino acid in solution is affected by hydration, and thus in solution the volume of a compactly folded protein is smaller than that of its component amino acids. However, in practice volume additivity per se does not appear to be the dominant effect, because the additive Gladstone-Dale model works well for many typical proteins, including HEWL, the control protein in this set. This may be because the effect would largely be expected to impact aliphatic amino acid sidechains, which are generally buried inside the protein interior, but have low polarizability and thus contribute little to the refractive index. For surface-exposed residues, previous experimental studies have found that at room temperature and below, hydration of charged and non-polar sidechains is similar to that observed in small model compounds (e.g. isolated amino acids), while significant deviations are observed for the hydration of polar neutral sidechains [41].
Water molecules bound to the surface of a protein behave differently from those solvating small polar molecules because each water molecule can form hydrogen bonds with multiple polar groups on the protein surface, resulting in a network of ordered solvation water that influences the compressibility more than the specific volume [42, 43, 44, 45]. These hydrogen bond networks line up water molecules, albeit transiently, impacting the electric field at the protein surface. The water layer around a biomolecule is dynamic and heterogeneous, and exact degree of ordering and the timescale of “bound” water dynamics remain controversial [46]. However, it is reasonable to expect protein hydration to have a non-negligible impact on refractive index. Subtle effects of the solution composition have previously been shown to impact refractivity, for example the measured dn/dc of lysozyme depends on the buffer compound used [47].
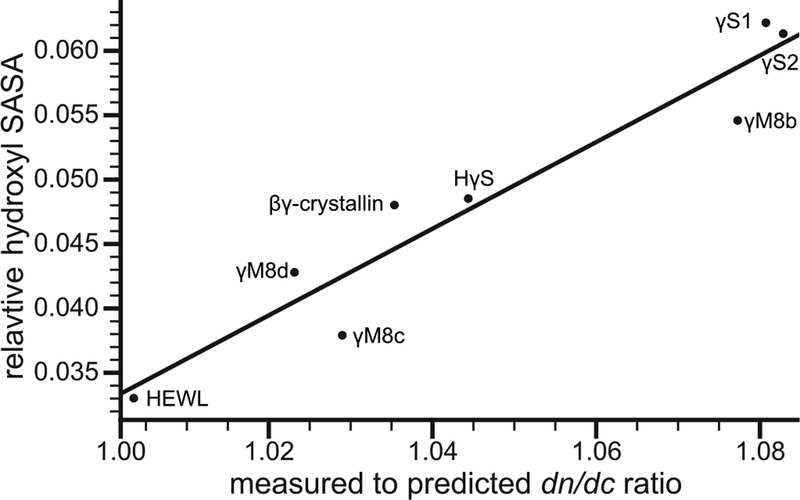
Examination of the structural models for our protein set revealed a positive correlation between the solvent-exposed surface area (SASA) of hydroxyl groups and the deviation from predicted dn/dc values (Figure 3). Hydroxyl groups are highly polar and can both donate and accept hydrogen bonds, contributing to the formation of the water network at the protein surface. This correlation supports the hypothesis that protein hydration plays a role in the dn/dc discrepancies we observe in lens proteins and provides a rationale for future experimental studies of their hydration properties. Prior experiments have suggested that the hydration shells of eye lens crystallin proteins are particularly robust, highlighting a possible mechanism of selection for high refractivity as well as enhanced solubility [48].
Figure 3.
Relative hydroxyl SASA correlates with the measured to predicted dn/dc ratio. The relationship was fit to a linear regression that follows the form Shyd = 0.336x − 0.304 with an R2 of 0.906, in which Shyd and x are the fraction of hydroxyl SASA and measured to predicted dn/dc ratio respectively.
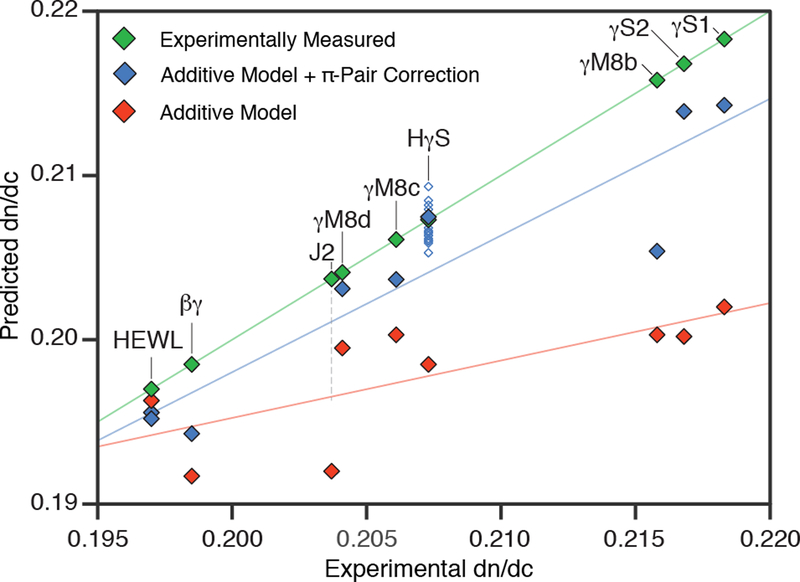
Another factor that may influence the protein dn/dc is that the polarizabilities of individual amino acids in the context of a folded protein need not be isotropic; residues may interact with their neighbors to produce local (much smaller than the wavelength of light) regions of larger polarizability. Some of the most polarizable amino acid side chains, e.g. Trp, Phe, Tyr, His, and Arg, are also highly anisoptropic in shape, raising the possibility of highly specific interactions held in place by the packing of the protein interior. Surface residues may also adopt particular conformations via strong interactions such as salt bridges or cation-π interactions. These effects are probably not independent, as changes in the compressibility of the molecule also influence its polarizability [49]. To approximate the effect of polarizable amino acid interactions, we applied a correction factor to the additive dn/dc model from Zhao et al. In this correction, applying a small positive and negative weight for π-π and cation-π interactions, respectively, improves prediction accuracy (Figure 4). More experimental data is needed to develop a more complete theory of protein refractive index in lens proteins. In particular, this π-pair correction may be refined using the detailed angular information about the relative orientations of key side chains that is only available from high-resolution structures, while experimental measurements of the hydration shell mobility will help to clarify the role of surface hydration.
Figure 4.
Experimental dn/dc values (green), values predicted from the additive model of Zhao et al (red) and additive model values plus the π-pair correction (blue) are plotted as a function of the experimental dn/dc. Corrected predictions are shown as filled diamonds for the lowest energy structure and empty diamonds for alternate confirmations where they are available. Two filled diamonds are shown representing the two lysozyme crystal structures, while no predictions are shown for J2-crystallin, as no previously solved structures were sufficiently similar for confident structural modeling. Additional unfilled diamonds are shown for human γS-crystallin to represent alternate low energy NMR conformations. Regression lines are shown as visual guides for model comparison.
Conclusion
In summary, the measured refractive index values for all the lens crystallins investigated here is higher than that predicted using the prevailing model, indicating that factors other than amino acid composition are involved in producing the high refractivity of lens proteins. The difference is particularly striking for γS1-, γS2-, and γM8b-crystallin from the Antarctic toothfish. We propose two hypotheses for the origin of this effect, which may work independently or in concert. The arrangement of hydroxyl groups on the surface may affect the protein hydration structure and hence the dipole moment and polarizability. Alternatively, the effect of short-range interactions between highly polarizable amino acids may cause local regions of anisotropic polarizability. We propose a correction to the additive model based on the idea that π-π interactions contribute more to the refractive index than the sum of the amino acid polarizabilities. For the proteins studied here, this π-pair model improves agreement between predicted and measured values, although further refinement is needed. Structure determination efforts for these proteins and experiments probing their hydration shells are expected to provide further insight into the mechanisms underlying the high refractive indices of eye lens proteins. Other remaining questions include the behavior of these proteins at higher concentrations, where self-organization becomes important, as well as the concentration gradient and differential distribution of these proteins in the lens.
Supplementary Material
Acknowledgments
The authors thank Stephen White for providing access to instrumentation in his laboratory, Craig Martens and Carter Butts for helpful discussions, Andrew Meyer and Wyatt Instruments for assistance with the refractometer, and Dmitry Fishman for excellent management of the UCI Laser Spectroscopy Facility. This work was supported by the National Science Foundation awards DMR 1410415 and DMS 1361425, and National Institutes of Health awards 1R01EY021514 and 1R01EY025328 to RWM and collaborators. KWR was supported by an NSF graduate fellowship under award DGE 1633631.
Footnotes
Supplementary Information
The molecular models used for calculating the hydroxyl SASA and the π-pair correction term for the Dissotichus mawsoni γS1-, γS2-, γM8b-, γM8c-, and γM8d-crystallins are available for download.
References
- [1].Slingsby Christine, Wistow Graeme J., and Clark Alice R.. Evolution of crystallins for a role in the vertebrate eye lens. Protein Science, 22(4):367–380, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Wistow Graeme J. and Piatigorsky Joram. Lens crystallins: The evolution and expression of proteins for a highly specialized tissue. Annual Review of Biochemistry, 57:479–504, 1988. [DOI] [PubMed] [Google Scholar]
- [3].Zhao H, Brown PH, and Schuck P. On the distribution of protein refractive index increments. Biophysical Journal, 100:2309–2317, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Zhao Huaying, Chen Yingwei, Rezabkova Lenka, Wu Zhengrong, Wistow Graeme, and Schuck Peter. Solution properties of γ-crystallins: Hydration of fish and mammal γ-crystallins. Protein Science, 23(1):88–99, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Horwitz J. Alpha-crystallin can function as a molecular chaperone. Proceedings of the National Academy of Sciences of the United States of America, 89(21):10449–10453, November 1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Weadick Cameron J. and Chang Belinda S. W.. Molecular evolution of the βγ lens crystallin superfamily: evidence for a retained ancestral function in γn crystallins. Molecular Biology and Evolution, 26:1127–1142, 2009. [DOI] [PubMed] [Google Scholar]
- [7].Piatigorsky J and Wistow G. The recruitment of crystallins: new functions precede gene duplication. Science, 252:1078–1079, 1991. [DOI] [PubMed] [Google Scholar]
- [8].Tomarev S, snd Chung SI and Piatigorsky J. Glutathione S-transferase and S-crystallins of cephalopods: evolution from active enzyme to lens-refractive proteins. Journal of Molecular Evolution, 41:1048–1056, 1995. [DOI] [PubMed] [Google Scholar]
- [9].Tan Wei-Hung, Cheng Shu-Chun, Liu Yu-Tung, Wu Cheng-Guo, Lin Min-Han, Chen Chiao-Che, Lin Chao-Hsiung, and Chou Chi-Yuan. Structure of a highly active cephalopod S-crystallin mutant: New molecular evidence for evolution from an active enzyme into lens-refractive protein. Scientific Reports, 6:31176, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Wistow Graeme J., Mulders John W. M., and Wilfried W. de Jong. The enzyme lactate dehydrogenase as a structural protein in avian and crocodilian lenses. Nature, 326:622–624, 1987. [DOI] [PubMed] [Google Scholar]
- [11].Kozmik Z, Shivalingappa K, Ruzickova J, Jonasova K, Paces V, Vlcek C, and Piatigorsky J. Cubazoan crystallins: evidence for convergent evolution of pax regulatory sequences. Evolution & Development, 10:52–61, 2008. [DOI] [PubMed] [Google Scholar]
- [12].Slingsby C and Graeme J. Wistow. Functions of crystallins in and out of lens: Roles in elongated and post-mitotic cells. Progress in Biophysics and Molecular Biology, 115:52–67, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Huglin MB. Specific refractive index increments of polymer solutions. part i. literature values. Journal of Applied Polymer Science, 9:3963–4001, 1965. [Google Scholar]
- [14].Wen Jie, Arakawa Tsutomu, and Philo John S.. Size-exclusion chromatography with on-line light-scattering, absorbance, and refractive index detectors for studying proteins and their interactions. Analytical Biochemistry, 240(2):155–166, 1996. [DOI] [PubMed] [Google Scholar]
- [15].Ye Hongping. Simultaneous determination of protein aggregation, degradation, and absolute molecular weight by size exclusion chromatography–multiangle laser light scattering. Analytical Biochemistry, 356(1):76–85, 2006. [DOI] [PubMed] [Google Scholar]
- [16].Barer R and Joseph S. Refractometry of living cells. The Quarterly Journal of Microscopical Science, 95:399–423, 1954. [Google Scholar]
- [17].Mahendiran K, Elie C, Nebel J-C, Ryan A, and Pierscionek BK. Primary sequence contribution to the optical function of the eye lens. Scientific Reports, 4:5195, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Fredericks WJ, Hammonds MC, Howard SB, and Rosenberger F. Density, thermal expansivity, viscosity and refractive index of lysozyme solutions at crystal growth concentrations. Journal of Crystal Growth, 141:183–192, 1994. [Google Scholar]
- [19].Pierscionek Barbara, Smith George, and Augusteyn Robert C. The refractive increments of bovine α-, β-and γ-crystallins. Vision Research, 27(9):1539–1541, 1987. [DOI] [PubMed] [Google Scholar]
- [20].Tan C-Y and Huang Y-X. Dependence of refractive index on concentrations and temperature in electrolyte solution, polar solution, nonpolar solution, and protein solutions. Journal of Chemical & Engineering Data, 60:2827–2833, 2015. [Google Scholar]
- [21].Brubaker WD, Freites JA, Golchert KJ, Shapiro RA, Morikis V, Tobias DJ, and Martin RW. Separating instability from aggregation propensity in γS-crystallin variants. Biophys. J, 100(2):498–506, January 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Kozlyuk Natalia, Sengupta Suvrajit, Bierma Jan C., and Martin Rachel W. Calcium binding dramatically stabilizes an ancestral crystallin fold in tunicate βγ-crystallin. Biochemistry, 55(50):6961–6968, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].McMeekin Thomas L, Wilensky Mildred, and Groves Merton L. Refractive indices of proteins in relation to amino acid composition and specific volume. Biochemical and Biophysical Research Communications, 7(2):151–156, 1962. [Google Scholar]
- [24].McMeekin Thomas L., Groves Merton L., and Hipp Norbert J.. Refractive indices of amino acids, proteins, and related substances In Amino Acids and Serum Proteins, chapter 4, pages 54–66. ACS Publications, 1964. [Google Scholar]
- [25].Zhao H, Brown PH, Magone MT, and Schuck P. The molecular refractive function of lens γ-crystallins. Journal of Molecular Biology, 411(3):680–699, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Cohn Edwin J. and Edsall John T.. Density and apparent specific volume of proteins In Proteins, amino acids, and peptides as ions and dipolar ions, chapter 16, pages 370–381. Reinhold Publishing Corporation, New York, 1943. [Google Scholar]
- [27].Barer R and Joseph S. Refractometry of living cells: Part i. basic principles. Journal of Cell Science, 3(32):399–423, 1954. [Google Scholar]
- [28].Heller Wilfried. Remarks on refractive index mixture rules. The Journal of Physical Chemistry, 69(4):1123–1129, 1965. [Google Scholar]
- [29].Perlmann Gertrude E. and Longsworth LG. The specific refractive increment of some purified proteins. Journal of the American Chemical Society, 70(8):2719–2724, 1948. [DOI] [PubMed] [Google Scholar]
- [30].Coquelle N, Brewster AS, Kapp U, Shilova A, Weinhausen B, Burghammer M, and Colletier JP. Raster-scanning serial protein crystallography using micro- and nano-focused synchrotron beams. Acta Crystallographica, Section D: Biological Crystallography, 71:1184–1196, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Kingsley Carolyn N., Brubaker William D., Markovic Stefan, Diehl Anne, Brindley Amanda J., Oschkinat Hartmut, and Martin RW. Preferential, specific binding of human αB-crystallin to a cataract-related variant of γS-crystallin. Structure, 21:2221–2227, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Shimeld SM, Purkiss AG, Dirks RP, Bateman OA, Slingsby C, and Lubsen NH. Urochordate betagamma-crystallin and the evolutionary origin of the vertebrate eye lens. Current Biology, 15:1684–1689, 2005. [DOI] [PubMed] [Google Scholar]
- [33].Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, and Bourne PE. The protein data bank. Nucleic Acids Research, 28:235–242, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Kim David E, Chivian Dylan, and Baker David. Protein structure prediction and analysis using the Robetta server. Nucleic Acids Research, 32(suppl 2):W526–W531, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Pettersen Eric F., Goddard Thomas D., Huang Conrad C., Couch Gregory S., Greenblatt Daniel M., Meng Elaine C., and Ferrin Thomas E.. UCSF chimera–a visualization system for exploratory research and analysis. Journal of Computational Chemistry, 25(13):1605–1612, 2004. [DOI] [PubMed] [Google Scholar]
- [36].Sanner Michel F., Olson Arthur J., and Spehner Jean-Claude. Reduced surface: An e cient way to compute molecular surfaces. Biopolymers, 38(3):305–320, March 1996. [DOI] [PubMed] [Google Scholar]
- [37].Gibaud Thomas, Cardinaux Frederic, Bergenholtz Johan, Stradner Anna, and Schurtenberger Peter. Phase separation and dynamical arrest for particles interacting with mixed potentials-the case of globular proteins revisited. Soft Matter, 7:857–860, 2011. [Google Scholar]
- [38].Kiss Andor J., Mirarefi Amir Y., Ramakrishnan Subramanian, Zukoski Charles F., DeVries Arthur L., and Cheng Chi-Hing C.. Cold-stable eye lens crystallins of the Antarctic nototheniid toothfish Dissostichus mawsoni Norman. Journal of Experimental Biology, 207:4633–4649, 2004. [DOI] [PubMed] [Google Scholar]
- [39].Kratohvil JP, Dezelic G, and Dezelic N On the refractive index increment of bovine plasma albumin at low concentrations. Archives of Biochemistry and Biophysics, 106:381–385, 1964. [DOI] [PubMed] [Google Scholar]
- [40].Böttcher CJF. Theory of electric polarization, volume 1. Elsevier Science Publishers B.V., Sara Burgerhartstraat 25, PO Box 211, 1000 AE Amsterdam, The Netherlands, second edition, 1973. [Google Scholar]
- [41].Chalikian Tigran V., Totrov Maxim, Abagyan Ruben, and Breslauer Kenneth J.. The hydration of globular proteins as derived from volume and compressibility measurements: Cross correlating thermodynamic and structural data. Journal of Molecular Biology, 260:588–603, 1996. [DOI] [PubMed] [Google Scholar]
- [42].Kharakoz DP. Volumetric properties of proteins and their analogs in diluted water solutions. 1. Partial volumes of amino acids at 15–55 °C. Biophysical Chemistry, 34:5634–5642, 1989. [DOI] [PubMed] [Google Scholar]
- [43].Kharakoz DP. Volumetric properties of proteins and their analogs in diluted water solutions. 2. Partial adiabatic compressibilities of amino acids at 15–70 °C. J. Phys. Chem, 95:5634–5642, 1991. [DOI] [PubMed] [Google Scholar]
- [44].Kharakoz DP. Partial molar volumes of molecules of arbitrary shape and the effect of hydrogen bonding with water. Journal of Solution Chemistry, 21:569–595, 1992. [Google Scholar]
- [45].Kharakoz DP and Sarvazyan AP. Hydrational and intrinsic compressibilities of globular proteins. Biopolymers, 33:11–26, 1993. [DOI] [PubMed] [Google Scholar]
- [46].Laage Damien, Elsaesser Thomas, and Hynes James T.. Water dynamics in the hydration shells of biomolecules. Chemical Reviews, 117:1069410725, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Ball Vincent and Ramsden Jeremy J.. Buffer dependence of refractive index increments of protein solutions. Biopolymers, 46(7):489–492, December 1998. [Google Scholar]
- [48].Huang Kuo-Ying, Kingsley Carolyn N., Sheil Ryan, Cheng Chi-Yuan, Bierma Jan C., Roskamp Kyle W., Khago Domarin, Martin Rachel W., and Han Songi. Stability of protein-specific hydration shell on crowding. Journal of the American Chemical Society, 138:5392–5402, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Donald Kelling J.. Electronic compressibility and polarizability: Origins of a correlation. Journal of Physical Chemistry A, 110(6):2283–2289, 2006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.