Deep Reinforcement Learning in Medicine

Abstract

Reinforcement learning has achieved tremendous success in recent years, notably in complex games such as Atari, Go, and chess. In large part, this success has been made possible by powerful function approximation methods in the form of deep neural networks. The objective of this paper is to introduce the basic concepts of reinforcement learning, explain how reinforcement learning can be effectively combined with deep learning, and explore how deep reinforcement learning could be useful in a medical context.

Introduction

Reinforcement learning (RL) algorithms have experienced unprecedented success in the last few years, reaching human-level performance in several domains, including Atari video games [1] or the ancient games of Go [2] and chess [3]. This success has been largely enabled by the use of advanced function approximation techniques in combination with large-scale data generation from self-play games. The aim of this paper is to introduce basic RL algorithms and describe state-of-the-art extensions of these algorithms to deep learning. We also discuss the potential of RL in medicine and review the literature to study existing practical applications of RL. Even though RL offers several benefits in comparison to other artificial intelligence (AI) techniques, such as the ability to optimize long-term benefit to patients rather than immediate benefit, there are a number of obstacles that have to be overcome in order to apply RL on a large scale.

Reinforcement Learning

RL is an area of machine learning concerned with sequential decision problems [4]. Concretely, a learner or agent interacts with an environment by taking actions, and the aim of the agent is to maximize its expected cumulative reward. Each action affects the next, and the agent cannot simply maximize the immediate reward that it will get, but rather has to plan ahead and select actions that will maximize reward in the long run.

Notation: Given a finite set X, a probability distribution on X is a vector µ ∈ R^X whose elements are non-negative (i.e., µ(x) ≥ 0 for each x ∈ X) and whose sum equals 1 (i.e., Σ_xµ(x) = 1). We use Δ(X) = {µ ∈ R^X: Σ_xµ(x) = 1, µ(x) ≥ 0 (∀x)} to denote the set of all such probability distributions.

Markov Decision Processes

Sequential decision problems are usually modelled mathematically as Markov decision processes, or MDPs. An MDP is a tuple M = (S, A, P, r), where

• S is the finite state space,

• A is the finite action space,

• P: S × A → Δ(S) is the transition function, with P (s′ ∣ s, a) denoting the probability of moving to state s′ when taking action a in state s,

• r: S × A → R is the reward function, with r (s, a) denoting the expected reward obtained when taking action a in state s.

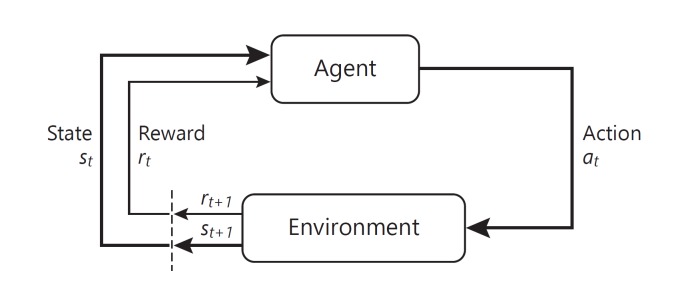
Intuitively, the agent controls which action to select, while the environment controls the outcome of each action. In each round t, the agent observes a state s_t ∈ S and selects an action a_t ∈ A. As a result, the environment returns a new state s_{t + 1} ∼ P (• ∣ s_t, a_t) and reward r_{t+ 1} ∼ r (s_t, a_t). This process is illustrated in Figure 1. By repeating the procedure for t = 0, 1, 2, ... the result is a trajectory

$$s_0,a_0,r_1,s_1,a_1,r_2,s_2,a_2,r_3,s_3,\mathrm{....}$$

The aim of the agent is to select actions as to maximize some measure of expected cumulative reward. The most common reward criterion is the discounted cumulative reward

$$E\left[r_1+\gamma r_2+{\gamma }^2{r}_2+\mathrm{...}\right]=E\left[\sum _{t-1}^{\infty }{\gamma }^{t-1}{r}_t\right],$$

where γ ∈ (0, 1] is a discount factor which ensures that the sum remains bounded.

Fig. 1.

Illustration of the agent-environment interface [4].

The decision strategy of the agent is represented by a policy π: S → Δ (A), with π (a | s) denoting the probability that the agent selects action a in state s. For each policy π, we can define an associated value function V^π, which measures how much expected reward the agent will accumulate from a given state when acting according to π. Specifically, the value in state s is defined as

$$V^{\pi }(s)=E\left[\sum _{t-1}^{\infty }{\gamma }^{t-1}{r}_t|s_0=s\right].$$

The values of consecutive states satisfy a recursive relationship called the Bellman equations:

$$V^{\pi }(s)=\sum _a\pi (a|s)\left(r(s,a)+\gamma \sum _{s^{\text{'}}}P(s^{\text{'}}|s,a)V^{\pi }(s^{\text{'}})\right).$$

As an alternative to V^π, we can instead define an action-value function Q^π, which measures how much expected reward the agent will accumulate from a given state when taking a specific action and then acting according to π. The action-value for state s and action a is defined as

$$Q^{\pi }(s,a)=E\left[\sum _{t-1}^{\infty }{\gamma }^{t-1}{r}_t|s_0=s,a_0=a\right]$$

There is a straightforward relationship between the value function V^π and action-value function Q^π:

$$V^{\pi }(s)=\sum _a\pi (a|s)Q^{\pi }(s,a),Q^{\pi }(s,a)=r(s,a)+\gamma \sum _{s^{\text{'}}}P(s^{\text{'}}|s,a)V^{\pi }(s^{\text{'}})$$

Consequently, the Bellman equations can be stated either for V^π or for Q^π.

We can also define the optimal value function V* as the maximum amount of expected reward that an agent can accumulate from a given state. The optimal value function in state s is given by V* (s) = max_πV^π (s), i.e., the maximum value among the individual policies. The optimal policy π* is the policy that attains the maximum value in each state s, i.e., π* (• ∣ s) = arg max_π V^π (s). The optimal values of consecutive states satisfy the optimal Bellman equations

$$V^{*}(s)=\underset{a}{max}\left(r(s,a)+\gamma \sum _{s^{\text{'}}}P(s^{\text{'}}|s,a)V^{*}(s^{\text{'}})\right)$$

Just as before, we can instead define the optimal action-value function Q*, which is related to V* as follows:

$$V^{*}(s)=\underset{a}{max}{Q}^{*}(s,a),Q^{*}(s,a)=r(s,a)+\gamma \sum _{s^{\text{'}}}P(s^{\text{'}}|s,a)V^{*}(s^{\text{'}})$$

RL Algorithms

Most RL algorithms work by maintaining an estimate πˆ of the optimal policy, an estimate Vˆ of the optimal value function, and/or an estimate Qˆ of the optimal action-value function. If the transition function P and reward function r are known, πˆ and Vˆ can be estimated directly. Specifically, from the Bellman equations we can derive a Bellman operator T^π which can be applied to a value function Vˆ to produce a new value function T^πVˆ defined as

$$T^{\pi }\widehat{V}(s)=\sum _a\pi (a|a)\left(r(s,a)+\gamma \sum _{s^{\text{'}}}P(s^{\text{'}}|s,a)\widehat{V}(s^{\text{'}})\right).$$

Likewise, from the optimal Bellman equations we can derive an optimal Bellman operator T* that, when applied to a value function Vˆ, is defined as

$$T^{*}\widehat{V}(s)=\underset{a}{max}\left(r(s,a)+\gamma \sum _{s^{\text{'}}}P(s^{\text{'}}|s,a)\widehat{V}(s^{\text{'}})\right).$$

Value iteration works by repeatedly applying the optimal Bellman operator T* to an initial value function estimate Vˆ₀:

$${\widehat{V}}_{k+1}=T^{*}{\widehat{V}}_k,k=0,1,2,\mathrm{...}$$

If the value of each state is stored in a table, value iteration is guaranteed to eventually converge to the optimal value function V*.

Policy iteration instead starts with an initial policy estimate πˆ₀ and alternates between a policy estimation step and a policy improvement step. In the policy estimation step, we simply estimate the value function Vˆ^πˆk associated with the current policy πˆ_k. To do so, we can repeatedly apply the Bellman operator T^πˆk to an initial value function estimate Vˆ₀:

$${\widehat{V}}_{n+1}=T^{{\widehat{\pi }}_k}{\widehat{V}}_n,n=0,1,2,\mathrm{...}$$

In the policy improvement step, we update the policy such that it is greedy with respect to the value function estimate Vˆ^πˆk:

$${\widehat{\pi }}_{k+1}=arg\underset{\pi }{max}{T}^{\pi }{\widehat{V}}^{{\pi }_k}.$$

If the value of each state is stored in a table, policy iteration is also guaranteed to eventually converge to the optimal value function V*.

If the transition function P and reward function r are unknown, we have to resort to different techniques. In this case, πˆ, Vˆ, and Qˆ have to be estimated from transitions on the form s_t, a_t, r_{t+ 1}, s_{t+ 1}. Unlike value iteration and policy iteration, which update the values of all states in each iteration, temporal difference (TD) methods update the value of a single state for a given transition. The most popular TD method is Q-learning [5], which maintains an estimate Qˆ_t of the optimal action-value function, which is updated after each transition (s_t, a_t, r_{t+ 1}, s_{t+ 1}). The new estimate Qˆ_{t+ 1} is identical to Qˆ_t for each state-action pair different from (s_t, a_t), while Qˆ_{t+ 1} (s_t, a_t) is given by

$${\widehat{Q}}_{t+1}(s_t,a_t)=(1-{\alpha }_t){\widehat{Q}}_t(s_t,a_t)+{\alpha }_t\left(r_{t+1}+\gamma \underset{a}{max}{\widehat{Q}}_t(s_{t+1},a)\right).$$

Here, α_t is a learning rate. If the value of each state-action pair is stored in a table and α_t is appropriately tuned, Q-learning is guaranteed to eventually converge to the optimal action-value function Q*, even if the transition function P and reward function r are unknown.

Deep RL

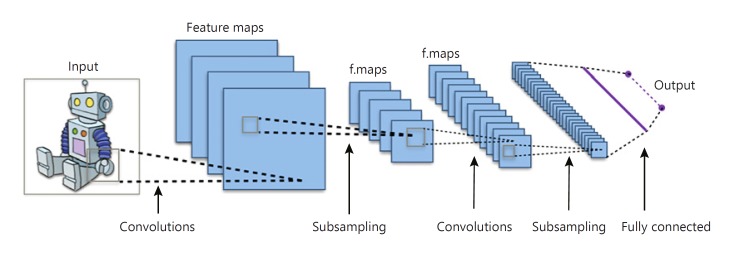
In most realistic domains, the state space S is too large to store the estimated value function Vˆ in a table. In this case, it is common to parameterize Vˆ_θ (or πˆ_θ, Qˆ_θ) on some parameter vector θ. The value in a state is completely determined by the current parameters in θ, and the update rules for RL algorithms are modified such that they no longer update the values of states directly, but rather the parameters in θ. In deep RL, Vˆ_θ (or πˆ_θ, Qˆ_θ) is represented using a deep neural network, with θ being the parameters of the network. When the input is an image, a convolutional neural network is typically deployed, such as the one in Figure 2.

Fig. 2.

Convolutional neural network. By Aphex 34 (CC BY-SA 4.0 [https://creativecommons.org/licences/by-sa/4.0]), from Wikimedia Commons.

A deep Q network, or DQN [1], is a deep neural network that estimates the action-value function Qˆ_θ. Given a transition s_t, a_t, r_{t+ 1}, s_{t+ 1}, the parameters θ of the neural network are updated as to minimize the Bellman error

$$r_{t+1}+\gamma \underset{a}{max}{\widehat{Q}}_{\Theta }(s_{t+1},a)-{\widehat{Q}}_{\Theta }(s_t,a_t).$$

In order to prevent overfitting, the algorithm performs a technique called experience replay in which many transitions are stored in a database. In each iteration, a number of transitions are sampled at random from the database in order to update the network parameters θ.

Asynchronous advantage actor-critic, or A3C [6], maintains both an estimate πˆ_θ of the policy (the actor) and an estimate Vˆ_ϕ of the value function (the critic). Given a transition (s_t, a_t, r_{t+ 1}, s_{t+ 1}), the parameter vector θ of πˆ_θ is updated using the regularized policy gradient rule

$${\nabla }_{\Theta }log{\widehat{\pi }}_{\Theta }(a_t|s_t){\widehat{A}}_{\Phi }(s_t,a_t)+\beta {\nabla }_{\Theta }H({\widehat{\pi }}_{\Theta }(•|s_t)),$$

where Aˆ_ϕ (s_t, a_t) is an estimate of the advantage function

$${\widehat{A}}_{\Phi }(s_t,a_t)=r_{t+1}+\gamma {\widehat{V}}_{\Phi }(s_{t+1})-{\widehat{V}}_{\Phi }(s_t),$$

H(πˆ_θ (• ∣ s_t)) is the entropy of the policy πˆ_θ in state s_t, and the parameter β controls the amount of regularization. The stability of the algorithm increases by using n-step returns, i.e., reward accumulated during n consecutive transitions. Moreover, the vectors θ and ϕ often share parameters, e.g., in a neural network setup all non-output layers are shared, and only the output layers differ for πˆ_θ and Vˆ_ϕ.

AlphaZero [3, 7] also maintains both a policy estimate πˆ_θ and a value estimate Vˆ_ϕ. The parameters are not updated using the policy gradient rule; rather, the algorithm performs Monte-Carlo tree search (MCTS) to estimate a target action distribution p(•) given by the empirical visitation count of each branch of the search tree (MCTS also determines which action a_t to perform next). The parameters are then updated using the loss function

$$l={(R_t-{\widehat{V}}_{\Phi }(s_t))}^2-P{(•)}^{T}log{\widehat{\pi }}_{\Theta }(•|s_t)+\beta |\left|\Theta \right|{|}^2,$$

where R_t is the observed return from state s_t, and β again controls the amount of regularization.

RL in Medicine

Many decision problems in medicine are by nature sequential. When a patient visits a doctor, the doctor has to decide which treatment to administer to the patient. Later, when the patient returns, the treatment previously administered affects their current state, and consequently the next decision regarding future treatment. This type of decision problem can be effectively modelled as an MDP and solved using RL algorithms.

In most AI systems implemented in medicine, the sequential nature of decisions is ignored, and the systems instead base their decisions exclusively on the current state of patients. RL offers an attractive alternative to such systems, taking into account not only the immediate effect of treatment, but also the long-term benefit to the patient.

In spite of the potential of RL in medicine, there are a number of obstacles that have to be overcome in order to apply RL algorithms in the hospital. RL algorithms typically learn by trial-and-error, but submitting patients to exploratory treatment strategies is of course not an option in practice. Instead, RL algorithms would have to learn from existing data collected using fixed treatment strategies. This process is called off-policy learning and will play an important role in practical RL algorithms, especially in a medical setting.

Another important issue is to establish what the reward should be, which in turn determines the behavior of the optimal policy. Defining an appropriate reward function involves weighing different factors against each other, such as the monetary cost of a given treatment versus the life expectancy of a patient. This dilemma is not exclusive to RL, however, and is already being discussed on a large scale in different countries.

There exist several examples of medical RL applications in the literature. RL has been used to develop treatment strategies for epilepsy [8] and lung cancer [9]. An approach based on deep RL was recently proposed for developing treatment strategies based on medical registry data [10]. Deep RL has also been used to learn treatment policies for sepsis [11].

In nephrology, the problem of anemia treatment in hemodialysis patients is particularly well-suited to model as a sequential decision-making problem. A common treatment for patients with chronic kidney disease are erythropoiesis-stimulating agents (ESAs), but the effects of ESAs are unpredictable, making it necessary to closely monitor the patient's condition. At regular time intervals, the medical team has to decide what action to take, and in turn, this action will affect the patient's condition in the future. Several authors have proposed using RL to control the administration of ESAs [12, 13].

Statement of Ethics

The author has no ethical conflicts to disclose.

Disclosure Statement

The author has no conflicts of interest to declare.