On the scaling behavior of water diffusion in human brain white matter

Abstract

Development of therapies for neurological disorders depends on our ability to non-invasively diagnose and monitor the progression of underlying pathologies at the cellular level. Physics and physiology limit the resolution of human MRI to be orders of magnitude coarser than cell dimensions. Here we identify and quantify the MRI signal coming from within micrometer-thin axons in human white matter tracts in vivo, by utilizing the sensitivity of diffusion MRI to Brownian motion of water molecules restricted by cell walls. We study a specific power-law scaling of the diffusion MRI signal with the diffusion weighting, predicted for water confined to narrow axons, and quantify axonal water fraction and orientation dispersion.

1. Introduction

As MRI hardware development approaches physical and physiological limits, the fundamental scientific challenge becomes to bridge the remaining two-to-three orders-of-magnitude gap between the typical mm-scale macroscopic imaging resolution, and the µm-scale tissue cellular structure, where physiological and pathological processes occur. From the basic physics standpoint, Brownian motion of spin-carrying (water) molecules provides the desired micrometer length scale for probing cellular architecture (Tanner, 1979) far below the nominal resolution. This has fueled research on diffusion MRI (dMRI) as a microstructure-sensitive in vivo imaging modality (Le Bihan, 2003; Le Bihan et al., 1986; Callaghan et al., 1988; Basser et al., 1994; Jones, 2010; Beaulieu, 2002). The sensitivity to tissue microstructure, however, is bound to be indirect, and cellular parameters can only be quantified by virtue of biophysical modeling, which links biomedical imaging with the fundamental physics paradigms (Lerch et al., 2017; Kiselev, 2017; Novikov et al., 2016; Jespersen, 2018; Novikov et al., 2018a).

The viability of model-based “super-resolution” MRI rests on validating the specific biophysical model assumptions in each tissue type. In neuronal white matter (WM), the basic assumption underpinning most biophysical models (Kroenke et al., 2004; Assaf et al., 2004; Jespersen et al., 2007; Assaf et al., 2008; Jespersen et al., 2010; Alexander et al., 2010; Fieremans et al., 2011; Sotiropoulos et al., 2012; Zhang et al., 2012; Novikov et al., 2014; Burcaw et al., 2015; Fieremans et al., 2016; Jensen et al., 2016; Novikov et al., 2018b; Reisert et al., 2017) is compartmentalization — i.e. representing the dMRI signal as a sum of independent contributions from separate pools of water, corresponding to locally anisotropic intra- and extra-axonal spaces, Fig. 1.

Figure 1: Microstructural origin of dMRI signal:

The existing conjecture (Kroenke et al., 2004; Jespersen et al., 2007, 2010; Fieremans et al., 2011; Zhang et al., 2012; Novikov et al., 2015; Jensen et al., 2016; Novikov et al., 2016; Reisert et al., 2017; Novikov et al., 2018b) presents water diffusion in WM (a, b) as restricted diffusion in an array of axons, represented by “sticks” (red) embedded in the hindered extra-axonal water (blue), whereas contribution of myelin water (yellow) is considered to be negligible due to its short T₂. (c) Schematic representation for water diffusion properties of an individual stick. Given the diffusion time t ∼ 100 ms, the associated diffusion length scale of ≃ 10 µm is at least two orders of magnitude smaller than the imaging resolution (d). Hence, the measured intra-axonal signal reflects the averaging over an ensemble of sticks, whose directions are captured by an orientational distribution function $\mathcal{P}\left(\widehat{\mathbf{n}}\right)$. (e) Qualitatively, only the directions within the range $\delta \theta \sim {\left(b{D}_a^{\parallel }\right)}^{-1/2}\ll 1$ transverse to the diffusion direction $\widehat{\mathbf{g}}$ contribute to the observed signal at large b, yielding the asymptotic signal scaling (1) solely from intra-axonal water because the extra-axonal signal decays exponentially fast with b.

The defining architectural signature of neuronal tissue from the water diffusion standpoint has been the conjecture (Kroenke et al., 2004; Jespersen et al., 2007) of infinitely narrow impermeable channels (“sticks”) representing axonal compartment (and possibly glial cell processes) inside which diffusion is locally effectively one-dimensional, with diffusivity $D_a^{\parallel }$, while the radial intra-axonal diffusivity $D_a^{\perp }$ can be considered negligible. This stick picture for axons was first introduced by Kroenke et al. (2004), in the diffusion study of N-acetyl-L-aspartate (NAA) in the rat brain. As NAA resides predominantly inside neurons, its spectroscopically-selected dMRI signal avoided the extra-neuronal contributions (Palombo et al., 2016). However, the use of NAA in the human MRI is greatly hampered due to its ~ 10,000 times smaller signal relative to water.

Since then, a plethora of microstructural WM models for water dMRI was built around the stick assumption (Jespersen et al., 2007, 2010; Fieremans et al., 2011; Sotiropoulos et al., 2012; Zhang et al., 2012; Novikov et al., 2014, 2018b; Jensen et al., 2016; Reisert et al., 2017; Novikov et al., 2016; Veraart et al., 2017), with the differences between them being largely about how the orientational dispersion of the sticks is parametrized, and how the water diffusion in the extra-axonal space is described. Alternatively, another family of WM models based on cylinders with finite diameter and non-negligible $D_a^{\perp }$, has been proposed (Assaf et al., 2004, 2008; Alexander et al., 2010), with the intent of measuring the inner axonal diameters in vivo (Assaf et al., 2013; Horowitz et al., 2015). The diameter values (Alexander et al., 2010; Innocenti et al., 2015) and the model assumptions (Burcaw et al., 2015; Fieremans et al., 2016) were recently contested.

The proven ability to map the corresponding directional diffusion coefficients inside axons and outside them in the extra-axonal space ($D_e^{\parallel }$ and $D_e^{\perp }$), Fig. 1, as well as the compartment water fractions would turn dMRI into a unique non-invasive scientific instrument. Such an instrument would potentially be able to discern between specific intra- and extra-cellular disease processes, such as demyelination (Kochunov et al., 2016; Jelescu et al., 2016), axonal loss (Kochunov et al., 2016; Jelescu et al., 2016), beading (Budde and Frank, 2010), oedema and inflammation (Unterberg et al., 2004), and provide objective quantitative metrics for disease progression.

However, the Achilles’s heel of model-based approaches has been the lack of validation of underlying model assumptions. As histology is not directly related to a diffusion measurement, it can neither quantify MRI-relevant markers of cell integrity, such as all of the estimated diffusion coefficients, and membrane permeability responsible for possible inter-compartmental exchange, nor can it prove the overarching picture of sticks (Kroenke et al., 2004; Jespersen et al., 2007) or cylinders (Assaf et al., 2004, 2008) for the effective-medium description (Novikov et al., 2016) of diffusion inside neurites, Fig. 1. Even the comparison of MRI-estimated axonal diameters with those from histology is nontrivial. Indeed, histological tissue preparation might uncontrollably change its properties (Shepherd et al., 2009), introducing uncertainties in quantitative model validation.

Here we approach the fundamental model validation challenge by focusing on the functional form of the dMRI signal. We borrow this validation paradigm from the physical sciences, where numerous fundamental phenomena have been observed in this way, completely indirectly, by studying nontrivial functional dependencies in highly tailored measurements. In particular, a power-law scaling of the dMRI signal:

$$S\left(b\right)\simeq \beta \cdot b^{-\alpha }+\gamma ,$$ (1)

with exponent α = 1/2, and a nearly zero offset γ ~ −0.01. ${S|}_{b=0}$, would establish the following key microstructural WM signatures:

(i) The b^−1/2 term (Kroenke et al., 2004; Jensen et al., 2016; McKinnon et al., 2017) originates from within one-dimensional “sticks”, with $\beta \propto {f/\left(D_a^{\parallel }\right)}^{1/2}$, where f is the T₂-weighted axonal water fraction. Observing this particular signal decay demonstrates that isolating the intra-axonal contribution to the signal and, as such, achieving compartmental specificity is feasible, Figs. 2–3.

Figure 2: Observation of power law (1) with α = 1/2:

(a,b) Asymptotically linear scaling of the isotropically averaged signal $\tilde{S}\left(b\right)$ as a function of $1/\sqrt{b}$ in all WM voxels. (c) For each subject, the average WM signal decay is shown (solid line), as well as the linear approximation for b > 7 ms/µm² (dashed). The boxed window of interest of (c) is enlarged in (d) and shown in a double logarithmic scale (e). (f, g) The maps and histograms of α and γ for a 35 years-old female volunteer are shown, with α nearly constant (blue) within WM tracts. Models (ii) and (iii) were used to estimate α and γ, respectively.

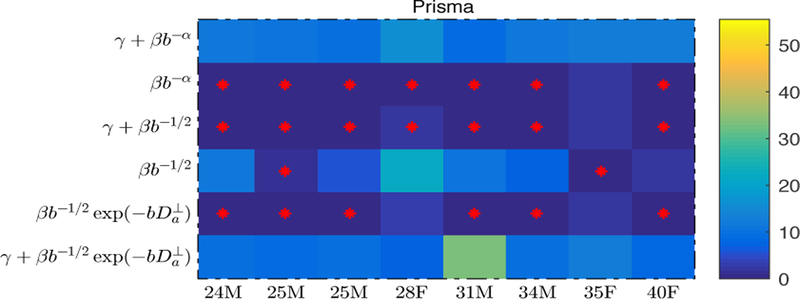
Figure 3: Model selection:

The corrected AIC values are shown for each model (rows) and each subject (columns) in the color-encoded matrix. Instead of showing the actual values, we show their difference to the subject-specific minimum ∆AICc. Red crosses indicates all models with an AICc that is not significantly (Burnham and Anderson, 2002) larger than the smallest one, i.e. ∆AICc < 2. This analysis shows that (i) models with fixed α = 1/2 should be preferred over the others; (ii) Fit quality benefits from adding a negative intercept γ to the power scaling.

(ii) The stability and persistence of α = 1/2 across WM indicates (a) diffusion MRI is practically insensitive to the inner-axonal radii on modern clinical MRI systems and (b) the existence of a notable fraction of axons for which the exchange with extra-axonal water is not relevant on the clinical dMRI time scales t ≲ 100 ms, Figs. 4–5.

Figure 4: Effects of the residual extra-axonal diffusion and finite axonal radii.

Simulations with varying $D_e^{\perp }$ demonstrate the feasibility to identify the power law exponent α = 1/2 if axons have radii according to values reported in the histology studies of Aboitiz et al. (Aboitiz et al., 1992) (solid lines) or Caminiti et al. (Caminiti et al., 2009) (dashed lines), when corrected by a shrinkage factor between η = 1 and 2 (cf. Methods). Comparison with Fig. 2 (observed curves falling within the greyed-out area) excludes strong tissue shrinkage, η ≳ 2.

Figure 5:

The distribution of $D_a^{\perp }$ estimated via the truncated power law, i.e. model (V) in Fig. 3, for all WM voxels (all scanner-specific subjects pooled). The data shows a low precision for the estimator of $D_a^{\perp }$. Despite the small yet positive mean value and the associated negative intercept in Fig. 2, a large number of WM voxels yield biophysically implausible $D_a^{\perp }$ < 0 values.

(iii) By further studying the scaling behavior as a function of b and direction relative to a WM fiber tract, we decouple f from $D_a^{\parallel }$. This demonstrates that isolating the intra-axonal contribution to the signal, and quantifying various intra-axonal parameters, is realistic on modern clinical MRI systems, Figs. 6.

Figure 6: Scaling of the directional high-b signal:

The distribution of the probability-normalized distribution of ${\tilde{S}}_b\left(\theta \right)$ as a function of ${\sin }^2\overline{\theta }$ is non-Gaussian (a) and its variance ${\sigma }_b^2$ (computed as the slope of ln $\tilde{S}$ vs ${\sin }^2\overline{\theta }$, panel (a)) decays as 1/b, panel (b). The intercept and slope of the variance as a function of 1/b returns an in vivo estimate of the intrinsic axonal orientational dispersion ${\sigma }_a^2$ and intra-axonal diffusivity $D_a^{\parallel }$, respectively, panel (c). Axonal water fraction f is estimated using $D_a^{\parallel }$ and the parameter β from equation (1).

(iv) The fraction of fully restricted, immobile water (that is not attenuated with the increasing b) is negligible in the clinically accessible regime, Fig. 7.

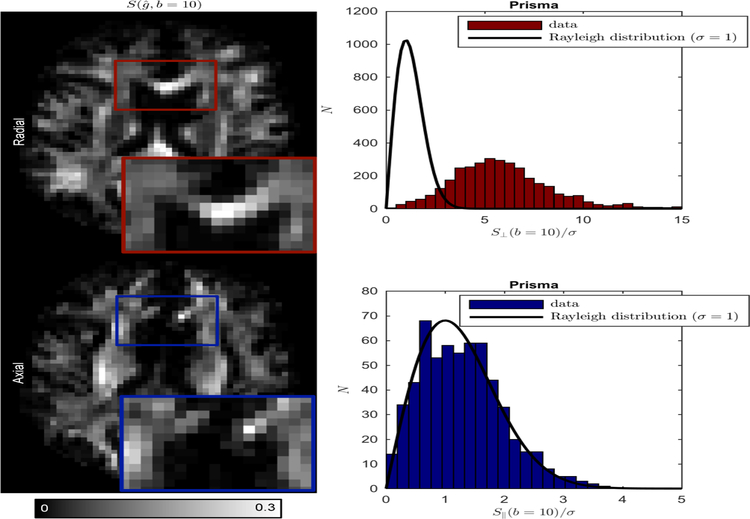
Figure 7:

Full suppression of directional signal ${\tilde{S}}_b\left(\theta \right)$ from single-fiber voxels is observed in the directions approximately parallel to the underlying axonal fibre (axial); signal statistics for θ ≤ 20◦ (blue bars) obeys the Rayleigh distribution, i.e. SNR=0 (solid line). In the radial directions, SNR ~ 3 even at b = 10 ms/µm².

2. Theory: From a “stick” to the power law scaling

The dMRI signal $S=\int \text{d}\mathbf{r}\hspace{0.17em}{e}^{-i\mathbf{q}r}{G}_{t,\mathbf{r}}$ is the Fourier transform of the ensemble average propagator G_t,r, which is the distribution of the displacement of the water molecules r, or the displacement of the center-of-mass of their trajectories for finite-pulse width (Callaghan, 1991; Mitra and Halperin, 1995). To probe the microstructure, we focus on varying q, given by the area under the gradient pulse (Callaghan, 1991), in the broadest possible range, while keeping the diffusion time t fixed. In this way, we achieve the diffusion-weighting b = q²t up to 10 ms/µm², an order of magnitude greater than typical b ~1 ms/µm² used in the clinic.

The asymptotic power law ${S|}_{b\to \infty }\sim b^{-\alpha }$ with α = 1/2 can only originate from intra-axonal water in the limit of zero stick radius (Kroenke et al., 2004; Jensen et al., 2016; McKinnon et al., 2017). Indeed, consider the dMRI signal (henceforth normalized to ${S|}_{b=0}\equiv 1$)

$$S\left(\widehat{\mathbf{g}},b\right)=f\int \text{d}\widehat{\mathbf{n}}\mathcal{P}\left(\widehat{\mathbf{n}}\right){\psi }_{\widehat{\mathbf{n}}}\left(\widehat{\mathbf{g}},b\right)\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{S}^{\text{eas}}\left(\widehat{\mathbf{g}},b\right)\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{f}_{\text{im}}$$ (2)

in the unit direction$\widehat{\mathbf{g}}$. The first term comes from the collection of narrow cylinders (or sticks) representing axons and possibly glial cell processes, with the net T₂-weighted (Veraart et al., 2017) water fraction f, and parameterized by the orientational distribution function (ODF) $\mathcal{P}\left(\widehat{\mathbf{n}}\right)$, Fig. 1. The intra-axonal response function, i.e. the signal from water inside an axon pointing in the direction $\widehat{\mathbf{n}}$,

$${\psi }_{\widehat{\mathbf{n}}}\left(\widehat{\mathbf{g}},b\right)=e^{-b{D}_a^{\perp }\left[1-{\left(\widehat{\mathbf{g}}\widehat{n}\right)}^2\right]+\mathcal{O}\left(b^2\right)}{e}^{-b{D}_a^{\parallel }{\left(\widehat{\mathbf{g}}\widehat{n}\right)}^2},$$ (3)

factorizes into a non-Gaussian restricted diffusion propagator in the direction transverse to the axon (where $O(b^2)$ symbolizes the terms of the order q⁴ and above), and a simple Gaussian diffusion propagator along the axon, under the assumption that the t → ∞ limit in this direction has been reached.

If the stick assumption is correct, such that $b{D}_a^{\perp }\ll 1$ 1 for all achievable b, and the transverse dynamics can be fully neglected, the response (3) simplifies to a Gaussian one-dimensional propagator ${\psi }_{\widehat{\mathbf{n}}}\left(\widehat{\mathbf{g}},b\right)\equiv e^{-b{D}_a^{\parallel }{\left(\widehat{\mathbf{g}}\widehat{n}\right)}^2}$. For large b, such that $b{D}_a^{\parallel }\gg 1$, this response yields a non-negligible contribution only from axons oriented within a thin “pancake” $\left|\widehat{\mathbf{n}}\cdot \widehat{\mathbf{g}}\right|\underset{˜}{<}{\left(b{D}_a^{\parallel }\right)}^{-1/2}$ nearly transverse to $\widehat{\mathbf{g}}$, Fig. 1(e), whose thickness scaling as b^−1/2 results in the first term of Eq. (1), Fig. 2.

The extra-axonal contribution $S^{\text{eas}}\left(\widehat{\mathbf{g}},b\right)\sim e^{-b{D}_e\left(\widehat{\mathbf{g}}\right)}$, coming from water diffusion in a simply-connected space characterized by a finite diffusion coefficient $D_e\left(\widehat{\mathbf{g}}\right)$ in any direction $\widehat{\mathbf{g}}$ (with $D_e\left(\widehat{\mathbf{g}}\right)\ge D_e^{\perp }$, Fig. 1), decays exponentially faster than the intra-axonal signal, by virtue of $e^{-b{D}_e^{\perp }}\ll 1$ for large b, and can be eventually neglected, as shown below.

The last term, $f_{\text{im}}\equiv {S|}_{b\to \infty }$, is the possible contribution of immobile (fully restricted) water, that does not experience diffusion attenuation. If the intra-axonal diffusion can indeed be described by diffusion inside infinitely-narrow sticks, then the power law offset $\gamma \equiv f_{\text{im}}\ge 0$ in Eq. (1) would measure the immobile water fraction.

It is essential, for the asymptotic scaling (1) to hold and to originate solely from “intra-stick” water, that the dMRI signal exactly transverse to a stick, $\widehat{\mathbf{g}}\perp \widehat{\mathbf{n}},$, is not suppressed: ${\psi }_{\widehat{\mathbf{n}}\perp \widehat{\mathbf{g}}}$ does not decay at large b, equivalent to a negligible transverse diffusion coefficient, $b{D}_a^{\perp }\ll 1$ (Fig. 1).

Here we use a diffusion time t of about 50 ms; at this time scale, the residual time-dependence of the diffusion metrics is relatively small (Fieremans et al., 2016; Lee et al., 2017). Furthermore, residual t-dependence of $D_a^{\parallel }$, leading to a finite intra-axonal kurtosis $K_a^{\parallel }\left(t\right)$, does not change the scaling behavior (1): The saddle-point estimate

$$f\hspace{0.17em}{\int }_0^1\text{d}x\hspace{0.17em}{e}^{-b{D}_a^{\parallel }{x}^2}\left[1+\frac{k}{6}{\left(b{D}_a^{\parallel }{x}^2\right)}^2\right]\simeq \beta \left[1+\frac{k}{8}\right]b^{-1/2},\hspace{1em}x=\widehat{\mathbf{g}}\widehat{n},$$

renormalizes the prefactor β, keeping the exponent α = 1/2.

Either the sensitivity of MR to a finite axonal radius, or a notable exchange rate between intra- and extra-axonal water, would alter the very particular b^−1/2 scaling (1). In particular, according to Eq. (3), a finite $D_a^{\perp }$ would result in the intra-axonal signal decay $~e^{-b{D}_a^{\perp }+\mathcal{O}\left(b^2\right)}\cdot b^{-1/2}$ (for a fixed t), i.e. a truncated power law.

Averaging the signal over diffusion directions for each b cancels the ODF shape (Jespersen et al., 2013; Kaden et al., 2016; Szczepankiewicz et al., 2015; Lasivc et al., 2014), $\tilde{S}\left(b\right)=\int \text{d}\widehat{\mathbf{n}}\mathcal{P}\left(\widehat{\mathbf{n}}\right)\hspace{0.17em}\int \text{d}\widehat{\mathbf{g}}\hspace{0.17em}f{e}^{-b{D}_a^{\parallel }{\left(\widehat{\mathbf{g}}\widehat{n}\right)}^2}\simeq \frac{\sqrt{\pi }}{2}f{\left(b{D}_a^{\parallel }\right)}^{-1/2}$, since $\int \text{d}\widehat{\mathbf{g}}{\psi }_{\widehat{\mathbf{n}}}\left(\widehat{\mathbf{g}},b\right)$ is independent of fiber direction $\widehat{\mathbf{n}}$, and the ODF is normalized to $\int \text{d}\widehat{\mathbf{n}}\mathcal{P}\left(\widehat{\mathbf{n}}\right)\equiv 1$. This yields the prefactor $\beta =\sqrt{\pi /4}\cdot f/{\left(D_a^{\parallel }\right)}^{1/2}$ in Eq. (1) for the direction-averaged signal in terms of the intra-axonal parameters f and $D_a^{\parallel }$.

3. Methods

3.1. Data

A total of eight healthy volunteers, 25 to 40 years old, underwent MR imaging after obtaining informed consent. The cohort consisted of 5 males and 3 females. The scans were performed at NYU Langone Health on a clinical Siemens Prisma 3T scanner equipped with a 80 mT/m gradient system, using a 64-channel receiver head coil. The body coil was used for transmission. An echoplanar readout diffusion-weighted sequence was used to acquire the dMRI data. Diffusion weighting was applied along 60 isotropically distributed gradient directions for each of the 21 b-values that were equidistantly distributed in the range [0, 10 ms/µm²] with a step of 0.5 ms/µm². That acquisition took two hours. Note that for 4 out of the 8 subjects, we only acquired the b = 0 and b ≥ 5 ms/µm² images (with the same step in b) to limit the total scan time to one hour. Diffusion gradient pulses had a width of δ = 35.1 ms, separation ∆ = 50.9 ms and maximal amplitude of 80 mT/m. Following imaging parameters were kept constant throughout the data acquisition sequence: TR/TE : 4000/105 ms, matrix: 80 × 80, NEX: 1, in-plane resolution: 3 × 3 mm², slice thickness: 3 mm, slices: 38, parallel imaging: GRAPPA with acceleration factor 2, reconstructed using the adaptive combine algorithm to ensure Rician data distribution, multiband acceleration with factor 2, and no partial Fourier. The average SNR for ${S|}_{b=0}$ was 30.

3.2. Data processing

MPPCA noise estimation and denoising (Veraart et al., 2016) allowed to strongly reduce the noise in the data and to estimate the noise map σ(x) by exploiting the inherent redundancy in diffusion MRI data. The positive signal bias, inherent to low-SNR magnitude MR data, was removed by using the method of moments (Koay and Basser, 2006), where the denoised signal was used as a proxy for the Rician expectation value. Denoised and Rice-floor-corrected images were subsequently corrected for Gibbs ringing (Kellner et al., 2016), geometric eddy current distortions and subject motion (Andersson and Sotiropoulos, 2016). We used tract-density imaging (Calamante et al., 2010) based on whole-brain probabilistic fiber-tracking (Tournier et al., 2012) of the b = 5 ms/µm²-shell for identifying all WM voxels. To avoid voxels affected by partial voluming with gray matter, a more conservative segmentation was obtained by omitting all voxels with a fractional anisotropy smaller than 0.6.

3.3. Noise propagation and effect of finite axonal radii

To evaluate the feasibility of detecting the α = 1/2 power law scaling, Rice-distributed synthetic data was generated for the same imaging protocol using a two-compartmental signal-generating model of orientationally dispersed WM. Without the loss of generality, we choose $\mathcal{P}\left(\widehat{\mathbf{n}}\right)$ to be the axially symmetric Watson distribution: $\mathcal{P}\left(\widehat{\mathbf{n}}\right)=M{\left(1/2,3/2,\kappa \right)}^{-1}{e}^{\kappa {\left(\widehat{\mathbf{g}}\widehat{n}\right)}^2}$, where M is a confluent hypergeometric function and κ is the concentration parameter that describes the axonal dispersion. The hindered extra-axonal signal

$$S^{\text{eas}}\left(\widehat{\mathbf{g}},b\right)=\left(1-f\right)e^{-b{D}_e^{\perp }}\int \text{d}\widehat{\mathbf{n}}\mathcal{P}\left(\widehat{\mathbf{n}}\right)e^{-b\left(D_e^{\parallel }-D_e^{\perp }\right){\left(\widehat{\mathbf{g}}\widehat{n}\right)}^2}$$ (4)

was parameterized by axial diffusivity $D_e^{\parallel }$ and transverse diffusivity $D_e^{\perp }$, relative to each axonal fiber in direction $\widehat{\mathbf{n}}$, Fig. 1. $D_e^{\parallel }$ was sampled from a normal distribution with mean±sd 2 ±0.2 µm²/ms, whereas the effect of varying $D_e^{\perp }$ was evaluated by sampling from distributions with mean values ${\overline{D}}_e^{\perp }$ = 0.25, 0.50, 0.75 µm²/ms, and standard deviation of 0.1. The intra-axonal compartment had f = 0.65 ± 0.10, $D_a^{\parallel }$ = 2 0.2 µm²/ms (cf. Fig. 6e), Watson concentration parameter κ ranging from 0.1 to 30, and finite axon radii r_i. Radial signal attenuation within the impermeable cylinders (van Gelderen et al., 1994) accounted for the axonal radii distribution by adding the signals for every r_i weighted by r², using r_i from the bins of the measured distributions (Aboitiz et al., 1992; Caminiti et al., 2009).

To account for possible tissue shrinkage in histology, we multiplied the digitized histograms (Aboitiz et al., 1992; Caminiti et al., 2009) with a uniform shrinkage factor η = {1, 1.5, 2, 2.5, 3}, implying that in vivo axons are η times thicker than in histology. We also used η = 0 to simulate the effect of zero-radius axons. Note that the shrinkage factor is histologically expected (Aboitiz et al., 1992) be at most ≈ 30% (η ≈ 1.43). No immobile water was added, f_im = 0. For each η, 1000 “voxels” were simulated by sampling the ground truth values in their respective intervals, with SNR = 30 for ${S|}_{b=0}$, to mimic our in vivo data sets. Processing of the simulated data included denoising and Rician bias correction, as described above.

3.4. Model selection:

Fit robustness with respect to the number of degrees of freedom, Fig. 3, was evaluated by considering the full, nested, and extended models to equation (1) for b ≥ 7 ms/µm². Specifically, the evaluated models were:

(i) $\gamma +\beta b^{-\alpha }$ (i.e., equation (1));

(ii) $\beta b^{-\alpha };$

(iii) $\gamma +\beta b^{-1/2};$

(iv) $\beta b^{-1/2};$

(v) $\beta e^{-b{D}_a^{\perp }}{b}^{-1/2};$ and

(vi) $\gamma +\beta e^{-b{D}_a^{\perp }}{b}^{-1/2}.$

We used a “trust region” nonlinear least squares estimator for the parameters α, β, γ, and/or $D_a^{\perp }$ with fixed starting points 0.5, 0.3, 0, and 0, respectively. We compared the relative fit quality of the generic power law (i, ii), “stick” (iii, iv), and “cylindrical” (v, vi) models to the WM- and direction-averaged signal decays by means of the corrected Akaike information criterion (AICc), which includes a penalty term for the number of parameters (Burnham and Anderson, 2002). Fully aware of how unreliable blind goodness-of-fit criteria can be for the model selection (Novikov et al., 2018a), we discuss the qualitative, systematic differences between models and data, and also consider the scaling of directional signal, as described next.

3.5. Scaling of directional intra-axonal signal

The signal S ($\widehat{\mathbf{g}}$, b) encodes rich information, that can be explored to decouple f from $D_a^{\parallel }$, to estimate the axonal orientational dispersion σ_a, and to estimate the immobile water fraction. For this analysis, we select the subset of WM voxels that are characterized by a single fiber population (SFP) (Tax et al., 2014), and focus on the signal ${\tilde{S}}_b\left(\theta \right)$ as a function of the angle θ between the gradient direction $\widehat{\mathbf{g}}$ and the principal fiber direction ${\widehat{\mathbf{n}}}_{\mathbf{0}}$ (determined as a principal diffusion tensor direction).

First, by fitting a Rician distribution to all signals that are near parallel, i.e. θ < 0, using a maximum likelihood estimator, we obtain an estimate of the fraction of fully restricted signal in the parallel direction. Such signal might arise from the immobile water fraction, that is, the so-called dot compartment (Stanisz et al., 1997; Alexander et al., 2010; Dhital et al., 2017), or from near perpendicular fiber crossings.

Second, we study the functional decay of ${\tilde{S}}_b\left(\theta \right)$ as a function of b. To increase precision, we averaged ${\tilde{S}}_b\left(\theta \right)$ over all SFP voxels, normalizing voxel-wise contributions by the spatially-dependent noise level (Veraart et al., 2016). Consequently, we here ignore the potentially spatially varying nature of f, $D_a^{\parallel }$, and σ_a and focus on the WM-averaged values.

Our method rests on the following intuition: For $b{D}_a^{\parallel }\to \infty$, the stick response function becomes infinitely sharp, such that the corresponding ${\tilde{S}}_{b\to \infty }\left(\theta \right)\propto \tilde{\mathcal{P}}\left(\overline{\theta }\right)$, where the complementary angle $\overline{\theta }=\pi /2-\theta$ Fig. 1e. Since we bin the distribution ${\tilde{S}}_b\left(\theta \right)$ only as a function of the polar angle θ to reduce the effects of noise, our average SFP ODF $\tilde{\mathcal{P}}\left(\widehat{\mathbf{n}}\right)\equiv \tilde{\mathcal{P}}\left(\overline{\theta }\right)$ will be axially symmetric.

By focusing on the small-$\overline{\theta }$, Gaussian part $\tilde{\mathcal{P}}\left(\overline{\theta }\right)\sim e^{-{\sin }^2\overline{\theta }/2{\sigma }_a^2}$ of the ODF, we can deconvolve its intrinsic variance ${\sigma }_a^2$ from a sequence of finite-b measurements. In the $b{D}_a^{\parallel }\gg 1$ limit, the signal ${\tilde{S}}_b\left(\theta \right)\sim e^{-{\sin }^2\overline{\theta }/2{\sigma }_b^2}$ approaches the Gaussian shape with the variance being a sum of intrinsic variance and the variance from the stick response function:

$${\sigma }_b^2={\sigma }_a^2+\frac{1}{2b{D}_a^{\parallel }}.$$ (5)

A proof of this relation is given in the Appendix.

4. Results

4.1. Scaling behavior of the angular-averaged signal

Figure 2(a,b) demonstrates the asymptotic behavior (1) based on diffusion measurements in all WM voxels (colored lines) with b up to 10 ms/µm². As an average of power-law contributions (over directions and voxels) with the same α yields the same power law, the asymptotic behavior (1) becomes most pronounced for the WM- and direction-averaged signals (orange and blue lines in Fig. 2a–b, respectively), and is reproducible in every subject, Fig. 2c–e.

We interpret the signal excess $\tilde{S}\left(b\right)$ over the straight line at smaller b ≲ 7 ms/µm² as corresponding to the residual extra-axonal contribution ${\tilde{S}}^{\text{eas}}\left(b\right)$, second term in Eq. (2), that gets eventually suppressed. This b value thereby gives us a useful measure of the diffusion weightings necessary to practically fully suppress the extra-axonal space contribution to the signal.

Recognizing the expected intra-axonal functional form means that beyond b ≳ 7 ms/µm², the observed signal is now assumed to originate from the inside axons only. This is akin to the spectroscopic selection of the intra-neurite signal using NAA (Kroenke et al., 2004), — albeit here, for water, we rely on the diffusion weighting instead of the proton frequency shift.

We notice from Fig. 2, however, that the stick picture is incomplete: an extrapolation to infinite b, i.e. to $1/\sqrt{b}\to 0$, yields a small but significant negative offset γ, of the order of a few per cent of the non-attenuated ${S|}_{b=0}$ signal, in all subjects. However, Fig. 3 suggests that adding $D_a^{\perp }$ to the power law form does not improve the fit quality significantly for any of the subjects.

4.2. Insensitivity to axon diameters

In Fig. 4 we argue that a slight, yet significant (significance level of 0.05) bias in the estimation in α and γ is likely due to residual exponentially decaying extra-axonal signal, i.e. a signature of strongly hindered radial extra-axonal diffusion ($D_e^{\perp }$≈ 0.5 µm²/ms) (Burcaw et al., 2015; Fieremans et al., 2016). The biases can theoretically be attributed to finite axonal radii. Indeed, the negative γ could mathematically also be explained by the exponential envelope exp($-b{D}_a^{\perp }$). However, the simulations predict that our measurements are insensitive to axonal radii if they fall within the range obtained by histology, with a correction factor η ≲ 2 (Aboitiz et al., 1992; Caminiti et al., 2009). Moreover, comparing our simulations with in vivo data (Fig. 2) excludes strong tissue shrinkage η ≳ 2

In Fig. 5, the distribution of $D_a^{\perp }$ for WM voxels and all subjects, estimated using the ODF-independent equation $\beta e^{-b{D}_a^{\perp }}{b}^{-1/2}$, is shown for all subjects. Biophysically implausible negative $D_a^{\perp }$ are observed in approximately 35% of all WM voxels. This means that the voxelwise estimation of $D_a^{\perp }$ and the associated axon radius is impractical on a state-of-the-art clinical scanner with 80 mT/m gradients due to an insufficient contrast-to-noise ratio of the signal attenuation of restricted diffusion in cylinders, cf. van Gelderen et al. (1994). This result is in agreement with theoretical considerations of Nilsson et al. (2017).

4.3. Scaling of directional intra-axonal signal

In Fig. 6b, we observe that the signal variance ${\sigma }_b^2$, cf. Eq. 5, calculated via the slope of ${\tilde{S}}_b$ with respect to ${\sin }^2\overline{\theta }$ around $\overline{\theta }=0$, indeed scales linearly with 1/b in all subjects. As our analytical calculation in Methods shows, this scaling of the variance has the same biophysical origin as the signal scaling (1)—the b-dependent width of the “pancake” stick response function, Fig. 1e—confirming our picture of asymptotic sensitivity only to the intra-axonal water within narrow impermeable sticks. It further allows us to determine both the intrinsic fiber orientational dispersion σ_a, and the intra-axonal diffusivity $D_a^{\parallel }$ separately from the axonal water fraction f. Note that σ_a and $D_a^{\parallel }$ are directly derived from fitting Eq. 5 whereas f can be extracted from $\beta \propto {f/\left(D_a^{\parallel }\right)}^{1/2}$ (Eq. 1) after the independent estimation of $D_a^{\parallel }$. This shows the added value of studying the directional signal variance, as compared to the overall signal magnitude for a given direction, or the directional average $\tilde{S}$ (Fig. 2), in which these quantities are mixed in the parameter β.

We estimate the intra-axonal diffusivity $D_a^{\parallel }$ to be in the range [1.5, 2.5] µm²/ms, whereas the T₂-weighted relative axonal water fraction f ranges between 0.6 − 0.7 amongst all subjects (Fig. 6c).

Extrapolating the observed linear function to the 1/b = 0 intercept provides an in vivo estimate of intrinsic ODF dispersion σ_a for the single fiber population. The estimated dispersion angle sin⁻¹ σ_a ≈ 17◦ in all subjects is in excellent agreement with previous 2D and 3D histological studies yielding dispersion ≈ 18◦ (Schilling et al., 2018; Ronen et al., 2014; Leergaard et al., 2010).

4.4. Immobile water

We show that strong directional dependence of the unprocessed magnitude signal $S(\widehat{\mathbf{g}},b)$ provides evidence for the lack of an isotropically restricted component, i.e. f_im can be neglected in Eq. (2), Fig. 7. Although we observe a remarkably high signal-to-noise ratio SNR ≈ 3 even for a strong diffusion weighting b = 10 ms/µm² in the radial direction (θ ≈ 90◦, $\widehat{\mathbf{g}}\perp {\widehat{\mathbf{n}}}_0$), the signal ${\tilde{S}}_b\left(\theta \right)$ in the axial direction, binned within the cone θ ≤ 20◦ (when $\widehat{\mathbf{g}}$ is almost parallel to the principal fiber direction), is fully suppressed, as it reaches the Rician noise floor $\tilde{S}/\sigma =\sqrt{\pi }/2$ for the magnitude MR images. Notably, the statistical properties of the axial signal are characterized by the Rayleigh distribution (Rician distribution with zero signal), the black lines in Fig. 7 drawn without any adjustable parameters, corroborating the accuracy of our noise estimation method (Veraart et al., 2016) and our conclusion about the unobservable f_im. Fitting the Rician distribution with parameters f_im and σ to the axial signals sets an upper bound of 0.2% for f_im, an order-of-magnitude improvement over the recently found bound of about 2% (Dhital et al., 2017), and shows that the estimated σ differs from that estimated using our MP-PCA method (Veraart et al., 2016) by ~ 1%. Note that unlike all other experiments, we here used the unprocessed magnitude data in order to preserve that noise statistics.

5. Discussion

This work interprets the in vivo human diffusion-weighted MRI signal decay at high b-values in terms of of a scale-invariant functional form S ~ b^−1/2. Experimental detection of specific functional forms – a validation paradigm borrowed from the physical sciences (Novikov et al., 2018a) – is instrumental for selecting the family of plausible microstructural models, and for non-invasively validating their assumptions.

The observation of the power-law scaling of the diffusion MR signal with exponent 1/2 at strong diffusion-weighted regimes for clinical scanners would provide indirect validation of the stick model, which is commonly adopted in the community as a building block for biophysical models of diffusion in the white matter.

The b^−1/2-scaling has previously been suggested by McKin-non et al. (2017). However, in comparison with their work, our data is unusually rich due to the dense sampling of b-shells, up to 21, with a maximal b-value of 10ms/µm², enabling a more precise assessment of the signal scaling, especially because of a better suppression of the extra-axonal signal contributions. Furthermore, we exploit the directional information contained in the scaling (5) from the collection of SFP voxels, which provides an independent way to corroborate the “stick” assumption.

In this work, the b^−1/2-scaling has only been identified asymptotically, in a relatively narrow b-range, i.e. b = 7 to 10 ms/µm². Indeed, at lower b-values, the extra-axonal space still contributes significantly to the signal, while clinical hardware puts an upper bound on the maximally achievable b-value. In future work, we will further validate the power-law scaling in wider b-ranges (cf. Stumpf and Porter (2012)) by exploiting the strong gradient systems of the Siemens Connectom 3T scanner (G_max = 300 mT/m) and Bruker Aeon Ascend 16.4T (G_max = 3000 mT/m) to widen the b-range with a factor of 2.5 in humans and an order of magnitude in fixed brain tissue, respectively.

Another limitation of our study is the lack of a localized estimation of microstructural parameters f, $D_a^{\parallel }$, and ${\sigma }_a^2$ Although our method enables the decoupling of β – a necessity to break the degeneracy of two-compartmental models – in SFP voxels, it relies on a densely sampled signal ODF. We could only construct the ODF by concatenating the data from all SFP voxels. Although we hereby lose potential spatially varying trends of those parameters, we can generate average reference values that might provide insight in the recently debated branch selection problem if one can improve the precision of the experiment (Jelescu et al., 2016; Novikov et al., 2018b; Kunz et al., 2018).

Our results also contribute to the on-going debate (Horowitz et al., 2015; Innocenti et al., 2015; Burcaw et al., 2015) about the feasibility of in vivo axonal diameter mapping in the human brain on a clinical scanner. Histological studies extensively reported axonal diameters to be in the range 0.5 − 2 µm for human WM (Aboitiz et al., 1992; Caminiti et al., 2009), with only 1% of all axons having a diameter larger than 3 µm (Caminiti et al., 2009), while MRI-derived axonal diameters fall outside that range (Alexander et al., 2010; Horowitz et al., 2015; Huang et al., 2015). On the MRI side, the bias has been attributed to the volume-weighted contributions amplifying the tail of the distribution (Alexander et al., 2010; Burcaw et al., 2015), to the wide diffusion pulses reducing the effect of signal attenuation (van Gelderen et al., 1994; Burcaw et al., 2015), and to the effect of residual time-dependence of extra-axonal diffusion $D_e^{\perp }\left(t\right)$ overshadowing the relatively small $D_a^{\perp }\simeq r^2/4t$ (Burcaw et al., 2015; Fieremans et al., 2016; Lee et al., 2017). On the other hand, shrinkage during tissue fixation has been suggested as a potential shortcoming of histology (Horowitz et al., 2015), implying that in vivo axons are thicker than their histologically reported values. In simulations, we showed that the effect of strong tissue shrinkage by a factor η ≳ 2, for which the large MRI-derived axonal radii (Alexander et al., 2010; Horowitz et al., 2015) could make sense, leads to a qualitatively different form of S (b) with α notably exceeding 1/2, and unphysical γ < 0, both incompatible with our measurement.

The presence of isotropic immobile water has been conjectured (Stanisz et al., 1997) for ex vivo tissue, as water possibly trapped inside the bodies of glial cells such as the oligodendrocytes, and other small compartments (e.g. vesicles). However, in this study, we conclude that fraction of fully restricted, immobile water (that is not attenuated with the increasing b) is negligible in the living human white matter. For that, we demonstrated that the signal statistics along fibers at high b coincides with a Rayleigh distribution, i.e. Rician distribution for zero signal. This conclusion is in agreement with a recent dedicated experiments by (Dhital et al., 2017; Najac et al., 2014, 2016) using planar tensor encoding and diffusion-weighted spectroscopy, respectively. A translation of the results to ex vivo samples requires additional study. We hypothesize here that either the volume fraction of restricted compartments is too small, or their T₂ relaxation time is too short, or the water exchange rate is too fast on the scale of our diffusion time t ≈ 50 ms for treating them as coming from separate compartment.

The remarkably slow decay of the signal, $\sim 1/\sqrt{b}$, originating solely from within narrow neurites (predominantly axons) provides an exciting avenue for targeting intra-neurite water on modern clinical systems. The specificity to neurites, and the absence of the more isotropic extra-axonal signal, may potentially improve the recently contested performance (Maier-Hein et al., 2017) of fiber tractography, used in mapping brain anatomical connectivity and in presurgical planning, as well as increase precision in estimating biophysical parameters of microstructural tissue integrity, thereby fostering the translation of advanced diffusion MRI methods into clinical practice.

6. Conclusion

By exploring diffusion averaged signals up to 10 ms/µm², we here conclude that for the healthy white matter: (i) MRI is specific to intra-axonal signal if strong diffusion-weighting is applied. The intra-axonal signal does not decay exponentially as a function of b. Instead, it shows a very slow non-analytic decay, accessible on modern clinical scanners, retaining a notable part of the signal even at very large diffusion weightings. (ii) An apparent power law scaling of the signal with exponent α = 1/2 suggests that axons can be modeled as an array of zero-radius sticks, precluding axon diameter mapping on a clinical MR scanner. (iii) The specificity to the intra-axonal signal enables the estimation of reproducible markers of axonal structure and integrity, i.e. intra-axonal fraction, diffusivity, and dispersion. (iv) The fraction of fully restricted, immobile water is negligible in the living human white matter.

7. Appendix: Stick response deconvolution

The directional scaling of the first term of 2 can be used to quantify the parameters f, $D_a^{\parallel }$ and axonal orientational dispersion within major fiber tracts.

Assuming fiber tract orientation ${\widehat{\mathbf{n}}}_0\parallel \widehat{\mathbf{z}}$ and a sufficiently narrow axially-symmetric ODF $\mathcal{P}\left(\widehat{\mathbf{n}}\right)$, we can approximate the ODF by the Gaussian (Watson) shape in the vicinity of zˆ. In this limit, the intra-axonal contribution to the signal

$$\begin{gathered} S\left(\widehat{\mathbf{g}},b\right)=f{c}_k\int \text{d}\widehat{\mathbf{n}}\hspace{0.17em}{e}^{-\kappa \left(n_x^2+n_y^2\right)-b{D}_a^{\parallel }{\left(\widehat{\mathbf{g}}\widehat{n}\right)}^2} \\ \hspace{1em}\hspace{1em}\hspace{1em}=2f{c}_{\kappa }{\int }_{-\infty }^{\infty }\frac{\text{d}\lambda }{2\pi }{e}^{i\lambda }\int \frac{{\text{d}}^3\mathbf{n}}{4\pi }{e}^{-\mathbf{n}\mathcal{A}\mathbf{n}} \\ \hspace{1em}\hspace{1em}\hspace{1em}=\frac{f{c}_{\kappa }}{2\pi }{\int }_{-\infty }^{\infty }\frac{\text{d}\lambda }{2\pi }\frac{{\pi }^{3/2}{e}^{i\lambda }}{{\det }^{1/2}\mathcal{A}\left(\lambda \right)} \end{gathered}$$

where the ODF normalization c ≃ 2κ follows from $c_{\kappa }^{-1}={\int }_0^{\pi /2}\sin \theta \text{d}\theta \hspace{0.17em}{e}^{-\kappa {\sin }^2\theta }\simeq {\int }_0^{\infty }\theta \text{d}\theta \hspace{0.17em}{e}^{-\kappa {\theta }^2}=\frac{1}{2\kappa }$ in the narrow-ODF limit κ ≫ 1, and in the second equality we introduced the integration over the 3d space of n using the constraint $\delta \left(\left|\mathbf{n}\right|-1\right)=2\delta \left({\mathbf{n}}^2-1\right)\equiv 2\hspace{0.17em}\int \frac{\text{d}\lambda }{2\pi }{e}^{i\lambda \left(1-{\mathbf{n}}^2\right)}$, such that the symmetric matrix $\mathcal{A}=i\lambda +b{D}_a^{\parallel }\hspace{0.17em}\widehat{\mathbf{g}}\hspace{0.17em}\otimes \hspace{0.17em}\widehat{\mathbf{g}}+\kappa \left(1-\widehat{\mathbf{z}}\hspace{0.17em}\otimes \hspace{0.17em}\widehat{\mathbf{z}}\right)$. The 3d Gaussian integration is performed exactly by means of a unit-Jacobian orthogonal transformation $\mathbf{n}\to R\mathbf{n}$ diagonalizing $\mathcal{A}$, yielding the last equality. Using

$$\begin{gathered} \det \mathcal{A}=\left(i\lambda +\kappa \right)\left[{\left(i\lambda \right)}^2+\left(b{D}_a^{\parallel }+\kappa \right)\cdot i\lambda +\kappa b{D}_a^{\parallel }{g}_z^2\right] \\ \hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\equiv \left(i\lambda +\kappa \right)\left(i\lambda +x\_\right)\left(i\lambda +x_{+}\right) \end{gathered}$$

where $2x_{\pm }=b{D}_a^{\parallel }+\kappa +\sqrt{{\left(b{D}_a^{\parallel }+\kappa \right)}^2-4\kappa b{D}_a^{\parallel }{g}_z^2}$, and deforming the integration contour from the real axis into the upper half-plane of the complex variable λ according to the Jordan’s lemma, the resulting integration encircles the two branch cuts: between $ix\_\simeq i\kappa b{D}_a^{\parallel }{g}_z^2/\left(\kappa +b{D}_a^{\parallel }\right)$, and iκ, and between $i{x}_{+}\simeq i\left(b{D}_a^{\parallel }+\kappa -x\_\right)$ and i∞, along the positive imaginary axis. Parametrizing λ = iy, we obtain

$$\begin{gathered} S\left(\widehat{\mathbf{g}},b\right)=\frac{f{c}_{\kappa }}{2\sqrt{\pi }}[{\int }_{x\_}^{\kappa }\frac{\text{d}y\hspace{0.17em}{e}^{-y}}{\sqrt{\left(\kappa -y\right)\left(y-x\_\right)\left(x_{+}-y\right)}} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\int }_{x_{+}}^{\infty }\frac{\text{d}y\hspace{0.17em}{e}^{-y}}{\sqrt{\left(y-\kappa \right)\left(y-x\_\right)\left(y-x_{+}\right)}}]. \end{gathered}$$

Our goal is to find the dependence of the signal on $g_z=\cos \theta \equiv \sin \overline{\theta }$ (Fig. 1) in the limit $b{D}_a^{\parallel }\underset{˜}{>}\kappa \gg 1$, i.e. when our stick response function is sharper than the ODF, and the ODF is sufficiently sharp to justify using the Gaussian (Watson) shape around its apex. In this limit, the second term is exponentially suppressed as $\sim e^{-b{D}_a^{\parallel }}$ and can be neglected in comparison with the first term. The first term is dominated by the region around its lower bound $x\_\simeq \kappa g_z^2$ extending up to y ≲ 1 due to the exponentially decaying weight e^−y. Extending the upper bound from y = κ to y = ∞ would result in an exponentially negligible error; this in turn makes the resulting integral exactly solvable after neglecting the y-dependence under the square root, except around y = x₋:

$$\begin{gathered} S\left(\widehat{\mathbf{g}},b\right)\simeq \frac{f{c}_{\kappa }}{2\sqrt{\pi \kappa \left(x_{+}-x\_\right)}}{\int }_{x\_}^{\infty }\frac{\text{d}y\hspace{0.17em}{e}^{-y}}{\sqrt{y-x\_}} \\ \hspace{1em}\hspace{1em}\hspace{1em}=\frac{c_{\kappa }}{2\sqrt{\kappa }}\frac{e^{-x\_}}{\sqrt{x_{+}-x\_}}. \end{gathered}$$

As a result, we obtain the asymptotically Gaussian shape of the direction-dependent signal

$$S\left(\widehat{\mathbf{g}},b\right)=S_b\left(\overline{\theta }\right)\simeq \frac{f}{\sqrt{1+b{D}_a^{\parallel }/\kappa }}{e}^{-{\sin }^2\overline{\theta }/2{\sigma }_b^2}$$ (6)

with ${\sigma }_b^2=\frac{1}{2\kappa }+\frac{1}{2b{D}_a^{\parallel }}$, where the intrinsic ODF variance ${\sigma }_a^2=\frac{1}{2\kappa }$ is increased by that from the stick response function width, scaling as $\frac{1}{2b{D}_a^{\parallel }}\sim \frac{1}{b}$.