A G Protein-Based Model of Adaptation in Dictyostelium discoideum

Abstract

A new model is proposed based on signal transduction via G proteins for adaptation of the signal relay process in the cellular slime mold Dictyostelium discoideum. The kinetic constants involved in the model are estimated from Dictyostelium discoideum and other systems. A qualitative analysis of the model shows how adaptation arises, and numerical computations show that the model agrees with observations in both perfusion and suspension experiments. Several experiments that can serve to test the model are suggested.

1. INTRODUCTION

The cellular slime mold Dictyostelium discoideum (Dd hereafter) is a widely used system for the study of many developmental processes, including extracellular communication, signal transduction, chemotaxis, pattern formation, and differentiation [8]. In the presence of an adequate food supply the amoebas exist as free-ranging individuals, but when the food supply is exhausted an elaborate developmental program is initiated. After a period of starvation, cells attain relay competence, by which it is meant that they can detect an external cAMP pulse and respond to it by synthesizing and releasing cAMP. Experiments show that the response to cAMP has two separate components. One component is signal relay, which includes the adaptation of internal cAMP secretion to prolonged external cAMP stimuli. The other component includes cGMP synthesis and the effect of this on chemotaxis. Our objective here is to develop a new model for the cyclic AMP pathway and to explain how adaptation of the signal relay process occurs in this pathway. The cGMP pathway, which is linked to chemotaxis, is similar to the PI cycle found in mammalian cells [4, 15–17, 22]. Calcium is involved as a messenger in this pathway, and there appears to be some crosstalk between the chemotaxis-activating pathway and the signal relay pathway [41], but it is as yet not well enough defined to warrant detailed modeling.

There is a substantial body of experimental information on the input-output behavior of Dd under a variety of stimulus protocols [9–13], including short and prolonged stimuli and sequential stimuli. One important fact observed in these experiments is that the relay response adapts to constant stimuli over a range of four orders of magnitude in the stimulus amplitude. There are two components to relay adaptation: a rapid component that probably involves receptor modification and occurs on a time scale of minutes, and a slower component that involves down-regulation of receptors. Recent work on models of adaptation in signal relay are reported in [32]–[37], where an attempt was made to incorporate as many of the biochemical steps as possible. The two main biochemical pathways involved in the models are activation of adenylate cyclase via a simplified transduction scheme in which the enzyme and receptor are precoupled, and an inhibitory pathway in which calcium regulates the activity of the enzyme. The biochemical evidence for such control and the results of numerical computations that show that the input–output behavior of the cells is accurately described by this model are given in these papers. We will refer to this model as the Monk-Othmer model. The model developed here is similar in spirit but quite different in detail. Recent experimental evidence discussed later demonstrates the involvement of G proteins in the signal transduction pathway and shows that calcium is involved in the PI cycle pathway. This opens the way for a more detailed analysis of the signal transduction process and, in particular, raises the possibility that the rapid component of relay adaptation arises in the transduction pathway without any direct involvement of calcium. In the present model the inhibition arises from a parallel inhibitory channel that provides a type of feedforward control, whereas in the Monk-Othmer model the primary control is via direct feedback.

Signal transduction via G proteins has been studied in a number of systems, including Dd, but is best characterized in mammalian systems. Dd-specific results are given in Section 2, and suffice it here to say that it is reasonable to assume that there are G_s, and G_i proteins present in the membrane. In other systems it is known that they couple the effects of stimulus and inhibitor. We base the model for the adenylate cyclase–activating pathway on what is known for mammalian cells, but, of course, in Dd the stimulus signal and inhibitory signal coincide. Since the single external cAMP has the dual effect of stimulation and inhibition, it is necessary, in order to get adaptation, to have two different receptors for external cAMP, and we call these R_s, and R_i. A novel feature of our model is that the inhibitory effect of G_i is at the receptor level. The activated G_i binds with the cAMP–R_s, complex and terminates its capacity for activating G_s. The detailed rationale behind the model is given in Section 2. In Section 3 we derive the equations that describe the model. Conservation conditions and singular perturbation techniques are used to reduce the numbers of differential equations involved. Some qualitative analysis of the model is done in Section 4 in order to develop an intuitive understanding of how this model functions.

Numerical results are presented in Section 5. The results show good agreement with experimental data from perfusion experiments. As was found in previous papers [32–37], this implies that the model should also reproduce the results for suspension experiments and for wave propagation in aggregation fields. The former is verified in Section 6, and results on the latter will be reported elsewhere. The results suggest that the fast component of adaptation can arise entirely within the adenylate cyclase–activating pathway; no coupling to other components such as the calcium or PI cycles is needed. This does not rule out the possibility that the PI cycle is involved in the adaptation process in Dd, and there is evidence for crosstalk between the cAMP pathway and the PI cycle pathway in Dd [23, 41]. Of course, theoretical analysis can never prove a model, and some experiments to test it are proposed in Section 7. The predicted outcomes of the proposed experiments are obtained via computer simulations. In the Appendix we give estimates for the parameters involved in the system. Some of the data needed are available from experiments on Dd, and some are estimated from other systems.

2. THE SIGNAL PATHWAYS FROM STIMULUS TO cAMP GENERATION

2.1. HORMONAL CONTROL OF ADENYLATE CYCLASE ACTIVITY IN MAMMALIAN CELLS

Recent research on the role of G proteins in the activation of adenylate cyclase has established some of the main steps in transmembrane signal transduction in numerous systems [21, 26, 30, 43–45]. In this section we give a brief review of the results known for the mammalian cAMP pathway in order to establish a basis for the mathematical model developed later.

While there are different membrane-bound receptors for different stimuli in this pathway, they fall into two classes that are generally denoted R_s and R_i. R_s is the receptor for agonist signals H_s, such as epinephrine, glucagon, and the β-adrenergic agonists. Antagonist signals H_i are transduced through the R_i receptor, examples of which include the α₂-adrenoceptor and the muscarinic M₂ receptor. R_i receptors may also respond to stimulus hormones [3, 14,47], which is the case in Dd. The R_s receptors are coupled to a single pool of a G protein denoted G_s, which is a heterotrimeric protein comprising an α_s subunit, a β subunit, and a γ subunit.

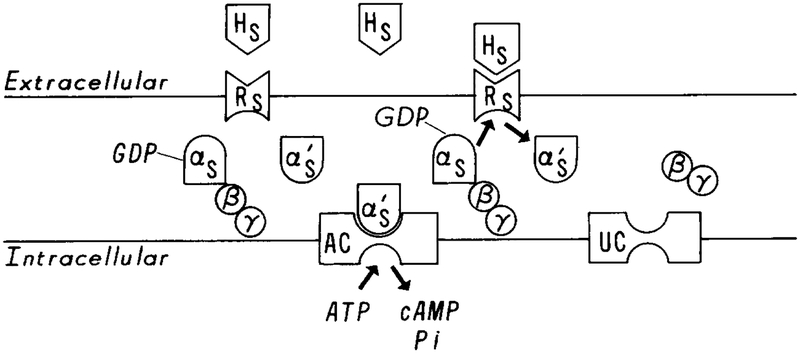
A typical scheme for signal transduction is shown in Figure 1. Upon binding of agonist to a receptor, the agonist–receptor complex H_sR_s catalyzes the conversion of G_s from the inactive GDP-binding state, to the active GTP-binding state, with the release of GDP and the βγ subunits. Binding of the active G_s protein, which we denote by ${\text{G}}_{\text{s}}^{\prime }$ or α_sGTP, with the unactivated adenylate cyclase, which we denote UC, converts the latter into the activated cyclase AC. α_sGTP is deactivated by the intrinsic GTPase activity of α_s. Modulo the basal rate for the unactivated cyclase, the rate at which cAMP is produced is proportional to the amount of agonist present, and a constant level of stimulus can sustain a constant level of cAMP production in the absence of adaptation.

FIG. 1.

A schematic diagram of the activation of adenylate cyclase via G_s proteins. H_s denotes the stimulus signal, R_s the stimulus receptor, α_sGDPβγ unactivated G_s protein, and UC unactivated adenylate cyclase. It is believed that upon binding of H_s with R_s, G_s is activated by the H_sR_s complex. This involves the release of the βγ subunits and the addition of GTP to the α_s chain. α_sGTP, which is denoted by ${\alpha }_s^{\prime }$ in this figure, then activates adenylate cyclase, which catalyzes the conversion of ATP to cAMP.

The reactions in the inhibitory pathway are not as well established. It is known that a specific protein G_i, which is the transducer of inhibitory signals, exists in the membrane. The mechanism for activating G_i is the same as that for activating G_s: H_iR_i catalyzes the exchange of GTP for GDP on G_i, which decomposes into βγ and α_iGTP. ${\text{G}}_{\text{i}}^{\prime }$ (or α_iGTP), the active state of G_i, then turns off activation of adenylate cyclase by a mechanism that is not yet completely understood. G_i also has a three- subunit structure comprising α_i, β, and γ subunits. The β and γ subunits are identical to the β and γ subunits of G_s, but α_i is different from from α_s.

Many of the details of the transducing process are not known, even in the best-characterized systems. Some of these are discussed briefly in order to explain how we arrived at the model.

• Is G_s precoupled with adenylate cyclase? The issue here is whether H_sR_s interacts with the G_sUC complex, or whether H_sR_s interacts with G_s first, releasing ${\text{G}}_{\text{s}}^{\prime }$, after which ${\text{G}}_{\text{s}}^{\prime }$ reacts with UC. Levitzki [27] argues that G_s is always coupled to adenylate cyclase in vivo. This argument is based on the work of Arad et al. [2] and on kinetic analysis, which indicates that the interaction between G_s and adenylate cyclase is not rate-limiting [27, 46]. Gilman [21] believes that this conclusion is not correct, based on the behavior in the presence of detergent and the excess of the amount of G_s over adenylate cyclase observed in vivo (cf. also [1] concerning the amounts of G_s and cyclase). Even though the experiments show that the rate is first-order in the hormone–receptor complex, one cannot conclude that G_s and UC are always bound; it may simply be that the rate of binding of ${\text{G}}_{\text{s}}^{\prime }$ to UC is large relative to other rates in the pathway, and this is what is assumed later in the model.

• Does ${\text{G}}_{\text{i}}^{\prime }$ interact directly with UC? In view of the fact that G_i and G_s have very similar structures, it is conceivable that ${\text{G}}_{\text{i}}^{\prime }$ interacts directly with adenylate cyclase, just as ${\text{G}}_{\text{s}}^{\prime }$ interacts with UC. If the inhibitory effect of ${\text{G}}_{\text{i}}^{\prime }$ is only competitive, then either there must be a large amount of ${\text{G}}_{\text{i}}^{\prime }$ present, or the binding of ${\text{G}}_{\text{i}}^{\prime }$ to UC must be very tight in order to turn off the signal. However, all attempts to identify a ${\text{G}}_{\text{i}}^{\prime }\text{AC}$ complex have failed [29]. Thus it is widely accepted that ${\text{G}}_{\text{i}}^{\prime }$ does not interact with UC directly to express the inhibitory effect.

• Does the subunit exchange hypothesis explain inhibition? Gilman proposed the “subunit exchange hypothesis” based on the observations that G_i is usually present at a higher concentration than G_s in vivo and that the subunits of β and γ in G_i and G_s are identical. He argued that the βγ subunits released by ${\text{G}}_{\text{i}}^{\prime }$ will have a much higher concentration than ${\text{G}}_{\text{s}}^{\prime }$ and can reduce the amount of free ${\text{G}}_{\text{s}}^{\prime }$ by displacing the reaction equilibrium toward the inactive G_s form [7, 19, 44].

There are several difficulties with this hypothesis, as was noted by Levitzki [29]. First, he argues that his recent work suggests that the βγ subunit plays no regulatory role. Second, if Gilman’s mechanism were operative, then the activation of any G protein with the same βγ subunit would result in the inhibition of adenylate cyclase, even if it is not in the pathway in question. In the analysis given in the following section it will be seen that even though βγ subunits may account for some inhibitory effect, it would not be enough to account for full adaptation in Dd.

• Does G_i or ${\text{G}}_{\text{i}}^{\prime }$ interact with H_sR_s? In [27] it is found that the β-adrenoceptor catalyzes the binding of GTPγS to G_i with an efficiency that is 30% of that for the activation of G_s. Levitzki remarks that “these interesting observations point to the possibility that G_i may mediate inhibition of adenylate cyclase not only directly on the catalytic subunit or via the βγ subunits released from G_i and scavenging α_s, but also exerting its inhibitory effect on stimulatory receptors.” Thus, G_i does not have to carry out its inhibitory effect through the interaction with adenylate cyclase or G_s, but can do so through H_sR_s [28], which means that the effects of G_s and G_i are not symmetric. Levitzki suggests that in the absence of hormone, R_s, is bound with G_i, and that binding of hormone frees that receptor to catalyze the activation of G_s. However, in Dd the agonist and antagonist are identical, and it is difficult to see how the signal would be turned off. Later in this section we describe a scheme for Dd in which ${\text{G}}_{\text{i}}^{\prime }$ interacts directly with H_sR_s.

2.2. THE EVIDENCE FOR G PROTEIN-BASED TRANSDUCTION IN Dd

Several classes of cAMP receptors have been identified in Dd, and the dissociation constants for these receptors have been measured [49, 50]. Recently, significant progress has been made in understanding the signal pathway leading to the activation of adenylate cyclase. Gilman [21] set forth criteria for determining whether G proteins are involved in signal transduction, and van Haastert and coworkers [5, 40, 50] have concluded that the adenylate cyclase activation pathway in Dd meets several of these criteria. A G_α protein (G_α2) that may be involved in signal transduction has been identified, and since it does not have a site for ADP ribosylation catalyzed by pertussis toxin [18], it may be involved in the stimulatory channel.

In other systems pertussis toxin catalyzes the ADP ribosylation of α_iGDP, which blocks its inhibitory effect. If there is a G_i protein that modulates inhibition in Dd, then one expects that adaptation would be abolished when pertussis toxin is applied, and this is precisely what is observed experimentally [39–41]. In the experiment the initial increase of cAMP was identical in control and pertussis toxin–treated cells, which suggests that activation of adenylate cyclase is not affected, but cAMP synthesis continued in toxin-treated cells, due to a strongly diminished desensitization. This suggests that pertussis toxin plays the same role in Dd as it does in mammalian cells. G_s is not affected by pertussis toxin; hence the stimulatory pathway is not affected.

It is also known that cAMP induces phosphorylation of the cAMP receptors in Dd [24, 25] and that this occurs on the same time scale as adaptation. Thus phosphorylation may be involved in adaptation, perhaps by interfering with the activation of a G_s protein. However, phosphorylation is not sufficient for adaptation, since pertussis toxin treatment blocks adaptation but does not interfere with receptor modification [40, 50]. This suggests that activation of a G_i protein is necessary for adaptation [42]. In our model we propose one scheme by which this might occur and show that it can produce the observed adaptation. To simplify the scheme we do not include a role for phosphorylation, but in the conclusion section we indicate how this can be incorporated and what effects this would have on the dynamics. This leaves us with three possible patterns of interactions for adaptation: (i) ${\text{G}}_{\text{i}}^{\prime }$ can interact with adenylate cyclase directly; (ii) ${\text{G}}_{\text{i}}^{\prime }$ may possibly turn off the signal by buffering ${\text{G}}_{\text{s}}^{\prime }$ via the βγ subunits; and (iii) ${\text{G}}_{\text{i}}^{\prime }$ can interact with cAMP–R_s directly.

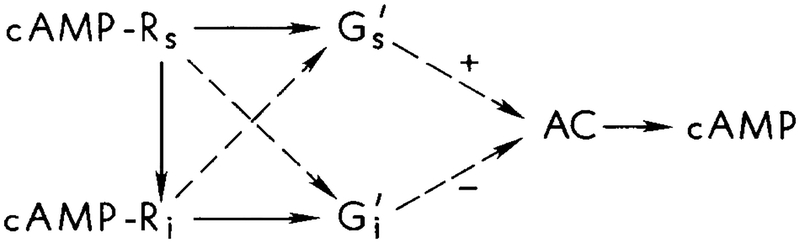
(i) If the G protein network is as in other systems, then it is unlikely that ${\text{G}}_{\text{i}}^{\prime }$ interacts with adenylate cyclase directly, and the scheme shown in Figure 2, which was suggested in [39]–[41], is questionable. However, such a scheme is not unworkable, for if we suppose that ${\text{G}}_{\text{i}}^{\prime }$ interacts with ${\text{G}}_{\text{s}}^{\prime }\text{AC}$ to turn off the enzyme, then numerical simulations indicate that the experimental results can be reproduced. This point will be elaborated in the conclusion section.

FIG. 2.

The scheme of interactions for the regulation of AC proposed by van Haastert and coworkers [39–41].

(ii) The ratio of G_s to G_i is very important here. If the concentration of G_i is much greater than that of G_s, then it is possible that the βγ subunits released from G_i can buffer ${\text{G}}_{\text{s}}^{\prime }$, and complete adaptation can result. However, if the concentration of G_s is greater than about 10% of G_i, there will be a significant amount of free ${\text{G}}_{\text{s}}^{\prime }$ and thus a significant steady-state rate of cAMP production, which is at variance with observations for Dd. Moreover, the concentrations of G_s and G_i proteins are approximately the same in Dd under the assumption that they are proportional to the concentrations of the corresponding receptors [49].

(iii) A model based on the interaction of ${\text{G}}_{\text{i}}^{\prime }$ with cAMP–R_s can explain the adaptation process and other experimental results. As we remarked earlier, it is difficult to obtain adaptation if G_i interacts directly with cAMP–R_s. Thus we propose the following scheme.

$$\begin{gathered} {\text{G}}_{\text{i}}^{\prime }+{\text{H}}_{\text{s}}{\text{R}}_{\text{s}}\to {\text{H}}_{\text{s}}{\text{R}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime } \\ {\text{H}}_{\text{s}}{\text{R}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }\to {\text{H}}_{\text{s}}+{\text{R}}_{\text{s}}+{\text{G}}_{\text{i}}^{\prime } \\ {\text{H}}_{\text{s}}{\text{R}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }\to {\text{H}}_{\text{s}}{\text{R}}_{\text{s}}+{\alpha }_{\text{i}}\text{GDP} \end{gathered}$$ (1)

This mechanism is supported by several facts.

• It is found in other systems that an increase in the GTP concentration causes a decrease in the concentration of the H_sR_s complex but has little effect on the H_iR_i complex [27, 31]. In our mechanism the decrease in [H_sR_s] due to the increase in [GTP] is mediated through the increase in $\left[{\text{G}}_{\text{i}}^{\prime }\right]$. The formation of ${\text{H}}_{\text{s}}{\text{R}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$ and its rapid decomposition leads to a decrease in the concentration of the H_sR_s complex.

• The affinity of R_s for H_s is decreased in the presence of ${\text{G}}_{\text{i}}^{\prime }$ [31, 49]. In the proposed scheme this results from the rapid decomposition of the ${\text{H}}_{\text{s}}{\text{R}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$ complex.

The detailed mechanism for relay adaptation, of which the above is one component, is described in the next section.

3. THE MATHEMATICAL MODEL

The reactions in the mechanism are as follows. Here and hereafter we use H to represent the extracellular cAMP stimulus.

(i) The Stimulus Pathway

$$\text{H}+{\text{R}}_{\text{s}}\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}{\text{HR}}_{\text{s}}$$ (2a)

$${\text{HR}}_{\text{s}}+{\text{G}}_{\text{s}}\underset{k_{-2}}{\overset{k_2}{\rightleftharpoons }}{\text{HR}}_{\text{s}}{\text{G}}_{\text{s}}$$ (2b)

$${\text{HR}}_{\text{s}}{\text{G}}_{\text{s}}+\text{GTP}\stackrel{{\widehat{k}}_3}{\to }{\text{HR}}_{\text{s}}+{\text{G}}_{\text{s}}^{\prime }+\text{GDP}+\beta \gamma$$ (2c)

$${\text{G}}_{\text{s}}^{\prime }+\text{UC}\underset{k_{-4}}{\overset{k_4}{\rightleftharpoons }}{\text{G}}_{\text{s}}^{\prime }\text{AC}$$ (2d)

$${\text{G}}_{\text{s}}^{\prime }\stackrel{k_{\text{s}}}{\to }{\alpha }_{\text{s}}\text{GDP}+{\text{P}}_{\text{i}}$$ (2e)

$${\text{G}}_{\text{s}}^{\prime }\text{AC}\stackrel{k_{\text{s}}}{\to }{\alpha }_{\text{s}}\text{GDP}+\text{UC}+{\text{P}}_{\text{i}}$$ (2f)

$${\alpha }_{\text{s}}\text{GDP}+\beta \gamma \stackrel{k_6}{\to }{\text{G}}_{\text{s}}$$ (2g)

(ii) The Inhibitory Pathway

$$\text{H}+{\text{R}}_{\text{i}}\underset{h_{-1}}{\overset{h_1}{\rightleftharpoons }}{\text{HR}}_{\text{i}}$$ (3a)

$${\text{HR}}_{\text{i}}+{\text{G}}_{\text{i}}\underset{h_{-2}}{\overset{h_2}{\rightleftharpoons }}{\text{HR}}_{\text{i}}{\text{G}}_{\text{i}}$$ (3b)

$${\text{HR}}_{\text{i}}{\text{G}}_{\text{i}}+\text{GTP}\stackrel{{\widehat{h}}_3}{\to }{\text{HR}}_{\text{i}}+{\text{G}}_{\text{i}}^{\prime }+\text{GDP}+\beta \gamma$$ (3c)

$${\text{G}}_{\text{i}}^{\prime }+{\text{HR}}_{\text{s}}\underset{h_{-4}}{\overset{h_4}{\rightleftharpoons }}{\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$$ (3d)

$${\text{G}}_{\text{i}}^{\prime }\stackrel{h_5}{\to }{\alpha }_{\text{i}}\text{GDP}+{\text{P}}_{\text{i}}$$ (3e)

$${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }\stackrel{h_6}{\to }\text{H}+{\text{R}}_{\text{s}}+{\text{G}}_{\text{i}}^{\prime }$$ (3f)

$${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }\stackrel{h_{\text{5}}}{\to }{\text{HR}}_{\text{s}}+{\alpha }_{\text{i}}\text{GDP}+{\text{P}}_{\text{i}}$$ (3g)

$${\alpha }_i\text{GDP}+\beta \gamma \stackrel{h_7}{\to }{\text{G}}_{\text{i}}$$ (3h)

(iii) Production and Secretion of Intracellular cAMP

$${\text{G}}_{\text{s}}^{\prime }\text{AC}+\text{ATP}\underset{{\widehat{l}}_{-1}}{\overset{{\widehat{l}}_1}{\rightleftharpoons }}{\text{G}}_{\text{s}}^{\prime }\text{AC}-\text{ATP}$$ (4a)

$${\text{G}}_{\text{s}}^{\prime }\text{AC}-\text{ATP}\stackrel{l_2}{\to }{\text{cAMP}}_i+{\text{G}}_{\text{s}}^{\prime }\text{AC}$$ (4b)

$${\text{cAMP}}_i+\text{iPDE}\underset{l_{-3}}{\overset{l_3}{\rightleftharpoons }}{\text{cAMP}}_i-\text{iPDE}$$ (4c)

$${\text{cAMP}}_i-\text{iPDE}\stackrel{l_4}{\to }\text{AMP}+\text{iPDE}$$ (4d)

$${\text{cAMP}}_i\stackrel{l_5}{\to }{\text{cAMP}}_o^{*}$$ (4e)

The definition of the symbols used in these reactions is given in Table 1, as are the mathematical symbols used later. The function l₅ is the secretion rate function, and we assume here that it is linear. In the perfusion experiments, the secreted cAMP must be distinguished from cAMP in the perfusate, since the former is radioactively labeled. We use an asterisk (*) to indicate the former.

TABLE 1.

The Variables and Their Symbols

Pathway	Species	Concentration	Meaning Function
Stimulus	HRS	y1(t)	Stimulus receptor bound with cAMP
	HRSGS	y2(t)	cAMP-Rs complex bound with Gs
	${\text{G}}_{\text{s}}^{\prime }$	y3(t)	Activated Gs protein
	${\text{G}}_{\text{s}}^{\prime }\text{AC}$	y4(t)	Activated adenylate cyclase
	αsGDP	y5(t)	Hydrolyzed ${\text{G}}_{\text{s}}^{\prime }$
Inhibitory	HRi	y6(t)	Inhibitory receptor bound with cAMP
	HRiGi	y7(t)	cAMP-R; complex bound with Gi
	${\text{G}}_{\text{i}}^{\prime }$	y8(t)	Activated Gi protein
	${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$	y9(t)	Activated Gi bound with HRS
	αiGDP	y10(t)	Hydrolyzed ${\text{G}}_{\text{i}}^{\prime }$
Generation and secretion	${\text{G}}_{\text{s}}^{\prime }\text{AC}-\text{ATP}$	y11(t)	Activated AC bound with ATP
	cAMPi	y12(t)	Intracellular cAMP
	iPDE-cAMPi	y13(t)	Intracellular iPDE-cAMP complex
	${\text{cAMP}}_o^{*}$	$y_{14}^{*}(t)$	Total amount of secreted cAMP

The basic assumptions concerning the transduction component of the model are the following.

• The G_s and G_i proteins exist unbound in the membrane and act as shuttle messengers in the presence of cAMP. In the inactive GDP-bound form, the α subunit of each has a high affinity for the βγ subunit.

• The βγ subunit is released upon the activation of the G protein. The βγ subunits of G_s and G_i are identical.

• The roles of G_s and G_i are not symmetric. ${\text{G}}_{\text{s}}^{\prime }$ combines with inactive adenylate cyclase and transforms it to its active form, while ${\text{G}}_{\text{i}}^{\prime }$ combines with the activated form of R_s, cAMP–R_s, and converts it to its inactive form R_s by releasing cAMP.

• The hydrolyzation rates of ${\text{G}}_x^{\prime }$, where x = s or i, are the same for all states, that is, for G_s, ${\text{G}}_{\text{s}}^{\prime }$, ${\text{G}}_{\text{s}}^{\prime }\text{AC}$, ${\text{G}}_{\text{s}}^{\prime }\text{AC}-\text{ATP}$ and for G_i, ${\text{G}}_{\text{i}}^{\prime }$, $\text{cAMP}-{\text{R}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$. (This assumption is not essential and can be easily changed. In reality, ${\text{G}}_{\text{s}}^{\prime }\text{AC}$, ${\text{G}}_{\text{s}}^{\prime }\text{AC}-\text{ATP}$, and $\text{cAMP}-{\text{R}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$ may have a higher rate of hydrolysis than ${\text{G}}_{\text{s}}^{\prime }$ and ${\text{G}}_{\text{i}}^{\prime }$).

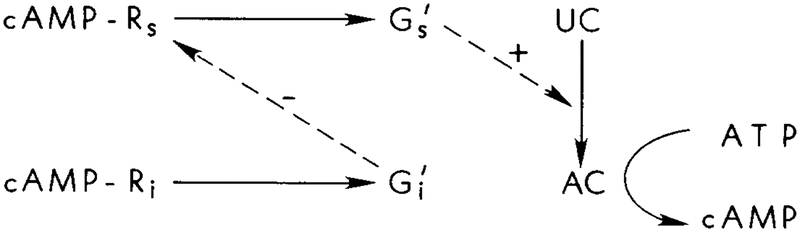
There are three interacting pathways involved: (1) the stimulus pathway, which involves signal transduction from extracellular cAMP to R_s, from R_s to G_s, and from G_s to adenylate cyclase; (2) the inhibitory pathway, in which the extracellular signal is transduced into an inhibitory intracellular signal; and (3) the pathway for the generation and secretion of intracellular cAMP. If extracellular cAMP is a dynamic variable, as in the suspension experiments, the stimulus, production, and secretion pathways form a positive feedback loop. This loop is controlled by negative feedback from the parallel inhibitory pathway, as shown in Figure 3. Clearly the dynamics will depend strongly on the characteristic time scales of the positive and negative feedback loops. When viewed at the level of cAMP production, which is the output, these parallel pathways constitute a feedforward control loop in which the disturbance signal is measured, processed, and used to turn off cAMP production and secretion (see Figure 3). The preset value for the system is the basal cAMP turnover rate of UC. The external disturbance is the increase in the extracellular cAMP concentration. This increase is detected by the “observer” R_i and by the “processor,” which is the inhibitory pathway. The feedforward signal acts at R_s, and in this way the “disturbance” is greatly reduced before it enters the “system,” which comprises G_s and UC.

FIG. 3.

A schematic diagram of the interactions in the proposed model. An extracellular cAMP stimulus serves as both the stimulus and the inhibitory signal. Adaptation arises from the action of ${\text{G}}_{\text{s}}^{\prime }$ on the hormone–receptor cmplex. Viewed at the level of cAMP production, this interaction produces a feedforward mechanism for the control of cAMP production.

Certain of the species involved in the model are assumed to be constant, and their effects are included in the kinetic constants. These are GTP, GDP, ATP, P_i, AMP, and other species that may influence the reactions. Furthermore, in the “mechanism” given below, we neglect unimportant back-reactions and reactions that generate short-lived intermediates such as HR_sα_sGTPβγ and ${\text{R}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$. Furthermore, we neglect the hydrolysis of activated adenylate cyclase bound with substrate, and we neglect the basal (unactivated) activity of the cyclase.

Notice that the nature of the reactions between ${\text{G}}_{\text{i}}^{\prime }$ and the cAMP–R_s complex is different than that of the reactions between ${\text{G}}_{\text{s}}^{\prime }$ and UC. The effect of ${\text{G}}_{\text{s}}^{\prime }$ is to increase the binding rate between ATP and adenylate cyclase by activating adenylate cyclase, while the effect of ${\text{G}}_{\text{i}}^{\prime }$ is to decrease the rate of the binding between extracellular cAMP and R_s by deactivating R_s. The rapid decomposition of $\text{cAMP}-{\text{R}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$ accounts for the apparent loss of affinity of R_s for extracellular cAMP. Of course, once the complex decomposes, extracellular cAMP can bind to the bare receptor again. An increase in the GTP concentration will cause an increase of ${\text{G}}_{\text{i}}^{\prime }$, which in turn causes a loss of affinity of R_s to extracellular cAMP and a decrease in the total amount of cMAI–R_s complex in the steady state.

For simplicity, we only display the differential equations for the variables y₁–y₁₄, since the remaining unknowns can be obtained from conservation conditions. There are seven conservation relations for the system, and the quantities that are determined by these relations are listed in Table 2. The differential equations for quantities in the stimulus pathway are

$$\begin{gathered} \frac{d{y}_1}{dt}=k_{1}H{z}_1-k_{-1}{y}_1-k_2{y}_1{z}_2+\left(k_{-2}+k_3\right)y_2-h_4{y}_1{y}_8+h_5{y}_9, \\ \frac{d{y}_2}{dt}=k_2{y}_1{z}_2-\left(k_{-2}+k_3\right)y_2, \\ \frac{d{y}_3}{dt}=k_3{y}_2-k_4{y}_3{z}_3-k_5{y}_3, \\ \frac{d{y}_4}{dt}=k_4{y}_3{z}_3-\left(k_5+l_1\right)y_4+\left(l_{-1}+l_2\right)y_{11}, \\ \frac{d{y}_5}{dt}=k_5\left(y_3+y_4\right)-k_6{y}_5{z}_6. \end{gathered}$$ (5)

The differential equations for quantities in the inhibitory pathway are

$$\begin{gathered} \frac{d{y}_6}{dt}=h_{1}H{z}_4-h_{-1}{y}_6-h_2{y}_6{z}_5+\left(h_{-2}+h_3\right)y_7, \\ \frac{d{y}_7}{dt}=h_2{y}_6{z}_5-\left(h_{-2}+h_3\right)y_7 \\ \frac{d{y}_8}{dt}=h_3{y}_7-h_4{y}_1{y}_8-h_5{y}_8+h_6{y}_9, \\ \frac{d{y}_9}{dt}=-\left(h_5+h_6\right)y_9+h_4{y}_1{y}_8, \\ \frac{d{y}_{10}}{dt}=h_5\left(y_8+y_9\right)-h_7{y}_{10}{z}_6. \end{gathered}$$ (6)

The differential equations for the production and secretion of intracellular cAMP are

$$\begin{gathered} \frac{d{y}_{11}}{dt}=l_1{y}_4-\left(l_{-1}+l_2\right)y_{11}, \\ \frac{d{y}_{12}}{dt}=l_2{y}_{11}-l_5{y}_{12}+l_{-3}{y}_{13}-l_3{y}_{12}{z}_7, \\ \frac{d{y}_{13}}{dt}=-\left(l_{-3}+l_4\right)y_{13}+l_3{y}_{12}{z}_7, \\ \frac{d{y}_{14}^{*}}{dt}=l_5{y}_{12}. \end{gathered}$$ (7)

Here $k_3\equiv {\widehat{k}}_3[\text{GTP}]$, $h_3\equiv {\widehat{h}}_3[\text{GTP}]$, and $l_1\equiv {\widehat{l}}_1[\text{ATP}]$.

TABLE 2.

The Quantities Determined by Conservation Conditions

Species	Concentration	Definition
Rs	z1(t)	Free Rs in membrane
Gs	z2(t)	Free Gs in membrane
UC	z3(t)	Free adenylate cyclase in the membrane
Ri	z4(t)	Free Ri in the membrane
Gi	z5(t)	Free Gi in the membrane
βγ	z6(t)	Free βγ subunits in the membrane
iPDE	z7(t)	Free PDE in the cytoplasm

The conservation relations that determine the dependent variables z_i, i = 1, …,7, are

$$\begin{gathered} y_1+y_2+y_9+z_1={\left[{\text{R}}_{\text{s}}\right]}_T, \\ {y}_2+y_3+y_4+y_5+y_{11}+z_2={\left[{\text{G}}_{\text{s}}\right]}_T, \\ {y}_4+y_{11}+z_3={\left[\text{UC}\right]}_T,y_6+y_7+z_4={\left[{\text{R}}_{\text{i}}\right]}_T, \\ {y}_7+y_8+y_9+y_{10}+z_5={\left[{\text{G}}_{\text{i}}\right]}_T, \\ {y}_3+y_4+y_5+y_8+y_9+y_{10}+y_{11}-z_6=0, \\ {y}_{13}+z_7={\left[\text{iPDE}\right]}_T, \end{gathered}$$ (8)

where subscript T denotes the initial value of a quantity. When these are solved for the z_i and the solutions used in (5)–(7), the result is a system of 13 equations in y₁, …, y₁₃, with at worst quadratic nonlinearities. The reader can easily show that the flow associated with these equations preserves positivity, that is, solutions of these equations that begin in the nonnegative cone of composition space remain there. Furthermore, it is easy to see that y₁, …, y₁₁ and y₁₃ remain bounded for all time, and the bounds are given in Table 3. If appropriate assumptions are made about the secretion function and the rate constants for adenylate cyclase and intracellular phosphodiesterase, then the same is true of y₁₂. Thus the governing equations are well-posed in the mathematical sense.

TABLE 3.

Bounds for the Independent and Dependent Dimensional Variables

0 ⩽ y1 ⩽ [Rs]T	0 ⩽ y8 ⩽ [Gi]T	0 ⩽ z1 ⩽ [Rs]T
0 ⩽ y2 ⩽ min([Rs]T, [Gs]T)	0 ⩽ y9 ⩽ min([Rs]T, [Gs]T)	0 ⩽ z2 ⩽ [Gs]T
0 ⩽ y3 ⩽ [Gs]T	0 ⩽ y10 ⩽ [Gi]T	0 ⩽ z3 ⩽ [UC]T
0 ⩽ y4 ⩽ min([Gs]T, [UC]T)	0 ⩽ y11 ⩽ min([Gs]T, [UC]T)	0 ⩽ z4 ⩽ [Ri]T
0 ⩽ y5 ⩽ [Gs]T	0 ⩽ y12 ⩽ ∞	0 ⩽ z5 ⩽ [Gi]T
0 ⩽ y6 ⩽ [Ri]T	0 ⩽ y13 ⩽ [iPDE]T	0 ⩽ z6 ⩽ [Gs]T + [Gi]T
0 ⩽ y7 ⩽ min([Ri]T, [Gi]T)	$0⩽y_{14}^{*}⩽\infty$	0 ⩽ z7 ⩽ [iPDE]T

4. ANALYSIS OF THE MODEL

In this section we describe the qualitative behavior of the model, we do a reduction that simplifies the system, and we analyze various components of the dynamics.

4.1. A QUALITATIVE DESCRIPTION OF ADAPTATION AND DEADAPTATION IN THE MODEL

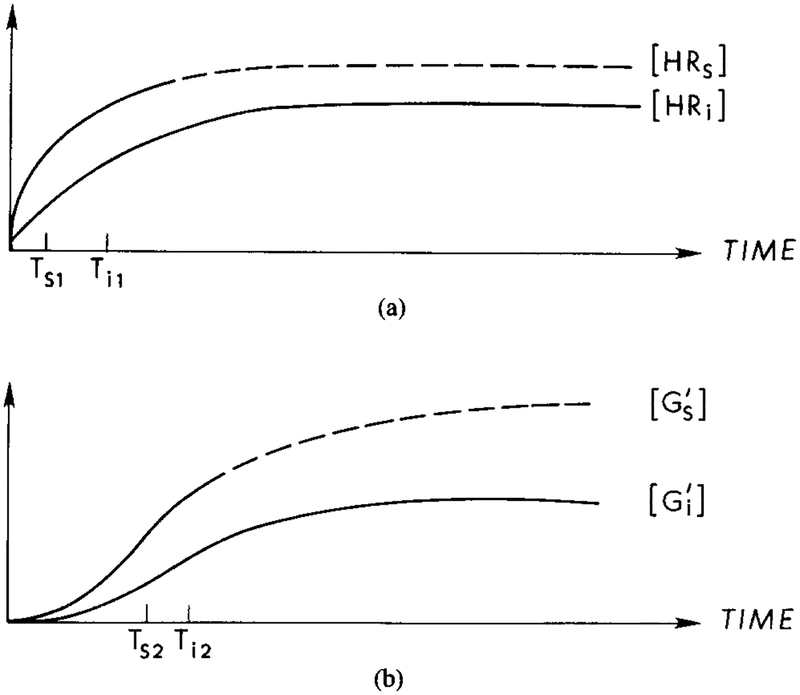
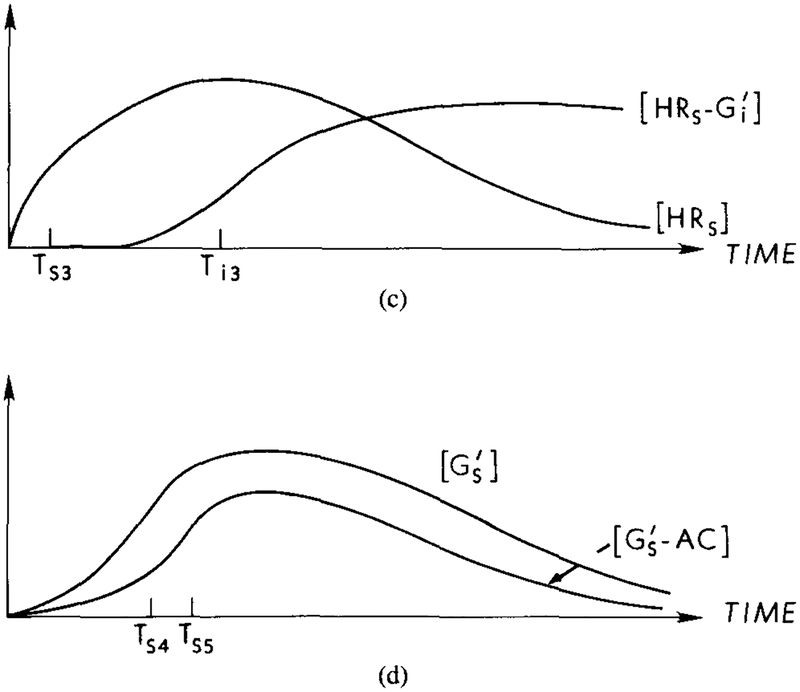
Suppose that a step change in the extracellular concentration of cAMP is introduced in a perfusion apparatus. Since agonist and antagonist are the same in Dd, ${\text{G}}_{\text{i}}^{\prime }$ and ${\text{G}}_{\text{s}}^{\prime }$ will be produced simultaneously. ${\text{G}}_{\text{s}}^{\prime }$ activates UC, while ${\text{G}}_{\text{i}}^{\prime }$ combines with HR_s to deactivate it. This blocks the further production of ${\text{G}}_{\text{s}}^{\prime }$, and the ${\text{G}}_{\text{s}}^{\prime }$ produced in response to the step will be degraded by hydrolysis. Thus there will be an initial burst of cAMP produced, but the activated adenylate cyclase will decay due to the hydrolysis of ${\text{G}}_{\text{s}}^{\prime }$. If a higher concentration is presented, then a new burst of ${\text{G}}_{\text{s}}^{\prime }$ and ${\text{G}}_{\text{i}}^{\prime }$ will be produced. As we shall see, if the time scales in the stimulatory and inhibitory channels are adjusted properly, this mechanism can produce the full range of observations in perfusion and suspension experiments. The qualitative time course of the various species following a step change in cAMP is shown in Figure 4. In [39], cAMP secretion was compared in pertussis-treated and untreated cells, and it was found that for the first 30 s of stimulus the secretion rates were the same. This indicates that the lag time in the inhibitory pathway, which is T_i1 + T_i2 in Figure 4, is of the order of 30 s.

FIG. 4.

A qualitative description of latency and adaptation in the signal transduction process under a constant stimulus. The time for activation of G protein is the major component of the latency between stimulus arrival and activation of the adenylate cyclase. Adaptation at the receptor level results from the interaction of ${\text{G}}_{\text{i}}^{\prime }$ with HR_s, which reduces the amount of activated G_s and cyclase. (a) Response curves for HR_s and HR_i under a constant stimulus. T_s1 and T_i1, represent the half-maximal times for the respective components. The dashed line indicates the response for HR_s in the absence of an inhibitory effect. (b) Response curves for the concentrations of ${\text{G}}_{\text{s}}^{\prime }$ and ${\text{G}}_{\text{i}}^{\prime }$. T_s2 and T_i2 represent the half-maximal times for the respective components. The dashed line indicates the response if the inhibitory effect is not present. (c) In the presence of ${\text{G}}_{\text{i}}^{\prime }$, HR_s is diminished due to the formation of ${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$. The half-maximal time, T_s3, for HR_s in the presence of ${\text{G}}_{\text{i}}^{\prime }$ is approximately the same as T_s1, whereas T_i3 > T_i2. (d) Response curves for the concentration of ${\text{G}}_{\text{s}}^{\prime }$ and ${\text{G}}_{\text{s}}^{\prime }\text{AC}$. The half-maximal time for ${\text{G}}_{\text{s}}^{\prime }$, T_s4, is approximately equal to T_s2, whereas the half-maximal time for ${\text{G}}_{\text{s}}^{\prime }\text{AC}$, T_s5, is greater than T_s4. The rate of cAMP_i production is proportional to the concentration of G_sAC.

If a constant cAMP stimulus that has been held long enough to produce full adaptation is terminated, the concentration of the HR_s and HR_i complexes will decay. Decay of HR_i, produces no new ${\text{G}}_{\text{i}}^{\prime }$, and the amount of ${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$ will decrease due to hydrolysis. Under the assumption that hydrolysis is first-order in the substrate, deadaptation occurs at an exponential rate when the stimulus is withdrawn.

4.2. NONDIMENSIONALIZATION AND REDUCTION OF THE EQUATIONS

Nondimensionalization.

We start by introducing dimensionless variables for the 14 independent concentration variables. The choices of dimensionless variables depend on the estimates of kinetic parameters, which are derived in the Appendix. The results are summarized in Tables 4 and 5.

TABLE 4.

Estimates of the Kinetic Parameters

Pathway	Parameter	Estimated value	Source
Stimulus	k1	7.5 s−1 μM−1	van Haastert and de Wit [49]
	k−1	0.45 s−1	van Haastert and de Wit [49]
	k2	1.0 × 103 m2/(μmol·s)	Gilman [21]
	k−2	0.0 s−1	Gilman [21]
	k3	1.0 × 103 s−1	Gilman [21]
	k4	1.0 × 104 m2/(μmol·s)
	k−4	0.0 s−1
	k5	0.0625 s−1	Gilman [21]
	k6	1.0 × 105 m2/(μmol·s)
Inhibitory	h1	2.2 s−1 μM−1	van Haastert and de Wit [49]
	h−1	1.0 s−1	van Haastert and de Wit [49]
	h2	40.0 m2/(μmol·s)	Dinauer et al. [13]
	h−2	0.0 s−1	Dinauer et al. [13]
	h3	4.0 × 102 s−1	Dinauer et al. [13]
	h4	5.0 × 106 m2/(μmol·s)
	h−4	0.0 s−1
	h5	7.5 × 10−3 s−1	Gerisch and Wick [20]
	h6	17.0 s−1	van Haastert and de Wit [49]
	h7	105 m2/(μmol·s)
cAMP generation and secretion	l	20.2 s−1	Levitzki [29]
	l−1	20.2 s−1	Levitzki [29]
	l2	202 s−1	Levitzki [29]
	l3	5.0 × 10−4 m3/(μmol·s)	Rapp et al. [37]
	l−3	0.0 s−1	Rapp et al. [37]
	l4	50 s−1	Rapp et al. [37]
	l5	0.157 s−1

TABLE 5.

Estimates for the Fixed Concentrations

Quantity conserved	Molecules per cell	Standard concentration
[Rs]T, [Gs]T, [UC]T	3.84 × 104	1.67 × 10−4 μmol/m2
[RilT [Gi]T	5.76 × 104	2.50 × 10−4 μmol/m2
[iPDE]T	7.28 × 105	1.73 × 103 μmol/m3

After nondimensionalization, one finds that the dimensionless variables fall into two categories: those that reach a pseudo-steady state rapidly, which we call the singular variables, and the remainder, which we call nonsingular variables. The mathematical symbols for singular variables are v_i, i = 1, …,6, and for nonsingular variables u_i, i = 1, …,8. The dimensionless variables and their relationship to the corresponding dimensional variables are listed in Table 6. The nondimensionalization gives rise to a number of small parameters, which are defined in Table 7. Other dimensionless kinetic parameters are listed in Table 8. Note that $\tau ~\mathcal{O}(1)$ corresponds to $t~\mathcal{O}(10\text{s})$.

TABLE 6.

The Relationship Between Dimensional and Dimensionless Variables

	Species	Dimensional form	Dimensionless form
Stimulus pathway	HRS	y1	u1 = y1/[Rs]T
	HRSGS	y2	$v_1=\frac{k_{-2}+k_3}{k_2{\left[{\text{R}}_{\text{s}}\right]}_T{\left[{\text{G}}_{\text{s}}\right]}_T}{y}_2$
	${\text{G}}_{\text{s}}^{\prime }$	y3	u2 = y3/[Gs]T
	${\text{G}}_{\text{s}}^{\prime }\text{AC}$	y4	u3 = y4/[UC]T
	αsGDP	y5	v2 = (k6/k5)y5
Inhibitory pathway	HRi	y6	u4 = y6/[Ri]T
	HRiGi	y7	${\nu }_3=\frac{h_{-2}+h_3}{h_2{\left[{\text{R}}_{\text{i}}\right]}_T{\left[{\text{G}}_{\text{i}}\right]}_T}{y}_7$
	${\text{G}}_{\text{i}}^{\prime }$	y8	u5 = y8/[Gi]T
	${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$	y9	u5 = y8/[Gi]T
	αiGDP	y10	v4 = (h7/h5)y10
cAMP generation and secretion	${\text{G}}_{\text{s}}^{\prime }\text{AC}-\text{ATP}$	y11	$v_5=\frac{l_{-1}+l_2}{l_1{\left[\text{UC}\right]}_T}{y}_{11}$
	cAMPi	y12	u7 = y12/[iPDE]T
	iPDE-cAMPi	y13	$v_6=\left(l_{-3}+l_4\right)y_{13}/l_3{\left[\text{iPDE}\right]}_T^2$
	${\text{cAMP}}_o^{*}$	$y_{14}^{*}$	$u_8^{*}=y_{14}^{*}/{\left[\text{iPDE}\right]}_T$
Time scale		t	τ = k5t

TABLE 7.

The Small Dimensionless Kinetic Parameters and Their Values

Small parameter	Relation to dimensional parameters	Value
ϵ1	k5/(k−2 + k3)	6.25 × 10−5
ϵ2	k5/k6[Gs]T	3.74 × 10−4
ϵ3	k5/(h−2 + h3)	1.56 × 10−4
ϵ4	k5/h7[Gi]T	2.50 × 10−4
ϵ5	k5/(l−1 + l2)	2.81 × 10−4
ϵ6	k5/(l−3 + l4)	1.56 × 10−3

TABLE 8.

Other Dimensionless Parameters and Their Values

	Dimensionless parameter	Relation to dimensional parameter	Value
Stimulus Pathway	αH	(k1/k5)H(t)	120 μM−1 × H(t)
	αl	k−1/k5	7.2
	α2	k2[Gs]T/k5	2.67
	α3	k3/(k−2 + k3)	1.0
	α4	k4[Gs]T/k5	26.7
Inhibitory Pathway	βH	(h1/k5)H(t)	35.2 μM−1 × H(t)
	β1	h−1/k5	16.0
	β2	h2[Gi]T/k5	0.16
	β3	h3/(h−2 + h3)	1.0
	β4	h4[Gi]T/k5	2.0 × 104
	β5	h5/k5	0.12
	β6	h6/k5	272.0
cAMP generation and secretion	γ1	l1/k5	323.2
	γ2	$\frac{l_2{[\text{UC}]}_T}{\left(l_{-1}+l_2\right){[\text{iPDE}]}_T}$	0.048
	γ3	(l−3 + l4)/l3[iPDE]T	57.7
	γ4	l4/k5	800.0
	γ5	l5/k5	0.224
Independent concentrations	cl	[Rs]T/[Gs]T	1.0
	c2	[Ri]T/[Gi]T	1.0
	c3	[Rs]T/[Gi]T	0.668
Dependent concentrations	c4	[UC]T/[Gs]T	1.0
	cl/c3	[Gi]T/[Gs]T	1.5

The dimensionless form of (5)–(7), wherein the conservation equations have been used to remove z_i, is as follows. The differential equations for the singular variables are

$$\begin{gathered} {ϵ}_1\frac{d{v}_1}{d\tau }=u_1-v_1-u_1\left(u_2+u_3+{ϵ}_1{c}_1{\alpha }_2{v}_1+{ϵ}_2{v}_2+{ϵ}_5{c}_1{\gamma }_1{v}_5\right), \\ {ϵ}_2\frac{d{v}_2}{d\tau }=u_2+u_3-v_2\left(u_2+u_3+\frac{c_1}{c_3}{u}_5+c_1{u}_6+{ϵ}_2{v}_2+{ϵ}_4\frac{c_1}{c_3}{\beta }_5{v}_4+{ϵ}_5{\gamma }_1{v}_5\right), \\ {ϵ}_3\frac{d{v}_3}{d\tau }=u_4-v_3-u_4\left(u_5+c_3{u}_6+{ϵ}_3{\beta }_2{v}_3+{ϵ}_4{c}_2{\beta }_5{v}_4\right), \\ {ϵ}_4\frac{d{v}_4}{d\tau }=u_5+c_3{u}_6-\frac{c_3}{c_1}{v}_4\left(u_2+u_3+\frac{c_1}{c_3}{u}_5+c_1{u}_6+{ϵ}_2{v}_2+{ϵ}_4\frac{c_1}{c_3}{\beta }_5{v}_4+{ϵ}_5{\gamma }_1{v}_5\right), \\ {ϵ}_5\frac{d{v}_5}{d\tau }=u_3-v_5, \\ {ϵ}_6\frac{d{v}_6}{d\tau }=u_7-v_6-\frac{1}{{\gamma }_3}{u}_7{v}_6, \end{gathered}$$ (9)

and the differential equations for the nonsingular variables are

$$\begin{gathered} \frac{d{u}_1}{d\tau }={\alpha }_H(\tau )-\left[{\alpha }_H(\tau )+{\alpha }_1+{\alpha }_2\right]u_1+\left[1-{ϵ}_1{\alpha }_H(\tau )\right]{\alpha }_2{v}_1+\left[{\beta }_5-{\alpha }_H(\tau )\right]u_6-{\beta }_4{u}_1{u}_5+{\alpha }_2{u}_1\left(u_2+u_3+{ϵ}_1{c}_1{\alpha }_2{v}_1{ϵ}_2{v}_2+{ϵ}_5{\gamma }_1{v}_5\right), \\ \frac{d{u}_2}{d\tau }={\alpha }_2{\alpha }_3{c}_1{v}_1-\left(1+{\alpha }_4\right)u_2+{\alpha }_4{u}_2\left(u_3+{ϵ}_5{\gamma }_1{v}_5\right), \\ \frac{d{u}_3}{d\tau }={\alpha }_4{u}_2-\left(1+{\gamma }_1\right)u_3+{\gamma }_1{v}_5-{\alpha }_4{u}_2\left(u_3+{ϵ}_5{\gamma }_1{v}_5\right), \\ \frac{d{u}_4}{d\tau }={\beta }_H(\tau )-\left[{\beta }_H(\tau )+{\beta }_1+{\beta }_2\right]u_4+\left[1-{ϵ}_3{\beta }_H(\tau )\right]{\beta }_2{v}_3+{\beta }_2{u}_4\left(u_5+c_3{u}_6+{ϵ}_3{\beta }_2{v}_3+{ϵ}_4{\beta }_5{v}_4\right), \\ \frac{d{u}_5}{d\tau }=-{\beta }_5{u}_5+{\beta }_6{c}_3{u}_6+{\beta }_2{\beta }_3{c}_2{v}_3-c_3{\beta }_4{u}_1{u}_5, \\ \frac{d{u}_6}{d\tau }=-\left({\beta }_5+{\beta }_6\right)u_6+{\beta }_4{u}_1{u}_5, \\ \frac{d{u}_7}{d\tau }={\gamma }_1{\gamma }_2{v}_5-{\gamma }_5{u}_7-\frac{l_3{\left[\text{iPDE}\right]}_T}{k_5}{u}_7+\frac{l_{-3}}{k_5{\gamma }_3}{v}_6+\frac{l_3{\left[\text{iPDE}\right]}_T}{k_5{\gamma }_3}{u}_7{v}_6, \\ \frac{d{u}_{\text{s}}^{*}}{d\tau }={\gamma }_5{u}_7. \end{gathered}$$ (10)

Upper and lower bounds for the solution in dimensionless terms are given in Table 9. In deriving these it is assumed that the initial conditions satisfy the conservation equations and lie inside the bounded region.

TABLE 9.

Bounds for the Dimensionless Variables

Nonsingular variable	Singular variable
0 ⩽ u1 ⩽ 1	$0⩽v_1⩽\text{min}\left(\frac{k_{-2}+k_3}{k_2{\left[{\text{R}}_{\text{s}}\right]}_T},\frac{k_{-2}+k_3}{k_2{\left[{\text{G}}_{\text{s}}\right]}_T}\right)$
0 ⩽ u2 ⩽ 1	0 ⩽ v2 ⩽ k6[Gs]T/k5
0 ⩽ u3 ⩽ min(l, [Gs]T/[UC]T)	$0⩽v_3⩽\text{min}\left(\frac{h_{-2}+h_3}{h_2{\left[{\text{R}}_{\text{i}}\right]}_T},\frac{h_{-2}+h_3}{h_2{\left[{\text{G}}_{\text{i}}\right]}_T}\right)$
0 ⩽ u4 ⩽ 1	0 ⩽ v4 ⩽ h7[Gi]T/h5
0 ⩽ u5 ⩽ 1	$0⩽v_5⩽\text{min}\left(\frac{l_{-1}+l_2}{l_1},\frac{\left(l_{-1}+l_2\right){\left[{\text{G}}_{\text{s}}\right]}_T}{l_1{[\text{UC}]}_T}\right)$
0 ⩽ u6 ⩽ min(l,[Gi]T/[Rs]T)	0 ⩽ v6 ⩽ (l−3 + l4)/l3[iPDE]T
0 ⩽ u7 ⩽ ∞	$0⩽u_8^{*}⩽\infty$

Simplification via Singular Perturbation.

On the τ time scale, the singular equations can be reduced to the algebraic system

$$\begin{gathered} u_1-v_1-u_1\left(u_2+u_3+{ϵ}_1{c}_1{\alpha }_2{v}_1+{ϵ}_2{v}_2+{ϵ}_5{c}_1{\gamma }_1{v}_5\right)=0, \\ {u}_2+u_3-v_2\left(u_2+u_3+\frac{c_1}{c_3}{u}_5+c_1{u}_6+{ϵ}_2{v}_2+{ϵ}_4\frac{c_1}{c_3}{\beta }_5{v}_4+{ϵ}_5{\gamma }_1{v}_5\right)=0, \\ {u}_4-v_3-u_4\left(u_5+c_3{u}_6+{ϵ}_3{\beta }_2{\nu }_3+{ϵ}_4{c}_2{\beta }_5{v}_4\right)=0, \\ {u}_5+c_3{u}_6-\frac{c_3}{c_1}{v}_4\left(u_2+u_3+\frac{c_1}{c_3}{u}_5+c_1{u}_6+{ϵ}_2{v}_2+{ϵ}_4\frac{c_1}{c_3}{\beta }_5{v}_4+{ϵ}_5{\gamma }_1{v}_5\right)=0, \\ {y}_3-v_5=0, \\ {u}_7-v_6-\left(1/{\gamma }_3\right)u_7{v}_6=0. \end{gathered}$$ (11)

The solution of this system to within terms of $\mathcal{O}\left({ϵ}_i\right)$ is

$$\begin{gathered} v_1=u_1-u_1\left(u_2+u_3\right), \\ {v}_2=\frac{u_2+u_3}{u_2+u_3+\left(c_1/c_3\right)u_5+c_1{u}_6}, \\ {v}_3=u_4-u_4\left(u_5+c_3{u}_6\right), \\ {v}_4=\frac{c_1\left(u_5+c_3{u}_6\right)}{c_3\left[u_2+u_3+\left(c_1/c_3\right)u_5+c_1{u}_6\right]}, \\ {v}_5=u_3, \\ {v}_6={\gamma }_3{u}_7/\left(u_7+{\gamma }_3\right). \end{gathered}$$ (12)

If we replace the v_i in Equation (10) by their pseudo-steady-state values given by Equation (12), then we get an ordinary differential equation system with seven independent variables. We can also approximate this differential equation system by dropping the $\mathcal{O}(ϵ)$ and higher order terms, where ϵ ≡ max{ϵ_i}. After some simplifications, we obtain the following system.

$$\begin{gathered} \frac{d{u}_1}{d\tau }={\alpha }_H(\tau )-\left[{\alpha }_H(\tau )+{\alpha }_1\right]u_1+\left[{\beta }_5-{\alpha }_H(\tau )\right]u_6-{\beta }_4{u}_1{u}_5, \\ \frac{d{u}_2}{d\tau }={\alpha }_2{\alpha }_3{c}_1{u}_1-\left(1+{\alpha }_4\right)u_2-{\alpha }_2{\alpha }_3{c}_1{u}_1\left(u_2+u_3\right)+{\alpha }_4{u}_2{u}_3, \\ \frac{d{u}_3}{d\tau }={\alpha }_4{u}_2-u_3-{\alpha }_4{u}_2{u}_3, \\ \frac{d{u}_4}{d\tau }={\beta }_H(\tau )-\left[{\beta }_H(\tau )+{\beta }_1\right]u_4, \\ \frac{d{u}_5}{d\tau }={\beta }_2{\beta }_3{c}_2{u}_4-{\beta }_5{u}_5+{\beta }_6{c}_3{u}_6-c_3{\beta }_4{u}_1{u}_5-{\beta }_2{\beta }_3{c}_2{u}_4\left(u_5+c_3{u}_6\right), \\ \frac{d{u}_6}{d\tau }=-\left({\beta }_5+{\beta }_6\right)u_6+{\beta }_4{u}_1{u}_5, \\ \frac{d{u}_7}{d\tau }={\gamma }_1{\gamma }_2{u}_3-{\gamma }_5{u}_7-\frac{{\gamma }_4{u}_7}{u_7+{\gamma }_3}, \\ \frac{d{u}_8^{*}}{d\tau }={\gamma }_5{u}_7. \end{gathered}$$ (13)

4.3. ANALYSIS OF THE COMPONENT STEPS

We next analyze the qualitative dynamics of the model. For convenience in relating the results to the biochemical steps, we do this in terms of the dimensional quantities. First we analyze various individual steps by uncoupling the pathways. The second part is devoted to the study of the coupled system. In this case the dynamics cannot be analyzed directly, but with certain simplifications we can analyze the steady-state behavior. This provides some qualitative understanding of how adaptation arises.

The Dynamics of G-Protein Activation.

We first suppose that k₄ = h₄ = 0, which suppresses activation of AC and inactivation of HR_s. This enables us to uncouple the three pathways and study the dynamics of G-protein activation.

First consider the binding to R_s, for which the reactions are (2a) and (2b). We invoke the pseudo-steady-state assumption for [HR_sG_s] to reduce the degrees of freedom, by setting

$$\frac{d\left[{\text{HR}}_{\text{s}}{\text{G}}_{\text{s}}\right]}{dt}=0.$$

In this way, we obtain the usual expression

$$\left[{\text{HR}}_{\text{s}}{\text{G}}_{\text{s}}\right]=\frac{k_2}{k_{-2}+k_3}\left[{\text{HR}}_{\text{s}}\right]\left[{\text{G}}_{\text{s}}\right],$$

and according to our estimates of parameters,

$$\frac{\left[{\text{HR}}_{\text{s}}{\text{G}}_{\text{s}}\right]}{{\left[{\text{R}}_{\text{s}}\right]}_T}=\frac{k_2{\left[{\text{R}}_{\text{s}}\right]}_T}{k_3}\left(\frac{\left[{\text{G}}_{\text{s}}\right]}{{\left[{\text{R}}_{\text{s}}\right]}_T}\right)\left(\frac{\left[{\text{HR}}_{\text{s}}\right]}{{\left[{\text{R}}_{\text{s}}\right]}_T}\right)⩽1.67\times {10}^{-4}\frac{\left[{\text{HR}}_{\text{s}}\right]}{{\left[{\text{R}}_{\text{s}}\right]}_T}.$$

Hence the amount of HR_sG_s is very small compared to [HR_S], and therefore we have the approximation

$$\begin{gathered} \frac{d\left[{\text{HR}}_{\text{s}}\right]}{dt}=k_1[\text{H}]\left[{\text{R}}_{\text{s}}\right]-k_{-1}\left[{\text{HR}}_{\text{s}}\right], \\ \left[{\text{HR}}_{\text{s}}\right]+\left[{\text{R}}_{\text{s}}\right]={\left[{\text{R}}_{\text{s}}\right]}_T \end{gathered}$$

or equivalently,

$$\frac{d{y}_1}{dt}=k_1[\text{H}]{\left[{\text{R}}_{\text{s}}\right]}_T-\left(k_1[\text{H}]+k_{-1}\right)y_1,y_1(0)=0.$$ (14)

Thus the response is

$$y_1(t)={\left[{\text{R}}_{\text{s}}\right]}_T\frac{[\text{H}]}{[\text{H}]+K_d}\left(1-e^{-\left(k_1[\text{H}]+k_{-1}\right)}t\right),$$ (15)

where K_d ≡ k₋₁/k₁ is the dissociation constant. This process is fast because k₋₁ is relatively large. The half-time for this process is

$$t^{0.5}=\frac{\text{ln}2}{k_1[\text{H}]+k_{-1}}<\frac{\text{ln}2}{k_{-1}}=1.54\text{s,}$$

and the steady-state response is

$$u_1^d\equiv \frac{{\left[{\text{HR}}_{\text{s}}\right]}_s}{{\left[{\text{R}}_{\text{s}}\right]}_T}=\frac{[\text{H}]}{[\text{H}]+K_d},$$ (16)

where [·]_s denotes the steady-state concentration of a species. A similar analysis can be done for the binding of cAMP to R_i.

Next we consider the activation of G_s by HR_s. The reactions involved are (2b), (2c), (2e), and (2g). Our estimates of the parameters (cf. Appendix) shows that k₆ is very large. Hence [α_sGDP] is small, and we simplify the analysis by setting [α_sGDP] = 0. The simplified reaction and conservation equations are

$$\begin{gathered} \frac{d\left[{\text{G}}_{\text{s}}^{\prime }\right]}{dt}=k_3\left[{\text{HR}}_{\text{s}}{\text{G}}_{\text{s}}\right]-k_5\left[{\text{G}}_{\text{s}}^{\prime }\right], \\ \left[{\text{HR}}_{\text{s}}{\text{G}}_{\text{s}}\right]=\frac{k_2}{k_{-2}+k_3}\left[{\text{HR}}_{\text{s}}\right]\left[{\text{G}}_{\text{s}}\right], \\ {\left[{\text{G}}_{\text{s}}\right]}_T=\left[{\text{G}}_{\text{s}}\right]+\left[{\text{G}}_{\text{s}}^{\prime }\right]+\left[{\text{HR}}_{\text{s}}{\text{G}}_{\text{s}}\right], \end{gathered}$$

and therefore

$$\frac{d{y}_3(t)}{dt}=k_{\text{on}}{\left[{\text{G}}_{\text{s}}\right]}_T-\left(k_{\text{on}}+k_{\text{s}}\right)y_3,y_3(0)=0,$$ (17)

where k_on = k₂k₃/(k₋₂ + k₃)[HR_s]. Here k_on is not a constant but is time-dependent. When the stimulus level is higher than 0.1 μM, the binding step is much faster than the activation of $G_s^{\prime }$. Hence we can suppose that the binding is in equilibrium and use the value of [HR_s] given by (16) in k_on. Consequently,

$$y_3(t)=\frac{k_{\text{on}}{\left[{\text{G}}_{\text{s}}\right]}_T}{k_{\text{on}}+k_5}\left(1-e^{-\left(k_{\text{on}}+k_5\right)}t\right).$$ (18)

When [H] is smaller than 0.1 μM, the speed of the binding step is comparable to that of activation of G_s. In this case we cannot get an explicit solution, but in any case, the half-time for this response is estimated by

$$t^{0.5}=(\text{ln}2)/\left(k_{\text{on}}+k_5\right).$$

Using the estimate of k_on and k_off, we find that

$$3.0\text{s}<t^{0.5}<11.1\text{s}.$$

Thus the steady-state response is given by

$$\frac{{\left[{\text{G}}_{\text{s}}^{\prime }\right]}_s}{{\left[{\text{G}}_{\text{s}}\right]}_T}=\frac{k_{\text{on}}}{k_{\text{on}}+k_5}=\frac{k_2{k}_3{\left[{\text{HR}}_{\text{s}}\right]}_s}{k_2{k}_3{\left[{\text{HR}}_{\text{s}}\right]}_s+\left(k_{-2}+k_3\right)k_{\text{5}}}.$$ (19)

A similar analysis can be done for the activation of G_i. The biochemical reactions involved are (3b), (3c), (3e), and (3h), since ${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }=0$. Because h₇ is large, we neglect [α_iGDP] and obtain the approximate solution

$$y_8(t)=\frac{h_{\text{on}}{\left[{\text{G}}_i\right]}_T}{h_{\text{on}}+h_5}\left(1-e^{-\left(h_{\text{on}}+h_5\right)}t\right),$$ (20)

where h_on = [h₂h₃/(h₋₂ + h₃)][HR_i]. The half-time for this response is

$$t^{0.5}=(\text{ln}2)/\left(h_{\text{on}}+h_5\right),$$

and using our estimates of h_on and h_off we obtain

$$39.6\text{s}<t^{0.5}<92.4\text{s}.$$

Thus in the absence of coupling, the delay in the buildup of $\left[{\text{G}}_{\text{i}}^{\prime }\right]$ is of the same order as the observed adaptation time.

The steady-state response is given by

$$\frac{{\left[{\text{G}}_{\text{i}}^{\prime }\right]}_s}{{\left[{\text{G}}_{\text{i}}\right]}_T}=\frac{h_{\text{on}}}{h_{\text{on}}+h_5}=\frac{h_2{h}_3{\left[{\text{HR}}_{\text{i}}\right]}_{\text{s}}}{h_2{h}_3{\left[{\text{HR}}_{\text{i}}\right]}_{\text{s}}+\left(h_{-2}+h_3\right)h_5}.$$

Table 10 shows the steady-state response of receptor binding and activation of the G proteins for different stimulus levels, using the parameter values estimated in the Appendix. From this table one sees how the fractions of the activated G proteins depend on the stimulus level.

TABLE 10.

The steady-state response of uncoupled stimulus and inhibitory pathways to external cAMP stimuli

[H](μM)	10−4	10−3	10−2	10−1	1	10
$\frac{{\left[{\text{HR}}_{\text{s}}\right]}_s}{{\left[{\text{R}}_{\text{s}}\right]}_T}\times 100$	0.17%	1.64%	14.3%	62.5%	94.0%	99.4%
$\frac{{\left[{\text{HR}}_{\text{i}}\right]}_s}{{\left[{\text{R}}_{\text{i}}\right]}_T}\times 100$	0.022%	0.22%	2.15%	18%	69.0%	95.7%
$\frac{{\left[{\text{G}}_{\text{s}}^{\prime }\right]}_s}{{\left[{\text{G}}_{\text{s}}\right]}_T}\times 100$	0.45%	4.36%	27.7%	62.6%	71.5%	72.7%
$\frac{{\left[{\text{G}}_{\text{i}}^{\prime }\right]}_s}{{\left[{\text{G}}_{\text{i}}\right]}_T}\times 100$	0.03%	0.29%	2.79%	19.4%	47.9%	57.1%

A Steady-State Analysis of the Coupled System.

In this section, we will do the steady-state analysis for the coupled pathways, that is, for the case of k₄ ≠ 0 and h₄ ≠ 0. The three pathways are coupled, and we cannot obtain an explicit solution, but we can obtain some quantitative insight into adaptation.

The binding of external stimulus H with R_i is the same as in the case for the decoupled system, but $\left[{\text{G}}_{\text{i}}^{\prime }\right]$ will be different, since a fraction of the ${\text{G}}_{\text{i}}^{\prime }$ will be bound to HR_s. Since we assume that ${\text{G}}_{\text{i}}^{\prime }$ decays at the same rate irrespective of what form it is in, we may consider the combined concentration of the two forms of ${\text{G}}_{\text{i}}^{\prime }$, namely, ${\text{G}}_{\text{i}}^{\prime }$ and ${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$.

Let ${\left[{\text{G}}_{\text{i}}^{\prime }\right[}^{*}$ denote this quantity:

$${\left[{\text{G}}_{\text{i}}^{\prime }\right]}^{*}=\left[{\text{G}}_{\text{i}}^{\prime }\right]+\left[{\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }\right].$$ (21)

Reactions (3d) and (3g) do not alter ${\left[{\text{G}}_{\text{i}}^{\prime }\right]}^{*}$, and therefore it is dynamically equivalent to $\left[{\text{G}}_{\text{i}}^{\prime }\right]$ in the preceding analysis. As a result,

$${\left[{\text{G}}_{\text{i}}^{\prime }\right]}^{*}=\frac{h_{\text{on}}{\left[{\text{G}}_{\text{i}}\right]}_T}{h_{\text{on}}+h_5}\left(1-e^{-\left(h_{\text{on}}+h_{\text{s}}\right)}t\right).$$ (22)

Now consider the equations for [HR_s] and $\left[{\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }\right]$. The differential equations are

$$\begin{gathered} \frac{d{y}_1}{dt}=k_1[\text{H}]\left({\left[{\text{R}}_{\text{s}}\right]}_T-y_1-y_9\right)-k_{-1}{y}_1-h_4{y}_1\left({\left[{\text{G}}_{\text{i}}^{\prime }\right]}^{*}-y_9\right), \\ \frac{d{y}_9}{dt}=k_4\left({\left[{\text{G}}_{\text{i}}^{\prime }\right]}^{*}-y_9\right)y_1-h_6{y}_9, \\ {y}_1(0)=y_9(0)=0. \end{gathered}$$ (23)

This system is closed since ${\left[{\text{G}}_{\text{i}}^{\prime }\right]}^{*}$ is given by (22), but we cannot find an explicit solution to it. Therefore we only do the steady-state analysis in order to obtain some insight as to how adaptation works in this step. With some simplifications we obtain the system

$$\begin{gathered} u_1^d-u_1-\frac{k_1[\text{H}]+h_6}{k_1[\text{H}]+k_{-1}}{u}_6=0, \\ {u}_1-\frac{{\left[{\text{R}}_{\text{s}}\right]}_T}{{\left[{\text{G}}_{\text{i}}^{\prime }\right]}_s^{*}}{u}_1{u}_6-\frac{h_6}{h_4{\left[{\text{G}}_{\text{i}}^{\prime }\right]}_s^{*}}{u}_6=0, \end{gathered}$$ (24)

where $u_1^d$ is given in (16). The approximate solution is

$$u_1=\left\{\frac{h_6}{h_6+h_4{\left[{\text{G}}_{\text{i}}\right]}_s^{*}\left(k_1[\text{H}]+h_6\right)/\left(k_1[\text{H}]+k_{-1}\right)}\right\}{u}_1^d,$$ (25)

and since u₁ = [HR_s]/[R_s]_T, this represents the unadapted portion of [HR_s]. From this equation one can deduce the following:

• An increase in h₄ causes a decrease in [HR_s]_s, by virtue of reaction (3d).

• An increase in ${\left[{\text{G}}_{\text{i}}^{\prime }\right]}_s^{*}$ causes a decrease in [HR_s]_s. This can occur, for example, by increasing h_on or [G_i]_T.

• An increase in h₆ leads to an increase in [HR_s]_s, because ${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$ decomposes faster.

One of the basic assumptions given in Section 3 is that the ${\text{G}}_{\text{s}}^{\prime }$ is hydrolyzed at the same rate irrespective of whether it is in free or bound form. An argument similar to that used to obtain ${\left[{\text{G}}_{\text{i}}^{\prime }\right]}^{*}$ shows that the combined concentrations of ${\text{G}}_{\text{s}}^{\prime }$, ${\text{G}}_{\text{s}}^{\prime }\text{AC}$, and ${\text{G}}_{\text{s}}^{\prime }\text{AC}-\text{ATP}$, which we denote ${\left[{\text{G}}_{\text{s}}^{\prime }\right]}_s^{*}$, is the same as the concentration of ${\text{G}}_{\text{s}}^{\prime }$ in the uncoupled system. Since [HR_s] is very small at steady state (see Table 11), it follows from (19) that ${\left[{\text{G}}_{\text{s}}^{\prime }\right]}_s$ and ${\left[{\text{G}}_{\text{s}}^{\prime }\text{AC}\right]}_s$, are small. The last row of Table 11 gives the values of ${\left[{\text{G}}_{\text{s}}^{\prime }\right]}_s^{*}$ corresponding to the parameters given in the Appendix. Thus we see that adaptation of internal cAMP production and secretion results from adaptation at the level of the stimulatory receptor.

TABLE 11.

The Steady-State Concentrations of Components in the Transduction Steps

[H] (μM)	10−4	10−3	10−2	10−1	1	10
$\frac{{\left[{\text{HR}}_{\text{i}}\right]}_{\text{s}}}{{\left[{\text{R}}_{\text{i}}\right]}_T}\times 100$	0.022%	0.22%	2.15%	18.0%	69.0%	95.7%
$\frac{{\left[{\text{G}}_{\text{i}}^{\prime }\right]}_s^{*}}{{\left[{\text{G}}_{\text{i}}\right]}_T}\times 100$	0.03%	0.29%	2.79%	19.4%	47.9%	57.1%
$\frac{{\left[{\text{HR}}_{\text{s}}\right]}_s}{{\left[{\text{R}}_{\text{s}}\right]}_T}\times 100$	0.093%	0.18%	0.21%	0.30%	1.01%	4.33%
$\frac{{\left[{\text{G}}_{\text{s}}^{\prime }\right]}_s^{*}}{{\left[{\text{G}}_{\text{s}}\right]}_T}\times 100$	0.03%	0.058%	0.067%	0.096%	0.32%	1,37%

5. NUMERICAL RESULTS

5.1. THE DYNAMICS OF THE UNCOUPLED SYSTEM

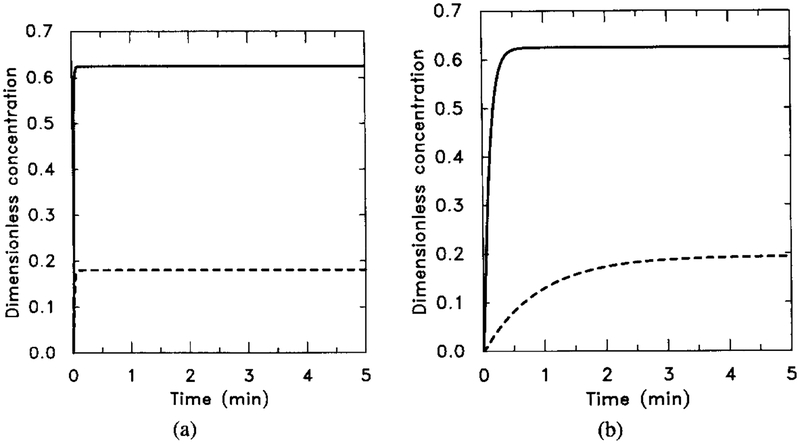
In the first set of simulations we let k₄ = h₄ = 0, with other parameters held at the values estimated in the Appendix. Typical response curves are shown in Figure 5 for a single-step stimulus. One can see that the response of both HR_s and HR_i is rapid; both reach their steady-state value within seconds. On the other hand, $\left[{\text{G}}_{\text{s}}^{\prime }\right]$ and $\left[{\text{G}}_{\text{i}}^{\prime }\right]$ increase on a much slower time scale, with the former increasing more rapidly and to a higher level than the latter.

FIG. 5.

The response of the uncoupled system. The stimulus is [H] = 0.1 μM for t ∈ (0, 5). The numerical results can be compared with the analytical results obtained from the analysis in Section 4 and with Figure 6 to verify the steady-state additivity of the uncoupled system. (a) The dimensionless concentrations of HR_s (solid line) and HR_i (dashed line). (b) The dimensionless concentrations of ${\text{G}}_{\text{s}}^{\prime }$ (solid line) and ${\text{G}}_{\text{i}}^{\prime }$ (dashed line). Note that the half-time for the buildup of ${\text{G}}_{\text{i}}^{\prime }$ agrees well with the theoretical estimate but that the rise time for ${\text{G}}_{\text{s}}^{\prime }$ is longer than the theoretical estimate. This discrepancy indicates that the pseudo-steady-state hypothesis applied to [HR_sG_s] is probably not valid on this time scale.

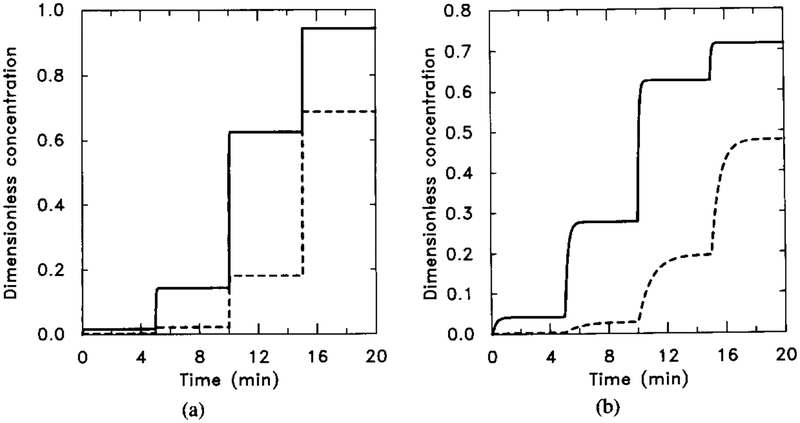
If the steady-state response for a certain level of stimulus is independent of the stimulus history, then we say that the system exhibits steady-state additivity. This property is illustrated in Figure 6, where we show the response to a sequence of lo-fold increases in the stimulus. Comparison of Figures 5 and 6 shows that the steady-state response to a single step to H = 0.1 μM is the same as the response to a multistep stimulus ending at the same level, but the time-dependent portions of the responses are completely different.

FIG. 6.

The response of the uncoupled system to sequential increases of the stimulus. The sequence is [H] = 0.001 μM for t ∈ (0, 5); [H] = 0.001 μM for t ∈ (5, 10); [H] = 0.1 μM for t ∈ (10, 15); and [H] = 1.0 μM for t ∈ (15, 20). (a) The dimensionless concentrations of HR_s (solid line) and HR_i (dashed line). (b) The dimensionless concentrations of ${\text{G}}_{\text{s}}^{\prime }$ (solid line) and ${\text{G}}_{\text{i}}^{\prime }$ (dahsed line).

The numerical responses for [HR_s], [HR_i], $\left[{\text{G}}_{\text{s}}^{\prime }\right]$, and $\left[{\text{G}}_{\text{i}}^{\prime }\right]$ are consistent with the results obtained from the qualitative analysis, which justifies the approximations we made in the previous section. We shall see later that [HR_s] changes significantly in the coupled system compared to the uncoupled system, while [HR_i] and ${\left[{\text{G}}_{\text{i}}^{\prime }\right]}^{*}$, which is the combined amount of $\left[{\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }\right]$ and $\left[{\text{G}}_{\text{i}}^{\prime }\right]$, change very little.

5.2. THE DYNAMICS OF THE COUPLED SYSTEM: EXPERIMENTAL AND NUMERICAL

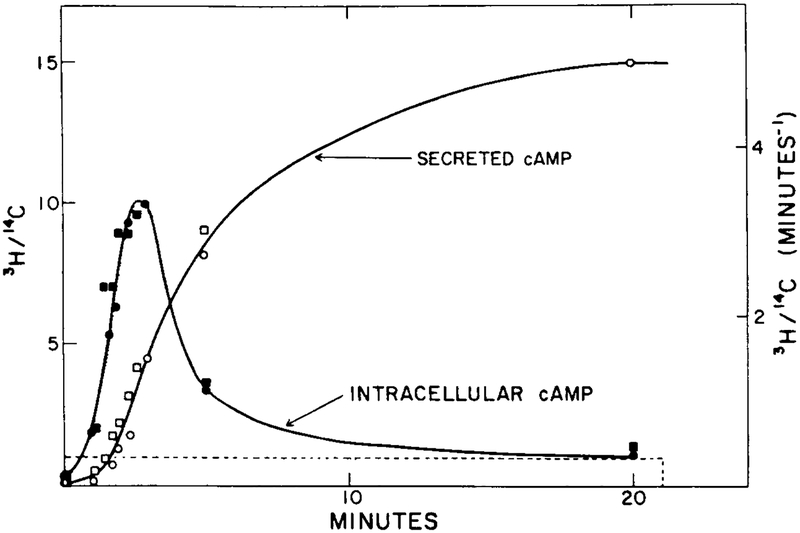
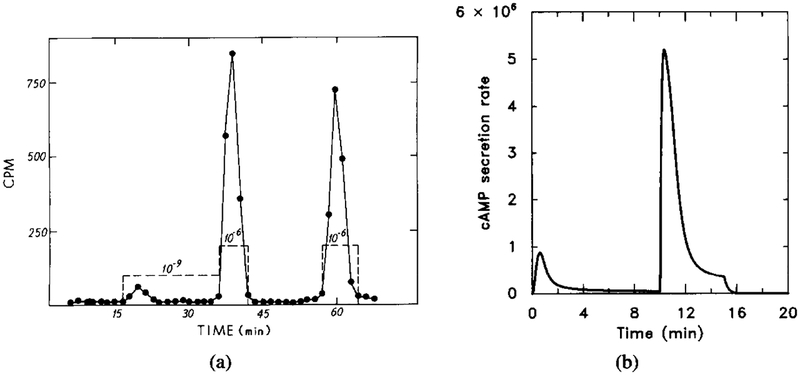
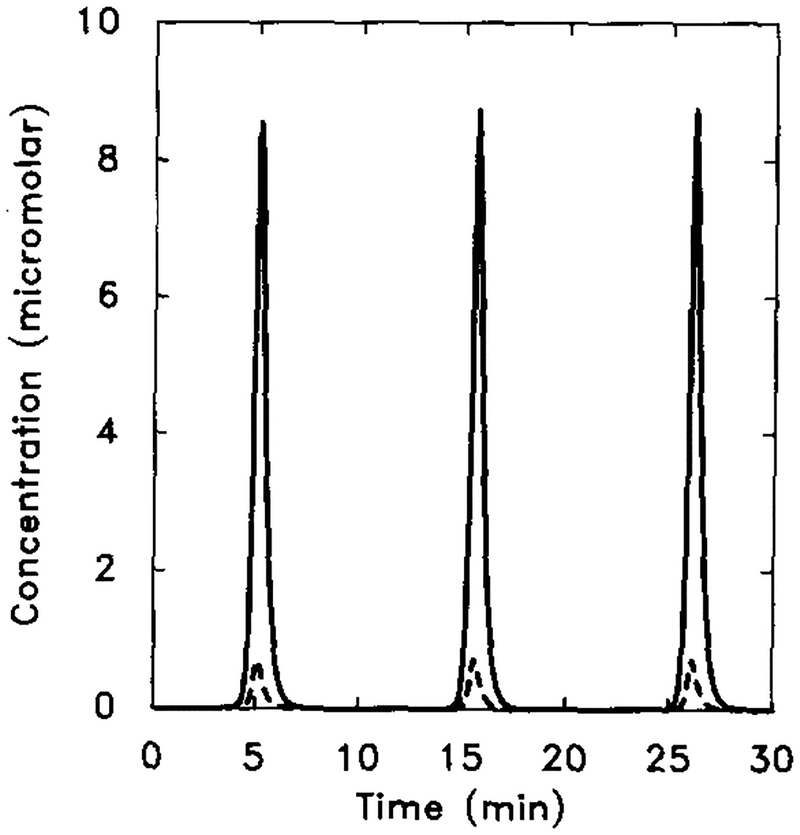
The perfusion experiments done by Devreotes and coworkers [10, 13] provide a benchmark against which an adaptation model can be tested. The result of a typical experiment is shown in Figure 7. Note that the secretion rate does not adapt perfectly in this experiment.

FIG. 7.

The experimental response of cAMP secretion to a single prolonged stimulus of 10⁻⁶ M extracellular cAMP (from [11]). The stimulus is a 20-min step function of 1 μM magnitude (dashed line). Two experimental results (circles and squares) are shown here for intracellular cAMP concentration (filled symbols) and cAMP secretion (open symbols).

The predicted cAMP secretion rate in response to the same stimulus is shown in Figure 8, where it is seen that the model also predicts incomplete adaptation. Note also that the predicted secretion rate peaks more rapidly for the estimated parameters than does the observed rate. The time to peak could be increased by decreasing either k₁ or k₄

FIG. 8.

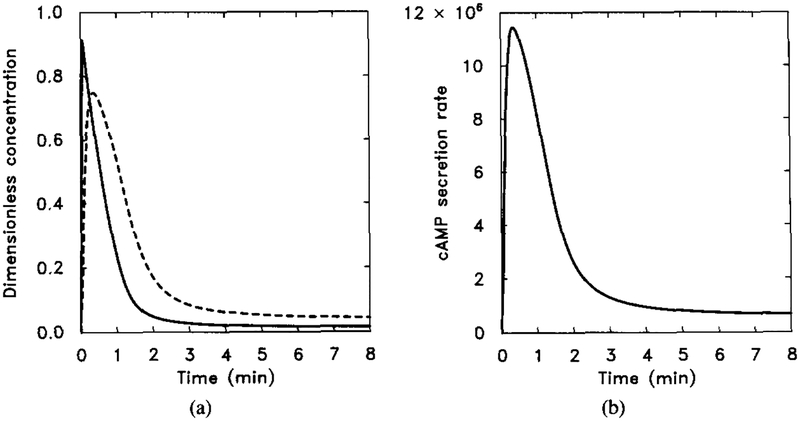
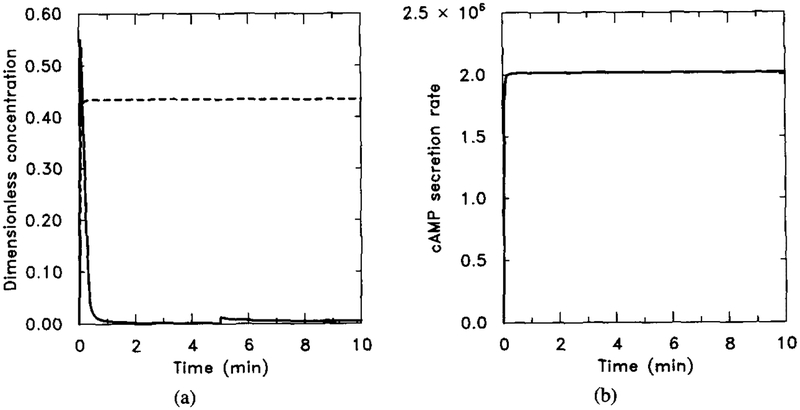
The response of the model to a prolonged stimulus of 10⁻⁶ M extracellular cAMP. The stimulus is [H] = 1.0 μM from t = 0 to t = 8 min. (a) The dimensionless concentrations of HR_s (solid line) and cAMP_i/10 (dashed line). (b) The dimensional secretion rate of cAMP_i in molecules per cell per minute. Compare with Figure 7 for experimental data.

The rapid buildup and decrease of [HR_s] shown in Figure 8a illustrates the fact that adaptation to a constant stimulus occurs at the receptor level. Since the time scale of [HR_s] is fast compared to the activation of G_s and adenylate cyclase, one can regard the signal carried by [HR_s] as a δ function with a certain magnitude that depends on the stimulus levels. That is, the interaction of the stimulatory and inhibitory pathways generates a signal like a δ function. If the signal transduction from G_s to adenylate cyclase can be approximately treated as a linear amplification process, then the response to this δ-function input would give the transient response of this process in a control-theoretic sense. However, the biochemical processes involved are not linear, but one should note that the response still has the shape of a first-order transient function.

As the stimulus level increases, the maximum secretion rate increases as well as the steady-state unadapted portion. Even at the largest stimulus level, the unadapted portion is less than 5% of the maximum rate. The parameter that has the strongest effect on the unadapted fraction is h₄. A five-fold increase in h₄ will decrease the unadapted fraction to an insignificant level at all the stimulus levels.

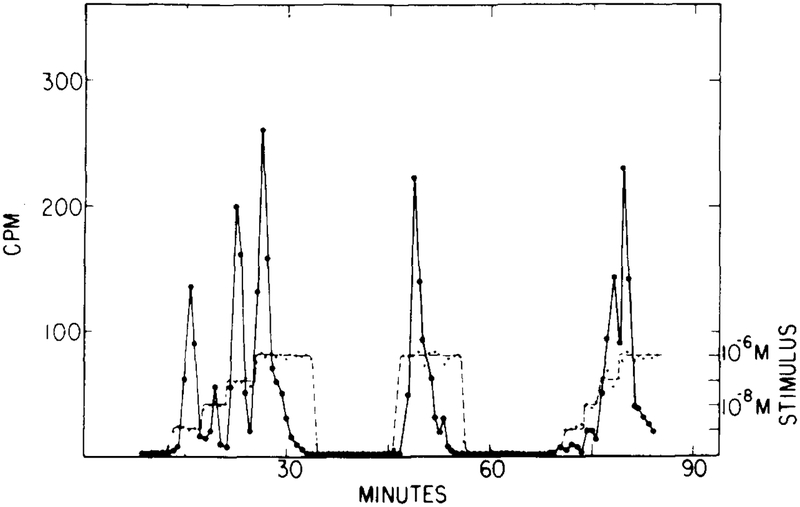
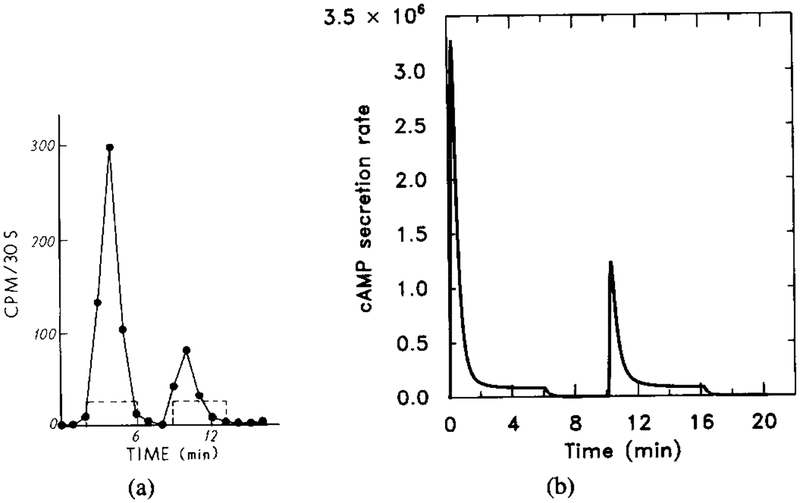
Figure 9 shows the response for a stimulus sequence of four steps, beginning with a step from 0 to 10⁻⁹, followed by three 10-fold increases.

FIG. 9.

The experimentally observed cAMP secretion in response to a multistep stimulus. The first step is from 0 to 10⁻⁹ M, and this is followed by three 10-fold increases. (Adapted from [9].)

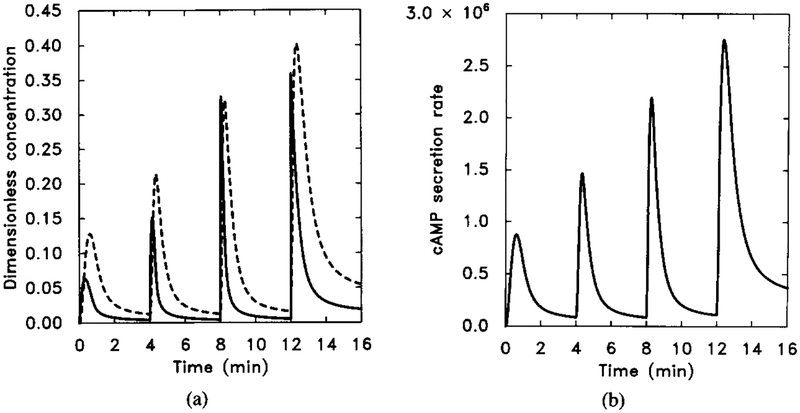
The computational results, using the parameters estimated in the Appendix, are shown in Figure 10. One sees that the response to the initial 10⁻⁹ M signal is too small compared to the experimental data. In order to get a significant initial response to a stimulus of 10⁻⁹ M, we changed the value of k₋₁ to 0.075, which is still in the range of the experimental values.

FIG. 10.

The numerical response of the system using the measured k₋₁. Starting at t = 0 min, extracellular cAMP was increased from 0 to 10⁻⁹ M and then to 10⁻⁶ M in three 10-fold steps of 4 min duration. Dimensional parameter values are given in Table 4. The dimensionless concentrations of HR_s (solid line) and cAMP_i/10 (dashed line).

Figure 11 shows the response, and one can see that now it is very similar to the experimental data. Hereafter we will use this value, with other parameters unchanged, for the numerical experiments. A similar result can be obtained by slowing the rise of ${\text{G}}_{\text{i}}^{\prime }$ somewhat.

FIG. 11.

The numerical response to sequential 10-fold increases of stimuli with k₋₁ in Table 4 changed from 0.45 to 0.075. Other parameter values are unchanged. The stimulus is the same as in Figure 10. (a) The dimensionless concentrations of HR_s (solid line) and cAMP_i/10 (dashed line). (b) The dimensional secretion rate of cAMP_i (molecules per cell per minute). Compare with Figure 9 for experimental data.

In Figure 9 the response to the second step of the stimulus sequence H = 10⁻⁸ M is small compared to the responses to other stimulus levels. This can be reproduced in the model by speeding up the response of the inhibitory channel. For example, by increasing h₂ and h₅ by a factor of 3, one obtains a response very similar to that shown in Figure 9.

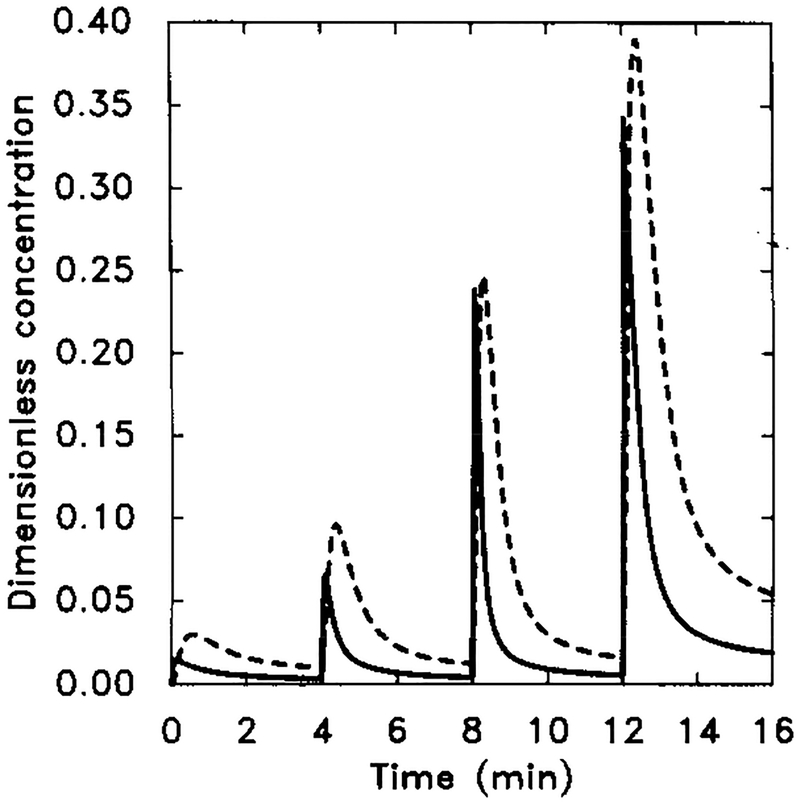
The simulations for a variety of stimuli are satisfactory using the parameter values given in Table 4, provided that k₁ is changed as above. This includes the response to a two-step sequential increase (Figure 12) and the two-step short time step stimulus (Figure 13). Experimental results and the simulation response curves are given here.

FIG. 12.

The experimental and model response to a two-step sequential stimulus. Note that after removal of the stimulus the unadapted portion decays very rapidly. The parameter value are the same as in Figure 11. The stimulus sequence is [H] = 10⁻⁹ M for t = 0 to t = 10, [H] = 10⁻⁶ M for t = 10 to t = 15, and [H] = 0 M for t = 15 to t = 20. (a) The experimentally observed response (adapted from [9]). (b) The dimensional secretion rate of cAMP_i in molecules per cell per minute.

FIG. 13.

The experimental and numerical response to short two-step stimuli. The time course of the extracellular cAMP stimulus is 10⁻⁸ M (t = 0–6), 0 M (t = 6–10), 10⁻⁸ M (t = 10–16), and 0 M (t = 16–20). This experiment probes the time course of deadaptation, because the magnitude of the response to the second stimulus depends upon the degree to which the cells have recovered from the first stimulus. Parameter values are the same in Figure 11. (a) Experimental results (adapted from [11]). (b) The dimensional secretion rate of cAMP_i (molecules per cell per minute). The response to the second signal of the same magnitude is much smaller because ${\text{G}}_{\text{i}}^{\prime }$ has not decayed completely. The magnitude of the second response increases with the elapsed time since the preceding signal.

We conclude that the model can explain adaptation at the transduction level, using parameter estimates based on experimental observations in Dd and mammalian systems. In the following section we show that the model can also reproduce the observed oscillations in suspensions.

6. SIMULATION OF SUSPENSION EXPERIMENTS

Thus far we have only dealt with the modeling of perfusion experiments, in which case the extracellular cAMP is a specified function of time. As we have demonstrated elsewhere [32, 33], the dynamics of other experimental configurations can also be described with perhaps changes in one or two parameters, once the input–output behavior of the cells is accurately described by a model. In this section we demonstrate this for the present model by analyzing the dynamics of suspensions. A detailed discussion of suspension experiments is given in [32].

6.1. SUSPENSION EXPERIMENTS AND A MATHEMATICAL MODEL

To describe the suspensions, we only have to append reactions for the extracellular dynamics and equations for the evolution of extracellular cAMP. The additional reactions arise from the presence of the extracellular enzymes.

$$\begin{gathered} {\text{cAMP}}_o+\text{mPDE}\underset{l_{-6}}{\overset{l_6}{\rightleftharpoons }}{\text{cAMP}}_o-\text{mPDE} \\ {\text{cAMP}}_o-\text{mPDE}\stackrel{l_7}{\to }\text{AMP} \\ {\text{cAMP}}_o+\text{ePDE}\underset{l_{-8}}{\overset{l_8}{\rightleftharpoons }}{\text{cAMP}}_o-\text{ePDE} \\ {\text{cAMP}}_o-\text{ePDE}\stackrel{l_9}{\to }\text{AMP} \end{gathered}$$ (26)

Here cAMP_o denotes extracellular cAMP, mPDE denotes membrane-bound phosphodiesterase, cAMP_o–mPDE denotes the complex between cAMP and mPDE on the extracellular membrane, ePDE denotes the extracellular phosphodiesterase in solution, and cAMP_o–ePDE denotes the ePDE–cAMP_o complex in the extracellular solution. Notice that cAMP_o, is different from H and ${\text{cAMP}}_o^{*}$.

The additional differential equations are

$$\begin{gathered} V_o\frac{d{y}_{14}}{dt}=N{V}_c{l}_5{y}_{12}+N{A}_c{l}_{-6}{y}_{15}+V_o{l}_{-8}{y}_{16}-N{A}_c{l}_6{y}_{14}{z}_8-N{V}_c{l}_8{y}_{14}{z}_9 \\ \frac{d{y}_{15}}{dt}=-\left(l_{-6}+l_7\right)y_{15}+l_6{y}_{14}{z}_8 \\ \frac{d{y}_{16}}{dt}=-\left(l_{-8}+l_9\right)y_{16}+l_8{y}_{14}{z}_9. \end{gathered}$$ (27)

Here N denotes the total number of cells, V_o denotes the extracellular volume, and A_c(V_c) denote the area (volume) per cell. In addition, y₁₄ stands for [cAMP_o], y₁₅ for [mPDE–cAMP_o,], y₁₆ for [ePDE–cAMP_o], z₈ for free [mPDE], and z₉ for the free [ePDE]. In addition, there are two other conservation equations:

$$y_{15}+z_8={\left[\text{mPDE}\right]}_T,y_{16}+z_9={\left[\text{ePDE}\right]}_T.$$ (28)

The newly introduced variables y₁₅ + y₁₆ are both positive and bounded. In fact, we have

$$0⩽y_{15}⩽{\left[\text{mPDE}\right]}_T,0⩽y_{16}⩽{\left[\text{ePDE}\right]}_T.$$

It follows from this that y14 is also bounded.

By scaling the new independent variables and introducing additional nondimensional parameters, we obtain a nondimensionalized system for the u_i and v_i. Most of the equations are the same as in Section 7. The newly introduced dimensionless parameters and singular variables are listed in Table 12. We use the same scaling for y₁₄ as $y_{14}^{*}$, u₈ = y₁₄/[iPDE]_T.

TABLE 12.

Additional Dimensionless Variables and Parameters

Parameters	Parameters	Variables
${\alpha }_0=\frac{k_1{\left[\text{iPDE}\right]}_T}{k_5}$	${\gamma }_8=\frac{l_{-8}+l_9}{l_8{\left[\text{iPDE}\right]}_T}$	$v_7=\frac{\left(l_{-6}+l_7\right)y_{15}}{l_6{\left[\text{iPDE}\right]}_T{\left[\text{mPDE}\right]}_T}$
${\beta }_0=\frac{h_1{\left[\text{iPDE}\right]}_T}{k_5}$	${\gamma }_9=\frac{l_9{\left[\text{ePDE}\right]}_T}{k_5{\left[\text{iPDE}\right]}_T}$	$v_8=\frac{\left(l_{-8}+l_9\right)y_{16}}{l_8{\left[\text{iPDE}\right]}_T{\left[\text{ePDE}\right]}_T}$
${\gamma }_6=\frac{\left(l_{-6}+l_7\right)}{l_6{\left[iPDE\right]}_T}$	${ϵ}_7=\frac{k_5}{\left(l_{-6}+l_7\right)}$
${\gamma }_7=\frac{l_7{\left[mPDE\right]}_T{A}_c}{k_5{\left[iPDE\right]}_T{V}_c}$	${ϵ}_8=\frac{k_5}{\left(l_{-8}+l_9\right)}$

The newly introduced singular differential equations are

$$\begin{gathered} {ϵ}_7\frac{d{v}_7}{d\tau }=u_8-v_7-\frac{1}{{\gamma }_6}{u}_8{v}_7, \\ {ϵ}_8\frac{d{v}_8}{d\tau }=u_8-v_8-\frac{1}{{\gamma }_8}{u}_8{v}_8. \end{gathered}$$ (29)

As before, we set the time derivatives for the singular variables equal to zero, solve the resulting system, and use the results in the equatidns for the nonsingular variables. The result is that the new nonsingular variables satisfy the following system.

$$\begin{gathered} \frac{d{u}_1}{d\tau }={\alpha }_0{u}_8-\left({\alpha }_0{u}_8+{\alpha }_1\right)u_1+\left({\beta }_5-{\alpha }_0{u}_8\right)u_6-{\beta }_4{u}_1{u}_5, \\ \frac{d{u}_4}{d\tau }={\beta }_0{u}_8-\left({\beta }_0{u}_8+{\beta }_1\right)u_4, \\ \frac{d{u}_8}{d\tau }=\frac{\rho }{1-\rho }\left[{\gamma }_5{u}_7-\frac{{\gamma }_7{u}_8}{u_8+{\gamma }_6}-\frac{{\gamma }_9{u}_8}{u_8+{\gamma }_9}\right] \end{gathered}$$ (30)

Here ρ is the ratio of cell volume to the total volume in an experiment, that is,

$$\rho =N{V}_c/\left(N{V}_c+V_o\right).$$

Using the parameter values given in the Appendix, we obtain the values for the dimensionless parameters given in Table 13.

TABLE 13.

Estimated Values for the New Dimensionless Parameters

α0 = 208.0	γ6 = 2.9	γ8= 4607	ρ = 0.14
β0 = 61.0	γ7 = 225.4	γ9 = 659.3

6.2. NUMERICAL SIMULATION OF SUSPENSION EXPERIMENTS

We have tested the model numerically both for the scaled system and the unscaled system. As is expected from the singular perturbation analysis, the simplified system approximates the original system very well.

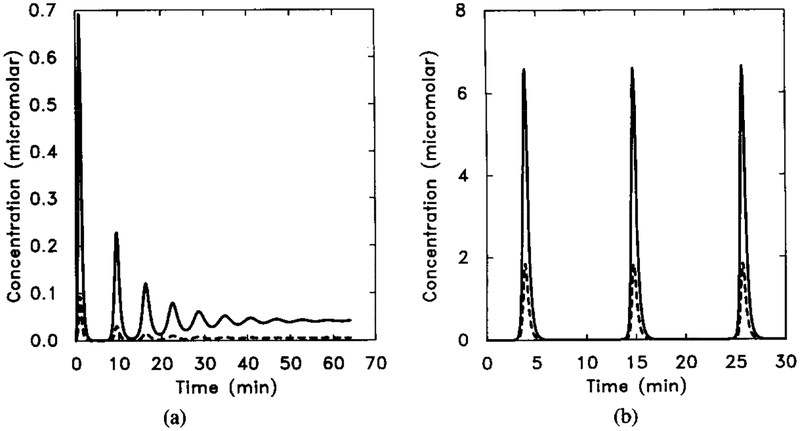
There are three types of qualitatively distinct dynamics in suspensions, depending on the parameter values chosen: (1) adaptation without oscillation, (2) decaying oscillations, and (3) stable oscillations. A typical response curve for each of the last two types is shown in Figure 14.

FIG. 14.

The dimensionless [cAMP_i] as a function of time, illustrating decaying oscillations. Parameter values are taken from Tables 8 and 13. The initial stimulus is [H] = 10⁻⁸ M. In this figure we scale both γ₂ and γ₅ by a factor f. Here γ₂ = f × 0.048, and γ₅ = f × 0.224, with f = 5.0. (b) A stable oscillation for f = 10.0. Shown are the dimensional intracellular cAMP concentration [cAMP_i] (solid line) and 10 times the extracellular cAMP concentration [cAMP_o] (dashed line).

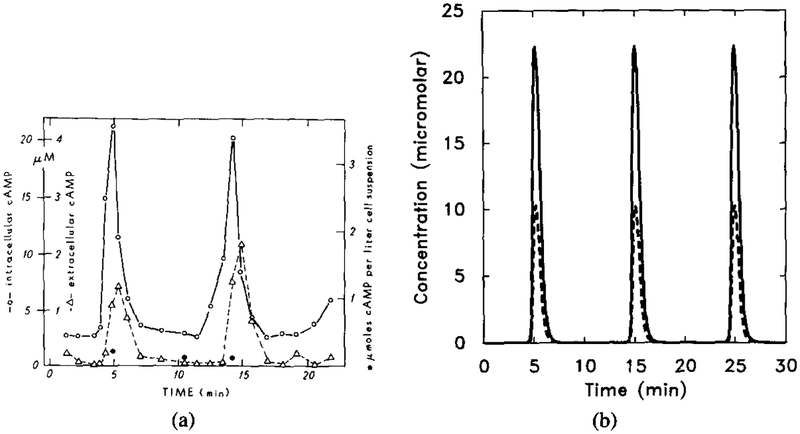
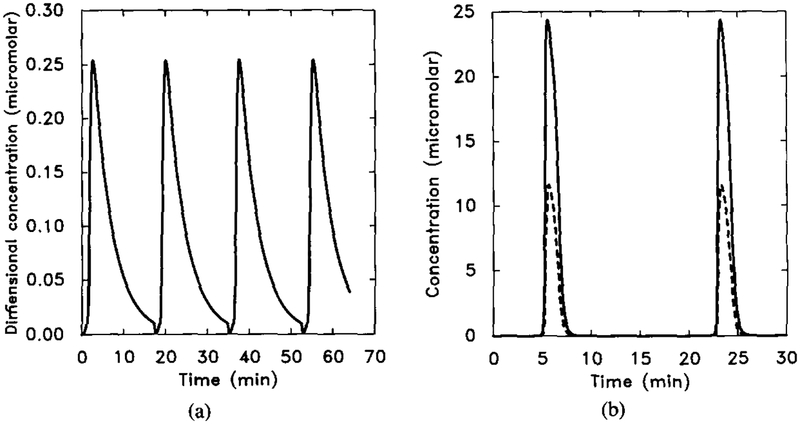
Since there are many parameters involved in the system, a complete demarcation of parameter space according to the type of response is difficult to obtain. However, if we keep certain variables fixed and let only one variable change, we can do a bifurcation analysis. Bifurcation analysis with respect to certain parameters that are known to change in different developmental stages (such as total amount of adenylate cyclase and the cAMP secretion rate) gives insight into how the dynamics change with the developmental stage. The results of this type of analysis were given in [32]. Here we simply illustrate that the experimentally observed oscillations can be reproduced with the model. Figure 15 shows (a) the experimental results and (b) the numerical results. One sees that the latter correspond well with the experimental data in both magnitude and frequency.

FIG. 15.

The experimental results for oscillations in suspensions and the corresponding numerical results. Parameter values are the same as in Figure 14 except f = 25.0. (a) Experimental measurements of intracellular (◯) and extracellular (Δ). Redrawn from Figure 2 of Gerisch and Wick [20]. (b) Dimensional intracellular cAMP concentration [cAMP_i] (solid line) and five times the extracellular cAMP concentration [cAMP_o] (dashed line).

The peak amplitude of the extracellular cAMP is very sensitive to the amount and the turnover rate of adenylate cyclase and to the activity of iPDE and mPDE. Figure 16 shows how a change of the values of mPDE and γ5 changes the magnitude of the response.

FIG. 16.

The magnitude of oscillation is significantly influenced by the parameters reflecting the activities of AC, iPDE, and mPDE. Here γ₆ is decreased by a factor of 10 (γ₆ = 0.29) and other parameter values are the same as in Figure 15. Shown are the dimensional intracellular cAMP concentration [cAMP_i] (solid line) and 10 times the extracellular cAMP concentration [cAMP_o] (dashed line).

On the other hand, the frequency of the oscillation is very sensitive to β2 ≡ h₂[G_i]_T/k₅ and β₅ = h₅/k₅. Figure 17 shows how the frequency can be changed by proportional changes in β₂ and β₅, which determine the slowest process in the system (see Appendix for the explanation).

FIG. 17.

An illustration of how changes in β₂ and β₅ significantly change the oscillation frequency. Here β₂ and β₅ are divided by a factor of 2. Other parameter values are the same as in Figure 15. Compare with Figure 15. (a) The dimensionless concentration of ${\text{G}}_{\text{i}}^{\prime }$. (b) Five times the intracellular cAMP concentration [cAMP_i] (solid line) and the extracellular cAMP concentration [cAMP_o] (dashed line).

7. EXPERIMENTAL TESTS OF THE MODEL

7.1. PROPOSED EXPERIMENTS

In this section we propose several experiments that can be used to test the model, and we describe the predictions made by the model for these experiments.

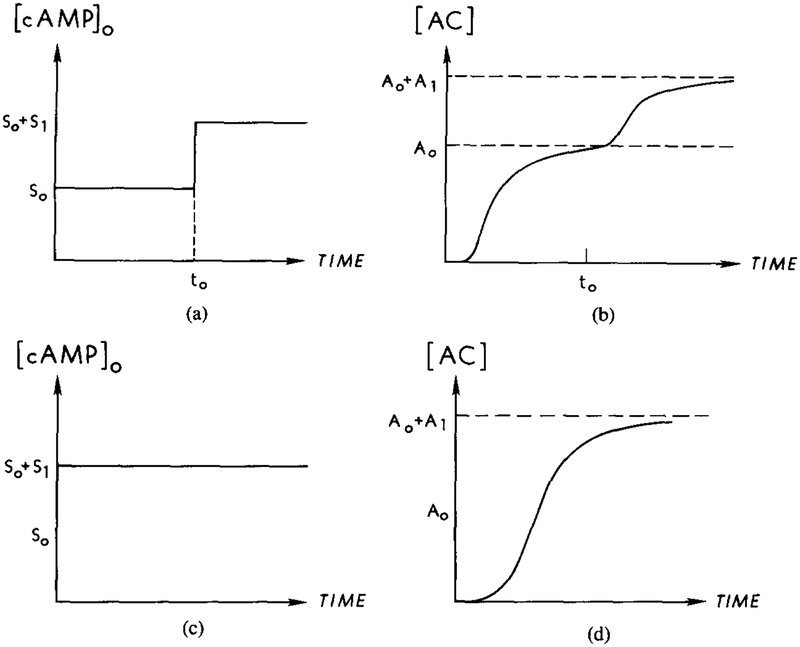
The effect of cholera toxin on adaptation of the relay response in Dictyostelium discoideum has not yet been reported. However, if we assume that cholera toxin acts on the G_s of Dd in the same way it acts on G_s in other cells, then it will block hydrolysis of activated G_s. When the agonist and antagonist are different, as in many other systems, the result of exposure to cholera toxin is that all of the UC is eventually converted into AC in the presence of a prolonged agonist signal. However, in Dd the agonist and antagonist are the same, and thus both signals arrive at the same time. As a result, in our model most of the HR_s complex is split rapidly, and only a small amount of adenylate cyclase is activated in a short time. Thus a small stimulus cannot turn on all the adenylate cyclase in a short time, and a further increase in the stimulus will cause a further increase in the AC activity. An interesting prediction of our model under cholera toxin treatment is the following.

Suppose that the external cAMP concentration is held at S₀ until time T₀ and that the amount of AC turned on is A₀ (see Figure 18). Next increase the external cAMP concentration by S₁ and hold it until T₁, and suppose that the corresponding increase of AC is A₁. Then the model predicts that for an external cAMP concentration of S₀ + S₁, the corresponding amount of adenylate cyclase that is activated for times of the order of T₁ will be A₀ + A₁, that is, the amount of AC activated is additive in a quasi-steady state. Since adaptation is not complete, the presence of some unadapted HR_s will eventually activate all the AC. However, the increase in AC activity due to the residual HR_s is slow, and the additivity should be observable on the experimental time scale. This prediction can be used to check our model.

FIG. 18.

The steady-state additivity of cAMP production in the response to an extracellular cAMP signal, predicted for cholera toxin–treated cells. The steady-state concentration should depend only on the final stage of extracellular stimulus and not on the stimulus history. (a) A two-step stimulus of magnitude from S₀ to S₀ + S₁. (b) The corresponding response of activated adenylate cyclase to the stimulus in (a). The steady-state concentration should be from A₀ to A₀ + A₁. (c) A single-step stimulus of magnitude S₀ + S₁. (d) The corresponding response of activated adenylate cyclase to the stimulus in (c).

Since we do not know whether cholera toxin interacts with G_s in Dd, we propose another experiment to check this model. If we use a nonhydrolyzable substitute such as GTPγS or Gpp[NH]p for GTP, activated AC will not be deactivated, just as in the case of cholera toxin treatment. On the other hand, the signal is also changed in the inhibitory pathway. A prolonged stimulus will result in the complete activation of G_i, and this will turn off further activation of AC. The pseudo-steady-state concentrations of ${\text{G}}_{\text{s}}^{\prime }$ and AC will be proportional to the stimulus level and will not decay.

The essential difference between the response of cholera toxin-treated cells and cells treated with GTPγS is in the response to a second cAMP signal of higher concentration. While the cholera toxin-treated cell should have the property of semiadditivity on a short time scale, the cells treated with GTPγS should have no response to the sequential increase of stimulus. Very little of the second stimulus will pass the receptor level, since most of the G_i is activated by the first signal. The newly generated population of HR_s will rapidly be bound with α_i-GTPγS and thus will not catalyze the transition from G_s to ${\text{G}}_{\text{s}}^{\prime }$. When Gpp[NY]p is used instead of GTPγS the time course of the response will be essentially the same, but there will be a slight decrease in the magnitude of the response because the affinity of α_i and α_s for Gpp[NH]p is not as high.

These two tests are not able to distinguish between our model and a model with direct inhibitory interaction between ${\text{G}}_{\text{i}}^{\prime }$ and ${\text{G}}_{\text{s}}^{\prime }-\text{AC}$. Both predict the same type of response for the two experiments. However, there is an experiment that can rule out the possibility of a direct interaction model, and this hinges on the possibility of measuring the activated ${\text{G}}_{\text{s}}^{\prime }$ concentration.

In the direct interaction inhibition model, the fraction of G_s activated will remain large under a constant stimulus. On the other hand, if adaptation occurs at the receptor level, as in our model, then after an initial burst following a step change in the stimulus, the fraction of G_s will return to a low level fixed by the stimulus, If it is possible to measure the time course of ${\text{G}}_{\text{s}}^{\prime }$ in the membrane, then the two models can be distinguished.

In the next section, we report the detailed predictions made by the model for these experiments.

7.2. NUMERICAL OUTPUTS FOR THE EXPERIMENTS

The first numerical experiment we do concerns the pertussis toxin-treated cells. The effect of pertussis toxin is simulated by letting h₂ = 0, which means that G_i cannot be activated. The numerical simulation predicts a near-linear increase in the total amount of cAMP secreted. This differs from the experimental result in [39]. The decrease in the cAMP secretion rate in the experiment results from the phosphorylation of receptors, which is not included in our model.

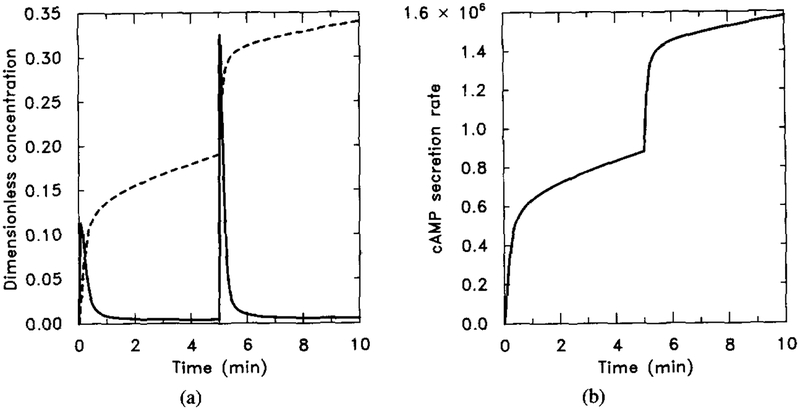
To simulate the effect of treatment with cholera toxin, we let k₅ = 0. Notice that here we cannot use the scaled system for the numerical experiment, because in that system k₅ is used to scale the time. The numerical output from the nonscaled system (5)–(8) is shown in Figure 19. The figure should be compared with Figure 18 to check the steady-state additivity property in this experiment. Notice that in Figure 18a, adaptation does occur at receptor level, but ${\text{G}}_{\text{s}}^{\prime }$ does not decay.

FIG. 19.

The effect of cholera toxin as predicted by the model. The result should be compared with Figure 18 to see the steady-state additivity. Parameter values are given in Table 4 with k₅ = 0 to mimic the effect of cholera toxin. The stimulus is 10⁻⁸ M for t ∈ (0, 5) and 10⁻⁷ M for t ∈ (5, 10). (a) Dimensionless concentrations of HR_s (solid line) and cAMP_i/10 (dashed line). (b) Dimensional secretion rate of cAMP_i (molecules per cell per minute).

If GTPγS is used instead of GTP, then both ${\text{G}}_{\text{s}}^{\prime }$ and ${\text{G}}_{\text{i}}^{\prime }$ are nonhydrolyzable. We mimic this by letting k₅ = h₅ = 0. The numerical output is shown in Figure 20. We see here that the first signal (H = 0.1 μM) can turn on almost all the ${\text{G}}_{\text{i}}^{\prime }$ after a certain time. The high level of ${\text{G}}_{\text{i}}^{\prime }$ blocks the response of the system to the second stimulus (H = 1 μM). The small increase in internal cAMP concentration and the increased secretion rate are due to the unadapted portion of HR_s, which is very small.

FIG. 20.

Numerical output for the experiment when GTP is replaced by GTPγS. The parameter values are the same as in Figure 19 with h₅ = 0 to simulate the fact that α_i-GTPγS is also nonhydrolyzable. The stimulus is 10⁻⁸ M for t ∈ (0, 5) and 10⁻⁷ M for t ∈ (5, 10). (a) Dimensionless concentrations of HR_s (solid line) and cAMP_i/10 (dashed line). (b) Dimensional secretion rate of cAMP_i (molecules per cell per minute). (b) should be compared with (b) in Figure 19.

8. CONCLUSIONS

We have developed a model for adaptation of the relay response in Dictyostelium discoideum and have shown that it can reproduce the experimental results available for perfusion and suspension experiments. As in the Monk-Othmer model, this has been done using the same parameters to model both perfusion and suspension experiments, except for those that are known to vary with developmental age. It was shown in [32], [33] that several modifications to the basic model presented there, such as the inclusion of time delays in the stimulus and adaptation pathways, do not alter the general conclusions reached, and the same conclusion undoubtedly applies here, although we have not checked this in detail. Certain aspects, such as the rise time of the production and secretion of cAMP, could be improved by tuning the parameters, but that is of secondary importance.

As we mentioned in Section 2.2, another possible mechanism for adaptation is based on direct interaction between ${\text{G}}_{\text{i}}^{\prime }$ and ${\text{G}}_{\text{s}}^{\prime }\text{AC}$. This would require a second G_i protein binding site on adenylate cyclase, such that when it is occupied with ${\text{G}}_{\text{i}}^{\prime }$ the activity of the cyclase is essentially zero. A kinetic scheme for this mechanism is as follows.

$$\begin{gathered} {\text{G}}_{\text{s}}^{\prime }+\text{UC}\rightleftharpoons {\text{G}}_{\text{s}}^{\prime }\text{AC} \\ {\text{G}}_{\text{s}}^{\prime }\text{AC}+{\text{G}}_{\text{i}}^{\prime }\to {\text{G}}_{\text{s}}^{\prime }\text{AC}-{\text{G}}_{\text{i}}^{\prime } \\ {\text{G}}_{\text{s}}^{\prime }\text{AC}-{\text{G}}_{\text{i}}^{\prime }\to {\alpha }_{\text{s}}\text{GDP}+\text{UC}+{\text{G}}_{\text{i}}^{\prime } \\ {\text{G}}_{\text{s}}^{\prime }\text{AC}-{\text{G}}_{\text{i}}^{\prime }\to {\text{G}}_{\text{s}}^{\prime }\text{AC}+{\alpha }_{\text{i}}\text{GDP} \end{gathered}$$ (31)

Our numerical simulations indicate that an adaptation model based on this mechanism can also reproduce the experimental observations in perfusion experiments. We have not checked this for the suspension experiments, but past experience indicates that it will function properly in that context as well. A model based on direct interaction of ${\text{G}}_{\text{i}}^{\prime }$ with the cyclase is similar in spirit to the Monk-Othmer model, wherein calcium plays the inhibitory role and interacts directly with the cyclase.

At present one cannot discriminate on theoretical grounds between the direct inhibition model described in this section and the model proposed and analyzed in this paper. However, the fact that a ${\text{G}}_{\text{i}}^{\prime }$–cyclase complex has not been found in other systems favors the latter model. Energetic considerations also favor the latter model, since adaptation at the level of the cyclase entails approximately twice the consumption of GTP in the presence of a constant signal. However, the final determination of a model hinges on identifying the details of the biochemical pathways from extracellular signal to cyclase.

A number of other models for cyclic AMP control and synthesis in Dictyostelium have appeared, and these were reviewed in [32] and [33]. Models involving receptor modification are motivated by the experimental fact that cAMP induces phosphorylation of the cAMP receptors in Dd [24,25] and that this occurs on the same time scale as adaptation. Thus phosphorylation may be involved in adaptation, perhaps by interfering with the activation of a G_s protein. However, as we mentioned earlier, phosphorylation is not sufficient for adaptation, since pertussis toxin treatment blocks adaptation but does not interfere with receptor modification [40, 50]. This suggests that activation of a G_i protein is necessary for adaptation [42]. In this paper we developed a mechanism based on this and showed that it can produce the observed adaptation. We have not incorporated a role for phosphorylation, but this is easily done and would not alter the basic conclusions, since it simply introduces alternative pathways for the intermediates, and the same dynamics are as predicted by the present model can be obtained by retuning the rate constants.

The model presented in this paper concerns only the relay response. However, cyclic AMP stimuli also trigger a chemotactic response, and to model the cellular response more completely we would have to incorporate cyclic GMP and perhaps other species [48]. Such a model is presently under development.

APPENDIX

In this appendix, we estimate the model parameters.

A.1. REACTION KINETIC CONSTANTS

Two classes of cAMP binding sites have been identified in relay competent Dd cells, which are denoted as the A site and B site [50]. The total number of sites is approximately (5–10)×10⁴ per cell [18]. The B sites comprise only about 4% of all binding sites, and it is believed that they are involved in the cGMP and chemotaxis pathways. We take the upper value of 10⁵ receptors per cell for the total binding sites, that is, 9.6 × 10⁴ for A sites. Of the A sites, about 40% are fast dissociation with high affinity (K_d = 60 nM), and about 60% are fast dissociation with low affinity (K_d = 450 nM). It is reasonable to assume that the high-affinity receptors of the A site are R_s and the low affinity ones are R_i, since usually G_i > G_s. The values of the binding and dissociation constants for the two receptor types are estimated as

$$\begin{gathered} k_1=7.5{\text{s}}^{-1}\mu {\text{M}}^{-1},k_{-1}=0.45{\text{s}}^{-1} \\ {h}_1=2.2{\text{s}}^{-1}\mu {\text{M}}^{-1}{h}_{-1}=1.0{\text{s}}^{-1} \end{gathered}$$

in [49].

Data on the rate of activation of G_s are reported in terms of the rate constant

$$k_{\text{on}}\equiv \frac{k_2{k}_3}{k_{-2}+k_3}\left[{\text{HR}}_{\text{s}}\right].$$

Levitzki [29] reported that k_on is in the range of 0.5–1.5 min⁻¹ for mammalian cells. Freissmuth et al. [19] reported a higher k_on, with a minimum of 2 min⁻¹. The latter estimate is more compatible with the observed rates of cAMP secretion in Dd (the secreted cAMP reaches its peak at about 1.5 min). There is no measurement of k_on reported for Dd, so we will take the value of k_on = 2.5 min⁻¹ = 0.0167 s⁻¹. Since

$$k_{\text{on}}=\frac{k_2{k}_3}{k_{-2}+k_3}\left[{\text{HR}}_{\text{s}}\right]=\frac{k_2{k}_3}{k_{-2}+k_3}\left(\frac{[\text{H}]{\left[{\text{R}}_{\text{s}}\right]}_T}{[\text{H}]+{\left[{\text{R}}_{\text{s}}\right]}_T}\right),$$

the value of k_on depends on the stimulus level. From this estimate for k_on we have to estimate k₂, k₋₂, and k₃. If we assume an intermediate stimulus level of [H] ~ 10⁻² μM, we have [HR_s]/[R_s]_T ~ 0.1, and therefore

$$\frac{k_{\text{on}}}{{\left[{\text{R}}_{\text{s}}\right]}_T}=\frac{0.1k_2{k}_3}{k_{-2}+k_3}.$$

The value for k₃ is reported as 10⁴ s⁻¹ in [19]. We still cannot obtain both k₂ and k₋₂, and therefore we assume that k₋₂ ≪ k₃. This means that the rate of dissociation of HR_sG_s is small compared with the rate of production of ${\text{G}}_{\text{s}}^{\prime }$, and with this assumption we obtain

$$k_2=10k_{\text{on}}/{\left[{\text{R}}_{\text{s}}\right]}_T=1000.0{\text{m}}^2/(\mu \text{mol}\cdot \text{s}).$$

The analysis for the estimation of h₂, h₋₂, and h₃ is very similar to that of h₂, h₋₂, h₃ but here there is no reported value of h_on. We can, however, use the cAMP secretion to estimate these kinetic constants. A typical value for the peak value of cAMP secretion is t^peak ~ 1.5 min, and we assume that the half-time of the inhibitory signal is

$$t_{0.5}^i=1.5t^{\text{peak}}=1.5\times 1.5=2.25\text{min}.$$

Knowing $t_{0.5}^i$, we can get an estimate of h_on from the dynamics of this pathway. Under the assumption of a pseudo-steady state, we have

$$h_{\text{on}}=(\text{ln}2)/t_{0.5}^i=5.13\times {10}^{-3}{\text{s}}^{-1}.$$

If we assume that the stimulus level to yield this value of h_on is [HR_i]/[R_i]_T ~ 0.5, then we can get an estimate for h₂, h₋₂, and h₃ in the same way as previously. The result is that

$$h_2=\frac{1}{0.5}\left(\frac{0.01}{{\left[{\text{R}}_{\text{i}}\right]}_T}\right)=40{\text{m}}^2/(\mu \text{mol}\cdot \text{s}),$$

h₋₂ = 0 s⁻¹, and h₃ = 400 s⁻¹.

Next we set k₄ and h₄. Based on the observation that the rate of production of cAMP is first-order in the receptor concentration, Levitzki argued that G_s is precoupled to the inactivated adenylate cyclase [27]. However, as we noted in the text, there is evidence that suggests that G_s shuttles between HR_s and adenylate cyclase. Whichever is correct, it is safe to assume, in the absence of Dd–specific information, that k₄ is large, and we use the value k₄ = 1 × 10⁴ m²/(μmol·s) for the numerical computations. For the same reasons we can assume that h₄ is very large, that is, that the affinity of ${\text{G}}_{\text{i}}^{\prime }$ to HR_s is very high, and in the numerical experiments we use k₄ = 5 × 10⁵ m²/(μmol·s).

There is uncertainty concerning the rate of hydrolysis of the activated G_s protein as well. Levitzki reports that k_off (≡ k₅) is in the range of 13–15 min⁻¹ [28], but Casey and Gilman [7] report a value of k_off of around 3 min⁻¹. For the numerical computations we use the value k₅ = 3.75 min⁻¹ = 0.0625 s⁻¹.

The rate of decay of ${\text{G}}_{\text{i}}^{\prime }$ is the slowest step involved in the oscillations in suspension experiments. Restimulation can only occur after ${\text{G}}_{\text{i}}^{\prime }$ has decayed to a low-level, which means that the period of the oscillations depends strongly on h_off. If we assume that the external cAMP is suddenly withdrawn from the extracellular medium, it will take about 4 half-lives of ${\text{G}}_{\text{i}}^{\prime }$ to degrade ~ 95% of existing ${\text{G}}_{\text{i}}^{\prime }$. However, extracellular cAMP is degraded only gradually by ePDE and mPDE, and thus the actual time for sufficient degradation of ${\text{G}}_{\text{i}}^{\prime }$ may be severalfold longer than if the signal is abruptly terminated. The observed time period for oscillation is about 10 min [38]. If we assume that the time is 1.5–1.75 times longer and note that

$$t^{0.5}=(\text{ln}2)/h_{\text{off}}$$

and

$$(1.5-1.75)\times 4\times t^{0.5}=10\text{min}=600\text{s,}$$

we find that

$$6.94\times {10}^{-3}{\text{s}}^{-1}<h_{\text{off}}<8.0\times {10}^{-3}{\text{s}}^{-1}.$$

We take a value of

$$h_{\text{off}}=h_5=7.5\times {10}^{-3}{\text{s}}^{-1}.$$

The rate of association between the βγ subunit and the hydrolyzed G proteins is set at

$$k_6=h_7={10}^5{\text{m}}^2/(\mu \text{moles}\cdot \text{s}).$$

This assumption is based on the known fact that α-GDP has a high affinity for βγ [21].

There is some experimental data that can be used for the estimation of h₆. van Haastert and de Wit [49] report that the high-affinity receptors are transformed to low-affinity receptors in the presence of prolonger stimuli. The interpretation of this in the context of our model is that ${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }$ has a much lower affinity for H then does R_s. There is no transformation between the two different binding sites R_s and R_i in our model; the transformation from high affinity to low affinity is due to the reaction

$${\text{HR}}_{\text{s}}{\text{G}}_{\text{i}}^{\prime }\stackrel{h_{\text{6}}}{\to }\text{H}+{\text{R}}_{\text{s}}+{\text{G}}_{\text{i}}^{\prime }.$$

It follows that the coupling of h₆ with k₁ should yield the same value of the affinity as for the low-affinity sites, which implies that

$$h_6/k_1=h_d=h_{-1}/h_1.$$

From this we obtain

$$h_6=(1.0/2.2)7.5=3.4{\text{s}}^{-1}.$$

The actual value of h₆ we used is

$$h_6=17.0{\text{s}}^{-1}.$$

Finally, we have to estimate the constants for adenylate cyclase, internal phosphodiesterase, and the secretion rate. It is reported in [29] that the typical value for the turnover number of activated adenylate cyclase is

$$l_{\text{cat}}=1100{\text{min}}^{-1}=18.4{\text{s}}^{-1}$$

provided the concentration of ATP is held constant. Under this condition, we have that

$$l_{\text{cat}}=l_1{l}_2/\left(l_{-1}+l_2\right).$$

Since this process is fast, the selection of l₁, l₋₁, l₂ has little effect on the dynamics on the time scale we focus on, provided that the combination of the chosen values of l₁, l₋₁, l₂ yields the correct value of l_cat. Thus we take l₁ = l₋₁ = 20.2 s⁻¹ and l₂ = 202 s⁻¹.

The kinetic constants for iPDE have been estimated from experiments in [32] and [37]. It is reported there that the Michaelis-Menten constants are

$$V_{\text{iPDE}}^{\text{max}}=l_4{\left[\text{iPDE}\right]}_T=86.67\mu \text{M}/\text{s}$$

and

$$K_{\text{iPDE}}=\left(l_{-3}+l_4\right)/l_3=10\mu \text{M}.$$

The individual value for each of the constants involved is unknown, but it is reasonable to assume that the turnover number of iPDE is not very high, since the function of iPDE is to hydrolyze excess cAMP so as to control the internal level of cAMP. For simplicity we take l₋₃ = 0 s⁻¹ and l₄ = 50 s⁻¹, and then we can get

$$\begin{gathered} l_3=5\mu {\text{M}}^{-1}{\text{s}}^{-1}=5\times {10}^{-3}{\text{m}}^3/(\mu \text{mol}\cdot \text{s}), \\ {\left[\text{iPDE}\right]}_T=1.7334\mu \text{M}=1.7334\times {10}^3\mu \text{mol}/{\text{m}}^3 \end{gathered}$$

Finally, it is reported in [11] that l₅ ranges from 0.34 min⁻¹ to 0.94 min⁻¹. We use the intermediate value

$$l_5=0.84{\text{min}}^{-1}=0.014{\text{s}}^{-1}.$$

A.2. CELL GEOMETRY AND CHEMICAL CONCENTRATIONS

The typical cell radius for Dd is 11 μm [6, 37]. If a spherical geometry is assumed, then

$$V_c=696.9\mu {\text{m}}^3\text{and}{A}_c=380.1\mu {\text{m}}^2$$

Concentrations are stated either per unit area or per unit volume. These can be converted to molecules per cell as follows:

$$\begin{gathered} y_i\text{(molecules}/\text{cell)}=2.29\times {10}^8{y}_i\left(\mu \text{mol}/{\text{m}}^2\right), \\ {y}_i(\text{molecules}/\text{cell})=4.20\times {10}^2{y}_i\left(\mu \text{mol}/{\text{m}}^3\right). \end{gathered}$$

Therefore

$${\left[\text{iPDE}\right]}_T=1.7334\mu \text{M}=7.28\times {10}^5\text{molecules}/\text{cell}$$

and

$$\begin{gathered} \left[{\text{R}}_{\text{s}}\right]\doteq 0.4\times 9.6\times {10}^4=3.84\times {10}^4\text{milecules}/\text{cell}, \\ \left[{\text{R}}_{\text{i}}\right]\doteq 0.6\times 9.6\times {10}^4=5.76\times {10}^4\text{milecules}/\text{cell}. \end{gathered}$$

At present there is little information about the concentrations of G_s and G_i. It is commonly claimed that the concentration of G proteins is higher than the concentration of receptors, and one estimate for mammalian cells give a value for G_s of 100,000 per cell [1]. It is believed that in Dd the number of G protein molecules is in the same range as that of receptors [39], and we take them as equal in our model. Thus

$$\left[{\text{G}}_{\text{s}}\right]=3.84\times {10}^4/\text{cell}\text{and}\left[{\text{G}}_{\text{i}}\right]=5.76\times {10}^4/\text{cell}.$$

The total amount of adenylate cyclase is equal to the concentration of G_s in some mammalian cells [29] (but not others, cf. [1]), and we assume that this is true in Dd as well. Thus we have

$${[\text{UC}]}_T=3.48\times {10}^4\text{molecules}/\text{cell},$$

and the corresponding concentrations are

$$\begin{gathered} {\left[{\text{R}}_{\text{s}}\right]}_T=1.67\times {10}^{-4}\mu \text{mol}/{\text{m}}^2,{\left[{\text{R}}_{\text{i}}\right]}_T=2.50\times {10}^{-4}\mu \text{mol}/{\text{m}}^2 \\ {\left[{\text{G}}_{\text{s}}\right]}_T=1.67\times {10}^{-4}\mu \text{mol}/{\text{m}}^2,{\left[{\text{G}}_{\text{i}}\right]}_T=2.50\times {10}^{-4}\mu \text{mol}/{\text{m}}^2 \end{gathered}$$

and

$${[\text{UC}]}_T=1.67\times {10}^{-4}\mu \text{mol}/{\text{m}}^2.$$

This assumption is not critical, for we set the overall production rate to match the observed concentrations and secretion rates.

A.3. PARAMETERS IN THE SUSPENSION EXPERIMENTS

The new parameters that must be estimated for the suspension experiments are $V_{\text{max}}^{\text{mPDE}}$, K_mPDE, $V_{\text{max}}^{\text{ePDE}}$, and K_ePDE, where

$$V_{\text{max}}^{\text{mPDE}}=l_7{\left[\text{mPDE}\right]}_T,K_{\text{mPDE}}=\left(l_{-6}+l_7\right)/l_6,$$ (A1)

$$V_{\text{max}}^{\text{ePDE}}=l_9{\left[\text{ePDE}\right]}_T,K_{\text{ePDE}}=\left(l_{-8}+l_9\right)/l_8.$$ (A2)

The values of these parameters have been estimated in [32] and [37].

$$\begin{gathered} V_{\text{max}}^{\text{mPDE}}=1.67\times {10}^6\text{molecules}/(\text{cell}\cdot \text{s})=7.29\times {10}^{-3}\mu {\text{mol}}^{-1}{\text{m}}^{-2}, \\ {K}_{\text{mPDE}}=0.5\mu \text{M,} \\ {V}_{\text{max}}^{\text{ePDE}}=3\times {10}^7\text{molecules}/(\text{cell}\cdot \text{s})=7.15\times {10}^4\mu {\text{mol}}^{-1}{\text{m}}^{-3}, \\ {K}_{\text{ePDE}}=1.3\text{mM}. \end{gathered}$$

In the numerical simulations, we used K_mPDE = 5.0 μM, $V_{\text{max}}^{\text{mPDE}}=4.48\times {10}^{-2}\mu {\text{mol}}^{-1}{\text{m}}^{-2}$, K_ePDE = 1.3 mM, and $V_{\text{max}}^{\text{ePDE}}=4.39\times {10}^5\mu {\text{mol}}^{-1}{\text{m}}^3$.