I. Introduction
Much is known about the molecular components involved in signal transduction and gene expression in a number of model systems in developmental biology, and the focus is now shifting to understanding how these components are integrated into networks, and how these networks transduce the inputs they receive and produce the desired pattern of gene expression. The major question is how the correct genes are turned on at the correct point in space at the correct time in development to produce the numerous cell types present in an adult. Gene expression during embryonic development is not a cell-autonomous process, because cell fate in a multicellular embryo usually depends on the cell’s location in the embryo. A spatially-graded distribution of factors that influence development can be used to induce spatially-varying differentiation, and this idea played a central role throughout the early history of theoretical work in the field and was later developed into the theory of positional information by Wolpert (1969). Formally the theory posits that a cell must ‘know’ its position relative to other cells in order to adopt the correct developmental pathway, but of course what a cell ‘knows’ is determined by the information it extracts from the past and current signals received. Pattern formation in development refers to the spatially- and temporally-organized expression of genes in a multicellular array, and positional information is viewed as a necessary part of this process. Frequently pattern formation results from the response of individual cells to a spatial pattern of chemicals called morphogens, a term coined by the British logician Alan Turing in a fundamental paper on pattern formation (Turing, 1952) (cf. Fig. 1). Currently morphogens are defined as secreted signaling molecules that (i) are produced in a restricted portion of a tissue, (ii) are transported by diffusion, active transport, relay mechanisms, or other means to the remainder of the tissue, (iii) are detected by specific receptors or bind to specific sites on DNA, and (iv) initiate an intracellular signal transduction cascade that initiates or terminates the expression of target genes in a concentration-dependent manner. Perhaps the earliest example of a morphogen was the Bicoid protein that is involved in anterior–posterior (AP) patterning in Drosophila (Frohnhöfer and Nüsslein-Volhard, 1986), but many more examples are now known, including Activin, Hedgehog, Wingless, and various members of the transforming growth factor family. Theoretical studies of how different modes of transport and transduction affect patterning are reported in Kerszberg and Wolpert (1998); Kerszberg (1999); Lander et al. (2002); Strigini (2005); Umulis et al. (2006) and many others.
Figure 1.
The classical paradigm for patterning along an axis. (A) A morphogen is produced by source cells at the left and diffuses away from the source, and diffusion and degradation of the morphogen establishes a decreasing distribution. Cells respond to the local concentration of the morphogen, which is assumed to be time-invariant, and adopt one of three distinct fates in a threshold-dependent manner. (B) Patterning mediated by morphogens can be sensitive to changes in the level of morphogen secretion or the overall size of the system, but with suitable modifications the model can produce scale-invariance. (C) The time-evolution of the morphogen distribution shown overshoots the steady state, which may not even be reached in the time available. (D) Morphogen fluctuations due to stochastic effects may lead to a noisy signal, particularly at low concentrations. (See color insert.)
Thus the problem of pattern formation in a given system becomes that of discovering the mechanisms of localized production and transport that generate positional information. The classic paradigm for this is the model shown in Fig. 1A, wherein a source at one boundary of a one-dimensional domain produces the morphogen, which diffuses throughout the domain and initiates gene transcription and cell differentiation in a threshold-dependent manner. This is a static viewpoint, in that cells simply sense the local concentration and respond to it, and neither the transient dynamics of the signal nor the history of exposure to it play any role in patterning. As we show in Sections II and III, patterning by this mechanism is sensitive to changes in length unless some special mechanisms are used to compensate for such changes, and we show in Section V that the history of exposure is important in some contexts.
In many developing systems the outcome is buffered to numerous perturbations, ranging from major ones such as separation of the cells at the 2-cell stage in Xenopus (which can lead to one smaller, but normal adult, and an amorphous mass of tissue), to less severe ones such as changes in the ambient temperature or the loss of one copy of a gene. Indeed, many loss-of function mutations of important developmental genes in higher organisms show weak or no phenotypic effects, as will be discussed later in the context of Drosophila. There are many other instances in which the developmental outcome is buffered to changes in environmental variables that affect reaction rates, transport rates, and other factors that control the morphogen distribution, and the general question is how systems are buffered against variations in such factors. Said otherwise, how robust are developmental processes, and what does robustness even mean in this context? Other mathematical questions regarding morphogen patterning that arise are illustrated in Fig. 1. For instance, how do different organisms within a species preserve proportion even though they vary substantially in body size? How do cells respond to a ‘noisy’ morphogen signal caused by low levels of the morphogen, as in some of the patterning events discussed later? How do cells respond to a morphogen that is evolving in time during the course of development? Mathematical models and analysis can shed light on these issues and suggest mechanisms for mitigating the deleterious effects of some of these factors.
In the following section we discuss robustness in the developmental context in a general framework, and thereafter we discuss specific examples in the context of anterior–posterior patterning (Section III), parasegment patterning (Section IV), and of dorsal–ventral patterning (Section V), all in Drosophila.
A. Drosophila melanogaster as a Model System
Drosophila melanogaster, which is the common fruit fly, has served as a model system to study many aspects of development for the past 100 years. Drosophila has a short life cycle, it is easily grown, the genome is sequenced, and many of the components of the signal transduction and gene control networks involved in patterning are known. However, less is known about how these networks produce the desired spatiotemporal pattern of gene expression. Development is a sequential process in which later stages build on earlier stages, but within stages there are often multiple feedback loops in signaling and gene control networks that may serve to buffer against perturbations caused by fluctuations in morphogen concentration and other components. Understanding the structural features in a network that ensure reliable patterning in the face of various perturbations is a major unresolved problem.
The Drosophila oocyte, or egg, is an approximately prolate ellipsoid that forms from a germline cell in the ovary (cf. Fig. 2). The egg is surrounded by a thin fluid-filled shell, the perivitelline (PV) space, that is bounded on the outside by the vitelline membrane. A coordinate system in the egg is first established by gradients of maternally-inherited cytoplasmic factors in the AP direction and by gradients of factors in the PV space in the dorsal–ventral (DV) direction. About fifty maternal genes set up the AP and DV axes, which provide the early positional information in the zygote. Zygotic gene expression is initiated by transcription factors produced from maternal RNA. Spatial patterning proceeds in stages: first the AP and DV axes are set up, then the whole domains are divided into broad regions, and finally smaller domains are established in which a unique set of zygotic genes is transcribed. The successive stages of patterning are initiated by a strictly-controlled hierarchy of gene expression in both the AP and DV directions. The former is shown in Fig. 3, which shows some of the interactions within and between levels. Both AP and DV patterning will be discussed in detail later, but first we discuss robustness in general terms.
Figure 2.
The definitions of the anterior–posterior (AP) and dorsal–ventral (DV) axes and the tissue types in Drosophila. (From Alberts et al., 1994, with permission.) See color insert.
Figure 3.
The expression patterns for some of the genes in the different classes (left column) and a representation of some of the feedback loops and cross interactions (right column). [Images on the left are taken from Crauk and Dostatni (2005) (*), from Fly-Base SDB-Online (**), and from Jaeger et al. (2004) (***).] See color insert.
II. Robustness in the Developmental Context
We define robustness as follows: a component, system or process is robust with respect to a given class of perturbations if its output or response is unchanged to within some tolerance by these perturbations, i.e., if the system is unlikely to ‘fail’ in the face of these perturbations. The perturbations can be in the inputs to the component, system or process, or they can be perturbations or alterations in the internal structure of the component or system. Explicit in this definition is that robustness can be defined at many different levels, that it can only be defined with respect to a specified class of perturbations of the inputs or internal structure, and that a system may be robust even if it contains nonrobust components. Conversely, a system comprised of robust components need not be robust itself. In the developmental context the system might be an entire developing embryo, or a portion thereof, the output could be the expression of a certain gene, the spatial pattern of tissue types, etc., and the perturbations might be knock-outs or overexpression of an upstream gene, the removal of a portion of the system, a mutation that interferes with a signal transduction pathway, variations in the amount of cellular constituents received at division time, and so on.
A. Structural Stability in Dynamical Systems
Since robustness is defined as insensitivity of the output, which is usually a prescribed function of the state of a system, to a defined class of perturbations, it should be possible to test for robustness if one has a model for the system. Thus consider a system whose state u evolves according to the finite system of ordinary differential equations of the form
| (1) |
Here u represents all the concentrations and other variables that define the state, p is a vector of constant parameters that appear in the model equations, and Φ represents time-dependent inputs. There are at least three classes of ‘perturbations’ we can consider, and these lead to three types of insensitivity or robustness.
Insensitivity with respect to inputs, by which we mean that in the long run the system ignores a certain class of inputs. This is a well-established notion in control theory and it is known that the system will ignore a given class of inputs if and only if it contains a subsystem that can generate the given class of inputs (Sontag, 2003). This is an example of a characteristic common to many sensory or signal transduction systems, and in that context the system is said to adapt to the specified inputs. In the developmental context this would imply that the system only responds to the transient changes in a signal and subtracts out the background signal.
Insensitivity with respect to changes in the model itself, which are reflected in changes to the function F. This is captured in the notion of coarseness or structural stability developed for dynamical systems: the system (1) is said to be structurally stable if its associated flow is orbit equivalent to the flow generated by any system in a sufficiently small neighborhood of it, using a suitable measure of closeness. In more prosaic terms this means that the family of solution curves in phase space ‘look alike.’ A global criterion for this kind of robustness, i.e., one valid for all values of the state u, is known for linear systems, but only local results are known in general. Said otherwise, one can test whether the output or state of the system is insensitive to small perturbations near a known solution, but in general not globally. These might include deletion of paths in a signal transduction network if the flux of signal or material flow along that pathway is sufficiently small.
Insensitivity with respect to changes in parameters. Strictly speaking this is a subset of 2, but this is the concept of robustness most frequently applied to signal transduction and gene control systems.
B. Sensitivity Analysis
There are well-established techniques for examining robustness or sensitivity of a mathematical model to changes in the parameters of the model. Suppose that the equations for the local dynamics, which could arise from a system of chemical reactions, are written as the system
| (2) |
Here we suppose that there are no time-dependent inputs and simply lump p and Φ in (1) together. At a steady state F(u, Φ) = 0, and we shall assume that det(Fu) ≠ 0, where det(·) denotes the determinant and the subscript denotes the partial derivative. This implies that locally there is a unique function us : Rm → Rn such that F(us(Φ), Φ) = 0. Differentiating the steady-state equation
| (3) |
with respect to Φ leads to
where is an n × m matrix when Φ has m components. By the above assumption Fu is invertible, so the steady-state sensitivity to Φ is
| (4) |
Obviously one can determine from this the sensitivity of any particular component.
Now consider a distributed problem described by a system of reaction–diffusion equations, and for simplicity consider only the steady-state problem. Let Ω ⊂ Rn be a given region of space with boundary ∂Ω, and write the governing equations as
| (5) |
where B incorporates the fluxes at the boundary. If we assume this has a unique solution us and differentiate the equation with respect to Φ as before, we obtain the following system.
| (6) |
One could easily compute the solution of the variational problem (6) in parallel with the solution of (5). From this one could see how different components vary at different points in space as the input fluxes or kinetic parameters are varied. As a result, one could, for example, study the sensitivity of the spatial location of a particular concentration level to changes in the kinetic parameters.
C. The Turing Theory of Spatial Pattern Formation and Scale Invariance
An alternative to the localized-source, distributed-response paradigm built into the French flag model of patterning, which requires preexisting differentiation of those cells that serve as sources, is to suppose that pattern formation is a self-organizing process. The classical model based on this idea is due to Turing (1952). A Turing model involves two or more chemical species, which he called morphogens, that react together and diffuse throughout the system. In Turing’s original analysis no cells were distinguished a priori; all could serve as sources or sinks of the morphogen. Moreover, Turing only considered periodic systems or closed surfaces, in which case no boundary conditions are needed. More generally, we call any system of reaction–diffusion equations for which the boundary conditions are of the same type for all species a Turing system.1 Turing showed for a two-component system that under suitable conditions on the kinetic interactions and diffusion coefficients a spatially-homogeneous stationary state can, as a result of slow variation in parameters such as kinetic coefficients, become unstable with respect to small nonuniform disturbances. Such instabilities, which Turing called symmetry-breaking because the homogeneous locally-isotropic stationary state becomes unstable and therefore dynamically inaccessible, can lead to either a spatially nonuniform stationary state or to more complicated dynamical behavior. Such transitions from uniform stationary states to spatially- and/or temporally-ordered states might in turn lead, via an unspecified ‘interpretation’ mechanism, to spatially-ordered differentiation. For mathematical simplicity most analyses of Turing models deal with instabilities of uniform stationary states, since numerical analysis is generally required for more general reference states. However, Turing himself recognized the biological unreality of this in stating that ‘most of an organism, most of the time is developing from one pattern to another, rather than from homogeneity into a pattern’ (Turing, 1952). In a classic example of theory preceding experiment, it took until 1990 to verify Turing’s theory in a system comprising chlorite, iodide and malonic acid (Castets et al., 1990), and there is still no conclusive evidence of biological examples that can be explained by his theory. Theoretical models for patterning of hair follicles related to Turing’s mechanism are well known (Claxton, 1964; Nagorcka and Mooney, 1982), but only recently have specific morphogens been suggested. Sick et al. (2006) suggest that Wnt and Dkk may function as morphogens in determining the hair follicle spacing in mice, and while this is potentially an important advance, much remains to be explained. For example, the underlying network governing expression of these species is certainly much more complex than the simple two-species model employed in the computations. Extension of Turing’s analysis leads to the structural conditions that guarantee Turing instabilities for any number of components (Othmer, 1980), and it may turn out after a more detailed analysis that this is the first biological system in which patterning is self-organized.
While Turing patterns show a degree of insensitivity to parameter variations, particularly if the condition that all species satisfy the same boundary conditions is relaxed (Dillon et al., 1994), it is quite sensitive to changes in the size of the system, particularly for more complex patterns that correspond to higher modes (Othmer and Pate, 1980). Thus it is usually difficult to guarantee that a given spatial pattern will persist under significant changes in diffusion coefficients, the kinetic parameters, or the length scale of the system, because the underlying instability that leads to a spatial pattern carries with it an intrinsic length scale defined by the kinetic parameters and the diffusion coefficients. This can be understood by realizing that the rate of diffusion depends on the gradient of concentration, hence on the spatial scale, whereas the kinetic interactions in a homogeneous system do not.
In a number of contexts to be discussed later, patterning in developing embryos occurs reliably even when the size changes by a factor of 2–3, and neither the Turing model nor the French flag model will produce a correctly-proportioned pattern under such changes. In the following section we propose a model that explains recent experimental results on scale-invariance of the Bicoid distribution in Drosophila, and as background for that we describe a general method for producing scale-invariant distributions of morphogen distributions set up by reaction and diffusion. Consider again the region Ω and now suppose that reaction and diffusion can occur both in the interior of the region and on the boundary. Let u (resp., v) denote the concentration of species in the interior (resp., on the boundary), the latter measured in units of M/L2T, and write the governing equations as follows.
| (7) |
| (8) |
| (9) |
Here R(u) denotes the reaction in the interior of the region, κ−1 is a characteristic time scale for the reactions, B0(u, x) denotes a specified input flux, B1(u, v, x) denotes reactions that occur on the boundary and involve u, Rb(v) denotes other reactions on the boundary, and n denotes the inward normal. All reaction rates are allowed to depend on x, since these may vary throughout the system. For simplicity we have omitted parameters in the rate functions.
By scale invariance of the morphogen distribution we mean that the solution of (7)–(9) (or at least one component) is unchanged, both in amplitude and spatial variation, when the system is dilated, either positively or negatively, within a given range. This implies that when the equations are transformed to relative coordinates (i.e., a scaled version of the original coordinates), the solution is unchanged in amplitude and spatial variation under specified changes in the size measure. To understand what must occur to produce scale-invariant morphogen distributions, we reduce (7)–(9) to a form that corresponds to the simplest model for positional information. Consider the one-dimensional, steady-state problem on the interval [0, L], with a specified flux at x = 0, linear decay in the interval [0, L], and zero flux at x = L. Thus
| (10) |
In scaled coordinates this becomes
| (11) |
where λ2 ≡ κL2/D and J = jL/D. The solution is
| (12) |
If the flux j is fixed, the factor J/λ is independent of L, since both J and λ are proportional to L. However, the shape function ϕ(ξ) depends on L, and as a result, so does the amplitude. Thus neither the shape nor the amplitude of the morphogen distribution is scale invariant; the distribution decays proportionally more rapidly the larger L is.
The shape ϕ(ξ) of the distribution is invariant under changes in L if λ is independent of L, and this can be achieved if either D ∝ L2 or κ ∝ L−2, but then the amplitude is not invariant. One can understand the origin of the problem from (7)–(9), for there one sees that in converting these equations to scaled coordinates the diffusion terms scale as L−2, whereas the boundary terms involving the normal derivative scale as L−1. Thus it is difficult to achieve invariance, even if the diffusion or kinetic coefficients scale properly, without scaling the input flux j. If the system is closed this problem disappears, and a mechanism for producing the required dependence of D or κ on L in the context of a generalized Turing problem is described elsewhere (Othmer and Pate, 1980).
Suppose that the morphogens are produced by all cells and that the boundary is closed, and there are no reactions on the boundary. Suppose also that all cells produce a control species at a constant rate R0, that the concentration of this species is zero at the boundary, and that this control species modulates the diffusion and/or kinetic coefficients. This leads to the system of equations
wherein c = (c1, c2,…, cn) is the vector of concentrations for the pattern-inducing species, C is the concentration of the control species that modulates either the diffusion coefficients or the kinetic coefficients, and D(C) and κ(C) reflect the dependence on C. It is easy to see that the steady state concentration of C scales as L2, and thus perfect scale-invariance is possible if Di (·) ∝ C or κ(·) ∝ C−1. In effect the control species can change the underlying metric by changing the diffusion coefficient, it can change the time scale by modulating the reaction rates, or it can do both. By relaxing the assumption that the control species is zero on the boundary, one can incorporate an influx of the control species and still achieve very weak dependence of the morphogen distributions on L. One can thereby achieve a controllable level of robustness with respect to changes in the size of the system (Othmer and Pate, 1980).
As a second example that incorporates receptor dynamics on one surface, suppose we specialize the general problem described by (7)–(9) to the geometry shown in Fig. 4. Assume that the surface reactions involve only binding to a receptor and decay of the receptor–ligand complex, and to simplify the analysis, suppose that whenever a receptor–ligand complex is internalized it is replaced by a bare receptor (Umulis et al., 2006). The surface z = 0 can be thought of as the receptor-filled outer mebrane that divides intra- and extracellular environments, as in Drosophila dorsal surface patterning, or as the cytoplasmic side of the inner membrane in which the nuclei are embedded in the Drosophila blastoderm. Let Lx, Ly, and Lz be the lengths in the x, y, and z directions, respectively, and let C be the concentration of a morphogen in the fluid and R the concentration of receptor on the surface z = 0. Suppose there is a fixed influx of C on the boundary x = 0, and zero flux on the remaining faces except z = 0; then the governing equations can be written as follows.
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
Equation (14) reflects the assumption that the steps by which an occupied receptor is internalized and a free receptor is recycled to the surface reach a steady state rapidly compared with other processes. As a result, the total receptor density is constant at every point on the surface z = 0, i.e., where RT is a constant.
Figure 4.
The geometry of a thin fluid layer over receptors embedded in a surface. See color insert.
To simplify this system we define the dimensionless variables the scaled coordinates ξ = x/Lx, η = y/Ly and ζ = z/LZ and the dimensionless time τ = t/T. The system then become
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
If we assume that Lz ≪ Lx, Ly the first equation can be averaged over ζ. In view of the boundary conditions, the solution must be constant in the η direction at steady state and the equations reduce to
| (23) |
| (24) |
where u now stands for the average over ζ, and
If u ≪ K then this reduces to
| (25) |
| (26) |
where
This system is identical to (11), given the assumed zero-flux boundary condition at ξ = 1, and therefore the dimensionless solution u is given by (12). Again we can ask under what conditions the shape and amplitude are scale-invariant, and now the answer may be different. Suppose that the total number of receptors is fixed, even though the lengths Lx and Ly may change. It is clear that the total number NT is
under the assumption that the density is uniform, and therefore
| (27) |
Since ks and D are constants, it is clear that λ will be independent of the length scale if (i) NT is constant, (ii) Lx and Ly scale by the same amount, and (iii) Lz is constant. Thus a uniform dilation in the x and y directions, no dilation in the z direction, and a constant total number of receptors produces a scale-invariant shape function. This is conceptually equivalent to embedding the receptors in a rubber sheet and stretching or shrinking the sheet uniformly in x and y without changing the thickness of the fluid layer. Given that λ is constant, it follows that the amplitude will be constant under size changes if J is constant, which holds if the total input flux over the surface x = 0 is constant under uniform dilations in x and y, since in that case j scales as .
III. Scaling of AP Patterning in Drosophila
A. Anterior–Posterior Patterning
Here and in later sections we describe only the primary genes and the effects of their products; a more complete description of the patterning process can be found in Gilbert (2006). When referring to genes and their products we italicize the former and capitalize the latter.
Three groups of maternal gene products, anterior, posterior and terminal, are involved in the first stage of AP patterning, in which anterior is distinguished from posterior. Four messenger RNAs (bicoid, hunchback, nanos, and caudal) are critical in this stage. These encode transcriptional and translational regulatory proteins that activate or repress the expression of certain zygotic genes. The maternally-inherited bicoid mRNA is localized at the anterior end of the unfertilized egg and is translated after fertilization. The Bicoid protein diffuses throughout the syncytial blastoderm and establishes a concentration gradient along the AP axis.
The posterior pattern is primarily controlled by the levels of Nanos and Caudal. nanos mRNA is localized at the posterior pole of the egg and Nanos suppresses translation of hunchback in the posterior. hunchback mRNA is both maternally-inherited and transcribed in the zygote, the former distributed uniformly throughout the egg. Zygotic transcription of hunchback is activated by high Bicoid levels and inhibited by Nanos and Pumilio. caudal mRNA is distributed uniformly, but a posterior-to-anterior gradient of Caudal is established by inhibition of Caudal synthesis by Bicoid.
Thus in the initial stage of AP patterning, Bicoid and maternal Hunchback activate hunchback expression throughout the anterior half of the embryo. By midcycle 14, this primary expression pattern of hunchback is replaced by a secondary pattern consisting of a variable anterior domain, a stripe at the position of parasegment 4 (described later), and a posterior cap (Margolis et al., 1995). In the next stage, which is initiated by Bicoid and Hunchback, the AP axis is divided into broad regions by the expression of the gap genes giant, kruppel, and knirps. kruppel is activated by a combination of Bicoid and low levels of Hunchback, but is repressed by high levels of Hunchback. This localizes kruppel expression to the center of the embryo, in parasegments 4–6. knirps is repressed by high levels of Hunchback, and therefore is expressed in parasegments 7–12. The details of how the boundaries of expression domains are determined are complex, but by an elaboration of further localization of expression the initial gradients of morphogens lead to the establishment of regions within the syncytial blastoderm that foreshadow the onset of segmentation, which follows formation of parasegments.
Expression of pair-rule genes defines the boundaries of the parasegments. These genes are expressed in 7 transverse stripes corresponding to every second parasegment: even-skipped in odd parasegments and fushi-tarazu in even parasegments. Their expression begins just before cellularization (midcycle 14) and after cellularization, each pair-rule gene is restricted to a few cells in seven stripes. Again, the details, which can be found in Gilbert (2006), are more complex, since each stripe is controlled by combinations of transcription factors. Segments are made from the posterior part of one parasegment and the anterior of the next. The last step for our purposes is expression of the segment polarity genes, which are discussed later. These pattern the 14 parasegments and stabilize parasegment and segment boundaries, thus defining the segmented structure of the abdomen.
B. Intra- and Interspecies Variations in the Bicoid Distribution
As we saw in Section II.C, a preset morphogen threshold in the French flag model described by (10) does not scale properly under changes in length, and unless there are downstream mechanisms for adjusting the response, there will be variation in the proportioning of an embryo into the different cell types. Since Bicoid is a primary determinant of AP patterning, it is important to determine how much variation there is in the spatial location of a threshold in Bicoid for activation of hunchback. It has been shown experimentally that there is significant variation in this threshold from embryo-to-embryo at early cycle 14, both in Drosophila and other closely-related dipteran species (Gregor et al., 2005). However, the shape and amplitude of the Bicoid distribution is essentially independent of the embryo size over a four-fold change in length when comparing different species (ibid). It was found that Hunch-back expression is less sensitive to embryo size in Drosophila, which suggested that there may be other mechanisms that cooperate or compete with Bicoid to control target gene expression (Aegerter-Wilmsen et al., 2005; Howard and ten Wolde, 2005; Houchmandzadeh et al., 2005). Other data suggests that at midcycle 14 the variation in the Bicoid threshold location in Drosophila is no greater than that in the boundary of hunchback expression, and thus Bicoid can control target gene expression precisely without additional factors or control schemes (Crauk and Dostatni, 2005). The high embryo-to-embryo variability of the Bicoid distribution observed in early cycle 14 may originate from the antibody staining methods (Houchmandzadeh et al., 2002; Crauk and Dostatni, 2005), or the distribution may sharpen in midcycle 14 by some unknown mechanism.
The analysis of Section II.C shows that the interspecies scaling of the Bicoid distribution could be achieved by scaling of the diffusion coefficients, scaling of the reaction rates, or a combination of the two. The experimental results in Gregor et al. (2005) show that the characteristic decay length in the notation of (11) scales as the length of the AP axis, which implies that in (10) is constant across species. These authors also show that the diffusion of similarly-sized molecules between different embryos does not change appreciably, and therefore the scale-invariance of the Bicoid distribution must be achieved by scaling the pseudo-first-order decay κ of Bicoid (Gregor et al., 2005). As we showed in Section II.C, this can be achieved if (i) the total number of binding sites is constant, (ii) the integrated input flux remains constant under scaling, and (iii) the morphogen is confined to a thin layer and the lateral dimensions of this layer each scale as L. The first of these conditions has been verified experimentally: the number of nuclei at cell cycle 14 is given by log2 Nnuc = 12.8 ± 0.2 nuclei for the species studied (Gregor et al., 2005). Condition (ii) will be met if the net production of Bicoid in an egg is constant across species, which can be achieved if either the amount of maternal RNA deposited in an egg is constant across species or the transcription rate is adjusted appropriately. The last condition has not been tested experimentally, but support for it stems from the fact that in embryos stained for Bicoid, the protein accumulates near the nuclei at the periphery and there appears to be less in the bulk cytoplasm (Gregor et al., 2005; Houchmandzadeh et al., 2002).
The proposed mechanism based on the simplified configuration in Fig. 4, in which the receptors are uniformly distributed, can account for perfect invariance. In the following section we show that in applying this to Drosophila, the discreteness of the nuclei does not affect this conclusion, and we show that some of the embryo-to-embryo variation in the location of a threshold may be accounted for by diffusion in the bulk cytoplasm.
C. The Effects of Discrete Nuclei and Diffusion in the Bulk Cytoplasm
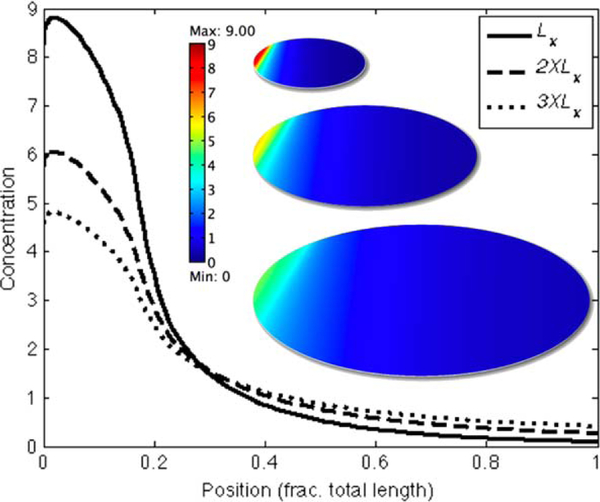
To investigate the applicability of the analytical solution to nonuniform uptake and release of transcription factors, we developed a computational model in which nuclei are arranged in a regular two-dimensional hexagonal array and the transcription factors are free to diffuse unhindered over the field of nuclei. Nuclei are round and their size remains constant under changes in the overall system lengths. The x- and y-directions can be scaled independently of each other and the nuclei spacing is determined by the centers of the dilated hexagonal packing. Fig. 5 shows a small section of the nuclei distribution for total lengths that vary 3-fold from the base case Lx to 3XLx. As in the analytical system, the steady-state distribution of morphogens in the nonuniform field exhibit perfect scale invariance as long as the ratio Ly/Lx remains constant. In the example here, this is demonstrated with a system that has regular hexagonal packing, but the details of the grid are not relevant: the solution remains scale invariant as long as Ly/Lx is constant. As expected, perfect scale invariance is not achieved when Ly/Lx is not constant. For instance, if only Lx is scaled while Ly remains fixed, the amplitude scales as while the dimensionless decay length scales as .
Figure 5.
(a) Section of nonuniform distributions of nuclei shows spacing for base case (left) Lx, Ly; and rescaled cases (middle) 2 × Lx, 2 × Ly; and (right) 3 × Lx, 3 × Ly. (b, c) shows the scaling of the decay length and amplitude for Lx (solid), 2XLx (dashed), and 3XLx (dotted). (d, e) same as (b, c) mapped to the interval [0, 1] and plotted logarithmically. The approximate analytical solution gotten by ignoring the growing exponential term in (12) is also shown (red dot–dash). The superimposed lines for Lx, 2 × Lx, and 3 × Lx in (d) and (e) demonstrate scale invariance of the nonuniform system. The nuclei were taken to be 2μm in diameter, the diffusion coefficient was 20 μ2/s and konRtot = 5.6 × 10−3. See color insert.
Fig. 6 shows the effect of incorporating diffusion in the bulk cytoplasm as well as in the thin layer at the periphery in a full 3D model of the embryo. One sees there that the profiles no longer scale perfectly, as they would without diffusion in the bulk, which suggests that one may be able to explain the embryo-to-embryo variability within species by effects such as this. A more detailed analysis of this and other aspects of scaling will be reported elsewhere (Umulis et al., 2007).
Figure 6.
The effect of diffusion throughout the cytoplasm on the scaling of Bicoid distributions. See color insert.
IV. Models of the Segment Polarity Network
As described earlier, the genes involved in spatial patterning are expressed in a temporal sequence that leads to successively more refined spatial patterns of expression. The gap and pair-rule genes are only expressed transiently, but the segment polarity genes, which pattern the parasegments, are expressed throughout the life of the fly. A parasegment comprises four cells, and the gene expression pattern is repeated in each of the fourteen parasegments. The network of gene and protein interactions at this stage are shown in Fig. 7. The stable expression pattern of wingless and engrailed, defines and maintains the borders between different parasegments (Wolpert et al., 2002). The segment polarity genes are first expressed after cellularization, and intercellular communication is an essential component at this stage.
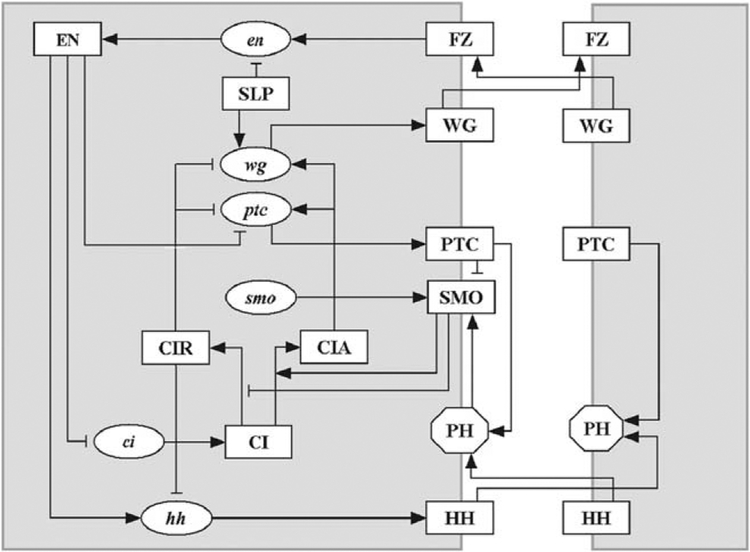
Figure 7.
The network of interactions between the segment polarity genes. The shape of the nodes indicates whether the corresponding substances are mRNAs (ellipses), proteins (rectangles) or protein complexes (octagons). The edges of the network signify either biochemical reactions (e.g., translation) or regulatory interactions (e.g., transcriptional activation). The edges are distinguished by their signatures, i.e., whether they are activating or inhibiting. Terminating arrows (→) indicate translation, post-translational modifications (in the case of CI), transcriptional activation or the promotion of a post-translational modification reaction (e.g., SMO determining the activation of CI). Terminating segments (⊣) indicate transcriptional inhibition or in the case of SMO, the inhibition of the post-translational modification reaction CI → CIR. From Albert and Othmer (2003) with permission. See color insert.
The major components involved are the transcription factor engrailed (EN), the cytosolic protein Cubitus Interruptus (CI), the secreted proteins Wingless (WG) and Hedgehog (HH), and the transmembrane proteins Patched (PTC) and Smoothened (SMO), the latter two of which are the receptor and an auxiliary protein involved in transduction of the HH signal. The pair-rule gene sloppy paired (slp) is activated earlier and expressed constitutively thereafter (Grossniklaus et al., 1992), and therefore serves as a constant input. A detailed description of the network and the biological justification for the activation and inhibition steps depicted in Fig. 7 is given in Albert and Othmer (2003).
The essential function of this network can be understood as follows. Label the full cell shown in Fig. 7 as i and the cell (shown partially) to the right of it as i + 1. If i + 1 expresses wingless protein WG, this upregulates EN production in i via the frizzled receptor and the intermediate protein Disheveled (not shown), and this in turn upregulates HH production in i and downregulates CI and ptc in i. Conversely, if i expresses HH, this upregulates CIA and WG production in i + 1, and thus there is a self-reinforcing feedback loop that encompasses both cells. The qualitative description suggests (a) that one should not see simultaneous expression of wg and either en or hh in the same cell, and that, (b) since all cells have the same network, the initial conditions will determine which cells express wg and which express en, hh. The results shown later will confirm these expectations.
The first detailed model for the segment polarity gene network was analyzed by von Dassow et al. (2000) and von Dassow and Odell (2002), who developed a continuous-state model of the core network of five genes (en, wg, ptc, ci, and hh) and their proteins. This is described in the following section. In this model and the Boolean model described later no account is taken of concentration variations within cells, but cell–cell interactions are included.
A. The Continuous-State Analysis of the Segment Polarity Gene Network
The model described in von Dassow et al. (2000) leads to differential equations of the following general form for mRNAs and proteins
Here [hh]i denotes the hedgehog mRNA in the ith cell and [HH]i,j denotes the corresponding protein between the ith and jth cells. When a single transcription factor controls gene expression, the transcription rate is given by a Hill function, but when multiple factors are involved the transcription rate is either a rational function of such functions, or a composition of them (cf. the supplemental material to von Dassow et al., 2000). These assumptions embody enormous simplifications of the underlying biochemical events, and a more realistic description would involve the probabilities of the various configurations of the promoter in the presence of activators and inhibitors. The transcription rate at any time could be set to a linear combination of these configurations, each weighted according to the rate of transcription in that configuration.
Suitable modifications of the initial network topology led to correct patterns of wild-type gene expression under wide variations in the kinetic constants in the rate laws, provided that the cooperativity in the Hill functions was sufficiently large. This insensitivity to parameters suggests that the essential features involved are the topology of the segment polarity network and the signatures of the interactions in the network (i.e., whether they are activating or inhibiting). In the next section we describe a Boolean model developed in Albert and Othmer (2003) that substantiates this prediction.
B. A Boolean Model for Control of the Segment Polarity Genes
The Boolean description of the segment polarity network is a discrete-time, discrete state model in which the state of each mRNA and protein is either 1 (ON) or 0 (OFF), and time is discretized into steps approximately equal to the duration of a transcription or translation event. Each mRNA or protein is represented by a node of a network, and the interactions between them are encoded as directed edges (see Fig. 7). The state of each node is 1 or 0, according as the corresponding substance is expressed or not, and the next state of node i is determined by a Boolean (logical) function of its state and the state of those nodes that have edges incident on it. The regulatory influences in the network are encoded in the connections shown in Fig. 7 and their signatures, by which we mean whether an edge corresponds to activation or inhibition of the terminal node. The Boolean interaction functions are then constructed from these interactions: the rules governing the transcription of an mRNA, for example, are determined by a Boolean function of the states of its transcriptional activators and inhibitors.
The Boolean rules used in the model are given in Table I; a detailed justification for them is given in Albert and Othmer (2003). The key assumptions underlying the updating rules are (i) the effect of transcriptional activators and inhibitors is never additive, but rather, inhibitors are dominant; (ii) the dependence of transcription and translation is an ON/OFF function of the state; (iii) mRNAs decay in one step if not transcribed; and (iv) transcription factors and proteins undergoing post-translational modification decay in one step if their transcript is not present. The rules give the expression of a node at time t + 1 as a function of the expression of its effector nodes at time t, except that we assume the expression of SLP does not change, and that the activation of SMO and the binding of PTC to HH are instantaneous.
Table I.
The Boolean rules used in the model
| Variable | Logical Functions Used for Updating |
|---|---|
| SLPi | |
| wgi | |
| WGi | |
| eni | |
| ENi | |
| hhi | |
| HHi | |
| ptci | |
| PTCi | |
| PHi | |
| SMOi | |
| cii | |
| CIi | |
| CIAi | |
| CIRi |
If is the state of the ith node (i = 1, 15) in the jth cell at time t, and x = (x11,…, xnN), then the next state of the network is , which defines a discrete dynamical system whose iteration determines the evolution of the state of all nodes. This discrete dynamical system is much easier to analyze than the differential equations; one simply prescribes an initial state for each node, and the state at the next time step is determined by the Boolean function for that node. A fixed point of is a time-invariant state of the system, whereas a fixed point of for some p > 1 represents a state that repeats periodically with least period p. The test for whether or not the model correctly predicts the observed spatial patterns is whether, starting from wild-type initial conditions, the state evolves to a fixed point that corresponds to this pattern. Since the objective is to describe the effect of the segment polarity genes in maintaining the parasegment border, the patterns of segment polarity genes formed before stage 8 are considered as initial states for the network, and the final stable state should reflect the wild type patterns observed in stage 11.
The initial state, based on the experimental observations of stage 8 embryos, includes a two-cell-wide SLP stripe in the posterior half of the parasegment, a single-cell-wide wg stripe in the most posterior part of the parasegment, single-cell-wide en and hh stripes in the most anterior part of the parasegment, and ci and ptc expressed in the posterior three-fourths of the parasegment [see Albert and Othmer (2003) and references therein]. The one-dimensional representation of the mRNA and protein patterns for this initial condition is shown in Fig. 8a. Beginning with this initial distribution, one finds that after 6 time steps the system reaches the stable fixed point represented by the pattern shown in Fig. 8b). This pattern agrees with the experimental observations of the wild type expression of the segment polarity genes after stage 11. Note that wg and WG are expressed in the most posterior cell of each parasegment, while en, EN, hh and HH are expressed in the most anterior cell of each parasegment, as is observed experimentally (Tabata et al., 1992; Ingham et al., 1991).
Figure 8.
Wild-type expression patterns of the segment polarity genes. (a) The initial state before stage 8 based on experimental observations. (b) The wild type stable state of the model if initialized with the pattern in (a). From Albert and Othmer (2003) with permission. See color insert.
One can also analyze the patterns that result from initial conditions other than wild-type, and for various mutants. Analysis of the steady states and their domains of attraction shows that the minimal prepatterning that leads to wild type stable expression is as follows:
wg is wild type,
en and hh are not expressed,
ptc is expressed in the third cell of the parasegment,
ci and the proteins are not expressed.
Broader initial expression of any node except PH, SMO, ci and CIR leads to a pattern with broad stripes in about 90% of the total number of initial states.
It is shown in Albert and Othmer (2003) that the family of possible stable steady states includes three well-known states corresponding to the wild type, broadened and nonsegmented patterns, and three states with very limited basins of attraction. Nevertheless, the existence of the latter steady states suggests the adaptability of the network to produce patterns other than those required in Drosophila embryogenesis. Additionally, if we relax the assumption of identical parasegments, the steady state patterns corresponding to individual parasegments can be combined to form diverse patternings of the whole ectoderm. For example, the wild type steady state and its double wg variant can be seamlessly integrated.
C. The Segment Polarity Network is a Simple Switching Network
The robustness observed in the continuous-state description suggested that the essential feature of the segment polarity network is the topology and signature of the interactions, not the details of the rate laws for the kinetic steps, and the Boolean model confirms this in most details. It reproduces the wild type expression pattern of these genes, as well as the ectopic expression patterns observed in various mutants. Furthermore, the Boolean representation enables one to do a complete analysis of the possible steady states, and allows for a more precise identification of the basin of attraction of each steady state. While both models reproduce the observed steady states of gene expression, the temporal evolution may not reflect the in vivo evolution of expression patterning for either model, since there is no data to compare the predictions with: both models can attain the steady state in the time available for patterning.
Various extensions of each model are possible. Several that can be tested in the continuous-state description are (i) the suitability of the simplified description of gene expression, and (ii) the effect of time delays in various steps. Recent analysis of the original ODE system shows that a number of components must function in an ON–OFF manner to achieve robustness (Ingolia, 2004), which provides indirect validation of the Boolean model. In the Boolean model it is assumed that the expression of proteins decays in one time step if their mRNAs are switched off, and this assumption induces on–off flickering and rearrangements in the expression pattern that slowly stabilize. An extension of the model that assumes that protein expression decays in two timesteps after the disappearance of the mRNA has been analyzed, and this two-step model leads to the same steady states as the original model, and all the conclusions regarding the initial state and gene mutations are preserved. The only change is in the transient dynamics, and generally the number of steps leading to a striped steady state decreases in the two-step model (cf. Albert and Othmer, 2003). One can also introduce a stochastic aspect into the Boolean functions by assigning probabilities that given Boolean functions are realized. For example, if one relaxes the rigid ‘inhibition dominates activation’ rule, and chooses this output probabilistically, then the network functions correctly if the output realizes the deterministic rule at least 75–80% of the time.
The success of the Boolean model of the segment polarity network suggests that the network has evolved to function as a simple switching network wherein genes (nodes) are either on or off; no graded response is needed and thus the details of the kinetic steps are not so important for understanding the steady state behavior. This may be true of many other gene control networks, such as the delta-notch signaling network. In any case, a Boolean description of a network facilitates the integration of qualitative observations on gene interactions into a coherent picture, and provides an easy verification of the sufficiency of these interactions (i.e., whether some steps are missing or whether some postulated interactions are incorrect).
V. Dorsal–Ventral Patterning in Drosophila
Establishment of a coordinate frame for DV patterning in the oocyte begins when the nucleus migrates from a central posterior position to a dorsal, anterior position. The nucleus expresses gurken, which establishes a cortical region of high gurken mRNA and protein levels. Gurken is a secreted growth factor that binds to receptors on the follicle cells surrounding the egg and results in a DV gradient of EGF receptor (Egfr) activation and up- or downregulation of target genes in the EGF pathway (Reeves et al., 2006). At least three genes expressed in follicle cells are involved: pipe, nudel, and windbeutel. Expression of pipe is repressed by Gurken, with the result that it is only expressed in the ventral 40% of the follicle cells. pipe encodes a protein similar to heparan sulfate 2-O-sulfotransferase that may modify ECM components to produce sites for the initiation of reactions that produce a ventralizing signal (Morisato and Anderson, 1994; Sen et al., 1998, 2000). Four maternal effect genes whose products are secreted into the PV space (gastrulation defective, snake, easter, and spatzle) are involved from the germline. The first three are serine proteases that act in a cascade whose end product is the activated form of the diffusible ligand Spätzle, which is secreted in an inactive form and cleaved in the ventral region. The active C-terminal fragment, denoted Spa*, binds to the receptor Toll, which is uniformly expressed at the surface of the embryo (Hashimoto et al., 1991). Toll in turn activates an intra-cellular cascade that stimulates the nuclear uptake of the transcription factor Dorsal (Dl). The graded distribution in the PV space of the diffusible ligand Spätzle results in graded activation of its receptor and graded nuclear uptake of the transcription factor Dorsal, which, combined with threshold responses for gene activation, subdivides the DV cross-section into three major regions: the ventral-most prospective mesoderm, the intermediate lateral ectoderm and neuroectoderm, and the dorsal ectoderm, where the amnioserosa is determined in the dorsal-most subregion (Morisato and Anderson, 1994). Absence of Dorsal allows expression of tolloid (tld), and decapentaplegic (dpp) genes in the lateral dorsal region, while zerknüllt (zen) and its protein are expressed in the dorsal-most region that defines the amnioserosa (Wolpert et al., 2002; Levine and Davidson, 2005) (cf. Fig. 9).
Figure 9.
A schematic of a cross-section of an embryo, showing the distribution of Dorsal, which sets the DV polarity (A), the major tissue types in a DV section (B), and the profiles of the major determinants of dorsal surface patterning and the interactions between these components. See color insert.
Maternal factors determine the position of lateral ectoderm relative to dorsal ectoderm, but zygotic genes sog and dpp, which are expressed uniformly in the former and latter domains, respectively, are required to maintain that initial subdivision and to define the amnioserosa. The bone morphogenetic proteins (BMPs), Sog and Dpp, are free to diffuse in the PV space (for a more detailed review of the biology of dorsal surface patterning see O’Connor et al., 2006). Dpp maintains expression of dorsally-acting genes, including itself, and Sog prevents Dpp from activating Dpp production in the lateral ectoderm (Biehs et al., 1996). At least five secreted zygotic gene products are required to specify dorsal ectoderm and the amnioserosa. These include Dpp and Screw (Scw) (which is another signaling BMP), two BMP inhibitors Sog and Twisted gastrulation (Tsg), and the protease Tolloid (Tld), which cleaves complexes of BMPs with Sog and/or Tsg, thereby freeing BMPs to bind to receptors (Biehs et al., 1996; Shimmi and O’Connor, 2003). The Type I receptors for Dpp (Thickvein: Tkv) and Scw (Saxophone: Sax) and the common Type II receptor Punt are all uniformly expressed in the embryo (Dorfman and Shilo, 2001). BMP signals are transduced by a heteromeric complex of Type I and II receptors, which phosphorylate members of the R-Smad family of transcription factors (Massague and Chen, 2000). Once phosphorylated, the R-Smads form a complex with a common Smad (co-Smad) and translocate to the nucleus where they regulate target gene activity. Signaling is assayed by the level of phosphorylated Mad (p-Mad), which initially appears in a dorsal strip 18–20 cells wide (20% of the circumference), but within ~40 minutes is refined to a strip 8–10 cells wide (Ross et al., 2001). Despite the fact that Scw is uniformly expressed, p-Mad expression only appears in the dorsal domain where Dpp is expressed, which shows that Mad phosphorylation requires simultaneous activation by Scw and Dpp (Nguyen et al., 1998). In fact, the early p-Mad pattern is not seen when Sax, Tkv, or Dpp are absent. However, several studies show that patterning of the dorsal region is robust to changes in the concentrations of some of the components in the signaling network. For example, heterozygous scw, sog, tld, or tsg mutant embryos are viable and do not show any apparent macroscopic phenotype (Mason et al., 1997; Eldar et al., 2002), despite broadened p-Mad expression for sogmutants (Shimmi et al., 2005; Wang and Ferguson, 2005).
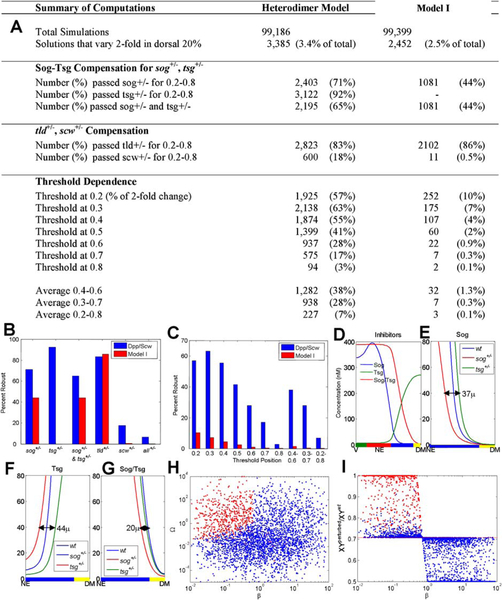
A major question concerning patterning in the dorsal region is how the BMP activity gradient is established. It is known that Sog and Tsg can form a trimeric complex with Dpp, thereby sequestering it, and that Sog in this complex can be cleaved by Tld, thereby releasing the ligand (Marques et al., 1997; Shimmi and O’Connor, 2003). The suggestion that facilitated transport of BMP may underly pattern formation within the dorsal domain of the embryo (Holley et al., 1995) could account for the fact that Sog and Tsg can have both positive and negative effects on the patterning process (Ross et al., 2001; Decotto and Ferguson, 2001). It has been widely believed that Sog, Tsg, and Tld can act to produce localization of BMPs at the dorsal midline, but how this occurs has remained unresolved until recently. A mathematical model by Eldar et al. (2002) took into account the formation of BMP–Sog dimers, incorporated the diffusion of Sog, BMP, and BMP–Sog, and allowed for the cleavage of Sog and BMP–Sog by Tld. Computational results showed that the model could produce a steady state distribution of BMPs that corresponds to the observed p-Mad distribution for certain choices of parameters, but analysis of the steady-state BMP distributions for wide ranges of the parameters showed that in most cases a prescribed threshold position of BMP shifted significantly with changes in the parameters. Halving the expression of tld, scw, and sog changed the threshold by less than 10% in only ~0.3% of the networks, and these were termed robust networks. Analysis of the robust networks showed insensitivity to most parameters, provided the following conditions were met (i) processing of Sog by Tld is BMP-dependent; (ii) unbound BMP does not diffuse; (iii) Dpp and Scw homodimer patterning is decoupled by the formation of the inhibitor complex Sog/Tsg; (iv) receptor binding is irreversible; and (v) Sog removes BMP from receptors (Eldar et al., 2002).
The first condition has been validated in vitro which suggests that analyzing a network for robustness properties can yield significant biological insight (Holley et al., 1996; Marques et al., 1997; Shimmi and O’Connor, 2003). Conditions (iv) and (v) have not been tested yet, but affinity assays may provide some insight into the validity of these requirements. Recently, it was demonstrated that the primary signaling molecule is a Dpp/Scw heterodimer, and that the loss of Scw precludes the formation of an extracellular Dpp gradient (Shimmi et al., 2005). Condition (ii) is more controversial: early experimental evidence suggested that BMP is indeed localized and this suggestion has been bolstered by extracellular Dpp-GFP staining using perivitelline injection (Eldar et al., 2002; Wang and Ferguson, 2005). However, in another study it was suggested that Dpp has an effective range of 15–20 cell diameters (Mizutani et al., 2005), while Scw can act over even larger distances (Wang and Ferguson, 2005).
To investigate establishment of the spatial pattern when the primary BMP can diffuse, a simple model was developed that could reproduce many of the observed phenotypes (Mizutani et al., 2005). Furthermore, it was demonstrated that embryos are not as robust with respect to changes in the level of Sog as previously reported, and that the mathematical model could not account for the large changes that are actually observed (Mizutani et al., 2005). Instead of limiting the diffusion of BMPs by reducing the diffusion coefficient, the extracellular BMP rapidly binds to immobile receptors and is degraded. This effectively limits the diffusion length of BMP to between 1 and 9 cell diameters and thus BMP is highly localized in the presence of diffusion.
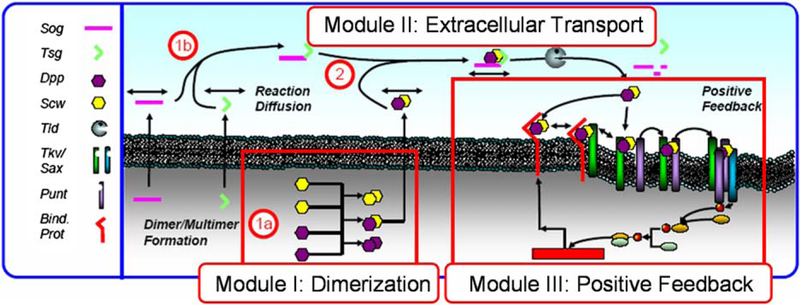
However one can ask whether freely diffusible Dpp can be redistributed by extracellular regulators to form the narrow, high-level signal at the dorsal midline of the embryo, even in the absence of receptors, or whether other transport mechanisms have to be invoked? If so, do the extracellular regulators Sog, Tsg, and Tld confer robustness with respect to changes in gene copy number, as is observed in heterozygous genetic mutants? The objectives in this section are three-fold. Firstly, the contributions of reaction and diffusion of Dpp with Sog, Tsg, and Tld are investigated to determine the balance of processes that lead to the transient evolution and steady-state spatial distribution of BMPs in the PV space. Since patterning occurs on a relatively short time scale, it is important to study both the transient evolution of the morphogen profile and the steady-state profile. Secondly, two models of extracellular transport are studied to determine what kinetic steps lower the sensitivity of the BMP distribution to reductions in gene copy number, as occurs in heterozygous mutants of sog, tsg, and tld. Also, since this is a fairly well-studied system, large-scale parameter screens of two patterning models are used to determine how sensitive the conclusions on robustness are to the specific choice of measurement method used, and the results are compared to those previously published for similar models (Eldar et al., 2002). Here it is shown that small changes in the kinetic structure of the model can enhance the robustness of extracellular patterning to changes in input. The cell-autonomous formation of Dpp/Scw before secretion into the PV-space along with dimerization of Sog and Tsg in the extracellular space buffer out changes in input independent of the specific method used to analyze the robustness. Lastly, we show that certain key aspects of the temporal evolution can be explained by incorporation of positive feedback in the signal transduction network. In order to investigate these aspects systematically we decompose the complete patterning system into three modules, as shown in Fig. 10.
Figure 10.
The modular description underlying the DV patterning model. 1a, 1b, and 2 show a two-stage dimerization cascade. (From Umulis et al., 2006, with permission.) See color insert.
A. The Model for DV Patterning
1. Dimerization of BMP Ligands and Extracellular Inhibitors
Mechanisms that confer robustness to changes in parameters, gene copy number, and other environmental conditions can be embedded in any stage in a hierarchical signal transduction system. For dorsal surface patterning, robustness can be gained or lost before secretion, during extracellular ligand patterning, or during receptor-signaling and feedback. Robustness of the full patterning model can be determined by analysis of each stage or module independently, followed by analysis of the linked modules. The first step at which compensation for reductions in the levels of ligand or inhibitor arises is during formation of the respective active ligand or inhibitor complexes. Dpp/Scw formation occurs intracellularly prior to secretion, whereas Sog/Tsg formation occurs in the PV-space. The local dynamics for heterodimer formation have been analyzed previously (Shimmi et al., 2005) and we review the main conclusions here.
Since the intracellular dimerization steps for Dpp/Scw formation occur in small volumes with high concentrations relative to the extracellular space, we assume that those processes equilibrate rapidly. This leads to the algebraic system
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
By defining the dimensionless variables , , , , and , the Eqs. (28)–(32) are simplified to:
| (33) |
| (34) |
| (35) |
| (36) |
wherein a(Ω) = 1 − 4Ω2, and b(λ, β, Ω) = 4Ω2(1 − β/λ) − 2. When Ω = 1/2, the relative change in production of the heterodimer to perturbations of the input is given by
| (37) |
| (38) |
| (39) |
| (40) |
| (41) |
| (42) |
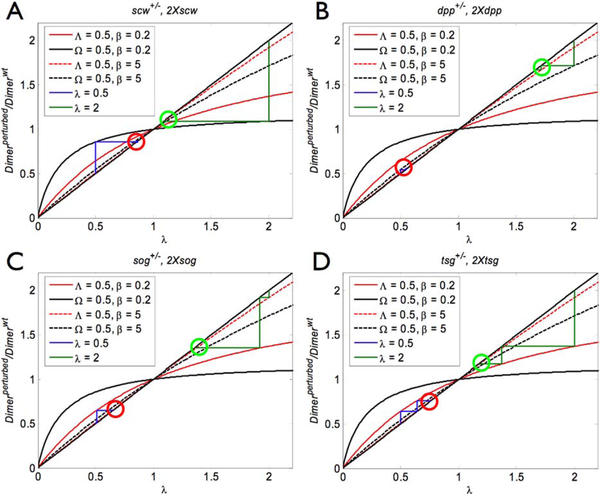
When heterodimer formation occurs according to this scheme, the level of compensation conferred on the heterodimer increases as the ratio of input production of monomer (β) decreases. As β approaches zero the ratio approaches 1, which means that the output production of the heterorodimer is unaffected. Formation of the heterodimer Dpp and Scw would significantly enhance the robustness of Dpp/Scw levels for changes in the production rate of Scw, but not Dpp, if Scw is present in slight excess. Example results showing the level of compensation for changes in the production of Dpp and Scw are shown in Figs. 11A and11B. The final compensation achieved by sequential dimerization of Dpp/Scw and Sog/Tsg is shown for 50% reductions in monomer production (lower red circle) and 100% increases in monomer production (upper green circle). The closer the output of the dimerization cascade is to 1, the greater the robustness of heterodimer output is to perturbations of the input.
Figure 11.
Heterodimer formation can reduce the effect of changes in the input, and a sequence of dimerization steps increases the robustness additively in the number of steps. Each curve in (A–D) shows the level of output heterodimer for changes in input monomer levels for different values of β with Ω = 0.5. The stairs indicate the level of compensation achieved for a sequence of dimerization reactions and the circles indicate the final level of heterodimer for reductions (red lower circle) and increases (green upper circle) for increases in the monomer input. Results are shown for reductions and increases in scw (A), dpp (B), sog (C), and tsg (D). See color insert.
The local dynamics for the production of the Sog/Tsg heterodimer is similar to the dimerization of Dpp and Scw with two key differences: Sog and Tsg binding is highly reversible since the molecules do not form a covalent bond, and secondly, Sog and Tsg do not form Sog–Sog and Tsg–Tsg homodimers once secreted (note: the Tsg molecule is actually a homodimer of two Tsg subunits which form before secretion and is irreversible). The local dynamics for Sog/Tsg formation can be represented by three ordinary differential equations:
| (43) |
| (44) |
| (45) |
We can solve the steady-state equations for Sog/Tsg and deduce the changes in output relative to changes in input. To simplify the results we define the dimensionless variables and the dimensionless parameters , where KST = k2γI /(k−2 + γI). This leads to the following dimensionless equations
| (46) |
| (47) |
and the solution of these is
| (48) |
| (49) |
wherein b = 1 + 2Λ(β − λ). Now the output ratio is
and the output level of heterodimer can be computed as before. The output for a two-level cascade of Sog/Tsg formation and binding to Dpp/Scw is shown in Figs. 11C and11D. It is clear that dimerization reduces the effect of changes in the levels of the input, but the magnitude of the effect depends on the input that is changed. For example, if Scw is in slight excess to Dpp, the output is less sensitive to changes in the level of Scw than Dpp and vice versa, and the compensation for changes in the level of Scw provides a filter in an early stage of patterning. The local dynamics for Sog and Tsg also suggest that dimerization could increase the level of robustness, but this has to be tested when transport is also included, and this is done in the following section.
2. Extracellular Patterning
We assume that the embryo is symmetric across a plane through the DV axis and orthogonal to the cross-section, and develop equations for the evolution of the species involved (Sog, Tsg, etc.) in an axial cross-section midway between the anterior and posterior poles of the embryo. In addition, since the PV space is narrow (~0.5 microns) in the direction normal to the inner membrane, we neglect variations in this direction and reduce the problem to one space dimension. The governing equations are as follows and descriptions of the variables are given in Table II.
II.
Dependent variables for the heterodimer-based model described by Eqs. (50)–(57) and the model due to Eldar et al. (2002) (to be defined later and referred to as Model I hereafter)
| Name | Description |
|---|---|
| Heterodimer model | |
| D | Dpp monomer |
| W | Scw monomer |
| DWin | Dpp/Scw (internal) |
| B | Dpp/Scw (PV space) |
| S | Sog |
| T | Tsg |
| I | Sog/Tsg |
| IB | Sog/Tsg–Dpp/Scw |
| Model I | |
| W | Scw monomer |
| W2in | Scw homodimer (internal) |
| W2 | Scw homodimer (PV space) |
| S | Sog |
| SW2 | Sog–Scw/Scw |
| (50) |
| (51) |
| (52) |
| (53) |
| (54) |
| (55) |
| (56) |
| (57) |
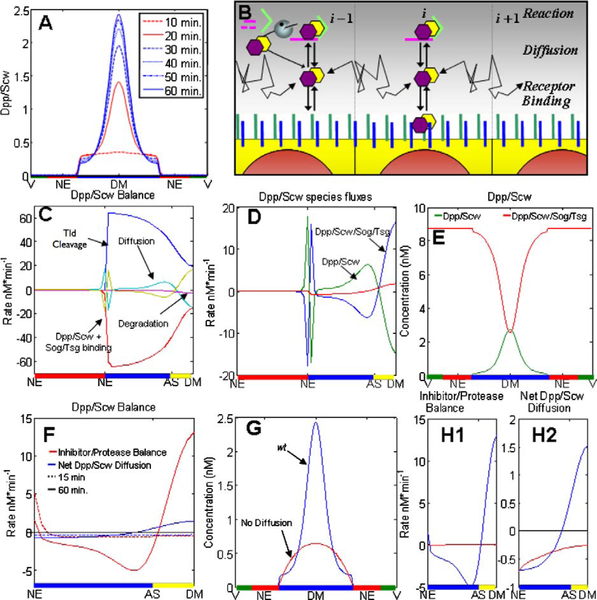
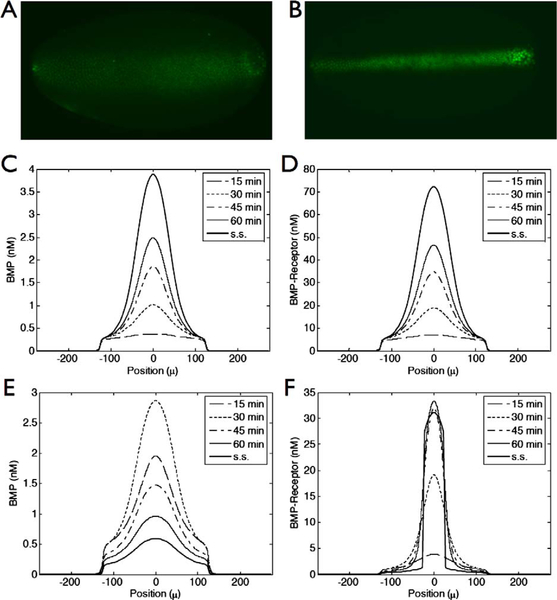
Numerical simulations of these equations were done with initial conditions set to zero for the levels of all species but Tld, which was uniformly distributed in the dorsal region. The results for the transient evolution of Dpp/Scw, assuming first-order degradation of Dpp/Scw, are shown at 15, 30, 45, and 60 minutes in Fig. 12A. One sees that the early profile (15 minutes) is broad and weak with a shallow peak near the dorsal midline. The shape at this time reflects the fact that Sog/Tsg is not yet present in sufficient quantities to sequester Dpp/Scw near the NE boundary. At 30 minutes the level of Sog/Tsg is high enough to foster localization of Dpp/Scw near the DM, and by 60 minutes, when the profile has essentially reached steady state, there are two distinct regions. Dpp/Scw levels are high near the DM, and with a suitable threshold in the downstream signal transduction pathway, the super-threshold region could specify the presumptive amnioserosa. Directly adjacent to the DM the profile is shallow and flat, which would produce a low level signal to specify the dorsal ectoderm. The evolution of the profile generally corresponds with the transient evolution of p-Mad in the embryo, but, as in previous models with time-independent BMP production, it does not capture the sharpening and contraction of the gradient (cf. Fig. 12A) (cf. Eldar et al., 2002; Mizutani et al., 2005, and the review in O’Connor et al., 2006).
Figure 12.
The transient Dpp/Scw activity gradient is established by interacting processes that limit receptor binding laterally and redistribute Dpp/Scw dorsally. (A) The temporal evolution of the spatial profile of Dpp/Scw/Tkv/Sax at the times indicated. (B) Schematic of reactions controlling localization of Dpp/Scw activity (for key see Fig. 10). (C–H) The spatial profile of Dpp/Scw, which determines the amount of bound receptor, results from a balance of Sog/Tsg binding, Tsg binding, and diffusion. (C) Spatial distribution of reaction and diffusion contributions to the shape of the Dpp/Scw activity distribution. Kinetic contributions from Sog/Tsg binding (red, rescaled 0.25×), Tsg (blue, rescaled 0.25×) are shown. Diffusion (blue/green) and degradation (purple) of Dpp/Scw reduces levels near the midline. (D) Dpp/Scw flux distribution in the dorsal region shows that diffusion of Dpp/Scw and Dpp/Scw/Tsg moves Dpp/Scw from the DM region toward the lateral regions while Dpp/Scw/Sog/Tsg redistributes Dpp/Scw towards the midline. (E) Spatial distribution of Dpp/Scw in various bound forms. (F) Net of Sog/Tsg binding and resupply from Tsg release after Tld cleavage (red) and net flux of Dpp/Scw in all forms (blue). Data is shown for 15 (dashed) and 60 (solid) minutes. (G) wt (blue) results are compared with solutions where the diffusion of Dpp/Scw/Sog/Tsg is set to zero (red). (H1) Inhibitor/Protease balance contributions to Dpp/Scw for cases described in (G). (H2) Contributions of combined Dpp/Scw redistribution for cases described in (G). The parameters used in the computations for these figures are given in the supplement to Umulis et al. (2006). See color insert.
3. Morphogen Gradient Shape Arises by Transport and Inhibitor/Protease Competition
We indicated earlier that the net rate of change of a species is the sum of contributions from various processes, and a plot of the spatial profiles of these individual contributions at 60 minutes is shown in Fig. 12C. The largest kinetic contributions to the local rate of change of Dpp/Scw in the dorsal region are from binding of Sog/Tsg and resupply from Dpp/Scw/Sog/Tsg after Sog is cleaved by Tld (Fig. 12C). The net contribution of these two processes (Fig. 12F) removes Dpp/Scw from the majority of the dorsal region (negative values) except near the dorsal midline where the net contribution is positive. Balancing the release of Dpp/Scw near the midline is diffusion and degradation (Fig. 12C).
The steady-state diffusion profiles of Dpp/Scw, and Dpp/Scw/Sog/Tsg are shown in Fig. 12D. One sees that the net Dpp/Scw flux is negative near the DM (i.e., Dpp/Scw diffuses away from the midline), positive near the AS boundary, and negative again near the NE boundary. In contrast, the Dpp/Scw/Sog/Tsg net flux is large and positive near the DM and the NE region, and negative in between. Thus there is a complicated pattern of diffusion of Dpp/Scw and its complexes. Since the complexes provide a source of Dpp/Scw after Tld processing, the Dpp/Scw profile reflects the balances between the diffusion of Dpp/Scw away from the midline and the facilitated diffusion of Dpp/Scw complexed with Sog/Tsg towards the midline. The spatial distributions of the various forms of Dpp/Scw are shown in Fig. 12E, and one sees there that the unbound form of Dpp/Scw is present at the lowest level of the two forms.
To understand the transient evolution of the Dpp/Scw profiles in Fig. 12A, we also examined the transient evolution of the kinetic terms for Sog/Tsg binding and Tld processing, as well as the evolution of the diffusion fluxes of all forms of Dpp/Scw (Fig. 12F). At 15 minutes, the net kinetic balance is negative (red, dashed) because Dpp/Scw binds rapidly to Sog/Tsg, but later the balance between binding and release is reversed. In addition, the net flux of Dpp/Scw near the midline is initially negative, which reflects the fact that all forms of Dpp/Scw diffuse away from the DM due to the localized binding to Sog at the NE boundary, which creates a sink. However this also reverses at later times (blue, solid). Later, the shoulders of the Dpp/Scw profile diminish as the peak near the dorsal midline increases, which is consistent with the transient evolution of the inhibitor/protease balance and net Dpp/Scw diffusion (Fig. 12F). To confirm our interpretation of the evolution, we set the diffusion coefficient of the Dpp/Scw/Sog/Tsg complex to zero. In Fig. 12G we show the profiles of Dpp/Scw after 60 minutes, for the wt and the nondiffusible Dpp/Scw/Sog/Tsg. Removing the diffusion of Dpp/Scw/Sog/Tsg reduces the maximum amplitude at the DM and abolishes the shoulder near the NE boundary. The changes in the balance between Tld processing and Sog/Tsg binding in the two cases, as well as the change in the net diffusion fluxes are shown in Figs. 12H1 and 12H2, respectively.
4. Simulations of Mutants Match Observed Phenotypes at Steady-State
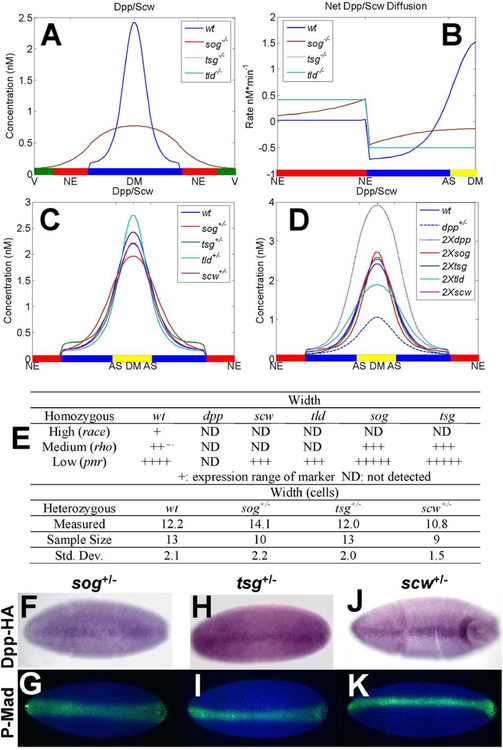
Next we examine the effect of mutations on patterning. We model the homozygous mutants sog−/−, tsg−/−, scw−/−, and tld−/− by computing Dpp/Scw profiles with the production rates for the appropriate component set to zero (e.g., Sog in a sog−/− mutant). The profiles for homozygous mutants are shown in Fig. 13A at 60 minutes, and the corresponding experimentally-observed phenotypes are listed in Fig. 13E. Sog mutants cannot redistribute the Dpp/Scw ligand, and this leads to broad and low morphogen distribution between the levels necessary to specify the dorsal ectoderm and presumptive amnioserosa. In sog and tsg mutants, the high level target race is lost, but, medium level rho, and low level pnr are expanded (Fig. 13E) (Jazwinska et al., 1999; Nguyen et al., 1998; Shimmi and O’Connor, 2003; Shimmi et al., 2005). This suggests that in mutant embryos the dorsal ectoderm enlarges at the expense of the presumptive amnioserosa, which does not form. Consistent with this finding is the observation that in a sog mutant, enough BMP diffuses into the neurogenic ectoderm to turn on dorsal genes (Biehs et al., 1996). In this case the only mechanism for redistribution is diffusion of Dpp/Scw (Fig. 13B). In the tld mutant, p-Mad expression is low and embryos are unable to fully specify dorsal ectoderm or amnioserosa. In the absence of Tld, the gradient of Dpp/Scw/Sog/Tsg that leads to transport toward the DM is lost and the net Dpp/Scw flux is slightly negative (Fig. 13B). Here Sog/Tsg sequesters Dpp/Scw throughout the PV space and facilitates the transport of Dpp/Scw out of the dorsal region. This effectively removes Dpp/Scw from the vicinity of the dorsal region, resulting in a strongly ventralized embryo.
Figure 13.
Homozygous and heterozygous computation results correspond well with observed pheno-types. (A) Dpp/Scw/Tkv/Sax profile is shown for wt (blue), and homozygous mutant sog- (red), tsg- (green), scw- (purple), and tld- (blue/green) after 60 minute of patterning time. (B) Net diffusion of Dpp/Scw in homozygous mutants. Dpp/Scw/Tkv/Sax profile is shown for (C) wt and heterozygous mutant sog+/−, tsg+/−, tld+/−, and scw+/−. (D) wt, dpp+/−, 2X dpp, and 2X scw. (E) Top: Summary of homozygous mutant target gene expression profiles (1, 11, 23, 26) (* denotes data not shown). Bottom: Width of p-Mad activity for heterozygous mutants. (F–K) Dpp-HA accumulates in a narrow stripe that corresponds well with p-Mad signaling in sog+/−, tsg+/−, and scw+/− heterozygotes. Staining techniques are as described in Shimmi et al. (2005). See color insert.
It was suggested previously that the p-Mad profile in Drosophila embryos was unchanged in heterozygous mutant embryos, but in that study the variability was not addressed (Eldar et al., 2002). We measured the width in cell numbers of the p-Mad stripe in various heterozygous mutant backgrounds wt (12.2), sog+/− (14.1), tsg+/− (12.0), and scw+/− (10.8) in 13, 10, 13, and 9 embryos, respectively, (cf. Figs. 13F–13K). The embryos are largely insensitive to reductions in copy number for these genes, but we note that sog+/− mutant embryos show an expansion in the width of the p-Mad stripe by about 2–3 cells (15–25%) on average. Others have also noted that the system is somewhat sensitive to sog gene copy number (Mizutani et al., 2005; Wang and Ferguson, 2005). To compare these data with the model predictions, we simulated heterozygous mutant profiles by reducing the input or level of the heterozygous factor by 50%. For certain choices of parameters, the Dpp/Scw morphogen distribution is insensitive to the heterozygous mutant genotypes for all reductions except Dpp (cf. Fig. 13C). Analysis of Model I showed that this insensitivity could only be achieved if (i) Dpp and Scw homodimer patterning is decoupled by formation of Sog/Tsg, and (ii) free BMP does not diffuse (Eldar et al., 2002), but these conditions are not necessary in the present model. Here the diffusion constant for Dpp/Scw was estimated from standard correlations to be 73 μ2 s−1 (Young et al., 1980), and all binding steps are reversible, which implies that free BMP is less tightly localized than in earlier models (Eldar et al., 2002).
5. Selective Use of Heterodimers Enhances Robustness: Extracellular Patterning
The spatial distributions of BMPs predicted by the heterodimer patterning model can also be tested for their sensitivity to changes in other kinetic components. To determine whether changes in the kinetic interactions of Dpp and Scw in the steps prior to secretion, or changes in the steps for the formation of Sog/Tsg heterodimers, enhance or reduce robustness of the spatial distributions of BMPs, a wide range of parameters was tested, and the results were compared to those predicted by Model I, given by Eqs. (58)–(62) below. The heterodimer-based model contains three heteromer formation steps, namely Sog + Tsg, Dpp + Scw, and Sog/Tsg + Dpp/Scw, whereas Model I contains only one, formation of BMP/Sog. We did not explicitly compare the model developed by Mizutani et al. (2005), but we expect the degree of robustness with respect to variations in Sog, Tsg, and Tld to be the same as in the heterodimer model, since both rely on the selective use of the Sog/Tsg heterodimer that binds to BMP and is cleaved by Tld.
| (58) |
| (59) |
| (60) |
| (61) |
| (62) |
In this case the balance on the homodimer is trivial, and leads to an input of BMP to the extracellular patterning of VinϕW/2VPV. Here Vin/Vpv = 1 × 10−3 and ϕW = 10 μMmin−1.
The protocol for the computations and comparisons is as follows. Parameters in both sets of equations were chosen randomly from uniform distributions, ranging over 5 orders of magnitude for the forward and reverse binding reactions (10−3–101 min−1 nM−1 or min−1), 4 orders of magnitude for the degradation/internalization rates (10−3–100 min−1), 3 orders of magnitude (0.01–1 nM s−1 cell−1) for the production rates, and 2 orders of magnitude (1 μ2 s−1–100 μ2 s−1) for the diffusion coefficients. Once a set of random parameter values is chosen, a base case or wt profile for each component is calculated, and the spatial distribution of each species is normalized by the maximum concentration of that component. It is observed experimentally that p-Mad staining occurs in the dorsal-most 10–15% cells, corresponding to the localization of Dpp/Scw (Figs. 3F–3K), and therefore we consider computational solutions that show at least a 2-fold change in the Dpp/Scw concentration within the dorsal-most 20% of the embryo suitable for specification of the amnioserosa. All other components are ignored in this criterion.
A total of 99,186 steady-state solutions were calculated for the heterodimer system and 99,399 solutions for Model I, and of these, 3385 (3.4%) were admissible in the heterodimer model, whereas 2452 (2.5%) for Model I met the criterion. Then for each admissible set of parameters, the spatial distributions for the heterozygous genotypes for sog+/− and tsg+/− were computed after reducing the production of each protein to 50% of the wt level. Each mutant profile was normalized by the wt maximum and then compared with the wt to determine the sensitivity of the BMP distribution to that perturbation of the input. Usually robustness is measured by the magnitude of the spatial shift of the ‘perturbed’ case versus the base case at a specified threshold value of the morphogen. However morphogens usually specify multiple targets in a concentration-dependent manner, and thus basing robustness on a single level is inappropriate: the entire shape of profile should be considered in a criterion for robustness. To illustrate the inadequacy of tests based on a single threshold, Fig. 14 shows an example ‘base case’ distribution (the triangle) and a ‘perturbed’ or mutant profile (the rectangle). If the threshold is set at the morphogen level 2 one would conclude that the profiles are robust, but they clearly are not, since threshold levels at position 1 (resp., 3) would indicate that the mutant profile is wider (resp., narrower) than the base case. There are many ways to measure the difference between two profiles and we use the following one for comparing wt and mutant profiles. Regard the morphogen level as the independent variable, invert the position–concentration relation for each profile to obtain position as a function of concentration, integrate the absolute value of the difference in the positions for the profiles, and divide by the concentration range. A mutant profile was judged admissible if the region of high intensity p-Mad staining, determined by computing the integral average of the absolute value of the differences between the wt and heterozygous cases over the central 60% (from 20–80%) of the wt profile, changed by less than 10 μ in the half-width of the embryo. This corresponds to a change of less than 4 cells with high intensity p-Mad staining in the entire dorsal region.
Figure 14.
An illustration of how fixing a single morhpogen threshold as the criterion for robustness can be misleading. See color insert.
6. Sog/Tsg Formation Compensates for Reductions in Both Sog and Tsg
In the heterodimer-based model, 71% of the sog+/− solutions shifted by less than 10 μm, whereas in Model I only 44% met the same criterion. More (92%) passed in the heterodimer-based model for reductions in the level of Tsg and 65% passed when compensation for 50% reductions in both Sog and Tsg were considered independently. This is still about 50% more than the monomer-based model. These data suggest that transport by the heteromeric complex Sog/Tsg enhances compensation for reductions in the levels of both Sog and Tsg (Figs. 15A–15C).
Figure 15.
Robustness of the heterodimer-based model. (A) Summary of computation results comparing the simplified heterodimer-based model (50)–(57) with a previous model based on monomers and homodimers. (B–C) Histograms show that the heterodimer-based model is less sensitive to most types of heterozygous mutant perturbations (B), and produces more robust hits at every threshold position chosen between 20 and 80% of wt (C). (D) The wt distribution of Sog, Tsg, and Sog/Tsg. (E–G) wt and sog+/− and tsg+/− distributions of Sog, Tsg, and Sog/Tsg. (H–I) Solutions robust with respect to scw+/− (red) vs nonrobust (blue) are shown for different values of Ω and β (H) and also for Dpp/Scwperturbed/Dpp/Scwwt vs β (I). See color insert.
Our previous analysis of heterodimer production suggested that Sog/Tsg formation can compensate for reductions of Tsg, and to a lesser extent Sog (Shimmi et al., 2005). The results here reflect this imbalance, in that there are many more solutions that are robust to decreases in Tsg and fewer for Sog. However, when compared to Model I, which incorporates only Sog, Sog/Tsg formation enhances robustness overall, and leads to more robust solutions when both heterozygotes sog+/− and tsg+/− are considered. Since Sog and Tsg diffuse in the PV space and form a Sog/Tsg complex that has a high affinity for BMP, the shift in their profiles under changes in their inputs provides insight into the origin of robustness. Fig. 15D shows the wt profiles of Sog, Tsg, and Sog/Tsg, and the mutant distributions for Sog, Tsg, and Sog/Tsg are shown in Figs. 15E–15G, respectively. Sog and Tsg compensate for the partial loss of the other component by shifting in the same direction, thereby reducing the effect of the perturbation on the formation of Sog/Tsg, and thus on the Sog/Tsg distribution. As expected, the buffering is not symmetric and the Sog/Tsg profile is more sensitive to reductions of Sog than Tsg, which agrees with the experimentally observed shift in p-Mad signaling. However, it is noteworthy that the Sog distribution itself is less sensitive to perturbations in the presence of Tsg, which suggests that perturbations are distributed to Tsg by the Sog/Tsg complex.
It was previously reported that patterning by BMPs is also insensitive to knock-downs in scw, i.e.„ there is no phenotypic change for scw+/− mutant genotypes (Eldar et al., 2002). We found that scw+/− embryos actually narrowed by about 1 nucleus on average (Fig. 13E). Computationally we found that in the heterodimer-based model 18% of the solutions were robust under reductions in Scw. This stands in sharp contrast to the results for Model I, for which only 0.5% of solutions passed the same test (Figs. 15A–15B).
When considering reductions in Tld, 83% of the perturbed met the criterion for insensitivity vs Model I’s 86%. Since Tld interactions in the two models are nearly equivalent, we would expect roughly the same number of robust solutions.
7. Robustness Depends on Threshold Position and Measurement
The number of solutions that passed the test for Model I (here 0.1%) is fewer than reported previously (0.3%), and the difference stems from the difference in the specific measure of robustness used. Here robustness is measured using an integral average over a majority of the wt profile, rather than judging robustness by the shift in location of a chosen threshold value. Indeed, if a narrower range or a specific threshold value is used, the number of robust solutions increases for both models. For a narrower range of the integral average and for threshold choices in 10% increments from 20% of the wt profile up to 80% (Figs. 15B–15C) the number of robust profiles increases from 7% (0.1%) to a maximum of 63% (10%) for the heterodimer model and Model I, respectively. The heterodimer-based model has significantly more robust solutions at all thresholds chosen between 0.2 and 0.8 of the wt maximum, ranging from 5.7–93 times, depending on the threshold position or range used (Fig. 15A).
B. The Role of Positive Feedback
Module I (dimerization) and II (extracellular transport) enhance the robustness by limiting the range of ligand diffusion and buffering changes in monomer levels by forming active heterodimers. However, the current extracellular patterning model with constant ligand production cannot reproduce the experimentally-observed transient evolution of p-Mad staining observed in wt embryos. One way to overcome this is to have a pulse or transient input of the BMP ligand (Eldar et al., 2002), but this is not likely to occur during development since dpp expression persists throughout cell cycle 14. Another possibility suggested by Wang and Ferguson (2005) is that BMP signaling initiates expression of a protein that enhances binding of Dpp to the receptors by localizing Dpp at the surface. When positive feedback of a surface bound BMP-binding protein is included in the BMP patterning model, the level of BMP-bound receptors contracts in time to produce a sharp distribution that corresponds well with embryonic p-Mad staining (Umulis et al., 2006). Positive feedback and receptor interactions make up the third module for dorsal surface patterning, which can be modeled as an autonomous unit since the receptors and other complexes do not diffuse. However, analysis of the third module’s contribution to overall patterning is more complex than for modules 1 and 2, since the extracellular distribution of Dpp and receptor processes are highly coupled (Umulis et al., 2006).
Interestingly, inclusion of positive feedback does not reduce the upstream contributions to robustness of patterning, and actually enhances the robustness of the mechanism to changes in the level of receptors (Umulis et al., 2006). Inclusion of positive feedback leads to a distribution of BMP bound receptors that contracts in time and ultimately produces a step-like profile due to a bi-stability in the local dynamics (Umulis et al., 2006) (see Fig. 16). Another interesting consequence of positive feedback is that the level of signaling is determined by the temporal course of exposure to extracellular BMP, rather than by the level at a fixed time. Thus the history of the ligand exposure rather than only the instantaneous level is important for the transient response in this patterning mechanism, as in other systems (Dillon and Othmer, 1999; Harfe et al., 2004). Dynamic interpretation of the morphogen has also been suggested in the context of anterior–posterior patterning (Bergmann et al., 2007).
Figure 16.
Positive feedback of a surface-bound BMP-binding protein leads to contraction of BMP-receptors towards the dorsal-midline in time. (A) early, and (B) late p-Mad distributions, showing the contraction in later stages. (C–F) Simulation results for the evolution of extracellular BMP and BMP-bound receptor levels in time for two versions of module III: (C–D) receptor mediated endocytosis, and (E–F) positive feedback of a BMP-binding protein. The level of BMP-bound receptors widens for any chosen threshold in (D). (F) The distribution of BMP-bound receptors contracts in time for low-levels, while growing in amplitude near the dorsal midline. See color insert.
VI. Conclusions
Mathematical models of embryonic development can provide insights into the complex interactions between spatial variations in morphogens, signal transduction, and intracellular response in patterning processes. Mechanistic models of specific processes based on our current understanding of them provide an additional tool to help in understanding the complex regulation of development. In addition to the fundamental biological questions concerning the structure of components and pathways, mathematical models introduce a host of new questions. For example, how do signal transduction networks respond to perturbations in the levels of molecules, and how do changes in the length of the system affect patterning? How can the often nonintuitive behavior observed in vivo be reconciled with in vitro data? What is the potential function of a novel gene? Incorporating mechanistic models during experimental design and data analysis will enrich our understanding of individual biological processes and of the system as an integrated unit rather than just the sum of its parts.
We have discussed a number of different aspects of robustness in Drosophila embryonic patterning, and have shown how the models lead to new insights concerning scale-invariance in AP patterning, the role of network topology and signature in the switching network used for control of the segment polarity genes, and the role of signaling via heterodimers in DV patterning. The modular decomposition of DV patterning described herein is based on the current understanding of the kinetic interactions between morphogens and inhibitors in the PV space, and incorporates the various dimeric forms of inhibitors and signaling BMPs.
Scale-invariance is a basic feature of a number of developmental processes. The conservation of morphogen binding sites and production between different size organisms may be a natural way to ensure scale-invariance without requiring additional levels of regulation such as feedback, opposing gradients or rescaling of the diffusion coefficients. A side effect of achieving scale-invariance by modulating the time scale of the kinetics (done here by invariance of the number of binding sites for different-sized embryos) is that the time to reach a steady-state distribution increases in proportion to the length of the system squared.
A rather surprising result is that the robustness of DV spatial patterning can essentially be predicted from an analysis of the local dynamics. Transport certainly plays a role in the establishment of the spatial distribution of all components, but the key property of the kinetic interactions that produces robustness is the use of heterodimeric species for both the primary signaling molecule (Dpp/Scw) and the primary inhibitor (Sog/Tsg). Previously we showed that the use of heterodimers, rather than monomers or homodimers, can compensate particularly well for changes in Scw, and that a cascade of stages in which heterodimers are dominant can provide a high degree of compensation (Shimmi et al., 2005). Here the analysis of the spatially-distributed system corroborates the earlier results and provides further evidence for the selective advantage of using heterodimers for signal transduction and morphogenesis. We found that robustness with respect to reductions in Scw requires that β = ϕDpp/ϕScw be less than 0.71 (Fig. 15H), which means that Scw production must be slightly larger than Dpp production. Robustness is also favored by large values of Ω = K1/2(K2K3)1/2, which means that heterodimer formation must be favored over the homodimer counterparts Dpp/Dpp and Scw/Scw. These results correspond well with our earlier analysis of a simplified system (Shimmi et al., 2005), as can be seen by a comparison of Fig. 15I herein and Fig. 6C in (Shimmi et al., 2005).
In the absence of positive feedback, tight localization of nanomolar levels of Dpp/Scw requires a binding rate of Dpp/Scw to the Sog/Tsg complex that approaches the theoretical maximum of ~109 M−1 s−1 (Keizer, 1987). The kinetics of Sog binding, Tld cleavage and receptor binding operate in a similar dynamic range with on-rates approximately 1000 times lower than the level necessary to localize BMPs in the absence of receptors, or at lower rates of Dpp (Eldar et al., 2002; Shimmi and O’Connor, 2003; Mizutani et al., 2005). Thus, while the tight localization of BMPs by Sog and Tsg is theoretically possible, other mechanisms are required to either limit the diffusion of Dpp/Scw or reinterpret the shallow gradient and amplify small differences in concentration. One possible mechanism that can produce the sharp p-Mad distribution is positive feedback on a factor that enhances Dpp binding to its receptor by localizing Dpp. Addition of positive feedback does not offset the robustness gained in upstream mechanisms, but rather enhances it with respect to changes in the level of receptors, when compared to simple equilibrium receptor binding and other similar mechanisms (Umulis et al., 2006). Positive feedback can lead to the contraction of p-Mad signaling in time, which is observed during dorsal surface patterning and also in a related signaling mechanism during wing vein patterning. Thus, the spatial refinement of components may be a general property of BMP pathways, and additional experiments are necessary to determine the nature of the positive feedback.
Acknowledgments
This research was funded in part by NIH Grant GM29123 and NSF Grants DMS-0317372 and DMS-0517884 to HGO, and by a Biotechnology Training Grant (DMU). MBO is an Investigator with the Howard Hughes Medical Institute.
Footnotes
Note added in proof
Since acceptance of this paper, two papers have appeared that deal with the issues discussed herein (Gregor et al., 2007a; Gregor et al., 2007b). Gregor et al. developed a Bicoid–GFP fusion protein to study the dynamics, reproducibility, and other aspects of morphogen patterning in the Drosophila syncytium, and they discuss theoretical approaches to the reliability of threshold determination.
Of course if there are sources or sinks at the boundary, as in (6), then there is also preexisting differentiation of some cells.
References
- Aegerter-Wilmsen T, Aegerter CM, and Bisseling T (2005). Model for the robust establishment of precise proportions in the early Drosophila embryo. J. Theor. Biol 234(1), 13–19. [DOI] [PubMed] [Google Scholar]
- Albert R, and Othmer HG (2003). The topology of the regulatory interactions predicts the expression pattern of the segment polarity genes in Drosophila melanogaster. J. Theor. Biol 223(1), 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberts B, Bray D, Lewis J, Raff M, Roberts K, and Watson JD (1994). “Molecular Biology of The Cell.” Garland Publishing Inc., New York. [Google Scholar]
- Bergmann S, Sandler O, Sberro H, Shnider S, Schejter E, Shilo B-Z, and Barkai N (2007). Presteady-state decoding of the Bicoid morphogen gradient. PLoS Biol. 5(2), e46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biehs B, Francois V, and Bier E (1996). The Drosophila short gastrulation gene prevents Dpp from autoactivating and suppressing neurogenesis in the neuroectoderm. Genes Dev 10(22), 2922–2934. [DOI] [PubMed] [Google Scholar]
- Castets V, Dulos E, and Kepper P.De. (1990). Experimental evidence of a sustained standing Turing-type nonequilibrium chemical pattern. Phys. Rev. Lett 64(24), 2953–2956. [DOI] [PubMed] [Google Scholar]
- Claxton JH (1964). The determination of patterns with special reference to that of the central primary skin follicles in sheep. J. Theor. Biol 7, 302–317. [DOI] [PubMed] [Google Scholar]
- Crauk O, and Dostatni N (2005). Bicoid determines sharp and precise target gene expression in the Drosophila embryo. Curr. Biol 15(21), 1888–1898. Comparative study. [DOI] [PubMed] [Google Scholar]
- Decotto E, and Ferguson EL (2001). A positive role for Short gastrulation in modulating BMP signaling during dorsoventral patterning in the Drosophila embryo. Development 128(19), 3831–3841. [DOI] [PubMed] [Google Scholar]
- Dillon R, and Othmer HG (1999). A mathematical model for outgrowth and spatial patterning of the vertebrate limb bud. J. Theor. Biol 197(3), 295–330. [DOI] [PubMed] [Google Scholar]
- Dillon R, Maini PK, and Othmer HG (1994). Pattern formation in generalized Turing systems. I. Steady-state patterns in systems with mixed boundary conditions. J. Math. Biol 32(4), 345–393. [Google Scholar]
- Dorfman R, and Shilo BZ (2001). Biphasic activation of the BMP pathway patterns the Drosophila embryonic dorsal region. Development 128(6), 965–972. [DOI] [PubMed] [Google Scholar]
- Eldar A, Dorfman R, Weiss D, Ashe H, Shilo BZ, and Barkai N (2002). Robustness of the BMP morphogen gradient in Drosophila embryonic patterning. Nature 419(6904), 304–308. [DOI] [PubMed] [Google Scholar]
- Frohnhöfer HG, and Nüsslein-Volhard C (1986). Manipulating the anteroposterior pattern of the Drosophila embryo. J. Embryol. Exp. Morphol. (October) 97(Suppl.), 169–179. [PubMed] [Google Scholar]
- Gilbert SF (2006). “Developmental Biology,” 8th ed Sinauer Associates, Inc., Sunderland, MA. [Google Scholar]
- Gregor T, Bialek W, de Ruyter van Steveninck RR, Tank DW, and Wieschaus EF (2005). Diffusion and scaling during early embryonic pattern formation. Proc. Natl. Acad. Sci. USA 102(51), 18403–18407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregor T, Wieschaus EF, McGregor AP, Bialek W, Tank DW (2007a). Stability and nuclear dynamics of the bicoid morphogen gradient. Cell 130(1), 141–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregor T, Tank DW, Wieschaus EF, Bialek W (2007b). Probing the limits to positional information. Cell 130(1), 153–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossniklaus U, Pearson RK, and Gehring WJ (1992). The Drosophila sloppy paired locus encodes two proteins involved in segmentation that show homology with mammalian transcription factors. Genes Dev. 6, 1030–1051. [DOI] [PubMed] [Google Scholar]
- Harfe BD, Scherz PJ, Nissim S, Tian H, McMahon AP, and Tabin CJ (2004). Evidence for an expansion-based temporal Shh gradient in specifying vertebrate digit identities. Cell 118(4), 517–528. [DOI] [PubMed] [Google Scholar]
- Hashimoto C, Gerttula S, and Anderson KV (1991). Plasma membrane localization of the Toll protein in the syncytial Drosophila embryo: Importance of transmembrane signaling for dorsal–ventral pattern formation. Development 111(8), 1021–1028. [DOI] [PubMed] [Google Scholar]
- Holley SA, Jackson PD, Sasai Y, Lu B, De Robertis EM, Hoffmann FM, and Ferguson EL (1995). A conserved system for dorsal–ventral patterning in insects and vertebrates involving sog and chordin. Nature 376, 249–253. [DOI] [PubMed] [Google Scholar]
- Holley SA, Neul JL, Attisano L, Wrana JL, Sasai Y, O’Connor MB, De Robertis EM, and Ferguson EL (1996). The Xenopus dorsalizing factor noggin ventralizes Drosophila embryos by preventing DPP from activating its receptor. Cell 86(4), 607–617. [DOI] [PubMed] [Google Scholar]
- Houchmandzadeh B, Wieschaus E, and Leibler S (2002). Establishment of developmental precision and proportions in the early Drosophila embryo. Nature 415(6873), 798–802. [DOI] [PubMed] [Google Scholar]
- Houchmandzadeh B, Wieschaus E, and Leibler S (2005). Precise domain specification in the developing Drosophila embryo. Phys. Rev. E Stat. Nonlin. Soft Matter. Phys 72(6 Pt 1), 061920. [DOI] [PubMed] [Google Scholar]
- Howard M, and ten Wolde PR (2005). Finding the center reliably: Robust patterns of developmental gene expression. Phys. Rev. Lett 95(20), 208103. [DOI] [PubMed] [Google Scholar]
- Ingham PW, Taylor AM, and Nakano Y (1991). Role of the Drosophila patched gene in positional signaling. Nature 353, 184–187. [DOI] [PubMed] [Google Scholar]
- Ingolia NT (2004). Topology and robustness in the Drosophila segment polarity network. PLoS Biol. 2(6), E123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaeger J, Surkova S, Blagov M, Janssens H, Kosman D, Kozlov KN, Myasnikova E, Vanario-Alonso CE, Samsonova M, Sharp DH, and Reinitz J (2004). Dynamic control of positional information in the early Drosophila embryo. Nature 430(6997), 368–371. [DOI] [PubMed] [Google Scholar]
- Jazwinska A, Rushlow C, and Roth S (1999). The role of brinker in mediating the graded response to Dpp in early Drosophila embryos. Development 126(15), 3323–3334. [DOI] [PubMed] [Google Scholar]
- Keizer J (1987). Diffusion effects on rapid bimolecular chemical reactions. Chem. Rev 87(1), 167–180. [Google Scholar]
- Kerszberg M (1999). Morphogen propagation and action: Towards molecular models. Semin. Cell Dev. Biol 10(3), 297–302. Review. [DOI] [PubMed] [Google Scholar]
- Kerszberg M, and Wolpert L (1998). Mechanisms for positional signaling by morphogen transport: A theoretical study. J. Theor. Biol 191(1), 103–114. [DOI] [PubMed] [Google Scholar]
- Lander A, Nie Q, and Wan FYM (2002). Do morphogen gradients arise by diffusion? Dev. Cell 2, 785–796. [DOI] [PubMed] [Google Scholar]
- Levine M, and Davidson EH (2005). Gene regulatory networks for development. Proc. Natl. Acad. Sci. USA 102(14), 4936–4942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margolis JS, Borowsky ML, Steingrimsson E, Shim CW, Lengyel JA, and Posakony JW (1995). Posterior stripe expression of hunchback is driven from two promoters by a common enhancer element. Development 121(9), 3067–3077. [DOI] [PubMed] [Google Scholar]
- Marques G, Musacchio M, Shimell MJ, Wunnenberg-Stapleton K, Cho KW, and O’Connor MB (1997). Production of a DPP activity gradient in the early Drosophila embryo through the opposing actions of the SOG and TLD proteins. Cell 91(3), 417–426. [DOI] [PubMed] [Google Scholar]
- Mason E, Williams S, Grotendorst G, and Marsha J (1997). Combinatorial signaling by twisted gastrulation and decapentaplegic. Mech. Dev 64(1–2), 61–75. [DOI] [PubMed] [Google Scholar]
- Massague J, and Chen YG (2000). Controlling TGF-beta signaling. Genes Dev. 14(6), 627–644. [PubMed] [Google Scholar]
- Mizutani CM, Nie Q, Wan FY, Zhang YT, Vilmos P, Sousa-Neves R, Bier E, Marsh JL, and Lander AD (2005). Formation of the BMP activity gradient in the Drosophila embryo. Dev. Cell 8(6), 915–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morisato D, and Anderson KV (1994). The spatzle gene encodes a component of the extracellular signaling pathway establishing the dorsal–ventral pattern of the Drosophila embryo. Cell 76, 677–688. [DOI] [PubMed] [Google Scholar]
- Nagorcka BN, and Mooney JR (1982). The role of a reaction–diffusion system in the formation of hair fibres. J. Theor. Biol 98, 575–607. [DOI] [PubMed] [Google Scholar]
- Nguyen M, Park S, Marques G, and Arora K (1998). Interpretation of a BMP activity gradient in Drosophila embryos depends on synergistic signaling by two type I receptors, SAX and TKV. Cell 95(4), 495–506. [DOI] [PubMed] [Google Scholar]
- O’Connor MB, Umulis DM, Othmer HG, and Blair SS (2006). Shaping BMP morphogen gradients in the Drosophila embryo and pupal wing. Development 133, 183–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Othmer HG (1980). Synchronized and differentiated modes of cellular dynamics In “Dynamics of Synergetic Systems” (Haken H, Ed.), Springer-Verlag, Berlin/London. [Google Scholar]
- Othmer HG, and Pate E (1980). Scale-invariance in reaction–diffusion models of spatial pattern formation. Proc. Natl. Acad. Sci. USA 77(7), 4180–4184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reeves GT, Muratov CB, Schupbach T, and Shvartsman SY (2006). Quantitative models of developmental pattern formation. Dev. Cell 11(3), 289–300. [DOI] [PubMed] [Google Scholar]
- Ross JJ, Shimmi O, Vilmos P, Petryk A, Kim H, Gaudenz K, Hermanson S, Ekker SC, O’Connor MB, and Marsh JL (2001). Twisted gastrulation is a conserved extracellular BMP antagonist. Nature 410(6827), 479–483. [DOI] [PubMed] [Google Scholar]
- Sen J, Goltz JS, Stevens L, and Stein D (1998). Spatially restricted expression of pipe in the Drosophila egg chamber defines embryonic dorsal–ventral polarity. Cell 95(4), 471–481. [DOI] [PubMed] [Google Scholar]
- Sen J, Goltz JS, Konsolaki M, Schupbach T, and Stein D (2000). Windbeutel is required for function and correct subcellular localization of the Drosophila patterning protein Pipe. Development 127(24), 5541–5550. [DOI] [PubMed] [Google Scholar]
- Shimmi O, and O’Connor MB (2003). Physical properties of Tld, Sog, Tsg, and Dpp protein interactions are predicted to help create a sharp boundary in Bmp signals during dorsoventral patterning of the Drosophila embryo. Development 130(19), 4673–4682. [DOI] [PubMed] [Google Scholar]
- Shimmi O, Umulis D, Othmer HG, and O’Connor MB (2005). Facilitated transport of a Dpp/Scw heterodimer by Sog/Tsg leads to robust patterning of the Drosophila blastoderm embryo. Cell 120(6), 873–886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sick S, Reinker S, Timmer J, and Schlake T (2006). WNT and DKK determine hair follicle spacing through a reaction–diffusion mechanism. Science 314(5804), 1447–1450. [DOI] [PubMed] [Google Scholar]
- Sontag ED (2003). Adaptation and regulation with signal detection implies internal model. Syst. Control Lett. 50, 119–126. [Google Scholar]
- Strigini M (2005). Mechanisms of morphogen movement. J. Neurobiol 64(4), 324–333. [DOI] [PubMed] [Google Scholar]
- Tabata T, Eaton S, and Kornberg TB (1992). The Drosophila hedgehog gene is expressed specifically in posterior compartment cells and is a target of engrailed regulation. Genes Dev. 6, 2635–2645. [DOI] [PubMed] [Google Scholar]
- Turing AM (1952). The chemical basis of morphogenesis. Philos. Trans. R. Soc. London Ser. B Biol. Sci 237, 37–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umulis DM, Serpe M, O’Connor MB, and Othmer HG (2006). Robust, bistable patterning of the dorsal surface of the Drosophila embryo. Proc. Natl. Acad. Sci. USA 103(31), 11613–11618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umulis DM, O’Connor MB, and Othmer HG (2007). Scale-invariance, Embryon. Dev (in preparation). [Google Scholar]
- von Dassow G, Meir E, Munro EM, and Odell GM (2000). The segment polarity network is a robust developmental module. Nature 406(6792), 188–192. [DOI] [PubMed] [Google Scholar]
- von Dassow G, and Odell GM (2002). Design and constraints of the Drosophila segment polarity module: Robust spatial patterning emerges from intertwined cell state switches. J. Exp. Zool 294(3), 179–215. [DOI] [PubMed] [Google Scholar]
- Wang YC, and Ferguson EL (2005). Spatial bistability of Dpp-receptor interactions during Drosophila dorsal–ventral patterning. Nature 434(7030), 229–234. [DOI] [PubMed] [Google Scholar]
- Wolpert L (1969). Positional information and the spatial pattern of cellular differentiation. J. Theor. Biol 25(1), 1–47. [DOI] [PubMed] [Google Scholar]
- Wolpert L, Beddington R, Jessel T, Lawrence P, Meyerowitz E, and Smith J (2002). “Principles of Development.” Oxford Univ. Press, New York, NY. [Google Scholar]
- Young ME, Carroad PA, and Bell RL (1980). Estimation of diffusion coefficients of proteins. Biotechnol. Bioeng 22, 947–955. [Google Scholar]