Rupture Resemblance Models May Correlate to Growth Rates of Intracranial Aneurysms: Preliminary Results

Abstract

Background:

Treatment of intracranial aneurysms (IAs) is largely guided by IA size and growth. Preliminary investigations have found a relationship between clinical factors and growth; yet, the relationship between morphologic and hemodynamic risk prediction models to IA growth is unknown.

Methods:

We analyzed serial images of 5 growing and 6 stable IAs. Rupture resemblance scores (RRSs) were calculated from 3D segmented images and computational fluid dynamics simulations. The morphologic (RRS_M), hemodynamic (RRS_H) and combination (RRS_C) scores leveraged IA size ratio (SR), wall shear stress (WSS) and oscillatory shear index (OSI). Comparisons of RRS, morphologic and hemodynamic characteristics were made between growing and stable IAs at the baseline time point and between the baseline and follow-up time points of the growing IAs. Additionally, we investigated the correlation of growth rate and RRS. Lastly, in the growing IA cases, the hemodynamics of growing and stable regions were compared.

Results:

Our results indicate that there is no statistical difference in parameters at the baseline time point; however, growing IAs tend to have a higher aspect ratio (AR), undulation index, and RRS_C. Additionally, we found a significant correlation between growth rate and baseline RRS of all three models (RRS_M, r=0.874, p<0.001; RRS_H, r=0.727, p=0.011; RRS_C, r=0.815, p=0.002). We also found that growing IAs significantly increased in AR (p=0.034), SR (p=0.034), and RRS_M (p=0.034). Lastly, our results show that stable and growing regions had statistically different WSS and OSI.

Conclusions:

Based on this preliminary study, we conjecture that aneurysms that resemble ruptured IAs may grow faster.

Introduction

In clinical settings, intracranial aneurysm (IA) growth is used as an indicator of potential rupture.^1–3 However, there is limited understanding regarding the characteristics that lead to growth or if growth can be predicted. Preliminary clinical studies have indicated that risk factors for IA rupture (including population, hypertension, age, IA location, history of subarachnoid hemorrhage, and IA size) can also predict IA growth.^3,4 Yet, it is unknown if other predictive models of rupture can perform similarly. Specifically, models that include morphologic and hemodynamic factors have not been studied.

A study by Xiang et al. analyzed a cohort of 204 ruptured and unruptured IAs and identified independently significant morphologic and hemodynamic characteristics of rupture.^5–7 Reconstructed angiographic images of patient IAs were used to analyze morphologic factors and to perform computational fluid dynamics (CFD). After multivariate logistic regression, three models, termed rupture resemblance scores (RRSs), were generated to calculate the resemblance of new unruptured IA cases to ruptured IAs. A high morphologic (RRS_M), hemodynamic (RRS_H), and combination (RRS_C) score result from high IA size ratio (SR), low wall shear stress (WSS) and high oscillatory shear index (OSI), and all three parameters combined. These models have shown to remain stable with increasing samples of ruptured and unruptured IAs.^6,7 However, it is unknown if these models can relate to IA growth.

In this study, we investigated the relationship of morphologic characteristics, hemodynamic characteristics and the RRS models to IA growth. We collected and analyzed five patients with growing IAs and six patients with stable IAs. Each case was analyzed at a baseline and follow-up time point. Morphologic and hemodynamic analyses were performed and RRS was calculated. Comparisons were made between growing and stable IAs at the baseline time point and then between baseline and follow-up time points of the growing IAs. Additionally, the correlation of RRS to growth rate was analyzed. Lastly, in each growing case, we compared the hemodynamics of stable and growing regions.

Materials and Methods

Population

Table 1 summarizes the clinical information of the patients used in this study. Eleven patients, including 5 growing and 6 stable cases, from Wakayama Rosai Hospital in Wakayama, Japan were analyzed. Patients with growing IAs were included if they presented with IAs that exhibited growth from a baseline (initial discovery) to a follow-up time point, underwent 3D imaging at both time points, were initially untreated, and had images with sufficient quality for reconstruction. Patients with stable IAs had the same selection criteria but only required a 3D image with sufficient image quality at the baseline time point. All stable cases were re-imaged at a later date by magnetic resonance angiography (MRA). All patients were female except for one (Stable 2). There was no difference in the patient age (stable 62±12 years; growing 62±9 years, p=0.941), follow-up time (stable 23±6 months; growing 33±11 months, p=0.112), or initial IA size (stable 3.24±0.74mm; growing 4.62±3.84mm, p=0.407) between the growing and stable IA groups.

Table 1.

Clinical information, follow-up time, and imaging information for the five growing and six stable IA cases.

	Location	Age (years)	Gender	Follow-up time (months)	Image	Modality	Resolution (mm)
Stable Cases
Stable 1	Left ICA	62	Female	25	Baseline	3DRA	0.097
Stable 2	Left MCA	73	Male	33	Baseline	3DRA	0.177
Stable 3	Center ICA	47	Female	25	Baseline	3DRA	0.097
Stable 4	ACOM	67	Female	23	Baseline	3DRA	0.097
Stable 5	Left MCA	74	Female	19	Baseline	3DCT	0.422
Stable 6	Left ICA	46	Female	14	Baseline	3DRA	0.097
Growing Cases
Growing 1	Right MCA	50	Female	49	Baseline	3DRA	0.198
					Follow-up	3DRA	0.198
Growing 2	Right Cavernous ICA	62	Female	23	Baseline	3DRA	0.327
					Follow-up	3DRA	0.327
Growing 3	Left PCoA	68	Female	38	Baseline	3DRA	0.327
					Follow-up	3DRA	0.198
Growing 4	Right MCA	74	Female	29	Baseline	3DCT	0.447
					Follow-up	3DRA	0.198
Growing 5	Right Cavernous ICA	56	Female	26	Baseline	3DCT	0.391
					Follow-up	3DRA	0.177

Abbreviations: 3DCT, three-dimensional computational tomographic angiography; 3DRA, three-dimensional rotational angiography; ICA, internal carotid artery; MCA, middle cerebral arterycommunicating arteryartery

At the time of the baseline image, Cases 1, 3 and 4 were not treated because they were small (<4mm). Cases 2 and 5 were not treated because they were located at the cavernous portion of the internal carotid artery. At the follow-up time point, Cases 1, 3, and 4 were treated by clipping and intraoperative images were obtained. Cases 2 and 5 were treated endovascularly, therefore, no intraoperative image was taken.

Image Acquisition and IA Model Generation

Table 1 summarizes the imaging technique and resolution of each image. A baseline image was acquired and analyzed for each IA and an additional follow-up image was acquired and analyzed for each patient with a growing IA. 3D rotational angiography (3DRA) or 3D computed tomographic angiography (3DCT) with 512 × 512 × 512 isotropic voxels was used for image acquisition. The 3DRA (Philips Xper, Philips Healthcare, Best, Netherlands) had a voxel size of 0.198 or 0.327 mm and the 3DCT (64 channel CT, Lightspeed VCT, GE Healthcare, Milwaukee, WI, USA) had a voxel size of 0.447 mm.

For precise morphological and hemodynamic calculations, 3D images were segmented and analyzed. Segmentation was performed in the open-source software Vascular Modeling Toolkit (vmtk.org).⁸ A threshold-based iso-surface was generated by a fast marching cubes algorithm.⁹ An experienced user manually selected the threshold for segmentation with assistance from a trained neurosurgeon and available intraoperative images.

From growing IAs the untrimmed baseline and follow-up geometries were co-registered in ANSYS ICEM CFD (ANSYS Inc., Canonsburg, PA) and the inlet and outlet(s) were cut at the same location. For all IAs, the outlets were cut at the next bifurcation and the inlets were manually extended 10 diameters to allow flow to fully develop. The inlet of all the models was the internal carotid artery.

Morphological Parameters

We calculated 3D morphologic parameters previously associated with rupture^5,10,11 and those related to the RRS score calculation. Detailed descriptions of the parameters can be found in previous publications.¹⁰ Briefly, IA size is the maximum perpendicular height of the aneurysm dome from the neck, SR is the IA size to parent vessel diameter, aspect ratio (AR) is the aneurysm size to the neck size, and undulation index (UI) is the degree of surface concavity. Automatic morphologic calculations of the aneurysm models were performed in AView, a research tool with the potential for IA management.¹²

CFD Methods

To simulate blood flow in the aneurysm models we performed pulsatile CFD simulations following the practices found in previous publications.⁵ Each aneurysm geometry was meshed using ANSYS ICEM CFD. The mesh contained tetrahedral elements with four refined prism layers at the wall. The average number of elements was 1.69 million (range 0.95 to 3.00 million).

CFD was performed in STAR-CCM+ (v. 10.06, CD-adapco, Melville, NY). A pulsatile waveform taken by a transcranial Doppler ultrasound measurement from a healthy subject was imposed at the inlet. A flow split condition was imposed at the outlets. Blood was assumed to be Newtonian with a density of 1056 kg/m³ and viscosity of 0.0035 N∙s/m². The transient Navier-Stokes equations were discretized using a second-order spatial upwind differencing scheme and second-order temporal scheme. A time step of 1 milliseconds was used. The simulation was run for three cycles to allow for convergence of the solution. The last cycle was extracted and used for analysis.

Hemodynamic Parameters

We quantified two previously proposed hemodynamic risk factors of rupture at for the baseline time point of all cases and the follow-up time point for the growing cases. A detailed description of hemodynamic parameters can be found in previous publications.^5,13,14 Briefly, WSS is the average friction force experienced at the wall. Normalized WSS is the temporal and spatial average of the aneurysmal WSS, normalized by the average WSS in the parent vessel. OSI is the directional change of the shear stress throughout the cardiac cycle.

Growth and Rupture Resemblance Models

To investigate the relationship of rupture resemblance models to growth we calculated the aneurysm’s growth rate and correlated it to the baseline RRS.^5,6 The growth rate is the change in IA size over the number of months. RRS quantifies the resemblance of an aneurysm to previously ruptured aneurysms from a database of 204 IAs (56 ruptured). Three models leverage morphological (RRS_M), hemodynamic (RRS_H) and both morphologic and hemodynamic parameters combined (RRS_C). RRS_M includes SR, RRS_H includes low WSS and high OSI, and RRS_C includes all three parameters. The calculation the odds (where RRS is the odds divided by one plus the odds) are described in Equations (1), (2), and (3):

$$Od{d}_M=e^{1.09\cdot SR-2.99}$$ (1)

$$Od{d}_H=e^{-0.73\cdot WSS+2.86\cdot OSI-0.12}$$ (2)

$$Od{d}_C=e^{0.73\cdot SR-0.45\cdot WSS+2.19\cdot OSI-2.09}$$ (3)

As with previous studies, each parameter was scaled to a range of 0 to 10 based on the previous population’s distribution.⁵

Comparison of Growing and Stable Regions

For the growing IA cases, the baseline and follow-up images were co-registered using CloudCompare (v.2.6.2, cloudcompare.org). An iterative closest point algorithm was used to minimize the distance between two point clouds consisting of mesh nodes to co-register the images. Then, using a custom MATLAB code (R2014a, The MathWorks Inc., Natick, MA), normal vectors of all nodes in the aneurysm on the baseline surface mesh were generated. A ray was extended in both positive and negative directions to find the intersection point with the follow-up aneurysm’s geometry. The distance was calculated using the coordinate of intersection point and the starting point of the ray for each node. The displacement was associated with its baseline hemodynamic parameter.

The displacement at each node was defined as either growing or stable. Consistent with previous studies, the growing nodes were those that had displacements greater than the image pixel length.¹⁵ In cases where baseline and follow-up images were acquired with two different image resolutions (Cases 3, 4, and 5), the larger pixel size was used.

Statistical Methods

We compared the morphologic and hemodynamic characteristics of the baseline and follow-up time points of the growing IAs by a paired t-test. Then, to investigate the difference in the growing and stable cases, we compared the baseline characteristics of the growing IAs to the characteristics of the stable IAs by an unpaired t-test. We also invested the correlation of the RRS models to growth rate by Pearson’s correlation. Lastly, for the growing IAs, we compared WSS and OSI of the growing and stable regions using a Wilcoxon rank sum test. For all statistical tests, a p-value of less than 0.05 was considered statistically significant. Statistical analyses were performed in IBM SPSS Statistics (v.22.0, IBM Corporation, Armonk, NY).

Results

The results of the analysis for Growing Cases 1–5 are shown in Figures 1–Figures 5, respectively. The co-registered images (A), the growing and stable regions (E), and the intraoperative image (F) describe the IA growth. From the co-registered images and intraoperative images, we qualitatively observed that the growing regions (pink) were associated with red, thin regions of the IA wall and did not seem to be associated with the location of an inflow jet. We also noted that Cases 1, 3, and 4, grew non-uniformly, while Cases 2 and 5 grew circumferentially. Additionally, aneurysmal hemodynamics are shown by streamlines (B), normalized WSS (C) and OSI (D) for both baseline and follow-up time points.

Figure 1. Case 1, a right middle cerebral artery aneurysm.

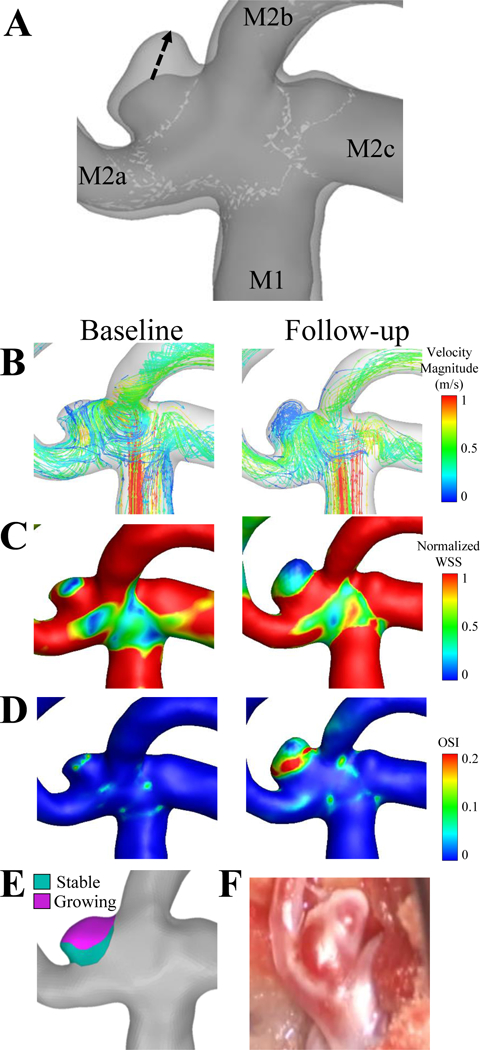
(A)The dashed arrows in the image of the co-registered images indicate that the growth from the baseline to the follow-up time points. The flow inlet (M1), and three outlets (M2a, M2b, M2c) are indicated on the co-registered images. (B) Velocity streamlines, (C) wall shear stress and (D) oscillatory shear index are shown for the baseline and follow-up time points. (E) The aneurysm was isolated and the growing (pink) and stable regions (teal) were isolated on the baseline geometry and hemodynamic parameters were compared. (F) An intraoperative image was taken at the follow-up time point (bottom right).

Figure 5. Case 5, a left internal carotid artery aneurysm.

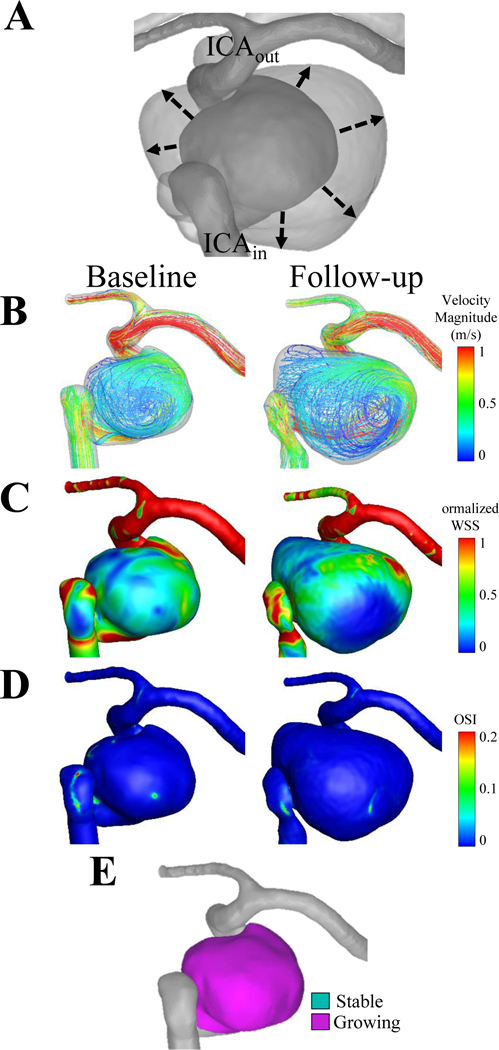
(A) The dashed line of the co-registered images indicates that the growth from the baseline to the follow-up time point was circumferential. The flow inlet (ICA_in) and the outlet (ICA_out) are shown on the co-registered images. (B) Velocity streamlines, (C) wall shear stress and (D) oscillatory shear index are shown for the baseline and follow-up time points. (E) The circumferential growth is confirmed by quantifying growing and stable regions.

Comparison of Growing and Stable IAs

Table 2 summarizes the morphological and hemodynamic parameters that were analyzed for the stable cases and the baseline and follow-up time points of each of the growing cases. When the characteristics of stable IAs were compared to growing IAs at the baseline time point there was no statistical differences; however, we observed at the growing cases had a higher AR (p=0.066), UI (p=0.086) and RRS_C (p=0.086). Additionally, as indicated in Figure 6(A), the average RRS for all three models was higher for the growing cases, although there was also no difference between the stable and the baseline scores of the growing cases.

Table 2.

Baseline and follow-up morphologic and hemodynamic characteristics and rupture resemblance scores for the five growing and six stable IA cases. The comparison of the baseline and follow-up characteristics of the growing IAs and the comparison of the baseline characteristics of the growing IAs and the characteristics of the stable IAs is shown.

	IA size (mm)	Volume (mm3)	AR	SR	UI	Normalized WSS	OSI (x10−2)	RRSM (%)	RRSH (%)	RRSC (%)
Stable Cases
Stable 1	2.80	16.9	0.90	1.04	0.010	1.55	0.55	10.0	1.1	1.6
Stable 2	2.51	10.6	0.73	1.24	0.055	2.21	0.80	12.4	0.2	0.7
Stable 3	4.61	49.1	1.30	1.29	0.055	0.83	0.97	13.1	22.8	14.5
Stable 4	3.11	15.9	0.98	1.31	0.034	1.29	0.58	13.4	2.8	3.6
Stable 5	3.41	33.7	0.91	1.30	0.023	1.23	0.30	13.2	2.1	2.7
Stable 6	2.99	16.1	0.94	1.02	0.017	0.90	0.87	9.8	16.1	9.2
Mean	3.24	23.7	0.96	1.20	0.032	1.33	0.68	12.0	7.5	5.4
SD	0.74	14.7	0.19	0.13	0.019	0.50	0.25	1.7	9.5	5.4
Growing Cases- Baseline
Growing 1	1.26	1.8	0.45	0.66	0.015	2.20	0.61	6.5	0.1	0.3
Growing 2	8.42	553.0	1.08	2.73	0.006	0.64	1.89	47.5	74.6	74.8
Growing 3	1.80	7.4	0.52	0.79	0.011	1.00	0.26	7.5	4.3	2.8
Growing 4	2.44	16.5	0.65	1.33	0.024	0.75	1.41	13.7	45.9	30.0
Growing 5	9.16	962.0	0.66	2.84	0.018	0.44	0.43	50.7	30.5	40.5
Mean	4.62	308.1	0.67	1.67	0.015	1.01	0.92	25.2	31.1	29.7
SD	3.84	435.0	0.24	1.05	0.007	0.70	0.70	22.1	30.8	30.6
Growing Cases- Follow-up
Growing 1	2.14	6.3	0.56	1.09	0.031	0.83	8.43	10.5	100.0	100.0
Growing 2	12.12	1595.0	1.19	4.81	0.006	0.39	1.19	92.2	67.1	91.7
Growing 3	3.13	22.7	0.75	1.56	0.037	0.69	0.45	17.4	15.9	12.3
Growing 4	6.23	67.6	1.18	3.00	0.179	0.65	0.27	55.9	13.5	28.3
Growing 5	15.52	3370.6	0.90	6.26	0.013	0.38	0.28	98.6	29.0	91.4
Mean	7.83	1012.4	0.92	3.34	0.053	0.59	2.12	54.9	45.1	64.7
SD	5.80	1482.0	0.27	2.18	0.071	0.20	3.55	40.9	37.4	41.1
Comparison
Stable vs. Baseline Growing Cases
p-value	0.407	0.140	0.066	0.298	0.086	0.407	0.448	0.174	0.165	0.086
Growing Cases: Baseline vs. Follow-up
p-value	0.031*	0.208	0.034*	0.034*	0.265	0.160	0.512	0.034*	0.569	0.129

Abbreviations: AR, aspect ratio; IA, intracranial aneurysm; OSI, oscillatory shear index; RRS_C, combination rupture resemblance score; RRS_H, hemodynamic rupture resemblance score; RRS_M, morphologic rupture resemblance score; SR, size ratio; UI, undulation index; WSS, wall shear stress

Figure 6. The relationship of growth to rupture resemblance scores (RRSs).

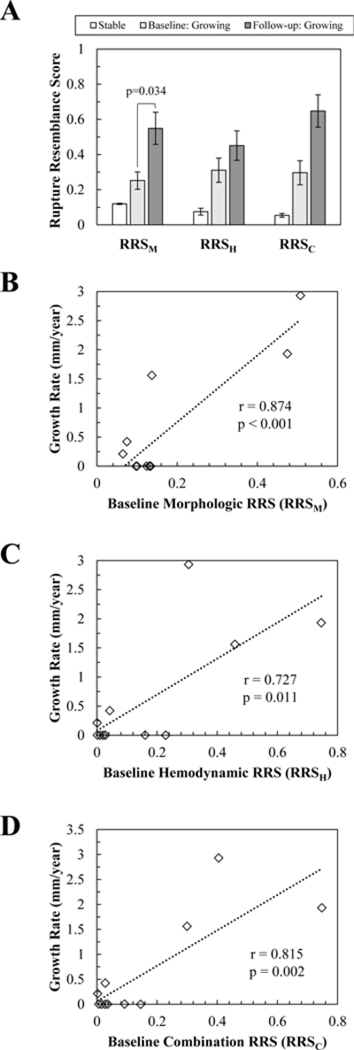
(A) Comparison of RRS between the stable cases and baseline and follow-up time points. (B)The correlation of growth rate to baseline morphologic, RRS_M, (C) hemodynamic, RRS_H, and (D) combination, RRS_C, models. A significant positive correlation between growth rate and RRS was found for all three models.

Comparison of Baseline and Follow-up Time Points for Growing IAs

As shown in Table 2, when the baseline and follow-up time points of the growing IAs were compared, we found that the IAs increased significantly in size (p=0.031), AR (p=0.034), and SR (p=0.034). As shown in Figure 6(A), the RRS_M (p=0.034) also significantly increased from baseline to follow-up time points. Additionally, although we observed a trend of increasing IA volume, UI, OSI, RRS_H, RRS_C and decreasing WSS after growth, none of these parameters were significantly different.

Relationship of Growth Rate and Rupture Resemblance Models

As Figure 6(B-D) shows, when we analyzed the correlation of growth rate and baseline RRS in all cases, a significant positive correlation was found. The morphologic (RRS_M r=0.874, p<0.001), hemodynamic (RRS_H r=0.727, p=0.011) and combination scores (RRS_C r=0.815, p=0.002) all showed significant and high Pearson correlation coefficients. This indicates that a higher baseline RRS is correlated to faster growth.

Quantification and Analysis of Growing Regions

As shown in Table 3, when the growing and stable regions of the growing IAs were compared, we found that the regions had different mean baseline normalized WSS and OSI, excluding normalized WSS in Case 3. Interestingly, Cases 1 and 4, two non-uniformly growing IAs, had lower WSS in growing regions compared to stable regions, while Cases 2 and 5, the circumferentially growing IA, had higher WSS in growing regions when compared to stable regions. Figures 1–5E show growing and stable regions on the baseline geometry as pink and teal regions, respectively.

Table 3.

Comparison of growing and stable regions in each of the growing IA cases. Stable and growing regions were compared based on the baseline normalized WSS and OSI.

	Region	Baseline Normalized WSS		Baseline OSI		Number of Points Analyzed
		Mean ± SD	p-value	Mean ± SD	p-value
Growing Case 1	Stable	2.91 ± 1.98	< 0.001	0.001 ± 0.001	< 0.001	1412
	Growing	2.35 ± 2.27		0.007 ± 0.018
Growing Case 2	Stable	0.39 ± 0.29	< 0.001	0.032 ± 0.044	< 0.001	2591
	Growing	0.62 ± 0.48		0.020 ± 0.034
Growing Case 3	Stable	1.23 ± 1.10	0.513	0.003 ± 0.009	< 0.001	880
	Growing	1.17 ± 0.80		0.002 ± 0.004
Growing Case 4	Stable	0.67 ± 0.63	< 0.001	0.010 ± 0.016	< 0.001	1192
	Growing	0.29 ± 0.16		0.017 ± 0.027
Growing Case 5	Stable	0.60 ± 0.26	0.015	0.002 ± 0.001	< 0.001	8151
	Growing	0.65 ± 0.51		0.003 ± 0.019

Abbreviations: OSI, oscillatory shear index; WSS, wall shear stress

Discussion

Intracranial aneurysm growth is used as an indicator of impending rupture. ^1–3 however, a limited number of studies have investigated if growth can be predicted. A clinical study by Bakes et al. demonstrated that the previously developed rupture risk PHASES score (which considered population, hypertension, age, IA location, history of subarachnoid hemorrhage, and IA size) could predict IA growth.³ Yet, it is unknown if prediction models that leverage morphologic and hemodynamic^5,16–18 factors can perform similarly. Therefore, we investigated if such a model, RRS, could relate to IA growth by conducting a preliminary analysis on growing and stable IAs.

In our current study, we observed a trend of a higher AR, UI, and RRS_C in growing IAs when compared to stable IAs at a baseline time point. However, these differences did not rise to the level of significance. Although our current findings do not aid in the identification of IAs with the potential for growth, it could justify the initial decision to observe the IAs and we do suspect this tend to persist in a larger data set. We did find a significant positive correlation between the baseline morphologic, hemodynamic, and combination RRS models to growth rate. Our results suggest that IAs with the highest growth rate will have the highest initial RRS. Specifically, our data suggest that if RRS_C is less than 0.20, the IA growth rate will be less than 0.5 mm/year. This rate of growth that is difficult to detect using CTA or MRA, and may not warrant treatment. Therefore, we suggest that IAs with an initially higher SR, lower WSS and higher OSI in IAs may warrant more frequent follow-up as their predicted growth rate is higher.

Abnormal WSS is known to effect vessel wall remodeling. Specifically, low WSS and high OSI conditions could trigger inflammatory cell-mediated destructive remodeling.¹⁹ Under this flow condition, endothelial cells become dysfunctional and promote inflammatory cell infiltration into the IA wall.^20,21 This may lead to the upregulation of matrix metalloproteinase^22–24 which causes wall remodeling and degradation. Ultimately, with enough destructive remodeling, this hemodynamic environment could result in IA growth and rupture. Our results suggest that when an IA subjected to inflammatory cell-mediated destructive remodeling, or low WSS and high OSI, faster growth may result.

As an IA undergoes destructive remodeling the geometric changes gives way to hemodynamic changes.^19,25 However, few longitudinal studies have investigated these changes over time. In this study, by examining baseline and follow-up images of growing IAs, we observed that, along with IA size, AR, SR and RRS_M significantly increased. An increase in AR, or the ratio of the aneurysm size to the neck plane, indicates that the IA size increases more rapidly than the neck. Similarly, an increase in SR, or the ratio of the aneurysm size to the parent vessel size, indicates that the parent vessel may remain relatively constant while the IA size increases. Each of these parameters has previously been associated with IA rupture in large statistical studies.^5,26–28 We also observed a large increase in the IA volume, UI (the quantification of the surface irregularity), and OSI, and a decrease in WSS from baseline to follow-up time points; however, they did not reach levels of significance. We conjecture that studies with increased sample sizes will find aneurysm growth is linked to increasingly aberrant wall shear stress and irregular surfaces.

It has been previously hypothesized that surface irregularity signifies the presence of intraluminal thrombus.^29,30 Intraluminal thrombus has been associated with the degeneration of the IA wall, which may lead an IA to become more rupture-prone.²⁴ With low flow conditions, a thrombus may trap inflammatory cells that promote destructive remodeling of the aneurysmal wall.²⁴ The inflammatory cells may give rise to a white irregular IA surface, akin to atherosclerosis.³¹ From intraoperative images of 3 cases, we observed that the IA wall after growth is heterogeneous, with both thick and thin regions interspersed. We qualitatively observed that growing regions tend to be associated with thinner regions of the IA wall with lower WSS. We speculate that the thin regions represent the newest remodeling and are areas where slower recirculating flow manifests in low WSS. If growth stabilizes, it is possible that these regions could give rise to intraluminal thrombus and develop into more white-ish regions. However, longitudinal studies that couples investigations of hemodynamic forces and histological studies of the IA wall are necessary to establish a more definitive link.²⁵

While, to the best of our knowledge, this study is one of only two CFD studies to implicate high OSI as a potential driving force for growth in multiple IAs,³² previous investigations have suggested that abnormal aneurysmal WSS is associated with IA growth and initiation.^19,33 A longitudinal study by Boussel et al. analyzed seven growing patient IAs and showed that growth occurs in regions of low WSS by statistically comparing 100 discretized regions on the aneurysm surface.³⁴ Additionally, Acevedo-Bolton et al. analyzed a single mid-basilar artery aneurysm with five follow-up time points.³⁵ They similarly reported that growing regions occurred in regions of low WSS. In a study by Sugiyama et al., a single patient with two uniquely growing aneurysms was analyzed.³² They found that non-uniform growth occurred under physiologic WSS conditions (0.45–1.20 Pa) and high velocity flow, while uniform growth occurred under low WSS (0.02– 0.45 Pa) and high OSI (0.29). In this study, if we consider low WSS as normalized aneurysmal WSS < 1 (or less than the parent vessel which is presumed to be physiologic WSS) and high OSI as > 0.92×10⁻² (the group-averaged mean), we find that both non-uniform and uniform (circumferential) growth can occur when baseline normalized WSS is low and OSI is high. Furthermore, when we compared WSS in growing and stable regions we found that non-uniform growth occurs under WSS that is lower than stable regions, while circumferential growth occurs under WSS that is higher than stable regions. Both growth types show different OSI (either high or low) in stable versus growing regions. This indicates that aberrant and non-uniform WSS may promote growth; however, larger studies are necessary.

Our findings have several limitations. First, the sample size is small and a larger number of cases is required to confirm the relationship of IA growth rate to RRS. Second, each IA case was examined only at two time points. Because the growing IAs exhibited growth at the first follow-up, the IAs were treated. The intermediary nature of the IA growth is unknown and it is unknown if the growing aneurysms experienced intermittent rapid growth or steady growth, or if the stable cases will remain stable at further time points. This study does not refute the possibility of exponential or linear growth as previously proposed.³⁶ Lastly, due to a lack of patient-specific information, several assumptions were made to make computational simulations tractable, including rigid walls, a Newtonian fluid, and non-patient-specific inflow and outflow boundary conditions.

Conclusions

In this study, we investigated if previously developed rupture resemblance scores (RRSs), which leverage hemodynamic and morphologic characteristics, could predict intracranial aneurysm growth. Our preliminary analysis of 5 growing and 6 stable IA cases found that IAs with a higher AR, UI, and RRS_C at the baseline time point tended to grow. Additionally, a higher RRS at a baseline time point was found to be significantly correlated with faster growth. We speculate that IAs that resemble ruptured IAs may grow faster.

Figure 2. Case 2, a right cavernous internal carotid artery aneurysm.

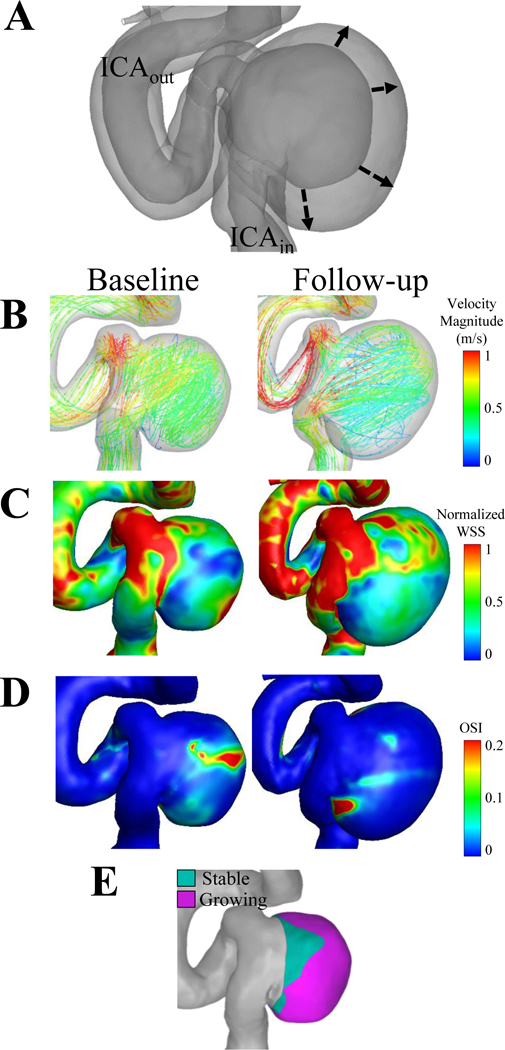
(A) The dashed lines of the co-registered images indicate that the direction of growth from the baseline to the follow-up times, and the flow inlet (ICA_in) and outlet (ICA_out) are indicated. (B) Velocity streamlines, (C) wall shear stress and (D) oscillatory shear index are shown for the baseline and follow-up time points. (E) By quantifying growing and stable regions, we found that the aneurysm grew circumferentially.

Figure 3. Case 3, a left posterior communicating artery aneurysm.

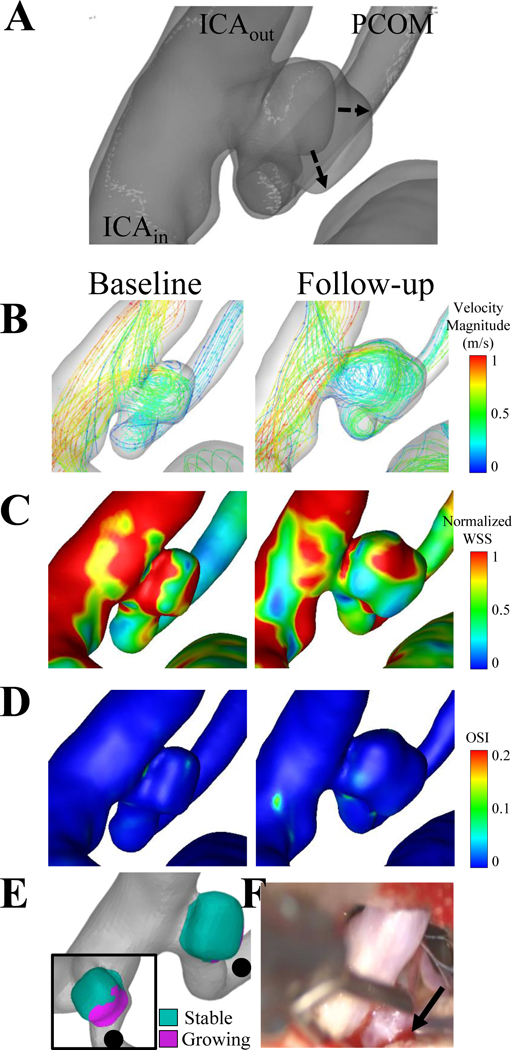
(A) The dashed lines of the co-registered images indicate that the growth from the baseline to the follow-up times was non-uniform. The flow inlet (ICA_in) and two flow outlets (ICA_out and PCOM) are indicated on the co-registered images. (B) Velocity streamlines, (C) wall shear stress and (D) oscillatory shear index are shown for the baseline and follow-up time points. (E) Two views are given to show the growing and stable regions, where the black dot indicates the posterior communicating artery. (F) The solid arrow on the intraoperative image shows the red region of the partially obstructed aneurysm sac.

Figure 4. Case 4, a right middle cerebral artery aneurysm.

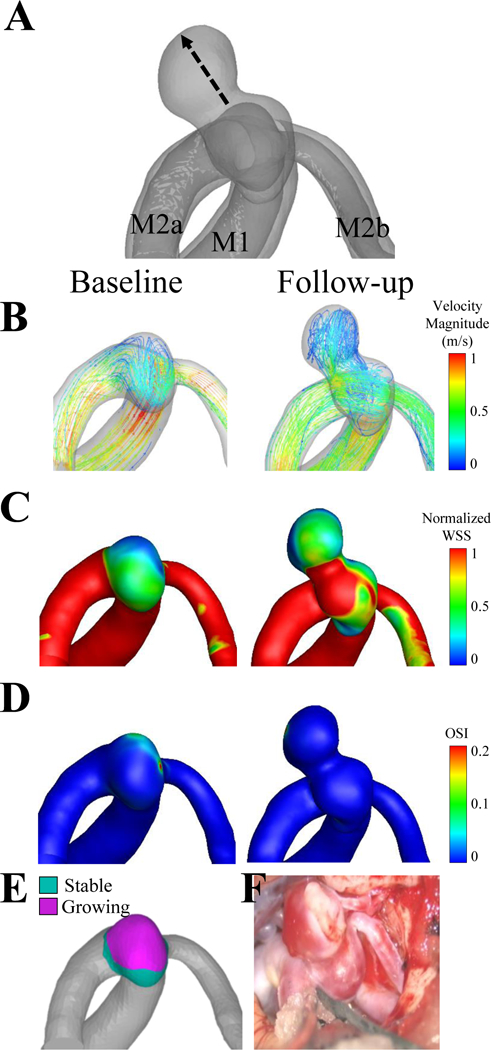
(A) The dashed line of the co-registered images indicates that the growth from the baseline to the follow-up time point was non-uniform. The flow inlet (M1) and two flow outlets (M2a, M2b) are indicated on the co-registered images. (B) Velocity streamlines, (C) wall shear stress and (D) oscillatory shear index are shown for the baseline and follow-up time points. (E) The non-uniform growth is confirmed by quantifying growing and stable regions. (F) The solid arrow on the intraoperative image indicates possible brain parenchyma.

List of Abbreviations:

3DCT

three-dimensional computed tomography

3DRA

three-dimensional rotational angiography

CFD

computational fluid dynamics

AR

aspect ratio

IA

intracranial aneurysm

OSI

oscillatory shear index

RRS

rupture resemblance score

RRSc

combination rupture resemblance score

RRS_H

hemodynamic rupture resemblance score

RRS_M

morphologic rupture resemblance score

SR

size ratio

UI

undulation index

WSS

wall shear stress