Single-shot ultrafast optical imaging

Abstract

Single-shot ultrafast optical imaging can capture two-dimensional transient scenes in the optical spectral range at ≥100 million frames per second. This rapidly evolving field surpasses conventional pump-probe methods by possessing the real-time imaging capability, which is indispensable for recording non-repeatable and difficult-to-reproduce events and for understanding physical, chemical, and biological mechanisms. In this mini-review, we survey comprehensively the state-of-the-art single-shot ultrafast optical imaging. Based on the illumination requirement, we categorized the field into active-detection and passive-detection domains. Depending on the specific image acquisition and reconstruction strategies, these two categories are further divided into a total of six sub-categories. Under each sub-category, we describe operating principles, present representative cutting-edge techniques with a particular emphasis on their methodology and applications, and discuss their advantages and challenges. Finally, we envision prospects of technical advancement in this field.

1. INTRODUCTION

Optical imaging of transient events in their actual time of occurrence exerts compelling scientific significance and practical merits. Occurring in two-dimensional (2D) space and at femtosecond to nanosecond timescales, these transient events reflect many important fundamental mechanisms in physics, chemistry, and biology [1–3]. Conventionally, the pump-probe methods have allowed capture of these dynamics through repeated measurements. However, many ultrafast phenomena are either non-repeatable or difficult-to-reproduce. Examples include optical rogue waves [4, 5], irreversible crystalline chemical reactions [6], light scattering in living tissue [7], shockwaves in laser-induced damage [8], and chaotic laser dynamics [9]. Under these circumstances, the pump-probe methods are inapplicable. In other cases, although reproducible, the ultrafast phenomena have significant shot-to-shot variations and low occurrence rates. Examples include dense plasma generation by high-power, low-repetition laser systems [10, 11] and laser-driven implosion in inertial confinement fusion [12]. For these cases, the pump-probe methods would lead to significant inaccuracy and low productivity.

To overcome the limitations in the pump-probe methods, many single-shot ultrafast optical imaging techniques have been developed in recent years. Here, “single-shot” describes capturing the entire dynamic process in real time (i.e., the actual duration in which an event occurs) without repeating the event. Extended from the established categorization [13, 14], we define “ultrafast” as imaging speeds at 100 million frames per second (Mfps) or above, which correspond to inter-frame time intervals of 10 ns or less. “Optical” refers to detecting photons in the extreme ultraviolet to the far-infrared spectral range. Finally, we restrict “imaging” to two-dimensional (2D, i.e., x, y). With the unique capability of recording non-repeatable and difficult-to-reproduce transient events, single-shot ultrafast optical imaging techniques have become indispensable for understanding fundamental scientific questions and for achieving high measurement accuracy and efficiency.

The prosperity of single-shot ultrafast optical imaging is built upon advances in three major scientific areas. The first contributor is the vast popularization and continuous progress in ultrafast laser systems [15], which enable producing pulses with femtosecond-level pulse widths and up to joule-level pulse energy. The ultrashort pulse width naturally offers outstanding temporal slicing capability. The wide bandwidth (e.g., ~30 nm for a 30-fs, 800 nm, Gaussian pulse) allows implementing different pulse shaping technologies [16] to attach various optical markers to the ultrashort pulses. The high pulse energy provides a sufficient photon count in each ultrashort time interval for obtaining images with a reasonable signal-to-noise ratio. All three features pave the way for the single-shot ultrafast recording of transient events. The second contributor is the incessantly improving performance of ultrafast detectors [17–22]. New device structures and state-of-the-art fabrication have enabled novel storage schemes, faster electronic responses, and higher sensitivity. These efforts have circumvented the limitations of conventional detectors in on-board storage and read-out speeds. The final contributor is the development of new computational frameworks in imaging science. Of particular interest is the effort to apply compressed sensing (CS) [23, 24] in spatial and temporal domains to overcome the speed limit of conventional optical imaging systems. These three major contributors have largely propelled the field of single-shot ultrafast optical imaging by improving existing techniques and by enabling new imaging concepts.

In this mini-review, we provide a comprehensive survey of the cutting-edge techniques in single-shot ultrafast optical imaging and their associated applications. The limited article length precludes covering the ever-expanding technical scope in this area, resulting in possible omission. We restrict the scope of this review by our above-described definition of single-shot ultrafast optical imaging. As a result, multiple-shot ultrafast optical imaging methods—including various pump-probe arrangements implemented via either temporal scanning by ultrashort probe pulses and ultrafast gated devices [25–29] or spatial scanning using zero-dimensional and one-dimensional (1D) ultrafast detectors [18, 30, 31]—are not discussed. In addition, existing single-shot optical imaging modalities at less than 100-Mfps imaging speeds, such as ultra-high-speed sensors [32], rotating mirror cameras [33], and time-stretching methods [34–36], are excluded. Finally, ultrafast imaging using non-optical sources, such as electron beams, x-rays, and terahertz radiations [37–39], falls out of the scope here. Interested readers can refer to the selected references listed herein and the extensive literature elsewhere.

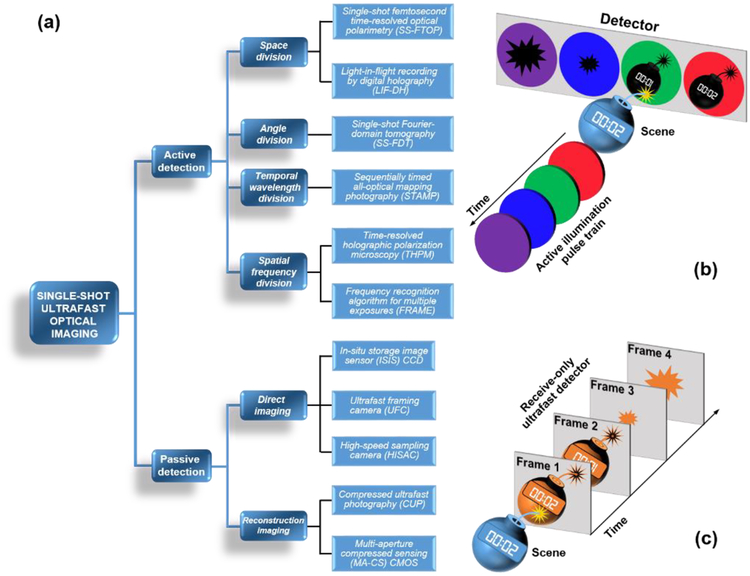
The subsequent sections are organized by the following conceptual structure [Fig. 1(a)]. According to the illumination requirement, single-shot ultrafast optical imaging can be categorized into active detection and passive detection. The active-detection domain exploits specially designed pulse trains for probing 2D transient events [Fig. 1(b)]. Depending on the optical marker carried by the pulse train, the active-detection domain can be further separated into four methods, namely space division, angle division, temporal wavelength division, and spatial frequency division. The passive-detection domain leverages receive-only ultrafast detectors to record 2D dynamic phenomena [Fig. 1(c)]. It is further divided into two image formation methods—direct imaging and reconstruction imaging. The in-depth description of each method starts by its basic principle, followed by the description of representative techniques, with their applications as well as their strengths and limitations. In the last section, a summary and an outlook are provided to conclude this mini-review.

Fig. 1.

(a) Categorization of single-shot ultrafast optical imaging in two detection domains and six methods with 11 representative techniques. (b) Conceptual illustration of active-detection-based single-shot ultrafast optical imaging. Colors represent different optical markers. (c) Conceptual illustration of passive-detection-based single-shot ultrafast optical imaging.

2. ACTIVE-DETECTION DOMAIN

In general, the active-detection domain works by using an ultrafast pulse train to probe a transient event in a single image acquisition. Each pulse in the pulse train is attached with a unique optical marker [e.g., different spatial positions, angles, wavelengths, states of polarization (SOPs), or spatial frequencies]. Leveraging the properties of these markers, novel detection mechanisms are deployed to separate the transmitted probe pulses after the transient scene in the spatial or spatial frequency domain to recover the (x, y, t) datacube. In the following, we will present four methods with six representative techniques in this domain.

A. Space division

The first method in this domain is space division. Extended from Muybridge’s famous imaging setup to capture a horse in motion [40], this method constructs a probe pulse train with each pulse occupies a different spatial and temporal position. Synchronized with a high-speed object traversing through the field of view (FOV), each probe pulse records object’s instantaneous position at the different time. These probe pulses are projected onto different spatial areas of a detector, which thus records the (x, y, t) information. Two representative techniques are presented in this sub-section.

1. Single-shot femtosecond time-resolved optical polarimetry (SS-FTOP)

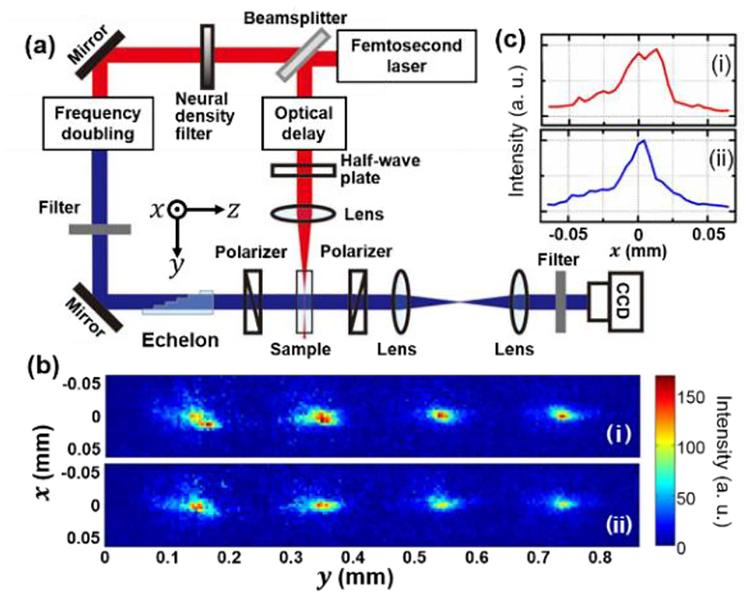
Figure 2(a) shows the schematic of the SS-FTOP system for imaging ultrashort pulse’s propagation in an optical nonlinear medium [41]. An ultrafast Ti:sapphire laser generated 800-nm, 65-fs pulses, which were split by a beam splitter to generate pump and probe pulses. The pump pulse, reflected from the beam splitter, passed through a half-wave plate for polarization control and then was focused into a 10-mm-long Kerr medium. The transmitted pulse from the beam splitter was frequency doubled by a β-barium borate (BBO) crystal. Then, it was incident on a four-step echelon [42], which had a step width of 0.54 mm and a step height of 0.2 mm. This echelon, therefore, produced four probe pulses with an inter-pulse time delay of 0.96 ps, corresponding to an imaging speed of 1.04 trillion frames per second (Tfps). These probe pulses were incident on the Kerr medium orthogonally to the pump pulse. The selected step width and height of the echelon allowed each probe pulses to arrive coincidentally with the propagating pump pulse in the Kerr medium. A pair of polarizers, whose polarization axes are rotated 90° relative to each other, sandwiched the Kerr medium [43]. As a result, the birefringence induced by the pump pulse allowed part of the probe pulses to be transmitted to a CCD camera. The transient polarization change thus provided contrast to image the pump pulse’s propagation. Each of the four recorded frames had 41×60 pixels (Prof. L. Yan, personal communication, May 2^nd, 2018). SS-FTOP’s temporal resolution, determined by the probe pulse width and pump pulse’s lateral size, was 276 fs.

Fig. 2.

Single-shot femtosecond time-resolved optical polarimetry (SS-FTOP) based on space division followed by varied time delays for imaging a single ultrashort pulse’s propagation in a Kerr medium (adapted from [41]). (a) Schematic of experimental setup. (b) Two sequences of single ultrashort pulses’ propagation. The time interval between adjacent frames is 0.96 ps. (c) Transverse intensity profiles of the first frames of the two single-shot observations in (b).

Figure 2(b) shows two sequences of propagation dynamics of single, 45-μJ laser pulses in the Kerr medium. In spite of nearly constant pulse energy, the captured pulse profiles varied from shot to shot, attributed to self-modulation-induced complex structures within the pump pulses [44]. As a detailed comparison, the transverse (i.e., x-axis) profiles of the first frames of both measurements [Fig. 2(c)] show different intensity distributions. In particular, two peaks are observed in the first measurement, indicating the formation of double filaments during the pump pulse’s propagation [44].

SS-FTOP can fully leverage the ultrashort laser pulse width to achieve exceptional temporal resolution and imaging speeds. With the recent progress in attosecond laser science [45, 46], the imaging speed could exceed one quadrillion (i.e., 10¹⁵) fps. However, this technique has three limitations. First, using the echelon to induce the time delay discretely, SS-FTOP has a limited sequence depth (i.e., the number of frames captured in one acquisition). In addition, the sequence depth conflicts with the imaging FOV. Finally, SS-FTOP can only image ultrafast moving objects with non-overlapping trajectory.

2. Light-in-flight (LIF) recording by holography

Invented in the 1970s [47], this technique records time-resolving holograms by using an ultrashort reference pulse sweeping through a holographic recording medium (e.g., a film [48] for conventional holography or a CCD camera [49] for digital holography). The pulse front of the obliquely incident reference pulse intersects with different spatial areas of the recorded holograms, generating time-resolved views of the transient event.

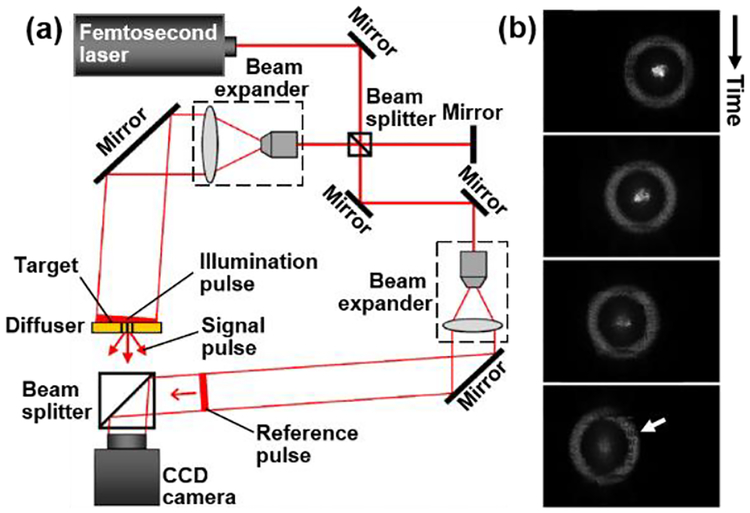
As an example, Fig. 3(a) illustrates a digital holography (DH) system for LIF recording of a femtosecond pulse’s sweeping motion on a patterned plate [50]. An ultrashort laser pulse (800-nm wavelength and 96-fs pulse width), from a mode-locked Ti:sapphire laser, was divided into an illumination pulse and a reference pulse. Both pulses were expanded and collimated by beam expanders. The illumination pulse was incident on a diffuser plate at 0.5° against the surface normal. A USAF resolution test chart was imprinted on the plate. The light scattered from the diffuser plate formed the signal pulse. The reference pulse was directed to a CCD camera with an incident angle of 0.5°. When the time of arrival of scattered photons coincided with that of the reference pulse, interference fringes were formed. Images were digitally reconstructed from the acquired hologram. The temporal resolution of LIF-DH was mainly determined by the FOV, incident angle, and coherence length [50].

Fig. 3.

Light-in-flight (LIF) recording by digital holography (DH) based on obliquely sweeping the reference pulse on the imaging plane, a form of space division [50]. (a) Experimental setup for recording the hologram. (b) Representative frames of single ultrashort laser pulses’ movement on a USAF resolution target. The time interval between frames is 192 fs. The white arrow points to the features of the USAF resolution target.

Figure 3(b) shows the sequence of the femtosecond laser pulse sweeping over the patterned plate. In this example, seven sub-holograms (512×512 pixels in size), extracted from the digitally recorded hologram, were used to reconstruct frames. The temporal resolution was 88 fs, corresponding to an effective imaging speed of 11.4 Tfps. In each frame, the bright spot at the center is the zeroth-order diffraction, and the reconstructed femtosecond laser pulse is shown as the circle. The USAF resolution target can be seen in the reconstructed frames. The sweeping motion of the femtosecond laser pulse is observed by sequentially displaying the reconstructed frames.

Akin to SS-FTOP, LIF holography fully leverages the ultrashort pulse width to achieve femtosecond-level temporal resolution. The sequence depth is also inversely proportional to the imaging FOV. Different from SS-FTOP, the FOV in LIF holography is tunable in reconstruction, which could provide a much-improved sequence depth. In addition, in theory, provided a sufficiently wide scattering angle and a long-coherence reference pulse, LIF holography could be used to image ultrafast moving objects with complex trajectories and other spatially-overlapped transient phenomena. However, the shape of the reconstructed object is determined by the geometry for which the condition of the same time-of-arrival between the pump and the probe pulses is satisfied [50]. The shape is also subject to observation positions [51]. Finally, based on interferometry, this technique cannot be implemented in imaging transient scenes with incoherent light emission.

B. Angle division

In the angle-division method, the transient event is probed from different angles in two typical arrangements. The first scheme uses an angularly separated and temporally distinguished ultrashort pulse train, which can be generated by dual echelons with focusing optics [52]. The second scheme uses longer pulses to cover the entire duration of the transient event. These pulses probe the transient events simultaneously. Each probe pulse records a projected view of the transient scene from a different angle. This scheme, implementing the Radon transformation in the spatiotemporal domain, allows leveraging well-established methods in medical imaging modalities, such as x-ray computed tomography (CT) and therefore has received extensive attention in recent years. Here, we discuss a representative second scheme.

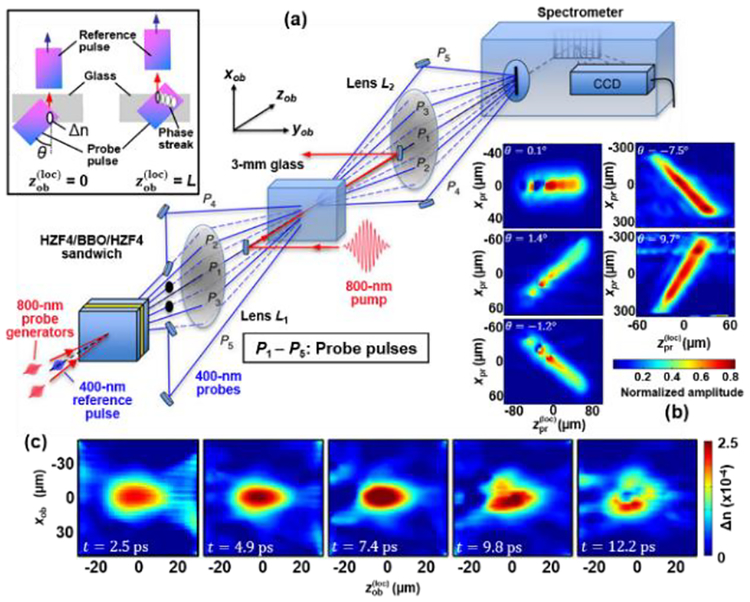
Figure 4(a) shows the system setup of single-shot frequency-domain tomography (SS-FDT) [53] for imaging transient refractive index perturbation. An 800-nm, 30-fs, 0.7-μJ pump pulse induced a transient refractive index structure (Δn) in a fused silica glass due to the nonlinear refractive index dependence and pump-generated plasma. This structure evolved at a luminal speed. In addition, a pair of pulses, directly split from the pump pulse (each with a 30-μJ pulse energy), were crossed spatiotemporally in a BBO crystal that was sandwiched by two HZF4 glasses. The first HZF4 glass generated a fan of up to eight 800 nm daughter pulses by cascaded four-wave mixing. The BBO crystal doubled the frequency as well as increased the number of pulses. The second HZF4 glass chirped these frequency-doubled daughter pulses to 600 fs. In the experiment, five angularly separated probe pulses were selected.

Fig. 4.

Single-shot frequency-domain tomography (SS-FDT) for imaging transient refractive index perturbation based on angle division followed by spectral imaging holography [53]. (a) Schematic of the experimental setup. Upper-left inset: principle of imprinting a phase streak in a probe pulse (adapted from [54]). θ, incident angle of the probe pulse; Δn, refractive index change. (b) Phase streaks induced by the evolving refractive index profile. x_pr and $z_{\mathrm{p}\mathrm{r}}^{\left(\mathrm{l}\mathrm{o}\mathrm{c}\right)}$, the transverse and the longitudinal coordinates of probe pulses. (c) Representative snapshots of the refractive index change using a pump energy of E = 0.7 μJ. x_ob and $z_{\mathrm{o}\mathrm{b}}^{\left(\mathrm{l}\mathrm{o}\mathrm{c}\right)}$, the transverse and the longitudinal coordinates of the object.

The HZF4/BBO/HZF4 structure was directly imaged onto the target plane. The five probe pulses illuminated the target with probing angles of θ. Because all the probe pulses were generated at the same time from the same origin, they overlapped both spatially and temporally at the target. The transient scene was measured by spectral imaging interferometry [54–56]. Specifically, the transient refractive index structure imprinted a phase streak in each probe pulse [see the upper-left inset in Fig. 4(a)]. Before these probe pulses arrived, a chirped 400-nm reference pulse, directly split from the pump pulse, recorded the phase reference. The reference pulse and the transmitted probe pulses were imaged to an entrance slit of an imaging spectrometer. Inside the spectrometer, a diffraction grating and focusing optics broadened both reference pulse and probe pulses, which overlapped temporally to form a frequency-domain hologram [57] on a CCD camera. In the experiment, this hologram recorded all five projected views of the transient event.

Three steps were taken in image reconstruction. First, a 1D inverse Fourier transform was taken to convert the spatial axis into the incident angle. This step, therefore, separated the five probe pulses in the spatial frequency domain. Second, by windowing, shifting, and inverse transforming the hologram area associated with each probe pulse, five phase streaks were retrieved [Fig. 4(b)]. Finally, these streaks were fed into a tomographic image reconstruction algorithm (e.g., algebraic reconstruction technique [53, 58]) to recover the evolution of the transient scene. The reconstructed movie had a 4.35 Tfps imaging speed, an approximately 3-ps temporal resolution, and a sequence depth of 60 frames. Each frame had 128×128 pixels in size [59].

Figure 4(c) shows representative frames of nonlinear optical dynamics induced by intense laser pulse’s propagation in a fused silica glass. The reconstructed movie has revealed that the pulse experienced self-focusing within 7.4 ps. Then, an upper spatial lobe split off from the main pulse appeared at 9.8 ps, attributed by laser filamentation. After that, a steep-walled index ‘hole’ was generated near the center of the profile at 12.2 ps, indicating that the generated plasma had induced a negative index change that locally offset the laser-induced positive nonlinear refractive index change.

The synergy of CT and spectral imaging interferometry has endowed SS-FDH with advantages of the large sequence depth, the ability of recording complex amplitude, and the capability of observing dynamic events along the probe pulses’ propagation directions. However, the sparse angular sampling results in artifacts that strongly affect the reconstructed images [60], which thus limits the spatial and temporal resolutions.

C. Temporal wavelength division

The third method in the active-detection domain is temporal wavelength division. Rooted in time-stretching imaging [34–36], the wavelength-division method attaches different wavelengths to individual pulses. After probing the transient scene, a 2D (x, y) image at a specific time point is stamped by unique spectral information. At the detection side, dispersive optical elements spectrally separate transmitted probe pulses, which allows directly obtaining the (x, y, t) datacube.

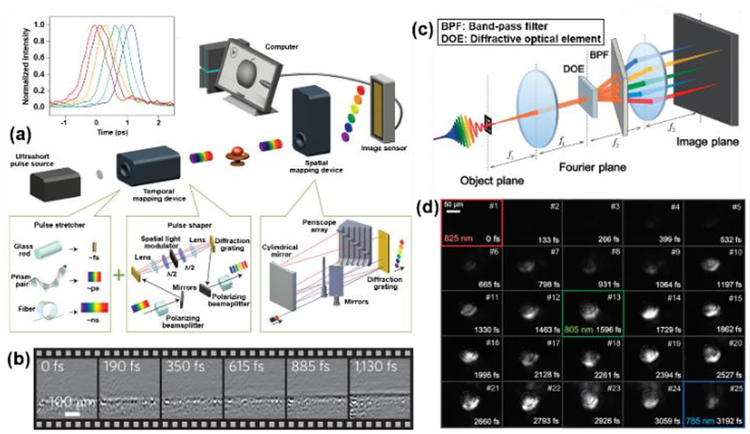
The representative technique discussed in this sub-section is the sequentially time all-optical mapping photography (STAMP) [61]. As shown in Fig. 5(a), a femtosecond pulse first passed through a temporal mapping device that comprised a pulse stretcher and a pulse shaper. Depending on specific experimental requirements, the pulse stretcher used different dispersing materials to increase the pulse width and to induce spectral chirping. Then, a classic 4f pulse shaper [62] filtered selective wavelengths, generating a pulse train containing six wavelength-encoded pulses [see an example in the upper-left inset in Fig. 5(a)] to probe the transient scene. After the scene, these transmitted pulses went through a spatial mapping unit, which used a diffraction grating and imaging optics to separate them in space. Finally, these pulses were recorded at different areas on an imaging sensor. Each frame has 450×450 pixels in size.

Fig. 5.

Sequentially timed all-optical mapping photography (STAMP) based on temporal wavelength division. (a) System schematic of STAMP [61]. Upper inset: normalized intensity profiles of the six probe pulses with an inter-frame time interval of 229 fs (corresponding to a frame rate of 4.4 Tfps) and an exposure time of 733 fs. Lower insets: schematics of the temporal mapping device and the spatial mapping device. (b) Single-shot imaging of electronic response and phonon formation at 4.4 Tfps [61]. (c) Schematic setup of spectrally filtered (SF)-STAMP [64]. f₁ and f₂, focal lengths of lenses. (d) Full sequence of crystalline-to-amorphous phase transition in Ge₂Sb₂Te₅ captured by the SF-STAMP system with an inter-frame time interval of 133 fs (corresponding to an imaging speed of 7.52 Tfps) and an exposure time of 465 fs [64].

The STAMP system has been deployed in visualizing light-induced plasmas and phonon propagation in materials. A 70-fs, 40-μJ laser pulse was cylindrically focused into a ferroelectric crystal wafer at room temperature to produce coherent phonon-polariton waves. The laser-induced electronic response and phonon formation were captured at 4.4 Tfps with an exposure time of 733 fs per frame [Fig. 5(b)]. The first two frames show the irregular and complex electronic response of the excited region in the crystal. The following three frames show an upward-propagating coherent vibration wave.

Since STAMP’s debut in 2014, various recent development [63–66] has reduced the system’s complexity and improve system’s specifications. For example, the schematic setup of the spectrally filtered (SF)-STAMP system [64] is shown in Fig. 5(c). SF-STAMP abandoned the pulse shaper in the temporal mapping device. Consequently, instead of using several temporally discrete probe pulses, SF-STAMP used a single frequency-chirped pulse to probe the transient event. At the detection side, SF-STAMP adopted a single-shot ultrafast pulse characterization setup [67, 68]. In particular, a diffractive optical element (DOE) generated spatially resolved replicas of the transmitted probe pulse. These replicas were incident to a tilted bandpass filter, which selected different transmissive wavelengths according to the incident angles [67]. Consequently, the sequence depth was equal to the number of replicas produced by the DOE. The imaging speed and the temporal resolution were limited by the transmissive wavelength range.

Figure 5(d) shows the full sequence (a total of 25 frames) of the crystalline-to-amorphous phase transition of Ge₂Sb₂Te₅ alloy captured by SF-STAMP at 7. 52 Tfps (with an exposure time of 465 fs). Each frame has 400×300 pixels in size. The gradual change in the probe laser transmission up to ~660 fs is clearly shown, demonstrating the phase transition process. In comparison with this amorphized area, the surrounding crystalline areas retained high reflectance. The sequence also shows that the phase change domain did not spatially spread to the surrounding area. This observation has verified the theoretical model that attributed the initiation of non-thermal amorphization to Ge-atom displacements from octahedral to tetrahedral sites [64, 69].

The SF-STAMP technique has achieved one of the highest imaging speeds (7.52 Tfps) in active-detection-based single-shot ultrafast optical imaging. The original STAMP system, although having a high light throughout, is restricted by a low sequence depth. SF-STAMP, although having increased the sequence depth, significantly sacrifices the light throughput. In addition, the trade-off between the pulse width and spectral bandwidth limits STAMP’s temporal resolution. Finally, they are applicable to only color-neutral objects.

D. Spatial frequency division

The last method discussed in the active-detection domain is spatial frequency division. It works by attaching different spatial carrier frequencies to probe pulses. The transmitted probe pulses are spatially superimposed at the detector. In the ensuing imaging reconstruction, temporal information associated with each probe pulse is separated at the spatial frequency domain, which allows recovering the (x, y, t) datacube. Two representative techniques are shown for this method.

1. Time-resolved holographic polarization microscopy (THPM)

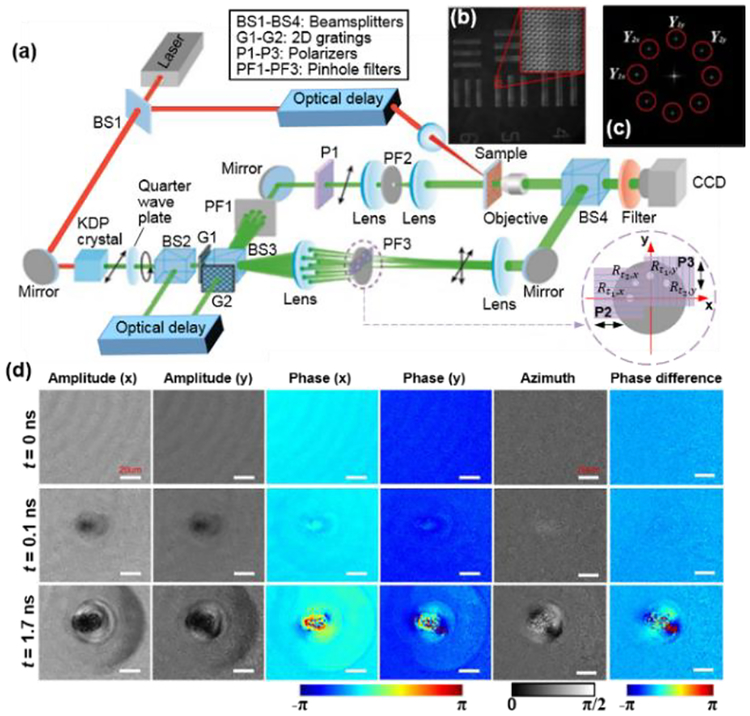
In the THPM system [Fig. 6(a)] [70], a pulsed laser generated a pump pulse and a probe pulse by using a beam splitter. The pump beam illuminated the sample. The probe pulse was first frequency doubled by a potassium dihydrogen phosphate crystal, tuned to circular polarization by a quarter wave plate, and then split by another beam splitter to two pulses with a time delay. Each probe pulse passed through a 2D grating and was further split to signal pulses and reference pulses. The orientation of the grating determined the polarization of diffracted light to be 45° with the x-axis. Two signal pulses were generated by selecting only the zeroth diffraction order from a pinhole filter. The reference pulses passed through a four-pinhole filter, on which two linear polarizers were placed side by side [see the lower-right inset in Fig. 6(a)]. The orientations of the linear polarizers P2 and P3 were along the x-axis and the y-axis, respectively. As a result, a total of four reference pulses (i.e., $R_{t_1,x},R_{t_1,y},R_{t_2,x},R_{t_2,y}$), each carrying a different combination of arrival times and SOPs, were generated. After the sample, the reference pulses interfered with the transmitted signal pulses with the same arrival times on a CCD camera (2048×2048 pixels). There, the interference fringes of signal pulse with the four reference pulses had different spatial frequencies. Therefore, a frequency multiplexed hologram was recorded [Fig. 6(b)].

Fig. 6.

Time-resolved holographic polarization microscopy (THPM) based on time delays and spatial frequency division of the reference pulses for imaging laser-induced damage of a mica lamina sample (adapted from [70]). (a) Schematic of experimental setup. Black arrows indicates the pulses’ SOPs. KDP, potassium dihydrogen phosphate. Lower-right inset: Generation of four reference pulses. (b) Recorded hologram of a USAF resolution target. The zoom-in picture shows the detailed interferometric pattern of this hologram. (c) Spatial frequency spectrum of (b). (d) Time-resolved multi-contrast imaging of ultrafast laser-induced damage in a mica lamina sample.

In image reconstruction, the acquired hologram was first Fourier transformed. Information carried by each carrier frequency was separated in the spatial frequency domain [Fig. 6(c)]. Then, by windowing, shifting, and inverse Fourier transforming of hologram associated with each carrier frequency, four images of complex amplitudes were retrieved. Finally, the phase information in the complex amplitude was used to calculate the SOP, in terms of azimuth and phase difference [71].

THPM has been used for real-time imaging of laser-induced damage [Fig. 6(d)]. A mica lamina plate, obtained by mechanical exfoliation, was the sample. A pump laser damaged the plate with an intensity of >40 J/cm². THPM has captured the initial amplitude and phase change at 0.1 ns and 1.7 ns after the pump pulse, corresponding to a sequence depth of two frames and an imaging speed of 625 Gfps. The images have revealed the generation and propagation of shock waves. In addition, the movie reflects non-uniform changes in amplitude and phase, which was due to the sample’s anisotropy. Furthermore, the SOP analysis revealed a phase change of 0.4π and an azimuth angle of ~36° at the initial stage. Complex structures in azimuth and phase difference were observed at the 1.7-ns delay, indicating anisotropic changes in transmission and refractive index in the process of laser irradiation.

2. Frequency recognition algorithm for multiple exposures (FRAME) imaging

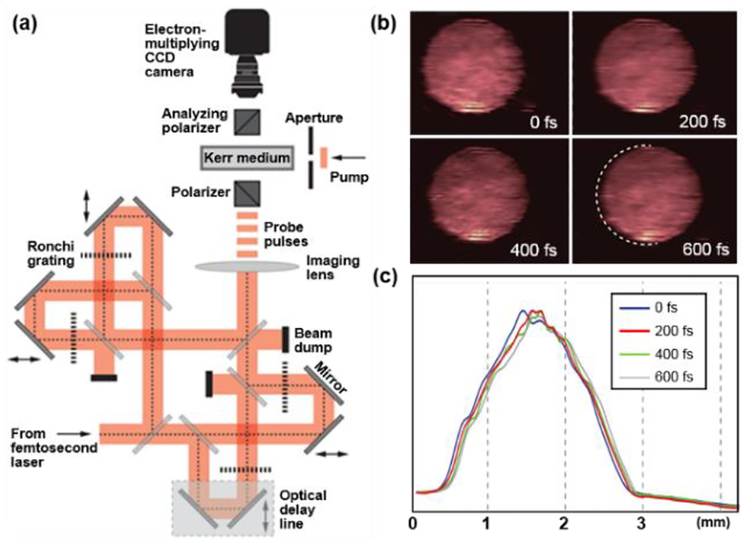
The second technique is the frequency recognition algorithm for multiple exposures (FRAME) imaging [72]. Instead of forming the fringes via interference, FRAME attaches various carrier frequencies to probe pulses using intensity modulation. In the setup [Fig. 7(a)], a 125-fs pulse output from an ultrafast laser was split into four sub-pulses, each having a specified time delay. The intensity profile of each sub-pulse was modulated by a Ronchi grating with an identical period but a unique orientation. These Ronchi gratings, providing sinusoidal intensity modulation to the probe pulses, were directly imaged to the measurement volume. As a result, the spatially modulated illumination patterns were superimposed onto the dynamic scene in the captured single image. In the spatial frequency domain, the carrier frequency of the sinusoidal pattern shifted the band-limited frequency content of the scene to unexploited areas. Thus, the temporal information of the scene, conveyed by sinusoidal patterns with different angles, were separated in the spatial frequency domain without any cross-talk. Following a similar procedure as THPM, the sequence could be recovered. The FRAME imaging system has captured the propagation of a femtosecond laser pulse through a CS₂ medium at imaging speeds up to 5 Tfps with a frame size of 1002×1004 pixels. The temporal resolution, limited by the imaging speed, was 200 fs. Using a similar Kerr-gate setup as the one in Fig. 2(a), transient refractive index change was used as the contrast to indicate the propagation of the pulse in the Kerr medium [Fig. 7(b) and (c)].

Fig. 7.

Frequency recognition algorithm for multiple exposures (FRAME) imaging based on spatial frequency division of the probe pulses [72]. (a) System schematic. (b) Sequence of reconstructed frames of a propagating femtosecond light pulse in a Kerr medium at 5 Tfps. The white dashed arc in 600-fs frame indicates the pulse’s position at 0 fs. (c) Vertically summed intensity profiles of (b).

Akin to the space-division method (Section 2A), the generation of the probe pulse train using the spatial frequency division method does not rely on dispersion. Thus, the preservation of the laser pulse’s entire spectrum allows simultaneously maximizing the frame rate and the temporal resolution. The carrier frequency can be attached via either interference or intensity modulation. The former offers the ability of directly measuring the complex amplitude of the transient event. The latter allows easy adaptation to other ultrashort light sources, such as sub-nanosecond flash lamps [73] and LEDs [74, 75]. By integrating imaging modalities that can sense other photon tags (e.g., polarization), it is possible to achieve high-dimensional imaging of ultrafast events. The major limitation of the frequency-division method, similar to the space-division counterpart, is the limited sequence depth. To increase the sequence depth, either the FOV or spatial resolution must be sacrificed.

3. PASSIVE-DETECTION DOMAIN

A transient event can also be passively captured in a single measurement. In this domain, the ultra-high temporal resolution is provided by receive-only ultrafast detectors without the need for active illumination. The transient event is either imaged directly or reconstructed computationally. Compared with active detection, passive detection has unique advantages in imaging self-luminescent and color-selective transient scenes or distant scenes that are light-years away. In the following, we will present two passive-detection methods implemented in five representative techniques.

A. Direct imaging

The first method in the passive-detection domain is direct imaging using novel ultrafast 2D imaging sensors. In spite of limitations in pixel counts, sequence depth, or light throughput, this method has the highest technological maturity, manifesting in the successful commercialization and wide applications of various products. Here, three representative techniques are discussed.

1. In-situ storage image sensor (ISIS) CCD

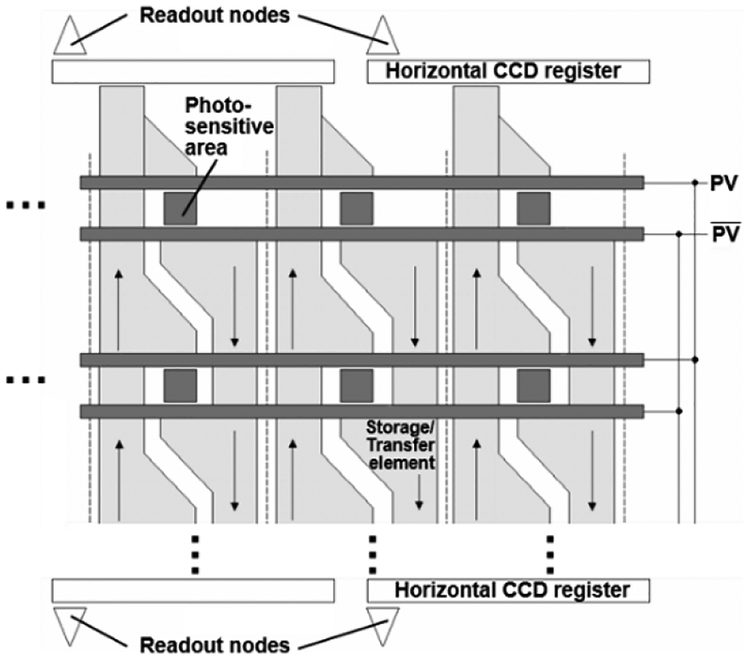
The ISIS CCD camera uses a novel charge transfer and storage structure to achieve ultra-high imaging speed. As an example, the ISIS CCD camera manufactured by DALSA [76] (Fig. 8) had 64×64 pixels, each with a 100-μm pitch. Each pixel contained a photosensitive area (varies from 10×10 μm² to 18×18 μm² in size, corresponding to a fill factor of 1–3%), two readout gates (PV and $\stackrel{-}{\mathrm{P}\mathrm{V}}$ in Fig. 8), and 16 charge storage/transfer elements (arranged into two groups of eight elements, with opposite transfer directions). Transfer elements from adjacent pixels constituted continuous two-phase CCD registers in the vertical direction. Horizontal CCD registers with multiport readout nodes were distributed at the top and the bottom of the sensor. The two readout gates, operating out of phase in burst mode, transferred photo-generated charges alternatingly into the up and down groups of storage elements within each frame’s exposure time of 10 ns (corresponding to an imaging speed of 100 Mfps). During image capturing, charges generated by the odd or even numbered frames filled up the storage elements on both sides without being read out, which is the bottleneck in speed. After a full integration cycle (16 exposures in total), the sensor was reset while all time-stamped charges were read out in a conventional manner. As a result, the inter-frame time interval could be decreased to the transfer time of an image signal to the in-situ storage [77]. The ultrafast imaging ability of this ISIS-based CCD camera has been demonstrated by imaging a 4-ns pulsed LED light source [76].

Fig. 8.

Structure of DALSA’s in-situ storage image sensor (ISIS) CCD camera based on on-chip charge transfer and storage (adapted from [76]). The sensor has 64×64 pixels while six are shown here. Arrows indicate the charge transfer directions.

The DALSA’s ISIS-based CCD camera, to our best knowledge, is currently the fastest CCD camera. Based on mature fabrication technologies, this camera holds great potential for being further developed towards a consumer product. However, currently, its limited number of pixels, low sequence depth, and extremely low fill factor, make this camera far below most users’ requirements [77].

2. Ultrafast framing camera (UFC)

In general, the UFC is built upon the operation of beam splitting with ultrafast time gating [17]. In an example [78] schematically shown in Fig. 9(a), a pyramidal beam splitter with an octagonal base generated eight replicated images of the transient scene. Each image was projected onto a time-gated intensified CCD camera. Onset and width of the time gate for each intensified CCD camera were precisely controlled to capture successive temporal slices [i.e., 2D spatial (x, y) information at a given time point] of the transient event. The recent advances in ultrafast electronics have enabled inter-frame time intervals as short as 10 ps and a gate time of 200 ps [79]. The implementation of new optical design has increased the sequence depth to 16 frames [80].

Fig. 9.

Ultrafast framing camera (UFC) based on beam splitting along with ultrafast time gating. (a) Schematic of a UFC [78]. (b) Schematic of shadowgraph imaging of cylindrical shock waves using a UFC (adapted from [84]). Inset: Configuration of the multi-layered target. (c) Sequence of captured shadowgraph frames showing the convergence and subsequent divergence of the shock waves generated by a laser excitation ring (red dashed circle in the first frame) in the target [84]. The shock front is pointed by the white arrows. Additional rings and structure instabilities are shown by the blue arrows and orange arrows, respectively.

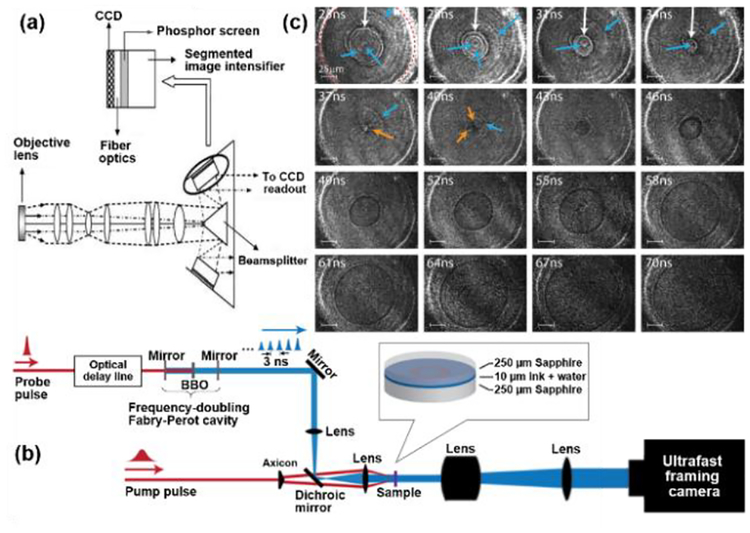
UFCs have been used in widespread applications, including ballistic testing, materials characterization, and fluid dynamics [81–83]. Figure 9(b) shows the setup of ultrafast imaging shadowgraphy of cylindrically propagating shock waves using the UFC [84]. In the experiment, a multi-stage amplified Ti:sapphire laser generated pump and probe pulses. The pump pulse, with a 150-ps pulse width and a 1-mJ pulse energy, was converted into a ring shape (with a 150-μm inner diameter and an 8-μm width) by a 0.5° axicon and a 30-mm-focal-length lens. This ring pattern was used to excite a shock wave on the target. The probe pulse, compressed to a 130-fs pulse width, passed through a frequency-doubling Fabry-Perot cavity. The output 400-nm probe pulse train was directed through the target of a 10-μm-thick ink-water layer that was sandwiched between two sapphire wafers. The transient density variations of the shock wave altered the refractive index in the target, causing light refraction in probe pulses. The transmitted probe pulses were imaged onto a UFC (Specialised Imaging, Inc.) that is able to capture 16 frames (1360×1024 pixels) with an imaging speed of 333 Mfps and a temporal resolution of 3 ns [80].

The single-shot ultrafast shock imaging has allowed tracking non-reproducible geometric instability [Fig. 9(c)]. The sequence revealed asymmetric structures of converging and diverging shock waves. While imperfect circles from the converging shock front were observed, the diverging wave maintained a nearly circular structure. The precise evolution was different in each shock event, which was characteristic of converging shock waves [85]. In addition, faint concentric rings [indicated by blue arrows in Fig. 9(c)] were seen in these events. Tracking these faint features has allowed detailed studies of shock behavior (e.g., substrate shocks and coupled wave interactions) [84].

3. High-speed sampling camera (HISAC)

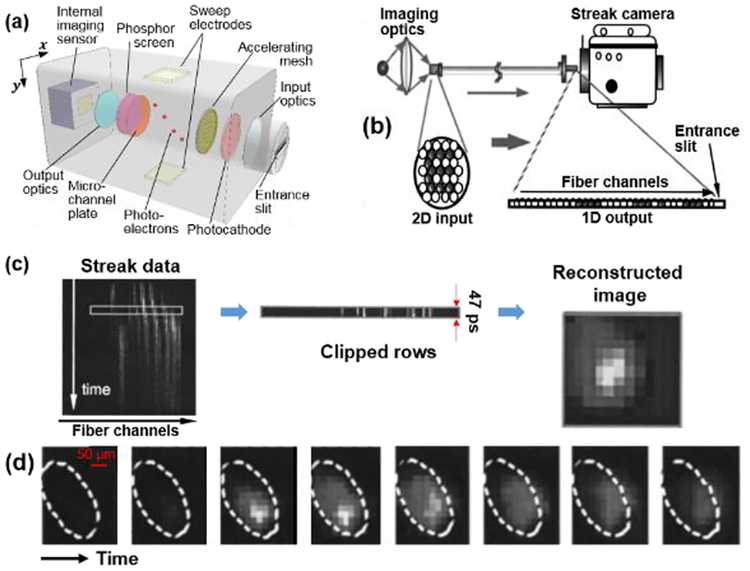
Streak cameras are ultrafast detectors with up to femtosecond temporal resolutions [22]. In the conventional operation [Fig. 10(a)], incident photons first pass through a narrow (typically 50–200 μm wide) entrance slit [along the x-axis in Fig. 10(a)]. The image of this entrance slit is formed on a photocathode, where photons are converted into photoelectrons via the photoelectric effect. These photoelectrons are accelerated by a pulling voltage and then passed between a pair of sweep electrodes. A linear voltage ramp is applied to the electrodes so that photoelectrons are deflected to different vertical positions [along the y-axis in Fig. 10(a)] according to their times of arrival. The deflected photoelectrons are amplified by a micro-channel plate and then converted back to photons by bombarding a phosphor screen. The phosphor screen is imaged onto an internal imaging sensor (e.g., a CCD or a CMOS camera), which records the time course with a 1D FOV [i.e., an (x, t) image at a specific y position]. Because the streak camera’s operation requires using one spatial axis on the internal imaging sensor to record the temporal information, the narrow entrance confines its FOV. Therefore, the conventional streak camera is a 1D ultrafast imaging device.

Fig. 10.

High-speed sampling camera (HISAC) based on remapping the scene from 2D to 1D in space and streak imaging. (a) Schematic of a streak camera. (b) Schematic of a high-speed sampling camera (HISAC) system. (c) Formation process of individual frames from the streak data. (d) Sequence showing shock wave breakthrough. The time interval between frames is ~336 ps. The laser focus is outlined by the white dashed circle. (b)-(d) are adapted from [87].

To overcome this limitation, various dimension-reduction imaging techniques [86–89] have been developed to allow direct imaging of a 2D transient scene by a streak camera. In general, this imaging modality maps a 2D image into a line to interface with the streak camera’s entrance slit, so that the streak camera can capture an (x, y, t) datacube in a single shot. As an example, Fig. 10(b) shows the system schematic of the high-speed sampling camera (HISAC) [87]. An optical telescope imaged the transient scene to a 2D-1D optical fiber bundle. The input end of this fiber bundle was arranged as a 2D fiber array (15×15) [90], which sampled the 2D spatial information of the relayed image. The 2D fiber array was remapped to a 1D configuration (1×225) at the output end that interfaced with a streak camera’s entrance slit. The ultrashort temporal resolution, provided by the streak camera, was 47 ps, corresponding to an imaging speed of 21.3 Gfps. A 2D frame at a specific time point was covered by reshaping one row on the streak image to 2D according to the optical fiber mapping [Fig. 10(c)]. Totally, the sequence depth was up to 240 frames.

HISAC has been implemented in many imaging applications, including heat propagation in solids [91], electron energy transport [92], and plasma dynamics [93]. As an example, Fig. 10(d) shows the dynamic spatial dependence of ablation pressure imaged by HISAC [87]. A 100-J, 1.053-μm laser pulse was loosely focused on a 10-μm-thick hemispherical plastic target. The sequence shows the shock breakthrough process. It revealed that the shock heating decreased with the incident angle, and the breakthrough speed was faster for smaller incident angles. This non-uniformity was ascribed to the angular dependence of pressure generated by the laser absorption.

The dimension-reduction-based streak imaging has an outstanding sequence depth. In addition, its temporal resolution is not bounded by the response time in electronics, which permits hundreds of Gfps to even Tfps imaging speed. However, its biggest limitation is the low number of fibers in the bundle, which produces either a low spatial resolution or a small FOV.

B. Reconstruction imaging

Despite the recent progress, existing ultrafast detectors, restricted by their operating principles, still have limitations, such as imaging FOV, pixel count, and sequence depth. To overcome these limitations, novel computational techniques are thus brought in. Of particular interest among existing computational techniques is compressed sensing (CS). In conventional imaging, the number of measurements is required to be equal to the number of pixels (or voxels) to precisely reproduce a scene. In contrast, CS allows underdetermined reconstruction of sparse scenes. The underlying rationale is that natural scenes possess sparsity when expressed in an appropriate space. In this case, many independent bases in the chosen space convey little to no useful information. Therefore, the number of measurements can be substantially compressed without excessive loss of image fidelity [94]. Here, two representative techniques are discussed.

1. Compressed ultrafast photography (CUP)

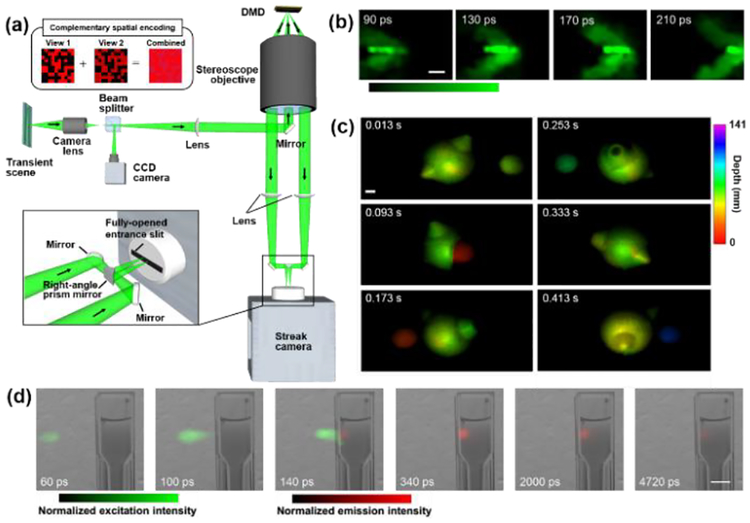
CUP synergistically combines CS with streak imaging [95]. Fig. 11(a) shows the schematic of lossless encoding CUP system [96, 97]. In data acquisition, the dynamic scene, denoted as I, was first imaged by a camera lens. Following the intermediate image plane, a beam splitter reflected half of the light to an external CCD camera. The other half of the light passed through the beam splitter and was imaged to a digital micromirror device (DMD) through a 4f system consisting of a tube lens and a stereoscope objective. The DMD, as a binary amplitude spatial light modulator [98], spatially encoded transient scenes with a pseudo-random binary pattern. Because each DMD pixel can be tilted to either +12° (ON state) or–12° (OFF state) from its surface normal, two spatially-encoded scenes, encoded by complementary patterns [see the upper inset in Fig. 11 (a)], were generated after the DMD. The light beams from both channels were collected by the same stereoscope objective, passed through tube lenses, planar mirrors and a right-angle prism mirror to form two images at separate horizontal positions on a fully-opened entrance port (5 mm×17 mm). Inside the streak camera, the spatially-encoded scenes experienced temporal shearing and spatiotemporal integration and were finally recorded by an internal CCD camera in the streak camera.

Fig. 11.

Compressed ultrafast photography (CUP) for single-shot real-time ultrafast optical imaging based on spatial encoding and 2D streaking followed by compressed-sensing reconstruction. (a) Schematic of the lossless-encoding CUP system [97]. DMD, digital micromirror device. Upper inset: Illustration of complementary spatial encoding. Lower inset: Close-up of the configuration before the streak camera’s entrance port (black box). (b) CUP of a propagating photonic Mach cone [96]. (c) CUP of dynamic volumetric imaging [104]. (d) CUP of spectrally resolved pulse-laser-pumped fluorescence emission [95]. Scale bar: 10 mm.

For image reconstruction, the acquired snapshots from the external CCD camera and the streak camera, denoted as E, were used as inputs for the two-step iterative shrinkage/thresholding algorithm [99], which solved the minimization problem of ${\text{min}}_I\left\{\frac{1}{2}\Vert E-\mathit{O}I{\Vert }_2^2+\beta \text{Φ}\left(I\right)\right\}$. Here O is a joint measurement operator that accounts for all operations in data acquisition, ${\Vert \bullet \Vert }_2$ denotes the l² norm, Φ(I) is a regularization function that promotes sparsity in the dynamic scene, and β is the regularization parameter. The solution to this minimization problem can be stably and accurately recovered, even with a highly compressed measurement [94, 100]. For the original CUP system [95], the reconstruction produced up to 350 frames in a movie with an imaging speed of up to 100 Gfps and with an effective exposure time of ~50 ps [101]. Each frame contained 150×150 pixels. The LLE-CUP system, while maintaining the imaging speed at 100 Gfps, improved the numbers of (x, y, t) pixels in the datacube to 330×200×300 [96]. Recently, a trillion-frame-per-second CUP (T-CUP) system, employing a femtosecond streak camera [102], has achieved an imaging speed of 10 Tfps, an effective exposure time of 0.58 ps, numbers of (x,y) pixels of 450×150 per frame, and a sequence depth of 350 frames [103].

CUP has been used for a number of applications. First, it allows the capture, for the first time, a scattering-induced photonic Mach cone [96]. A thin scattering plate assembly contained an air (mixed with dry ice) source tunnel that was sandwiched between two silicone-rubber (mixed with aluminum oxide powder) display panels. When an ultrashort laser pulse was launched into the source tunnel, the scattering events generated secondary sources of light that advanced superluminally to the light propagating in the display panels, forming a scattering-induced photonic Mach cone. CUP imaged the formation and propagation of a photonic Mach cone at 100 Gfps [Fig. 11(b)]. Second, by leveraging the ultrashort temporal resolution and the spatial encoding, CUP has enabled single-shot encrypted volumetric imaging [104]. Through the sequential imaging of the CCD camera inside the streak camera, high-speed volumetric imaging at 75 volume per second was demonstrated by using a two-ball object rotating at 150 revolutions per minute [Fig. 11(c)]. Finally, CUP has achieved single-shot spectrally resolved fluorescence lifetime mapping [95]. Showing in Fig. 11(d), Rhodamine 6G dye solution placed in a cuvette was excited by a single 7-ps laser pulse. The CUP system clearly captured both the excitation and the fluorescence emission processes. The movie has also allowed quantification of the fluorescence lifetime.

CUP exploits the spatial encoding and temporal shearing to tag each frame with a spatiotemporal “barcode”, which allows an (x, y, t) datacube to be compressively recorded as a snapshot with spatiotemporal mixing. This salient advantage overcomes the limitation in the FOV in conventional streak imaging, converting the streak camera into a 2D ultrafast optical detector. In addition, CUP’s recording paradigm allows fitting more frames onto the CCD surface area, which significantly improves the sequence depth while maintaining the inherent imaging speed of the streak camera. Compared with the LIF holography, CUP does not require the presence of a reference pulse, making it especially suitable for imaging incoherent light events (e.g., fluorescence emission). However, the spatiotemporal mixture in CUP trades spatial and temporal resolutions of a streak camera for the added spatial dimension.

2. Multiple-aperture compressed sensing (MA-CS) CMOS

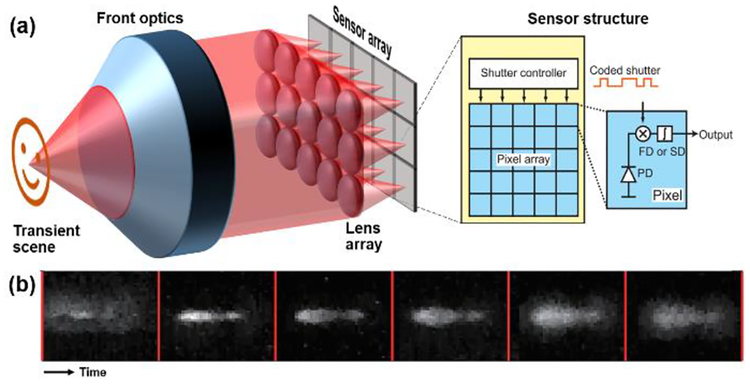
CS has also been implemented in the time domain with a CMOS sensor. Figure 12(a) shows the structure of the MA-CS CMOS sensor [105]. In image acquisition, a transient scene, I, first passed through the front optics. A 5×3 lens array (0.72 mm × 1.19 mm pitch size and 3-mm focal length), sampling the aperture plane, optically generated a total of 15 replicated images, each was formed onto an imaging sensor (64×108 pixels in size). A dynamic shutter, encoded by a unique binary random code sequence for each sensor, modulated the temporal integration process [106, 107]. The temporally encoded transient scene was spatiotemporally integrated on the sensor. The acquired data from all sensors, denoted by E, were fed into a compressed-sensing-based reconstruction algorithm [108, 109] that solved the inverse problem of ${\text{min}}_I{{\sum }_i\Vert D_{i}I\Vert }_{p}s.t.E=\mathit{A}I$. Here, D_iI is the discrete gradient of I at pixel i, ${‖\bullet ‖}_p$ means the p norm (p = 1 or 2), and A is the observation matrix. With the prior information about the 15 temporal codes and the assumption that all 15 images are spatially identical, the spatiotemporal datacube was recovered. The reconstructed frame rate and the temporal resolution, determined by the maximum operation frequency of the shutter controller, was 200 Mfps. Based on the captured 15 images, 32 frames could be recovered in the reconstructed movie.

Fig. 12.

Multiple-aperture compressed-sensing (MA-CS) CMOS sensor based on temporally encoding each of the image replicas (adapted from [105]). (a) System schematic. PD, photodiode; FD, float diffuser; SD, storage diode. (b) Temporally resolved frame of laser-pulse-induced plasma emission. The inter-frame time interval is 5 ns.

This sensor has been implemented in time-of-flight LIDAR [110] and plasma imaging [105]. As an example, Fig. 12(b) shows the plasma emission induced by an 8-ns, 532-nm laser pulse. The MA-CS CMOS sensor captured these dynamics in a period of 30 ns.

The implementation of the MA recording and CS overcomes the imaging speed limit in the conventional CMOS sensor. In addition, built upon the mature CMOS fabrication technology, the MA-CS CMOS sensor has great potential in increasing the pixel count. Moreover, different from the UFCs, a series of temporal gates, instead of one, was applied to the sensor, which significantly increased the light throughput. Finally, compared with the ISIS CCD camera, the fill factor of the MA-CS CMOS sensor has been improved to 16.7%. However, the MA recording scheme may face technical difficulties in scalability and parallax, which poses challenges in improving the sequence depth.

4. SUMMARY AND OUTLOOK

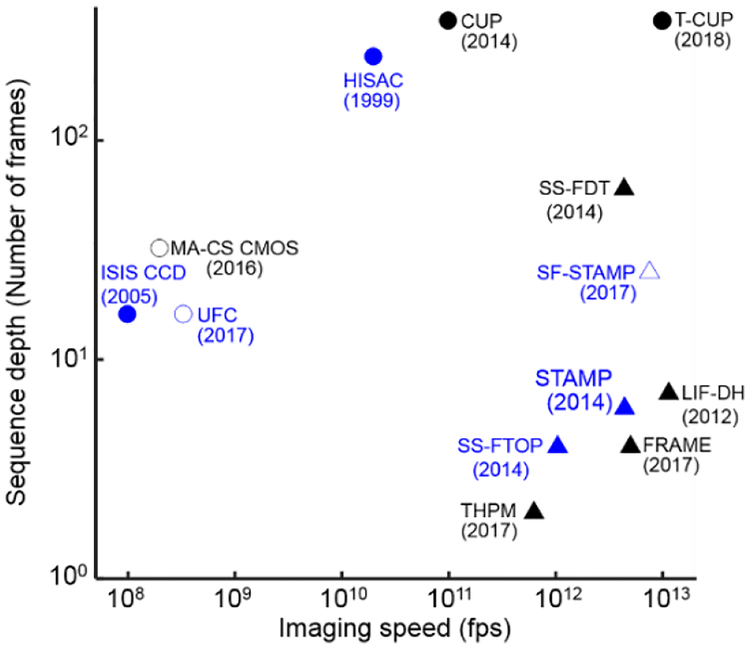
In this mini-review, based on the illumination requirement, we categorize single-shot ultrafast optical imaging into two general domains. According to specific image acquisition and reconstruction strategies, these domains are further divided into six methods. A total of 11 representative techniques have been surveyed from aspects of their underlying principles, system schematics, specifications, applications, as well as their advantages and limitations. This information is summarized in Table 1. In addition, Fig. 13 compares the sequence depths versus the imaging speeds of these techniques. In practice, researchers could use this table and figure as general guidelines to assess the fortes and bottlenecks, and select the most suitable technique for their specific studies.

Table 1.

Comparative summary of representative single-shot ultrafast optical imaging techniques

Imaging technique	Detection domain	Image formation	Imaging speed	Temporal resolution	Number of (x, y) pixels	Sequence depth	Light throughput	Selected applications
SS-FTOP [41]	Active	Direct	1.04 Tfps	276 fs	41×60	4	High	Laser pulse characterization [41]
LIF-DH [50]	Active	Reconstruction	11.4 Tfps	88 fs	512×512	7	High	Laser pulse characterization [50]
SS-FDT [53]	Active	Reconstruction	4.35 Tfps	3 ps	128×128	60	High	Nonlinear optical physics [53]
STAMP [61]	Active	Direct	4.4 Tfps	733 fs	450×450	6	High	Laser plasma; Phonon propagation [61]
SF-STAMP [64]	Active	Direct	7.52 Tfps	465 fs	400×300	25	Low[a]	Phase transition in alloys [64]
THPM [70]	Active	Reconstruction	625 Gfps	1.6 ns	2048×2048	2	High	Laser-induced damage [70]
FRAME [72]	Active	Reconstruction	5 Tfps	200 fs	1002×1004	4	High	Laser pulse characterization [72]
ISIS CCD [76]	Passive	Direct	100 Mfps	10 ns	64×64	16	High	Laser pulse characterization [76]
UFC [78]	Passive	Direct	333 Mfps	3 ns	1360×1024	16	Low[b]	Fluid dynamics [81]; Material characterization [82]; Shock wave dynamics [84]
HISAC [87]	Passive	Direct	21.3 Gfps	47 ps	15×15	240	High	Laser ablation [87]; Electron energy transport [92]; Plasma dynamics [93]
CUP [95]	Passive	Reconstruction	100 Gfps	50 ps	150×150	350	High	Fluorescence lifetime mapping [95]; Shock wave dynamics [96]; Time-of-flight volumetric imaging [104];
T-CUP [103]	Passive	Reconstruction	10 Tfps	0.58 ps	450×150	350	High	Laser pulse characterization [103]
MA-CS CMOS [105]	Passive	Reconstruction	200 Mfps	5 ns	64×108	32	Medium[c]	Plasma dynamics [105] Time-of-flight LIDAR [110]

^[a]The light throughput can be approximated estimated by the reciprocal of the sequence depth.

^[b]The light throughput is determined by τ_g/τ_s, where τ_g and τ_s are the width of ultrafast gating and that of the transient event, respectively.

^[c]50% in current MA-CS CMOS configuration. Specific light throughput depends on the ratio between “ON” and “OFF” pixels in temporal binary random encoding.

Fig. 13.

Comparison of representative single-shot ultrafast optical imaging techniques in imaging speeds and sequence depths. Triangles and circles represent active and passive detection domains. Blue and black colors represent the direct and reconstruction imaging methods, respectively. Solid and hollow marks represent high and low (including medium) light throughputs. The numbers in the parentheses are the years in which the techniques were published. CUP, Compressed ultrafast photography; T-CUP, Trillion-frames-per-second CUP; FRAME, Frequency recognition algorithm for multiple exposures; HISAC, High-speed sampling camera; ISIS CCD, In-situ storage image sensor CCD; LIF-DH, Light-in-flight recording by digital holography; MA-CS CMOS, Multi-aperture compressed sensing CMOS; SS-FDT, Single-shot Fourier-domain tomography; SS-FOP, Single-shot femtosecond time-resolved optical polarimetry; STAMP, Sequentially timed all-optical mapping photography; SF-STAMP, Spectral-filtering STAMP; THPM, Time-resolved holographic polarization microscopy; UFC, Ultrafast framing camera.

Single-shot ultrafast optical imaging will undoubtedly continue its fast evolution in the future. This interdisciplinary field is built upon the areas of laser science, optoelectronics, nonlinear optics, imaging theory, computational techniques, and information theory. Fast progress in these disciplines will create new imaging techniques and will improve the performance of existing techniques, both of which, in turn, will open new avenues for a wide range of laboratory and field applications [111–114]. In the following, we outline four prospects in system development.

First, the recent development of a number of emerging techniques suggests intriguing opportunities for significantly improving the specifications of existing single-shot ultrafast optical imaging modalities in the near future. For example, implementing the dual-echelon-based probing schemes [115, 116] could easily improve the sequence depth by approximately one order of magnitude for SS-FTOP (Section 2A). In addition, ptychographic ultrafast imaging [117] has been recently demonstrated in simulation. Spectral multiplexing tomography [118] has shown ultrafast imaging ability experimentally on single frame recording. Both techniques, having solved the issue of limited probing angles, could be implemented in SS-FDT (Section 2B) to reduce reconstruction artifacts and thus to improve spatial and temporal resolutions. As another example, time-stretching microscopy with GHz-level line rates has been demonstrated [119, 120]. Integrating a 2D disperser in these systems could result in new wavelength-division-based 2D ultrafast imaging (Section 2C). Finally, a high-speed image rotator [121] could increase the sequence depth of FRAME imaging (Section 2D). For the passive-detection domain, the highest speed limit of silicon sensors, in theory, has been predicted to be 90.1 Gfps [122]. Currently, a number of Gfps-level sensors are under development [77, 123, 124]. This recent progress could significantly improve the imaging FOV, pixel count, and sequence depth in ultrafast CCD and CMOS sensors (Section 3A). In addition, the advent of many femtosecond streak imaging techniques [125] could support the pursuit of the imaging speed of CUP (Section 3B) further toward hundreds of Tfps levels.

Second, computational techniques will exert a more significant role in single-shot ultrafast optical imaging. Optical realization of mathematical models can transfer some unique advantages in these models into the ultrafast optical imaging systems and thus has alleviated the hardware limitations in, for example, imaging speed for MA-CS CMOS (Section 3B). In addition, a number of established image construction algorithms used in tomography have been grafted to the spatiotemporal domain [e.g., the algebraic reconstruction technique for SS-FDT (Section 2B)]. It is therefore believed that this trend will continue, and more algorithms used in x-ray CT, magnetic resonance imaging, and ultrasound imaging may be applied in newly developed ultrafast optical imaging instruments. Finally, it is predicted that machine learning techniques [126, 127] will be implemented in the single-short ultrafast optical imaging to improve imaging reconstruction speed and accuracy.

Third, high-dimensional single-shot ultrafast optical imaging [128] will gain more attention. Many transient events may not be reflected by light intensity. Therefore, the ability to measure other optical contrasts, for example, phase and polarization, will significantly enhance the ability and the application scope of ultrafast optical imaging. A few techniques [e.g., SS-FTOP (Section 2A) and THPM (Section 2D)] have already explored this path. It is envisaged that imaging modalities that sense other optical contrasts (e.g., volumography, spectroscopy, and light-field photography) will be increasingly integrated into ultrafast optical imaging.

Finally, continuous streaming will be one of the ultimate milestones in single-shot ultrafast optical imaging. Working in the stroboscopic mode, current single-shot ultrafast imaging techniques still require a precise synchronization in imaging transient events, falling short in visualizing asynchronous processes. Towards this goal, innovations in large format imaging sensors [129], high-speed interfaces [130], ultrafast optical waveform recorders [131], can be leveraged. In addition, intelligent selection, reconstruction, and management of big data are also indispensable [132].