SLiM 3: Forward Genetic Simulations Beyond the Wright–Fisher Model

Abstract

With the desire to model population genetic processes under increasingly realistic scenarios, forward genetic simulations have become a critical part of the toolbox of modern evolutionary biology. The SLiM forward genetic simulation framework is one of the most powerful and widely used tools in this area. However, its foundation in the Wright–Fisher model has been found to pose an obstacle to implementing many types of models; it is difficult to adapt the Wright–Fisher model, with its many assumptions, to modeling ecologically realistic scenarios such as explicit space, overlapping generations, individual variation in reproduction, density-dependent population regulation, individual variation in dispersal or migration, local extinction and recolonization, mating between subpopulations, age structure, fitness-based survival and hard selection, emergent sex ratios, and so forth. In response to this need, we here introduce SLiM 3, which contains two key advancements aimed at abolishing these limitations. First, the new non-Wright–Fisher or “nonWF” model type provides a much more flexible foundation that allows the easy implementation of all of the above scenarios and many more. Second, SLiM 3 adds support for continuous space, including spatial interactions and spatial maps of environmental variables. We provide a conceptual overview of these new features, and present several example models to illustrate their use.

Introduction

Forward genetic simulations are playing an increasingly important role in evolutionary biology due to their ability to model a wide range of population genetic mechanisms and include a high level of ecological detail in the simulated scenario (Carvajal-Rodriguez 2010; Yuan et al. 2012; Bank et al. 2014; Hoban 2014; Thornton 2014; Haller and Messer 2017; Haller et al. 2018). The SLiM forward genetic simulation framework (Messer 2013; Haller and Messer 2017) has proved to be a powerful tool for this purpose, and constitutes one of the most widely used computational frameworks for implementing such simulations at the present time.

The National Cancer Institute’s Genetic Simulation Resources (GSR) website provides a comprehensive database of genetic simulation software tools (NCI 2018). At the time of writing, the GSR listed 42 packages supporting forward simulation; this includes many tools that are specialized for a particular type of model, as well as some tools that support a wide variety of evolutionary scenarios. SLiM’s popularity among these tools is based primarily upon three key attributes. First, it is highly scriptable, allowing the mechanics of the SLiM framework to be fundamentally modified and extended in many ways. At the same time, even fairly sophisticated evolutionary models can often be expressed in a page of code or less, since all of the core simulation code is provided by SLiM, yielding tremendous benefits compared with writing simulations from scratch in a language such as C++. Second, SLiM includes a full-featured graphical modeling environment, SLiMgui, that makes interactive model development, visual debugging, and hands-on exploration easy, with large benefits throughout the modeling process (Grimm 2002). And third, a great deal of work has been devoted to optimizing SLiM, making it run as efficiently as possible across a wide variety of simulation scenarios; these speed benefits are inherited for free by any model running within SLiM. The GSR does not provide performance comparisons, so users with performance concerns should run their own tests before settling upon a particular package; for comparing the features available in different packages, however, the GSR can be a very helpful resource.

In our contact with users of SLiM over the past years, one category of questions has predominated: how can SLiM simulations be constructed that go beyond the standard Wright–Fisher or “WF” model (Fisher 1922; Wright 1931)? This model, which has provided the conceptual foundation for all previous versions of SLiM (Messer 2013; Haller and Messer 2017), is defined by a number of simplifying assumptions. For example, the model assumes that generations are nonoverlapping and discrete, without any age structure or age-based differentiation among individuals. Another critical assumption of the model lies in the rules governing the generation of offspring from the parental population; in the standard WF model, the parents for each child in the next generation are drawn randomly from the previous generation with a probability proportional to each individual’s fitness. This makes it difficult to model variation in litter size, monogamous mating, and other such phenomena. Furthermore, since population size is an externally determined parameter in the WF model, it is often not clear how scenarios in which population size is an emergent variable—depending, for instance, on factors such as mean fitness, available habitat, and colonization history—should be accurately modeled in a WF framework.

Given the scope of the simplifying assumptions underlying the WF model, the desire among SLiM’s users to go beyond this model takes many forms, but they might be said to unify around the idea of more realistic spatial and ecological dynamics. For example, users have inquired whether it is possible to model the explicit movement of individuals over a continuous landscape, life cycles with overlapping generations, individual variation in reproduction, density-dependent population regulation, individual variation in dispersal or migration, local extinction and recolonization, mating between subpopulations, age structure, fitness-based survival and hard selection, emergent sex ratios, and more. Because SLiM 2 was already highly scriptable, and thus many of its internal dynamics could be modified through scripting, it was sometimes possible to work around the limitations inherited from the WF model; but those workarounds are often clumsy and laborious, and some types of models have simply proved difficult or impossible to implement in SLiM 2. Fundamentally, the Wright–Fisher model is not an ecological model, and so if we are to progress toward uniting genetics and evolutionary biology with ecology, the need for a more flexible foundation is clear.

In response to this need, we here introduce SLiM 3, which contains two major advances squarely aimed at these limitations. First, in addition to the traditional Wright–Fisher or WF model type of previous SLiM versions, SLiM 3 supports a new non-Wright–Fisher or “nonWF” model type that provides much greater flexibility in how key processes such as mate choice and reproduction, migration, fitness evaluation, survival, population regulation, and other related areas are implemented, allowing the explicit linking of evolutionary dynamics with ecological patterns and processes. Second, in addition to support for discrete subpopulations connected by migration, SLiM 3 now supports models that occupy continuous spatial landscapes, including built-in support for spatial maps that describe environmental characteristics, and for local spatial interactions such as spatial competition and mate choice. (Support for spatial models was introduced in SLiM 2.3, in fact, but is previously unpublished.)

SLiM 3 contains many other important additions as well. Most prominently, it adds support for “tree-sequence recording” (also called “pedigree recording”), a method of recording ancestry information in forward simulations (Kelleher et al. 2016, 2018). Tree-sequence recording can decrease simulation runtimes by several orders of magnitude, by allowing neutral mutations to be overlaid efficiently after forward simulation has completed and by allowing neutral burn-in to be done extremely efficiently with “recapitation”, and it provides several other major benefits as well (Kelleher et al. 2018; Haller et al. 2018). SLiM 3’s support for tree-sequence recording is discussed further in Haller et al. (2018). Other important changes in SLiM 3 since SLiM 2.0 (the last published version) include many additions and improvements to the Eidos scripting language (Haller 2016), many new methods provided by SLiM’s Eidos classes (Haller and Messer 2016), and many improvements to the SLiMgui graphical modeling environment. SLiM 3 also contains a great deal of optimization work to make simulations run faster. A few more specific improvements are worth mentioning too: a new Individual class representing simulated individuals, support for a variable mutation rate along the chromosome, a new recombination() callback mechanism for modifying recombination breakpoints at an individual level, and VCF format output, among others (a complete change list may be found in the SLiM manual).

Here, however, we will focus on what we believe to be the most important new features in SLiM 3: nonWF models and continuous space, the features that enable users to go beyond the Wright–Fisher model in SLiM. We will provide a conceptual overview of these features, and will demonstrate them with several examples.

The nonWF Simulation Model

Perhaps the easiest way to understand nonWF models is by looking at how they differ from the standard WF model type. The most important differences are in the following broad areas:

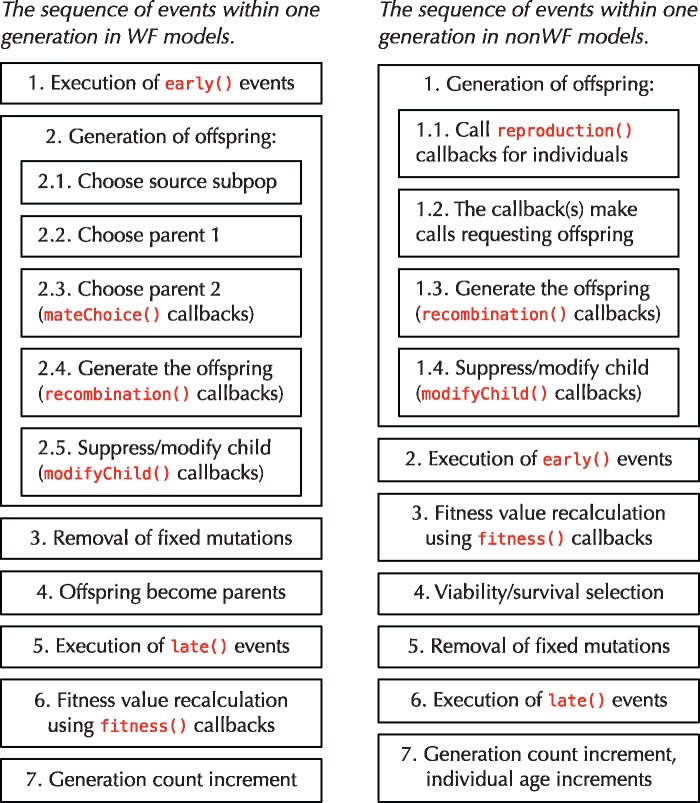
• Age structure. In WF models, generations are discrete and nonoverlapping; all individuals live for a single generation, during which they reproduce and then die. In nonWF models, by contrast, generations can be overlapping; individuals can live for multiple generations, until they die due to some cause (typically selection, old age, or bad luck). More fundamentally, the concept of a “generation” has been broadened. In nonWF models, each generation represents an opportunity to reproduce and/or die—a discretization of those events in time, providing a temporal structure to the model that could be based upon hours, days, seasons, or decades, but that is not necessarily related to the expected lifespan of individuals. Individuals in nonWF models have an age (measured in generations), the population thus has an age structure, and the model can implement whatever age-related behaviors are desired. The generation cycle in nonWF models is contrasted against that of WF models in figure 1 .

• Offspring generation. In WF models, offspring are generated by drawing parents from the individuals in the previous generation. The population size is a parameter of the model, determining how many offspring are to be generated in each generation; the selfing rate, cloning rate, and sex ratio are, similarly, population-level parameters. In nonWF models, by contrast, the script is much more directly in charge of the process of offspring generation; the script requests the generation of each offspring based upon individual state rather than population-level parameters. Calls are made from SLiM to reproduction() callbacks defined in the model script, and those callbacks determine which individuals reproduce, how they choose a mate or mates (if any), how many offspring they have, and so forth. The population size, selfing rate, cloning rate, and sex ratio are therefore no longer population-level parameters; instead, they are emergent properties of the model, consequences of the rules specified in script for the individual-based reproduction dynamics. The population size, for example, becomes a result of the balance between birth rates and death rates, often (but not necessarily) regulated by density-dependent viability selection implemented in the model.

• Migration. In WF models, migration between populations is modeled by specifying the fraction of offspring in a given target population that stem from parents in a given source population. Since this model of migration leads to offspring that occupy a different population from their parents, it most closely resembles a model of juvenile migration. In nonWF models, by contrast, migration is again handled more directly by the model script, which may call the takeMigrants() method to move individuals to a new population at any point in the generation cycle, enabling models where individuals migrate as juveniles, as adults, or at multiple times during their life. This focus on individual-level migration, rather than population-level migration rates, allows for the probability that a given individual will migrate to depend much more flexibly upon individual-level state. A wide range of scenarios can be modeled this way, such as sex-dependent migration, habitat choice, or condition-dependent migration. In such models, the overall migration rate between two populations is again an emergent property that depends on the specific composition of the population and the migration rules specified in script, rather than on a population-level rate.

• Fitness. In WF models, fitness influences the probability that an individual will be chosen as a parent for a child in the next generation; there is no built-in concept of selection-induced mortality. Fitness is therefore relative, resulting in a model of so-called “soft” selection in which greater success for some individuals necessarily comes at the price of diminished success for others. The overall population size is not affected by selection, since it is a model parameter rather than an emergent property of the underlying evolutionary and ecological dynamics. In nonWF models, by contrast, fitness directly influences the probability of survival for each individual during each generation; individuals with low fitness are less likely to survive. Fitness is therefore absolute, and selection is “hard” in such a model by default; as a result, population size will vary naturally with mean population fitness (although this may be compensated for by density-dependent selection or fecundity). Of course one may still model the effects of genetics upon reproductive success or fecundity, in a reproduction() callback, if desired.

Fig. 1.

A comparison of the generation cycles in WF models (left) versus nonWF models (right). Note that nonWF models have a viability/survival selection phase, immediately after fitness value recalculation, whereas in WF models fitness influences mating success and there is no concept of mortality-based selection. Events and callbacks are shown in red; these are points in the generation cycle when SLiM will call out to the script to provide custom behavior. So-called early() and late() events provide commonly used points in the generation cycle when the model script can intervene in SLiM’s operation, toward the beginning and the end of each generation respectively, to do model-specific tasks—generate output, handle interactions between individuals, move individuals in space, and so forth. As this figure illustrates, in WF models early() events come before offspring generation and late() events come after; in nonWF models, early() events come after offspring generation, whereas late() events, by virtue of being at the end of the generation cycle, in effect come before offspring generation (when it occurs at the beginning of the next generation). Callbacks, on the other hand, allow the script to override specific aspects of SLiM’s behavior, such as choosing mates, customizing generated offspring, calculating fitness effects, or generating custom recombination breakpoints. Most of these callbacks exist in both WF and nonWF models, but mateChoice() callbacks exist only in WF models, whereas reproduction() callbacks are only in nonWF models and handle mate choice as well as other reproduction-related duties.

These differences can be summarized by saying that nonWF models are more individual-based, more script-controlled, more emergent, and therefore more biologically realistic. However, they are also often more complex in certain ways, primarily because of the need to implement a reproduction() callback and to introduce some explicit mechanism of population regulation. In effect, with the power to more precisely control reproduction and population regulation comes the responsibility to more explicitly think about and specify those phenomena. Populations can be regulated by any of a wide variety of mechanisms, from density-dependent fecundity to resource competition to predation to territorial behavior to natural disasters (Hixon et al. 2002; Begon et al. 2006). Any of these mechanisms can be implemented in a nonWF model, but it is not done for you as it is in a WF model; the user must decide what mechanism(s) of population regulation are desired and implement them in the model’s script.

To provide an illustration of the relative ease with which such nonWF models can be specified in SLiM, we have supplied two example recipes (supplementary examples 1 and 2, Supplementary Material online). The first example is a very basic nonWF model in a population where viability depends on the carrying capacity of the population; the second example is a more sophisticated nonWF model with monogamous mating and effects of age on mating and fitness.

Continuous Space Models and Spatial Interactions

Continuous-space models in SLiM 3 are quite straightforward at the conceptual level. Continuous space is enabled with a call to initializeSLiMOptions() that provides a dimensionality: "x" for one spatial dimension, "xy" for two, or "xyz" for three; we will focus here on 2D models since that is probably the most common case. Individuals then have properties representing their x and y coordinates in the continuous 2D space, which can be accessed and set. The spatial boundaries of each subpopulation can be configured by the user; by default, the landscape will span the interval [0,1] in each dimension. Setting individual positions is the responsibility of the model, and the model determines what use, if any, is made of those positions; there is no automatic consequence of spatiality upon model dynamics. However, since there are common ways in which models often want spatiality to influence dynamics, two additional facilities are provided: interaction types, and spatial maps.

Interaction types are supported with a new Eidos class, InteractionType. An interaction type is defined with a call to initializeInteractionType(), and specifies two things: a distance metric that determines the interaction distance between two individuals, and an interaction formula that determines how the strength of interaction between two individuals varies with the distance between them. Once an interaction type is set up and evaluated, spatial queries can be made: what are the n closest neighbors to a given individual, what is the strength of interaction between individuals i and j, what is the total interaction strength exerted upon individual i by all other individuals in its subpopulation, and so forth. These queries are handled internally by highly optimized data structures such as k-d trees (Bentley 1975) and sparse arrays (Tewarson 1973), but those details are entirely hidden by SLiM, providing a way of implementing spatial interactions such as spatial competition and spatial mate choice that is both simple and fast.

Spatial maps are not represented with a separate class; instead, they are attached to subpopulations. A new spatial map can be defined with a call to the defineSpatialMap() method, and the value of a particular spatial map at a given point can then be queried with spatialMapValue(). Any number of spatial maps may be attached to a subpopulation; multiple maps are distinguished from each other by name. Each map defines a grid of values (of any resolution) that is superimposed across the spatial bounds of the subpopulation, either with or without interpolation of values between grid points. The scale of the map values, and the meaning attached to them, is entirely up to the model to define. One map might define elevation across the landscape, another temperature, and each of those maps might have consequences for survival, or fecundity, or movement, or any other aspect of the model.

Since much of this may seem rather abstract, we have again supplied two concrete examples (supplementary examples 3 and 4, Supplementary Material online). The first model is of a basic spatial population with local mate choice and competition; the second model introduces a heterogenous landscape and spatial extinction/recolonization dynamics.

Discussion

We have presented SLiM 3, a new major release of the SLiM forward genetic simulation framework. SLiM 3 provides many improvements over previous versions of SLiM, which are described in detail in the comprehensive documentation. Here we have focused on the two major features that enable SLiM 3 models to go beyond the limitations and assumptions of the Wright–Fisher model upon which all previous versions were based: the nonWF model type, and support for continuous space.

The nonWF model type affords the model control over each individual mating event. This makes it easy to control model characteristics such as mate-choice behavior, fecundity, and individual variation in reproduction. In nonWF models, fitness influences survival, not mating probability, by default, which allows more natural and realistic population dynamics. Other important model features that are relevant for realistic ecology, such as overlapping generations, age structure, and realistic migration/dispersal behavior, also emerge naturally in this design. However, the option to construct a WF model, as in previous SLiM versions, remains; this can be useful particularly when one wishes to compare a forward simulation model to an analytical model based upon Wright–Fisher assumptions.

Similarly, SLiM 3 provides the option of incorporating continuous space into a model, but models of discrete subpopulations connected by migration are also still supported. When continuous space is enabled, SLiM 3 provides a variety of useful tools for spatial modeling, such as spatial maps, which can define landscape characteristics that influence model dynamics, and a spatial interaction engine that can efficiently calculate interaction strengths between individuals and find nearby neighbors of an individual. SLiMgui also provides helpful visualizations for such models, making it easy to observe the dynamics that emerge from spatiality.

It should be emphasized that these features really dovetail with each other; in particular, ecologically realistic models involving continuous space should almost always be nonWF models. This is because the WF model imposes global population regulation upon the simulation; an overall size is set for each subpopulation, such that if density increases in one area of space (due to immigration, for example), absolute fitness will effectively decrease across the whole landscape. It is possible to compensate for this with appropriate fitness scaling, but it becomes quite complex if there is variation in local carrying capacity, immigration and emigration rates, variation in fecundity, etc.; the externally imposed population size of WF models is simply not designed to accommodate locally determined population density. The emergent population size and density in nonWF models, on the other hand, automatically accounts for whatever factors influence birth and death in the model. This is the reason that both of the continuous-space examples we presented are nonWF models; the influence upon local density of the sweep of a beneficial mutation in Example 3, or of the occasional disasters of Example 4, would be extremely difficult to model in a WF framework.

Many other new features of SLiM 3 have not been substantially discussed here. We urge all users to read about tree-sequence recording, which we believe to be a revolutionary new method that will considerably extend the horizon of what is possible in forward simulation (Haller et al. 2018). The SLiM manual (Haller and Messer 2016) now contains recipes and reference documentation for other new features, and the Eidos manual (Haller 2016) now documents new additions to the Eidos language. It is worth noting particularly that a great deal of optimization work has gone into SLiM 3, and it is generally much faster than previous versions, especially for large models with long chromosomes, which can be orders of magnitude faster than in previous versions. We have provided a performance comparison (supplementary results, Supplementary Material online) that illustrates these benefits and the performance tradeoffs involved with nonWF models and continuous space.

SLiM 3 is free, licensed under the GNU GPL, and is available on GitHub. Most users, however, will wish to download the release version from https://messerlab.org/slim/; the extensive manuals, with many examples, can be downloaded from the same website. We also encourage SLiM users to subscribe to the slim-discuss list at http://bit.ly/slim-discuss, where new versions are announced and users can ask questions and get help. The features that we have focused on here, nonWF models and continuous space, will enable many modeling scenarios that would have been difficult or impossible to model in previous versions of SLiM. We hope this will open up new frontiers in both applied and theoretical research.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.