Illustration of measurement error models for reducing biases in nutrition and obesity research using 2D body composition data

Abstract

Objective:

To illustrate the use and value of measurement error models for reducing biases when evaluating associations between body fat and having type 2 diabetes (T2D) or being physically active.

Methods:

Logistic regression models were used to evaluate T2D and physical activity among adults aged 19–80 years from the Photobody Study (n=558). Self-reported T2D and physical activity were categorized as “yes” or “no.” Body fat measured by 2D photographs was adjusted for bias using dual-energy X-ray absorptiometry scans as a reference. Three approaches were applied: regression calibration (RC), simulation extrapolation (SIMEX), and multiple imputation (MI).

Results:

Unadjusted 2D measures of body fat had upward biases of 30% and 233% for physical activity and T2D, respectively. For the physical activity model, RC-adjusted values had a 13% upward bias, whereas MI and SIMEX decreased the bias to 9% and 91%, respectively. For the T2D model, MI reduced the bias to 0%, whereas RC and SIMEX increased the upward bias to >300%.

Conclusions:

Of three statistical approaches to reducing biases due to measurement errors, MI performed best in comparison to RC and SIMEX. Measurement error methods can improve the reliability of analyses that look for relations between body fat measures and health outcomes.

INTRODUCTION

Measurement errors can manifest in healthcare research, particularly in obesity and nutrition studies in which self-reported measures are commonly used. It has been shown that self-reported measures, such as of dietary intake (1, 2), physical activity levels, smoking behavior (3), and alcohol intake (4), are all prone to measurement error. These errors can arise from multiple sources and often lead to biased statistical inference and incorrect conclusions. In nutritional epidemiology, measurement errors have led to statistical bias when evaluating the relationship between self-reported energy intake assessed by use of food frequency questionnaires (FFQ) (5–7) and chronic disease outcomes. Measurement errors can lead to biased estimates of the effects of error-prone measures on the outcomes of interest, loss of statistical power for detecting health outcomes due to potential excess variability, and an obscuring of the true features of the data (e.g., of linear and nonlinear trends and associations between data variables) (8, 9).

Measurement error (systematic and random error) in health research can arise from multiple sources (e.g., heart rate may be prone to within-individual variability in repeated measures due to the instrument or physiology of an individual), and measurement error can manifest in different patterns (e.g. consistent under-reporting or over-reporting of self-reported variables). In nutritional epidemiology, for example, error-prone measurements of energy intake—such as FFQ data, which may be subject to inaccurate responses due to participants’ inability to accurately recall food consumption—lead to biased estimates of the effects of diet on health outcomes (7).

Several statistical methods are available to reduce bias due to measurement error, including the classic regression calibration (RC) approach (10), multiple imputation (MI) (5, 11, 12), the maximum likelihood (ML) method (13), simulation extrapolation (SIMEX) (14, 15), and other methods (16–18). Prior studies showed improvements in statistical inference for FFQ data following RC in Spiegelman et al. (10, 19). Prentice et al. (6, 20) showed that unadjusted parameters of energy intake obtained from FFQs were not significantly associated with cancer; however, after bias-adjustment of measurement error using calibration methods, energy and protein density were indeed positively associated with cancer incidence (20). In this example, adjusting for measurement error improved the estimation of the association between diet and cancer, which further highlights the value of implementing these methods to improve estimation and reduce biases in statistical analyses. Similarly, calibrated or measurement error bias-adjusted energy consumption was positively associated with coronary artery disease risk (6), whereas unadjusted energy consumption was not.

Anthropometric measures, such as body mass index (BMI) (21, 22) and body fat percentage measured by 3D photonic scans (3DPS) or dual-energy X-ray absorptiometry (DXA) scans (23, 24), are also prone to inherent or unavoidable measurement error. While many body composition assessment methods are available, such as densitometry methods (e.g., air displacement or underwater weighing) and bioimpedance analysis, DXA scans are often the preferred method for estimating body fat. Furthermore, Garlie et al. showed that body fat percentage as estimated by 3DPS yielded 4.69–5.99% error relative to DXA (25). Hence, measurement error remains an issue in body composition data, and to our knowledge, the available statistical approaches for measurement error bias-adjustment have not yet been commonly adopted in body fat measures.

The purpose of this study was to illustrate the use and value of these methods to reduce potential biases due to measurement error when assessing the effects of body fat on two health outcomes: 1) the probability of having type 2 diabetes (T2D) and 2) the probability of being physically active (PA). In this study, we analyzed a unique dataset with body fat percentage estimated in two ways for all participants. First, body fat percentage was estimated by use of a novel 2D photographic-based method (BF_Photo), which was developed by Affuso et al. (26–28). This photographic method has shown to provide a valid estimate of body fat percentage compared to DXA in adults. However, this novel method may involve some inherent and unavoidable measurement error due to potentially lost information about muscle mass, bone mass, and fat mass, that may be lost when extracting body volume from 2D photographs and therefore may lead to biased estimates of body fat percentage. Second, body fat percentage was estimated by DXA (BF_DXA). The 2D photographic method has several advantages over DXA, such as its portability, low cost, convenience, and time efficiency. While BF_Photo estimates have been shown to be strongly correlated to BF_DXA (26, 28), here we assume that BF_DXA is the reference method, or is error-free, while BF_Photo is an error-prone body fat measure. In this work, three measurement error bias-adjustment techniques were applied to improve the predictions of health outcomes as estimated by BF_Photo by improving model parameters enough to yield results similar to those of the reference method, BF_DXA.

METHODS

Subjects:

Adults aged 19 to 80 years, living in Birmingham, Alabama, were recruited between November 2012 and September 2015 as part of the Photobody Study described in prior publications (26–28), and a subset of the data is used here. This subset included participants who were non-Hispanic Black or non-Hispanic White only. Participants who reported a “moderate” level of regular physical activity were excluded to allow for greater contrast between the individuals with low and high activity. Participants were recruited through advertisements placed in local newspapers and newsletters, flyers were placed throughout the community (e.g., college campus and other businesses), individuals were directly approached at community events (e.g., health fairs and other local events), and enrolled participants communicated to others by word of mouth. Individuals meeting the following criteria were enrolled in the study: 1) weight less than 450 lbs (weight limit of DXA equipment); 2) absence of conditions that would prevent participants from lying down for DXA scans or standing for taking photographs; 3) presence of health conditions that may alter body composition (e.g., cancer, cachexia, or rheumatoid arthritis); 4) no missing body parts (except a finger or toe); and 5) not pregnant. Written informed consent was obtained for each eligible participant. All participants were compensated $20.00 for their participation. This study was approved by the University of Alabama at Birmingham’s Institutional Review Board.

Demographics, physical activity, and health conditions:

Self-reported race/ethnicity, age, sex, medical history (health conditions and medication use), physical activity status, and T2D status were obtained through an interviewer-administered questionnaire. To assess physical activity status, participants were asked the question, “What is your current activity level (i.e., person’s average daily activity)?” and responded by selecting one of five options: “none,” “some,” “moderate,” “athlete,” or “elite athlete.” In this study, we grouped all participants into two physical activity groups: those who were not physically active (60.2%), which consisted of all individuals who reported either “none” or “some” regular physical activity, and the physically active group (39.8%), which consisted of participants who had “athlete” or “elite athlete” activity levels.

Body composition measurements:

Body composition was assessed for all participants using two approaches. First, DXA (encore 2011 version 13.6; GE Lunar iDXA Corporation, Madison, WI, encore 2011 version 13.6) scans were used to estimate percentage body fat, denoted BF_DXA. Second, 2D photographic images were processed for body volume and shape measures and were then used to calculate body fat percentage, denoted BF_Photo. This programming algorithm has been described in more detail elsewhere (26). Photographic images were obtained using a digital camera (Canon PowerShot - Model SX50; Cannon USA Inc., Melville, NY). All participants wore close-fitting tank tops (females only) and spandex shorts for body composition measurements in order to reduce measurement bias. Trained staff measured weight to the nearest 0.1 kg using a physician’s balance beam scale (Model 402LB; HealthOMeter, McCook, IL) and height to the nearest 0.1 cm using a stadiometer and these measurements were used to calculate BMI for each participant.

Statistical methods:

Descriptive statistics (mean ± SD) were calculated for the study sample. Mean body fat percentages (BF_DXA and BF_Photo) were assessed on the basis of physical activity and T2D status by one-way analysis of variance (ANOVA). Pearson correlation coefficients, r, were computed between pairs of model variables (e.g., age, height, weight, BF_DXA, and BF_Photo). Linear regression analyses were performed to compare body fat measures. Using Bland-Altman analyses, we investigated the distribution of absolute and relative differences between body fat measures to assess any biases in BF_Photo relative to BF_DXA (29). Logistic regression analyses were performed to predict: 1) the probability of having T2D and 2) the probability of being physically active. All statistical analyses were performed using SAS 9.4 (30) or R 3.2 (31) and with statistical significance accepted when P <0.05 (two-tailed).

Measurement error bias-adjustment methods:

Three measurement error bias-adjustment methods were used: RC, SIMEX, and MI. Details of the methods and algorithms are summarized in Appendices A–C. The RC method can be applied to an validation study (internal and external), when a gold standard or imperfect reference instrument is available (8, 19). However, for other studies, the non-iterative RC method can be used to approximate regression coefficients from regression models with measurement error in covariates when a reference method is not available (see (8, 19) for details). The RC method consists of estimating model parameters of the logistic model with error-prone variables and covariates, estimating regression coefficients for a linear model that relates the error-free to the error-prone variables, and subsequently using the estimated parameters from the linear model to obtain the RC-adjusted model parameters. The 95% confidence interval for the regression coefficients and their respective odds ratios were calculated using the variance-covariance matrix for the bias-adjusted model parameters (10, 19) (see Appendix A). RC was implemented using SAS macro %blinplus (7, 10, 19).

The SIMEX method, developed by Carroll et al (14), is a simulation-based approach that reduces the bias in parameter estimates due to measurement error by introducing random error into the model (5, 14, 15, 19). Simulated data with additive error terms were used to characterize the relation between model parameters and the amount of measurement error through a resampling approach. To characterize this trend, the parameter estimates were modeled as a function of the measurement error and corresponding mean regression coefficients. In the next step, the model parameter estimates for a model with error-free predictors were obtained by extrapolating back to the case of zero error (see Appendix B). This was implemented using the R ‘simex’ package (15).

The MI framework was applied by treating the true values of the variables with measurement error as a missing data problem (5, 11, 12), i.e., imputing the bias-adjusted values for unadjusted values. Multiple (for example m) values or “imputations” were imputed for each unadjusted value under the MI principle and used to replace the unadjusted value so that m datasets with only bias-adjusted values were generated. In the subsequent analysis, the m datasets were analyzed individually, yielding m statistics (for example, mean, parameter estimates, etc.). Eventually, the m statistics were combined into a single statistic using Rubin’s rule (32) (see Appendix C). The MI method has been implemented in many statistical software packages, such as SAS 9.4 (30), R 3.2 (31), and others (33, 34), so that bias adjustment by MI can also be utilized conveniently.

RESULTS

Body Composition Assessment:

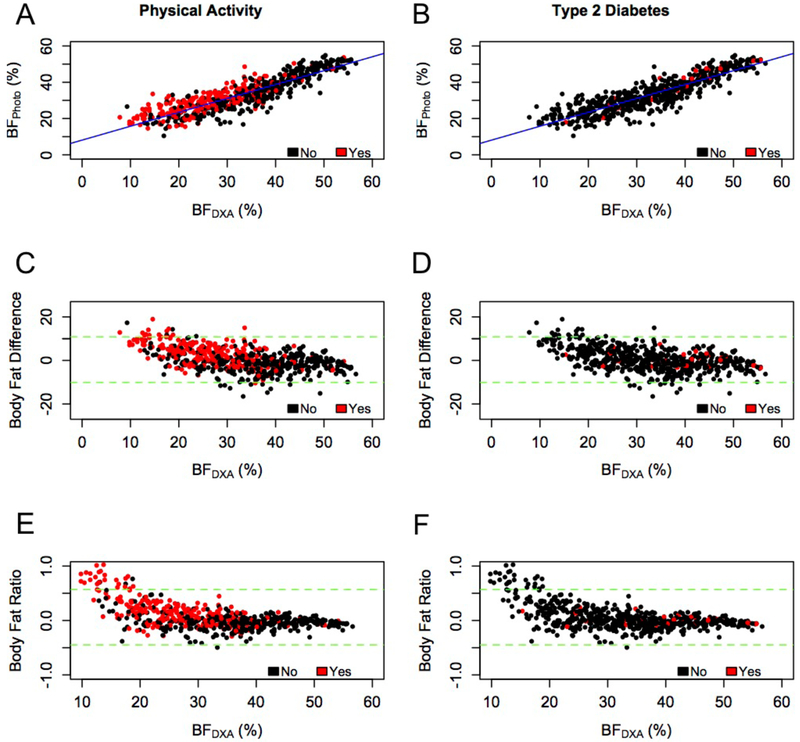
The sample consisted of non-Hispanic White (51%) and non-Hispanic Black (49%) adult men (46%) and women (54%) aged 39 ± 15 years (mean ± SD) with BMI of 28 ± 6 kg/m². About 5.3% of the participants self-reported having T2D, and 39.8% self-reported being physically active. Additional participant characteristics are summarized in Table 1. As expected, individuals considered to be physically active tended to have lower body fat percentages (Figure 1A). Body fat as estimated by BF_DXA and BF_Photo was significantly greater in the individuals who were not physically active (BF_DXA: 37 ± 10% and BF_Photo: 36 ± 10%) than in the physically active group (BF_DXA: 26 ± 9% and BF_Photo: 30 ± 7%; P < 0.0001). However, individuals with T2D had more variability in their body fat percentages (Figures 1B). Body fat estimates were significantly lower in individuals with T2D (BF_DXA: 32 ± 11% and BF_Photo: 33 ± 10%) than in those who did not report T2D (BF_DXA: 40 ± 10% and BF_Photo: 40 ± 9%; P < 0.0004).

Table 1:

Summary of participant characteristics.

	All (n=588)1	Men (n=270)	Women (n=318)
Age, years	39 ± 151	40 ± 16	38 ± 14
Height, cm	169.9 ± 9.8	177.3 ± 7.3	163.5 ± 6.7
Weight, kg	80.0 ± 19.8	85.2 ± 19.2	75.7 ± 19.2
BMI, kg/m2	27.7 ± 6.3	27 ± 5.5	28.3 ± 6.9
BFDXA , %	32.9 ± 11.2	26.1 ± 8.9	38.8 ± 9.5
BFPhoto , %	33.3 ± 9.7	26.6 ± 6.8	39.1 ± 7.9
Race, n (%)
Non-Hispanic White	297 (50.5)	145 (53.7)	152 (47.8)
Non-Hispanic Black	291 (49.5)	125 (46.3)	166 (52.2)
Physically Active (PA), n (%)
No	354 (60.2)	136 (50.4)	218 (68.5)
Yes	234 (39.8)	134 (49.6)	100 (31.5)
Type 2 Diabetes (T2D), n (%)
No	557 (94.7)	255 (94.4)	302 (95.0)2
Yes	31 (5.3)	15 (5.6)	16 (5.0)

¹Values are mean ± SD unless otherwise indicated.

Figure 1:

Associations and Agreements Between the Two Body Fat Percentage Estimates. BF_Photo and BF_DXA, by physical activity (left column) and type 2 diabetes (right column) outcomes for all participants (n=588). (A-B) BF_Photo strongly correlates with BF_DXA (r=0.88, P < 0.0001). Bland-Altman tests with 95% confidence intervals (dashed green lines) for the (C-D) absolute difference BF_Photo - BF_DXA and (E-F) relative difference (BF_Photo - BF_DXA)/ BF_DXA show that BF_Photo overestimated body fat percentage for individuals with lower body fat percentage

Pearson correlation coefficients (Table 2) indicated strong positive associations between BF_DXA and BF_Photo (r=0.88, P<0.0001; Figure 1). Bland-Altman analyses (Figure 1C–F) were performed to evaluate the amount of bias in the BF_Photo data due to measurement error. The absolute mean difference $\left({\widehat{u}}_{abs}\right)$ between BF_Photo and BF_DXA represents the average bias in body fat percentage. Here it was ${\widehat{u}}_{abs}=0.38\%$ for all participants as a group (slope=−13.94, P<0.0001), and the variance of this bias was ${\widehat{\sigma }}_{abs}^2=27.36$. The relative difference between BF_Photo and BF_DXA was 0.05% (95% CI: −0.44, 0.56).

Table 2:

Correlation and Variance-Covariance Summary.

	Pearson Correlation Coefficients						Variance-Covariance Values
	Age	Height	Weight	BFDXA	BFPhoto		Age	Height	Weight	BFdxa	BFPhoto
Age	1.00	−0.10	0.08a	0.22b	0.27b	Age	228.61	−15.09	24.35	37.65	38.85
Height		1.00	0.41b	−0.42b	−0.44b	Height		95.92	78.81	−46.24	−41.96
Weight			1.00	0.44b	0.49b	Weight			390.95	97.56	94.98
BFDXA				1.00	0.88b	BFDXA				124.83	95.66
BFPhoto					1.00	BFPhoto					93.851

¹Correlation coefficients with P < 0.05^a and P < 0.0001^b are shown.

Measurement Error Bias-Adjustment:

Parameters estimated from the logistic regression model with BF_DXA as the independent variable are denoted ${\widehat{\beta }}_{DXA}$, and similarly, those estimated using BF_Photo are denoted ${\widehat{\beta }}_{Photo}^{UC}$, where the superscript “UC” denotes an unadjusted parameter. Adjusted parameters of BF_Photo that are bias-adjusted are denoted with appropriate superscripts, i.e., ${\widehat{\beta }}_{Photo}^{MI}$ for the MI approach, ${\widehat{\beta }}_{Photo}^{RC}$ for the RC method, and ${\widehat{\beta }}_{Photo}^S$ for the SIMEX procedure.

Model coefficients for predicting the probability of being physically active are shown in Figure 2 and Table 3. The effect of BF_DXA on the odds of being physically active (${\widehat{\beta }}_{DXA}=-0.23$ [95% CI: −0.26, −0.19]; OR 0.79 [95% CI: 0.75, 0.82]; P<0.0001) was greater than that of BF_Photo (${\widehat{\beta }}_{Photo}^{UC}=-0.16$ [95% CI: −0.23, −0.08]; OR 0.84 [95% CI: 0.77, 0.92]; P=0.0002), which had an upward bias $\left({\widehat{\beta }}_{Photo}^{UC}>{\widehat{\beta }}_{DXA}\right)$. Similarly, an upward bias was observed for RC-adjusted estimates $\left({\widehat{\beta }}_{Photo}^{RC}>{\widehat{\beta }}_{DXA}\right)$, but a downward bias was found for SIMEX and MI $\left({\widehat{\beta }}_{Photo}^S,{\widehat{\beta }}_{Photo}^{MI}<{\widehat{\beta }}_{DXA}\right)$. To quantify the improvement of the measurement error bias-adjustment methods, the percentage changes for the adjusted model parameters, denoted Δβ (%), were calculated as the absolute change between the bias-adjusted parameter value (e.g.,${\widehat{\beta }}_{Photo}^{UC},{\widehat{\beta }}_{Photo}^{MI},{\widehat{\beta }}_{Photo}^{RC}$, and ${\widehat{\beta }}_{Photo}^S$) and the reference parameter value $\left({\widehat{\beta }}_{DXA}\right)$, divided by the absolute reference parameter value $\left({\widehat{\beta }}_{DXA}\right)$. The percentage change was lowest for MI (Δβ=9%), next lowest for RC (Δβ=13%), and significantly higher for SIMEX (Δβ=91%). Other significant covariates (adjusted and unadjusted) were age, sex, race, and weight (not shown); however, RC-adjusted age was not significant.

Figure 2:

Physical Activity Status Results. Parameters estimated with standard error bars for the probability of being physically active are shown for the error-free measurement (DXA), the unadjusted error-prone measurement (UC, Photo), and the three measurement error bias-adjusted cases (MI, RC, and S).

Table 3:

Summary of Physical Activity Results. Estimated model coefficients for body fat are shown for being physically active.

Model Coefficient	Parameter1	Estimate (95% CI)	%Δβ2,3	OR (95% CI)	P-value
Body Fat	${\widehat{\beta }}_{DXA}$	−0.23 (−0.26, −0.19)	-	0.79 (0.75, 0.82)	<0.0001
	${\widehat{\beta }}_{Photo}^{UC}$	−0.16 (−0.23, −0.08)	30 ↑	0.84 (0.77, 0.92)	0.0002
	${\widehat{\beta }}_{Photo}^{MI}$	−0.25 (−0.28, −0.21)	9.4 ↓	0.77 (0.73, 0.81)	<0.0001
	${\widehat{\beta }}_{Photo}^{RC}$	−0.20 (−0.31, −0.08)	13 ↑	0.81 (0.72, 0.91)	0.0008
	${\widehat{\beta }}_{Photo}^S$	−0.44 (−0.57, −0.30)	91 ↓	0.64 (0.55, 0.74)	<0.0001

¹Unadjusted BF_Photo $\left({\widehat{\beta }}_{Photo}^{UC}\right)$, multiple imputation $\left({\widehat{\beta }}_{Photo}^{MI}\right)$, regression calibration $\left({\widehat{\beta }}_{Photo}^{RC}\right)$, and SIMEX $\left({\widehat{\beta }}_{Photo}^S\right)$.

²The difference between ${\widehat{\beta }}_{DXA}$ and each parameter value (e.g. ${\widehat{\beta }}_{Photo}^{UC},{\widehat{\beta }}_{Photo}^{MI},{\widehat{\beta }}_{Photo}^{RC},\text{ and }{\widehat{\beta }}_{Photo}^S$. The percentage change, denoted Δβ (%), were calculated as the absolute change between the BF_Photo-based parameter value (e.g., ${\widehat{\beta }}_{Photo}^{UC},{\widehat{\beta }}_{Photo}^{MI},{\widehat{\beta }}_{Photo}^{RC},\text{ and }{\widehat{\beta }}_{Photo}^S$) and the reference parameter value $\left({\widehat{\beta }}_{DXA}\right)$ and the reference parameter value $\left({\widehat{\beta }}_{DXA}\right)$, divided by the absolute reference parameter value $\left({\widehat{\beta }}_{DXA}\right)$, and rounded.

³The ↑ represents upward bias $\left(\widehat{\beta }>{\widehat{\beta }}_{DXA}\right)$ and ↓ represents a downward bias $\left(\widehat{\beta }>{\widehat{\beta }}_{DXA}\right)$.

Model parameters estimated for predicting the probability of having T2D are shown in Table 4 and Figure 3. The effect of BF_DXA (${\widehat{\beta }}_{DXA}$=0.03 [95% CI: −0.04, 0.10]; OR 1.03 [95% CI: 0.95, 1.12]; P=0.4447) on the odds of having T2D was smaller in comparison to BF_Photo (${\widehat{\beta }}_{Photo}^{UC}$=0.10 [95% CI: −0.05, 0.25]; OR 1.11 [95% CI: 0.93, 1.32]; P=0.2188) and had an upward bias $\left({\widehat{\beta }}_{Photo}^{UC}>{\widehat{\beta }}_{DXA}\right)$. Both RC and SIMEX had an upward bias $\left({\widehat{\beta }}_{Photo}^{RC},{\widehat{\beta }}_{Photo}^S>{\widehat{\beta }}_{DXA}\right)$; however MI was unbiased $\left(\Delta \beta =0\%;{\widehat{\beta }}_{Photo}^{MI}={\widehat{\beta }}_{DXA}\right)$. The percentage change was over 300% for RC (Δβ=333%) and SIMEX (Δβ=800%). Parameter estimates for the age variable (adjusted and unadjusted) was the only significant predictor for T2D status (not shown), with the exception of SIMEX-adjusted age.

Table 4:

Summary of Type 2 Diabetes Results. Estimated model coefficients of body fat are shown for assessing type 2 diabetes status.

Model Coefficient	Parameter1	Estimate (95% CI)	%Δβ2,3	OR (95% CI)	P-value
Body Fat	${\widehat{\beta }}_{DXA}$	0.03 (−0.04, 0.10)	-	1.03 (0.95, 1.12)	0.4447
	${\widehat{\beta }}_{Photo}^{UC}$	0.10 (−0.05, 0.25)	233 ↑	1.11 (0.93, 1.32)	0.2188
	${\widehat{\beta }}_{Photo}^{MI}$	0.03 (−0.02, 0.08)	0	1.03 (0.96, 1.10)	0.3724
	${\widehat{\beta }}_{Photo}^{RC}$	0.13 (−0.06, 0.32)	333 ↑	1.14 (0.92, 1.41)	0.2245
	${\widehat{\beta }}_{Photo}^S$	0.27 (−0.02, 0.56)	800 ↑	1.32 (0.98, 1.77)	0.0653

¹Unadjusted BF_Photo $\left({\widehat{\beta }}_{Photo}^{UC}\right)$, multiple imputation $\left({\widehat{\beta }}_{Photo}^{MI}\right)$, regression calibration $\left({\widehat{\beta }}_{Photo}^{RC}\right)$, and SIMEX $\left({\widehat{\beta }}_{Photo}^S\right)$.

²The difference between ${\widehat{\beta }}_{DXA}$ and each parameter value (e.g. ${\widehat{\beta }}_{Photo}^{UC},{\widehat{\beta }}_{Photo}^{MI},{\widehat{\beta }}_{Photo}^{RC},\text{ and }{\widehat{\beta }}_{Photo}^S$. The percentage change, denoted Δβ (%), were calculated as the absolute change between the BF_Photo-based parameter value (e.g., ${\widehat{\beta }}_{Photo}^{UC},{\widehat{\beta }}_{Photo}^{MI},{\widehat{\beta }}_{Photo}^{RC},\text{ and }{\widehat{\beta }}_{Photo}^S$) and the reference parameter value $\left({\widehat{\beta }}_{DXA}\right)$, divided by the absolute reference parameter value $\left({\widehat{\beta }}_{DXA}\right)$, and rounded.

³The ↑ represents upward bias $\left(\widehat{\beta }>{\widehat{\beta }}_{DXA}\right)$ and ↓ represents a downward bias $\left(\widehat{\beta }>{\widehat{\beta }}_{DXA}\right)$.

Figure 3:

Type 2 Diabetes Status Results. Parameters estimated with standard error bars for the probability of having type 2 diabetes are shown for the error-free measurement (DXA), the unadjusted error bias-adjusted measurement (UC, Photo), and the three measurement error bias-adjusted cases (MI, RC, and S).

DISCUSSION

We presented and compared three measurement error bias-adjustment methods—RC, MI, and SIMEX—to reduce potential biases in statistical models used to evaluate the effect of body fat on health outcomes. The performances of these commonly used measurement error techniques were compared using body fat percentage estimated by DXA scans (BF_DXA) as the reference measure and a novel 2D photographic-based method (BF_Photo) as the error-prone measure. We applied the error bias-adjustment methods to a logistic model involving body fat to predict the probability of two health outcomes: having T2D or being physically active.

In this bi-ethnic sample of adults, BF_Photo and BF_DXA measures were strongly positively correlated; however, BF_Photo exhibited bias as measured by Bland-Altman analyses (see Figure 1). Body fat percentage (BF_Photo and BF_DXA) was lower in individuals with higher physical activity levels, compared to individuals who were not active, and was a significant predictor of being physically active (see Figure 1), which was expected on the basis of prior studies of body composition and physical activity levels (35, 36). This association of body fat with the probability that an individual is physically active was also observed when the population was stratified by race. In contrast, BF_Photo and BF_DXA were lower in participants with self-reported T2D, relative to individuals without T2D, which was not expected. That is, contrary to our expectations, excess body fat did not significantly increase the odds of having T2D in our cohort (see Table 4). Further, the association of body fat with the probability of having type 2 diabetes when the population was stratified by race were inconsistent, where it was statistically significant in some cases and not significant in others. However, the parameter estimates and 95% confidence intervals led to the conclusion that the association of body fat remained null, which is consistent with the findings shown in this study when the sample was analyzed as one group. Therefore, it is possible that our study participants with T2D had better body weight management than average: all participants with T2D reported being on medication(s) used for diabetes, weight loss, or other health conditions, which may explain the inverse relationship between body fat percentage and having T2D. The lower body fat percentage observed in participants with T2D could also be due to the cross-sectional design of the study, as well as the particular sample that volunteered to enroll in the study.

We also observed an upward bias from unadjusted BF_Photo data $\left({\widehat{\beta }}_{Photo}^{UC}>{\widehat{\beta }}_{DXA}\right)$ for models predicting the probability of being physically active and having T2D, which implies that unadjusted BF_Photo overestimates the effect of body fat on health outcomes. The performance of measurement error bias-adjustment methods to reduce this bias varied. For the physical activity model, SIMEX and MI methods led to a downward bias $\left({\widehat{\beta }}_{Photo}^S,{\widehat{\beta }}_{Photo}^{MI}<{\widehat{\beta }}_{DXA}\right)$, whereas the RC-adjusted estimate had an upward bias $\left({\widehat{\beta }}_{Photo}^{RC}>{\widehat{\beta }}_{DXA}\right)$; however, MI had the lowest percent change (Δβ=9%). Thus, MI performed the best, followed next by RC, and then the SIMEX method. For the T2D status model, both RC-adjusted and SIMEX-adjusted values had an upward bias $\left({\widehat{\beta }}_{Photo}^{RC},{\widehat{\beta }}_{Photo}^S>{\widehat{\beta }}_{DXA}\right)$, whereas the MI-adjusted estimate was unbiased $\left({\widehat{\beta }}_{Photo}^{MI}={\widehat{\beta }}_{DXA}\right)$ and therefore performed the best. The RC- and SIMEX-adjusted model parameters corresponding to body fat had percentage changes exceeding 300% and overestimated the effect of body fat percentage on the probability of having T2D. Hence, these results indicate that parameter estimates bias-adjusted by MI were closer to the reference estimates in comparison to RC and SIMEX. More specifically, MI-adjusted estimates consistently matched the estimates corresponding to BF_DXA for both T2D and physical activity outcomes. RC overestimated the effect of body fat $\left({\widehat{\beta }}_{Photo}^{RC}\right)$ the probability of having T2D, but improved the estimate of the effect of body fat $\left({\widehat{\beta }}_{Photo}^{RC}\right)$ on the probability of being physically active. However, SIMEX overestimated the effect of body fat $\left({\widehat{\beta }}_{Photo}^S\right)$ for both T2D and physical activity status outcomes. The standard error was greater for RC and SIMEX than for MI. Moreover, similar findings on the performance of MI, RC, and SIMEX for the bias-adjustment of parameter estimates have been reported in other studies (5, 11, 12, 37).

An advantage of our research is that we have concurrent body fat measures by DXA and a 2D photographic-based method for the entire sample. Another novel aspect of our work is the use of measurement error approaches to improve model parameters of body composition, which to our knowledge has not been done before. A limitation of this work is that the three error bias-adjustment methods that we implemented have different assumptions, which makes comparison of their performance difficult. For example, while MI may be the most effective method for measurement error bias-adjustment in this study, the imputation procedure includes T2D and physical activity outcome variables to simulate new datasets, thus improving its accuracy. In contrast to MI, the SIMEX and RC methods are completely different approaches with a different set of assumptions (see supplementary file for Appendices A–C). Further, it is important to note that the RC method can be applied to validation studies (internal and external), when a gold standard or reference measure is available (8, 19). However, in cases where this is not available, the non-iterative RC method can be used to adjust for measurement error in covariates (see (8, 19) for details). Another limitation is that these methods cannot address other biases such as those caused by unmeasured confounders and other biases. The results in our analyses are sensitive to all types of errors, not just measurement error, but also unmeasured confounders (38, 39). While these methods cannot address bias caused by unmeasured confounders, the measurement error models discussed here provide a valuable method for addressing measurement error when data are available and measurement error is a concern. Future work would be to consider unmeasured confounders when adjusting for measurement error. Lastly, another limitation is that the self-reported outcomes considered in this study, type 2 diabetes and physical activity, may potentially be misclassified, and therefore, could affect our results. However, the focus of this study is to assess the impacts of measurement error in the covariates on these outcomes. Future work would involve exploring the effects of errors on the outcomes.

In conclusion, this study demonstrates the value of measurement error bias-adjustment methods to improve model parameters in nutrition and obesity research studies. Our purpose was to introduce three statistical approaches for reducing biases due to measurement errors and illustrated its value using real data. We presented a practical example that involves evaluating the relationship between body fat and health outcomes. These tools were applied for a specific statistical model (logistic model) and dataset (body fat measured by DXA and a novel photographic-based method). Our results suggest that, overall, MI performed the best in adjusting for measurement error and can be used to minimize statistical bias caused by measurement error, a finding which is supported by other studies (11, 12). Furthermore, our study evaluated the case where the variance in the reference measure (DXA) is larger than the error-prone method (photographic), and here MI clearly outperforms all other methods. In summary, this study illustrates the utility and value of these methods for investigators conducting research where measurement error is a concern.

ANSWER THE STUDY IMPORTANCE QUESTIONS (3 bullet points).

1. What is already known about this subject?

   • Self-reported data are prone to measurement error.
   • Measurement error can lead to biased conclusions in statistical analyses.
   • Methods have been developed and applied for the bias-adjustment of self-reported data such as energy intake reported in food frequency questionnaires.
2. What does your study add?

   • This study illustrates the use of these methods for the bias-adjustment of body fat measures, which to our knowledge has not been done before.
   • This study compares the performance of three statistical approaches for measurement error bias-adjustment.
   • This study utilized a unique dataset with concurrent body fat measured by an assumed reference method (dual-energy x-ray absorptiometry scans) and an error-prone method (a novel 2D photographic-based method) for all participants.

APPENDIX A: RC

Adapting definitions from (11, 19), we briefly review RC theory. The RC method consists of estimating model parameters for the error-free model,

$$logit\left[\text{Pr }\left(Y|X,W\right)\right]={\alpha }^{*}+{\beta }_1^{*}X+{\beta }_2^{*}W,$$ (1)

where α^*, ${\beta }_1^{*}$, and ${\beta }_2^{*}$ are vectors of the model parameters. Y is the binary outcome and in this case represents physical activity status or type 2 diabetes status. X is a vector of error-free variables, which corresponds here to BF_DXA. The covariates, included in the vector W, are also assumed to be error-free; here, we used the covariates height, weight, age, sex, and race/ethnicity. We introduce the vector Z, which consists of the error-prone variable(s), or BF_Photo. The distribution of Z is assumed to be equivalent regardless of the binary outcome Y (e.g., Y = 0 and Y = 1), that is, Pr(Z | X, Y = 1) = Pr(Z | X, Y = 0). The RC method consists of the following steps:

Step 1: Estimate the logistic regression coefficients in the error-prone model,

$$logit\left[\text{Pr }\left(Y|Z,W\right)\right]={\alpha }^{UC}+{\beta }_1^{UC}Z+{\beta }_2^{UC}W,$$ (2)

where α^UC, ${\beta }_1^{UC}$, and ${\beta }_2^{UC}$ are vectors of the uncorrected (UC) model parameters.

Step 2: Estimate the regression coefficients that relate the error-prone variables to the error-free variables. The following multivariate (e.g., here defined as multiple dependent variables (43)) linear regression model is applied:

$$X={{\lambda }^{\prime }}_0+{\lambda }_{1}Z+{\lambda }_{2}W+e,$$ (3)

where ${{\lambda }^{\prime }}_0$, λ₁, and λ₂ are vectors of regression coefficients and e is the error vector, where e~N(0, Σ); that is, the errors follow normal distributions with a mean of zero.

Step 3: Estimate the RC-corrected model coefficients, ${\widehat{\beta }}^{RC}=\left({\widehat{\beta }}_1^{RC},{\widehat{\beta }}_2^{RC}\right)$. Using the assumption that the probability of Y = 1 in the study sample is small, then

$$\text{Pr}\left(Y|X,W\right)\cong \text{exp}\left[{\alpha }^{*}+{\beta }_1^{*}X+{\beta }_2^{*}W\right].$$ (4)

Substituting equation (3) into (4) and rearranging terms gives,

$$\text{Pr}\left(Y|Z,W\right)\cong \text{exp}\left[c+{\beta }_1^{*}{\lambda }_{1}Z+\left({\beta }_2^{*}+{\beta }_1^{*}{\lambda }_2\right)W\right],$$ (5)

where $c={\alpha }^{*}+{\beta }_1^{*}{\alpha }^{UC}$. The “multivariate linear approximation estimator” (11) yields

$$\widehat{\beta }*={\widehat{\beta }}^{RC}{\widehat{\lambda }}^{-1},$$ (6)

where ${\widehat{\beta }}^{RC}=\left({\widehat{\beta }}_1^{RC},{\widehat{\beta }}_2^{RC}\right)$ and $\widehat{\beta }*=\left({\widehat{\beta }}_1^{*},{\widehat{\beta }}_2^{*}\right)$. Here $\widehat{\lambda }=\left[\begin{array}{ll}{\widehat{\lambda }}_1\hfill & {\widehat{\lambda }}_2\hfill \\ 0\hfill & I\hfill \end{array}\right]$, where 0 is a matrix of zeroes and I is the the identity matrix. Hence, ${\widehat{\beta }}^{RC}={\widehat{\beta }}^{*}\widehat{\lambda }$, where ${\widehat{\beta }}_1^{RC}={\widehat{\beta }}_1^{*}{\widehat{\lambda }}_1$ and ${\widehat{\beta }}_2^{RC}={\widehat{\beta }}_1^{*}+{\widehat{\beta }}_2^{*}{\widehat{\lambda }}_2$.

Step 4: Estimate the variance-covariance matrix $Cov\left({\widehat{\beta }}_{j1}^{RC},{\widehat{\beta }}_{j2}^{RC}\right)$ (details are found in (11)).

Step 5: Estimate the 95% confidence interval for the jth true regression coefficient ${\widehat{\beta }}_j^{*}$ using ${\widehat{\beta }}_j^{*}\pm Z_{1-\alpha /2}\sqrt{Var\left({\widehat{\beta }}_j^{*}\right)}$. The 95% confidence interval of the corresponding odds ratio is calculated as $exp\left[{\widehat{\beta }}_j^{*}\pm Z_{1-\alpha /2}\sqrt{Var\left({\widehat{\beta }}_j^{*}\right)}\right]$.

APPENDIX B: SIMEX

The SIMEX method adjusts for bias in parameter estimates by first introducing random error into the model to uncover the relationship between model parameters and the amount of measurement error through a resampling approach and then extrapolating back to the case of no error to find the corrected model parameters (31–33). The SIMEX method consists of the following steps:

Step 1: Estimate the regression coefficients, ${\widehat{\beta }}^{UC}$, corresponding to the error-prone model given in Equation (2) and calculate the measurement error variance, ${\widehat{\sigma }}_U^2$, which is defined here as the variance of BF_DXA − BF_Photo.

Step 2: Implement a simulation step to generate and add random error, ϵ, to the error-prone variables. This gives a new measurement error variance, $\left(1+\theta \right){\widehat{\sigma }}_m^2$, where θ>0 and $ϵ~N\left(0,\theta {\widehat{\sigma }}_m^2\right)$. Past work shows that θ ∈ (0.5, 1, 1.5, 2) are the typical choices of the scale factor representing measurement error (33, 44).

Step 3: The simulations in Step 2 are repeated B times for each θ. Parameters are estimated for Equation (2), enoted ${\widehat{\beta }}^{\left({\theta }_j\right)}$, and then the mean regression coefficients for B iterations are calculated as follows: $\overline{\widehat{\beta }}\left({\theta }_j\right)=\frac{1}{B}{\sum }_{i=1}^B{\widehat{\beta }}^{\left(i,{\theta }_j\right)}$, where j = 1, …, k scale factors (here k = 4).

Step 4: Determine the extrapolant function for each model parameter, β_l, by identifying the functional relationship (i.e., linear or quadratic) between each regression coefficient and θ_j. This is defined as ${\beta }_l=f\left(\theta ,{\beta }_l^{(\theta )}\right)$ for each of the l = 1, … , n model parameters.

Step 5: Then extrapolate back to the case of zero error to get the “true” estimate. This yields the final estimates for ${\beta }_l=f\left({\theta }_0=-1,{\beta }_l^{(\theta )}\right)$, which is considered the case of no measurement error. The standard errors for the regression coefficients and 95% confidence intervals for the odds ratio were calculated.

APPENDIX C: MI

The MI method corrects for measurement error by generating values that represent the unobserved true data using the known relationships between variable(s) of interest and covariate(s). Here, BF_DXA is imputed based on the associations and distributions of variables in the data. The relationships among variables can be estimated using the Markov Chain Monte Carlo (MCMC) method under the multivariate normal distribution assumption or using the chained equations approach. The latter approach was used in this study and includes the following steps:

Step 1: Estimate regression coefficients, ${\widehat{\gamma }}_k$, where k = 1, … ,7 and residual variance ${\widehat{\sigma }}^2$ for the model relating BF_DXA and BF_Photo for subjects with both BF_DXA and BF_Photo measures:

$$B{F}_{DXA}={\gamma }_0+{\gamma }_{1}B{F}_{Photo}+{\gamma }_{2}Age+{\gamma }_{3}Sex+{\gamma }_{4}Race+{\gamma }_{5}Height+{\gamma }_{6}Weight+{\gamma }_{7}Outcome+ϵ,$$ (7)

where the variable Outcome represents either being PA for the PA model or having T2D in the T2D model and ϵ~N(0,σ²).

Step 2: For n subjects with BF_Photo only, the value of BF_DXA is treated as missing, denoted as X_i, where i = 1, … , n. Then a possible value of ${\widehat{X}}_i$ is randomly drawn from a normal distribution such that ${\widehat{X}}_i~N\left({\widehat{\mu }}_l,{\widehat{\sigma }}^2\right)$, where ${\mu }_i={\widehat{\gamma }}_0+{\widehat{\gamma }}_{1}B{F}_{Photo,i}+{\widehat{\gamma }}_{2}Ag{e}_i+{\widehat{\gamma }}_{3}Se{x}_i+{\widehat{\gamma }}_{4}Rac{e}_i+{\widehat{\gamma }}_{5}Heigh{t}_i+{\widehat{\gamma }}_{6}Weigh{t}_i+{\widehat{\gamma }}_{7}Outcom{e}_i$ for i = 1, … , n.

Step 3: Repeat Step 2 m times to generate m datasets with corrected BF_Photo values (imputed BF_DXA).

Step 4: A multivariable logistic regression (defined as a model with multiple dependent variables (45)) is used to evaluate the association between outcome and independent variables for each of the m datasets, yielding m sets of parameter estimates. By Rubin’s method, the m sets of parameter estimates can be combined into a single set of parameter estimates. For example for each model parameter : $\overline{\beta }=\frac{1}{m}{\sum }_{j=1}^m{\widehat{\beta }}_j$. Lastly, standard errors for the estimates and 95% confidence intervals for the odds ratio were calculated.