Abstract
Brain imaging studies have revealed that functional and structural brain connectivity in the so-called triple network (i.e., default mode network (DMN), salience network (SN) and central executive network (CEN)) are consistently altered in schizophrenia. However, similar changes have also been found in patients with major depressive disorder, prompting the question of specific triple network signatures for the two disorders. In this study, we proposed Supervised Convex Nonnegative Matrix Factorization (SCNMF) to extract distributed multi-modal brain patterns. These patterns distinguish schizophrenia and major depressive disorder in a latent low-dimensional space of the triple brain network. Specifically, 21 patients of schizophrenia and 25 patients of major depressive disorder were assessed by T1-weighted, diffusion-weighted, and resting-state functional MRIs. Individual structural and functional connectivity networks, based on pre-defined regions of the triple network were constructed, respectively. Afterwards, SCNMF was employed to extract the discriminative patterns. Experiments indicate that SCNMF allows extracting the low-rank discriminative patterns between the two disorders, achieving a classification accuracy of 82.6% based on the extracted functional and structural abnormalities with support vector machine. Experimental results show the specific brain patterns for schizophrenia and major depressive disorder that are multi-modal, complex, and distributed in the triple network. Parts of the prefrontal cortex including superior frontal gyri showed variation between patients with schizophrenia and major depression due to structural properties. In terms of functional properties, the middle cingulate cortex, inferior parietal lobule, and cingulate cortex were the most discriminative regions.
Keywords: Schizophrenia, Major depressive disorder, Triple network, Brain connectivity, Nonnegative matrix factorization
Highlights
-
•
Specific changes in SZP and MDD are complex but subtle, and distributed in triple networks.
-
•
Low-rank network signatures on multi-modal data well separate SZP and MDD.
-
•
Group-specific latent disrupted patterns are uncovered with SCNMF.
1. Introduction
Schizophrenia (SZP) and major depressive disorder (MDD) are the two most common psychiatric disorders with high life-long prevalence of about 1% (Kuhn and Gallinat, 2013; Lehrer et al., 2005) and 15% (Kahn and Sommer, 2015; McGrath et al., 2008), respectively. According to the diagnostic manuals of the American Psychiatric Association (DSM-5) (Association, 2013) and World Health Organization (ICD-10) (Organization, 2004), brain disorders are defined by behavioral and mental symptom patterns and their courses. Concerning biological signs, schizophrenia and depression are characterized by multiple brain alternations (Jarskog et al., 2007; Owen et al., 2016), especially in large-scale intrinsic brain networks (Dong et al., 2017; He et al., 2018; Kaiser et al., 2015; Wotruba et al., 2014). Large-scale brain networks are of special interest since (1) impairments at micro-scales converge on changes in large-scales. (2) impairments of large-scale systems are thought to mediate behavioral phenotypes (Park and Friston, 2013). Large-scale intrinsic brain networks are defined by the specific functional connectivity of ongoing, slowly fluctuating brain activity, which is typically measured by correlated resting-state functional magnetic resonance imaging (rs-fMRI) signal time courses (Fox and Raichle, 2007). They represent a basic form of organized brain activity (Buckner et al., 2013), which is impacted in both depression and schizophrenia (Kaiser et al., 2015; Shao et al., 2018; Whitfield-Gabrieli et al., 2009). Particularly three networks are affected, i.e., the default mode network (DMN), salience network (SN) and central executive network (CEN), which together constitute the so-called triple network (Menon, 2011). Recent meta-analyses of rs-fMRI studies demonstrated extended patterns of increased and decreased functional connectivity in DMN, SN, and CEN in both schizophrenia and depression (Dong et al., 2017; Kaiser et al., 2015). This overlap of dysconnectivity across both disorders, however, prompts the question of the disorder-specific network changes in the triple network, i.e., are these discriminative patterns of dysconnectivity within the triple network separating schizophrenia from major depression.
Concerning discriminative patterns, a large body of neuroimaging techniques has been employed to uncover the specific functional and/or structural changes in schizophrenia and major depressive disorder. They usually discriminate the two disorders using diverse classification algorithms (Arbabshirani et al., 2017). For instance, in the study of Iwabuchi et al. (2013), GM and WM maps were measured by structural MRI, and support vector machine (SVM) (Cortes and Vapnik, 1995) was introduced to classify schizophrenia and healthy control with 66.6%–77% accuracy. Venkataraman et al. (2012) employed rs-fMRI to determine the large-scale functional connectivity in schizophrenia and healthy control, and random forests classification algorithm (Breiman, 2001) was adopted to perform a classification task, yielding 75% accuracy. Serpa et al. (2014) investigated major depression disorder with gray matter (GM), white matter (WM) and regional analysis of brain volumes in normalized space (RAVENS) to distinguish MDD from healthy control with SVM. Similarly, Cao et al. (2014) used SVM to identify major depressive disorder with functional connections (FC).
In the work (Koutsouleris et al., 2015), principal component analysis (PCA) (Jolliffe, 2011) and recursive feature elimination (RFE) (Guyon et al., 2002) were jointly used to acquire significant features. Finally, a linear SVM was introduced to separate patients of schizophrenia from those of depression based on structural brain changes, which achieved an accuracy of 78%. These previous works indicate that the two disorders can be separated by brain characteristics. These findings together with the multitude of not totally convergent disorder signatures of previous imaging studies (Bora et al., 2012; Frodl et al., 2008; Kaiser et al., 2015; Kieseppa et al., 2010; Liao et al., 2013; Orliac et al., 2013), suggest that the specific changes in the two disorders might be complex, subtle, and distributed across the triple networks.
Therefore, we propose a new variant of nonnegative matrix factorization method, which aims to uncover the complex and subtle structural and functional connectivity changes in patients of schizophrenia and major depressive disorder. Specifically, patients with major depressive disorder, schizophrenia and healthy controls were assessed by T1-weighted, diffusion-weighted and rs-fMRI. The brain structural and functional connectivity networks were constructed based on the predefined sub-regions of DMN, SN, and CEN, respectively. Afterwards, the Supervised Convex Nonnegative Matrix Factorization (SCNMF) was proposed to capture the complex patterns between major depressive disorder and schizophrenia. Experiments indicate that SCNMF allows extracting group-specific subspace network patterns to distinguish between patients with major depression and schizophrenia (82.61% classification accuracy, 80.95% specificity and 84.00% sensitivity). Finally, these structural and functional group-specific low-rank network patterns are further explained in the original brain network space with a backtracking strategy.
2. Materials and methods
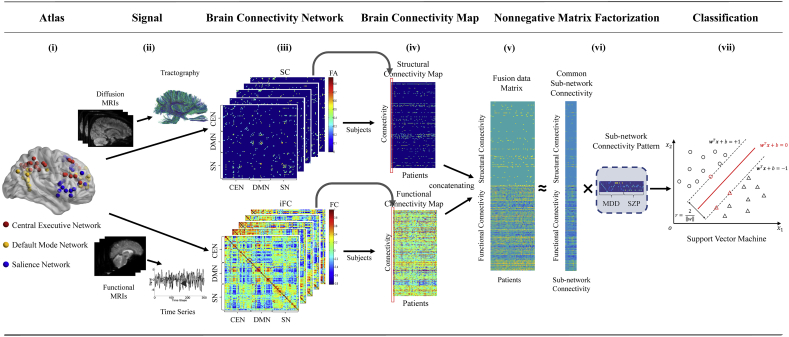
To exploit low-rank network signatures in patients of schizophrenia and major depressive disorder, a non-negative matrix factorization approach is proposed, which involves the following steps: data acquisition, brain network construction, brain connectivity map construction, and NMF-based prediction (Fig. 1).
Fig. 1.
The flowchart of group-specific patterns discovering between Schizophrenia and Major Depressive Disorder with Nonnegative Matrix Factorization. (i) The triple network nodes are identified via an ICA based method. The brain image is visualized by BrainNet toolbox (Xia et al., 2013). (ii) Diffusion MRI and functional MRI data are respectively preprocessed to tractography and time series as described in Section 2.3. (iii) Individual structural and functional connectivity networks, 105 × 105 matrices, are constructed. (iv) Structural and functional connectivity maps of 25 MDD and 21 SZP patients with 5460 brain network connectivity are performed. (v) With leave-one-out cross validation strategy, structural and functional connectivity maps were concatenated as joint data matrix for multimodal case. (vi) The joint data matrix is decomposed into latent space, consisting of basis matrix and encoding patterns, by Supervised Convex Nonnegative Matrix Factorization. (vii) The extracted patterns of each patient are converted to support vector machine as features for training and classification.
2.1. Subjects
Twenty-one patients with schizophrenia and twenty-five patients with major depression participated in current study (Table 1). The data used in our study have been described in detail previously in (Manoliu et al., 2014a) and (Meng et al., 2014). In brief, the study was approved by the local Ethics Committee of Technische Universität München, Klinikum rechts der Isar. All participants provided informed consent in accordance with the Human Research Committee guidelines of Technische Universität München. Patients were in-patients and recruited from the Department of Psychiatry of the Technische Universität München by treating psychiatrists, while healthy controls were recruited from the area of Munich by word-of-mouth advertising. Participants' examination included medical history, psychiatric interview, and psychometric assessment. Psychiatric diagnoses were based on DSM-IV (Association, 2000). The Structured Clinical Interview for DSM-IV was used to assess the presence of psychiatric diagnoses (Spitzer et al., 1992). Severity of clinical symptoms was measured with the Hamilton Rating Scale for Depression (Hamilton, 1960) and the Positive and Negative Symptom Scale (Kay et al., 1987). The global level of social, occupational, and psychological functioning was measured with the Global Assessment of Functioning Scale (Spitzer et al., 1992).
Table 1.
Demographic and clinical characteristics.
| SZP (n = 21) | MDD (n = 25) | Controls (n = 28) | pa | |
|---|---|---|---|---|
| Age (years) | 34.0(12.3) | 48.8 (14.8) | 42.0(17.5) | <0.05 |
| Sex (f/m) | 11/10 | 13/12 | 18/10 | |
| PANSS, total | 80.8(20.8) | 35.2 (3.4) | 30.7(0.8) | <0.01 |
| PANSS, positive | 19.1(5.9) | 7.8 (1.1) | 7.29(0.53) | <0.01 |
| PANSS, negative | 19.1(6.1) | 10.0 (2.3) | 7.32(0.55) | <0.01 |
| HAM-D | 9.0(5.9) | 22 (7.1) | 0.9(1.1) | <0.01 |
| GAF | 41.5 (11.6) | 50 (10.5) | 99.5 (1.1) | <0.01 |
Statistical testing was based on ANOVA. Abbreviations: SZP schizophrenia; MDD major depressive disorder; PANSS, Positive and Negative Syndrome Scale; Ham-D Hamilton depression scale; GAF Global Assessment of Functioning Scale.
For schizophrenic patients, schizophrenia was the primary diagnosis. All included patients were diagnosed with paranoid schizophrenia during acute psychosis as indicated by clinical exacerbation and increased positive symptom scores on the PANSS. Seven out of twenty-one patients had significant hallucinations (PANSS P3 ≥ 3) and 14 subjects had delusions (P1 ≥ 3). Due to increased vulnerability of psychotic patients, treating psychiatrists ensured very carefully that patients were able to provide informed consent for the study. Patients were free of any current or past depressive or manic episode, major depression, bipolar disorder, and substance abuse (except nicotine). Two out of twenty-one patients were free of antipsychotic medication; other patients received mono- or dual-therapy with atypical antipsychotics. For depressive patients, major depression was the primary diagnosis. These patients had recurrent major depression with current depressive episode. They were free of current or past psychotic symptoms, schizophrenia, schizoaffective disorder, bipolar disorder, and substance abuse. One depressive patient was free of any psychotropic medication during MRI assessment, other patients were treated by mono-, dual-, or triple-therapy including antidepressants and neuroleptics. All healthy controls were free of any current or past neurological or psychiatric disorder or psychotropic medication. More detailed information of patients is summarized in Table 1.
2.2. MRI data acquisition
All subjects underwent T1-weighted, diffusion-weighted imaging (DWI), and resting-state-functional MRI (rs-fMRI) in a 3 T Philips Achieva using an eight-channel phased-array head coil. Participants were instructed to keep their eyes closed and not to fall asleep during the 10-minute rs-fMRI scans. We verified that subjects stayed awake by interrogating via intercom immediately after the rs-fMRI scan. Brief medical examination before and after scanning validated patients' mental stability and investigated whether they had feelings of odd situations during the scanning. No patient dropped out during the scanning session.
2.3. Brain network construction
2.3.1. Extraction of triple networks with independent component analysis
Nodes of DMN, SN and CEN were pre-defined by analysis of rs-fMRI data of an independent sample of healthy controls. Briefly, 28 healthy controls were scanned on the same MRI scanner by the same rs-fMRI sequence. Data were preprocessed (motion correction, smoothing, and normalization) and analyzed by independent component analysis as described in (Manoliu et al., 2014b). Components-of-interest were selected by spatial regression for given templates (Uddin et al., 2011). Nodes of default mode, salience and central executive network were defined as spherical regions-of-interest (ROI) of 3 mm radius and local peaks of networks. In total, 105 ROIs were generated to represent three networks of interest: 38 ROIs for cortical central executive network, 30 ROIs for cortical default mode and 37 ROIs for cortical salience network. The following analyses are based on these nodes.
2.3.2. Diffusion-based tractography and structural connectivity (SC)
To evaluate tract-based SC across network nodes, tractography of individual DTI data was performed and related to cortical network ROIs. In brief, firstly, network ROIs were transformed in individual DTI space, and reduced to volumes without cerebral spinal fluid and with fractional anisotropy (FA) < 0.2 indicating gray matter. Secondly, after motion correction and voxel-wise diffusion tensor calculation, the deterministic fiber tracking algorithm TEND (Lazar et al., 2003) was applied, with all voxels with FA > 0.3 being selected as seed points of fiber tracking (Lazar et al., 2003). Tracking stopped in voxels with FA < 0.2 or physiologically implausible curvature of the track (>60°) (Lazar et al., 2003). Thirdly, the output of both ROI-based cortical parcellation and diffusion tractography were combined to construct an individual structural connectivity network for each subject. Connectivity of each pair of ROIs was measured by fibers across the two regions. If there exists at least one fiber with end-points in one pair of regions (e.g., region i and region j), the two cortical regions are assumed to be connected (Hagmann et al., 2008; Shao et al., 2012). For each connection, FAij was used to reflect the weighted edge of a network, and was defined as the mean value of FA across all voxel connecting fibers between the two cortical regions.
2.3.3. Functional MRI and intrinsic functional connectivity (iFC)
To evaluate iFC across network nodes, rs-MRI signal correlation analysis in (Meng et al., 2014) was performed. Preprocessing included head motion correction, spatial normalization into the standard stereotactic space of Montreal Neurological Institute with isotropic voxel of 3 × 3 × 3 mm3, and spatial smoothing with a 6 × 6 × 6 mm3 Gaussian kernel to reduce spatial noise. Then data quality was tested in-depth, particularly concerning motion-induced artifacts. Temporal signal-to-noise ratio and point-to-point head motion were estimated for each subject (Luo et al., 2015; Van Dijk et al., 2012). Excessive head motion (cumulative motion translation or rotation >3 mm or > 3° and mean point-to-point translation or rotation > 0.15 mm or >0.1°) was applied as an exclusion criterion. Point-to-point motion was defined as the absolute displacement of each brain volume compared with its previous volume. None of the participants had to be excluded. ANOVA and post-hoc t-tests yielded no significant differences between groups regarding mean point-to-point translation or rotation of any direction (ANOVA, p > .19) as well as temporal signal-to-noise ratio (ANOVA, p > .40). To construct iFC networks, for each ROI, time series of rs-fMRI signal were extracted from each voxel, averaged within each ROI, and then regressed against confounding covariates (comprising six time courses of head motion and signals derived from whole gray matter, white matter and cerebrospinal fluid). To estimate the intrinsic functional connectivity among different ROIs, Pearson's correlation coefficients (Rij) of corresponding time courses of any two ROIs i and j, were computed and transformed to z-values zij via r-to-z Fisher transformation. Finally, for each individual subject, the iFC within and between CEN, DMN and SN, respectively, was represented by corresponding ensembles of zij.
2.4. Brain connectivity map
As mentioned, for each subject, we constructed structural and functional connectivity networks across 105 nodes on the triple network, respectively. The two connectivity networks were thus represented as two 105 × 105 data matrices. Since the two matrices are symmetric, only the lower triangular part of the two matrices was respectively reshaped as a m-dimensional vector, where m = (105 × (105 − 1))/2 = 5460 is the number of connections. Afterwards, the vectors derived from all patients with SZP and MDD were concatenated as two structural and functional connectivity maps (i.e., two m × n matrices, and n = 25 + 21 = 46), where each column represents the structural or functional connectivity for a subject. A multimodal connectivity map was obtained after concatenating the two maps together. In the following, we would work on the structural, functional and multimodal (both structural and functional) connectivity maps.
2.5. Classification via supervised convex nonnegative matrix factorization
In this study, we extracted complex but subtle changes of brain network in latent space via NMF. In recent years, NMF has been increasingly adopted in brain MRI data analysis to tackle multi-modal data sets (Anderson et al., 2014; Arbabshirani et al., 2017). However, nonnegative matrix factorization techniques in existing neuroimaging data studies are usually unsupervised (Anderson et al., 2014; Sotiras et al., 2015; Stamile et al., 2017). In this paper, we introduced a new supervised NMF to discover discriminative low-rank patterns in latent space as signatures, aiming to boost the classification performance.
2.5.1. Nonnegative matrix factorization
Formally, NMF aims to factorize a data matrix X into two non-negative lower dimensional matrices: a basis matrix A and a coefficient matrix S.
| (1) |
where ‖ · ‖F2 is the Frobenius norm. In the context of neuroimaging data analysis,X = [x1, … , xn] ∈ ℝ + m×n corresponds to the structural or functional connectivity map, where n is the number of subjects, and m is the number of connections for each subject. A ∈ ℝ + m×k is the basis matrix and its values show how much each structural or functional connection is involved in the encoding latent space. S ∈ ℝ + n×k is the coefficient matrix representing individual patterns in latent space. In addition, k is the latent dimensionality which is determined based on the application at hand.
2.5.2. Supervised convex nonnegative matrix factorization
Original nonnegative matrix factorization (Lee and Seung, 1999) was proposed to extract latent patterns with a nonnegative constraint. Compared with other matrix factorizations without the constraint, such as dictionary learning (Eavani et al., 2015; Mairal et al., 2012), it could not decompose mixed-sign data. As shown in Eq. (1), the basis matrix A and coefficient matrix S of original NMF should be nonnegative. It means that the data X with negative values could not be decomposed to the product of these two matrices. In the neuroimaging analysis, the absolute value of functional connectivity means the strength of a correlation between two nodes in time series, and the sign represents the direction of this correlation. To apply NMF on the functional connectivity, the negative correlation should be well handled. If we simply remove negative values, the data will lose much information. Therefore, a strategy should be introduced to handle negative values in our study.
In unsupervised NMF, the extracted latent patterns may not have strong discriminative power to separate disorders. Therefore, the introduction of a supervised term would guide NMF to simultaneously aim at representing raw data in a low-dimensional space and distinguishing subjects with different disorders. Adding the class information into NMF will make the derived patterns discriminative. Recent studies have introduced different supervised constraints in the matrix factorization process. For example, by imposing Fisher constraints, Jia and Turk (2004) developed the Fisher NMF (FNMF). By enforcing the spatial locality and the separability between classes simultaneously, Zafeiriou et al. (2006) proposed the discriminant NMF (DNMF). The manifold regularization was adopted by Guan et al. (2011) for the manifold regularization and margin maximization to NMF (called MD-NMF). In addition, jointly exploiting both limited labeled and plenty of unlabeled data, Lee et al. (2010) introduced a semi-supervised of NMF (SSNMF). Recently, Shao et al. (2017) employed a cluster-based constraint to explore common and distinct patterns (CDNMF).
To better leverage the label information and well handle non-negative values in functional connectivity map, we proposed a new supervised NMF, called SCNMF. Specifically, the SCNMF algorithm jointly incorporates structural and functional connectivity maps and group information. The objective function is as follows.
| (2) |
where the first term is the objective function of Convex-NMF (Ding et al., 2010) and the second term is one kind of supervised term (Lee et al., 2010). Convex NMF is also of nonnegative constraint. However, it replaces the nonnegative basis matrix A ∈ ℝ + m×k with the product of a data matrix X ∈ ℝ ± m×n and a nonnegative basis matrix B ∈ ℝ + n×k. This part is conceivable of mixed-sign values. Therefore, it is possible for Convex NMF to handle negative data while retaining the benefit of the nonnegative constraint. Meanwhile, the supervised term is to ensure that patients of the same disorders could be mapped to the same label by adding the penalty term with label information. The label matrix Y = [y1, … , yn] ∈ ℝ + l×n is encoded that each column yi consists of zero elements except the jth entry which has one if instance xi belongs to class j. l is the number of psychiatric disorder classes. In addition, C ∈ ℝl×k is a basis matrix for label matrix Y, and λ is a tradeoff parameter to balance the importance of the supervised term.
To keep the nonnegative property of the basis and coefficient matrices in the updates, a multiplication iterative strategy was applied. The update rules of the three matrices are given as follows.
| (3) |
| (4) |
| (5) |
Moreover, we can obtain the test data in the latent space as follows.
| (6) |
where
| (7) |
| (8) |
and X could be an arbitrary matrix here. Usually, the denominator of Eqs. (3–5) is added with a small positive number to ensure divisors non-zero. In our experiments, we set it as 10−9.
2.5.3. Support vector machine
Support Vector Machine (SVM) (Cortes and Vapnik, 1995) was used to classify samples into one of two classes, i.e., patients with schizophrenia and major depressive disorder. SVM is a basic and powerful classifier used in many applications. It constructs a separating hyperplane between the training instances of both classes. The learned hyperplane is of the maximum margin with different class instances near the distinct hyperplane, called support vectors. In learning stage, given n patient training data xi ∈ ℝm (i = 1, … , n), and label vector Y ∈ ℝn×1 where yi ∈ {1, −1}, the objective function is
| (9) |
where εi is nonnegative variable, β is a penalty parameter (which is set as 1 by default) and yi is the class label. In addition, w is a k dimensional vector of weights, b is a bias scalar. In the classification stage, given patient data x, the linear SVM predicts the class of patients with the following function.
| (10) |
where f(x) is the classification function, and sign(⋅) is the sign function.
2.5.4. Classification with extracted patterns
Building upon the learned patterns via SCNMF, we classified the two disorders with support vector machine. Specifically, the classification procedure involves the following steps:
-
a)
Concatenating structural and functional connectivity maps of patients as the joint connectivity matrix X.
-
b)
Adopting leave-one-out cross validation strategy to partition multi-modal connectivity matrix X into Xtrain and Xtest for each fold.
-
c)
For each fold, decomposing Xtrain into basis matrix A and latent pattern matrix Strain via SCNMF, which does alternate iterations with Eqs. (3), (4), (5).
-
d)
Obtaining the new test data Stest in the latent space by Eq. (6).
-
e)
Training linear SVM classifier with train data Strain and classify with test data Stest. The prediction performance is the average of all folds.
2.6. Interpretation analysis
In this section, we exploited the potential complex and subtle changes based on the extracted patterns via interpretation analysis. The value of the weight vector w reflects the importance of extracted patterns during distinguishing different disorders. Therefore, it provides an intuitive way to reveal the statistical correlation between the extracted patterns and disorders. Since nonnegative matrix factorization is a linear transformation, weights on latent components could be traced back to structural or functional connections without losses. Specifically, the value of basis matrix A is the product of the raw data X and the basis matrix B in SCNMF. It could be regarded as a transform matrix, which transforms the raw data into latent components, and thus can reversely trace the extracted patterns back.
Under the same scale, the feature weights imply the importance that how much the classifier considers corresponding features during the classification. Thereby the classification contribution (CC) of structural and functional connections could be obtained via tracing the weight vector w back to structural and functional connectivity with the basis matrix A as follows.
| (11) |
Therefore, we can measure the contribution of each connection to a correct classification via the backtracking strategy. Namely, once a subject is correctly classified, we computed the contribution of each connection with Eq. (11), and then averaged the contributions of each connection for all correct classifications to measure its discriminative power (DP):
| (12) |
where means the predicted label of the test subject in each fold, and N is the number of total folds.
It is worth mentioning that machine learning models usually guarantee to achieve a locally optimal point. The weights of the model tend to capture a subset of features that are necessary to achieve a good performance (Haufe et al., 2014). Without sufficient data, the model cannot generalize well for all cases. So, the interpretation analysis here is merely a guideline.
2.7. Evaluation
2.7.1. Selection of comparison algorithms
To demonstrate the effectiveness of our proposed approach, we compared it with several classification paradigms, including Decision Tree (Quinlan, 1993), Naïve Bayes (Domingos and Pazzani, 1997), Support Vector Machine (SVM) (Cortes and Vapnik, 1995) and K-Nearest Neighbor (KNN) (Aha et al., 1991). Also several feature selection methods were also investigated for comparison, including chi square test (Pearson, 1894), Pearson correlation coefficient (PCC) (Pearson, 1895), maximal information coefficient (MIC) (Reshef et al., 2011) and recursive feature elimination RFE (Guyon et al., 2002). In addition, a part of unsupervised dimension reduction approaches was also considered, such as PCA (Jolliffe, 2011), naïve NMF (Lee and Seung, 1999), Convex NMF (Ding et al., 2010) and SSNMF (Lee et al., 2010). Moreover, we tested the method in (Koutsouleris et al., 2015), which is involved with both PCA and RFE. All methods, including SCNMF, were performed on the same constructed connectivity maps and evaluated via leave-one-out cross validation strategy.
For classification paradigms, the decision tree algorithm was C4.5 (Quinlan, 1993) and the parameter of the nearest neighbor number in KNN was tuned in the range of (3, 5, 7, 9). In SVM model, the kernel function was chosen as the linear kernel. All feature selection and dimension reduction methods were followed with linear SVM. The RFE was applied with the weights of linear SVM as correlation coefficients. The trade-off parameter λ was set as 1 in SSNMF and SCNMF. In addition, with the nonnegative constraint, the value of functional connectivity map was normalized from 0 to1 for naïve NMF and SSNMF. The exact number of estimated components in all feature selection and dimension reduction approaches was tuned to achieve the best results.
For the initialization, we applied the original initialization method in Convex NMF (Ding et al., 2010) to stabilize and optimize result. Specifically, S was initialized as S(0) = H + 0.2E, where E is a matrix with all elements being one, and H = (h1, h2, … , hk) is the cluster indicator matrix. Here, Hik = {0, 1} and the ones indicate cluster membership of each instance, obtained from K-means cluster algorithm. To fix the cluster result, we set the first k instances as initial center points. Moreover, B was initialized as B(0) = (H + 0.2E)D−1, where D = diag (d1, d2, … , dk) is a diagonal matrix with corresponding element being the count of points in each cluster. In addition, C was randomly initialized.
2.7.2. Evaluation metrics
In this study, we report the accuracy, sensitivity and specificity to evaluate the classification.
performance, which are formally defined as follows.
| (13) |
where TP, FP, TN and FN are the number of truly classified positive instances (MDD patients classified as MDD patients), falsely classified positive instances (SZP patients classified as MDD patients), truly classified negative instances (SZP patients classified as SZP patients) and falsely classified negative instances (MDD patients classified as SZP patients), respectively.
3. Results
3.1. Classification result
The classification performance is summarized in Table 2. Experimental results demonstrated that SCNMF achieved a better classification accuracy with multi-modal data (Two-Sample t-test with baseline methods showing p-value < .05), compared to changeless accuracy or even retrogression of other baseline methods with multi-modal data. With leave-one-out cross validation strategy, we found that the SCNMF with SVM on multi-modal connectivity connections yielded an accuracy of 82.61% (p-value < .01 and 95%-confidence interval: 71.23 to 93.99%) with a specificity of 80.95% and sensitivity of 84.00%.
Table 2.
Classification accuracies of proposed and baseline methods.
| Model | SCa | FCb | SC + FC |
|---|---|---|---|
| Decision Tree | 54.35% | 60.87% | 60.87% |
| Naïve Bayes | 56.52% | 60.87% | 71.74% |
| k-NN | 54.35% | 71.74% | 54.35% |
| SVM | 63.04% | 60.87% | 63.04% |
| Chi2 test | 67.39% | 71.74% | 67.39% |
| PCC | 67.39% | 71.74% | 71.74% |
| MIC | 67.39% | 69.57% | 67.39% |
| RFE | 69.57% | 71.74% | 71.74% |
| PCA | 67.39% | 71.74% | 73.91% |
| PCA + RFE | 67.39% | 71.74% | 76.09% |
| Naïve NMF | 63.04% | 73.91% | 76.09% |
| SSNMF | 69.57% | 73.91% | 78.26% |
| Convex NMF | 65.22% | 73.91% | 78.26% |
| SCNMF | 69.57% | 73.91% | 82.61% |
SC is structural connectivity.
FC is functional connectivity. This table reports the best performances of the proposed and baseline methods with tuned parameters. SCNMF achieved such performances with the latent dimensionality as 15, 39, 9 for SC, FC and multi-modal case, respectively.
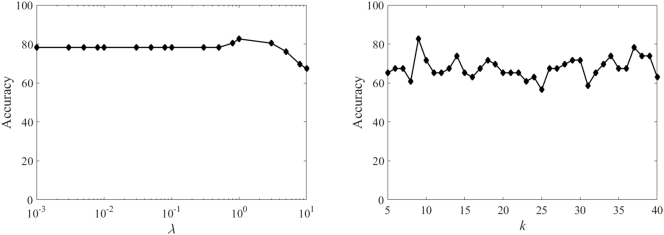
Furthermore, the performance of the proposed method SCNMF with different values of balance parameter λ and latent dimension k is shown in Fig. 2. From the figure, we can observe that SCNMF yields the best result when λ = 1 and k = 9. The results against balance parameter λ are relatively stable in a long range from 0.001 to 5, while the classification performance is fluctuated with different values of latent dimension k. We further discussed the tuning strategy of these two parameters in Section 4.1.
Fig. 2.
The sensitivity of the balance parameter λ and estimated dimension k on classification accuracy.
3.2. Group-specific network signatures discovery
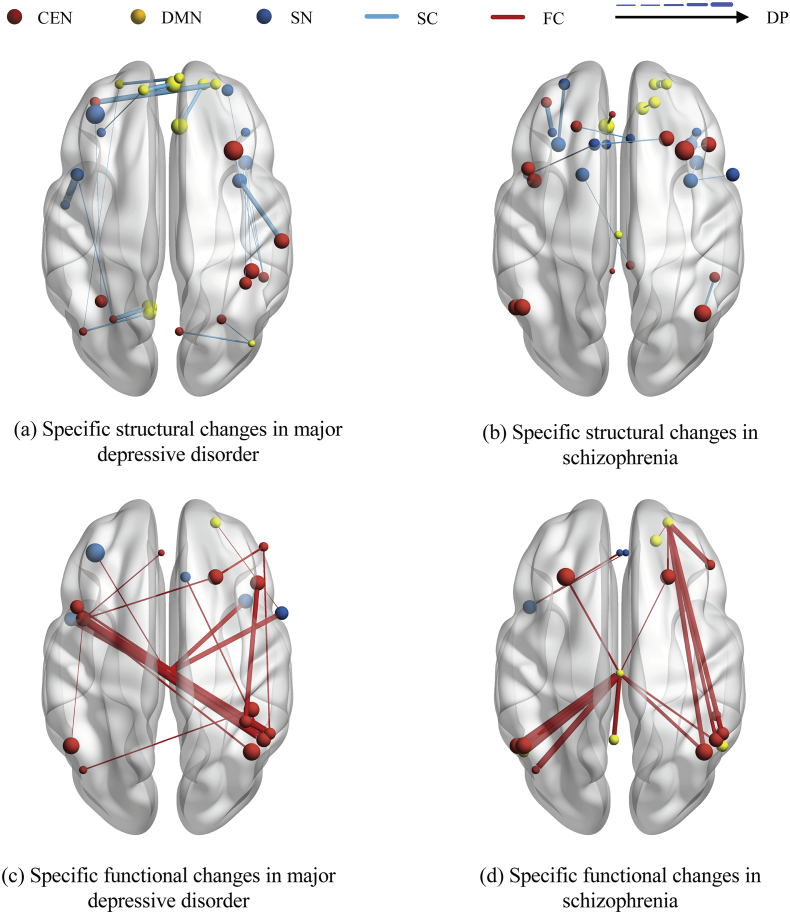
For the trained linear classifier, its knowledge, represented as the value of weights w, demonstrates effectiveness of each latent pattern. They could be traced back to structural and functional connections by the basis matrix A of nonnegative matrix factorization for discovering connections with high discriminative power. In Fig. 3, we illustrated the discriminative connections with value of DP for each psychiatric disorder, and listed these connections with names in Table 3.
Fig. 3.
The illustration of group-specific multi-modal network signatures. The discovered most discriminative structural and functional connections in current study of schizophrenia and major depressive disorder are respectively demonstrated. The top 20 discriminative connections for each psychiatric disorder. The effectiveness of structural and functional connections was traced back from the weight of classifier. The brain regions in triple network, and structural and functional connections could be distinguished by colours, and the volume of brain regions and the discriminative power are demonstrated by size.
Table 3.
Discriminative structural and functional connections between major depressive disorder and schizophrenia.
| A: Discriminative structural connections between major depressive disorder and schizophrenia | |||||
|---|---|---|---|---|---|
| MDD |
SZP |
||||
| Name (ALL) | Name (ALL) | DP | Name (ALL) | Name (ALL) | DP |
| Frontal_Inf_Oper_L | Temporal_Sup_L | 1.14 | Frontal_Sup_Medial_R | Frontal_Sup_R | 0.78 |
| Frontal_Mid_L | Frontal_Sup_R | 1.07 | Insula_R | Frontal_Inf_Tri_L | 0.76 |
| Frontal_Sup_Medial_R | Frontal_Sup_L | 1.06 | Frontal_Mid_L | Frontal_Inf_Tri_L | 0.65 |
| Postcentral_R | Insula_R | 1.04 | Parietal_Inf_L | Angular_L | 0.59 |
| Occipital_Mid_L | Calcarine_L | 1.04 | Frontal_Inf_Orb_L | Frontal_Sup_L | 0.58 |
| Cingulum_Ant_R | Frontal_Sup_Medial_R | 1.01 | Frontal_Sup_Medial_L | Cingulum_Ant_L | 0.57 |
| Frontal_Sup_Medial_R | Frontal_Sup_L | 0.99 | Angular_L | Temporal_Mid_L | 0.54 |
| Angular_L | Precuneus_L | 0.95 | Angular_R | SupraMarginal_R | 0.54 |
| Precuneus_R | Occipital_Mid_R | 0.94 | Frontal_Sup_R | Cingulum_Ant_R | 0.52 |
| Occipital_Mid_L | Frontal_Inf_Oper_L | 0.93 | Insula_L | Frontal_Inf_Orb_L | 0.52 |
| Frontal_Sup_L | Frontal_Inf_Tri_L | 0.92 | Temporal_Pole_Sup_L | Frontal_Sup_Medial_L | 0.51 |
| Occipital_Sup_R | Occipital_Mid_R | 0.92 | Frontal_Sup_R | Frontal_Sup_Medial_L | 0.51 |
| Parietal_Inf_R | Insula_R | 0.92 | Frontal_Sup_Medial_L | Cingulum_Mid_R | 0.51 |
| SupraMarginal_R | Frontal_Mid_R | 0.91 | Insula_R | Insula_R | 0.51 |
| SupraMarginal_R | Insula_R | 0.91 | Frontal_Sup_L | Frontal_Sup_Medial_R | 0.50 |
| SupraMarginal_R | Frontal_Sup_R | 0.91 | Insula_R | Frontal_Inf_Oper_R | 0.49 |
| Frontal_Mid_R | Frontal_Inf_Tri_L | 0.91 | Frontal_Mid_R | Frontal_Inf_Tri_R | 0.48 |
| Angular_L | Frontal_Sup_L | 0.91 | Precuneus_L | Frontal_Inf_Oper_L | 0.48 |
| Parietal_Inf_L | Frontal_Mid_L | 0.91 | Cingulum_Mid_R | Frontal_Sup_L | 0.48 |
| Parietal_Sup_R | Insula_R | 0.91 | Cingulum_Mid_L | Cingulum_Mid_L | 0.48 |
| B: Discriminative functional connections between major depressive disorder and schizophrenia | |||||
|---|---|---|---|---|---|
| MDD |
SZP |
||||
| Name (ALL) | Name (ALL) | DP | Name (ALL) | Name (ALL) | DP |
| Parietal_Inf_R | Precuneus_L | 0.74 | Cingulum_Mid_L | Angular_L | 1.04 |
| Parietal_Inf_R | Precuneus_L | 0.73 | Angular_L | Cingulum_Mid_L | 1.02 |
| Cingulum_Mid_L | Temporal_Sup_L | 0.73 | Angular_L | Cingulum_Mid_L | 0.99 |
| Cingulum_Mid_L | Frontal_Inf_Oper_R | 0.69 | Frontal_Inf_Tri_R | Frontal_Sup_R | 0.95 |
| Frontal_Inf_Tri_R | Parietal_Sup_R | 0.68 | Parietal_Inf_R | Frontal_Sup_R | 0.92 |
| Cingulum_Mid_L | Temporal_Pole_Sup_L | 0.67 | Angular_R | Frontal_Sup_R | 0.92 |
| Cingulum_Mid_L | Insula_R | 0.67 | Cingulum_Mid_L | Cingulum_Post_L | 0.90 |
| Parietal_Inf_R | Frontal_Inf_Oper_L | 0.63 | Parietal_Inf_L | Cingulum_Mid_L | 0.88 |
| Angular_R | Precuneus_L | 0.62 | Parietal_Inf_R | Frontal_Sup_R | 0.87 |
| Frontal_Sup_R | Frontal_Mid_R | 0.62 | Angular_R | Cingulum_Mid_L | 0.85 |
| Frontal_Sup_R | Precuneus_L | 0.62 | Temporal_Mid_L | Cingulum_Mid_L | 0.81 |
| Parietal_Inf_R | Cingulum_Mid_R | 0.62 | Cingulum_Mid_L | Angular_R | 0.81 |
| Parietal_Inf_R | Parietal_Sup_R | 0.61 | Frontal_Mid_L | Cingulum_Mid_L | 0.80 |
| Parietal_Inf_R | Frontal_Mid_R | 0.61 | Frontal_Sup_R | Frontal_Sup_R | 0.79 |
| Angular_L | Parietal_Inf_R | 0.61 | Insula_L | Cingulum_Ant_L | 0.79 |
| Frontal_Sup_Medial_L | Precuneus_L | 0.61 | Frontal_Sup_R | Cingulum_Mid_L | 0.76 |
| Cingulum_Mid_L | Frontal_Mid_L | 0.61 | Angular_R | Frontal_Sup_R | 0.75 |
| Parietal_Inf_L | Precuneus_L | 0.60 | Insula_L | Cingulum_Ant_R | 0.75 |
| Frontal_Sup_R | Frontal_Inf_Oper_R | 0.60 | Frontal_Sup_R | Frontal_Sup_R | 0.74 |
| Parietal_Inf_R | Frontal_Inf_Oper_L | 0.59 | SupraMarginal_R | Frontal_Sup_R | 0.74 |
4. Discussion
In the study, measures of functional and structural brain connectivity together with nonnegative matrix factorization technique were used to study multi-modal triple network signatures to separate schizophrenia from major depressive disorder. The proposed approach, called SCNMF, extracts low-rank network patterns in a latent space, with these patterns discriminating both disorders with a classification accuracy of 82.6%.
4.1. A new approach to uncover low-rank network patterns
The basic hypothesis in the study is that specific changes in structural and functional connectivity of the two disorders are complex, subtle, and distributed across the three brain networks. Such disrupted patterns result in the difficulty of distinguishing the two disorders in the original data space. Therefore, we proposed a new NMF-based approach, called SCNMF, which aims at extracting these changes in a latent space instead of the original data space. As mentioned above, the idea of NMF is to represent raw data in a low-dimensional space to discover the hidden patterns. Experiment results showed a good classification performance with the extracted low-rank network patterns discovered by SCNMF. In addition, to interpret our results well, the discovered patterns in a latent space were further interpreted as the specific disrupted changes of structural and functional connectivity in the original space with a traceback strategy. Findings of current study suggest that low-rank network patterns may have the potential of providing an imaging- and network-based signatures for the distinction between major depressive disorder and schizophrenia. It further indicates that NMF-based approaches provide a deeper insight into the study of psychiatric disorders, which is also demonstrated by recent works (Shao et al., 2017).
4.2. High classification performance on multi-modal data
In Table 2, we can see that SCNMF yields good performances in both single-modal and multi-modal cases. Specifically, it produces 69.57% and 73.91% classification accuracy with structural connectivity and functional connectivity respectively. For multi-modal data analysis, SCNMF achieves 82.61% classification accuracy (with 80.95% specificity and 84.00% sensitivity). The high performance achieved by SCNMF is of the following potential reasons: (1) For most neuroimaging studies, the data is often with high dimensionality, which not only brings the computing complexity, but more importantly, causes a well-known effect of “curse of dimensionality” (Hughes, 1968), where most traditional classification algorithms tend to fail. Therefore, the dimensionality reduction of subspace learning introduced in this study provides a potential way to tackle this problem. (2) For high-dimensional neuroimaging data, the disrupted patterns are usually embedded in a lower space (i.e., a low-dimensional latent space). It is because that not all features contribute to an effective representation. An intuitive example is a 2-D manifold embedded in 3-D space. These patterns may be complex and subtle (e.g., the group-specific changes of MDD and SZP, shown in Fig. 3), and traditional approaches are difficult to master this situation. The proposed approach allows capturing these distributed changes effectively by imposing the supervised constraint on NMF. As mentioned in the introduction, previous works could also yield a good performance with a dimension reduction and feature selection (Koutsouleris et al., 2015). In all, the highly discriminative power of extracted patterns shows our approach is a promising way to analyze multi-modal data.
4.3. Group-specific disrupted patterns in schizophrenia and major depressive disorder
Half of specific structural changes of schizophrenia determined in this study was embodied in the prefrontal cortex. Correspondingly, abnormalities of the prefrontal cortex in schizophrenia over health controls have been extensively documented at the regional, edge and sub-network level (Fornito et al., 2011; Salvador et al., 2010; Zhou et al., 2007). In addition, the volume change of angular gyrus in schizophrenia has been noticed (Niznikiewicz et al., 2000), causing abnormal angular gyrus asymmetry. Neuroimaging studies of schizophrenia have also shown volume and cortical thickness reductions in a network of gray matter structures including insula, anterior cingulate gyrus and prefrontal cortex (Bora et al., 2011; Busatto et al., 2010; van Haren et al., 2011). On the other hand, we can observe that the specific disrupted changes in major depressive disorder are distributed in the three triple networks (Table 2, Fig. 3). Specifically, superior frontal gyri in default mode network is discovered as a ‘hotspot’. Prefrontal cortex including left medial frontal gyrus and superior frontal gyrus in salience network are identified, which is consistent with a large number of previous works (Glahn et al., 2008; Honea et al., 2008; Hoptman et al., 2008; Kyriakopoulos et al., 2008; Reetz et al., 2008). Reduced volumes of subgenual cingulate and anterior cingulate cortex have been shown in patients with major depressive disorder relative to controls (Bora et al., 2012; Hajek et al., 2008; Koolschijn et al., 2009; Videbech and Ravnkilde, 2004). Moreover, reduced volume and thinning of prefrontal, insular and cingulate regions were reportedly related to MDD symptoms (Du et al., 2012; Hajek et al., 2008; Taki et al., 2005; Tu et al., 2012). Interestingly, occipital cortex, besides left middle occipital gyrus determined as a prominent region in this study, was documented about GABA concentration changes in patients with major depressive disorder compared to health controls (Maciag et al., 2010; Sanacora et al., 2002). In addition, the parietal lobule is interpreted as a structural pattern to determine major depressive disorder in this study. However, its functional abnormalities were almost reported when compared to health controls. It seems to be a potential special discriminative pattern.
At the functional level, functional connectivity was identified to play an important role in distinguishing schizophrenia from major depressive disorders. Interestingly, middle cingulate cortex was discovered as the most prominent region for distinguishing schizophrenia from major depressive disorders in functional connectivity. However, the functional specificity of middle cingulate gyrus in schizophrenia was rarely reported, and thus it should be paid attention to. In the study, the left inferior parietal lobule (especially angular gyrus) in central executive network is also considered as a key region in schizophrenia, consistent with the finding of previous literatures when it is compared with health controls (Minzenberg et al., 2009; Salgado-Pineda et al., 2004; Torrey, 2007). The strongly affected regions in language-related areas (Broca's area and the inferior parietal lobule), as well as the anterior insula seemed to be reasonable, since a recent meta-analysis concluded that the auditory hallucinations in schizophrenia patients is associated with aberrant activity bilaterally in those regions (Jardri et al., 2011). In addition, in line with the finding of current study, widespread patterns of brain activity deficits in prefrontal and posterior cingulate have been found in patients with schizophrenia against health controls (Kuhn and Gallinat, 2013). Moreover, inferior parietal lobule and cingulate cortex are considered the most prominent in major depressive disorder. It seems reasonable since the parietal lobe dysfunction has been identified by the cerebral blood flow data (Mayberg et al., 1999; Sackeim et al., 1990) and limbic-paralimbic (subgenual cingulate) blood flow were identified to increase in sadness (Baker et al., 1997; George et al., 1995). Also impaired episodic memory in patients with major depressive disorder has been discovered to associate with left medial temporal dysfunction (Brody et al., 2001). In addition, functional abnormalities in prefrontal cortex and the precuneus have also been identified in depression relative to healthy controls (Baxter Jr. et al., 1989; Frodl et al., 2010; Mayberg, 1994).
4.4. Potential limitations
Although SCNMF has some advantages over many state-of-the-art algorithms, it also has the following limitations: (1) The determination of parameters, such as the balance parameter λ and latent dimensionality k, is an open question of dimension reduction methods, including nonnegative matrix factorization. Usually, the suggestion interval of balance parameter λ is between 0.01 and 1, and the number of estimated components k should be less than the minimum of instance number n and feature number m. In practice, they can be estimated on the validation set based on the classification performance. Apart from that, several intrinsic dimensionality estimation methods can be employed, which can be found in the drtoolbox (Van der Maaten et al., 2007). (2) Moreover, this neuroimaging study worked on a relatively small sample set. Therefore, classification results, especially upon baseline methods, are conceivably limited in accuracy. By extracting discriminative latent patterns in a new subspace, the proposed approach SCNMF provides a new venue to separate two disorders with high classification performance. Meanwhile, it is worth reminding readers that although the proposed method promises a good performance, with data limitation, the discovered patterns may not be that general. (3) Although the meaning and unit of the structural and functional connectivity values are the same, different ranges of features would cause different variances of data. It may make the machine learning method hard to capture effective patterns.
5. Conclusion
In this study, we examined the complex but subtle network changes in schizophrenia and major depressive disorder via supervised nonnegative matrix factorization. This method integrates structural and functional connections in three intrinsic brain networks into low-rank patterns, allowing discovering group-specific differences effectively. Experimental results show a good classification performance, further demonstrating the discriminative power of extracted patterns.
Conflict of interest
The authors declare no conflict of interest.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (61403062, 61433014 to J.S., 41601025 to Q.Y.), Science-Technology Foundation for Young Scientist of SiChuan Province (2016JQ0007 to J.S.), The Sichuan Provincial Soft Science Research Program (2017ZR0208 to Q.Y.), The National Key Research and Development Program of China (2016YFB0502303), and the German Federal Ministry of Education and Research (BMBF 01EV0710 to A.M.W., BMBF 01ER0803 to C.S.)
References
- Aha D.W., Kibler D., Albert M.K. Instance-based learning algorithms. Mach. Learn. 1991;6:37–66. [Google Scholar]
- Anderson A., Douglas P.K., Kerr W.T., Haynes V.S., Yuille A.L., Xie J.W., Wu Y.N., Brown J.A., Cohen M.S. Non-negative matrix factorization of multimodal MRI, fMRI and phenotypic data reveals differential changes in default mode subnetworks in ADHD. Neuroimage. 2014;102:207–219. doi: 10.1016/j.neuroimage.2013.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arbabshirani M.R., Plis S., Sui J., Calhoun V.D. Single subject prediction of brain disorders in neuroimaging: promises and pitfalls. Neuroimage. 2017;145:137–165. doi: 10.1016/j.neuroimage.2016.02.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Association, AP . American Psychiatric Association; Washington, DC: 2000. Diagnostic and Statistical Manual of Mental Disorders-IV-TR. [Google Scholar]
- Association, AP . American Psychiatric Pub; 2013. Diagnostic and Statistical Manual of Mental Disorders (DSM-5®) [Google Scholar]
- Baker S.C., Frith C.D., Dolan R.J. The interaction between mood and cognitive function studied with PET. Psychol. Med. 1997;27:565–578. doi: 10.1017/s0033291797004856. [DOI] [PubMed] [Google Scholar]
- Baxter L.R., Jr., Schwartz J.M., Phelps M.E., Mazziotta J.C., Guze B.H., Selin C.E., Gerner R.H., Sumida R.M. Reduction of prefrontal cortex glucose metabolism common to three types of depression. Arch. Gen. Psychiatry. 1989;46:243–250. doi: 10.1001/archpsyc.1989.01810030049007. [DOI] [PubMed] [Google Scholar]
- Bora E., Fornito A., Radua J., Walterfang M., Seal M., Wood S.J., Yucel M., Velakoulis D., Pantelis C. Neuroanatomical abnormalities in schizophrenia: a multimodal voxelwise meta-analysis and meta-regression analysis. Schizophr. Res. 2011;127:46–57. doi: 10.1016/j.schres.2010.12.020. [DOI] [PubMed] [Google Scholar]
- Bora E., Fornito A., Pantelis C., Yucel M. Gray matter abnormalities in Major Depressive Disorder: a meta-analysis of voxel based morphometry studies. J. Affect. Disord. 2012;138:9–18. doi: 10.1016/j.jad.2011.03.049. [DOI] [PubMed] [Google Scholar]
- Breiman L. Random forests. Mach. Learn. 2001;45:5–32. [Google Scholar]
- Brody A.L., Barsom M.W., Bota R.G., Saxena S. Seminars in Clinical Neuropsychiatry. Vol. 6. 2001. Prefrontal-subcortical and limbic circuit mediation of major depressive disorder; pp. 102–112. [DOI] [PubMed] [Google Scholar]
- Buckner R.L., Krienen F.M., Yeo B.T.T. Opportunities and limitations of intrinsic functional connectivity MRI. Nat. Neurosci. 2013;16:832–837. doi: 10.1038/nn.3423. [DOI] [PubMed] [Google Scholar]
- Busatto G.F., Zanetti M.V., Schaufelberger M.S., Crippa J.A.S. Brain anatomical abnormalities in schizophrenia: neurodevelopmental origins and patterns of progression over time. Adv. Schizophr. Res. 2010;2009:113–148. [Google Scholar]
- Cao L.L., Guo S.X., Xue Z.M., Hu Y., Liu H.H., Mwansisya T.E., Pu W.D., Yang B., Liu C., Feng J.F., Chen E.Y.H., Liu Z.N. Aberrant functional connectivity for diagnosis of major depressive disorder: a discriminant analysis. Psychiatry Clin. Neurosci. 2014;68:110–119. doi: 10.1111/pcn.12106. [DOI] [PubMed] [Google Scholar]
- Cortes C., Vapnik V. Support-vector networks. Mach. Learn. 1995;20:273–297. [Google Scholar]
- Ding C., Li T., Jordan M.I. Convex and semi-nonnegative matrix factorizations. IEEE Trans. Pattern Anal. Mach. Intell. 2010;32:45–55. doi: 10.1109/TPAMI.2008.277. [DOI] [PubMed] [Google Scholar]
- Domingos P., Pazzani M. On the optimality of the simple Bayesian classifier under zero-one loss. Mach. Learn. 1997;29:103–130. [Google Scholar]
- Dong D., Wang Y., Chang X., Luo C., Yao D. Dysfunction of large-scale brain networks in schizophrenia: a meta-analysis of resting-state functional connectivity. Schizophr. Bull. 2017;44(1):168–181. doi: 10.1093/schbul/sbx034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du M.Y., Wu Q.Z., Yue Q., Li J., Liao Y., Kuang W.H., Huang X.Q., Chan R.C.K., Mechelli A., Gong Q.Y. Voxelwise meta-analysis of gray matter reduction in major depressive disorder. Prog. Neuro-Psychopharmacol. Biol. Psychiatry. 2012;36:11–16. doi: 10.1016/j.pnpbp.2011.09.014. [DOI] [PubMed] [Google Scholar]
- Eavani H., Satterthwaite T.D., Filipovych R., Gur R.E., Gur R.C., Davatzikos C. Identifying sparse connectivity patterns in the brain using resting-state fMRI. Neuroimage. 2015;105:286–299. doi: 10.1016/j.neuroimage.2014.09.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fornito A., Yoon J., Zalesky A., Bullmore E.T., Carter C.S. General and specific functional connectivity disturbances in first-episode schizophrenia during cognitive control performance. Biol. Psychiatry. 2011;70:64–72. doi: 10.1016/j.biopsych.2011.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox M.D., Raichle M.E. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat. Rev. Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- Frodl T.S., Koutsouleris N., Bottlender R., Born C., Jager M., Scupin I., Reiser M., Moller H.J., Meisenzahl E.M. Depression-related variation in brain morphology over 3 years - effects of stress? Arch. Gen. Psychiatry. 2008;65:1156–1165. doi: 10.1001/archpsyc.65.10.1156. [DOI] [PubMed] [Google Scholar]
- Frodl T., Bokde A.L.W., Scheuerecker J., Lisiecka D., Schoepf V., Hampel H., Moller H.J., Bruckmann H., Wiesmann M., Meisenzahl E. Functional connectivity bias of the orbitofrontal cortex in drug-free patients with major depression. Biol. Psychiatry. 2010;67:161–167. doi: 10.1016/j.biopsych.2009.08.022. [DOI] [PubMed] [Google Scholar]
- George M.S., Ketter T.A., Parekh P.I., Horwitz B., Herscovitch P., Post R.M. Brain activity during transient sadness and happiness in healthy women. Am. J. Psychiatr. 1995;152:341–351. doi: 10.1176/ajp.152.3.341. [DOI] [PubMed] [Google Scholar]
- Glahn D.C., Laird A.R., Ellison-Wright I., Thelen S.M., Robinson J.L., Lancaster J.L., Bullmore E.T., Fox P.T. Meta-analysis of gray matter anomalies in schizophrenia: application of anatomic likelihood estimation and network analysis. Biol. Psychiatry. 2008;64:774–781. doi: 10.1016/j.biopsych.2008.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan N., Tao D., Luo Z., Yuan B. Manifold regularized discriminative nonnegative matrix factorization with fast gradient descent. IEEE Trans. Image Process. 2011;20:2030–2048. doi: 10.1109/TIP.2011.2105496. [DOI] [PubMed] [Google Scholar]
- Guyon I., Weston J., Barnhill S., Vapnik V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002;46:389–422. [Google Scholar]
- Hagmann P., Cammoun L., Gigandet X., Meuli R., Honey C.J., Wedeen V., Sporns O. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008;6:1479–1493. doi: 10.1371/journal.pbio.0060159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hajek T., Kozeny J., Kopecek M., Alda M., Hoschl C. Reduced subgenual cingulate volumes in mood disorders: a meta-analysis. J. Psychiatry Neurosci. 2008;33:91–99. [PMC free article] [PubMed] [Google Scholar]
- Hamilton M. A rating scale for depression. J. Neurol. Neurosurg. Psychiatry. 1960;23:56–62. doi: 10.1136/jnnp.23.1.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Haren N.E.M., Schnack H.G., Cahn W., van den Heuvel M.P., Lepage C., Collins L., Evans A.C., Pol H.E.H., Kahn R.S. Changes in cortical thickness during the course of illness in schizophrenia. Arch. Gen. Psychiatry. 2011;68:871–880. doi: 10.1001/archgenpsychiatry.2011.88. [DOI] [PubMed] [Google Scholar]
- Haufe S., Meinecke F., Gorgen K., Dahne S., Haynes J.D., Blankertz B., Biessgmann F. On the interpretation of weight vectors of linear models in multivariate neuroimaging. Neuroimage. 2014;87:96–110. doi: 10.1016/j.neuroimage.2013.10.067. [DOI] [PubMed] [Google Scholar]
- He H., Yang M., Duan M.J., Chen X., Lai Y.X., Xia Y., Shao J.M., Biswal B.B., Luo C., Yao D.Z. Music intervention leads to increased insular connectivity and improved clinical symptoms in schizophrenia. Front. Neurosci. 2018;11:15. doi: 10.3389/fnins.2017.00744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honea R.A., Meyer-Lindenberg A., Hobbs K.B., Pezawas L., Mattay V.S., Egan M.F., Verchinski B., Passingham R.E., Weinberger D.R., Callicott J.H. Is gray matter volume an intermediate phenotype for schizophrenia? A voxel-based morphometry study of patients with schizophrenia and their healthy siblings. Biol. Psychiatry. 2008;63:465–474. doi: 10.1016/j.biopsych.2007.05.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoptman M.J., Nierenberg J., Bertisch H.C., Catalano D., Ardekani B.A., Branch C.A., DeLisi L.E. A DTI study of white matter microstructure in individuals at high genetic risk for schizophrenia. Schizophr. Res. 2008;106:115–124. doi: 10.1016/j.schres.2008.07.023. [DOI] [PubMed] [Google Scholar]
- Hughes G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory. 1968;14:55–63. [Google Scholar]
- Iwabuchi S.J., Liddle P.F., Palaniyappan L. Clinical utility of machine-learning approaches in schizophrenia: improving diagnostic confidence for translational neuroimaging. Front. Psychiatry. 2013;4:95. doi: 10.3389/fpsyt.2013.00095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jardri R., Pouchet A., Pins D., Thomas P. Cortical activations during auditory verbal hallucinations in schizophrenia: a coordinate-based meta-analysis. Am. J. Psychiatr. 2011;168:73–81. doi: 10.1176/appi.ajp.2010.09101522. [DOI] [PubMed] [Google Scholar]
- Jarskog L.F., Miyamoto S., Lieberman J.A. Annual Review of Medicine. Annual Reviews, Palo Alto. 2007. Schizophrenia: New pathological insights and therapies; pp. 49–61. [DOI] [PubMed] [Google Scholar]
- Jia Y.W.Y., Turk C.H.M. Proc. Asian Conf. on Comp. Vision. Citeseer. 2004. Fisher non-negative matrix factorization for learning local features; pp. 27–30. [Google Scholar]
- Jolliffe I. International Encyclopedia of Statistical Science. Springer; 2011. Principal component analysis; pp. 1094–1096. [Google Scholar]
- Kahn R.S., Sommer I.E. The neurobiology and treatment of first-episode schizophrenia. Mol. Psychiatry. 2015;20:84–97. doi: 10.1038/mp.2014.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser R.H., Andrews-Hanna J.R., Wager T.D., Pizzagalli D.A. Large-scale network dysfunction in major depressive disorder a meta-analysis of resting-state functional connectivity. JAMA Psychiatry. 2015;72:603–611. doi: 10.1001/jamapsychiatry.2015.0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay S.R., Fiszbein A., Opler L.A. The positive and negative syndrome scale (PANSS) for schizophrenia. Schizophr. Bull. 1987;13:261–276. doi: 10.1093/schbul/13.2.261. [DOI] [PubMed] [Google Scholar]
- Kieseppa T., Eerola M., Mantyla R., Neuvonen T., Poutanen V.P., Luoma K., Tuulio-Henriksson A., Jylha P., Mantere O., Melartin T., Rytsala H., Vuorilehto M., Isometsa E. Major depressive disorder and white matter abnormalities: a diffusion tensor imaging study with tract-based spatial statistics. J. Affect. Disord. 2010;120:240–244. doi: 10.1016/j.jad.2009.04.023. [DOI] [PubMed] [Google Scholar]
- Koolschijn P., van Haren N.E.M., Lensvelt-Mulders G., Pol H.E.H., Kahn R.S. Brain volume abnormalities in major depressive disorder: a meta-analysis of magnetic resonance imaging studies. Hum. Brain Mapp. 2009;30:3719–3735. doi: 10.1002/hbm.20801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koutsouleris N., Meisenzahl E.M., Borgwardt S., Riecher-Rossler A., Frodl T., Kambeitz J., Kohler Y., Falkai P., Moller H.J., Reiser M., Davatzikos C. Individualized differential diagnosis of schizophrenia and mood disorders using neuroanatomical biomarkers. Brain. 2015;138:2059–2073. doi: 10.1093/brain/awv111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn S., Gallinat J. Resting-state brain activity in schizophrenia and major depression: a quantitative meta-analysis. Schizophr. Bull. 2013;39:358–365. doi: 10.1093/schbul/sbr151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kyriakopoulos M., Vyas N.S., Barker G.J., Chitnis X.A., Frangou S. A diffusion tensor imaging study of white matter in early-onset schizophrenia. Biol. Psychiatry. 2008;63:519–523. doi: 10.1016/j.biopsych.2007.05.021. [DOI] [PubMed] [Google Scholar]
- Lazar M., Weinstein D.M., Tsuruda J.S., Hasan K.M., Arfanakis K., Meyerand M.E., Badie B., Rowley H.A., Haughton V., Field A., Alexander A.L. White matter tractography using diffusion tensor deflection. Hum. Brain Mapp. 2003;18:306–321. doi: 10.1002/hbm.10102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D.D., Seung H.S. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401:788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- Lee H., Yoo J., Choi S. Semi-supervised nonnegative matrix factorization. IEEE Signal Process. Lett. 2010;17:4–7. [Google Scholar]
- Lehrer D.S., Christian B.T., Mantil J., Murray A.C., Buchsbaum B.R., Oakes T.R., Byne W., Kemether E.M., Buchsbaum M.S. Thalamic and prefrontal FDG uptake in never medicated patients with schizophrenia. Am. J. Psychiatr. 2005;162:931–938. doi: 10.1176/appi.ajp.162.5.931. [DOI] [PubMed] [Google Scholar]
- Liao Y., Huang X.Q., Wu Q.Z., Yang C., Kuang W.H., Du M.Y., Lui S., Yue Q., Chan R.C.K., Kemp G.J., Gong Q.Y. Is depression a disconnection syndrome? Meta-analysis of diffusion tensor imaging studies in patients with MDD. J. Psychiatry Neurosci. 2013;38:49–56. doi: 10.1503/jpn.110180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo C., Zhang Y.D., Cao W.F., Huang Y., Yang F., Wang J.J., Tu S.P., Wang X.M., Yao D.Z. Altered structural and functional feature of striato-cortical circuit in benign epilepsy with centrotemporal spikes. Int. J. Neural Syst. 2015;25:13. doi: 10.1142/S0129065715500276. [DOI] [PubMed] [Google Scholar]
- Maciag D., Hughes J., O'Dwyer G., Pride Y., Stockmeier C.A., Sanacora G., Rajkowska G. Reduced density of calbindin immunoreactive GABAergic neurons in the occipital cortex in major depression: relevance to neuroimaging studies. Biol. Psychiatry. 2010;67:465–470. doi: 10.1016/j.biopsych.2009.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mairal J., Bach F., Ponce J. Task-driven dictionary learning. IEEE Trans. Pattern Anal. Mach. Intell. 2012;34:791–804. doi: 10.1109/TPAMI.2011.156. [DOI] [PubMed] [Google Scholar]
- Manoliu A., Meng C., Brandl F., Doll A., Tahmasian M., Scherr M., Schwerthoffer D., Zimmer C., Forstl H., Bauml J., Riedl V., Wohlschlager A.M., Sorg C. Insular dysfunction within the salience network is associated with severity of symptoms and aberrant inter-network connectivity in major depressive disorder. Front. Hum. Neurosci. 2014;7:17. doi: 10.3389/fnhum.2013.00930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manoliu A., Riedl V., Zherdin A., Muhlau M., Schwerthoffer D., Scherr M., Peters H., Zimmer C., Forstl H., Bauml J., Wohlschlager A.M., Sorg C. Aberrant dependence of default mode/central executive network interactions on anterior insular salience network activity in schizophrenia. Schizophr. Bull. 2014;40:428–437. doi: 10.1093/schbul/sbt037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayberg H.S. Frontal-lobe dysfunction in secondary depression. J. Neuropsychiatr. Clin. Neurosci. 1994;6:428–442. doi: 10.1176/jnp.6.4.428. [DOI] [PubMed] [Google Scholar]
- Mayberg H.S., Liotti M., Brannan S.K., McGinnis S., Mahurin R.K., Jerabek P.A., Silva J.A., Tekell J.L., Martin C.C., Lancaster J.L., Fox P.T. Reciprocal limbic-cortical function and negative mood: converging PET findings in depression and normal sadness. Am. J. Psychiatr. 1999;156:675–682. doi: 10.1176/ajp.156.5.675. [DOI] [PubMed] [Google Scholar]
- McGrath J., Saha S., Chant D., Welham J. Schizophrenia: a concise overview of incidence, prevalence, and mortality. Epidemiol. Rev. 2008;30:67–76. doi: 10.1093/epirev/mxn001. [DOI] [PubMed] [Google Scholar]
- Meng C., Brandl F., Tahmasian M., Shao J.M., Manoliu A., Scherr M., Schwerthoffer D., Bauml J., Forstl H., Zimmer C., Wohlschlager A.M., Riedl V., Sorg C. Aberrant topology of striatum's connectivity is associated with the number of episodes in depression. Brain. 2014;137:598–609. doi: 10.1093/brain/awt290. [DOI] [PubMed] [Google Scholar]
- Menon V. Large-scale brain networks and psychopathology: a unifying triple network model. Trends Cogn. Sci. 2011;15:483–506. doi: 10.1016/j.tics.2011.08.003. [DOI] [PubMed] [Google Scholar]
- Minzenberg M.J., Laird A.R., Thelen S., Carter C.S., Glahn D.C. Meta-analysis of 41 functional neuroimaging studies of executive function in schizophrenia. Arch. Gen. Psychiatry. 2009;66:811–822. doi: 10.1001/archgenpsychiatry.2009.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niznikiewicz M., Donnino R., McCarley R.W., Nestor P.G., Iosifescu D.V., O'Donnell B., Levitt J., Shenton M.E. Abnormal angular gyrus asymmetry in schizophrenia. Am. J. Psychiatr. 2000;157:428–437. doi: 10.1176/appi.ajp.157.3.428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Organization, WH . World Health Organization; 2004. International Statistical Classification of Diseases and Related Health Problems. [Google Scholar]
- Orliac F., Naveau M., Joliot M., Delcroix N., Razafimandimby A., Brazo P., Dollfus S., Delamillieure P. Links among resting-state default-mode network, salience network, and symptomatology in schizophrenia. Schizophr. Res. 2013;148:74–80. doi: 10.1016/j.schres.2013.05.007. [DOI] [PubMed] [Google Scholar]
- Owen M.J., Sawa A., Mortensen P.B. Schizophrenia. Lancet. 2016;388:86–97. doi: 10.1016/S0140-6736(15)01121-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park H.J., Friston K.J. Structural and functional brain networks: from connections to cognition. Science. 2013;342:579. doi: 10.1126/science.1238411. [DOI] [PubMed] [Google Scholar]
- Pearson K. Contributions to the mathematical theory of evolution. Philos. Trans. R. Soc. Lond. A. 1894;185:71–110. [Google Scholar]
- Pearson K. Note on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895;58:240–242. [Google Scholar]
- Quinlan J.R. Morgan Kaufmann; San Mateo, CA: 1993. C4.5: Programs for Machine Learning. [Google Scholar]
- Reetz K., Lencer R., Steinlechner S., Gaser C., Hagenah J., Buchel C., Petersen D., Kock N., Djarmati A., Siebner H.R., Klein C., Binkofski F. Limbic and frontal cortical degeneration is associated with psychiatric symptoms in PINK1 mutation carriers. Biol. Psychiatry. 2008;64:241–247. doi: 10.1016/j.biopsych.2007.12.010. [DOI] [PubMed] [Google Scholar]
- Reshef D.N., Reshef Y.A., Finucane H.K., Grossman S.R., McVean G., Turnbaugh P.J., Lander E.S., Mitzenmacher M., Sabeti P.C. Detecting novel associations in large data sets. Science. 2011;334:1518–1524. doi: 10.1126/science.1205438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sackeim H.A., Prohovnik I., Moeller J.R., Brown R.P., Apter S., Prudic J., Devanand D.P., Mukherjee S. Regional cerebral blood flow in mood disorders. I. Comparison of major depressives and normal controls at rest. Arch. Gen. Psychiatry. 1990;47:60–70. doi: 10.1001/archpsyc.1990.01810130062009. [DOI] [PubMed] [Google Scholar]
- Salgado-Pineda P., Junque C., Vendrell P., Baeza I., Bargallo N., Falcon C., Bernardo M. Decreased cerebral activation during CPT performance: structural and functional deficits in schizophrenic patients. Neuroimage. 2004;21:840–847. doi: 10.1016/j.neuroimage.2003.10.027. [DOI] [PubMed] [Google Scholar]
- Salvador R., Sarro S., Gomar J.J., Ortiz-Gil J., Vila F., Capdevila A., Bullmore E.T., McKenna P.J., Pomarol-Clotet E. Overall brain connectivity maps show cortico-subcortical abnormalities in schizophrenia. Hum. Brain Mapp. 2010;31:2003–2014. doi: 10.1002/hbm.20993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanacora G., Mason G.F., Rothman D.L., Krystal J.H. Increased occipital cortex GABA concentrations in depressed patients after therapy with selective serotonin reuptake inhibitors. Am. J. Psychiatr. 2002;159:663–665. doi: 10.1176/appi.ajp.159.4.663. [DOI] [PubMed] [Google Scholar]
- Serpa M.H., Ou Y.M., Schaufelberger M.S., Doshi J., Ferreira L.K., Machado-Vieira R., Menezes P.R., Scazufca M., Davatzikos C., Busatto G.F., Zanetti M.V. Neuroanatomical classification in a population-based sample of psychotic major depression and bipolar I disorder with 1 year of diagnostic stability. Biomed. Res. Int. 2014;9 doi: 10.1155/2014/706157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao J.M., Myers N., Yang Q.L., Feng J., Plant C., Bohm C., Forstl H., Kurz A., Zimmer C., Meng C., Riedl V., Wohlschlager A., Sorg C. Prediction of Alzheimer's disease using individual structural connectivity networks. Neurobiol. Aging. 2012;33:2756–2765. doi: 10.1016/j.neurobiolaging.2012.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao J., Yu Z., Li P., Han W., Sorg C., Yang Q. Data Mining (ICDM), 2017 IEEE 17th International Conference on. IEEE; 2017. Exploring common and distinct structural connectivity patterns between schizophrenia and major depression via cluster-driven nonnegative matrix factorization. [Google Scholar]
- Shao J., Meng C., Tahmasian M., Brandl F., Yang Q., Luo G., Luo C., Yao D., Gao L., Riedl V., Wohlschlager A., Sorg C. Common and distinct changes of default mode and salience network in schizophrenia and major depression. Brain Imaging Behav. 2018;12:1708–1719. doi: 10.1007/s11682-018-9838-8. [DOI] [PubMed] [Google Scholar]
- Sotiras A., Resnick S.M., Davatzikos C. Finding imaging patterns of structural covariance via Non-Negative Matrix Factorization. Neuroimage. 2015;108:1–16. doi: 10.1016/j.neuroimage.2014.11.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spitzer R.L., Williams J.B.W., Gibbon M., First M.B. The structured clinical interview for DSM-III-R (SCID) .1. history, rationale, and description. Arch. Gen. Psychiatry. 1992;49:624–629. doi: 10.1001/archpsyc.1992.01820080032005. [DOI] [PubMed] [Google Scholar]
- Stamile C., Kocevar G., Cotton F., Maes F., Sappey-Marinier D., Van Huffel S. Multiparametric non-negative matrix factorization for longitudinal variations detection in white-matter fiber bundles. IEEE J. Biomed. Health Informatics. 2017;21:1393–1402. doi: 10.1109/JBHI.2016.2597963. [DOI] [PubMed] [Google Scholar]
- Taki Y., Kinomura S., Awata S., Inoue K., Sato K., Ito H., Goto R., Uchida S., Tsuji I., Arai H., Kawashima R., Fukuda H. Male elderly subthreshold depression patients have smaller volume of medial part of prefrontal cortex and precentral gyrus compared with age-matched normal subjects: a voxel-based morphometry. J. Affect. Disord. 2005;88:313–320. doi: 10.1016/j.jad.2005.08.003. [DOI] [PubMed] [Google Scholar]
- Torrey E.F. Schizophrenia and the inferior parietal lobule. Schizophr. Res. 2007;97:215–225. doi: 10.1016/j.schres.2007.08.023. [DOI] [PubMed] [Google Scholar]
- Tu P.C., Chen L.F., Hsieh J.C., Bai Y.M., Li C.T., Su T.P. Regional cortical thinning in patients with major depressive disorder: a surface-based morphometry study. Psychiatry Res. Neuroimaging. 2012;202:206–213. doi: 10.1016/j.pscychresns.2011.07.011. [DOI] [PubMed] [Google Scholar]
- Uddin L.Q., Supekar K.S., Ryali S., Menon V. Dynamic reconfiguration of structural and functional connectivity across core neurocognitive brain networks with development. J. Neurosci. 2011;31:18578–18589. doi: 10.1523/JNEUROSCI.4465-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Maaten L., Postma E.O., van den Herik H.J. MICC, Maastricht University; 2007. Matlab Toolbox for Dimensionality Reduction. [Google Scholar]
- Van Dijk K.R.A., Sabuncu M.R., Buckner R.L. The influence of head motion on intrinsic functional connectivity MRI. Neuroimage. 2012;59:431–438. doi: 10.1016/j.neuroimage.2011.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venkataraman A., Whitford T.J., Westin C.F., Golland P., Kubicki M. Whole brain resting state functional connectivity abnormalities in schizophrenia. Schizophr. Res. 2012;139:7–12. doi: 10.1016/j.schres.2012.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Videbech P., Ravnkilde B. Hippocampal volume and depression: a meta-analysis of MRI studies. Am. J. Psychiatr. 2004;161:1957–1966. doi: 10.1176/appi.ajp.161.11.1957. [DOI] [PubMed] [Google Scholar]
- Whitfield-Gabrieli S., Thermenos H.W., Milanovic S., Tsuang M.T., Faraone S.V., McCarley R.W., Shenton M.E., Green A.I., Nieto-Castanon A., LaViolette P., Wojcik J., Gabrieli J.D.E., Seidman L.J. Hyperactivity and hyperconnectivity of the default network in schizophrenia and in first-degree relatives of persons with schizophrenia. Proc. Natl. Acad. Sci. U. S. A. 2009;106:1279–1284. doi: 10.1073/pnas.0809141106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wotruba D., Michels L., Buechler R., Metzler S., Theodoridou A., Gerstenberg M., Walitza S., Kollias S., Rossler W., Heekeren K. Aberrant coupling within and across the default mode, task-positive, and salience network in subjects at risk for psychosis. Schizophr. Bull. 2014;40:1095–1104. doi: 10.1093/schbul/sbt161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia M.R., Wang J.H., He Y. BrainNet viewer: a network visualization tool for human brain connectomics. PLoS One. 2013;8:15. doi: 10.1371/journal.pone.0068910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zafeiriou S., Tefas A., Buciu I., Pitas I. Exploiting discriminant information in nonnegative matrix factorization with application to frontal face verification. IEEE Trans. Neural Netw. 2006;17:683–695. doi: 10.1109/TNN.2006.873291. [DOI] [PubMed] [Google Scholar]
- Zhou Y., Liang M., Tian L.X., Wang K., Hao Y.H., Liu H.H., Liu Z.N., Jiang T.Z. Functional disintegration in paranoid schizophrenia using resting-state fMRI. Schizophr. Res. 2007;97:194–205. doi: 10.1016/j.schres.2007.05.029. [DOI] [PubMed] [Google Scholar]