Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Aug 6;5(9):3594–3600. doi: 10.1021/acsphotonics.8b00425

Nanoimaging and Control of Molecular Vibrations through Electromagnetically Induced Scattering Reaching the Strong Coupling Regime

Eric A Muller †,*, Benjamin Pollard †, Hans A Bechtel ‡, Ronen Adato §, Dordaneh Etezadi ⊥, Hatice Altug ⊥, Markus B Raschke †,*
PMCID: PMC6390704  PMID: 30828589

Abstract

graphic file with name ph-2018-00425x_0005.jpg

Optical resonators can enhance light–matter interaction, modify intrinsic molecular properties such as radiative emission rates, and create new molecule–photon hybrid quantum states. To date, corresponding implementations are based on electronic transitions in the visible spectral region with large transition dipoles yet hampered by fast femtosecond electronic dephasing. In contrast, coupling molecular vibrations with their weaker dipoles to infrared optical resonators has been less explored, despite long-lived coherences with 2 orders of magnitude longer dephasing times. Here, we achieve excitation of molecular vibrations through configurable optical interactions of a nanotip with an infrared resonant nanowire that supports tunable bright and nonradiative dark modes. The resulting antenna–vibrational coupling up to 47 ± 5 cm–1 exceeds the intrinsic dephasing rate of the molecular vibration, leading to hybridization and mode splitting. We observe nanotip-induced quantum interference of vibrational excitation pathways in spectroscopic nanoimaging, which we model classically as plasmonic electromagnetically induced scattering as the phase-controlled extension of the classical analogue of electromagnetically induced transparency and absorption. Our results present a new regime of IR spectroscopy for applications of vibrational coherence from quantum computing to optical control of chemical reactions.

Keywords: plasmonics, molecular vibrations, strong coupling, optical antennas, tip-enhanced, scattering-scanning near-field optical microscopy (s-SNOM), synchrotron infrared nanoscale spectroscopy

Optical resonators, from microcavities to plasmonic nanoparticles, have garnered significant attention for their ability to enhance light–matter interaction. Hybridized states of the resonator and an emitter such as a molecular transition can be used for quantum coherent control,1 single-photon sources,2 quantum information processing,3 slow light,4 and optical control of photocatalysis.5 Optical resonators can modify excitation and decay of molecular states, with an effect proportional to the quality factor and inverse mode volume (Q/V) of the optical resonator.6,7 Coherent energy transfer between molecular transitions and optical states of the resonator is readily achieved in high-Q microcavities yet with diffraction-limited mode volumes. Recent advances in nanophotonic devices, such as optical antennas and plasmonic nanoparticles, have utilized an associated extreme mode confinement as small as 10–6 V/λ3 to achieve strong coupling with molecular or quantum dot electronic transitions in the visible spectral region.8−12 However, the fast, 10s of femtosecond dephasing times of both electronic transitions and plasmonic resonators13 present a significant obstacle to applications of electronic strong coupling for coherent control or quantum information processing.

In contrast, at infrared (IR) wavelengths, molecular vibrations offer dephasing times of picoseconds or greater and as long as millisecond radiative lifetimes. Coupling between molecular vibrations and IR nano-optical resonators primarily has been utilized for enhanced detection sensitivity, as previously demonstrated at visible wavelengths14 through surface-enhanced infrared absorption (SEIRA)15,16 or for nanoscale imaging in IR scattering-scanning near-field optical microscopy (s-SNOM).17,18 Although a rich coherent and phase-controlled light–matter interaction regime is expected using molecular vibrations,19−21 the coherent interaction regime of strong coupling has only recently been reached through microcavities,22 surface plasmons,23 or hyperbolic phonons, yet in ensemble measurements and with moderate mode volumes not yet reaching the level of nanoconfinement achievable with metallic optical antennas.

Nanoscale optical antennas enable greater confinement of the light, and the combination of multiple antennas can give rise to new phenomena including yet greater confinement in nanoscale gaps, increased Q-factors, and dark-to-bright mode conversion.24−26 Constructive and destructive interference between multiple excitation pathways of coupled antennas can result in either enhancement of a transition or optical transparency at the frequency of an absorption. Similar to electromagnetically induced transparency and aborption (EIT and EIA) observed in multilevel atoms,27 optical antennas have been used to achieve the plasmonic analogues of both EIT and EIA with similar Fano-type line shapes as well as spectral regions of high transmission or absorption.28−33 The plasmonic analogue of EIT can be understood through classical models of coupled harmonic oscillators, with the coupling field in coherent EIT replaced by a classial spring and leading to similar phenomena.34,35 Such coupling of multiple resonators through near-field interactions may overcome the limits of the small vibrational dipole moment and take advantage of the long vibrational coherence times for controlled light–matter interactions. However, to date, optical antennas have relied on fixed near-field coupling with limited control of excitation and emission pathways.

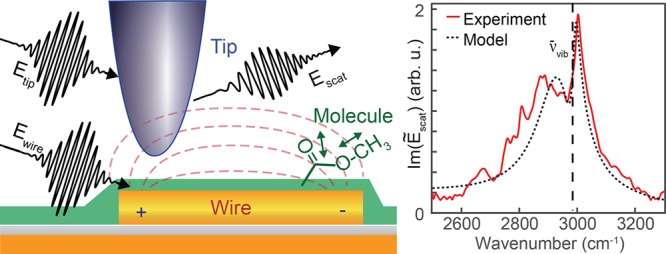
In this work, we demonstrate the combination of a nanowire and a nanotip for configurable optical interactions with molecular vibrations. As shown in Figure 1A, through near-field interaction, we couple a nanowire antenna with high Q-factor to a nanotip with low Q-factor and fast radiative dephasing. We use the nanotip as an active and perturbative optical element, where we modify vibrational excitation pathways through 3D positioning relative to the nanowire. We measure coupling and energy transfer through spectrally resolved scattering from the nanotip analogous to broadband IR s-SNOM. As vibrational model oscillators, we use the carbonyl stretch and the C–H stretch from a thin film of poly(methyl methacrylate) (PMMA) on the nanowire. We achieve coupling strength to the molecular vibration of 47 ± 5 cm–1 through the nanowire and 35 ± 5 cm–1 through the nanotip, respectively, both of which exceed the intrinsic dephasing rate of the molecular vibration. Interference between competing optical pathways of the nanotip and nanowire gives rise to phase-controlled vibrational excitation and control. Similar to the classical analogues of EIT and EIA, we can induce sharp spectral dips and peaks respectively at the vibrational resonance through controlled coupling to both nanotip and nanowire, which we describe as classical electromagnetically induced scattering (EIS). Our results thus demonstrate IR vibrational spectroscopy approaching the strong coupling regime with modification of radiative emission and control of vibrational coherence though coupled nanophotonic resonators.

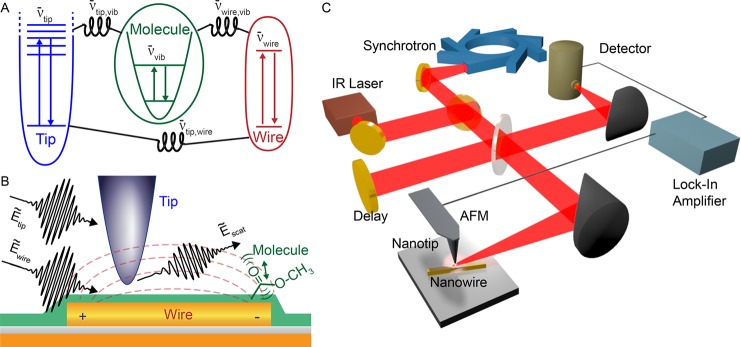
Figure 1.

Figure 1

Open in a new tab

(A) Nanotip, nanowire, and molecular vibration are coupled in the near field with coupling strengths ν̅tip,wire, ν̅wire,vib, and ν̅tip,vib. (B) Conceptual experimental implementation with nanotip positioned above the nanowire with PMMA molecular thin film. (C) Broadband IR light from a synchrotron or narrow-band laser illuminates the nanowire and nanotip, positioned by an atomic force microscope (AFM). Tip-scattered light is interferometrically detected and demodulated by a lock-in amplifier.

Experiment

We couple a resonant nanowire antenna, a broadband nanotip antenna, and molecular vibration as schematically depicted in Figure 1B. The nanotip antenna couples to the nanowire antenna through the evanescent near field, with phase and coupling strength tunable by 3D tip positioning as shown in Figure 1C, using an atomic force microscope (AFM) operating in intermittent contact mode (modified Nano-IRs2, Anasys Instruments Inc., and modified Innova, Veeco Instruments Inc.).

Gold IR nanowire antennas were fabricated with large Q = 12–14 and long dephasing times (Γwire = 120–140 cm–1) on a Au ground plane with a 90 nm MgF2 spacer layer. This configuration reduces the radiative damping of the nanowire,15 thus extending its dephasing time. The antenna dipole resonances cover the range from 1950 cm–1 (5.2 μm) to 1450 cm–1 (6.9 μm), with nanowire lengths of 1.5 to 2.1 μm, following the expected effective wavelength scaling.15,36 Simple metalized AFM tips (Pt/Ir coated, Nanosensors) provide the desired broadband and weakly frequency-dependent IR response for the nanotip antenna, as demonstrated previously.37 To access molecular vibrational modes, the nanowire is covered with an 8 nm thick PMMA film, which supports carbonyl stretch at 1730 cm–1 and the C–H stretch at 2995 cm–1, with narrow line widths of Γvib = 21 ± 3 cm–1 and Γvib = 34 ± 5 cm–1, respectively, as determined by FTIR. The near-field coupling strength between nanowire and molecular vibration is ν̅wire,vib = 47 ± 5 cm–1 with this geometry, as determined from coupling-induced splitting of IR absorption spectra. (For further details of device preparation and characterization see Supporting Information.)

The coupled nanotip and nanowire are illuminated by vertically polarized light, which is focused by an off-axis parabolic mirror (NA = 0.35). For broadband spectroscopy, we use IR s-SNOM in the implementation of synchrotron infrared nanospectroscopy (SINS) (Beamline 5.4, Advanced Light Source) spanning the multioctave range 700–5000 cm–1.37 For narrow-band IR imaging, we used a tunable quantum cascade laser (QCL, Daylight Solutions). Interferometrically detected tip-scattered near-field quadrature Re(Ẽscat) and Im(Ẽscat) are then measured by lock-in demodulation at the second harmonic of the cantilever motion as described previously37 (further experimental details and modeling of lock-in detection in Supporting Information).

Results

Tip-Tunable EIT through Bright Mode Antenna

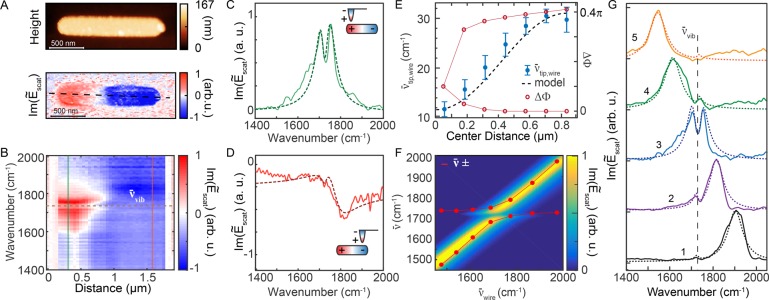
In the following experiments, we both measure and modify the coupling between nanotip, nanowire, and molecular vibration. Figure 2A shows AFM topography and the corresponding Im(Ẽscat) image of a nanowire at 1775 cm–1 near its antenna resonance. The sign of Im(Ẽscat) changes across the nanowire due to near-field interaction between nanotip and nanowire (details in Supporting Information). We measure the near-field interaction as a spatiospectral line scan of Im(Ẽscat) (Figure 2B) along the length of the nanowire (dashed line in Figure 2A). The spectrum of Im(Ẽscat) has a primarily absorptive character on the left antenna terminal with opposite sign on the right antenna terminal. Figure 2C and D show corresponding spectra at the respective locations indicated in Figure 2B. With the nanotip on the left (Figure 2C, green), Im(Ẽscat) is positive and the molecular vibration appears as a pronounced spectral dip at 1730 cm–1 (EIT). In contrast, on the right (Figure 2D, orange), Im(Ẽscat) is negative and blue-shifted.

Figure 2.

Figure 2

Open in a new tab

(A) AFM topography (top) and s-SNOM (bottom) image of Im(Ẽscat) at 1775 cm–1 as a function of nanotip position above the nanowire. Scale bars: 500 nm. (B) Spectrally resolved transect of Im(Ẽscat) along the dashed line in (A). (C, D) Im(Ẽscat) measured at nanowire terminals (solid) with corresponding fits (dashed) from locations indicated in (B). (E) Nanotip position dependent change in relative phase delay of nanotip versus nanowire excitation ΔΦ to the left and right of the nanotip center and coupling strength ν̅tip,wire from calculated fits to the Im(Ẽscat) line scan in (B). (F) Surface plot of calculated Im(Ẽscat) as a function of ν̅wire. Coupling-induced splitting of nanowire and vibrational modes shown as ν̅± (red). (G) Im(Ẽscat) spectra (solid) and corresponding calculated fits (dotted) for a series of nanowires with varying lengths.

We describe our experimental results through a quantiative model for a system of three coupled classical harmonic oscillators in an extension of previous two-oscillator models.34,35 We solve for the scattered field from the tip, Ẽscat(38)

graphic file with name ph-2018-00425x_m001.jpg 1

In this expression, the frequency-dependent optical response of each oscillator is given by gwire, gtip, and gvib, with corresponding resonance frequencies ν̅tip, ν̅wire, and ν̅vib and damping rates γtip, γwire, and γvib. We include near-field coupling between the components as the coupling strengths ν̅tip,wire and ν̅wire,vib, with ν̅tip,vib found to be negligibly small. External far-field illumination drives both the nanotip Ẽtip and nanowire with field Ẽwire and optical phase retardation between the two given by ΔΦ (details in Supporting Information).

We use eq 1 to fit to tip-scattered spectra Im(Ẽscat), with carbonyl and nanowire resonance parameters and ν̅wire,vib = 47 cm–1 from above as fixed and ν̅tip,wire and ΔΦ as the only variables. From the combined fit (red and green dashed lines), we obtain ν̅tip,wire = 30 ± 5 cm–1 for both terminals. This value of ν̅tip,wirealready approaches the coupling strength of the nanowire to the far field with associated radiative emission.

Fitting the spatiospectral line scan (Figure 2E) as a function of nanotip position, we find ν̅tip,wire varies from as small as 12 ± 2 cm–1 at the nanowire center to its maximum value at the terminals. That variation in ν̅tip,wire follows a sinusoidal behavior (black dashed line), which is in excellent agreement with the current distribution of a resonant λ/2 antenna.36Figure 2E also shows the phase difference ΔΦ of the tip and nanowire driving fields, which varies by (0.4 ± 0.1)π between the two terminals of the nanowire. It is the combination of both ν̅tip,wire and ΔΦ that accounts for the variation in sign and line shape of Im(Ẽscat), thus providing a handle to tune the optical response of the coupled system as further illustrated below.

We next vary the nanowire length in order to tune its optical resonance and control coupling within the system. Figure 2F,G show Im(Ẽscat) for a series of nanowires measured with the nanotip positioned ∼100 nm from the left edge of each nanowire. The initially small carbonyl peak at 1730 cm–1 (Figure 2G, black) increases in intensity and shifts in frequency as the nanowire is tuned, becoming a spectral hole near degeneracy (Figure 2G, blue). The entire data set can be described accurately by model calculations through variation in nanowire resonance only, with fixed parameters for previously determined coupling ν̅tip,wire as above. Shown as a surface plot in Figure 2F is the resulting dependence of Im(Ẽscat) as a function of nanowire resonance, which reveals an avoided crossing between the two peaks. From a comparison between the avoided crossing in Im(Ẽscat) with far-field measurements of the nanowire–vibration hybridized mode ν̅± (red circles), we can attribute peak shifts to the classical coupling frequency in analogy to Rabi splitting from near-field interactions between molecular vibration and the nanowire.

Phase-Tunable EIT and EIA through Dark Mode Antenna

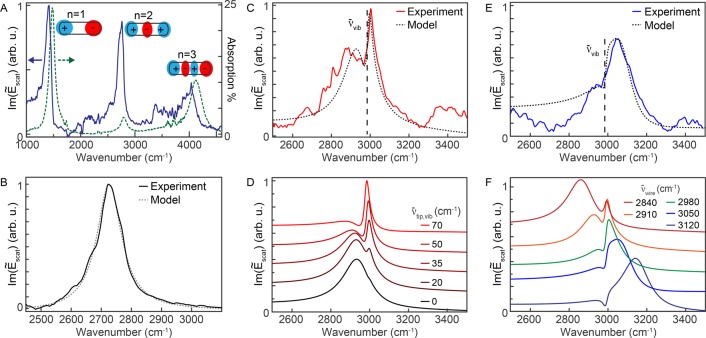
In the experiments described above, the vibrational excitation occurs primarily through the nanowire with little contribution from the tip, i.e., ν̅tip,vib ≪ ν̅wire,vib. Under these conditions the phase of the vibrational excitation cannot yet be tuned significantly by the presence of the nanotip, and thus no control over the EIT line shape is obtained. This constraint can be lifted if we further reduce the far-field radiative emission of the nanowire by employing optically forbidden overtone resonances in order to increase the contribution of the broadband nanotip excitation. Figure 3A (green dotted) shows an IR absorption spectrum with the fundamental and overtone antenna resonances n = 1, 2, and 3 for a nanowire with length 2.1 μm. The n = 2 mode at 2790 cm–1 is symmetry forbidden and only weakly driven in the far field due to a residual asymmetry in the k-vector distribution of the IR focus, while the quadrupole mode at 4130 cm–1 is again optically allowed yet weaker. In contrast, the n = 2 mode can effectively be excited by near-field coupling with the nanotip, as seen in Figure 3A, with Im{Ẽscat} (blue) of nearly equal intensity for the n = 1 and n = 2 modes. The zoomed-in spectrum (Figure 3B), Im{Ẽscat}, for n = 2 measured near the terminal of the nanowire, is fit to eq 1 with Γwire = 175 ± 15 cm–1. This corresponds to a Q-factor of 16 (i.e., larger than the Q-factor of 12–14 for n = 1), as expected with the reduced radiative damping for n = 2.

Figure 3.

Figure 3

Open in a new tab

(A) Fundamental and overtone resonances (n = 1, 2, 3) of the nanowire (dashed green line) measured by FTIR. Im{Ẽscat} (solid blue line) with nanotip positioned above the nanowire terminal. (B) Im{Ẽscat} for n = 2 response with ν̅wire= 2790 cm–1 with corresponding calculated fit (dotted) using eq 2. (C) Im{Ẽscat} for ν̅wire = 2960 cm–1 with corresponding calculated fit (dotted) to EIS using eq 2. (D) Calculated spectra show transition into vibrational EIS as a function of ν̅tip,vib. (E) Im{Ẽscat} for ν̅wire = 3100 cm–1 with corresponding fit (dotted) to EIS. (F) Calculated spectra show transition of vibrational response from EIT (spectral hole) to EIA (peak) as a function of ν̅wire nanowire resonance frequency.

Increased vibrational excitation through the nanotip and interference with excitation by the dark antenna mode of the nanowire now provide an additional means to control molecular vibrations. As an example, Figure 3C shows Im(Ẽscat) for the n = 2 mode red detuned to 2950 cm–1 with respect to the C–H alkyl stretch mode at 2995 cm–1, with the nanotip positioned on one terminal of the nanowire. The C–H vibration now appears as a narrow peak (EIA) on the blue side of the nanowire response.

We expand the coupled oscillator model shown above in eq 1 to include the increased coupling between the nanotip and molecular vibrations ν̅tip,vib, (details in Supporting Information), expressed as

graphic file with name ph-2018-00425x_m002.jpg 2

We fit the measured Im(Ẽscat) in Figure 3C using eq 2 now with ν̅tip,vib and ΔΦ as fit parameters, with (dotted lines) calculated fit for ν̅tip,vib = 35 ± 5 cm–1. Note that the peak cannot be accounted for without explicitly treating the contribution of ν̅tip,vib. Figure 3D models the transition from small values of ν̅tip,vib, where the vibration is barely observed within the broad response of the nanowire, to a sharp peak at the vibrational resonance with an EIA line shape that appears as ν̅tip,vib becomes larger. The calculated small optical response of the molecular vibration with nanowire but no nanotip (black) is in agreement with the far-field absorption measurement, in which vibrational response of the C–H remains unresolved, only becoming apparent with interaction through both ν̅wire,vib and ν̅tip,vib.

Figure 3E shows corresponding data with the dark mode nanowire resonance blue detuned to 3100 cm–1, with the C–H response only manifesting itself as a weak shoulder or dip on the low-frequency side (EIT). The corresponding fit (dotted line) yields the same value of ν̅tip,vib = 35 ± 5 cm–1 as above. The model calculations in Figure 3F show the transition when tuning the nanowire resonance frequency ν̅wire for a fixed ν̅tip,vib = 35 cm–1 from the EIT to EIA regime. For ν̅wire < ν̅vib (red), the vibration appears as a small peak, which changes into a spectral hole for ν̅wire > ν̅vib (blue). Thus, with ν̅tip,vib ≃ ν̅wire,vib achieved with the nanowire dark antenna modes only, the vibrational response is significantly greater than with either the nanotip or nanowire alone, and a qualitatively distinct spectral response arises compared to the response observed for the bright mode antenna resonance.

Lastly, we show how the relative phase through nanotip versus nanowire excitation pathways changes the spectral response of the molecular vibration itself without tuning the antenna resonance. Nanotip positioning provides an additional degree of freedom through ΔΦ to tune constructive or destructive interference between nanotip and nanowire excitation pathways. Figure 4A shows calculated Im(Ẽscat) as a function of ΔΦ, which we tune from −2/3 π to 2/3 π. We find that, through nanotip positioning alone, we can transition the optical response of the system from an EIT to EIA line shape, similarly to the nanowire length dependence above. The change in sign for the vibrational response only occurs with ν̅tip,vib ≃ ν̅wire,vib and is not apparent for ν̅tip,vib ≪ ν̅wire,vib, indicating the importance of the coupling strength for both excitation pathways in order to observe the interference.

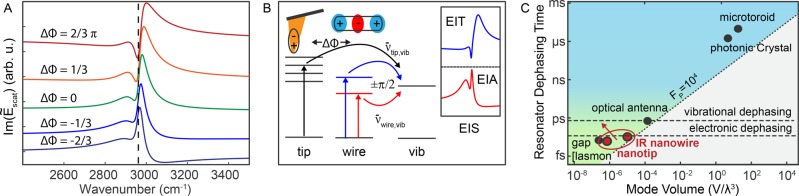
Figure 4.

Figure 4

Open in a new tab

(A) Calculated spectra showing change in EIS interference as a function of ΔΦ. (B) Schematic showing pathways for phase-delayed interference with red- and blue-detuned nanowire, additionally controlled through ΔΦ. Calculated EIS (inset) with EIA (red) and EIT (blue) line shape for constructive and destructive interference, respectively. (C) Dephasing rate and mode volume of nano- and microresonators. Dashed line indicates a Purcell factor Fp of 104 for IR resonances. Mode volume and dephasing of nanoresonators from (red) this work and (black) previous demonstrations.8,11

Discussion

Figure 4B illustrates the mechanisms leading to the observed interference in Im(Ẽscat), which occurs due to constructive or destructive interaction between the two vibrational excitation pathways through ν̅tip,vib and ν̅wire,vib. As a red-detuned nanowire resonance approaches the vibrational frequency, a narrow peak appears above the broader nanowire response (red EIA), whereas blue-detuning of the nanowire resonance leads to EIT line shapes (blue). We understand this as resulting from optical phase retardation of the nanowire, which shifts by ±π/2 on either side of the vibrational resonance, while the broadband optical response of the nanotip remains constant. Similarly, the phase difference ΔΦ between nanotip and nanowire driving fields can create an analogous change in the phase of vibrational excitation. This interference between nanotip and nanowire excitation pathways leads to both constructive (EIA) and destructive (EIT) interference in vibrational excitation, which is universally described as plasmonic electromagnetically induced scattering.

As shown in Figure 4C, the coupling rate to molecular vibrations can be understood through the Purcell factor, F ∝ Q/V, which is closely related to the dephasing time. Purcell factors for resonant metal nanotips have been shown to be as high as 106,8,39 which can be even greater than the highest values of 105 observed in photonic crystals or microtoroids.11 Although the dephasing rate of the nanotip (∼10 fs) is significantly faster than the nanowire (∼100 fs) (Figure 4C red circles), the correspondingly smaller mode volume allows for an enhanced optical density of states and Purcell factor that is comparable to that achievable in diffraction-limited optical resonators and could be further improved through either reduced damping or designs that enable greater mode volume confinement (red arrow). The extreme mode confinement of both nanowires and nanotips thus enables enhancement and interference between vibrational excitation pathways at ultrafast time scales.

Molecular vibrations offer a platform for coherent interactions with photonic states of optical antennas, with interactions lasting picoseconds or longer due to inherently long dephasing times. Hybrid states of molecular vibrations formed through coupling to optical antennas can modify the nuclear ground state potential energy surface, which has been demonstrated to potentially control the rates and outcomes of molecular reactions.40 Similarly, it is possible to affect the outcome of chemical reactions or create quantum logic gates using specific initial vibrational superposition of states in molecular systems, which are prepared by shaped femtosecond pulses.19−21 We show that it is possible to build on these demonstration experiments both to modify the nuclear potential energy surface and to prepare specific vibrational superposition of states by near-field coupling of molecular vibrations to one or more nanophotonic resonators. Our approach builds on previously reported designs of optical antennas or metamaterials with fixed geometries,1,29−32 and we achieve controllable plasmonic EIS with moleucular vibrations through both coupling and driving phase of a nanotip and nanowire with tunable near-field interactions.

With dipole-allowed bright modes of the nanowire, we already observe EIT of the vibration with modification of the nanotip–nanowire coupling, tuning ν̅tip,wire simply by nanotip positioning. Using optically dark modes of the nanowire opens interference of vibrational excitation pathways through both the nanowire ν̅wire,vib and nanotip ν̅tip,vib, leading to the classical analogues of both EIT and EIA. The coupling between the molecular vibration and the light field of the nanowire is as high as ν̅wire,vib = 47 ± 5 cm–1 (100 fs) in addition to coupling to the nanotip of as high as ν̅tip,vib = 35 ± 5 cm–1 (150 fs). Both are greater than the 20–30 cm–1 (∼250 fs) intrinsic vibrational dephasing rate, enabling the much sought-after control of vibrational dephasing pathways. The oscillating nanotip provides a means to selectively detect the scattering signal associated with the near-field interactions, and it may be possible to extend our work to utilize the distance-dependent coupling and associated interference by utilizing extremely small tapping amplitudes with few-nanometer tip–sample gaps.

These results therefore open a range of possibilities toward coherent interactions and strong coupling with molecular vibrations by utilizing molecular vibrations with large transition dipoles, antennas with long dephasing times, and tunable interactions between nanophotonic antennas. Potential applications range from single- and few-molecule femtosecond spectroscopy to nanoimaging, quantum information processing, and optical control of photocatalysis.

Acknowledgments

We acknowledge funding from the NSF Science and Technology Center on Real-Time Functional Imaging under DMR-1548924. The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under contract no. DE-AC02-05CH11231. H.A. acknowledges European Commission Horizon 2020 Grant no. FETOPEN-737071 and Consolidator Grant no. ERC-CoG-2015 VIBRANT-BIO. The authors would like to acknowledge Dordaneh Etezadi for her assistance with electron beam lithography and evaporation. We acknowledge W. E. Lewis, O. Khatib, M. C. Martin, B. Metzger, and F. Menges for stimulating discussions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsphotonics.8b00425.

  • Additional technical information including experimental methods; details and derivation of the coupled oscillator model; precharacterization measurements of the nanowire, nanotip, and molecular vibration; calculations accounting for the lock-in demodulation scheme; and additional near-field measurements (PDF)

The authors declare no competing financial interest.

Supplementary Material

ph8b00425_si_001.pdf (3.6MB, pdf)

References

  1. Arju N.; Ma T.; Khanikaev A.; Purtseladze D.; Shvets G. Optical Realization of Double-Continuum Fano Interference and Coherent Control in Plasmonic Metasurfaces. Phys. Rev. Lett. 2015, 114, 237403. 10.1103/PhysRevLett.114.237403. [DOI] [PubMed] [Google Scholar]
  2. Claudon J.; Bleuse J.; Malik N. S.; Bazin M.; Jaffrennou P.; Gregersen N.; Sauvan C.; Lalanne P.; Gérard J.-M. A highly efficient single-photon source based on a quantum dot in a photonic nanowire. Nat. Photonics 2010, 4, 174. 10.1038/nphoton.2009.287x. [DOI] [Google Scholar]
  3. Engheta N. Circuits with light at nanoscales: optical nanocircuits inspired by metamaterials. Science 2007, 317, 1698–702. 10.1126/science.1133268. [DOI] [PubMed] [Google Scholar]
  4. Safavi-Naeini A. H.; Alegre T. P. M.; Chan J.; Eichenfield M.; Winger M.; Lin Q.; Hill J. T.; Chang D. E.; Painter O. Electromagnetically induced transparency and slow light with optomechanics. Nature 2011, 472, 69–73. 10.1038/nature09933. [DOI] [PubMed] [Google Scholar]
  5. Linic S.; Aslam U.; Boerigter C.; Morabito M. Photochemical transformations on plasmonic metal nanoparticles. Nat. Mater. 2015, 14, 567–576. 10.1038/nmat4281. [DOI] [PubMed] [Google Scholar]
  6. Busson M. P.; Bidault S. Selective Excitation of Single Molecules Coupled to the Bright Mode of a Plasmonic Cavity. Nano Lett. 2014, 14, 284–288. 10.1021/nl403963y. [DOI] [PubMed] [Google Scholar]
  7. Akselrod G. M.; Argyropoulos C.; Hoang T. B.; Ciracì C.; Fang C.; Huang J.; Smith D. R.; Mikkelsen M. H. Probing the mechanisms of large Purcell enhancement in plasmonic nanoantennas. Nat. Photonics 2014, 8, 835–840. 10.1038/nphoton.2014.228. [DOI] [Google Scholar]
  8. Chikkaraddy R.; de Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Zhang Y.; Meng Q.-S.; Zhang L.; Luo Y.; Yu Y.-J.; Yang B.; Zhang Y.; Esteban R.; Aizpurua J.; Luo Y.; Yang J.-L.; Dong Z.-C.; Hou J. G. Sub-nanometre control of the coherent interaction between a single molecule and a plasmonic nanocavity. Nat. Commun. 2017, 8, 15225. 10.1038/ncomms15225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Wu X.; Gray S. K.; Pelton M. Quantum-dot-induced transparency in a nanoscale plasmonic resonator. Opt. Express 2010, 18, 23633–23645. 10.1364/OE.18.023633. [DOI] [PubMed] [Google Scholar]
  11. Agio M. Optical antennas as nanoscale resonators. Nanoscale 2012, 4, 692–706. 10.1039/C1NR11116G. [DOI] [PubMed] [Google Scholar]
  12. Derom S.; Vincent R.; Bouhelier A.; des Francs G. C. Resonance quality, radiative/ohmic losses and modal volume of Mie plasmons. EPL 2012, 98, 47008. 10.1209/0295-5075/98/47008. [DOI] [Google Scholar]
  13. Vasa P.; Wang W.; Pomraenke R.; Lammers M.; Maiuri M.; Manzoni C.; Cerullo G.; Lienau C. Real-time observation of ultrafast Rabi oscillations between excitons and plasmons in metal nanostructures with J-aggregates. Nat. Photonics 2013, 7, 128. 10.1038/nphoton.2012.340. [DOI] [Google Scholar]
  14. Ambjörnsson T.; Mukhopadhyay G.; Apell S. P.; Käll M. Resonant coupling between localized plasmons and anisotropic molecular coatings in ellipsoidal metal nanoparticles. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 085412. 10.1103/PhysRevB.73.085412. [DOI] [Google Scholar]
  15. Adato R.; Artar A.; Erramilli S.; Altug H. Engineered Absorption Enhancement and Induced Transparency in Coupled Molecular and Plasmonic Resonator Systems. Nano Lett. 2013, 13, 2584–2591. 10.1021/nl400689q. [DOI] [PubMed] [Google Scholar]
  16. Rodrigo D.; Limaj O.; Janner D.; Etezadi D.; García de Abajo F. J.; Pruneri V.; Altug H.. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. 10.1126/science.aab2051. [DOI] [PubMed] [Google Scholar]
  17. Ropers C.; Neacsu C. C.; Elsaesser T.; Albrecht M.; Raschke M. B.; Lienau C. Grating-Coupling of Surface Plasmons onto Metallic Tips: A Nanoconfined Light Source. Nano Lett. 2007, 7, 2784–2788. 10.1021/nl071340m. [DOI] [PubMed] [Google Scholar]
  18. Alonso-González P.; Albella P.; Schnell M.; Chen J.; Huth F.; García-Etxarri A.; Casanova F.; Golmar F.; Arzubiaga L.; Hueso L.; Aizpurua J.; Hillenbrand R. Resolving the electromagnetic mechanism of surface-enhanced light scattering at single hot spots. Nat. Commun. 2012, 3, 684. 10.1038/ncomms1674. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kubel M.; Siemering R.; Burger C.; Kling N. G.; Li H.; Alnaser A.; Bergues B.; Zherebtsov S.; Azzeer A.; Ben-Itzhak I.; Moshammer R.; de Vivie-Riedle R.; Kling M. Steering Proton Migration in Hydrocarbons Using Intense Few-Cycle Laser Fields. Phys. Rev. Lett. 2016, 116, 193001. 10.1103/PhysRevLett.116.193001. [DOI] [PubMed] [Google Scholar]
  20. Zhai L.; Zheng Y. Intramolecular energy transfer, entanglement, and decoherence in molecular systems. Phys. Rev. A: At., Mol., Opt. Phys. 2013, 88, 012504. 10.1103/PhysRevA.88.012504. [DOI] [Google Scholar]
  21. Tesch C. M.; de Vivie-Riedle R. Quantum Computation with Vibrationally Excited Molecules. Phys. Rev. Lett. 2002, 89, 157901. 10.1103/PhysRevLett.89.157901. [DOI] [PubMed] [Google Scholar]
  22. Long J. P.; Simpkins B. S. Coherent Coupling between a Molecular Vibration and Fabry–Perot Optical Cavity to Give Hybridized States in the Strong Coupling Limit. ACS Photonics 2015, 2, 130–136. 10.1021/ph5003347. [DOI] [Google Scholar]
  23. Memmi H.; Benson O.; Sadofev S.; Kalusniak S. Strong Coupling between Surface Plasmon Polaritons and Molecular Vibrations. Phys. Rev. Lett. 2017, 118, 126802. 10.1103/PhysRevLett.118.126802. [DOI] [PubMed] [Google Scholar]
  24. Fromm D. P.; Sundaramurthy A.; Schuck P. J.; Kino G.; Moerner W. E.. Gap-Dependent Optical Coupling of Single ‘‘Bowtie’’ Nanoantennas Resonant in the Visible. Nano Lett. 2004, 4, 957–961. 10.1021/nl049951r. [DOI] [Google Scholar]
  25. Panaro S.; Nazir A.; Liberale C.; Das G.; Wang H.; De Angelis F.; Proietti Zaccaria R.; Di Fabrizio E.; Toma A. Dark to Bright Mode Conversion on Dipolar Nanoantennas: A Symmetry-Breaking Approach. ACS Photonics 2014, 1, 310–314. 10.1021/ph500044w. [DOI] [Google Scholar]
  26. Demichel O.; Petit M.; Colas des Francs G.; Bouhelier A.; Hertz E.; Billard F.; de Fornel F.; Cluzel B. Selective excitation of bright and dark plasmonic resonances of single gold nanorods. Opt. Express 2014, 22, 15088–15096. 10.1364/OE.22.015088. [DOI] [PubMed] [Google Scholar]
  27. Fleischhauer M.; Imamoglu A.; Marangos J. P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. 10.1103/RevModPhys.77.633. [DOI] [Google Scholar]
  28. Zhang S.; Genov D. A.; Wang Y.; Liu M.; Zhang X. Plasmon-Induced Transparency in Metamaterials. Phys. Rev. Lett. 2008, 101, 047401. 10.1103/PhysRevLett.101.047401. [DOI] [PubMed] [Google Scholar]
  29. Taubert R.; Hentschel M.; Kästel J.; Giessen H. Classical Analog of Electromagnetically Induced Absorption in Plasmonics. Nano Lett. 2012, 12, 1367–1371. 10.1021/nl2039748. [DOI] [PubMed] [Google Scholar]
  30. Sun Y.; Yang Y.; Chen H.; Zhu S. Dephasing-Induced Control of Interference Nature in Three-Level Electromagnetically Induced Tansparency Systems. Sci. Rep. 2015, 5, 16370. 10.1038/srep16370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Osley E. J.; Biris C. G.; Thompson P. G.; Jahromi R. R. F.; Warburton P. A.; Panoiu N. C. Fano Resonance Resulting from a Tunable Interaction between Molecular Vibrational Modes and a Double Continuum of a Plasmonic Metamolecule. Phys. Rev. Lett. 2013, 110, 087402. 10.1103/PhysRevLett.110.087402. [DOI] [PubMed] [Google Scholar]
  32. Zhang X.; Xu N.; Qu K.; Tian Z.; Singh R.; Han J.; Agarwal G. S.; Zhang W. Electromagnetically induced absorption in a three-resonator metasurface system. Sci. Rep. 2015, 5, 10737. 10.1038/srep10737. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Liu N.; Langguth L.; Weiss T.; Kästel J.; Fleischhauer M.; Pfau T.; Giessen H. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nat. Mater. 2009, 8, 758–762. 10.1038/nmat2495. [DOI] [PubMed] [Google Scholar]
  34. Joe Y. S.; Satanin A. M.; Kim C. S. Classical analogy of Fano resonances. Phys. Scr. 2006, 74, 259–266. 10.1088/0031-8949/74/2/020. [DOI] [Google Scholar]
  35. Souza J. A.; Cabral L.; Oliveira R. R.; Villas-Boas C. J. Electromagnetically-induced-transparency-related phenomena and their mechanical analogs. Phys. Rev. A: At., Mol., Opt. Phys. 2015, 92, 023818. 10.1103/PhysRevA.92.023818. [DOI] [Google Scholar]
  36. Olmon R. L.; Rang M.; Krenz P. M.; Lail B. A.; Saraf L. V.; Boreman G. D.; Raschke M. B. Determination of Electric-Field, Magnetic-Field, and Electric-Current Distributions of Infrared Optical Antennas: A Near-Field Optical Vector Network Analyzer. Phys. Rev. Lett. 2010, 105, 167403. 10.1103/PhysRevLett.105.167403. [DOI] [PubMed] [Google Scholar]
  37. Bechtel H. A.; Muller E. A.; Olmon R. L.; Martin M. C.; Raschke M. B. Ultrabroadband infrared nanospectroscopic imaging. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 7191–7196. 10.1073/pnas.1400502111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Kravtsov V.; Berweger S.; Atkin J. M.; Raschke M. B. Control of Plasmon Emission and Dynamics at the Transition from Classical to Quantum Coupling. Nano Lett. 2014, 14, 5270–5275. 10.1021/nl502297t. [DOI] [PubMed] [Google Scholar]
  39. Park K.-D.; Jiang T.; Clark G.; Xu X.; Raschke M. B. Radiative control of dark excitons at room temperature by nano-optical antenna-tip Purcell effect. Nat. Nanotechnol. 2018, 13, 59–64. 10.1038/s41565-017-0003-0. [DOI] [PubMed] [Google Scholar]
  40. Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying chemical landscapes by coupling to vacuum fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ph8b00425_si_001.pdf (3.6MB, pdf)

Articles from ACS Photonics are provided here courtesy of American Chemical Society

RESOURCES