Abstract
In this paper a numerical study is presented that concentrates on the influence of the interface roughness that develops during plastic deformation of a metal, on the work of adhesion and on the change of interface energy upon contact with a glassy polymer. The polymer coating is described with a constitutive law that mimics the behavior of Poly-Ethylene Terephthalate. It includes an elastic part, a yield stress, softening and hardening with increasing strains. For the interface between the metal and the polymer a mixed-mode (mode I and II) stress-separation law is applied that defines the interface energy and an interaction length scale. At the onset of deformation the surface of the substrate has a self-affine roughness characterized by the so-called Hurst exponent, a correlation length and an rms roughness amplitude, that evolves as a function of increasing strain. The findings are the following: the interface energy decreases until the strain at yield of the polymer coating. Interestingly, after yielding as the polymer starts to soften macroscopically, the decreasing average stress levels result in partial recovery of the interface energy at the interface. At higher strains, when macroscopic hardening develops the recovery of the interface stops and the interface energy decreases. The effect of coating thickness is discussed as well as the physical relevance of various model parameters.
Keywords: Shear Band, Interface Energy, Polymer Coating, Cohesive Zone, Hurst Exponent
Introduction
Polymer-coated metal sheets are rather recent products of steel manufacturers that are used in various applications in food and automotive industry. In the manufacturing process severe plastic deformation is used to obtain the final shapes of the end products. A drawback of plastic deformation is the intrinsic roughening of the surface of the metal caused by dislocation activity. This paper concentrates on the implications of the roughening process for the mechanical properties of the combined metal–polymer system. Clearly the subject is closely related to that of a large number of papers discussing the impact of roughness on the work of adhesion W, e.g [1–7]. However, this paper sets itself apart from earlier research because it emphasizes on: First, the evolution of roughness of the metal as a mechanical loading mechanism of a metal–polymer interface; second, the coupling between the metal substrate and the polymer coating using a stress-separation law; and third, the polymer behavior including yielding, softening and hardening. In the following these points are briefly discussed in the framework of the current understanding.
During uniaxial deformation, a metal surface roughens. A height-height correlation function C(r,ɛ) of the interface may be defined as [8]
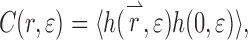 |
1 |
where 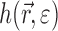 is the height of the surface at a strain
is the height of the surface at a strain 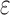 and at the position
and at the position 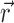 . It has been shown [9, 10] that for all strains
. It has been shown [9, 10] that for all strains 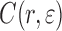 of a surface of a uniaxially deformed metal can be approximated by:
of a surface of a uniaxially deformed metal can be approximated by:
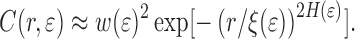 |
2 |
Equation 2 describes the surface roughness in a statistical sense with three parameters: the rms roughness amplitude w above a certain lateral correlation length ξ, and a Hurst exponent H characterizing the self-affine geometry below ξ. For a uniaxially deforming metal these surface parameters are a function of the applied strain 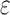 . From experiments parameterized fits for
. From experiments parameterized fits for 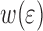 ,
, 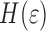 and
and 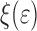 may be determined (see also [9, 11]).
may be determined (see also [9, 11]).
The topics addressed here are the work of adhesion W between such a self-affine roughening metal–polymer system, the dependence of W on the parameters w, H and ξ, and the evolution of W as a function of uniaxial strain 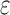 .
.
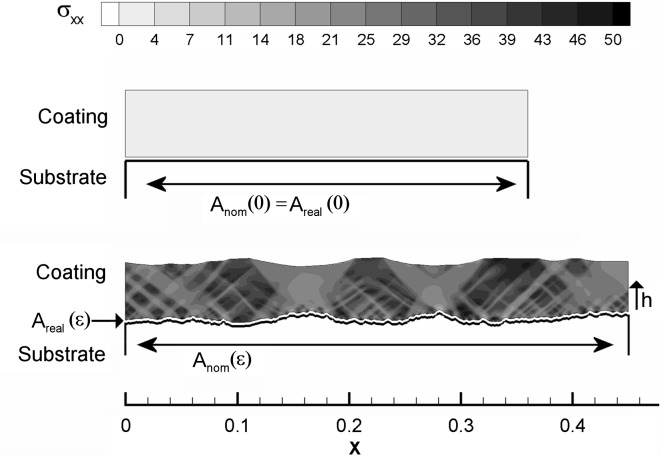
Figure 1 illustrates the problem under consideration, and introduces a number of relevant quantities. It shows a metal and polymer in contact across an interface at zero strain, and also at a higher strain value. The area of contact increases upon straining, the average stress in the polymer increases, and roughness develops at the interface, which is accompanied by stress concentrations. These stress concentrations can lead to local delamination. Also, note the appearance of shear bands in the polymer, caused by the intrinsic softening that characterizes the post-yield deformation behavior of typical glassy polymers. The impact of all of these phenomena on the work of adhesion W is the subject of this paper.
Fig. 1.
Schematic representation of some model parameters at two stages in the deformation process (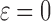 and
and 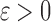 )
)
For a metal (m) and a polymer (p) coming into contact across an area A 0 the work of adhesion W per unit area is defined as:
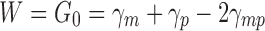 |
3 |
where γm and γp represent the surface energies and γ pm the interface energy. During uniaxial deformation at a strain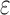 the nominal (projected) contact area A
nom is given by:
the nominal (projected) contact area A
nom is given by:
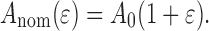 |
4 |
Due to roughening of the metal surface the real contact area A
real at a strain 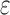 is larger than A
nom(
is larger than A
nom(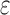 ) and is given by
) and is given by
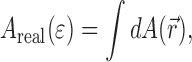 |
5 |
where the integral is taken over all positions 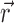 on the nominal surface.
on the nominal surface.
The work of adhesion 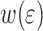 at a strain
at a strain 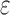 can be approximated by:
can be approximated by:
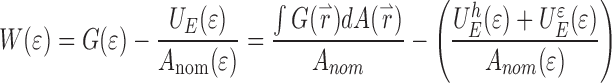 |
6 |
here 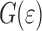 represents all surface and interface terms and
represents all surface and interface terms and 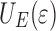 is the elastic energy stored in the bulk of the materials. The elastic energy is split in two terms:
is the elastic energy stored in the bulk of the materials. The elastic energy is split in two terms:
First, 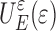 represents the average energy stored in a deformed block of material in case the surface does not roughen and may be approximated by
represents the average energy stored in a deformed block of material in case the surface does not roughen and may be approximated by
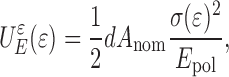 |
7 |
where d is the layer thickness, 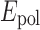 is the Young’s modulus of the polymer. Due to the substantial difference of the elastic moduli the metal can be regarded as a rigid solid and is omitted from the energy balance.
is the Young’s modulus of the polymer. Due to the substantial difference of the elastic moduli the metal can be regarded as a rigid solid and is omitted from the energy balance.
Second, 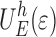 represents the elastic energy contribution of the roughening interface.
represents the elastic energy contribution of the roughening interface.
The term 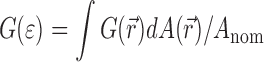 takes into account the two competing effects of roughening on the interface energy, on the one hand an increase in real contact area, and on the other hand local delamination caused by the stresses acting on the interface.
takes into account the two competing effects of roughening on the interface energy, on the one hand an increase in real contact area, and on the other hand local delamination caused by the stresses acting on the interface.
So far, the interface was described in terms of energies only. In reality stresses are transferred across the interface until delamination occurs, see Fig. 1. The interface can be described in terms of a stress-separation law (e.g 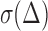 with
with 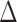 the displacement at the interface. Traction and shear stresses, i.e.
the displacement at the interface. Traction and shear stresses, i.e. 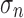 , and
, and 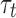 respectively, and resulting displacements (
respectively, and resulting displacements (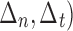 may have components normal and tangential to the interface. The work of adhesion W enters in a natural way as
may have components normal and tangential to the interface. The work of adhesion W enters in a natural way as
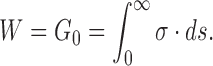 |
8 |
(short cut of: 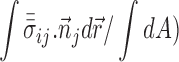
G 0 again contains all surface and interface terms. One can now also define
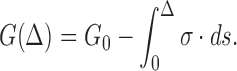 |
9 |
In a physical sense 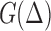 represents the remaining work needed to separate two surfaces in the presence of a pre-applied stress. In the case of a roughening surface as considered here, the stresses at a certain position stem from the height differences, e.g. areas of the interface between two roughness peaks experience a local opening stress.
represents the remaining work needed to separate two surfaces in the presence of a pre-applied stress. In the case of a roughening surface as considered here, the stresses at a certain position stem from the height differences, e.g. areas of the interface between two roughness peaks experience a local opening stress.
The separate contributions of interface and bulk to the work of adhesion and their dependence on the strain are a key issue. In the following our numerical approach is described that takes into account all the aforementioned features.
Model description
The numerical model describes the interface between steel and PET and it will capture the following three aspects: Polymer deformation; roughening of the metal surface; interaction between metal and polymer across the surface. The representation of the PET layer is a finite element model built from quadrilaterals representing a size of 1 × 1 μm2 [12, 13]. The initial length of the system is 2049 μm and the initial thickness h of the PET film is 60 μm unless mentioned otherwise. In the calculations the ‘metal’ substrate is taken to be rigid. This is a reasonable approximation, since the elastic modulus of steel is typical of the order of 200 GPa and therefore the thin polymer coating is expected to have little effect on its roughening behavior.
Polymer constitutive behavior
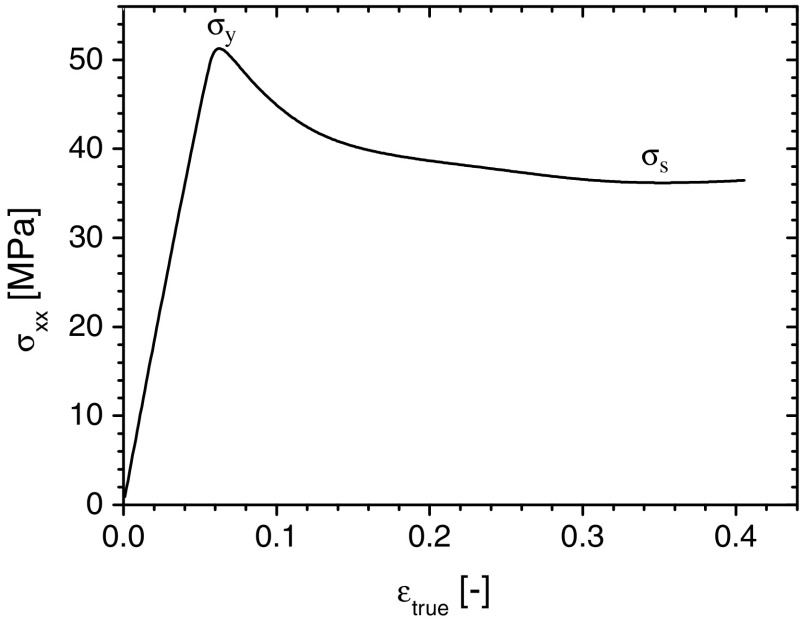
The constitutive behavior used for the polymer is described in [12] and the response and values of the parameters are given in the caption of Fig. 2. Here the curve is plotted as a function of the true strain 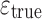 , which is defined as
, which is defined as 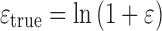 . The regime of the polymer is purely elastic and after yielding the polymer starts to soften. In this regime shear bands occur as a result of localization. Eventually, hardening (onset just visible in the figure) will stop the localization.
. The regime of the polymer is purely elastic and after yielding the polymer starts to soften. In this regime shear bands occur as a result of localization. Eventually, hardening (onset just visible in the figure) will stop the localization.
Fig. 2.
Stress–strain relationship for PET, using the following values as defined in [12]: E/s 0 = 7.76; s ss/s 0 = 0.774; As 0/T = 91.99; h/s 0 = 3.90; α = 0.25; N = 12.602; C R/s 0 = 0.132
Roughening of the metal surface
One of the simplifications in the approach proposed here is to parameterize the roughness evolution of a metal surface as a function of strain, and to assume that the roughness evolution at a polymer–metal interface is essentially identical to this because of the large difference in elastic moduli of typical metals (∼100 s of GPa) and glassy polymers (∼1 GPa).
The surface morphology for as received rolled stainless steel (with an averaged grain size equal to 11.7 μm and a plate thickness of 500 μm) was determined experimentally with confocal microscopy [9] during uniaxial tensile experiments and characterized by the following empirical relationships as a function of strain  :
:
 |
10 |
with  μm, C
1 = 6.1 and
μm, C
1 = 6.1 and  μm. The Hurst exponent H was found to be insensitive to strain and is taken to be constant
μm. The Hurst exponent H was found to be insensitive to strain and is taken to be constant
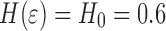 . The correlation length ξ increases with the strain in the tensile direction. A qualitatively similar behavior was also found for other materials (Fe, Al, [10]). From experimental results least square fits to Eq. 10 were performed [9]. A recursive refinement algorithm [11] was used to simulate surfaces with the characteristics described by Eq. 10. A detailed example of the roughness evolution in the numerical model is displayed in [9], a few stages of which are apparent from Fig. 3.
. The correlation length ξ increases with the strain in the tensile direction. A qualitatively similar behavior was also found for other materials (Fe, Al, [10]). From experimental results least square fits to Eq. 10 were performed [9]. A recursive refinement algorithm [11] was used to simulate surfaces with the characteristics described by Eq. 10. A detailed example of the roughness evolution in the numerical model is displayed in [9], a few stages of which are apparent from Fig. 3.
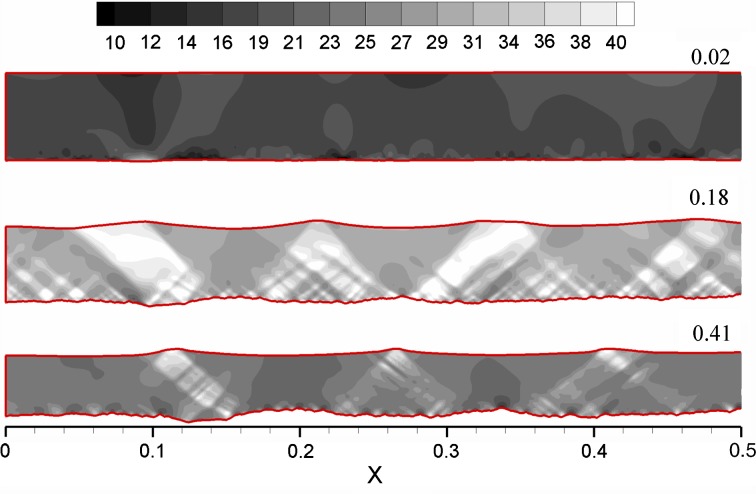
Fig. 3.
Typical results of stress fields in the PET caused by strain induced roughening of the substrate, showing σxx in the PET. Three cases are shown for 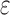 in the elastic (top), softening (middle) and hardening (bottom) region of the polymer stress–strain curve
in the elastic (top), softening (middle) and hardening (bottom) region of the polymer stress–strain curve
Interaction between metal and polymer
In finite element models, stress-separation laws are commonly known as “cohesive zones” and different kinds have been discussed in the literature. In the numerical calculations presented here the interface was implemented as a rate-independent mixed-mode cohesive zone of the type described in [14]. This type defines coupled stress separation laws  (tractions) and
(tractions) and 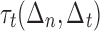 (shear stresses) at the interface, with
(shear stresses) at the interface, with 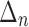 and
and 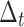 coordinates normal and parallel to the interface, respectively. The distance
coordinates normal and parallel to the interface, respectively. The distance 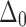 is defined as the point at which the opening stress
is defined as the point at which the opening stress 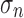 attains its maximum value
attains its maximum value 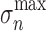 . Unless stated otherwise the parameters used for the cohesive zone in this paper are: normal-to-shear stress ratio
. Unless stated otherwise the parameters used for the cohesive zone in this paper are: normal-to-shear stress ratio 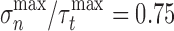 , interface energy
, interface energy 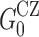 = 30 J/m2, working distance
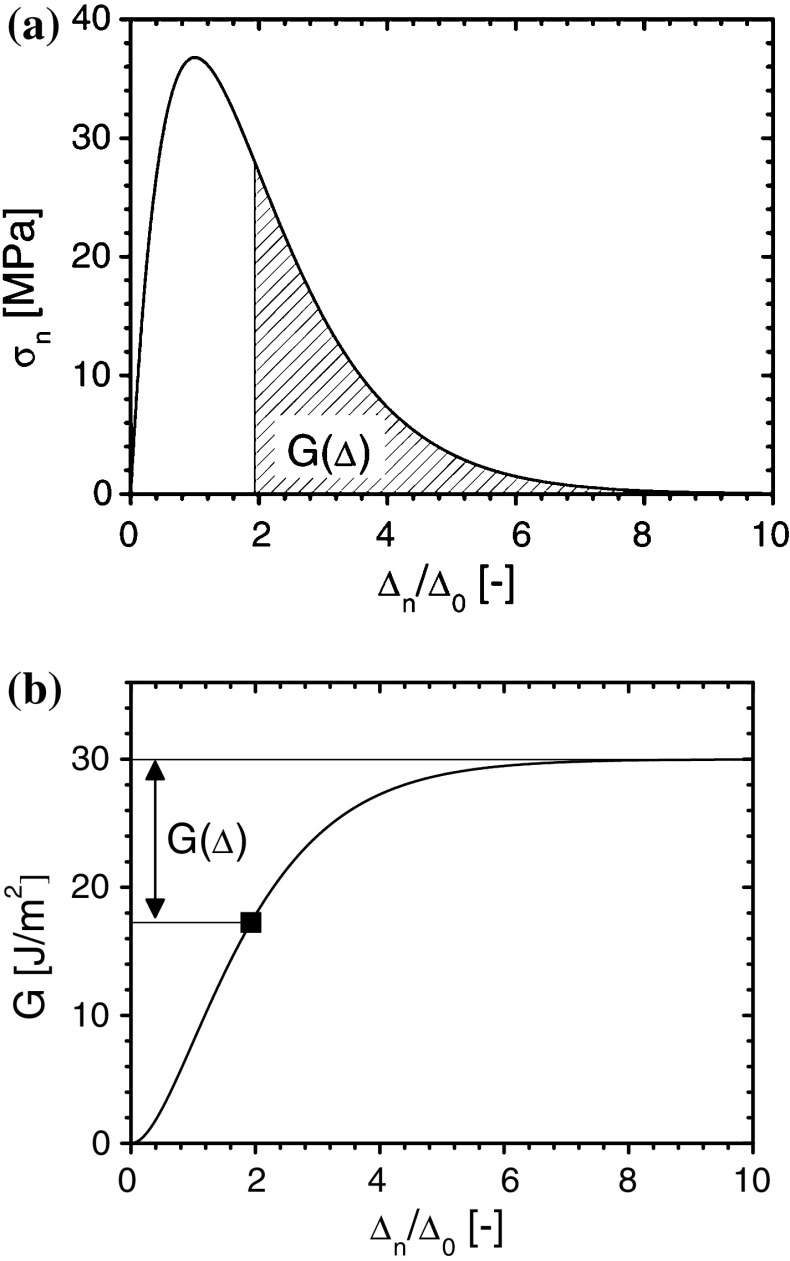
= 30 J/m2, working distance 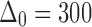 nm and σmaxn = 36.8 MPa. To illustrate the key features of the cohesive zone
nm and σmaxn = 36.8 MPa. To illustrate the key features of the cohesive zone 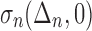 is shown in Fig. 4.
is shown in Fig. 4.
Fig. 4.
Characteristics of the cohesive zone (a) σn(Δn,0) plotted as function of Δn/Δ0 (b)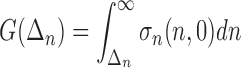 plotted as function of Δn/Δ0
plotted as function of Δn/Δ0
For each interface element the surface area and stress state are calculated. The interface energy can be calculated analogous to Eq. 9 as:
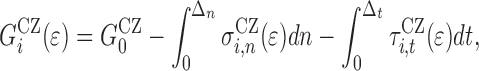 |
11 |
where G
CZ0 refers to G
0 of the cohesive zone (see Eq. 8), 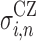 is the stress normal and
is the stress normal and 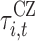 the stress parallel to the interface element i. In this work we are interested in
the stress parallel to the interface element i. In this work we are interested in 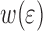 and therefore in
and therefore in 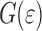 and
and 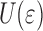 . In the context of the numerical model we define
. In the context of the numerical model we define 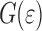 as follows:
as follows:
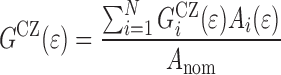 |
12 |
with i running over the discrete elements in the model, 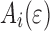 and
and 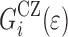 are the surface area and the interface energy of the i-th element, respectively.
are the surface area and the interface energy of the i-th element, respectively.
Since all energies in the following are derived from the numerical model the superscript CZ will be dropped.
Simulation of deformation
In the calculations the composite is loaded in uniaxial plane strain up to strains of 50% (in steps of 0.1%). At each step the following boundary conditions (see Fig. 5) are imposed on the PET and the cohesive zone. At the side of the PET at x = 0 displacements along x are imposed while displacements along y are free. Similar boundary conditions are applied at x = L(ɛ). Along the interface displacements in the substrate are constrained in all directions. Displacements in the polymer are not restricted and coupled to those in the substrate by the stress-separation laws incorporated in the cohesive zone. At each strain step the positions of the substrate nodes are updated in x (to reflect the increase in strain) and y (to reflect the increase in roughness).
Fig. 5.
Schematic representation of the boundary conditions at low strain (gray) and higher strain (black)
Results
A typical result of the calculation is shown in Fig. 3. The figure shows 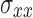 distribution in the PET at strains for three different stages depicted in Fig. 2: elastic I, softening II, and hardening III. Clearly visible are localized shear bands and roughening of the polymer surface during the softening and hardening regime.
distribution in the PET at strains for three different stages depicted in Fig. 2: elastic I, softening II, and hardening III. Clearly visible are localized shear bands and roughening of the polymer surface during the softening and hardening regime.
A series of calculations was carried out in which the parameters describing the roughness and the parameters describing the cohesive zone were varied. For these calculations 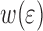 and
and  were studied and are discussed below.
were studied and are discussed below.
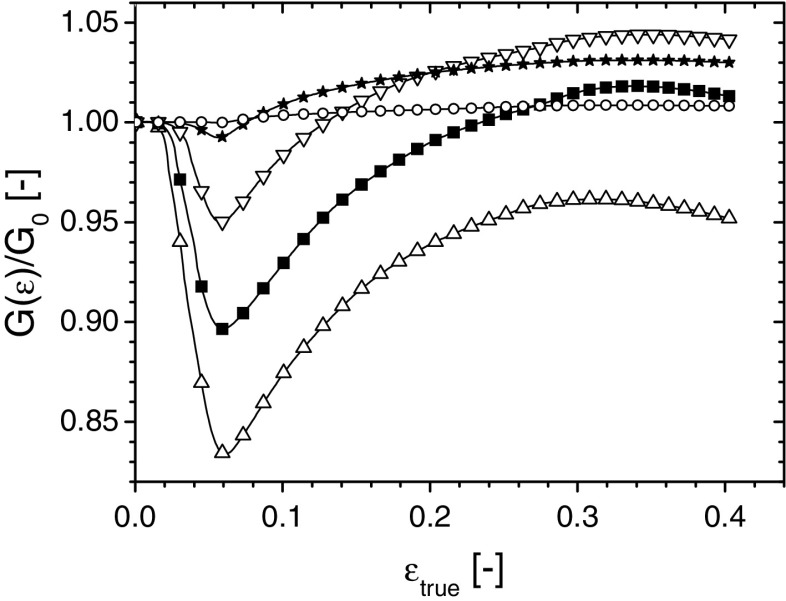
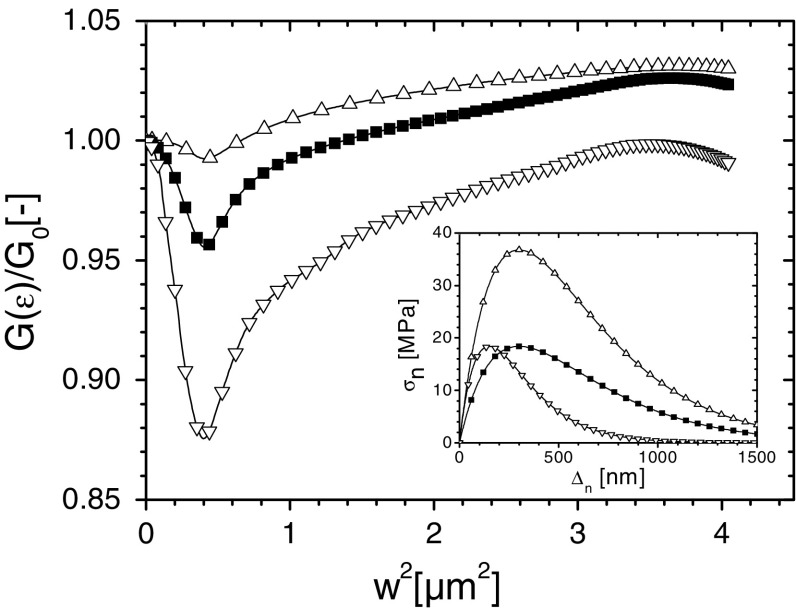
General characteristics of G(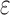 )
)
All graphs of 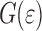 display a number of characteristic features. These will be discussed using Fig. 6 that shows the dependence of
display a number of characteristic features. These will be discussed using Fig. 6 that shows the dependence of 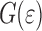 on
on 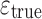 . (Note that in the figures
. (Note that in the figures
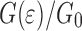 has been plotted, rather than
has been plotted, rather than
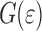 . Three stages can be distinguished.
. Three stages can be distinguished. 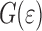 decreases initially, approximately up to
decreases initially, approximately up to 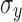 (stage I) and then starts to increase (stage II), after which it passes through a maximum and decreases again (stage III). Depending on
(stage I) and then starts to increase (stage II), after which it passes through a maximum and decreases again (stage III). Depending on 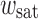 the maximum may be either below or above G
0.
the maximum may be either below or above G
0.
Fig. 6.
Normalized interface energy 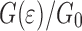 as function of
as function of 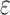 for different values of
for different values of 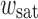 :
:  w
sat = 1.1 μm; ★ w
sat = 2.2 μm;
w
sat = 1.1 μm; ★ w
sat = 2.2 μm; 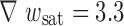 μm;
μm; 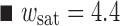 μm and
μm and 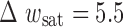 μm
μm
The physical interpretation of the three stages is as follows: in stage I, “delamination” due to the loading of interface by the coating dominates and 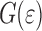 decreases. In stage II the area increase due to roughening dominates because during this stage the stress in polymer is limited by
decreases. In stage II the area increase due to roughening dominates because during this stage the stress in polymer is limited by 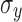 . Finally, in stage III the polymer starts to work harden, the load at the interface increases and delamination proceeds. This effect levels off because of the saturation of the roughness amplitude with increasing strain. The interpretation of the three stages is confirmed in Fig. 7a and b showing the effects of delamination and area increase respectively.
. Finally, in stage III the polymer starts to work harden, the load at the interface increases and delamination proceeds. This effect levels off because of the saturation of the roughness amplitude with increasing strain. The interpretation of the three stages is confirmed in Fig. 7a and b showing the effects of delamination and area increase respectively.
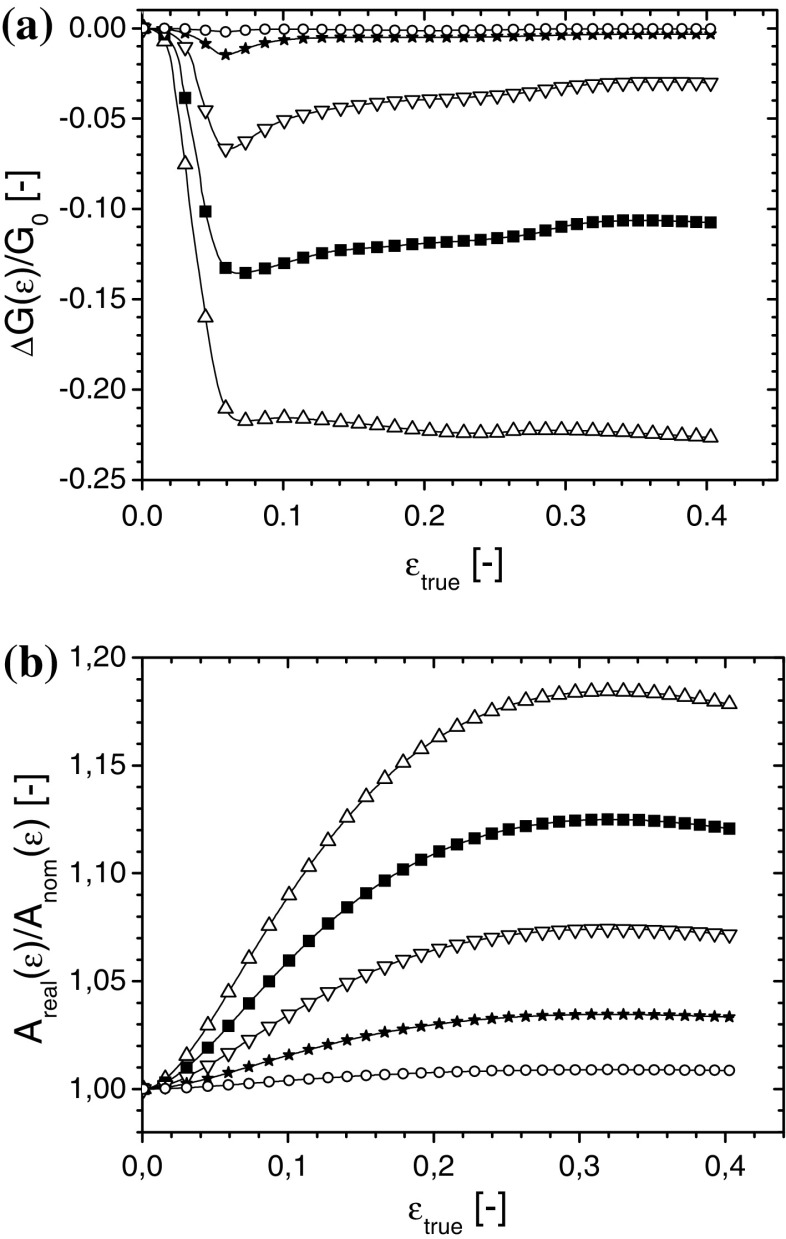
Fig. 7.
Normalized interface energy 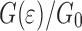 (same data as in Fig. 6) separated into the contribution (a)
(same data as in Fig. 6) separated into the contribution (a) 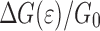 and (b)
and (b) 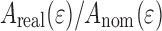
Here it is useful to split the effect of the roughness and the increase in surface area (as shown in Fig. 7a and b):
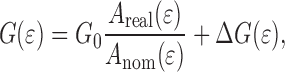 |
13 |
where the effect of the roughness on the change of interface energy upon contact is
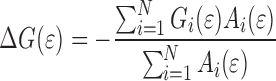 |
14 |
and the surface area increase effect is
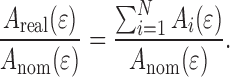 |
15 |
Figure 7a shows the reduction in interface energy as indicated in Eq. 14. This effectively removes the effect of increasing area and gives an indication of the decrease in
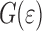 caused by the loading of the interface. At the onset
caused by the loading of the interface. At the onset
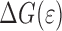 decreases rapidly (approximately linearly with w
2). At the yield point of the polymer the rate of decrease of
decreases rapidly (approximately linearly with w
2). At the yield point of the polymer the rate of decrease of
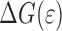 reduces considerably, and in fact for low
reduces considerably, and in fact for low 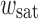 the interface partly recovers due to the softening of the polymer layer, and the reduced stresses acting on the interface as a cause of that.
the interface partly recovers due to the softening of the polymer layer, and the reduced stresses acting on the interface as a cause of that.
Figure 7b shows
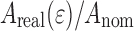 which exhibits a monotonous increase due to roughening up to a maximum where the increase in nominal area starts dominating the effects of the increase of
which exhibits a monotonous increase due to roughening up to a maximum where the increase in nominal area starts dominating the effects of the increase of 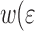 ).
).
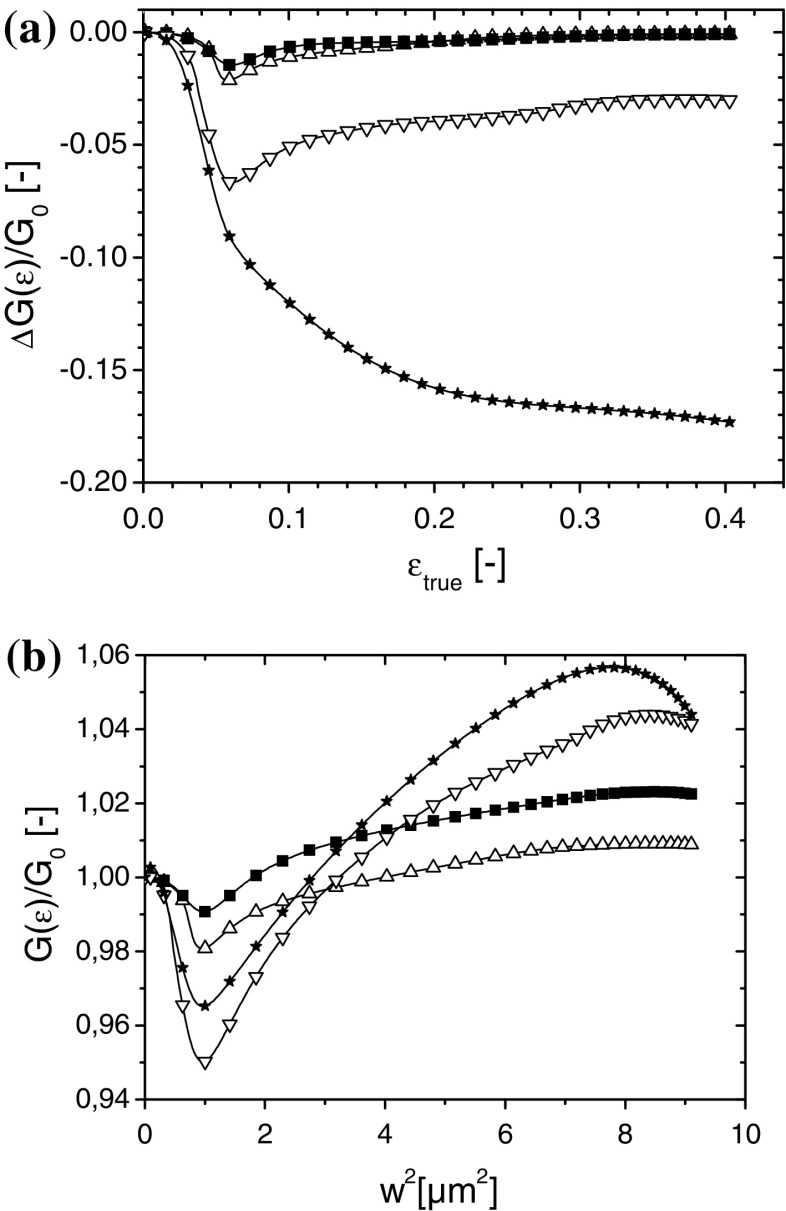
G(ɛ) as function of w, H and 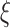
In the previous section the general behavior of 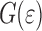 was illustrated, and curves at different
was illustrated, and curves at different 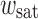 were presented. The situation remains roughly the same if we change other parameters describing the self-affinity, the correlation length
were presented. The situation remains roughly the same if we change other parameters describing the self-affinity, the correlation length 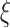 and the Hurst exponent H. A low value of H results in rapid fluctuation on a short length scale, and this leads to a larger decrease in
and the Hurst exponent H. A low value of H results in rapid fluctuation on a short length scale, and this leads to a larger decrease in 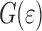 at low strains (Fig. 8a) and to a continuing delamination above the yield point. However, the overall effect is still compensated by the faster increase in surface area (Fig. 8b).
at low strains (Fig. 8a) and to a continuing delamination above the yield point. However, the overall effect is still compensated by the faster increase in surface area (Fig. 8b).
Fig. 8.
(a) ΔG(ε)/G
0 as a function of 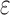 , and (b)
, and (b)
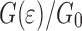 as a function of w
2. For all curves
as a function of w
2. For all curves  μm. Hurst exponents H: ★ H = 0.4;
μm. Hurst exponents H: ★ H = 0.4; 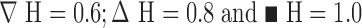
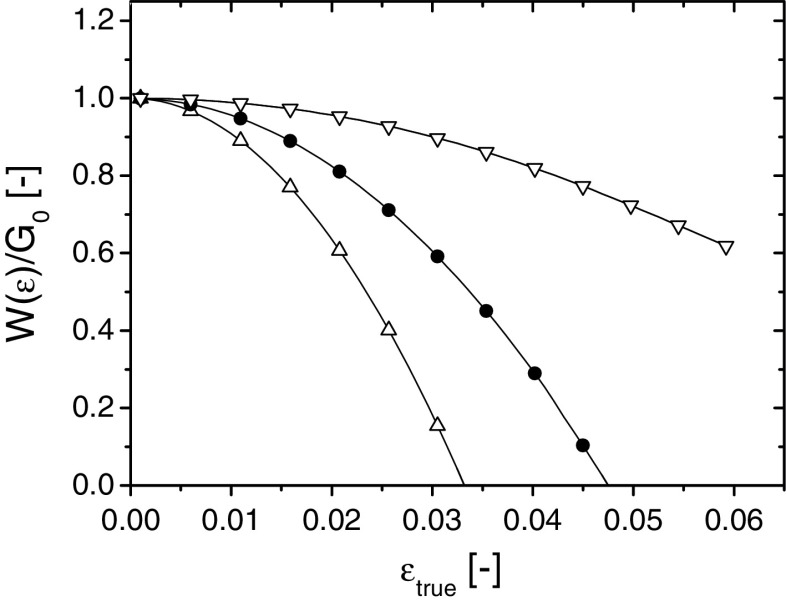
W(ɛ) as a function of layer thickness
We note that the effects shown in the previous section do not take into account the elastic energy stored in the layer. Figure 9 shows  , similar to Figs. 6 and 7b for layers of different thickness. For all layer thickness the behavior of G is qualitatively similar. Figure 10 shows
, similar to Figs. 6 and 7b for layers of different thickness. For all layer thickness the behavior of G is qualitatively similar. Figure 10 shows 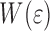 up to the strain at yielding.
up to the strain at yielding. 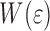 equal to zero indicates that the interface becomes metastable to fracture. Clearly,
equal to zero indicates that the interface becomes metastable to fracture. Clearly, 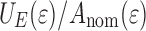 dominates
dominates 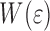 . For the 10 μm coating
. For the 10 μm coating 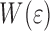 decreases to a value of about 0.6 at the yield strain, indicating that this coating is stable against delamination.
decreases to a value of about 0.6 at the yield strain, indicating that this coating is stable against delamination. 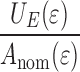 increases linearly with d, and for the coatings of 30 μm and of 60 μm the energy
increases linearly with d, and for the coatings of 30 μm and of 60 μm the energy 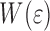 turns out to be smaller than zero and therefore these situations are metastable.
turns out to be smaller than zero and therefore these situations are metastable.
Fig. 9.
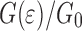 as a function of w
2. For all curves
as a function of w
2. For all curves 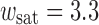 μm. Thickness h:
μm. Thickness h: 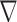 h = 10 μm; • h = 30 μm and Δ h = 60 μm
h = 10 μm; • h = 30 μm and Δ h = 60 μm
Fig. 10.
Work of adhesion W of the system for different coating thickness h: ∇ h = 10 μm; • h = 30 μm and Δ h = 60 μm (same dataset as Fig. 9)
Discussion
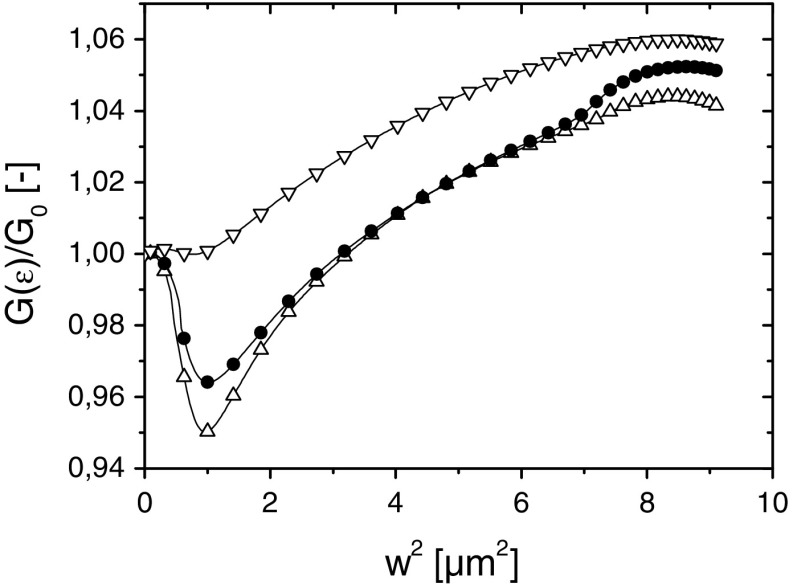
A relevant point of discussion is the influence of the cohesive zone on the results. In Fig. 11 the results for three different parameter sets describing the cohesive zone (in the inset) are shown. Regardless of the parameter values of the cohesive zone the same qualitative behavior of the 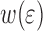 is found, i.e. weakening, recovery and renewed weakening.
is found, i.e. weakening, recovery and renewed weakening.
Fig. 11.
Normalized effective interface energy
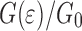 as a function of the squared rms roughness (
as a function of the squared rms roughness (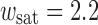 ) for different G
0 and working distance Δ0:
) for different G
0 and working distance Δ0: 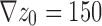 nm,
nm, 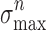 = 18.4 MPa and G
0 = 7.5 J/m2;
= 18.4 MPa and G
0 = 7.5 J/m2; 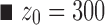 nm,
nm, 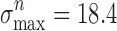 MPa and G
0 = 15 J/m2; Δz
0 = 300 nm,
MPa and G
0 = 15 J/m2; Δz
0 = 300 nm, 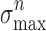 = 36.8 MPa and G
0 = 30 J/m2
= 36.8 MPa and G
0 = 30 J/m2
Another interesting aspect is the relation to analytical results relating 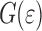 to the roughness of interfaces. In the literature analytical studies have been reported for situations [15, 16] in which a flat elastic body is brought into perfect contact with a rigid rough body (see appendix A for a brief overview of these treatments).
to the roughness of interfaces. In the literature analytical studies have been reported for situations [15, 16] in which a flat elastic body is brought into perfect contact with a rigid rough body (see appendix A for a brief overview of these treatments).
The physical picture emerging from these analytical results is the following: Roughness increases the real contact area at the interface and this effect contributes to an increase of the change of interface energy upon contact. On the other hand for complete contact to occur elastic energy is stored in the material and this contributes to a decrease in interface energy. Depending on the properties of interface, substrate and polymer (geometric as well as elastic) one of these two effects dominates and in fact a critical modulus E c can be defined for the polymer layer that separates these two regimes [15]. For E c it is found that
 |
16 |
with
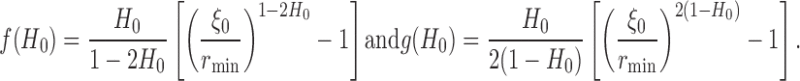 |
17 |
Here r
min represents the smallest length scale in the system (in our case 1 μm). In the case of PET and steel and for a substrate geometry typical for the ones discussed here we find 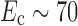 MPa which means that E
PET >> E
c. So, based on the analytical approach the interfaces are expected to show a decrease in interface energy for increasing roughness. An expression for
MPa which means that E
PET >> E
c. So, based on the analytical approach the interfaces are expected to show a decrease in interface energy for increasing roughness. An expression for 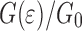 is given in [15] (see Appendix A for a derivation and a description of the assumptions):
is given in [15] (see Appendix A for a derivation and a description of the assumptions):
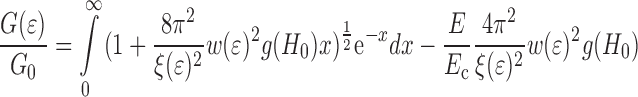 |
18 |
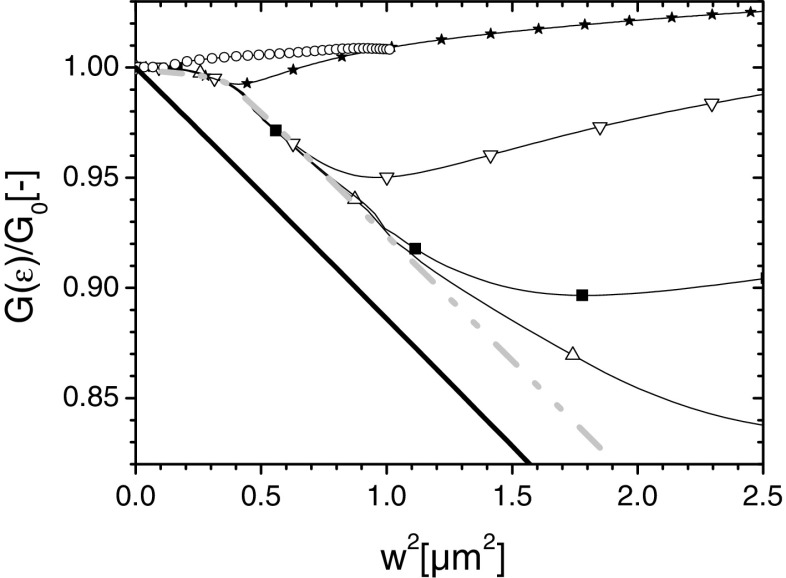
In Fig. 12 a comparison is made between this analytical solution and a number of results from the numerical simulations (Fig. 6). To compare both cases it is necessary to introduce an effective modulus E that reflects the elastic properties of both the cohesive zone and the polymer coating. In the graph a value of 118 MPa is used.
Fig. 12.
Comparison of the results of Eq. 17 (with E = 118 MPa) indicated with the drawn line and numerical results 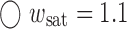 μm; ★
μm; ★ 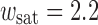 μm;
μm; 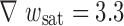 μm;
μm; 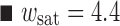 μm and
μm and  μm. An enveloping curve (dash-dot) accentuate the response of the numerical model in case the PET behaves elastically
μm. An enveloping curve (dash-dot) accentuate the response of the numerical model in case the PET behaves elastically
The figure shows that the analytic result (indicated by a drawn line) predicts a monotonous linear decrease of 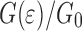 as a function of
as a function of 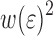 . We note that the existence of an enveloping curve (indicated by a dash-dot line in the figure) may be inferred from the numerical simulations (also shown in Fig. 11). This shows that as long as the PET is in the elastic regime the interface energy depends only on
. We note that the existence of an enveloping curve (indicated by a dash-dot line in the figure) may be inferred from the numerical simulations (also shown in Fig. 11). This shows that as long as the PET is in the elastic regime the interface energy depends only on 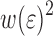 which is in qualitative accordance with the analytical results. A difference in this respect is the occurrence of a non-linear regime at low strains for the numerical solutions which is due to the description of the interface with a stress-separation law with a certain working distance. Decreasing the interaction distance for the cohesive zone will lead to a closer correspondence with the analytical result.
which is in qualitative accordance with the analytical results. A difference in this respect is the occurrence of a non-linear regime at low strains for the numerical solutions which is due to the description of the interface with a stress-separation law with a certain working distance. Decreasing the interaction distance for the cohesive zone will lead to a closer correspondence with the analytical result.
Deviation from the enveloping curve occurs for all numerical calculations as soon as the average strain in the PET reaches the yield strain. The value of 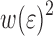 at which this occurs depends on
at which this occurs depends on 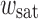 . It can be seen that for small
. It can be seen that for small 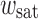 the deviations from the envelope curve occur for very low
the deviations from the envelope curve occur for very low 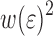 . The softening that occurs in the PET above the yield strain leads to an increase or partial recovery of
. The softening that occurs in the PET above the yield strain leads to an increase or partial recovery of 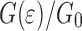 , a behavior that differs drastically from what is expected from the analytical result.
, a behavior that differs drastically from what is expected from the analytical result.
Conclusion
The following generic picture emerges that describes the energetics of a strained ductile glassy polymer layer with a roughening interface:
At the interface local delamination leading to a decrease in adhered area competes with roughening that leads to an increase in adhered area.
A decrease of the interface energy occurs in the regime where the polymer deforms elastically, a (partial) recovery occurs during the softening phase of the polymer followed by a renewed decrease during the hardening phase of the polymer coating.
For layers of practical thickness the elastic energy stored in the polymer coating by straining at the yield stress dominates the work of adhesion and the stability of the interface against delamination.
Acknowledgements
This work was financially supported by the Netherlands Technology Foundation STW (project number GTF.4901).
Appendix A
In the literature analytical studies have been reported for situations [15, 16] in which a flat elastic body is brought into perfect contact with a rigid rough body. Using the definitions in Eqs. 3–7 and accounting for the self-affine character of the surface it can be shown that the results in [15, 16] are equivalent to:
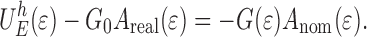 |
19 |
For 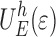 , the elastic energy in the polymer due to the surface roughness only, it is found that [15, 16]:
, the elastic energy in the polymer due to the surface roughness only, it is found that [15, 16]:
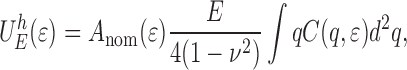 |
20 |
where q is defined as 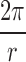 and
and
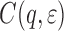 is the Fourier transform of the substrate height–height correlation function
is the Fourier transform of the substrate height–height correlation function 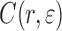 defined in Eq. 1 [17–20]. For the term
defined in Eq. 1 [17–20]. For the term 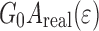 it is found that
it is found that
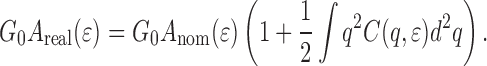 |
21 |
For 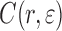 with scaling properties given by Eq. 2,
with scaling properties given by Eq. 2, 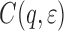 scales as
scales as 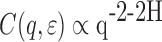 if
if 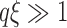 , and as
, and as  if
if 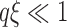 . Using the latter relation together with Eqs. 19, 20 and 21 results in Eq. 18. These results hold when a number of criteria are met, most importantly
. Using the latter relation together with Eqs. 19, 20 and 21 results in Eq. 18. These results hold when a number of criteria are met, most importantly 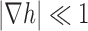 and the surfaces should stay in complete contact.
and the surfaces should stay in complete contact.
References
- 1.Hertz H. J Reine Angew Math. 1882;92:156. [Google Scholar]
- 2.Archard JF. Proc R Soc London Ser A. 1957;243:190. doi: 10.1098/rspa.1957.0214. [DOI] [Google Scholar]
- 3.Greenwood JA, Williamson JBP. Proc R Soc London Ser A. 1960;295:300. [Google Scholar]
- 4.Johnson KL. Contact Mechanics. Cambridge: Cambridge University Press; 1985. [Google Scholar]
- 5.Bush AW, Gibson RD, Thomas TR. Wear. 1975;35:87. doi: 10.1016/0043-1648(75)90145-3. [DOI] [Google Scholar]
- 6.Persson BNJ, Bucher F, Chiaia B. Phys Rev B. 2002;65(18):184106. doi: 10.1103/PhysRevB.65.184106. [DOI] [Google Scholar]
- 7.Hyun S, Pei L, Molinari JF, Robbins MO. Phys Rev E. 2004;70(2):026117. doi: 10.1103/PhysRevE.70.026117. [DOI] [PubMed] [Google Scholar]
- 8.Zhao Y, Wang GC, Lu TM (2001) Characterization of amorphous and crystalline rough surface. Principles and applications. Academic Press
- 9.van Tijum R, Vellinga WP, De Hosson JThM (2005) Linking length scales in the mechanical behavior of materials. In: Rudd RE, Balk TJ, Windl W, Bernstein N (eds) MRS Proceedings Volume 882E, EE3.2
- 10.Wouters O, Vellinga WP, van Tijum R, De Hosson JThM. Acta Mater. 2005;53:4043–4050. doi: 10.1016/j.actamat.2005.05.007. [DOI] [Google Scholar]
- 11.van Tijum R., De Hosson J. Th. M. Effects of self-affine surface roughness on the adhesion of metal-polymer interfaces. Journal of Materials Science. 2005;40(13):3503–3508. doi: 10.1007/s10853-005-0414-4. [DOI] [Google Scholar]
- 12.Van der Giessen E (1997) Eur J Mech, A/Solids 16(special issue):87
- 13.Abdul-Baqi A, Van der Giessen E. Int J Solid Struct. 2002;39(6):1427. doi: 10.1016/S0020-7683(01)00280-3. [DOI] [Google Scholar]
- 14.Xu XP, Needleman A. Model Simul Mater Sci Eng. 1993;1:111. doi: 10.1088/0965-0393/1/2/001. [DOI] [Google Scholar]
- 15.Persson BNJ, Tosatti E. J Chem Phys. 2001;115:5597. doi: 10.1063/1.1398300. [DOI] [Google Scholar]
- 16.Palasantzas G, De Hosson JThM. Phys Rev E. 2003;67:021604–1–6. doi: 10.1103/PhysRevE.67.021604. [DOI] [PubMed] [Google Scholar]
- 17.Krim J, Palasantzas G. Int J Mod Phys B. 1995;9:599. doi: 10.1142/S0217979295000239. [DOI] [Google Scholar]
- 18.Meakin P. Fractals, scaling, and growth far from equilibrium. Cambridge: Cambridge University Press; 1998. [Google Scholar]
- 19.Sinha SK, Sirota EB, Garoff S, Stanley HB. Phys Rev B. 1988;38:2297. doi: 10.1103/PhysRevB.38.2297. [DOI] [PubMed] [Google Scholar]
- 20.Yang HN, Lu TM. Phys Rev E. 1995;51:2479. doi: 10.1103/PhysRevB.51.2479. [DOI] [PubMed] [Google Scholar]