Learning-induced changes in selectivity and interactions of GABAergic interneuron classes in visual cortex

Summary

Learning increases the selectivity of cortical representations for behaviorally relevant stimuli, but how this occurs through changes in activity of different cell types remains unclear. We imaged simultaneously responses of pyramidal cells (PYR), and parvalbumin (PV), somatostatin (SOM), and vasoactive intestinal peptide (VIP) inhibitory interneurons in primary visual cortex while mice learned to discriminate two visual patterns. Learning increased the selectivity for both stimuli in subsets of PYR, PV and SOM cells but not VIP cells. Strikingly, PV neurons became as selective as PYR cells and less correlated with stimulus preference of the local network. A linear dynamical system model revealed that PYR to PV interactions reorganized such that stimulus selective PYR-PV subnetworks emerged during learning. In contrast, SOM cells became decorrelated from the local network and may gate selectivity changes. Thus, learning shapes the activity and interactions of multiple cell classes as the network becomes more selective for processing of behaviorally relevant stimuli.

Introduction

Learning exerts a powerful influence on how cortical circuits process sensory information. Cortical representations become more selective when sensory stimuli acquire behavioral relevance during learning(Recanzone et al., 1993; Schoups et al., 2001; Yang and Maunsell, 2004; Rutkowski and Weinberger, 2005; Blake et al., 2006; Li et al., 2008; Wiest et al., 2010; Gdalyahu et al., 2012; Goltstein et al., 2013; Yan et al., 2014; Poort et al., 2015; Chen et al., 2015a). These improvements in sensory coding take place in richly interconnected networks containing principal excitatory neurons as well as multiple classes of GABAergic interneurons, each with distinct molecular, cellular and connectional properties(Markram et al., 2004; Xu et al., 2010; Pfeffer et al., 2013; Kepecs and Fishell, 2014; Jiang et al., 2015). Yet how learning changes the responses and interactions of excitatory and inhibitory cell classes remains poorly understood.

Specific classes of inhibitory interneurons have been implicated in plasticity of cortical circuits with sensory experience and learning(Maffei et al., 2006; Letzkus et al., 2011; Kuhlman et al., 2013; Makino and Komiyama, 2015; Kato et al., 2015; Chen et al., 2015b; Sachidhanandam et al., 2016; Kaplan et al., 2016). In principle, inhibitory neurons could gate the plasticity of inputs onto pyramidal cells(Kuhlman et al., 2013; van Versendaal et al., 2012; Barnes et al., 2015) as well as inhibit or disinhibit their responses to specific sensory stimuli(Makino and Komiyama, 2015; Kato et al., 2015; Chen et al., 2015b; Sachidhanandam et al., 2016). However, it is not known whether learning can enhance the response selectivity for behaviorally relevant stimuli in specific classes of interneurons and thus provide more stimulus-specific inhibition to the network. Moreover, each interneuron class has been suggested to act as a functionally (and thus computationally) homogeneous unit during sensory or behavioral events(Kato et al., 2015; Kvitsiani et al., 2013; Pi et al., 2013; Hangya et al., 2014; Pinto and Dan, 2015; Karnani et al., 2016), but it is not clear whether learning leads to homogeneous response changes within each interneuron class. Finally, due to the dense connectivity of cortical networks, any change in responses in one group of interneurons could lead to complex changes in responses of neurons belonging to other classes. The majority of previous work has studied changes in a single class of interneurons at a time. A few studies have measured the activity of multiple cell classes(Karnani et al., 2016; Kerlin et al., 2010; Wilson et al., 2017), while others have used model-based methodologies incorporating multiple cell classes(Kuchibhotla et al., 2017; Litwin-Kumar et al., 2016) or have modelled population data from a single cell class(Harris et al., 2003; Pillow et al., 2008). However, there are no studies yet that provide a model-based fit of concurrent activity in multiple identified cell classes that account for the influences of the local population on each cell. As a result it is not well understood how learning modifies the functional interactions between multiple cortical interneuron classes to support more selective processing of sensory information.

To address these questions we imaged simultaneously the responses of four classes of cortical neurons: putative pyramidal cells (PYR), and parvalbumin (PV), somatostatin (SOM), and vasoactive intestinal peptide (VIP) expressing interneurons in layer 2/3 (L2/3) of the primary visual cortex before and after mice learnt a visual discrimination task. In each cell class we observed heterogeneous responses to behaviorally relevant visual stimuli as well as diverse response changes with learning. Most strikingly, learning led to a strong increase in the stimulus selectivity of PV cells. A linear dynamical system (LDS) model revealed a reorganization of interactions between PYR and PV cells and the emergence of stimulus specific PYR-PV subnetworks. In contrast, SOM-PYR interactions seemed to gate response plasticity, as the degree of correlation with the SOM population before learning predicted the extent of selectivity increase in PYR cells. Concurrently, SOM cells became decoupled from the local network during learning, which may facilitate further plasticity. These results underscore the complex and concerted nature of network-wide changes in activity across multiple cell classes during learning.

Results

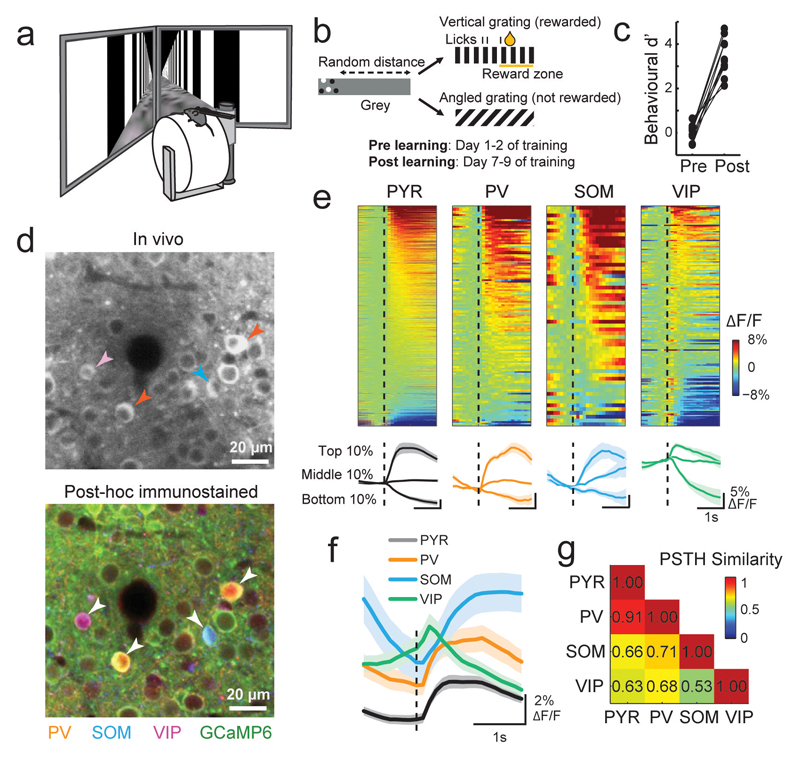
To understand how learning changes the responses of different cell types in V1, we trained mice to perform a visual discrimination task in a virtual reality environment(Poort et al., 2015) (Fig. 1a). Head-fixed mice learnt a go-no go discrimination task (Fig. 1b) in which they ran through a virtual approach corridor where the walls displayed a short stretch of circle patterns followed by gray for a random distance, before they were abruptly presented with one of two grating patterns. Mice were rewarded for licking a reward spout only in response to vertical gratings. No punishment was given for licking in response to angled gratings (40° relative to vertical). All mice learnt to discriminate the two stimuli, starting at chance performance (behavioral d’ close to zero) and reaching our threshold criterion of d’ > 2.0 within 9 days (~85% accuracy, Fig. 1c, sign test, P = 0.008, N = 8 mice).

Figure 1. Simultaneous two-photon imaging of multiple cell classes during a visual discrimination task in virtual reality.

(a) Virtual reality setup. (b) Schematic of behavioral task. Mice were rewarded for licking a reward spout when presented with vertical and not angled gratings. (c) Behavioral discrimination performance (behavioral d’) across learning (N = 8 mice). Connected points represent individual mice. (d) Top, example region of an in-vivo image plane with GCaMP6f expressing neurons. Bottom, same region after post-hoc immunostaining for PV, SOM and VIP (orange, blue and magenta, respectively) and image registration to match the in-vivo plane. Identified interneurons are indicated by arrowheads. (e) Top, average responses to the vertical grating of all recorded neurons of each cell type after learning. Calcium responses are baseline corrected (subtraction of baseline ΔF/F -0.5 to 0 s before stimulus onset), and aligned to grating onset (dashed line). Cells are sorted by their average response amplitude 0-1 s from stimulus onset. Number of cells included in each plot: 1249, 132, 58 and 175 for PYR, PV, SOM and VIP, respectively, N = 8 mice. Bottom, average responses of cells from the top, middle and bottom 10th percentiles of grating-evoked response amplitudes of each cell class. Shaded area represents SEM. (f) Average response to the vertical grating of all cells from each cell class after learning. (g) Similarity of response profiles to the vertical grating of all pairs of cell classes attained with a random forest decoder to classify single cells to one of two classes based on the shape of their average baseline-subtracted PSTH (see Online Methods). PSTH similarity score = 2 × (1- classification accuracy). Scores near 0 and 1 indicate low and high PSTH similarity between two cell classes respectively.

We used viral vectors to express the calcium indicator GCaMP6f(Chen et al., 2013) in V1 and recorded responses of populations of L2/3 cells during the task before and after learning using two-photon calcium imaging. We then re-identified the same neurons in co-registered, immunohistochemically stained brain sections of the same animals and detected simultaneously imaged PV-positive, SOM-positive and VIP-positive interneurons(Kerlin et al., 2010; Keller and Martin, 2015) (Fig. 1d, Supplementary Fig. 1). Immuno-unlabeled cells were classified as putative PYR cells(Rudy et al., 2011).

We first characterized the responses of the four cell classes while mice engaged in visual discrimination. The activity of many cells in each class was modulated by the onset of the task-relevant grating stimuli (Fig. 1e, Supplementary Fig. 2a, b). The average peri-stimulus time histograms (PSTHs) revealed cell class-specific response profiles (Fig. 1f, Supplementary Fig. 2c); while VIP cell responses preceded and peaked close to stimulus onset, the responses of SOM cells were delayed relative to PYR and PV cells after stimulus onset (Fig. 1f, Supplementary Fig. 2d). The average activities of SOM and VIP cells exhibited opposing response profiles and were thus most different from each other, whereas responses of PYR and PV cells were most similar (Fig. 1g, Supplementary Fig. 2e).

Importantly, despite differences in average response profiles, the responses of individual neurons within each cell class were highly heterogeneous, including stimulus-evoked increases and decreases in activity (Fig. 1e, Supplementary Fig. 2a, b). Within-class response diversity was also apparent in responses triggered by the onset of running, and the delivery of reward or an odor (Supplementary Fig. 3). Thus, grating-evoked response profiles are broadly different between cell classes, but also heterogeneous within each cell class.

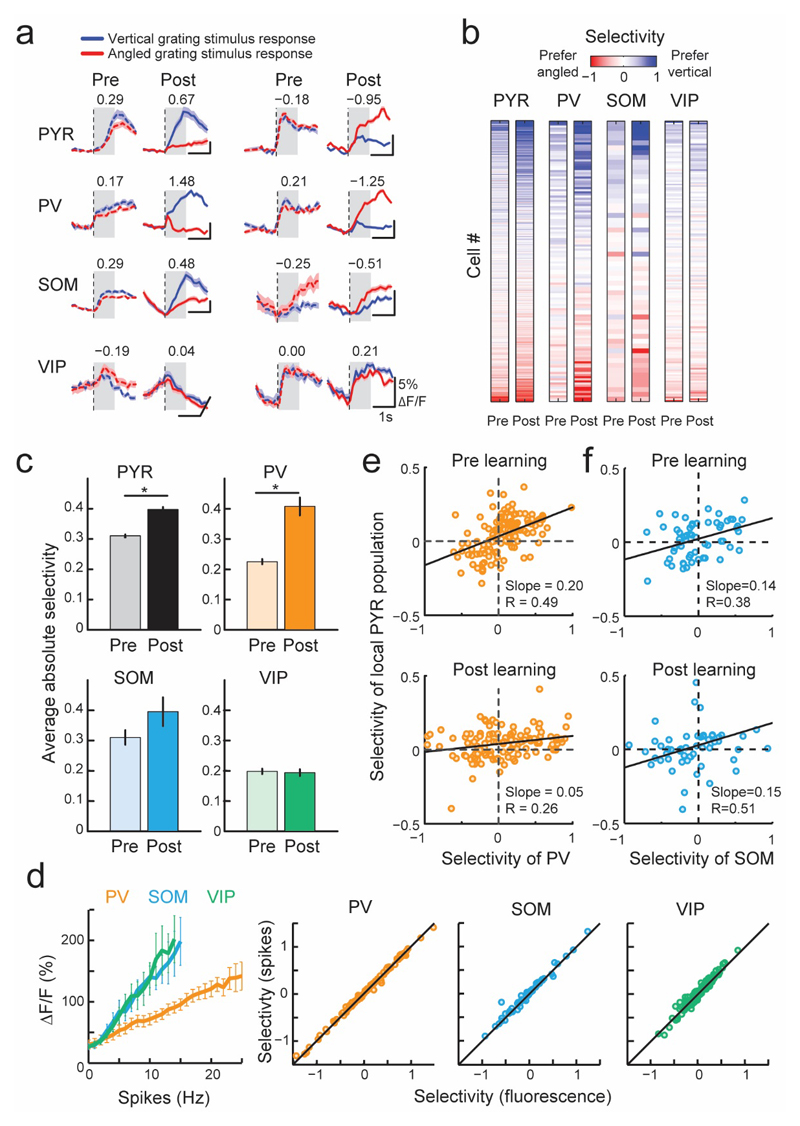
During learning, the responses to task-relevant grating stimuli changed in subsets of neurons from all cell classes, including both increases and decreases in response amplitude (Supplementary Fig. 4), as well as changes in the average population response of different cell types over the course of several days (Supplementary Fig. 4a, d). This was associated in varying degrees of stimulus selectivity changes in individual cells (difference in the responses to the vertical and angled grating stimuli normalized by the response variability, see Online Methods and Fig. 2a, b). On average, PYR cells significantly increased their stimulus selectivity, as reported previously (average absolute selectivity pre learning, 0.31 ± 0.32 (mean ± std), post learning 0.41 ± 0.45, sign test, P < 10^-7, N = 1249)(Poort et al., 2015). Notably, selectivity also increased robustly in PV cells, which became as selective as PYR cells for the task-relevant stimuli (Fig. 2b, c, pre learning 0.25 ± 0.20, post learning 0.43 ± 0.38, sign test, P = 0.002, N = 132). Although on average the selectivity of the SOM interneurons did not change significantly (pre learning 0.27 ± 0.18, post learning 0.40 ± 0.46, P = 0.51, N = 58), a specific subpopulation became more selective (Fig. 2b, c): SOM cells that were negatively correlated with VIP cells after learning exhibited larger changes in selectivity, and had significantly higher selectivity in mice that learned the task (Supplementary Fig. 5). In contrast, VIP cells were poorly selective for behaviorally relevant stimuli, which remained unchanged after learning (pre learning 0.19 ± 0.17, post learning 0.19 ± 0.16, P = 1.00, N = 175). We found that changes in eye position, pupil size, eye movements, running and licking could not account for the increased selectivity of responses after learning (Supplementary Fig. 6d-h). Furthermore, the increased response selectivity was specific to the task-relevant grating stimuli and was not observed in the approach corridor (Supplementary Fig. 6i).

Figure 2. Response amplitude and selectivity changes with learning in different cell classes.

(a) Average responses to vertical (blue line) and angled (red line) grating stimuli before (dashed line) and after learning (solid line) of example neurons from different cell classes. Numbers indicate selectivity to the grating stimuli, calculated in a window 0-1s from grating stimulus onset (gray shading). Positive and negative values indicate vertical and angled preference, respectively. Shaded area represents SEM. (b) Grating selectivity of the same cells (rows) before (pre) and after (post) learning (columns). Cells were ordered by their mean pre and post learning selectivity. Numbers of cells recorded both pre and post learning: 1249 PYR, 132 PV, 58 SOM and 175 VIP cells here and elsewhere, N = 8 mice. (c) Mean absolute selectivity of each cell class before and after learning. Error bars represent SEM. *, P < 10^-5. (d) Left, relationship between action potential firing rate and calcium transient size in simultaneous loose patch and GCaMP6 recordings from the three interneuron classes in visual cortex slices. Error bars represent SEM. Right, comparison of selectivity values computed from measured fluorescence (x-axis) and inferred firing rate (y-axis) in PV, SOM, and VIP interneurons. Correlation coefficients 1.00, 0.99, 0.97 for PV, SOM and VIP respectively (e, f) Relationship between the selectivity of individual PV cells (e) or SOM cells (f) and the mean selectivity of the local PYR population within 100 μm distance from each PV or SOM cell, before (top) and after learning (bottom).

To test that the increased preference for task-relevant stimuli was not a result of nonlinearities in the relationship between a neuron’s firing rate and calcium concentration, we performed loose-patch recordings of spiking activity while simultaneously imaging GCaMP6 calcium fluorescence in from the three interneuron classes in visual cortex slices. We found a near-linear relationship between firing rate and associated calcium fluorescence changes for all interneurons (PV = 13, SOM = 17 and VIP = 11 cells). The slope of this relationship was lower for PV cells than for SOM and VIP cells (Fig. 2d), possibly reflecting different calcium buffering capacities of these GABAergic populations(Hu et al., 2014). The relationship between firing rate and fluorescence changes allowed us to infer the firing rates of all imaged cells based on measured calcium transients on each trial. The selectivity values obtained from the inferred firing rate closely matched those obtained from calcium signals in each interneuron class (Fig. 2d, average absolute selectivity of inferred spike rate pre learning 0.25, 0.27, 0.20; post learning 0.43, 0.39, 0.20 in PV, SOM and VIP cells, respectively). Thus, the observed changes in selectivity during learning were unlikely to arise from differences in calcium signal nonlinearities of the three classes of interneuron.

The increased selectivity of PV cells for the grating stimuli was unexpected given that these interneurons are thought to broadly integrate the activity of surrounding PYR cells(Kerlin et al., 2010; Bock et al., 2011; Hofer et al., 2011; Scholl et al., 2015), thus providing local inhibition proportional to the average local activity levels. Indeed, we observed a positive correlation between PV cell selectivity and that of the average activity of nearby PYR cells (within 100 μm from the PV cell) before learning (Fig. 2e top, slope = 0.2, confidence intervals (CI) 0.14 to 0.26, R = 0.49). However, the slope of this relationship decreased with learning (Fig. 2e bottom, slope = 0.05, CI 0.02 to 0.10, reduction in slope bootstrap test P < 10^-4, R = 0.26). Thus, the emergence of selective responses for behaviorally relevant stimuli in PV cells was associated with their activity becoming more independent from the average stimulus preference of the surrounding PYR cells. In contrast, the relationship between the selectivity of SOM cells and surrounding PYR cells remained constant with learning (Fig. 2f, slope before learning 0.14, CI 0.04 to 0.24, and after learning 0.15, CI 0.05 to 0.25, no significant change in slope with learning, P > 0.05).

These results suggest that improvements in response selectivity during learning are associated with a restructuring of firing interdependencies between different cell types in visual cortex. PV cells might become more strongly influenced by external (top down or bottom up) inputs and driven less by surrounding PYR cells after learning. Alternatively, individual PV cells might acquire more selective input from subsets of PYR cells with specific stimulus-preferences during learning, causing them to respond more selectively and thus reflect local network activity to a lesser degree. These two hypotheses predict distinct changes in firing interdependencies between different cell types in visual cortex over learning. If a cell type were to decouple from the surrounding network and become more strongly influenced by external inputs, its co-fluctuations with neighbouring cells would decrease substantially. In contrast, if a cell maintained selective associations with neighbouring cells of a given stimulus preference, co-fluctuations with those neighbouring cells would not strongly decrease after learning. The first, but not the second alternative would predict that co-fluctuations between PV neurons and the local network should decrease.

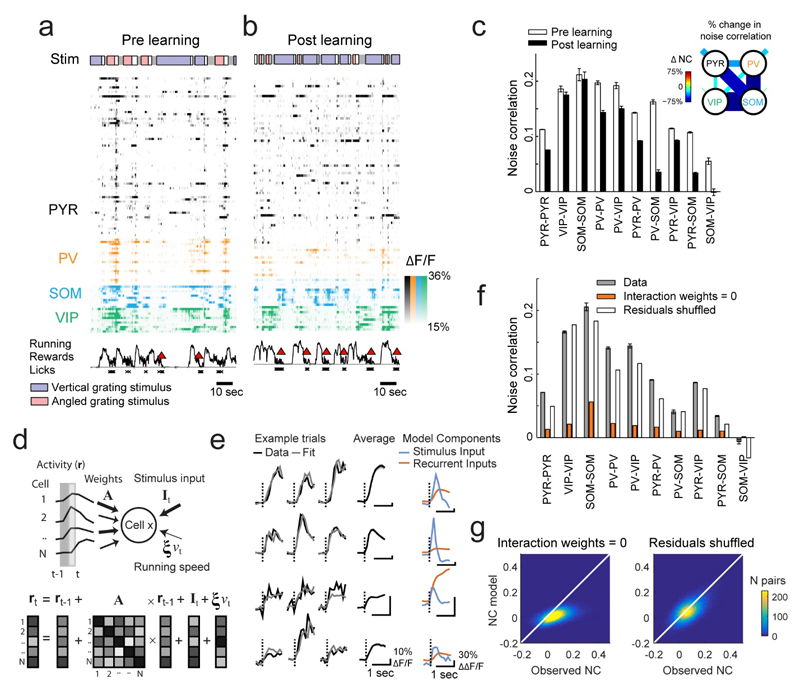
To distinguish between these hypotheses, we computed noise correlations during the visual stimulus period between pairs of neurons within and across cell classes, before and after learning (Figs. 3a-c, Supplementary Fig. 7). Noise correlations reflect the stimulus-independent trial-to-trial covariability of responses, and thus provide an estimate of mutual connectivity and shared inputs(Cohen and Kohn, 2011; Cossell et al., 2015). We found that learning decreased noise correlations both within and between cell classes (sign test, all Ps < 10^-4, with the exception of SOM-SOM cell pairs, P = 0.35), indicating that firing in the network became more independent (Fig. 3c). Notably, the activity of SOM cells became strongly decorrelated from that of PYR, PV and VIP cells, while in contrast PV cells showed less decorrelation (Fig. 3c, inset). SOM cells in particular thus seemed to become uncoupled from the local network during learning. Changes in eye position, pupil size, eye movements, running or licking could not account for the observed changes in noise correlations with learning (Supplementary Fig. 8).

Figure 3. Concerted changes in interactions and neuronal selectivity with learning.

(a, b) Example responses of simultaneously imaged neurons before (a) and after learning (b). Colored bars on top indicate stimuli encountered by the mouse as it traversed the virtual corridor: blue and red indicate vertical and angled gratings, gray and white indicate corridor walls in gray or with dots, respectively. Running (black line), reward delivery (red triangle) and licks (crosses) are indicated below. Only a quarter of the PYR cells are shown for clarity. (c) Noise correlations measured during the vertical grating response (0-1 s from stimulus onset) between cell pairs of each combination of cell classes, before and after learning. Error bars represent SEM here and elsewhere. Inset: relative changes in noise correlation over learning between and within all cell classes, as indicated by line thickness and color code. Shorter line segments show relative change in correlations between cells of the same type. (d) The linear dynamical system model fits single trial responses by estimating the contribution of stimulus-locked input, recurrent inputs from the local cell population and running speed. (e) Example traces of responses and model fit on three single trials (columns) from 4 cells (rows) along with each cell's average response (black), stimulus input (blue) and average recurrent input (red). (f) Average post learning noise correlations observed (gray), or simulated after setting interaction weights to zero (orange) or shuffling residuals (white). (g) Scatter density plot of observed versus simulated pairwise noise correlations (NC), after setting interaction weights to zero or shuffling residuals.

We sought to assess in more detail the extent to which the activity of individual cells in the network was influenced by inputs from the local network or by stimulus-related, external input, and whether changes in these influences over learning could account for the observed changes in selectivity and correlations. To address these questions, we fit the data to a linear dynamical system (LDS) model which predicted the activity of each cell based on two main components: (1) a weighted contribution of inputs from all other simultaneously recorded cells on the previous time step (the recurrent input), and (2) a contribution from a trial-invariant stimulus-locked input (the stimulus input, Fig. 3a, b). When the LDS model is fit to the data, the interaction weights organize to best capture the covariance of the responses across the population, whereas the stimulus input to each cell organizes to exactly capture the average PSTH of each cell (see Online Methods). We also included an input proportional to running speed in the model, but this had a negligible contribution to the responses (Supplemental Fig. 9a). Any remaining unexplained response variability was assigned to a residual term.

To test whether the model captured the data well, we asked if the observed noise correlations were accounted for by the interaction weights between cells in the model (see Online Methods). On simulating the network responses with all interaction weights set to zero, average noise correlations were greatly diminished compared to the data (Fig. 3f, average over all cells 0.013 from 0.077). Moreover, both shuffling or setting interaction weights to zero heavily disrupted the pattern of individual pairwise noise correlations (Fig. 3g, observed versus simulated: R² = xx; setting weights to zero: R² = -0.18; shuffling weights: R² = xx). In contrast, simulating responses with the residuals shuffled, which removed any correlations not captured by the model, had a much smaller effect on noise correlations and left their patterns largely intact (Fig. 3f, g, average over all cells 0.056 from 0.077; observed versus simulated; shuffling residuals: R² = 0.59). Thus, in addition to the PSTH of each cell, the model also captured the correlated trial-by-trial response fluctuations across the population using a fixed set of interaction weights (also see Supplementary Fig. 9b for the fit to pre learning data). This implies that neuronal co-fluctuations observed before and after learning (Fig. 3b) could be accounted for by the interaction weights between cells. Interestingly, although the model was blind to cell type, we observed cell class specific differences in interaction weights and their changes over learning (Supplementary. Fig. 9c).

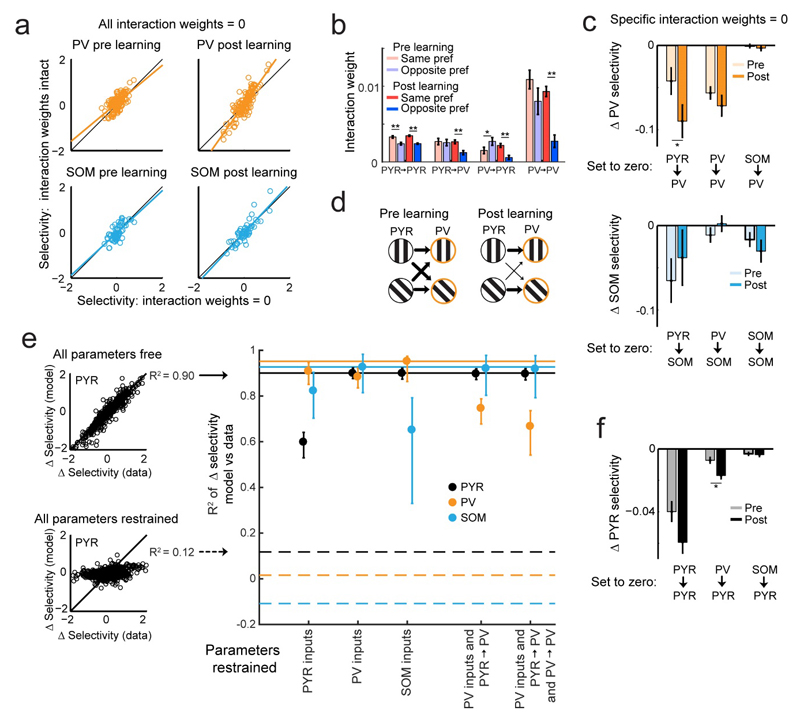
Manipulating the interaction weights in the model allowed us to determine the extent to which the recurrent local network accounted for the stimulus selectivity of interneurons. We deleted all interaction weights and simulated the responses of the population (see Online Methods). Pre learning, the selectivity of PV and SOM cells did not change on deleting interaction weights. However, post learning, deletion of interaction weights resulted in a significant reduction in PV selectivity (Fig. 4a, slope before learning 0.83, CI 0.64 to 1.03, slope after learning, 1.41, CI 1.24 to 1.56, P < 10^-4), while no such effect was observed in SOM cells (slope before learning 0.93 CI 0.72 to 1.18, slope after learning 1.08 CI 0.87 to 1.35, P > 0.05, also see Supplementary Fig. 10a). Moreover, we found that the effect of specifically deleting PYR to PV interaction weights on reducing PV selectivity increased after learning (Fig. 4c, top, sign test P < 0.05) while the effect of weight deletions did not change with learning for SOM cells (Fig. 4c, bottom, all Ps > 0.05). This result suggests a reorganisation of local PYR interaction weights onto PV cells during learning. Indeed, we found that post learning, PYR to PV and PV to PV weights were significantly higher between cells which preferred the same grating stimulus compared to cells with opposite preference (Fig. 4b, P-values < 10^-3, Wilcoxon rank-sum test). No such differences were observed either pre or post learning for PYR to SOM or SOM to SOM weights (Fig. Supplementary 10b, all P-values > 0.05). Thus, selective interactions between PV cells and subsets of PYR cells with similar stimulus preference emerged with learning, consistent with the learning-related development of selective PYR-PV subnetworks.

Figure 4. Relationship between neuronal selectivity and changes in interactions between different cell classes.

(a) Effect of removing weights between all cells in the LDS model on selectivity in PV (top) and SOM cells (bottom) before (left) and after (right) learning. N = 132 PV and 58 SOM cells here and below. (b) Interaction weights in LDS model before and after learning for cell pairs with the same or different stimulus-input preference (see Online Methods). **, P < 10^-3; *, P < 0.05 here and elsewhere. (c) Effect of specific weight removal on the selectivity change over learning (Δselectivity) in PV (top) and SOM cells (bottom). (d) Schematic depicting how PYR to PV interaction weights (arrows of different thickness) rearrange to provide selective inputs to PV cells after learning. (e) LDS model jointly fit across learning. Left: allowing all (top, free) or no parameters (bottom, restrained) to differ pre and post learning results in high or low R² between observed and simulated Δselectivity over learning of PYR cells, respectively. N = 1249 PYR cells, here and below. R² values with all or no free parameters indicated by horizontal lines on right for PYR, PV and SOM cells. Right, R² values obtained for different cell classes in joint LDS fits while restraining specific parameters from changing pre to post learning. Error bars represent bootstrapped 90% confidence intervals. (f) Effect of specific weight removal on Δselectivity in PYR cells.

To establish whether PYR to PV interaction weights were required to change over learning to account for the observed selectivity changes, we jointly fit the LDS model to the pre- and post-learning data, while constraining specific parameters (stimulus inputs or interaction weights) to remain fixed across learning and allowing others to vary. Holding all or none of the parameters fixed gave poor or good fits of selectivity changes during learning respectively (Fig. 4e left, indicated by horizontal lines in right panel). When stimulus inputs to SOM or PYR cells were held fixed over learning, not surprisingly, the model failed to fully capture the observed selectivity changes in these cell types (Fig. 4e right, bootstrap test on the difference between model with all parameters free compared to model with parameters fixed, both P-values < 0.002, see Online Methods). In contrast, changes in PV selectivity were significantly disrupted only when stimulus inputs to PV cells as well as PYR to PV interaction weights were both constrained to remain fixed across learning (P < 0.002, also see Supplementary Fig. 10c). This effect was stronger when PV to PV weights were additionally constrained (P = XX). Thus, in contrast to SOM and PYR cells, the changes in PV selectivity were affected only when both stimulus-locked drive and local interactions with PYR cells were fixed across learning.

Importantly, the increased post learning selectivity of PV cells further boosts the selectivity of PYR cells. Specific deletion of PV to PYR weights reduced PYR selectivity, and the effect was greater after learning (Fig. 4f, P < 10^-3). In contrast, the effect of deleting SOM and PYR cell weights on PYR cells did not change with learning (Fig. 4f, P > 0.05).

Taken together, these results indicate a key functional difference between PV and SOM interneurons. Post learning, PV cells may integrate activity more selectively from local PYR cells to in turn provide more selective inhibition to the network after learning. In contrast, SOM cells appear to become uncoupled from the local network and might be influenced more by external sources after learning.

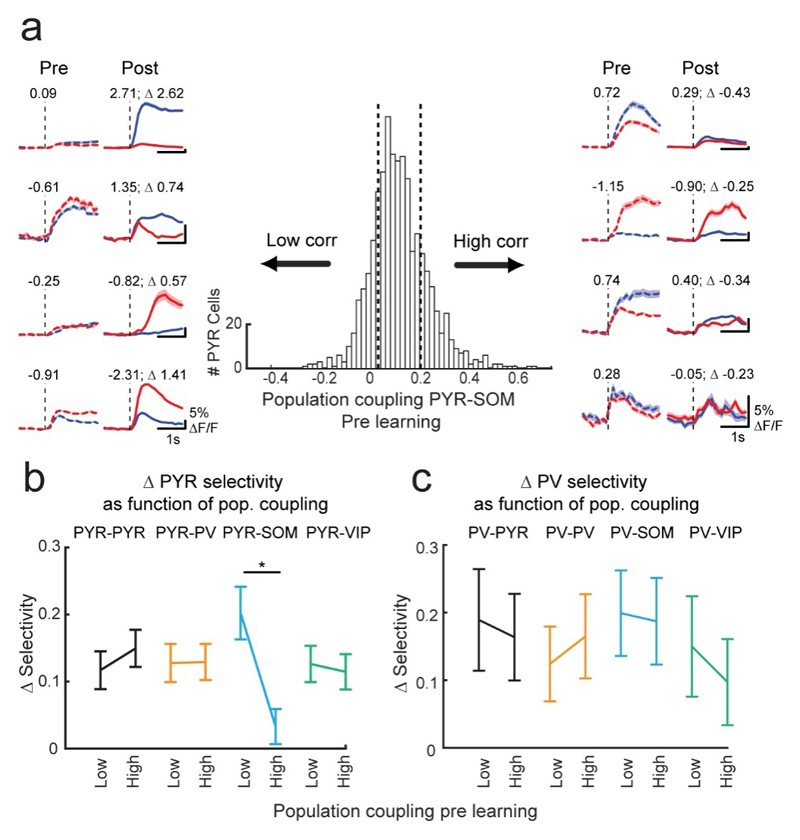
SOM cells target the apical dendrites of PYR cells. This might enable them to gate the influence of top-down learning-related signals arriving in layer 1(Yavorska and Wehr, 2016; Zhang et al., 2014). Thus, PYR cells that experience SOM mediated dendritic inhibition synchronous with their bottom up stimulus drive may be unable to pair top down and bottom up inputs, and thus may not exhibit learning-related selectivity changes. We selected PYR cells with high noise correlations with the average activity of the SOM population before learning (top 20th percentile), and found that this subset of PYR cells exhibited very low selectivity increases during learning (Fig. 5a, right, Fig. 5b). Conversely, PYR cells with the lowest noise correlations with the SOM population (bottom 20th percentile) showed a significantly larger learning-induced increase in selectivity (Fig. 5a, left, Fig. 5b). This dependence of PYR cell selectivity changes on their coupling to the SOM population was only apparent before but not after learning (Supplementary Fig. 11), and the degree of coupling with PV, VIP or PYR populations could not predict selectivity changes in PYR cells (Fig. 5b). PV cells, which also significantly increased selectivity with learning displayed no such relationship with SOM cell population activity (Fig. 5c), consistent with the notion that PV cells may be less influenced by top-down input, but might inherit their selectivity from the PYR network.

Figure 5. Degree of coupling with the SOM cell population is related to PYR cell selectivity increase.

(a) Centre: distribution of pre learning noise correlations between individual PYR cells and the average activity of the SOM cell population, N = 1249 PYR cells. Vertical dashed lines denote top and bottom 20th percentiles. Average grating responses pre and post learning of example PYR cells with low and high pre learning SOM cell population coupling (left and right, 4 example cells each). Numbers indicate selectivity. (b,c) Difference in the absolute selectivity pre and post learning (Δselectivity) of PYR cells (b) and PV cells (c) with low and high (bottom and top 20^th percentiles) coupling to the four cell type populations. **, P < 10^-3, N = 250 PYR cells (b) and 26 PV cells (c) in each group. Error bars represent SEM.

Discussion

Response heterogeneity within interneuron classes

Previous studies in various cortical areas have suggested that interneurons of a given molecularly defined class can act as a relatively homogenous functional unit during specific sensory or behavioral events, including high activity correlations between cells of the same class(Kato et al., 2015; Sachidhanandam et al., 2016; Kvitsiani et al., 2013; Pi et al., 2013; Hangya et al., 2014; Pinto and Dan, 2015; Karnani et al., 2016). We found that activity correlations across cell classes (e.g. PV-VIP cell pairs) can be as high as those within a class (e.g. PV-PV, VIP-VIP pairs). This implies that functional cell ensembles or subnetworks can span multiple cell types. Importantly, however, we observed a substantial within-class heterogeneity in responses aligned to onsets of behaviorally relevant grating stimuli, running, reward and odour delivery, as well as in learning-related response changes of PV, SOM and VIP interneurons in visual cortex. The fact that neurons within each cell class can be functionally diverse may not be surprising given that each molecularly defined class comprises cells with various morphologies, network connectivity and intrinsic properties(Markram et al., 2004; Kepecs and Fishell, 2014; Jiang et al., 2015; Runyan and Sur, 2013; Tasic et al., 2016). The challenge for future studies is to establish the extent to which the heterogeneous behavior of single cells is captured by the diversity of cell types within an interneuron class and to determine any brain-state and region-specific differences in their activity.

Learning increases selectivity of specific cell types and reorganizes their interactions

We show that learning changes the selectivity and functional interactions of multiple classes of inhibitory interneurons in V1. Our results demonstrate that the relationship between neurons within and across cell classes and their contribution to network function is not static, but that it can change with experience(Kuhlman et al., 2011). We found that PV cells were poorly selective for task-relevant grating stimuli before learning. This is consistent with observations that PV cells broadly integrate inputs from their neighbors and therefore display broad visual stimulus tuning in mouse V1(Kerlin et al., 2010; Bock et al., 2011; Hofer et al., 2011; Scholl et al., 2015). After learning, however, PV cells became selective and their tuning was less related to the preference of the average surrounding network. This result implied a rearrangement of interactions between PYR and PV cells. To estimate interactions between individual cells in a network, we developed a quantitative measure of interaction strength using a linear dynamical system model. The model fit a static weight matrix with which it captured the trial to trial activity fluctuations between each cell pair during a recording. This provided two significant insights. First, the origins of noise correlations in a neural network have been debated. Here we suggest that noise correlations can to a large extent be accounted for by concurrent functional interactions with simple linear dynamics. Second, in the LDS model PYR to PV interaction weights became specific for stimulus preference during learning and significantly contributed to PV selectivity changes. The model therefore suggests that learning induces plasticity in excitatory connections onto PV cells. Changes in PYR to PV interactions might lead to the emergence of stimulus selective PYR-PV subnetworks, implying that PV cells may integrate local excitatory inputs more specifically as a function of learned stimulus relevance. These effects were cell class specific and not observed in interactions of PYR and SOM cells. Rather, SOM cells became uncoupled from the local network during learning, raising the possibility that their activity during stimulus presentation increasingly reflects signals from long-range inputs (ref Makino,Komiyama). In the future, these hypotheses could be tested directly by assessing the local and long-range connectivity of PYR, PV and SOM neurons with specific response properties (Hofer et al., 2011; Ko et al., 2011) in naive and expert mice.

Irrespective of origin, the increased selectivity of PV and SOM subpopulations implies an increase in the amount of selective inhibition in the local network, which we suggest further sharpens cortical representations of task-relevant sensory stimuli(Alitto and Dan, 2010; Harris and Mrsic-Flogel, 2013). In contrast, VIP cells remained unselective throughout learning, suggesting they do not play a direct role in shaping selective PYR cell responses after learning, but they may contribute to the decorrelation of SOM cell activity from the local network (Pfeffer and Scanziani; Lee and Rudy, and the recent Sur NN paper).

Increase in PYR selectivity is gated

SOM cells have been shown to be important for learning, as well as exhibiting changes in their activity and bouton density in concert with learning-related changes in PYR cells (cichon&Gan 2015 nature, Makino Komiyama, chen, Komiyama). Here we find that already in naïve animals the degree of correlated activity with the SOM cell population predicts how strongly PYR neurons increase their selectivity during learning. We therefore suggest that SOM cells gate learning-related plasticity, by preventing PYR cells that are highly correlated with the SOM population from increasing their stimulus selectivity. Pairing of top-down and bottom-up inputs arriving in apical and basal dendrites respectively is important for forming new associations(Larkum, 2013), and SOM cells preferentially inhibit apical dendrites. If PYR cells respond to a visual, bottom-up input that also correlated with activity in a subpopulation of SOM cells, they may receive concurrent SOM mediated inhibition of the apical dendrite which may prevent the association of visual and top down inputs. High correlations with SOM cells may thus prevent learning related plasticity, while low correlations are permissive of plasticity. We observe a strong decorrelation of SOM cells from the rest of the network during learning. This may serve as a mechanism to increase plasticity of V1 circuits in general as visual stimuli become behaviorally relevant. Thus as mice learn the behavioral relevance of visual, their visual circuits may become primed to more readily undergo additional learning-related changes, for instance to facilitate further associations between visual stimuli and behavioral signals.

Our results highlight the existence of functional diversity across and within three molecularly defined cell classes of interneurons. The heterogeneous nature of experience-dependent response changes in different inhibitory neurons suggests that optogenetic manipulations of entire cell classes may not be the most appropriate approach for investigating the circuit mechanisms of cortical processing and plasticity, and may require precisely targeted interventions with cellular resolution(Packer et al., 2015; Rickgauer et al., 2014). Taken together, our results emphasize that learning-induced changes in cortical circuits are highly interdependent, involving interactions between specific subsets of neurons across multiple cell classes.

Online Methods

Experimental procedures for the behavioral task and two-photon calcium imaging have been described in detail in a previous study(Poort et al., 2015).

Animals and surgical procedures

All experimental procedures were carried out in accordance with institutional animal welfare guidelines and licensed by the Swiss cantonal veterinary office. Mice used in this study were C57Bl/6 wild type mice obtained from Janvier Labs (4 males, 1 female), crosses between Rosa-CAG-LSL-tdTomato (JAX: 007914) and PV-Cre (JAX: 008069) (3 males), and crosses between Rosa-CAG-LSL-tdTomato and VIP-Cre (JAX: 010908) (1 male, 1 female) all obtained from Jackson Laboratory. The crosses expressed tdTomato in PV and VIP interneurons respectively and were used for comparison of immunohistochemical labelling with genetic labelling, which was consistently found to be very high (typically >90%). Mice aged between postnatal days 48-58 were anaesthetized with a mixture of Fentanyl (0.05 mg kg−1), Midazolam (5 mg kg−1), and Medetomidin (0.5 mg kg−1). Additional drugs provided analgesia (Rimadyl 6 mg/kg), anti-inflammatory effects (dexamethasone, 1.6 mg/kg), and reduced mucus secretions (atropine, 0.04 mg kg−1). A circular craniotomy (4 mm diameter) was made over the right primary visual cortex (V1) and a virus expressing GCaMP6f (AAV2.1-syn-GCaMP6-WPRE(Chen et al., 2013), vector core, University of Pennsylvania Gene Therapy Program) was injected in 1-3 sites using glass pipettes and a pressure micro-injection system (Picospritzer III, Parker). The craniotomy was then sealed with a glass cover slip and cyano-acrylic glue (Loctite) and a custom machined aluminium head-plate was cemented onto the skull using dental cement (C&B Superbond). Antibiotic (Baytril 0.4 mg kg−1) and analgesia (buprenorphine 0.08 mg kg−1) was given at the end of surgery and repeatedly during recovery of the animal. Imaging and behavioral training started approximately three weeks after surgery.

Two-photon calcium imaging

Imaging was performed using a custom-built resonant scanning two-photon microscope and a Spectra Physics MaiTai eHP laser with a DeepSee prechirper (< 70 fs pulse width, 80 MHz repetition rate) at 940 nm using a Nikon 16× 0.8 NA objective. Images of 750 × 750 pixels and a field of view of 350 µm × 350 µm were acquired using a 12 kHz resonant scanner (Cambridge Technology) and an FPGA module (PXIe-7965R FlexRIO, National Instruments) with an imaging rate of 32 Hz. We used a piezo Z-scanner (P-726.1CD, Physik Instrumente) to scan 4 planes with 20 µm spacing, resulting in an imaging rate of 8 Hz for each imaging plane.

The microscope was controlled using custom software written in Labview (National Instruments). Two-photon calcium imaging of GCaMP6-labelled neurons in layer 2/3 (typically 150-300 µm below the cortical surface) was performed before and after learning in 8 mice (pre learning: either first or second day of training; post learning: either day 7, 8 or 9 of training). Before each recording session the same imaging site was found by matching anatomical land marks. Mice with bone re-growth under the window, or poor viral expression were excluded from the study.

Image stacks were first corrected for motion by maximizing the cross-correlation of all frames with a reference image(Guizar-Sicairos et al., 2008). The reference image was an average of 30 successive frames and it was selected by computing for 30 candidate reference images (at linearly spaced positions in the recording stack) the x- and y-shift to 100 single frames (also linearly spaced) to obtain the most typical reference image with the smallest average shift. Regions of interest (ROIs) were selected by manually assigning pixels to individual cells by inspecting individual frames, as well as the average and maximum projections of the imaging stacks. Frames with motion shifts exceeding 5 microns (Euclidean distance) relative to neighbouring frames were rejected (on average 0.11% of all frames, range 0 to 1.05%).

Behavioral training and discrimination task

Mice were trained in a visual discrimination task in a virtual corridor over 9 days. Mice had free access to water, but were food deprived to maintain at least 85% of their free-feeding body weight (typically 85-90%, 2-3 g of standard food pellets per animal per day). Before the onset of training in the task, animals became accustomed to handling and gentle restraint over two to three days, before they were head-fixed and trained to run on a styrofoam cylinder (20 cm diameter, on a ball-bearing mounted axis) in the dark for two to four days. This period was also used to find suitable imaging sites. A reward delivery spout was positioned near the snout of the mouse, and licks were detected using a piezo disc sensor and custom electronics. The reward was a 10% solution of soya infant milk powder (SMA Wysoy) delivered by opening a pinch valve (NResearch) controlled through custom electronics. The mice’s running speed on the cylinder was detected with an optical mouse (Logitech G700, USB polling rate of 125 to 1000 Hz). This signal was used to control the speed at which mice moved through a virtual environment that was presented on two screens in front of them. The virtual environment consisted of linear corridors created in a gaming engine (Unity), and the position in the environment was controlled by custom software written in Labview (National Instruments). The luminance of visual stimuli was corrected using a luminance meter (Konica Minolta, LS-100).

A trial started when the mouse was positioned at a starting point in an approach corridor with walls showing black (0.1cd m⁻²) and white (10.9cd m⁻²) circles on a gray background (luminance 5.5cd m⁻²). Black and white circles were present for a short distance (111 cm) followed by a random distance of gray walls (minimum usually 74-185 cm, additional random delay chosen from an exponential distribution with mean 37 cm). Mice were then randomly teleported to one of two grating corridors (length 111 cm) with either a vertical grating pattern (square wave gratings, 100% contrast) or an angled grating pattern (rotated 40° relative to vertical) on the walls. We estimate the spatial frequency of the gratings in the centre of the screen to be ~0.05 cycles per degree, and temporal frequency at the average running speed ~4 Hz. In the vertical grating corridor, the mouse could trigger the delivery of a reward, a drop of soy milk, by licking the spout after it had entered a ‘reward zone’ a short distance (55.5 cm) into the grating corridor (mice typically started licking in anticipation of the reward zone). This was considered a 'hit' trial. If an animal did not lick by the end of the reward zone, shortly before the end of the vertical grating corridor (92.5 cm from the start), it was given a drop of reward by default and this was considered a 'miss' trial (this rarely happened after the first few sessions). In the angled grating corridor, the mouse did not receive a reward, and a single lick or more in this corridor was considered a 'false alarm' (FA) trial. No punishment was given. During initial stages of training the probability of non-rewarded trials was occasionally increased to discourage unrewarded licking (probability of angled grating trials 50-70%). We quantified the performance of the mouse using a behavioral d-prime: bd′ = Φ⁻(H) − Φ⁻¹(F), where Φ⁻¹ is the normal inverse cumulative distribution function, H is the rate of hit trials and F is the rate of false alarm trials.

Mice were trained in an olfactory discrimination task in the dark after reaching high levels of performance in the visual discrimination task. Mice were presented with one of two odor stimuli after a random delay (delays determined using the same method as the visual task): 10% soya milk odor (go stimulus, licking was rewarded with a drop of soya milk) or 10% soya milk with 0.1% limonene mixture odor (no-go stimulus, no reward for licking). Odors were delivered through a flow dilution olfactometer calibrated with a mini PID (Aurora) at 10-20% saturated vapor concentration of the above solutions, and at 1 L/min flow rate.

Immunohistochemistry and image registration

Brains were fixed by transcardial perfusion with 4 % paraformaldehyde (PFA) in phosphate buffer 0.1 M followed by 24 hours of post-fixation in the same solution at 4°C. The whole brains were incubated successively in 20 ml of 10 %, 20 % and 30 % sucrose in phosphate buffer saline (PBS) at 4°C for 1, 8 and 12 hours respectively. For antigen retrieval, the brains underwent two freeze-thaw cycles in liquid nitrogen, followed by three 10 minute washes in PBS. The brains were then sliced tangentially to the surface of visual cortex. 80 µm slices were cut on a vibratome (Zeiss Hydrax V50) and washed three times for 10 minutes each in PBS.

Slices were blocked overnight at room temperature with blocking buffer (Triton X-100 2 %, goat serum 10 %, NaN₃ 0.04 % in PBS), incubated in primary antibodies in blocking buffer for twelve hours at room temperature and 2.5 days at 4°C, rinsed three times for one minute and three times for ten minutes in PBS and finally incubated in secondary antibodies in blocking buffer for one day at room temperature. Slices were then rinsed three times for one minute and three times for ten minutes in PBS before being mounted on slides in DABCO-PVA (2.5 % DABCO, 10 % polyvinyl alcohol (Sigma; Type II), 5 % glycerol and 25 mM Tris buffer at pH 8.7).

The following primary antibodies were applied in blocking buffer:

Target	Host	Dilution	Supplier
Parvalbumin	Goat	1/500	Swant (PVG-213)
Parvalbumin	Mouse	1/1000	Swant (PV 235)
Vasoactive intestinal peptide	Rabbit	1/500	ImmunoStar anti-VIP (#20077)
Somastostatin	Rat	1/200	Millipore (MAB354)

The following secondary antibodies were applied in blocking buffer:

Genotype	Primary	Secondary	Code number
WT	Mouse-anti PV	DyLight 405	715-475-150
	Rabbit-anti VIP	Rhodamine Red X	711-295-152
	Rat-anti SOM	Alexa 647	712-605-153
PV-tdTomato	Mouse-anti PV	Alexa 594	715-585-151
	Rabbit-anti VIP	Alexa 647	711-605-152
	Rat-anti SOM	DyLight 405	712-475-153
VIP-tdTomato	Goat-anti PV	DyLight 405	705-475-147
	Rabbit-anti VIP	Rhodamine Red X	711-295-152
	Rat-anti SOM	Alexa 647	712-605-153

All secondary antibodies were from Jackson ImmunoResearch and were used at 1/200 dilution in blocking buffer.

The slices were imaged with a confocal microscope (Zeiss LSM 700), and confocal z-stacks were compared with the previously acquired in vivo imaging planes and z-stacks of the recording sites(Keller and Martin, 2015; Kerlin et al., 2010). We determined the approximate location of the injection site using GCaMP6 fluorescence, and then used blood vessel patterns and cellular morphology to identify the imaging site. We matched at least three points in the confocal z-stack to points in the in vivo imaging plane to obtain a 3-dimensional transformation matrix which was applied to the entire confocal z-stack. Cells were then manually identified and assigned to cell classes based on immunostaining.

To measure the overlap of labelling by transgenic mouse lines and immunostaining, we performed immunostaining on PV, SOM, and VIP transgenic mice (2 mice each) expressing tdTomato in the respective interneuron class, and determined the percentage of overlap between immunostaining and transgenic marker expression, which in each case was above 90%.

Genotype	Immuno +	Also tdTomato +	Percent
PV	250	236	94.4%
SOM	167	164	98.2%
VIP	152	139	91.4%

We further measured the percentage of transgenically labelled cells that were also identified as belonging to the same interneuron class by immunostaining:

Genotype	tdTomato +	Also Immuno +	Percent
PV	312	289	92.6%
SOM	278	195	70.1%
VIP	233	188	85.4%

These values are, however, more relevant for studies relying on transgenic mouse lines to categorise cell classes. The lower values of overlap for SOM cells have been previously reported (Pfeffer et al 2013, Tasic et al, 2016).

Simultaneous loose patch and fluorescence measurements

Crosses between PV-Cre (JAX: 008069) and Rosa-CAG-LSL-tdTomato (JAX: 007914) (4 males) were injected with GCaMP6f expressing AAV virus (AAV1.Syn.GCaMP6f.WPRE, vector core, University of Pennsylvania Gene Therapy Program) and VIP-Cre (JAX: 010908, 3 males) or SOM-Cre (JAX: 013044, 3 females) mice were injected with AAV1.Syn.Flex.GCaMP6f.WPRE.SV40, (vector core, University of Pennsylvania Gene Therapy Program) in V1 at P27-P40. After 9-16 days, animals were anesthetized with pentobarbital (150mg/kg), and brains were intracardially perfused by ice cold Choline Chloride solution containing 110 mM Choline chloride, 11.60 mM Na- ascorbate, 7 mM MgCl₂, 3.10 mM Na-Pyruvate, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 25 mM NaHCO₃, and 25 mM D-Glucose bubbled with a 5% CO₂, 95% O₂ mixture. Coronal slices of cortex (350 µm) were cut in the same Choline chloride solution using a VT1200S vibratome (Leica). After 30 minutes at 32 degrees in ACSF containing 125 mM NaCl, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 26 mM NaHCO₃, 2 mM MgCl₂, 1 mM CaCl₂, 25 mM D-Glucose bubbled with a 5% CO₂, 95% O₂ mixture, slices were brought to room temperature.

Loose patch recordings were performed at 32 degrees in ACSF. Pipettes (5-7 MΩ) filled with 5 mM KCl, 115 mM K-gluconate, 10 mM K-HEPES, 4 mM MgATP, 0.3 mM NaGTP, 10 mM Na-phosphocreatine, 0.1% w/v biocytin were lowered in the bath. Fluorescent cells were targeted for loose-cell patch clamp recordings (seal > 50 MΩ). To induce activity in otherwise quiet slices, a second glass pipette with a potassium-based solution was placed above the recorded cell and slight positive pressure was applied to trigger activity in the recorded neuron. This pipette contained a mixture of internal solution and a diluting solution in 3:7 ratio. The diluting solution contained 150 mM NaCl, 2.5 mM KCl and 10 mM Hepes (final potassium concentration 48 mM). Electrophysiological signals were acquired using a Multiclamp 700B (Axon instruments) filtered between 1 Hz to 2 KHz and digitized at 20 KHz with a NI-PCI6229 (National Instruments) and acquired with WinWCP (John Dempster, University of Strathclyde). Extracellular spikes were detected using custom Python scripts. Simultaneous two-photon imaging was performed at 34 Hz frame rate using a custom-built two-photon microscope at a wavelength of 940 nm, through a 16× water immersion objective (0.8 NA, Nikon).

Data analysis

Image stacks were corrected for motion and regions of interest (ROIs) were selected for each cell in each session. Raw fluorescence time series F(t) were obtained for each cell by averaging across pixels within each ROI. Baseline fluorescence F₀(t) was computed by smoothing F(t) (causal moving average of 0.375s) and determining for each time point the minimum value in the preceding 600s time window (120s for slice experiments). The change in fluorescence relative to baseline, ΔF/F, was computed by taking the difference between F and F₀, and dividing by F₀. To test the influence of out-of-focus fluorescence from the neuropil surrounding cell body ROIs on neuronal responses of the difference cell classes and learning-related changes, we repeated the key analyses after adapting the method of Ref. (Chen et al., 2013) to correct for neuropil contamination of calcium traces (Supplementary Fig. 12). We created for each cell a neuropil mask by extending the ROI by 25μm and taking all pixels that were more than 10μm away from the cell boundary, excluding pixels assigned to other cells. In order to avoid including segments of dendrites and axons in the neuropil mask, we computed for each pixel the average fluorescence across all frames, and excluded pixels that were more than 2 standard deviations brighter than the mean across all pixels in the neuropil mask. We performed a robust regression on the relationship between the fluorescence values of the ROI and neuropil mask. By inspecting the slope of this regression in a sample of our dataset we obtained a factor of 0.7 by which we multiplied the neuropil mask fluorescence before subtracting it from the ROI fluorescence.

Responses were analyzed separately for the vertical and angled grating corridor by aligning neuronal activity to the onset of the grating corridors. We used a Wilcoxon rank-sum test to determine if the response of a cell (average ΔF/F in a time window of 0-1 s after grating onset) was significantly different for vertical and angled gratings (P < 0.05). Within stimulus conditions, we used a Wilcoxon signed-rank test to determine if the response (ΔF/F 0-1 s) to the gratings significantly increased or decreased relative to baseline (-0.5 to 0 s). For visualizing stimulus-evoked responses (Fig. 1e, Supplementary Fig. 2a, b, 3, 4b, e), and for computing the change in stimulus-evoked responses with learning (Supplementary Fig. 4c, f), we subtracted the pre-stimulus baseline (-0.5 to 0 s before stimulus onset) from the average response. For each cell the time to peak response was defined as the time of the maximum of the average ΔF/F in the window of -0.5 to 2s after stimulus onset (Supplementary Fig. 2d).

We quantified the selectivity of each cell as the selectivity index (SI) which was the difference between the mean response (0-1 s) to the vertical and angled grating divided by the pooled standard deviation. The selectivity was positive for cells that preferred the vertical grating and negative for cells that preferred the angled grating. To obtain an average measure of the selectivity across a population of cells including vertical and angled preferring cells, we took the average of the absolute selectivity of all cells (Fig. 2c, Supplementary Fig. 6d-i, 13a). We calculated the selectivity of the local PYR population around each interneuron by averaging the responses of all PYR cells within 100 μm distance, to the two grating stimuli (Fig. 2e, f, Supplementary Fig. 12b). We calculated the confidence intervals for the slope in these figures by a bootstrap procedure where we randomly selected cells with replacement 10,000 times to obtain the 2.5 and 97.5 percentiles. The P value was given by the percentage of bootstrapped pre learning slope values that were lower than the post learning slope multiplied by two (two-sided test). To compute Δselectivity, we subtracted the absolute selectivity before learning from the absolute selectivity after learning (Fig. 4c, d, Fig. 5, Supplementary Fig. 12).

We used the Pearson correlation coefficient to quantify the correlation between responses of pairs of cells. The significance of the correlation coefficient was determined using Student's t-distribution. Noise correlation was computed by first subtracting for each trial and each cell the average responses across all trials. For analysis of noise correlations, we only included cells that significantly responded to grating stimulus onset. Changes in noise correlations with learning between different cell types (Fig. 3c) were tested using a sign test with Bonferroni correction on all cells imaged pre and post learning.

We quantified differences between response profiles across cell classes by using a random forest decoder that classified cells to one of two classes based on the shape of the baseline-subtracted response, averaged across all trials (Fig. 1g, Supplementary Fig. 2e). For a given pair of cell classes, we randomly picked 20 cells of each class to train the decoder (Matlab function TreeBagger, with parameters N_trees = 32, minleaf = 5), and estimated the accuracy of classifying the cells of each class that were not used for training. We repeated this procedure 1000 times for each pair of cell classes and averaged the accuracies to obtain the classification accuracy. In order to estimate the baseline classification accuracy, we randomly picked two sets of 20 cells from the same class to train the decoder. We used the classification accuracy (CA) to compute the similarity score SS = 2×(1-CA), where scores near 0 and 1 indicate low and high PSTH similarity between two cell classes respectively.

Linear Dynamical System Model

We modelled the activity of simultaneously imaged neurons with a linear dynamical system. The interactions between cells were modelled with a weight matrix A. The stimulus drive to each cell was modelled with an input time series I_t which was fixed across trials for a given stimulus, where t indexes time relative to stimulus onset. Running speed related modulation of responses was modelled as an additional input $\xi v_t^{\left(i\right)},$ where ξ is a vector of coefficients that determines the speed modulation of each cell and $v_t^{\left(i\right)}$ is the running speed at time sample t on trial i.

For each imaging session, we extracted trials spanning -1 to 1 s relative to the onset of the two grating stimuli and the onset of the grey pre-stimulus period. We then fit the following equation to the population activity:

$${\mathbf{\text{r}}}_t^{\left(i\right)}={\mathbf{\text{r}}}_{t-1}^{\left(i\right)}+{\mathbf{\text{Ar}}}_{t-1}^{\left(i\right)}+{\mathbf{\text{I}}}_t+\xi v_t^{\left(i\right)}+e_t^{\left(i\right)}$$ (1)

by minimizing the sum of squared residuals over all trials i and time samples $t:{\mathbf{\text{r}}}_t^{\left(i\right)}\left\{\mathbf{\text{A}};{\mathbf{\text{I}}}_t;\xi \right\}=\text{arg}\text{min}({\displaystyle {\sum }_{i,t}\parallel {\mathbf{\text{e}}}_t^{\left(i\right)}{\parallel }^2}).$ A and ξ were set to be stimulus-independent whereas I_t was set to be stimulus-dependent. The model was fit separately pre and post learning to infer the changes in parameters with learning. Model fitting was blind to cell type.

To analyze the contribution of neuronal interactions and stimulus-related inputs to the measured responses we derived analytical expressions for the responses produced by the model under a given set of parameters:

$${\mathbf{\text{r}}}_{\text{t}}^{\left(i\right)}={\left(\mathbf{\text{A}}+\text{𝕀}\right)}^t{\mathbf{\text{r}}}_0^{\left(i\right)}+{\displaystyle {\sum }_{\tau =1}^t{\left(\mathbf{\text{A}}+\text{𝕀}\right)}^{\text{t}-\tau }({\mathbf{\text{I}}}_{\text{t}}+\mathbf{\xi }{\text{v}}_{\tau }^{\left(i\right)}+{\mathbf{\text{e}}}_{\tau }^{\left(i\right)})}$$ (2)

where ${\mathbf{\text{r}}}_0^{\left(i\right)}$ is the measured activity one time step before trial onset (note that trial onset begins 1 second before stimulus onset) and 𝕀 is the identity matrix. Using this equation, we computed the population responses when weights were deleted (set to zero) and when residuals were shuffled (Fig. 3f, g). In the model, the interaction weights are a function of only the covariance of the data (see Equation.XXX) and the residuals contain any variability not captured by the model. The degree to which the observed covariance was accounted for by correlations in the residuals was assessed by simulating the responses after shuffling the residuals. To determine the degree to which the observed covariance was accounted for by interaction weights, we simulated responses after shuffling or deleting the interaction weights. These manipulations allowed us to test whether the model captured the coordinated variability in the data using a set of parameters fixed across trials, without requiring any additional unexplained inputs that covary across trials or time.

To shuffle residuals in Fig. 3f, g, we randomly permuted the trial labels of the residuals across all vertical stimulus trials separately for each cell and then computed the responses according to Equation (2) by substituting the shuffled residuals. Having calculated the responses under residual shuffling, we then computed pair-wise noise correlations using the same method as for the experimental data. We repeated this for 100 random shuffles and averaged over the noise correlations generated by these shuffles for each cell pair. To calculate the noise correlations when interactions are removed (Fig. 3f, g), we set all off-diagonal elements of the interaction matrix A to zero and then computed the responses according to Equation (2). We again calculated the noise correlations of these responses as above. To quantify the quality of the fit after shuffling residuals and removing interactions we computed R².

To compute the selectivity of responses following weight deletions we set all off-diagonal weights of a given type to zero (leaving diagonal elements of the weight matrix intact), calculated responses as above, and averaged responses for each cell to the vertical and angled stimulus similar to the experimental data. Because the interaction weights in the LDS organize to best capture the variance in the data (see below), deleting weights removes the majority of simulated response variance. We therefore used the measured variance to calculate selectivity after weight deletions.

To test whether interaction weights identified by the model were dependent on the stimulus-input preference of the cell (Fig. 4b). We separated cell pairs into groups according to the mean stimulus input they received in the 0 to 1 s window from stimulus onset at the vertical and angled gratings. If both cells in the pair had a larger stimulus input at the same grating, they were considered to have the same grating preference (either to the vertical or angled stimulus), otherwise they were considered to have opposite preferences. We measured the mean interaction weight between cell pairs that preferred the same or different gratings. Only cells whose responses were significantly different to the vertical and angled gratings were included in the analysis (criterion P < 0.05, Wilcoxon rank-sum test).

To determine whether the effect a of specific weight deletion changed with learning, we computed the selectivity index with all weights intact SI_full and the selectivity with a specific weight deleted SI_del pre and post learning, and then compared |SI_del,pre| − |SI_full,pre| to |SI_del,post| − |SI_full,post| using a sign test.

To fit the model across learning while constraining certain parameters to remain fixed, we fit Equation (1) jointly to the pre and post learning trials for each mouse by minimizing the sum of squared residuals across all combined pre and post learning trials with a subset of parameters free to take on different values for pre and post learning trials and a subset set to be the same for pre and post learning trials.

To compute the changes of selectivity across learning generated by a model with a given set of parameters fixed, we shuffled the trial labels of the residuals across the combined set of pre and post learning trials (leaving the residuals across cells and time within a given trial intact). We then recomputed the responses using Equation (2) by substituting the shuffled residuals, and computed the selectivity of these responses pre and post learning. We repeated this process for 100 random shuffles and averaged the resulting selectivity over shuffles. We then computed the R² value of the model-generated change in selectivity vs the change in selectivity observed in the data. To generate confidence intervals for these R² values we performed a bootstrap over cells.

To perform hypothesis testing that two models (Model 1 and Model 2) generated R² values that differed more than would be expected by chance, we performed a model-based bootstrap. For the model-based bootstrap, we first fit the data to Model 1. We then generated a new dataset from Model 1 by randomly resampling residuals (with replacement) and computing responses according to Equation (2). Next, we fit Models 1 and 2 to the dataset generated from Model 1, and computed the R² of the change in selectivity generated by these models against the change in selectivity in the simulated dataset from Model 1. We repeated this process 500 times to obtain a distribution of the difference in R² between Model 1 and Model 2 that would be expected if the data were generated by Model 1.