Abstract
Research into cellular engineered bone grafts offers a promising solution to problems associated with the currently used auto- and allografts. Bioreactor systems can facilitate the development of functional cellular bone grafts by augmenting mass transport through media convection and shear flow-induced mechanical stimulation. Developing successful and reproducible protocols for growing bone tissue in vitro is dependent on tuning the bioreactor operating conditions to the specific cell type and graft design. This process, largely reliant on a trial-and-error approach, is challenging, time-consuming and expensive. Modelling can streamline the process by providing further insight into the effect of the bioreactor environment on the cell culture, and by identifying a beneficial range of operational settings to stimulate tissue production. Models can explore the impact of changing flow speeds, scaffold properties, and nutrient and growth factor concentrations. Aiming to act as an introductory reference for bone tissue engineers looking to direct their experimental work, this article presents a comprehensive framework of mathematical models on various aspects of bioreactor bone cultures and overviews modelling case studies from literature.
Keywords: Mathematical modelling, bioreactors, bone tissue engineering, parameterisation
Background
There is a high demand for functional bone grafts to treat bone trauma, with approximately 2 million procedures performed annually worldwide.1,2 They are applied in reconstructive interventions after tumour recession, in spinal fusions and in the treatment of non-union fractures (defined by a failure to heal 6 months after the injury). Non-unions occur at a rate of 2% of all fractures,3 and at 5% of long bone fractures.4 Their prevalence is projected to increase as the population ages.1 Non-unions are more common after high-impact open fractures, associated with severe damage to the blood vessels near the injury.3 Smoking, alcohol consumption, obesity and diabetes, which lead to reduced mineralisation and constriction of blood vessels, are further risk factors5 causing a predisposition to non-union fractures.
The current gold standard in bone grafting is to use autologous or allogeneic implants to induce osteo-regeneration. Complications such as haematoma, blood loss, infection and neurovascular injuries occur in up to 39% of autologous graft patients.6 There is a danger of chronic pain, cosmetic deformity and even increased probability of subsequent fracture at the donor site.6 Currently, the rate of surgical revisions after bone grafting procedures is high – for autologous grafting, it is 17%; for treatment with recombinant human bone morphogenetic proteins (rhBMPs), 22%; and for allografts, above 30%.7 This motivates the need to develop new therapeutic strategies, one of which is tissue engineering. Tissue engineering has the potential to contribute in this arena as a histocompatible solution which delivers the patient’s own cells in a graft of controllable size and shape.
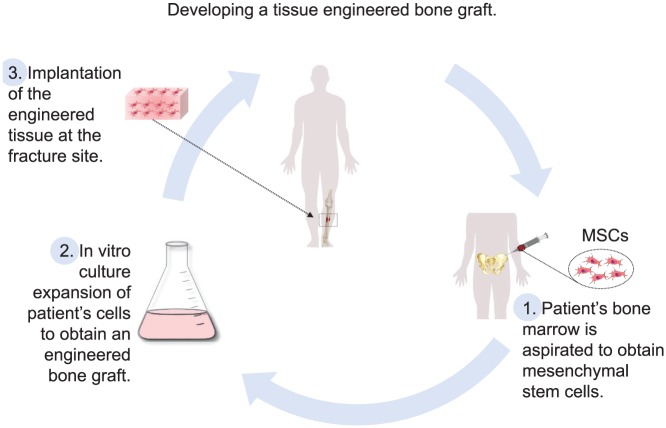
The established strategy for cell-based engineered bone grafts is to grow an autologous cell population in vitro on biocompatible three-dimensional (3D) scaffolds until a functional graft is produced.8–11 This is then implanted in vivo at the fracture site to induce and promote healing (Figure 1).
Figure 1.
Diagram demonstrating the main bone tissue engineering paradigm: (1) obtaining the patient’s stem cells from a bone marrow aspirate; (2) expanding the cell culture to clinically relevant numbers and achieving homogeneous seeding of the biocompatible scaffold; and (3) implanting the tissue engineered construct at the fracture site.
The cell component of engineered grafts is essential to improve engineered bone graft performance as shown in preclinical trials.12–14 Cells enable the grafts to be osteoinductive,15 with the seeded cells driving the remodelling process inside critically sized defects too large to be bridged by the surrounding native cells.16 This is especially pertinent for patients who suffer from decreased activity of osteoprogenitors due to comorbidities such as diabetes and osteoporosis.5,17 The cell types used in grafts can be osteogenic cells such as osteoblasts, dedicated engineered osteoprogenitor cell lines or stem cells – mesenchymal stem cells (MSCs), human induced pluripotent stem cells (hiPSCs) or human embryonic stem cells (hESCs).2,9,15,17,18 As the natural osteogenic precursors,9,19 MSCs are commonly identified to be the best cell source.8,20,21 They have long been used in different cell therapies and are preferred as a result of their potential for self-renewal and multilineage differentiation.2 They also act as immunosuppressors in vivo,15 enabling allogeneic transplantation.22,23
MSCs-based engineered bone grafts have been used in a number of single or small-cohort clinical studies to treat long bone fractures and dental or facial defects.8,15 These studies demonstrated the potential of the new therapy to successfully promote bone healing in cases where autologous grafting was deemed unsuitable. However, biopsies taken in the clinical studies have indicated that the grafted MSCs had difficulty forming new bone.15 While no clinical studies have evaluated the efficacy of the engineered grafts in comparison with control groups treated with autografts or allografts, in preclinical testing, cell-based tissue engineered constructs have not performed as well as autografts.24,25
Therefore, generating fully functional bone grafts remains an outstanding tissue engineering problem.18 The desired grafts should deliver a clinically relevant, uniformly spread cell mass,10 sufficient to induce healing.19–21 The inferior performance of current engineered grafts in comparison with autografts could be the result of deficiencies in the in vitro culture used to scale-up the grafts to sizes fit for the clinic. Mimicking the in vivo environment as closely as possible, for instance, by preserving 3D cell-to-cell contact, is essential to maintaining cellular functionality and phenotype.9,11,26 Growing cell cultures on premade scaffolds, on spherical microcarriers, or as multicellular spheroids, are some of the techniques available to retain the complex architecture of cellular signalling and improve tissue viability.26 The main challenge then is to prevent mass transfer limitations in these cultures.10,27,28 Exposure of the cells to severe hypoxia in vitro could impair their potential for differentiation and mineralisation.29,30 Hypoxia is especially common in static cultures, where transport is diffusion-only dependent, and constructs grown there have a proliferating periphery but a necrotic core.10
Bioreactors, however, provide dynamic mixing of the culture medium through convection. Thus, they augment mass transport and provide a controlled environment, crucial for developing reproducible protocols.10,11 Apart from delivering higher nutrient concentrations, they recreate the in vivo environment more realistically as the flow passing through the 3D construct mimics the interstitial flow between the blood and lymphatic vessels experienced in bone tissue in vivo.31 The fluid shear stresses thus induced trigger bone tissue mineralisation,11 which has been shown to be sensitive to mechanical cues.32,33 Overall, flow in bioreactors facilitates osteogenic differentiation and proliferation, and improves seeding efficiency and homogeneity of cell spreading in constructs cultured under convective conditions.34
Despite the considerable advances in bioreactor systems for tissue engineering, preclinical testing has not shown significant improvement in in vivo performance of bone grafts grown in vitro in bioreactors rather than in static cultures.34 Further work is needed to select the appropriate bioreactor operating conditions to develop reproducible protocols for producing more functional bone grafts. Better understanding of how the multiple factors (fluid flow, nutrient distribution and flow shear stress) inside dynamic bioreactors affect in vitro tissue morphogenesis is required. This is where mathematical and computational modelling can be immensely useful by elucidating the complex underlying processes and enabling the comparison of various culture conditions in a quick and efficient manner.
Significance of mathematical modelling in bioreactor systems for bone tissue engineering
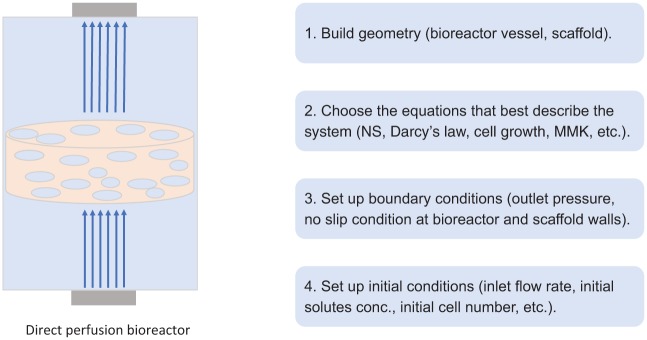
Mathematical modelling can be used to study and improve specific experimental tissue engineering protocols and outcomes. The models can simulate the chemical, physical and biological components of the culture and study their interactions in a cause-and-effect manner. Before choosing the appropriate equations to model these components, which are overviewed in the section ‘Continuum and discrete models’, the correct geometry needs to be prescribed for both the culture vessel and the tissue construct (Figure 2). To finish setting the model, initial and boundary conditions need to be imposed.
Figure 2.
Figure showing the steps of setting up a mathematical model: (1) building the geometry of the investigated system; (2) choosing the system of equations to describe the culture; (3) and (4) imposing the appropriate initial and boundary conditions. These are the essential stages required to set up a basic functional mathematical model of a cell culture.
The model can then produce detailed quantitative spatial and temporal knowledge of the flow velocities, chemical distributions and shear stresses inside the in vitro culture. Crucially, the level of insight offered by modelling cannot be obtained by means of experimentation in isolation.
The main benefit of bioreactors, convection, is the most challenging to characterise. It determines both nutrient mixing and the fluid shear force experienced by the cells, affecting tissue development. While experiments such as particle image velocimetry (PIV) cannot easily quantify the flow field in the system, computational fluid dynamics (CFD) can be applied to simulate the flow based on the scaffold and bioreactor geometry. Fluid flow can then be used to estimate the fluid shear stress stimulation on the cells and calculate solute fields of nutrients and waste products.
Using models to predict culture outcomes in this way requires robust calibration of simulation results against experimental data.28,35,36 Custom-designed, small-scale experiments, characterising the culture in terms of cell number, metabolite concentration or media acidity, for example, can be a convenient and quick source of such data.
These parameterised models then allow different culture protocols to be tested, saving both time and resources in comparison with using only experimentation. The models can be used to make more objective comparisons between the culture conditions in different bioreactors and predict and assess the cell-type-specific response in terms of universal criteria such as the size and cell density of the produced tissue construct. This can inform which bioreactor is suitable for scaling up the production of engineered tissue to clinically relevant sizes. Furthermore, the models can propose the convection regime within the bioreactor which optimises nutrient delivery and mechanical stimulation in the culture. Increasing the flow rate to minimise the presence of anoxic regions has to be balanced against potential cellular damage as a result of excessive flow shear stresses.33 More efficient application of chemical factors and their spatial location can also be informed by modelling, for instance, media supplements to induce osteogenesis or rhBMPs to trigger bone development.37
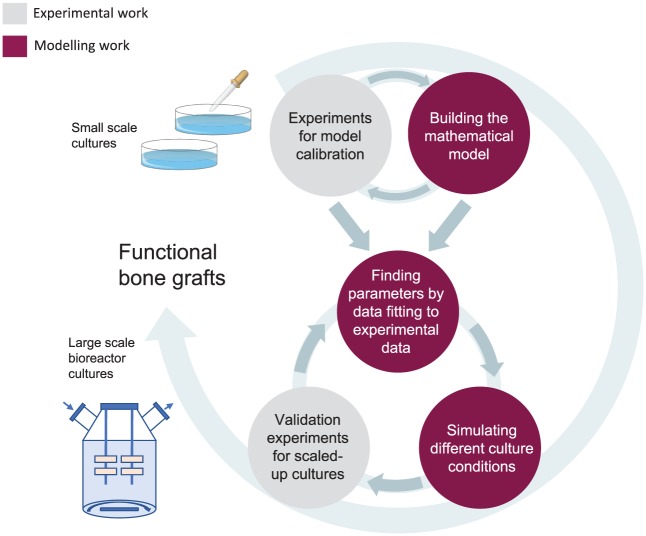
A strong collaboration between modelling and experimentation, where dedicated experiments inform models which in turn suggest improvements to the in vitro protocols, is crucial to the development of successful tissue engineering strategies (Figure 3). This has the potential to streamline the development of functional engineered grafts for clinical testing as novel treatments.18 Nevertheless, it is important to highlight that models are only approximate representations of the biological reality, and their results need to be experimentally validated.
Figure 3.
Diagram demonstrating the collaboration between modelling and experimentation, culminating in the development of protocols for large-scale tissue engineering informed by experiment-parameterised models. Calibration experiments can be used to inform a mathematical model, which can then be parameterised to the experimental measurements. The parameterised model can then provide predictions about the effect of different operating conditions on culture growth, proposing a range which improves cell yield. Upon an experimental validation of these suggestions and implementing any necessary adjustments, new robust and more efficient protocols for bone tissue engineering are developed.
A review by Vetsch et al.38 summarises the progress achieved in modelling culture systems for bone tissue engineering. While studies of both the mechanical and biological environment for multiple bioreactors are presented, the bulk of the work focuses on the mechanical aspects. The tissue and its evolution with time are not often considered in the cited studies, and these are highly important components in developing clinical therapies.
Here, we overview mathematical models of in vitro cultures for bone tissue engineering in the literature. The traditional dynamic systems – spinner flasks, rotating wall, perfusion and hollow fibre bioreactors – are considered. Technologies under development, such as magnetic force bioreactors and mechanical conditioning systems,10,11 which provide direct mechanical stimulation by stretching or compression, are also included. A comprehensive framework of equations, modelling various aspects of the tissue culture, is presented, aiming to act as a summary for bone tissue engineers looking to complement and optimise their experimental work. We highlight the three major model components: (1) flow and pressure profiles, and resulting mechanical forces; (2) nutrient distribution, time-dependent diffusion and consumption by the tissue; and (3) cell behaviour, growth and spreading. Case studies are provided, where modelling investigations focus on one or a combination of these to inform, for instance, the relationship between flow and cell response,39–41 to design scaffold structure42 or to advise oxygen requirements.43,44
Continuum and discrete models
There are two main approaches to the mathematical representation of bioreactor systems and the tissues cultured in them – continuum and discrete models. Continuum models provide a description of the averaged behaviour of the system. They are based on the assumption that the cells and tissue are a number of continuous materials able to occupy the same space.45 Homogenisation techniques based on microscopic considerations can be employed to derive the constitutive relationships describing the properties of and interactions between the material phases. In the absence of theoretical laws, empirically inferred dependencies can be found through experiments. Continuum models naturally represent large populations of cells and accommodate the fluid dynamics theory with the Navier–Stokes (NS) equations.
In contrast, discrete models treat cells as a combination of separate entities. Computational algorithms, which determine cell fate based on preset criteria, are used to model the evolution of the cell lineage. Complex behaviour such as movement of individual cells, intercellular interaction and signalling processes can be recreated, as well as phenomena such as cellular division and self-organisation into clusters.45 Discrete models are most commonly aimed at improving the fundamental understanding of tissue formation.
Both modelling strategies have their merits and provide a unique insight. Discrete models preserve a high level of detail about the stochastic nature of cell-level processes. A crucial limitation is finding appropriate values for the unknown parameters, which are nearly impossible to measure experimentally at the scale of individual cells. Computational costs make it prohibitive to capture large cell populations, rendering discrete models ill-suited to evaluate the overall performance of bioreactor systems and to design optimal protocols for clinically relevant tissue samples.45
Continuum macro-scale models are more useful for this purpose. They provide sufficient information about the chemical and mechanical environment even in constructs with very complex geometries.11 Simplifications to analytical or asymptotic solutions can be made (eg. using disparate timescales for transport versus cell processes), reducing the dependence on numerical computations and facilitating comparisons to experiments. A drawback of continuum models is the loss of individual cell-scale data, important when interested, for instance, in the random motility of cells or the development of spatial inhomogeneity in tissue constructs.46,47
In the context of developing predictive models based on experimental work, it is important to consider the nature of the experimental data available. For example, if imaging data on individual cells are available, then a discrete model could be appropriate. However, if the only information about cell number is an averaged estimation from DNA or absorbance-based assays, then only a continuum model would be suitable. Furthermore, as continuum and discrete models approach the modelling of the key culture components differently, one modelling approach may be more amenable than the other to a particular setup. For example, there is not a readily established method of simulating chemical distribution in discrete models, which might make them unsuitable for a model with an emphasis on metabolic behaviour. Discrete models are also associated with a larger number of free parameters, which may hinder the ability to perform meaningful parameterisation of the model.
An important feature of any model is the scale: pore (micro) or construct (macro) scale, at which the process of tissue growth is considered. Both continuum and discrete models apply different techniques and relationships to describe the behaviour of biological tissues at the micro- or macro-scale, as overviewed in the following sections. Increasingly, however, instead of focusing on one scale, multiscale models are developed which use homogenisation multiscale asymptotics or volume averaging approaches to derive averaged models determined by micro-scale features.48–50 A good introduction into the theory can be found in the study of Davit et al.51 Such multiscale models can have either a discrete or continuous formulation at the micro-scale and are continuous at the macro-scale.
Within the context of tissue engineering of bone and related tissues and processes, material properties are determined at the micro-scale by exploiting repetitive unit cells or representative volume elements (RVEs) in the geometry, often informed by micro-computed tomography (CT) images.52–54 The material properties (density, elastic and poroelastic modulus) resulting from this approach are a function of the volume fraction of different homogeneous material phases (pores, scaffold and tissue) within the RVE. Homogenised stiffness tensors can incorporate these material properties for each scale: micro, meso or macro.55 Downscaling schemes can then be used to derive the stress and strain levels at the micro-scale from known mechanical loads at the macro-scale to model bone remodelling driven by pore-specific mechanosensation.56,57 In contrast, some models exploit the separation of the micro- and macro-scales through asymptotic techniques and applying knowledge of the pore-scale, derive construct-level models, for example, to obtain Darcy-type description of mass transport58 or poroelastic continuum formulations of tissue growth resulting from nutrient exchange with the liquid phase.59
In the following section, we present the most common modelling approaches relevant to in vitro cultures, before going on to discuss their application to specific bioreactor setups.
Modelling the flow environment
As discussed, one of the most fundamental benefits of mathematical modelling in tissue engineering is the ability to quantify the fluid dynamics of the system. Continuum models use the NS equations for mass conservation
| (1) |
and momentum conservation
| (2) |
to describe the flow of free culture media,60 where u (m/s) is the velocity vector, (kg/m3) is the density, is the body force due to gravity, (Pa) is the pressure and µ (N∙s/m2) is the viscosity. The media is usually considered to be an incompressible Newtonian fluid with constant viscosity and density,61 reducing equations (1) and (2) to
| (3) |
and
| (4) |
The left-hand side of equation (4) describes the inertial forces, where the first term is the time-dependent change in momentum and the second term is the momentum change due to convection. The right-hand side of the equation includes the pressure force (), the body force due to gravity and the viscous force. Once the initial and boundary conditions have been prescribed, the equation is solved to obtain the velocity field (u) and the pressure. These can then be used to evaluate the transport of nutrients and waste products.
The NS equations can be applied to the free flow at both the macro- and the micro-scale in all bioreactor systems, provided the fluid is Newtonian. NS equations have, for instance, been used to model the complex semi-turbulent flows in spinner flasks.62 They are often applied to quantify the bulk flow in 3D models of perfusion cultures40,44,63,64 and the flow of media through the lumen in hollow fibre reactors.65,66
Velocity and pressure in rotating wall bioreactors are also found using the NS equations,67 unless they are experimentally determined68 or computed using a drag-coefficient-based strategy.36 Applied to this bioreactor system, NS equations are considered in the rotational frame of reference, where the effect of the Coriolis and centrifugal forces have to be included in addition to the hydrodynamic and gravitational forces. The velocity and pressure information is then coupled to the descriptions of scaffold motion to predict the movement of scaffolds inside the bioreactor. The acceleration of these objects due to the net combination of gravitational, buoyancy, centrifugal, Coriolis and drag forces36,67 is determined. Pollack et al.69 and Cummings and Waters70 use this approach to find the velocity and trajectory of scaffolds or microcarriers inside rotating wall bioreactors.
At the micro-scale (cell-scale), detailed information about the geometry alongside appropriate boundary conditions is sufficient to solve the entire flow field applying the NS equations. Advanced imaging tools such as micro-CT (µ-CT) scans of scaffolds provide 3D images with a resolution of 30–70 µm or smaller. These geometries are then used as the substrate for fluid flow simulations. CFD finite element models, combined with no-slip and no-flux boundary conditions on the fluid–solid interface, and appropriate initial conditions found from macro-scale solutions, are applied.41,64 While the micro-scale velocity and pressure field solutions are very detailed, obtaining them is computationally intensive and the solutions are difficult to validate experimentally, as it is usually difficult to make measurements at this length scale. It is often prohibitive to model large scaffold volumes in their entirety, so often the preferred option is to model instead representative smaller elements. Such practice is employed, for example, in order to quantify the errors of macro-scale estimates and evaluate their reliability.41
At the macro-scale, while NS equations are suitable for free media flow, they cannot be used for flow through porous media (scaffolds). In those cases, an estimate derived from the averaged behaviour at the micro-scale is used. One such estimate is Darcy’s law37
| (5) |
where (m2) is the permeability of the porous medium. The flux is proportional to and occurs in the direction of the pressure drop and is reduced as viscosity increases. The permeability can either be measured experimentally or prescribed as a function of the micro-scale geometry using constitutive laws or mathematical averaging techniques.58
Sometimes, a variation of Darcy’s law – Brinkman’s equation71 – is adopted to incorporate viscous shear effects72
| (6) |
where is the effective Brinkman’s viscosity of the porous medium, while (%) is its porosity. Brinkman’s equation is valid only when the volume fraction of the solid is small.73
Either equation is typically adopted for flow through scaffolds in perfusion bioreactors.63,64 They are also used in hollow fibre bioreactors for the flow across the fibre membrane and inside the extra-capillary space to capture the flow properties of a cell-packed tissue matrix.65,66
Discrete models, however, use the lattice Boltzmann (LB) method to describe the flow. The LB approach adopts the molecular theory of fluids and uses an algorithm to calculate the velocity of each molecule. This method provides a second-order computational approximation to the NS equations and is also easily and efficiently implemented computationally. It readily integrates with micro-tomography scans of scaffold geometries, so it is capable of capturing detailed information about the flow at the micro-structure while requiring less computational power than continuum micro-scale models, making it an attractive modelling choice. It has commonly been applied to the complex flow through porous scaffolds in perfusion bioreactors39,74 where resolving stresses at the micro-scale is essential for the culture optimisation.
Modelling the mechanical environment due to fluid flow
The trajectory and magnitude of the flow can then be used to determine the fluid shear stress exerted on the cells or as an approximation, the scaffold walls. The total wall shear stress (WSS) at any position75 in a scaffold can be calculated by
| (7) |
where
| (8) |
and (m/s) are the three components of velocity in the and directions, respectively, in the Cartesian coordinate system (Figure 4(a)). Gutierrez and Crumpler75 used this approach to explore flow shear stress dependency on scaffold geometry in rotating wall bioreactors, aiming to propose scaffold designs which eliminate damagingly high shear on cells. NS-based fluid flow simulations were used to model the WSS on the scaffold surface of a disc-shaped scaffold. With the goal of reducing maximum WSS and increasing the homogeneity of the stress field across the surface, an alternative spheroid geometry was proposed where sharp edges were removed, as they are points of critical stress, and the surface area was maximised.
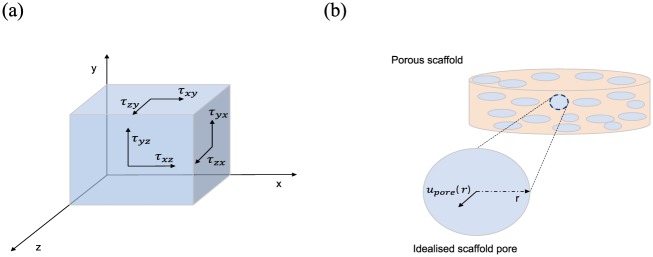
Figure 4.
(a) A 3D graphical representation of the shear stresses, exemplified on the sides of a box, which are used to calculate the wall shear stress (equations (7) and (8)); (b) an example of an idealised perfectly circular pore, which is used to calculate the velocity inside the pore and subsequently the wall shear stress exerted on the pore walls (equations (9)–(11)).
This micro-scale CFD approach for finding WSS has also been used for perfusion44 and rotating wall bioreactors, as well as mechanical conditioning systems.42
In contrast, the procedure for finding shear stresses in macro-scale continuum models is less straightforward. Darcy’s law provides an approximation for the macro-scale velocity as a function of position, which can be rescaled to estimate the average velocity inside a typical pore76
| (9) |
where (m/s) is the velocity found using Darcy’s law, (%) is the porosity of the scaffold and (0–1) is the corresponding tortuosity. The unknown average velocity inside a pore, (m/s), is an average measure based on a typical pore shape and size (Figure 4(b)), and it is informative to find the velocity in the radial direction : , modelling the pores as cylindrical ducts with a diameter (m) and considering Poiseuille’s flow of an incompressible Newtonian fluid
| (10) |
The WSS, (Pa), can then be found using a simplified version of equation (7) since the flow is one-dimensional
| (11) |
In discrete models, the velocity field found with the LB method, , can be used to estimate the WSS as shown by Porter et al.39
| (12) |
The derivatives of each velocity component with respect to the three dimensions are found by means of a finite difference formula for each lattice voxel in the discrete model.39 This fluid shear stress information can be used to efficiently compare different scaffold geometries and flow settings without sacrificing crucial detail about the micro-scale architecture of the system as done in macro-scale continuum models. This procedure also requires less computational power to simulate full system volumes than micro-scale continuum models.
Modelling the transport of chemical species
Nutrients such as oxygen, waste products such as lactate, and growth factors11 affect the proliferation, differentiation and migration of cells in vitro. Having a detailed map of chemical concentrations in the culture is, therefore, necessary for controlling the cell environment. Assuming Fickian diffusion and prescribing the initial and boundary conditions, the distribution of any solute is modelled using mass conservation to give an advection–reaction–diffusion system
| (13) |
where (mol/m3) is the concentration of species , (m/s) is the media flow velocity, (m2/s) is the corresponding coefficient of diffusion and (mol/s∙m3) is a term representing the metabolic reaction.44,77
Consumption or production can be modelled using reaction kinetics equations, for example, zero-order kinetics
| (14) |
or first-order kinetics
| (15) |
In zero-order kinetics, the reaction rate is independent of the concentration of the substrate , while in first-order kinetics, it is linearly dependent on it.
Oxygen is often the limiting nutrient in in vitro cultures due to its low coefficient of diffusion, and the inability to saturate the culture with it due to the toxicity of hyperoxia.78–82 Modelling its consumption realistically is, therefore, necessary in order to reliably simulate oxygen availability. This metabolic reaction has most closely been captured by the Michaelis–Menten kinetics (MMK) relation83 for enzyme-catalysed reactions. In the case of oxygen, the MMK rate of consumption is often84–86 given by
| (16) |
where (mol/s∙m3) is the maximum rate of the reaction, while (mol/m3) is the Michaelis–Menten constant which is equal to the concentration at which the reaction rate is half the maximum ().87 can also be reported per cell (mol/s∙cell), in which case it is multiplied by the cell density (cell/m3). Both and are determined through a Lineweaver–Burk plot constructed by empirically measuring the reaction rate at various concentrations of the substrate (in this case, oxygen).88 Glucose consumption, of interest as glucose is the main source of energy to cells cultured in vitro,89 is also modelled through MMK.
The diffusion coefficient must capture the properties of the substrate through which the solute diffuses. Matrix deposition increases the density of the construct and reduces its porosity and permeability. To account for the new tissue and the loss of permeability, time- and space-dependent functions for the diffusion coefficients () are introduced in models aiming to track transport limitations due to tissue growth.76,77 Galban and Locke84 develop an effective diffusion coefficient as a function of the cell volume fraction based on Maxwell’s formula. Chung et al.63 similarly employ Maxwell’s relationship for the change in diffusion and use Carman–Kozeny’s equation for the reduction in permeability due to cell proliferation.
While these equations are often introduced in perfusion systems,63,76 they have been successfully shown for mechanical conditioning systems,77 and in the more general case within a scaffold.84
Alternatively, depending on the question addressed with the model, provided a continuous free flow of fresh media in the bioreactor, advantage can be taken of the timescale disparity between transport and growth phenomena. In such cases, a constant diffusion coefficient is appropriate.
Mass transport through engineered tissue constructs can also be altered by the deformation of the elastic scaffold materials under the influence of fluid flow. This effect is described by poroelastic or poroviscoelastic models. The increase in pore size due to fluid exerting pressure on the walls affects the flow velocity and consequently also nutrient transport. Models couple Darcy’s equation (equation (5)) to analytical structural analysis describing the displacement of elastic or viscoelastic materials under loading.77 Porosity, permeability and mechanical properties of the construct are determined using the theory of mixtures, based on the volume fractions of the extracellular matrix (ECM) and the scaffold. The change in mechanical properties due to deposition of ECM can be captured by a stored energy density function.77 This function can also take into account the history of mechanical strain experienced by the construct, where mechanical stimulation creates a stiffer, less pliant matrix.77 These models are more suitable for perfusion and mechanical conditioning systems, where the constructs experience fluid pressures and forces high enough to cause deformation.
Discrete models do not offer the capability of modelling nutrient mixing by themselves. Instead, they can be interfaced with information about nutrient distribution obtained using continuum methods and develop hybrid models. In these cases, velocity profiles obtained using the LB method are applied in continuum advection–diffusion equations for solute concentration.74
Modelling the biological species: cells and tissues
Next, we discuss models used to investigate the response of the tissue to the chemical and mechanical environment in the culture. While not all studies include this component in their analysis, it is essential for models aiming to develop improved culture protocols. The influence of a range of culture conditions on the behaviour of the cells or tissues (including ECM) is of primary interest.
Continuum models
In continuum models, the theory of mixtures is usually employed to describe cell populations or tissues. The theory evaluates the properties of composite tissues as a function of the volume fraction of their constitutive components.11 Conservation of mass37
| (17) |
and momentum equations40 are written for each phase
| (18) |
where (N/m2) is the stress tensor for each phase, (N/m3) is the force per unit volume between each phase and (0–1) is the volume fraction of each phase: culture medium, cells or ECM. The sum of all phases adds up to 1 () following conservation of mass. The biological component can also be modelled as a single-phase material, for instance, cells only, where equation (17) is used again and (cell/m3) is the cell density and the conservation of mass law above does not apply.
Equation (17) accounts for diffusive () and convective () transport of each biological phase, which are applied depending on its nature. For instance, cells are usually considered a single phase, which does not experience convection and diffuses slowly to account for random cell migration.
Cell migration can also be directed by mechanotaxis (e.g. response to materials and stress fields) or by chemotaxis, for example, towards higher concentrations of growth factors or nutrients such as oxygen.11 An additional chemotaxis term77 can be introduced in equation (17)
where is the cell fraction, (m2/s) is the chemotactic sensitivity, is the saturation cell density (cell/m3) and is the concentration of the chemical attractant.
The conservation of momentum equation (equation (18)) captures the force balance between different phases. This includes interactions between cell populations, the cells and the scaffold, and the cells and the medium.37
The reaction term in equation (17) can be used to incorporate more complex processes, such as tissue evolution through cell proliferation or deposition of ECM.11 A function determining cell growth or ECM synthesis can be introduced. Cell growth functions usually include proliferation () and death () terms which are dependent on the available cell volume fraction () and the concentration of nutrients ()
| (19) |
A commonly chosen90,91 form for equation (19) is the logistic growth law, written here in terms of cell density (cell/m3)
| (20) |
which is saturated at maximum cell density . Cell growth in this equation depends on the local oxygen concentration (mol/m3), which is assumed to be the limiting nutrient with a linear effect. In this case, the death (apoptosis) term is a constant, (cell/m3⋅s), but it can be modified further. The proliferation constant is denoted by the coefficient (m3/mol⋅s).
Another common model of cell proliferation is the exponential model which assumes the entire population as dividing at a rate (1/s)
| (21) |
where is the initial cell fraction. This growth model has also been modified to include the more complex asymmetric characteristics of heterogeneous mixtures of dividing and non-dividing cell populations, as overviewed by MacArthur et al.92 These modified models are especially applicable to stem cell populations, where terminally differentiated cells enter a resting state and no longer undergo mitosis.
While the modified Contois growth kinetics is also commonly applied to represent cell proliferation,63,84 linear growth40 and mass-structured population balance equations35 have been used as well. Lappa36 proposes a model in which organic tissue development is based on crystal growth dynamics.
Continuum models are able to reproduce the biophysical and biochemical environment in the bioreactor and use it to predict the level of cell proliferation and differentiation.11 Oxygen concentration affects the rate of proliferation, and the inhibitive effect of anoxic conditions is often depicted using a linear dependency on oxygen availability (equation (20)). However, it has been shown that high levels of oxygen can also be toxic to the cell population.30 Soares and Sacks77 propose a cell growth function where proliferation is reduced under anoxic and toxicly high oxygen levels. Similarly, Lappa36 presents a system of equations which account for the effect of both nutrient availability and mechanical stimulation on matrix deposition. While the biochemical effect is linear, the suggested shear stress dependency is non-linear. Chapman et al.93 also consider the effect of both environmental cues (oxygen and shear stress) on cell aggregate growth in hollow fibre bioreactors. They adopt a step function and pinpoint a very small window of operating conditions which augment growth due to the balance between the two opposing processes: nutrient supply and shear stress damage. Shakeel et al.76 apply a step function where proliferation is promoted at intermediate levels of shear stress and stopped at higher levels as determined experimentally by Cartmell et al.33 O’Dea et al.,40 Soares and Sacks77 and Pearson et al.37 also consider the impact of the mechanical environment, incorporating a shear stress-dependent tissue expansion term due to either stretching77 or fluid flow.37,40
The growth models discussed so far are only some of the examples used in the literature. They are strictly cell-type specific and their parameters can be found only in conjunction with experimentation.
Discrete models
All discrete models have a spatial domain that is discretised into individual points as part of a lattice. The models consist of differential equations applicable at distinct locations or governed by computational algorithms.94 There are a number of methods which allow discrete models to represent the behaviour of cells:
Cellular automata models – they are based on a set of discrete states, time cycles and space coordinates. The subsequent states of the system are directed by random walk algorithms representing migration, where the future cell position is chosen stochastically out of those closest to the current one. After a fixed period of time, the cells duplicate, again occupying a randomly selected location. Example of this approach in practice can be found in the studies of Galbusera et al.,74 Chung et al.,95 Cheng et al.96 and Byrne et al.47
Agent-based models – apart from modelling cells as discrete entities in the same manner as in cellular automata models, information about the shape and size of the cells is also incorporated.94
Cellular Potts models – discrete lattice Monte Carlo model capable of representing migration, proliferation and aggregation. Movement happens in the direction which minimises the local Hamiltonian energy function, while aggregation is driven by cell–cell contact energies.94
Cell force-based models – cells are entities which possess individual properties – location, orientation, state of stress and active forces they could exert in response to their micro-environment. Force equilibrium laws incorporate components of viscous drag and cell–matrix and cell–cell interactions.94
Furthermore, discrete models can incorporate information about the fluid velocity, (m/s), and the shear strain () to find the parameter used in an algorithm which directs differentiation47
| (22) |
where coefficients and (m/s) are found experimentally in a study examining the effect of mechanical stimulation on differentiation evidenced by bone fracture healing histology.47 The velocity and strain can be found using the discrete LB technique or by virtue of poroelastic finite element modelling for multiphase materials.46,47 Depending on the value of the coefficient , the cells differentiate into fibroblasts, chondrocytes or osteoblasts. Very low values of (which means very low levels of mechanical stimulation) lead to tissue resorption, low values to osteoblasts, intermediate levels to chondrocytes and high levels to fibroblasts.46 The cell lineage predictions obtained are then used to calculate the new material properties within each finite element, by once again applying the theory of mixtures. The development of the tissue phenotype is discretised into distinct time steps at which the tissue mechanical properties are updated. Young’s modulus, bulk modulus, permeability and Poisson’s ratio are determined as a function of the volume fraction of all the phenotypes occupying the lattice element. This algorithm allows for the simulation of complex morphological structures.
Having summarised the different modelling frameworks for flow, solutes and biological species in the literature, next we overview how they have been applied to gain insight into bioreactor systems.
Bioreactor types
Employing bioreactor cultures for tissue engineering applications is essential for the transition to large-scale production of tissue substitutes grown in vitro. Bioreactors can efficiently maintain the physiological requirements and provide in vivo-like mechanical and chemical cues to the cells, necessary to facilitate the development of functional grafts.34
Most importantly, they offer unrivalled control of the culture environment, enabling reproducibility of protocols and the ability to monitor the culture in real time. Bioreactor systems are also versatile and provide a suitable in vitro platform for a wide variety of tissue engineering applications ranging from bottom-up self-assembling constructs to scaffold-based co-culture tissues.10 Here, we focus on systems which have shown potential to improve the outcome of bone substitute cultures in comparison with static cultures – spinner flasks; rotating wall, perfusion and hollow fibre bioreactors; and mechanical conditioning and magnetic force systems. This promising potential can be fully realised only by closely tailoring the conditions in the bioreactor to the specific culture, which can be expedited by collaboration between experimentation and modelling as demonstrated by the case studies in this section.
Spinner-flask bioreactors
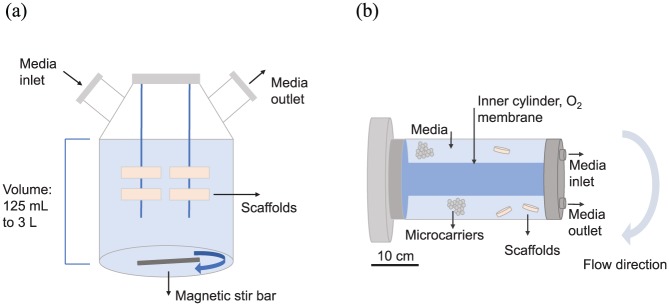
Spinner flasks are some of the systems most often used for bone tissue in vitro cultures, as they have been shown to improve mineralisation and proliferation in scaffolds34,97 in comparison with static cultures. The relatively simple spinner flasks (Figure 5(a)) depend on a stir bar at the bottom of the chamber to provide fluid flow to convect the suspended cylindrical scaffolds which are attached to needles hanging from the top.10,34 ECM deposition and cell differentiation are mainly enhanced at the periphery of the scaffold, where the benefits of convective transport, high nutrient concentration, and shear stress stimulation are most apparent.97 While constructs grown in spinner flasks are significantly more mineralised and cellularised than those in static cultures, this has not been shown yet to translate to significantly improved bone formation after implantation of the constructs in vivo.34 The flow, furthermore, cannot penetrate the entirety of large 3D tissues, which imposes limitations on the maximum volume to be cultured in spinner flasks (100–800 mm3).34,85 Therefore, modelling tools can be applied to study the flow environment and consequently inform flow settings for particular construct sizes or propose scaffold designs to control shear stresses experienced by the cells.
Figure 5.
(a) Diagram of a spinner flask. It is commercially available and can either be reusable (glass) or disposable (plastic). The stir bar can be magnetic or a rotating paddle, rotating from 20 to 120 rpm, but optimal rotational speeds are determined empirically. The lid could also incorporate a porous membrane through which oxygenation can occur. (b) Schematic diagram of a rotating wall bioreactor. The inner cylinder usually has a porous membrane that allows oxygenation. There are commercially available products, with volumes ranging from 10 to 500 mL, but custom-made bioreactors are also in use. Scaffold sizes of up to 10 cm3 are reported in the literature. Typical rotational speeds in slow turning lateral vessels (STLVs) range from 5 to 36 rpm.32
The work by Galban and Locke84 is one of the first instances of mathematical modelling used to examine the effect of space and mass transport limitations on tissue growth in vitro. They based the model on experimental work performed by Freed et al.28 who found that the proliferation rate of chondrocytes cultured in spinner flasks on biodegradable polyglycolic acid (PGA) scaffolds was inhibited with increasing scaffold thickness and seeding cell density. Galban and Locke84 hypothesised that this was caused by mass transport limitations and developed a mathematical model to explore this in more detail. They proposed a two-phase model – the cell phase (cells and ECM) and the void phase (polymer scaffold and the media). A volume averaging method, based on timescale disparity between transport and cell growth, was applied to reduce the complexity of the system. A main benefit of this approach is that it allows the modelling of temporal and spatial concentration profiles that develop as a result of diffusion, metabolic activity and tissue growth, which are particularly challenging to extract experimentally. The model was used to compare the spatial distribution of cells in two scaffolds with different thicknesses, by keeping all other parameters constant. The simulations replicated the experimental observation that increased scaffold thickness exacerbates mass transfer limitations in the centre of the construct. A greater spatial variation of cellular distribution in the thicker scaffold was revealed. However, the comparison between modelling and experimental results was only qualitative and validation was based on observing the same trends in cell growth. The model did not recreate the experimental environment ideally, for example, realistic nutrient depletion in the bulk media and flow shear forces exerted on the cells were not considered. Importantly, the model proposed a framework to track changing mass transfer properties within a scaffold due to a proliferating culture, but without parameterisation, it cannot be used to inform different protocols. Nevertheless, it is a good qualitative approximation of the temporal and spatial formation of cartilage tissue in vitro.
Crucially, the specific flow regimes unique to spinner flasks were not addressed in the study of Galban and Locke.84 Without having a good understanding of the shear stresses acting on the cultured construct, the choice of flow setting is arbitrary. Sucosky et al.62 proposed a validated framework for characterising the flow environment in spinner flasks. They used the experimental setup proposed by Freed and Vunjak-Novakovic68 and confirmed CFD-simulated fluid velocities against PIV measurements. Cells were not explicitly considered, unlike the study by Galban and Locke.84 Computational models first looked at shear stresses on the outside of the scaffolds and inside its porous structure. Maximum values (2.5 dyn/cm2) were detected at the lower corners of the scaffold, while the bottom was subjected to the smallest stresses. At the experimentally applied rotational velocities of 50 minrevolutions per minute (rpm), turbulence was the leading influence on the mean flow and shear stress, indicating substantial changes at lower velocities with more laminar flows.
Darcy’s law was applied for the flow through the porous scaffold, but because experimental measurement of the actual cell-construct time-dependent permeability was not available, only theoretical trend-revealing estimates were made in the case of low- and very high permeabilities. If this framework is coupled to the effective permeability and diffusion coefficients proposed by Galban and Locke84 in their tissue-growth model, this validated flow model could be a very useful tool able to provide settings for spinner-flask bioreactor operation.
Rotating wall bioreactors
Rotating wall bioreactors (Figure 5(b)) consist of two concentric cylinders rotating about their horizontal axis. Cultured cells and media fill the space between them.10 Oxygenation usually occurs through a membrane covering the inner cylinder which is filled with oxygen. Positive tissue engineering results have been seen using this system, including increased proliferation and osteogenic differentiation in comparison with static cultures. This bioreactor type also facilitates the use of bottom-up tissue engineering for anchorage-dependent cells seeded on microcarriers which readily form tissue aggregates.10 Rotating wall vessels have often been compared to spinner flasks,68,98–100 but results have not conclusively shown which system performs better.101 Rotating wall vessel performance is very sensitive to the choice of scaffold size and material, and flow regime, leading to a large variation in culture outcome. For instance, microcarrier cultures can experience reduced ECM formation and proliferation when the microcarrier material is denser than water due to carrier collisions with the walls of the bioreactor chamber.97 If the rotation speeds are reduced to meet the conditions for free-fall of the scaffolds, then the low shear forces induced might provide suboptimal mechanical stimulation. The performance of rotating wall vessels could greatly be benefitted by a modelling tool informing bioreactor flow regimes to maintain this balance. With this view, one of the main motivations of the extensive modelling work performed is to develop a mathematical framework which predicts construct movement within the rotating vessel.69,102
An early work by Freed and Vunjak-Novakovic68 aimed to estimate the hydrodynamic stresses on chondrocyte-seeded polymer constructs in a settling regime where they are in a state of free-fall around a fixed point. Desiring more insight into the culture conditions in their experiments in a slow turning lateral vessel (STLV), the authors applied a simple two-dimensional (2D) force balance analysis to estimate the relative velocity of the construct with respect to the fluid flow and the resulting shear stresses on the construct. The relative velocity of the construct was validated against an experimental measurement of the construct settling velocity over a distance of 15 cm, and a hydrodynamic stress value of 1.5 dyn/cm2 was found to act on the scaffold. Freed and Vunjak-Novakovic68 used this information to motivate their hypothesis that the velocity and stresses in the rotating vessel provided sufficient nutrient transport and mechanical stimulation, while maintaining smaller mechanical forces in comparison with spinner-flask bioreactors, thus enhancing the homogeneity of cellular and matrix distribution.
While this simplified model only considers a single situation, later works aim to provide more universal capabilities for understanding construct trajectory and resulting stresses. Pollack et al.69 modelled microcarrier motion in a high aspect ratio vessel (HARV) rotating bioreactor. The authors solved the equation of motion analytically and computationally for two types of carriers – lighter and heavier than water. Their results were validated against images from a custom-made particle tracking system. The analytical solutions showed that for microcarriers denser than the culture medium, collision with the walls of the bioreactor chamber occurred, which would cause excessive mechanical damage and hamper proliferation and cluster formation. Microcarrier behaviour was simulated under different rotational velocities to examine whether the settling regime, inducing lower levels of shear stress, was maintained.
Building on this work, Kwon et al.102 developed a model with the goal of predicting the optimal rotating speed to avoid sedimentation of microcarriers of different sizes. They also investigated oxygen diffusion and which flow regime optimised its availability at the centre of the chamber. A two-phase model, separating the medium and the bead–cell phases, was used, and an element of bead-to-bead collision was included. It was found that an increase in microcarrier size had to be accompanied by an increase in the rotational velocity of the bioreactor. However, an optimal mid-range velocity for each carrier size was identified that prevented sedimentation and also maintained microcarriers trajectory away from the wall, thus minimising bead–wall collisions. Oxygen availability was enhanced with increased carrier size, as that improved the convection in the chamber. The model was validated by qualitative comparison to published experimental data of microcarrier positions inside the bioreactor. This model is a good basis for a tool that can be used to set bioreactor operating conditions, but it can be revised by including cell behaviour and considering the effects of shear stress.
This is the focus of Pisu et al.35 who modelled the tissue and chemical environment in a rotating bioreactor. The authors applied reaction–diffusion equations (equation (13)) and a cell population balance equation to estimate cell proliferation and glycosaminoglycan (GAG) synthesis throughout the construct. GAG production was modelled as a first-order kinetic reaction, inhibited by oxygen, and population growth was linearly dependent on oxygen concentration. The model was parameterised against experimental data obtained by Obradovic et al.,85 who also employed a similar mathematical model for the concentration of oxygen and GAG, but used a regression curve fit of in vitro cell density data as a function of scaffold position and time. Pisu et al.35 parameterised proliferation to experimental data where the cells were cultured at 80 mmHg oxygen partial pressure in the media, while all other parameters were kept as found in the literature. The model was then validated quantitatively against data for cells cultured at 40 mmHg oxygen partial pressure in terms of GAG concentration as a function of position at the end of the experimental run. Simulations were found to be quantitatively very similar to the experimental data. The proposed framework offers the ability to predict cell number and GAG content under varying oxygen concentrations at the late stages of cultures (10 days to 5 weeks). It requires further histological validation before it can be used to design operating conditions and control the shape and size of the produced construct.
Although the predictive ability of the model by Pisu et al.35 is impressive, it does not consider the flow environment and presents an incomplete picture of the whole bioreactor system. Waters et al.67 and Cummings and Waters70 undertook this and developed a comprehensive framework to investigate flow regimes, shear stresses and nutrient transport in both HARV and STLV rotating bioreactors. The main difference between the two bioreactors is in their aspect ratio – the ratio of their length to radius. HARVs have larger radii compared to their length, while STLVs are longer with smaller radii. Waters et al.67 combined modelling and experimentation to examine tissue aggregation of MCF-7 human breast carcinoma cells suspended in the bioreactors. Experimental observations showed the assembly of smooth cylindrical nodules at rotation levels up until a certain threshold value, above which the cell clusters were irregularly shaped. The smooth nodule was found to consist of a proliferating periphery and a necrotic core and was denser than the media. Waters et al.67 hypothesised that the mechanical forces acting on the cluster determined its morphology and tested this by examining the mechanical stability of the construct under small-amplitude oscillations. They modelled the interior cells as a viscous fluid, which was distinct from the viscous fluid representing the culture media. The proliferating cell layer was modelled as an extensible membrane of constant tension. The governing equations applied were the continuity (equation (1)) and the NS equations (equation (2)). The asymptotic analytical solutions indicated that bioreactor geometry affected the shape of the cultured tissue, and that more irregularity in shape was to be expected using a HARV than an STLV, which preserved stability even at higher rotational velocities. For the second part of the study,70 the model was expanded to calculate the trajectory of a circular construct in the HARV and to find nutrient transport and tissue-growth rate in the free-fall settling state. The fluid problem was reduced to a flow going around a moving circular object. Due to the large Peclet number (ratio of convective to diffusive timescales), nutrient transport was modelled with convection along the streamlines, and diffusion across them. The tissue-growth rate was linearly proportional to local nutrient concentration. The authors took advantage of the disparity in timescales and solved sequentially for the construct trajectory (based on the force balance), flow velocity, nutrient concentration and tissue growth. Theoretically, three states of particle movement were found: (1) object stays in a fixed position (fixed); (2) object oscillates around a fixed position off the centre of the chamber without crossing it (settling); and (3) scaffold rotates around a fixed point in an orbit with a larger radius, but still away from the wall (orbital). The investigators performed an experimental study,103 in which these findings were compared to a cylindrical scaffold cultured in a vertically rotating bioreactor. The asymptotic solution for the construct trajectory in each of the three states was qualitatively and quantitatively validated. This series of studies culminated in the proposal of a simple imaging system to follow the scaffold’s displacement from its position due to growth, which alongside the model could help calculate the change in density and adjust the rotational speed in order to maintain the desired location away from the bioreactor walls. While this model provides reasonably good particle movement estimates, it is worth noting that shear stress assessment and its effect on tissue formation were not incorporated.
Lappa36 addressed this and developed a comprehensive model that assumed tissue growth resembled growth of organic protein crystals. The aim was to have a parameterised, validated model which could simulate entire tissue culture environments and outcomes, and especially the shape and size of the produced tissue. The model considered the tissue-growth rate, nutrient concentration and flow profile. The author investigated specifically the later stage of ECM expansion (10 days to 6 weeks) of a cartilage construct cultured in a free-fall state in a rotating wall bioreactor and compared simulations to experimental data by Obradovic et al.85 Tissue growth was assumed to positively correlate to the steepness of the nutrient concentration gradient and the local shear stress, thus capturing the two main governing factors while maintaining relative simplicity. The equation modelling the effect of fluid shear and oxygen availability on ECM deposition was parameterised against experimental data by Obradovic et al.85 for the growth rate of the construct. Simulations with different values of the parameter were performed, and the value leading to the closest match to the experimental rate was chosen. This ensured the model’s predictive ability about the shape of the scaffold. Qualitative validation of the parameterised model showed very good agreement with morphological measurements and shape of the cartilage grown in vitro by Obradovic et al.85 at the end of 6 weeks. Lappa36 showed that increasing the size of the construct accelerated growth at the lower edges of the scaffold where the flow is strongest and both mass transfer and shear stress are enhanced, which mirrored experimental observations. The validated parameterised model can predict the shape of different construct sizes and flow conditions given the same cell type is used. Nevertheless, the model overestimated the symmetry of the system, and as a further improvement could be extended to 3D, and validated against separate experimental data in a more quantitative manner.
Perfusion bioreactors
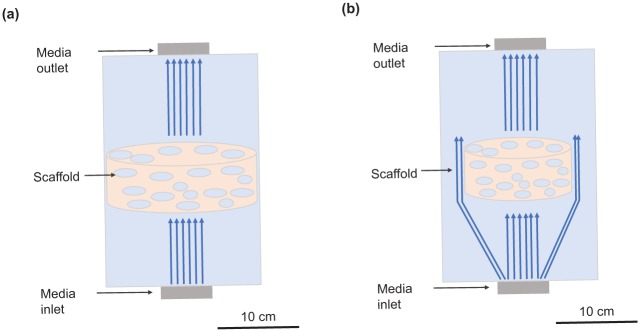
In perfusion bioreactors, the medium is pumped through the bioreactor chamber. Indirect perfusion (Figure 6(a)) leads to enhanced flow around the scaffold, while direct perfusion (Figure 6(b)) ensures the fluid flows through the scaffold which improves nutrient transport to the centre of 3D scaffolds in comparison with spinner flasks and rotating wall systems.34 Both the rate of osteoblastic differentiation and calcium deposition are increased and larger constructs can be cultured, as a result of continuous or pulsatile flow.10 In particular, a cyclic flow which provides a recovery period for the cells has shown promising results.101 However, direct perfusion bioreactors require the presence of a custom-made casing around the scaffold to ensure the fluid flows through rather than around it. This makes their wide adoption in automated cultures more challenging. Nevertheless, both systems have been observed to significantly increase the quality of tissue formation after implantation in vivo in comparison with grafts grown in static cultures. Protocols involving these bioreactors could greatly benefit from mathematical modelling to inform the inlet flow rate so that nutrient concentration is kept sufficiently high downstream in the construct. It can also be used to find the shear stresses induced by inlet flow rates in experiments, and infer the range within which tissue growth stimulation occurs. This can be developed further to design scaffolds to control the stresses exerted on the cell population within them.
Figure 6.
(a) Diagram of an indirect perfusion bioreactor. Indirect perfusion bioreactors are usually custom-made and support flow rates from 0.01 to 1 mL/min. Scaffold sizes of up to 14 mm in diameter are reported in the literature. (b) Diagram of a direct perfusion bioreactor. Direct perfusion bioreactors are usually custom-made to fit tightly around the scaffold. They usually require smaller flow rates than indirect perfusion bioreactors as here the flow is forced through the scaffold. This is due to the very small gap between the scaffold and the wall which requires more pressure to force flow through it and shifts the preferential flow through the scaffold. Maximum scaffold size reported in literature is 20 mm in diameter.34
A large number of models investigate the effect of flow on oxygen distribution throughout the construct, with both continuum63,64,86 and discrete74 approaches adopted. The semi-discrete model of Galbusera et al.74 employed the LB method to model velocity in a perfusion bioreactor on the micro-level. The authors compared the evolution of cell number and oxygen distribution under static and perfusion conditions (0.1 mm/s). One of the unique characteristics of this model is representing the cells as cellular automata – instead of using a continuum model, the cells were modelled individually, allowing for their random movement, proliferation and cluster formation, thus providing a more realistic micro-scale simulation of cellular position in space. The results of the simulations recreated well the expected exponential cell population growth which reached a maximum value and levelled off due to lack of space. The range of oxygen concentrations observed throughout the scaffold was significantly reduced in the presence of convection – the value at the downstream boundary in the perfusion bioreactor given the same cell number was 85% that of the inlet, up from 40% in static culture.
Continuum models showed similar results. Zhao et al.86 combined modelling and experimentation to analyse the effect of different culture conditions on cell growth, oxygen consumption and oxygen concentration of hMSCs seeded on 3D scaffolds. They compared static and perfusion systems, culturing constructs with an average volume of 1 cm3 for up to 40 days. Cell proliferation in an exponential growth model was matched to the data obtained in the experiments. Parameter estimation was also applied to find an expression for the specific oxygen consumption rate with a quadratic regression. The lactic acid to glucose ratio was found experimentally to be higher in the static culture, indicating a lower level of aerobic glycolysis probably due to lower levels of oxygen. This was confirmed by the mathematical simulations of oxygen concentration in the static cell layer which was less than half that in the perfusion system. The model highlighted how lack of flow limited nutrient availability which substantially affected proliferation and metabolism.
Cioffi et al.64 developed a similar parameterised model. Their simulations used two different flow rates: 0.3 and 0.03 mL/min through a polymer foam scaffold with a porosity of 80%. The biological element of the model was greatly simplified and instead of incorporating a cell growth model, experiments using human chondrocytes were performed to approximate a value for the maximum volumetric oxygen consumption rate. The effect of cells and ECM were not considered, which made the model applicable to the first few days of culture only. Velocity profiles and oxygen concentrations obtained in the macro-scale model were applied as boundary conditions in a micro-scale model. Higher and more homogeneous oxygen profiles were observed at the higher flow rate, with approximately equal velocity and oxygen concentrations throughout the scaffold at a given distance from the inlet. The micro-scale model indicated that average velocities and shear stress inside the pores of the scaffold at the lower flow rate were approximately 10-fold smaller. It could be concluded from the simulations that essentially all cells would not experience anoxia at the 0.3-mL/min inlet flow rate. For the lower flow rate, however, 6% of the scaffold had local oxygen concentration below 1% partial pressure, mainly at the periphery and near the outlet. This estimate could go up to 17% using a more conservative analysis, suggesting that while the lower flow rate reduces shear stress, it might not be able to support cell viability throughout the construct. The frameworks proposed by both Zhao et al.86 and Cioffi et al.64 can be used to prescribe the appropriate flow rates to ensure nutrient availability under different culture conditions.
The models could further be expanded to reflect longer timescales by incorporating effects of cell growth and ECM deposition, which affect the construct permeability and the effective diffusion coefficients. Chung et al.63 proposed a framework which addresses this. They modelled cell proliferation and nutrient consumption in scaffolds cultured under direct perfusion for 30 days. While the NS equations were used for the flow in the bulk media, Brinkman’s equation for flow through porous media was employed for the scaffold. The permeability of the construct was reduced with time on account of tissue formation by employing a Carman–Kozeny-type equation to find time-dependent shear stresses. Maxwell’s formula described the effective diffusion coefficient of the nutrient by accounting for the increasing cell number. The authors investigated how increasing the flow affects nutrient distribution and cell proliferation. As expected, enhanced mass transport increased nutrient availability and boosted the growth rate of the cell volume fraction, which reached an asymptotic value due to self-saturation. Average stresses inside the pores, estimated with Darcy’s law, were predicted to increase with time and cell growth. The average values (between 0.12 and 0.5 MPa) were found to be in good agreement with previously published modelling results.39 However, the potential for excessive shear forces to detrimentally affect proliferation and ECM formation was not considered.
This was the focus of the work by Porter et al.39 who simulated mechanical stresses experienced by scaffolds in direct perfusion bioreactors to assess and compare the findings of studies where differences in the flow rate and scaffold architectures affected cell proliferation and matrix mineralisation rates. The authors applied the discrete LB method to represent the complex scaffold microstructure obtained from a micro-CT scan in order to reduce the computational power required. The study was tailored to the in vitro investigation by Cartmell et al.33 – the same scaffold material was chosen and the generated shear stresses from the experimentally reported flow rates were estimated. The velocity profiles corresponding to the four different flow rates applied experimentally (0.01, 0.1, 0.2 and 1.0 mL/min) were obtained and applied to the entire structure following the procedure set out in the study of Martys and Chen.104 The authors reported that the micro-scale shear stress at a flow rate of 0.01 mL/min (which was shown to be beneficial to proliferation by Cartmell et al.33) was 5 × 10−5 Pa. Mineralisation of the matrix was observed at flow rates up to 0.2 mL/min (corresponding to 1 × 10−3 Pa shear stress), above which cellular death was more prominent. Stress estimates with the LB method underestimate analytical solutions by 16% according to the authors. Higher resolution tomographic scans would improve accuracy and also increase the computational power required to run the simulations.
The optimal shear stresses found by Porter et al.39 were applied by Pierre and Oddou44 in their investigation of the mechanical environment and nutrient (oxygen) availability in large constructs (2 cm2) cultured in perfusion systems. The model aimed to propose inlet flow rates balancing shear stress stimulation and nutrient availability. Numerical solutions indicated that a flow rate of 0.1 mm/s provided sufficient oxygenation along the entire length of channels inside the scaffold, but induced excessive shear stresses. The investigators performed a number of different simulations reducing the inlet flow rate, but found that a decrease of 75% in the initial rate leads to the development of hypoxic areas downstream in the channel. Consequently, a very fine-tuned compromise has to be achieved between selecting a perfusion rate sufficient to maintain oxygen availability and maintaining the shear stress experienced by the cells at levels which promote cell viability and matrix formation.
In order to do so reliably, the model should relate cell growth to shear stresses, as proposed by O’Dea et al.40 Their multiphase model focused on predicting the response of the cells to the mechanical environment – due to either fluid shear or intercellular pressure, in a direct perfusion bioreactor. The presence of the scaffold was not taken into account while both phases were modelled as viscous fluids. The initial analysis with a constant proliferation rate concluded that excessive flow rates could flush the tissue construct out of the bioreactor before any meaningful growth could take place. Cell loss due to convection is an inherent perfusion bioreactor design problem that has often been unduly neglected in previous modelling studies. The model predicted the exponential increase in width and volume fraction of the cell phase. The study then continued with an investigation of the impact of the mechanical environment in the bioreactor on the proliferation rate of the cell phase. Three distinct stages were defined for the behaviour of the cells, defined by preset threshold pressure values. Intermediate stress levels caused an increase in growth in comparison with low levels due to enhanced ECM deposition. Above a certain higher stress value, proliferation was set to zero and apoptosis occurred. The complex pressure profile in the bioreactor created a non-uniform construct. The model could be augmented by parameterising the threshold values which determine the relationship between cell growth and shear stress.
Guyot et al.41 performed an in-depth analysis of the mechanical stresses acting on a single cell attached to a 3D scaffold inside a direct perfusion bioreactor to reveal the complex effects of precise cell position and orientation, scaffold geometry and flow direction on micro-scale stresses. Atomic force microscopy measurements of human periosteal derived cells (hPDCs) were taken to find their Young’s modulus, which was used in the simulations. The flow inside the scaffold was solved first on the bioreactor scale using the NS equations, and the values obtained were used as boundary conditions for the micro-scale model. The cell was mechanically defined by its stretching stiffness, bending stiffness (estimated experimentally), bulk modulus and nucleus stiffness. Four different configurations were simulated, with the cell positioned along the flow, facing the flow, bridging a corner and within a three-cell cluster facing the flow. All cases were subjected to a flow rate of 1 mL/min. While very small deformations were observed in all cases, maximal tensions around 0.005 Pa and maximal shear stresses of 0.16 Pa were estimated for the flow facing the cell and cluster. Crucially, the stresses were not reduced due to shielding in the cluster configuration. Even though the simulations produced very small strains, they nevertheless could still be sufficient in activating mechano-regulated osteogenesis. The authors also compared their results for maximum and average shear stress on the cells to the values for the scaffold walls and found that the maximum ones are double those for the scaffold, while the average values were considerably lower. These results suggest that scaffold-estimated shear stresses are suitable indicators of the mechanical stimulation on the cells in this culture when used to inform protocols. No comparison was made with biological experiments to try to elucidate the cellular response to the simulated mechanical forces, but the findings presented here for both scaffold WSS and maximum cell shear stress were in excess of the optimal values evaluated by Porter et al.39 This study demonstrates the power modelling offers for bioreactor process precision control and is a marked step towards understanding the nature of mechanotransduction and the effect of the local mechanical environment on long-term cellular response.
Hollow fibre bioreactors
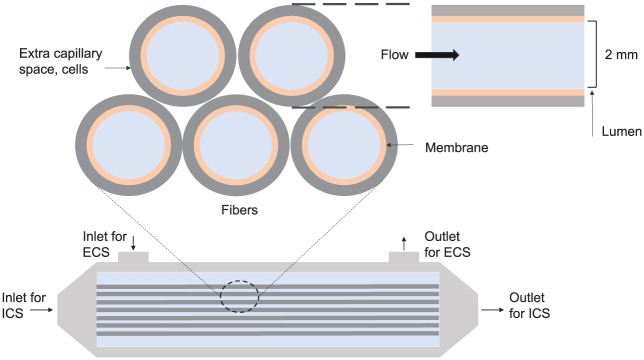
Hollow fibre bioreactors offer the possibility of enhanced transport through the cellular construct without the drawback of excessive shear stress on the cells. Hollow fibre bioreactors consist of fibres through which culture medium is perfused (Figure 7), while cells can be seeded either on their outer surface or in the matrix between them. The presence of the fibre membrane shields the cells from unduly high shear stresses while simultaneously providing the needed mass transport to the inside of the engineered tissue. Hollow fibre bioreactors reduce the chemicals and labour required for their operation and are immensely more cell density–efficient than flask cultures.66 The fibre cultures are considered angiogenesis-inducive after implantation in vivo due to their resemblance to capillaries. They have shown promising results for bone tissue cultures, demonstrating that the PLGA fibres supported bone differentiation and proliferation.105,106 It was found that the alkaline phosphatase activity was increased and more collagen was deposited after in vivo implantation in mice when compared to constructs grown in static conditions. Modelling can improve these cultures by prescribing inlet flow rates and outlet pressures which ensure sufficient mass transfer across the fibre membrane, while still adequately nourishing the downstream parts of the culture.
Figure 7.
Diagram of a hollow fibre bioreactor. The media flows in the lumen (intra-capillary space (ICS)) and passes through the membrane to the extra capillary space (ECS) where the cells are. Flow also goes in and out of the extra capillary space. The typical length of the fibres is 10 cm (adapted from the study of Shipley et al.43).
A pioneering work107 used modelling to propose bioreactor dimensions that would ensure appropriate oxygen concentration for various cell cluster configurations in the bioreactor. The authors highlighted the development of non-uniform cell and matrix distributions inside the annular space of the fibre (on the outside of the lumen and membrane). Convection–diffusion equations were used to report the transport of nutrients (glucose, oxygen, other carbon substrates and proteins) across the membrane, and a zero-order reaction kinetics term was added to the annular region where the tissue resided. The nature of matrix deposition in that region was considered to be inhomogeneous, with a number of void channels developing where fluid could flow around the cellular clumps. An analysis was performed on the oxygen concentration associated with a number of distinct idealised configurations of tissue growth. Appropriate dimensions for the bioreactor were proposed that would support a viable tissue culture for each case by maintaining acceptable oxygen levels. The consideration of non-uniform cell distributions inherent to long-term cultures in the design of cultures for tissue engineering is crucial for ensuring positive outcomes.
Another early analytical work focused on quantifying the flow inside the fibres, representing them as porous tubes.65 Brinkman’s equation was applied to the flow in the porous wall combined with Darcy’s law for the permeability, while NS equation was used for the flow in the lumen. The authors reported flow velocities and pressures corresponding to different inlet conditions and Reynolds numbers. The flow was assumed to be laminar and incompressible, and the simulation results were in a good qualitative agreement with experimentally obtained velocities in a previous study which measured velocities with magnetic resonance imaging (MRI).
While this analysis proposed dimensions for the lumen and length of the fibre, it does not allow for direct application to real-life problems interested in selecting operating conditions for hollow fibre bioreactors, as done by Shipley et al.66 In this later study, theoretical expressions to help determine the flow settings for the bioreactor were found. The model investigated the flow environment inside a single fibre from the hollow fibre bioreactor and was parameterised using experimental data obtained in-house to find the permeability of the membrane. It was then validated against data obtained using a different flow rate. Parameters such as the inlet flow rate, outlet pressure, and membrane properties were pinpointed as the main determinants of the flow environment inside the extra capillary space (ECS). Flow was modelled through the application of the NS equations, and Darcy’s law for flow across the membrane. The model was reduced which allowed the derivation of a simple equation describing the relationship between the operating parameters (inlet and outlet flow rate, and pressure). Worked examples were provided, which demonstrated the usefulness of the expression to experimentalists aiming to provide a certain level of permeation.
The model by Shipley et al.66 did not incorporate a reference to the cell phase or consider changes in the distribution of nutrients. A subsequent study43 considered the limiting effect of oxygen availability in the ECS of a single fibre. The objective was to define operating conditions such as length of the fibre, flow rate and depth of the ECS, in order to maintain a level of oxygenation sufficient to support the given cell culture. Constant cell number and a homogeneous cell distribution were assumed, while oxygen consumption was represented by MMK. First, an analytical solution was obtained for a case in which oxygen concentration is high enough to reduce its consumption to zero-order kinetics, and an expression for the flow rate was derived. This analysis showed that the amount of oxygen depended on the radial position and the distance from the inlet. A second case, in which zero-order kinetics was replaced with the full Michaelis–Menten equation, was solved numerically. The analytical and numerical solutions were validated against each other and a good quantitative agreement was observed (3.4% discrepancy). The authors reviewed both high and low cell oxygen requirement cases and showed how the bioreactor settings depended on the cell type and the oxygen consumption rate. They demonstrated the relationship between the length of the lumen and the flow regime on the one hand and the cell-specific metabolic parameters on the other, showing the informative potential of the model.
A framework proposed by Pearson et al.37 illustrates how modelling can be used to select more efficient operation of this system. The goal was to minimise the amount of bone growth factor (BMP-2) used due to its very high cost, while still obtaining desirable outcomes. A 2D multiphase model was proposed – the scaffold, medium, differentiated and undifferentiated cells were explicitly considered. The role of excessive flow in flushing the cells out of the system was incorporated. Solutions were obtained numerically for the ratio of differentiated to undifferentiated cells, the yield of differentiated cells and the growth factor uptake. The authors first considered a hypothesis where differentiation was dependent solely on BMP-2 according to a Michaelis–Menten term. Results conclusively showed that increasing inlet concentrations of BMP-2 led to higher cell numbers. Then, a comparison was drawn between two particular concentrations which produced a desirable final cell number. It was determined that while the higher concentration was associated with an insignificant increase in cell number, it disproportionately inflated the amount of consumed growth factor and was not an efficient choice. The second hypothesis under consideration was that both the growth factor and the flow shear stress influenced differentiation. The function representing the effect of shear stress caused up-regulation only between two threshold mid-range values, taking into account the insufficient stimulation of low values and the mechanical damage due to high values. The combination of factors elicited a non-monotonic behaviour, where no steady state for the differentiated cell fraction was obtained, and the extent of differentiation sensitivity was revealed. It was found that the gain in proliferation when using very high BMP-2 inlet concentrations was not significant enough to warrant the 30% rise in cost required to supply the additional amount of chemical. The model requires a parameterisation through comparison with experimental data about the cellular response to BMP-2 and flow shear to better predict in vitro results. However, it is an excellent example of modelling applied in tissue engineering to fine tune growth factor use which can be easily adapted to different cell types.
Bioreactor systems for mechanical conditioning
Special mechanical conditioning systems have been developed with the goal of ensuring that the forces applied to the engineered bone tissue are close to those experienced in vivo, thus safeguarding against mechanical failure of the construct upon implantation.10 One example of such a system is presented in Figure 8(a), where perfusion is applied in conjunction with compression from a piston. There are some limitations to the system, for instance, guaranteeing long-term sterility might be challenging due to the presence of the piston – an external part.10 Stronger scaffold materials with longer degradation times, able to transmit the desired forces to the cells without failing mechanically, need to be used. These bioreactors are, nevertheless, very useful culture systems, as the combination of compression and fluid shear is more conducive to alkaline phosphatase activity and deposition of bone proteins – osteocalcin and osteopontin.10,34 Mineralised matrix is also deposited at the critical loading points, creating constructs with sufficient mechanical strength in a more rapid manner.10
Figure 8.
(a) Schematic diagram of a compression perfusion mechanical conditioning bioreactor. Apart from media perfusion and the flow-generated shear stress, additional mechanical stimulation is provided by a compression piston. A strain of magnitude of 1% is applied cyclically at a frequency of 1 Hz. The design is based on the bioreactor system developed by El Haj and Cartmell.10 (b) Diagram of a magnetic force bioreactor. Magnetic biocompatible nanoparticles modified with RGD peptides attach to cell membrane receptors. When the magnetic field is applied by means of a magnetic plate outside the bioreactor chamber, the magnetic force acts on the beads and causes translational motion and strain on the membrane, providing mechanical stimulation. Cells are of typical size 15–30 µm (figure of cell adapted from the study of Owen and Newsome108).
The effective use of these bioreactors requires knowing precisely what the applied strains and stresses are so as to prevent any damaging effects, which can be achieved through modelling. Zhao et al.42 aimed to accomplish this as they explored the impact of design parameters such as porosity, pore size and overall architecture of scaffolds in dynamic compression-conditioning systems with and without perfusion on shear stresses. They also compared the two mechanical conditioning systems to a perfusion-only system. The presence of laminar or turbulent flow regime was determined based on the Reynolds number, after which computational fluid dynamics were used to estimate the flow profiles inside the interconnected network of pores. A fluid–structure model identified the stress on the scaffold. Pore size was found to be the dominant determinant of the induced WSS inside the scaffold, with smaller pore sizes leading to higher interior velocities and therefore higher shear stresses. The combined influence of flow and compression was estimated to be larger than the sum of each separately. An expression for finding shear stress was derived which could be used to select inlet flow rates and scaffold designs to confer the required stimulation.
This work, however, needs to be viewed in the context of cellular response, the knowledge of which can be obtained through in vitro experimentation. A number of studies take this approach and propose frameworks which simulate how the tissue reacts to the complex mechanical environment. The models proposed by Milan et al.46 and Byrne et al.47 modelled the effect of different compressive load conditions on tissue phenotype. In both, a 3D finite element study simulated the mechanical loading from a rigid plate pressing on the top of the scaffold, with the tissue and the fluid displaced in the process. The main difference between the two models is that Milan et al.46 used cyclic loading instead of the constant load applied by Byrne et al.47 The mechanical properties of each construct element were determined using the theory of mixtures, accounting for changes in the scaffold, cell number and phenotype. The cell population model incorporated migration and division following a stochastic random walk algorithm which chose at random a new position for motile cells and triggered mitosis at regular intervals. A previously parametrised109 mechanoregulated model was employed which directed the differentiation of MSCs into either fibroblasts, chondrocytes or osteoblasts. The level of shear strain and fluid velocity determined cell fate, including tissue resorption at very low values of mechanical stimulation.
Milan et al.46 examined a high number of strain and force initial conditions and identified a small range which produced a homogeneous tissue phenotype. Their model used geometry from micro-CT scans to improve predictability, but the gains from this were counteracted by not incorporating scaffold degradation. Byrne et al.,47 however, were particularly interested in this aspect. They hypothesised that it is possible to maximise tissue formation by exploring the relationship between the degradation rate, porosity and Young’s modulus, allowing them to select the highest possible degradation rate and porosity (leading to increased tissue growth), without compromising the mechanical integrity of the construct or applying high loads on the tissue. A regular 3D printed scaffold was assumed for the simulations, and three values each for porosity, Young’s modulus and dissolution rate were compared. The simulations suggested that low compressive loads were more beneficial to the development of mature bone tissue. Even at low loading conditions, very high levels of scaffold dissolution would lead to mechanical failure before sufficient differentiation could occur and sufficient natural strength could be developed. Sets of scaffold parameters (porosity, strength and scaffold degradation rate) which maximised the amount of resulting bone were identified. It was found that high porosity general enhanced bone tissue deposition, while a trade-off between dissolution rate and Young’s modulus was required to maintain the mechanical stability of the construct.
One of the limitations of these comprehensive models is that the effect of ECM deposition on nutrient mass transport and cell movement was not considered. Mass transfer hampered by inhomogeneous ECM formation can affect cell viability and differentiation, and change the nature of the construct. The models could also be improved by accounting for the influence of the chemical environment on differentiation, either by nutrient or growth factor availability.
Models based on different mechanical conditioning bioreactors have also been developed. Soares and Sacks77 studied a system based on stretching of the tissue. Theoretical predictions were combined with experimental work to develop a model simulating tissue formation directed by mechanical stimuli. A complex cell model accounting for proliferation, death (dependent on nutrient availability) and chemotaxis, was adopted alongside a multiphase framework for ECM deposition. The model considered the manifold effect of oxygen on cell growth – limiting at low concentration and toxic at high. Mechanical properties of ECM synthesis was stimulated by stretching. The model produced qualitatively close outcomes to the experimental results with vascular smooth muscle cells for both static culture and stretching. Substantially different outcomes for the two types of cultures were produced, showing that the model could distinguish well between them. Stretching augmented the formation of collagen and the uniformity of the construct composition. The simulations indicated that the frequency of stretching had a more significant and pronounced impact than the amount of flexure. The model provided a very comprehensive framework for investigating the tissue engineering process in mechanical conditioning systems, with its capacity for considering transport phenomena, reaction kinetics, chemotaxis, nutrient-regulated cell apoptosis and growth, and synthesis of ECM due to mechanical force. Despite the study concerning cardiac tissue, it could be adapted to compression conditions for bone tissue engineering and be used to investigate the suitability of operating parameters, especially the required strain and frequency of the mechanical stimulation applied. In contrast to the two previously discussed models, the current results were validated against experimental data, confirming the model is a sound approximation.
Magnetic force bioreactor
Another encouraging novel technology for administering mechanical stimulation is the use of magnetic forces to apply strain directly to the cytoplasmic cell membrane (Figure 8(b)). This is done through manipulating biocompatible magnetic nanoparticles attached to receptors on the membrane or on ion channel membrane proteins.10 This system enables unprecedented control of the stress applied. It does not require the use of slowly degrading scaffold biomaterials which are generally needed to transmit loads onto the cells in traditional mechanical conditioning systems, or pose the risk of infection from external objects designed to impart loads.10 Magnetic force bioreactors are especially favourable to the formation of bone and cartilage tissue due to the augmented delivery of mechanical stimulation. Results have indicated that bone matrix proteins are up-regulated using this system in comparison with non-particle controls.10 Higher expression of osteogenic genes and mineral-to-matrix ratio was reported by Hu et al.110 During the long-term in vitro culture, osteopontin activity was also increased in comparison with controls. Cartmell and colleagues111,112 performed toxicity studies of the magnetic particles and no negative effect was detected. An important consideration for developing the magnetic force bioreactor for future use is its incorporation alongside a system providing sufficient medium mixing. The challenge is to accomplish this without causing undue mechanical stress, while also allowing the easy estimation of the entire mechanical stimulation.
A theoretical framework to inform the design of a magnetic force system was proposed by Dobson et al.113 The authors discussed the merits of this system and its potential to provide a 3D force field which could facilitate the development of truly complex tissues. The strength of the magnetic field and its gradient were pinpointed as the main components which determine the magnetic force acting on the tissue and theoretical expressions describing their effect were presented. The next step is to build a model, which accounts for the cellular response to the magnetic forces, calibrated to the body of in vitro experimental work performed. This can be used to select what level of magnetic force stimulation is required and provide an excellent tool to develop this bioreactor as an established tissue engineering culture system.
Discussion and conclusion
Modelling is essential to develop clinically relevant tissue engineering therapies. It provides invaluable assistance to advance this field which has so far been largely developed empirically. Modelling can serve two main roles – as a method to test hypotheses and as a tool for obtaining quantitative predictions about the state of tissue cultures. The large body of experimental research on engineering tissue formation in vitro indicates trends in its morphogenesis, for instance, the stimulating effect of convected cultures.34 These empirical observations give rise to a number of hypotheses which could explain them, for instance, that local oxygen concentration affects cellular differentiation and tissue phenotype or that flow shear stress mediates ECM synthesis. Modelling provides the means to test these theories in a methodical manner and determine whether either one or both are the main drivers of this behaviour. It can also provide more insight into the mechanism of this influence, as has been shown by Soares and Sacks77 who in the process of studying this exact question also revealed the intricate relationship between the frequency and the strength of mechanical stimulation. Different hypotheses have also been tested through modelling, ranging from confirming the impact of flow stability in rotating wall bioreactors on the shape of constructs67 to transport limitation-driven inhomogeneity in cartilage tissues grown in spinner flasks.84
Modelling is also indispensable for the quantitative information it can provide about cultures, informing further experimental work. Its versatility in investigating a wide range of culture settings in a wide array of experimental setups can focus operating conditions to those identified as most promising. Bioreactor dimensions can be informed,107 levels of shear stress can be prescribed39 and culture protocols can be made more efficient.37 Table 1 summarises the models overviewed here and how they can be used to further develop experimental protocols for each bioreactor type. Examples where modelling is placed in the context of experimental work, either by comparison to published data or by performing in-house experiments, are highlighted.
Table 1.
Comparison between the different bioreactor types, and modelling approaches to them, summarising research in the field.
| Bioreactor system | Bioreactor application | Model purpose | Combination between modelling and experiments |
|---|---|---|---|
| Spinner flask | Good for scaffold cultures, typically disc-shaped (4–10 mm diameter). In vitro, it performs better than static cultures and comparable to rotating wall bioreactors, but no significant improvement after implantation. |
Multiphase model to study effect of mass transport on homegeneity of tissues.84
Validated CFD model for flow and wall shear stresses.62 |
Galban and Locke84 compared the cell growth model to previously published experimental data. Sucosky et al.62 validated the CFD simulations to experimental PIV measurements. |
| Rotating wall | Good for scaffolds (discs of 4–65 mm diameter) and microcarriers. Important to ensure no collision with walls or sedimentation. |
Force balance for hydrodynamic stress68 and equations of motion for the scaffold trajectory.69,102 Parameterised and validated model for proliferation and GAG content due to O2 concentration.35 Comprehensive models of flow, shear stress, O2 concentration and cell behaviour used to predict construct shape36 or position.67 | Freed and Vunjak-Novakovic68 measured terminal velocity experimentally, while Cummings et al.103 and Pollack et al.69 validated particle trajectories in-house with object imaging systems. Pisu et al.,35 Lappa36 and Kwon et al.102 validated to published experimental data. |
| Perfusion | Common scaffold shapes: cylinders, cubes, discs (typical size: 4–20 mm diameter). Studies have reported better performance upon implantation in vivo in comparison with constructs grown in static cultures.34 |
Parameterised discrete and continuum models for flow, O2 concentration and cell growth,64,74,86 including long-term evolving tissues.63 Finding shear stresses as a result of flow rates,39 predicting flow settings44 and cell response.39–41 | Zhao et al.86 and Cioffi et al.64 parameterised cell growth and O2 uptake in-house. Porter et al.39 used modelling to find shear stresses from a reported experimental study. Guyot et al.41 measured the physical properties of cells in-house to use in model. |
| Hollow fibre | Good for tissue that requires assistance with angiogenesis; fibres can be biodegradable for complete integration with the tissue. Example length of a fibre is 10 cm. | CFD flow simulations for flow characterisation,65 choosing bioreactor dimensions to maintain oxygenation107 and providing theoretical expressions to select flow settings for desired permeation and oxygenation.43,66 Multiphase cell model to develop more efficient protocols by selecting the minimal effective amount of BMP-2 (Pearson, Oliver and Shipley).37 | Pangrle et al.65 validated velocity profiles with results from MRI scans. Shipley et al.66 parametrised mass transfer properties of the membrane to experimental data. |
| Mechanical conditioning | Good for constructs that are designed for load-bearing applications. | A fluid–structure interaction model to determine shear stress under different porosity and pore size.42 Models predicting tissue phenotype46,47 and tissue formation77 under different loading conditions. | Soares and Sacks77 validated their model to in-house experimental data. Milan et al.46 and Byrne et al.47 used previously parameterised differentiation model. Zhao et al.42 derived an expression for setting bioreactor conditions but did not validate simulations. |
| Magnetic force | Good for constructs requiring complex morphology as it allows for precise application of force-directed morphogenesis. | Theoretical expressions for estimating the magnetic force acting on the cell membrane.113 | Bioreactor system is in development and no research has been produced as of yet where both modelling and experimentation are used to improve its operation. |
CFD: computational fluid dynamics; PIV: particle image velocimetry; GAG: glycosaminoglycan; MRI: magnetic resonance imaging; BMP-2: bone morphogenetic protein-2
Highly informative models can only be obtained when simulations match the in vitro reality, best achieved by specifically fitting model parameters to experimental measurements. Data-fitted coefficients specific to cell behaviour (i.e. rate of proliferation and nutrients uptake) are key to informing improved culture conditions. While non-parameterised models can reveal trends in in vitro tissue morphogenesis,40,63 developing tissue engineering protocols for clinical applications through modelling is dependent on a robust parameterisation procedure. Implicit in this is a comprehensive knowledge of the experimental data and methods, as a result of which comparisons to data published in the literature are often only qualitative.84 Lappa36 use data in the literature to find the coefficient defining the effect of shear stress on the tissue-growth rate, while Soares and Sacks77 find the relationship between collagen concentration and Young’s modulus, although there is less confidence in the value of parameters found in this manner. In-house parameterisation is also challenging, often confined to finding a single coefficient66 or forced to accommodate large standard deviations when finding cell-data parameters.86 Nevertheless, providing useful information about the impact of shear stress on the tissue is particularly benefitted by parameterisation in models ranging from studying the response of a single cell41 to predicting construct-wide phenotype evolution46,47 and distinguishing between the effect of different bioreactor systems and flow regimes on bone tissue maturation.39
Such parameterised models can bring about a fundamental change in the way culture conditions are selected and lead to a step-change in the quality of engineered bone grafts. While there is a lot of progress in the field of mathematical modelling on cell cultures, it is only in the context of collaboration with experimental work that it can be used to scale-up tissue engineering production and develop products for the clinic.
Footnotes
Declaration of conflicting interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship and/or publication of this article.
Funding: This work was supported by the Rosetrees Trust through research grant no. A696.
ORCID iDs: Iva Burova  https://orcid.org/0000-0003-3936-8673
https://orcid.org/0000-0003-3936-8673
Ivan Wall  https://orcid.org/0000-0001-6294-8348
https://orcid.org/0000-0001-6294-8348
References
- 1. Amini AR, Laurencin CT, Nukavarapu SP. Bone tissue engineering: recent advances and challenges. Crit Rev Biomed Eng 2012; 40(5): 363–408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Campana V, Milano G, Pagano E, et al. Bone substitutes in orthopaedic surgery: from basic science to clinical practice. J Mater Sci Mater Med 2014; 25(10): 2445–2461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Mills LA, Aitken SA, Simpson AHRW. The risk of non-union per fracture: current myths and revised figures from a population of over 4 million adults. Acta Orthop 2017; 88(4): 434–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Nandra R, Grover L, Porter K. Fracture non-union epidemiology and treatment. Trauma 2016; 18(1): 3–11. [Google Scholar]
- 5. Copuroglu C, Calori GM, Giannoudis PV. Fracture non-union: who is at risk? Injury 2013; 44(11): 1379–1382. [DOI] [PubMed] [Google Scholar]
- 6. Kinaci A, Neuhaus V, Ring DC. Trends in bone graft use in the United States. Orthopedics 2014; 37(9): e783–e788. [DOI] [PubMed] [Google Scholar]
- 7. Flierl MA, Smith WR, Mauffrey C, et al. Outcomes and complication rates of different bone grafting modalities in long bone fracture nonunions: a retrospective cohort study in 182 patients. J Orthop Surg Res 2013; 8: 33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Quarto R, Mastrogiacomo M, Cancedda R, et al. Repair of large bone defects with the use of autologous bone marrow stromal cells. N Engl J Med 2001; 344(5): 385–386. [DOI] [PubMed] [Google Scholar]
- 9. Marolt D, Knezevic M, Vunjak-Novakovic G. Bone tissue engineering with human stem cells. Stem Cell Res Ther 2010; 1(2): 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. El Haj AJ, Cartmell SH. Bioreactors for bone tissue engineering. Proc IMechE, Part H: J Engineering in Medicine 2010; 224(12): 1523–1532. [DOI] [PubMed] [Google Scholar]
- 11. O’Dea RD, Byrne HM, Waters SL. Continuum modelling of in vitro tissue engineering: a review. In: Geris L. (ed.) Computational modeling in tissue engineering (studies in mechanobiology, tissue engineering and biomaterials), vol. 10 Berlin: Springer, 2012, pp. 229–266. [Google Scholar]
- 12. Kon E, Muraglia A, Corsi A, et al. Autologous bone marrow stromal cells loaded onto porous hydroxyapatite ceramic accelerate bone repair in critical-size defects of sheep long bones. J Biomed Mater Res 2000; 49(3): 328–337. [DOI] [PubMed] [Google Scholar]
- 13. Bruder SP, Kraus KH, Goldberg VM, et al. The effect of implants loaded with autologous mesenchymal stem cells on the healing of canine segmental bone defects. J Bone Joint Surg Am 1998; 80(7): 985–996. [DOI] [PubMed] [Google Scholar]
- 14. Kruyt MC, de Bruijn JD, Wilson CE, et al. Viable osteogenic cells are obligatory for tissue-engineered ectopic bone formation in goats. Tissue Eng 2003; 9(2): 327–336. [DOI] [PubMed] [Google Scholar]
- 15. Chatterjea A, Meijer G, van Blitterswijk C, et al. Clinical application of human mesenchymal stromal cells for bone tissue engineering. Stem Cells Int 2010; 2010: 215625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Brydone AS, Meek D, Maclaine S. Bone grafting, orthopaedic biomaterials, and the clinical need for bone engineering. Proc IMechE, Part H: J Engineering in Medicine 2010; 224(12): 1329–1343. [DOI] [PubMed] [Google Scholar]
- 17. Hollinger JO, Winn S, Bonadio J. Options for tissue engineering to address challenges of the aging skeleton. Tissue Eng 2000; 6(4): 341–350. [DOI] [PubMed] [Google Scholar]
- 18. Geris L, Gerisch A, Schugart RC. Mathematical modeling in wound healing, bone regeneration and tissue engineering. Acta Biotheor 2010; 58(4): 355–367. [DOI] [PubMed] [Google Scholar]
- 19. De Long WG, Einhorn TA, Koval K, et al. Bone grafts and bone graft substitutes in orthopaedic trauma surgery: a critical analysis. J Bone Joint Surg Am 2007; 89(3): 649–658. [DOI] [PubMed] [Google Scholar]
- 20. Connolly JF, Guse R, Tiedeman J, et al. Autologous marrow injection as a substitute for operative grafting of tibial nonunions. Clin Orthop Relat Res 1991; 266: 259–270. [PubMed] [Google Scholar]
- 21. Hernigou PH, Poignard A, Beaujean F, et al. Percutaneous autologous bone-marrow grafting for nonunions. J Bone Joint Surg Am 2005; 87(7): 1430–1437. [DOI] [PubMed] [Google Scholar]
- 22. Le Blanc K, Rasmusson I, Sundberg B, et al. Treatment of severe acute graft-versus-host disease with third party haploidentical mesenchymal stem cells. Lancet 2004; 363(9419): 1439–1441. [DOI] [PubMed] [Google Scholar]
- 23. Arinzeh TL, Peter SJ, Archambault MP, et al. Allogeneic mesenchymal stem cells regenerate bone in a critical-sized canine segmental defect. J Bone Joint Surg Am 2003; 85-A(10): 1927–1935. [DOI] [PubMed] [Google Scholar]
- 24. Reichert JC, Cipitria A, Epari DR, et al. A tissue engineering solution for segmental defect regeneration in load-bearing long bones. Sci Transl Med 2012; 4(141): 141ra93. [DOI] [PubMed] [Google Scholar]
- 25. Bensaïd W, Oudina K, Viateau V, et al. De novo reconstruction of functional bone by tissue engineering in the metatarsal sheep model. Tissue Eng 2005; 11(5–6): 814–824. [DOI] [PubMed] [Google Scholar]
- 26. Lin RZ, Chang HY. Recent advances in three-dimensional multicellular spheroid culture for biomedical research. Biotechnol J 2008; 3(9–10): 1172–1184. [DOI] [PubMed] [Google Scholar]
- 27. Muschler GF, Nakamoto C, Griffith LG. Engineering principles of clinical cell-based tissue engineering. J Bone Joint Surg Am 2004; 86-A(7): 1541–1558. [DOI] [PubMed] [Google Scholar]
- 28. Freed LE, Marquis JC, Langer R, et al. Kinetics of chondrocyte growth in cell-polymer implants. Biotechnol Bioeng 1994; 43(7): 597–604. [DOI] [PubMed] [Google Scholar]
- 29. Nicolaije C, Koedam M, van Leeuwen JP. Decreased oxygen tension lowers reactive oxygen species and apoptosis and inhibits osteoblast matrix mineralization through changes in early osteoblast differentiation. J Cell Physiol 2012; 227(4): 1309–1318. [DOI] [PubMed] [Google Scholar]
- 30. Tuncay OC, Ho D, Barker MK. Oxygen tension regulates osteoblast function. Am J Orthod Dentofacial Orthop 1994; 105(5): 457–463. [DOI] [PubMed] [Google Scholar]
- 31. Griffith LG, Swartz MA. Capturing complex 3D tissue physiology in vitro. Nat Rev Mol Cell Biol 2006; 7(3): 211–224. [DOI] [PubMed] [Google Scholar]
- 32. Yu X, Botchwey EA, Levine EM, et al. Bioreactor-based bone tissue engineering: the influence of dynamic flow on osteoblast phenotypic expression and matrix mineralization. Proc Natl Acad Sci U S A 2004; 101(31): 11203–11208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Cartmell SH, Porter BD, García AJ, et al. Effects of medium perfusion rate on cell-seeded three-dimensional bone constructs in vitro. Tissue Eng 2003; 9(6): 1197–1203. [DOI] [PubMed] [Google Scholar]
- 34. Sladkova M, de Peppo G. Bioreactor systems for human bone tissue engineering. Processes 2014; 2(2): 494–525. [Google Scholar]
- 35. Pisu M, Lai N, Cincotti A, et al. A simulation model for the growth of engineered cartilage on polymeric scaffolds. Int J Chem React Eng 2003; 1(1): 1–13. [Google Scholar]
- 36. Lappa M. Organic tissues in rotating bioreactors: fluid-mechanical aspects, dynamic growth models, and morphological evolution. Biotechnol Bioeng 2003; 84(5): 518–532. [DOI] [PubMed] [Google Scholar]
- 37. Pearson NC, Oliver JM, Shipley RJ, et al. A multiphase model for chemically- and mechanically- induced cell differentiation in a hollow fibre membrane bioreactor: minimising growth factor consumption. Biomech Model Mechanobiol 2016; 15(3): 683–700. [DOI] [PubMed] [Google Scholar]
- 38. Vetsch JR, Muller R, Hofmann S. The evolution of simulation techniques for dynamic bone tissue engineering in bioreactors. J Tissue Eng Regen Med 2015; 9(8): 903–917. [DOI] [PubMed] [Google Scholar]
- 39. Porter B, Zauel R, Stockman H, et al. 3-D computational modeling of media flow through scaffolds in a perfusion bioreactor. J Biomech 2005; 38(3): 543–549. [DOI] [PubMed] [Google Scholar]
- 40. O’Dea RD, Waters SL, Byrne HM. A two-fluid model for tissue growth within a dynamic flow environment. Eur J Appl Math 2008; 19: 607–634. [Google Scholar]
- 41. Guyot Y, Smeets B, Odenthal T, et al. Immersed boundary models for quantifying flow-induced mechanical stimuli on stem cells seeded on 3D scaffolds in perfusion bioreactors. PLoS Comput Biol 2016; 12(9): e1005108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Zhao F, Vaughan TJ, McNamara LM. Quantification of fluid shear stress in bone tissue engineering scaffolds with spherical and cubical pore architectures. Biomech Model Mechanobiol 2016; 15(3): 561–577. [DOI] [PubMed] [Google Scholar]
- 43. Shipley RJ, Davidson AJ, Chan K, et al. A strategy to determine operating parameters in tissue engineering hollow fiber bioreactors. Biotechnol Bioeng 2011; 108(6): 1450–1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Pierre J, Oddou C. Engineered bone culture in a perfusion bioreactor: a 2D computational study of stationary mass and momentum transport. Comput Methods Biomech Biomed Engin 2007; 10(6): 429–438. [DOI] [PubMed] [Google Scholar]
- 45. Sengers BG, Taylor M, Please CP, et al. Computational modelling of cell spreading and tissue regeneration in porous scaffolds. Biomaterials 2007; 28(10): 1926–1940. [DOI] [PubMed] [Google Scholar]
- 46. Milan JL, Planell JA, Lacroix D. Simulation of bone tissue formation within a porous scaffold under dynamic compression. Biomech Model Mechanobiol 2010; 9(5): 583–596. [DOI] [PubMed] [Google Scholar]
- 47. Byrne DP, Lacroix D, Planell JA, et al. Simulation of tissue differentiation in a scaffold as a function of porosity, Young’s modulus and dissolution rate: application of mechanobiological models in tissue engineering. Biomaterials 2007; 28(36): 5544–5554. [DOI] [PubMed] [Google Scholar]
- 48. Zubkov V, Combes AN, Short K, et al. A spatially-averaged mathematical model of kidney branching morphogenesis. J Theor Biol 2015; 379: 24–37. [DOI] [PubMed] [Google Scholar]
- 49. O’Dea RD, Nelson MR, El Haj AJ, et al. A multiscale analysis of nutrient transport and biological tissue growth in vitro. Math Med Biol 2015; 32(3): 345–366. [DOI] [PubMed] [Google Scholar]
- 50. Holden EC, Collis J, Brook BS, et al. A multiphase multiscale model for nutrient limited tissue growth. ANZIAM J 2018; 59: 499–532. [Google Scholar]
- 51. Davit Y, Bell CG, Byrne HM, et al. Homogenization via formal multiscale asymptotics and volume averaging: how do the two techniques compare? Adv Water Res 2013; 62: 178–206. [Google Scholar]
- 52. Scheiner S, Sinibaldi R, Pichler B, et al. Micromechanics of bone tissue-engineering scaffolds, based on resolution error-cleared computer tomography. Biomaterials 2009; 30(12): 2411–2419. [DOI] [PubMed] [Google Scholar]
- 53. Fernandes PR, Rodrigues HC, Guedes JM, et al. Multiscale modelling on bone mechanics – application to tissue engineering and bone quality analysis. IFAC Proc Vol 2012; 45: 1013–1017. [Google Scholar]
- 54. Fritsch A, Hellmich C, Young P. Micromechanics-derived scaling relations for poroelasticity and strength of brittle porous polycrystals. J Appl Mech 2013; 80: 020905. [Google Scholar]
- 55. Scheiner S, Komlev VS, Gurin AN, et al. Multiscale mathematical modeling in dental tissue engineering: toward computer-aided design of a regenerative system based on hydroxyapatite granules, focussing on early and mid-term stiffness recovery. Front Physiol 2016; 7: 383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Scheiner S, Komlev VS, Hellmich C. Strength increase during ceramic biomaterial-induced bone regeneration: a micromechanical study. Int J Fract 2016; 202(2): 217–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Pastrama M-I, Scheiner S, Pivonka P, et al. A mathematical multiscale model of bone remodeling, accounting for pore space-specific mechanosensation. Bone 2018; 107: 208–221. [DOI] [PubMed] [Google Scholar]
- 58. Shipley RJ, Jones GW, Dyson RJ, et al. Design criteria for a printed tissue engineering construct: a mathematical homogenization approach. J Theor Biol 2009; 259(3): 489–502. [DOI] [PubMed] [Google Scholar]
- 59. Penta R, Ambrosi D, Shipley RJ. Effective governing equations for poroelastic growing media. Quart J Mech Appl Math 2014; 67(1): 69–91. [Google Scholar]
- 60. White FM. Fluid mechanics. 4th ed. New: York: McGraw-Hill, 2017. [Google Scholar]
- 61. Acheson DJ. Elementary fluid dynamics. Oxford: Oxford University Press, 1991. [Google Scholar]
- 62. Sucosky P, Osorio DF, Brown JB, et al. Fluid mechanics of a spinner-flask bioreactor. Biotechnol Bioeng 2004; 85(1): 34–46. [DOI] [PubMed] [Google Scholar]
- 63. Chung CA, Chen CW, Chen CP, et al. Enhancement of cell growth in tissue-engineering constructs under direct perfusion: modeling and simulation. Biotechnol Bioeng 2007; 97(6): 1603–1616. [DOI] [PubMed] [Google Scholar]
- 64. Cioffi M, Kuffer J, Strobel S, et al. Computational evaluation of oxygen and shear stress distributions in 3D perfusion culture systems: macro-scale and micro-structured models. J Biomech 2008; 41(14): 2918–2925. [DOI] [PubMed] [Google Scholar]
- 65. Pangrle BJ, Alexandrou AN, Dixon AG, et al. An analysis of laminar fluid flow in porous tube and shell systems. Chem Eng Sci 1991; 46(11): 2847–2855. [Google Scholar]
- 66. Shipley RJ, Waters SL, Ellis MJ. Definition and validation of operating equations for poly(vinyl alcohol)-poly(lactide-co-glycolide) microfiltration membrane-scaffold bioreactors. Biotechnol Bioeng 2010; 107(2): 382–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Waters SL, Cummings LJ, Shakesheff KM, et al. Tissue growth in a rotating bioreactor. Part I: mechanical stability. Math Med Biol 2006; 23(4): 311–337. [DOI] [PubMed] [Google Scholar]
- 68. Freed LE, Vunjak-Novakovic G. Cultivation of cell-polymer tissue constructs in simulated microgravity. Biotechnol Bioeng 1995; 46(4): 306–313. [DOI] [PubMed] [Google Scholar]
- 69. Pollack SR, Meaney DF, Levine EM, et al. Numerical model and experimental validation of microcarrier motion in a rotating bioreactor. Tissue Eng 2000; 6(5): 519–530. [DOI] [PubMed] [Google Scholar]
- 70. Cummings LJ, Waters SL. Tissue growth in a rotating bioreactor. Part II: fluid flow and nutrient transport problems. Math Med Biol 2007; 24(2): 169–208. [DOI] [PubMed] [Google Scholar]
- 71. Hidalgo-Bastida LA, Thirunavukkarasu S, Griffiths S, et al. Modeling and design of optimal flow perfusion bioreactors for tissue engineering applications. Biotechnol Bioeng 2012; 109(4): 1095–1099. [DOI] [PubMed] [Google Scholar]
- 72. Brinkman HC. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Flow Turbul Combust 1949; 1(1): 27–34. [Google Scholar]
- 73. Lundgren TS. Slow flow through stationary random beds and suspensions of spheres. J Fluid Mech 1972; 51(2): 273–299. [Google Scholar]
- 74. Galbusera F, Cioffi M, Raimondi MT, et al. Computational modeling of combined cell population dynamics and oxygen transport in engineered tissue subject to interstitial perfusion. Comput Methods Biomech Biomed Eng 2007; 10(4): 279–287. [DOI] [PubMed] [Google Scholar]
- 75. Gutierrez RA, Crumpler ET. Potential effect of geometry on wall shear stress distribution across scaffold surfaces. Ann Biomed Eng 2008; 36(1): 77–85. [DOI] [PubMed] [Google Scholar]
- 76. Shakeel M, Matthews PC, Graham RS, et al. A continuum model of cell proliferation and nutrient transport in a perfusion bioreactor. Math Med Biol 2013; 30(1): 21–44. [DOI] [PubMed] [Google Scholar]
- 77. Soares JS, Sacks MS. A triphasic constrained mixture model of engineered tissue formation under in vitro dynamic mechanical conditioning. Biomech Model Mechanobiol 2016; 15(2): 293–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Sturrock JE, Nunn JF. Chromosomal damage and mutations after exposure of Chinese hamster cells to high concentrations of oxygen. Mutat Res 1978; 57(1): 27–33. [DOI] [PubMed] [Google Scholar]
- 79. Balin AK, Goodman DBP, Rasmussen H, et al. The effect of oxygen tension on cellular growth and metabolism was studied in actively growing WI-38 cells. J Cell Physiol 1976; 89(2): 235–249. [DOI] [PubMed] [Google Scholar]
- 80. Burdon RH. Oxidative stress in cultured animal cells. In: Spier RE, Griffiths JB. (eds) Animal cell biotechnology, vol. 6. New York: Academic Press, 1994, pp. 129–160. [Google Scholar]
- 81. Helt CE, Rancourt RC, Staversky RJ, et al. p53-dependent induction of p21Cip1/WAF1/Sdi1 protects against oxygen-induced toxicity. Toxicol Sci 2001; 63(2): 214–222. [DOI] [PubMed] [Google Scholar]
- 82. Gray DH, Hamblen DL. The effects of hyperoxia upon bone in organ culture. Clin Orthop Relat Res 1976; 119: 225–230. [PubMed] [Google Scholar]
- 83. Buerk DG, Saidel GM. Local kinetics of oxygen metabolism in brain and liver tissues. Microvasc Res 1978; 16(3): 391–405. [DOI] [PubMed] [Google Scholar]
- 84. Galban CJ, Locke BR. Effects of spatial variation of cells and nutrient and product concentrations coupled with product inhibition on cell growth in a polymer scaffold. Biotechnol Bioeng 1999; 64(6): 633–643. [PubMed] [Google Scholar]
- 85. Obradovic B, Meldon JH, Freed LE, et al. Glycosaminoglycan deposition in engineered cartilage: experiments and mathematical model. AIChE J 2000; 46: 1860–1871. [Google Scholar]
- 86. Zhao F, Pathi P, Grayson W, et al. Effects of oxygen transport on 3-D human mesenchymal stem cell metabolic activity in perfusion and static cultures: experiments and mathematical model. Biotechnol Prog 2005; 21(4): 1269–1280. [DOI] [PubMed] [Google Scholar]
- 87. Pilling MJ, Seakins PW. Reaction kinetics. Oxford: Oxford University Press, 1996. [Google Scholar]
- 88. Biotol. Bioprocess technology: modelling and transport phenomena (Biotol series). Oxford: Butterworth-Heinemann, 1992, pp. 244–250. [Google Scholar]
- 89. Liu Y, Munoz N, Bunnell BA, et al. Density-dependent metabolic heterogeneity in human mesenchymal stem cells. Stem Cells 2015; 33(11): 3368–3381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Shakeel M. 2-D coupled computational model of biological cell proliferation and nutrient delivery in a perfusion bioreactor. Math Biosci 2013; 242(1): 86–94. [DOI] [PubMed] [Google Scholar]
- 91. Ambard D, Swider P. A predictive mechano-biological model of the bone-implant healing. Eur J Mech A Solids 2006; 25(6): 927–937. [Google Scholar]
- 92. MacArthur BD, Please CP, Taylor M, et al. Mathematical modelling of skeletal repair. Biochem Biophys Res Commun 2004; 313(4): 825–833. [DOI] [PubMed] [Google Scholar]
- 93. Chapman LAC, Shipley RJ, Whiteley JP, et al. Optimising cell aggregate expansion in a perfused hollow fibre bioreactor via mathematical modelling. PLoS ONE 2014; 9(8): e105813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Geris L. Computational modeling in tissue engineering: Berlin: Springer, 2013. [Google Scholar]
- 95. Chung CA, Lin T-H, Chen S-D, et al. Hybrid cellular automaton modeling of nutrient modulated cell growth in tissue engineering constructs. J Theor Biol 2010; 262(2): 267–278. [DOI] [PubMed] [Google Scholar]
- 96. Cheng G, Markenscoff P, Zygourakis K. A 3D hybrid model for tissue growth: the interplay between cell population and mass transport dynamics. Biophys J 2009; 97(2): 401–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97. Yeatts AB, Fisher JP. Bone tissue engineering bioreactors: dynamic culture and the influence of shear stress. Bone 2011; 48(2): 171–181. [DOI] [PubMed] [Google Scholar]
- 98. Song K, Liu T, Cui Z, et al. Three-dimensional fabrication of engineered bone with human bio-derived bone scaffolds in a rotating wall vessel bioreactor. J Biomed Mater Res A 2008; 86(2): 323–332. [DOI] [PubMed] [Google Scholar]
- 99. Zhang Z-Y, Teoh SH, Teo EY, et al. A comparison of bioreactors for culture of fetal mesenchymal stem cells for bone tissue engineering. Biomaterials 2010; 31(33): 8684–8695. [DOI] [PubMed] [Google Scholar]
- 100. Sikavitsas VI, Bancroft GN, Mikos AG. Formation of three-dimensional cell/polymer constructs for bone tissue engineering in a spinner flask and a rotating wall vessel bioreactor. J Biomed Mater Res 2002; 62(1): 136–148. [DOI] [PubMed] [Google Scholar]
- 101. Carpentier B, Layrolle P, Legallais C. Bioreactors for bone tissue engineering. Int J Artif Organs 2011; 34(3): 259–270. [DOI] [PubMed] [Google Scholar]
- 102. Kwon O, Devarakonda SB, Sankovic JM, et al. Oxygen transport and consumption by suspended cells in microgravity: a multiphase analysis. Biotechnol Bioeng 2008; 99(1): 99–107. [DOI] [PubMed] [Google Scholar]
- 103. Cummings LJ, Sawyer NBE, Morgan SP, et al. Tracking large solid constructs suspended in a rotating bioreactor: a combined experimental and theoretical study. Biotechnol Bioeng 2009; 104(6): 1224–1234. [DOI] [PubMed] [Google Scholar]
- 104. Martys NS, Chen H. Simulation of multicomponent fluids in complex three-dimensional geometries by the lattice Boltzmann method. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics 1996; 53(1): 743–750. [DOI] [PubMed] [Google Scholar]
- 105. Ellis MJ, Chaudhuri JB. Human bone derived cell culture on PLGA flat sheet membranes of different lactide: glycolide ratio. Biotechnol Bioeng 2008; 101(2): 369–377. [DOI] [PubMed] [Google Scholar]
- 106. Morgan SM, Tilley S, Perera S, et al. Expansion of human bone marrow stromal cells on poly-(DL-lactide-co-glycolide) (PDL LGA) hollow fibres designed for use in skeletal tissue engineering. Biomaterials 2007; 28(35): 5332–5343. [DOI] [PubMed] [Google Scholar]
- 107. Cima LG, Blanch HW, Wilke CR. A theoretical and experimental evaluation of a novel radial-flow hollow fiber reactor for mammalian cell culture. Bioprocess Eng 1990; 5(1): 19–30. [Google Scholar]
- 108. Owen A, Newsome PN. Mesenchymal stromal cell therapy in liver disease: opportunities and lessons to be learnt. Am J Physiol Gastrointest Liver Physiol 2015; 309(10): G791–G800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Prendergast PJ, Huiskes R, Soballe K. Biophysical stimuli on cells during tissue differentiation at implant interfaces. J Biomech 1997; 30(6): 539–548. [DOI] [PubMed] [Google Scholar]
- 110. Hu B, El Haj AJ, Dobson J. Receptor-targeted, magneto-mechanical stimulation of osteogenic differentiation of human bone marrow-derived mesenchymal stem cells. Int J Mol Sci 2013; 14(9): 19276–19293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Cartmell SH, Dobson J, Verschueren S, et al. Mechanical conditioning of bone cells in vitro using magnetic microparticle technology. Eur Cell Mater 2002; 4: 130–131. [Google Scholar]
- 112. Cartmell SH, Hughes S, Dobson J, et al. Preliminary analysis of magnetic particle techniques for activating mechanotransduction in bone cells. In: Proceedings of the IEEE-EMBS special topic conference on molecular, cellular and tissue engineering, Genoa, 9 June 2002, pp. 87–88. New York: IEEE. [Google Scholar]
- 113. Dobson J, Keramane A, El Haj AJ. Theory and applications of a magnetic force bioreactor. Eur Cell Mater 2002; 4: 42–44. [Google Scholar]