Dissociable Forms of Uncertainty-Driven Representational Change Across the Human Brain

Abstract

Environmental change can lead decision makers to shift rapidly among different behavioral regimes. These behavioral shifts can be accompanied by rapid changes in the firing pattern of neural networks. However, it is unknown what the populations of neurons that participate in such “network reset” phenomena are representing. Here, we investigated the following: (1) whether and where rapid changes in multivariate activity patterns are observable with fMRI during periods of rapid behavioral change and (2) what types of representations give rise to these phenomena. We did so by examining fluctuations in multivoxel patterns of BOLD activity from male and female human subjects making sequential inferences about the state of a partially observable and discontinuously changing variable. We found that, within the context of this sequential inference task, the multivariate patterns of activity in a number of cortical regions contain representations that change more rapidly during periods of uncertainty following a change in behavioral context. In motor cortex, this phenomenon was indicative of discontinuous change in behavioral outputs, whereas in visual regions, the same basic phenomenon was evoked by tracking of salient environmental changes. In most other cortical regions, including dorsolateral prefrontal and anterior cingulate cortex, the phenomenon was most consistent with directly encoding the degree of uncertainty. However, in a few other regions, including orbitofrontal cortex, the phenomenon was best explained by representations of a shifting context that evolve more rapidly during periods of rapid learning. These representations may provide a dynamic substrate for learning that facilitates rapid disengagement from learned responses during periods of change.

SIGNIFICANCE STATEMENT Brain activity patterns tend to change more rapidly during periods of uncertainty and behavioral adjustment, yet the computational role of such rapid transitions is poorly understood. Here, we identify brain regions with fMRI BOLD activity patterns that change more rapidly during periods of behavioral adjustment and use computational modeling to attribute the phenomenon to specific causes. We demonstrate that the phenomenon emerges in different brain regions for different computational reasons, the most common being the representation of uncertainty itself, but that, in a selective subset of regions including orbitofrontal cortex, the phenomenon was best explained as a shifting latent state signal that may serve to control the degree to which recent temporal context affects ongoing expectations.

Introduction

Neural populations in rodent prefrontal cortex can undergo abrupt changes in firing concomitant with changes in performance in rule-based tasks (Durstewitz et al., 2010; Powell and Redish, 2016). Similar phenomena have been observed in the multivoxel patterns in human fMRI data preceding changes in task strategy, leading to the notion that such changes might correspond to an “aha moment” at which the brain reorganizes to produce a new task set (Schuck et al., 2015). In rodent learning tasks that involve discontinuously changing reward contingencies, abrupt changes in firing of neurons in medial frontal cortex are observed more frequently during periods of uncertainty, during which animals appear to be searching for the best behavioral policy (Karlsson et al., 2012). It is unclear to what extent such phenomena are specific to medial frontal populations or to what extent they might have an analog in human learning. Furthermore, although these “network resets” during periods of uncertainty are thought to play a role in behavioral flexibility in changing environments (Tervo et al., 2014), the exact computational role of abrupt changes in such neural representations remains unknown.

A number of different computational factors could explain previously observed network reset phenomena. First, and most simply, such abrupt changes would be expected in a neural representation of the current behavioral policy, which in some cases may be directly related to the motor program. Successful execution of learning requires maintenance and updating of a behavioral policy, which would tend to change more rapidly during periods of uncertainty.

Alternatively, reset phenomena might result from representation of higher-order computational variables used to appropriately calibrate the rate of learning. Recent work has highlighted a number of computational variables that are important for successful learning in the presence of discontinuous environmental changes (change points). In particular, humans tend to increase rates of learning according to the probability with which a given outcome reflects a change point in the behavioral contingency (“change point probability,” CPP) and according to the relative imprecision of their estimate of the current contingency (“relative uncertainty,” RU) (Nassar et al., 2010, 2012). These computational variables both increase following change points, albeit with different dynamics, to mediate rapid incorporation of new information during and after periods of environmental change. CPP and RU correlate with BOLD responses across a wide swath of brain regions, including some that jointly reflect both variables and some that uniquely reflect either CPP or uncertainty (McGuire et al., 2014). In principle, neural representations of either computational factor might involve patterns of activation that mimic “network reset” phenomena, yet this possibility has never been tested directly.

Another signal that might give rise to reset-like dynamics is a continuously evolving latent state representation. Latent states, which represent the relevant behavioral context in cases where it is not directly observable, can improve learning in the face of abstract stimulus categories or repeated episodes by efficiently partitioning learning across distinct behaviorally relevant contexts (Gershman and Niv, 2010). Although previous work has focused primarily on the advantage of such representations for rapid reinstatement of previously learned behaviors (Gershman et al., 2010; Wilson et al., 2014), another advantage of such representations is that they could facilitate rapid disengagement from established behaviors that are no longer relevant. By appropriately partitioning data collected over time in a changing environment, such a mechanism could aid learning even if previously encountered environmental states do not recur. To accomplish this, such a latent state representation would need to evolve faster after a period of environmental change to effectively disengage from the previous behavioral context (Prescott Adams and MacKay, 2007; Wilson et al., 2010). Although previous work has suggested that orbitofrontal cortex (OFC) might represent latent task states (Klein-Flügge et al., 2013; Stalnaker et al., 2014; Howard et al., 2015; Schuck et al., 2016; Howard and Kahnt, 2018), it is unclear whether such representations transition dynamically during periods of rapid learning as would be necessary to efficiently mediate disengagement of learned responses that are rendered irrelevant by environmental change.

Here, we investigated whether and where uncertainty-linked network resets are observable in human fMRI data and evaluated the most likely computational explanation for these phenomena in individual brain regions. We did so using a multistep approach. First, we identified signals that change rapidly from trial to trial during periods of uncertainty and rapid learning and potentially correspond to network resets (Karlsson et al., 2012). Second, we generalized this notion of representational change across pairs of nonconsecutive trials using representational similarity analysis (RSA) (Nili et al., 2014). Third, we formalized a set of candidate computational explanations for network-reset phenomena and allowed these explanations to compete to explain multivariate brain activity (Kragel et al., 2018).

We observed rapid changes in multivariate activity patterns across widespread cortical regions during periods of uncertainty and rapid learning. Using RSA, we showed that patterns in motor regions were best described as reflecting behavioral policy, patterns of activation in occipital regions were best described as registering the occurrence of change points, and patterns across much of the rest of the cortex appeared to reflect uncertainty. However, patterns of activation in a small number of regions including OFC were most consistent with dynamic latent state representations, suggesting a possible role for the OFC in translating learning signals into state changes that effectively disengage from behaviors learned in contexts that are no longer relevant.

Materials and Methods

Behavioral task and analysis.

Thirty-two human subjects (17 female, 15 male) performed a computerized predictive inference task in an MRI scanner while undergoing functional neuroimaging. On each trial, subjects were required to move a bucket to a new location at some point on the horizontal axis of a screen using a joystick controlled by the right hand and starting from a “home position” at the right edge of the screen. Subjects were instructed to move the bucket to the inferred position of a helicopter, which was occluded by clouds, and thus not directly observable. Subjects had 3 s to place the bucket in their preferred location, after which the helicopter would drop a bag that contained either high value or neutral items (value designated by color, the animation of the falling bag lasted 1 s). The primary information in the task was provided by the horizontal location of the bag, which was selected at random on each trial from a normal distribution centered on the true helicopter location (incentivizing bucket placement under the inferred helicopter location) and with a SD that was manipulated blockwise. Subjects completed four task blocks of 120 trials each (two blocks of high/low SD). On the majority of trials (90%), the helicopter would remain in the same location as in the previous trial, but occasionally (10%), the helicopter would relocate to a new position along the horizontal axis of the screen (selected randomly and uniformly). Because subjects could not see the helicopter, they were forced to infer its position based on history of previous bag locations and in some cases were required to recognize and respond to a change in helicopter location. A more in-depth description of the behavioral task and an extensive characterization of subject behavior are available in our previous report (McGuire et al., 2014).

MRI data acquisition and preprocessing.

T1-weighted MPRAGE structural images (0.9375 × 0.9375 × 1 mm voxels, 192 × 256 matrix, 160 axial slices, TI = 1100 ms, TR = 1630 ms, TE = 3.11 ms, flip angle = 15°), T2*-weighted EPI functional data (3 mm isotropic voxels, 64 × 64 matrix, 42 axial slices tilted 30° from the AC-PC plane, TR = 2500 ms, TE = 25 ms, flip angle = 75°), and field map images (TR = 1000 ms, TE = 2.69 and 5.27 ms, flip angle = 60°) were acquired on a 3 T Siemens Trio with a 32 channel head coil. Functional data were acquired in 4 runs, each of which lasted 9 min and 25 s (226 images).

Data were preprocessed using AFNI (Cox, 1996, 2012) and FSL (Jenkinson et al., 2002, 2012; Smith et al., 2004) in the following steps: (1) slice timing correction (AFNI's 3dTshift); (2) motion correction (FSL's MCFLIRT); (3) field map-based geometric undistortion, alignment with structural images, and registration to the MNI template (FSL's FLIRT and FNIRT); (4) spatial smoothing with a 6 mm FWHM Gaussian kernel (FSL's fslmaths); and (5) outlier attenuation (AFNI's 3dDespike) and intensity-scaling by a single grand-mean value in each run (FSL's fslmaths). The resulting functional time series was deconvolved to estimate trial activations at the time of the bag drop using the least-squares-separate method (Mumford et al., 2012) implemented in MATLAB with inclusion of six rigid body motion parameters and 16 low-order cosine components (four per run) as regressors of no interest. Our decision to model the bag drop time point (as in our previous reports; Nassar et al., 2012; McGuire et al., 2014) was motivated by our interest in how the bag locations would affect internal representations. In practice, however, the rapid nature of our task prohibits us from making strong claims regarding the specificity of our results to a given task phase.

Alternative preprocessing pipelines were also used to verify the robustness of our findings (see Tables 2 and 3). In one such pipeline, the spatial smoothing was omitted from the pipeline described above and instead spatial smoothing with a 6 mm FWHM Gaussian kernel was applied to the coefficient maps resulting from RSA. Another alternative preprocessing strategy omitted spatial smoothing and also implemented spatial prewhitening to emphasize high-frequency components of the spatial patterns (Walther et al., 2016).

Table 2.

Peak voxel locations corresponding to behavioral policy, relative uncertainty, change point probability and shifting latent state representations after RSA

Coefficient	Voxels	Max t-value	x	y	z	Label
Behavioral policy	1058	6.5	27	−57	−18	R fusiform cortex
	295	5.2	−34	−27	64	L precentral gyrus (motor)
Change point probability	4191	10.0	21	−90	7	Occipital pole
Uncertainty	29582	10.5	−7	−66	52	Precuneus
	Local max	9.0	−19	−84	−18	L occipital fusiform
	Local max	8.6	−1	−39	58	Postcentral gyrus
	Local max	8.5	30	13	61	R middle frontal gyrus
	Local max	8.4	6	16	52	Paracingulate gyrus
Shifting latent state	3581	5.5	−58	−6	−33	L middle temporal gyrus
	2096	6.0	−37	64	−3	Orbitofrontal cortex
	1290	6.0	−19	−72	64	Superior lateral occipital complex
	443	4.4	60	−6	−36	R middle temporal gyrus

Shown are cluster size (in voxels) and maximum (t-statistic) and MNI coordinates for each cluster from the competing computations RSA analysis on unsmoothed data surviving multiple-comparisons correction (spatial smoothing performed on RSA coefficients before multiple comparisons correction; see Fig 3-1).

Table 3.

Robustness checks in the regions of interest showing a significant effect of shifting latent state (from peak voxel of clusters reported in Table 1)

Region/model	Mean beta	t-value	p-value (uncorrected)
Inferior temporal gyrus (−61, −24, −24)
Prewhitened	0.0375	3.68	8.78e-4
Minimal model	0.0693	4.57	7.37e-5
Time-shifted	0.0729	4.19	2.14e-4
Occipitoparietal cortex (21, −69, 67)
Prewhitened	0.0624	3.16	0.00347
Minimal model	0.0372	1.13	0.265
Time-shifted	0.0859	4.09	2.81e-4
Left orbitofrontal cortex (−16, 49, −15)
Prewhitened	0.0256	2.27	0.0304
Minimal model	0.0517	3.43	0.00172
Time-shifted	0.0720	3.98	3.91e-4
Superior parietal lobule (−28, −48, 52)
Prewhitened	0.0175	1.82	0.0792
Minimal model	0.0116	0.547	0.588
Time-shifted	0.0656	4.22	2.00e-4
Right orbitofrontal cortex (27, 43, −18)
Prewhitened	0.0271	2.18	0.0367
Minimal model	0.0586	3.93	4.45e-4
Time-shifted	0.0640	4.06	3.11e-4
Occipital pole (−13, −93, −9)
Prewhitened	0.0243	2.68	0.0116
Minimal model	0.0539	3.47	0.00153
Time-shifted	0.0426	3.08	0.00435

Peak-centered spheres were re-analyzed in three ways. The prewhitened analysis used unsmoothed voxels that were spatially prewhitened (Walther et al., 2016). The minimal model analysis used a regression model that only contained an intercept, the latent state predictor, and 15 off-diagonal autocorrelation terms. The time-shifted analysis used a time-shifted “shifting latent state” regressor in which representations at the time of outcome on a given trial were modeled as reflecting the beliefs that would guide behavior on the subsequent trial. This was offset by one trial from our original analysis, which assumed that representations upon viewing an outcome would reflect the beliefs that were formed in anticipation of that outcome rather than the updated ones that incorporated it.

Computing normative dynamic learning rates.

Successful task performance required contending with imperfect cues about helicopter location (variability in the distribution of bag locations), as well as changes in helicopter location, which rendered past bag locations irrelevant to future ones. Optimal inference under such conditions can be achieved by applying Bayes rule to maintain and update a probability distribution over potential periods of stability, or run length (Prescott Adams and MacKay, 2007; Wilson et al., 2010). This solution can be approximated by using a single representative value for the run length, rather than maintaining the full distribution, yielding an error-driven learning rule in which the learning rate is adjusted dynamically from trial-to-trial as follows:

where B_t is the underlying belief about helicopter location on trial t, δ is the prediction error on trial t (Difference between bag location and belief), and α is a dynamic learning rate, which varies from trial to trial and controls the influence of prediction errors on updated beliefs (Nassar et al., 2010, 2012).

Dynamic learning rates depend on CPP, which is the probability that the helicopter relocated since the previous outcome was observed, and RU, which reflects the fraction of uncertainty over the position of the upcoming bag location that is attributable to uncertainty about the current helicopter position (see Fig. 1C; Nassar et al., 2016):

where Ω_t is the CPP and τ_t is the RU on trial t.

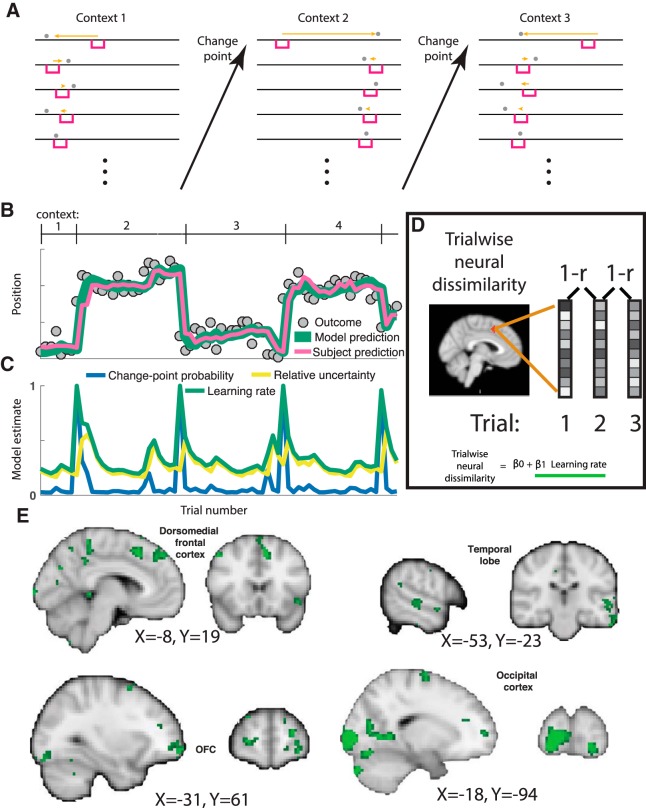
Figure 1.

Trialwise neural dissimilarity is increased after change points during periods of rapid learning for multiple brain regions. A, Participants were asked to move a bucket (pink rectangle) on each trial to the location most likely to deliver a reward (in the form of a bag containing coins). On each trial (stacked vertically), the participant would observe an outcome (bag location; gray circle) that they could use to update their bucket placement for the subsequent trial (orange arrow). Most contiguous trials were generated from the same context, which was defined by a fixed outcome distribution; however, at occasional change points, the context (mean outcome location) shifted abruptly and unpredictably. B, Example sequence of outcomes (gray circles) and corresponding participant bucket placements (pink line) plotted across trials. C, Participant bucket placements were well described by a normative learning model (green line) that adjusts learning rate according to CPP and RU, which are updated according to the model on each trial and evolve over time. D, Trialwise measures of neural dissimilarity were computed on each trial as one minus the correlation coefficient between contiguous trial activations within a searchlight and regressed onto learning rates from the normative learning model to identify brain regions with BOLD activations that evolved more rapidly during periods of rapid learning. E, Diverse array of brain regions including occipital regions, dorsomedial prefrontal cortex, OFC, and temporal regions displayed neural changes that were positively related to learning (green clusters). All images are thresholded at p = 0.001, uncorrected.

These latent variables were updated on each trial with a parameter-free normative model that took subject prediction errors as an input according to the following set of recursive equations:

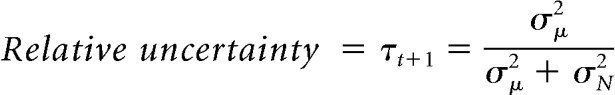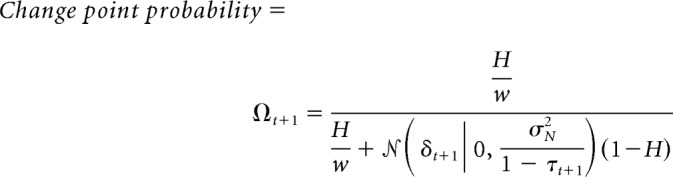where σ_μ² is the total variance in beliefs about the helicopter location (the generative mean), σ_N² is the variance in the distribution of outcomes (bag drops) around that mean, δ_t is the prediction error, H is the hazard rate, and w is the width of the screen. For a full derivation of the model and terms, see Nassar et al. (2010) and for a complete description of the method for estimating latent variables, see Nassar et al. (2016).

Multivariate fMRI analysis.

Multivariate analyses were conducted in spherical searchlights (radius = 3 voxels) across the entire brain. Within each searchlight, the neural dissimilarity between each pair of trials was computed as one minus the spatial Pearson correlation between the voxelwise activations for those trials.

Trial-to-trial dissimilarity analysis.

Trial-to-trial dissimilarity scores were extracted by extracting the i = j − 1 diagonal elements from the dissimilarity matrix, which corresponded to the dissimilarity between adjacent trials (see Fig. 1D). The dissimilarity scores were regressed onto an explanatory matrix containing an intercept, and dynamic learning rates prescribed by a normative learning model, yielding one coefficient of interest per subject, per searchlight.

As described above, dynamic learning rates depended on two factors: CPP and RU. In general, CPP and RU were both increased after change points, albeit with different latencies, leading to learning rates that decay slowly as a function of time within context. Learning rates quantifying sensitivity to information provided on trial j were aligned with the trial-to-trial dissimilarity between trials j and j+1. Therefore, our analysis targeted patterns of activity whose degree of change between trials j and j+1 reflected normative learning predicted to occur from the outcome presented on trial j. The first 3 trials from each block were removed from analysis as they occurred at the onset of fMRI acquisition. Correlations between model-derived quantities (CPP, RU, normative learning rate) and the six rigid body motion parameters (estimated from MCFLIRT and deconvolved using the least-squares-separate method as described above) were uniformly small (mean Pearson R² across participants < 0.009 for each of the 18 pairwise correlations) as were correlations with absolute relative displacements in the same measures (mean Pearson R² across participants < 0.008 for each of the 18 pairwise correlations).

RSA.

Trial-to-trial dissimilarity analysis described above could be thought of as a special case of the general idea that the similarity between each pair of trials might be inversely related to the learning done between them. Because this pattern of similarity is what might be expected to emerge from a representation of the latent task state, which transitions abruptly from one context to the next and remains relatively stable after many trials in a well learned context, we will refer to it as the shifting latent state dissimilarity matrix. The hypothesis matrix for shifting latent states was generated by computing the extent to which the inference on trial i would factor into the inference on trial j, assuming normative learning as follows:

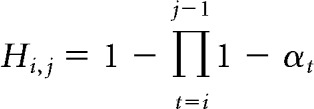where H is the shifting latent state dissimilarity matrix and α is the learning rate prescribed by a normative model (Nassar et al., 2010), such that more prescribed learning between two trials corresponded to higher values of α, a smaller product term, and thus a greater dissimilarity. The i = j − 1 diagonal of this matrix is 1 − (1 − α_t), or just α_t, and thus equivalent to the vector of trial-to-trial dissimilarities described above. However, the shifting latent state hypothesis matrix also includes information about other elements in the matrix, potentially offering a more powerful construct to ask a similar question. We investigated whether this similarity structure was reflected in the neural dissimilarity between trials in each spherical searchlight. The lower triangle of the neural dissimilarity matrix was regressed onto a hypothesis matrix that included an intercept, the shifting latent state hypothesis matrix (lower triangle), and 15 dummy variables designed to remove the influence of autocorrelation on the coefficient of interest. These autocorrelation terms were derived from 15 off-diagonal binary matrices in which a single off-diagonal (i = j − 1; i = j − 2; i = j − 3 … i = j − 15) was set to one. These matrices were constructed to account for any variance in the neural dissimilarity matrices that could be explained by a fixed signal autocorrelation. To be sure that autocorrelation could not affect our analysis of interest, we also set all elements of the shifting latent state similarity matrix that fell outside of this range (trials separated by more than 15 trials) to the maximum dissimilarity value.

Dissociating computational explanations with RSA.

To better understand the computations that give rise to rapid changes in neural patterns during periods of learning after a helicopter relocation, we constructed an exhaustive set of hypothesis matrices and conducted a RSA in which these representations could compete with the shifting latent state matrix described above to explain structure in neural dissimilarity matrices. Therefore, this analysis included the same shifting latent state matrix, but also included hypothesis matrices for various factors that could relate to task uncertainty, learning, or explain nuisance variance in the neural dissimilarity matrices. Hypothesis matrices were generated for three additional explanatory variables of interest: (1) subject prediction (behavioral policy), (2) RU, and (3) CPP. We also included six additional nuisance variables: (4) the bag drop's location, (5) the signed prediction error (i.e., the distance between the prediction and the bag drop), (6) high CPP (to account for patterns of activity that may asymmetrically encode CPP), (7) high RU (to account for patterns of activity that may asymmetrically encode RU), (8) outcome reward value, and (9) task block. For factors 1–5 and 8, element (i,j) of the hypothesis matrix corresponded to the absolute difference in that factor on trials i and j. For factor 9, dissimilarity values were set to 0 for trials in the same block and 1 for trials in different blocks. Dissimilarity matrices for factors 6 and 7 were computed as one minus the multiplicative interaction of the model variable (6 = CPP, 7 = RU) on trials i and j such that similarity was only hypothesized when the model-derived term took on a high value on both trials. These terms allowed the model to capture asymmetric representations of the two factors governing learning in our model, such as a representation that converged for values of high RU, but did not show any consistent pattern of activation when RU was low.

The lower triangle of the neural dissimilarity matrix was extracted and regressed onto an explanatory matrix consisting of an intercept and the lower triangle of all hypothesis/nuisance matrices (including the shifting latent state and nuisance autocorrelation terms), yielding one coefficient per variable, per subject, per searchlight (Chikazoe et al., 2014; Kragel et al., 2018). Group-level analyses were conducted by computing t-statistics across subjects for each variable and searchlight. Cluster-based permutation testing using cluster mass with a cluster forming threshold of p < 0.001 and an α of 0.01 was used to identify significant activations (FSL's randomise) (Nichols and Holmes, 2002).

Results

To determine how neural signals change during periods of uncertainty, we reanalyzed data from a previously published study that included recordings of fMRI BOLD signal and behavioral responses of human participants in a predictive inference task (McGuire et al., 2014). Participants played a video game in which they tried to get as many coins as possible (redeemable for money) by catching bags of coins dropped from a hidden helicopter in the sky. Therefore, on each task trial, participants estimated the state of an unobservable variable (the position of a helicopter) based on the history of an observable variable (the position of bags dropped from that helicopter) (McGuire et al., 2014). The task included abrupt change points at which the position of the helicopter was resampled from a uniform distribution, which forced participants to rapidly revise beliefs about the helicopter location to maintain successful task performance. Here, we refer to periods of consistent helicopter position as contexts (Fig. 1A) such that the task could be described as requiring dynamic belief updating both within (Fig. 1A, vertical) and across (Fig. 1A, horizontal) contexts.

As we described in our previous report, adjustments in the rate at which participants revised beliefs in response to new information were well described by a normative learning model that adjusted learning according to two computational variables: CPP and RU (Fig. 1B, compare pink and green lines; McGuire et al., 2014; Nassar et al., 2016). CPP reflects the Bayesian posterior probability that the helicopter has relocated on the current trial and is largest on trials with large spatial prediction errors (Fig. 1C, blue line). RU captures the degree to which uncertainty about the true helicopter location should drive learning, is greatest on the trial after a spike in CPP, and decays as a function of trials thereafter (Fig. 1C, yellow line). Both of these factors affect the sensitivity of ongoing beliefs to new information (e.g., bag locations), which can be expressed in terms of a dynamic learning rate (Fig. 1C, green). We sought to identify relationships between the sensitivity of behavior to incoming information (i.e., learning rate) and the sensitivity of neural representations to the same information.

Representations change rapidly during learning

The trial-to-trial dissimilarity in multivariate voxel activation patterns was related to the dynamic learning rates prescribed by the normative model (Fig. 1D). Trialwise neural dissimilarity was computed for each pair of sequentially adjacent trials using a whole-brain searchlight procedure and regressed onto an explanatory matrix that included model-based estimates of dynamic learning rates. A constellation of regions showed patterns of activation that changed more rapidly during periods of rapid learning after change points (Fig. 1E). These regions included OFC, but also clusters in dorsomedial frontal cortex (DMFC), occipital cortex, and temporal lobe. Therefore, with a simple measure of representational change, we identified neural signals with representations that updated more rapidly during periods of learning in multiple brain regions (Karlsson et al., 2012).

Testing for shifting latent state representations using RSA

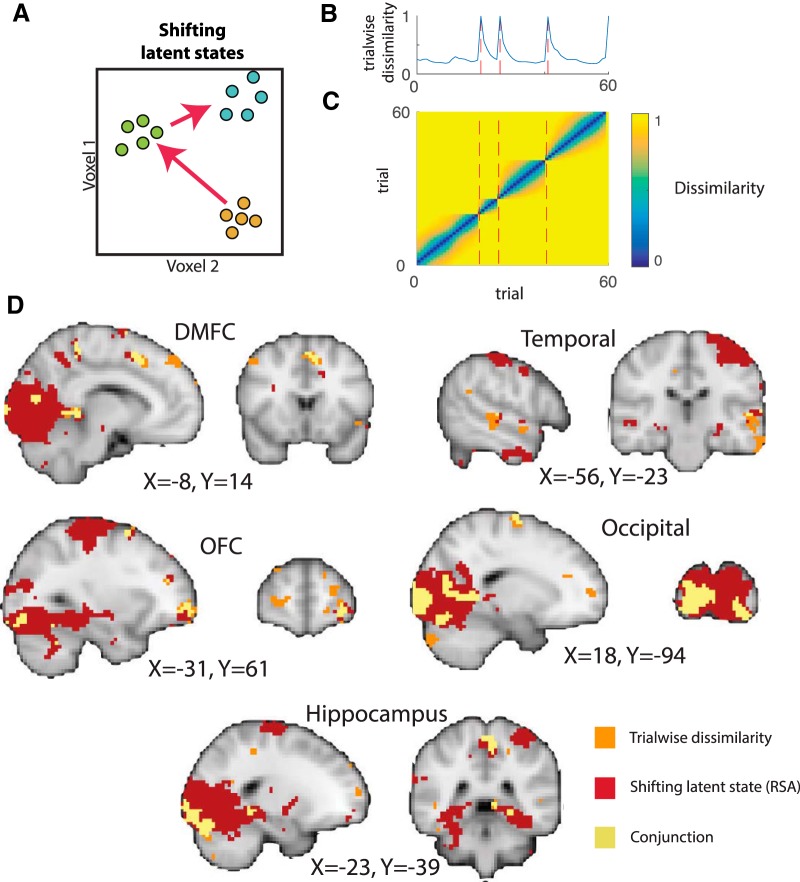
We next exploited RSA to extend and generalize the analysis above by incorporating information about the pairwise dissimilarity for all pairs of trials, not merely adjacent trial pairs. We hypothesized that the dissimilarity in neural representation for any pair of trials would depend on the cumulative amount of learning expected to occur between them under the normative model (see Materials and Methods). The hypothesized pattern of dissimilarity across trials is equivalent to what we would expect from a latent state representation that shifted rapidly at abrupt context transitions and concomitant periods of rapid learning, but remained relatively stable in periods when the statistics of the environment were stationary (Fig. 2A). The pattern of dissimilarities predicted across adjacent trials using this strategy is exactly equivalent to the learning rates that served as the explanatory variable in the previous analysis (Fig. 2B), but this generalization also makes predictions about the pattern of dissimilarities that would be observed across nonadjacent trials (Fig. 2C). We used a searchlight to identify brain regions in which the neural dissimilarity matrix was positively associated with this hypothetical “shifting state representation” hypothesis matrix while controlling for fixed autocorrelation in the similarity structure (see Materials and Methods). A significant association was observed in a set of regions that overlapped with the results from the trialwise dissimilarity analysis, including clusters in OFC, DMFC, occipital, and temporal regions (Fig. 2D). As might be expected by the increased power because of the nonadjacent trial comparisons afforded by RSA analysis, we also identified additional regions that were not clearly indicated by our previous analysis, including a number of visual regions, left motor cortex, and bilateral hippocampus (Fig. 2D).

Figure 2.

RSA reveals additional brain regions with representations that evolve more rapidly during periods of learning. A, In principle, rapid changes in neural representation coincident with learning might reflect a dynamic state representation that transitions rapidly at changes in context (see Fig. 1A) and evolves more slowly as subjects develop accurate representations of the context. B, C, This would lead to greater trialwise dissimilarity immediately after change points in task context (blue line indicates simulated trialwise dissimilarity; red dashed lines indicate change points) (B), but also to unique patterns of dissimilarity across nonadjacent trials (C). D, Searchlight RSA to identify such patterns revealed a constellation of regions (red) that overlapped substantially with that identified in the trialwise similarity analysis (orange; conjunction depicted in yellow) and also included additional regions such as left motor cortex, visual cortex, and hippocampus. All images are thresholded at p = 0.001, uncorrected.

Distinguishing between computational explanations for representational change

We next sought to arbitrate among multiple possible causes for the varying rates of representational change. The rapid evolution of neural representations after change points might reflect different underlying computations in different brain regions. Our analysis focused on four candidate computations that could all theoretically drive network reset-like phenomena.

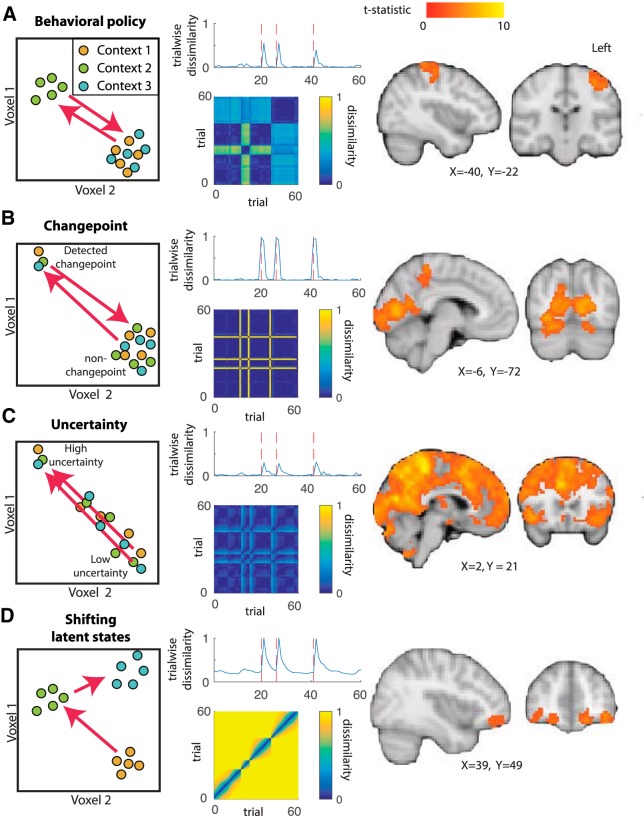
First, we considered the possibility that a brain region might reflect the behavioral policy of the participant. In our experimental task, the behavioral policy was reported directly by positioning a bucket at the predicted location (using a joystick) on each trial. For a given helicopter position, participants tended to place the bucket in a similar location, but changes in helicopter location corresponded to large changes in the bucket placement, which would correspond to abrupt transitions in a representation of behavioral policy after change points (Fig. 3A). Occasionally, a new helicopter position was similar to one that had previously been encountered, such that a similar behavioral policy might be used in two temporally separated contexts (Fig. 3A, contexts 1 and 3).

Figure 3.

Dissociable explanations for task-driven changes in trialwise dissimilarity. Left, Context changes could affect different sorts of representations that are thought to be involved in task performance. A change in context could elicit a large representational change (arrows) in the behavioral policy (A), an internal assessment of CPP (B), the current level of RU (C), or a latent state that shifts in proportion to learning (D). Middle, Each of these representations would predict increased trialwise dissimilarity after change points (top, red dotted lines indicate change points). However, dissimilarity matrices constructed across all trials (adjacent and nonadjacent) reveal unique representational profiles for each source of change point related dissimilarity (bottom). Right, Patterns of voxel activations across trials revealed an anatomical dissociation among representations of behavioral policy (A; left motor cortex), CPP (B; occipital cortex), RU (C; widespread), and shifting latent states (D; OFC). Brain images in each panel reflect t-statistic maps thresholded at p < 0.01 after correction for multiple comparisons. For analogous results using an alternative preprocessing pipeline (i.e., no smoothing before RSA), see extended data Figure 3-1.

Figure 3-1

RSA results are robust to spatial smoothing. This extended data figure is an exact replication of figure 3, except that the analysis differed in the following ways: 1) RSA was performed on BOLD data that had not been spatially smoothed, and 2) spatial smoothing with a 6mm FWHM Gaussian kernel was applied to the coefficient maps resulting from RSA. Left: Context changes could affect different sorts of representations that are thought to be involved in task performance. A change in context could elicit a large representational change (arrows) in the behavioral policy (A), an internal assessment of change-point probability (B), the current level of relative uncertainty (C), or a latent state that shifts in proportion to learning (D). Middle: Each of these representations would predict increased trialwise dissimilarity after change points (top, red dotted lines indicate change points). However, dissimilarity matrices constructed across all trials (adjacent and non-adjacent) reveal unique representational profiles for each source of change-point related dissimilarity (bottom). Right: Patterns of voxel activations across trials revealed an anatomical dissociation between representations of behavioral policy (A; left motor cortex), change-point probability (B; occipital cortex), relative uncertainty (C; widespread), and shifting latent states (D; orbitofrontal cortex). All maps are thresholded at p < 0.01 after correction for multiple comparisons, except the behavioral policy map in which this threshold was increased to include display of the motor cortical representation for which the cluster corrected p value was 0.011. Statistics for significant clusters are reported in table 2. Download Figure 3-1, EPS file ^{(4.2MB, eps)}

A second possible explanation for rapid representational change after change points is that the representations could reflect the current level of CPP or RU. CPP changes most dramatically at a change in the context (Fig. 1C), leading to predicted trialwise neural dissimilarity time courses that do the same (Fig. 3B). The level of RU changes most rapidly immediately after change points (Fig. 1C) and a neural representation of RU should do the same (Fig. 3C). However, either of these representations should return to a fixed pattern for all epochs across the experimental session that share the same level of CPP or RU regardless of the current helicopter position (Fig. 3B,C).

A final computational explanation for rapid representational changes after change points is that such a signal may reflect a latent state that is used to partition learning across distinct contexts (Wilson et al., 2014). For example, each new helicopter position could be reasonably thought of as a new temporal context during which learning from prior contexts should be discounted to minimize interference (Fig. 1A). Because the helicopter position cannot be resolved exactly, such a context representation would be expected to evolve over time in proportion to the rate of learning about the current context. This idea was formalized in Figure 2 and, as described previously, would lead to latent state representations that change rapidly at change points and immediately afterward and change only minimally during periods of prolonged stability (Fig. 3D). Unlike the other computational factors discussed above, a latent state representation would not necessarily exhibit any systematic similarity relation between one context and another because our task did not include situations in which the helicopter returned exactly to a previously occupied position. Such a latent state signal might provide an evolving substrate to which outcomes could be linked to achieve rational adjustments of learning.

Each of these representations would yield more rapid changes in neural patterns after change points in our task and, indeed, they make very similar predictions for how neural dissimilarity metrics between adjacent trials should evolve over time (Fig. 3, middle column, top plots). Predictions of trial-to-trial dissimilarity made for the four candidate computations were highly correlated (all average pairwise Pearson correlations were >0.45, with predictions for shifting latent representations particularly highly correlated with those for RU, r = 0.80, and those for behavioral policy, r = 0.74), suggesting that the representations of these computations could not be distinguished based on adjacent trial dissimilarity alone.

However, the four candidate representations differed drastically in their predictions about the dissimilarity for nonadjacent pairs of trials. We constructed hypothesis matrices for each candidate representation by considering the expected difference in the computation of interest across all possible pairs of trials. These hypothesis matrices highlight qualitative features of each candidate computation; behavioral policy frequently undergoes abrupt shifts, but often takes on a similar value to a previous state, CPP highlights differences between change point and non-change-point trials, RU highlights the differences between high RU and other trials, and shifting latent states capture differences largely near the diagonal (Fig. 3, middle column, bottom). Consistent with these qualitative differences, correlations between the hypothesis matrices for the different candidate representations were relatively low (all pairwise r < 0.16), suggesting that the candidate representations could be efficiently distinguished when considering the entire pairwise dissimilarity matrix.

We exploited these distinct predictions using an RSA approach that allowed alternative explanations of representational change to compete to explain the observed neural dissimilarity matrix. Neural dissimilarity was computed for each pair of trials as one minus the spatial correlation of trial activations across voxels in a searchlight and regressed onto an explanatory matrix that included the hypothesis matrices for all four candidate representations, along with a number of other explanatory terms designed to account for factors changing throughout the task and simple sources of variability such as autocorrelation (see Materials and Methods).

RSA supported distinct explanations for representational change in different anatomical regions. Behavioral policy provided a good description of BOLD activity patterns in left motor cortex (contralateral to the hand used to move the joystick and execute the behavioral policy) and visual cortex (Fig. 3A, right, Table 1). Representations of CPP were prominent in occipital cortex and precuneus (Fig. 3B, Table 1). Representations of RU were widespread across the brain and included DMFC, dorsolateral prefrontal cortex, bilateral parietal cortices, insula, as well as some occipital and temporal regions (Fig. 3C, right). Patterns of activation consistent with a latent state that shifts according to assessment of the current context were prominent in OFC and temporal cortex (Fig. 3D, right, Table 1).

Table 1.

Peak voxel locations corresponding to behavioral policy, relative uncertainty, change point probability, and shifting latent state representations before RSA

Coefficient	Voxels	Max t-value	x	y	z	Label
Behavioral policy	841	6.37	27	−60	−18	Temporal occipital fusiform
	389	6.03	−37	−21	58	L precentral gyrus (left motor)
Change point probability	3795	8.13	12	−93	−6	Occipital pole
Uncertainty	29941	11.4	−4	−63	49	Precuneus
	Local max	9.4	−22	−90	−15	Occipital fusiform gyrus
	Local max	8.6	9	22	37	Anterior cingulate cortex
	Local max	8.3	15	−54	1	Lingual gyrus
	Local max	8	51	−39	55	Supramarginal gyrus
	Local max	8	48	16	1	Insula
Shifting latent state	869	6.02	−61	−24	−24	Inferior temporal gyrus (posterior)
	231	5.48	21	−69	67	Occipitoparietal cortex
	220	5.56	−16	49	−15	L OFC
	220	5.2	−28	−48	52	Superior parietal lobule
	199	5	27	43	−18	R OFC
	181	5.6	−13	−93	−9	Occipital pole

Shown are cluster size (in voxels) and maximum (t-statistic) and MNI coordinates for each cluster from the competing computations RSA analysis on spatially smoothed data surviving multiple-comparisons correction.

The relationship between the neural dissimilarity in OFC and the dissimilarity structure predicted by a shifting latent state signal was unlikely to be an artifact of motion or eye movements. Normative learning rate, the primary driver of the shifting latent state hypothesis matrix, was not correlated with motion parameters to any significant degree (average Pearson R² across subjects <0.006 for each of the 6 motion parameters), nor was it correlated with eye movements in a follow-up study using the same task run outside of the scanner (McGuire et al., 2014).

Our findings were robust to analysis choices including those affecting the spatial frequency of our multivariate fMRI signals. There is active debate over best practices in preprocessing fMRI data for RSA, with some work supporting liberal spatial smoothing of raw data before analysis (Op de Beeck, 2010; Hendriks et al., 2017) and other work suggesting that excessive spatial smoothing can dampen signals of interest by reducing high-frequency components of the signal (Gardumi et al., 2016). Because we had no a priori predictions about the spatial scale of our signal, we repeated our full RSA on unsmoothed fMRI data, instead adding an additional smoothing step after RSA on the resulting coefficient maps. This analysis yielded very similar results to our original analysis (cf. Fig. 3-1, with Fig. 3), including similar shifting latent state effects in OFC (Fig. 3-1D, right, and Table 2). An ROI analysis applied to peak voxels for the shifting latent state regressor in our primary analysis (Table 1) that further emphasized high-frequency components of spatial pattern by using a prewhitening procedure (Walther et al., 2016) confirmed that OFC latent state representations were evident even when neural dissimilarity was restricted to high-spatial-frequency information (p < 0.05; Table 3).

The observed shifting latent state effects in OFC were not driven by relationships between additional explanatory variables included in the regression model because exclusion of other explanatory variables yielded very similar relationships (Table 3). It is noteworthy that this was not true of all clusters that survived whole-brain correction in our RSA; clusters identified in left superior parietal lobule and right occipital cortex were not related to the shifting latent state predictions in isolation (Table 3). Furthermore, the relationship between shifting latent state predictions and OFC patterns of activation was also robust to our assumptions about the exact timing of learning; a time-shifted version of the shifting latent state hypothesis matrix that assumed learning occurred immediately upon observing a trial outcome could also describe similarity patterns observed in right and left OFC (Table 3).

In summary, whereas we found a number of regions that showed rapidly changing representations during periods of uncertainty following a context change, these reset-like phenomena were due to dissociable computational explanations. Although a few regions were implicated in representing behavioral policy or CPP, most of these regions reflected RU and a smaller subset of regions including OFC were consistent with representing a latent state that is adjusted according to changes in context.

Discussion

Neural representations in rodent medial frontal cortex rapidly change during periods of uncertainty (Karlsson et al., 2012). Here, we demonstrate, in the context of a dynamic learning task, that such rapid representational changes are present in the BOLD signal in widespread cortical and subcortical regions. Furthermore, we show that these rapid representational changes are consistent with several different computational explanations, which could be teased apart by considering the similarity structure of nonadjacent trials through RSA.

Our analyses revealed distinct explanations for rapid representational changes in different brain regions. Focal representations of behavioral policy and CPP were identified in motor and visual cortex, respectively, whereas widespread representations of RU were observed throughout the brain. In addition, a small number of brain areas including the OFC had patterns of activation consistent with a form of shifting latent state representation that could speed disengagement from well learned responses in a changing context.

Perhaps most straightforwardly, our analysis revealed that left motor cortex contained representations consistent with behavioral policy. In our task, this policy was completely concordant with the physical movement necessary to implement the behavioral policy. Therefore, we interpret these results as a consequence of our experimental design, which required subjects to provide an analog behavioral output of their behavioral policy with their right hand on each task trial. Therefore, this result was likely driven, at least in part, by a univariate effect of movement magnitude in the contralateral motor cortex.

Two other computations that we identified using this approach, CPP and RU, had been the focus of a previous study using this same dataset (McGuire et al., 2014). In the case of CPP, both univariate and RSA analyses revealed occipital cortex and precuneus as the locus of neural representation (Fig. 2C; McGuire et al., 2014). However, RU representations identified using RSA were considerably more widespread than those identified through univariate activations (Fig. 2C; McGuire et al., 2014). This broader set of areas included some regions that were activated in the univariate analysis (e.g., DMFC), some that were deactivated in the univariate analysis (e.g., ventromedial prefrontal cortex), and some that were not identified in univariate analyses at all (e.g., temporal cortex). The near-ubiquitous cortical representation of RU revealed by RSA is somewhat analogous to the widespread representations of reward prediction errors that have been identified using multivariate fMRI analysis methods (Vickery et al., 2011). Interestingly, both reward prediction errors and RU have been suggested to be signaled through brainstem neuromodulatory systems that could potentially have widespread effects throughout the brain (Schultz et al., 1997; Yu and Dayan, 2005; Doya, 2008; Nassar et al., 2012).

In addition to providing a more sensitive tool to identify well specified computational variables, RSA also allowed us to look for patterns of activity that could not easily be detected in univariate analyses. In particular, it allowed us to look for neural representations of a dynamically shifting state representation without making strong assumptions about what the signal would look like at any given moment. It has been proposed that state representations provided by the OFC might serve to hasten learning in environments that include a small number of repeated contexts (Gershman and Niv, 2010; Wilson et al., 2014; Schuck et al., 2016). This proposal is supported by observations that OFC representations encode the predicted identities of action outcomes (Klein-Flügge et al., 2013; Stalnaker et al., 2014; Howard et al., 2015; Howard and Kahnt, 2018), can reflect a probability distribution over the causal source of outcomes (Chan et al., 2016), and can be used to decode latent states that control action–outcome contingency (Schuck et al., 2016). Here, we hypothesized that shifts in the same type of latent state representations might implement the rapid learning that should and does follow change points in outcome contingencies (Prescott Adams and MacKay, 2007; Nassar et al., 2010; Wilson et al., 2010). Such an implementation could make use of existing computational elements to efficiently partition learned associations that pertain to distinct and unrelated contexts, effectively creating the product partitions necessary for optimal inference amid change points (Prescott Adams and MacKay, 2007).

Consistent with this idea, we identified signals in OFC consistent with a shifting state signal that changed more rapidly during periods of learning. The region of OFC that we identified included both lateral regions (Fig. 3D), which are similar to those where outcome identity representations have previously been observed (Howard and Kahnt, 2018), and more medial regions (Fig. 3D), which are closer to where state representations have previously been reported (Schuck et al., 2016). Nonetheless, the OFC regions in which we identify shifting state signals are still somewhat lateral to those reported by Schuck et al. (2016) and future work should investigate whether the sorts of abrupt transitions in representation that we identify here indeed occur the same regions as those that seem to represent state within a cognitive map of task space.

A neural population that encoded such a shifting state signal would be well positioned to transform a direct representation of dynamic learning rate, such as the population that has been identified in cortical regions (Behrens et al., 2007; Krugel et al., 2009; McGuire et al., 2014) and thought to be broadcast through noradrenergic neuromodulation (Yu and Dayan, 2005; Nassar et al., 2012; Browning et al., 2015) into a proportional change in associative strength. Using a learning signal to control the rate of contextual shift could enable a simple associative neural network to accomplish the type of adaptive learning that has previously been modeled as a delta-rule update with a varying learning rate. In such a case, increases in apparent learning would be implemented through changes in the substrate for learning or the active latent state rather than by adjusting associative strength per se.

Representations of latent state that transition dynamically from one context to the next are similar in spirit to the concept of event segmentation in episodic memory (Ezzyat and Davachi, 2011). Segmenting events is useful in that it can allow memories that are embedded within the same event but separated in time to share associations, whereas memories that may be closer in time but embedded in separate events are maintained separately, preventing interference (Reynolds et al., 2007). One mechanism through which segmentation could be achieved involves dynamic adjustment of the time constant in slowly fluctuating temporal context signals to effectively “reset” context at event boundaries (Howard and Kahana, 2002; Howard et al., 2011; Manning et al., 2011). Our data suggest a link between this aspect of episodic encoding and the dynamic adjustments of learning that have been observed at context boundaries (Behrens et al., 2007; Nassar et al., 2010; McGuire et al., 2014). However, aspects of our findings also raise questions about the extent of this link. Although our results could be interpreted as supporting roles for OFC and temporal lobe in segmenting contexts, we did not observe the same phenomenon in the hippocampus, which is thought to play a key role in event segmentation (Ezzyat and Davachi, 2014; Hsieh et al., 2014; Shapiro, 2014). Instead, we found that representations in hippocampus, like many other brain regions, were best explained as representing uncertainty itself. One potentially relevant detail is that previous contexts were not systematically revisited in our task, reducing demands for episodic retrieval. An interesting avenue for future work would be to determine how the representations that we identified respond when the context abruptly returns to a previously encountered state, such as might require a form of mental time travel for successful performance (Manning et al., 2011).

Our results, especially regarding the OFC, demonstrate the utility of analyzing the representational similarity of multivoxel patterns of activity in concert with computational modeling. Such an approach allowed us to identify neural representations consistent with a specific computational role for OFC, which in principle could not have been isolated in our task with univariate activation or multivariate classification analyses.

In summary, we show that shifts in the statistics of the environment during a dynamic learning task induced both elevated learning and changes in neural representation. These changes in neural representation were attributed to specific computations using RSA. Our results identified widespread representations of RU throughout the brain, together with more focal representations of CPP and behavioral policy. In addition, a small number of brain areas including the OFC had patterns of activation consistent with a shifting latent state representation that could speed unlearning of irrelevant information in a changing context.