Pelvic Organ Segmentation Using Distinctive Curve Guided Fully Convolutional Networks

Abstract

Accurate segmentation of pelvic organs (i.e., prostate, bladder and rectum) from CT image is crucial for effective prostate cancer radiotherapy. However, it is a challenging task due to 1) low soft tissue contrast in CT images and 2) large shape and appearance variations of pelvic organs. In this paper, we employ a two-stage deep learning based method, with a novel distinctive curve guided fully convolutional network (FCN), to solve the aforementioned challenges. Specifically, the first stage is for fast and robust organ detection in the raw CT images. It is designed as a coarse segmentation network to provide region proposals for three pelvic organs. The second stage is for fine segmentation of each organ, based on the region proposal results. To better identify those indistinguishable pelvic organ boundaries, a novel morphological representation, namely distinctive curve, is also introduced to help better conduct the precise segmentation. To implement this, in this second stage, a multi-task FCN is initially utilized to learn the distinctive curve and the segmentation map separately, and then combine these two tasks to produce accurate segmentation map. The final segmentation results of all three pelvic organs are generated by a weighted max-voting strategy. We have conducted exhaustive experiments on a large and diverse pelvic CT dataset for evaluating our proposed method. The experimental results demonstrate that our proposed method is accurate and robust for this challenging segmentation task, by also outperforming the state-of-the-art segmentation methods.

I. INTRODUCTION

PROSTATE cancer is a common cancer among men, which is the third leading cause of cancer death in America [1]. Clinically, radiotherapy is the most effective treatment for prostate cancer. For radiotherapy, computed tomography (CT) imaging is necessary since it conveys tissue density information which can be used for dose planning. During radiotherapy, the high-energy ray should be focused on the prostate, while is spare on the nearby normal organs, i.e., bladder and rectum. Thus, in the planning stage, accurate segmentation of these three pelvic organs is required. Manual delineation of pelvic organs is a routine strategy in the clinic. However, it is less effective and quite time-consuming even for experienced clinicians. Therefore, developing an effective segmentation algorithm with superior accuracy and robustness is of high demand.

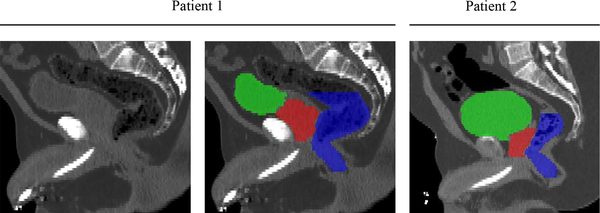
However, accurate segmentation of three pelvic organs is challenging due to the following two reasons. 1) Low soft tissue contrast in CT images. As shown in Fig. 1, the contrast among prostate, bladder and rectum is quite low, and the organ boundaries are very difficult to distinguish. Also, the appearance patterns of these three organs are similar to their neighboring tissues, which makes it difficult to identify them. 2) Large anatomical variations. The pelvic organs are all deformable soft tissues, and thus both shape and appearance of these three organs can have large variations across different individuals, as can also be observed in Fig. 1.

Fig. 1.

CT images of pelvic regions in two typical patients. Red denotes the prostate, Green denotes the bladder, and Blue denotes the rectum. We can observe 1) low soft tissue contrast in these CT images, and 2) large shape and appearance variations of these three organs across subjects.

Recently, deep leaning methods have shown their outstanding performance particularly for the segmentation tasks [2], [3], [4], [5], [6], due to their strong non-linear modeling capability. However, these networks cannot be directly applied for the CT pelvic organ segmentation due to indistinguishable shape and border. To address this issue, in this paper, we propose to employ the morphological representation to help enhance the accuracy and robustness of the conventional deep network for this challenging segmentation task.

Generally, two kinds of shape representations, i.e., landmarks and surface, are widely adopted in previous studies to help represent the organ shapes [7], [8]. For the landmark-based representation, some landmarks with anatomical significance are identified to serve as the cue for guiding the subsequent shape segmentation or analysis. Although landmarks can be identified efficiently, it is not an accurate shape representation for the pelvic organs in CT due to the following two reasons. 1) It is difficult to guarantee anatomical consistency of the identified landmarks across different individuals. 2) Since pelvic organs may have large anatomical variations, several landmarks are not sufficient to represent the whole shape of each organ.

On the other hand, the surface is a more informative representation that can describe the whole organ boundary. However, there is lots of redundant information by using the surface, which makes it less efficient to represent the organ shape. Also, for the pelvic CT images, it is difficult to obtain accurate surface representations of the prostate, bladder and rectum.

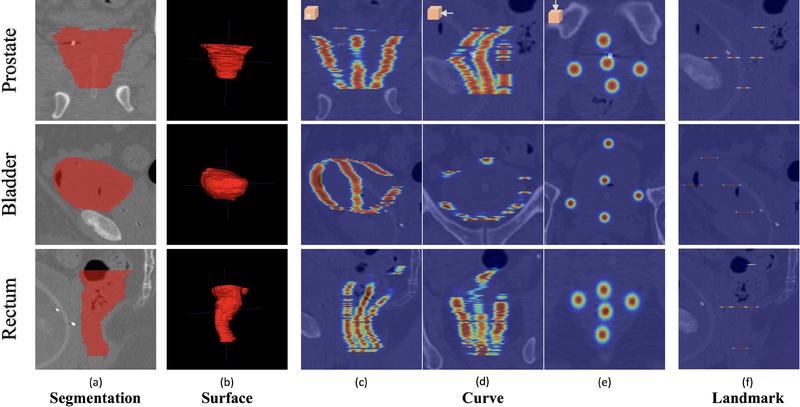
To address the aforementioned issues of two existing shape representations for pelvic organs, we introduce a novel shape representation, namely distinctive curves, to more accurately and efficiently represent the organ shapes in pelvic CT images. The comparison of landmark, surface and distinctive curve are shown in Fig. 2.

Fig. 2.

The comparison of four types of shape representation for three pelvic organs: segmentations (a), surface (b), curve (c-e), and landmark (f). For better visualization, we set the raw image as the background in (c-f) to provide references. Besides, we enlarge each point of the curves and landmarks in a Gaussian way. Note that, in each view, not all the segmentations, distinctive curves or landmarks are visible.

Basically, the distinctive curve can be regarded as a sequential set of points, sparsely delineating the whole organ shape. Obviously, the distinctive curve can take advantages of both landmarks and surface, and is thus an informative and efficient shape representation.

In this paper, we propose a two-stage, distinctive curve guided fully convolutional neural network (FCN) to tackle the challenging pelvic CT segmentation problem. Under the guidance of the beneficial morphological representation, i.e., the distinctive curve, the learning ability of the FCN is significantly improved and an accurate and robust segmentation model is well established.

Our contributions are three-fold:

• To address the issues of the unclear boundary and large shape variation for the pelvic organs in CT images, we introduce a novel shape representation, i.e., the distinctive curve, to enhance the capability of the conventional FCN for the challenging segmentation task. The distinctive curve is also learned automatically. The generalization of the FCN can thus be significantly improved under the guidance of this informative morphological representation, which eventually contributes to accurate pelvic segmentation.

• In order to better identify the main pelvic organs in the whole CT image, we propose a two-stage framework to segment the pelvic organs progressively. The first stage is designed to efficiently identify the organ region, and the second stage is used to perform accurate segmentation. Under this framework, even small pelvic organs can also be segmented robustly and accurately from the whole CT image.

• We perform comprehensive experiments on a dataset with 313 CT images from the 313 patients. Our proposed method can consistently outperform the state-of-the-art methods, showing the potential to be applied to real clinical applications.

II. RELATED WORK

The proposed algorithm in this paper is a learning-based segmentation method. Also, the distinctive curve delineation is related with landmark detection. Thus, in this section, we will review two kinds of methods, i.e., learning-based segmentation methods and landmark detection methods.

A. Learning-based Segmentation

Learning-based segmentation methods have achieved remarkable performance in recent years [9], [10], [11], [12], [4], [13], [14], [15]. In this kind of methods, the segmentation task is usually regarded as a classification or regression problem, with the goal of explicitly labeling each voxel in CT image to the target object or background. A semi-automated prostate segmentation method [14] is proposed by applying the spatially-constrained transductive lasso on coupled local region features for joint feature selection. Then, the selected features are used to classify the voxels into different classes. In order to enhance the learning capability, some additional information has also been incorporated into the learning framework. For example, Gao et al. [9] proposed to learn a displacement regressor to predict 3D displacement, which can be used to assist the classifier learning for accurate pelvic organ segmentation. Lay et al. [16] proposed to build a discriminative classifier by employing the landmarks, which was detected via the global and local texture information jointly. Shao et al. [8] presented a boundary detector based on a regression forest, and then used it as shape prior to guide accurate prostate segmentation.

One main limitation of the aforementioned learning-based methods is that we need to predefine the features for the specific learning model, such as Haar-like [17], Gabor [18], SIFT [19], etc. In this case, the distinctiveness of the features may significantly influence the learning accuracy. To address this limitation, deep learning methods have been widely used, in which the features can be learned automatically and effectively, i.e., through convolutional neural networks (CNN) [20]. Cha et al. [13] combined deep networks with level sets to improve the segmentation accuracy of the bladder. However, the per-pixel prediction is less efficient in the application stage. The Fully Convolutional neural Networks (FCN) [2] can generate dense pixel-wise predictions, which is efficient and has been shown outstanding performance for segmentation tasks. Nie et al. [21] employed an FCN to segment isointense infant brain via multiple modality images. Men et al. [5] proposed a multi-scale FCN based network to robustly segment the clinical target volume and organs at risk for rectal cancer. Nevertheless, due to the limited size of medical image dataset, the generalization can be hardly guaranteed during the training. To alleviate this issue, a special FCN, namely U-net [3], was proposed to incorporate low-level and high-level features to train the model. In this network, the limited data information is more efficiently used to achieve better performance. Accordingly, in this paper, we will use U-net as the basic architecture to construct our networks.

B. Landmark Detection

Basically, landmark detection is a common task in many computer vision applications, such as human body estimation [22], organ detection [7], and face image analysis [23]. In medical images, landmarks are defined as the locations that possess anatomical significance and can be used to effectively describe the structures of variant organs, e.g., brain [24], [25], pelvic organs [26], fingers [27] and etc. For example, Gao et al. [26] detected landmarks through a displacement vector based regression model. The displacement vector for each voxel was defined from the current location to the target landmark. Zhang et al. [7] detected landmarks of brain MRI using the group comparison method and then adopted these detected landmarks for Alzheimer’s disease (AD) diagnosis.

Recently, the deep learning based methods were also applied for landmark detection. For example, Zheng et al. [28] built a landmark detector based on FCN by composing a shallow network with a deep network. In this work, instead of directly regressing the landmark position, a heatmap was first fitted to the landmark location via a Gaussian kernel, and then used as the regression target to make the network more robust and powerful. Based on the work proposed in [22], Payer et al. [27] also adopted FCN to regress finger landmarks. Actually, the distinctive curve proposed in this paper can be regarded as the sequential landmarks (without correspondences), yet more robust and accurate for describing the indistinguishable pelvic organ boundaries. We have also adopted FCN network to detect the distinctive curve.

III. METHOD

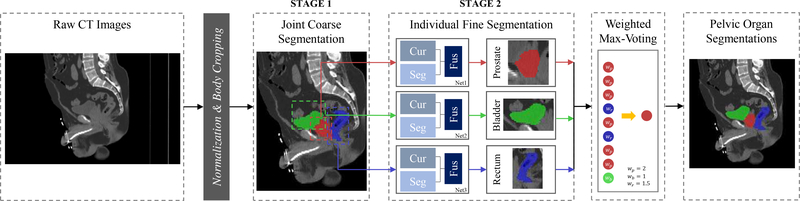
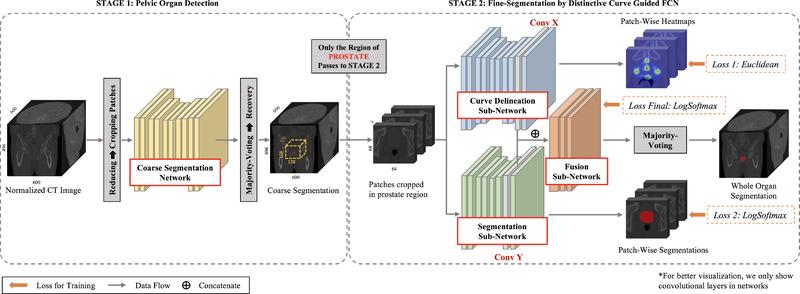
To accurately segment the prostate, bladder and rectum from the raw CT image, we propose a distinctive curve guided FCN, with the whole pipeline illustrated in Fig. 3. Since the raw CT image covers a large region of the human body while the target pelvic organs are relatively small, a two-stage framework is further designed to robustly segment pelvic organs from coarse level to fine level. The first stage is implemented with an FCN, which is designed for the pelvic organ detection from the raw CT image. In this stage, two stable regions, i.e., left and right femoral heads, are employed as references to better identify the target pelvic organs as well as differentiate them with other similar tissues. The details of this stage will be introduced in Section III-A. The second stage is the distinctive curve guided FCN, which is designed for accurate pelvic organ segmentation based on the detected regions from the first stage. In this second stage, for each organ, a multi-task FCN is first utilized to learn the distinctive curve and the segmentation maps separately, and then combine these two tasks together to produce the segmentation result. The details of this second stage will be elaborated in Section III-B. Finally, a weighted max-voting algorithm is proposed to generate the whole 3D segmentation for all three pelvic organs, with the results shown in the right dashed box of Fig. 3. The details of this part will be described in Section III-C.

Fig. 3.

The pipeline of the proposed method. Note that 2D view is shown for better visualization, although real CT images are in 3D. “w_p”, “w_b” and “w_r” denote the weights of prostate, bladder and rectum in the final weighted Max-Voting.

A. Stage 1: Pelvic Organ Detection

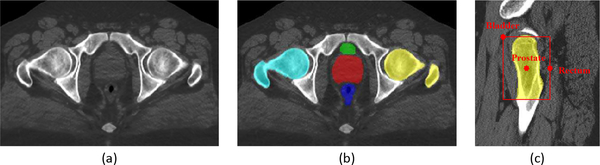
The aim of this first stage is to effectively detect the target organ location from the raw CT image, and then provide the region proposal of each organ (resulting in a bounding box) to the stage 2 for fine segmentation. Conventional region proposal methods often regress some locations about the organ, e.g., the mass center [29], to determine the organ region. However, it cannot work effectively for the pelvic organs that are adjacent to each other and also difficult to distinguish. To locate each organ region accurately, we here perform a joint organ localization/segmentation, rather than regressing each of their locations separately. Additionally, two stable pelvic bones, i.e., the right and left femoral heads, are also incorporated into the joint organ segmentation task, to help better identify the target pelvic organs, as shown in Fig. 5.

Fig. 5.

(a) A slice of a raw CT image. (b) The labeled five pelvic organs. Cyan denotes the left femoral head, and Yellow denotes the right femoral head. (c) The reference locations generated by the two femoral heads (symmetrically) for prostate, bladder and rectum, respectively. We use the right femoral head as instance.

1). Joint Coarse Segmentation for Pelvic Organs:

To effectively perform the organ region proposal, in this first stage, we perform coarse segmentation of all five pelvic organs jointly, which can be deemed as a 6-class classification problem, i.e., five classes for the organs (prostate, bladder, rectum, left femoral head and right femoral head) and one class for the background and remaining regions. An FCN is designed to fast jointly segment the five organs based on the down-sampled CT image. There are two kinds of benefit using the down-sampled CT image. 1) Coarse segmentation satisfies the goal of accurate region proposal, and also using down-sampled image can make the algorithm more efficient. 2) More global contextual information can be considered during the network learning, which helps better identify the indistinguishable pelvic organs in the raw CT image. Specifically, before segmentation, we use a reducing step, to down-sample the original CT image to its 1/4 size for the coarse segmentation. Then, after segmentation, we use a recovery step to up-sample the down-sampled segmentation result to the original resolution, which is, used to propose the organ region.

For the joint segmentation task, we adopt a U-net [3] like architecture, as illustrated in the first part of Fig. 4. The contracting path is composed of several convolutional layers with three times max pooling, while the expanding path is deployed by several convolutional layers with three times transposed convolution. In the expanding path, the output feature maps concatenate with the corresponding scale feature maps in the contracting path, and then feed into the subsequent convolutional layers. The final output is the class label for each voxel of the whole image. The detailed architecture of the coarse segmentation network is shown in Table I. To lower the memory load, we employ patch-wise training rather than the training on the whole image, and the patches are cropped in 2D image slice. Specifically, the input of the network is the patches extracted from five sequential slices (two slices before and two slices after the middle slice), and the output is the corresponding label patch of the middle slice. In this way, the adequate neighborhood information of the 3D image can be well leveraged to better train the segmentation model. Then, the coarse segmentation of the five pelvic organs will be used for the following organ region proposal.

Fig. 4.

The architecture of the two-stage segmentation of prostate, bladder and rectum. Prostate segmentation is used as an example in this figure. Note that the combination of segmentations of the three pelvic organs after separate fine organ segmentations is not illustrated in this figure.

TABLE I.

The detailed architectures of the coarse segmentation network (CoarseNet) and the two sub-networks: Segmentation sub-network (SNet) and Curve delineation sub-network (CNet). The ”Params” include: 1) the kernel size and the number of channels; 2) ”Pad” for the spatial padding; 3) ”Str.” for the stride; 4) ”2× Pooling” for the block being followed by a 2×2 max-pooling layer. Please note the number of the convolutional layers in each ”Conv” block as listed below.

Layers	Params	Number of Layers
		CoarseNet	SNet	CNet
Conv1	3 × 3 × 32; Pad: 1; Str.: 1; 2× Pooling	2	2	3
Conv2	3 × 3 × 32; Pad: 1; Str.: 1; 2× Pooling	1	1	3
Conv3	3 × 3 × 32; Pad: 1; Str.: 1; 2× Pooling	1	1	3
Deconv4	2 × 2 × 32; Pad: 0; Str.: 2	1	1	1
Concatenate	Conv3 & Deconv 4	1	1	1
Conv4	3 × 3 × 32; Pad: 1; Str.: 1	1	1	2
Deconv5	2 × 2 × 32; Pad: 0; Str.: 2	1	1	1
Concatenate	Conv2 & Deconv 5	1	1	1
Conv6	3 × 3 × 32; Pad: 1; Str.: 1	1	1	2
Deconv6	2 × 2 × 32; Pad: 0; Str.: 2	1	1	1
Concatenate	Conv1 & Deconv 6	1	1	1
ConvX/Y	3 × 3 × 32; Pad: 1; Str.: 1	2	1 + ConvY	2 + ConvX
LastConv	Specific	1 × 1 × 6; Pad: 0; Str.: 0	1 × 1 × 2; Pad: 0; Str.: 0	1 × 1 × 5; Pad: 0; Str.: 0
LogSoftmax Loss Euclidean Loss	Loss weight: 1 Loss weight: 0.1	1 -	1 -	- 1

2). Organ Region Proposal:

Based on the coarse segmentation of the five pelvic organs, we introduce a mixed localization method to robustly locate the centroid of the three target pelvic organs, i.e., prostate, bladder and rectum, under the guidance of the two more stable organs, i.e., the left and right femoral heads. As shown in Fig. 5, the bone region is salient in CT, and also the shape and appearances of femoral heads are stable even across different individuals. Thus, it is easy to obtain accurate segmentations of femoral heads. As the femoral heads are spatially close to the prostate, bladder and rectum, they can provide a beneficial reference to help better identify the three organs. Then, the final centroid of each organ can be obtained via the following three steps. 1) A rough centroid is first obtained via the coarse segmentation. 2) A reference centroid is estimated based on the femoral heads, which is calculated by averaging the corresponding reference points on two femoral heads, as shown in Fig. 5.(c). These reference points are defined by adopting the prior knowledge of the spatial locations of human organs, between the femoral heads and the pelvic organs. Thus, the reference centroid can provide estimated locations of the pelvic organs based on the salient femoral heads, and the rough centroid can provide the locations based on the coarse organ segmentations. 3) The final centroid is then calculated by averaging the results of the previous two steps. Obviously, the mixed result is more stable than using one of the previous estimations for organ localization.

Once the centroid is determined, we crop region for each organ from the raw CT image. To easy implement, the region sizes of the prostate, bladder and rectum are 128×128×128, 160×160×128 and 128×128×160, respectively. The region sizes are large enough to cover the different organs across individuals. After organ region proposal, we can then perform the fine segmentation based on the specific regions in Stage 2.

B. Stage 2: Fine-Segmentation by Distinctive Curve Guided FCN

In this second stage, we perform the fine segmentation for each target organ individually, based on the proposed region from Stage 1. A distinctive curve guided FCN is proposed, as illustrated in the right part of Fig. 4. Initially, a multitask learning is first performed to train the distinctive curve delineation and segmentation tasks separately. Then, the high-level feature maps of these two tasks are combined to work together for the accurate segmentation.

1). Distinctive Curve Delineation:

We introduce a novel shape representation, namely distinctive curve, to serve as a supplementary guidance to help the network better learn the segmentation task. Obviously, the distinctive curve can provide a strong reference for the organ shape, as shown in Fig. 2; thus it can help the segmentation network better capture unclear boundaries between adjacent organs in CT image. The distinctive curve delineation is also learned by another FCN, where the ground truth of the curve is defined in the training stage. Specifically, for each slice, we use the anteriormost, posteriormost, left, and right points of the organ boundary to indicate the organ boundary, and also use the center points of the organ to indicate the skeleton of each organ. When composing the points of each slice in the entire image, the distinctive curves can be generated, with the four curves located on the organ surface and one curve located in the middle of the organ. Obviously, in each slice, the curves are represented by several points, which can be detected by a certain point/landmark detection method. Here, we follow the scheme in [22], in which an FCN is adopted to estimate the heatmaps of points/landmarks, rather than directly regressing their locations, as shown in Fig. 4. Specifically, each heatmap is defined by fitting a Gaussian kernel to each landmark location upon the whole image. Then, we can build the FCN based regression network for detecting the points/landmarks in each image slice. Once all points are detected, the distinctive curves can be obtained accordingly.

2). Network Architecture:

The proposed distinctive curve guided FCN is organ-specific, with each model consisting of three sub-networks, i.e., the curve delineation sub-network, the segmentation sub-network, and the fusion sub-network, as shown in Fig. 4. These three tasks are trained simultaneously so that they can work cooperatively for the final segmentation task. Specifically, for each organ, we first crop patches from the region proposal (generated by Stage 1). Then, the same patches are fed into the curve delineation and segmentation sub-networks. We set these two sub-networks with different architectures. The segmentation sub-network is a simple U-Net following the same architecture with the coarse segmentation network in Stage 1. The number of input 2D slices is three. The curve delineation sub-network utilizes more convolutional layers, in order to capture more structural information.

Unlike the conventional multi-task deep networks that often share the low-level and mid-level features across different tasks [23], our proposed architecture only combines the high-level feature maps. As reported by [30], this kind of fusion can better preserve the respective information of each task and improve the performance. Specifically, we concatenate the second top layer feature maps from the two sub-networks (denoted as ConvX and ConvY in Fig. 4), and then train the fusion sub-network that includes two convolutional layers with the filter size of 3 × 3 and the channel size of 32. We show the architecture details in Table I. Note that, the Rectification Linear Unit (ReLU) is used as the activation function after each convolutional layer. The parameters of the whole network can be updated by the m tasks (m = 3 in this case) simultaneously in one back-propagation process. In this learning scenario, the loss of each task t is given by Loss_t with the weight λ_t. Thus the final loss of the whole network is defined as:

$$\text{Loss}=\sum _{t=1}^m{\lambda }_{t}Los{s}_{\text{t}}$$ (1)

The loss of curve delineation sub-network is the Euclidean loss, while the loss of segmentation and fusion sub-network is the Logarithmic Softmax loss. During the training stage, for each organ, we first pre-trained the curve delineation and segmentation sub-networks separately and then composed their features to train the fusion sub-network (by fixing all parameters of the previous two sub-networks). Finally, the whole network is optimized together via a standard backpropagation [20].

C. Weighted Max-Voting

In the testing stage, we use a sliding-window method to crop densely overlapped image patches from the raw CT image, and feed them into the trained model to predict the label maps. Obviously, one voxel can have two different kinds of overlapping predictions. 1) Since the three organs are adjacent, the region proposals of three organs can have overlap. Then, the same voxel may be labeled differently via the networks trained for different organs. 2) For the trained network of a specific organ, one voxel will have overlapping predictions since the testing patches have overlap. To effectively fuse these two kinds of overlapping predictions, we propose a weighted max-voting approach to make accurate predictions. First, given a voxel x_i, if it is labeled for the different segmentation networks (e.g., labeled as prostate in prostate segmentation network and also labeled as bladder in bladder segmentation network), the final label will be obtained by selecting the maximum weighted probability, which is defined as:

$$y_i=\arg \underset{c}{\max }{w}_c\sum _{i=1}^{n_{ic}}{y}_{ic}$$ (2)

where n_ic is the number of predictions for organ C, y_i is the predict probability for i-th voxel and c is the index for organ C. w_c = w_p = 2,w_b = 1,w_r = 1.5 is the weight parameter for class c. n is the number of overlapped patches.

We set different weights for different organs here to balance the aforementioned two problems. Intuitively, if all of the three networks have high confidences to predict as their organs, the final prediction at a certain voxel will be prostate. This will protect the prostate segmentations as they are very sensitive to the final results, and accurate segmentation for prostate is more important than that for bladder and rectum in clinical applications. If the networks have different confidences of their predictions, the final segmentations may vary based on the assigned weights.

IV. EXPERIMENTAL RESULTS

A. Algorithm Setting

The experimental dataset consists of 313 CT scans from 313 prostate cancer patients acquired during the planning stage of radiotherapy, where 35 of 313 CT scans are contrast enhanced. The image size is 512 × 512 × (61 ~ 508), with in-plane resolution as 0.932 ~ 1.365 mm, and slice thickness as 1 ~ 3 mm. These images were collected from the North Carolina Cancer Hospital, using different scanners, with different image sizes and resolution. The patient positions also vary across different subjects, thus further increasing the variability of the acquired CT images. For the preprocessing, we use the trilinear interpolation to resample all the images to the same resolution (1 × 1 × 1 mm³) and then crop the image by excluding non-body regions. The contours delineated and agreed by two experienced physicians are adopted as the ground truth.

To eliminate the singular values in the CT images, we saturate all the intensity values into [0,1000]. The input data from each image is decremented by the mean of the whole image. Because the large magnitude of signals will destroy the signal propagation of the deep networks, we normalize all the intensities into the range of [−1,1]. We perform five-fold cross-validation to conduct fair comparisons with the state-of-the-art methods. Specifically, in each round, one fold is used for testing and the remaining four folds are used for training and validation (with a ratio of 7:1). We repeat this procedure five times until all the five folds are traversed as the testing set.

The dataset we used is challenging for segmentation due to the following reasons: 1) using different machines from different manufactories for image acquisition; 2) acquiring CT images in different angles, positions and organ statuses; 3) unclear organ boundaries. 4) the large amount of noise. 5) the use of only a single planning CT image for each patient, thus large shape and appearance variation across subjects.

B. Implementation Details

1). Parameter Setting & Testing Time:

The highly remarked open-source framework Caffe [31] is used to implement our method. We train the whole network using the standard Stochastic Gradient Descent (SGD) algorithm by an invasion learning rate, from 10⁻⁴ to 10⁻⁸ with a decreasing rate of 1×10⁻⁴ per iteration until reaching the manual stop learning rate. We use the momentum of 0.9 to make a tradeoff between the last observed image and the newly coming image. All the network parameters are initialized by Xavier’s method [32].

In the training process, we also crop patches randomly through the whole image in Stage 1 and the organ regions in Stage 2. In the testing process, we crop (the overlapped) patches regularly with a constant step size. The patch size is set to 64×64×5 for stage 1, and 64×64×3 for Stage 2. And the networks are trained by using the training CT images. We do not use the pre-trained models as they do not meet the required input size of our method. The experiments are conducted on an NVidia Titan X powered workstation. The computational time for testing one raw CT image is less than 1 minute, with only 1 second used for Stage 1.

C. Segmentation Results

1). Metrics:

To evaluate the segmentation performance, the volumetric overlap (DSC, PPV, SEN) and surface distance (ASD) are used, as defined below.

1. Dice similarity coefficient (DSC):

   $$DSC=\frac{2\Vert Vo{l}_{gt}\cap Vo{l}_{seg}\Vert }{\Vert Vo{l}_{gt}\Vert +\Vert Vo{l}_{seg}\Vert }$$ (3)
2. Positive predictive value (PPV) and Sensitivity (SEN):

   $$PPV=\frac{\Vert Vo{l}_{gt}\cap Vo{l}_{seg}\Vert }{\Vert Vo{l}_{seg}\Vert }SEN=\frac{\Vert Vo{l}_{gt}\cap Vo{l}_{seg}\Vert }{\Vert Vo{l}_{gt}\Vert }$$ (4)
3. Average surface distance (ASD):

   $$\begin{gathered} ASD=\frac{1}{2}\{mean\underset{{}_{a\in Vo{l}_{\mathit{gt}},b\in Vo{l}_{seg}}}{\min }d(a,b) \\ +mean\underset{{}_{a\in Vo{l}_{seg},b\in Vo{l}_{gt}}}{\min }d(a,b)\} \end{gathered}$$ (5)

   where V ol_seg denotes the voxel set of predicted volume, V ol_gt denotes the voxel set of ground truth volume, and d(a,b) denotes the Euclidean distance between a and b.

   We here define a new metric, i.e., Average object coverage rate (AOCR), to evaluate the accuracy of the region proposal in Stage 1 in our method, as below.

4. Average object coverage rate (AOCR):

   $$AOCR=\Vert Vo{l}_{in}\Vert /\Vert Vo{l}_{gt}\Vert$$ (6)

   where V ol_in denotes the voxel set of organ volume inside the cropped organ region.

2). Organ Region Detection:

Here, we present the organ detection results in Stage 1. We compare the region proposal results using the original CT image (Original) and using the down-sampled image (Fast), as given in Table II. Since we regard this task as a coarse segmentation task, the DSC values of the three target organs are also provided. From Table II, we can observe that, although the DSC values of the three target organs are not higher by using the proposed down-sampled images, the proposed region is still similar compared with the case of using the original image, both of which can cover the whole organ. But the efficiency is largely improved by using the proposed fast detection strategy, which is more than 300 times faster than using the original image.

TABLE II.

The mean DSC of coarse organ segmentation (Pro: prostate; Bla: bladder; Rec: rectum) and the mean AOCR of region detection results.

Methods	DSC			AOCR	Time(s)
	Pro	Bla	Rec
Original	0.70	0.82	0.67	1	380
Fast	0.67	0.77	0.57	1	1

3). Evaluation on Network Design:

a). Evaluation on Number of Slices.

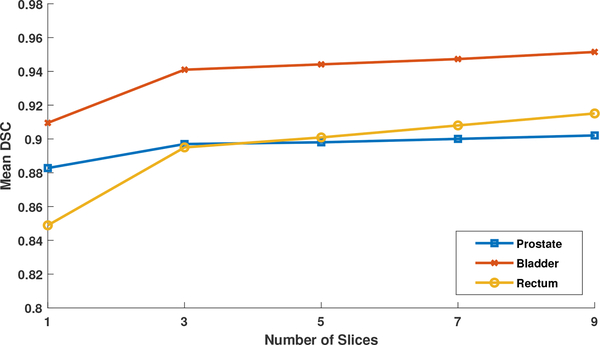
In our method, we use the sequential slices as input to predict the segmentation map of the middle slice. Fig. 6 shows the influence of the number of input slices in Stage 2. We do not evaluate the performance in Stage 1, since the segmentation performance of Stage 1 does not affect the final segmentation results as verified in the previous section. As shown in Fig. 6, by using more slice as input, the results are not very sensitive to the number of input slices when it reaches three. However, more input slices make the network computationally expensive. Thus, we finally choose the three as the number of input slices.

Fig. 6.

The mean DSCs of the proposed method for prostate, bladder and rectum segmentations with respect to the use of different number of input slices 1,3,5,7,9.

b). Evaluation on Network Structure.

In order to evaluate the contribution of our proposed two-stage multi-task network design, we compare our proposed network (Proposed) with 1) the case of directly using one segmentation network (Seg-One) and 2) the case of using the two-stage design, but with no guidance from distinctive curve delineation sub-network (Seg-noCur). For fair comparison, the architecture of Seg-One and the segmentation network in the second stage of Seg-noCur are the same as the architecture of the proposed method, by only removing the “Last Conv” layer of CNet and the guidance of curve delineation. The mean DSC values of the target pelvic organs after segmentation are reported in Table III. The results by Seg-One in Table III shows that the direct use of FCN cannot produce reasonable results, for this challenging pelvic CT segmentation task. The segmentation performance is improved by employing the proposed two-stage framework, as shown by results by Seg-noCur in Table III. This demonstrates the effectiveness of the proposed two-stage framework in segmenting the relatively small organs from the raw CT image, since the organ region can be first detected robustly and then refined on the detected region. The p-value for Seg-noCur and Proposed is calculated and reported in the rightmost column. The best performance is achieved by our proposed distinctive curve guided multi-task FCN, with significantly improved DSC values of all the three organs. From these results, we can summarize that: 1) the proposed distinctive curve is effective in providing shape information for better identifying unclear organ boundaries; 2) the multi-task learning strategy allows better use of complementary information from different tasks, for final accurate segmentation. In addition, since prostate and rectum is more difficult than segmenting bladder, the improvements by using the distinctive curve on prostate and rectum segmentations are more obvious than on bladder segmentation. This further verifies the effectiveness of using the distinctive curve, especially for indistinguishable organ boundaries.

TABLE III.

Quantitative comparison of DSC for segmentation of three pelvic organs on the planning CT images of 313 patients. (The best results are indicated in bold)

Organ	Seg-One	Seg-noCur	Proposed	p-value
Prostate	0.72 ± 0.11	0.79 ± 0.07	0.89 ± 0.02	4.06 × 10−22
Bladder	0.83 ± 0.08	0.88 ± 0.08	0.94 ± 0.03	1.31 × 10−9
Rectum	0.70 ± 0.14	0.75 ± 0.11	0.89 ± 0.05	4.91 × 10−24

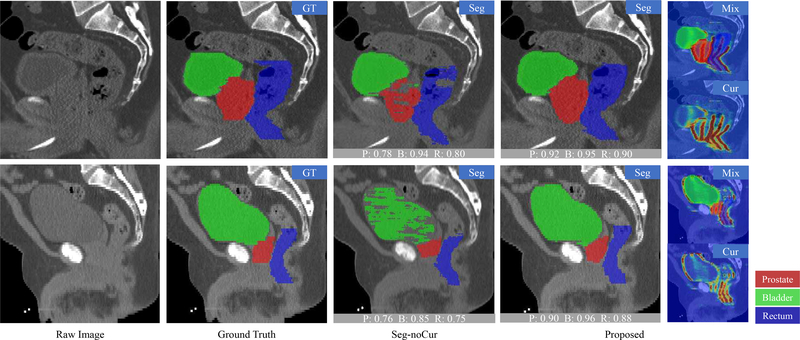
c). Visual Results.

The segmentation results of prostate, bladder and rectum by using the Seg-noCur method and the proposed method are visualized in Fig. 7. For better visualization, we display only the part of raw CT image with three target organs. As can be seen from Fig. 7, the prostate and the rectum are more difficult to segment than the bladder, due to their unclear boundaries. Therefore, Seg-noCur obtains similar results with our proposed method for bladder segmentation. But, for the prostate and rectum, our proposed method achieves much better segmentation results compared with Seg-noCur. From these visualization results, we can also observe the crucial role of the distinctive curve in guiding the segmentation of the prostate and rectum with very low tissue contrast.

Fig. 7.

Visualization of the segmentation results of prostate, bladder and rectum by using the proposed method and Seg-noCur method. The curve delineation results are also provided. The gray block at the bottom of the image denotes the DSC of this image. “P” denotes the prostate, “B” denotes the bladder, and “R” denotes the rectum. The probabilities of the curves are marked from blue to red, which indicates the probabilities from low to high.

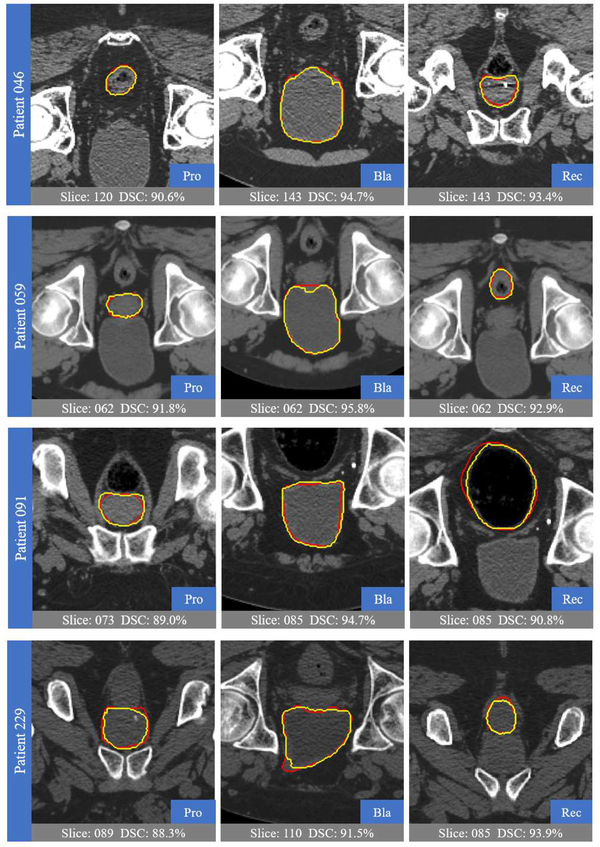
Fig. 8 shows the ground truths and automatic segmentations of four randomly-selected patients from the testing data. As can be observed, our proposed method can well delineate the organ boundaries, with high overlaps of automatic and ground-truth segmentation results, despite large shape variation of pelvic organs and the unclear boundaries in CT images.

Fig. 8.

Visual comparison between the segmentation results of our proposed method (yellow) and the ground truth (red).

4). Comparison with State-of-the-art Methods:

Now we compare our proposed method with the state-of-the-art methods. Here, we compare with six methods, as briefly introduced below.

• Martines et al.’s method [33], which introduced a Bayesian framework to initialize the segmentation and then deformed it by a local deformation function.

• Lay et al.’s method [16], which adopted landmarks as guidance to initialize the organ shapes. Landmarks were detected by using both local and global context information. This method takes the similar assumption as our proposed method.

• Lu et al.’s method [34], which took additional information to help infer organ boundaries, thus improving the segmentation performance.

• Shao et al.’s method [8], which utilized a deformable model-based segmentation method, by adopting the shape prior generated from a regression forest trained on organ boundaries.

• Gao et al.’s method [35], [9], which were also based on deformable models to jointly learn a classifier and a regressor for pelvic organ segmentation.

a). DSC and ASD.

Table IV compare the segmentation performance of our proposed method with the six state-of-the-art methods on prostate, bladder and rectum segmentations, using the mean DSC and ASD (mm) with standard deviation. Among the state-of-the-art methods, Gao et al.’s method in [9] has achieved the best performance. The Seg-noCur is not competitive with Gao et al.’s method in [9], while our proposed method consistently wins the best performance for segmentations of all three organs. Specifically, Gao et al.’s method in [9] leverages all the voxels to learn for a general displacement regressor to draw the organ boundaries explicitly, and our proposed method introduces the distinctive curve to effectively guide the segmentation. Besides, Gao et al.’s method in [9] is implemented as a four-step hierarchical framework, while our proposed method is a two-stage framework. Additionally, our proposed method also wins the best performance in term of ASD. The ASD for prostate is 1.86mm in [8] and 1.77mm in [9]. In our method, under the guidance of the distinctive curve, we obtain further improvement of 0.43mm compared with [9]. For the bladder, similar improvement can also be achieved. For the rectum, our proposed method has the comparable performance with [9]; note that Gao et al.’s method in [9] employs the smooth surface as the guidance, while our proposed method used only the distinctive curve, which is more efficient to describe. Also, our proposed method directly deals with the raw image data without preprocessing steps. All these results demonstrate the effectiveness of our proposed method in the segmentation of pelvic organs.

TABLE IV.

Quantitative comparisons of DSC and ASD (mm) for segmentations of three pelvic organs (i.e., prostate, bladder, rectum) on the planning CT images of 313 patients. (The best results are indicated in bold)

Methods	Prostate		Bladder		Rectum
	DSC	ASD	DSC	ASD	DSC	ASD
Martinez [33]	0.87 ± 0.07	-	0.89 ± 0.08	-	0.82 ± 0.06	-
Lay [16]	-	3.57 ± 2.01	-	3.08 ± 2.25	-	3.97 ± 1.43
Lu [34]	-	2.37 ± 0.89	-	2.81 ± 1.86	-	4.23 ± 1.46
Shao [8]	0.88 ± 0.02	1.86 ± 0.21	0.86 ± 0.05	2.22 ± 1.01	0.84 ± 0.04	2.21 ± 0.50
Gao [35]	0.86 ± 0.05	1.85 ± 0.74	0.91 ± 0.10	1.71 ± 3.74	0.79 ± 0.20	2.13 ± 2.97
Gao [9]	0.87 ± 0.04	1.77 ± 0.66	0.92 ± 0.05	1.37 ± 0.82	0.88 ± 0.05	1.38 ± 0.75
Seg-noCur	0.79 ± 0.07	2.65 ± 1.54	0.88 ± 0.08	2.28 ± 1.20	0.75 ± 0.11	4.02 ± 2.03
Proposed	0.89 ± 0.02	1.34 ± 0.64	0.94 ± 0.03	0.94 ± 0.76	0.89 ± 0.05	1.38 ± 1.63

b). PPV and SEN.

We further compare the segmentation results in term of PPV and SEN with Gao et al.’s method in [9] as well as other four state-of-the-art methods, which are described below.

• Rousson et al. [36]’s method, which incorporated a Bayesian framework to impose shape constraint on prostate, due to the partially visible of this organ.

• Costa et al.’s method [37], which used different segmentation techniques for prostate and bladder, with the assumption that the shape of prostate is statistically stable while the shape of bladder is of large variance.

• Freeman et al.’s method [38], which incorporated shape and appearance information for segmentation.

• Chen et al.’s method [39], which introduced anatomical constraints for active shape models to enhance the segmentation ability.

Since different papers work on different organs, we report the separate results in two different tables (Table V and VI) for a fair comparison. Among these existing methods, Gao et al.’s method in [9] gets the best performance in most cases. However, our proposed method still wins the best overall performance compared with Gao et al.’s method in [9]. For example, the PPV is consistently improved in all cases, while the SEN is improved on the bladder.

TABLE V.

Quantitative comparisons of Mean SEN and PPV for the prostate and bladder segmentation results. (The best results are indicated in bold)

Method	Prostate		Bladder
	SEN	PPV	SEN	PPV
Rousson [36]	0.84	0.79	-	-
Costa [37]	0.81	0.85	0.75	0.80
Gao [9]	0.88	0.85	0.94	0.92
Proposed	0.88	0.92	0.93	0.95

TABLE VI.

Quantitative comparisons of Median SEN and PPV for the prostate and rectum segmentation results. (The best results are indicated in bold)

Method	Prostate		Rectum
	SEN	PPV	SEN	PPV
Freedman [38]	0.83	0.85	0.74	0.85
Chen [39]	0.84	0.87	0.71	0.76
Gao [9]	0.90	0.86	0.91	0.89
Proposed	0.88	0.93	0.90	0.93

The slightly lower SEN by our proposed method also indicates that our method has less issue on over-segmentation. Actually, since the pelvic boundaries are unclear in CT images, the over-segmentation is more likely to happen for the automatic segmentation algorithms. In this case, by using the distinctive curve, our proposed method has a higher capacity for dealing with the indistinctive boundaries. Less over-segmentation is also important in clinical applications for well protecting normal tissue during radiotherapy, and eventually minimizing side effects.

V. DISCUSION AND CONCLUSION

We have proposed a two-stage distinctive curve guided FCN to tackle the pelvic organ segmentation task in CT images. We employed Stage 1 to robustly detect the prostate, bladder and rectum in the raw CT image, and Stage 2 to accurately segment these three organs. Specifically, in Stage 2, we introduced a novel shape representation, namely distinctive curve, to help the network better identify the unclear organ boundaries. Experimental results on a large diverse dataset demonstrated both the accuracy and robustness of our proposed method, better than the state-of-the-art segmentation methods.

Although the proposed method has shown its promising results in the experiments, we also found it may not work perfectly to accurately segment organ boundaries in some cases (See the last row of Fig. 8). As a pixel-wise method, the proposed method may have some under-segmentation results in some specific slices.

In the future work, we will further improve method from the following two aspects. 1) In this work, we simplify the curve delineation task as a sequential landmark detection task. We may further investigate a more effective way to more robustly and accurately delineate the distinctive curves. 2) The distinctive curve is adopted as a cue for the segmentation task. However, this shape delineation can be further explored. For example, we may use these curves to generate the organ surface that can guide a deformable model for further segmentation refinement.