Amelogenin as a Promoter of Nucleation and Crystal Growth of Apatite

Abstract

Human dental enamel forms over a period of 2 – 4 years by substituting the enamel matrix, a protein gel mostly composed of a single protein, amelogenin with fibrous apatite nanocrystals. Self-assembly of amelogenin and the products of its selective proteolytic digestion are presumed to direct the growth of apatite fibers and their organization into bundles that eventually comprise the mature enamel, the hardest tissue in the mammalian body. This work aimed to establish the physicochemical and biochemical conditions for the growth of apatite crystals under the control of a recombinant amelogenin matrix (rH174) in combination with a programmable titration system. The growth of apatite substrates was initiated in the presence of self-assembling amelogenin particles. A series of constant titration rate experiments was performed that allowed for a gradual increase of the calcium and/or phosphate concentrations in the protein suspensions. We observed a significant amount of apatite crystals formed on the substrates following the titration of rH174 sols that comprised the initial supersaturation ratio equal to zero. The protein layers adsorbed onto the substrate apatite crystals were shown to act as promoters of nucleation and growth of calcium phosphates subsequently grown on the substrate surface. Nucleation lag time experiments have showed that rH174 tends to accelerate precipitation from metastable calcium phosphate solutions in proportion to its concentration. Despite their mainly hydrophobic nature, amelogenin nanospheres, the size and surface charge properties of which were analyzed using dynamic light scattering, acted as a nucleating agent for the crystallization of apatite. The biomimetic experimental setting applied in this study proves as convenient for gaining insight into the fundamental nature of the process of amelogenesis.

Introduction

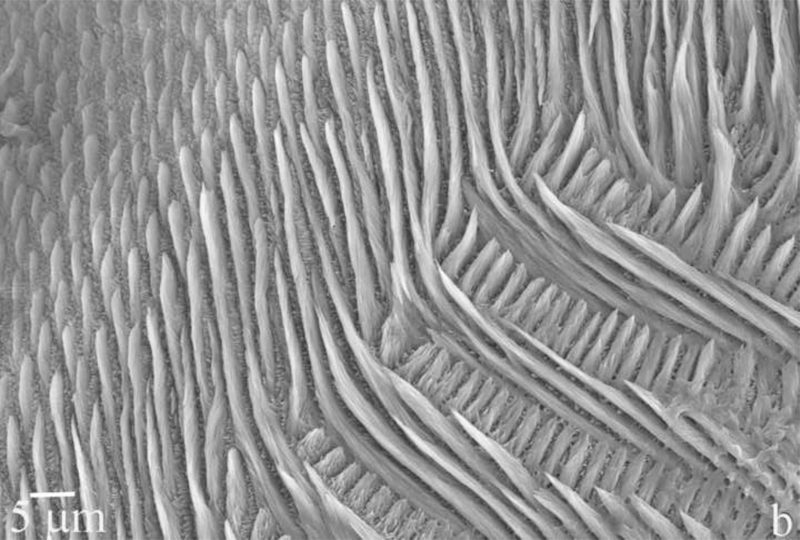
Dental enamel is a unique biological material in many senses. For one, it is the hardest tissue in the mammalian body. Secondly, its microstructure dominated by parallel rods [1,2], composed of bundles of 40 – 60 nm wide apatite crystals with the aspect ratio of up to 1:10⁴. And thirdly, it is the most mineralized tissue in the human body, comprising 96 – 98 wt% of the mineral phase, apatite, which is best described by the stoichiometric formula (Ca,Z)₁₀(PO₄,Y)₆(OH,X)₂, where Z = Na⁺, Mg²⁺, K⁺, Sr²⁺, etc., Y = CO₃^2-, HPO₄^2-, and X = Cl^-, F^-. The microstructural and morphological difference of apatite crystals in enamel compared to those present in bone and dentin have suggested that the mechanism of formation of apatite crystals in enamel may be markedly different from the organic-template-based one associated with collagenous hard tissues, such as bone or dentin [3]. Understanding the mechanism of amelogenesis on nano and molecular scales is of major potential significance for reparative dentistry [4]. Microstructures of tooth enamel in goat and mouse species are shown in Fig.1.

Fig.1.

Scanning electron micrographs showing the microstructure of the tooth enamel in goat (a) and mouse (b) species.

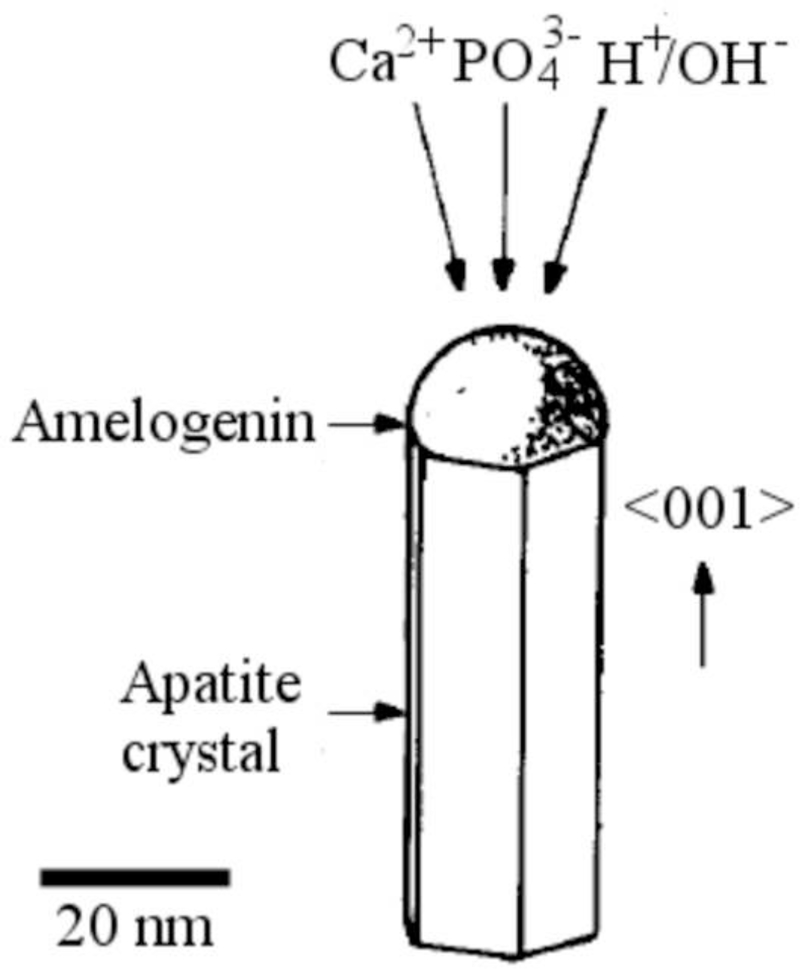
The imitation of amelogenesis in vitro as the central subject of this study has been based on the hypothesis that 20 – 40 nm sized spherical assemblies of rH174 in aqueous sols will control the substrate-specific growth of the apatite seeds during a continuous supply of Ca²⁺ and PO₄^3- ions at low degrees of saturation. The aim of this study has been to assess the validity of the current model describing the chemical mechanism of matrix-guided crystal growth during enamel maturation based on the assumption that amelogenin nanospheres preferentially adsorb onto (hk0) faces of the growing apatite crystals, thereby allowing the surrounding Ca²⁺ and PO₄^3- ions to bind onto (001) crystal faces solely and forcing the uniaxial growth of apatite crystals along the [1] axis [5]. A confirmation of this model in vivo is, however, still being sought for. A natural implication of this model is that amelogenin plays the role of a growth inhibitor in the course of amelogenesis [6,7]. In contrast, there are a few studies demonstrating that under specific conditions, amelogenin can act as a promoter of nucleation of a calcium orthophosphate phase [8–10]. Tarasevich et al. furthermore came to the conclusion that amelogenin may act both as a nucleation promoter and inhibitor [11], confirming a well-known fact that macromolecules often exhibit different crystallization effects depending on their concentration [12]. These models call for more complex models of amelogenesis, such as those based on the mesoscale co-assembly of amelogenin oligomers and apatite nanocrystals [9]. In this work, we provide experimental insights and arguments that speak in favor of the capacity of amelogenin to promote nucleation and growth of calcium phosphate from lowly supersaturated solutions with respect to apatite.

Experimental

The experimental setting applied in this study was modified from a previous one [13], and is displayed in Fig.2. The programmed titration was performed with 1 ml burettes, using a Titrino 751 GDP titration device in combination with a Dosimat 755 (Brinkmann-Metrohm) controlled by computer software (Tiamo 1.2, Brinkmann-Methrohm). The basic procedure was as follows. The reaction suspension comprising 5 ml of 0.2 – 1.6 mg/ml rH174, 20 mM Tris/HCl buffer, different concentrations of KH₂PO₄ and CaCl₂, and 0.02 % NaN₃ (introduced to the system in the given sequence) at pH 7.40 +− 0.01 was prepared in a glass vessel, which was kept at 37 °C via a circulating water bath (Fig.2). The two buffered titrant solutions (20 mM Tris/HCl, pH 7.40 +− 0.02) comprising the separate precursor ions (CaCl₂ and KH₂PO₄) and the electrolyte (142 mmoll⁻¹ KCl) up to the level of the physiological ionic strength were then being injected into the reaction suspension at a controlled rate of 84 nl/min, i.e., 1.2 ml/day, cumulatively, in pulses equal to 1 μl in volume, throughout a 7-day period of time. The initial and titrant calcium and phosphate concentrations, as well as the titration rates were modified in different experiments with the purpose of investigating the effects of different variables. Table 1 shows different ionic concentrations and titration modes applied. The crystal growth was initiated on glass ceramic substrates comprising embedded fluoroapatite (FAP) crystals with surface-exposed (001) faces (Fig.2) [14]. Prior to their usage, the substrates were polished using 1 and 0.25 μm diamond paste. Subsequently, their surface was covered with a drop of 0.5 mM HF for 30 seconds so as to etch the glass phase and bring the FAP crystal surface 5 – 15 nm higher relative to the surrounding silica glass matrix. A single substrate was sampled out each day, rinsed with 3–4 droplets of distilled water, dried with dust-free canned air, and evaluated for the crystal growth properties using Atomic Force Microscopy (AFM, Nanoscope III, Digital Instruments) and Scanning Electron Microscopy (SEM, DS130C, Topcon). Tapping-mode AFM was applied using Si-tips with a radius of about 5 nm (Supersharp, Nanosensors, Neuchatel, Switzerland). The crystal heights were measured using the section analysis tool in NanoScope software. Heights of twelve randomly chosen peaks in three different 10 × 10 μm AFM images were measured and the average values were plotted as a function of the titration volume. Recombinant human rH174 was previously synthesized via their expression in BL21(DE3) plysS Escherichia coli [15,16]. The concentration of Ca²⁺ in the reaction solution was followed using a calcium ion-selective electrode (pHoenix), while PO₄^3- concentration was measured from 20 μl aliquots using atomic absorption spectrophotometry (Milton Roy, Genesys 5).

Fig.2.

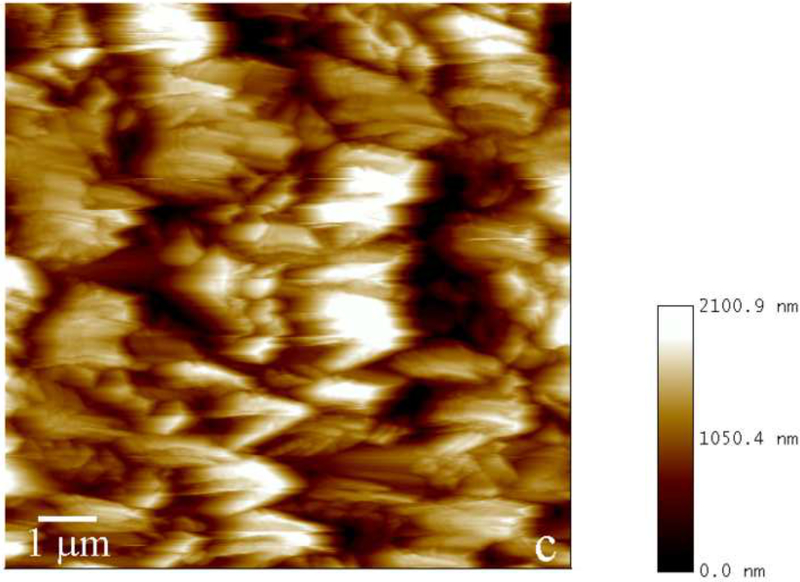
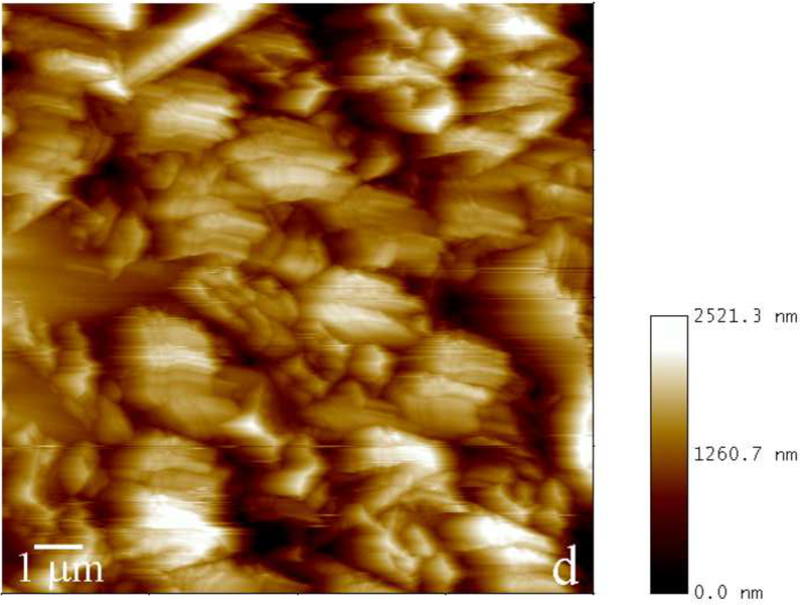
Reaction vessel used in the dynamic precipitation experiments (a), including the AFM images of nanospherical (b) and nanofibrous (c) assemblies of rH174 present in the reaction suspension and of the surface of FAP/glass ceramic composites used as crystal growth substrates (d).

Table 1.

Different ionic concentrations in the initial reaction systems and in the titrant solutions for different apatite crystallization experiments.

System	Initial [Ca2+] (mM)	Initial [PO43−] (mM)	Titrant [Ca2+] (mM)	Titrant [PO43−] (mM)	Cumulative titration rate (ml/day)	pH
I	1.6	1.0	8.2	5.0	1.2	7.4
II	4.1	0	8.2	5.0	1.2	7.4
III	0	2.5	8.2	5.0	1.2	7.4

The degrees of saturation (DS) at different reaction times were calculated using an algorithm based on Debye-Hückel equation [17], while taking into account the solvent evaporation rate at ca. 1 ml/day:

$$\text{DS}={\text{pK}}_{\text{sp}}-\text{pQ}$$ (Eq.1)

where Q is the ionic activity product of the solution, and K_sp is the solubility product of hydroxyapatite (Ca₅(PO₄)₃OH, HAP), the negative logarithm of which was taken as equal to 58.65. Activity coefficients were calculated through logγ = - Az_i² / (I^1/2 + Ba_i), where A is a temperature dependent constant equal to 0.5115 at 25 °C. B and a_i are, like A, constants depending on temperature, dielectric constant of the solution and Debye screening length; a_i = 6 × 10⁻⁸ for Ca²⁺; 9 × 10⁻⁸ for H⁺; and 4 × 10⁻⁸ for PO₄^3- ions. The algorithm approximated the protein-bound fraction of Ca²⁺ and corrected the free [Ca²⁺] using a relationship established for Ca²⁺-binding proteins in saliva [18]. Supersaturation ratio (S) for precipitation/dissolution of hydroxyapatite can be represented as:

$$\text{S}=\text{Q}/{\text{K}}_{\text{sp}}={\{{\text{Ca}}^{2+}\}}^5{\{{{\text{PO}}_{\text{4}}}^{3-}\}}^3\{{\text{OH}}^{-}\}/{\text{K}}_{\text{sp}}$$ (Eq.2)

Nucleation lag time, a.k.a. the induction time, was determined by continuously measuring pH of a 5 ml suspension composed of rH174 in different concentrations (0 – 0.84 mM), 1.6 mM CaCl₂, 1.0 mM KH₂PO₄ and 150 mM KCl kept in a sealed borosilicate glass vessel at 37 °C (DS = 10.9). The resulting pH vs. time curves yielded nucleation lag times as the intersections of tangents over the initially flat levels of pH (7.40 +− 0.02) and over the subsequent pH drop caused by the release of protons following precipitation of apatite:

$$10{\text{Ca}}^{2+}+6{{\text{HPO}}_{\text{4}}}^{2-}+2{\text{H}}_2\text{O}={\text{Ca}}_{10}{\left({\text{PO}}_4\right)}_6{(\text{OH})}_2+8{\text{H}}^{+}$$ (Eq.3)

Dynamic light scattering (DLS) and electrophoretic analyses of colloidal suspensions of rH174 and hydroxyapatite were carried out on Malvern Zetasizer Nano-ZS device, as follows. One milliliter of solution comprising 20 mM Tris/HCl and 150 mM KCl at pH 7.55 was added to 1 mg of HAP, vortexed and centrifuged at 4000 rpm for 3 min. The supernatant dispersion was then extracted, set to pH 7.40 +− 0.02, and analyzed. HAP powder was prepared according to the procedure described previously [19,20]. The same buffered electrolyte solution was added to 0.4 mg of rH174, followed by vortexing and centrifugation. The supernatant was separated, diluted twice, set to pH 7.40 +− 0.02, and analyzed for size and ζ-potential.

Results and discussion

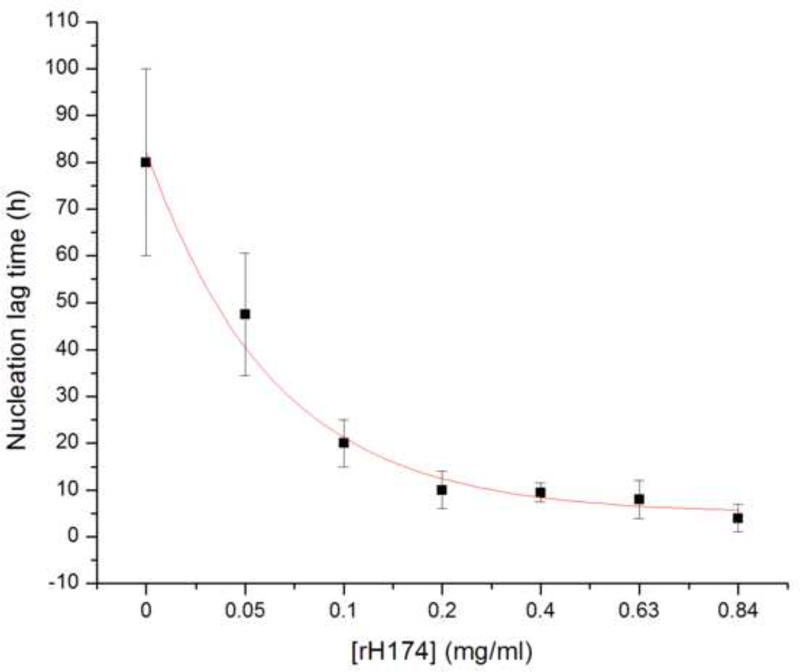
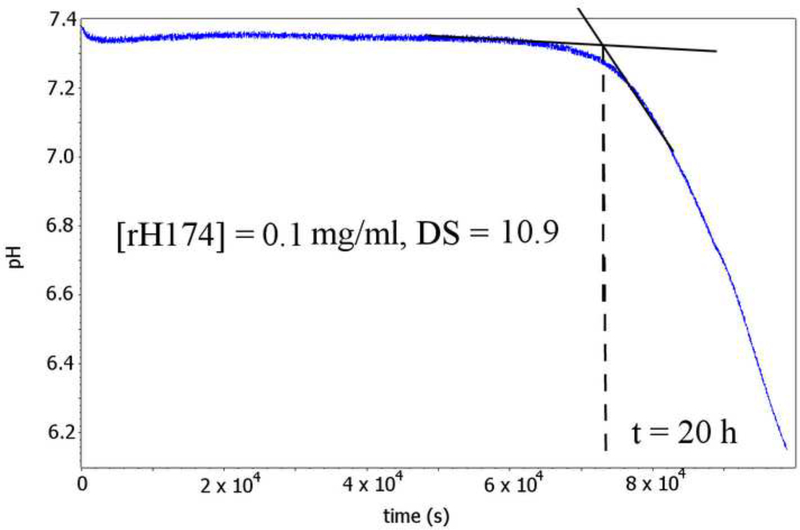
The first indication of the nucleation-promoting capacities of rH174 comes from nucleation lag time (τ) experiments, the results of which are shown in Fig.3. As the concentration of rH174 in a reaction system with DS = 10.9 with respect to apatite is raised from 0 to 0.84 mg/ml, τ exponentially drops from 80 +- 20 h to 6 +- 3 h. The exponential function fitting the experimentally derived τ vs. [rH174] dependence is τ = Ae^-[rH174]/β, where A and β are dimensionless units equal to 150 and 1.5, respectively, and τ and [rH174] are given in units of seconds and mg/ml, respectively. Fig.3b shows a typical pH vs. time curve for [rH174] = 0.1 mg/ml and the deducted induction time of 20 h. The general theory states that the flat pH vs. t line prior to the drop reflects the formation of unstable calcium phosphate embryos and amorphous units with low content of OH^- groups [21.22]. As precipitation of OH^- groups has an acidifying effect on the suspension, whereas their substitution of HPO₄^2- groups in the initial amorphous precipitate has the opposite effect, only when the stoichiometric content of OH^- groups in the calcium phosphate precipitate approaches the one of apatite (i.e., one ninth of the total growth units), the drop in the pH of the solution becomes detectable. Such a model assumes the formation of apatite via numerous transient phases (starting from an amorphous phase and frequently including octacalcium phosphate at low DS values and physiological pHs), and is often supported by the empirical Ostwald-Lussac’s rule, although its validity in the protein-governed crystal growth is questionable.

Fig.3.

Nucleation lag time for the precipitation of apatite as a function of [rH174] (a), and a typical pH vs reaction time curve from which the induction time is extrapolated (b).

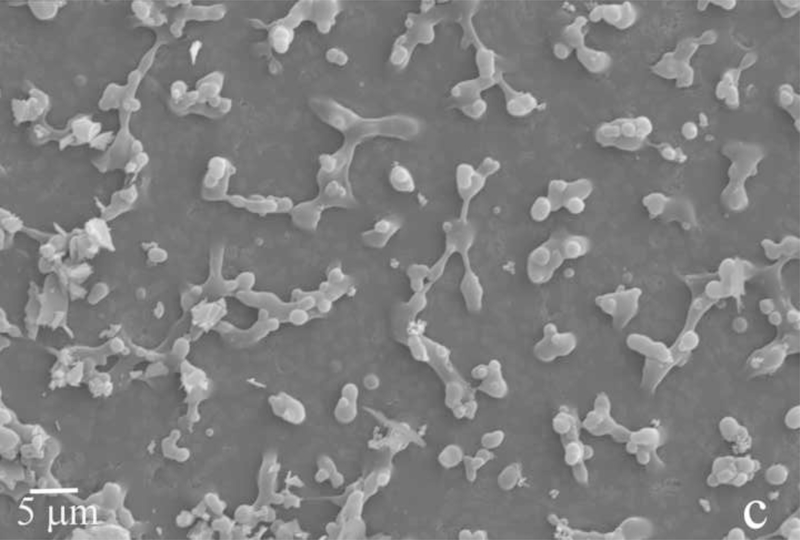
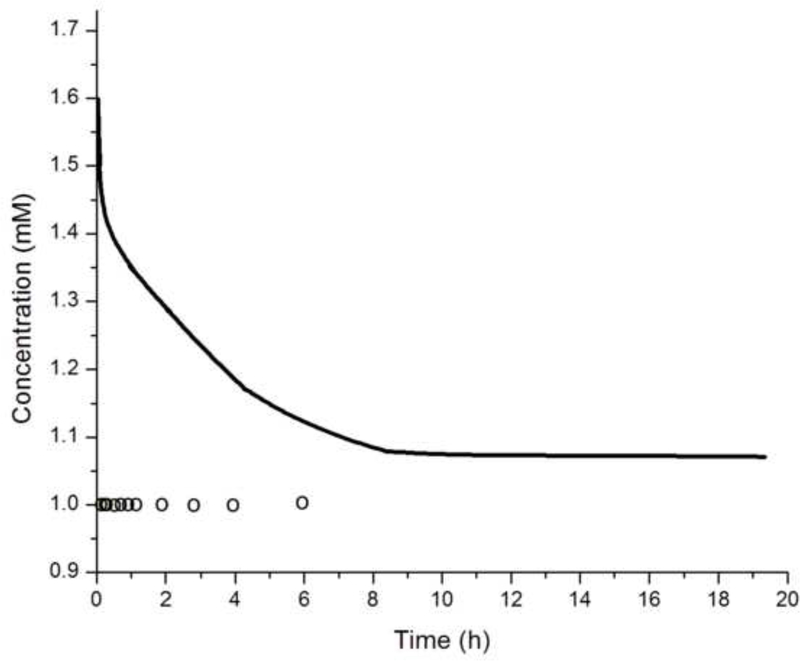
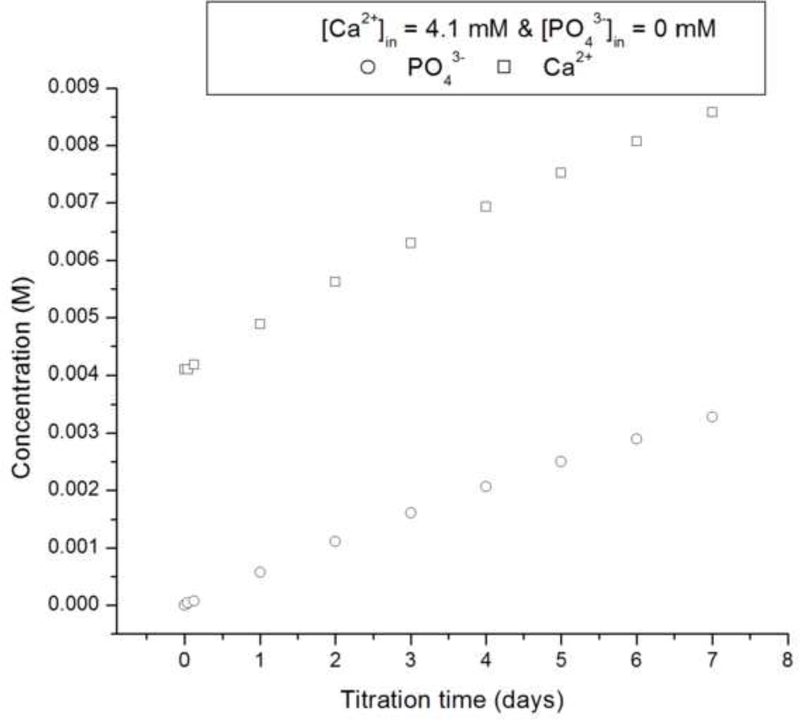
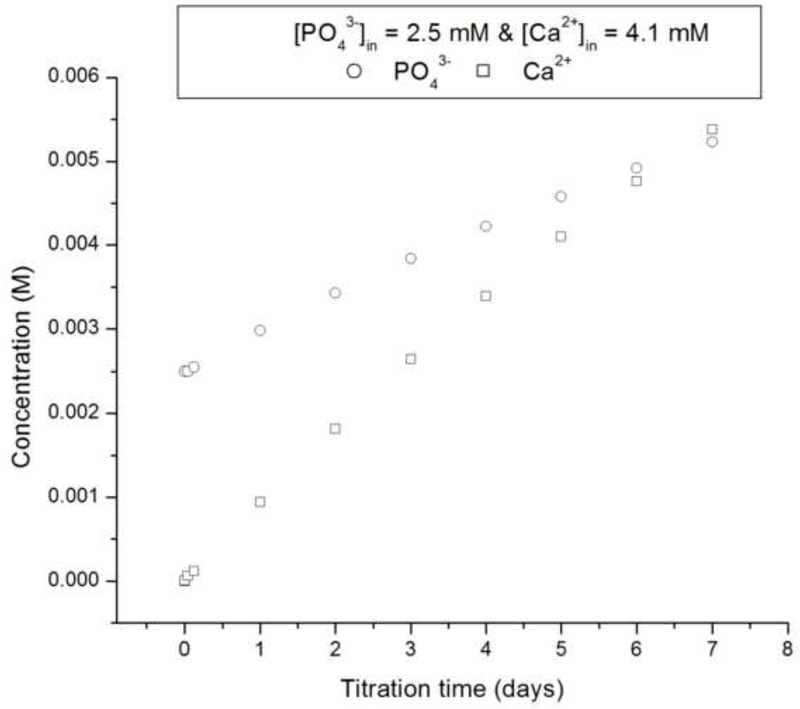
The crystallization runs with reaction solutions initially comprising metastable solutions with respect to apatite (system I, DS = 10.9) did not produce significant growth of the substrate crystals (d ~ 100 – 140 nm), irrespective of whether the proteolytic reaction was initiated or not, as well as irrespective of the rH174 concentration in 0.2 – 1.6 mg/ml range. SEM images shown in Figs.4–5 demonstrate that the growth of the substrate FAP crystals was negligible even after 10 ml of the titration volume in system I (Fig.4b), whereas the substrates sampled out from system III eventually become fully covered with the plate-shaped calcium phosphate crystals (Fig.4d). Fig.4c also shows that the crystal formation leading to extensive substrate coverage begins specifically in the areas in which protein layers were deposited earlier. Results of the crystal height analyses shown in Fig.6 also demonstrate that the crystal growth in system I is significantly less compared to that in systems II and III, which initially comprised an undersaturated sol with supersaturation ratio equal to zero. The reason may be that an amorphous or other transient calcium phosphate phase formed upon mixing the ionic components solution (1.6 mM CaCl₂ and 1 mM KH₂PO₄) with rH174. A presumed formation of the initial nuclei as associated with the suspended rH174 nanospheres rather than with the substrate crystals enforces the subsequent crystal growth to take place outside of the FAP surface provided by the glass-ceramic substrates. The evidence for this comes from following the concentration of free Ca²⁺ ions in the solution over time, as demonstrated in Fig.7a. A drop in the calcium levels from the initial 1.6 mM to 1.1 mM following mixing the initial calcium and phosphate solution with rH174 occurred over the first 8 hours. As only 0.06 mM of Ca²⁺ ions can be shown to remain in form of calcium phosphate complexes in the solution [17], the rest of the concentration drop has to be associated with the sequestration by the protein and the consequent formation of amorphous or transient nanosized calcium phosphate phases [23]. The level of phosphates similarly drops, from the initial 1.0 mM to 0.7 mM, but only after mixing rH174 with both calcium and phosphate ions. Otherwise, as shown in Fig.7a, free concentration of phosphate species in solution stays unchanged at 1.0 mM after adding 0.4 mg/ml rH174 to it and aging for up to 6 h, indicating no binding of PO₄^3- to the protein. These results suggest a higher affinity of rH174 to bind calcium than phosphate ions. Previously reported results based on using atomic absorption spectroscopy similarly indicated drops in Ca²⁺ levels in rH174 sols but relatively constant phosphate levels therein during a set of constant composition experiments [13]. The initial drop in Ca²⁺ levels corresponds well to the results of a study by Le et al., who reported sequestration of calcium ions by rH174 monomers, resulting in approximately 6 Ca²⁺ ions bound to a single rH174 molecule [24]. Hence 0.12 mM of Ca²⁺ would be required to fully saturate rH174 molecules in concentration of 0.4 mg/ml rH174. This model explains the immediate drop from [Ca²⁺] = 1.60 mM to [Ca²⁺] = 1.47 mM following mixing of the given amount of CaCl₂ with 0.4 mg/ml rH174.

Fig.4.

SEM images of the FAP substrates sampled out from systems I (a, b) and III (c, d) after 2.7 ml (a, c) and 10 ml (b, d) of the titration volume.

Fig.5.

SEM images of the FAP substrates sampled out from system II, comprising 0.4 (a) and 0.8 mg/ml (b) rH174, after 10 ml of the titration volume.

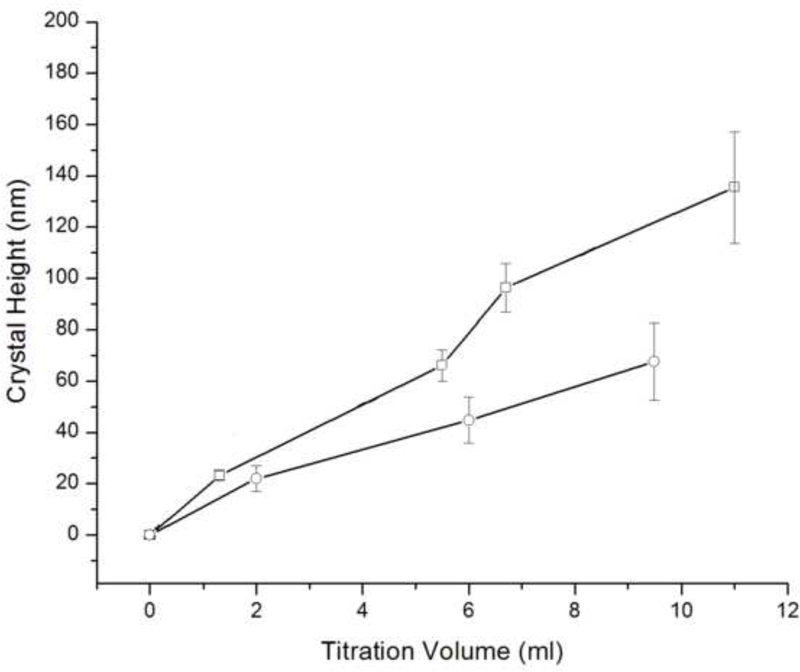
Fig.6.

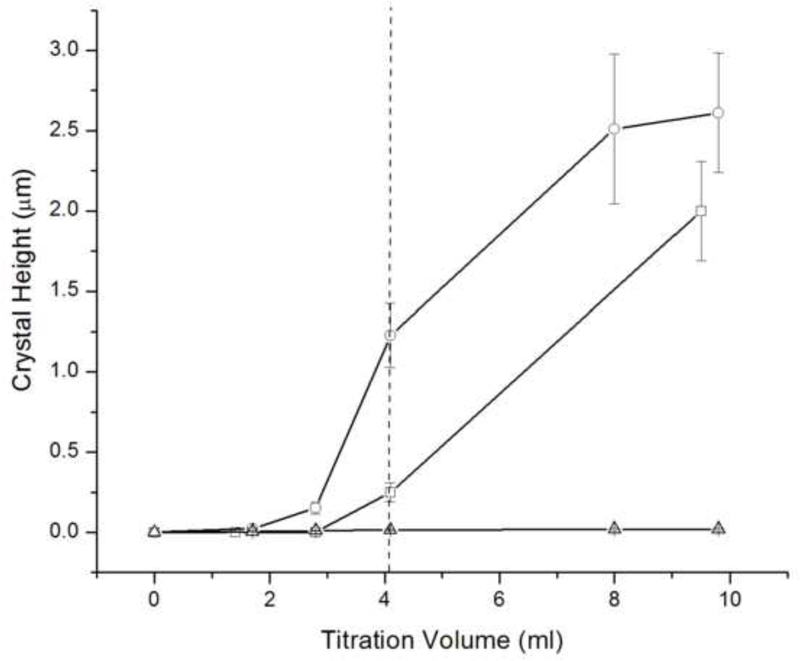
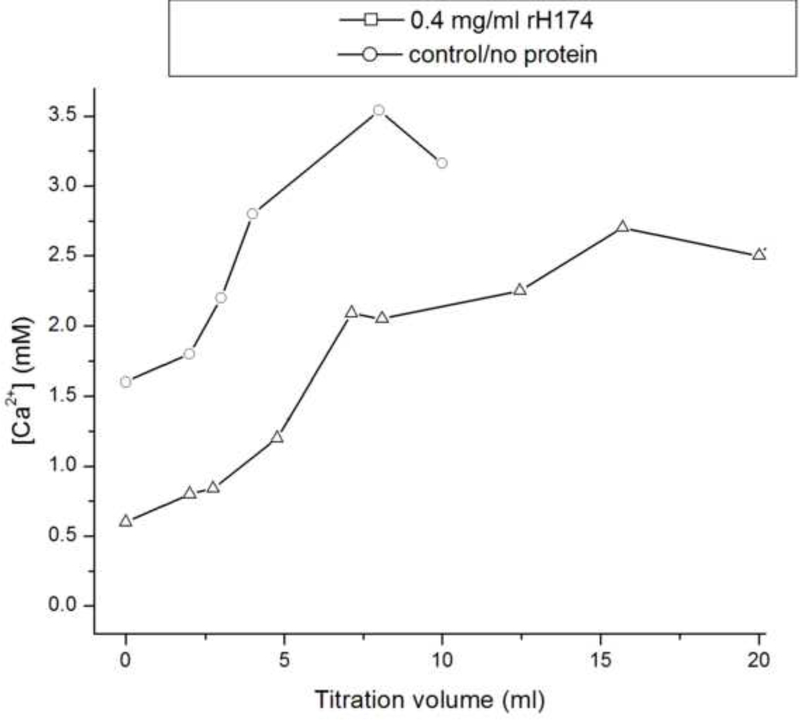
The average height of apatite crystals grown in system I after different titration volumes compared between 0.4 mg/ml rH174 sample (-□-) and a control sample with no protein (-o-) (a), and of apatite crystals grown in systems III (-o-) and II (-□-) with 0.4 mg/ml rH174, as compared to the control sample with no protein (-Δ-) (b).

Fig.7.

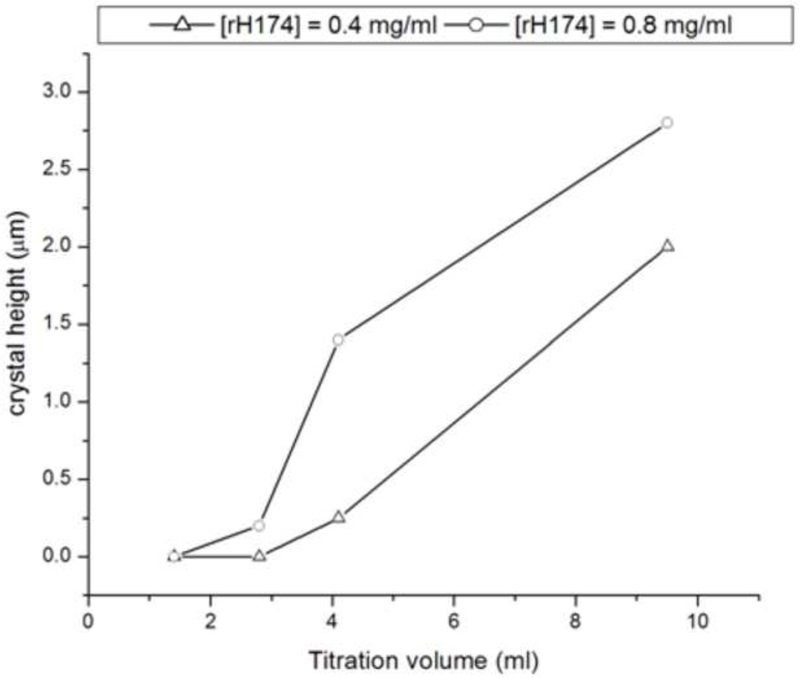
(a) Concentrations of free Ca²⁺ (straight line) and PO₄^3- (circles) during aging of a sol containing 0.4 mg/ml rH174, 1.6 mM CaCl₂, 1.0 mM KH₂PO₄, and 150 mM KCl at 37 °C (continuous line) and 0.4 mg/ml rH174, 1.0 mM KH₂PO₄, and 150 mM KCl at 37 °C (circles); (b) Height of the crystalline layer grown in system II at [rH174] = 0.4 mg/ml (-Δ-) and [rH174] = 0.8 mg/ml (-o-) versus the titration volume.

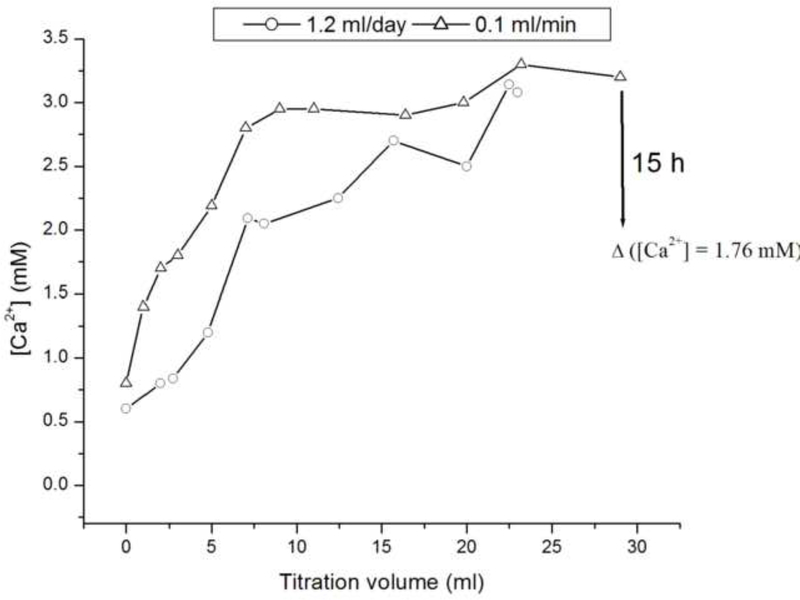
Fig.8a shows that although the levels of free Ca²⁺ measured at the start of the control, protein-free experiment (system I) equal the initially set concentration of 1.6 mM, there is a drop in [Ca²⁺] following the mixing of precursor ionic and peptide components. The subsequent increase in the Ca²⁺ levels is due to titration, and the plateaus reached after different reaction times signify the onsets of precipitation from the solution. Whereas the control, protein-free system reaches [Ca²⁺] = 3.5 mM before it homogeneously precipitates, forming particles in the solution, the supersaturation levels for the protein-containing samples are significantly lower and proportional to the amount of the peptides exposed to the solvent. Thus, the system composed of rH174 only reaches critical supersaturation at [Ca²⁺] = 2 mM, whereas the system with the proteolytic digestion of rH174 reaches the critical levels at [Ca²⁺] = 1.3 mM. This is the first indication that rH174 itself promotes precipitation of calcium phosphate at a lower DS compared with non-protein solutions. Fig.8b demonstrates the effect of rate of addition of titrants into the reaction vessel, in such a way that increasing the titration rate leads to a higher [Ca²⁺] at any given titration volume. The system titrated at the rate of 0.1 ml/min thus reaches higher critical supersaturation levels compared to the system titrated at 1.2 ml/day (i.e., at [Ca²⁺] = 3 mM vs. [Ca²⁺] = 2 mM, respectively), indicating the effect of the nucleation lag time in transcending the energy barrier imposed on the reaction path of the system towards crystallizing its ionic content into apatite form. The observed immediate drop in [Ca²⁺] in the presence of rH174 particularly emphasized in the presence of H₂PO₄^- and HPO₄^2- species points at the immediate formation of amorphous or crystalline solid units in the protein suspension, which explains the low growth rate under such circumstances.

Fig.8.

The concentrations of calcium ions in the supernatant reaction solutions after different titration volumes for the titration rate of 1.2 ml/day and for protein-free solution (-o-) and rH174-comprising solution (-Δ-) (a), and for the rH174-comprising solution and the titration rates of 1.2 ml/day and 0.1 ml/min (b).

Figs.4 and 6a show that the protein-containing systems of type I produce more crystal growth compared to the control runs performed with no rH174. The same and an even more drastic trend is detected in case of systems II and III, which are typified by a slow increase in DS starting from undersaturated state with respect to all calcium phosphate phases (Fig.6b). Whereas the crystals grown in the protein-free systems II and III exhibit heights of less than 100 nm after the 7-day titration, the thickness of crystalline deposits in rH174-containing runs exceeds 1 μm, suggesting a crucial importance of rH174 for a controlled, surface-specific growth of apatite under conditions employed in these experiments. Carrying out a protein-free experiment under the low pH conditions of system VII, although at higher concentrations of calcium and phosphate ions compared to systems I - VI, similarly did not yield any significant crystal growth even after longest reaction times. As indicated by the peak in [Ca²⁺] in the control solution over time (Fig.8a), the titration eventually results in precipitation of a visible calcium phosphate powder, which does not adhere to the FAP substrates, indicating the necessity of the presence of rH174 to promote surface-specific growth of the substrate crystals under the applied conditions.

As significant amount of a mineralized layer is observed only in the presence of rH174, it clearly indicates its role as a nucleation and crystal growth promoting agent. The crystal growth rate and the reaction time when the substrates become fully covered with apatite layers of more than 1 μm in thickness are in this case also proportional to the amount of rH174 employed. Fig.9 thus displays AFM images of FAP substrates sampled out after identical reaction times from system II comprising 0.4 and 0.8 mg/ml rH174. Whereas the former sample is barely covered with the precipitate, apatite layers exceeding 1 μm in thickness were detected in the latter sample. Also, Fig.10 shows the crystallization of FAP seeds from system III as in its initial stages at [rH174] = 0.4 mg/ml after 2.8 ml of titration volume (Fig.10a), whereas already after 2.6 ml of titration the substrates are completely covered with the crystalline deposits when [rH174] = 1.6 mg/ml (Fig.10d). In contrast, it takes ~ 4 ml of the titration volume to fully cover the reference level of glass in system III employing [rH174] = 0.4 mg/ml (Fig.10c). During all that time and even after 10 ml of the titration volume, no significant crystal growth is observed in the protein-free control samples (Fig.10b).

Fig.9.

Phase mode AFM images showing an incomplete (a) and complete (b) coverage of the substrate with apatite for [rH174] = 0.4 mg/ml and 0.8 mg/ml, respectively, after 4 ml of titration volume in system II.

Fig.10.

AFM images of the crystallization substrates in system III with: [rH174] = 0.4 mg/ml, V_t = 2.8 ml (a), [rH174] = 0 mg/ml, V_t = 8 ml (b), [rH174] = 0.4 mg/ml, V_t = 4 ml (c), and [rH174] = 1.6 mg/ml, V_t = 2.6 ml (d).

Although it is evident from Fig.10a that the apatite growth starts specifically on FAP crystals (there are no signs of homogeneously precipitated crystals deposited on the surrounding glass), the crystals eventually branch out, resulting in a complete coverage of the substrate surface. At the point when the reference level of glass becomes covered with the crystalline phase (2 – 3 μm of crystal height), it is difficult to measure the real crystal height owing to the limit of the AFM scanner movement in z-direction. The plateau denoting unchanging crystal growth in Fig.6b thus stands forth as an artifact coinciding with reaching the limits in the AFM imaging resolution. SEM analysis of the cross-sections of the glass-ceramic seeds yielded values of ~ 50 μm for the apatite layer thickness after 7 days of titration, as visible from Fig.11. Hence, the crystal growths reached in these experiments have mimicked the order of magnitude of the growth rate of enamel in vivo: ~ 3 μm/day.

Fig.11.

SEM of the cross-section of an FAP/glass substrate sampled out from system III after 7 days of titration time.

At a sufficiently low concentration, such as 0.2 mg/ml, rH174 is already incapable of promoting the extensive crystallization of apatite that fully covers the seeds as observed with [rH174] ≥ 0.4 mg/ml. Instead of promoting the growth of the FAP substrates, nucleation and crystal formation occur in the solution, as indicated by agglomerated particles on the substrate surface, without attachment to the seed crystals. In contrast to that, at [rH174] ≥ 0.4 mg/ml, the first signs of crystallization are observed on the FAP substrates rather than in the solution or on the surrounding glass surface, as can be seen from Fig.10a. Therefore, not only does rH174 need to be adsorbed onto the growing crystals at a low DS, but its concentration also needs to be sufficient in order for the protein-controlled crystal growth to be initiated. In case of 0.2 mg/ml, only 5 % of titrated Ca²⁺ precipitated after the titration volume of 1.2 ml, and 70 % were precipitated after 7 ml. Since no significant growth on the FAP substrate (> 1 μm) was observed during the entire run, the precipitation is expected to have primarily occurred in the solution with the dispersed rH174 nanospheres acting as nucleation surfaces. A high enough concentration of the dispersed rH174 is apparently required to induce its adsorption onto apatite in a level sufficient to foster the formation of architectures that promote the protein-controlled crystal growth.

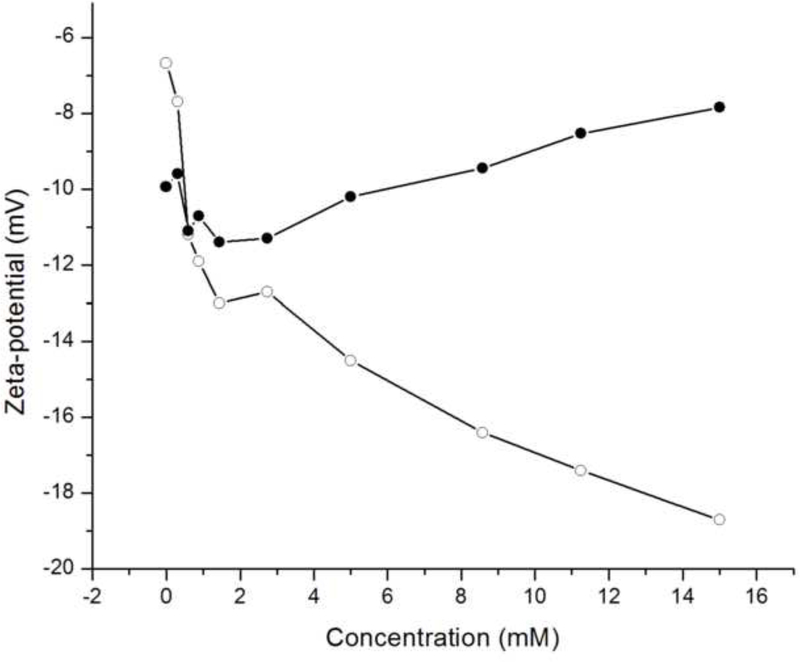
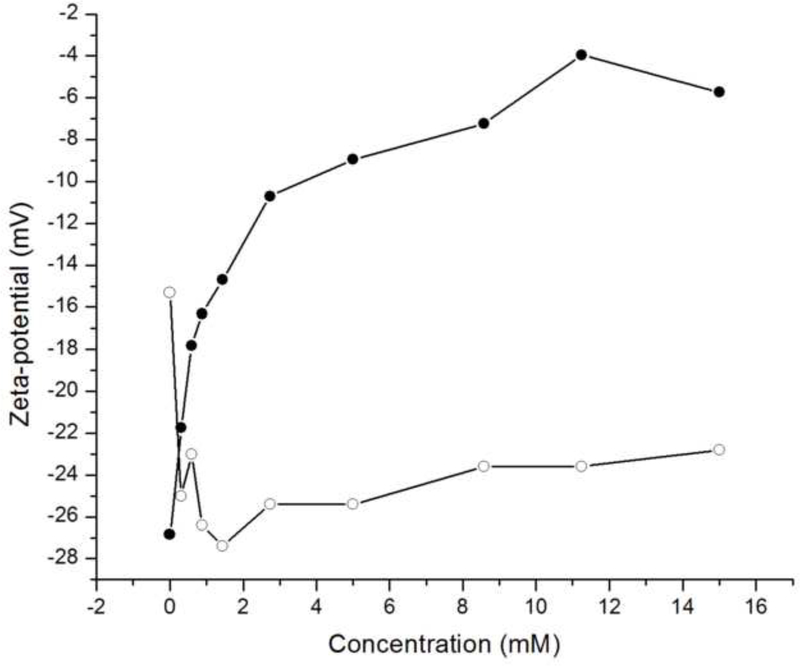
Phosphate ions are not bound to the rH174 nanospheres but are still present in the shear plane of the rH174 particles, as evidenced by a drop in ζ-potential of rH174 nanospheres caused by their titration with KH₂PO₄ shown in Fig.12a. Namely, as rH174 nanospheres are titrated with KH₂PO₄ at pH 7.4, ζ-potential of the nanospheres first drops from – 7 to – 13 mV after the addition of 1 mM of KH₂PO_4. After the shear plane of rH174 particles becomes partly saturated with respect to the PO₄^3- ions, the drop in ζ-potential becomes less intensive: from – 13 to – 19 mV in the concentration range of 1 – 15 mM of KH₂PO₄. On the other hand, the titration with CaCl₂ does not produce any significant change of the ζ-potential of rH174 nanospheres at pH 7.4 (Fig.12a). The reason may be that the complete saturation of rH174 molecules with Ca²⁺ would require only 0.12 mM Ca²⁺ at most, as previously discussed. Any additional titration of Ca²⁺ would in that case most probably not affect ζ-potential of rH174. The same electrophoretic titration analysis carried out on hydroxyapatite nanoparticles resulted in a specific adsorption of both Ca²⁺ and PO₄^3- ions onto rH174 nanospheres (Fig.12b). On one hand, the apatite structure is known both for its easy exchangeability of lattice components, mainly OH^- and Ca²⁺ ions, and a high mobility of the surface layer. The latter contributes to its relatively high electrical conductivity and facile remodeling in bone. On another hand, apatite is a sparsely soluble salt. These two arguments combined speak in favor of complex surface properties of apatite. Owing to an intensive exchange of ions between the solution and the particle surface, the titrated Ca²⁺ and PO₄^3- tend to enter either the Stern layer or the slipping plane of the hydrodynamic sphere surrounding the apatite particles, as could be evidenced from Fig.12b.

Fig.12.

ζ-potential of rH174 nanospheres (a) and hydroxyapatite nanoparticles (b) at pH 7.40 +− 0.02 vs. ionic concentration of calcium (-●-) and phosphate (-o-) species

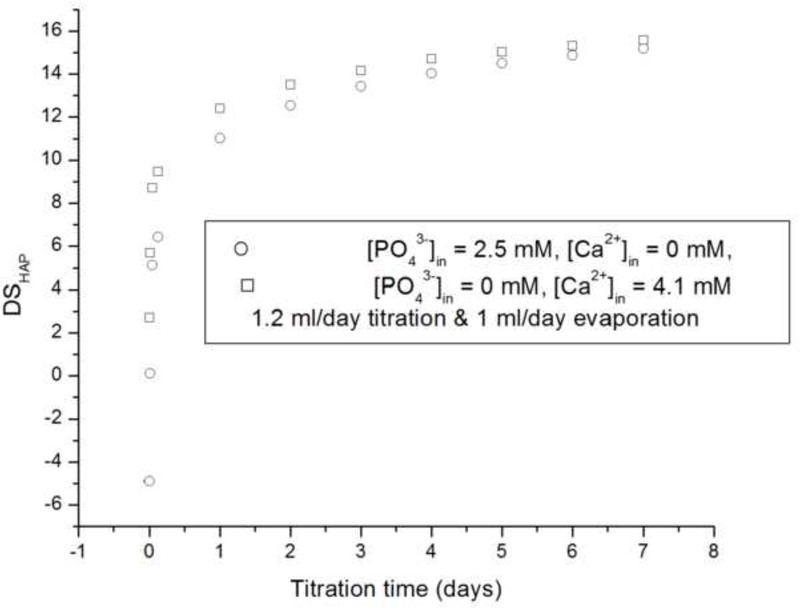
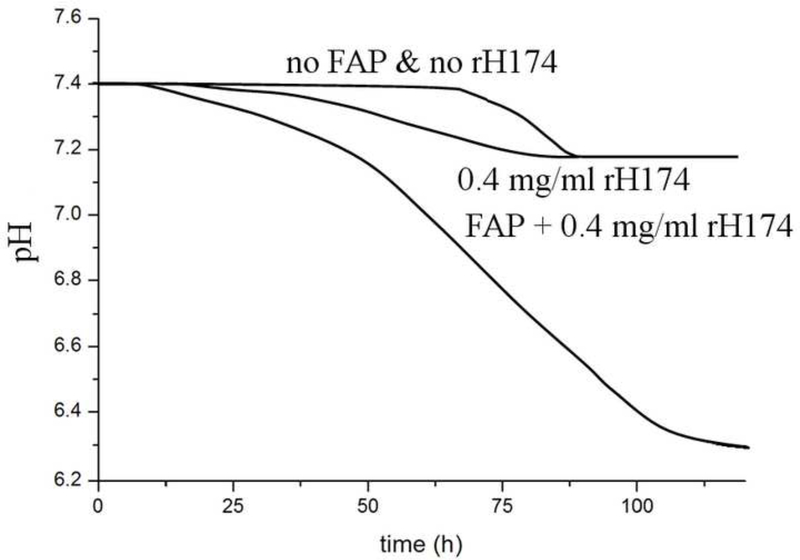
Starting with DS < 0 and then gradually increasing DS by titration (systems II and III) produces more favorable conditions for the crystal growth, thereby avoiding homogeneous nucleation in the solution occurring when starting with DS > 0 (system I). As DS gradually increases starting from an undersaturated state (Fig.13a-c), the conditions for heterogeneous nucleation on the substrate surface or the diffusional growth of FAP seeds are reached prior to those for homogenous nucleation in the solution. FAP substrates and rH174 in synergy create more favorable conditions for the precipitation of apatite than rH174 per se, which is demonstrated in Fig.13d. Although rH174 alone is able to decrease the nucleation lag time for crystallization of apatite from a metastable calcium phosphate solution (DS = 10.9), this effect is more pronounced when apatite seeds are introduced in the system too.

Fig.13.

The calculated values for calcium (□) and phosphate (o) concentrations (a,b) and DS (c) in the reaction suspension with the assumption of no precipitation for systems II (a, c) and III (b, c) versus the reaction time; pH vs time curves for the aging of metastable solutions of Ca²⁺ and H_xPO₄^x−3 (DS = 10.9 with respect to apatite) at 37 °C with and without the FAP substrates and 0.4 mg/ml rH174 (d).

Comparison between systems II and III furthermore yields conclusions about the nature of the amelogenin-guided formation of apatite. Namely, whereas starting with initially high levels of phosphates in the reaction system and no Ca²⁺ present at all (system III) results in extensive crystal formation at shorter reaction times compared to the system II wherein high levels of Ca²⁺ and no PO₄^3- comprise the reaction system initially. These results are in agreement with a previous AFM study in which the growth rate of brushite was shown to be inversely proportional to Ca/PO₄ ratio in the solution [25]. Further, Kokubo’s classical method of producing HAP precipitate on the surface of a bioglass immersed in simulated body fluid (SBF; [Ca²⁺] = 2.5 mM, [H_xPO₄^x−3] = 1.0 mM, pH 7.4) [26] has recently been modified by substituting SBF with an alkaline, pH 8.5 solution of Na₂HPO₄, thus demonstrating that the formation of apatite facilely takes place under extremely low [Ca²⁺], provided the concentration of phosphates remains comparatively high [27,28]. Whereas DS = 12.5, which approximately signifies the critical DS for homogeneous nucleation of calcium phosphate, is reached after 24 h for system II, it is reached after 48 h in case of system III, and yet the higher crystal growth was observed in case of the latter system (Fig.6b). Hence, it is not merely a higher DS that contributes to the higher rate of crystal growth. The fact that it is the high content of phosphates and a low content of Ca²⁺ that leads to a more efficient crystal growth suggests that the amelogenin-guided growth of apatite is mainly a Ca²⁺-controlled process. These data are also in agreement with the fact that the biological environment in which enamel crystals grow comprises 4 – 10 times higher concentration of phosphates (2 – 5 mM) than that of calcium (0.4 – 0.6 mM) [29].

In view of the results presented hereby where precipitation is more favored at high concentrations of phosphates and low Ca²⁺ contents than vice versa, as well as in view of the detected decrease in the ionic contents of the solution in contact with the rH174 sols when a more pronounced drop was observed for Ca²⁺ rather than for phosphates, the following model can be proposed: Ca²⁺ ions are tightly bound and precisely coordinated on the surface of amelogenin nanospheres, whereas phosphate ions bind less tightly to amelogenin surface and diffuse in the ionic layers adjacent to amelogenin particle surface. According to the ζ-potential analysis, they also tend to position themselves within the shear plane of the hydrodynamic radius of amelogenin particles, where they are free to diffuse and yet contribute to ζ-potential of the particles.

Amelogenin assemblies may act not as inhibitors of the growth of apatite, but as bridges or channels that selectively deliver Ca²⁺ and phosphate ions or amorphous units assembled on the surface of the protein from the solution onto the surface of the growing crystals. Previous research has shown that the adsorption of amelogenin onto the exposed crystalline faces of the seed crystals presents the first step for a controlled, substrate-specific growth to take place [30,31]. As shown in Fig.14, as the titration proceeds and S is gradually increased from zero to values that correspond to the supersaturated state, amelogenin layers adsorbed on the FAP substrate surface (Fig.14a) start to nucleate calcium phosphate within their droplet-shaped deposits (Fig.14b). A gradual increase in the calcium content from the mineral-free initial amelogenin deposits (Fig.14a) to the mineral-containing amelogenin layers that nucleate calcium phosphate crystals within (Fig.14b) was confirmed by means of EDX analysis (Fig.14). The subsequent growth of the underlying crystals has proceeded in less controlled fashion, yielding plate-shaped apatite particles (Fig.14c) that eventually uniformly cover the substrate surface (Fig.4d) rather than well-aligned nanofibers typical of apatite in enamel. It is possible that ameloblasts regulate the rate and the direction of the growth of individual apatite fibers within the enamel by controlling the density of amelogenin adsorbed onto the crystalline faces. Mineralization of dental enamel may thus be modulated by a dynamic adsorption/desorption of amelogenin onto the growing apatite surface. Most of the evidence in favor of the nucleation-promoting behavior of amelogenin has so far come from experiments utilizing comparatively low protein concentrations. On the other hand, enamel matrix is a gel ([rH174] > 300 mg/ml) rather than a sol, with water dispersed within the protein network instead of vice versa. In view of that, it is possible that the local concentration of amelogenin in contact with (hk0) faces of apatite is higher than in the layers adjacent to the faster growing (001) faces. These layers of lower density in contact with the (001) face are closest to the ameloblast surface and are thus most accessible to their control. The role of the adsorbed protein layers may be to assist in controllable delivery of precursor ions onto the crystalline surface. The presence of hydrophobic domains within amelogenin structure may be important in ensuring the proper delivery of the ionic growth units, as already known to exist in the case of ionic channels on cell membranes [32]. Although there has not been any confirmation of the ability of amelogenins to “channel” calcium and phosphate ions through its structure, the results presented here indicate that substrate-specific crystal growth occurs only insofar as amelogenin adsorbed onto the seeds mediates concentration of precursor ions, their nucleation and surface growth (Fig.14). Strictly speaking, with largely undetermined secondary structure of amelogenin, it can only be speculated about its 3D structure and the ion-channeling function. Thus, previously determined β-spirals formed by a series of β-turns in the secondary structure of folded amelogenin [33,34] may modulate electric potential along the canals in the interior of the protein chain and assist in channeling Ca²⁺ ions, which is a common structural effect among membranous channel proteins [35]. In addition to channeling ions, hydrophobic ionophores soluble in the lipid membrane layers may also be involved in the active transport of ions [36]. In that sense, the 100 – 150 kDa lipoprotein ATPase complex that releases the bound Ca²⁺ ions on one side while simultaneously releasing protons on the other may serve as a model for the possible role that amelogenin may play in the transport of ions onto the growing apatite faces. Namely, as in accordance with Eq. 3, an increase in acidity follows the formation of apatite, which implies that conditions for a simultaneous controlled delivery of ions to the mineralization front and dissipation of the released H⁺/H₃O⁺ ions to the surrounding amelogenin gel need to be ensured.

Fig.14.

Evolution of the FAP/glass substrate surface during the titration of amelogenin sols in system III, from the titration times of 24 h (a) to 48 h (b) to 72 h (c).

The proposed mechanism bears resemblance to the one describing the formation of silicon nanowires in the vapor-liquid-solid (VLS) process, during which nanodroplets of gold deposited on top of silicon wafers attract silicon atoms from the vapor, and after becoming supersaturated with respect to silicon begin to precipitate it, building well-aligned nanowires oriented perpendicular to the underlying surface [37,38]. Similarly to the conditions for growth of plate-shaped apatite particles from amelogenin deposits on FAP substrates in our experiments, the gradual increase in saturation levels allows for the highly substrate-specific and oriented growth of the elongated crystals (Fig.15). In addition, as our previous study has pointed out that pH 7.4 lies close to the boundary of the pH zone wherein amelogenin nanospheres aggregate forming microsized entities [39], ameloblasts may be able to vary the density of the protein matrix at the nano scale by varying local pH, particularly since pH of the enamel matrix exhibits modulations in the range of 6.2 – 7.6 [40]. Ameloblasts are able to adjust the pH of the enamel fluid, and their rhythmical change from smooth to ruffled ended cells is accompanied by a local pH change in the surrounding enamel fluid from nearly physiological (7.2 – 7.4) to slightly acidic (6.1 – 6.8) [41]. Furthermore, as ζ-potential of hydroxyapatite is negative in the entire pH range of its stability, whereas rH174 exhibits isoelectric point at 6.8 +− 0.2 [39], subtle pH changes can be applied to modify the intensity of the attraction between the protein and the mineral phase, which is the topic of our current studies. Thus, at pH < 6.8 +− 0.2, the protein and the mineral surfaces would be oppositely charged, whereas at pH > 6.8 +− 0.2, they would carry the same, negative charge. The underlying Tomes’ process may be furthermore crucial in aligning the apatite fibers along the same direction and preventing their random tilting in space. Insofar as the effect of cellular orchestration of growth in the enamel morphogenesis can be elucidated and demarcated from the growth guided by the protein self-assembly, the grounds for a prosperous biomimetics of morphogenesis of this remarkable tissue would be set forth.

Fig.15.

Hypothesized model for the protein-controlled crystal growth in amelogenesis based on the adsorbed amelogenin assemblies, such as nanospheres, channeling either calcium and phosphate ions from the solution or amorphous calcium phosphate entities formed through a precise coordination of Ca²⁺ bound to the protein and phosphate ions diffusing in the hydrodynamic layer of the protein particles onto the growing crystal surface. Adapted with permission from Ref. [37].

Conclusions

In this paper we have reported conditions under which recombinant human amelogenin, the main protein of the developing enamel matrix, acted as a promoter of a substrate-specific nucleation and crystal growth of apatite. The capacity of amelogenin to promote nucleation and crystal growth increased in direct proportion with its concentration. Biomimetic conditions under which crystallization proceeded as driven by the ability of amelogenin to concentrate and nucleate ionic growth units within its deposited layers, rather than by the thermodynamic propensities of the solution, were established. It was shown that the titration of rH174 sols has to proceed starting from sols with the initial supersaturation ratio with respect to apatite equal to zero in order for the conditions for a significant substrate-specific growth of apatite crystals to be reached. A mechanism for the amelogenin-guided crystal growth based on the observed nucleation of calcium phosphate within amelogenin layers deposited on the substrate surface was proposed. By offering arguments that support the thesis that amelogenin may act as a promoter of the growth of apatite crystals in enamel and that its adsorption onto the underlying crystals presents the starting point in their controlled growth, we have challenged the reigning hypothesis which states that the role of amelogenin assemblies is to block the approach of ions to the growing crystals.

*Research Highlights.

• In this paper we have reported conditions under which recombinant human amelogenin, the main protein of the developing enamel matrix, acted as a promoter of a substrate-specific nucleation and crystal growth of apatite.

• The capacity of amelogenin to promote nucleation and crystal growth increased in direct proportion with its concentration.

• A significant amount of apatite crystals formed on the substrates following the titration of amelogenin sols that comprised the starting supersaturation ratio equal to zero.

• The biomimetic experimental setting applied in this study proves as convenient for gaining insight into the fundamental nature of the process of amelogenesis.