Ecological significance of light quality in optimizing plant defence

Abstract

Plants balance the allocation of resources between growth and defence to optimize fitness in a competitive environment. Perception of neighbour‐detection cues, such as a low ratio of red to far‐red (R:FR) radiation, activates a suite of shade‐avoidance responses that include stem elongation and upward leaf movement, whilst simultaneously downregulating defence. This downregulation is hypothesized to benefit the plant either by mediating the growth‐defence balance in favour of growth in high plant densities or, alternatively, by mediating defence of individual leaves such that those most photosynthetically productive are best protected. To test these hypotheses, we used a 3D functional–structural plant model of Brassica nigra that mechanistically simulates the interactions between plant architecture, herbivory, and the light environment. Our results show that plant‐level defence expression is a strong determinant of plant fitness and that leaf‐level defence mediation by R:FR can provide a fitness benefit in high densities. However, optimal plant‐level defence expression does not decrease monotonically with plant density, indicating that R:FR mediation of defence alone is not enough to optimize defence between densities. Therefore, assessing the ecological significance of R:FR‐mediated defence is paramount to better understand the evolution of this physiological linkage and its implications for crop breeding.

Short abstract

Plants use ratios of red to far‐red (R:FR) light to predict future competition and to subsequently activate shade‐avoidance responses and downregulate defences. R:FR‐mediated defence is suggested to be advantageous to decrease plant defence with increasing plant competition and to adjust defence to the photosynthetic value of a leaf as signalled by R:FR. Using a 3D plant model, this study shows that adjusting leaf‐level defence can result in a fitness benefit to the plant, whereas R:FR ratios alone cannot account for the optimal relation between the level of plant defence and the degree of competition.

1. INTRODUCTION

Plants growing in high densities suffer more from pests and diseases compared with plants in low densities (Burdon & Chilvers, 1982). As many plants in nature and most of our food crops grow at high densities, exploring the causes and functionality of this phenomenon is of both scientific and societal interest. A number of explanations have been proposed for this phenomenon, such as the relation between plant density and light availability, microclimate, and dispersal ability of pathogens or pests (Ratnadass, Fernandes, Avelino, & Habib, 2012). Recently, evidence has accumulated that the same density‐dependent light cues play an important role in regulating defence levels as well as shade avoidance responses (Ballaré & Pierik, 2017). To avoid future shading by their neighbours, plants exhibit a suite of responses to bring leaves into a favourable position with respect to the light gradient. These responses are termed the shade‐avoidance syndrome (SAS) and include, but are not restricted to, stem elongation, an upward change of the leaf angle, and petiole elongation (Ballaré & Pierik, 2017; Fraser, Hayes, & Franklin, 2016).

An important light cue that is used by plants to detect future shading is the red to far‐red ratio (R:FR; Ballaré, Scopel, & Sanchez, 1990; Novoplansky, Cohen, & Sachs, 1990). Red light is readily absorbed by plant tissues whereas most far‐red radiation is reflected and transmitted. Hence, the R:FR ratio in a developing canopy decreases over time, and R:FR will be lower in dense canopies than in open canopies. In addition to inducing a shade avoidance response, a low R:FR ratio represses the activity of the jasmonate pathway—a phytohormonal pathway involved in plant defence against necrotrophic pathogens and chewing insects (Leone, Keller, Cerrudo, & Ballaré, 2014). In this way, shade‐avoidance responses and defence are intertwined at the level of signal transduction networks through a common light cue, R:FR, resulting in an increased susceptibility to pathogens and insects in competitive environments characterized by a low R:FR (de Wit et al., 2013; Leone et al., 2014; Moreno, Tao, Chory, & Ballare, 2009).

Two important hypotheses have been put forward why plants downregulate their defence when perceiving a low R:FR (de Vries, Evers, & Poelman, 2017). First, it is hypothesized that defence is suppressed by a low R:FR ratio to balance growth and defence, such that competitive strength through SAS is favoured over defence at high plant density (Ballaré & Pierik, 2017). This downregulation may be understood from the perspective of evolutionary game theory (EGT; Anten & Vermeulen, 2016; Maynard Smith, 1982). EGT predicts that in a competitive environment natural selection can drive expression of plant traits away from the population‐level optimum (hereafter called simple optimum) and towards a competitive optimum (Parker & Smith, 1990), which is termed a tragedy of the commons (TOC; Falster & Westoby, 2003; McNickle & Dybzinski, 2013). Competition for resources may lead to overexpression of plant traits related to resource acquisition at the expense of other traits, such as defence against herbivores, leading to trade‐offs between growth and defence‐related traits (Züst & Agrawal, 2017). Thus, one would expect the optimal level of defence in high plant densities to be lower than the optimal level of defence at lower plant densities, making the R:FR ratio a signal that can potentially regulate plant defence expression between plant densities.

Second, it is hypothesized that R:FR regulates defence expression to optimize the distribution of defences within the plant (Ballaré, 2014). The locally perceived R:FR ratio signals the future value of a leaf in terms of photosynthetic gain, warranting the regulation of leaf defence expression by R:FR (Ballaré, 2014; Izaguirre, Mazza, Astigueta, Ciarla, & Ballaré, 2013). Plants are known to vary the defence investment of a leaf as a function of the value of that leaf in terms of the current investment of limited resources and the future acquisition of those resources (Koricheva & Barton, 2012), as predicted by optimal defence theory (Cipollini, Walters, & Voelckel, 2014; McKey, 1974). Differences in leaf value arise from the light gradient in the canopy, with leaves in the bottom of the canopy generally being of lower value due to them intercepting less light and therefore having less potential for photosynthetic gain. Furthermore, leaf defence levels are often correlated to leaf age as plants move secondary metabolites away from older leaves and towards younger leaves that are generally situated in areas of high light intensity (Lambdon, Hassall, Boar, & Mithen, 2003; van Dam, Witte, Theuring, & Hartmann, 1995), although Zangerl (1986) did not find such a pattern.

The downregulation of defences by a low R:FR ratio can have negative consequences for crops if this response makes their defence levels fall below the simple optimum in high plant densities, in which crops are typically grown (Campos et al., 2016). This suboptimal defence expression at the population level can potentially be the result of a TOC driven by an internal resource trade‐off between defence and shade avoidance growth. To counteract this potential for suboptimal defence expression in crop plants, it has been suggested to decouple defence from neighbour proximity perception in crops so that their defence expression is not lowered in high planting densities (Ballaré & Pierik, 2017; Campos et al., 2016). This decoupling potentially increases crop performance by elevating plant defence expression towards the simple optimum, and can reduce pesticide use by elevating‐the plant's natural ability to defend itself. However, decoupling defence from R:FR signalling potentially impairs the ability of the plant to distribute defences within the canopy according to leaf value. Optimizing defence distribution in the canopy can increase plant performance by maximizing defence expression in the most valuable leaves although reducing costs by minimizing defence expression in less valuable leaves.

The aim of this study is to elucidate the role of R:FR in mediating defence expression across densities and within a canopy to optimize plant fitness in an evolutionary setting and how this translates to crop performance. Therefore, we aim to quantify (a) the optimum level of whole‐plant‐defence expression under intragenotypic competition (plants compete with neighbours adopting the same level of defence), (b) the optimum level of whole‐plant‐defence expression under intergenotypic competition (plants compete with neighbours adopting a different level of defence), (c) how defence mediation by locally perceived R:FR cues impacts plant fitness under intergenotypic competition (plants that mediate defence by R:FR compete with neighbours that keep defence levels constant across leaves), and (d) how decoupling R:FR regulation of defence affects plant fitness in mono‐stands (plants that mediate defence by R:FR compete against neighbours that adopt the same strategy).

The interaction between plant competition for light and its impact on the optimum level of defence expression under herbivore attack is studied using functional–structural plant (FSP) modelling (Evers, 2016; Evers, Letort, Renton, & Kang, 2018; Godin & Sinoquet, 2005; Vos et al., 2010). FSP models simulate the growth and development of individual plants in three dimensions using source‐sink dynamics (Evers et al., 2010; Evers & Bastiaans, 2016; Ma et al., 2018) and functional responses to light cues (Bongers, Pierik, Anten, & Evers, 2018, de Vries, Poelman, Anten, & Evers, 2018; Evers et al., 2007), as they compete for light. FSP modelling is the only approach that mechanistically simulates the feedback between plant architecture and light cues such as R:FR, that change plant architecture, which in turn modifies the R:FR cue, and so forth.

2. METHODS

To elucidate the effect of R:FR regulation of plant defence on plant fitness in a competitive environment, we used Brassica nigra as model species. B. nigra occurs in a wide range of plant densities (Lankau & Strauss, 2008); exhibits a strong morphological response to competition, resulting in distinctly different plant phenotypes (Ballaré & Pierik, 2017; Pantazopoulou et al., 2017); and is widely used as a model plant in the field of plant–herbivore interactions (Broekgaarden et al., 2011; Lankau & Strauss, 2008; van Dam & Raaijmakers, 2006). We expanded an FSP model of B. nigra growth and development (de Vries, Poelman, et al., 2018), which has been developed in the FSP‐modelling platform GroImp (Hemmerling, Kniemeyer, Lanwert, Kurth, & Buck‐Sorlin, 2008). The model mechanistically simulated on a daily‐basis plant growth and development through light‐driven source‐sink dynamics and functional responses of plant architecture to R:FR cues (for a detailed model description, see de Vries, Poelman, et al. (2018)). The architectural responses to changes in R:FR that determine stem elongation, branching, leaf size, and leaf angle were parameterized and tested using detailed field measurements on architecture, biomass, and seed production (de Vries, Poelman, et al., 2018). Plant performance and fitness were emergent properties of the model that arose from dynamic interactions between plants and the feedback between plant architecture and the light environment, as altered by plant growth and leaf herbivory. Total seed mass after one growing season (124 days) was taken as measure of its fitness, which was reasonable considering that we model an annual plant.

We expanded the existing model with a plant‐defence module that described defence expression at the leaf level as a function of local R:FR perception. The investment in plant defence interacted with plant growth through source‐sink dynamics and reduced herbivore damage, as explained in the sections below.

2.1. Plant defence

The model described plant defence as the biomass allocated towards a pool of secondary metabolites that may be distributed over the leaves of the plant (see Table 1 for parameter values). The model distinguished between two groups of plant strategies with either (a) a constant leaf‐defence expression or (b) a leaf‐defence expression regulated by local R:FR perception. For the first group, the potential leaf‐defence expression (D _pot,i, g defence [e.g.. secondary metabolites]) of leaf i was a function of the biomass of the leaf (L _i, g) and the maximum leaf defence expression that is realized if resources are not limiting (D _max, g defence g⁻¹ leaf).

$$D_{\mathit{pot},i}=D_{\mathit{max}}*L_{i,}$$ (1)

$$D_{\mathit{pot},i}=\frac{D_{\mathit{max}}*L_i}{1+e^{-10\left(R:F{R}_i-R:F{R}_0\right)}}.$$ (2)

Table 1.

Model parameters related for herbivory and plant defence

Description	Name	Value	Unit	Eq.
Maximum defence investment	Dmax	Variable (0–0.2)	g defence g−1 leaf	1, 2
R:FR where D pot = 0.5*D max	R:FR 0	Variable (0.45–0.85)	umol red umol−1 farred	2
Construction costs of defence	cc	15	g glucose g−1 biomass	3, 5
Maintenance respiration rate	rm	0.02	g glucose g−1 biomass	3, 5
Potential herbivore damage	h pot	0.005	dimensionless	7
Herbivore damage reduction coefficient	c	0.18	g defence g−1 leaf	7

Note. R:FR: red to far‐red.

For the second group, in which the potential leaf level defence expression (D _pot,i, g defence) was regulated by the perceived R:FR, we assumed the potential level of defence of that leaf (D_{pot, i}) to be related to the R:FR perceived at the leaf tip (Equation 2; Pantazopoulou et al., 2017). We made this assumption because data on the location of R:FR perception affecting defence are lacking, and in this way, a single cue is used to model SAS and defence. The functional form relating defence expression to R:FR is not known. For this reason, a sigmoidal relationship was chosen to ensure that D_{pot, i} does not reach levels below a minimum or above a maximum level of defence at low‐ and high‐R:FR ratios, respectively. Furthermore, we tested a range of parameter combinations of the logistic functions to simulate different defence responses to R:FR (see scenarios below). The potential level of defence was dependent on the maximum leaf defence expression at high R:FR ratios (D _max, g defence g⁻¹ leaf), the biomass of the leaf (L _i, g), the R:FR perception on the leaf tip (R:FR_i), and a parameter that describes the R:FR ratio where D _pot,i is 0.5*D _max—R:FR₀; Equation 1, Table 1 for parameter values. D _pot,i reflected the defence level that is realized if resources are not limiting. At every time step, the potential biomass a plant allocated to defence was calculated from the difference between current whole plant‐defence biomass and potential defence expression of all leaves on the plant. The energy requirement of maintaining and growing the pool of secondary metabolites available to the plant was called the sink strength (Sink _D, g glucose/d). Sink _D consisted of two components: a cost to construct new defensive compounds and a cost to maintain current defence, Equation 3. The construction costs included the machinery to synthesize, transport, reallocate, and store defensive compounds such as glucosinolates and were calculated by multiplying the requested defence investment with the construction costs of defence (cc, g glucose g⁻¹ defensive compound). The costs of maintenance were calculated from the current whole plant defence biomass (D, g) and a parameter for maintenance respiration (rm, g glucose g⁻¹ biomass). With D _pot,i representing the potential defence investment in an individual leaf i, and rm the maintenance costs of the current pool of secondary metabolites. Note that when the suppression of defence was mediated by R:FR (second group of strategies), it acted through D _pot,i and hence lowered the defence sink strength.

The allocation of assimilates to defence (C _{D, g}) is limited either by the growth potential of the pool of defensive compounds (Sink _D , g) or by the availability of photosynthates that can be allocated to defence $\left(\frac{S*\mathit{Sin}{k}_D}{{\sum }_{i=1}^n{\mathit{\text{Sink}}}_{,i}}\right)$. The latter is a function of the total available assimilates (S, g) and the combined sink strength of all sink organs in the plant (Sink _i, g). We assumed that, when assimilates were limiting, all plant organs received assimilates proportional to their demand (Equation 4) (Evers et al., 2010; Evers & Bastiaans, 2016).

$$C_D=\mathit{\text{min}}\left(\mathit{Sin}{k}_D,\frac{S*\mathit{Sin}{k}_D}{{\sum }_{i=1}^n{\mathit{\text{Sink}}}_{,i}}\right).$$ (4)

The pool of secondary metabolites available for distribution in the next time step (D _t + 1, g) was calculated from the pool of secondary metabolites of the current time step (D, g), adding the assimilates allocated to defence whilst subtracting maintenance and construction costs, Equation 5.

$$D_{t+1}=D+\frac{C_D-\mathit{rm}D}{\mathit{cc}}.$$ (5)

The pool of secondary metabolites was then distributed over the leaves, with the defence allocated to a leaf (D _i, g) being proportionate to their contribution to the total potential plant defence expression—ΣD _pot,i, g; Equation 6.

$$D_i=\frac{D_{\mathit{pot},i}{D}_{t+1}}{{\sum }_{i=1}^n{D}_{\mathit{pot},i}}.$$ (6)

2.2. Herbivore damage

Herbivore damage was simulated by assuming that potential leaf damage was proportional to the biomass of the leaf, irrespective of its position in the canopy. This baseline assumption was made to ensure that there was no a priori advantage of distributing leaf defence to leaves of a given age, size, or position in the canopy. The actual leaf damage depended on the defence level of that leaf and the feeding rate of the insect herbivore. We assumed that feeding rate increased linearly with thermal time to match plant growth and development—tt GDD (growing degree days; Bale et al., 2002).

$$h_i=h_{\mathit{pot}}\left(1-\frac{\frac{D_{L,i}}{L_i}}{\frac{D_{L,i}}{L_i}+c}\right)\mathit{tt}.$$ (7)

With herbivore damage on the leaf level (h _i, dimensionless) being a function of the potential feeding rate per unit of growing degree days (h _pot, GDD⁻¹), the thermal time of the current time step (tt, GDD), the defence present in the leaf (D _i, g) relative to the biomass of the leaf (L _i, g), and a parameter c (g defence g⁻¹ leaf) that described the leaf defence level at which herbivore damage was reduced by half.

The proportion leaf area removed scaled linearly with a proportional decrease in leaf biomass—L _i; Equation 8—as we assumed that specific leaf area was constant over time and over leaf ranks and that defensive compounds were homogeneously distributed within a leaf.

$$\frac{d{L}_i}{\mathit{dt}}=-L_i{h}_i.$$ (8)

3. SIMULATIONS

To test whether regulation of defence by R:FR is beneficial to plant fitness, we compared the performance of plants that had a constant defence distribution over their leaves (Group 1) with plants that regulated the leaf defence expression by local R:FR perception (Group 2). We tested a variety of plant defence strategies that differed in the maximum level of defence expression (Dmax in Equation 1 and 2. Ranging from 0, entailing no defence expression, to 0.2 and the distribution of defence over their leaves, which is either constant (Group 1) or regulated by R:FR—Group 2; R:FR₀ in Equation 2, ranging from 0.45 to 0.85. The model simulated plots of four by four plants, where plants competed either with neighbours adopting the same strategy (mono‐stands and intragenotypic competition) or neighbours adopting a different strategy with the two plant strategies arranged in a checkerboard pattern (mixed stands and intergenotypic competition). This plot was cloned 625 times to simulate a large field of 10.000 plants for light model calculations. Every time step, the model calculated the light interception of an individual plant by averaging the light interception of its 625 clones. This approach was used to eliminate border effects in light conditions and their effect on plant growth. The simulations spanned a growing season of 124 days (31 March to 2 August), with average daily temperature, average daily insolation, and solar angle typical for the Netherlands at a latitude of 52°.

4. SCENARIOS

We simulated four subsequent scenarios to elucidate the effect of defence regulation by R:FR in the context of natural selection and crop performance in a range of plant densities (100, 44, and 25 plants/m²; see Figure 1 for an overview).

1. First, we determined the optimal level of defence for plants with a constant defence distribution over their leaves (Group 1), growing in one of three plant densities (25, 44, and 100 plants/m²) and competing with plants with the same level of defence. By varying the level of defence expression from 0.0–0.2 g/g leaf—D _max, Equation 1—in all plants simultaneously, the level of defence that led to the highest seed production was assumed to be the population‐level optimum for that density (the simple optimum).

2. Second, we determined the optimal level of defence of plants with a constant distribution of defence over their leaves (Group 1) growing in mixed stands in one of three plant densities (25, 44, and 100 plants/m²). We simulated seven strategies, each with an incremental increase in potential leaf defence expression (0–0.12 g/g leaf, with increments of 0.02) and simulated each strategy competing with a less defended strategy and with a better defended strategy (e.g., 0 vs. 0.02, 0.02 vs. 0.04, 0.04 vs. 0.06, and etc.). The strategy that outcompeted both the less defended and the better defended competitor was assumed to express the optimal level of defence under intergenotypic competition at the given plant density (the competitive optimum).

3. Third, we tested the possible fitness benefit of regulating defence by R:FR for plants growing in mixed stands in one of three plant densities (25, 44, and 100 plants/m²). In each stand, plants were arranged in a checkerboard pattern where plants that regulated defence by R:FR (Group 2) were competing with plants with a constant leaf defence expression (Group 1) that matched the competitive optimum obtained from Scenario 2. We tested 20 strategies of R:FR regulating plants that differed in their maximum leaf defence expression—D _max, Equation 2, 0.4–1.2 in steps of 0.2—and their sensitivity to the R:FR signal, R:FR ₀, Equation 2, 0.45–0.85 in steps of 0.1. By varying both parameters, we explored the benefit of R:FR regulation as a way to distribute defence according to expected leaf value and how this distribution of defence impacts the optimal level of whole‐plant defence expression.

4. Fourth, to test the consequences of decoupling defence from the R:FR cue when plants are grown in monoculture, we selected the strategies of R:FR‐regulating plants that outcompeted the plants expressing the competitive optimum with a constant leaf defence expression. These plant strategies were grown in mono‐stands and compared with the mono‐stand performance of the competitive optimum established in Scenario 2 to assess the effect of R:FR mediation of leaf level defence on crop performance.

Figure 1.

Schematic outline of the four model scenarios. In the first scenario (top left), we seek for the simple optimal level of defence of plants that homogeneously defend their leaves. In the second step, we test the competitive optimum level of defence, by competition between individuals that homogeneously distribute defence over the leaves that vary slightly in their level of defence. Competing strategies (represented by the different colours) are positioned in a checkerboard design. The competitive optimum is selected to compete with plants that regulate defence by red to far‐red (R:FR; Scenario 3). Plants that regulate defence by R:FR and perform better compared with plants that homogeneously defend their leaves are grown in mono‐stands to test if the benefit of (Cipollini, 2004) regulating defence still pays off when growing in competition with plants that have the same strategy (Scenario 4). Each scenario is repeated in three densities to explore whether a plant that regulates defence by R:FR can approach the competitive optimum in each density through a single response curve. See main text for definitions of simple and competitive optimum [Colour figure can be viewed at wileyonlinelibrary.com]

To account for model stochasticity (caused by random variation in seed orientation, potential leaf and stem length, and the maximum number of phytomers), we ran 20 simulation for scenario's 1, 2, and 4 and 40 replications for scenario 3.

5. RESULTS

5.1. Plant density

Plant morphology changed with an increase in plant density, which reduced the number of branches and leaf size, and increased leaf angle (Figure 2). In addition, the R:FR ratio perceived by the plants differed across densities, both temporally and spatially (de Vries, Poelman, et al., 2018). The initial drop in R:FR was stronger and came earlier with an increase in plant density, initiating the morphological changes associated to the increase in plant density (Figure S1).

Figure 2.

Visual representation of the Brassica nigra phenotype in three plant densities, showing the architectural changes related to branching dynamics, leaf size, and leaf angle in response to plant density [Colour figure can be viewed at wileyonlinelibrary.com]

5.2. Scenario 1

In the first scenario, the optimal‐defence level of plants that distribute defence homogeneously over their leaves was determined (simple optimum; Figure 3). At all densities, an optimum‐defence level was found that yielded highest seed production, represented by the peaks in the lines presented in Figure 3. The optimal level of defence was highest at 44 plants/m² at 0.12 g defence per gram leaf. At the low density of 25 plants/m² and the high density of 100 plants/m², the optimum defence levels were lower: 0.08 and 0.04 g defence per gram leaf, respectively.

Figure 3.

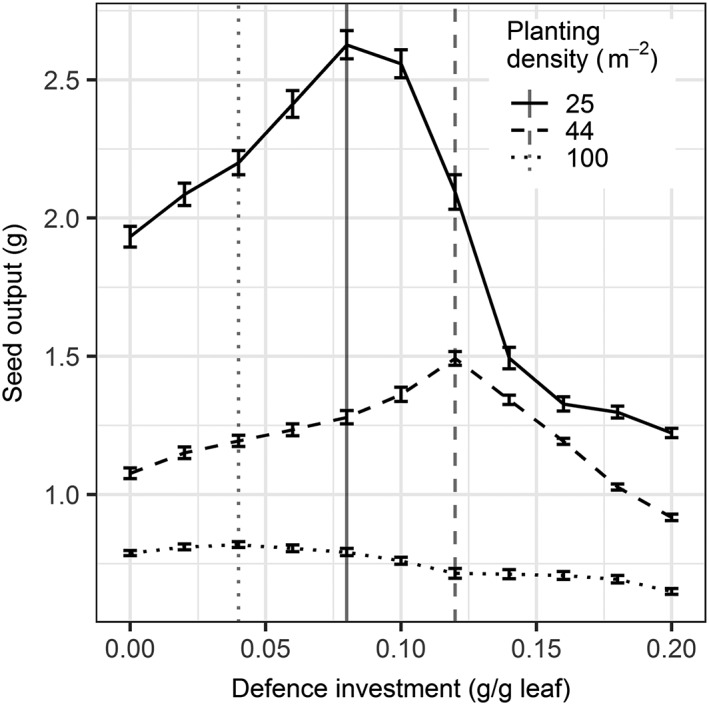
The relationship between investment in defence (g defence/g plant biomass) and seed production (grams) of plants that distribute defence homogeneously over leaves for three different densities (line type) and a given level of herbivory. The vertical lines denote the optimum levels of defence for each density. Error bars represent standard error of the mean seed output (n = 20)

5.3. Scenario 2

In the second scenario, the competitive optimum level of defence expression was determined by simulating mixtures of two plant strategies, one better defended than the other, with incremental increases in plant defence investment in both strategies. At lower defence investments, the better defended plants reached a higher fitness than the less defended plants, whereas at higher defence investments, the less defended plants reached a higher fitness than the better defended plants. (Figure 4). The transition point, defined as the competitive optimum, was found to depend on plant density and was estimated at 0.04 for a density of 25 and 100 plants/m² and 0.06 for plants in a density of 44 plants/m². Thus, the competitive optimum level of defence was lower than the simple optimum in two lower densities, whereas for the highest density the competitive optimum level of defence was equal to the simple‐defence optimum (Table 2).

Figure 4.

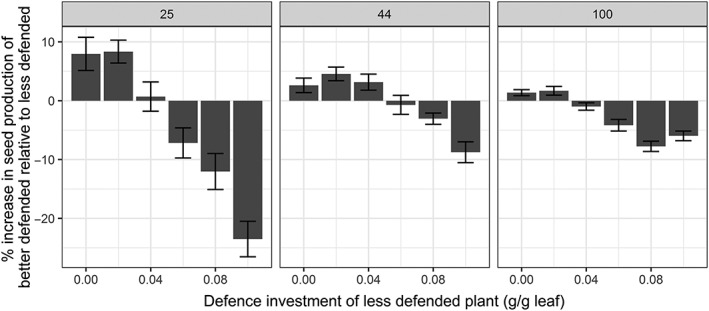
The relative change (%) in seed production for plants that invest 0.02 g/g more in defence compared with the defence investment (g/g) of the lesser defended competitors in three plant densities (25, 44, and 100 plants/m²). At low level of defence, it pays off to be better defended (increase in fitness). Increasing defence investment above an intermediate level of defence investment does not pay off anymore. This defence level is defined as the competitive optimum. Error bars represent standard error of the mean seed output (n = 20)

Table 2.

Optimal level of defence at various plant densities and the respective seed output

Plant density (plants/m2)	Simple optimum defence (g/g)	Competitive optimum defence (g/g)	Seed output (simple optimum)	Seed output (competitive optimum)
25	0.08	0.04	2.63	2.23
44	0.12	0.06	1.49	1.28
100	0.04	0.04	1.19	1.19

5.4. Scenario 3

In plants that regulate their defence expression by R:FR, the potential defence investment at the leaf level was constrained by local R:FR perception of the leaf as described by Equation 2, whereas the actual defence investment was also dependent on the availability of substrates (see Figure 5). Moreover, leaf‐defence levels decreased with leaf rank, except for the youngest five leaves that are still clustered in buds and, therefore, perceive a lower R:FR than expected based on rank (Figure S2).

Figure 5.

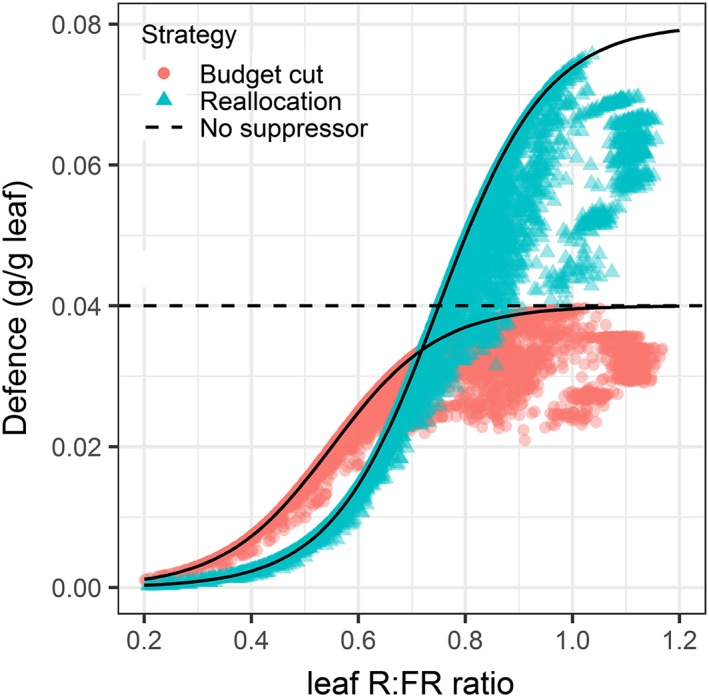
The relationship between red to far‐red (R:FR) ratio perceived by the leaf and the defence level (g/g leaf) the next day of two representative (out of 20 simulated) strategies that regulate defence by R:FR, one strategy that reduces the overall investment in defence through suppressing defence in leaves with low R:FR (budget cut; red dots; D _max 0.04, R:FR₀ 0.55) and a strategy that has the same overall investment in defence as the strategy that does not regulate defence upon R:FR but allocates defence according to the leaf R:FR (reallocation; blue triangles; D_max 0.08, R:FR₀ 0.75). The black lines represent the potential level of defence in the leaf (D _pot) and the coloured dots the realized level of defence in a leaf (D _i). The dotted line represents the level of defence in a plant that distributes defence homogeneously over the leaves. See Equation 2 for details [Colour figure can be viewed at wileyonlinelibrary.com]

Regulating defence by R:FR was found to be slightly beneficial compared with plants that distribute defence homogeneously over the leaves but only for specific shapes of the R:FR response curve (Equation 2; Figure 6; Figure S3). Supressing defence in leaves perceiving a low R:FR ratio without raising the maximum level of defence did slightly pay off at the highest density (D _max = 0.04, R:FR₀ = 0.45 in Figure S3) but not at the lower densities. In contrast, the R:FR regulating strategies that outperformed the homogeneously defending plant increased defence investment in leaves perceiving a high R:FR ratio and decreased defence investment in leaves perceiving a low R:FR ratio. For example, at a density of 100 plants/m² _, leaves perceiving a high R:FR ratio (1.2) were defended a factor 1.5–2 higher, whereas leaves perceiving a low R:FR ratio (0.4) were defended 8–17 times less compared with a homogeneously defended plant.

Figure 6.

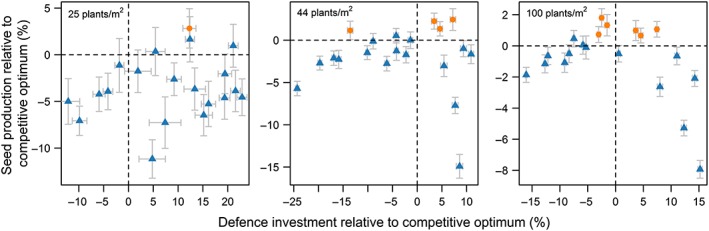
Relationship between the mean relative change in investment in defence (%) and associated change in seed production (%) of a strategy that regulated defence by R:FR relative to a strategy that distributes defence homogeneously over the canopy. The points represent different combinations of D _max (defence investment in leaves with high R:FR) and R:FR₀ representing the R:FR ratio where D _max is 0.5*D _max. The orange dots represent strategies that have a fitness benefit and the blue triangles strategies that perform equal or worse than a strategy that distributes defence homogeneously over the canopy. Error bars represent standard error of the means and are based on 40 replications [Colour figure can be viewed at wileyonlinelibrary.com]

The benefit of regulating defence in response to R:FR was different for the three densities. At the lowest density, only one strategy (D _max 0.06 and R:FR₀ 0.55 in Figure S3) was found to outperform the homogeneous defender, whereas at the two higher densities, various R:FR response curves were found to perform better than the homogeneous defender. In those densities, the best performing R:FR‐regulating strategies expressed a whole‐plant‐defence level that was close to that of the competitive optimum level of defence expression (Figure 6; Figure S4).

5.5. Scenario 4

The strategy with a D_max of 0.06 and an R:FR₀ ratio of 0.55 approximated the fitness of the best performing homogeneous defender in each of the three densities most closely, with an average 0.34% fitness difference. Furthermore, seed production of the two best performing strategies that regulate defence by R:FR when competing against similar individuals was not substantially higher compared with the optimal strategies that do not regulate defence by R:FR (Table 3). This shows that although R:FR‐regulated defence gives an advantage when competing with plants that distribute defence homogenously over the plant (Figure 6), this benefit disappears when competing against plants that adopt the same R:FR‐regulating strategy.

Table 3.

Seed production (grams ± se) of the best performing strategies for three different plant densities. For these densities, the performance of the best homogeneous defender, the overall best R:FR regulating strategy across all densities, and the best R:FR regulating strategy in a given density are shown

	Seed production (grams ± se)
Plant strategy	25 plants m−2	44 plants m−2	100 plants m−2
Competitive optimum (homogeneous defender)	2.20 ± 0.04	1.23 ± 0.02	0.81 ± 0.01
Overall best R:FR regulator across all densities	2.24 ± 0.03	1.18 ± 0.02	0.81 ± 0.02
Best R:FR regulator in a given density	2.24 ± 0.03	1.28 ± 0.02	0.82 ± 0.01

Note. R:FR: red to far‐red.

6. DISCUSSION

The aim of this study was to investigate the fitness benefits of regulating defence by R:FR as a mechanism to optimize either (a) whole‐plant‐defence expression over a range of densities or (b) the distribution of defence over the leaves such that those with the highest potential for future photosynthetic gain are better protected. The model simulations showed that plant‐level defence investment is a strong determinant of plant fitness and that the optimum defence level varies between densities. However, the optimal plant defence investment did not monotonically decrease with planting density but was highest at intermediate densities. This suggests that R:FR mediation of plant defence alone is not sufficient to optimize plant level defence expression between densities as the relation between R:FR and plant density does not coincide with the relation between optimal plant‐level‐defence expression and plant density. Our results further show that adjusting leaf‐level defence according to the value predicted by its perceived R:FR ratio can provide a fitness benefit that is more pronounced at higher plant densities.

6.1. The benefit of regulating defence by R:FR across densities

The model analysis showed that the simple and competitive optimum‐defence‐levels increased with plant density but decreased again when plant density further increased (Scenarios 1 and 2). This nonlinear relation between optimal defence expression and plant density is the result of the interplay between the costs and benefits of defence, which are in turn affected by the strength of competition, the light environment, and density‐determined plant phenotype (Figure 2). One might expect the highest level of defence at intermediate densities if the costs of defence increase faster with plant density than the benefits of defence. At low density, plants are able to tolerate herbivore damage because of a low ratio of self to nonself shading, that is, removal of leaf area will likely lead to an increased light capture of the underlying leaves of the same plant (Trumble, Kolodny‐Hirsch, & Ting, 1993) and may induce new branches, enabling greater potential for passive compensatory growth (Anten, Martínez‐Ramos, & Ackerly, 2003). Thus, at low densities, the optimal strategy may be to tolerate herbivory and minimize investment in defence (McNickle & Evans, 2018; Strauss & Agrawal, 1999). Conversely, at high densities, the ratio of self to non‐self shading is much lower due to the exponential increase in nonself shading with an increase in plant density and a decrease in plant size due to competition for limited resources. As a consequence, leaf area loss due to herbivory very likely increases the light interception of neighbouring plants rather than of the other leaves of the same plant. Hence, the benefits of defence will increase with plant density as the plant's ability to tolerate herbivory decreases with plant density. The relative direct costs of defence also increase with density, as the photosynthetic gain per unit leaf area decreases with density. Furthermore, any investment in defence comes at the expense of an investment in leaf area or stem growth and reduces future light capture (Douma, Vermeulen, Poelman, Dicke, & Anten, 2017). Thus, at low densities, plant defence may not pay off because of a larger passive ability for regrowth due to increased branching and a large degree of self‐shading, whereas at very high densities defence may not pay off because investment in resource acquisition is more important. Hence, one would expect the highest levels of defence at intermediate densities, which is confirmed by the model simulations.

Our model results only partly agree with the hypothesis that plants regulate defence by R:FR to optimally grow and defend at different plant densities (Ballaré & Pierik, 2017), as optimal‐defence expression did not decrease monotonically with plant density. Thus, no single strategy that regulated defence by R:FR realized a fitness equal to or higher than the competitive optimum at each of the three densities (Figure 6). However, in natural settings, the selective pressure on the sensitivity of defence to R:FR depends on the range and frequency in which possible densities are encountered by the plant and the selective pressure exerted by these densities. B. nigra naturally grows in disturbed soils where initially it may grow solitary, whereas its seedlings occur at high densities (>50 per m²) and mostly encounter intraspecific and intergenotypic competition (Lankau & Strauss, 2008). However, individuals occurring at later successional stages mostly encounter interspecific competition as other plant species have entered the plant community. The selection pressure exerted at high plant densities is not only dependent on the competitive pressure resulting from the high density but also on the plant species present in the community and how these interact with other species in the community.

6.2. The benefit of regulating defence within a canopy by R:FR

Plants that mediated leaf‐level defence through locally perceived R:FR cues distributed defensive compounds such that leaves perceiving a high R:FR ratio are relatively better defended and leaves perceiving a low R:FR are relatively less defended compared with plants with a homogeneous defence distribution. This reallocation of defence within the canopy resulted in a small (a few percent) but distinct fitness benefit that was more pronounced at higher plant densities. However, almost all strategies (14–19 out of the modelled 20) with R:FR mediation of leaf‐level defence yielded a lower fitness compared with plants that homogeneously defended the plant, most likely because it led to a suboptimal change in whole plant defence expression (Figure 6). Particularly at the two highest densities, the strategies that yielded a fitness benefit expressed a whole‐plant defence level that was close to the competitive defence optimum. This suggests that the selection on whole‐plant defence expression is an important constraint on the optimal distribution of defence within the canopy. Furthermore, the fitness benefit of distributing defence by local R:FR perception arose only in the case of intergenotypic competition, whereas under intragenotypic competition, plants hardly benefitted from distributing leaf level defence in response to R:FR (Scenario 4).

The optimal relation of leaf‐level defence to R:FR was different for each density (Figure 6). First, the information relayed by a gradient in the light climate changes with plant density as the ratio of self to nonself shading decreases with an increase in plant density. Thus, a given R:FR ratio implies more neighbour shading at high density compared with the same R:FR ratio at a low density and to gain a competitive advantage at high density plants require a stronger response to R:FR. In reality, plants often use multiple cues, including volatiles, touching, and other light cues, to detect neighbour presence (Pierik, Mommer, & Voesenek, 2013) and have a localized perception for these neighbour detection cues (de Wit et al., 2012; Pantazopoulou et al., 2017), which may allow them to better differentiate between self and nonself shading. Secondly, as the leaf area index increases with density, the gradient in R:FR is steeper in high densities compared with low densities (Figure S3). This results in a stronger gradient in leaf value and, therefore, stronger selection on a gradient in leaf‐defence expression. Finally, the variation in fitness benefit of R:FR mediation of defence increased with a decrease in plant density, resulting from a more heterogeneous light environment at the lowest density (as indicated by larger variation in leaf‐level photosynthesis; Figure S1). This may cause processes such as branching into local canopy gaps to have a relatively big effect on plant fitness compared with the effects of R:FR mediation of defence.

Plants are known to express a higher level of defence in younger leaves (Koricheva & Barton, 2012), following gradients in the allocation and acquisition of limited resources conform to optimal defence theory. The model developed in this study did not assume a relationship between leaf age and defence expression, but the simulated relation between defence expression and local R:FR perception did predict a qualitatively similar decrease in defence expression over the life span of a leaf as experimental and modelling studies that relate defence to leaf age (Ohnmeiss & Baldwin, 2000; Van Dam, De Jong, Iwasa, & Kubo, 1996), but see (Barto & Cipollini, 2005; Figure S2). In dicots such as B. nigra, a low R:FR ratio is expected to coincide with leaf age as the youngest leaves tend to be produced from apical meristems at the top of the canopy where R:FR ratio is high, as opposed to the situation for many grasses. To date, the effect of leaf age and plant development on leaf sensitivity to R:FR is unknown, but is needed to assess the significance of R:FR in regulating defence within the plant. Research on passion flower (Passiflora edulis) in which different branches were exposed to different light quality cues suggests that defence regulation by R:FR is a local response that can exist alongside a leaf age regulation of defence expression (Izaguirre et al., 2013). However, in erect herbaceous species such as B. nigra, leaf age and leaf R:FR are correlated. Therefore, it remains to be tested to what extent R:FR can regulate local defence expression independent of leaf age. The degree to which R:FR can mediate defence independent of leaf age will affect the degree to which R:FR mediation is beneficial.

The above example illustrates that to fully appreciate the possible benefit of downregulating defence in response to a low R:FR ratio, the effect of plant ontogeny and physiology on sensitivity to R:FR needs to be taken into account. As the R:FR ratio drops quickly early in the development of canopies and given the asymmetry of competition for light, investing in shade avoidance in that stage is probably more important than to invest in defence—particularly if attack is uncertain. Moreover, as the largest increase in plant defence is observed in the seedling stage (Barton & Koricheva, 2010), R:FR‐dependent regulation of defence may be particularly useful early on in plant development to optimally adapt to the growing conditions. Furthermore, as leaf area accumulates during the growing season, leading to a lower R:FR ratio, regulation of defence by R:FR will lead to reduced defence levels over the growing season which may be beneficial as the return on investment of leaves developed later in the season is lower (Douma et al., 2017).

6.3. Consequences of decoupling R:FR and defence for crop growth

It has been suggested that decoupling defence from R:FR in crops could avoid a level of defence expression that is suboptimal for the field‐level performance of the crop (Ballaré & Pierik, 2017; Campos et al., 2016). Decoupling defence from R:FR perception may be a relatively easy way to increase whole‐plant defence levels because the JAZ genes responsible for this coupling have been identified in Arabidopsis. However, the benefit of such decoupling depends on the density at which the crop is planted and the difference between the simple and competitive optima in defence expression at that density. The model indicated that plant fitness of the competitive optimum was lower compared with that of the simple optimum, pointing to a tragedy of the commons (Augner, Fagerstrom, & Tuomi, 1991). Furthermore, the difference between simple and competitive optima was dependent on plant density. An increase in plant density initially increased the difference between simple and competitive optima but brought the two closer together at high plant density. This suggests that the benefit of decoupling defence and R:FR in crop plants depends on the density in which the crop is planted. Furthermore, our results suggest that the changes in defence distribution within the canopy as a result of decoupling defence from R:FR hardly affects field level performance, contrary to our initial hypothesis (Scenario 4). Yet, whether the decoupling indeed leads to a notable increase in plant defence in (field) crops depends on the importance of other processes governing leaf defence, such as plant development (Barton & Koricheva, 2010), other light cues such as UV‐B (Qi et al., 2018) and plant volatiles (Cortes, Weldegergis, Boccalandro, Dicke, & Ballare, 2016; Karban, Yang, & Edwards, 2013; Kegge & Pierik, 2010).

6.4. Interactions between plant‐defence expression and the herbivore community

The model assumes that herbivore damage done to a plant is solely determined by temperature and leaf biomass and is, therefore, assumed to be independent of the interactions between the plant and herbivore communities. Plant‐mediated changes in the composition and distribution of the herbivore community can be strong determinants of plant fitness and can, therefore, exert selection pressure on plant‐defence expression for three reasons (de Vries et al., 2017; Poelman & Kessler, 2016; Stam et al., 2014). First, the advantage of a defence gradient is expected to become even stronger when insect herbivores prefer to feed on young leaves near the tip of the branches. Second, the gradient in leaf defence expression within a canopy as established by R:FR can benefit the plant by dispersing herbivore damage away from young leaves (Cipollini et al., 2014), which is shown to benefit plants in competition with conspecifics, but only under high herbivore pressure (de Vries, Evers, Dicke, & Poelman, 2018; de Vries, Poelman, et al., 2018). If this effect would have been included in this study, it would have resulted in a bigger advantage of R:FR‐mediated defence. Third, whole‐plant defence expression is known to impact host‐selection preference of insect herbivores, attracting specialist herbivores and repelling generalist herbivores (Badenes‐Perez, Gershenzon, & Heckel, 2014). How those selective forces interact with R:FR mediated defence in a canopy remains to be seen. Finally, the identity and abundance of insect herbivore species may change with planting density, which may lead to changes in the optimal level of defence and the defence response to R:FR predicted by our model (Joshi et al., 2008; Otway, Hector, & lawton, 2005; Rhainds & English‐Loeb, 2003). If plants in high densities experience relatively lower herbivory per unit biomass compared with lower plant densities, the optimal level of defence may increase. Thus, the ecological significance of the role of the R:FR ratio in mediation of plant defence needs to be assessed in the light of the temporal and spatial dynamics and the composition of insect herbivore communities (de Vries et al., 2017).

Supporting information

Figure S1. The relative increase in seed production (%) for plants that regulate leaf‐level defence by R:FR when competing against plants that distribute defence homogeneously over the canopy (blue: increase in fitness, red decrease in fitness) (scenario 3). Left panel: strategies that compromise total defence investment by suppressing defence in leaves with low R:FR (budget cut). The budget cut increases with increasing midpoint (R:FR0) values. Right panels: strategies that reallocate defence by R:FR with varying Dmax (columns). The rows represent three planting densities (100, 44 and 25 9 plants/m2). Error bars represent standard error of the mean seed output (n = 40).

Figure S2. The total amount of invested in defence for the homogenously defending strategy (black) and the by R:FR defence suppressing strategy (red and blue). Red color indicates that the strategy has a lower fitness compared to the homogeneous defender, while blue indicates a strategy with an average higher fitness compared to the homogeneous defender (see figure S1). The midpoints (x‐axis) and the maximum (columns) of the defence‐suppression curves are varied, in two densities (rows; plants/m2).

Figure S3. Relationship between thermal time and the range in R:FR ratio (upper 95% and lower 5% quantile) perceived by leafs in three different planting densities (upper panel), and the standard deviation in Amax.

Figure S4. The relationship between leaf rank and the investment in defence (g/g leaf) for a plant density of 0.1 plants/m2 and different Dmax (columns) and different midpoints (R:FR0; colours) of plants about halfway the growing season. The blue shaded area indicates the combination of Dmax and R:FR0 that results in a higher fitness compared to a plant that does not suppress its defence in response to R:FR.

Douma C, de Vries J, Poelman H, Dicke M, Anten PR, Evers B. Ecological significance of light quality in optimizing plant defence. Plant Cell Environ. 2019;42:1065–1077. 10.1111/pce.13524