Computational Approaches to Design and Test Plant Synthetic Metabolic Pathways^,

Computational approaches to design and in silico test synthetic metabolic pathways can revolutionize plant synthetic biology applications in crop improvement.

Abstract

Successfully designed and implemented plant-specific synthetic metabolic pathways hold promise to increase crop yield and nutritional value. Advances in synthetic biology have already demonstrated the capacity to design artificial biological pathways whose behavior can be predicted and controlled in microbial systems. However, the transfer of these advances to model plants and crops faces the lack of characterization of plant cellular pathways and increased complexity due to compartmentalization and multicellularity. Modern computational developments provide the means to test the feasibility of plant synthetic metabolic pathways despite gaps in the accumulated knowledge of plant metabolism. Here, we provide a succinct systematic review of optimization-based and retrobiosynthesis approaches that can be used to design and in silico test synthetic metabolic pathways in large-scale plant context-specific metabolic models. In addition, by surveying the existing case studies, we highlight the challenges that these approaches face when applied to plants. Emphasis is placed on understanding the effect that metabolic designs can have on native metabolism, particularly with respect to metabolite concentrations and thermodynamics of biochemical reactions. In addition, we discuss the computational developments that may help to transform the identified challenges into opportunities for plant synthetic biology.

The Food and Agricultural Organization of the United Nations projects that food production will need to increase by 70% if the global population reaches 9.1 billion by 2050 (FAO, 2009). While modern advances in crop breeding have resulted in varieties with greater yield, pest resistance, and climate adaptability (Crossa et al., 2017), these developments are often achieved at the cost of a decreased nutrient content (e.g. proteins and vitamins B₆, E, and C; Davis et al., 2004). Therefore, there is a pressing need for developing novel strategies and approaches to adequately meet the projected increase in the global food demand without sacrificing food quality. The emerging field of plant synthetic biology offers a promising means to address these challenges.

Plant synthetic biology aims at applying engineering principles to the design and alteration of plant systems as well as to the de novo construction of artificial biological pathways whose behavior in plants can be predicted, controlled, and, ultimately, programmed (Schwille, 2011; Liu and Stewart, 2015; Glass and Alon, 2018). Since plant yield and nutritional value directly depend on metabolically assembled building blocks, in silico design, testing, and experimental validation of synthetic metabolic pathways provide a roadmap for rational manipulation of these agronomically important plant traits. On the one hand, a partial understanding of plant metabolic networks and their characteristics is required to rationally design and test synthetic metabolic pathways. On the other hand, the experimental validation of a multitude of designs is made feasible by approaches that allow an in silico assessment of their effects on engineered plants. Therefore, further advances in assembling plant metabolic network models and the development of novel computational approaches to arrive at feasible synthetic metabolic pathways may revolutionize plant synthetic biology.

We first provide a succinct view of models of plant metabolic networks that enable the understanding of key phenotypes affecting nutritional value and yield, namely, metabolic pools (i.e. concentration of metabolites) and biochemical reaction rates. We then offer a systematic review of computational approaches to design and in silico test synthetic metabolic pathways not only in plants but also in other organisms. Many of these approaches are based on advances that synthetic biology has achieved in microbial systems (Liu and Stewart, 2015). While the same design principles and concepts are readily applicable to plants, the transfer between species faces challenges due to the increase in complexity and diversity of plant cell types, tissues, and organs (Cook et al., 2014). The experimental validation of synthetic metabolic pathways is realized by engineering a regulatory network of interacting proteins, RNA, and DNA; comprehensive reviews already provide a critical summary of advances in synthetic biology techniques and technologies to achieve this step (Ellis et al., 2009; Lim, 2010), and we do not cover them here. Finally, we point at the key challenges in the area of synthetic metabolic pathways and the computational developments that may help to address them.

PLANT METABOLIC NETWORKS AND INVESTIGATION OF SYNTHETIC METABOLIC PATHWAYS

Metabolism encompasses the entirety of biochemical reactions that shape the metabolic pools in an organism. The availability of fully assembled genomes of key model plants and crops (CoGepedia, 2011) and approaches to annotate gene functions (Rhee and Mutwil, 2014) makes it possible to develop and further refine mathematical models of plant metabolism (Nikoloski et al., 2015). The quality and accuracy of metabolic models (and, consequently, of the resulting predictions) ultimately depend on the extensiveness of the underlying gene annotations. Annotation of gene function in plants still lags behind (e.g. with respect to secondary metabolism or enzymes with multiple functions), which imposes limitations to understanding the possible system-wide effects of a synthetic metabolic pathway.

One way of modeling (plant) metabolism is to mathematically describe the change of each metabolic pool in terms of the biochemical reactions that directly contribute to its production and depletion (Fig. 1A). Each reaction in a metabolic network can carry flux, denoting the rate at which substrate molecules are transformed into product molecules (Fig. 1A). The rate of a reaction depends on the activity of the enzymes that catalyze the reaction (if not spontaneous) and the concentration of metabolites, either entering the reactions as substrates or as allosteric regulators of enzyme activity. We will denote with x the concentration of metabolites and with θ the parameters of the reaction rates (e.g. mass action rate constants, Michaelis-Menten constants, catalytic rates, and concentration of active enzyme). In addition, we will use 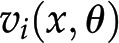to denote the rate of the biochemical reaction 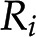, which depends on x and θ, as stated before, and 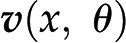to denote an array (vector) that gathers the rates of all reactions.

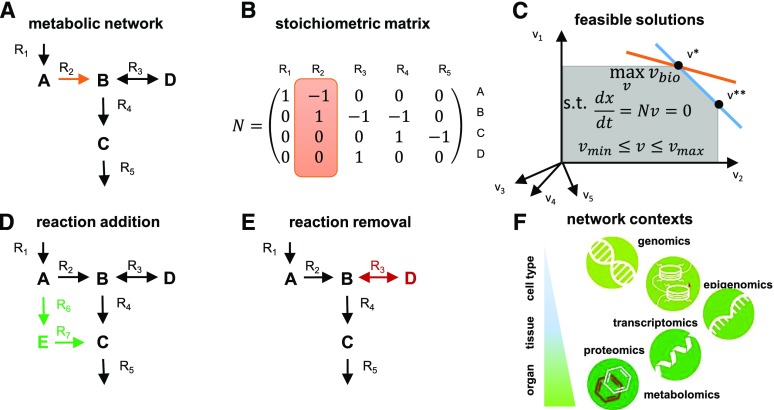
Figure 1.

Constraint-based modeling of metabolic networks. A, A metabolic network is a collection of biochemical reactions exchanging metabolites with the environment and interconverting them into the building blocks of biomass and energy. The network includes five reactions and four metabolites, A to D. B, Stoichiometric matrix of the metabolic network shown in A. Highlighted is reaction 2, converting one molecule of the substrate B into one molecule of the product C. C, Feasible solutions (gray) are compatible with the steady-state constraints, whereby there is no change in the concentration of metabolite over time (i.e. 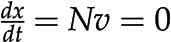) and flux capacity bounds (i.e. 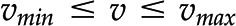). The optimum for the objective function, 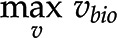, in orange is associated with a unique optimum flux distribution (v*), while 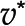and 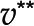are two optimal flux distributions for the objective function in blue. Note that the optimal objective value at 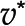and 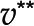are the same. D, Addition of reactions 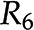and 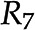leads to the introduction of metabolite E. E, Removal of reaction 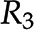leads to the removal of metabolite D. F, Context-specific metabolic networks are obtained by considering constraints from different profiling technologies applicable to single cell types, tissues, organs, and entire organisms.

Moreover, each metabolic reaction can be described by the stoichiometry of its substrates and products. The collection of the stoichiometry of all reactions in a metabolic network yields a so-called stoichiometric matrix, denoted by N. The rows of a stoichiometric matrix represent metabolites and the columns stand for reactions. Negative and positive entries in a stoichiometric matrix denote the molarity with which a metabolite enters a reaction as a substrate and a product, respectively (Fig. 1B). The stoichiometry ensures that reactions are balanced with respect to mass and charge (i.e. no matter and energy are produced or consumed out of nowhere).

Given the concepts of stoichiometric matrix and reaction rates, the change of metabolic pools over time, denoted by 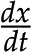, is then given by 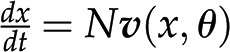. From this expression, we can conclude that, given the same initial concentrations of metabolites, the change in the metabolic pools over time may be affected by alteration to the stoichiometric matrix N, alterations in the reaction rates (i.e. the way in which rates depend on metabolic pools and other parameters [as described in 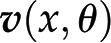], or both. Since large-scale metabolic networks include reactions involved in synthesis and degradation of key building blocks and energy currencies, this modeling framework provides the means to assess the effects of a synthetic metabolic pathway on cellular economy and (re)distribution of resources in a (plant) cell.

Depending on the level of abstraction, the stoichiometric matrix can either represent a microcompartment, an organelle, or an entire plant cell as well as interacting cells, tissues, organs, or an entire plant. Data from transcriptomics, proteomics, and metabolomics profiling platforms as well as flux estimates from labeling studies have indicated that not all biochemical reactions are active across all plant cell types, tissues, or organs, referred to as cellular contexts (Zur et al., 2010; Fig. 1F). For instance, there is a distinction between the metabolism of guard and mesophyll cells in an Arabidopsis (Arabidopsis thaliana) leaf (Robaina-Estévez et al., 2017), between the metabolism of different cell types in an Arabidopsis root (Scheunemann et al., 2018), or between metabolism of bundle sheath and mesophyll cells over a maize (Zea mays) leaf developmental gradient (Bogart and Myers, 2016). Therefore, recent advances in plant metabolic modeling have focused on extraction of context-specific metabolic networks (Machado and Herrgård, 2014; Robaina Estévez and Nikoloski, 2014) and their integration into larger models of interacting organs (Grafahrend-Belau et al., 2013; Gomes de Oliveira Dal’Molin et al., 2015). Table 1 summarizes the key properties of the existing large-scale models of plant metabolism that provide the basis for in silico testing of synthetic metabolic pathways to provide novel plant metabolic functions.

Table 1. Survey of existing plant genome-scale metabolic network reconstructions and some of their properties.

Rice, Oryza sativa; sorghum, Sorghum bicolor; sugarcane, Saccharum officinarum; tomato, Solanum lycopersicum.

Model Organism	Context	No. of Compartments/Reactions/Metabolites	References
C3 plants
Arabidopsis	Heterotrophic cell culture	2/1,336/1,231	Poolman et al. (2009)
Arabidopsis (AraGEM)	Photosynthetic and nonphotosynthetic tissues	5/1,567/1,748	de Oliveira Dal’Molin et al. (2010)
Arabidopsis (iRS1597)	Photosynthetic and nonphotosynthetic tissues	5/1,985/1,825	Saha et al. (2011)
Arabidopsis (context and tissue specific)	Condition-specific models for compartmented cell, cell culture, cotyledon, flower bud, open flower, root, juvenile leaf, and silique	7/1,929/1,410	Mintz-Oron et al. (2012)
Arabidopsis	Heterotrophic cell culture	5/2,769/2,618	Cheung et al. (2013)
Arabidopsis	Leaf metabolism over a day-night cycle	5/5,609/5,235	Cheung et al. (2014)
Arabidopsis (AraCORE)	Photoautotrophically growing leaf cell	4/549/407	Arnold and Nikoloski (2014)
Arabidopsis	Plant primary and secondary metabolism	8/6,399/6,236	Seaver et al. (2015)
Arabidopsis	Multitissue whole-plant model	6/9,727/10,733	Gomes de Oliveira Dal’Molin et al. (2015)
Arabidopsis	Mesophyll and guard cell	4/455/374	Robaina-Estévez et al. (2017)
Arabidopsis	Root, stele, endodermis, cortex and epidermis (atrichoblasts), xylem, phloem, and pericycle cells	8/2,199/1,813	Scheunemann et al. (2018)
Rice	Developing leaf cell	3/1,736/1,484	Poolman et al. (2013)
Rice (iOS2164)	Single leaf cell	7/2,441/1,999	Lakshmanan et al. (2015)
Tomato (iHY3410)	Single leaf cell	5/2,143/1,998	Yuan et al. (2016)
C4 plants
Maize, sorghum, sugarcane (C4GEM)	Mesophyll and bundle sheath cells	5/1,588/1,775	Dal’Molin et al. (2010)
Maize (iRS1563)	Single cell	5/1,798/1,820	Saha et al. (2011)
Maize (iEB5204)	Single leaf cell	12/1,535/1,125	Bogart and Myers (2016)
Maize (iEB2140)	Single leaf cell	12/635/603	Bogart and Myers (2016)
Maize (iEB2140x2)	Mesophyll and bundle sheath cells in developing maize leaf	19/1,268/1,121	Bogart and Myers (2016)
Maize	Bundle sheath and mesophyll cells	7/8,525/9,153	Simons et al. (2014)
Maize (full and tissue specific)	Plant primary and secondary metabolism, leaf cell, embryo cell, endosperm cell	8/6,458/6,250	Seaver et al. (2015)
Crassulacean acid metabolism plants
Crassulacean acid metabolism	Leaf cell day-night cycle	25/1,312/1,112	Shameer et al. (2018)

Due to the differences in the metabolic capabilities of various plant cell contexts, it is important to consider the following: (1) which function is supposed to be modified or de novo engineered, (2) what is the context in which the function is to be performed, (3) whether the function involves biochemical reactions that span several spatial contexts (e.g. multiple organelles), and (4) the consequences of performing the altered or novel function to the selected plant context and the plant as a whole. Resolving these issues via metabolic modeling can eventually result in a successfully engineered synthetic metabolic pathway in a specific plant context.

The last question can be readily addressed with approaches from the constraint-based modeling framework (Bordbar et al., 2014), with Flux Balance Analysis (FBA) as the first and most prominent representative. FBA assumes that the system is operating at steady state, whereby there is no change of metabolite pools over time. Mathematically, this assumption implies that 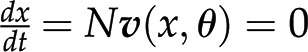. Focusing on the reaction rates, the expression 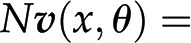0 results in a system of linear equations 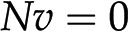, with the reaction rates, 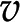, as unknowns. Each linear equation models a steady state of a particular metabolite. Since the number of reactions is typically larger than the number of metabolites (i.e. number of equations), the system of linear equations 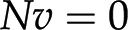usually has infinitely many solutions (Fig. 1C). To restrict the set of solutions to 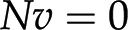and arrive at the reaction rates in a given context, additional biochemically relevant constraints can be imposed. For instance, all reactions are assumed to operate between some (generic) upper and lower flux boundaries (i.e. 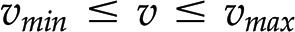; Fig; 1C), while some reactions may be known to operate in a single direction (i.e. ) in a given context. Moreover, the inputs and outputs of the system can also be measured and used as constraints (i.e. 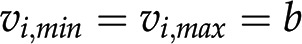, where b is a measured flux). The set of flux distributions 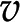that satisfy 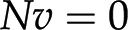and the other enumerated constraints is called a feasible space (gray area in Fig. 1C). To further narrow down the feasible space, one assumes that the biological system optimizes an objective, such as biomass produced per unit of input substrate (Feist and Palsson, 2010). This leads to a linear program, whose solution is the optimal biomass yield (equations in Fig. 1C). Biomass yield is modeled via a so-called biomass reaction whose stoichiometry corresponds to the contribution of specific precursors to grams of dry weight (Feist and Palsson, 2010). Since the problem is modeled as a linear problem, there is a single optimal value for the objective. However, this objective may be realized by a single or multiple flux distributions (orange and blue lines, respectively, in Fig. 1C). Another common objective is the minimization of the sum of fluxes, a proxy for the cost of the enzymatic machinery (Holzhütter, 2004; Sweetlove and Ratcliffe, 2011). This objective is used with the idea of obtaining a single optimal flux distribution, thus obtaining the rates of all reactions in the modeled network.

Since FBA is a linear programming problem, one can readily investigate the sensitivity of the objective value to changing a constraint, denoted as a shadow price for the constraint. For a constraint that corresponds to a resource, the shadow price indicates the increase in yield when the resource is increased by a unit. Since the constraint associated with a metabolite corresponds to the steady state (balance) for the metabolite, determining the shadow price indicates how the imbalance of that metabolite affects the objective (Reznik et al., 2013). Therefore, extensions of FBA may allow insights to the effect of changes in metabolite pools on the performance of the biological system (see “Criteria for Ranking Pathways” below).

Given the FBA framework, one can readily investigate how a modification of the network structure, encoded in the stoichiometric network, affects a selected cellular objective as well as the production of particular target metabolites. There are several possibilities with respect to the modification of the stoichiometric network, including reaction removal and reaction addition, and, as a result of these, removal and addition of metabolites, respectively (Fig. 1, D and E). The added reactions may correspond to enzyme functions that either exist in nature or need to be engineered. As a result, the changes of the network structure have recently been categorized into five levels of metabolic engineering, corresponding to native metabolism, copy and paste, mix and match of enzymes, as well as novel enzyme reactions and novel enzyme chemistries (Erb et al., 2017). Identifying reaction removals, additions, or combinations thereof that lead to a desired modification of a target compound is a common problem in metabolic engineering of microorganisms for which there are readily available constraint-based solutions, such as optKnock (Burgard et al., 2003), optStrain (Pharkya et al., 2004), optReg (Pharkya and Maranas, 2006), optForce (Ranganathan et al., 2010), and EMILiO (Yang et al., 2011), to name a few. For instance, optStrain can be employed to determine pathway modifications, through reaction additions with nonnative functionalities and reaction removal to divert flux away from competing functions, for improved plant growth (Pharkya et al., 2004). These constraint-based solutions are suitable for designing and testing copy-and-paste as well as mix-and-match metabolic engineering strategies.

One typical example of a mix-and-match strategy in plant science is photorespiratory bypasses, which have been experimentally shown to result in increased growth in Arabidopsis (Kebeish et al., 2007; Maier et al., 2012). These pathways aim at diverting flux away from photorespiration and back into the Calvin-Benson cycle, thus increasing carbon fixation. They do so by altering the metabolism of glycolate, a toxic by-product of photosynthesis, in the chloroplast. The Kebeish bypass consists of glycolate dehydrogenase, tartronate semialdehyde carboxylase, and 2-hydroxy-3-oxopropionate reductase, transforming glycolate into glycerate that can be converted into 3-phosphoglycerate, a Calvin-Benson cycle intermediate (Kebeish et al., 2007). The Maier bypass consists of a complete glycolate catabolic cycle, including glycolate oxidase, malate synthase, and catalase (from Escherichia coli). By interconversions in the glycolate cycle, one molecule of glycolate is converted into two molecules of CO₂. Therefore, while the Kebeish bypass reintroduces three-quarters of the glycerate into Calvin-Benson cycle intermediates, the Maier bypass operates without recycling of 3-phosphoglycerate. Three implementations of these bypasses were recently tested in tobacco (Nicotiana tabacum) along with RNA interference to down-regulate a native chloroplast glycolate transporter in the photorespiratory pathway. The first employed five genes from the glycolate oxidation pathway in E. coli; the second used plant glycolate oxidase and malate synthase and E. coli catalase; the third implementation employed plant malate synthase and a green algal glycolate dehydrogenase. One of the 17 construct designs of the three pathways resulted in a biomass increase greater than 25% in the field. We note that these strategies were not designed and tested in silico and were a result of searching for ways to divert flux away from processes considered as wasteful.

A recent computational study has identified that mimicking the experimental findings with constraint-based modeling approaches is possible only upon consideration of additional constraints on the ratio of the Rubisco carboxylation and oxygenation reactions (Basler et al., 2016). The key findings of this study indicate that constraint-based approaches have to be refined to consider plant-specific constraints if they are to be used in plant synthetic biology, particularly in conjunction with the design of synthetic metabolic pathways, to further enhance a desired plant function (Maia et al., 2015). In the following section, we survey the computational approaches for design of synthetic metabolic pathways and their application in plant science.

COMPUTATIONAL APPROACHES TO DESIGN SYNTHETIC METABOLIC PATHWAYS

The design of a synthetic metabolic pathway begins with specification of the metabolic function to be achieved by engineering. In the case of improving nutritional value of a crop, the metabolic function corresponds to the production of a target compound (e.g. vitamin C). In the case of carbon fixation, it denotes the production of a key intermediate of carbon metabolism that serves as a building block of more complex molecules (e.g. glyceraldehyde-3-phosphate; Bar-Even et al., 2010). In the case of growth, the metabolic function can be a combination of key constituents of biomass (Chan et al., 2017). Finally, the metabolic function may also include a nonnative target compound that is not present in a plant metabolic network.

Given a target compound, the design of a synthetic metabolic pathway may start from known substrate compounds, or the substrates may not be provided and should be determined as a part of the pathway design. As a result, one can distinguish two groups of computational approaches for the design of synthetic metabolic pathways, with prespecified or without specified substrates (Fig. 2). These scenarios roughly lead to two classes of computational approaches: optimization based and retrobiosynthesis, respectively (Box 1). The retrobiosynthesis approaches can also be applied to determine pathways connecting a specified substrate and target. We do not survey approaches that deal with defining and searching for pathways in a given network, as those are reviewed elsewhere (Wang et al., 2017).

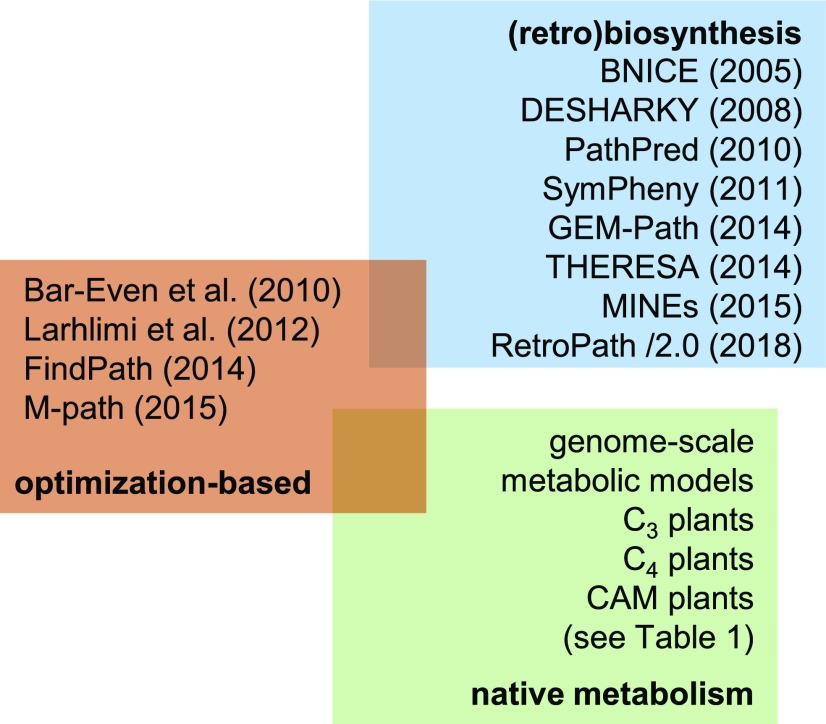
Figure 2.

Overview of approaches for the design of synthetic metabolic pathways. The existing approaches can be roughly grouped into optimization based (red rectangle) and retrobiosynthesis focused (blue rectangle). Selected approaches are listed alongside the year of their publication. The designed pathways are to be validated in a context-specific plant metabolic network (green rectangle and Table 1). The ultimate scenario should embed the design of a plant metabolic network in the context in which it is to operate. CAM, Crassulacean acid metabolism.

Optimization-Based Approaches

The computational approaches in this group aim to identify a set of biochemical reaction steps that lead from given substrates to a desired target compound. The existing approaches in this group fall in the class of constraint-based modeling approaches, which have been instrumental for advances in systems biology (Bordbar et al., 2014). For instance, FindPath (Vieira et al., 2014) aims to predict metabolic pathways enabling the conversion of one or more nonnative compounds (i.e. molecules not present in the metabolic network) into any (specified) target metabolite of a given metabolic network. The approach necessitates data on all known metabolic conversions of the product of interest as well as the metabolism of the context in which the pathway is to be engineered. For biochemically meaningful results, the approach requires that the reactions are mass and charge balanced and that their reversibility is known. Given such an assembled network, the approach searches for an elementary flux mode (Klamt and Stelling, 2003; i.e. a minimal subset of reactions that can operate at steady state and connect the source to the target). For instance, in Figure 3, there are three pathways, illustrated in red, connecting the source (A) to the target (C). These pathways support steady state; in addition, they are minimal, in the sense that each one of them cannot be expressed as a sum of the others. Although the enumeration of elementary flux modes is a challenging computational task in real-world metabolic networks (due to the very large number of such pathways), FindPath can be applied to large-scale reaction networks due to the specification of sources and/or targets.

Figure 3.

Optimization-based approaches for synthetic metabolic pathway design. Source and target compounds, A and C, respectively, are shown in a network of biochemical reactions. FindPath (Vieira et al., 2014) is based on the concept of minimal subnetworks of reactions that can operate at steady state, called elementary flux modes. Elementary flux modes leading from source A to target C are marked in red. The approach of Bar-Even et al. (2010) seeks a minimum flux subnetwork, marked in red, obtained via a linear program that minimizes total flux 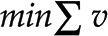under steady-state constraints 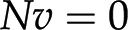and a fixed value, c, for the out-flux, 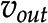. Stoichiometric capacitance (Larhlimi et al., 2012) maximizes the theoretical production of a target by predicting a synthetic reaction that can be decomposed into respective enzyme-catalyzed reactions. The latter can also be determined by the randomized optimization approach called M-path (Araki et al., 2015).

In contrast to FindPath, the approach of Bar-Even et al. (2010) starts with a generic network of documented metabolic conversions (obtained by modification of KEGG; Kanehisa et al., 2014) upon removal of cofactors, while ensuring mass balancing. This approach aims to identify synthetic carbon fixation pathways that start from CO₂ or HCO₃⁻ and produce glyceraldehyde-3-phosphate as a target. To this end, a linear programming formulation is used, whereby the total flux through the pathway is minimized while flux is allowed only through a subset of kinetically superior carboxylation enzymes (Fig. 3). The authors report and further analyze only one solution for each subset of carboxylation enzymes allowed to carry flux, although multiple alternative solutions may be possible, providing further opportunities for exploring this feasible approach for design of in silico pathways.

The approach of Larhlimi et al. (2012) aims to characterize the maximum theoretically possible product yield and to engineer networks with optimal conversion capability by predicting a biochemically feasible synthetic reaction called stoichiometric capacitance (Fig. 3). The approach is formulated as a mixed integer linear program that maximizes a function of interest (i.e. biomass production) while allowing the insertion of an additional synthetic reaction. In addition, the approach was extended to predict a decomposition of the synthetic (net) reaction into a subset of thermodynamically feasible biochemical reactions (see “Criteria for Ranking Pathways”; Fig. 3). While the approach provides an interesting way to couple the design of a synthetic pathway with the metabolic network of the context in which the function should be engineered, the decomposition step may lead to infeasibilities and, like the approach of Bar-Even et al. (2010), alternative solutions will have to be considered. The decomposition step can be employed to arrive at a subset of reactions that can substitute the steps of the enzymatic mechanisms of a single, less efficient enzyme. For instance, Bar-Even (2018) has employed this strategy to propose a substitution for Rubisco’s enzymatic mechanism, which consists of an isomerase, biotin-dependent carboxylase, and carbon-carbon hydrolase.

The M-path approach aims to find a combination of reaction feature vectors, given by the difference between chemical features of products and substrates of reactions, that result in a given pathway feature vector (Araki et al., 2015). Therefore, the approach requires a set of reaction feature vectors and solves iteratively integer linear programs on a random subset of reaction feature vectors (Fig. 3). The pathway is then stitched together from the obtained solutions by ordering the reaction feature vectors and matching of the intermediates.

Due to their low computational complexity and the possibility for investigation of pathway design concomitantly with its effects on the plant cell context, the approaches in this group have great potential for generating realizable designs. However, except for the approach of Bar-Even et al. (2010) applied to the problem of carbon fixation, the approaches in this group have not been employed to design plant-specific synthetic metabolic pathways.

Retrobiosynthesis Approaches

The retrobiosynthesis approach constructs pathways from a given target compound by repeatedly applying chemical reaction rules to the obtained intermediates until a desired native compound has been reached (Fig. 4). It fulfills the key promise of synthetic biology to design pathways that are not limited to enzymes and biosynthetic routes that exist in nature. Retrobiosynthesis can be regarded as walking backward from a given molecule while satisfying basic chemical principles. In doing so, one has to ensure that the generated reaction transformation steps can be realized with known enzymes or with enzymes that can be engineered (Brunk et al., 2012). The presence of multimolecular reactions in the backward-walking strategy used in retrobiosynthesis approaches causes computational issues due to combinatorial explosion, since the pathway is to be expanded for more than one intermediate. This is a pressing issue despite the observation that pairs of key compounds (e.g. precursors to biomass) are connected by a minimal number of enzymatic steps (Noor et al., 2010; see “Pathway Pruning”).

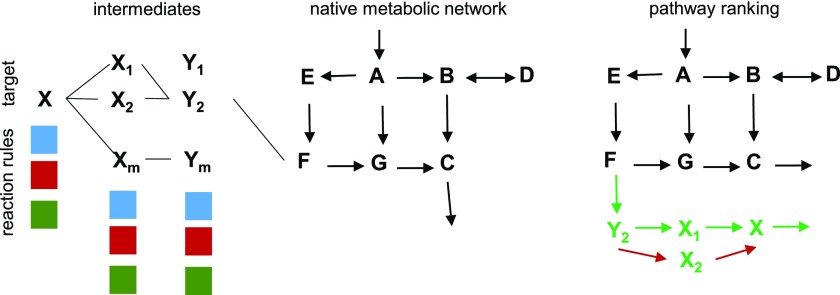
Figure 4.

Retrobiosynthesis approaches for synthetic metabolic pathway design. Reaction rules (colored boxes) are applied to the target to obtain a set of intermediates to which the reaction rules are iteratively applied until a compound from the native metabolic network is reached. Metabolite X can be synthesized from F via two pathways, F→ Y₂ → X₁ → X and F→ Y₂ → X₂ → X. The two pathways are ranked based on different criteria, such as thermodynamics, concentration of metabolites, enzyme costs, and effects on native metabolism (e.g. production of metabolite C). The reactions marked in red are not feasible due to unfavorable thermodynamics.

During the last two decades, a range of computational approaches have been proposed that can help to improve pathway design. Their main difference is with respect to the representation of the reaction rules used. As pointed out by Delépine et al. (2018), reaction rules can be encoded in at least four different ways by employing Bond-Electron matrices (Dugundji and Ugi, 1973), reaction SMARTS (Daylight, 2017), RDM patterns (Oh et al., 2007), and reaction signatures (Carbonell et al., 2014). Given a selected encoding, there are two strategies that have been followed: (1) establish a fixed set of reaction rules that covers the classes of reactions of interest and (2) automatically compute flexible rules based on a set of given reactions and representation of compounds.

With respect to the first strategy, the Enzyme Commission (EC) classification provides a standardized, hierarchical, numerical classification of enzymes (Webb, 1992). The complete EC number of an enzyme consists of four numbers defining with increasing detail the enzyme class and subclasses to which the enzyme belongs. Although all reactions that have the same first three parts of an EC number should follow the same chemistry, some do not share the common substructures and cannot be encoded in the same way by SMARTS. Moreover, relying on EC numbers would neglect some reactions that have not yet been assigned to any of the existing enzyme classes (Webb, 1992). Nevertheless, a fixed set of rules, such as those defined by EC numbers, allows for easy manual checking and verification. This strategy is used by SymPheny (Yim et al., 2011), MINEs (Jeffryes et al., 2015), BNICE (Hatzimanikatis et al., 2005) and an extension thereof (Hadadi et al., 2016), DESHARKY (Rodrigo et al., 2008), PathPred (Moriya et al., 2010), GEM-Path (Campodonico et al., 2014), THERESA (Liu et al., 2014), and the approach of Cho et al. (2010). These approaches employ different sets of biochemical pathways and databases of metabolic networks, including MetRxn (Kumar et al., 2012), KEGG (Tanabe and Kanehisa, 2012), BioCyc (Caspi et al., 2016), Plant Metabolic Network (Schläpfer et al., 2017), and PubChem (Hähnke et al., 2018).

The second strategy is implemented by RetroPath and its extension, RetroPath 2.0 (Delépine et al., 2018). It uses a flexible way to incorporate different levels of structural detail by considering atoms in the reaction center (i.e. atoms that change configuration upon the reaction taking place) and their neighborhoods at different distance heights. By varying the distance used to define a neighborhood, RetroPath 2.0 facilitates the control of the number of reactions in the generated synthetic metabolic pathway.

One way to address the noted issue of combinatorial explosion is to remove ubiquitous compounds (e.g. ATP and water). Another way consists of dividing multimolecular reactions into several unimolecular reactions at the expense of losing representational rigor and careful bookkeeping. This approach is used in RetroPath2.0, BNICE, THERESA, and GEM-Path (Hatzimanikatis et al., 2005; Campodonico et al., 2014; Liu et al., 2014; Delépine et al., 2018).

Pathway Pruning

Regardless of whether one uses fixed or flexible reaction rules, even when a single compound is used as a seed of the iterative application of reaction rules, the number of generated intermediates and reactions grows exponentially. Therefore, the exhaustive enumeration becomes unfeasible and means for controlling the growth of possible pathways should be considered. There are several strategies that can be used, and they deal with ensuring that the reactions can be realized with currently annotated enzymes and that intermediates have suitable properties. For instance, in BNICE, the pruning of pathways is implemented in the application of reaction rules, so that only predefined classes of compounds and reactions are allowed to be used. In RetroPath, a reaction and respective intermediates are pruned if there is no suitable documented enzyme that can catalyze the proposed transformation, assessed by machine learning approaches (Faulon et al., 2008; Mellor et al., 2016). GEM-Path follows a similar approach and accepts a reaction if there is high enough similarity of substrates of a reference reaction based on chemoinformatics measures (e.g. Tanimoto coefficient; Campodonico et al., 2014). This step of pathway pruning has been termed qualitative pruning (Hadadi and Hatzimanikatis, 2015).

CRITERIA FOR RANKING PATHWAYS

There are multiple criteria that can be used to select from the list of generated synthetic metabolic pathways by the outlined algorithms. For instance, Dale et al. (2010) enumerate more than 100 pathway characteristics, grouped based on reaction evidence, genome context, taxonomic range, pathway connectivity, and biochemical properties, to name just a few (Dale et al., 2010). These characteristics have been used in ranking of pathways based on machine learning approaches (e.g. support vector machines). Since biochemical properties relate to the thermodynamics of reactions, metabolite concentrations, their toxicity and regulation of metabolic state, and the protein burden (i.e. cost) of the pathway are the key determinants of a feasible and realizable pathway, these characteristics are of high importance when designing and in silico testing synthetic pathways. Here, we survey the key computational developments that can be used to analyze the aforementioned characteristics.

Thermodynamics

Energetically unfavorable pathways can be removed from further analysis by considering the thermodynamics of individual reactions and generated pathways. To perform this analysis, one requires the standard Gibbs free energy of reactions, which can be obtained following the group contribution method (Jankowski et al., 2008). An estimate of standard Gibbs free energy is associated uncertainty, which renders it difficult to pinpoint (ir)reversibility of reactions under standard conditions. To estimate the Gibbs free energy under physiologically relevant conditions, data on metabolite concentrations can be used, if available. This approach also requires data on pH in different plant cellular compartments (Benčina, 2013) to estimate standard Gibbs free energy of reactions across different compartments. In addition, estimation of standard Gibbs free energy is also challenging due to the observation that a metabolic pool is usually partitioned into subpools of different ionic strengths (Haraldsdóttir, 2014). The existing approximations of the Gibbs free energy have been used in ranking of carbon fixation pathways (Bar-Even et al., 2010), while estimated standard Gibbs free energies are used by other approaches discussed above.

If data about metabolite concentrations, along with estimates of concentration ranges for metabolites as well as information about pH in different plant cellular compartments, are available, Thermodynamics-based Flux Balance Analysis (TFBA; Henry et al., 2007) can in principle be employed to adjust the ranges for estimated standard Gibbs free energy to in vivo-like conditions. TFBA can be regarded as an extension of FBA in which the additional constraint, that a reaction that carries positive flux is associated with a negative Gibbs free energy, must be satisfied. This approach guarantees that the generated pathway is feasible and allows the simultaneous estimate of the maximum pathway yield, an idea followed in BNICE and GEM-Path. Similarly, one can use the max-min driving force to determine the degree to which a pathway is constrained by a low thermodynamic driving force (Noor et al., 2014). However, obtaining a large-scale metabolic model that integrates this type of data is still an open problem even for model plants and crops. The availability of such models will facilitate estimation of the effects of alternation in pH and cellular energy status due to the incorporation of a synthetic metabolic pathway.

Concentration of Metabolites

Changes in a metabolic network by insertion of a pathway are likely to affect the metabolic state of the plant system, by modifying the concentration and activity of enzymes as well as the concentration of metabolites. Since metabolites are interdependent not only due to the substrate-product relationships but also due to regulatory effects, changes in the metabolic makeup of a cell will have effects on the key kinetic properties (e.g. stability and robustness) of the pathway and the network as a whole.

If the metabolic pathway introduces nonnative intermediates, it must be guaranteed that they do not accumulate to toxic concentrations. For instance, RetroPath incorporates a machine learning approach that predicts toxicity levels (i.e. half minimal inhibitory concentration) based on a library of 150 tested compounds (Planson et al., 2012), while DeepTox relies on a deep learning algorithm to identify potentially toxic effects of compounds (Mayr et al., 2016). However, these approaches provide a classification of intermediates as toxic or not but do not provide the means to predict metabolite concentrations in diverse cellular scenarios.

As indicated above, due to the steady-state assumption and the flux-centered focus, constraint-based approaches amount to solving a set of linear equations for the reaction fluxes. However, actual fluxes are integrated outcomes of the activity of available enzymes, their posttranscriptional and allosteric regulation, as well as metabolite levels. Mathematically, each reaction rate is described as a nonlinear function 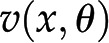, such that each steady-state flux distribution is accompanied by a steady state of metabolite concentrations. The latter can be obtained by solving the system of equations 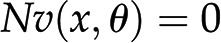, which are often nonlinear in the metabolite pool sizes x. Therefore, while the results from FBA are independent of enzyme-kinetic parameters, any predictions about metabolite concentrations in a steady state necessitate the inclusion of specific kinetic rate equations (Töpfer et al., 2015).

The development of approaches to predict concentration profiles with limited information on reaction kinetics is therefore key for testing the feasibility of a synthetic pathway. Although shadow prices (Reznik et al., 2013) and chemical properties (Bar-Even et al., 2011) of compounds have been proposed as means to estimate changes in concentrations, they show poor prediction performance in different scenarios. TFBA provides means to inspect the effect on the engineered pathway of metabolite concentrations, although the resulting ranges are often large for comparisons of scenarios. In addition, metabolic Tug-of-War (Tepper et al., 2013), which extends the approach for calculating the max-min driving force by assuming that the cell operates toward minimizing the metabolic load and enzyme costs, allows the estimation of absolute metabolite concentrations with a nonlinear optimization approach. The resulting correlations between predicted and measured concentrations is between 0.45 and 0.64 in E. coli and Clostridium acetobutylicum under different growth conditions. A recently proposed approach based on mass action modeling of reaction rates has established a connection between concentration of specific metabolites, ratio of selected fluxes, and a few reaction rate constants. This approach thus allows making predictions about metabolite concentrations with limited parameterization of large-scale metabolic networks by applying constraint-based modeling (Kueken et al., 2018). For networks endowed with mass action kinetics, the approach provides excellent quantitative predictions when a limited set of parameter values are presented; in addition, it provides good qualitative predictions (Pearson correlation of at least 0.6 and Spearman correlation of 0.75) for real-world data sets from E. coli.

Of these approaches, only shadow prices have been used in ranking of pathways in DESHARKY (Rodrigo et al., 2008), while the others will require extensions for routine application in ranking of synthetic pathways. By employing the constraint-based modeling framework, the existing approaches forgo the consideration of allosteric regulations, which is another determinant of understanding the effect that a metabolic transformation can have on (plant) metabolism.

Enzyme Costs

Synthetic pathways can also be ranked based on the burden that the enzymes of the engineered pathway impose on the network. This is the approach taken in DESHARKY to calculate the effect of transcription and translation of the necessary enzymes for a synthetic pathway in a given context (Rodrigo et al., 2008). Another possibility is to use the inverse of an enzyme’s specific activity as its cost, which has been used to calculate the cost of alternative carbon fixation pathways (Bar-Even et al., 2010). Like the case of metabolite concentrations, protein costs can also be estimated by constraint-based approaches with the assumption of a particular kinetic rate law (Noor et al., 2016). There are currently no clear criteria as to which of these approaches provides advantages, since there is no systematic study that investigates their performance in diverse cellular scenarios.

CHALLENGES AND OPPORTUNITIES FOR PLANT SYNTHETIC BIOLOGY

Plant synthetic biology provides the means to engineer synthetic metabolic pathways that when introduced in a specific plant cell type will provide alteration of its function in a predictable desired direction. Interestingly, most if not all in silico strategies for alteration of plant metabolism are a result of in vivo testing of designs, with little support from modeling studies, despite roadmaps that call for model-driven in silico design and optimization of pathways (Zhu et al., 2010). The likely reasons for not adapting approaches for model-driven design of synthetic metabolic pathways are the following two challenges: (1) augmenting knowledge about specific plant cell types, their interactions, and joint function in the context of the entire plant, and (2) selecting feasible metabolic pathways (see Outstanding Questions).

Further developments are needed to annotate plant enzymes and characterize the plant metabolic space. This is particularly relevant given the promiscuity of enzymes in secondary plant metabolism, which has led to exceptional chemodiversity in plants (Weng et al., 2012). This challenge can be tackled by modern developments in plant systems biology that integrate genomics, transcriptomics, proteomics, and metabolomics data (Kliebenstein, 2014; Tohge et al., 2015). Revealing novel promiscuous enzyme functions in plants and other organisms will provide the possibility for engineering enzymes through directed evolution (Tracewell and Arnold, 2009; Chakraborty et al., 2013), which can then be used for the execution of pathway designs. These challenges go hand in hand with development of plant cell type-specific models and their integration into tissue and organ-level models.

Metabolic pathways in plants may span different compartments (e.g. photorespiration), and this is also conceivable for synthetic pathways. These pathways may offer increases in a desired function, however at the cost of having to manipulate organellar transporters (as demonstrated in the most recent examples from Ort’s lab [South et al., 2019]). Therefore, another key challenge includes the characterization of intracellular transporters and their appropriate inclusion in context-specific plant metabolic models. Addressing this issue will help improve the understanding of the effects that changes in one compartment may have in others.

From the systematic review of approaches for design of synthetic metabolic pathways, it becomes apparent that the likelihood for realizing a pathway can be increased if these approaches are directly coupled with in silico prediction of the pathway’s effects in the plant cell context. For instance, synthetic pathways can alter pH, energy status, and the reducing power of a plant compartment, cell, and organ. Therefore, future developments of computational approaches will have to be dedicated to understanding the effect that synthetic pathways have on native metabolism, particularly with respect to enzyme activities, metabolite concentrations, and reaction reversibility, all affected by the changes of the key parameters enumerated above. These developments must strike a compromise between the usage of meaningful characterization of enzyme kinetic forms and the number of parameters used, so as to reduce the effects of uncertainties and missing information about parameter values. In addition, they must consider as many plant-specific constraints as possible, to result in realistic predictions and selection of feasible metabolic designs. These developments will provide a tractable way to understand the difficulties of the execution of pathways that are now facile to design in silico.