Multinomial Extension of Propensity Score Trimming Methods: A Simulation Study

Abstract

Crump et al. (Biometrika. 2009;96(1):187–199), Stürmer et al. (Am J Epidemiol. 2010;172(7):843–854), and Walker et al. (Comp Eff Res. 2013;2013(3):11–20) proposed propensity score (PS) trimming methods as a means to improve efficiency (Crump) or reduce confounding (Stürmer and Walker). We generalized the trimming definitions by considering multinomial PSs, one for each treatment, and proved that these proposed definitions reduce to the original binary definitions when we have only 2 treatment groups. We then examined the performance of the proposed multinomial trimming methods in the setting of 3 treatment groups, in which subjects with extreme PSs more likely had unmeasured confounders. Inverse probability of treatment weights, matching weights, and overlap weights were used to control for measured confounders. All 3 methods reduced bias regardless of the weighting methods in most scenarios. Multinomial Stürmer and Walker trimming were more successful in bias reduction when the 3 treatment groups had very different sizes (10:10:80). Variance reduction, seen in all methods with inverse probability of treatment weights but not with matching weights or overlap weights, was more successful with multinomial Crump and Stürmer trimming. In conclusion, our proposed definitions of multinomial PS trimming methods were beneficial within our simulation settings that focused on the influence of unmeasured confounders.

Epidemiologists use propensity score (PS) methods (1–3) to evaluate the comparability of subjects in alternative exposure groups and to aid in control of imbalances between groups. Several authors (4–6) have suggested trimming the tails of the PS distribution. Crump et al. (4) suggested trimming to improve imprecision of inverse probability of treatment weight (IPTW) (7) estimators. Stürmer et al. (5) developed their trimming method to reduce bias by unmeasured confounders. Walker et al. (6) proposed a covariate overlap assessment tool that also serves as a trimming tool. They all focused on 2-group comparisons.

Many diseases now have 3 or more treatment options from which patients and physicians must choose. Conducting head-to-head clinical trials is the ideal way to establish equivalence or differences of efficacy and safety. However, it is not generally feasible to compare more than 2 medications in head-to-head trials. As such, observational comparative effectiveness (or safety) research (CER) studies are increasingly used for comparing multiple treatment choices.

Multiple-group CER, conducted among 3 or more active treatment agents, seeks to answer the question: “Given a population of patients requiring treatment and without contraindications to any of several approved options, which treatment is most appropriate among a range of available options?” Although the active comparator design (8) is a useful design to improve covariate balance, the presence of unmeasured confounders remains a concern. As reasoned by the authors above (5, 6), PS trimming has the potential to mitigate the bias by unmeasured confounders by focusing on a subset of subjects with better treatment equipoise. However, PS trimming strategies, as well as their performance, are not well established in the context of multiple-group CER. In this work, we have proposed general strategies for PS trimming for CER involving 3 or more treatment groups, illustrating their characteristics in empirical data examples and evaluating how they perform in simulated scenarios with 3 treatment groups.

METHODS

Existing PS trimming methods in the 2-group setting

To our knowledge, there are at least 3 PS trimming strategies often considered in epidemiologic studies involving PS methods (4–6) (Figure 1, Table 1, Web Appendix 1, Web Figures 1 and 2, available at https://academic.oup.com/aje). Let I be the set of indices {1, ..., n} indexing individuals in the entire study sample of sample size n. Let A_i ∈ {0,1} be the binary treatment indicator for individual i and e_i = P[A_i = 1 | X_i] be the PS for this individual given the covariate vector status X_i. Crump’s trimming method is defined as follows (4):

$$I_c=\{i\in I:e_i\in [{\mathrm{\alpha }}_c,1-{\mathrm{\alpha }}_c]\}$$

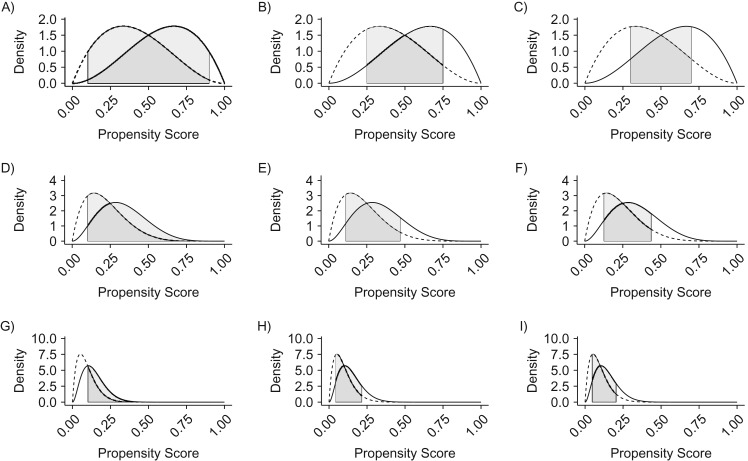
Figure 1.

Visual explanation of 3 existing 2-group trimming methods, using simulated data. A) Crump method (4), 50% treated; B) Stürmer method (5), 50% treated; C) Walker method (6), 50% treated; D) Crump method, 25% treated; E) Stürmer method, 25% treated; F) Walker method, 25% treated; G) Crump method, 10% treated; H) Stürmer method, 10% treated; I) Walker method, 10% treated. The hypothetical propensity-score distribution densities were generated from beta distributions. The dotted line represents the propensity score density in the untreated group, whereas the solid line represents the propensity score density in the treated group. In each panel, the gray region represents the retention region that applies to both treated and untreated groups. Individuals outside the retention region are removed regardless of their treatment status. Crump trimming is the same regardless of the prevalence, whereas the other 2 methods adapt to skewed propensity score distributions due to less frequent treatment. See Web Figures 1 and 2 for further examples.

Table 1.

Existing Propensity Score Trimming Method Definitions for a Binary Treatment and Proposed Propensity Score Trimming Method Definitions for a Multinomial Treatment^a

First Author, Year (Reference No.)	Original Binary Definitionb	Proposed Multinomial Definitionc
Crump et al., 2009 (4)	$I_c=\{i\in I:e_i\in [{\mathrm{\alpha }}_c,1-{\mathrm{\alpha }}_c]{\}}^d$	$I_{J,c}=\{i\in I_J:e_{ji}\ge {\mathrm{\alpha }}_{J,c}\forall j\in \{0,1,\dots ,J\}\}$
Stürmer et al., 2010 (5)	$I_s=\{i\in I:e_i\in \left[F_{e_i|A_i}^{-1}\left({\mathrm{\alpha }}_s|1\right),F_{e_i|A_i}^{-1}\left(1-{\mathrm{\alpha }}_s|0\right)\right]{\}}^e$	$I_{J,s}=\left\{i\in I_J:e_{ji}\ge F_{e_{ji}|A_i}^{-1}\left({\mathrm{\alpha }}_{J,s}|j\right)\forall j\in \{0,1,\dots ,J\}\right\}$
Walker et al., 2013 (6)	$I_w=\{i\in I:{\mathrm{\pi }}_i\in \left[{\mathrm{\alpha }}_w,1-{\mathrm{\alpha }}_w\right]{\}}^f$	$I_{J,w}=\left\{i\in I_J:{\mathrm{\pi }}_{ji}\ge {\mathrm{\alpha }}_{J,w}\forall j\in \{0,1,\dots ,J\}\right\}$

^a In all original and proposed methods, the same retention region is applied to every treatment group. See Web Appendix 2 for equivalence of the proposed methods to the original binary methods and proposed tentative thresholds in the multinomial setting.

^b Binary notations are as follows. I = {1, …, n}: set of individual indices; I_x: subset of individual indices retained by method x; A_i ∈ {0,1}: binary treatment indicator for individual i; e_i: propensity score for individual i; F⁻¹_ei|Ai: inverse cumulative distribution function of e_i conditional on A_i; π_i: preference score for individual i; α_x: trimming threshold by method x.

^c Multinomial notations are as follows. I_J = {1, …, n}: set of individual indices with J + 1 groups; I_J,x: subset of individual indices retained by method x; A_i ∈ {0,1, …, J}: multinomial treatment indicator for individual I; e_ji: propensity score for individual i for treatment j; F⁻¹_eji|Ai: inverse cumulative distribution function of e_ji conditional on A_i; π_ji: preference score for individual i for treatment j; α_J,x: trimming threshold by method x with J + 1 groups.

^d Crump et al.’s rule-of-thumb threshold for α_c was 0.1.

^e α_s were 0.01, 0.025, and 0.05 in Stürmer et al.’s simulation.

^f Walker et al.’s rule-of-thumb threshold for α_w was 0.3.

Crump et al. proved that the estimated treatment effect based on IPTW has the optimal precision for a specific choice of α_c. In practice, they suggested using α_c = 0.1 as a rule-of-thumb threshold that worked in a wide range of PS distributions in achieving near-optimal precision. At this threshold, the trimming method dictates that everyone who receives an IPTW of greater than 10 or less than 10/9 be removed.

Using the inverse of the cumulative distribution function of PS conditional on the treatment group F_ei|Ai, Stürmer’s asymmetric trimming method can be written as follows (5):

$$I_s=\left\{i\in I:e_i\in \left[F_{e_i|A_i}^{-1}\left({\mathrm{\alpha }}_s|1\right),F_{e_i|A_i}^{-1}\left(1-{\mathrm{\alpha }}_s|0\right)\right]\right\}$$

Rather than defining symmetric retention region around 0.5 as in Crump, this definition is based on the distribution of the PS in 2 treatment groups. The lower bound L is defined by the 100 × α_sth percentile of PS in the treated, and the upper bound U is defined by the 100 × (1−α_s)th percentile of PS in the untreated. Importantly, once this retention region [L, U] is constructed, every individual, both treated and untreated, outside this region is removed from the analytical data set. This is necessary to avoid artificially introducing PS nonoverlap. They examined 0.01, 0.025, and 0.05 for α_s. The rationale for this trimming strategy is to remove those who received a treatment choice that is contrary to the prediction: low-PS treated individuals and high-PS untreated individuals. They argued that these individuals were more likely to have strong unmeasured risk factors influencing the observed treatment choice.

Another trimming strategy, proposed by Walker et al. (6), is defined on the scale of the preference score, which is a monotone transformation of the PS, adjusting for treatment prevalence p and denoted as π_i here:

$$I_w=\left\{i\in I:{\mathrm{\pi }}_i\in \left[{\mathrm{\alpha }}_w,1-{\mathrm{\alpha }}_w\right]\right\}$$

They used α_w = 0.3 although it was not validated. The rationale for this trimming strategy is to keep patients with PS close to the mean PS in the trimmed cohort. The mean PS in the population equals the treatment prevalence. Therefore, one can argue that those individuals with e_i = p are the average patients most representative of the population of interest. The preference score transformation re-centers the distribution around such average patients. As a result, the trimming thresholds on the preference score scale are symmetric around 0.5.

Extension to the multinomial setting

In the 2-group setting of treated versus untreated, we need to consider only one scalar PS for the probability of being treated, P[A_i = 1 | X_i]. However, in the multinomial setting with J + 1 treatment groups, it helps to consider a PS vector e_i = (e_0i, e_1i, ..., e_Ji)^T having one probability of assignment for each one of the J + 1 treatment groups (9) where e_ji = P[A_i = j | X_i] for j ∈ {0,1, …, J}. The sum of the J + 1 elements is constrained to 1. We have introduced a corresponding generalization of the preference score transformation using the group prevalence p_j (see Web Appendix 2).

We can extend the definition of trimming using these generalized definitions of scores. The proposed definitions for the setting with J + 1 treatment groups are given in Table 1. Multinomial Crump trimming retains subjects who have all PSs above the threshold α_J,c. Multinomial Stürmer trimming is asymmetrical in that the lower threshold for each PS is different, unlike multinomial Crump trimming. The lower threshold is the 100α_J,cth percentile of each PS in the corresponding treatment group. Multinomial Walker trimming is similar to multinomial Crump trimming except for the use of a preference score in place of PS. We define only the lower threshold. Trimming the upper tail is implicit because individuals who have a very high PS for one treatment have very low PSs for the other treatments. These definitions reduce to the original definitions when there are only 2 groups (Web Appendix 2). These lower thresholds are indexed with J to indicate the need to adjust for the number of groups J + 1. This adjustment is required because the threshold values used in the 2-group setting can become too strict as the number of treatment groups increases. We used tentative values for our 3-group empirical illustration (Table 2).

Table 2.

Tentative Threshold Values for Propensity Score Trimming in the 3-Group Setting in Comparison With the Original Threshold Values for the 2-Group Setting

Study	No. of Groups	Crump et al.a	Stürmer et al.b	Walker et al.c
Original	2	0.100	0.050	0.300
Ours	3	0.067	0.033	0.200

^a Propensity score scale (4).

^b Group-specific propensity score quantile scale (5).

^c Preference score scale (6).

Empirical data illustration in the 3-group setting

We have illustrated how the trimming methods worked in the 3-group setting using observational data sets (10, 11) (Web Appendix 3) and visualization with ternary plots (12). A ternary plot is a triangle-shaped 2-dimensional representation of 3-dimensional data that sum to a constant (Web Figures 3 and 4). A point distant from a corner, for example, far from the top corner labeled 0, represents an individual with a low probability of being in group 0. The midpoint represents an individual with equal probabilities for all 3 groups. We also created an interactive web application that emulates a PS distribution (13).

Web Figure 5 shows the results of the 3 trimming methods on 3 different observational data sets. All proposed multinomial trimming methods resulted in triangular retention regions. Crump trimming resulted in fixed trimming bounds regardless of the PS distribution. The other 2 methods were adaptive to the observed PS distribution. In the example of 3 cyclooxygenase-2 selective inhibitors (10), all 3 groups were of similar sizes (32,684 celecoxib users, 24,124 rofecoxib users, and 26,582 valdecoxib users) and had comparable distributions of patient characteristics, resulting in a concentrated cluster of all 3 groups on top of each other. Crump trimming retained all subjects. The other 2 methods retained most subjects.

We found 23,532 naproxen users, 21,880 ibuprofen users, and 5,261 diclofenac users in the nonselective nonsteroidal anti-inflammatory drugs example (10). Users were still similar across treatment groups as illustrated by their clustering, but the small size of the diclofenac group resulted in the off-centered location of the observations and off-centered bounds for Stürmer and Walker trimming. All 3 methods trimmed similar proportions in this specific instance.

When the indications were different, as expected in the diabetes medication example (11), the distribution of PSs became more visibly separated (distinct colors), leading to small percentages of subjects remaining after trimming. This can reduce efficiency, but more importantly, it might be necessary to narrow cohort eligibility criteria to provide more comparable groups. We had a disproportionately large sulfonylurea group (n = 113,429), followed by the insulin (n = 18,294) and the glucagon-like peptide 1 agonist (n = 14,278) groups. This imbalance again resulted in off-centered bounds for Stürmer and Walker trimming.

Simulation setup

We conducted a simulation study to examine the influence of the proposed multinomial PS trimming methods in combination with different PS confounding-adjustment methods on bias and efficiency in the setting of a CER with 3 treatment groups. The reporting follows the recommendations of Morris et al. (14). The simulation suite was written in R (R Foundation for Statistical Computing, Vienna, Austria) (15).

Data-generating mechanism

We detailed the formulation of the data-generating models in Web Appendix 4. Briefly, to introduce unmeasured confounders in the tails of the PS distribution, we extended the data-generating mechanism developed by Stürmer et al. (5) in the 2-group setting to the 3-group setting (Web Figures 6 and 7). Covariates X₁ through X₆ were considered the base variables that were measured, whereas covariates X₇ through X₉ were considered the rare confounders that remained unmeasured. As in Stürmer et al. (5), we calculated a tentative PS based on the measured covariates. The unmeasured binary covariates were then generated based on the tentative PS such that X₇ = 1 was more prevalent in those who had a high tentative propensity for group 0; X₈ = 1 was more prevalent in those who had a high tentative propensity for group 1; and X₉ = 1 was more prevalent in those who had a high tentative propensity for group 2. After constructing the full set of covariates both measured and unmeasured, the true PS was assigned based on coefficients given to all the covariates. The unmeasured covariates had strong “contraindication effects.” For example, when X₇ was present in an individual with a high tentative propensity of receiving treatment 0, this treatment assignment became much less likely (X₇ serving as a strong contraindication to an otherwise preferred treatment). Treatment A_i was then generated as a 3-group multinomial random variable taking on one of {0, 1, 2}. The outcome Y_i was a Poisson count random variable based on a linear predictor dependent on all the covariates and treatment. A log-link model was chosen to eliminate the problem of noncollapsibility (16), which complicates the calculation of true effects (Web Appendix 4).

Methods to be evaluated

We compared the 3 types of multinomial PS trimming methods defined above in combination with different confounding-adjustment methods. Each trimming method was examined at several trimming thresholds to compare alternative cutoffs (Web Appendix 4). We used the 3-group IPTW (7), matching weights (MW) (17, 18), and overlap weights (OW) (19–21) as confounding adjustment methods. Consideration of these 3 weighting schemes permitted evaluation of the sensitivity of any observed benefit of trimming to this choice.

Estimand of interest

We estimated the alternatively weighted log rate ratios for contrasts of group 1 versus group 0, group 2 versus group 0, and group 2 versus group 1 in the overall study population as well as in the PS-trimmed cohort.

Performance measures

The trimmed sample size, bias, standard error, and mean squared errors were examined.

RESULTS

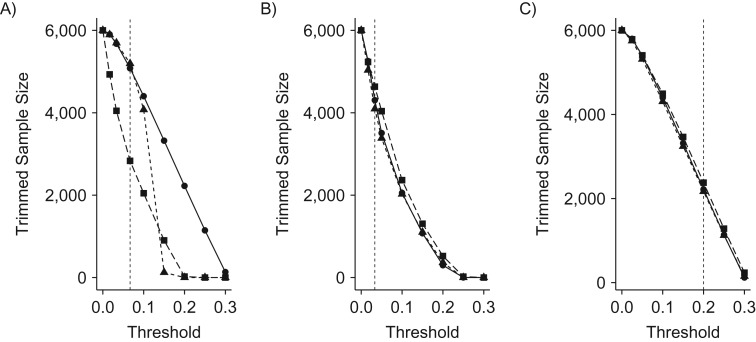
We examined 9 scenarios of varying data configurations, each conducted 500 times. Figure 2 shows the sample size decrease after trimming (methods as the columns of panels) at different thresholds (x-axis). The strength of unmeasured confounding did not affect the proportion of trimmed observations, because this strength of unmeasured confounding was manipulated by changing the coefficients for the outcome-generating model but not the treatment-generating model. The size of trimmed cohorts after trimming differed according to the treatment prevalence in the Crump trimming because these trimming thresholds did not adapt to the skewed distribution of PS as seen in the empirical examples (Web Figure 5). In the 10:10:80 setting, in particular, the center of the PS distribution was close to group 2 (right lower corner in the ternary plot), resulting in a larger proportion of the cohort trimmed by this method. Walker trimming provided most similar numbers of patients remaining in the cohort regardless of the treatment prevalence. This is because the Walker trimming region is around the average PS (i.e., a region where the treatment prevalence coincides with the full-sample prevalence).

Figure 2.

Simulated samples size after trimming at different thresholds, using simulated data. The scales for the thresholds were the propensity score scale for the Crump method (4) (A), quantiles of propensity score for the Stürmer method (5) (B), and the preference score scale for the Walker method (6) (C). The vertical broken hairlines are at the tentative thresholds used for the empirical data illustration. The solid line with circles represents the 33:33:33 treatment prevalence. The dotted line with triangles represents the 10:45:45 treatment prevalence. The broken line with squares represents the 10:10:80 treatment prevalence. The original sample size was n = 6,000 in all prevalence scenarios. Both Stürmer and Walker methods trimmed similarly regardless of treatment prevalence given that they accommodated skewed PS distributions. Crump trimming, on the other hand, trimmed differently at the same trimming threshold across treatment prevalence scenarios.

Web Figure 8 illustrates the bias in the setting of moderate unmeasured confounding with different treatment prevalence, various trimming methods, and trimming thresholds. The bias in the unadjusted analysis at trimming threshold zero (no trimming) shows the direction and magnitude of the total confounding including both measured and unmeasured confounding. As expected from the principle of restriction as a measure to control confounding (if variables do not vary in the analysis cohort, they cannot confound), trimming reduced the bias in unadjusted analyses until the threshold where the cohort became too small for outcome analyses. Use of MW and OW resulted in a reduction of bias even without trimming. However, a small bias persisted in the other direction except for the 1-versus-0 contrast. Bias of similar magnitude appeared in the other direction with IPTW. Reduction in residual confounding was seen for all weighting methods. The only exception was that in the 10:10:80 treatment prevalence scenario, the bias increased for 2-versus-0 and 2-versus-1 contrasts with Crump trimming beyond the 1/60 threshold. The reason for exacerbated bias seems to be the very skewed PS distribution. The average PS vector corresponded to the marginal prevalence (i.e., (0.1, 0.1, 0.8)^T). Therefore, group 2 would distribute closer to the left lower corner in the ternary plot, preferentially trimmed by Crump trimming. Estimation was less reliable for contrasts involving group 2 as a result. Stürmer and Walker trimming performed similarly regardless of the treatment prevalence. Overcorrection occurred with PS trimming in the 1-versus-0 contrast, in which MW and OW did not have residual confounding. Further trimming resulted in a return to less biased estimates. See also Web Figures 9 and 10.

Web Figure 11 illustrates the corresponding simulation standard error of estimates. IPTW standard error took a convex shape, initially benefiting from trimming but eventually increasing due to the small sample sizes after trimming. This IPTW standard-error reduction appeared in all 3 trimming methods, although only Crump trimming was proposed for improved precision. Among the thresholds examined in the simulation, the smallest standard error was attained at around 0.07 for Crump, 0.03 for Stürmer, and 0.1 for Walker trimming, indicating that the rule-of-thumb threshold of 0.2 for Walker trimming increased standard error in our simulation scenarios. Neither MW nor OW standard error clearly benefited from trimming. Stürmer trimming, in particular, resulted in a quick increase in standard error with MW and OW. Compared with other methods, Crump trimming seemed to offer the minimum IPTW standard error in the absence of unmeasured confounding (Web Figure 12). See Web Figure 13 for strong unmeasured confounding.

Web Figure 14 illustrates the mean squared errors of the estimators calculated as variance + bias², which represents the variability around the true value of the parameter. The variance term dominated the bias term with moderate unmeasured confounding. For IPTW, the minimum mean squared error was achieved at around 0.07 with Crump trimming, 0.017 for Stürmer trimming, and 0.05–0.10 for Walker trimming. The results for MW and OW were similar although the initial decrease in mean squared error was seen only in some settings (2-versus-0 and 2-versus-1 contrasts, particularly with 10:45:45 treatment prevalence). For the 1-versus-0 contrast, no apparent benefit was observed with any of the trimming methods or thresholds. See also Web Figures 15 and 16.

DISCUSSION

Several PS trimming methods have been proposed to improve the validity and efficiency of 2-group observational studies requiring PS-based confounding control (4–6). We extended these trimming methods to the multinomial treatment setting and conducted a simulation study in the 3-group setting. We specifically examined the interplay of bias introduced by confounders present in the tails of PS distribution and the variance of estimators with increasing trimming. All methods reduced bias in IPTW, MW, and OW estimators in most scenarios. However, multinomial Stürmer and Walker trimming were more successful in bias reduction when the 3 treatment groups had very different sizes (10:10:80), skewing the PS distribution. Trimming a small fraction of observations in all 3 methods decreased variance for IPTW but not for MW or OW. At the proposed rule-of-thumb thresholds, multinomial Crump and Stürmer trimming achieved variance reduction better in our simulation scenarios.

For the specific purpose of reducing bias by unmeasured confounders in the tails of multinomial PS distributions, Stürmer and Walker trimming might be better suited when the prevalence of treatment groups is quite different. Stürmer and others have suggested that this type of unmeasured confounding bias might be a reason for apparent “treatment effect heterogeneity” (truly a bias) seen in the tails of binary PS in the 2-group observational study setting (5, 22). This bias can also happen in the multinomial setting in the presence of a strong indication for one of the drugs or a strong contraindication against one of the drugs that is unmeasured. Diabetes medications provide an illustrative example. Those who have severe diabetes and observable clinical indications for insulin might be found in one of the oral medication groups. Such patients are more likely to have unobserved contraindications for insulin such as frailty, which could strongly influence many outcomes. We simulated this type of setting and demonstrated that trimming reduced the bias by strong unmeasured contraindications.

Progressively stricter trimming reduced bias, but this was at the cost of efficiency once the trimmed sample size became too small. In the simulation scenarios that we examined, we found that relatively limited PS trimming gave the best balance of bias and variance as assessed by mean squared errors. In our simulation, Walker trimming retained the fewest subjects, although this can vary depending on the PS distribution.

Another critical trade-off is the changing estimand when treatment effect heterogeneity exists. The target of inference, the population of individuals for whom we estimate the treatment effects, changes with trimming. Although PS trimming, a form of restriction, is expected to improve the validity of inference as long as all groups are trimmed in the same manner (23), the generalizability might be compromised. However, the type of patients retained after trimming can be argued to be patients with reasonable chances of being assigned to any of the treatment groups (i.e., individuals for whom CER is most relevant (6)), In practice, one should vary the trimming threshold to examine the sensitivity of the results related to progressively stricter trimming thresholds (24).

Our focus was bias by unmeasured risk factors that were more prevalent in the tails of PS distribution. This focus can be considered a multinomial equivalent of what Stürmer et al. examined (5). Importantly, the original intentions of the methods from Crump et al. (4) and Walker et al. (6) were somewhat different from those of Stürmer et al. Crump et al. emphasized the efficiency argument given that the PS model was correct and unmeasured confounding was absent. Their method’s strength is the proven minimum variance with IPTW under some constraints, although multinomial Crump trimming also reduced residual bias in most settings in our simulation. Interestingly, multinomial Stürmer and Walker trimming also reduced the variance of the IPTW estimator, albeit to a lesser extent. MW (17, 18) and OW (19–21) were more efficient than IPTW; thus, no trimming methods examined improved the efficiency of MW or OW estimators. One might argue that PS trimming is of little benefit for MW and OW. However, small bias reduction did occur even for MW and OW. Walker et al. (6) focused primarily on identifying CER settings where unmeasured confounding might be less of a concern. The tool’s role as a trimming tool was secondary. In our simulation study focusing on reducing unmeasured confounding bias in a given data set, we found that smaller thresholds (0.05 to 0.10 rather than proposed 0.20) were sufficient to reduce confounding.

Another potential approach to unmeasured confounding worth mentioning is PS calibration (25, 26). The important difference here is the requirement for an additional external validation data set that contains variables that are unmeasured confounders in the main data set. Our use of PS trimming to control for unmeasured confounding instead relies on the assumption that the tails of the PS contain individuals with unmeasured factors.

Although our definitions of multinomial PS trimming are natural extensions of the original binary PS trimming, they are not the only extensions. For example, PS trimming can be extended by considering all possible pairwise PSs rather than the single multinomial PS. However, the complexity of implementation increases more rapidly for the pairwise definition than for the multinomial definition. Importantly, all pairwise PSs must be defined for all patients. The pairwise PS for the A-versus-B contrast is estimated on groups A and B. However, we must assign this pairwise PS for the A-versus-B contrast even for those who are in group C. This counterintuitive approach is necessary to define the same retention region for all treatment groups and to capture those who are in equipoise for all treatment options. Otherwise, the principle of PS methods, assuring similar distribution of covariates in all treatment groups, is violated. The multinomial approach considers all treatment groups simultaneously; thus, it is not unnatural to assign all J + 1 probabilities of treatment assignment for each individual. It also has the advantage of having only one PS model rather than all possible pairwise PS models, which need to be fitted separately on relevant pairwise subsets of the entire data set.

Our study assumed that the relevant a priori clinical question was the comparison of treatment among subjects who had some chance of receiving any one of the multiple treatments. This assumption was an important rationale for modeling all groups in one multinomial PS model. On the other hand, we could construct pairwise PS and a pairwise PS-trimmed cohort for each one of the pairwise contrasts. The potential problem here is that each pairwise comparison might have a different target population. Having different target populations could cause nontransitive results, for example, A is better than B; B is better than C; but A is worse than C (27). The pairwise approach is more acceptable when we have one group that is the reference group or the drug-of-interest group. In this case, only the pairwise contrasts involving this one group are relevant, making nontransitivity less of a concern. These 2 approaches might result in similar and transitive effect estimates if those who are in pairwise equipoise are also in equipoise among all groups. If this does not hold, the multinomial trimming likely results in a small trimmed cohort as the separation between groups in the PS space might be greater. Ideally, investigators should assess the appropriateness of a multigroup CER question a priori. When multinomial PS trimming results in a much smaller cohort than the original, one might need to reconsider whether the data and eligibility criteria give sufficient overlap among groups to justify multigroup CER (6, 28).

The implications of a simulation study should be considered within the limitations of the data-generation process. We introduced unmeasured confounding in the tails of PS distributions similarly to Stürmer et al. (5), which involved a somewhat specialized 2-step covariate generation. The use of a count outcome in our simulation was for simplicity and consistency with the previous study (5). In theory, PS trimming is agnostic of the type of outcome because only PSs are used. However, difficult settings such as a rare binary outcome might affect the 3 trimming approaches differently.

In conclusion, we proposed a multinomial extension of the existing 2-group PS trimming methods and examined their performance with 3 treatment groups. The extensions of Stürmer and Walker’s PS trimming methods reduced bias in 3-group exposure settings even with highly imbalanced treatment frequencies. In practice, examining how effect estimates vary at various trimming thresholds can be a useful sensitivity analysis to assess potential unmeasured confounding in the tails of a multinomial PS.

Abbreviations

CER

comparative effectiveness research

IPTW

inverse probability of treatment weights

MW

matching weights

OW

overlap weights

PS

propensity score