Neural Quadratic Discriminant Analysis: Nonlinear decoding with V1-like computation

Abstract

Linear-nonlinear (LN) models and their extensions have proven successful in describing transformations from stimuli to spiking responses of neurons in early stages of sensory hierarchies. Neural responses at later stages are highly nonlinear, and have generally been better characterized in terms of their decoding performance on pre-specified tasks. Here, we develop a biologically plausible decoding model for classification tasks, that we refer to as neural Quadratic Discriminant Analysis (nQDA). Specifically, we reformulate an optimal quadratic classifier as an LN-LN computation, analogous to “subunit” encoding models that have been used to describe responses in retina and primary visual cortex. We propose a physiological mechanism by which the parameters of the nQDA classifier could be optimized, using a supervised variant of a Hebbian learning rule. As an example of its applicability, we show that nQDA provides a better account than many comparable alternatives for the transformation between neural representations in two high-level brain areas recorded as monkeys performed a visual delayed-match-to-sample task.

Introduction

Sensory “encoding” models, which describe how the inputs to a neuron are converted into its responses, have proven effective in a broad array of sensory modalities, brain areas, and species (e.g. Eggermont, Aertsen and Johannesma 1983, Jones and Palmer 1987, DiCarlo, Johnson and Hsiao 1998). Within vision, classic examples include the center-surround receptive field of a retinal ganglion cell (Enroth-Cugell and Robson 1966), the energy model of V1 complex cell (Adelson and Bergen 1985), and the divisive normalization model of gain control (Heeger 1992); as well as their more contemporary variants (e.g. Keat, Reinagel, Reid and Meister 2001, Rust, Schwartz, Movshon and Simoncelli 2005, Sharpee et al. 2006, Pillow et al. 2008, Carandini and Heeger 2011). Considerable effort has been devoted to developing and refining techniques for fitting these models to data derived from a single experiment (reviewed by Ringach and Shapley 2004, Schwartz, Pillow, Rust and Simoncelli 2006, Wu, David and Gallant 2006, Sharpee 2013). Successes were originally confined to brain areas positioned in early stages of the visual hierarchy, but have since been extended to intermediate stages (David, Hayden and Gallant 2006, Rust, Mante, Simoncelli and Movshon 2006, Willmore, Prenger and Gallant 2010, Mineault, Khawaja, Butts and Pack 2012, Sharpee, Kouh and Reynolds 2013). However, extending this approach to high-level brain areas has proven much more difficult.

One obstacle is that the techniques that have been developed to fit encoding models generally rely on a quantitative description of the inputs to the cells being fit. For example, encoding models of neurons within area MT have been fit based on a simulated population of inputs arriving from area V1 (Rust, Mante, Simoncelli and Movshon 2006). Similar methods have been applied in V2 (Willmore, Prenger and Gallant 2010), V4 (David, Hayden and Gallant 2006, Sharpee, Kouh and Reynolds 2013), and MST (Mineault, Khawaja, Butts and Pack 2012). But these approaches can only extend our understanding one stage beyond what is already relatively well-understood.

An additional challenge arises from the fact that neural responses at higher stages become increasingly affected by behavioral task and context, and models for the “decoding” of task performance have generally been more successful than those for the “encoding” of sensory stimuli (Hung, Kreiman, Poggio and DiCarlo 2005, DiCarlo and Cox 2007, Churchland et al. 2012, Mante, Sussillo, Shenoy and Newsome 2013, Pagan, Urban, Wohl and Rust 2013, Rigotti et al. 2013). These decoders have been generally assumed to be linear. And while the relative successes of handful of nonlinear (as compared to linear) decoders have been evaluated with neural data (Bialek, de Ruyter van Steveninck, Rieke and Warland 1996, Yu et al. 2007, Graf, Kohn, Jazayeri and Movshon 2011, Astrand et al. 2014), the neural mechanisms underlying nonlinear decoding remain unclear.

Arguably, what is needed to bridge this gap in describing high-level neural computations are techniques that 1) allow us to fit and evaluate biologically plausible descriptions of how the inputs to a brain area are transformed into its output responses in order to perform a specific task, 2) do not depend on a complete, quantitative description of how the inputs are derived from stimuli, and 3) can capture nonlinear transformations commonly found in neural responses. Here we develop such an approach. We reformulate a quadratic decoder, optimized for a pre-specified classification task, as a linear-nonlinear-linear-nonlinear (LN-LN) cascade model, analogous to models used for describing encoding in early visual areas. We show that this computation, which we call neural Quadratic Discriminant Analysis (nQDA), can account for the increase in classification performance between high-level visual brain areas IT and perirhinal cortex during a target search task. We also introduce a biologically plausible supervised learning rule for optimizing the parameters of nQDA.

Results

nQDA, a nonlinear decoder expressed as an LN-LN model

Consider the problem of classifying a set of inputs (e.g., “Is observed input X a member of group A or group B?”) based on a population of neural responses. The simplest solution is to assume a linear classifier, expressed as:

$$f_{\mathit{\text{LIN}}}(r)=m^{T}r+k$$ (1)

where r is the N-dimensional population response vector, m^Tr is the weighted sum (inner product) of the responses with N-dimensional vector of weights m, and k is a scalar constant. The class assignment (A versus B) is determined by the sign of the output (positive versus negative, respectively). The decision boundary corresponds to a hyperplane in the population response space, positioned such that it separates the two classes (Fisher 1936, Cortes and Vapnik 1995; Fig. 1a, top left). Many algorithms are available for fitting the parameters (m,k) (Duda, Hart and Stork 2000) and the “best” choice depends on the distribution of the data, noise properties, and the costs of making mistakes. When the population responses for each class are Gaussian distributed, with equal covariance, the maximum likelihood solution is the Fisher Linear Discriminant (FLD; Fisher 1936). FLD parameters may be expressed directly as:

$$m={\sum }^{-1}·({\mu }_1-{\mu }_2)k=\frac{1}{2}·\left[\right({\mu }_2^T·{\sum }^{-1}·{\mu }_2)-({\mu }_1^T·{\sum }^{-1}·{\mu }_1\left)\right]$$ (2)

where μ_i indicates the mean population response vector for the ith class and Σ is the common response covariance matrix. If the two covariances differ, this is typically replaced with their average, $\sum =\frac{1}{2}·({\sum }_1+{\sum }_2)$, although this is no longer the maximum likelihood solution.

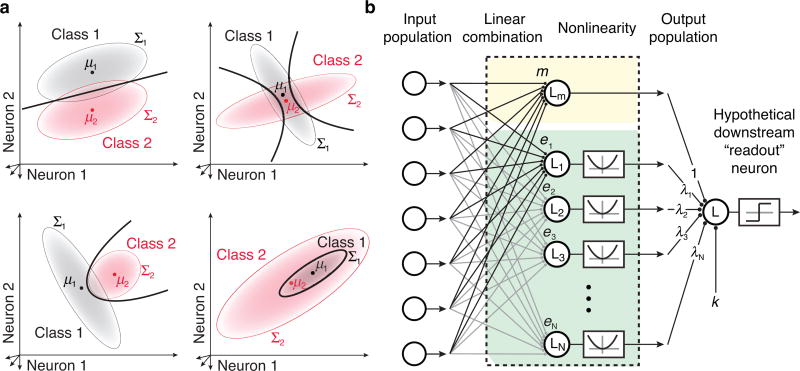
Figure 1. The nQDA framework.

a) Optimal quadratic discrimination boundaries (black lines) for four example pairs of population response distributions. Hypothetical class distributions are each multivariate Gaussian (indicated by red and gray elliptical regions), with means μ₁ and μ₂, and covariances Σ₁ and Σ₂. Top left: a scenario in which the means of the two classes differ and the covariances are matched. In this special case, the optimal classifier is linear; Top right: a scenario in which the means of the two classes are similar and a linear classifier alone is an ineffective decision boundary. Instead, the optimal classifier uses a pair of parabolic boundaries. Bottom left: an example with differing mean and covariance, yielding a single parabolic boundary. Bottom right: an example yielding an elliptical boundary. b) Depiction of the nQDA model, which implements the optimal quadratic classifier (Equations 3,4) as an LN-LN model (Equation 6). The first LN transformation is achieved with a bank of linear filters, with all but the first followed by a squaring nonlinearity. The outputs of these individual LN units are combined via a weighted sum, followed by a threshold function which determines the class membership.

Linear classifiers are considered biologically plausible - a weighted sum of inputs from the population in question, followed by a threshold nonlinearity. But linear classifiers are limited, relying on differences between the means of the class response distributions. Arguably, the simplest nonlinear extension is to include a quadratic term in the classifier:

$$f_{\mathit{\text{QUAD}}}(r)=r^T\mathit{\text{Qr}}+m^{T}r+k$$ (3)

where Q is an N-by-N symmetric matrix. As with the linear classifier, the class assignment is determined by the sign of this function. Similar to linear classifiers, multiple methods exist for fitting the parameters of a quadratic classifier (e.g. Kendall 1966, Hofmann, Schölkopf and Smola 2008). When the population responses are Gaussian-distributed, the maximum likelihood solution (known as Quadratic Discriminant Analysis (QDA; Kendall 1966)) corresponds to:

$$Q=\frac{1}{2}·({\sum }_2^{-1}-{\sum }_1^{-1});m={\sum }_1^{-1}{\mu }_1-{\sum }_2^{-1}{\mu }_2;$$ (4)

$$k=-\frac{1}{2}\left(\text{log}\right|{\sum }_1|-\text{log}|{\sum }_2|+{\mu }_1^T{\sum }_1^{-1}{\mu }_1-{\mu }_2^T{\sum }_2^{-1}{\mu }_2)$$

The incorporation of the quadratic term creates a more powerful classifier, which exploits differences in covariance, generally resulting in curved decision boundaries in the population response space (Fig. 1a).

Despite their potential for decoding information embedded in a population, it is not obvious how a brain area would implement QDA. Toward this end, and inspired by the successes of quadratic encoding models, we have reformulated QDA into a more biologically plausible framework. We first expand the quadratic term r^TQr (Equation 3) into a set of linear-nonlinear operations, using the eigendecomposition of Q. Specifically, we write Q = EΛE^T, where E = [e₁ e₂ ⋯ e_N] and $\mathrm{\Lambda }=\left[\begin{array}{cccc}\hfill {\lambda }_1\hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill {\lambda }_2\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill {\lambda }_N\hfill \end{array}\right]$. With this expansion, the quadratic term r^TQr of Equation 3 becomes:

$$r^T\mathit{\text{Qr}}=r^T\left(E\mathrm{\Lambda }{E}^T\right)r=\left(r^{T}E\right)\mathrm{\Lambda }\left(E^{T}r\right)={\left(E^{T}r\right)}^T\mathrm{\Lambda }\left(E^{T}r\right)=\sum _{i=1}^N{\lambda }_i·{\left(e_i^{T}r\right)}^2$$ (5)

That is, the term r^TQr can be computed as a linear projection of the response vector r onto the eigenvectors of Q, followed by a squaring nonlinearity, and a final linear re-combination weighted by the eigenvalues of Q. Substituting this back into the expression for QDA (Equation 3) yields:

$$f_{\mathit{\text{QUAD}}}=\sum _{i=1}^N{\lambda }_i{(e_i^{T}r)}^2+m^{T}r+k$$ (6)

This equation, combined with the final thresholding (decision) nonlinearity, specifies an LN-LN computation, as illustrated in Fig. 1b, which we refer to as neural QDA (nQDA).

Geometrical intuition of nQDA

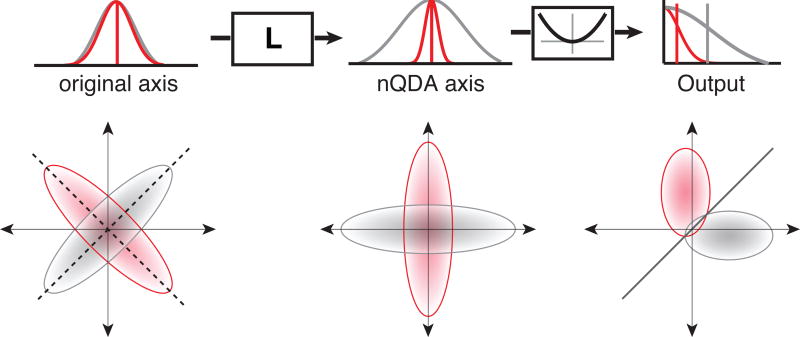
In this section, we provide an intuitive, geometrical description of how the nQDA computation converts the nonlinearly separable population representation of two classes into a more linearly separable format. In general, the information available to separate two classes can be regarded in terms of discrepancies between the moments of the two class distributions (i.e. mean, covariance, skew, …). Consequently, if the two classes are identical in all of their moments they cannot be separated. The second term of the nQDA solution (Equation 6) corresponds to a linear neuron which gathers the mean differences (i.e. the linearly separable information) present in the input population.

In contrast, the first term of Equation 6 is a sum over a set of nonlinear neurons that act to transform nonlinearly separable information available in the input population into a linearly separable format. In particular, differences in variance are converted into differences in mean. To achieve this, the linear weights of this set of nonlinear neurons serve to rotate the input space to a coordinate system that captures the largest/smallest differences in inverse covariances (Fig 2, left). Equivalently, since $\frac{1}{{\sigma }_1^2}-\frac{1}{{\sigma }_2^2}=\frac{{\sigma }_2^2-{\sigma }_1^2}{{\sigma }_1^2·{\sigma }_2^2}$, this rotation maximizes the normalized variance differences between the projected responses for the two (Fig. 2, middle). Squaring these linearly transformed responses acts to convert the variance differences into mean differences (Fig. 2, right). These mean differences allow linear separation of the response clouds corresponding to the two classes in the output population.

Figure 2. Geometrical intuition of nQDA.

Left, Response distributions of a hypothetical population to two classes, for which both the response mean and variance of each individual neuron are matched, but the class covariances differ. Dashed lines indicate nQDA axes (Equation 5). Center, Population responses linearly transformed to nQDA axes, along which the responses exhibit large relative variance differences between the two classes. Right, The squaring nonlinearity converts these variance differences into mean differences, and the resulting class distributions are more readily separated by a linear classifier (black line).

nQDA replicates the transformation between IT and PRh

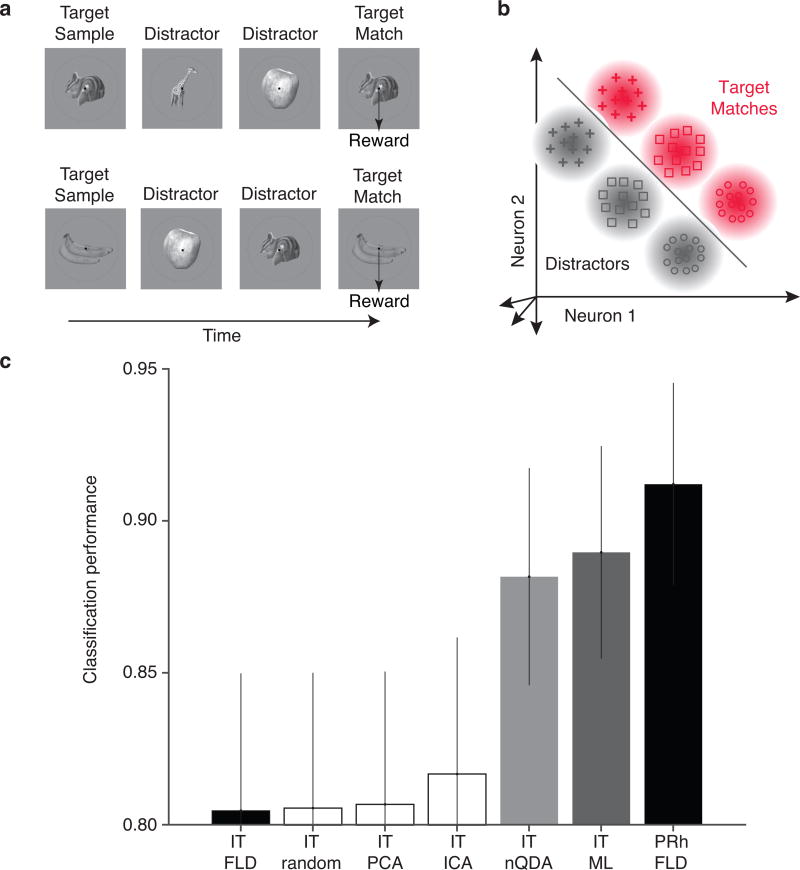
To determine the degree to which nQDA is useful for modeling neural data, we used it to characterize the transformation between responses of inferotemporal cortex (IT) and perirhinal cortex (PRh). Specifically, we recorded neural responses from IT and PRh as monkeys performed a delayed-match-to-sample sequential visual target search task that required them to indicate when different target images appeared within sequences of distractors (Fig. 3a).

Figure 3. Application of nQDA to recorded neural responses.

a) We recorded neural responses in IT and perirhinal cortex (PRh) as monkeys performed a delayed-match-to-sample task. On each trial, monkeys were presented with a cue indicating the identity of the target (“target sample”), followed by a random number of distractors and a target match. Monkeys were required to indicate when the target match appeared. b) Response clouds of two hypothetical neurons to target matches (red) and distractors (gray), where different shapes indicate different images. As described previously (Pagan, Urban, Wohl and Rust 2013), this task can be reformulated as a two-way classification between the set of responses to all the images presented as target matches versus the set of responses to the same images presented as distractors. c) Trial-level cross-validated classification performance of different decoders applied to IT, along with a linear decoder applied to PRh. Plotted are the mean performance values, with error bars indicating bootstrapped estimates of standard error. Classifiers include: an FLD decoder applied to IT and PRh (black); LN-LN decoders that include random, PCA and ICA decompositions applied to IT followed by optimized marginal nonlinearities and a final, FLD linear decoder (white); the nonlinear nQDA decoder applied to IT (light gray); and a nonlinear, maximum likelihood decoder applied to IT (dark gray).

On each trial, monkeys sequentially viewed images while maintaining fixation and indicated when they saw a target image by shifting gaze to a response dot on the screen. Our experimental design included four images presented in all possible combinations as a visual stimulus, and as an intended target, resulting in 16 experimental conditions. We held the target image fixed for short blocks of trials and we presented the same images as both targets and distractors in different blocks that were repeated several times. As monkeys performed this task, we recorded neural responses in IT or PRh using multichannel probes. To quantify the population response on any given trial, we counted spikes in a window starting 50 ms after stimulus onset (to allow time for signals to reach these brain areas) and ending at 220 ms, which always precedes the monkeys’ eye movement responses. Here we present results based on population data concatenated across experimental sessions into larger “pseudopopulations” of 164 neurons for each brain area, following on our earlier report that factors specific to simultaneously recorded populations (i.e. noise correlations) do not affect population performance (Pagan, Urban, Wohl and Rust 2013; Supp Fig S2).

This task can be envisioned as two-way classification of the same images presented as “target matches” (i.e. looking at and for the same image, for which the monkey is instructed to make an eye movement) versus “distractors” (i.e. looking at and for different images, for which the monkey is instructed to maintain fixation; Fig 3b). To avoid the possibility that population performance could rely on factors other than the “target match” signal, we used an equal number of target matches and distractors (i.e. at any one time we selected a subset of 4 of 12 possible distractors) and we explored all possible subsets of distractors that spanned all visual stimuli and all targets (see Methods).

As reported previously (Pagan, Urban, Wohl and Rust 2013), we found that total information for this classification was approximately matched in IT and PRh but that it was more linearly separable in PRh. This result is recapitulated in Figure 3c, where trial-level cross-validated performance of a linear decoder in PRh (“PRh FLD”) is seen to be similar to the performance of a nonlinear maximum likelihood decoder applied to IT (“IT ML”), suggesting that the linearly separable, task-relevant information contained within PRh is also largely present in its inputs arriving from IT. However, the performance of a linear classifier acting directly on IT responses (“IT FLD”) is significantly worse that the ML performance, suggesting that the information is nonlinearly embedded within IT. These results are consistent with a feed-forward mechanism in which PRh performs computations to increase linear separability of its IT inputs (Pagan, Urban, Wohl and Rust 2013, Pagan and Rust 2014).

We wondered how well nQDA could “mimic” computations performed by PRh, when applied to inputs arriving from IT. We found that a 164-dimensional nQDA-transformed IT population (Fig. 3c, “IT nQDA”) performed significantly better than a linear read-out of IT (p=0.022), nearly as well as the upper bound imposed by the ML read-out of the same data, and comparably to a linear read-out of PRh. These results suggest that nQDA is largely successful at capturing the nonlinear transformation of target match information from IT to PRh.

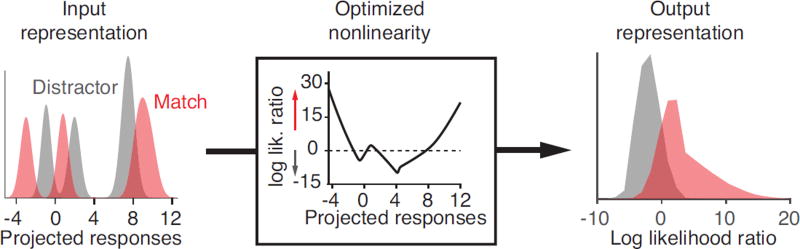
We also considered whether a number of alternative LN-LN models could account for PRh computation. The structure of each of these alternative LN-LN models mirrored the structure of nQDA (Fig. 1b, Equation 6) insofar as each model began by projecting the same inputs onto a bank of linear filters, each followed by a scalar nonlinearity, and the resulting output values were combined using a final linear decoder. From a geometric perspective, these initial linear transformations can be interpreted as projections onto different sets of axes that span the original input space (Fig. 2), and our goal was to compare alternative methods for selecting these axes (i.e. random, PCA and ICA) with nQDA. For each model, the first axis of the linear transformation was chosen to be the same as the first nQDA axis (thus preserving the linearly separable information that already existed in IT), while the remaining axes were chosen using one of several methods (described below). Whereas nQDA used a fixed (squaring) nonlinearity, we allowed each of these alternative models to use a different nonlinearity for each axis, chosen as the log likelihood ratio between the projected responses to matches and distractors (see Methods, Fig. 8).

Figure 8. Computing the optimal nonlinearity for each alternative nonlinear classifier axis.

The distributions of the responses to each condition, projected along each axis, were modeled as Gaussian distributions and the responses to the set of target matches and set of distractors were each modeled by mixtures of these Gaussian distributions. To compute an optimized nonlinearity that maximally separated the means of the target matches and distractors, we computed the log likelihood ratio between the mixture of Gaussians for matches and the mixture of Gaussians for distractors. This optimized nonlinearity was computed using the training data, and was applied to the test data following the application of different linear projections to obtain the results in Figure 3c.

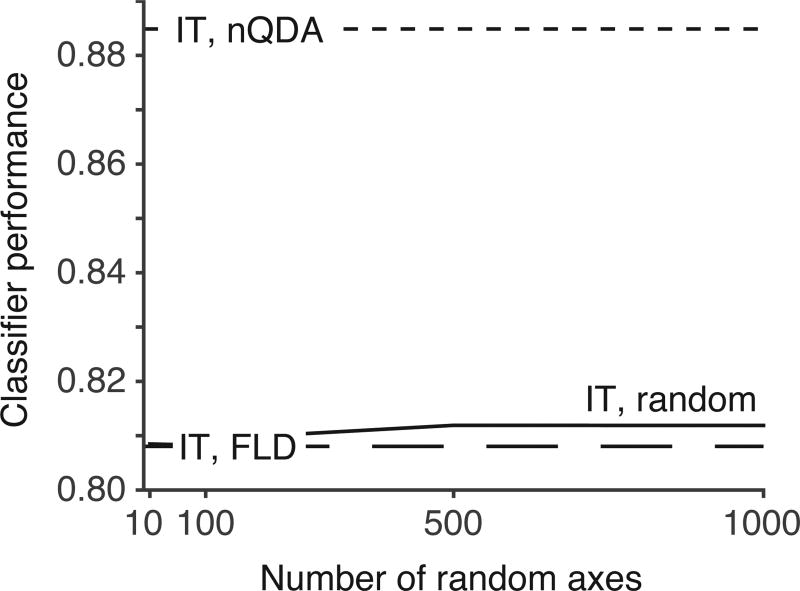
For the first alternative model, we chose 164 random, orthogonal axes (equal to the number of IT neurons). On average, this transformation did not exhibit better performance than the FLD applied to IT data (Fig. 3c). The performance of a random linear transformation can be improved by increasing the output dimensionality, but we found that using up to 1,000 random axes only led to a small improvement (Fig. 4). It is worth noting, however, that a random linear transformation with output dimensionality equal to the number of degrees of freedom in the linear and quadratic terms in Equation 3 (N + N(N+1)/2; in our case, ~14,000 axes) can exactly match the performance of nQDA.¹

Figure 4. Performance of an LN-LN model with random axes improves marginally with increasing output dimensionality.

Classifier performance is shown as a function of number of random axes. In contrast to the analysis depicted in Fig 3c “IT random”, which used a randomly chosen, orthogonal set of axes (with dimensionality N=164, equal to that of the input space), here each random axis was selected independently. These randomly weighted inputs were then passed through a nonlinearity optimized for each axis and the responses were combined using a final, linear decoder. For comparison the FLD and nQDA decoders applied to IT (i.e. the same values in Fig 3c) are also indicated (dashed lines).

We also investigated whether an LN-LN model based on PCA or Independent Component Analysis (ICA) linear transformations could match the performance of nQDA. We fit both methods to training subsets of IT population response to 4 target match and 4 distractor conditions (exploring all possible distractor subsets that spanned the four visual and four target dimensions, as described above), and we kept all the resulting dimensions. We found that a model using PCA as the initial linear transformation could not replicate the transformation from IT to PRh (Fig. 3c, “IT PCA”). Similarly, we found that, despite a modest increase in performance over random projections and PCA, ICA also failed to replicate the transformation from IT to PRh (Fig. 3c, “IT ICA”). In summary, these results show that the optimal quadratic classifier implemented with nQDA provides an efficient (in terms of the number of cells) explanation of the transformation between high-level brain areas IT and PRh, surpassing other LN-LN models with optimized (non-quadratic) nonlinearities.

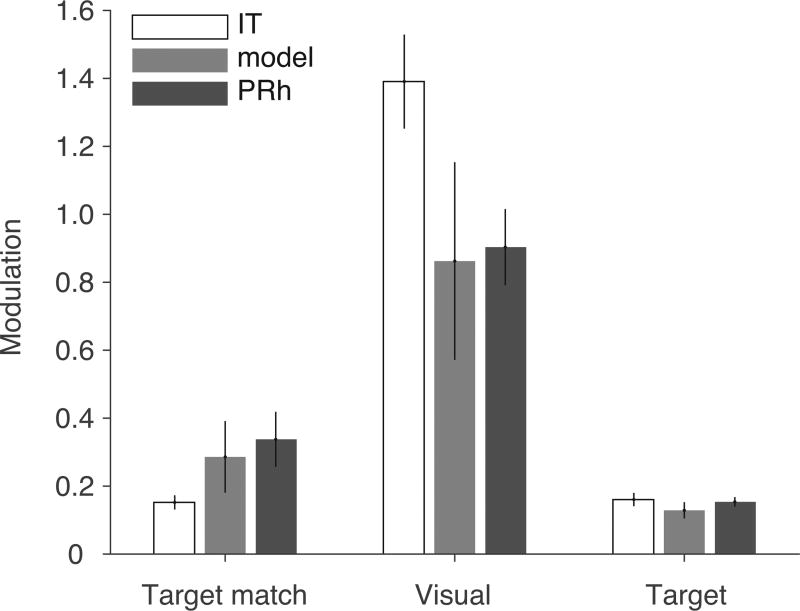
As an additional assessment of the degree to which nQDA replicated the transformation from IT to PRh, we examined the relative amounts of different task-relevant signals represented within the two brain areas. Specifically, we decomposed each neuron’s responses into three component signals: 1) “visual” modulation (i.e. response modulation by changes in the identity of the visual stimulus), 2) “target” modulation (i.e. response modulation by changes in the identity of the target) and 3) “target match” modulation (i.e. modulation by changing whether a condition is a target match or a distractor), using the techniques described by (Pagan and Rust 2014; see Methods). We quantified the strength of each of these signals by estimating the proportion of spike count variance they accounted for, relative to the total variance across trials. As expected from the population performance results, the amount of target match signal increased from IT to PRh and the nQDA model replicated this increase (Fig 5, ‘Target match’). Additionally, the amount of visual signal (which reflects visual image identity) decreased from IT to PRh, and this decrease was also replicated by the nQDA model (Fig 5, ‘Visual’). Although the target match signal is similar to what was optimized by nQDA, visual signals were not directly fit by our procedure and replication of their decrease from IT to PRh is thus non-trivial. We found no differences in the amount of target signal (which reflects target identity) between IT, PRh and the model (Fig 5, ‘Target’). These results provide additional support that nQDA captures transformations between IT and PRh.

Figure 5. nQDA replicates differences in signal magnitudes between IT and PRh.

The responses of each neuron were decomposed into different types of task-relevant signals by quantifying, for each neuron, the amount of spike count variance (around the grand mean spike count) that could be attributed to changes in experimental conditions, including: “Target match” (whether a condition was a target match or distractor); “Visual” (image identity); and “Target” (target identity) (see Methods). These signal variances were then normalized by each neuron’s trial-by-trial variance, averaged across conditions, to obtain unitless quantities that reflect the ratio of each type of signal relative to the noise. Shown are the means and standard errors of these signal measures, computed for each population.

Biologically plausible learning of nQDA parameters

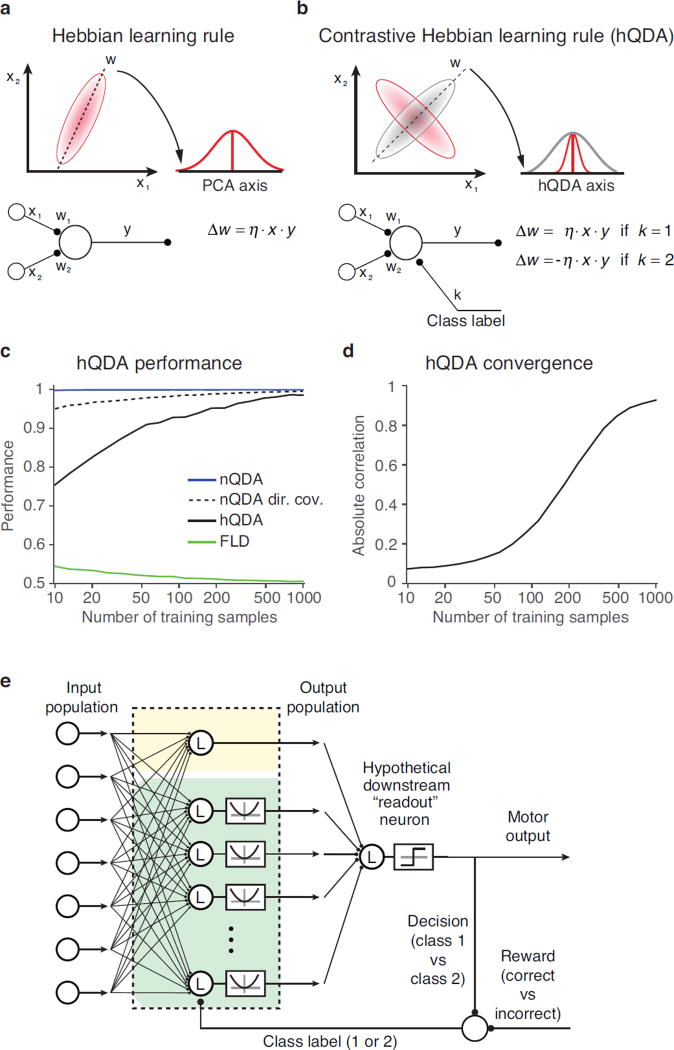
In the previous section, the parameters of an nQDA transformation were optimized by estimating the mean and covariance of the IT population responses to each of the classes, and inserting these into Equations 4 and 5. We wondered how neural populations could learn these parameters, without direct knowledge of the class covariances, and without computing the eigendecomposition of the difference of the inverse covariances. While we lack a full solution to this problem, we have gained insight into the special case in which the two class distributions have matched eigenvectors but different eigenvalues (i.e. two input distributions with variance distributed along the same axes but in different amounts, including possible differences in rank order). For this case, a supervised extension to a Hebbian learning algorithm converges to nQDA weights and we refer to this algorithm as “Hebbian QDA” (hQDA).

We first note that when the eigenvectors of two covariance matrices are matched, the eigendecomposition of difference of the inverse covariances (necessary for nQDA, Equation 4), can be computed via the eigendecomposition of the difference of the covariances. This emerges from the well-known fact that the eigenvectors of a matrix are the same as those of its inverse. Given this, we show that a simple local learning rule converges to the eigenvectors of the difference between class covariances. The hQDA learning rule is an extension of previous work by Oja, who revealed that a Hebbian learning algorithm converges to the first PCA principal component (Oja 1982). To review that work, we consider a simple scenario where a model neuron receives only two inputs, x₁ and x₂ which are weighted by synaptic weights w₁ and w₂ (Fig. 6a). The model neuron produces the output y as the linear combination of the 2-dimensional vectors x and w:

$$y=x^{T}w$$ (7)

According to Hebbian learning, weights w₁ and w₂ are increased when the activity of inputs and output are correlated, i.e. when the input and the output “fire together”, they “wire together”. This is achieved by modifying the weights by a quantity Δw proportional to the vector of inputs x, scaled by the output value y, and by a constant coefficient η called the learning rate:

$$\mathrm{\Delta }w=\eta ·x·y$$ (8)

Substituting y from Equation 7 leads to:

$$\mathrm{\Delta }w=\eta ·x·x^{T}w$$ (9)

Finally, by taking the mean value of Δw, we obtain the following equation:

$$\langle \mathrm{\Delta }w\rangle =\langle \eta ·x·x^{T}w\rangle =\eta ·\langle x·x^T\rangle w=\eta ·\sum ·w$$ (10)

where we used angle brackets 〈·〉 to denote averages, and Σ to indicate the covariance of x. The solution of this equation (Oja 1982) reveals that Hebbian learning converge to weights corresponding to the leading eigenvector of the covariance matrix, i.e. to the first Principal Component (Fig. 6a).

Figure 6. Approximate nQDA parameters can be learned with a supervised, Hebbian rule, hQDA.

a) As described previously by Oja (Oja 1982), the Hebbian algorithm recovers the first PCA axis. Top, the population response distribution for two hypothetical neurons to two classes of stimuli. The first Principal Component axis (dotted line) captures the axis with maximum variance, summed across conditions. Bottom, depiction of a neuron that receives inputs from the two neurons depicted at the top, and whose weights are modified according to a classic Hebbian rule. Application of the Hebbian rule results in the convergence of the input weights to the first PCA axis. b) Top, the population response distributions for two hypothetical neurons to two classes of stimuli. The first hQDA axis captures the axis with maximum variance difference (dotted). Bottom, depiction of the same neuron as shown in panel a but with an additional input that indicates the class label for each condition. The contrastive Hebbian rule is implemented in this framework by switching the sign of the classic Hebbian term according to this label. c) Cross-validated classification performance of a number of decoders applied to a neurally-inspired dataset (see text), plotted as a function of the training set size. Classifiers include: FLD (green); nQDA (blue); hQDA (black); and nQDA with the use of direct covariances instead of inverse covariances (black, dashed). hQDA was set to retrieve 6 axes, i.e. equal to the number of informative dimensions in the input space (see Methods). d) Average absolute correlation between the axes obtained by applying hQDA to the same simulated data and the corresponding closed-form eigenvectors computed via the difference of covariances. Convergence to closed-form axes is shown as function of the size of the training set. e) Diagram for model in which the contrastive Hebbian rule could be used to learn the hQDA parameters, where the “class label” is determined for each condition as a combination of the decision and whether the decision was rewarded.

The hQDA algorithm is inspired by the Hebbian rule (Equation 10), but it contains the modification that the model neuron receives an additional “top-down” supervision signal that specifies the class k of the current input (Fig. 6b; e.g., k=1 for target matches and k=2 for distractors). This top-down input acts to switch the sign of the learning rule between the two classes: it adopts a Hebbian rule for one class and an anti-Hebbian rule for the other and as such, we refer to it as a “contrastive” Hebbian rule:

$$\{\begin{array}{cc}\hfill \mathrm{\Delta }w=\eta ·x·y\hfill & \hfill \text{if }\mathrm{k}=1\hfill \\ \hfill \mathrm{\Delta }w=-\eta ·x·y\hfill & \hfill \text{if }\mathrm{k}=2\hfill \end{array}$$ (11)

If we now substitute Equation 7 into Equation 11 we obtain:

$$\{\begin{array}{cc}\hfill \mathrm{\Delta }w=\eta ·x·x·w\hfill & \hfill \text{if }\mathrm{k}=1\hfill \\ \hfill \mathrm{\Delta }w=-\eta ·x·x·w\hfill & \hfill \text{if }\mathrm{k}=2\hfill \end{array}$$ (12)

Taking the average value of Δw we get:

$$\langle \mathrm{\Delta }w\rangle =\langle \eta ·x_{k=1}·x_{k=1}·w\rangle -\langle \eta ·x_{k=2}·x_{k=2}·w\rangle =\dots \dots =\eta ·\langle x_{k=1}·x_{k=1}\rangle ·w-\eta ·\langle x_{k=2}·x_{k=2}\rangle ·w=\eta ·({\sum }_1-{\sum }_2)·w$$ (13)

where x_{k =1} indicates the inputs labeled for class 1, x_{k =2} indicates those of class 2, Σ₁ is the covariance for the inputs labeled for class 1, and Σ₂ is the covariance for those of class 2. Note that this expression is equivalent to Equation 10, with the exception that the covariance matrix Σ is now substituted by the covariance difference Σ₁ − Σ₂. Consequently, the weights now converge to the leading eigenvector of the difference of the covariance matrices, i.e. to the axis with maximum variance difference, as determined by nQDA (Fig. 6b).

Two additional modifications are required to recover the hQDA weights. First, to avoid an unbounded exponential increase of the synaptic weights we implement Oja’s correction (Oja 1982):

$$\{\begin{array}{cc}\hfill \mathrm{\Delta }w=\eta ·x·y-\eta ·y^2·w\hfill & \hfill \text{if }\mathrm{k}=1\hfill \\ \hfill \mathrm{\Delta }w=-\eta ·x·y-\eta ·y^2·w\hfill & \hfill \text{if }\mathrm{k}=2\hfill \end{array}$$ (14)

Second, an elaboration is required to recover the weights of the neurons beyond the first. This can be achieved using Sanger’s rule (Sanger 1989), in which each successive neuron forces its weights to be orthogonal to all previously defined neurons:

$$\{\begin{array}{cc}\hfill \mathrm{\Delta }w=\eta ·x·y-\eta ·y^2·w-\eta ·y·\sum _i{y}^{(i)}·w^{(i)}\hfill & \hfill \text{if }\mathrm{k}=1\hfill \\ \hfill \mathrm{\Delta }w=-\eta ·x·y-\eta ·y^2·w-\eta ·y·\sum _i{y}^{(i)}·w^{(i)}\hfill & \hfill \text{if }\mathrm{k}=2\hfill \end{array}$$ (15)

where y⁽ⁱ⁾ is the output of the i-th model neuron, and w⁽ⁱ⁾ are the weights of the i-th model neuron.

hQDA is only guaranteed to converge to the same axes as nQDA when the eigenvalues of the two covariance matrices are identical, and we thus wanted to assess how well hQDA performs under realistic conditions. Because the IT dataset described above included too few conditions to evaluate hQDA, we performed a simulation in which we sampled a large number of artificial population responses from two multivariate Gaussian distributions matched to the covariances matrices estimated from our data. To simplify the interpretation of this simulation, we subtracted the mean of each class-conditioned distribution, so that only differences in the covariances carried useful information. Figure 6d shows the classification performance of hQDA and other decoders as a function of the size of the training set. In this simulation, nQDA (blue) performed near 100% whereas FLD (green) performed near chance, as expected due to of the absence of linearly separable information. To separately evaluate issues related to the approximation of the difference of the inverse covariances (with the difference of covariances) and other issues related to hQDA implementation, we began by determining performance when we applied a version of nQDA in which the axes were computed as the eigenvectors of the difference of the two covariance matrices (see Methods). Performance of this classifier converged to nQDA performance (Fig 6c, black dashed), suggesting that this is a reasonable approximation under the conditions imposed in this data-inspired simulation. Next we recovered these axes using hQDA (see Methods) and found that it converged to nQDA performance in ~1000 training trials (Fig 6c, black solid). As another measure of hQDA convergence, we computed the absolute value of the correlation between the axes retrieved by hQDA and the eigenvectors of the difference of the covariance matrices. As shown in Fig. 6d, the average correlation between the hQDA axes and the closed-form solutions is > 0.85 after ~500 training trials. Together these results suggest that hQDA does indeed converge to the axes predicted by Equation 13, and can do so with a reasonable amount of training data.

Unlike Hebbian learning, contrastive Hebbian learning as we have described it requires an input that signals the class of the current condition. How might such an input be computed? Figure 6e shows a simple model demonstrating how this signal might be generated during training via a reinforcement learning algorithm. On each trial, a subject generates a behavioral decision (predicting whether each condition belongs to class 1 or 2), and receives a reward for correct responses. Class identity can uniquely be determined on each trial based on the combination of the predicted class and whether or not a reward was received: the presence of a reward confirms that the predicted label was correct whereas the absence of a reward indicates that the predicted label was incorrect and that it should thus be switched. Our model proposes that information is used to compute the class label (i.e. k=1 for target matches or k=2 for distractors) and is then fed-back as an input for contrastive Hebbian learning. Inputs that combine decision and reward information to mediate the modification of feed-forward weights have been proposed by others (Law and Gold 2009) and could be implemented biophysically via dopaminergic inputs, which are potent in PRh (Akil and Lewis 1993, Richmond 2006). Under this scenario, dopaminergic inputs could act as a gate for turning learning “on” and “off” and would thus prevent learning when it is inappropriate for it to occur (e.g., as a result of the cue period responses in our task; Soltani and Wang 2006, Izhikevich 2007).

Discussion

Quantitative descriptions of the computations implemented by higher brain areas have been difficult to develop. The responses of neurons in these areas are highly nonlinear functions of sensory inputs, requiring complex parameterization and large amounts of data. Alternatively, fitting simpler models to the computations performed only by the neurons in a given area generally relies on a precise description of the inputs to that area. Here we have used the structure of low-level encoding models as a basis for constructing decoding models to describe computation in higher stages. Our solution, neural Quadratic Discriminant Analysis (nQDA), reformulates an optimal quadratic classifier as a linear-nonlinear, linear-nonlinear (LN-LN) cascade model, in which input arriving from a population of neurons is transformed at the first stage by a bank of linear filters, followed by squaring nonlinearities, and a final read-out with a second LN stage. The model provides both a means of fitting neural data with an optimal classifier, as well as a biologically plausible description of neural mechanism.

We arrived at nQDA via our previous attempts to account for the transformation between two high-level brain areas, IT and perirhinal cortex (Pagan, Urban, Wohl and Rust 2013). In that work we fit a specific LN-LN classifier model (in which pairs of IT cells combined to form pairs of perirhinal neurons) via a brute force parameter search. Here we’ve used the insight gained from the pairwise model – that increased linear separability can be accomplished by converting class variance differences into mean differences via squaring – to develop a more general solution. Specifically, we’ve generalized this procedure to multiple dimensions by deriving it as a form of QDA, (Equations 3–6), shown that nQDA provides a better account of a transformation between two high-level brain areas than a number of comparable alternatives (Fig 3–4); and developed a biologically plausible learning rule that can be used to estimate nQDA parameters, hQDA (Fig 6).

Similarities between computation in PRh and V1

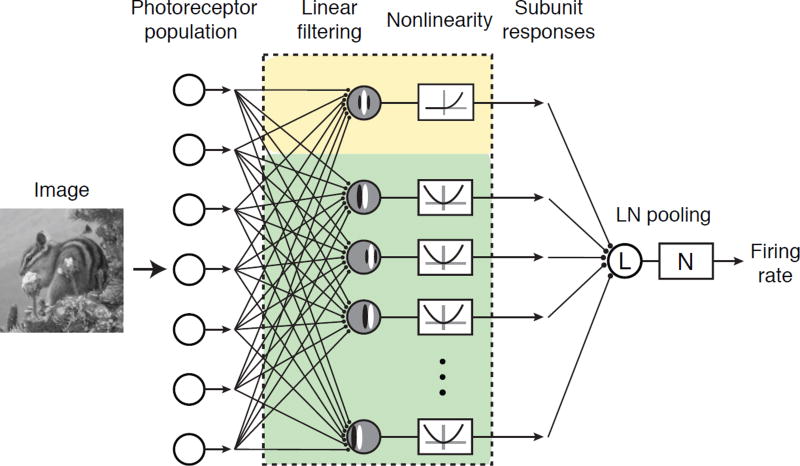
Although nQDA was designed from a decoding perspective, its structure (Fig. 1b) is qualitatively similar to functional models commonly used to describe neural computation in V1 (Fig 7). In their simplest form, the response of a V1 simple cell, including selectivity for orientation, spatial frequency, and phase is captured by an oriented linear filter followed by a threshold (Heeger 1992) and the phase invariance of the V1 complex cell is captured by the two oriented linear filters of differing phase whose responses are squared and summed (Adelson and Bergen 1985). In previous work, we and others have proposed a more elaborate LN-LN “subunit” model to capture the continuum of cells whose response properties lie between simple and complex (Rust, Schwartz, Movshon and Simoncelli 2005, Touryan, Felsen and Dan 2005, Lochmann, Blanche and Butts 2013). In this model, one subunit consists of a linear filter that is halfwave rectified and squared, the other subunits consist of linear filters followed by squaring, and all subunit responses are combined via a weighted sum, followed by a final response nonlinearity (Fig. 7). This model can be fit to neural data using spike-triggered covariance (Rust, Schwartz, Movshon and Simoncelli 2005, Touryan, Felsen and Dan 2005, Lochmann, Blanche and Butts 2013), or more direct maximum likelihood methods (Vintch, Movshon and Simoncelli 2015). The structure of this generalized V1 model bears a remarkable resemblance to the nQDA model framework (compare Fig. 1b and Fig. 7): an LN-LN model in which one (linear) subunit combines with a bank of nonlinear subunits whose responses are squared.

Figure 7. A generalized encoding description of V1 computation.

Shown is the generalized LN-LN subunit model proposed to describe the conversion of visual images in to the firing rate responses of individual V1 neurons. In the first LN stage, the stimulus is passed through a bank of linear filters followed by squaring, with the exception of the first subunit (which is half-squared). These responses are combined via a weighted sum, and the result is passed through a final nonlinearity. Note the similarity between the structure of this model and nQDA (Fig. 1b).

Despite their structural similarity, the V1 subunit model and the nQDA computation aim to describe different phenomena: the V1 model is a single-neuron description of the transformation of a visual image into a firing rate response, whereas the nQDA framework is a population-level description of the conversion of an input population response into the solution for a predefined classification task. Nevertheless, a notable similarity between the models is that the parameters recovered by both procedures are not uniquely constrained. Consequently, care must be taken in interpreting both the “subunits” of the V1 model and the parameters of the nQDA “model neurons” as biological elements. In the case of the V1 model, this can be observed empirically from the recovery of multi-lobed, physiologically implausible linear filters that span the same linear subspace as more plausible, localized, shifted subunits (Rust, Schwartz, Movshon and Simoncelli 2005, Lochmann, Blanche and Butts 2013, Vintch, Movshon and Simoncelli 2015). In the case of nQDA, the recovered “model neurons” are probably best regarded as “meta-neurons” that each represent something like a functional pool of individual neurons within the brain area of interest. In light of these issues, the advantage of both types of descriptions is that they each provide an intuitive, quantitative account of an input/output transformation that can then be used to guide future experiments as well as constrain more specific accounts of their biological implementation.

Links between nQDA and other proposed transformations

While decoding has become a widely used tool for studying the representational content of neural populations, it has seldom been used as a substrate for explicit modeling of neural response. Linear classifiers are commonly used to describe decision tasks, and their physiological implementation is straightforward (i.e. a weighted sum followed by a threshold), but the degree to which the brain implements such decoders is not known, and even less is known about nonlinear population decoders. The quadratic nQDA decoder developed here has a complexity that is well matched to the computational capabilities of one stage of neural processing (e.g, a cortical area). Our results suggest that this type of decoder is sufficient to capture the transformation that perirhinal cortex performs on the inputs arriving from IT (Fig. 3c). The reformulation of QDA into an LN-LN framework also allowed us to arrive at an intuitive geometric description of the neural mechanisms used to create linear separability – that is, by finding the input dimensions with maximal variance differences and converting those into mean differences with squaring (Fig. 2). Finally, the LN-LN reformulation leads to a physiologically plausible contrastive Hebbian learning algorithm capable of approximating nQDA parameters (Fig 6).

Our results demonstrate that nQDA provides a better account of the transformation between two high-level brain areas, IT and perirhinal cortex, than a number of comparable alternatives. Each transformation consisted of a linear transformation of the inputs followed by a nonlinearity constrained to operate separately on each of the resulting responses. We found that a random linear transformation, using up to 1,000 axes, failed to increase linear separability, suggesting that the randomly connected networks that have been proposed for other systems (Sussillo and Abbott 2009, Caron, Ruta, Abbott and Axel 2013) are not a good description for these particular brain areas and this particular task. The inability of PCA to replicate the transformation (Fig. 3c) is largely explained by the fact that the response modulation in IT is primarily visual (Pagan, Urban, Wohl and Rust 2013), and thus PCA recovers dimensions along which the distributions to target matches and distractors are highly overlapping, whereas increasing linear separability requires finding the dimensions along which the distributions of the two classes differ. The fact that ICA performs better that PCA can be understood in the context of the success of nQDA: directions along which the variance of two classes differ the most will also tend to have large kurtosis (since the distribution of inputs is a mixture of two distributions with very different variance), and thus are also likely to be found by ICA. However, nQDA did in fact outperform ICA, in part because of the additional information provided by the (supervised) class labels.

We evaluated the degree to which nQDA could replicate a two-way discrimination between target matches and distractors by assessing trial-level, cross-validated classification performance applied to data recorded from IT. While we found robust cross-validated performance across trials (Fig 3c), nQDA applied to this data set does not generalize well across conditions (not shown). We suspect that this is because the data set is relatively small (i.e. 16 total conditions) whereas generalization requires a considerable amount of data to accurately sample the covariance. While acquiring large data sets from the brains of awake, behaving animals is considerably more challenging than other situations in which generalization is typically applied (e.g., raw images or neural responses in animals that are passively viewing rapidly presented images, (Cadieu et al. 2014, Yamins et al. 2014)), we see expanding these data sets as an important future step of this modeling effort. We also note that our results do not guarantee that nQDA will provide an equally good account of other high-level transformations, such as the multi-way classifications required for invariant object recognition (i.e. Determining which of N possible objects is in view).

How might the brain learn the nQDA transformation?

Above we demonstrate that the parameters of nQDA can be learned by neurons via a local, supervised rule, hQDA (Fig. 6). Our learning rule closely resembles classic Hebbian descriptions of synaptic plasticity (Oja 1982, Sanger 1989, Hebb 2002), with the addition of an extra input that acts to switch the sign of the learning rule. Such an approach is reminiscent of the “contrastive Hebbian” (Hinton and Sejnowski 1986) and “contrastive divergence” (Hinton 2002) approaches that are generally adopted to train Boltzmann Machines. Notably, this learning algorithm is supervised and the best performing unsupervised algorithm that we applied (ICA) did not perform well. However, unsupervised algorithms have been used successfully in contexts similar to the ones we describe here (Wiskott and Sejnowski 2002, Serre, Wolf and Poggio 2005, Cadieu and Olshausen 2008), and it remains unclear whether hQDA could be reformulated in an unsupervised context. We have also offered speculative suggestions of how hQDA might be implemented in the brain (Fig 6e). One difficulty is the incorporation of Sanger’s rule, which forces the nQDA axes to be orthogonal (Equation 15). In his original proposal of the rule, Sanger speculated that this might be achieved via lateral or other competitive interactions between neurons (Sanger 1989).

The value of quantitative descriptions at higher stages

Finally, the importance of techniques for fitting quantitative models to account for high-level computation is worth noting. While it is tempting to assume that the types of complex response properties exhibited by high-level brain areas result from neural computations that are themselves complex, this need not be the case. Rather, the responses of neurons in a high-level brain area reflect the net effect of computations up to that point of processing, and seemingly complex responses can arise from cascading many stages of simple computation. Consequently, determining the computations that a high-level brain area implements requires separating the response properties that a brain area inherits from its inputs from the ones that are computed de novo. The results we have presented here suggest that, at least for the task of visual target identification, the computations implemented by perirhinal cortex bear a striking resemblance to the computations implemented at the earliest stage of visual cortical processing.

Methods

The experimental procedures involved in collecting that data are described in detail in (Pagan, Urban, Wohl and Rust 2013) and are briefly summarized here. All procedures were performed in accordance with the guidelines of the University of Pennsylvania Institutional Animal Care and Use Committee.

We recorded neural responses in IT and PRh as monkeys performed a delayed-match-to-sample task that required treating the same images as targets and as distractors on different trials (Fig. 3a). Monkeys initiated each trial by fixating a small dot. After a brief delay, a sample of the target image for that trial was presented, followed by a sequence of 0–3 distractors, and then by a target match. Monkeys were trained to maintain fixation during the presentation of the distractors and to make a saccade to a dot when the target match appeared. The same four images were used during all the experiments, and were presented in all possible combinations as a visual stimulus and as a target, thus resulting in a total of 16 conditions. Target matches that were presented after the maximal number of distractors (n=3) occurred with 100% probability and were discarded from the analysis; all other conditions were included (e.g., distractors presented at the first, second, or third positions). For each condition, we collected at least 20 repeats on correct trials. Spikes were counted in a window 50–220 ms following stimulus onset.

Population performance

To measure the amount and format of task-relevant information contained in each neural population, we performed a variety of cross-validated classification analyses of whether each condition was a target match or a distractor (Pagan, Urban, Wohl and Rust 2013). For all analyses, we considered population response vectors of N neurons (where N=164 in IT and PRh). The cross-validation procedure involved randomly assigning 18 trials from each condition to compute the representation (“training set”), setting aside one trial from each condition to optimize classifier parameters (“parameter set”), and finally using the remaining trial from each condition to test the performance of the classifier (“test set”). The number of target matches and distractors was matched on each iteration of the procedure (four from each class). Moreover, distractors were chosen to span all visual stimuli and all targets, to avoid the possibility that classifiers could rely on “visual” or “target” information alone, leading to nine valid sets of four distractors. While we note that this changes the ratio of target matches and distractors for the classification analysis (4 target matches / 4 distractors) as compared to the actual experiment (4 target matches / 12 distractors), the monkeys’ high performance on this task (averages of 94% and 92% for each of two monkeys) suggests that they were not simply relying on these suboptimal information sources (which would plateau at 66% correct) but rather computing the actual target match signal. The performance value for each iteration was computed as the mean of the eight test binary values (0 = wrong; 1 = correct), averaged across all nine valid choices of the distractor set. Mean and standard error were computed as the mean and standard deviation across 2000 iterations of the resampling procedure. To compare IT FLD and nQDA performance, we report a P value as an evaluation of the probability that differences in the mean performance values that we observed were due to chance. We compute this probability as the fraction of 2,000 iterations on which the difference was flipped in sign relative to the actual difference between the means of the full data set.

Before applying each classifier, the responses of each neuron were normalized to have zero mean and unit standard deviation across all training trials to ensure that the classifier parameters were assigned based on a combination of response magnitude and trial-by-trial variability rather than response magnitude alone. Responses could not be normalized before applying the Maximum likelihood classifier, because the classifier assumes inputs are Poisson-distributed and non-negative. We tested several types of classifiers (Fig 3c):

FLD linear classifier

The expression for the FLD classifier is presented in Equation 2. To minimize the impact of trial variability on our covariance estimates, we began by averaging the responses to each condition across the set of training trials, and we then computed the means and covariances for the neural population using a regularized estimate equal to a linear combination of the sample covariance Σ and the identity matrix I:

$${\hat{\sum }}_i=\gamma ·{\sum }_i+(1-\gamma )·I$$ (16)

On each iteration of resampling procedure, the regularizing parameter γ was optimized using the “training set” and the γ that produced the best performance was chosen to compute the actual performance using the separately measured “test set”. The final FLD performance values were then computed by averaging the performances on the test set across all iterations.

Maximum likelihood classifier

The maximum likelihood classifier is described in detail in (Pagan, Urban, Wohl and Rust 2013). Briefly, we used the set of training trials to compute the average response r_uc of each neuron u to each condition c, and (consistent with our data), we modeled the likelihood that a test response k was generated from a particular condition as a Poisson-distributed variable:

$$L_{u,c}(k)=\frac{{\left(r_{\mathit{\text{uc}}}\right)}^k·e^{-r_{\mathit{\text{uc}}}}}{k!}$$ (17)

The likelihood that a population response vector was generated in response to each condition was then computed as the product of the likelihoods of the individual neurons. Finally, we computed the likelihood that a test response vector arose from the category “target match” versus the category “distractor” as the mean of the likelihoods for target matches and distractors, respectively, and we assigned the classification label to the category with the higher likelihood.

nQDA

nQDA parameters were calculated as described in Equations 4–6 using the regularized covariances described in Equation 16.

Alternative nonlinear classifiers

We compared nQDA performance with three alternative nonlinear classifiers that (like nQDA) began by applying an initial linear transformation of the original IT space. Below we describe the computation of 1) the linear weights (axes) for each type of classifier, 2) the nonlinearities applied to these linearly transformed responses, and 3) the final linear weighting used to combine the transformed responses into the classifier signal (which is then thresholded to obtain the classification response).

1. Linear weights: For all three alternative nonlinear classifiers, we computed the parameters for one “linear” model neuron in the same manner as nQDA to ensure that we preserved the linearly separable information that already existed in IT. The computation of random axes (Fig. 3c, “IT random”) involved selecting a 164-dimensional random rotation matrix (Mezzadri 2006). When larger numbers of random axes were considered (Fig. 4), they were generated independently from a multivariate Gaussian distribution with zero mean and unitary standard deviation. The PCA axes (Fig. 3c, “IT PCA”) were chosen as the eigenvectors of the covariance matrix computed from the combined responses to both target matches and distractors. The ICA axes (Fig. 3c, “IT ICA”) were chosen as those along which the kurtosis of the projected responses was maximal, and they were computed using the fastICA package (http://research.ics.aalto.fi/ica/fastica). Finally, the nQDA axes (Fig. 3c, “IT nQDA”) were computed as described in the Results section.

2. Nonlinearities: Following the computation of the linear weights, an optimal nonlinearity was fit independently for each axis (with the exception of the linear axis) using the distribution of the projected responses for target matches and for distractors, obtained from the training data (Fig 8). This nonlinearity is optimal in the sense that it is designed to maximally separate the output values for matches from the output values for distractors in a manner very similar to the “ratio of Gaussians” method (Pillow and Simoncelli 2006). To compute the optimal nonlinearity for a particular axis, we modeled the distribution of responses to each match condition and each distractor condition as a Gaussian distribution, having the mean and the variance of the responses after the initial linear transformation. We then computed the log likelihood ratio between the mixture of Gaussians associated with matches and the mixture of Gaussians associated with distractors. This procedure assigned positive values to responses that are likely to be matches, and negative values to responses that are likely to be distractors.

3. The final linear read-out: For each alternative classifier, the weights of the final linear decoer were computed via the regularized FLD described by Equation 16 (in contrast to pooling via the eigenvalues as described for nQDA, Equation 6). As described above, computation of FLD weights included optimizing a single regularization parameter γ using the “parameter set”, whereas classifier performances were computed using the separately measured “test set”. Consequently, computation of both nQDA and each of these alternative nonlinear classifiers included the cross-validated optimization of a single, regularization parameter.

Quantifying neural signals

To parse neural responses into different types of task-relevant signals, we applied the method described by (Pagan and Rust 2014). Briefly, because our experimental design included all possible combinations of each of 4 images presented as a target match and as a distractor, we can re-express the 16-element vector reflecting the mean spike count of each unit to each condition as a weighted sum of 16 task-relevant “signals” by projecting it onto an orthonormal basis that we have designed specifically to capture different types of modulation (Pagan and Rust 2014; Fig 1d) and then combining components that reflect the same type of modulation (e.g., changes in visual identity). Shown in Fig. 5 are modulation magnitudes, each which reflect spike count variance (around the grand mean) that result from changes in: visual stimulus identity (“visual”), target identity (“target”) and whether each condition was a target match or a distractor (“target match”). These variances are normalized by each unit’s trial variance, computed as the variance across the 20 repeated trials for each condition and then averaged across conditions, to obtain a unitless quantity that reflects the ratio of each type of signal relative to the noise.

Data-inspired simulation

To evaluate how well the hQDA contrastive Hebbian learning algorithm converged to nQDA parameters (Fig 7c), we performed a data-inspired simulation that allowed us to generate the large number of trials necessary to evaluate convergence. Specifically, we computed the covariance matrices of the 167 IT neurons included in our data set across the 4 matches, and the covariance matrix across 4 distractors, and we then drew 167-dimensional vectors (up to 1000 for training and always 1000 for testing) from two multivariate Gaussian distributions whose covariances matched those of the data, and whose means were set to 0. This procedure was repeated 1000 times for each condition. On each iteration of the simulation, the 4 distractors were chosen randomly with the constraint of spanning all four visual stimuli and targets. We then used different numbers of training samples to fit the decoders, and we evaluated classification performances using the testing data (Fig. 7d).

With the exception of different numbers of training and testing trials, FLD and nQDA were implemented as described above. To implement hQDA, the weights were randomly initialized (from a standard multivariate normal distribution), and were updated following the presentation of each training sample according to the learning rule described by Equation 15. The learning rate was decreased as the learning proceeded, with the learning rate η_i used for the n-th training sample set to:

$${\eta }_i=\frac{{\eta }_0}{1+\frac{n}{N}}$$ (18)

where N is the total number of training samples, and the initial learning rate η₀ was set to 0.001. Because our data contained 4 matches and 4 distractors and the mean of each distribution was set to 0, the dimensionality of the training data was equal to 6. As a consequence, only 6 axes contained meaningful information to aid classification performance, and we thus restricted hQDA to learn 6 axes. More specifically, 3 axes were learned by adopting a positive Hebbian term for the “match” class, and a negative Hebbian term for the “distractor” class (thus retrieving axes where the match variance was larger than the distractor variance), and 3 axes were learned using the opposite association (thus retrieving the axes where distractor variance was larger than match variance). Because the simulated data did not contain any differences between the means of the two distributions, hQDA was implemented here without the linear axis (Fig.1b, yellow), thus focusing only on the squared axes (Fig.1b, green). Following squaring of the hQDA responses, they were combined via a final FLD (trained as described above).

We also implemented a modified version of nQDA in which axes were computed as the eigenvectors of the difference of the two covariance matrices, as opposed the difference of the inverse covariances (Fig 6c, black dashed). As with hQDA: we only computed the 6 axes associated with non-zero eigenvalues, we squared the resulting responses, and we combined the responses via a final FLD.