Optimal mechanical properties of a scaffold for cartilage regeneration using finite element analysis

Abstract

The development of successful scaffolds for bone tissue engineering requires concurrent engineering that combines different research fields. In previous studies, phenomenological computational models predicted the mechanical properties of a scaffold in a simple loading condition using the mechano-regulation theory. Therefore, the aim of this study is to predict the mechanical properties of an optimum scaffold required for cartilage regeneration using three-dimensional knee joint developed from medical imaging and mechano-regulation theory. It was predicted that the scaffold with optimal mechanical properties would result in greater amounts of cartilage tissue formation than without a scaffold. The results demonstrated the ability of the algorithms to design optimized scaffolds with target properties and confirmed the applicability of set techniques for bone tissue engineering. The scaffolds were optimized to suit the site-specific loading requirements, and the results reveal a new approach for computational simulations in tissue engineering.

Introduction

Osteoarthritis (OA) is a degenerative disease that may affect the knee joint, including the articular cartilage, subchondral bone, and periarticular tissue. Poor intrinsic healing potential of damaged cartilage leads to progressive degradation and subsequent widespread degeneration of a joint and is a major clinical problem in OA treatment.^1,2 Recently, cell-based tissue engineering was used to address the issue of articular cartilage repair by filling a cartilage lesion with a mechanically stable hyaline cartilage-like substance which does not deteriorate over time and integrates well with the surrounding tissue.^3–6

Specifically, mesenchymal stem cells (MSCs) are an attractive cell source for regenerative medicine. They can be harvested in a minimally invasive manner, and they are easily isolated and expanded with multipotentiality, including chondrogenesis.^7,8 The MSC implantation route focuses on the efficiency of travel of cells to the target organs and tissues. Direct intra-articular injection of MSCs into the OA knee is the most commonly used treatment.⁹ However, simple injection is insufficient to obtain the improved cell engraftment, because directly injected cells have limited cell retention and survival at the target site.^10–12 Therefore, tissue-engineered scaffolds may be needed to treat patients with large cartilage lesions. A fundamental tissue engineering design hypothesis is that the scaffold should provide a biomimetic mechanical environment for the initial function and sufficient porosity for cell migration and cell/gene delivery.¹³ This hypothesis presents conflicting design requirements since matching tissue stiffness, especially the stiffness of the used region, requires denser material while cell migration/delivery requires a more porous material.¹³ However, such requirements are generally accepted, and their specific quantitative embodiments are not widely rejected.¹³ For example, in bone tissue engineering, the requirement of temporary scaffold function is potentially indicated by the stiffness and strength, although the optimal magnitudes of the quantities are not defined. Conventional wisdom states that scaffolds should be designed to match healthy tissue stiffness and strength while maintaining an interconnected pore network for cell migration and nutrient transport.^14,15 The evaluation of the characteristics for various scaffolds and their mechanical behaviors requires a significant amount of in vitro and in vivo testing. It is time consuming, complex, expensive, and inaccurate because of the heterogeneity of tissues.¹⁶ However, finite element (FE) analysis provides the possibility of investigating the behavior of tissues and scaffolds, such as structural deformation, stress distributions, and the cartilage regeneration status in complex structures, to determine the mechanical and clinical requirements of scaffolds.¹⁶ In addition, mechano-regulation algorithms were introduced to evaluate possible relationships between mechanical stimulation and cell and tissue differentiation, in particular cartilage regeneration.^17,18

Boccaccio et al.¹⁹ studied to bridge the gap by developing a mechanobiology-based optimization algorithm aimed to determine the optimal graded porosity distribution in functionally graded scaffolds. They also suggested the algorithm that, combining parametric FE models of scaffolds with numerical optimization methods and a computational mechano-regulation model, is able to predict the optimal scaffold microstructure.²⁰ In addition, Dias et al.²¹ suggested that a topology optimization algorithm is proposed as a technique to design scaffolds that meet specific requirements for mass transport and mechanical load bearing. However, they performed it under simple loading conditions.

Therefore, the aim of this study is to determine the optimum material properties of the scaffold for cartilage regeneration using mechano-regulation theory and an FE model under gait cycle conditions. We compared the results of the tissue differentiation process of MSCs with and without scaffolds during cartilage regeneration. We hypothesized that applying a scaffold with optimized material properties would be remarkably effective for cartilage regeneration in knee joint OA.

Materials and methods

A computational model was developed to represent the temporal and spatial distributions of fibrous tissue, cartilage, and bone, regulated through cellular activity. The activities of the four cell types, namely MSCs, fibroblasts, chondrocytes, and osteoblasts, are dependent on mechanical stimulation.^17,18,22,23 At each time point and location, each cell type can migrate, proliferate, differentiate, and/or undergo apoptosis based on their mechanical stimulation and the activity of other cell types in the environment. They can also provide a matrix or stimulate matrix degradation.

Two different FE models are used, namely a mechanical poroelastic model and a cell model with a newly developed element formulation that represents cell activities. The two different models run in parallel and transfer data through subroutines. The entire callus is assumed to include granulation tissue at the beginning of the stimulation regimen.²⁴ Differentiation of the granulation tissue in a given element toward the fibrous tissue, cartilage, or bone was subsequently determined by the stimulus factor (S) based on equation (1) as follows

$$s=\frac{r}{a}+\frac{v}{b}$$ (1)

where γ denotes the octahedral shear strain, ν denotes the fluid velocity, and a (3.75%) and b (3 μm/s) denote the scaling factors for each stimulus. Based on the mechano-regulation theory, S > 3 is predicted to be a fibrous connective tissue, 1 < S <3 indicates cartilage, 0.53 < S < 1 indicates immature woven bone, 0.01 < S < 0.53 indicates mature woven bone, and 0 < S < 0.01 indicates bone resorption.^{17,18,22–24}

The poroelastic material properties were updated according to a rule of mixtures based on the concentration of cells in a given element (n_c), volume fractions (φ_j), material properties of the granulation tissue, and j types of the differentiated tissues in the element. For example, Young’s modulus (E) for a given element was calculated based on equation (2) as follows

$$E=\frac{\left(n_c^{max}-n_c\right)}{n_c^{max}}{E}_{granulation}+\frac{n_c}{n_c^{max}}\sum _{j=1}^{n_t}{E}_j{\phi }_j$$ (2)

where $n_c^{max}$ denotes the maximum number of cells that can occupy any single element, and E_j denotes Young’s modulus of the jth differentiated tissue. The volume fraction φ_j of a given type of differentiated tissue was evaluated as the fraction of the last 10 iterations wherein the differentiated tissue type was predicted in the element. This enabled the material properties to change gradually, thus preventing instability in the algorithm.²⁴ Each material property was calculated for each element with the formula using a custom FORTRAN script.

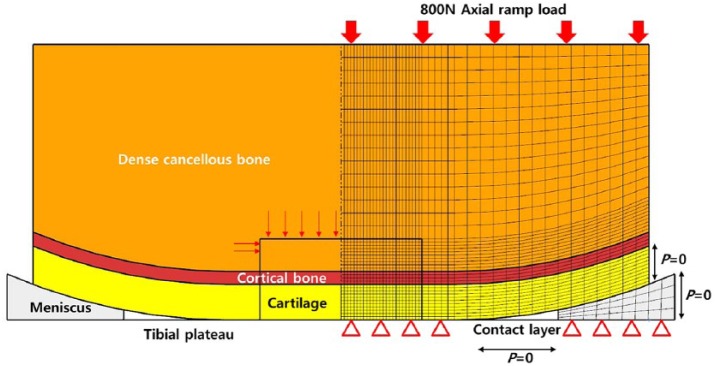
Two poroelastic FE models were developed in the study. The first model corresponded to the FE model that was validated with respect to an FE model in a previous study (Figure 1).¹⁸ A full thickness defect was incorporated into the FE model. The cartilage layer exhibited a thickness of 2 mm, and it was assumed to be uniform across the femoral condyle, which was approximated as a flattened semi-sphere of radius of 20 mm consisting of a 1 mm deep layer of cortical bone overlaying a dense cancellous bone. The tibial plateau was modeled as a rigid contact layer, and its permeability was assumed to be identical to that of cartilage. An 800 N axial ramp load was applied for 0.5 s. All the tissues were modeled as biphasic using the mechano-regulation theory. The material properties used for each tissue type are listed in Table 1.^25–27 In a manner similar to a previous study, cartilage defect size was modeled as 5 mm, and the cell concentration and concentration of each tissue type within the defect were compared.¹⁸

Figure 1.

Schematic of phenomenological axi-symmetric biphasic FE knee models constructed using mechano-regulation theory including a cartilage layer, cortical bone, cartilage, and meniscus for validation.

Table 1.

The material properties used for each tissue type.

	Young’s modulus (MPa)	Poisson’s ratio
Cartilage	15	0.47
Meniscus	120 (circumferential direction)	0.20 (circumferential and radial direction)
	20 (axial and radial direction)	0.30 (axial direction)

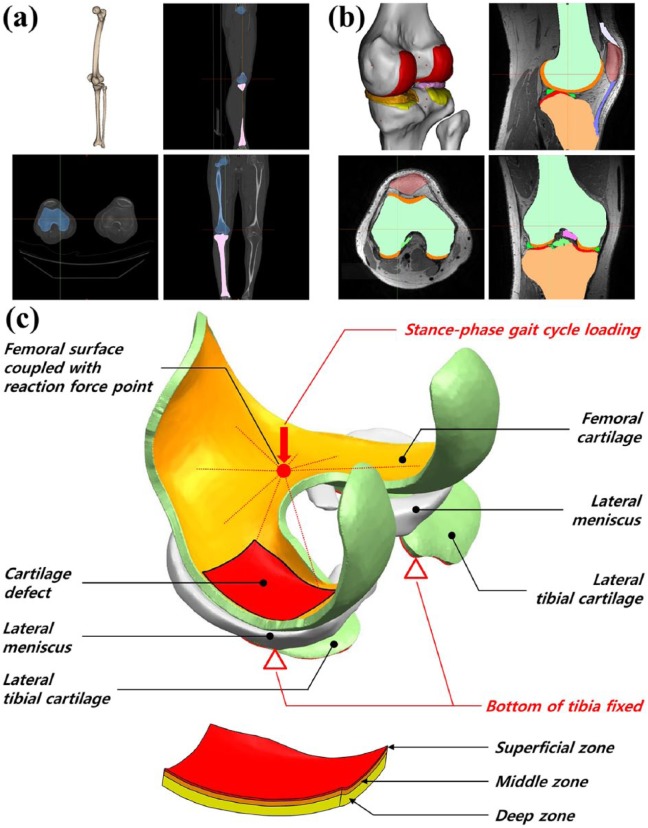
The second model was applied to a real clinical case, and a three-dimensional (3D) knee joint model was developed. The FE model used was previously developed for another study (Figure 2).^25,26 In brief, a 3D FE model of a normal knee joint was developed using data from computed tomography (CT) and magnetic resonance imaging (MRI) scans of a healthy 37-year-old male subject. The CT and MRI models were developed with a slice thickness of 0.1 and 0.4 mm, respectively. In contrast to the phenomenological model, the model was developed for the tibial cartilage to describe an actual clinical situation. Forty iterations were performed in order to simulate 5 days per week of stimulation for 8 weeks. Contact was modeled between the femoral cartilage and meniscus, meniscus and tibial cartilage, and femoral cartilage and tibial cartilage for both medial and lateral sides, and this resulted in a total of six contact pairs. The components were not penetrating. The second model was modeled with 2 cm² area and 3 mm depth. However, it is not easy to represent cartilage defect to microfracture technique or osteochondral autograft transfer in this volume. The boundary condition was a stance-phase gait cycle from the ISO 14243-1 standard.²⁸ The bottom surface of the medial and lateral tibial cartilage was fixed, whereas that of the femoral cartilage was fixed with a coupling constraint option to a reference point located at the middle-central point between the medial and lateral epicondyles of the femur.²⁹ This allowed us to control the femoral motion with respect to the tibia by the changes in boundary conditions at the reference. The duration of the single gait cycle loading was 0.6 s. Subsequently, femoral movement with respect to tibia in gait cycle, including two rotations (extension–flexion, internal–external) and two translations (anterior–posterior, lateral–medial), was obtained from the previous study.⁴ By allowing unrestricted varus–valgus rotation, the medial and lateral femoral cartilages were allowed to be in contact with the surfaces of tibial cartilage during the entire stance phase of the gait cycle. All FE analyses were completed using ABAQUS 6.5 (Abaqus, Inc., East Providence, RI, USA), and the mechano-regulation theory was a user-defined subroutine constructed using FORTRAN code.

Figure 2.

3D knee model developed from (a) CT for bone reconstruction and (b) MRI for soft tissue reconstruction. (c) Schematic of the cartilage defect model, depth-wise composition of the femoral cartilage, and boundary conditions for cartilage regeneration prediction.

In addition, in order to examine the influence of a scaffold on the cartilage defect repair, the optimal mechanical properties of the scaffold were applied to the FE model of the defect. The material properties of the scaffold were divided into three regions, and optimization was performed in the superficial, middle, and deep zones. The superficial, middle, and deep zones were maintained at 12%, 26%, and 62% of the full cartilage thickness, respectively (Figure 2).³⁰ The material properties of the scaffold were optimized using Isight (version 5.9; Dassault Systèmes, Vélizy-Villacoublay Cedex, France). The optimization was conducted using the nondominated sorting genetic algorithm 2 (NSGA2). It was introduced in a previous study as an appropriate method for solving multi-objective problems.^26,31 The optimization was performed to determine the material property that leads to the optimal regeneration of cartilage. The objective function is set to consider optimal properties those that keep the stimulus factor (S) between 1 and 3. Young’s modulus and permeability were determined in each layer.

Results

Model validation

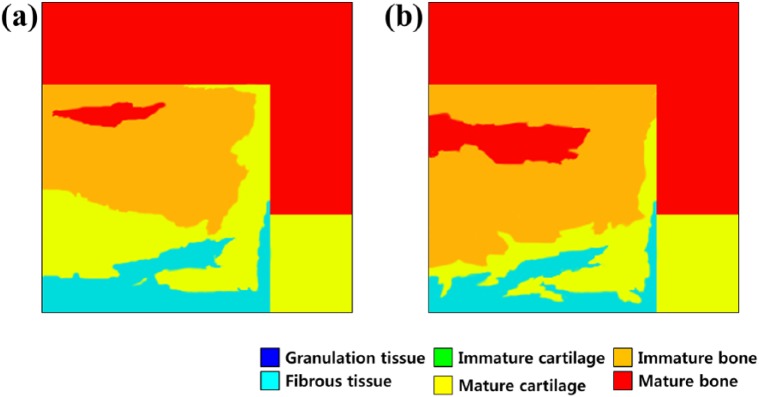
Figure 3 shows the phenomenological computational model of the predicted patterns of tissue differentiation in cartilage defects. This results in higher cell death predictions in the superficial layer of the repair tissue since MSCs differentiate into fibroblasts and undergo death in the high-strain environment. The tendency was also determined in a study conducted by Kelly and Prendergast.¹⁸ Figure 4 shows the cell concentration and each tissue type as a comparison between the present study and the Kelly and Prendergast¹⁸ study. A minor difference was observed, although the overall trend was significantly consistent. Specifically, after the simulation, fibrous tissue formation (18% in the present study and 16% in the previous study) and bone formation (61% in the present study and 64% in the previous study) were predicted.

Figure 3.

Predicted patterns of tissue differentiation with 5 mm cartilage defect in simulation with (a) 25 iterations and (b) 50 iterations.

Figure 4.

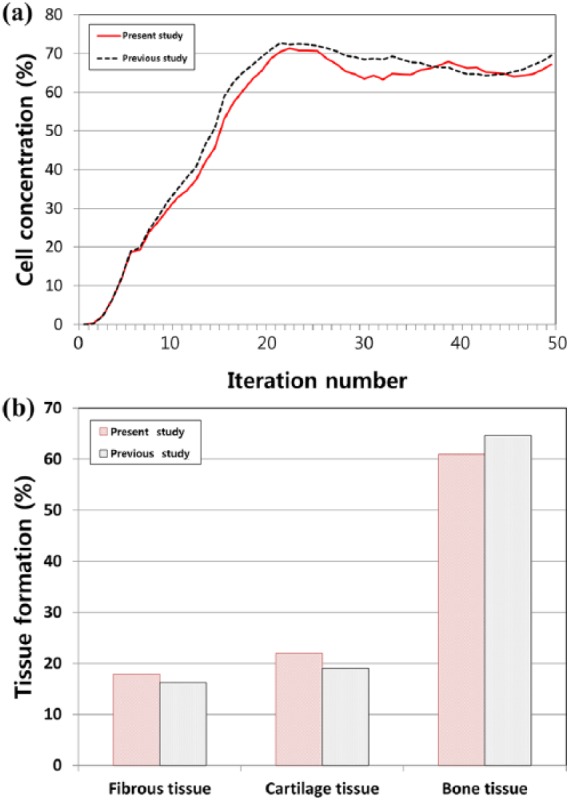
Comparison of prediction for (a) cell concentration at the articular surface and (b) tissue types percentage between this study and a previous study for validation.

Effect of scaffold with optimal mechanical properties and without scaffold condition

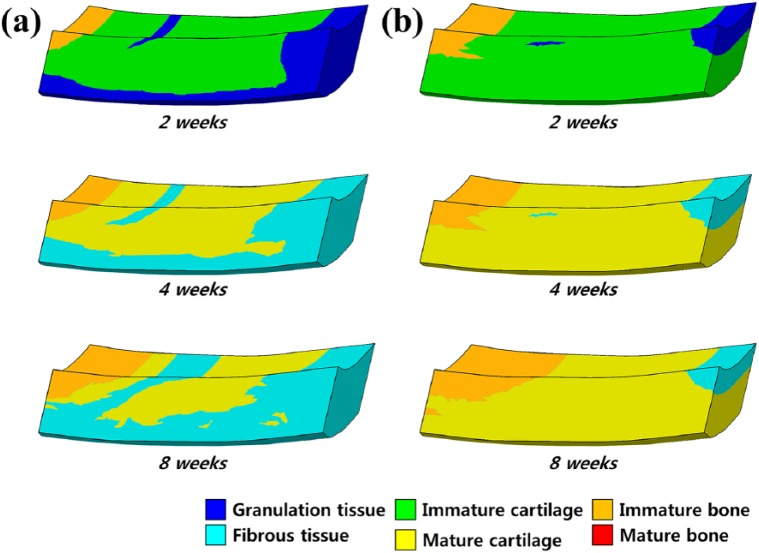
Figure 5 shows the scaffold with optimal mechanical properties and without scaffold for tissue differentiation in cartilage defects during the gait cycle loading. In the condition without scaffold, the simulations indicate that the defect was partially shielded from the load by the adjacent intact cartilage, and that the stimulus within the defect was low. The regeneration tissue begins to stiffen and to support the load, and chondrogenesis is favored within the center of the defect. Fibrous tissue is predicted to form at the articular surface due to the high magnitudes of strain and fluid flow in the region of tissue regeneration. After a period of 4 weeks, regions of cartilage begin to differentiate into the fibrous tissue, ultimately resulting in a reduction in the amount of cartilage within the defect. The predicted patterns of tissue differentiation in the implantation of a scaffold with optimal mechanical properties significantly differ from that predicted during regeneration under the without scaffold condition. Increased cartilage formation is predicted when the simulation of defect regeneration progresses with a higher proportion of the defect exhibiting cartilage tissue with optimal mechanical properties of the scaffold. During repair under the condition without scaffold, cell death is predicted at the articular surface due to the high strain. Implantation of a scaffold with optimal mechanical properties was predicted to prevent cell death due to lower strains experienced by cells in the presence of a scaffold (Figure 6). After 40 iterations, 68% and 21% amounts of cartilage tissue formation were predicted in the scaffold with optimal mechanical properties model and in the model without scaffold, respectively (Figure 7). The optimized material properties are listed in Table 2.

Figure 5.

Comparison of the pattern predictions for tissue differentiation in a cartilage defect during gait cycle: spontaneous regeneration (a) without scaffold and (b) in scaffold with optimal mechanical properties.

Figure 6.

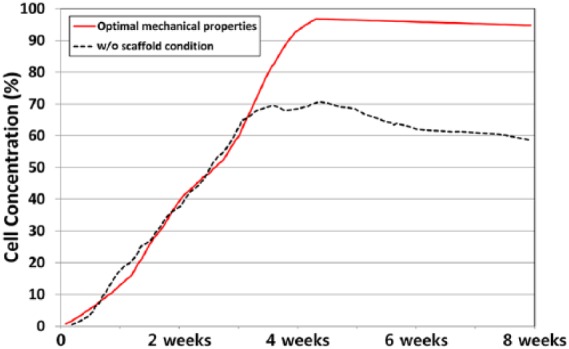
Comparison of cell concentration prediction between cases without scaffold and with a scaffold having optimal mechanical properties.

Figure 7.

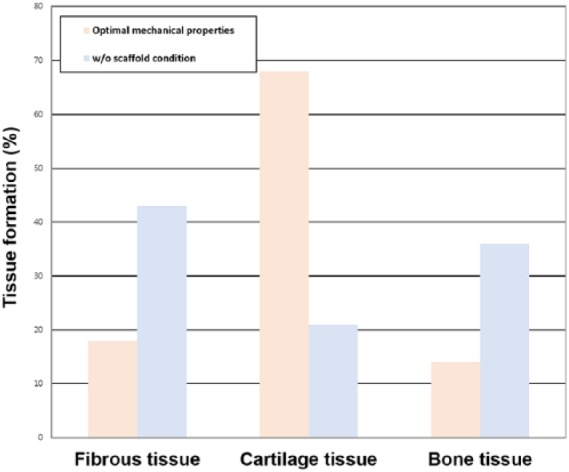
Tissue differentiation of different tissue phenotypes in calluses during the regeneration process after 8 weeks.

Table 2.

The optimized material properties of the scaffold.

	E (MPa)		v		G (MPa)	Permeability (m4/Ns × 10−14)
	In plane	Out of plane	In plane	Out of plane	Out of plane
Superficial zone	22.4	0.4	0.44	0.05	12.2	0.5
Middle zone	18.2	0.46	0.42	0.08	9.4	1
Deep zone	7.5	0.46	0.42	0.14	4.4	2

Discussion

The most important finding of the study was that the scaffold with optimal mechanical properties was effective in cartilage regeneration in the cartilage defect. Implantation of a scaffold with optimal mechanical properties was predicted to prevent cell death and to lead greater amounts of cartilage tissue formation. Cartilage primarily provides a biomechanical function, and therefore, tissue engineering strategies must ultimately produce the most essential mechanical properties of native cartilage.¹ The appropriate delivery of MSCs into the cartilage lesion is important for durable cartilage regeneration in the MSC-based treatment of OA.³² Recently, direct intra-articular injection of MSCs into the OA knee was evaluated in several studies. However, a simple injection is insufficient to achieve improved cell engraftment because directly injected cells exhibit limited cell retention and survival at the target site.^10,11,12

In our previous study,³³ MSC implantation was performed based on arthroscopic guidance according to the local adherent technique reported by Koga et al.³⁴ to further optimize implantation and prevent cell loss. However, we found that large cartilage lesions showed significantly worse outcomes, and we concluded that the development of an advanced surgical procedure with tissue-engineered scaffolds was needed to treat patients with large cartilage lesions.³³ Recently, our study indicated that clinical and arthroscopic outcomes of MSC implantation were encouraging for OA knees in both groups in the study, although there were no significant differences in the outcome scores between groups.³² However, with respect to second-look arthroscopy, better International Cartilage Repair Society (ICRS) grades were observed with scaffold MSC implantation.³² Furthermore, a recent study compared the clinical and second-look arthroscopic outcomes of an arthroscopic MSC injection and arthroscopic MSC implantation in patients with knee OA.³⁵ The principal finding was that a greater improvement in cartilage regeneration was achieved based on the ICRS cartilage repair grades with second-look arthroscopic surgery, and subsequent improved clinical outcomes were observed in patients with knee OA who underwent MSC implantation with a scaffold, than in patients who received an MSC injection with platelet-rich plasma.³⁵ Although MSC implantation demonstrated high clinical efficacy for articular cartilage regeneration in knee OA, there is a paucity of information on the known influential mechanical properties of a scaffold on cartilage regeneration after MSC implantation.^32,33,35,36 In previous studies, it was shown that it is essential for scaffolds to provide mechanical and mass transport properties that are as close as possible to those of normal tissues to improve tissue regeneration.³⁷

Scaffolds are considered as an active component that should provide a proper mechanical environment to maintain structural integrity at the defect site and transmit appropriate mechanical stimuli to the newly generated tissues.³⁷ However, these studies did not explore the optimal properties that should be possessed by a scaffold for optimal cartilage regeneration. For example, the suggestions on the optimal pore size or porosities for tissue repair are inconsistent. Furthermore, different levels of mass transport environment have been shown to lead to differentiation of various cell types and degrees of tissue regeneration.³⁸

As previously mentioned, many studies investigated on scaffold design and optimization of material properties. Challis et al.³⁹ optimized the structure of scaffolds by jointly maximizing scaffold stiffness and diffusive transport in the interconnected pores. They found that the stiffness of the scaffolds is matched to that of bone by choosing a suitable scaffold porosity. Uth et al.⁴⁰ reported the development of biological/synthetic scaffolds for bone tissue engineering using 3D bioplotting. In addition, a previous phenomenological computational model indicated the importance of the mechanical properties of a scaffold for cartilage regeneration.¹⁸ However, they used a simple geometry model in their study. Their model did not include tibial cartilage and used simple static loading instead of a realistic loading.¹⁸ In order to investigate the correlations between functional environments and tissue regeneration, scaffolds with controlled mechanical properties are necessary.

Optimal tailored mechanical properties of scaffold were designed and predicted using 3D knee joint model developed from medical imaging in our study. Moreover, gait cycle loading condition was applied to represent realistic human gait motion. The results indicated that the optimum material properties were more effective in the case with a scaffold than in the case without scaffold. In addition, the mechanical properties changed with respect to the superficial, middle, and deep layers. This type of trend was also determined in a previous study.¹⁸ However, the suggested mechanical properties were different due to differences in the loading condition and geometry between the proposed model and the model in the previous study.¹⁸ If the scaffold was excessively stiff, then the amount of fibrous tissue formation predicted to form increased due to the increase in the magnitude of fluid flow within the defect. Increases in the stiffness of the scaffold also reduced the thickness of the repair cartilage due to further progression of the osseous front. An advantage is that reducing the permeability of the scaffold decreases the amount of fibrous tissue formation within the defect.¹⁸ However, if the permeability of the scaffold was excessively low, the amount of fibrous tissue formation within the defect was predicted to increase. The increased octahedral shear strain in the superficial layer of the defect increased the stimulus for fibrous tissue formation and increased cell death at the articular surface. The increase in strain also increased the cell death at the articular surface. Preventing the formation of superficial fibrous tissue and any subsequent cell death by implanting a scaffold with the appropriate mechanical properties was beneficial in preventing long-term failure of the repair tissue.

In this study, only mechanical properties were focused on as design variables. However, it is necessary to consider the geometric parameters of the scaffold including the pore structure and shape of the structure. The development of biodegradable materials with sufficient mechanical properties, such as stiffness, is desired for applications in cartilage repair engineering. In addition, a biological treatment combined with bioactive factors could constitute other design variables that improve the regeneration process. The optimization studies indicated that the optimal mechanical properties of the scaffold that minimize the evaluation function can be determined by the computational simulation of cartilage regeneration, and that the proposed framework for optimal mechanical properties of a scaffold exhibits a potential to be applied to clinical issues. The optimized scaffold introduced in the study can be determined as a template for future scaffold design in which the mechanical properties of the scaffold are also dependent on specific factors such as the size and weight of a patient and the location of the defect. Future studies could involve designing patient-specific scaffolds based on computer simulations as proposed in the present study.

This study has several limitations. First, the geometric parameters of the scaffold were not considered. However, the purpose of the study was to determine the appropriate material property for cartilage regeneration in each layer, and therefore, the design parameter for each material property will be examined in a future study. Second, the developed models did not consider the migration into the defect from the exposed cancellous bone MSCs, and instead, it was assumed that all present MSCs are the result of implantation. Third, the study assumed that a single iteration of the algorithm represented a day of regeneration. Finally, histology from only a single time point was examined, and thus, it is unknown whether the simulation accurately predicts tissue differentiation patterns at earlier time points. Additional computational and in vivo studies are required to compare the predicted tissue distribution and material properties to those observed in vivo.

In conclusion, a mechano-regulation-theory-based FE approach of cartilage tissue regeneration using optimal scaffolds was derived and implemented to evaluate and analyze the scaffold mechanical properties parameters that directly influence cartilage regeneration. The results indicated that an optimum scaffold was effective in cartilage regeneration when compared to the condition without scaffold. Although further experimental validation is necessary, the model is still useful in assessing scaffold design and analyzing scaffold parameters in cartilage regeneration.