Abstract
The current study aimed to develop multiple diagnosis models for colorectal cancer (CRC) based on data from The Cancer Genome Atlas database and analysis with artificial neural networks in order to enhance CRC diagnosis methods. A genetic algorithm and mean impact value were used to select genes to be used as numerical encoded parameters to reflect cancer metastasis or aggression. Back propagation and learning vector quantization neural networks were used to build four diagnosis models: Cancer/Normal, M0/M1, carcinoembryonic antigen (CEA) <5/≥5 and Clinical stage I–II/III–IV. The performance of each model was evaluated by predictive accuracy (ACC), the area under the receiver operating characteristic curve (AUC) and a 10-fold cross-validation test. The ACC and AUC of the Cancer/Normal, M0/M1, CEA and Clinical stage models were 100%, 1.000; 87.14%, 0.670; 100%, 1.000; and 100%, 1.000, respectively. The 10-fold cross-validation test of the ACC values and sensitivity for each test were 93.75–99.39%, 1.0000; 80.58–88.24%, 0.9286–1.0000; 67.21–92.31%, 0.7091–1.0000; and 59.13–68.85%, 0.6017–0.6585, respectively. The diagnosis models developed in the current study combined gene expression profiling data and artificial intelligence algorithms to create tools for improved diagnosis of CRC.
Keywords: diagnosis model, colorectal cancer, artificial neural networks
Introduction
Colorectal cancer (CRC) is one of the most common malignant tumors and one of the most serious health problems worldwide (1). In China, the morbidity and mortality of CRC are both ranked fifth for all cancer types, responsible for 191,000 cancer-associated cases of mortality in 2015 (2,3).
The diagnosis of CRC at an early stage is crucial to enhance the success of treatment approaches. However, the detection and management of CRC is challenging due to the variable nature of the disease (4). To the best of our knowledge, there are no reliable predictors of CRC development or rate of progression and the diagnosis of CRC is inadequate. Effective systems to predict the occurrence and aggression of this malignancy are urgently required (5). Previously, Saghapouret and Sehhati (6) used a logistic regression model and artificial neural networks (ANNs) as two nonlinear models to establish a two-stage hybrid modeling procedure for prediction of metastasis in advanced CRC. Additionally, Chen et al (7) developed a proteomic approach for the simultaneous detection and analysis of multiple proteins to distinguish individuals with CRC from healthy individuals.
ANNs are a family of models inspired by biological neural networks that are used to estimate functions that depend on a large number of generally unknown inputs (8,9). ANNs constitute a class of flexible nonlinear models designed to mimic biological neural systems (10). ANNs are generally presented as systems of interconnected neurons that exchange messages with each other (10). Each connection has a numerical weight that can be adjusted based on experience, making ANNs adaptive to inputs and capable of learning (10). ANNs have been applied in many different areas and employed to solve medical diagnostic problems (10).
ANN is a mathematical and computational method that has been applied for diagnosis and prognosis prediction in several cancer types. Previously, this method has achieved higher sensitivity and specificity compared with traditional procedures (11–13). Recently, Peng et al (14) established a scoring system based on an ANN model which could better predict the long-term prognosis for patients with stage IIA colon cancer following radical surgery and screen out individuals at high risk of further aggressive progression. This study identified that decreased expression of TGFBR2 and increased expression of β-catenin, MAPK, TGF-β and pin1 may be predictive of a poor 10-year survival outcome.
The aim of the current study was to use ANN to build multiple CRC diagnosis models based on a dataset from The Cancer Genome Atlas (TCGA). The diagnosis models included: Cancer/Normal, M0/M1 (M0, without distant metastasis; M1, with distant metastasis), carcinoembryonic antigen (CEA) <5/≥5 µg/l and Clinical stage I–II/III–IV. The models were generated to help clinicians diagnose patients with CRC, predict the postoperative outcome and screen high-risk prognostic subgroups.
Materials and methods
Data collection
The mRNA expression data used in the current study was downloaded from TCGA (https://cancergenome.nih.gov/). The publically available dataset contained relatively large and diverse CRC RNA-seq expression data, with a total of 633 samples (15). Samples in which the respective clinical data were missing were deleted. A total of 328 samples were used in the current study. The dataset used in the Cancer/Normal contained 287 CRC samples and 41 healthy colorectal samples and M0/M1 models contained 189 M0 samples and 39 M1 samples. The database was filtered according to CEA classification and clinical stage for the CEA and Clinical stage models. Detailed information regarding the size of the relevant datasets is presented in Table I.
Table I.
Datasets used in the four diagnosis models.
| Datasets | Cancer/normal, n | M0/M1, n | CEA <5/≥5, n | Clinical stage I–II/III–IV, n |
|---|---|---|---|---|
| TCGA_colorectal cancer | 287/41 | 189/39 | 79/43 | 155/101 |
TCGA, The Cancer Genome Atlas; M0, without distant metastasis; M1, with distant metastasis; CEA, carcinoembryonic antigen.
Genetic algorithm (GA)
A GA is an optimization method used to identify the best solution to a problem by applying Darwin's evolution hypothesis and different genetic functions, including crossover and mutation (16,17). GA was proposed by John Holland in the early 1970s (18). Compared to traditional optimization and search procedures, GA is a stochastic method used to solve optimization problems, particularly when there is little or no prior knowledge about the process to be controlled (19,20). In the current study, GA was used as a robust nonlinear statistical method for variable selection. The feature genes selected by GA were used as numerical encoded parameters to denote cancerous, metastatic or healthy samples.
Mean impact value (MIV)
MIV is considered to be one of the best indicators to evaluate the impact of input variables for neural cells in a neural network (21). Each input variable of the training samples, comprising of the 171 samples used for model 2 generation (Table II), was increased and decreased by 10% to create two new samples for the simulation function. Then the mean of the difference between values of simulation was calculated to provide the variable MIV. A well-trained neural network model based on MIV is theoretically capable of selecting the most important gene (22).
Table II.
Number of samples used in training sets and test sets.
| Diagnosis model | |||||
|---|---|---|---|---|---|
| Use | Total sample, n | Cancer/normal, n | M0/M1, n | CEA <5/≥5, n | Clinical stage I–II/III–IV, n |
| Training set | 246 | 215/31 | – | – | – |
| Test set | 82 | 72/10 | – | – | – |
| Training set | 171 | – | 140/31 | – | – |
| Test set | 57 | – | 49/8 | – | – |
| Training set | 92 | – | – | 60/32 | – |
| Test set | 30 | – | – | 19/11 | – |
| Training set | 208 | – | – | – | 118/90 |
| Test set | 69 | – | – | – | 37/32 |
M0, without distant metastasis; M1, with distant metastasis; CEA, carcinoembryonic antigen.
ANNs: Back propagation (BP) and learning vector quantization (LVQ) models
In the current study, two types of ANN were used to build multiple diagnosis models: BP and LVQ. The BP neural network includes three layers: An input layer, a hidden layer and an output layer. The first layer has input neurons, which send data via synapses to a hidden layer of neurons, which have synapses to the third layer of output neurons (9,23). The LVQ neural network was a method of training neural networks for pattern classification (24,25). This network architecture includes the input layer, representing the space of inputs in the X dimension, the competition layer, which models the space of the inputs, and the output layer, in which decisions are made. In the current study, both algorithm programs were created using Matlab software (version 2010b; MathWorks, Natick, MA, USA).
Evaluation of diagnosis models
The overall performance of the four models was evaluated by two distinct approaches: Predictive accuracy (ACC) and the area under the curve (AUC) of a receiver operating characteristic (ROC) curve for an independent dataset test. The stability of the models was evaluated using a 10-fold cross-validation test (26). ACC was defined as follows: ACC=(∑TP+TN)/N, where TP was the true positive, TN was the true negative and N was the total number of predicted samples.
The ability of a test to identify true positives and negatives in a dataset was measured by sensitivity and specificity as follows (27): Sensitivity = TP/(TP+FN) and specificity = TN/(TN+FP), where FN was the false negative and FP was the false positive.
An ROC curve demonstrates the efficacy of a test by identifying both the sensitivity and specificity for different cutoff points (27). ROC curve analysis was performed with R software (version 3.2.0; http://www.r-project.org/). The most frequently used criterion for comparing multiple ROC curves is the AUC, which can range from 0.5 (poor performance of prediction model/no discrimination) to 1.0 (ideal performance of prediction model/high discrimination) (28).
For 10-fold cross-validation testing, the dataset was randomly divided into 10 sets, nine of which were used to set the parameters of the predictive algorithm. ACC of the algorithm was then evaluated against the remaining set. This procedure was repeated 10 times before the sensitivity and specificity against different parameters were calculated by an ROC curve for 10 test datasets.
Results and Discussion
Feature gene selection
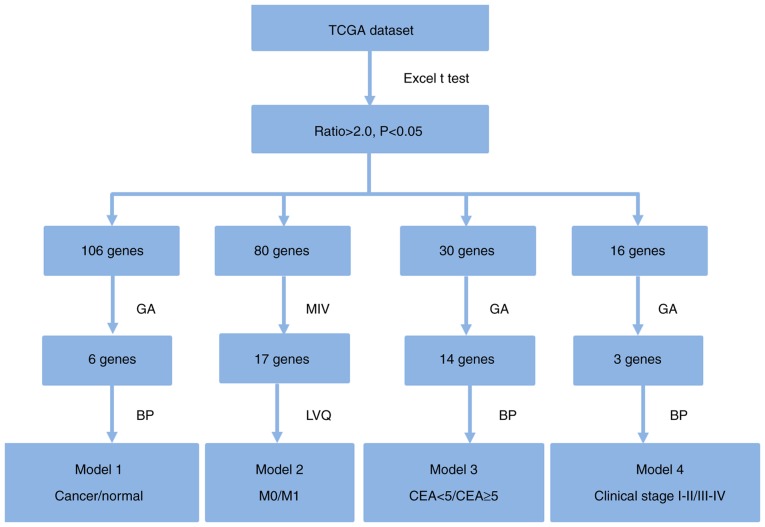
The CRC mRNA expression data from TCGA was divided into four different groups: Cancer/Normal (model 1), M0/M1 (model 2), CEA <5/≥5 (model 3) and Clinical stage I–II/III–IV (model 4). A flow chart outlining the feature genes selection method is presented in Fig. 1. Briefly, P-values and ratio values were calculated for all candidate genes by performing a t-test between every two groups using Excel 2007 (Microsoft Corporation, Redmond, WA, USA). Genes were selected with P<0.05 and ratio >2 for further analysis. The number of genes passing this first selection criteria for model 1, 2, 3 and 4 were 106, 80, 30 and 16, respectively. For selection of the most important genes, GA was run 1,000 times with different initial population sets. A population of good models was obtained. These genes were used to construct diagnosis models using the BP and LVQ techniques. Six, 17, 14 and three feature genes were selected to build models 1, 2, 3 and 4, respectively. Gene selection information is presented in Tables II and III.
Figure 1.
Flow chart for building colorectal cancer diagnosis models. TCGA, The Cancer Genome Atlas; GA, genetic algorithm; MIV, mean impact value; BP, back propagation; LVQ, learning vector quantization; M0, without distant metastasis; M1, with distant metastasis; CEA, carcinoembryonic antigen.
Table III.
Diagnostic genes used in diagnosis models.
| Diagnosis model | Gene symbol | mRNA description | Ratio | Regulation |
|---|---|---|---|---|
| Cancer/normal | MT1M | Metallothionein 1M | 57.35 | Down |
| Cancer/normal | ATP1A2 | ATPase Na+/K+ Transporting Subunit Alpha 2 | 45.00 | Down |
| Cancer/normal | ALPI | Alkaline Phosphatase, Intestinal | 43.49 | Down |
| Cancer/normal | LOC646627 | Uncharacterized LOC646627 | 43.23 | Down |
| Cancer/normal | TMEM72 | Transmembrane Protein 72 | 34.31 | Down |
| Cancer/normal | CPNE7 | Copine 7 | 33.87 | Up |
| M0/M1 | ALPPL2 | Alkaline Phosphatase, Placental Like 2 | 2.08 | Down |
| M0/M1 | ALPP | Alkaline Phosphatase, Placental | 2.35 | Down |
| M0/M1 | CACNG4 | Calcium Voltage-Gated Channel Auxiliary Subunit Gamma 4 | 2.60 | Down |
| M0/M1 | CAMK2B | Calcium/Calmodulin Dependent Protein Kinase II Beta | 2.30 | Down |
| M0/M1 | DLX3 | Distal-Less Homeobox 3 | 2.87 | Down |
| M0/M1 | FREM2 | FRAS1 Related Extracellular Matrix Protein 2 | 2.52 | Down |
| M0/M1 | GPR81 | Hydroxycarboxylic Acid Receptor 1 | 2.14 | Down |
| M0/M1 | HEPHL1 | Hephaestin Like 1 | 2.25 | Down |
| M0/M1 | KRT6A | Keratin 6A | 2.24 | Down |
| M0/M1 | LOC100133545 | MRPL23 antisense RNA 1 | 2.62 | Down |
| M0/M1 | LOC440173 | Uncharacterized LOC440173 | 2.03 | Down |
| M0/M1 | MAP7D2 | MAP7 Domain Containing 2 | 2.21 | Down |
| M0/M1 | MSLN | Mesothelin | 2.05 | Down |
| M0/M1 | PSCA | Prostate Stem Cell Antigen | 2.19 | Down |
| M0/M1 | SCEL | Sciellin | 2.39 | Down |
| M0/M1 | SLC14A1 | Solute Carrier Family 14 Member 1 (Kidd Blood Group) | 3.47 | Down |
| M0/M1 | SLC15A1 | Solute Carrier Family 15 Member 1 | 2.08 | Down |
| CEA <5/≥5 | ADH6 | Alcohol Dehydrogenase 6 (Class V) | 2.17 | Down |
| CEA <5/≥5 | AHSG | Alpha-2-HS-Glycoprotein | 2.05 | Down |
| CEA <5/≥5 | CCL25 | C-C Motif Chemokine Ligand 25 | 3.34 | Down |
| CEA <5/≥5 | CPLX2 | Complexin 2 | 2.36 | Down |
| CEA <5/≥5 | DEFA5 | Defensin Alpha 5 | 4.40 | Down |
| CEA <5/≥5 | DKK4 | Dickkopf WNT Signaling Pathway Inhibitor 4 | 2.25 | Down |
| CEA <5/≥5 | ELF5 | E74 Like ETS Transcription Factor 5 | 2.39 | Up |
| CEA <5/≥5 | EMX1 | Empty Spiracles Homeobox 1 | 3.04 | Down |
| CEA <5/≥5 | FABP4 | Fatty Acid Binding Protein 4 | 2.19 | Up |
| CEA <5/≥5 | GNG4 | G Protein Subunit Gamma 4 | 2.58 | Up |
| CEA <5/≥5 | IGFL2 | IGF Like Family Member 2 | 2.08 | Down |
| CEA <5/≥5 | NOS2 | Nitric Oxide Synthase 2 | 2.31 | Down |
| CEA <5/≥5 | SVOPL | SVOP Like | 2.07 | Up |
| CEA <5/≥5 | TNFRSF6B | Tumor Necrosis Factor Receptor Superfamily 6b | 2.11 | Down |
| Clinical stage | LY6G6D | Lymphocyte Antigen 6 Complex, Locus G6D | 2.01 | Down |
| I–II/III–IV | ||||
| Clinical stage | PALM3 | Paralemmin 3 | 2.23 | Down |
| I–II/III–IV | ||||
| Clinical stage | PRKAA2 | Protein Kinase AMP-Activated Catalytic Subunit Alpha 2 | 2.14 | Down |
| I–II/III–IV |
M0, without distant metastasis; M1, with distant metastasis; CEA, carcinoembryonic antigen.
Cancer/normal diagnosis model
Using the GA method, six feature genes (upregulated: CPNE7; downregulated: MT1M, ATP1A2, ALPI, LOC646627 and TMEM72) were obtained to create the Cancer/Normal diagnosis model.
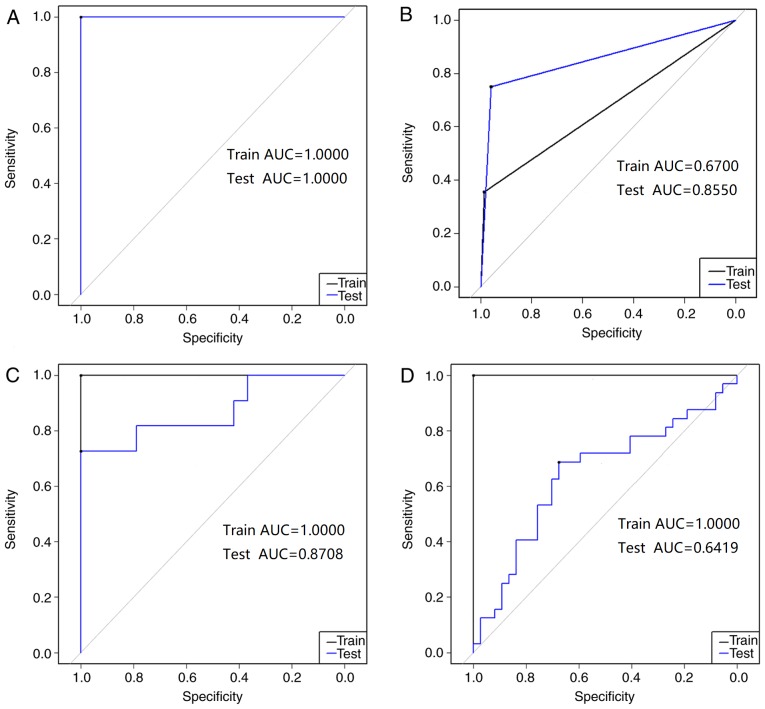
Here, the TCGA dataset was divided into a training set containing 246 samples that was used for model generation and a test set with 82 samples that was used to evaluate the model. The ACC and AUC of the training sets and test sets are presented in Table IV. Fig. 2A presents the ROC for the Cancer/Normal diagnosis model. The ACC and AUC were 100% and 1.000, respectively, for both the training set and the test set. AUC was applied to quantify the comprehensive performance of the prediction model. Therefore, the aforementioned statistical data indicated that the proposed Cancer/Normal diagnosis model exhibited a good ability to predict patients with cancer compared with healthy individuals.
Table IV.
Diagnosis model testing results.
| Diagnosis model | Use | ACC, % | AUC |
|---|---|---|---|
| Cancer/Normal | Training set | 100.00 | 1.0000 |
| Cancer/Normal | Test set | 100.00 | 1.0000 |
| M0/M1 | Training set | 87.14 | 0.6700 |
| M0/M1 | Test set | 92.98 | 0.8550 |
| CEA <5/≥5 | Training set | 100.00 | 1.0000 |
| CEA <5/≥5 | Test set | 80.00 | 0.8708 |
| Clinical stage I–II/III–IV | Training set | 100.00 | 1.0000 |
| Clinical stage I–II/III–IV | Test set | 65.22 | 0.6419 |
M0, without distant metastasis; M1, with distant metastasis; CEA, carcinoembryonic antigen; ACC, accuracy; AUC, area under curve.
Figure 2.
Training set and test set receiver operating characteristic curves for the four colorectal cancer diagnosis models. (A) Cancer/normal. (B) M0/M1 (without distant metastasis/with distant metastasis). (C) Carcinoembryonic antigen <5/≥5. (D) Clinical stage I–II/III–IV. AUC, area under curve.
The stability of the model was evaluated using a 10-fold cross-validation test and the results are presented in Table V. The ACC values of the Cancer/Normal diagnosis model in all 10 tests were in the range 93.75–99.39% and the sensitivity values were all 1.0000, suggesting that the Cancer/Normal diagnosis model has promising reliability and efficacy to identify cancer tissues against different test datasets.
Table V.
10-fold cross validation of diagnosis model TCGA training sets.
| Cancer/normal | M0/M1 | CEA <5/≥5 | Clinical stage I–II/III–IV | |||||
|---|---|---|---|---|---|---|---|---|
| 10-fold cross | ACC | Sen | ACC | Sen | ACC | Sen | ACC | Sen |
| 10-1 | 0.9375 | 1.0000 | 0.8824 | 1.0000 | 0.9231 | 1.0000 | 0.6000 | 0.6364 |
| 10-2 | 0.9692 | 1.0000 | 0.8824 | 1.0000 | 0.8000 | 0.9375 | 0.6829 | 0.6087 |
| 10-3 | 0.9796 | 1.0000 | 0.8431 | 0.9762 | 0.7568 | 0.8750 | 0.6885 | 0.6176 |
| 10-4 | 0.9847 | 1.0000 | 0.8088 | 0.9496 | 0.7551 | 0.8438 | 0.6707 | 0.6304 |
| 10-5 | 0.9878 | 1.0000 | 0.8118 | 0.9429 | 0.7377 | 0.7750 | 0.6602 | 0.6552 |
| 10-6 | 0.9898 | 1.0000 | 0.8058 | 0.9286 | 0.6986 | 0.7234 | 0.6452 | 0.6429 |
| 10-7 | 0.9913 | 1.0000 | 0.8083 | 0.9388 | 0.6744 | 0.7091 | 0.6414 | 0.6585 |
| 10-8 | 0.9924 | 1.0000 | 0.8102 | 0.9464 | 0.6735 | 0.7143 | 0.6024 | 0.6170 |
| 10-9 | 0.9923 | 1.0000 | 0.8117 | 0.9524 | 0.6909 | 0.7324 | 0.5936 | 0.6038 |
| 10-10 | 0.9939 | 1.0000 | 0.8187 | 0.9571 | 0.6721 | 0.7215 | 0.5913 | 0.6017 |
M0, without distant metastasis; M1, with distant metastasis; CEA, carcinoembryonic antigen; ACC, accuracy; Sen, sensitivity.
M0/M1 diagnosis model
M0 represents CRC without distant metastasis, while M1 represents CRC with distant metastasis. Distant metastasis is the main cause of cancer-associated cases of mortality for patients with CRC (29). The common organs for CRC distant metastasis are the liver and lung (30). As a result, M1 indicates a high risk of poor prognosis (31).
Following establishment of the BP diagnosis model to distinguish between cancer patients and healthy patients, the LVQ neural network was used to develop the M0/M1 diagnosis model with a training set of 171 samples, based on 17 feature genes selected by the MIV method (downregulated: ALPPL2, ALPP, CACNG4, CAMK2B, DLX3, FREM2, GPR81, HEPHL1, KRT6A, LOC100133545, LOC440173, MAP7D2, MSLN, PSCA, SCEL, SLC14A1 and SLC15A1). The test set consisted of 57 samples.
As presented in Table IV and Fig. 2B, the ACC of the training set in the LVQ model was 87.14% and the AUC was 0.670. The ACC of the test set was 92.98% and the AUC was 0.855. The AUC value is an indicator of the efficacy of the diagnosis model; an AUC close to 1.0 indicates a high overall efficacy of the test. The test set of M0/M1 diagnosis model had an AUC of approximately 0.9, suggesting that it had a relatively high ability to identify the distant metastasis tissues against the tissues without distant metastasis. The statistical data of the test set indicated that the M0/M1 diagnosis model had the ability to predict patients with and without metastasis.
ACC values for the LVQ M0/M1 diagnosis model in all 10-fold cross-validation tests were in the range 80.58–88.24% and the sensitivity was in the range 0.9286–1.0000 (Table IV). These results verified that the M0/M1 diagnosis model had a good statistical significance.
CEA <5/≥5 diagnosis model
CEA is an immunoglobulin cell adhesion molecule that is considered to be a marker for CRC (32). Previously, Spindler et al (33) reported that elevated preoperative CEA is a risk factor for aggressive tumor biology and poor prognosis for patients with CRC. CEA was also identified as an independent factor for shorter relapse-free survival and shorter overall survival (OS). Furthermore, elevated preoperative CEA has also been demonstrated to not only improve staging of CRC, but also guide adjuvant chemotherapy (34). Therefore, it is important to develop a CEA <5/≥5 diagnosis model to improve diagnosis and therapy for patients with CRC.
The BP neural network was used to develop a CEA <5/≥5 diagnosis model with a training set of 92 samples which contained 60 CEA <5 and 32 CEA ≥5 samples based on 14 feature genes (upregulated: ELF5, FABP4, GNG4 and SVOPL; downregulated: ADH6, AHSG, CCL25, CPLX2, DEFA5, DKK4, EMX1, IGFL2, NOS2 and TNFRSF6B) selected by the GA method. The TCGA test set contained 30 samples (19 CEA <5 and 11 CEA ≥5 samples).
The CEA <5/≥5 diagnosis model had a good ability to predict patients with CEA <5/≥5 in the training set and the test set. As presented in Table IV and Fig. 2C, the ACC for the training set was 100% and the AUC was 1.000. The ACC for the test set was 80% and the AUC was 0.8708. These statistical data indicate that the test set accuracy of the CEA <5/≥5 model is >80%.
The ACC values of the CEA <5/≥5 diagnosis model in all 10-fold cross-validation tests were in the range 67.21–92.31% and the sensitivity values were in the range 0.7091–1.0000 (Table V). This demonstrates that the accuracy and sensitivity ranges of the training set are relatively large but it still has ACC >67.21%, sensitivity >0.7091. Demonstrating that the model has ability to diagnose disease.
Clinical stage I–II/III–IV diagnosis model
The clinical stage of disease is an indicator of prognosis for patients with CRC. Clinical stage I–II is considered early stage, while clinical stage III–IV is considered to be late stage (35,36).
The current study generated a clinical stage I–II/III–IV diagnosis model using the BP neural network to assist with CRC diagnosis. A BP neural network was used to develop the model with a training set containing 208 samples and a test set containing 69 samples based on three feature genes (downregulated: LY6G6D, PALM3 and PRKAA2) selected by the GA method.
As presented in Table IV and Fig. 2D, the clinical stage I–II/III–IV diagnosis model training set had an ACC of 100% and an AUC of 1.0000. The ACC of the test set was 65.22% and the AUC was 0.6419. Meanwhile, the ACC values of this diagnosis model in all 10-fold cross-validation tests were in the range 59.13–68.85% and the sensitivity values were in the range 0.6017–0.6585 (Table V). This result indicates that although the training set for the Clinical stage I–II/III–IV diagnosis model has a high accuracy, the model is unreliable as the accuracy of the test set is only 65.22%.
Survival analysis
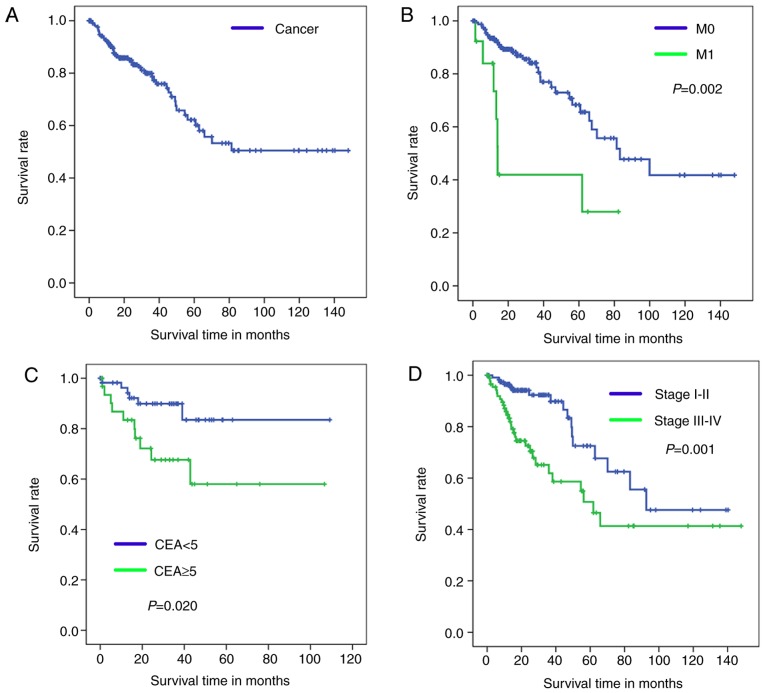
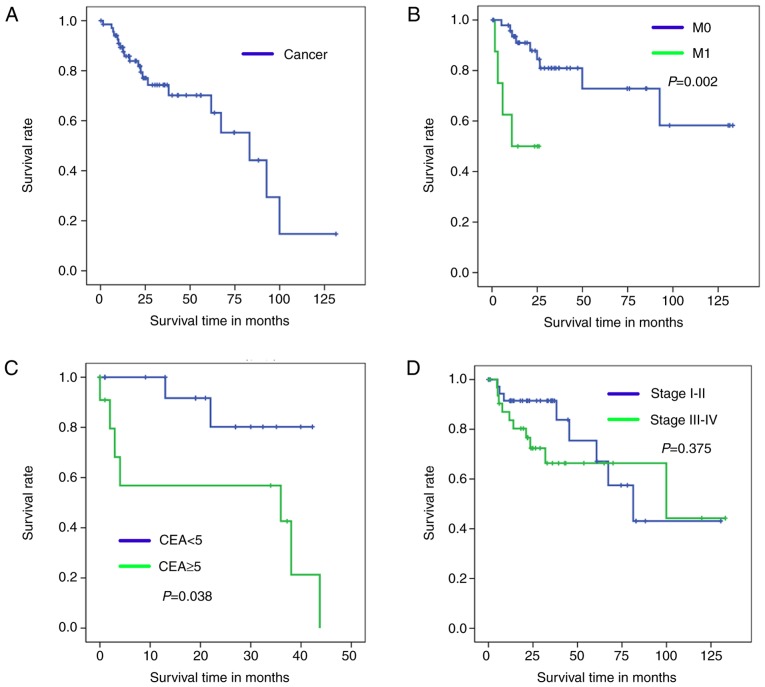
Kaplan-Meier analysis with a log-rank test was used to determine OS of patients in the four diagnosis models. According to the results of these models, Kaplan-Meier survival curves of overall survival are presented in Fig. 3 (training set) and Fig. 4 (test set).
Figure 3.
Kaplan-Meier survival curves for training set patients with colorectal cancer. (A) Cancer/Normal. (B) M0/M1 (without distant metastasis/with distant metastasis). (C) Carcinoembryonic antigen <5/≥5. (D) Clinical stage I–II/III–IV. CEA, carcinoembryonic antigen.
Figure 4.
Kaplan-Meier survival curves for test set patients with colorectal cancer. (A) Cancer/Normal. (B) M0/M1 (without distant metastasis/with distant metastasis). (C) Carcinoembryonic antigen <5/≥5. (D) Clinical stage I–II/III–IV. CEA, carcinoembryonic antigen.
The healthy tissue and tumor tissue originated from the same sample, therefore, these paired samples have the same sample number and OS time so only one OS curve can be presented in Figs. 3A and 4A. Fig. 3B-D demonstrates significant differences in the OS between patients in the M0 and M1 groups (P=0.002; Fig. 3B), CEA <5 and CEA ≥5 groups (P=0.020; Fig. 3C), and stage I–II and III–IV groups (P=0.001; Fig. 3D).
By comparing the Kaplan-Meier survival curve for the test set to OS (Fig. 4A), it can be concluded that the Cancer/Normal diagnosis model was successfully established. Furthermore, the current study effectively distinguished cancer samples into a favorable and unfavorable diagnosis group according to their M0/M1 and CEA index. As demonstrated in Fig. 4B and C, a significant difference was identified in the OS rates of patients in the M1 and CEA ≥5 groups compared with those in the M0 and CEA ≥5 groups (Fig 4B, P=0.002; Fig. 4C, P=0.038).
As illustrated in Fig. 4D, no statistically significant difference was identified in the OS time of the stage I–II groups compared with the stage III–IV groups (P=0.375). Fig. 4D also demonstrates that there was no significant difference in the OS rate of the two groups after 100 months. Therefore, the clinical stage I–II/III–IV model is not suitable for predicting prognosis of patients with CRC.
In conclusion, the current study established multiple novel diagnosis models for human CRC based on TCGA data using the ANN method. Feature genes were selected by GA and MIV methods, which represent characteristics of tumor and healthy samples that were used to generate the diagnosis models. Analysis demonstrated that the BP and LVQ models have strong predictive abilities with high ACC and AUC values in both the training and test sets, as well as robust stability, with notable accuracy and sensitivity values determined by 10-fold cross-validation. The M0/M1 and CEA <5/≥5 diagnosis models demonstrated a high ability to predict patient prognosis. The Cancer/Normal, M0/M1, CEA <5/≥5 and Clinical stage diagnosis models created in the current study, used a variety of artificial intelligence algorithms combined with an RNA-seq dataset to assist with human CRC diagnosis and postoperative outcome prediction.
Acknowledgements
Not applicable.
Glossary
Abbreviations
- CRC
colorectal cancer
- ANN
artificial neural network
- GA
genetic algorithm
Funding
The study was supported by grants from the National Natural Science Foundation of China (grant no. 81272556), the Science and Technology Project of Guangdong Province (grant no. 2017A030311035) and the Science and Technology Program of Guangzhou, China (grant no. 2014Y2-00137).
Availability of data and materials
All data generated or analysed during this study are included in this published article.
Authors' contributions
QW, WL, JC, JW and ZC designed the study and wrote the manuscript; TZ, JZ, BZ and PY collected and analysed the data. All authors read and approved the final manuscript.
Ethics approval and consent to participate
Not applicable.
Patient consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
References
- 1.Torre LA, Bray F, Siegel RL, Ferlay J, Lortet-Tieulent J, Jemal A. Global cancer statistics, 2012. CA Cancer J Clin. 2015;65:87–108. doi: 10.3322/caac.21262. [DOI] [PubMed] [Google Scholar]
- 2.Chen W, Zheng R, Zhang S, Zeng H, Xia C, Zuo T, Yang Z, Zou X, He J. Cancer incidence and mortality in China, 2013. Cancer Letters. 2017;401:63–71. doi: 10.1016/j.canlet.2017.04.024. [DOI] [PubMed] [Google Scholar]
- 3.Chen W, Zheng R, Baade PD, Zhang S, Zeng H, Bray F, Jemal A, Yu XQ, He J. Cancer statistics in China, 2015. CA Cancer J Clin. 2016;66:115–132. doi: 10.3322/caac.21338. [DOI] [PubMed] [Google Scholar]
- 4.Quah HM, Chou JF, Gonen M, Shia J, Schrag D, Landmann RG, Guillem JG, Paty PB, Temple LK, Wong WD, Weiser MR. Identification of patients with high-risk stage II colon cancer for adjuvant therapy. Dis Colon Rectum. 2008;51:503–507. doi: 10.1007/s10350-008-9246-z. [DOI] [PubMed] [Google Scholar]
- 5.de Gramont A, Hubbard J, Shi Q, O'Connell MJ, Buyse M, Benedetti J, Bot B, O'Callaghan C, Yothers G, Goldberg RM, et al. Association between disease-free survival and overall survival when survival is prolonged after recurrence in patients receiving cytotoxic adjuvant therapy for colon cancer: Simulations based on the 20,800 Patient ACCENT Data Set. J Clin Oncol Official. 2010;28:460–465. doi: 10.1200/JCO.2009.23.1407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Saghapour E, Sehhati M. Prediction of metastasis in advanced colorectal carcinomas using CGH data. J Theor Biol. 2017;429:116–123. doi: 10.1016/j.jtbi.2017.06.024. [DOI] [PubMed] [Google Scholar]
- 7.Chen YD, Zheng S, Yu JK, Hu X. Artificial neural networks analysis of surface-enhanced laser desorption/ionization mass spectra of serum protein pattern distinguishes colorectal cancer from healthy population. Clin Cancer Res. 2004;10:8380–8385. doi: 10.1158/1078-0432.CCR-1162-03. [DOI] [PubMed] [Google Scholar]
- 8.Hagan MT, Demuth HB, Beale M. Neural network design. InWseas International Conference on Circuits. 1997;357 [Google Scholar]
- 9.Kuan CM. Artificial Neural Networks. Ieas Working Paper Academic Research. 2006;1:1–23. [Google Scholar]
- 10.Shi HY, Lee KT, Wang JJ, Sun DP, Lee HH, Chiu CC. Artificial neural network model for predicting 5-year mortality after surgery for hepatocellular carcinoma: A nationwide study. J Gastrointest Surg. 2012;16:2126–2131. doi: 10.1007/s11605-012-1986-3. [DOI] [PubMed] [Google Scholar]
- 11.Spelt L, Nilsson J, Andersson R, Andersson B. Artificial neural networks-a method for prediction of survival following liver resection for colorectal cancer metastases. Eur J Surg Oncol. 2013;39:648–654. doi: 10.1016/j.ejso.2013.02.024. [DOI] [PubMed] [Google Scholar]
- 12.Tsao CW, Liu CY, Cha TL, Wu ST, Sun GH, Yu DS, Chen HI, Chang SY, Chen SC, Hsu CY. Artificial neural network for predicting pathological stage of clinically localized prostate cancer in a Taiwanese population. J Chin Med Assoc. 2014;77:513–518. doi: 10.1016/j.jcma.2014.06.014. [DOI] [PubMed] [Google Scholar]
- 13.Hu HP, Niu ZJ, Bai YP, Tan XH. Cancer classification based on gene expression using neural networks. Genet Mol Res. 2015;14:17605–17611. doi: 10.4238/2015.December.21.33. [DOI] [PubMed] [Google Scholar]
- 14.Peng JH, Fang YJ, Li CX, Ou QJ, Jiang W, Lu SX, Lu ZH, Li PX, Yun JP, Zhang RX, et al. A scoring system based on artificial neural network for predicting 10-year survival in stage II A colon cancer patients after radical surgery. Oncotarget. 2016;7:22939–22947. doi: 10.18632/oncotarget.8217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cancer Genome Atlas Network: Comprehensive molecular characterization of human colon and rectal cancer. Nature. 2012;487:330–337. doi: 10.1038/nature11252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Whitley D. A genetic algorithm tutorial. Stat Comput. 1994;4:65–85. doi: 10.1007/BF00175354. [DOI] [Google Scholar]
- 17.Shaefer CG. Springer; New York, NY: 1993. Genetic algorithm; p. 819. [Google Scholar]
- 18.Mitchell M, Forrest S, Holland JH. MIT Press; Cambridge, MA: 1992. The royal road for genetic algorithms: Fitness landscapes and GA Performance. In: Proceedings of the First European Conference on Artificial Life; pp. 245–254. [Google Scholar]
- 19.Zhang X, Zhang X, Li Q, Sun Z, Song L, Sun T. Support vector machine applied to study on quantitative structure-retention relationships of polybrominated diphenyl ether congeners. Chromatographia. 2014;77:1387–1398. doi: 10.1007/s10337-014-2735-4. [DOI] [Google Scholar]
- 20.Jalaliheravi M, Kyani A. Application of genetic algorithm-kernel partial least square as a novel nonlinear feature selection method: Activity of carbonic anhydrase II inhibitors. Eur J Med Chem. 2007;42:649–659. doi: 10.1016/j.ejmech.2006.12.020. [DOI] [PubMed] [Google Scholar]
- 21.Fu ZG, Qi MF, Jing Y. IEEE; Shanghai: 2012. Regression forecast of main steam flow based on mean impact value and support vector regression. In: Proceedings of Asia Pacific Power and Energy Engineering Conference; pp. 1–5. [Google Scholar]
- 22.Jiang JL, Su X, Zhang H, Zhang XH, Yuan YJ. A novel approach to active compounds identification based on support vector regression model and mean impact value. Chem Biol Drug Des. 2013;81:650–657. doi: 10.1111/cbdd.12111. [DOI] [PubMed] [Google Scholar]
- 23.Hagan MT, Beale M. Neural network design China Machine Press. 2002 [Google Scholar]
- 24.Hassoun MH. Fundamentals of artificial neural networks. Proceedings of the IEEE. 1996;84:906. doi: 10.1109/JPROC.1996.503146. [DOI] [Google Scholar]
- 25.Boubaker M, Khalifa KB, Girau B, Dogui M, Bedoui MH. On-line arithmetic based reprogrammable hardware implementation of LVQ neural network for alertness classification. IJCSNS Int J Comput Science Netw Secur. 2008;8:260–266. [Google Scholar]
- 26.Jiang FN, He HC, Zhang YQ, Yang DL, Huang JH, Zhu YX, Mo RJ, Chen G, Yang SB, Chen YR, et al. An integrative proteomics and interaction network-based classifier for prostate cancer diagnosis. PLoS One. 2013;8:e63941. doi: 10.1371/journal.pone.0063941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Baldi P, Brunak S, Chauvin Y, Andersen CA, Nielsen H. Assessing the accuracy of prediction algorithms for classification: An overview. Bioinformatics. 2000;16:412–424. doi: 10.1093/bioinformatics/16.5.412. [DOI] [PubMed] [Google Scholar]
- 28.Sun Y, Goodison S. Optimizing molecular signatures for predicting prostate cancer recurrence. Prostate. 2009;69:1119–1127. doi: 10.1002/pros.20961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Heinzerling JH, Anthony T, Livingston EH, Huerta S. Predictors of distant metastasis and mortality in patients with stage II colorectal cancer. Am Surg. 2007;73:230–238. [PubMed] [Google Scholar]
- 30.He F, Chen H, Yang P. Wu Q, Zhang T, Wang C, Wei J, Chen Z, Hu H, Li W, Cao J. Gankyrin sustains PI3K/GSK-3β/β-catenin signal activation and promotes colorectal cancer aggressiveness and progression. Oncotarget. 2016;7:81156–81171. doi: 10.18632/oncotarget.13215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Akkoca AN, Yanık S, Ozdemir ZT, Cihan FG, Sayar S, Cincin TG, Cam A, Ozer C. TNM and modified dukes staging along with the demographic characteristics of patients with colorectal carcinoma. Int J Clin Exp Med. 2014;7:2828–2835. [PMC free article] [PubMed] [Google Scholar]
- 32.Ullenhag GJ, Frödin JE, Jeddi-Tehrani M, Strigard K, Eriksson E, Samanci A, Choudhury A, Nilsson B, Rossmann ED, Mosolits S, Mellstedt H. Durable carcinoembryonic antigen (CEA)-specific humoral and cellular immune responses in colorectal carcinoma patients vaccinated with recombinant CEA and granulocyte/macrophage colony-stimulating factor. Clin Cancer Res. 2004;10:3273–3281. doi: 10.1158/1078-0432.CCR-03-0706. [DOI] [PubMed] [Google Scholar]
- 33.Spindler KLG, Christensen IJ, Nielsen HJ, Jakobsen A, Brünner N. TIMP-1 and CEA as biomarkers in third-line treatment with irinotecan and cetuximab for metastatic colorectal cancer. Tumour Biol. 2015;36:4301–4308. doi: 10.1007/s13277-015-3069-z. [DOI] [PubMed] [Google Scholar]
- 34.Aldulaymi B, Christensen IJ, Sölétormos G, Jess P, Nielsen SE, Brünner N, Nielsen HJ. Changes in soluble CEA and TIMP-1 levels during adjuvant chemotherapy for stage III colon cancer. Anticancer Res. 2010;30:233–237. [PubMed] [Google Scholar]
- 35.Liu LG, Yan XB, Xie RT, Jin ZM, Yang Y. Stromal expression of vimentin predicts the clinical outcome of stage II colorectal cancer for high-risk patients. Med Sci Monit. 2017;23:2897. doi: 10.12659/MSM.904486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lee KW, Lee SS, Kim SB, Sohn BH, Lee HS, Jang HJ, Park YY, Kopetz S, Kim SS, Oh SC, Lee JS. Significant association of oncogene YAP1 with poor prognosis and cetuximab resistance in colorectal cancer patients. Clin Cancer Res. 2015;21:357–364. doi: 10.1158/1078-0432.CCR-14-1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analysed during this study are included in this published article.