Abstract

The supramolecular chromatin fiber is governed by molecular scale energetics and interactions. Such energetics originate from the fiber’s building block, the nucleosome core particle (NCP). In recent years, the chromatin fiber has been examined through perturbative methods in attempts to extract the energetics of nucleosome association in the fiber. This body of work has led to different results from experiments and simulations concerning the nucleosome–nucleosome energetics. Here, we expand on previous experiments and use coarse-grained simulations to evaluate the energetics inherent to nucleosomes across a variety of parameters in configurational and environmental space. Through this effort, we are able to uncover molecular processes that are critical to understanding the 30 nm chromatin fiber structure. In particular, we describe the NCP–NCP interactions by relying on an anisotropic energetic landscape, rather than a single potential energy value. The attractions in that landscape arise predominantly from the highly anisotropic interactions provided by the NCP histone N-terminal domain (NTD) tails. Our results are found to be in good agreement with recent nucleosome interaction experiments that suggest a maximum interaction energy of 2.69kBT. Furthermore, we examine the influence of crucial epigenetic modifications, such as acetylation of the H4 tail, and how they modify the underlying landscape. Our results for acetylated NCP interactions are also in agreement with experiment. We additionally find an induced chirality in NCP–NCP interactions upon acetylation that reduces interactions which would correspond to a left-handed superhelical chromatin fiber.
Short abstract
This work reveals the internucleosome free energy landscape for normal and acetyl-H4 nucleosomes. Then, it infers the structural features of chromatin and how they vary with epigenetic modifications.
Introduction
The process by which eukaryotic DNA is hierarchically packaged into the cell nucleus is epicentric to cell function and introduces steric barriers for DNA processes such as replication, transcription, and repair. At the smallest length scales, 147 base pairs of DNA are wrapped 1.7 times superhelically around a histone octamer comprised of an H3–H4 tetramer and two H2A–H2B dimers. The resulting packaging unit is known as the nucleosome core particle (NCP).1−3 These NCPs then form a “beads-on-a-string” fiber that can self-associate into the chromatin fiber.3 The dynamic ability of chromatin to locally condense and decondense is central to epigenomic regulation. Despite its crucial role in biology, we have a limited understanding of chromatin’s condensed structure and condensation mechanism.
Available evidence on the secondary condensed chromatin structure has led to debate over the last several decades.3−8 Two primary secondary structures of chromatin have been observed in vitro: the one-start solenoid fiber9 and the two-start zigzag.10 Discussion has gradually shifted from a defined secondary structure in vitro toward a disordered, but dynamic, network of proteins and DNA in vivo.11 Such a disordered state is supported by recent results from advanced imaging techniques.12−14
Attempts to measure different structural and energetic features of the condensed DNA fiber have relied on approaches that capture the energetics of deformation, such as optical and magnetic tweezers. These tools probe the energetics of chromatin through extension of a single fiber.15 More specifically, the groups of Bustamante and van Noort have extracted the average association energy of nucleosomes under varying tensions and pull rates.16,17 Differing experimental conditions such as salinity, fiber length, and relaxed chromatin fiber ultimately incur into discrepancies in the average nucleosome–nucleosome interaction energy (3.2kBT and 13.4kBT, respectively). As previously mentioned, the condensed fiber is not a well-defined structure, which introduces additional sources of uncertainty. As a result, we have yet to develop a comprehensive and definitive understanding of the nucleosome–nucleosome interaction energy. An important feature that must also be taken into account is the highly anisotropic distribution of charges that comprise the nucleosome, which results in anisotropic interactions between nucleosomes. With this in mind, it is difficult to define internucleosome energies by relying on an individual order parameter.
The anisotropic and dynamic distribution of charges on the NCP can be partially attributed to the flexibility and availability of the N-terminal domain (NTD) histone tails. These tails are rich in positively charged lysine and arginine residues that attract negatively charged DNA and negatively charged histone residues.18 The H3 and H4 tails have been studied in the context of their positively charged residues and positioning on the NCP;19−21 they are grafted at the dyad axis and the sides of the nucleosome, respectively, which is of particular importance for chromatin fiber condensation.1 Recently, these tails have been reported to be mobile in the presence of highly dense chromatin fibers, further supporting that the availability of these tails serves to stabilize condensed fibers.22 Despite its length and flexibility, the H3 tail is believed to predominantly stabilize intranucleosome interactions, rather than internucleosome interactions in the absence of divalent salt.23 In contrast, the H4 tail predominantly contributes to internucleosome interactions; it interacts with the H2A acidic patch at the 16th lysine residue (H4K16), which provides a strong electrostatic contribution to internucleosome energetics.18,21,24,25 Removal of this interaction can be accomplished through methods such as acetylation or tail removal, which lead to a decrease in internucleosome energetics and chromatin fiber unfolding. It has also been shown through chromatin array cross-linking studies that H4K16 acetylation provides the same energetic decrease as acetylation of the H4 tail at the 5th, 8th, 12th, and 16th lysines combined.26 This is further supported by a recent study which demonstrated that removal and acetylation of the H4 tail leads to a significant decrease in the internucleosome interaction energy.27
The histone tails also serve as hosts to epigenetic processes. These tails contain specific residues that are subject to post-translational modifications (PTMs), including methylation, acetylation, and ubiquitination,28,29 which regulate and maintain nuclear functions such as transcription and DNA repair. Of particular interest to this work are the charged residues (e.g., lysine, arginine, histidine) that lose their charge upon acetylation. Electrostatic interactions are inherently long-ranged and play a significant role in regulating biological functionality. These charged residues can mediate nucleosome–nucleosome and nucleosome–DNA interactions, contributing to fiber condensation. Of these charged residues, lysines, especially those occurring on the H4 and H3 NTD, have been the focus of numerous epigenetic studies for their potential to be acetylated or methylated.19,29−33 It has also been proposed that acetylation of the tails reduces their flexibility and therefore diminishes their ability to reach other nucleosomes.21,34 Note that irregular methylation or acetylation of lysine residues, such as H3K4 and H3K27, has also been linked to carcinogenesis.35,36
The innate connection between PTMs and internucleosome energetics implies that epigenetic states can be linked to the structure of the chromatin fiber. Thus, an understanding of the energetics at play in the condensation of the chromatin fiber is important for studies of epigenetic states. Despite this connection, concrete links between epigenetic state and chromatin structure have yet to be drawn. The chromatin fiber is dynamic and sensitive to environmental conditions, making it difficult to disentangle the various energetic contributions to structure by relying solely on experimental deformation studies. Theoretical and computational studies could help elucidate a number of molecular-level processes that, until now, have been hidden in the experimental data.
It is important to emphasize that chromatin modeling efforts have relied extensively on available chromatin fiber experiments.37−41 In particular, the three site per nucleotide (3SPN) combined with the atomic-interaction-based coarse-grained (AICG) model has been useful in studies of the nucleosome.37,38 The model has shown good agreement with experimental results on nucleosome energetics and dynamics, including competitive reconstitution experiments that study binding strength of DNA sequence to the histone octomer,42 force-induced nucleosome–DNA unraveling,43 and nucleosome repositioning mechanism analyses.44
Building on that work, in what follows we use the 3SPN and AICG nucleosome models to examine the interaction energy landscape between unmodified and modified nucleosomes, and we study the effects of several modifications on chromatin structure. In doing so, we aim to identify some of the key internucleosome interactions that are relevant to chromatin condensation. Here we note that similar work at the atomistic scale has allowed researchers to extract key structural aspects of the tails when the nucleosomes are stacked.21,45 Building on that work, here we quantify the anisotropic internucleosome free energy landscape and provide new insights into previously reported nucleosome interaction energies by considering the roles of varying orientations, salt concentrations, and counterion condensation. We also consider the effects of lysine acetylation on the H4 tails, which lead to energetic decreases that are consistent with experimental findings.46 Finally, we examine how H4 lysine acetylation induces chirality of the nucleosome interaction energy landscape, away from a left-handed superhelical motif.5,10
Methods
Nucleosome Core Particle Model
Our work is carried out with the 3SPN.2C42 coarse-grained DNA model, parametrized using X3DNA.47 The 3SPN.2C model represents a nucleotide with three sites: one for the sugar, one for the phosphate, and one for the base. We make use of the most recent version of the model, where there is no attractive Lennard–Jones potential added between the DNA and histones.44 As 3SPN.2C is a sequence-dependent model, we use the strongly binding 601 DNA sequence in view of its extensive use in experiments.48 In future efforts, we will consider the effect of DNA sequence on the results reported here. The histone octomer is represented using the AICG protein model applied to the 1KX5 nucleosome crystal structure, generated using CafeMol.38,49−51 Electrostatics are treated at the level of Debye–Hückel theory. A temperature of 300 K and a salt concentration of 150 mM are used in all calculations unless otherwise noted, resulting in a Debye length of λd = 7.84 Å. The simulation time step in all calculations is 20 fs. Post-translational acetylations are incorporated into our model by setting the charges of those amino acids to zero. Note that evaluation of the results for different methods of acetylation are discussed in the Supporting Information.
In order to quantify the pair potential between nucleosomes, we make use of a second coarse-grained NCP realization. The second NCP is a copy of the first, and we move and rotate it into its designated orientation and location. The system is then restrained at those relative orientations, varying only the center of mass separation for our calculations. This approach is justified given the symmetry of the nucleosome core particle. Before gathering statistics, the nucleosomes are equilibrated for 20 ns at their respective orientations.
Nucleosome Orientation and Restraint
We define six distinct groups of histone residues that serve to restrain the two nucleosomes at their designated orientation. These six groups are located at the nucleosome dyad, the nucleosome center of mass, and an edge orthogonal to the dyad axis of the nucleosome. We provide a detailed description of the specific protein sites that comprise these groupings in the Supporting Information. For any calculation, a center of mass separation vector of any two groupings serves to define the orientational vectors, (f̂, û,v̂), which we use to define the orientation of each NCP. For our system, f̂ corresponds to the vector orthogonal to the face of the nucleosome, û corresponds to the vector through the dyad, and v̂ corresponds to the vector orthogonal to both û and f̂. Any given free energy calculation makes use of five orientational restraints between the two nucleosomes. These restraints are applied by attaching harmonic springs to a specific value of the angle between subsequent vectors in the nucleosomes. The vector combinations and values that correspond to each orientation are given in Table 1.
Table 1. Definition of Nucleosome–Nucleosome Orientations for Pair-Potential Calculations.
| orientation | A | B | C | D |
|---|---|---|---|---|
| ûi · ûj | 1 | 0 | 1 | 0 |
| ûi · r̂ij | 0 | 1 | 0 | 0 |
| ûj · r̂ij | 0 | 0 | 0 | 0 |
| v̂i · r̂ij | 0 | 0 | 1 | 1 |
| v̂j · r̂ij | 0 | 0 | 1 | 1 |
The orientations highlighted in the snapshots in Figure 1 are defined by the center of mass separation distance, rcom, and the orientations of the nucleosome reference unit vectors, f̂, û, and v̂. The “stacked” interaction is reminiscent of nucleosome stacking in the 30 nm fiber proposed by Finch and Klug9 and maximizes internucleosome tail interactions. Every other orientation favors unique histone tail interactions (e.g., rotated interaction highlights the interactions of the H2A or H2B). Additionally, the nucleosome pair orientations were held away from the dyad so as to avoid DNA unwrapping events that may alter the calculations. To keep DNA from unwrapping, a small spring force was included between the ends of the DNA and the dyad. We note that this spring diminishes the effect of intranucleosomal positioning on these calculations, which is a parameter that will be considered in future calculations using a more coarse grained representation of DNA.
Figure 1.
Nucleosome pair potential system orientations and resulting energetic landscape. Orientations of the nucleosomes considered here are shown on the left. The axes represent each nucleosome’s coordinate system. The red axis is the nucleosome dyad vector, the blue is orthogonal to the face of the nucleosome, and the green is orthogonal to the other two. (A) The “stacked” nucleosome orientation. (B) The “side–side” nucleosome orientation. (C) The “rotated-stack” orientation. (D) The “rotated-side” orientation. (E) Free energy landscape, where the colors correspond to the orientation shown to the left. Error bars shown are approximately the same order as the thickness of the lines.
Free Energy Calculations
For free energy calculations, we use umbrella sampling with the weighted histogram analysis method (WHAM).52,53 Convergence was determined by calculating the free energy of the system from a subset of the time series. When each subset overlapped with the overall curve, the simulation was deemed converged. The error bars on each curve originate from an average over three independent umbrella sampling calculations.
The primary order parameter for the simulations was the center of mass distance, rcom, ranging from 50 to 150 Å, which was divided into 20 umbrella sampling windows. The 2D surface was generated from a 2D umbrella calculation that varied rcom and ϕ, the offset angle from restraint orientation A, where
| 1 |
This was calculated over 112 umbrella sampling windows, 14 for distances by 8 for angles. The rotational free energy simulation held rcom fixed at the calculated global nucleosome minimum of 63.3 Å with the same restraints at orientation A, except θ, defined by eq 2, which was varied from −180 to +180°.
| 2 |
In order to ensure unique states for ±θ, the negative sign criteria was determined by (ûi × ûj)·rcom ≤ 0. For the case of >0, the positive sign was chosen.
The contact probabilities in Figure 2 were calculated through analysis of the resulting umbrella trajectories. For each trajectory, the center of mass distance was calculated and binned over the collective variable distance from 50 to 150 Å. In the event that the farthest any charged histone tail residue was within one Debye length of the opposite nucleosome, that interaction was recorded. The probabilities were evaluated over a range of at least three umbrella trajectories, each of 2 μs. Contacts were recorded every 50000 time steps to ensure that they corresponded to uncorrelated configurations.
Figure 2.
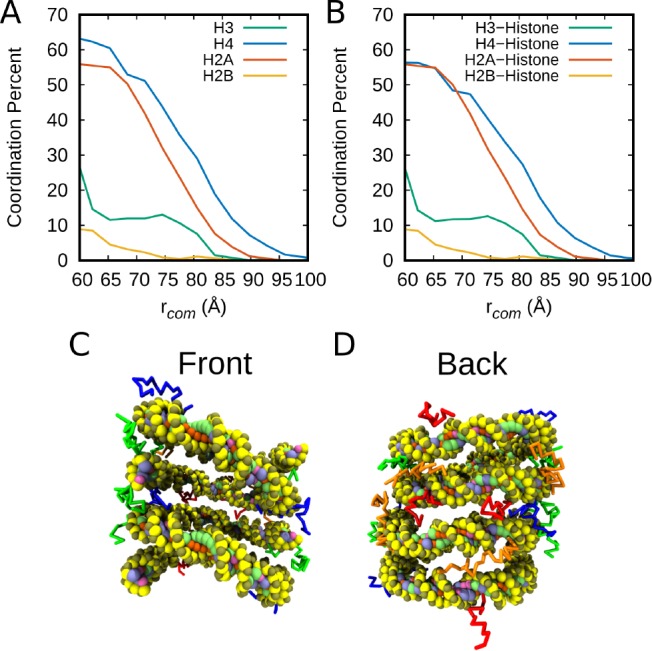
Coordination analysis of the tails with regards to the “stacked” orientation. Results were calculated on the basis of sites within 1 Debye length for each snapshot, λd. (A) Percentage of interactions with the other nucleosome, including both DNA and histone contacts. (B) Fraction of contact sites that were histone contacts as compared to DNA. (C) Schematic of histone tails in the dinucleosome system from the front to highlight positioning of the H3 and H4 tails. (D) Histone tail snapshot from the back to highlight positioning of the H2A and H2B tails. The colors of the tails correspond to the graphs, and the histone core is removed for ease of viewing.
Results
A schematic representation of the orientations used in this work is shown in Figure 1. With the orientations chosen, the systems are subsequently restrained so that only rcom varies. This allows us to evaluate not only the energy of attraction between two nucleosomes at unique orientations but also the inherent range of the interactions.
The strongest internucleosome interaction occurs at the stacked configuration, with a potential minimum of 15.0kBT at a separation of 63.3 Å (Figure 1E). This result agrees with previous experimental and computational work that cites accessibility of positively charged sites on the histone tails as significant contributors to internucleosome interactions.30,31 Here, we notice a decay to zero after ∼2.5 Debye lengths (λd = 7.84) from the minimum at a separation of 83 Å. The other notable minima show that the "rotated-stack" orientation exhibits a well of 11.2kBT at a slightly larger separation of 80.8 Å, and the "side-by-side" orientations both show a much reduced interaction minimum of 4.5kBT at a separation of 116.0 Å. The "rotated-stack" form has more histone tail contacts in comparison to either the "rotated-side" or the "side-side" orientations. We note that the energy scales obtained from this first-order calculation are in quantitative agreement with the 13.4kBT reported by Kruithof et al.16
Degree of Freedom Reduction
We extend our nucleosome interaction free energy definition by also evaluating the effect of nucleosomal rotation. The results of Funke et al. demonstrate that rotation of the nucleosomes results in little change to the pair potential. In this vein, we expect that a rotation of one nucleosome relative to the other (while the positional orientation is kept unchanged) should not alter the number of histone contacts and therefore the energetics of the system. Through this order parameter, we strengthen our results by demonstrating that rotation of the nucleosomes at their energetic minima does not significantly influence the internucleosome interactions.
To accomplish this, we generate a free energy surface for rotation at the global simulation minima (stacked orientation, 63.3 Å). In this orientation the top nucleosome is rotated 360°, as shown in Figure 3. The curve (Figure 3) shows that this rotation result in a very low energetic change. We notice that the largest change is ∼2kBT, which is a minimal change relative to the minimum of 15.0kBT. This demonstrates that a rotational change is not a key determinant of the interaction landscape, which motivates us to analyze the histone tails further.
Figure 3.

Reduction of degrees of freedom through stacked rotation of the nucleosomes. On the left is a schematic representation of the definitions of ±θ used from simulation. On the right panel is the free energy of rotation of two stacked nucleosomes. At most the interaction is a difference of ∼2kBT. We show through this graph that separation distance and orientations are a much more dominant determinant of nucleosome interactions than relative rotation.
Histone Tail Contributions
Of particular importance for this dinucleosome system is the ability to connect physical changes in the interaction landscape to modifications to the nucleosomes. The most relevant of these modifications are post-translational modifications. Through chemical modifications to the histone tails, chromatin can be regulated to become more accessible or even further condensed. With this system, we link PTMs, namely histone H4 acetylation, to free energy landscape modifications.
We first break down the contribution of each histone tail on the free energy landscape to determine the relative importance of each tail. The role played by the histone tails in mediating internucleosome energetics is analyzed here through a set of contact probability curves for each tail on the opposing nucleosome (Figure 2). These curves are calculated by assessing the probability that a residue is in contact with an opposite nucleosome. To expand upon these results, the calculations are separated into two categories: histone tail–protein internucleosome contacts and total contact probability (Figure 2). Both are provided to demonstrate that a greater fraction of total internucleosome interactions come from histone–histone interactions.
Looking at the breakdown of the most common tail interactions, we find that the H4 and H2A tails have the greatest probability of reaching the opposite nucleosome. We note that the long and flexible H3 tail provides significantly fewer contacts than either the H4 or H2A tails. This observation is consistent with recent evidence that the H3 tail mediates linker DNA and intranucleosome interactions, rather than internucleosome interactions in the absence of divalent salt.23,33
A surprising feature of this analysis is the number of contacts of the H2A tail relative to the H4 tail. To understand this result, we consider the structure of the nucleosome and the histone tails. Despite its strong coordination to the opposite nucleosome, the H2A tail contains the smallest number of positive residues. In order of lowest to highest in number of positively charged residues, the histone tails are H2A (5) < H4 (8) = H2B (8) < H3 (10).1 The contributions of these tails to the free energy are a result of the number of positive residues and the accessibility of these tails to the opposing nucleosome. The positioning of the H2A and H4 tails on the nucleosome face make them highly accessible to the opposing nucleosome, as can be seen in Figure 2 C and D. These results suggest that accessibility of the histone tails and, to a lesser extent, the number of positively charged residues influence the coordination probability of the tails. Here we conclude that the H4 tail contributes the most to the free energy results in Figure 1, followed by the H2A tail.
While coordination and the number of positive residues is a qualitative argument for the free energy, we still lack a quantitative understanding of these tails on the free energy surface. The free energy provided by these tails is an important metric for understanding the physical basis of biological processes such as transcription. From our results of tail contacts, we show that the H4 tail has the highest amount of contacts and residues. The literature suggests that post-translational modifications contribute greatly to chromatin dynamics, including fiber condensation. In particular, the acetylation of the H4 tail is highly associated with regions of transcriptionally active chromatin. Through this modification, positively charged lysine amino acids become neutral acetyl-lysine. This modification suggests that transcriptional regulation can be linked to internucleosome energetic changes. As a result, we incorporate such modifications of the nucleosome into the workflow and evaluate their effect on the potential landscape.
To evaluate this effect, we calculate the free energy surface for nucleosomes with acetylated tails (Figure 4). It can be seen from the modified interaction landscape that the “stacked” configuration changes from 15.0kBT to 10.4kBT. Additionally, minor reductions are calculated in the minimum of the other interactions. The “rotated–stack” in this case reduces to 10.2kBT, the “side–side” reduces to 4.21kBT, and the “rotated–side” reduces to 3.99kBT. This result suggests that the acetylated H4 tail predominantly affects the “stacked” orientation.
Figure 4.
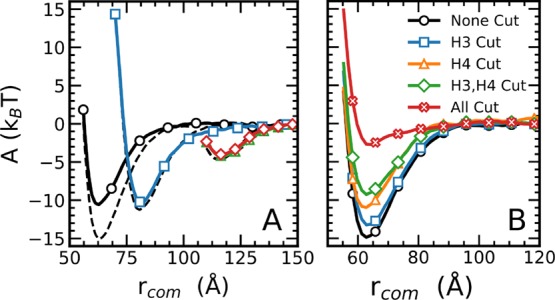
Free energy contributions of the histone tails. (A) The full landscape subject to H4 histone acetylation. The unmodified landscape is shown for comparison as dashed lines. The comparison shows that acetylation predominantly affects the stacked pair potential. (B) Effect of removing H3, H4, both H3 and H4, and all the histone tails. The energy decreases with each tail removal. The H4 tail provides a larger energy of 3.8kBT contribution in comparison to the H3 tail of 1.5kBT. Removal of all tails decreased the energy to 2.72kBT.
Building on this finding, we choose only the stacked configuration as the focal point for studying the effects of further modifications. We decide to highlight the energetics of the histone tails through both the removal of a small contact tail (H3) and a large contact tail (H4) and assess the resultant free energy landscape (Figure 4). By removing the H3 and H4 tails and all of the tails, we notice that the H4 tail does indeed provide a larger energetic effect on the pair potential in comparison to the H3 tail. We also note that removal and acetylation of the H4 tail shows no difference in free energy (see the Supporting Information). Additionally, even when the H3 and H4 tails are removed, a significant energy well of 8kBT persists. We expect a large portion of this to correspond to H2A interactions and, to a lesser extent, H2B. This is consistent with previous findings that the H2A tail provides a non-negligible interaction to the pair potential, as well as to a lesser extent the H2B. As expected, the pair potential interaction drops significantly upon removal of all tails, further proving that the energetic contribution is predominantly in the flexible histone tails. The effect of acetylations are further examined through multiple charge-removal analyses.
To understand modifications further, we analyze the potential chirality induced in the “stacked” interactions. We determined that the stacked interactions are predominantly modified but are unsure if this is a symmetric change across the face of the NCP. Prior analysis of NCP crystal structures has shown that the chromatin fiber exhibits a preferred left-handed superhelical structure.5,10 We expect that decondensed fibers must have some inherent energetics that preserve this structure. To examine the potential of transcription further, we assess the H4 modified landscape through multiple continuous orientations of the two nucleosomes. A 2D surface is constructed to highlight this area of largest attraction under both acetyl-H4 and unmodified nucleosome interactions. A comparison of the two and the difference between the two surfaces are shown in Figure 5.
Figure 5.
Analyzing the effect of H4 acetylation on the stacked nucleosome interaction. On top are snapshots of the different configurations for the calculations. A positive value of ϕ corresponds to a right-handed superhelical structure, and a negative value of ϕ corresponds to a left-handed motif. Below is the 2D internucleosome surface free energy difference calculated using two-dimensional umbrella sampling with nucleosome separation distance, r, and angle, ϕ. The free energy of the standard surface with no modifications is in the leftmost panel. In the middle is the free energy of the acetylated surface with reference color bar to the left for both the left and middle panels. The free energy difference between the two surfaces is shown as the rightmost panel with reference color bar shown to the right.
It can be seen in Figure 5 that there are small lobes above and below the center, corresponding to the “stacked” orientation seen in Figure 1. Upon acetylation of the H4 tail in Figure 5, it can also be noticed that the bottom lobe disappears relative to the minimum, which is highlighted by the difference spike in the same area in Figure 5. This suggests that the bottom lobe corresponds to H4 tail contacts providing a significant free energy reduction to the surface. Specifically, this region, what we are referring to as the “H4-contact lobe”, highlights the energetics that must arise at the nucleosome for local transcription of the fiber to occur. Consistent with theory, these interactions support a left-handed superhelical structure and are disrupted upon acetylation of the H4 tail, demonstrating an induced repulsive chirality.32
Ionic Environment on Dinucleosome Interactions
With a better understanding of the direct internucleosome energetics, we now turn our attention to environmental effects. The cell heavily regulates ionic conditions, as disruptions or stresses can result in cell death.54 We investigate how the structure of chromatin can be altered in the event of deviations in ionic environment. For all prior calculations we used a salt concentration of 150 mM, representing physiological salt strength. Experimental work has pointed to the salt concentration playing a significant role in changing the chromatin fiber structure.55,56 These effects propagate from modifying local to global chromatin structure. We examine the effect of local and long-range solution effects with two approaches: changing both the environmental salt concentration and including localized ionic coordination. Keeping close to physiological concentrations, the resultant nucleosome–nucleosome interaction strength is evaluated at 150 ± 25 mM. We show the effect of salt concentrations changes in Figure 4. Of importance, we see a minimal shift of ∼1 Å/25 mM in terms of separation distance, showing that the monovalent salt slightly affects the range of these interactions, but not significantly. However, we observe large changes in the interaction depth. The minima depth for a 25 mM decrease in the monovalent salt shows a 5.73kBT increase in strength, while a 25 mM increase in salt concentration results in a decrease in depth by 4.25kBT. These results suggest that the NCP physics are highly sensitive to changes in monovalent salt concentration and implicate altered chromatin structure in cell death.
We have thus far neglected the effects of counterion condensation on the pair potential landscape. The charge distribution from exposed DNA on opposing nucleosomes satisfies the condition required by Manning counterion condensation theory.37,57 From Hinckley et al. it is suggested that 3SPN.2 carries a counterion effective charge of 0.6.37 As such, the landscape is re-evaluated with the inclusion of counterion condensation as a means to incorporate local ion effects into the system. Counterion condensation in this model consists of a reduction in potential between internucleosome histone–DNA contacts shown in the Supporting Information. The results can be observed in Figure 6.
Figure 6.

Effects of ionic conditions on nucleosome interaction. (A) Energetic changes to the stacked nucleosome energy with varying salt concentrations. (B) Comparison of our results to experiment. This comparison shows good quantitative agreement for both the depth and location of the minima of the normal and H4-acetylated simulations.
It can be seen from Figure 6B that the energy minimum shifts significantly with counterion condensation from 63.3 to 68.8 Å and include drops of the interaction potential from 15.0 to 2.69kBT. This significant reduction is in quantitative agreement with the results from Funke et al. and Cui et al.17,27 The incorporation of post-translational modifications into the landscape shows that the deepest minimum reduces even further to 1.70kBT showing good agreement with experimental results. We show in Figure 6B that both the depths of the wells and the location of the minimum from experiment agree with those of the counterion condensation calculations. While we note the quantitative agreement with experiment for the location and depth of the wells, we find these results to be of shorter range than in experiments. We note that Manning condensation and Debye–Hückel electrostatics are only a first-order approximation of the environment; more rigorous electrostatic treatments will be considered in the future. Additionally, we acknowledge that divalent salts are present in the cell nucleus. Such salts are likely to influence the interactions examined in this work and will also be investigated in a future study.
Conclusion
In this work we have examined the primary factors that govern the strength and shape of the interaction landscape between two nucleosomes. The underlying pair potentials are highly anisotropic, but their strength is well correlated with histone tail contacts. Predominantly, we show that the H4 and H2A NTD provide more tail contacts and a greater contribution to internucleosome interactions. We also demonstrate that acetylation of the H4 tail, an epigenetic mark associated with active genes, is directly related to a free energy change in chromatin structure, which has been theorized for decades.29,58 We have also uncovered an induced chirality in the strongest interaction configuration upon acetylation of the H4 histone tail, suggesting that acetylation of the H4 tail disrupts the left-handed superhelical organization of the chromatin fiber. Upon consideration of local and global ion effects, one arrives at a free energy landscape that is in good agreement with available experimental reports. The results further predict a high sensitivity of the chromatin fiber structure to the ionic environment in the cell. The results reported here agree quantitatively with experiment. Taken together, the internucleosome interactions studied in this work paint a clearer picture of the energies associated with the chromatin fiber and pave the way for studies of higher length scale chromatin toward an energetic analysis of the 30 nm fiber.
Acknowledgments
The authors thank Andrés Córdoba, Ashley Guo, Emre Sevgen, Ryan McAvoy, Cody Bezik, and Lucas Antony for helpful discussions of this work. The development of the 3SPN.2C model was supported by the NSF under grant EFRI EEC 1830969. We further acknowledge computational resources provided by the Midway Research Computing Center at the University of Chicago.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00836.
Detailed description of simulation restraints and considerations (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Luger K.; Mäder a. W.; Richmond R. K.; Sargent D. F.; Richmond T. J. Crystal structure of the nucleosome core particle at 2.8 A resolution. Nature 1997, 389, 251–260. 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- Richmond T. J.; Finch J. T.; Rushton B.; Rhodes D.; Klug A. Structure of the nucleosome core particle at 7 resolution. Nature 1984, 311, 532–537. 10.1038/311532a0. [DOI] [PubMed] [Google Scholar]
- Kornberg R. D. Chromatin structure: a repeating unit of histones and DNA. Science (Washington, DC, U. S.) 1974, 184, 868–871. 10.1126/science.184.4139.868. [DOI] [PubMed] [Google Scholar]
- Robinson P. J.; An W.; Routh A.; Martino F.; Chapman L.; Roeder R. G.; Rhodes D. 30 nm Chromatin Fibre Decompaction Requires both H4-K16 Acetylation and Linker Histone Eviction. J. Mol. Biol. 2008, 381, 816–825. 10.1016/j.jmb.2008.04.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodcock C. L. F.; Frado L. L. Y.; Rattner J. B. The higher-order structure of chromatin: Evidence for a helical ribbon arrangement. J. Cell Biol. 1984, 99, 42–52. 10.1083/jcb.99.1.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Holde K. E.Cell; Springer: New York, 1989; Springer Series in Molecular Biology 2, Vol. 59, pp 243–244. [Google Scholar]
- Dorigo B. Nucleosome Arrays Reveal the Two-Start Organization of the Chromatin Fiber. Science 2004, 306, 1571–1573. 10.1126/science.1103124. [DOI] [PubMed] [Google Scholar]
- Williams S. P.; Athey B. D.; Muglia L. J.; Schappe R. S.; Gough A. H.; Langmore J. P. Chromatin fibers are left-handed double helices with diameter and mass per unit length that depend on linker length. Biophys. J. 1986, 49, 233–248. 10.1016/S0006-3495(86)83637-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finch J. T.; Klug A. Solenoidal model for superstructure in chromatin. Proc. Natl. Acad. Sci. U. S. A. 1976, 73, 1897–901. 10.1073/pnas.73.6.1897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song F.; Chen P.; Sun D.; Wang M.; Dong L.; Liang D.; Xu R. M.; Zhu P.; Li G. Cryo-EM study of the chromatin fiber reveals a double helix twisted by tetranucleosomal units. Science 2014, 344, 376–380. 10.1126/science.1251413. [DOI] [PubMed] [Google Scholar]
- Maeshima K.; Hihara S.; Eltsov M. Chromatin structure: Does the 30-nm fibre exist in vivo?. Curr. Opin. Cell Biol. 2010, 22, 291–297. 10.1016/j.ceb.2010.03.001. [DOI] [PubMed] [Google Scholar]
- Ou H. D.; Phan S.; Deerinck T. J.; Thor A.; Ellisman M. H.; O’Shea C. C. ChromEMT: Visualizing 3D chromatin structure and compaction in interphase and mitotic cells. Science 2017, 357, eaag0025. 10.1126/science.aag0025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong B.; Almassalha L. M.; Stypula-Cyrus Y.; Urban B. E.; Chandler J. E.; Nguyen T.-Q.; Sun C.; Zhang H. F.; Backman V. Superresolution intrinsic fluorescence imaging of chromatin utilizing native, unmodified nucleic acids for contrast. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, 9716. 10.1073/pnas.1602202113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almassalha L. M.; Tiwari A.; Ruhoff P. T.; Stypula-Cyrus Y.; Cherkezyan L.; Matsuda H.; Dela Cruz M. A.; Chandler J. E.; White C.; Maneval C.; Subramanian H.; Szleifer I.; Roy H. K.; Backman V. The global relationship between chromatin physical topology, fractal structure, and gene expression. Sci. Rep. 2017, 7, 41061. 10.1038/srep41061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leuba S. H.; Karymov M. A.; Liu Y.; Lindsay S. M.; Zlatanova J. Mechanically stretching single chromatin fibers. Gene Therapy and Molecular Biology Gene Ther Mol. Biol. 1999, 4, 297–301. [Google Scholar]
- Kruithof M.; Chien F.-T.; Routh A.; Logie C.; Rhodes D.; van Noort J. Single-molecule force spectroscopy reveals a highly compliant helical folding for the 30-nm chromatin fiber. Nat. Struct. Mol. Biol. 2009, 16, 534–40. 10.1038/nsmb.1590. [DOI] [PubMed] [Google Scholar]
- Cui Y.; Bustamante C. Pulling a single chromatin fiber reveals the forces that maintain its higher-order structure. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 127–132. 10.1073/pnas.97.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erler J.; Zhang R.; Petridis L.; Cheng X.; Smith J. C.; Langowski J. The Role of Histone Tails in the Nucleosome: A Computational Study. Biophys. J. 2014, 107, 2911–2922. 10.1016/j.bpj.2014.10.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepenella S.; Murphy K. J.; Hayes J. J. Intra- and inter-nucleosome interactions of the core histone tail domains in higher-order chromatin structure. Chromosoma 2014, 123, 3–13. 10.1007/s00412-013-0435-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B.; Zheng W.; Papoian G. A.; Wolynes P. G. Exploring the Free Energy Landscape of Nucleosomes. J. Am. Chem. Soc. 2016, 138, 8126–8133. 10.1021/jacs.6b02893. [DOI] [PubMed] [Google Scholar]
- Collepardo-Guevara R.; Portella G.; Vendruscolo M.; Frenkel D.; Schlick T.; Orozco M. Chromatin unfolding by epigenetic modifications explained by dramatic impairment of internucleosome interactions: A multiscale computational study. J. Am. Chem. Soc. 2015, 137, 10205–10215. 10.1021/jacs.5b04086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao M.; Nadaud P. S.; Bernier M. W.; North J. A.; Hammel P. C.; Poirier M. G.; Jaroniec C. P. Histone H3 and H4 N-terminal tails in nucleosome arrays at cellular concentrations probed by magic angle spinning NMR spectroscopy. J. Am. Chem. Soc. 2013, 135, 15278–15281. 10.1021/ja407526s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng C.; Lu X.; Hansen J. C.; Hayes J. J. Salt-dependent intra- and internucleosomal interactions of the H3 tail domain in a model oligonucleosomal array. J. Biol. Chem. 2005, 280, 33552–33557. 10.1074/jbc.M507241200. [DOI] [PubMed] [Google Scholar]
- Pepenella S.; Murphy K. J.; Hayes J. J. A distinct switch in interactions of the histone H4 tail domain upon salt-dependent folding of nucleosome arrays. J. Biol. Chem. 2014, 289, 27342–27351. 10.1074/jbc.M114.595140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kan P.-Y.; Caterino T. L.; Hayes J. J. The H4 Tail Domain Participates in Intra- and Internucleosome Interactions with Protein and DNA during Folding and Oligomerization of Nucleosome Arrays. Mol. Cell. Biol. 2009, 29, 538–546. 10.1128/MCB.01343-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allahverdi A.; Yang R.; Korolev N.; Fan Y.; Davey C. A.; Liu C. F.; Nordenskiöld L. The effects of histone H4 tail acetylations on cation-induced chromatin folding and self-association. Nucleic Acids Res. 2011, 39, 1680–1691. 10.1093/nar/gkq900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funke J. J.; Ketterer P.; Lieleg C.; Schunter S.; Korber P.; Dietz H. Uncovering the forces between nucleosomes using DNA origami. Science Advances 2016, 2, e1600974–e1600974. 10.1126/sciadv.1600974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenfeld G.; Groudine M. Controlling the double helix. Nature 2003, 421, 448–453. 10.1038/nature01411. [DOI] [PubMed] [Google Scholar]
- Allfrey V. G.; Faulkner R.; Mirsky A. E. Acetylation and Methylation of Histones and Their Possible Role in the Regulation of Rna Synthesis. Proc. Natl. Acad. Sci. U. S. A. 1964, 51, 786–794. 10.1073/pnas.51.5.786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strahl B. D.; Allis C. D. The language of covalent histone modifications. Nature 2000, 403, 41–45. 10.1038/47412. [DOI] [PubMed] [Google Scholar]
- Jenuwein T. Translating the Histone Code. Science 2001, 293, 1074–1080. 10.1126/science.1063127. [DOI] [PubMed] [Google Scholar]
- Wakamori M.; Fujii Y.; Suka N.; Shirouzu M.; Sakamoto K.; Umehara T.; Yokoyama S. Intra- and inter-nucleosomal interactions of the histone H4 tail revealed with a human nucleosome core particle with genetically-incorporated H4 tetra-acetylation. Sci. Rep. 2015, 5, 17204. 10.1038/srep17204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z.; Kono H. Distinct Roles of Histone H3 and H2A Tails in Nucleosome Stability. Sci. Rep. 2016, 6, 31437. 10.1038/srep31437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R.; Erler J.; Langowski J. Histone Acetylation Regulates Chromatin Accessibility: Role of H4K16 in Inter-nucleosome Interaction. Biophys. J. 2017, 112, 450–459. 10.1016/j.bpj.2016.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piunti A.; Shilatifard A. Epigenetic balance of gene expression by polycomb and compass families. Science 2016, 352, aad9780. 10.1126/science.aad9780. [DOI] [PubMed] [Google Scholar]
- Cierpicki T.; Risner L. E.; Grembecka J.; Lukasik S. M.; Popovic R.; Omonkowska M.; Shultis D. D.; Zeleznik-Le N. J.; Bushweller J. H. Structure of the MLL CXXC domain–DNA complex and its functional role in MLL-AF9 leukemia. Nat. Struct. Mol. Biol. 2010, 17, 62–68. 10.1038/nsmb.1714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinckley D. M.; Freeman G. S.; Whitmer J. K.; De Pablo J. J. An experimentally-informed coarse-grained 3-site-per-nucleotide model of DNA: Structure, thermodynamics, and dynamics of hybridization. J. Chem. Phys. 2013, 139, 144903. 10.1063/1.4822042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W. F.; Wolynes P. G.; Takada S. Frustration, specific sequence dependence, and nonlinearity in large-amplitude fluctuations of allosteric proteins. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 3504–3509. 10.1073/pnas.1018983108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grigoryev S. A.; Arya G.; Correll S.; Woodcock C. L.; Schlick T. Evidence for heteromorphic chromatin fibers from analysis of nucleosome interactions. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 13317–13322. 10.1073/pnas.0903280106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koslover E. F.; Fuller C. J.; Straight A. F.; Spakowitz A. J. Local geometry and elasticity in compact chromatin structure. Biophys. J. 2010, 99, 3941–3950. 10.1016/j.bpj.2010.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takada S.; Kanada R.; Tan C.; Terakawa T.; Li W.; Kenzaki H. Modeling Structural Dynamics of Biomolecular Complexes by Coarse-Grained Molecular Simulations. Acc. Chem. Res. 2015, 48, 3026–3035. 10.1021/acs.accounts.5b00338. [DOI] [PubMed] [Google Scholar]
- Freeman G. S.; Hinckley D. M.; Lequieu J. P.; Whitmer J. K.; De Pablo J. J. Coarse-grained modeling of DNA curvature. J. Chem. Phys. 2014, 141, 165103. 10.1063/1.4897649. [DOI] [PubMed] [Google Scholar]
- Lequieu J.; Córdoba A.; Schwartz D. C.; de Pablo J. J. Tension-Dependent Free Energies of Nucleosome Unwrapping. ACS Cent. Sci. 2016, 2, 660–666. 10.1021/acscentsci.6b00201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lequieu J.; Schwartz D. C.; de Pablo J. J. In silico evidence for sequence-dependent nucleosome sliding. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, E9197. 10.1073/pnas.1705685114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saurabh S.; Glaser M. A.; Lansac Y.; Maiti P. K. Atomistic Simulation of Stacked Nucleosome Core Particles: Tail Bridging, the H4 Tail, and Effect of Hydrophobic Forces. J. Phys. Chem. B 2016, 120, 3048–3060. 10.1021/acs.jpcb.5b11863. [DOI] [PubMed] [Google Scholar]
- Kurdistani S. K.; Grunstein M. Histone acetylation and deacetylation in yeast. Nat. Rev. Mol. Cell Biol. 2003, 4, 276–284. 10.1038/nrm1075. [DOI] [PubMed] [Google Scholar]
- Lu X. J.; Olson W. K. 3DNA: A software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003, 31, 5108–5121. 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowary P. T.; Widom J. New DNA sequence rules for high affinity binding to histone octamer and sequence-directed nucleosome positioning. J. Mol. Biol. 1998, 276, 19–42. 10.1006/jmbi.1997.1494. [DOI] [PubMed] [Google Scholar]
- Richmond T. J.; Davey C. A. The structure of DNA in the nucleosome core. Nature 2003, 423, 145–50. 10.1038/nature01595. [DOI] [PubMed] [Google Scholar]
- Davey C. A.; Sargent D. F.; Luger K.; Maeder A. W.; Richmond T. J. Solvent mediated interactions in the structure of the nucleosome core particle at 1.9 Å resolution. J. Mol. Biol. 2002, 319, 1097–1113. 10.1016/S0022-2836(02)00386-8. [DOI] [PubMed] [Google Scholar]
- Kenzaki H.; Koga N.; Hori N.; Kanada R.; Li W.; Okazaki K. I.; Yao X. Q.; Takada S. CafeMol: A coarse-grained biomolecular simulator for simulating proteins at work. J. Chem. Theory Comput. 2011, 7, 1979–1989. 10.1021/ct2001045. [DOI] [PubMed] [Google Scholar]
- Kästner J. Umbrella sampling. Wiley Interdisciplinary Reviews: Computational Molecular Science 2011, 1, 932–942. 10.1002/wcms.66. [DOI] [Google Scholar]
- Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R. H.; Kollman P. A. Multidimensional free-energy calculations using the weighted histogram analysis method. J. Comput. Chem. 1995, 16, 1339–1350. 10.1002/jcc.540161104. [DOI] [Google Scholar]
- Huh G. H.; Damsz B.; Matsumoto T. K.; Reddy M. P.; Rus A. M.; Ibeas J. I.; Narasimhan M. L.; Bressan R. A.; Hasegawa P. M. Salt causes ion disequilibrium-induced programmed cell death in yeast and plants. Plant J. 2002, 29, 649–659. 10.1046/j.0960-7412.2001.01247.x. [DOI] [PubMed] [Google Scholar]
- Routh A.; Sandin S.; Rhodes D. Nucleosome repeat length and linker histone stoichiometry determine chromatin fiber structure. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 8872–7. 10.1073/pnas.0802336105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen J. C.; Ausio J.; Stanik V. H.; van Holde K. E. Homogeneous Reconstituted Oligonucleosomes, Evidence for Salt-Dependent Folding in the Absence of Histone H1. Biochemistry 1989, 28, 9129–9136. 10.1021/bi00449a026. [DOI] [PubMed] [Google Scholar]
- Manning G. S. Limiting laws and counterion condensation in polyelectrolyte solutions. 7. Electrophoretic mobility and conductance. J. Phys. Chem. 1981, 85, 1506–1515. 10.1021/j150611a011. [DOI] [Google Scholar]
- Bowman G. D.; Poirier M. G. Post-translational modifications of histones that influence nucleosome dynamics. Chem. Rev. 2015, 115, 2274–2295. 10.1021/cr500350x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




