Spider dragline silk exhibits a self-powered torsion actuation driven by humidity, potentially acting as a novel torsional actuator.
Abstract
Self-powered actuation driven by ambient humidity is of practical interest for applications such as hygroscopic artificial muscles. We demonstrate that spider dragline silk exhibits a humidity-induced torsional deformation of more than 300°/mm. When the relative humidity reaches a threshold of about 70%, the dragline silk starts to generate a large twist deformation independent of spider species. The torsional actuation can be precisely controlled by regulating the relative humidity. The behavior of humidity-induced twist is related to the supercontraction behavior of spider dragline silk. Specifically, molecular simulations of MaSp1 and MaSp2 proteins in dragline silk reveal that the unique torsional property originates from the presence of proline in MaSp2. The large proline rings also contribute to steric exclusion and disruption of hydrogen bonding in the molecule. This property of dragline silk and its structural origin can inspire novel design of torsional actuators or artificial muscles and enable the development of designer biomaterials.
INTRODUCTION
Spider dragline silk from the major ampullate gland is an extraordinary biopolymer fiber that surpasses most synthetic fibers in mechanical toughness through a balance of strength and extensibility (1–3). High thermal conductivity (4), peculiar torsion dynamics (5, 6), and exceptional vibration propagation properties (7) are also recently reported for spider dragline silk. Adding more distinctiveness to this natural fiber, it also displays a giant shape-memory effect upon exposure to water, an effect termed supercontraction (8–11). These remarkable physical properties of spider dragline silk are attributed to its unique hierarchical structure and morphology (12). Understanding of the structure-property relationship of spider silk, i.e., a quantified structural description to account for its outstanding mechanical properties, would certainly benefit the overall understanding of the precise physical nature of biomaterials.
It is known that spider dragline silk is particularly sensitive to water. When wetted or saturated in a high relative humidity (RH) atmosphere, dragline silk can shrink up to 50% in length concomitantly with radial swelling (about twofold increase of the diameter) (8–11). It is generally accepted that, at high humidity, water can disrupt the hydrogen bonds to increase molecular mobility such that molecular entropy can drive the noncrystalline regions to rearrange to lower energetic configurations (3, 10, 13). This rearrangement results in the phenomenon of supercontraction. Recent studies reveal that supercontraction may find original applications in the field of artificial muscles or tensile actuators (9, 14, 15). For instance, the powerful cyclic contractions/relaxations of spider dragline silk allow it to act as a high-performance “muscle,” generating a mechanical work 50 times larger than that of the human muscle of equivalent mass (9). Also, Blackledge et al. (9, 10) and Lin et al. (14) found that the spider silks from Nephila clavipes and Ornithoctonus huwena display a reproducible “shrink-stretch” behavior driven by water or humidity, which allows an efficient weight lifting in a cyclic manner. Recently, several promising torsional artificial muscles from synthetic polymers (16, 17), carbon nanotubes (18, 19), and graphene-made fibers (20), driven by electrochemical cells, humidity, or temperature, have been reported and attracted much attention. Nevertheless, although the torsional properties of spider dragline silk are of practical interest, the fundamental structural origin of its torsional behavior and the related applications have been less explored (5). Moreover, it remains unclear how humidity or water may also affect the torsional behavior of spider dragline silk and whether this is related to the supercontraction.
In this study, we report a humidity-induced torsional behavior of spider dragline silk and demonstrate the effect of spider species and possible structural origins of the torsional response. This unique behavior of spider dragline silk is compared to that of other control fibers, e.g., Bombyx mori silk, Kevlar fiber, and human hair. Experiments are specifically designed to reveal the torsional responses of dragline silk to increasing humidity in a stepwise fashion and to cyclically changing humidity. To understand the mechanism of structural twist behavior at the molecular level, we performed atomistic simulations of the two-component proteins MaSp1 and MaSp2. The possible relations between the observed twist deformation driven by humidity and the molecular structural characteristics of dragline silk are proposed.
RESULTS
Materials and apparatus
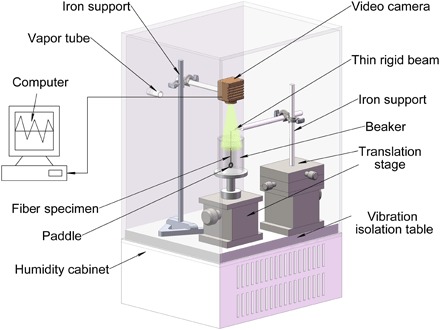
Dragline silks used here were from spiders of Nephila pilipes, Nephila edulis, and Argiope versicolor. The technique for collecting spider silk samples has been introduced in the previous studies (6, 11). For comparison purposes, control fiber specimens, including typical silk fiber from B. mori cocoon, keratin protein fiber of human hair, and synthetic polymer fiber of Kevlar, were also chosen for testing. An apparatus based on image processing (6, 21) for studying the humidity-driven torsional actuation of thin fibers with a ring-shaped paddle is illustrated in Fig. 1. A torsion pendulum made of a single fiber was enclosed within a humidity cabinet. The motion of the pendulum with increasing or decreasing the RH was recorded by a video camera. Two different protocols were designed to investigate the response of spider dragline silks to changes in humidity. One protocol is to increase the RH in a stepwise manner and then maintain a high RH for a long period. The other is to cyclically change the RH from 40 to 100% and then back to 40% for five times.
Fig. 1. Schematic diagram of the apparatus for measuring the torsional actuation of silks or other fibers driven by the RH.
Response of control fibers to changes in RH
We first performed screening tests on the three control fibers, i.e., B. mori silk, human hair, and Kevlar fiber. The scanning electron microscopy (SEM) images of these samples are given in Fig. 2 (A to C). Note that the human hair fiber is much thicker than the B. mori silk and Kevlar fiber. The experimental results are shown in Fig. 2D. With linearly increasing RH from 40 to nearly 100%, hair and Kevlar fibers display only slight signal of twist, whereas B. mori silk displays an initial clockwise twist and then a counterclockwise turnback. Nevertheless, these twist signals are so negligible that they may not be of interest as torsional actuators. It should be mentioned that RH is widely reported to make curly hair curlier, i.e., decreases the radius of curvature, or even frizzy (22). However, here, we tested straight Asian-type hair, which was anyway held straight by tension during the measurement. Therefore, our experiments show no effects on curl or frizziness under humidity.
Fig. 2. SEM images of the fibers and the responses to environmental humidity stimulus.
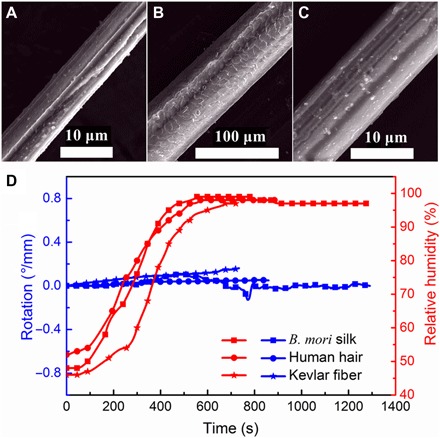
(A) B. mori silk (7.7 ± 0.3 μm in diameter). (B) Human hair (68.7 ± 2.5 μm in diameter). (C) Kevlar fiber (10.7 ± 0.2 μm in diameter). (D) Torsional responses of the representative fibers to environmental humidity: B. mori silk fiber (65.1 mm in length), human hair (69.5 mm in length), and Kevlar fiber (86.9 mm in length). A negligible twist driven by humidity can be seen in these fibers.
Response of spider dragline silk to monotonic increase in RH
Humidity-induced cyclic contractions/relaxations of dragline silk from different spider species have been observed in previous studies (9, 10, 14). However, whether there is a torsional actuation driven by humidity in dragline silk is unknown. Figure 3 (A and C) shows the torsional responses of N. pilipes and A. versicolor spider dragline silks, respectively, increasing RH in a stepwise fashion and then maintaining a high-level RH (>90%). An instant torsional response was actuated above the threshold of RH for both dragline silks. For the N. pilipes dragline silk, when the RH reached ~68%, the actuation was triggered; whereas for A. versicolor, the critical RH was ~70%. The responses of the two dragline silks to a change in RH appear varied. The surface of the dragline silk after testing became much rougher than that of the virgin one (see, e.g., fig. S1). The hanging paddle weighed about 0.1 g, which is about 36,000 times the weight of the silk [~2.75 μg; estimated using a density of 1.3 g cm−3 as indicated by Blackledge et al. (9)]. However, the paddle can still be rotated by the torque generated in N. pilipes spider dragline silk under high humidity. At the end of the test, N. pilipes spider dragline silk achieved a torsional deformation of about 255°/mm to only one direction. This value is even larger than that generated by recently reported carbon nanotube artificial muscles (250°/mm) powered by electricity (18, 23) and is thousands of times the values reported for other actuators based on shape-memory alloy and conducting polymers with twist deformation ability of 0.15° and 0.01°/mm, respectively. The maximum rotation speed of the paddle of about 35°/s (see Fig. 3B) was maintained for ~100 s. If the influence of air drag is neglected, then the initial angular acceleration of the paddle is a = 0.25°/s2 (see Fig. 3B). Because the moment of inertia of the paddle was I ≈ 0.48 × 10−9 kg·m2, the available start-up torque is at least τ = Ia ≈ 0.002 nN·m, which equates 759 nN·m for every gram of twisting dragline mass. Supplementary data for the N. pilipes spider dragline silk to monotonic increase on RH is given in fig. S2.
Fig. 3. Torsional actuation of spider dragline silks with increasing the RH from 40 to 100%.
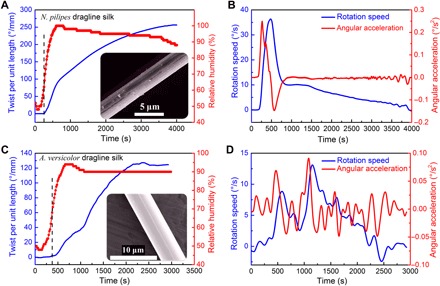
(A) Torsional actuation of N. pilipes spider dragline silk (121 mm in length, 3.1 ± 0.1 μm in diameter). (B) Rotation speed (blue line) and angular acceleration (red line) of the torsional actuation of N. pilipes spider dragline silk. (C) Torsional actuation of A. versicolor spider dragline silk (87.9 mm in length, 6.7 ± 0.1 μm in diameter). (D) The rotation speed (blue line) and angular acceleration (red line) of A. versicolor spider dragline silk. Inset shows the SEM images of representative silks.
For the A. versicolor dragline silk, the torsional actuation started at a RH value of ~70% (Fig. 3C). While RH was maintained at >90% for a period of about 2400 s, the rotation continued and gradually reached a plateau maximum value of 127°/mm. Although this value is lower than that of N. pilipes dragline silk, it is still comparable to that of carbon nanotube “muscles” (18). The peak value of the rotation speed of ~13.1°/s (see Fig. 3D) is still impressive given that the actuating silk fiber was loaded by a paddle with 41,000 times the fiber mass. However, the initial angular acceleration of the paddle of about 0.07°/s2 is only a quarter of that for N. pilipes dragline silk. Comparing Fig. 3 (B and D), one may note that the twist behavior of A. versicolor dragline silk was not as continuous as that of N. pilipes silk, and the angular speed experienced much fluctuation. It is unexpected that the two kinds of spider dragline silks have these different rotational responses.
Response of spider dragline silk to cyclical changes in RH
The results from cyclical humidity changes for torsional responses of three species of spider dragline silk are given in Fig. 4. The RH was changed from 40 to 100% and then to 40% for five times. When the RH was below the threshold level, the dragline silk remained still, and when the threshold level was reached, the twist of dragline silks was triggered immediately. The threshold of RH for torsional actuation of the N. pilipes silk was 68%, as observed in the experiments (Figs. 3A and 4A). The thresholds of RH for torsional actuation of both A. versicolor and N. edulis spider dragline silks were around 70%, as repeatedly shown in Fig. 4 (B and C). The sensitive torsional response of the dragline silk to humidity could provide a precise way for controlling twist deformation. As indicated by the vertical dashed lines in Fig. 4 (A to C), when the RH dropped below the threshold level and continued to decline, the twist deformation of the N. pilipes dragline silk was maintained, whereas the A. versicolor and N. edulis dragline silks reversed the twist slightly or rather noticeably. Yet, the slight recoverable twist upon decreasing RH below the threshold level was also observed in the dragline silk from another N. pilipes spider (see fig. S3). It is indicated that the humidity-induced torsional behavior of dragline silks may vary, given that different spider individuals produce varied molecular structure in silk (24). In the following RH cycles, the twist deformation developed further for all the dragline silk species despite some reversing at the moment of RH dropping below the threshold. After 5 cycles of RH changes, the overall generated rotation is ~130°/mm for both N. pilipes spider silk (the value can be larger for other spider individuals; see, for example, fig. S3A) and N. edulis spider silk (see Fig. 4, A and C), while ~120°/mm for A. versicolor spider silk (Fig. 4B). However, during the later RH cycles, both the twist speed and the angular acceleration showed a tendency to decrease, indicating that the torsional deformation was approaching a saturation state. Similarly, the initial angular acceleration for N. edulis spider dragline silk in Fig. 4C was 0.20°/s2, and the moment of inertia of the paddle was 0.49 × 10−9 kg·m2, so the start-up torque was at least ~0.0017 nN·m.
Fig. 4. Torsional actuation of dragline silks to RH cyclically changing from ~40 to ~100%.
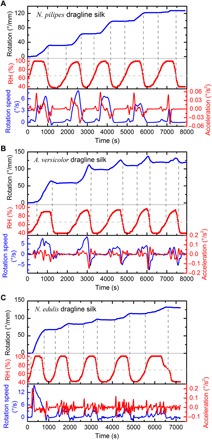
(A) N. pilipes dragline silk (98 mm in length, 3.1 ± 0.1 μm in diameter). (B) A. versicolor dragline silk (87.9 mm in length, 6.7 ± 0.1 μm in diameter). (C) N. edulis dragline silk (82 mm in length, 2.8 ± 0.1 μm in diameter). The horizontal dashed lines indicate the RH thresholds for the triggering of twist. The vertical dashed lines indicate the start and end of the induced twist. Note that the rotation direction of clockwise direction observed from top to bottom paddle is consistent for all silk samples.
All tested dragline silks generated twists to the same clockwise direction viewed from the top of the paddle. The length change of dragline silks before and after each test was carefully measured with the camera, and it is found that all the silks were elongated by ~5 to 10%. Unfortunately, the energy analysis of the torsional actuation of dragline silks driven by humidity is not available since the torque in a single wet silk is tiny (<0.1 nN·m) and we do not attempt to measure it. An enhanced torsion tester for microfibers (25, 26) is needed in the future study for determining the humidity-sinduced torque, which is as important as the supercontraction stress in wet spider dragline (8).
Physical mechanisms for humidity-induced twist in dragline silks on a molecular level
Comparing Figs. 2 and 3, we find that the humidity-induced twist is a unique characteristic of spider dragline silk. To reveal the underlying mechanism of this behavior, we need to understand first the molecular structure and morphology of spider dragline silk, including the specific secondary structures and the hierarchical structural organization.
Previous studies agree that the spider dragline silk has a skin-core organization with a bundle of compact nanofibrils (27–29). Each nanofibril is a semicrystalline polymer consisting of orientated nanocrystalline β-sheets with a high degree of internal hydrogen bonding embedded in an “amorphous” matrix (1, 3, 27, 28, 30, 31). One specific structural representation of the amorphous matrix mainly contains glycine-rich random chains and moderately oriented helical structures (28). The secondary structure of a typical dragline silk consists of helices, β-sheet crystals, β-turns, and other conformations (3, 32, 33). We recorded Raman spectra for the spider dragline silks studied here (see figs. S4 to S6). According to the work of Shao et al. (34) and Lefevre et al. (35), the Raman band assignments for the specific bond vibrations of the silks are given in table S1. The existence of the peak at about 1668 cm−1 in the amide I region of the silk proteins and the peak at around 1230 cm−1 in the amide III region revealed that insignificant change occurred in the basic conformations of the dragline silk before and after twist actuation (see fig. S4). Yet, more comprehensive characterization of dragline silk, e.g., x-ray diffraction (36) or solid-state nuclear magnetic resonance (28), is expected in the future experiment to further reveal its percent crystallinity and molecular structure at different humidity levels.
Two major proteins are normally found in dragline silks with similar sequence across species (37). For example, the Nephila family spider dragline silk contains spidroins I and II (14); Araneus diadematus spider dragline silk contains A. diadematus fibroin 3 and 4 (ADF3 and ADF4) (15). However, the detailed composition of the two proteins in silks has been studied very rarely. To illustrate the physical mechanism of the humidity-induced twist of dragline silks, we constructed atomistic models for the MaSp1 and MaSp2 proteins of the dragline silk from N. clavipes spider (38, 39) in the presence of water, based on molecular models derived by Keten et al. (27, 32, 40). Each model consists of 15 antiparallel polypeptide chains, with a central poly-Ala region with densely hydrogen-bonded β-sheets, surrounded by amorphous domains on each end. The models are meant to reflect the relaxed molecular conformations of the two proteins in water. MaSp1 consists mainly of GGX-type repeats, (where G denotes glycine, and X represents a subset of amino acids) followed by a glycine and alanine (GA) and poly-Ala domain. By comparison, MaSp2 has proline-rich GPGXX repeats and a poly-Ala region. Proline has been reported to affect the supercontraction ability of various dragline species (33, 41). However, it is unclear how proline is affecting the torsional response of dragline silk.
To address this question, we developed a protocol (see fig. S7) to calculate the molecular chirality of the proteins by tracking the projection of the centroid-centric angle of any three polypeptide chains (or triplets) traveling down from the top to the bottom of the model (see fig. S8). For MaSp2, the angle displacements between the two ends of the molecule are from −60° to −110° (Fig. 5A and fig. S9), depending on triplets considered, and the slope of the angle values is consistently negative, meaning that the chains are twisting to the clockwise direction, if observed from the top of the structure. This result is in good agreement with the experimental result. By contrast, MaSp1 followed a pattern with alternating positive and negative slopes in the angle (Fig. 5B and fig. S10). Maximum angle displacements in MaSp1 are smaller than those in the MaSp2, reduced by a factor of 2 to 3, depending on the triplets considered.
Fig. 5. Mechanisms for humidity-induced torsion in dragline silks on a molecular level.
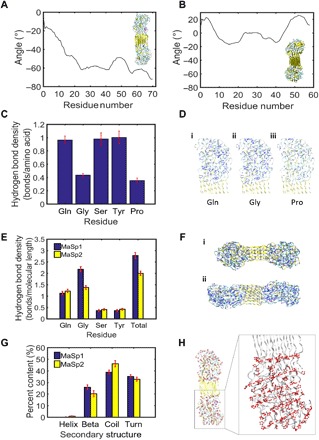
(A) Representative angle displacement curve for MaSp2, showing consistent and negative angles traveling down the strands, which corresponds to clockwise twist. Inset shows molecular model of MaSp2. (B) Representative angle displacement curve for MaSp1, showing alternating positive and negative angles. Inset shows molecular model of MaSp1. (C) Hydrogen bond density scaled by the number of those residues present in the MaSp2 sequence. Proline shows the lowest hydrogen bond density compared to other residues. (D) Hydrogen bonds (shown in blue) within a 3-Å radius around (i) glutamine (Gln), (ii) glycine (Gly), and (iii) proline (Pro). (E) Hydrogen bond density scaled by end-to-end molecular length within a 3-Å radius around amino acids Glu, Gly, Ser, Tyr, and all amino acids in sequences MaSp1 and MaSp2. (F) Hydrogen bonds shown in blue in (i) MaSp1 and (ii) MaSp2 molecules. (G) Secondary structure content in MaSp1 and MaSp2. (H) The location of proline residues (with proline rings shown in red) in MaSp2 depicts a striated, linear ring orientation. Zoomed panel shows dotted guiding lines representative of linear proline ring orientation. Error bars in (C), (E), and (G) show SD over 1 ns.
The presence of proline in MaSp2 produces a more pronounced unidirectional twist at the single-molecule scale. As mentioned, the striated, linear proline ring orientation may force the molecule into a twisted pattern. The steric exclusion effect of the large proline rings can be seen with the disruption of hydrogen bonding around the proline sites along the molecule (see Fig. 5, C and D). As compared to other amino acids, such as serine and glutamine, the occurrence of proline reduces the hydrogen bond density from 1 to 0.4. We note that glycine appears to have a similarly low hydrogen bond density in its vicinity simply because the density is reported as a scaled value by the number of relevant amino acids, and glycine is the dominant amino acid in the sequence. We also observe that hydrogen bonds are more sparsely distributed in MaSp2 compared to MaSp1 (see Fig. 5, E and F), and the total proline contribution reduces the hydrogen bond density in MaSp2 by 20%. Nevertheless, as shown in Fig. 5G, the overall conformation composition in MaSp1 and MaSp2 does not show notable difference. Figure 5H illustrates the orientation of proline rings within MaSp2, which we propose results in its characteristic twist.
While the molecular simulations at the protein level can explain the observed silk behavior, that is not to exclude the possibility of larger-scale mechanisms, too. In the future, it will be interesting to consider how multiscale assembly of silk protein may contribute to enhancing and propagating torsional effects observed at the molecular scale into the micro- and macroscales.
DISCUSSION
Two structural changes have been discussed for the supercontraction behavior of spider dragline silk, which could be extended to the humidity-induced twist deformation observed here. The first change is the relaxation of the oriented structure to coiled structures when high RH is reached to trigger the glass transition of the structure. In our experiment, the silk fiber was subject to a tensile stress of >30 MPa, which could completely restrain the relaxation of the structures according to the experiments of Blackledge et al. (10) and Guan et al. (11). The fact that the silk fiber did not contract in our experiment suggested that this structural relaxation did not take effect. On the contrary, the fiber experienced elongation, and it may be explained that the moisture softened the silk to result in slight strain increase under the same tensile stress. It should be noted that, when we performed molecular simulations on MaSp1 and MaSp2 proteins, we did not apply any tensile stress to the silk proteins. Therefore, no elongation of silk proteins is seen in the simulations.
The second structural change is proposed to be the structural transition of proline containing segment from straight form to twisted form. Previous studies have revealed that the contraction ratio for supercontraction of spider dragline silk depends on the proline content of the dragline silk (11). The occurrence of proline in an amino acid (AA) sequence, in a natural solution environment, often relates to turn or twisted conformation. Swirling of dragline silk is evident during supercontraction, which suggests a twist conformation formation or destruction. Nevertheless, this mechanism has not been separated from that of glass transition–induced structural relaxation. In our experiment, the longitudinal contraction was restrained by the stress from the paddle. However, strong torsional responses were generated under the RH threshold that could trigger the twist relaxation during normal supercontraction. It could be further deduced that the restraining stress for proline twisting should be greater than the stress given by the paddle in the current setup. Future experiments could be designed to explore the tensile stress dependence of the twist deformation induced by humidity.
Both the current experiment and the simulation strongly support the hypothesized mechanism of humidity-induced proline twisting in the RH-induced structural changes of dragline silks. Moreover, the observed right-handed twist in dragline also suggests that the helical structures, mainly proline-rich coils (10, 11), must have chirality. Because the three control fibers, B. mori silk, hair, and Kevlar fiber, do not contain proline, this hypothesis would predict that these fibers would not twist under high RH. We did expect to find a correlation between the proline content in the three different dragline silks and their torsional deformation. However, because the AA composition and full protein sequence for A. versicolor and N. pilipes spider draglines are unavailable, there is still insufficient information about the molecular structure of the two kinds of spider dragline silks to adequately explain their differences in humidity-induced rotational responses.
Without requiring any twist insertion to provide actuation, the torsional actuation of dragline silk is driven by high humidity, which does not require any mechanical twist insertion. Spider dragline silk can generate a huge twist (up to 255°/mm for N. pilipes and 127°/mm for A. versicolor spider dragline silks) under >70% RH. The torsional actuation can be controlled simply by tuning the level of RH. The generated power in dragline silk is not passive but an active change of state in response to humidity that must have an associated driving force, and hence, it could be served as a potential rotary actuator. The molecular dynamics simulation reveals that the proline-rich MaSp2 protein plays an important role for the humidity-induced twist in spider dragline silk. Through using the molecular-level structural changes, the humidity-induced twist turns the dragline silk to act as a torsional actuator. This finding may eventually lead to the development of humidity-driven soft robots, novel sensors, smart textiles, or green energy production devices.
MATERIALS AND METHODS
Collection of spider dragline silk and sample preparation
The N. pilipes and A. versicolor spiders, purchased from Xishuangbanna Tropical Botanical Garden of the Chinese Academy of Sciences, were raised in glass chambers of the laboratory with ornamental tree-branch vegetation. The spiders were watered and fed on moths regularly. Three adult female N. pilipes spiders with masses around 2 g were selected for forced silking by following the procedures introduced in note S1 for the spider silk harvesting. Dragline silk was first pulled out using a tweezer from the spinnerets of fully awake spiders and attached to the mandrel of the reeling device using adhesive tape. The custom-made reeling mandrel is made from high-density polyethylene, which the silk can be wound onto but not stuck to. The double-thread dragline silks were collected at a constant speed of 11 mm/s. For torsional measurements, silks were transferred from the spool to sample holders. The double-thread dragline silk was carefully separated into two individual threads at its end under a microscope (VHX-500F, KEYENCE). The collected silks were stored under room conditions (around 20°C and 55% RH) and were tested within 1 month of collection. The same method was used to collect dragline silks from three A. versicolor spiders with masses ranging from 0.22 to 0.60 g. The N. edulis spider dragline silks were collected in the Oxford Silk Group using similar procedures (11). For comparison, typical polymer fibers, e.g., B. mori silk, Kevlar fiber, and human hair, are also used. The B. mori silk was unraveled from a cocoon; the Kevlar fiber was purchased from the SOVETL company (China); and the human hair was collected from a laboratory member, which is a typical Asian hair—straight, dark brown in color, and with an oval/circular cross section.
Morphology and structure characterization
SEM images were obtained using a Quanta 3D FEG DualBeam with an accelerating voltage of 10 kV. Raman spectra were measured using a LabRAM HR800 (HORIBA Jobin Yvon Co. Ltd.) using a 532-nm Nd:YAG laser with an incident power of 5 mW.
Experimental methods
The schematic diagram of the torsion tester at different humidity is shown in Fig. 1. The paddle made of two bonded washers was left free to swing and rotate for at least 1 hour until equilibrium of steady state was reached. A video camera connected to a computer was fixed right above the specimen to record the real-time responses of the specimen to the change of RH. An image processing program was developed to determine the rotation of the paddle (21). The apparatus was placed in an environmental chamber with RH control from 40 to 100% at a precision of 2%. Certain RH was achieved through mixing water vapor with dry air. The RH was measured by a sensor within the chamber and displayed on the electronic screen. To minimize the influence of vapor flow, the paddle was enclosed in a transparent, cylindrical acrylic chamber. The recorded torsional actuation of the pendulum as twist angles versus time under different RH was analyzed.
Molecular dynamics simulation
Replica exchange molecular dynamics (REMD) (42) was adopted here to achieve native (equilibrium) structures within the time scales accessible to molecular dynamics simulation. REMD is an efficient approach to studying folding and aggregation of proteins since it allows the system to overcome energy barriers and local minima corresponding to non-native structures of proteins (43) and assists the progress of identifying the native (equilibrium) protein structures from the amino acid sequence. The simulation protocol for identifying the nanostructure of spider silk proteins has been described previously by Keten and Buehler (32, 40), and see also the flow chart in fig. S7. Assemblies of short segments of MaSp1 and MaSp2 proteins of dragline silk of N. clavipes spider (38, 39) were studied. The sample sequence of MaSp1 is
GGAGQGGYGGLGSQGAGRGGLGGQGAGAAAAAAGGAGQGGYGGLGSQGAGRGGLGGQGAG, and the sample sequence of MaSp2 is GPGQQGPGGYGPGQQGPGGYGPGQQGPSGPGSAAAAAAAAGPGQQGPGGYGPGQQGPGGYGPGQQGPSGPGS.
Bolded regions refer to β-sheet–rich regions (crystal domains). Models include 15 antiparallel strands. Both models were simulated in the presence of water.
Determination of twist angle at the molecular level
The method for calculation of angle displacement at molecular level is illustrated in fig. S8. First, each starting structure was preprocessed to filter out noise and obtain a cleaner structure for data extraction. A three-way moving average filter was used. Overall, structure patterns were maintained after filtering. Following filtering, 3 of 15 strands were selected in the model. These triplets were selected to best represent the overall structure, so perimeter strands were primarily used. Amino acids located at the same position in each of the three strands were selected to form a triangle. Alpha carbon positions from the amino acids on each triplet were projected onto the xy plane. At a position downstream on the strand (10 residues down in the example, see fig. S8), another triangle was formed to calculate angle displacement (and corresponding twist) between the two triangles sampled. The coordinates of the three points in both triangles were adjusted relative to the aligned centroids of the triangles. Twist angle was measured as an average of the angle displacement for the three points.
Supplementary Material
Acknowledgments
We acknowledge J. Guan of Beihang University for many valuable suggestions and constructive comments on earlier drafts. We also wish to thank F. Vollrath of University of Oxford for providing the N. edulis spider silk, Y. Sun of Zhejiang University for the Raman characterization, and Z. Qin of MIT for the helpful discussion. We acknowledge the Analytical and Testing Center of HUST and the Center for Nanoscale Characterization of WNLO for the characterization support. Funding: This work is financially supported by the National Natural Science Foundation of China (nos. 11702103, 11472114, and 11772138), the Natural Science Foundation of Hubei Province (no. 2015CFB394), and the Young Elite Scientist Sponsorship Program by CAST (no. 2016QNRC001). D.L. and D.J.D. are grateful for the financial support from the EU’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement no. 704292. A.T., C.C.H., and M.J.B. acknowledge support from the NIH (U01 EB014956) and from the MIT Undergraduate Research Opportunities Program (UROP), as well as ONR N000141612333. Author contributions: D.L. and Y.H. designed the research. D.L., S.Z., and J.L. collected the spider dragline silks. D.L., M.Y., and L.Y. performed the experiments. A.T., C.C.H., and M.J.B. carried out the molecular simulations. D.L., D.J.D., C.C.H., and A.T. analyzed the results. D.L., A.T., C.C.H., S.Z., D.J.D., and M.J.B. wrote the paper. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/3/eaau9183/DC1
Fig. S1. SEM images of the N. pilipes spider dragline silk before and after testing.
Fig. S2. Twist of the N. pilipes spider dragline silk with increasing RH from 40 to 100%.
Fig. S3. Twist of the N. pilipes spider dragline silk to RH cyclically changing from ~40 to ~100%.
Fig. S4. Raman spectrum of the N. pilipes spider dragline silk.
Fig. S5. Raman spectrum of the virgin dragline silk of N. edulis spider.
Fig. S6. Raman spectrum of the virgin dragline silk of A. versicolor spider.
Fig. S7. Flow chart for the molecular dynamics simulation and the determination of molecular twist.
Fig. S8. Approach to estimating molecular twist.
Fig. S9. Angle displacement between residue 0 and residue 1 to 70 for MaSp2 protein.
Fig. S10. Angle displacement between residue 0 and residue 1 to 70 for MaSp1 protein.
Table S1. Raman band assignment for the N. pilipes, N. edulis, and A. versicolor dragline silks.
Note S1. Supplementary method for the spider silk harvesting.
REFERENCES AND NOTES
- 1.Vollrath F., Knight D. P., Liquid crystalline spinning of spider silk. Nature 410, 541–548 (2001). [DOI] [PubMed] [Google Scholar]
- 2.Omenetto F. G., Kaplan D. L., New opportunities for an ancient material. Science 329, 528–531 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gosline J. M., Guerette P. A., Ortlepp C. S., Savage K. N., The mechanical design of spider silks: From fibroin sequence to mechanical function. J. Exp. Biol. 202, 3295–3303 (1999). [DOI] [PubMed] [Google Scholar]
- 4.Huang X., Liu G., Wang X., New secrets of spider silk: Exceptionally high thermal conductivity and its abnormal change under stretching. Adv. Mater. 24, 1482–1486 (2012). [DOI] [PubMed] [Google Scholar]
- 5.Emile O., Le Floch A., Vollrath F., Biopolymers: Shape memory in spider draglines. Nature 440, 621–621 (2006). [DOI] [PubMed] [Google Scholar]
- 6.Liu D., Yu L., He Y., Peng K., Liu J., Guan J., Dunstan D. J., Peculiar torsion dynamical response of spider dragline silk. Appl. Phys. Lett. 111, 013701 (2017). [Google Scholar]
- 7.Mortimer B., Gordon S. D., Holland C., Siviour C. R., Vollrath F., Windmill J. F., The speed of sound in silk: Linking material performance to biological function. Adv. Mater. 26, 5179–5183 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bell F. I., McEwen I. J., Viney C., Supercontraction stress in wet spider dragline. Nature 416, 37 (2002). [DOI] [PubMed] [Google Scholar]
- 9.Agnarsson I., Dhinojwala A., Sahni V., Blackledge T. A., Spider silk as a novel high performance biomimetic muscle driven by humidity. J. Exp. Biol. 212, 1990–1994 (2009). [DOI] [PubMed] [Google Scholar]
- 10.Blackledge T. A., Boutry C., Wong S. C., Baji A., Dhinojwala A., Sahni V., Agnarsson I., How super is supercontraction? Persistent versus cyclic responses to humidity in spider dragline silk. J. Exp. Biol. 212, 1980–1988 (2009). [DOI] [PubMed] [Google Scholar]
- 11.Guan J., Vollrath F., Porter D., Two mechanisms for supercontraction in Nephila spider dragline silk. Biomacromolecules 12, 4030–4035 (2011). [DOI] [PubMed] [Google Scholar]
- 12.Lefèvre T., Auger M., Spider silk as a blueprint for greener materials: A review. Int. Mater. Rev. 61, 127–153 (2016). [Google Scholar]
- 13.Giesa T., Schuetz R., Fratzl P., Buehler M. J., Masic A., Unraveling the molecular requirements for macroscopic silk supercontraction. ACS Nano 11, 9750–9758 (2017). [DOI] [PubMed] [Google Scholar]
- 14.Lin S., Zhu J., Li X., Guo Y., Fang Y., Cheng H., Zhu H., Water-driven actuation of Ornithoctonus huwena spider silk fibers. Appl. Phys. Lett. 110, 053103 (2017). [Google Scholar]
- 15.Elettro H., Neukirch S., Vollrath F., Antkowiak A., In-drop capillary spooling of spider capture thread inspires hybrid fibers with mixed solid-liquid mechanical properties. Proc. Natl. Acad. Sci. U.S.A. 113, 6143–6147 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Haines C. S., Lima M. D., Li N., Spinks G. M., Foroughi J., Madden J. D., Kim S. H., Fang S., Jung de Andrade M., Göktepe F., Göktepe Ö., Mirvakili S. M., Naficy S., Lepró X., Oh J., Kozlov M. E., Kim S. J., Xu X., Swedlove B. J., Wallace G. G., Baughman R. H., Artificial muscles from fishing line and sewing thread. Science 343, 868–872 (2014). [DOI] [PubMed] [Google Scholar]
- 17.Liu Z. F., Fang S., Moura F. A., Ding J. N., Jiang N., Di J., Zhang M., Lepró X., Galvao D. S., Haines C. S., Yuan N. Y., Yin S. G., Lee D. W., Wang R., Wang H. Y., Lv W., Dong C., Zhang R. C., Chen M. J., Yin Q., Chong Y. T., Zhang R., Wang X., Lima M. D., Ovalle-Robles R., Qian D., Lu H., Baughman R. H., Hierarchically buckled sheath-core fibers for superelastic electronics, sensors, and muscles. Science 349, 400–404 (2015). [DOI] [PubMed] [Google Scholar]
- 18.Foroughi J., Spinks G. M., Wallace G. G., Oh J., Kozlov M. E., Fang S., Mirfakhrai T., Madden J. D. W., Shin M. K., Kim S. J., Baughman R. H., Torsional carbon nanotube artificial muscles. Science 334, 494–497 (2011). [DOI] [PubMed] [Google Scholar]
- 19.Lima M. D., Li N., Jung de Andrade M., Fang S., Oh J., Spinks G. M., Kozlov M. E., Haines C. S., Suh D., Foroughi J., Kim S. J., Chen Y., Ware T., Shin M. K., Machado L. D., Fonseca A. F., Madden J. D. W., Voit W. E., Galvao D. S., Baughman R. H., Electrically, chemically, and photonically powered torsional and tensile actuation of hybrid carbon nanotube yarn muscles. Science 338, 928–932 (2012). [DOI] [PubMed] [Google Scholar]
- 20.Noiseux D. U., Similarity laws of the internal damping of stranded cables in transverse vibrations. IEEE. T. Power Delivery 7, 1574–1581 (1992). [Google Scholar]
- 21.Yu L., Liu D., Peng K., He Y., An improved torsion pendulum based on image processing for single fibers. Meas. Sci. Technol. 27, 075601 (2016). [Google Scholar]
- 22.C. R. Robbins, Chemical and Physical Behavior of Human Hair (Springer Berlin Heidelberg, 2012). [Google Scholar]
- 23.Chun K.-Y., Hyeong Kim S., Kyoon Shin M., Hoon Kwon C., Park J., T. Kim Y., Spinks G. M., Lima M. D., Haines C. S., Baughman R. H., Jeong Kim S., Hybrid carbon nanotube yarn artificial muscle inspired by spider dragline silk. Nat. Commun. 5, 3322 (2014). [DOI] [PubMed] [Google Scholar]
- 24.Yang Z., Liivak O., Seidel A., LaVerde G., Zax D. B., Jelinski L. W., Supercontraction and backbone dynamics in spider silk: 13C and 2H NMR studies. J. Am. Chem. Soc. 122, 9019–9025 (2000). [Google Scholar]
- 25.Liu D., He Y., Dunstan D. J., Zhang B., Gan Z., Hu P., Ding H., Anomalous plasticity in the cyclic torsion of micron scale metallic wires. Phys. Rev. Lett. 110, 244301 (2013). [DOI] [PubMed] [Google Scholar]
- 26.Liu D., Peng K., He Y., Direct measurement of torsional properties of single fibers. Meas. Sci. Technol. 27, 115017 (2016). [Google Scholar]
- 27.Keten S., Xu Z., Ihle B., Buehler M. J., Nanoconfinement controls stiffness, strength and mechanical toughness of β-sheet crystals in silk. Nat. Mater. 9, 359–367 (2010). [DOI] [PubMed] [Google Scholar]
- 28.van Beek J., Hess S., Vollrath F., Meier B. H., The molecular structure of spider dragline silk: Folding and orientation of the protein backbone. Proc. Natl. Acad. Sci. U.S.A. 99, 10266–10271 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li S., McGhie A., Tang S. L., New internal structure of spider dragline silk revealed by atomic force microscopy. Biophys. J. 66, 1209–1212 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Simmons A. H., Michal C. A., Jelinski L. W., Molecular orientation and two-component nature of the crystalline fraction of spider dragline silk. Science 271, 84–87 (1996). [DOI] [PubMed] [Google Scholar]
- 31.Oroudjev E., Soares J., Arcidiacono S., Thompson J. B., Fossey S. A., Hansma H. G., Segmented nanofibers of spider dragline silk: Atomic force microscopy and single-molecule force spectroscopy. Proc. Natl. Acad. Sci. U.S.A. 99, 6460–6465 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Keten S., Buehler M. J., Atomistic model of the spider silk nanostructure. Appl. Phys. Lett. 96, 153701 (2010). [Google Scholar]
- 33.Giesa T., Perry C. C., Buehler M. J., Secondary structure transition and critical stress for a model of spider silk assembly. Biomacromolecules 17, 427–436 (2016). [DOI] [PubMed] [Google Scholar]
- 34.Shao Z., Vollrath F., Sirichaisit J., Young R. J., Analysis of spider silk in native and supercontracted states using Raman spectroscopy. Polymer 40, 2493–2500 (1999). [Google Scholar]
- 35.Lefevre T., Rousseau M. E., Pézolet M., Protein secondary structure and orientation in silk as revealed by Raman spectromicroscopy. Biophys. J. 92, 2885–2895 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Riekel C., Bränden C., Craig C., Ferrero C., Heidelbach F., Müller M., Aspects of X-ray diffraction on single spider fibers. Int. J. Biol. Macromol. 24, 179–186 (1999). [DOI] [PubMed] [Google Scholar]
- 37.Gatesy J., Hayashi C., Motriuk D., Woods J., Lewis R., Extreme diversity, conservation, and convergence of spider silk fibroin sequences. Science 291, 2603–2605 (2001). [DOI] [PubMed] [Google Scholar]
- 38.Hayashi C. Y., Shipley N. H., Lewis R. V., Hypotheses that correlate the sequence, structure, and mechanical properties of spider silk proteins. Int. J. Biol. Macromol. 24, 271–275 (1999). [DOI] [PubMed] [Google Scholar]
- 39.Holland G. P., Creager M. S., Jenkins J. E., Lewis R. V., Yarger J. L., Determining secondary structure in spider dragline silk by carbon-carbon correlation solid-state NMR spectroscopy. J. Am. Chem. Soc. 130, 9871–9877 (2008). [DOI] [PubMed] [Google Scholar]
- 40.Keten S., Buehler M. J., Nanostructure and molecular mechanics of spider dragline silk protein assemblies. J. R. Soc. Interface 7, 1709–1721 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Liu Y., Shao Z., Vollrath F., Relationships between supercontraction and mechanical properties of spider silk. Nat. Mater. 4, 901–905 (2005). [DOI] [PubMed] [Google Scholar]
- 42.Sugita Y., Okamoto Y., Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 314, 141–151 (1999). [Google Scholar]
- 43.Miyashita N., Straub J. E., Thirumalai D., Sugita Y., Transmembrane structures of amyloid precursor protein dimer predicted by replica-exchange molecular dynamics simulations. J. Am. Chem. Soc. 131, 3438–3439 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/3/eaau9183/DC1
Fig. S1. SEM images of the N. pilipes spider dragline silk before and after testing.
Fig. S2. Twist of the N. pilipes spider dragline silk with increasing RH from 40 to 100%.
Fig. S3. Twist of the N. pilipes spider dragline silk to RH cyclically changing from ~40 to ~100%.
Fig. S4. Raman spectrum of the N. pilipes spider dragline silk.
Fig. S5. Raman spectrum of the virgin dragline silk of N. edulis spider.
Fig. S6. Raman spectrum of the virgin dragline silk of A. versicolor spider.
Fig. S7. Flow chart for the molecular dynamics simulation and the determination of molecular twist.
Fig. S8. Approach to estimating molecular twist.
Fig. S9. Angle displacement between residue 0 and residue 1 to 70 for MaSp2 protein.
Fig. S10. Angle displacement between residue 0 and residue 1 to 70 for MaSp1 protein.
Table S1. Raman band assignment for the N. pilipes, N. edulis, and A. versicolor dragline silks.
Note S1. Supplementary method for the spider silk harvesting.


