Spin-charge-lattice coupling in YBaCuFeO₅: Optical properties and first-principles calculations

Abstract

We combined spectroscopic ellipsometry, Raman scattering spectroscopy, and first-principles calculations to explore the optical properties of YBaCuFeO₅ single crystals. Measuring the optical absorption spectrum of YBaCuFeO₅ at room temperature revealed a direct optical band gap at approximately 1.41 eV and five bands near 1.69, 2.47, 3.16, 4.26, and 5.54 eV. Based on first-principles calculations, the observed optical excitations were appropriately assigned. Analysis of the temperature dependence of the band gap indicated anomalies in antiferromagnetic phase transition at 455 and 175 K. Additionally, a hardening in the frequency of the E_g phonon mode was observed at 175 K. The value of the spin–phonon coupling constant was 15.7 mRy/Ų. These results suggest a complex nature of spin–charge–lattice interactions in YBaCuFeO₅.

Introduction

Since YBaCuFeO₅ was synthesized in 1988¹ and treated as an impurity phase in the Fe-doped high-temperature copper oxides of YBa₂Cu₃O₇, this compound has received substantial research attention because of its complex physical properties and potential practical applications^2–14. YBaCuFeO₅ is tetragonal in structure and belongs to the P4/mmm space group^1,4,6,7. The building block consists of a CuFeO₁₀ bilayer of corner-sharing CuO₅ and FeO₅ square pyramids. Y³⁺ cations separate the CuFeO₁₀ bilayer, and the Ba²⁺ ions are located within the bilayer; this structure resembles the crystal structure in YBa₂Cu₃O₇. Much of the research interest concerning YBaCuFeO₅ has been focused on the compound’s complex magnetic structures^2,4–9. YBaCuFeO₅ displays a commensurate antiferromagnetic structure at approximately T_N1 = 440 K and an incommensurate spiral antiferromagnetic structure at temperatures below T_N2 = 230 K. Recent reports of magnetism-driven ferroelectricity at T_N2 = 230 K and a large electric polarization (0.4 μC/cm²) observed in YBaCuFeO₅^10,11,13 have led to further explorations of the possibilities for new functional devices based on the magnetoelectric effect of this material^15–18.

Numerous studies have examined magnetization, Mossbauer, neutron powder diffraction, and dielectric measurements, but the optical and phonon properties of YBaCuFeO₅ have remained largely unexplored³. Moreover, previous studies on YBaCuFeO₅ have been limited to powder samples. Recently, we modified the traveling-solvent floating-zone technique and used it to synthesize high-quality YBaCuFeO₅ single crystals¹⁹. Consecutive anisotropic antiferromagnetic phase transitions were observed at approximately 455 and 170 K^19,20. In the present study, we combined spectroscopic ellipsometry, Raman scattering spectroscopy, and first-principles calculations to determine the electronic structure and lattice dynamics of YBaCuFeO₅. Clarification of the microscopic characteristics that govern the material’s optical and phononic excitations is critical for further development of device applications. In this study, we also examined the correlation of the optical response with the magnetic phase transitions of YBaCuFeO₅. The findings of this investigation may help elucidate the nature of spin–charge–lattice coupling in this system and in related multiferroic materials.

Technical Details

Experiment

YBaCuFeO₅ single crystals were grown using a modified traveling-solvent floating-zone method. The details of sample preparation were as reported previously¹⁹. The crystals that formed on the bc-surface exhibited disk shapes of 5-mm diameter and 2-mm thickness. The (100) axis is the floating-zone growth direction. For each batch, crystals were characterized using synchrotron x-ray powder diffraction, dc resistivity, and magnetization measurements^19,20. Figure 1 presents the profiles for x-ray powder diffraction of YBaCuFeO₅ at 300 and 90 K. The spectra did not change significantly with temperature, which implied that no structural phase transition occurred within the temperature range investigated. Only after cooling below 300 K did YBaCuFeO₅ exhibit a decrease in the a and c lattice constants.

Figure 1.

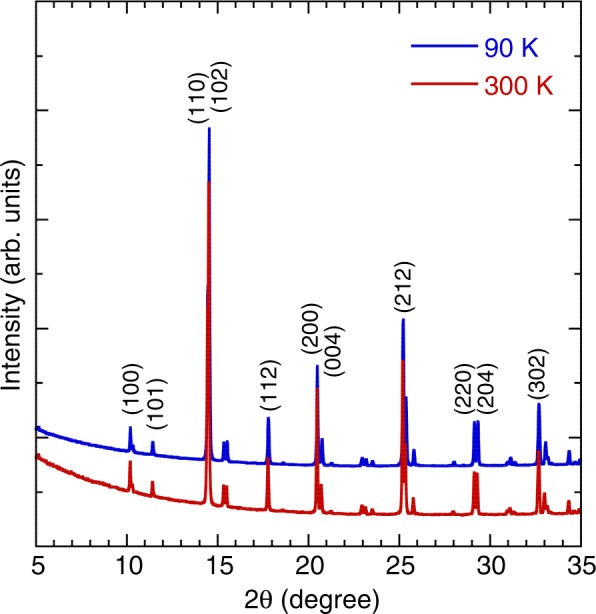
X-ray powder diffraction patterns of YBaCuFeO₅ at 300 and 90 K.

Spectroscopic ellipsometric measurements were conducted under angles of incidence between 60° and 75° and over a spectral range of 0.73 to 6.42 eV using a Woollam M-2000U ellipsometer. For temperature-dependent measurements between 4.3 and 500 K, the ellipsometer was equipped with an ultrahigh-vacuum cryostat. Raman scattering experiments were performed in a backscattering geometry with a laser-excitation wavelength of 532 nm. The linearly polarized light was focused to a 3-μm-diameter spot on the sample surface, and the scattered light was collected and dispersed using a SENTERRA spectrometer equipped with a 1024-pixel-wide charge-coupled detector. The polarizations of incident and scattered light were set such that the incident and scattered lights were parallel and perpendicular (cross) to each other. The spectral resolutions achieved using these instruments are typically less than 1 cm⁻¹. To avoid heating effects, the laser power was set to 0.2 mW. The sample was placed in a continuous-flow helium cryostat and Linkam heating stage, enabling measurements of the sample under temperatures of 10–700 K.

Theoretical methods

To investigate the electronic structure of YBaCuFeO₅, we modeled several YBaCuFeO₅ systems using density functional theory (DFT) calculations in the Vienna ab initio Simulation Package (VASP)^21,22. The electron wavefunctions were expanded in plane wave basis sets with an energy cutoff of 550 eV. Perdew–Burke–Ernzerhof (PBE) functional approximation was applied to the electron exchange correlation energy²³. The 5s4p4d4s, 6s5s5p, 4s3d, 4s3d, and 2s2p orbitals of Y, Ba, Cu, Fe, and O atom species were treated as valence electrons, and the pseudopotentials of core electrons were generated using the projector augmented-wave method^24,25. A 5 × 5 × 3 gamma-centered k-point mesh was applied to establish the optimized structures and absorption coefficients. The bandgap sizes of metal oxides are underestimated in DFT calculations; therefore, additional Hubbard-U potentials²⁶ were applied to Cu (U = 1 eV, J = 0 eV) and Fe (U = 6 eV, J = 0 eV) atom species. To enable observation of the G-type antiferromagnetic feature and of variation in the arrangement of Cu and Fe atoms, models with supercells comprising 2 × 2 × 2 formula cells were constructed (see supplementary information). In terms of one formula cell, the optimized lattice constants, a and c, ranged from 3.884 to 3.917 Å and 7.786 to 7.847 Å; these values were in favorable agreement with the experimental data²⁰.

Results and Discussion

Electronic excitations

Figure 2(a) presents the room-temperature real ε₁ and imaginary ε₂ parts of the dielectric function ε(ω) of YBaCuFeO₅ obtained from spectroscopic ellipsometry analysis. We observed a dispersive response in ε₁ with an overall positive value, which reflected typical behavior for a semiconductor. Optical transitions were identifiable in the spectra based on resonance and antiresonance features, which appeared at the same energy in ε₂ and ε₁, respectively. Notably, the spectrum ε₂ of YBaCuFeO₅ was dominated by optical transitions, for which detailed analysis is presented subsequently. We fitted the spectra reasonably well using a classical Lorentzian model for the complex dielectric function²⁷

$$\mathrm{\epsilon }(\omega )={\mathrm{\epsilon }}_{\infty }+{\sum }_{j=1}^N\frac{{\omega }_{pj}^2}{\left({\omega }_j^2-{\omega }^2\right)-i\omega {\gamma }_j}$$ 1

where ω_j, γ_j, and ω_pj represent the frequency, damping, and oscillator strength of the jth Lorentzian contribution. ε_∞ is the permittivity due to high-frequency electronic excitations. Figure 2(b) illustrates the room-temperature optical absorption spectrum. This absorption spectrum can also be modeled reasonably well by using Lorentzian oscillators. As the photon energies increased, the absorption gradually increased; three bands were manifested near 1.69, 2.47, and 3.16 eV; a maximum value was reached at approximately 4.26 eV, and a higher band was manifested at approximately 5.54 eV. In a normal solid, the absorption coefficient α(E) is accepted and is based on contributions from both direct and indirect band gap transitions²⁸. The absorption coefficient is given by

$$\alpha \left(E\right)=A{(E-E_{g,dir})}^{0.5}+B{(E-E_{g,indir}\mp E_{ph})}^2,$$ 2

where E_g,dir and E_g,ind are the magnitudes of direct and indirect gaps, respectively; E_ph is the emitted (absorbed) phonon energy, and A and B are constants. This model, which assumes a simple band shape, enables extraction of the direct energy gap when α² is plotted as a function of photon energy. The inset of Fig. 2(b) illustrates the direct band gap of 1.41 ± 0.01 eV at 300 K.

Figure 2.

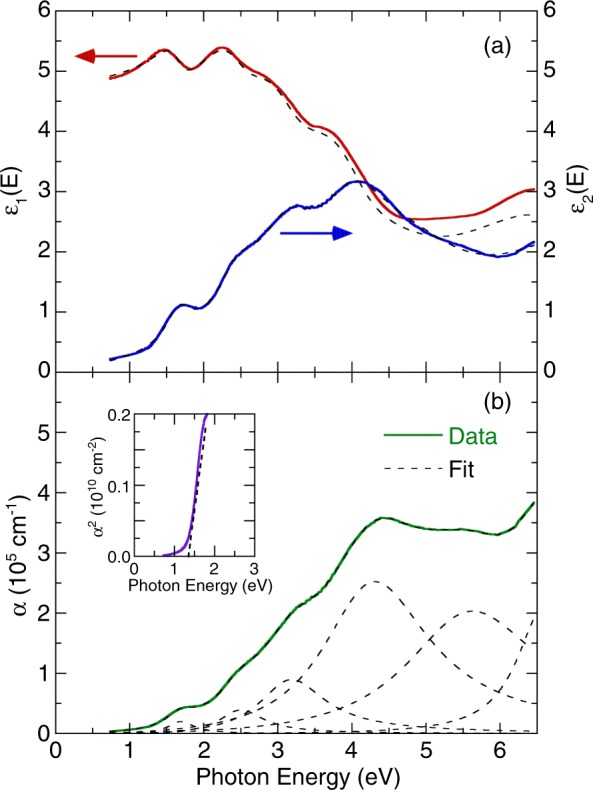
(a) Dielectric function for YBaCuFeO₅ at room temperature. (b) Optical absorption coefficient of YBaCuFeO₅ at room temperature. The dashed lines indicate the best fit from the Lorentzian model. The inset illustrates the direct band gap analysis of YBaCuFeO₅.

Figure 3 illustrates the temperature dependence of the optical absorption spectra. As the temperature was lowered, all optical absorptions exhibited shifts of the peak positions to higher energies and narrowing of linewidths. Figure 4 indicates the temperature dependence of the energy band gap. The gap became hardening as the temperature decreased. In principle, the observed blueshift value of the band gap energy with decreasing temperature in semiconductors can be described using the Bose–Einstein model²⁹

$$E_g\left(T\right)=E_g\left(0\right)-\frac{2a_B}{\exp \left({\mathrm{\Theta }}_B/T\right)-1},$$ 3

where E_g(0) is the band gap energy at 0 K; a_B represents the strength of the electron–phonon interactions; and Θ_B is the average phonon temperature. Our fitting results indicated that the band gap energy toward 0 K was approximately 1.45 ± 0.01 eV. The strength of the electron–phonon interactions a_B and the average phonon temperature Θ_B were 102 meV and 496 K, respectively. These values are larger than those obtained for other multiferroic oxides, such as BiFeO₃^30,31, thus reflecting a strong electron-phonon interaction in YBaCuFeO₅. As is evident from Fig. 4, the Bose–Einstein model reproduced the overall temperature dependence of the band gap in YBaCuFeO₅ satisfactorily. However, the band gap deviated from the theoretical prediction at 455 and 175 K, which suggested spin–charge interactions. Similar coupling behavior has been observed in other multiferroic materials, such as BiFeO₃^31,32, h-LuFeO₃³³, and LuFe₂O₄³⁴.

Figure 3.

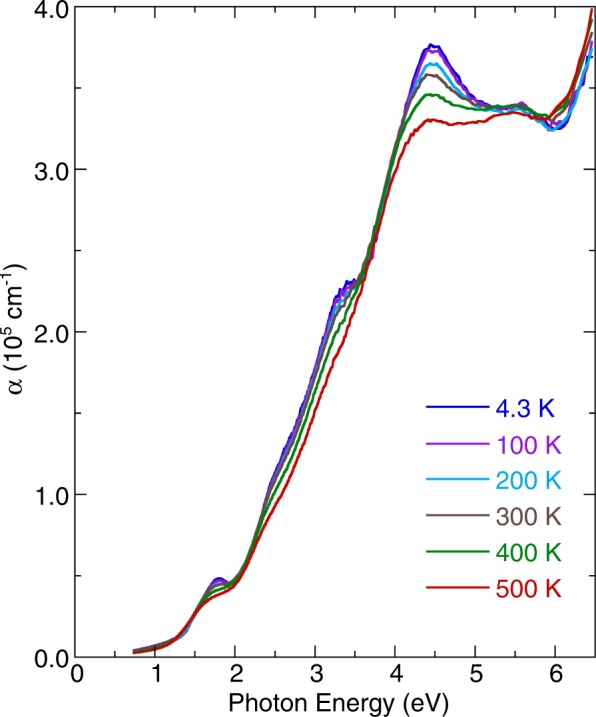
Temperature dependence of the optical absorption spectra of YBaCuFeO₅.

Figure 4.

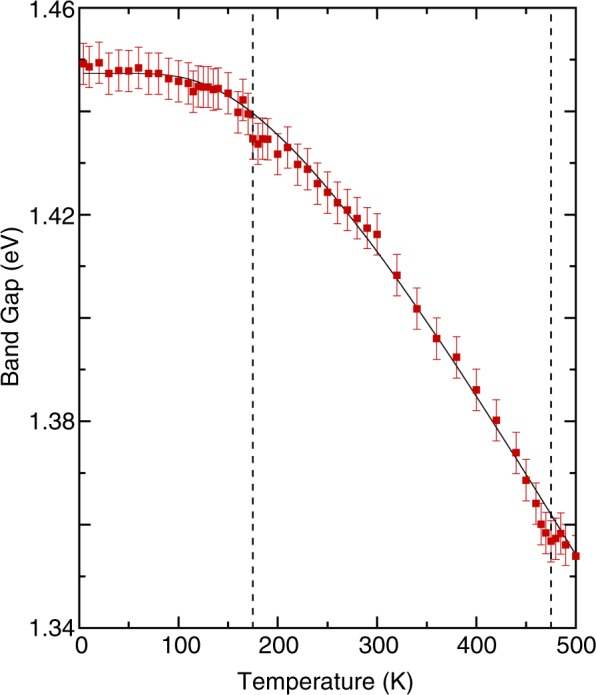
The energy band gap as a function of temperature for YBaCuFeO₅. The thin solid line indicates the result of the fitting using the Bose–Einstein model. Vertical dashed lines denote transition temperatures.

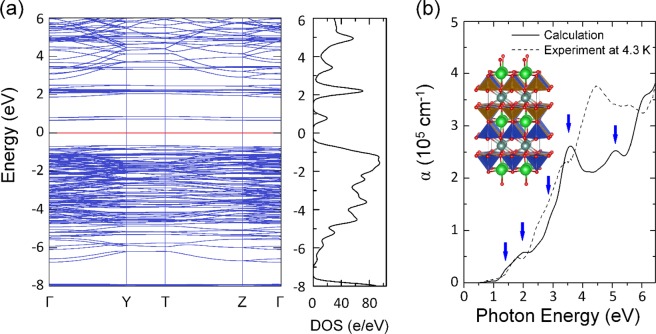
To understand the nature of the observed absorption peaks in YBaCuFeO₅, we calculated the electronic band structure, density of states (DOS), and optical absorption coefficient, and the results are presented in Fig. 5. In a previous report¹³, Morin et al. simulated YBaCuFeO₅ models using DFT calculations with 10 arrangements of Cu and Fe atoms. However, optical absorption spectra and electronic band structure were not assessed in their work, and these properties are critical for analyzing the optical properties of YBaCuFeO₅. We reinspected the crystal structure and electronic properties of the five models with the lowest energies from those in the study of Morin et al.¹³. In addition, we examined two models of slightly higher energies than the five previously mentioned models (see supplementary information). These two models were not investigated by Morin et al. We discovered that only one of the new models could reproduce the absorption spectrum presented in Fig. 2(b). The structure of the simulation model is depicted in Fig. 5(b).

Figure 5.

(a) Calculated electronic band structure, density of states (DOS), and (b) calculated and experimental optical absorption coefficient of YBaCuFeO₅. The inset in (b) depicts the atomic structure of the simulation model with dark cyan, green, blue, brown, and red spheres representing the Y, Ba, Cu, Fe, and O atoms, respectively. The pyramids formed by oxygen atoms embracing Cu and Fe atoms are also highlighted.

The electronic band structure of YBaCuFeO₅ (Fig. 5(a)) revealed that both the valence-band maximum and the conduction-band minimum were flat from the Γ to Y points of the Brillouin zone. The calculated direct band gap of YBaCuFeO₅ was approximately 1.36 eV, which was consistent with the experimental results. Furthermore, the shape and peak positions of the calculated optical coefficient spectrum (Fig. 5(b)) exhibited favorable agreement with the experimental data. Electronic excitations occurred at approximately 1.45, 2.0, 2.9, 3.5, and 5.1 eV. According to the DOS analysis (see supplementary information), the observed excitation near 1.45 eV was due to transitions from the 3d_xy orbitals of Cu or Fe atoms to the 3d_x²_−y² orbitals of Cu or Fe atoms. The absorption peak near 2.0 eV was attributed to transitions from the 3d_xz/yz orbitals of Cu or Fe atoms to the 3d_x²_−y² orbitals of Cu or Fe atoms. These symmetry-forbidden d-d transitions were possible due to strong hybridization of Cu or Fe 3d and O 2p states. The observed 2.9-, 3.5-, and 5.1-eV absorption peaks were assigned to the charge–transfer excitations from the 2p orbitals of O atoms to the 3d orbitals of Cu or Fe atoms.

Vibrational properties

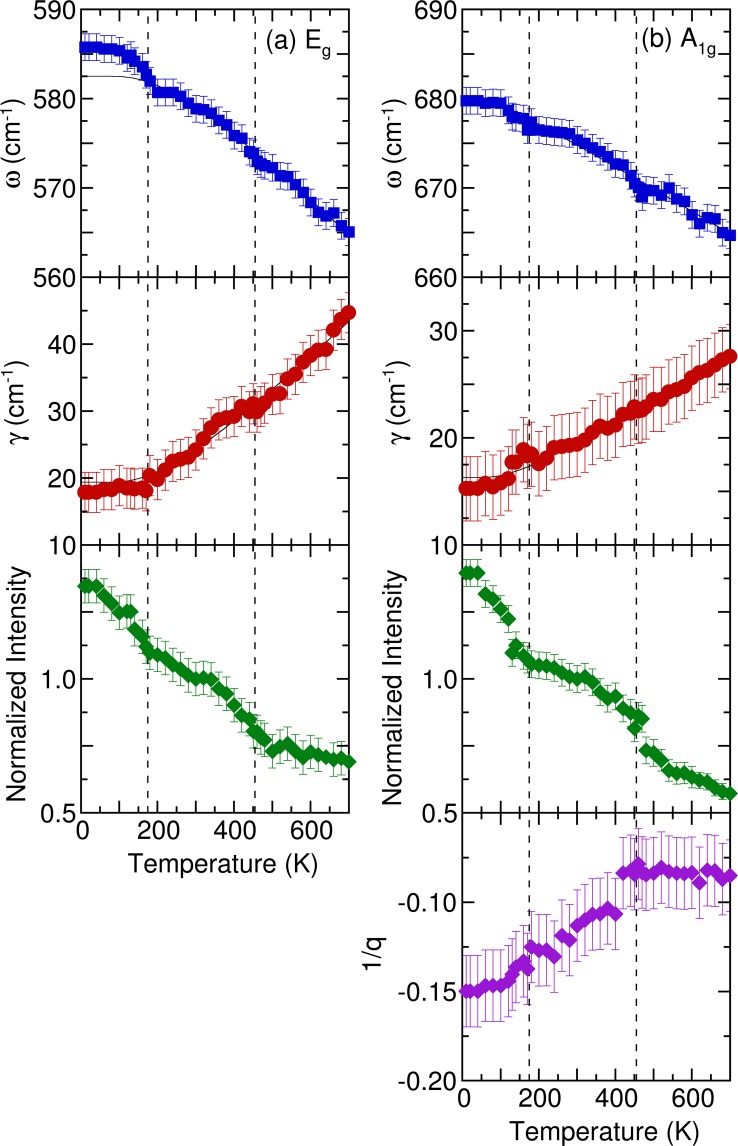
Figure 6(a) depicts the room-temperature Raman scattering spectrum of YBaCuFeO₅. The spectrum comprised six first-order Raman phonon modes. We fitted these phonon peaks using a standard Lorentzian profile. According to factor group analysis, the structure of YBaCuFeO₅ is tetragonal (space group P4/mmm) with one formula unit per primitive cell. The irreducible representation of the phonon modes at the center of the Brillouin zone is given by Γ = 2A_1g + B_1g + 3E_g + 5A_2u + 6E_u + B_2u³. These modes are classified as Raman active (2A_1g + B_1g + 3E_g), infrared active (4A_2u + 5E_u), acoustic (A_2u + E_u), and silent (B_2u). The inset of Fig. 6(a) illustrates polarized Raman scattering spectra of parallel and cross measurements. The 456 and 675 cm⁻¹ modes exhibited stronger intensities in the parallel configuration, indicating that they were of A_1g characters. By contrast, the 579 cm⁻¹ mode in cross geometry was stronger than other phonon peaks, thus demonstrating E_g symmetry. The E_g mode involves in-plane O-Cu/Fe-O bending motions, whereas the A_1g mode results from out-of-plane Cu/Fe-O stretching motions³. Additionally, the low-intensity broad phonon mode observed at approximately 1267 cm⁻¹ should be ascribed to multiphonon processes^35–37. In the present study, the 675 cm⁻¹ A_1g phonon mode exhibited an asymmetric line shape, indicating a strong interaction between the lattice vibrations and a magnetic continuum. As presented in the inset of Fig. 6(b), this mode was fitted using a standard Fano profile³⁸ as follows: I(ω) = I₀ (ε + q)²/(1 + ε²), where ε = (ω – ω₀)/Γ; ω₀ is the phonon frequency; Γ is the linewidth; and q is the asymmetry factor of the phonon mode.

Figure 6.

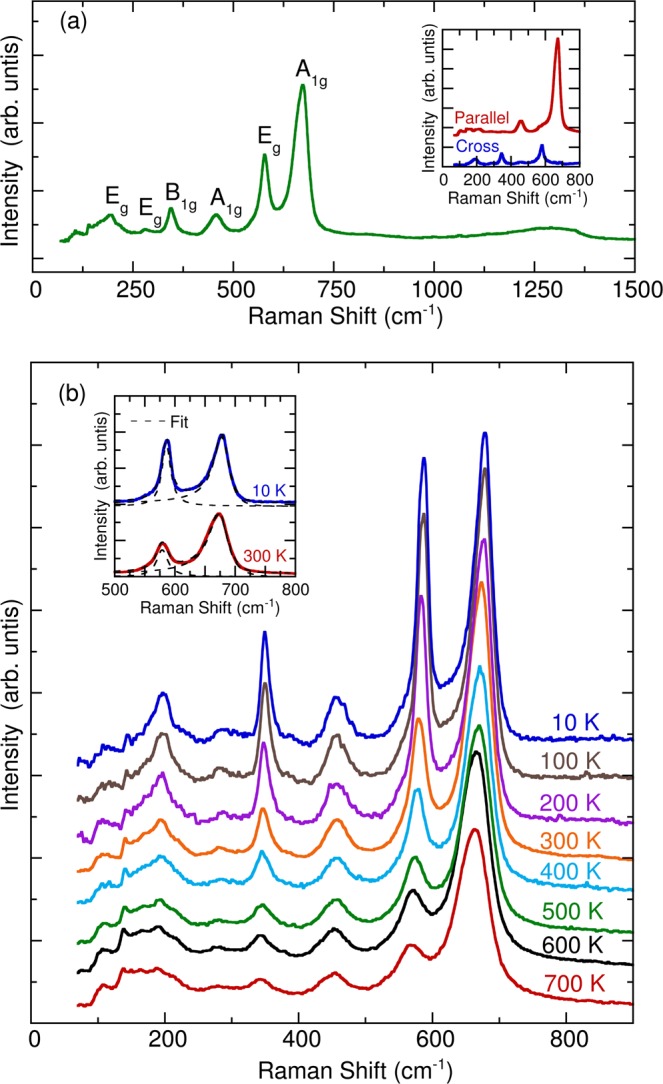
(a) Unpolarized Raman scattering spectrum of YBaCuFeO₅ at room temperature. The inset illustrates the Raman scattering spectra in parallel and cross scattering geometries. (b) Temperature dependence of unpolarized Raman scattering spectra of YBaCuFeO₅. The inset denotes the fitting results of spectra at 300 and 10 K using the Lorentzian and Fano models.

Figure 6(b) indicates the temperature dependence of the Raman scattering spectra of YBaCuFeO₅. With decreasing temperatures, the peak positions of all phonon modes shifted to higher frequencies, and the resonance linewidth narrowed. However, the phonon parameters of the 579 cm⁻¹ E_g and 675 cm⁻¹ A_1g modes behaved peculiarly at 455 and 175 K. Figure 7 further illustrates the frequency, linewidth, normalized intensity, and asymmetry factors of these two modes as functions of temperature. The frequencies and linewidths of the 579 cm⁻¹ E_g and 675 cm⁻¹ A_1g modes changed discontinuously at 455 and 175 K. Furthermore, the oscillator strengths of the two modes increased below 455 K. In a normal anharmonic solid, a nearly temperature-independent oscillator strength is expected, and at decreasing temperature, the phonon frequency should increase while linewidth decreases. Anharmonic interactions are relevant to high-order terms of atomic vibrations, which are beyond traditional harmonic terms. The temperature-dependent phonon frequency and linewidth can be written as³⁹

$$\omega \left(T\right)={\omega }_O+A\left[1+\frac{2}{\exp (\hslash \mathrm{\omega }/k_{B}T)-1}\right],$$ 4

and

$$\gamma \left(T\right)={\gamma }_O+B\left[1+\frac{2}{\exp \left(\hslash \mathrm{\omega }/k_{B}T\right)-1}\right],$$ 5

where ω_o and γ_o are the intrinsic frequency of the optical phonon mode and the linewidth broadening that results from defects. Parameters A and B are the anharmonic coefficients, and $\frac{1}{[\exp (\hslash {\omega }_o/2k_{B}T)-1]}$ corresponds to the thermal population factor of acoustic modes. For analysis of anharmonic contributions to the 579 cm⁻¹ E_g mode, the values of ω_o (≈582.5 cm⁻¹), _γo (≈19 cm⁻¹), A (≈−4.5), and B (≈1.8) were determined. For the 675 cm⁻¹ A_1g mode, the values of ω_o (≈682.9 cm⁻¹), _γo (≈16 cm⁻¹), A (≈−4.9), and B (≈1.2) were determined. Parameter A was negative, indicating that with an increase in temperature, the peak shifted to a lower frequency because of anharmonic phonon decay. By contrast, parameter B was positive, reflecting linewidth narrowing with a decrease in the temperature. The thin solid lines in Fig. 7(a,b) represent theoretical predictions based on Eqs (4, 5). The 675 cm⁻¹ A_1g mode exhibited a slight deviation from the usual anharmonic contribution to the temperature dependence of the phonon frequency and linewidth through the 455 and 175 K antiferromagnetic ordering transitions. By contrast, the 579 cm⁻¹ E_g mode hardened significantly below 175 K. Because the YBaCuFeO₅ exhibited no drastic temperature dependence in terms of crystal structure and lattice parameters, the phonon anomalies below the antiferromagnetic ordering temperature were attributed to spin–phonon interactions. Similar magnetoelastic coupling has been detected in other multiferroic materials, such as HoMnO₃⁴⁰, BiFeO₃⁴¹_, and Y₂CoMnO₆⁴².

Figure 7.

Temperature dependence of the frequency, linewidth, normalized intensity, and asymmetry factors of (a) E_g and (b) A_1g phonon modes of YBaCuFeO₅. The thin solid lines indicate the results of the fitting from the anharmonic model. Vertical dashed lines denote transition temperatures.

As indicated in Fig. 7(a), the frequency of the 579 cm⁻¹ E_g mode deviated considerably from the theoretical predictions to below the antiferromagnetic phase transition temperature of 175 K. This effect was attributed to the renormalization of the in-plane E_g phonon induced by magnetic ordering, usually understood as a sign of coupling between the lattice and spin degrees of freedom. The spin–phonon coupling constant can be calculated from frequency–shift data using the expression⁴³

$${\left(\mathrm{\Delta }\omega \right)}_{SP}=\frac{{\lambda }_{eff}}{{\omega }_{\mathit{0}}}{\left[\frac{M_{sub}(T)}{4{\mu }_B}\right]}^2,$$ 6

where (Δω)_SP is the difference between the phonon frequency values at 10 K from the theoretical prediction and experimental data; ω_o is the value from Eq. (4); M_sub(T) is the sublattice magnetic susceptibility with the external magnetic field along the ab plane; and λ_eff is the spin–phonon coupling constant. In the present study, we used the magnetic susceptibility with the external magnetic field along the ab plane and estimated the spin–phonon coupling constant to be 15.7 mRy/Ų. The magnitude of this value was comparable to those obtained for other multiferroic manganites^44–46.

Summary

We employed both spectroscopic ellipsometry and Raman scattering spectroscopy to investigate the electronic structure and lattice dynamics of YBaCuFeO₅ single crystals. We also characterized the optical transitions by comparing the experimental data and the results of first-principles calculations. The optical absorption spectrum of YBaCuFeO₅ at room temperature revealed Cu/Fe d to d on-site transitions at approximately 1.69 and 2.47 eV and O 2p to Cu/Fe 3d charge–transfer transitions at approximately 3.16, 4.26, and 5.54 eV. YBaCuFeO₅ exhibited a direct band gap of 1.41 ± 0.01 eV at 300 K. The band gap presented anomalies through antiferromagnetic phase transition temperatures at 455 and 175 K. Moreover, the temperature dependence of in-plane E_g phonon mode exhibited a hardening below 175 K. The spin–phonon coupling constant was estimated to be 15.7 mRy/Ų. These results confirmed a strong coupling of spin, charge, and lattice degrees of freedom in YBaCuFeO₅.

Author Contributions

H.L.L. conceived the idea and designed the experiments. H.W.C. performed the experiments. Y.C.L., F.C.C., and C.H.D. prepared the samples. Y.W.C. and J.L.K. performed the first-principles calculations and theoretical analyses. H.W.C., Y.W.C., and H.L.L. wrote the paper. All the authors discussed the results and commented on the manuscript.

Competing Interests

The authors declare no competing interests.

Electronic supplementary material

Supplementary information accompanies this paper at 10.1038/s41598-019-39031-6.