The primacy of rhythm: how discrete actions merge into a stable rhythmic pattern

Abstract

This study examined how humans spontaneously merge a sequence of discrete actions into a rhythmic pattern, even when periodicity is not required. Two experiments used a virtual throwing task, in which subjects performed a long sequence of discrete throwing movements, aiming to hit a virtual target. In experiment 1, subjects performed the task for 11 sessions. Although there was no instruction to perform rhythmically, the variability of the interthrow intervals decreased to a level comparable to that of synchronizing with a metronome; furthermore, dwell times shortened or even disappeared with practice. Floquet multipliers and decreasing variability of the arm trajectories estimated in state space indicated an increasing degree of dynamic stability. Subjects who achieved a higher level of periodicity and stability also displayed higher accuracy in the throwing task. To directly test whether rhythmicity affected performance, experiment 2 disrupted the evolving continuity and periodicity by enforcing a pause between successive throws. This discrete group performed significantly worse and with higher variability in their arm trajectories than the self-paced group. These findings are discussed in the context of previous neuroimaging results showing that rhythmic movements involve significantly fewer cortical and subcortical activations than discrete movements and therefore may pose a computationally more parsimonious solution. Such emerging stable rhythms in neuromotor subsystems may serve as building blocks or dynamic primitives for complex actions. The tendency for humans to spontaneously fall into a rhythm in voluntary movements is consistent with the ubiquity of rhythms at all levels of the physiological system.

NEW & NOTEWORTHY When performing a series of throws to hit a target, humans spontaneously merged successive actions into a continuous approximately periodic pattern. The degree of rhythmicity and stability correlated with hitting accuracy. Enforcing irregular pauses between throws to disrupt the rhythm deteriorated performance. Stable rhythmic patterns may simplify control of movement and serve as dynamic primitives for more complex actions. This observation reveals that biological systems tend to exhibit rhythmic behavior consistent with a plethora of physiological processes.

INTRODUCTION

It is a well-known but intriguing observation that humans “fall into step” when walking side by side with a friend. When listening to music, one may inadvertently tap one’s foot to the beat, and when the audience applauds after a concert even a large collective of clapping hands can converge to a common rhythm (Strogatz 1994; Strogatz and Stewart 1993). More subtle synchronization occurs during social interactions when people unknowingly mimic each other’s rhythm in speech or body movements (Tolston et al. 2014). Such uni- and bidirectional synchronization between two or more oscillations is observed in a host of biological, physical, and social systems (Phillips-Silver et al. 2010; Strogatz 1994, 2004).

However, what happens if there is no external rhythm to synchronize with or if there is not even a rhythm at the outset? When humans repeat similar movements over a prolonged time, such as repetitive actions in the workplace, they sometimes experience themselves to be “in the flow,” a subjective state that can occur when a sequence of movements becomes increasingly more regular or periodic. Motivated by this anecdotal observation, the present study examined how people spontaneously fall into a rhythm when performing a series of discrete, goal-directed movements in the absence of any periodic cues. How does the repetition of similar movements performed at no specific intervals develop into a rhythmic pattern? Does this rhythmic pattern show features of dynamic stability, and if so, do such stable dynamics enable better performance? A brief caveat on terminology upfront: although “rhythm” in music and dance can be associated with a complex temporal pattern, we refer to rhythm as “approximately periodic” behavior, whereas strict “periodicity” is defined as a sequence of events separated by identical intervals. Furthermore, a rhythmic time series is continuous, in contrast to discrete movements that are separated by pauses (Hogan and Sternad 2007).

Rhythms are ubiquitous in the human body, including cortical, cardiac, respiratory, circadian rhythms, and tremor, both in functional and pathological expressions. These oscillations occur at many different temporal and spatial scales, comprising orders of magnitudes from 10⁻³ s in neural or informational processes to distributional processes operating at 10⁰ and 10¹ and the metabolic system at 10⁵ s (Moser et al. 2006). These different mechanisms are coupled within and across spatiotemporal scales, likely to also manifest as rhythms at the behavioral level. In return, behavioral rhythmicity may help to maintain the entrainment among the physiological processes of the body. For example, disturbances of the circadian rhythm lead to desynchronization between physiological rhythms, experienced as jetlag (Haus and Smolensky 2006). An extensive body of research has modeled these rhythms as nonlinear oscillators that, when coupled, can account for synchronized behavior in nature, ranging from circadian rhythms to the synchronous behavior of fireflies (Ermentrout and Kopell 1991; Kopell and Ermentrout 1986; Pikovsky et al. 2000; Rinzel and Ermentrout 1998; Strogatz 1994; Winfree 1967, 1990).

Recognition of the fundamental nature of rhythmicity in biological and physical systems is also the basis for a proposition in motor control: human movements rely on and exploit dynamic primitives; one such primitive is oscillations or rhythms (Hogan and Sternad 2012, 2013; Ijspeertet al. 2013; Ronsse et al. 2009; Schaal et al. 2000; Sternad 2008). Several previous lines of work have provided evidence that rhythmic movements are a basic form of organization that the neuro-mechanical system assembles and may use as building blocks in the control of voluntary movements. Importantly, these rhythmic patterns, or dynamic primitives, are presumed to have attractor properties, i.e., they have limit-cycle dynamics. Such stable oscillations arise at the neural level but may also comprise the neuromechanical system (de Rugy and Sternad 2003; Ronsse et al. 2009; Strogatz and Stewart 1993). The primary example has been legged locomotion that has been modeled as coupled oscillators (Full and Koditschek 1999; Ijspeert et al. 2013; Ochoa et al. 2017; Taga et al. 1991). However, biological movements are not only rhythmic but also display vastly more complex behaviors. Hence, several studies have suggested that other stable attractors exist, such as fixed points that are the basis for discrete point-to-point movements (Ijspeert et al. 2013; Ronsse et al. 2009; Sternad et al. 2000). Even chaotic attractors have been discussed as contributors to the observed variability (Raftery et al. 2008). Recent work has emphasized that, for interactions with objects, impedance is also needed as a dynamic operator (Hogan and Sternad 2012, 2013). If humans indeed fall into a stable rhythm when performing a series of actions, then this would provide strong support that rhythmic behavior is an attractor and a dynamic primitive for human behavior.

To investigate the spontaneous development of rhythmicity, we examined how human subjects practiced a virtual throwing task with the sole goal to hit a target. The instruction only emphasized that the target should be hit accurately, and rhythmicity was not mentioned. In experiment 1, subjects performed the throwing task across 11 days with a total of 2,640 throws (240 throws per day). As subjects indeed converged to a rhythm, experiment 2 explicitly disrupted the timing of the throwing movements by cuing the throws at random times between successive throws. As the task was modified to be less challenging, 6 days of practice proved sufficient (120 trials per day, 720 total). In both experiments, continuous kinematic data of the arm movements were collected across all trials on 1 day. In addition to performance error, the arm trajectories were analyzed for signatures of rhythmicity and stability. Following Hogan and Sternad (2007), rhythmicity was defined by the degree of periodicity and continuity. The degree of dynamic stability was assessed by computing Floquet multipliers and variability at the Poincaré section. Finally, we assessed whether rhythmicity and stability in behavior correlated with task performance.

We hypothesized that the discrete throwing actions merge into a rhythmic sequence, identified by an approximately constant period and decreasing number and duration of pauses between movements (hypothesis 1). Subjects with higher degrees of rhythmicity and stability of their arm trajectories achieve better task performance (hypothesis 2). With increasing rhythmicity, the degree of stability of movements increases (hypothesis 3). When instructed to pause between successive throws, subjects perform worse than during self-paced rhythmic behavior (hypothesis 4). Results were indeed supportive of the hypotheses and allowed us to conclude that stable rhythmic behavior is foundational for good task performance. This is consistent with the proposition that humans exploit dynamic primitives to not only simplify control, but also improve performance. When allowed to exploit stable attractor behavior, humans may free up attention for accuracy demands.

METHODS

Participants

Fifteen right-handed subjects (20.5 ± 2.8 yr; 7 women, 8 men) were recruited for experiment 1. All subjects were compensated with $55 after completing the 11 data collection sessions on 11 separate days. In experiment 2, 16 right-handed subjects (20.7 ± 2.8 yr; 9 women, 7 men) took part and were randomly assigned to one of two groups. Subjects received $30 after completing the six daily sessions of data collection. None of the subjects had any prior experience with the experimental task. All subjects signed the consent form of the protocol before the data collection; the study was approved by the Institutional Review Board at the Northeastern University.

Experimental Task and Apparatus

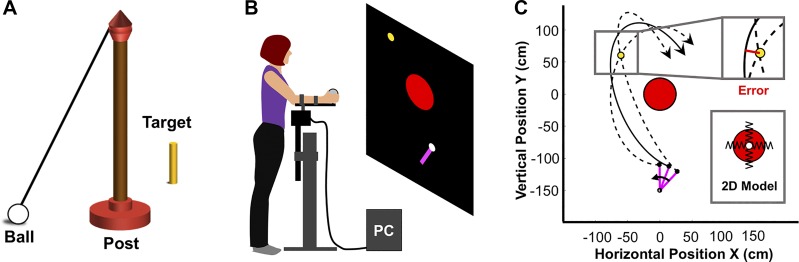
The experiments used a virtual throwing task that was based on the British pub game Skittles, which is similar to American tetherball (Fig. 1A) (Cohen and Sternad 2012; Hasson et al. 2016; Müller and Sternad 2004; Zhang et al. 2018). In this game, subjects throw a ball tethered to the top of a vertical post to hit a target skittle(s) on the opposite side of the post. For the virtual rendering, this task was presented as a top-down view on a backprojection screen (2 × 2 m) in front of the subject (distance to subject 1.50 m). The large red circle depicts the top-down view of the post; the smaller yellow circle represents the target to be hit (Fig. 1B). The purple bar corresponds to the subject’s arm/manipulandum and displayed his/her movements in real time. The white circle at the end of the bar is the ball to be thrown.

Fig. 1.

Experimental task and set-up. A: real skittles game. B: virtual skittles game and how subjects interact with the virtual workspace. The subject stands in front of the backprojection screen, rests her arm on a manipulandum, and throws the ball around the red center post to hit the yellow target in the virtual workspace. C: top-down view with of post (red circle) and ball trajectories around the target (yellow). The ball trajectory describes an elliptic path around the post. The pink bars denote the rotating arm. 3 exemplary trajectories with the 2 dashed-line trajectories going through the target despite different release angle and velocities demonstrate the redundancy of the task. The solid line has a non-0 error, highlighted in the inset. The second inset shows a schematic of the 2D spring model for generating the trajectory of the virtual ball [see details of the model in Zhang et al. (2018)].

To perform the throwing movements, subjects rested their forearm on a manipulandum that restricted their movements to rotations in the horizontal plane (Fig. 1B). A wooden ball was fixed to the end of the manipulandum that had a force sensor attached to it (Interlink Electronics, Camarillo, CA). To initiate the throw, subjects grasped the ball and pressed their index finger on the force sensor to hold the virtual ball. To throw the ball, subjects moved their forearm and released the finger from the pressure sensor as in a Frisbee throw. Releasing the finger from the force sensor initiated the ball flight, and the ball trajectory was calculated from the online-measured angular position and velocity of the manipulandum at the release moment. After release, the ball traversed an elliptic trajectory around the post as shown in Fig. 1C. The top-down view simplified the physics of the task to a two-dimensional system in which the ball was suspended by two orthogonal, massless springs (Fig. 1C, inset). The equilibrium point of the ball was at the origin, which was defined at the center of the post location. The two dashed lines in Fig. 1C show ball trajectories that went through the target with zero error. Note that these two trajectories were released with two different arm angles and velocities. This exemplifies the redundancy of the task; zero error could be achieved with many different combinations of release angle and velocity. The solid line represents a trajectory that passed the target with a non-zero error, as further highlighted in the zoomed view in the inset.

In experiment 1, the angular position of the manipulandum of the first five subjects was recorded with an analog potentiometer (Vishay Spectrol, Shelton, CT). However, this potentiometer was not sufficiently sensitive in detecting the angle change when the velocity was low. Hence, the potentiometer was replaced with a digital encoder (BEI Sensors, Goleta, CA) to collect the remaining 10 subjects in experiment 1 and subsequently all 16 subjects in experiment 2.

In experiment 1, the diameter of the ball and the target were 5 cm, and the diameter of the post was 50 cm; in experiment 2, ball and target were 2.5 cm, and the post was 25 cm in diameter. These changes made the task of hitting the target easier. The error of each throw was defined as the shortest distance between the ball path and the center of the target (Fig. 1C, inset). When the error was less than a threshold, set to be 1.1 cm in experiment 1 and 1.8 cm in experiment 2, the color of the target changed from yellow to green to indicate a successful target hit.

The physical model that generated the ball trajectories consisted of the ball fixed to the center location by two orthogonal massless springs; the rest position of the ball defined the origin of the workspace coordinates, coincident with the location of the center of the post (Fig. 1C). The equations for the ball position in the x- and y-directions at time t were

$$x\left(t\right)=A_x\text{sin}\left(\omega t+{\phi }_x\right)e^{-\frac{t}{\tau }}$$ (1)

$$y\left(t\right)=A_y\text{sin}\left(\omega t+{\phi }_y\right)e^{-\frac{t}{\tau }}$$ (2)

The frequency ω denotes the natural frequency of the springs. The amplitudes A_x and A_y and the phases φ_x and φ_y of the springs were determined by the position and velocity of the ball at the moment of release. The exponential term with the time constant τ created a small damping effect on the ball trajectory. Details of the physical model were presented in previous studies (Cohen and Sternad 2009; Hasson et al. 2016; Müller and Sternad 2004; Zhang et al. 2018).

Experimental Design and Task Specifications

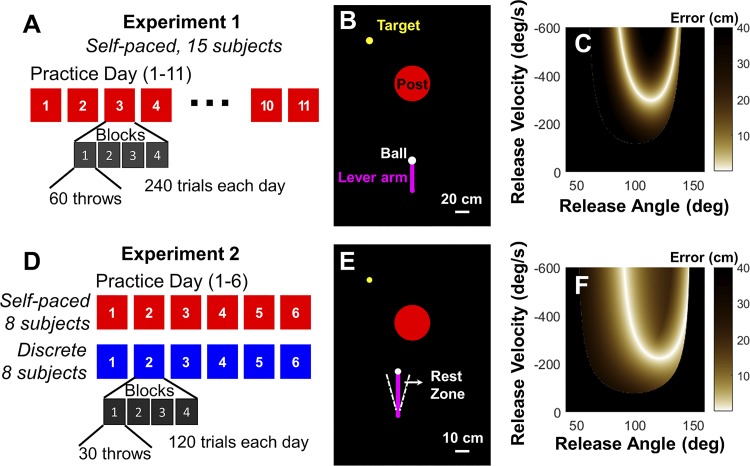
Figure 2 overviews the specific experimental design, the virtual workspace, and the solution space for the two experiments. In experiment 1, 15 subjects performed 11 days of practice, with 240 throws parsed into 4 blocks of 60 throws with a brief rest between each block (2,640 throws in total). Each session lasted ~20 min (Fig. 2A). The subjects were instructed to hit the target (yellow) as accurately as possible and to avoid the center post (red). If the distance from the target was within the error threshold, the target color turned green to signal success. Importantly, they did not receive any cues about the temporal sequence of the throws, and they could wait between throws as long as they wanted or needed. The target was located at (−60 cm, 60 cm) referenced to the center post (0 cm, 0 cm); the natural frequency ω of the springs was 3.16 rad/s, and the time constant τ was 20 s. The pivot of the manipulandum was located at (0 cm, −150 cm), and length of the lever arm was 40 cm (Fig. 2B). The threshold for the error was 1.1 cm. After subjects released the ball, the elliptic trajectory was drawn on the screen for 1.4 s. During this time, the ball could not be grasped, and the initiation of a new throw had to wait for this minimum time.

Fig. 2.

Experimental design, virtual workspace, and solution space of the 2 skittle task variations used in experiments 1 and 2. A: experimental design of experiment 1 with 11 days of practice. B: virtual workspace of experiment 1. C: solution space of experiment 1. Brown shades indicate the performance error for each pair of release angle and velocity in the state space. D: experimental design of experiment 2 with 6 days of practice for 2 groups. E: virtual workspace of experiment 2. F: solution space of experiment 2.

An important property of the task is redundancy; a successful hit can be achieved with more than one ball release. As elaborated previously, both angular position and velocity determine the ball trajectory, and one value of error can be achieved by a mathematically infinite number of different combinations of angular position and velocity, defining a solution manifold (Müller and Sternad 2009; Sternad et al. 2014; Zhang et al. 2018). This feature of the task is illustrated in Fig. 2, C and F, in which angular position and velocity span the execution space and performance error defines the result space; different color shadings indicate the different levels of error. All solutions with zero error define a one-dimensional solution manifold. Although this feature was not used for the primary performance analysis, the solution manifold was important for the analysis of the Floquet multipliers (see below).

In experiment 2, 16 subjects were randomly assigned either to a self-paced group or to a discrete group. Both groups practiced the throwing task for 6 consecutive days with only 120 throws on each practice day, parsed into 4 blocks of 30 throws (720 throws in total, Fig. 2D). Subjects in the self-paced group received the same instruction as in experiment 1. Subjects in the discrete group were asked to position their arm in a rest zone at 90 ± 15 deg after each throw; this rest zone was indicated on the screen by two white dashed lines (Fig. 2E). Subjects waited until they received a verbal cue from the experimenter to start the next throw. This cue was timed by a computer to be 7 s after the initiation of the previous throw. As a throw lasted ~2 s, the instructed pause between successive throws was ~5 s. As the actual duration of each throw varied and the pause was relatively long, subjects did not perceive the interval as periodic.

The parameters of the task were modified to reduce the challenge and ensure relatively fast development of rhythmicity and also to test the generalization of the results from experiment 1. After pilot tests of different task conditions, the following parameters were chosen: target location (−30, 30 cm), ω = 3.14 rad/s, τ = 13.6 s, error threshold = 1.8 cm. The pivot of the manipulandum was also slightly shifted to the left and was located at (−10 cm, −65 cm) with a length of 30 cm. These modified parameters changed the result space and the solution manifold (Fig. 2F). Although the solution manifold retained its U shape, the lighter color shadings indicate that the errors were smaller for a broader range of angle-velocity combinations. Hence this solution space enabled subjects to achieve target hits faster and was therefore also likely to facilitate faster development of rhythmicity.

Dependent Measures

Success rate and performance errors.

A first measure of task performance was the success rate or percentage of successful trials per day, i.e., throws with errors below threshold. A related but finer-grained measure of performance was the error, defined by the minimum distance between the target and the ball trajectory (Fig. 1C). The median error over all trials per day summarized each subject’s daily performance.

Periodicity of interthrow intervals.

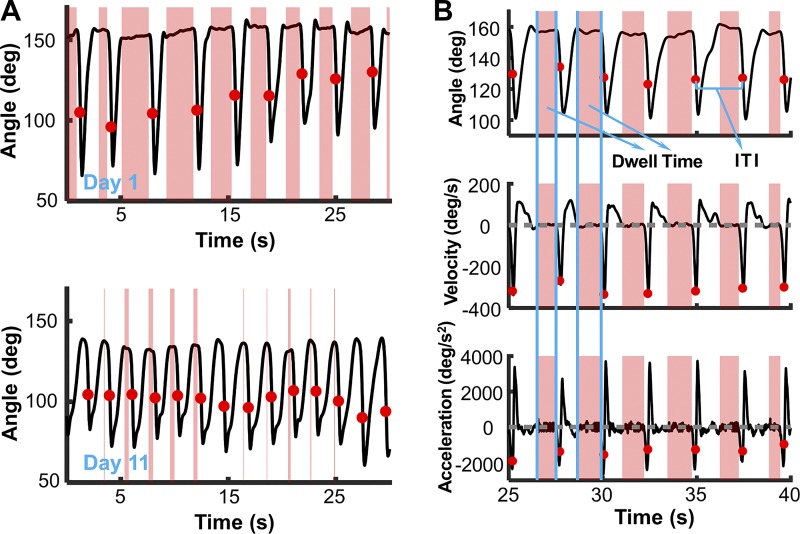
Periodicity is one essential characteristic of rhythmic movement, i.e., the same posture or event should recur at invariant intervals (Hogan and Sternad 2007). However, strict periodicity is unlikely to be present in human behavior, and in common understanding rhythmicity implies some variation around a constant interval. Figure 3A displays the time series of a self-paced trial of one subject on day 1 and on day 11. The red points mark the moments of ball release; the pink-shaded areas denote dwell times. Comparison of day 1 and day 11 clearly illustrates that the successive throws developed into an approximately periodic, i.e., rhythmic sequence. To quantify the degree of periodicity, the moments of ball release served as landmarks; the interval between two successive releases defined the interthrow interval (ITI). The median of all ITIs per day characterized each subject’s performance; ITIs longer than 10 s were removed, as they indicated a voluntary rest. The periodicity of movement was estimated by the dispersion of ITI, quantified by the quartile variation coefficient (QVC) of ITI for each day, as the distribution of ITI was highly leptokurtic and skewed (Bonett 2006)

$$\text{QVC}-\text{ITI}=\frac{Q_3-Q_1}{Q_3+Q_1}$$ (3)

where Q₁ refers to the 25th percentile and Q₃ to the 75th percentile of the distribution.

Fig. 3.

Representative time series of self-paced movement trajectories of the arm and calculation of interthrow interval (ITI) and dwell time. A: example time series of angular displacements of the arm over a segment of repeated throws for a single subject on day 1 and day 11. The red dots denote the moment of ball release; the pink-shaded sections denote the dwell duration (see methods for calculation details). The number and duration of the dwell times visibly decreased on day 11 below. B: angular position, velocity, and acceleration of a trial segment with 7 throws. The ITI was defined as the duration between 2 successive ball releases. The pink-shaded segments indicate the identified dwell times in the arm movement.

Number and duration of dwell times.

Following definitions by Hogan and Sternad (2007), discrete movements were defined by dwell times between successive movements, whereas rhythmic movements do not have such pauses. Comparing day 1 with day 11 in Fig. 3A suggests that the dwell times indeed shortened or completely disappeared with practice. To quantify how the discrete throwing movements merged into a continuous sequence, the number and durations of dwell times between trials were quantified. Dwell time was defined as the interval between the termination of one throw to the initiation of the next throw (Fig. 3B).

For the identification of onset and offset of each throw, the angular position was smoothed with a Savitzky-Golay filter using a second-order polynomial model; the window length of the smoothing filter was set to 100 ms. Angular velocity was approximated by the slope of a linear fit to 20 smoothed-angle samples before the current time point; acceleration was calculated with the same method as for the velocity. The onset of a throw was indicated when the velocity surpassed 5 deg/s for 10 ms, and the acceleration continuously exceeded 50 deg/s² for 10 ms for the first time. The offset was identified when velocity returned to values smaller than 5 deg/s and acceleration remained smaller than 50 deg/s² for 10 ms. The time interval between an offset and onset of the next throw quantified the dwell time. If no clear initiation or termination was detected, the adjacent throws were considered part of continuous movements (Fig. 3A, bottom). For all subjects, dwell times longer than 10 s were removed, indicating an explicit rest. This only happened six times in experiment 1 and never happened in experiment 2. The total number and the summed durations of dwell times per practice day served as two dependent measures for rhythmicity.

Variability and stability in state space.

Previous work has highlighted that discrete and rhythmic movements have different flow topologies in state space (Huys et al. 2014; Schöner 1990; Sternad et al. 1998). We therefore plotted arm trajectories in state space, spanned by angular position and velocity, and examined their variability using Poincaré sections (Fig. 4). A Poincaré section is an (n−1)-dimensional surface that cuts through the flow in n-dimensional state space (Rasband 1997; Strogatz 1994). The Poincaré map is a discrete representation of the periodic flow of a continuous dynamical system, defined by the successive crossings of the Poincaré section. The topology of the Poincaré map and the Poincaré plot were previously examined to quantify the stability of human locomotion (Dingwell and Kang 2006; Hurmuzlu et al. 1994) and other physiological data, such as cardiac and respiratory signals (Glass and Mackey 1988; Honerkamp 1983; Winfree 1990).

Fig. 4.

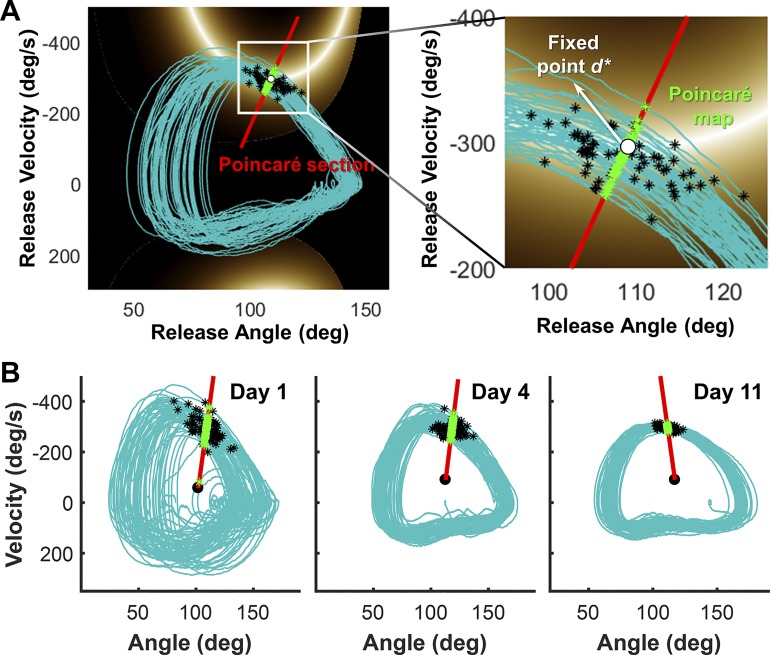
Representative movement trajectories of the arm in state space and the Poincaré map. A: illustration of the Poincaré section and the Poincaré map in state space. The blue line is the continuous hand trajectory of 60 successive throws in 1 block. The black asterisks on the arm trajectory represent the ball releases. The red line between the origin of the plot and the mean of the ball releases represents the Poincaré section. The green stars represent the projections of the release points onto the Poincaré section and represent the Poincaré map. Inset: zoomed depiction of the same plot. The white point at the intersection of the solution manifold and the Poincaré section is the assumed fixed point, as this represents the 0-error point on the section. B: arm trajectories on day 1, day 4, and day 11 to illustrate how the trajectories become less variable with practice. Note that this decreased variability is not necessary for task success, as any release on the manifold leads to 0 error.

Figure 4 shows exemplary orbits of the arm trajectories in state space (blue), together with the ball releases, denoted by black asterisks. Note that the state space is spanned by angle and velocity of the arm movements; when each state is viewed as a release of the ball trajectory, then each state also has an associated error. This is illustrated by the color shades as used previously in Fig. 2, C and F. The blue trajectories are intersected by a red line from the origin through the ball releases, the Poincaré section. The origin of the Poincaré section was determined for each subject and block separately as follows

$$\text{center}\left(\text{angle,velocity}\right)=\frac{P_{2.5}\left(\text{angle,velocity}\right)+P_{97.5}\left(\text{angle,velocity}\right)}{2}$$ (4)

where P_2.5 is the 2.5th percentile of the distribution of all angles and velocities, P_97.5 represents the 97.5th percentile. The second point defining the section was the average location of release points in each block, determined by the mean of the position and velocity values. Note that samples of the arm trajectory frequently did not lie exactly on the Poincaré section. Therefore, for each cycle of arm trajectory, the point closest to the Poincaré section ($\widehat{d_t}$) was selected. The projections of all $\widehat{d_t}$ onto the Poincaré section rendered the Poincaré map d = [d₁, d₂, …, d_t].

Before the calculations of the Poincaré section and the Poincaré map, the state space was normalized. Therefore, the trajectories of all blocks of each subject were pooled, and the position and velocity axes were normalized by setting the average maximum and minimum of each variable to 1 and −1. The normalization was kept constant for each individual across all practice days when calculating the variability in Poincaré map and the Floquet multipliers. This allowed us to measure the changing variability across practice days. To maintain differences across subjects, each subject was normalized separately.

Stability in state space.

To quantify the degree of stability of rhythmic movements, the Floquet multiplier has been widely used as a measure (Ahn and Hogan 2015; Hurmuzlu and Basdogan 1994; Kuo 1999). Human walking has been a primary application, and the moment of heel strike was chosen as the landmark for the Poincaré map. For the throwing movements, the cycle-by-cycle stability was characterized by the Floquet multiplier defined from the Poincaré map of the arm trajectories:

$$d_{t+1}-d^{*}=\lambda \left(d_t-d^{*}\right)$$ (5)

where λ is the Floquet Multiplier, d_t and d_t+1 represent the states at the tth and (t+1)-th cycle, and d* is the fixed point. A smaller Floquet multiplier value indicates faster convergence to the fixed point and therefore higher stability of the movement.

Previous studies on locomotion defined the fixed point d* as the average value of d, implying that different values of d presented fluctuations around the mean that converged to the fixed point. However, in this study the mean value was not necessarily equivalent to the desired task performance and therefore did not represent the best estimate for the fixed point. A better choice was the point at which the performance error was zero. This value d* was given by the solution manifold and its intersection with the Poincaré map (Fig. 4A, inset). The Floquet multiplier was then defined by the eigenvalue of the one-dimensional map, determined by the slope of a simple linear regression of d_t+1 on d_t.

However, a recent study by Ahn and Hogan (2015) demonstrated that the estimation based on linear regression and related methods by Burg, Yule, and Walker (Burg 1967; Walker 1931; Yule 1927) resulted in systematic overestimations of λ because of the limited length and the presence of noise in human behavioral data. Therefore, we applied their suggested correction method to obtain an unbiased estimate of the FM. This value $\widehat{\lambda }$ was calculated as follows:

$$\widehat{\lambda }={\widehat{\lambda }}_{\text{YW}}+\frac{{\widehat{\lambda }}_{\text{Burg}}{}^3-{\widehat{\lambda }}_{\text{Burg}}{}^{2n+1}}{\left(n-1\right)\left(1-{\widehat{\lambda }}_{\text{Burg}}{}^2\right)}$$ (6)

where ${\widehat{\lambda }}_{\text{YW}}=\frac{{{\displaystyle \sum }}_{i=1}^{n-1}{x}_i{x}_{i+1}}{{{\displaystyle \sum }}_{i=1}^{n-1}{x}_i^2}$ represented the Yule-Walker equation and ${\widehat{\lambda }}_{\text{Burg}}$ represented the Floquet multiplier calculated with Burg’s method based on spectral estimation.

Statistical Analysis

To characterize how performance and rhythmicity changed with practice in experiment 1, all eight dependent measures, median error, success rate, median ITI, QVC-ITI, total duration and total number of dwell times per block, mean STD-PM, and the FM of four blocks were subjected to one-way, repeated-measures ANOVAs with practice day as the within-subjects factor. Greenhouse-Geisser corrections were applied when the sphericity assumption was violated (Kirk 1982). Pairwise post hoc tests between practice days specified the change across days. To further assess whether rhythmicity in arm movements was associated with the performance error, Pearson’s correlation coefficients were computed between error and each of the dependent measures for each practice day.

In experiment 2, 2 (group) × 6 (practice days) repeated-measures ANOVAs were applied on the same dependent measures to determine whether discretizing movement influenced the performance. The same Pearson’s correlation coefficients were calculated for the discrete and the self-paced group.

RESULTS

Experiment 1

Task performance: success rate and error.

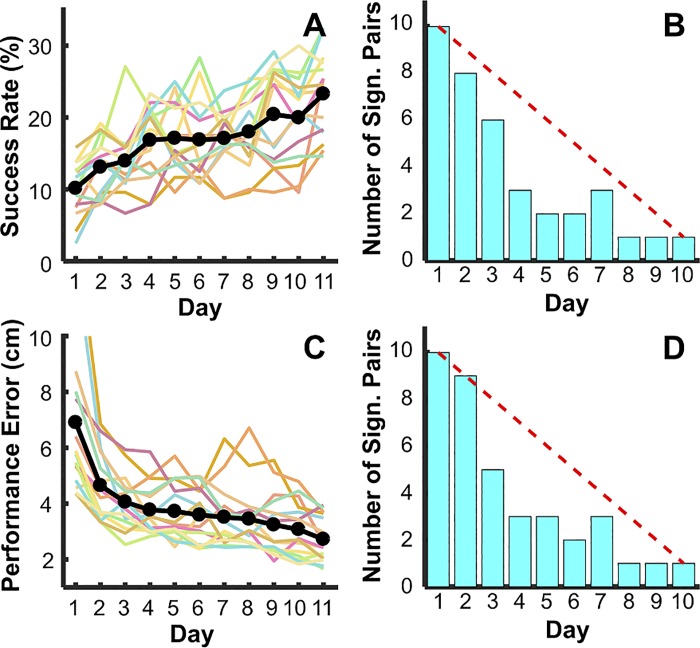
Figure 5 shows that the success rate increased and the error decreased for all subjects across the 11 days of practice, as should be expected in this novel task. Individual subjects’ median values per day are represented by different colors, and the black points show the mean performance of the 15 subjects. The one-way ANOVA confirmed that the success rate significantly increased from 10.14 ± 3.79% to 23.28 ± 5.90%, F(5.50, 77.00) = 17.56, P < 0.001, partial η² = 0.56 (Fig. 5A). Concomitantly, the errors significantly decreased from 6.90 cm ± 2.94 cm to 2.72 cm ± 0.80 cm, F(1.88, 26.29) = 22.71, P < 0.001, partial η² = 0.62 (Fig. 5C). With only very few exceptions, there was a continuous trend across all days, suggesting that improvement occurred throughout day 11.

Fig. 5.

Task performance in experiment 1. A: success rates on all 11 days of practice. The colored lines represent the individual participants’ performances; the black line and points show the mean values of all subjects per day. B: number of pairwise t-tests of success rate between practice days. The performance of each day was compared with all following days in a pairwise fashion. The bar chart shows the number of significant t-tests with P ≤ 0.05 (maximum 10 comparisons on day 1, maximum 9 comparisons on day 2, etc.). The red dashed line indicates the total number of t-tests per day. C: performance error across 11 days of practice. D: number of significant t-tests in pairwise comparisons between each day and its successive days.

To determine whether performance changed across days, pairwise t-tests compared the performance on each day with each of the following days. The bar charts in Fig. 5, B and D, show the total number of significant comparisons for each day; the red dashed line indicates the number of t-tests performed on each day. Comparing the actual number of significant pairings with this maximum number illustrates that both success rate and performance error decreased from day 1 to all other days at the beginning, with fewer significant changes in the middle but still some improvements at the final practice days. This performance improvement is to be expected but serves as the basis for further examination of rhythmicity and stability.

Rhythmicity: periodicity of ITIs.

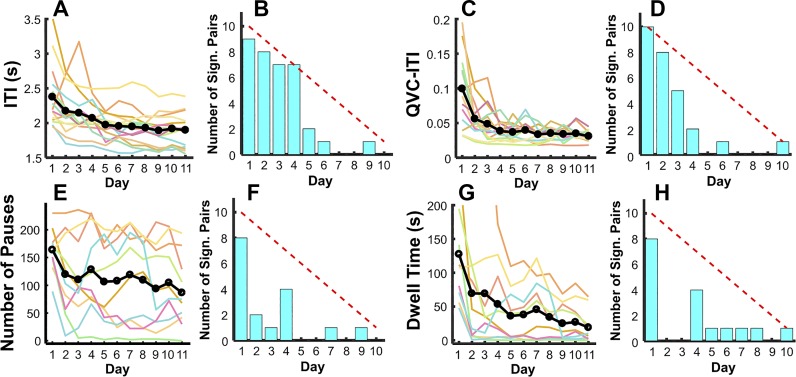
Both the ITI and its variability, QVC-ITI, decreased across practice days (Fig. 6, A and C). The ITI decreased from 2.38 ± 0.45 s to 1.90 ± 0.24 s, F(2.47, 34.55) = 12.42, P < 0.001, partial η² = 0.47. Although subjects became faster as practice progressed, their periodicity was not bounded by the minimum time between throws; this minimum time was the 1.4-s interval after ball release until it could be grasped again. Individual subjects varied in their ITI between 1.5 and 2.5 s. Pairwise comparisons between practice days suggested that subjects decreased the interval between throws predominantly during the first 4 days and then maintained their ITI on further days of practice (Fig. 6B).

Fig. 6.

Measures of periodicity and rhythmicity in experiment 1, including interthrow-interval (ITI), variability of ITI (QVC-ITI), and number and total duration of dwell times. A and B: ITI across 11 days of practice and number of significant differences for each day with subsequent days. C and D: variability of the QVC-ITI across 11 days of practice and the number of significant differences of each day with subsequent days. E and F: total duration of dwell times across 11 days of practice and number of significant differences of each day with subsequent days. G and H: number of pauses across 11 days and number of significant differences for each day with subsequent days. All metrics show significant changes over the 11 days of practice.

The periodicity estimate QVC-ITI also decreased significantly from 0.10 ± 0.05 to 0.03 ± 0.01, F(2.13, 29.78) = 17.45, P < 0.001, partial η² = 0.56. Similar to ITI, QVC-ITI significantly dropped from day 1 to day 2, continued by a slow monotonic change until day 5 (Fig. 6D). These results support hypothesis 1, showing that subjects developed increasingly periodic arm movements. It is also noteworthy that the variability of ITI reached a level equivalent of 5%; this is very low, as even rhythmic movements synchronized with a metronome show similar variability.

Correlation between periodicity and error.

For each day, the performance errors of all subjects were correlated with their respective ITI and QVC-ITI (Table 1). ITI appeared unrelated to error, and subjects who performed with shorter ITIs were not necessarily worse than those individuals with longer time between throws. Such relation might be conjectured if one assumed that error detection and correction would require time before each throw. In contrast, QVC-ITI showed significant correlations with mean error on early practice days (days 1–4). These results only weakly supported hypothesis 2.

Table 1.

Pearson correlation coefficients r between performance error and other dependent measures in experiment 1

	ITI, s		QVC-ITI		Number of Pauses		Dwell Time, s		STD-PM		FM
Practice Day	r	Sig.	r	Sig.	r	Sig.	r	Sig.	r	Sig.	r	Sig.
Day 1	0.36		0.67	†	−0.16		0.30		0.72	†	0.81	‡
Day 2	−0.10		0.42		−0.27		−0.23		0.73	†	0.45
Day 3	0.10		0.61	*	0.01		0.09		0.75	†	0.53	*
Day 4	0.07		0.73	†	0.18		0.35		0.76	†	0.57	*
Day 5	−0.28		0.48		−0.02		0.23		0.92	‡	0.5
Day 6	−0.27		0.63	*	−0.01		0.03		0.64	†	0.62	*
Day 7	0.15		0.41		0.20		0.06		0.80	‡	0.84	‡
Day 8	0.01		0.20		0.29		0.37		0.65	†	0.85	‡
Day 9	−0.15		0.10		0.37		0.34		0.89	‡	0.77	†
Day 10	−0.19		0.31		0.35		0.41		0.73	†	0.75	†
Day 11	−0.11		0.57		0.22		0.21		0.72	†	0.47

ITI, interthrow interval; QVC-ITI, quartile variation coefficient of ITI, Sig., significance.

^*0.01< P < 0.05,

^†0.001< P < 0.01,

^‡P < 0.001.

The boldface numbers indicate the correlations that were significant.

Rhythmicity: dwell time and number and duration of pauses.

The number and duration of pauses could only be calculated for the 10 subjects whose data were collected with the optical encoder (the potentiometer used for the first 5 subjects did not allow accurate detection of initiation and termination of movement). Figure 6, E and G, shows the number of pauses and dwell times across the 11 practice days. Overall, subjects inserted fewer pauses with practice, seen in the declining number of pauses per day from 163.90 ± 38.50 times to 86.70 ± 62.75 times, F(3.68, 33.11) = 4.75, P = 0.005, partial η² = 0.35. However, there was also a marked divergence between individuals; 4 subjects decreased at the beginning and retained only 15–50 pauses per day until the end, whereas the other 6 subjects fluctuated more across practice and retained between 100–200 pauses (the maximum number was 236 per day).

Unlike the pauses, however, most subjects significantly reduced their dwell times from a block total of 127.56 ± 71.70 s to 19.06 ± 23.93 s, F(2.03, 18.24) = 5.48, P = 0.013, partial η² = 0.38. Pairwise comparisons showed that both number of pauses and total dwell time dropped fast from day 1 to day 2 and then reached an asymptote after day 4 (Fig. 6, F and H). These changes are in support of hypothesis 1. However, counter to hypothesis 2, there was no significant correlation between performance error and number of pauses and dwell time (Table 1).

Variability in state space: variability of Poincaré map.

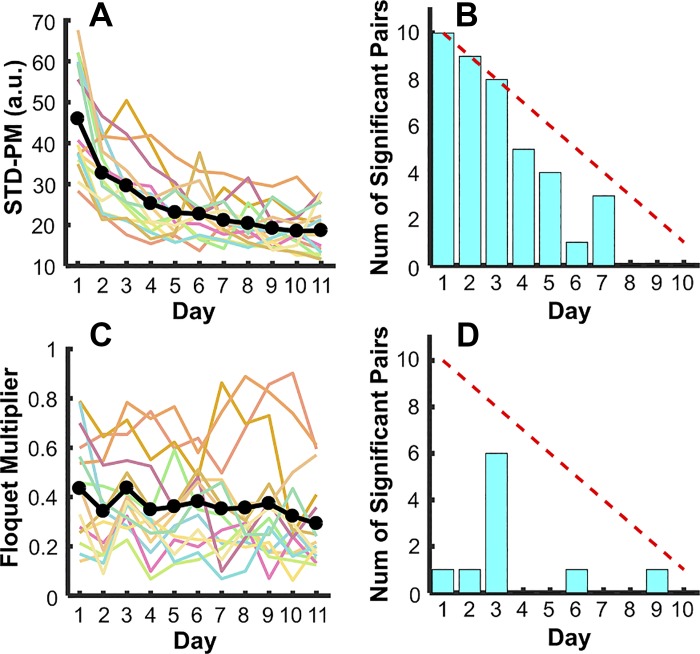
The variability of the arm trajectory was quantified in state space, drawing a Poincaré section through the mean release points (Fig. 4). The standard deviations of the intersections at the Poincaré map were determined for each block, STD-PM, and then averaged across each day. As illustrated in Fig. 4B, the trajectories of the orbits across three exemplary days of a single subject became tighter and less variable. This observation was summarized in the average STD-PM of each day that significantly decreased from 45.94 ± 13.41 to 18.65 ± 6.12, F(3.12, 44.32) = 35.5, P < 0.001, partial η² = 0.72. Smaller STD-PM indicated that the hand trajectories recurred in every movement cycle with a similar state. This reduction in variability developed quickly over the first 3 days, then kept decreasing from day 4 to day 7 before it started to plateau on day 8 (Fig. 7B). This decrease was supportive of hypothesis 3.

Fig. 7.

Measures of variability and stability in state space in experiment 1. A and B: variability on the Poincaré map STD-PM across 11 days of practice and number of significant differences for each day with subsequent days. C and D: values of Floquet multipliers across 11 days of practice and number of significant differences for each day with subsequent days. Although variability decreases, the Floquet multiplier values remain invariant but show large intersubject differences.

Stability in state space: Floquet multipliers.

The Floquet multipliers were calculated within each block and then averaged across the four blocks for each day. To begin, all Floquet multiplier values in the 10 subjects were <1, indicating that the rhythmic arm movements were dynamically stable (Fig. 7C). However, counter to hypothesis 3, movements within each subject did not become more stable as the changes of Floquet Multiplier across practice days were not significant, F(4.67, 65.34) = 2.05, P = 0.09, partial η² = 0.13. The individual subjects maintained similar Floquet multiplier levels or fluctuated across practice without any consistent trend. This was also reflected in the few significant pairwise comparisons (Fig. 7D).

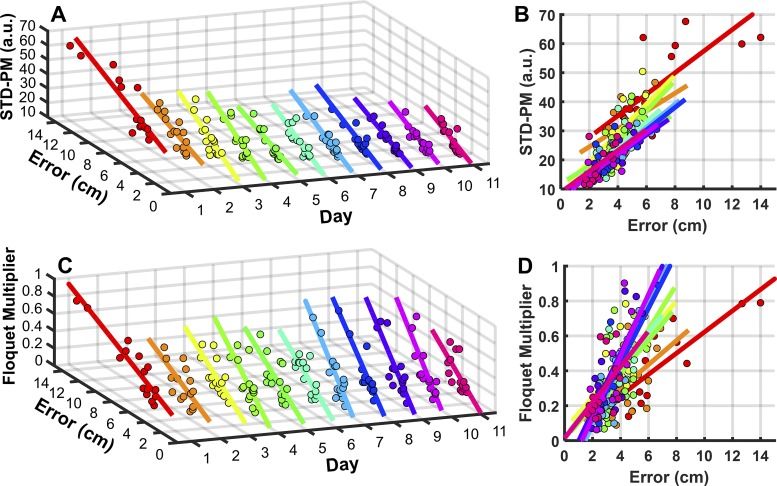
However, the actual Floquet multiplier values differed significantly between the subjects. When we performed Pearson correlations between the performance error and the two stability metrics, strong positive correlations were revealed on all days (Table 1). Figure 8 visualizes these consistent results for both STD-FM and Floquet multiplier across all 11 days of practice. Figure 8, A and B, shows that subjects who had lower state space variability tended to perform better in the target-oriented throwing, as expected by hypothesis 3. The same strong positive correlations in Fig. 8, C and D, demonstrate that subjects who had smaller Floquet multiplier, i.e., higher stability, performed with lower errors.

Fig. 8.

Correlation between variability and stability measures and performance. A: correlation between variability, defined as the standard deviations of the Poincaré map (STD-PM), and performance error for each day. The lines represent the correlations across subjects for each day. B: same correlations plotted in 2D to highlight the changing slopes across days. C: correlation between Floquet multiplier and performance error for each day. The lines represent the correlation across subjects for each day. D: same correlations plotted in 2D to highlight the changing slopes across days.

Experiment 2

Two new groups of subjects performed the same skittles task but with a different target configuration and solution space that lowered the task difficulty. We expected that, with an easier task, rhythmicity should develop faster. Furthermore, if this task variation achieved comparable results, then this would also demonstrate some generality of the results in experiment 1.

Task performance: success rate and error.

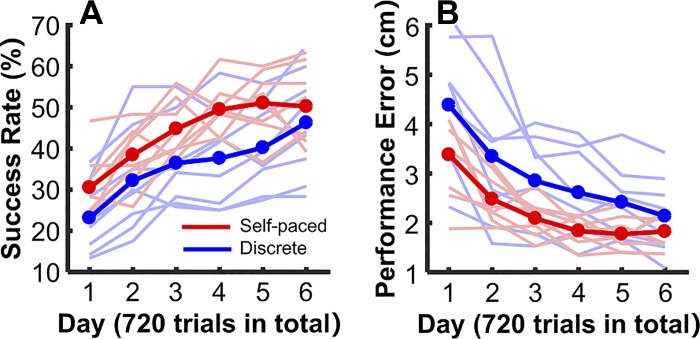
A first analysis of success rate and performance error clearly revealed that the self-paced group was better in the two metrics of task performance than the discrete group. As Fig. 9, A and B, illustrates, 6 days of practice with only 120 throws on each day was sufficient to show signs of approaching a plateau in success rate and performance error. The two-way ANOVA underscored that success rate significantly increased over days, F(3.11, 43.51) = 37.10, P < 0.001, partial η² = 0.73 (Fig. 9A), whereas the error significantly decreased in both groups, F(1.97, 27.62) = 27.83, P < 0.001, partial η² = 0.67 (Fig. 9B). More central to the hypothesis was that the subjects in the self-paced group showed a higher average success rate and lower errors than the discrete group. Although this group difference did not reach the level of significance for the success rate (P = 0.079), the advantage for the self-paced group was significant in the performance error, probably because error had a finer-grained resolution than the threshold-based binary success rate, F(1,14) = 4.86, P = 0.045, partial η² = 0.26. This result supported hypothesis 4.

Fig. 9.

Task performance in experiment 2. The blue and red lines represent the subject means of the discrete group and the self-paced groups, respectively. The light blue and light red lines show the individual subjects’ performance in the 2 experimental groups. A: success rate across 6 days of practice. B: performance error across 6 days of practice.

One potential caveat is that there were no significant interactions (both measures P > 0.28) allowing for the possibility that the difference in performance might have been due to differences between the group’s general skill level. To probe whether this group difference was present at the very beginning of the experiment, we also compared the measures between the self-paced and the discrete group on day 1 using two-sample independent t-tests. Neither success rate nor performance error were significantly different (P > 0.05); the differences only became significant on days 4 and 5. This subtle divergence did not reach significance in the interaction of the ANOVA. However, these results indicate that it was not differences in skill level between the two groups that brought about the overall better performance of the self-paced group. Rather, it was the disruption of the flow of successive throws that impacted performance.

Periodicity: ITIs.

Measures of periodicity were only applicable for the self-paced group. Table 2 summarizes mean values of ITI and QVC-ITI over six practice days. Although a small visible decrease in both ITI and QVC-ITI was discernible, these changes did not reach significance in a one-way ANOVA. Because the target location in experiment 2 was less difficult to hit, subjects fell into a rhythm very early in practice and maintained the same regularity until the end of the much shorter practice. This is reflected in the very low QVC-ITI that reached 5% very early in practice. In fact, both ITI and QVC-ITI reached the same level as in in experiment 1 on day 3. Hence, despite little change across practice days, the rhythmicity measures still replicated those of experiment 1 and were consistent with hypothesis 1.

Table 2.

Measures of rhythmicity in experiment 2

Practice Day	ITI, s	QVC-ITI	Dwell Time, s	Number of Pauses
Day 1	2.45 ± 0.48	0.07 ± 0.02	71.70 ± 64.76	87.38 ± 26.23
Day 2	2.42 ± 0.52	0.05 ± 0.05	72.13 ± 64.38	81.25 ± 35.17
Day 3	2.31 ± 0.34	0.05 ± 0.02	56.82 ± 43.22	83.75 ± 34.95
Day 4	2.16 ± 0.24	0.05 ± 0.01	40.72 ± 33.74	79.00 ± 36.70
Day 5	2.17 ± 0.27	0.04 ± 0.01	48.30 ± 40.70	85.63 ± 34.37
Day 6	2.11 ± 0.23	0.04 ± 0.01	38.59 ± 33.70	83.50 ± 36.09

Values are means ± SE. ITI, interthrow interval; QVC-ITI, quartile variation coefficient of ITI.

Rhythmicity: number and duration of dwell times.

As for periodicity, the measures for rhythmicity, i.e., number and duration of dwell times, could only be determined for the self-paced group. The one-way ANOVA showed no consistent changes in the number and duration of dwell times over the 6 days; 2 subjects decreased their number of pauses, whereas 3 decreased their dwell times among all 8 subjects. Comparing the mean values in Table 2, it becomes evident that the initial values were already very low and close to the values at the end of experiment 1. Hence, these low levels allowed for very little change.

Stability: periodicity in state space.

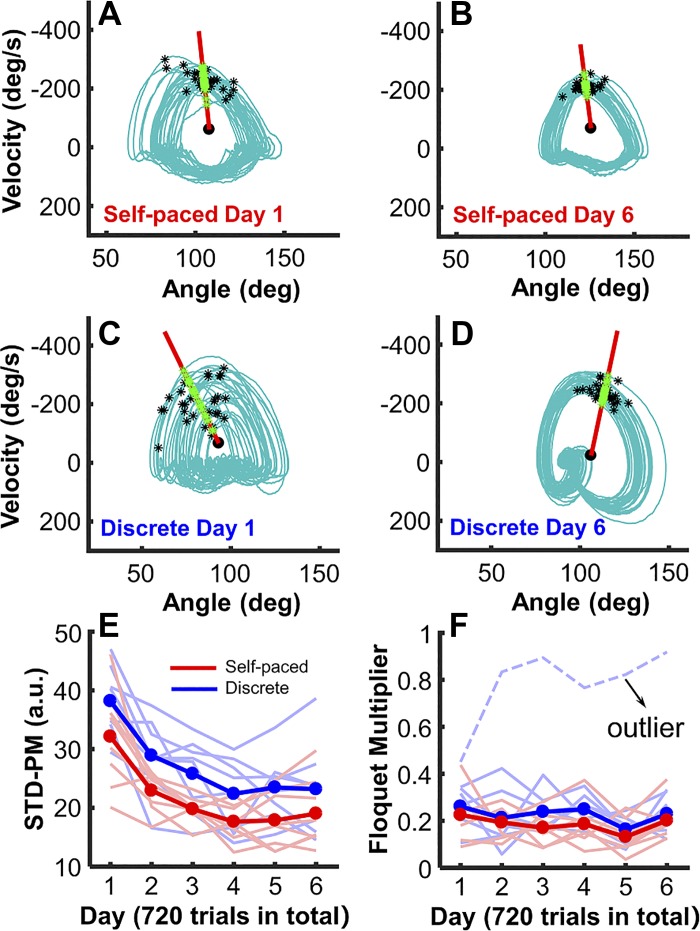
Although the rhythmicity measures did not detect significant changes across days, the stability measures were sufficiently sensitive to reveal changes. Both groups decreased their variability in state space, STD-PM, over 6 days of practice as in experiment 2, F(2.65, 37.09) = 31.25, P < 0.001, partial η² = 0.691 (Fig. 10E). In addition, there was a significant difference between the self-paced group and the discrete group in STD-PM, F(1, 14) = 6.20, P = 0.026, partial η² = 0.307, indicating that the self-paced group performed with lower variability, i.e., higher periodicity, than the discrete group. These results aligned with expectations from hypothesis 1.

Fig. 10.

Measures of variability and stability in state space in experiment 2. A and B: arm trajectories on day 1 and day 4 of an exemplary subject form the self-paced group. C and D: arm trajectories on day 1 and day 4 of an exemplary subject form the discrete group. E: standard deviations at the Poincaré section STD-PM across 6 days of practice. F: Floquet multiplier across 6 days of practice. The 2 groups improve across the 6 days, and they differ in performance measures. The variability (Bodfish et al. 2000) and stability measures show the same pattern as in experiment 1.

As for success rate and error, the pattern might also be produced by two groups with different skill level. Therefore, we again focused on the 120 trials of day 1 to analyze the initial difference between the groups. A two-sample t-test did not reveal any difference (P > 0.05). In contrast, the same comparisons for day 2, 3, and 5 did detect a statistical difference. Although these t-tests were not corrected for multiple comparisons, they nevertheless suggest that group difference only arose as a result of the two different timing instructions.

Stability in state space.

As summarized in Fig. 10F, the Floquet multiplier values of both groups were between 0 and 0.4, with the exception of one extreme outlier in the discrete group. Note that this subject was not an outlier in the other performance measures, suggesting that subjects could indeed perform with the entire range of Floquet multipliers. As in experiment 1, there were no significant effects across practice days (P = 0.07) nor between the two groups (P = 0.08). Pearson correlations between the performance error and the two stability measures were summarized in Table 3. As can be seen, STD-PM in the discrete group correlated significantly with error in 5 out of 6 days, consistent with hypothesis 3. The lack of correlation may be ascribed to the fewer subjects that displayed a smaller range of Floquet multiplier values than in experiment 1.

Table 3.

Pearson correlation coefficients r between error and dependent measures in experiment 2

	Self-Paced Group				Discrete Group
	STD-PM		FM		STD-PM		FM
Practice Day	r	Sig.	r	Sig.	r	Sig.	r	Sig.
Day 1	0.61		0.38		0.76	*	0.16
Day 2	0.24		−0.22		0.53		0.71
Day 3	0.49		−0.27		0.87	†	0.79	*
Day 4	0.60		−0.27		0.76	*	−0.21
Day 5	0.75	*	−0.27		0.93	†	0.57
Day 6	0.65		−0.34		0.91	†	0.21

Sig., significance.

^*0.01< P < 0.05,

^†0.001< P < 0.01.

The boldface numbers indicate statistically significant correlations.

DISCUSSION

The findings of the two experiments conclusively demonstrate that subjects spontaneously developed a stable rhythm when performing a sequence of similar movements. Rhythmicity was defined by metrics that quantified the degree of periodicity and continuity. Stability was evaluated in state space using the Poincaré map. Experiment 1 documented how subjects spontaneously developed rhythmicity over extensive practice; variability of ITIs decreased, and pauses between throws became fewer and shorter (hypothesis 1). Subjects with higher degrees of rhythmicity and stability of their arm trajectory also achieved better task performance (hypothesis 2). Although variability at the Poincaré section noticeably decreased, stability as quantified by the Floquet multipliers did not change with practice (counter hypothesis 3). Nonetheless, subjects that exhibited smaller Floquet multiplier values, indicating higher stability, performed with smaller errors. Experiment 2 explicitly disrupted periodicity and continuity, which had a negative effect on errors and success rate, as predicted by hypothesis 4.

At first glance, the observation that subjects fall into rhythm may appear almost trivial, as it concurs with intuitive experiences and anecdotal observations. However, it needs to be reiterated that in the throwing movements, the explicit and only goal of the subjects was to minimize their error when aiming to hit a target. The intervals between successive ball releases became increasingly invariant, without explicit awareness of this development. The variability of the ITIs in both the 11-day-long but also in the shorter practice dropped to levels as low as 5%. This variability is comparable to variability reported in studies on tapping to a metronome, a task in which the subject intends to move as periodically as possible in synchrony with a metronome (Repp 2010; Repp and Steinman 2010). Why do people get attracted to a rhythm?

More specifically, why should initiation of each successive movement be constrained to an almost periodic pattern? Furthermore, why could it be beneficial to eliminate pauses between individual throws? Assuming error correction is the predominant process in this practice, it might appear advantageous to flexibly adjust the intervals between attempts to allow for processing of the error and to update the motor command of the next attempt (Diedrichsen et al. 2010; Wolpert et al. 2011). Indeed, as expected, performance significantly improved with practice, attesting to gradual corrections of errors despite the self-imposed time constraints (Fig. 5). However, this appears counterintuitive because, when connecting the successive movements into a continuous flow, there are no controlled initial conditions for each new throw. Instead, previous errors may seamlessly propagate into the next cycle and compromise error correction. It could be reasoned that the best conditions for improving each throw is to set the arm to the exact same initial conditions so that the error correction is applied to invariant starting conditions. However, increased rhythmicity left the overt performance in experiment 1 largely unaffected. The lack of correlation between errors and ITIs seemed to suggest that there was no time constraint for error processing, at least not across subjects (Table 1). Neither did the elimination of pauses affect performance success directly. Only when the continuous flow was explicitly perturbed in experiment 1 and a pause was imposed by the experimenter was the performance negatively affected. Note that there was no instruction to initiate as fast as possible upon the cue that might have distracted the subject’s attention.

Instead, performance improvements appeared to be mediated by the emerging stability properties of the rhythmic movement. The variability of the Poincaré map clearly decreased with practice, underscoring the decrease in the overt variability of the ITI (Figs. 6 and 7). It is important to note that this increasing consistency in state space is not required for consistent task performance, as the task is redundant. The result space has a solution manifold with mathematically infinite solutions, and the system can visit any point at or close to the solution manifold without any overt effect on performance (Fig. 2, C and F). The Floquet multiplier itself, a measure of the evolution around the fixed point, or zero error solution in this case, was positive with higher values indicating a lower degree of stability. While the Floquet multiplier did not change across practice, counter to expectations, it varied widely across subjects, and the values strongly correlated with subjects’ throwing proficiency (Figs. 7C and 8C). These results suggest that stability of the rhythmic arm movements supported good performance. However, a caveat is necessary: Floquet multiplier analysis rests on the assumption that the performance is at a limit-cycle attractor. Hence, a stronger test of stability would be to apply perturbations (e.g., Kay et al. 1991).

One plausible explanation for the emerging rhythmicity could be that subjects get attracted to the resonant frequency of the oscillating limb, which may confer an energetically parsimonious solution as smaller input forces generate higher amplitude output. Such an argument has been supported by a number of studies in locomotion in which the human or animal tends to prefer a frequency that coincides with the minimum of metabolical energy consumption (Hoyt and Taylor 1981; Snaterse et al. 2011). Other work demonstrated that the preferred frequencies scale proportional to the resonant frequency of the limb (Holt et al. 1990, 1995; Turvey et al. 1988). For the human arm moving in the horizontal plane (as in skittles), several studies have assessed stiffness and damping (Bennett 1993; Bennett et al. 1992; Latash 1992), but the resonant frequency itself has been given less attention. With the use of perturbation methods, these studies quantified the stiffness of the neuromuscular complex and its variations throughout the cycle. However, not only do these stiffness estimates vary across the cycle, different studies also identified widely different stiffness values, ranging between 2 and 18 N-m/rad (Bennett et al. 1992) and 6 to 22 N-m/rad (Latash 1992). This is probably due to different choices of movement frequencies and specified movement amplitudes. Another set of studies examined rhythmic movements in the sagittal plane, in which the pendular movements are also subject to restoring torques attributable to gravity, absent in movements in the horizontal plane in which stiffness alone is the determinant (Bingham et al. 1991). For forearm movements swinging in the sagittal plane, Hatsopoulos and Warren (1996) estimated the resonant frequency to be around 1.2 Hz and the joint stiffness to be 0.4 N-m/rad. This study demonstrated that subjects indeed exploited the resonant frequency when allowed to swing their limb at their preferred frequency.

To assess whether the limb movements in the skittles task converged to their respective resonant frequencies with potential energy savings, it would be necessary to know not only the inertial parameters of the limb and the manipulandum, but also the values for the muscle stiffness and damping. Moreover, as visible in the phase portrait in Fig. 4, the throwing task goes beyond simple forearm oscillations and includes accentuated hand opening for the ball release. Furthermore, the effective resonant frequency should probably not only be defined for the moving forearm plus hand, but also include the ball trajectory, as its dynamics is coupled to the hand. Quantifying this “resonant frequency” over the entire perception-action cycle is clearly a challenge. To conclude, although it is possible or even plausible that the emerging ITI converges to a period that affords low metabolic cost or effort, this is hard to quantitatively support at this point.

One benefit of rhythmic performance with dynamic stability is its robustness with respect to perturbations and noise (Longtin et al. 1990; Stark 1962). By definition, any system with stable limit-cycle dynamics rejects small errors and noise and returns to its stable attractor without requiring explicit corrections. Empirical support that this feature of dynamic systems is relevant for human motor behavior has been provided in a series of studies on rhythmically bouncing a ball to a target height (de Rugy and Sternad 2003; Huber and Sternad 2015; Sternad et al. 2000, 2001a, 2001b). Although the racket can contact the ball at any phase of the racket movement and achieve the desired target amplitude, mathematical analyses showed that only contacts at the decelerating portion of the racket trajectory show dynamic stability. Subjects indeed converged to this phase of contact with practice, without being explicitly aware of it. These studies argued that exploiting dynamic stability is a computationally parsimonious solution, obviating computationally demanding error correction (Schaal et al. 1996; Sternad 2017; Wei et al. 2007). However, in contrast to the throwing movements, bouncing a ball in the air is a rhythmic activity, and subjects were instructed to rhythmically bounce the ball. When performing a sequence of throws, periodic movements were not required.

From a neurophysiological perspective, rhythmic movements may confer an advantage because they may involve fewer high-level neural resources. Using fMRI imaging, Schaal, Sternad, and colleagues (Schaal et al. 2004) demonstrated that rhythmic wrist movements required significantly fewer cortical and subcortical areas than discrete movements that were voluntarily separated by random pauses. Discrete movements were associated with bilateral parietal and cerebellar activation, not seen in self-paced rhythmic movements. Presumably, control of rhythmic movements is deferred to subcortical and possibly brainstem areas although these brain regions were not recorded. This view is also supported by a study on patients with stroke that revealed less impairment in rhythmic movements compared with discrete movements in patients with cortical stroke (Leconte et al. 2016). If rhythmic movements can be maintained with fewer demands on higher-level cortical control, then they may free up computational capacity for other control processes.

This preference for stable rhythmic actions is also good support for the proposition in motor control that movements are generated by dynamic primitives. Previous work has argued that the control of the complex human system requires modules to simplify control of the high-dimensional and redundant system. Several lines of research have pursued such modules in the muscular organization and identified functional low-dimensional synergies (d’Avella et al. 2003, 2006; Ivanenko et al. 2004; Tresch et al. 1999). For example, several studies examined locomotion in humans and identified four or five synergies in muscle activation in control of the movement (Dominici et al. 2011; Ivanenko et al. 2004, 2005). Examining walking on a narrow beam, dancers exhibited better control of balance, which was associated with additional synergies (Sawers et al. 2015).

In contrast to muscle synergies, a dynamic systems perspective proposes that modules or primitives are defined over the neuromuscular substrate within the context of a behavioral task. Sternad and colleagues (Schaal and Sternad 1998; Schaal et al. 2000; Sternad 2008; Sternad et al. 2000) have proposed stable attractors as modules that are assembled over the neuromechanical system. Recognizing that the neuromechanical system is nonlinear, stable attractors can take the form of fixed points and limit-cycles, generating discrete and rhythmic movements, respectively. Such stable subsystems may combine to perform more complex movements as a combination of both (de Rugy and Sternad 2003; Ronsse et al. 2009; Sternad et al. 2000). More recently, Hogan and Sternad (2012, 2013) proposed that a third primitive, impedance, is needed to ensure stable physical interactions with objects and the environment. They outline a nonlinear equivalent network as a model for integrating the primitives into interactive behavior.

Although the observations have been recorded in the ideal conditions of the laboratory, the phenomenon is likely to uphold in more realistic conditions with environmental disturbances, just as the rhythmicity of walking and running is maintained on uneven terrain. How robust this tendency is requires further investigation. It is noteworthy though that this preference for rhythmic movements is also consistent with several clinical observations. For example, individuals with severe autism frequently are urged to perform repetitive movements, such as hand flapping and body rocking, that seem to have a calming effect (Bodfish et al. 2000; Goldman et al. 2009). Individuals with chronic schizophrenia frequently display purposeless repetitive movements, and antipsychotic drugs can induce low-frequency large-amplitude tremor (Burke et al. 1982). Furthermore, it is well known that one cardinal symptom of Parkinson disease is tremor with higher-amplitude and lower frequency compared with healthy physiological tremor (Heldman et al. 2011). A similar manifestation of uncontrolled oscillations is essential tremor, another widespread but still understudied neurological disorder (Archer et al. 2018a, 2018b; Elble 2017). These pathological manifestations suggest that, when the nervous system is impaired, oscillations as a more basic form of organization can emerge.

As a final speculation, we want to return to the recognition that the human system is a complex hierarchy of interconnected oscillations at different temporal and spatial scales. As many scientists in chronobiology have pointed out, the human body comprises a hierarchy of oscillatory processes at a vast range of orders of magnitudes, starting with periods 10⁻³ and 10⁻¹ s at the level of neuronal signals, to 10⁰–10² s at the level of cardiac and respiratory processes, to the level of the metabolic system with 10³ to 10⁵ s and even higher in circadian and reproduction cycles. The behavioral level of volitional movements is at the order of 10⁰ s. However, the intriguing fact is that movements are under volitional control and can take on many complex nonrhythmic patterns. The observation that a sequence of volitional movements tend to shape into a rhythmic pattern suggests that it falls in line with the hierarchical system whenever possible.

Returning to the subjective association of rhythmic movements with “being in a zone,” signaling a comfortable state, this may suggest that rhythmic behaviors have beneficial effects on the human system, just as rocking has soothing effect on an infant (Ko et al. 2016). We conclude by proposing that the central nervous system can make use of this intrinsic tendency and exploit such temporary rhythmic patterns as building blocks or primitives to construct more complex movement patterns. We recognize that much of these interpretations are still highly speculative and call for more research in this direction.

GRANTS

This study was supported by the National Institutes of Health R01-HD087089, R01-HD081346, and the National Science Foundation, NSF-EAGER 1548514, NSF-NRI 1637854, awarded to D. Sternad.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

D.S. conceived and designed research; Z.Z. performed experiments; Z.Z. analyzed data; Z.Z. and D.S. interpreted results of experiments; Z.Z. prepared figures; Z.Z. and D.S. drafted manuscript; Z.Z. and D.S. edited and revised manuscript; Z.Z. and D.S. approved final version of manuscript.