Theta-gamma cascades and running speed

Abstract

Oscillations in the hippocampal local field potential at theta and gamma frequencies are prominent during awake behavior and have demonstrated several behavioral correlates. Both oscillations have been observed to increase in amplitude and frequency as a function of running speed. Previous investigations, however, have examined the relationship between speed and each of these oscillation bands separately. Based on energy cascade models where “…perturbations of slow frequencies cause a cascade of energy dissipation at all frequency scales” (Buzsaki G. Rhythms of the Brain, 2006), we hypothesized that cross-frequency interactions between theta and gamma should increase as a function of speed. We examined these relationships across multiple layers of the CA1 subregion, which correspond to synaptic zones receiving different afferents. Across layers, we found a reliable correlation between the power of theta and the power of gamma, indicative of an amplitude-amplitude relationship. Moreover, there was an increase in the coherence between the power of gamma and the phase of theta, demonstrating increased phase-amplitude coupling with speed. Finally, at higher velocities, phase entrainment between theta and gamma increases. These results have important implications and provide new insights regarding how theta and gamma are integrated for neuronal circuit dynamics, with coupling strength determined by the excitatory drive within the hippocampus. Specifically, rather than arguing that different frequencies can be attributed to different psychological processes, we contend that cognitive processes occur across multiple frequency bands simultaneously with organization occurring as a function of the amount of energy iteratively propagated through the brain.

NEW & NOTEWORTHY Often, the theta and gamma oscillations in the hippocampus have been believed to be a consequence of two marginally overlapping phenomena. This perspective, however, runs counter to an alternative hypothesis in which a slow-frequency, high-amplitude oscillation provides energy that cascades into higher frequency, lower amplitude oscillations. We found that as running speed increases, all measures of cross-frequency theta-gamma coupling intensify, providing evidence in favor of the energy cascade hypothesis.

INTRODUCTION

The observation that changes in local field potential (LFP) oscillations correlate with the behavioral state of an animal has a long history (for review, see Buzsáki 2005). Nevertheless, the mechanisms that generate and organize oscillatory activity are still opaque. For example, it has been proposed that different LFP oscillations and their couplings support different processes and network functions (Belluscio et al. 2012; Bieri et al. 2014; Colgin et al. 2009; Gloveli et al. 2005; Lisman and Jensen 2013; Tort et al. 2008, 2009). However, the neurophysiological mechanisms responsible for integrating neuron spiking and oscillations across temporal scales to support cognition have yet to be elucidated. The observation that hippocampal neuron firing rate (McNaughton et al. 1983; Maurer et al. 2005), theta power (Sheremet et al. 2016 and others), and gamma power (Ahmed and Mehta 2012; Chen et al. 2011; Kemere et al. 2013; Zheng et al. 2015) all increase with faster running speeds suggests that synaptic potentials organization across the macroscopic scale (theta) to the microscopic level of the single units. Specifically, slow oscillations reflect the entrainment of a large volume of neurons. Briefly, the phasic reentry of anatomical connections can give rise to oscillatory entrainment: the larger the reentrant pathway, the more neurons involved, the greater the axonal conduction delay, and, therefore, the slower the oscillatory frequency (Buzsaki 2006; Buzsáki 2013; Edelman 1987). These global slow oscillations are poised to “coordinate” local events (Buzsáki and Draguhn 2004). Gamma, on the mesoscopic level, is an inevitable pattern when fast excitation and inhibition compete (Buzsaki 2006; Buzsáki et al. 2004; Buzsáki and Wang 2012; Wang and Buzsáki 1996). On the microscopic scale, basket cells, entrained by the global theta rhythm, appear to be critical in gamma generation given their fast time course and perisomatic terminals onto pyramidal cells (Buzsaki 2006; Freund and Buzsáki 1996). Thus, during theta states, large-scale activation provides the input necessary for inhibitory and excitatory processes to compete on the mesoscale level (generating high-amplitude gamma). Above, we suggested that inhibition and excitation compete rather than cooperate. Credibly, the distinction is a matter of perspective. However, this choice was made to retain congruence with the “compromise in competition” models of energy cascade (e.g., Wang et al. 2016). Briefly, the nervous system must be able to propagate activity from one region to the next without letting excitation become a rhythmic seizure. For a seizure to occur, excitatory dynamics would have to “win out.” Thus, when normal cognitive processes are considered, inhibition and excitation compete to a point of optimal network activity.

Previously, we have demonstrated increases in single-unit firing rate with rat running speed (Maurer et al. 2005). Furthermore, accompanying the increase in firing rate, we found changes in sequence compression (defined as the ratio of the rate of cell assembly transition to the rat’s actual velocity; see Dragoi and Buzsáki 2006; Skaggs et al. 1996) at faster running speed (Maurer et al. 2012). With respect to the LFP, these changes are accompanied by an increase in theta power, theta frequency, and the number of theta harmonics (Sheremet et al. 2016). Finally, we revealed that pyramidal cells and interneurons interact through putative monosynaptic connections to organize spike firing times (Maurer et al. 2006). Therefore, on the basis of these findings and the role of interneurons in shaping gamma oscillations, we sought to empirically test the hypothesis that theta and gamma couple in proportion to the amount of activity into the network by examining power-power correlations and power-phase relationships between these oscillations as a function of running speed. “Energy” in this context can be roughly considered to be the amount of synaptic input, either excitatory or inhibitory, that is known to be influenced by behavioral state and shape oscillatory potentials. Specifically, the LFP measures the potential of an electromagnetic field. The variance of the electromagnetic field is proportional, by a multiplicative constant (that is, the dielectric constant), to the energy of the field in the unit volume. In general, the electromagnetic field changes in proportion to behavioral state, and specifically, synaptic potentials and other local ionic exchanges (Buzsáki et al. 2012; Vanderwolf 1969).

Importantly, hippocampal synaptic inputs from different afferents are associated with distinct lamina, suggesting that the relationship between behavioral state and LFP dynamics may not be uniform across different input zones. Specifically, the CA1 subregion of the hippocampus has four distinct lamina: stratum oriens, pyramidale, radiatum, and lacunosum-moleculare. The stratum lacunosum-moleculare region of CA1 neurons receives input from the layer III of the entorhinal cortex (Witter et al. 1988), nucleus reuniens (Wouterlood et al. 1990), and amygdala (Pikkarainen et al. 1999), and inhibitory input from somatostatin-positive cells (Freund and Buzsáki 1996). The stratum radiatum and oriens receive CA3 Schaeffer collateral and commissural fibers (Hjorth-Simonsen 1973; Ishizuka et al. 1990). The stratum pyramidale receives relatively fewer synaptic inputs than the other layers, but this layer is the primary target of parvalbumin-positive inhibitory cells (Freund and Buzsáki 1996). Given these anatomical distinctions, it is conceivable that there could be a laminar sensitivity to theta-gamma oscillatory coupling as a function of movement speed. Specifically, because speed sensitivity neurons have been observed in the entorhinal cortex (Kropff et al. 2015) and the input into the distal dendrites of CA1 neurons appears to be more powerful than the CA3 input to the radiatum (Brun et al. 2002, 2008; Jarsky et al. 2005), it is conceivable that cross-frequency coupling is greatest in the lacunosum-moleculare relative to the radiatum.

The current study investigated the potential interaction between gamma (50–120 Hz; Bragin et al. 1995; Chrobak and Buzsáki 1998; Leung 1992; Penttonen et al. 1998; Stumpf 1965) and theta (6–10 Hz) oscillation (Green and Arduini 1954; Jung and Kornmüller 1938; Vanderwolf 1969) across hippocampal CA1 laminae as a function of running speed. Should low- and high-frequency rhythms arise from distinct circuit and biophysical mechanisms, then synaptic activation in support of each oscillation should be dissociable, as would be evidenced by unrelated changes in power across frequencies. Alternatively, if different frequencies of the LFP spectrum are part of a unitary process, then all forms of cross-frequency coupling should increase when the power in one frequency band is altered. The current data support the latter prediction, adding to an emerging framework that high-amplitude slow oscillations dissipate to influence all temporal scales of the LFP spectrum.

MATERIALS AND METHODS

Subjects and Behavioral Training

All behavioral procedures were performed in accordance with the National Institutes of Health guidelines for rodents and with protocols approved by the University of Florida Institutional Animal Care and Use Committee. A total of five 4- to 10-mo-old Fisher344-Brown Norway rats (Taconic) were used in the present study. This was a mixed-sex cohort comprising r530♂, r538♂, r544♀, r547♂, and r695♀ (where r is rat and ♂ and ♀ indicate male and female sex, respectively) to integrate sex as a biological variable and begin to alleviate the disparity in research focused exclusively on males (Clayton 2016). In the present study, we had no a priori predictions that sex would alter oscillations of the hippocampus, because single-unit physiology is relatively consistent in female animals across estrous (Tropp et al. 2005). On arrival, rats were allowed to acclimate to the colony room for 1 wk. The rats were housed individually and maintained on a 12:12-h light-dark cycle. All training sessions and electrophysiological recordings took place during the dark phase of the rats’ light-dark cycle. Training consisted of shaping the rats to traverse a circular track for food reward (45 mg of unflavored dustless precision pellets, product no. F0021; BioServ, Flemington, NJ). During this time, their body weight was slowly reduced to 85% of their arrival baseline. Once the rats reliably performed more than one lap per minute, they were implanted with a custom single-shank silicon probe from NeuroNexus (Ann Arbor, MI). This probe was designed such that 32 recording sites, each with a recording area of 177 μm², were spaced 60 μm apart, allowing incremental recording across the hippocampal lamina. In preparation for surgery, the probe was cleaned in a 4% dilution of Contrad detergent (Decon Contrad 70 liquid detergent; Fisher Scientific) and then rinsed in distilled water (Vandecasteele et al. 2012).

Surgical Procedures

Surgery and all other animal care and procedures were conducted in accordance with the NIH Guide for the Care and Use of Laboratory Animals and approved by the Institutional Animal Care and Use Committee at the University of Florida. Rats were initially sedated in an induction chamber. Once anesthetized, the rat was transferred to a nose cone. The head was shaved, with care taken to avoid the whiskers. The rat was then transferred to the stereotaxic frame, with the ear bars gently secured and the front teeth placed over the incisor bar. The stereotaxic nose cone was secured, ensuring that the rat was appropriately inhaling the anesthesia. During surgical implantation, the rats were maintained under anesthesia with isoflurane administered at doses ranging from 0.5 to 2.5%. Next, ophthalmic ointment was applied, and “tanning shades,” fabricated out of foil, were placed over, but not touching, the eyes to minimize direct light exposure. Multiple cycles of skin cleaning, using betadine followed by alcohol, were applied before the first incision from approximately the forehead to just behind the ears. The remaining fascia was blunt dissected away, and bone bleeding was mitigated through application of bone wax or cautery. Once the location of bregma was determined, the site of the craniotomy was located and a 3 × 3-mm contour was drilled out, but not completed. This was followed by the placement of seven anchor screws in the bone as well as a reference over the cerebellum and a ground screw placed over the cortex. Once the screws were secured, a thin layer of dental acrylic (Grip cement industrial grade, no. 675571 powder, no. 675572 solvent; Dentsply Caulk, Milford, DE) was applied, with care taken to not obscure the craniotomy location. Finally, the craniotomy location was completed, with irrigation and bleeding managed as necessary once the bone fragment was removed. Next, a portion of the dura was removed, with care taken to avoid damaging the vessels and the surface of the neocortex. Small bleeding was managed with saline irrigation and gel foam (sterile absorbable gelatin sponges; Pharmacia & Upjohn, Kalamazoo, MI, a division of Pfizer, New York, NY). The probe implant coordinates targeted the dorsal hippocampus (anteroposterior: −3.2 mm, mediolateral: 1.5 relative to bregma, dorsoventral: −3.7 to brain surface).

Once the probe was in place, the craniotomy was covered with Silastic (Kwik-Sil; World Precision Instruments, Sarasota, FL) and then secured to the anchor screws with dental acrylic. Four copper mesh flaps were placed around the probe, providing protection as well as acting as a potential Faraday cage. The wires from the reference and ground screws were soldered to the appropriate pins of the connector. Adjacent regions of the copper mesh flaps were soldered together to ensure their electrical continuity, and the ground wire soldered to the copper mesh with care taken to isolate the reference from contact with the ground. Once the probe was secured, the rat received 10 ml of sterile saline as well as Metacam (1.0 mg/kg) subcutaneously (generic nonsteroidal anti-inflammatory meloxicam; Boehringer Ingelheim Vetmedica, St. Joseph, MO). The rat was placed in a cage and monitored constantly until fully recovered. Over the next 7 days, the rat was monitored to ensure recovery and no behavioral anomalies. Metacam was administered the day following surgery, as well. Antibiotics (sulfamethoxazole-trimethoprim oral suspension, 200 mg/40 mg per 5 ml; Aurobindo Pharma USA, Dayton, NJ) were administered in the rat mash for an additional 5 days.

Neurophysiology

Following recovery from surgery, rats were retrained to run unidirectionally on a circle track (outer diameter: 115 cm, inner diameter: 88 cm), receiving food reward at a single location. For r530, r544, and r695, data were only analyzed from the circle track conditions. To deal with low velocities from the circle track data sets, additional data sets for r538 and r539 from running on the figure-eight track (112 cm wide × 91 cm long) were used. In this task, rats were rewarded on successful spatial alternations. Only data sets in which the rats performed more than 85% of trials correctly were used. The LFP was recorded on a Tucker-Davis neurophysiology system (PZ2 preamplifier and RZ2 processor; Tucker-Davis Technologies, Alachua, FL) at ~24 kHz. The animal’s position was recorded at 30 frames/s (Tucker-Davis). Spatial resolution was 3.68 pixels/cm.

Analyses and Statistics

Speed was calculated as the average derivative of position in 1-s epochs. The LFP data were analyzed in MATLAB (The MathWorks, Natick, MA) using custom-written code as well as code imported from the HOSAtoolbox (Swami et al. 2003). Raw LFP records sampled at 24 kHz (Tucker-Davis system) were low-pass filtered down to 2 kHz and divided into sequences of 1,024 time samples (~0.5 s). The analysis of the LFP in the current study was based on standard techniques used for stationary signals (Papoulis and Pillai 2002; Priestley 1981) as previously described in Sheremet et al. (2016). Briefly, we assume that the LFP time series is a stochastic process, stationary in the relevant statistics, and decompose it using the discrete Fourier transform (DFT). The Fourier transform time sequences are reduced to the nonredundant frequency domain of 1 Hz ≤ ω ≤ 1 kHz (where ω are the analyzed frequencies), with a frequency increment of 1 Hz.

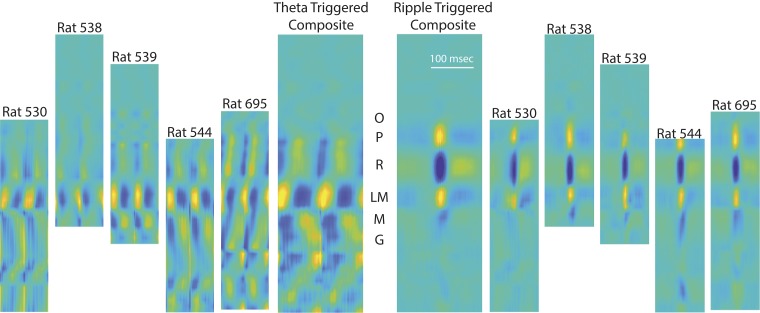
Electrode position along the CA1-dentate axis was determined initially via visual inspection of the LFP, followed by traditional current source density analyses (Bragin et al. 1995; Buzsáki et al. 1986; Mitzdorf 1985; Rappelsberger et al. 1981). Shifts in the phase of theta from stratum oriens to the dentate (Buzsáki et al. 1983; Leung 1984; Winson 1978) as well as the regional distribution of currents (triggered on ripples) revealed sources and sinks that directly related to input layers (Fig. 1; Sullivan et al. 2011; Ylinen et al. 1995a).

Fig. 1.

Use of current source density for electrode localization across rats. Left: current source density of the raw local field potential (LFP) triggered on the maximum positive deflection of the filtered theta rhythm, with time normalized to 2 cycles of the hippocampal theta rhythm. Right: individual rat current source density plots for the unfiltered LFP, triggered on the maximum positive-going ripple in the pyramidal cell layer (sources are warm colors, sinks are cool colors). To identify the layers across each rat, composite images (center) were generated with the output compared with that of prior publications (Bragin et al. 1995; Buzsáki 2015; Sullivan et al. 2011). Both the theta and ripple current source density analyses were calculated during either awake-behavior or rest epochs. To account for differences in hippocampal size, the current source density images were cross-correlated with each other to determine appropriate alignment and compression. For the purposes of the current analyses, the oriens (O), pyramidal layer (P), stratum radiatum (R), lacunosum-moleculare (LM), molecular layer (M), and upper granule layer (G) were identified.

Detection of fundamental frequencies.

An import issue that resides in the field is the ability to detect the fundamental frequencies that are present in the LFP rhythm that are potentially distinct from the f^−α background activity. To address this, we implemented the method of calculating the correlation coefficients of the spectrogram as outlined by Masimore et al. (2004, 2005). The power cross-correlograms were obtained by estimating the correlation coefficients between all the frequency pairs in the output of the DFT (see above). Importantly, as discussed by Masimore et al. (2004, 2005), this method allows the fundamental frequencies of the LFP to be identified without filtering as well as determination of any potential interactions across different oscillatory bands.

Power-power correlations.

To investigate the relationship between theta and gamma power, the LFP recordings were downsampled to 2 kHz and split into 1-s segments. To remove epochs with potential noise, an LFP quality control algorithm was applied to remove segments with either 1) too large or too small variance [>3·mean(variance) or <0.1·mean(variance)] or 2) maximum (or minimum) LFP recording with 10 SD from the mean [maximum(LFP) > mean(LFP) + 10 SD(LFP) or minimum(LFP) < mean(LFP) − 10 SD(LFP)]. The mean speed for each segment was computed, and only segments with mean speed larger than 5 cm/s were included for this analysis. For each segment, the power spectrum was estimated with the multitaper method. The first three digital prolate spheroidal sequences (DPSS) were used to get the tapered spectrum estimations. Tapered spectrum estimations were computed with 2,000 fast Fourier transform (FFT) points, and averaging over these spectrum estimations generated the multitaper spectrum. The power of the LFP in a given frequency range is the area under the power spectrum curve within that frequency range. Each observation in the power-power correlation analysis is the power of theta (6–10 Hz) and gamma (50–120 Hz) for a 1-s segment.

Phase-power coherence.

The LFP recordings were downsampled to 2,000 Hz, split into 1-s segments, and sorted according to their corresponding average speed into four classes [0,5], (5,15], (15,35], and >35 cm/s. If X(t) is a 1-s time series segment that belongs to a given speed class, the corresponding power time series Y_f1(t) at frequency f₁ was obtained by using wavelet transform. The wavelet transform decomposes X(t) into the timescale domain, and Y_f1(t) is the modulus square of wavelet transform at the scale whose central frequency is f₁. The Fourier transforms of time series X(t) and Y_f1(t) are $\widehat{X}\left(f\right)$ and $\widehat{Y}\left(f\right)$, and the cross-spectrum between X(t) and Y_f1(t) is $〈\widehat{X}\left(f\right){\widehat{Y}}^{*}\left(f\right)〉$ where $〈.〉$ is the expected-value operator. The phase-power coherence is defined as the modulus of the cross-spectrum $\widehat{X}{\widehat{Y}}^{*}$ normalized by the power spectra of X and Y_f1, and the mathematical expression for phase-power coherence is $\left|\frac{〈\widehat{X}{\widehat{Y}}^{*}〉}{{\left(〈\widehat{X}{\widehat{X}}^{*}〉〈\widehat{Y}{\widehat{Y}}^{*}〉\right)}^{1/2}}\right|$. Informally, the phase-power coherence measures how much the power time series of frequency component f₁ is modulated by frequency components f in the original signal.

For example, if the time series X(t) has a fast oscillation component with frequency f_FO whose amplitude is modulated by a slow oscillation with frequency f_SO, this component can be written as A(t) sin(2πf_FOt + ϕ₁) with a slow-varying envelope A(t) = C sin(2πf_SOt + ϕ₂), where C is a constant and ϕ₁ and ϕ₂ are phases. The wavelet transform decomposes the original time series into scale-time domain, and at the scale whose central frequency is f_FO, the modulus of wavelet transform Y_fFO(t) approximates the envelope A(t). If the original time series also has a frequency component with frequency f_SO and this frequency component is phase-locked with A(t), then the cross-spectrum between X(t) and Y_fFO(t) will exhibit high coherence value at frequency f_SO, which indicates the amplitude of fast oscillation is correlated with the phase of slow oscillation. In Fig. 5, the y-axis represents the frequency component whose envelope is obtained by wavelet transform, and the x-axis represents the modulation frequency.

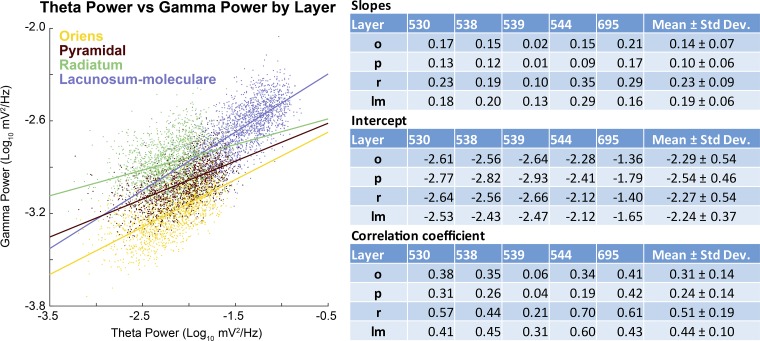
Fig. 5.

Correlation of theta power to gamma power. Left: scatter plot and least-squared regression lines for theta and gamma power across the layers of rat 695. Note that there is a clear positive trend across all layers, although it is strongest in the lacunosum-moleculare. Right: table containing the individual rat data (slope, intercept, and correlation coefficient) by layer (o, oriens; p, pyramidal layer; r, radiatum; lm, lacunosum-moleculare), as well as averages (means ± SD).

Bispectrum and bicoherence.

The bispectrum has been thoroughly reviewed in terms of both statistical and mathematical background (Harris 1967) as well as its application to nonlinear wave interaction (Kim and Powers 1979). As noted in our prior publication (Sheremet et al. 2016) as well as by others, bispectral analysis (the Fourier transform of the third-order cumulant) quantifies the degree of phase coupling between the frequencies of the LFP, whereas the bicoherence quantifies the degree of cross-frequency coupling independent from the amplitude (Barnett et al. 1971; Bullock et al. 1997; Gloveli et al. 2005; Hagihira et al. 2001; Li et al. 2009; Muthuswamy et al. 1999; Ning and Bronzino 1989; Shahbazi Avarvand et al. 2018; Sigl and Chamoun 1994; Wang et al. 2017). Thorough discussion of bicoherence and bispectral analysis as well as considerations relative to other methods have been described elsewhere (Aru et al. 2015; Dumermuth et al. 1971; Kovach et al. 2018).

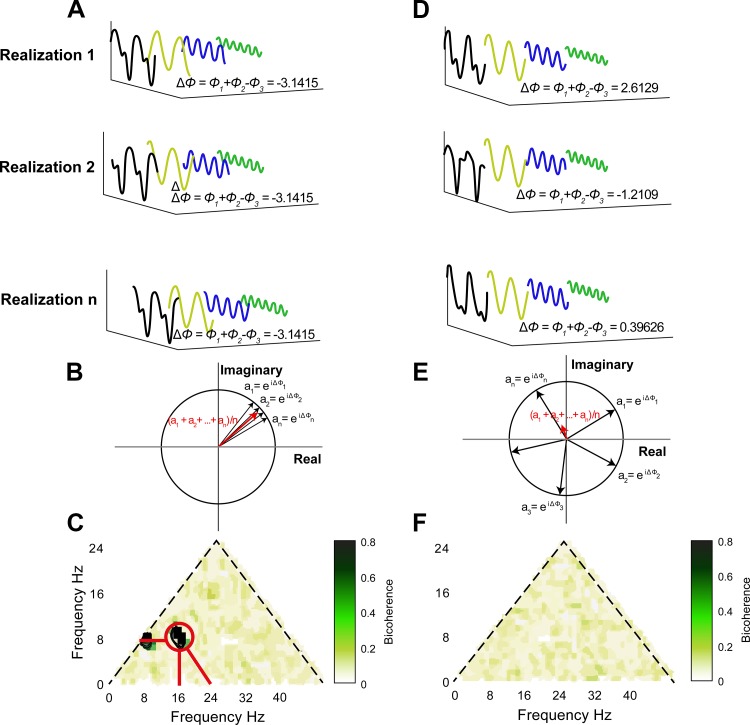
The utility of the bispectrum can be illustrated as follows. In the instances of “no coupling,” three independent waves (ω₁, ω₂, and ω₁ + ω₂) will have statistically independent phases relative to each other, resulting in a random phase mixing when estimated over multiple realizations. In these instances, the bispectrum will take a zero value. When three waves are nonlinearly coupled, however, a phase coherence will exist between ω₁, ω₂, and ω₁ + ω₂, resulting in a nonzero bispectral value (Fig. 2; Kim et al. 1980). To analyze for nonlinear phase coupling between hippocampal LFP frequencies, the data were analyzed in MATLAB (The MathWorks) using custom-written code as well as code imported from the HOSAtoolbox (Swami et al. 2003) for bispectral analysis. It is necessary to reiterate that the nonlinearity of a time series is expressed by the phase correlation across different frequencies. We used the lowest order (third order) phase coupling, described by the bispectrum and first used in ocean waves by Hasselmann (1963), to analyze the hippocampal LFP, as we previously described in Sheremet et al. (2016). It is emphasized here, as well as elsewhere (Pradhan et al. 2012; Van Milligen et al. 1995), that the bispectrum measures phase coupling, defined to occur when the sum of phases between two frequencies is equal to the value of a third frequency plus a constant. Furthermore, the real and imaginary parts of the normalized bispectrum provide information regarding how cross-frequency interactions contribute to skewness and asymmetry, respectively (for more information, see Sheremet et al. 2016).

Fig. 2.

Bicoherence illustration. A: time series with triad phase coupling (black line) resolved into Fourier series where the main components are 3 sinusoidal waves with frequencies: f₁ = 8 Hz (yellow), f₂ = 16 Hz (blue), and f₃ = f₁ + f₂ = 24 Hz (green). The biphase of the 3 waves is defined as $\Delta \varphi ={\varphi }_{f_1}+{\varphi }_{f_2}-{\varphi }_{f_3}$. The biphase is almost constant over realizations. Averaging biphase vectors over realizations $\frac{{\sum }_{k=1}^n{e}^{i\Delta {\varphi }_k}}{n}\approx e^{i\Delta {\varphi }_k}$ gives a complex number that has the norm close to 1, as shown in B. The frequency triad (f₁, f₂, f₃) corresponds to the significant region (marked with red circle) in bicoherence plot in C. C shows the modulus of the averaged biphase vectors $\left|\frac{{\sum }_{k=1}^n{e}^{i\Delta {\varphi }_k}}{n}\right|$ for all the frequency triads. The contour lines in C outline the 99% significance level on zero bicoherence, which is suggested by Elgar and Guza (1985) as $\sqrt{\raisebox{1ex}{$6$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}$. The marked significant region indicates the frequency of three waves: 8, 16, and 24 Hz (indicated with red lines). The y = x boundary of the bicoherence plot in C is imposed by the symmetry property of bicoherence, and the x + y = 50 boundary is imposed by the up limit of the frequency range of interest (f_x + f_y = 50 Hz). In C, there is another significant region (8, 8, and 16 Hz), which implies this triad is also phase coupled. D: time series without triad phase coupling (black line) and the Fourier series components with frequency f₁ = 8 Hz (orange), f₂ = 16 Hz (blue), and f₃ = 24 Hz (green). The biphase Δϕ distributes randomly, and the biphase vectors $e^{i\Delta {\varphi }_k}$ cancel each other when averaged over realizations, as shown in E, which gives a bicoherence plot without any significant regions, as shown in F.

To associate our analysis with speed, the 1 s of LFP for the bispectrum was stored with the mean speed for the same temporal epoch. Based on mean velocities of every segment, we classified each LFP segment into four speed ranges: 0.001 to 5, 5 to 15, 15 to 35, and >35 cm/s. For statistical comparisons, average nonlinearity was calculated for the 5–15 and the >35 cm/s speed bins.

RESULTS

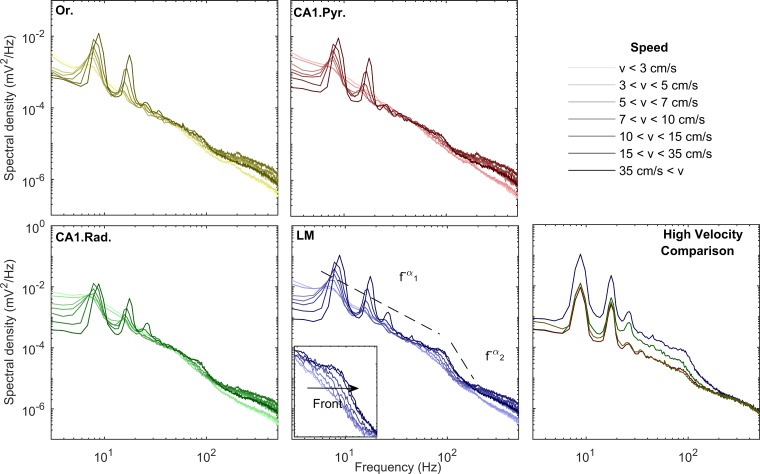
For a preliminary measure of laminar differences of LFP, we calculated the power spectral density in the CA1 oriens (Or), stratum pyramidale (CA1.Pyr), radiatum (CA1.Rad), and lacunosum-moleculare (LM) as a function of speed (Fig. 3). Our observations of the power spectra can be characterized in general as having a power law f^−α structure. However, unlike previous reports, the spectral slope α is not constant throughout the entire frequency range. Instead, two or more domains with distinct slopes can be identified, most evident in the LM. With preliminary analyses across layers of the power spectral density, cross-frequency phase-power coherence, and bicoherence analyses, these domains formed rather well-defined frequency intervals that can be associated with theta (6–10 Hz) and its harmonics (16, 24, 32, 40, and 48 Hz; see nonlinear analysis below); gamma (broadly defined as ~50–120 Hz, similar to Bragin et al. 1995); and fast oscillations (>120 Hz). Adjacent hippocampal layers also exhibited harmonics of theta, although not as prominent as the LM region. In agreement with previous results (Bragin et al. 1995), theta and gamma power are higher in the LM than in the other CA1 layers.

Fig. 3.

Changes in power spectral density as a function of velocity and CA1 layer (transition from lighter to darker hues indicates low to high velocities). Across all layers, the increases in theta and theta harmonic with speed are associated with an increase in gamma power. Spectral shapes in all layers follow a power law of the type f^−α. Remarkably, the lacunosum-moleculare (LM) layers exhibit different slopes between the frequency domains that encompass theta and its harmonics and the gamma range. This phenomenon becomes apparent in all regions when all high-velocity power spectra across layers are compared (bottom right). Furthermore, as power increases in the gamma range, the spectrum preserves its slope and shifts to the right, creating the appearance of a moving front (inset in LM). In agreement with prior work (Bragin et al. 1995), the CA1 oriens (Or.) and pyramidal layer (CA1.Pyr.) exhibit the least energetic gamma range of all the layers examined. CA1.Rad., CA1 stratum radiatum.

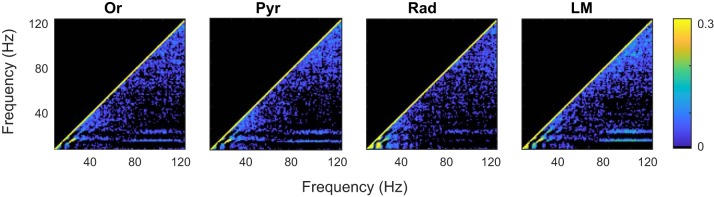
In the frequency range 50–120 Hz, the distribution of power acquires the form of a front of constant slope shifting to the right, toward higher frequencies as running speed increases (inset in Fig. 3). This effect is observed across all layers. Whereas the increase in theta power with speed is in congruence with models by which theta is driven by an external input (Buzsáki 2002; Holsheimer et al. 1982), the shifting gamma front is indicative of a change in circuit dynamics. Specifically, previous work on central pattern generators suggests that high-frequency oscillations can increase as a function of neural drive (Shik et al. 1969). To test this hypothesis relative to the hippocampus, we examined power-power correlations between the theta and gamma bands. Before performing this analysis, however, it is necessary to identify the predominant frequencies of theta and gamma. Therefore, in accordance with Masimore et al. (2004, 2005), characteristic frequencies of interest were determined by calculating the correlation coefficients of the Fourier transform (Fig. 4). Notably, this method is also capable of identify interactions across frequencies. This method clearly identified interactions among theta and its harmonics (<40 Hz) across all layers, as well as between theta and gamma, with the gamma range covering 50–120 Hz. Therefore, these frequency ranges were used for the present analyses.

Fig. 4.

Average correlation coefficients of Fourier transform across all rats for the identification of fundamental frequencies in the hippocampal local field potential (LFP). As previously described, correlations along the diagonal are equal to 1 (each value will be correlated with itself); correlations slightly off the diagonal are the correlations with adjacent frequencies, because rhythmic oscillations have a nonzero width; and the off-axis correlations indicate that 2 oscillatory bands showed high power at similar times, suggestive of an interaction (see Masimore et al. 2004, 2005). In all regions, there are notable “dots” of correlations at ~40 Hz and below, indicative of theta and its harmonics (Sheremet et al. 2016; see below). Farther off-axis, there is a correlation between ~80–120 Hz and theta as well as its harmonics. Therefore, we constrained our analysis to examine the harmonics and, because there is no evidence for subdivided bands of gamma in our data (e.g., Colgin et al. 2009), a broad oscillatory band that maintains congruence with Bragin et al. (1995; 50–120 Hz). Because the cross-correlation is symmetric, the upper part of the panel is set to 0. For all plots, values below 0.03 are set to black. Or, oriens; Pyr, CA1 pyramidal layer; Rad, radiatum; LM, lacunosum-moleculare; 𝑣, speed.

Notably, in accordance with the idea that the gamma frequency component of the LFP is excited by the same input as theta, this first-pass analysis revealed that there are “power-power” correlations. To explore this further, we calculated power for hippocampal theta (narrowly defined as 6–10 Hz for this analysis) relative to gamma power (using a range from 50 to 120 Hz) in 1-s windows. By correlating the power of the hippocampal theta rhythm against the power of the gamma within the same region, it is possible to determine whether a power-power relationship exists (Fig. 5). Across lamina and rats, there was a significant relationship between theta power and gamma power with, on average, 16% of the variance in gamma power being explained by theta power (P = 0.04). Note that this value of the explained variance (EV) meets or exceeds values used in the field of hippocampal reactivation (Euston et al. 2007; Hoffman and McNaughton 2002; Kudrimoti et al. 1999; Lansink et al. 2008; Pennartz et al. 2004). Although beyond the scope of the present article, in line with the cascade theory, we hypothesize that a model accounting for more frequencies, such as the multiple harmonics of theta, would increase the observed EV value. Interestingly, the correlation coefficients between theta and gamma power significantly differed between hippocampal lamina [F_(3,12) = 10.21, P = 0.001]. In fact, the correlation between theta and gamma power was highest in the CA1.Rad (r = 0.51) and lowest in the CA1.Pyr (r = 0.24). Simple orthogonal contrasts comparing the CA1.Rad to the other CA1 lamina indicated that the theta-gamma power correlation was significantly greater in the CA1.Rad compared with the Or [F_(1,4) = 19.74, P = 0.01] and the CA1.Pyr [F_(1,4) = 16.98, P = 0.02]. In contrast, the correlation between theta and gamma power was not significantly different between the CA1.Rad and LM [F_(1,4) = 2.11, P = 0.22]. These data indicate that theta and gamma power are strongly correlated across all layers and that this relationship is particularly evident in the CA1.Rad and LM.

The slope of the relationship between theta and gamma power provides information regarding the rate at which activity transfers across frequency bands. The slope was significantly different across hippocampal laminae [F_(3,12) = 7.52, P = 0.004]. The slope was greatest in the CA1.Rad (b = 0.23, where b is the slope) and smallest in the CA1.Pyr (b = 0.11). Simple orthogonal contrasts comparing the CA1.Rad to the other CA1 lamina indicated that the slope of the theta-gamma power relationship was significantly greater in the CA1.Rad compared with the Or [F_(1,4) = 10.64, P = 0.03] and CA1.Pyr [F_(1,4) = 14.63, P = 0.02]. In contrast, the slope of the theta-gamma power relationship was not significantly different between the CA1.Rad and LM [F_(1,4) = 2.11, P = 0.22]. This observation is not trivial, because it runs counter to contemporary models in which neural oscillations considered to be independent and multiplexed (Akam and Kullmann 2014; McLelland and VanRullen 2016). Multiplexing implies that different frequencies, supported by orthogonal populations of neurons (e.g., Gloveli et al. 2005), can vary their activity independently of each other (which would be evident should theta-to-gamma power exhibit little to no correlation). Rather, these observations indicate that, across layers, gamma increases power in proportion to the amount of theta activity, supporting the hypothesis that external neural drive (theta) provides the activity that supports the amplitude of the gamma oscillation.

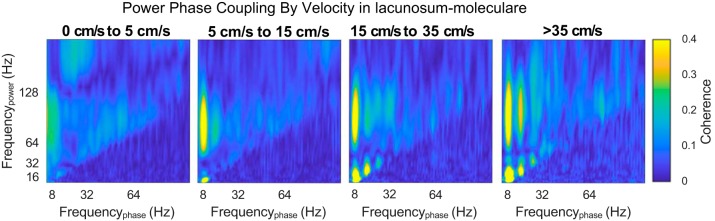
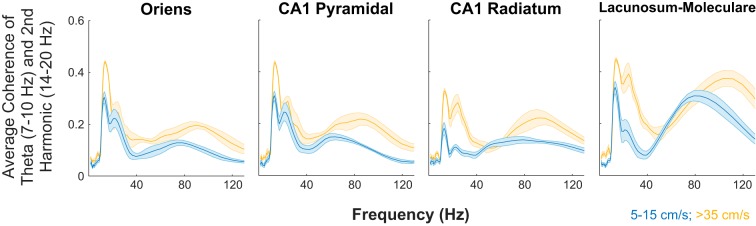
Although there was a significant, positive correlation between theta and gamma power and power increases with speed, it may be argued that these results do not fully encompass cross-frequency interactions, let alone demonstrate dependency. Therefore, we investigated the average cross-frequency phase-power coherence (Colgin et al. 2009) as a function of speed (Michaels et al. 2018). Across layers, gamma power-theta phase coherence increased as a function of speed (Fig. 6). As theta transitions from a sinusoidal oscillation to a “sawtooth” shape with increasing speed, higher order harmonics are cast in the spectral decomposition (Buzsáki et al. 1983; Sheremet et al. 2016; Terrazas et al. 2005). Notably, phase-power coherence also increased between the harmonics of theta with speed as well as between the phase of the 16-Hz harmonic and the power of gamma. Because 16 Hz is not an independent oscillation from theta but simply an oscillatory deformation, the interaction between theta and gamma encompasses both the 8- and 16-Hz components. Therefore, to quantify the power-phase coherence increase with speed, the average coherence was calculated for theta phase (7–10 Hz)-gamma power and harmonic phase (14–20 Hz)-gamma power. Averaging across the range of frequencies in Fig. 5 provides the bin width to ensure that the change in theta and harmonic frequencies with speed are taken into consideration (Hinman et al. 2011; Terrazas et al. 2005). Comparison of the high-speed bin (>35 cm/s) and low-speed bin (5–15 cm/s) revealed a consistent increase in gamma power and the phase of the theta complex (Fig. 7).

Fig. 6,

Example cross-frequency coherence between oscillatory power and oscillatory phase as a function of velocity for the lacunosum-moleculare. As velocity increases, there are low-frequency interactions between theta and its harmonics (below 40 Hz). Because harmonics by definition are integer, phase-locked components to a fundamental oscillation, and because the deformation of theta from sinusoid to sawtooth increases with velocity (Buzsáki et al. 1983; Sheremet et al. 2016; Terrazas et al. 2005), this effect is to be expected. Interestingly, there is a notable increase in the coupling between theta phase and gamma power, as well as theta harmonic phase and gamma power, with velocity. Our effect is largely in agreement with the observations of Michaels et al. (2018).

Fig. 7.

Average cross-frequency coherence for theta (7–10 Hz) and the 2nd harmonic (14–20 Hz) phase. When the coherence is averaged for these specific phases, there is a considerable change in cross-frequency coherence with velocity. Each panel shows the individual layers of the hippocampus, with yellow as the high-velocity (>35 cm/s) bin and blue as the 5–15 cm/s bin. The lines and shading depict the mean ± SE (n = 5). Note that in the gamma range, greater than ~50 Hz, there is an increase in coherence that is associated with a shift of the maximum value to higher frequencies (see Fig. 3). The changes in the low-value frequencies, <40 Hz, are attributed to the higher order harmonics of theta (e.g., 24 and 32 Hz; see bicoherence analysis in Figs. 8 and 9).

Because the power and phase of theta both exhibited a strong influence on gamma power, which increases in magnitude as a function of speed, it is suggested that the two oscillations are in fact part of a unitary process. Rather than the hippocampal spectra being akin to decomposition of an orchestra, with different frequencies attributable to specific, noninteracting instruments, it appears that there is a direct dependency that is analogous to ocean waves in which waves of different length form a cooperative system in which they sustain each other (e.g., Longuet-Higgins 1992). Stated simply, the LFP of the hippocampus reflects a multiscale phenomenon, driven by a flow of energy from low to high frequencies across the spectrum (Buzsaki 2006). In this energy cascade framework, it would be suggested that theta-gamma interactions are dependent, with the degree of phase-phase interactions directly proportional to energy/activity in the network. However, the analytical approaches of cross-frequency phase-phase coupling have been recently called into question, due to distortions in filtering and not accounting for harmonics (Scheffer-Teixeira and Tort 2016). As described in materials and methods, bicoherence has been used extensively to quantify the degree of cross-frequency phase-phase coupling in the LFP, investigating the relationship between a wide band of frequencies, and can be implemented to directly identify harmonics. Therefore, we investigated the degree of phase coupling within hippocampal layers as a function of speed using bicoherence analyses.

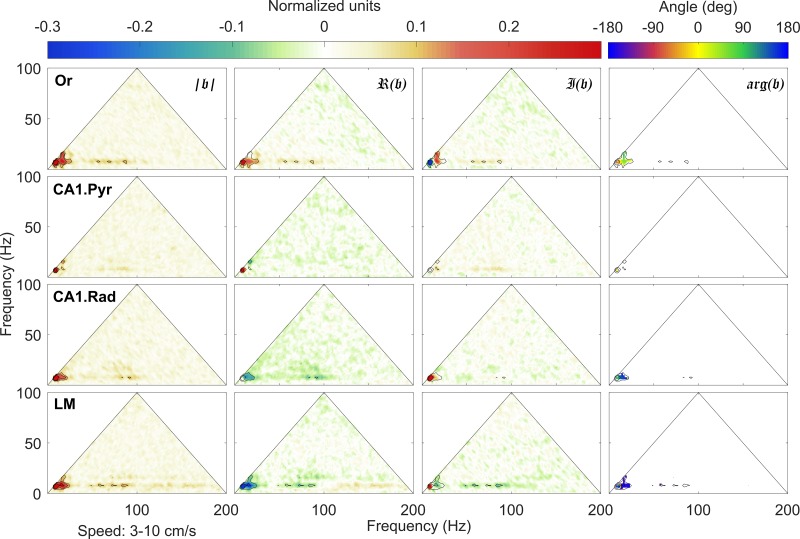
As previously reported, bispectral estimates of theta and the respective harmonics show significant variability with rat running speed, with limited significant interactions at speeds of 3–10 cm/s (Fig. 8). In contrast, at higher running speeds (i.e., >40 cm/s; Fig. 9), the bispectral map shows a rich phase-coupling structure. In agreement with the observations of power spectral density evolution (Fig. 3), strong phase coupling develops between theta (theta frequency f_θ ≈ 8 Hz) and its harmonics (f_θ, with n = 2, 3, 4, …), with peaks detectable at frequencies below ~50 Hz, at various strengths, across all layers. It is worth emphasizing that the development of theta harmonics strongly coupled to theta indicates a nonlinear deformation of the theta rhythm toward positive skewness and asymmetry and should not be attributed to the generation of additional, statistically independent rhythms. Rather, the sawtooth shape of theta causes a 48-Hz frequency to register in the oscillatory decomposition of LFP.

Fig. 8.

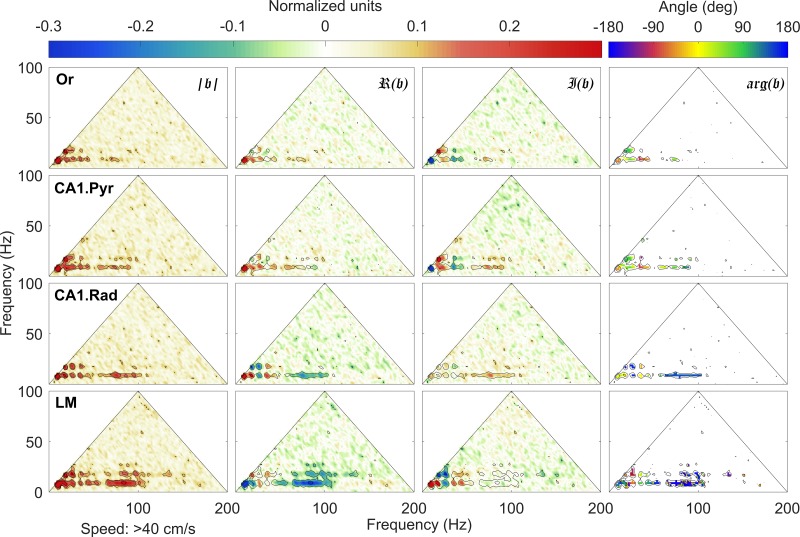
Normalized bispectrum at low speeds (3 cm/s < 𝑣 < 10 cm/s). An in-depth explanation of the bicoherence plot can be found in Sheremet et al. (2016). Briefly, the triangular region represents the area containing nonredundant information for the discrete Fourier transform. Columns (left to right) show the bicoherence |𝔟|, the real ℜ(𝔟) (skewness) and imaginary 𝔍(𝔟) (asymmetry) parts of the normalized bispectrum 𝔟, and the biphase arg(𝔟). The first three can be interpreted as nonlinearity strength and measures of the contribution of different triads to the skewness and asymmetry of the local field potential (LFP), respectively. Peak in the bispectral estimate represents a phase-coupled triplet (f₁, f₂, f₁ + f₂), where f_j, j = 1, 2 are frequency bands in the Fourier representation. The observations in each row correspond to a given hippocampal layer. For each layer, black contours mark the significant bicoherence value of 0.1 (with 300 degrees of freedom, zero-mean bicoherence is <0.1 at 95% confidence level). Or, oriens; CA1.Pyr, pyramidal layer; CA1.Rad, radiatum; LM, lacunosum-moleculare.

Fig. 9.

Normalized bispectrum at high speeds (𝑣 > 35 cm/s). Same organization as in Fig. 8, where columns (left to right) show the bicoherence |𝔟|, the real ℜ(𝔟) (skewness) and imaginary 𝔍(𝔟) (asymmetry) parts of the normalized bispectrum 𝔟, and the biphase arg(𝔟). Note the development of multiple regions of high bicoherence |𝔟|, notably 1) t theta (theta frequency f_θ ≈ 8 Hz) and its harmonics (nf_θ, with n = 2, 3, 4, …), with peaks detectable up to 48 Hz across all layers, and 2) theta and a wide gamma band spanning approximately the interval between 60 and 100 Hz. The lacunosum-moleculare (LM) exhibits the richest nonlinear structures of the 4 layers examined with gamma coupling to the first harmonic of theta. Or, oriens; CA1.Pyr, pyramidal layer; CA1.Rad, radiatum.

Furthermore, the increase of theta power and nonlinearity is accompanied by the development of significant phase coupling between theta and gamma oscillations, related to interaction between rhythms, rather than to nonlinear shape deformation. Theta-gamma coupling covers the entire gamma frequency band (the wide bands located at 50 Hz < f₁ < 100 Hz and f₂ ≈ 8 Hz). The effect is again strongest in the LM, where interacting triads of the form (f_γ, f_θ, f_γ + f_θ) and (f_γ, 2f_θ, f_γ + 2f_θ) are obvious, where f is a frequency in the gamma band. Because the location and magnitude of the bicoherence peaks identify and measure the intensity of cross-phase interactions, the strength of the nonlinear coupling can be quantified by integrating the bicoherence over the region of interest (Fig. 10). In agreement with the results presented in Sheremet et al. (2016), the nonlinearity was significantly greater at faster running speeds [F_(1,16) = 31.09, P = 0.001; repeated measures]. Moreover, nonlinearity also varied significantly as a function of CA1 laminae [F_(3,16) = 11.96, P = 0.001], with the LM being significantly more nonlinear compared with the other three laminae [P < 0.002 for all comparisons, Tukey’s honestly significant difference (HSD)]. The bicoherence values across the Or, CA1.Pyr, and CA1.Rad, however, were not significantly different (P > 0.76 for all comparisons). The difference in nonlinearity between low and high velocities did not significantly interact with layer [F_(3,16) = 0.21, P = 0.89], indicating that the impact of faster speeds on nonlinearity was similar across all CA1 laminae.

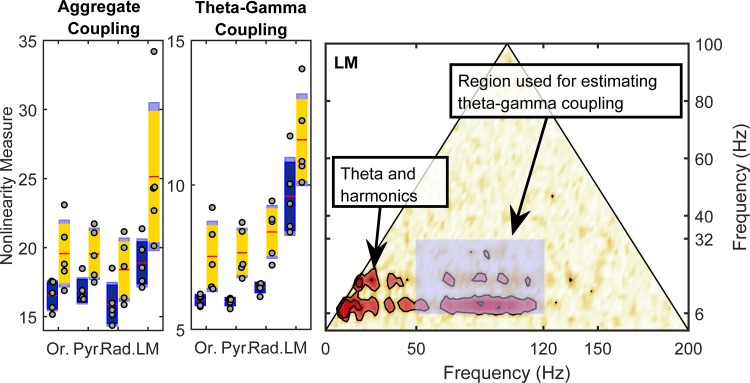
Fig. 10.

Estimate of nonlinear cross-frequency phase coupling. Left: total overall strength of nonlinearity, estimated by summing the bicoherence over its entire definition domain. Estimates are shown for speed bins at 5–15 cm/s (blue) and >35cm/s (yellow). Middle: strength of nonlinear coupling between theta (and harmonics) and gamma rhythms, estimated by summing the bicoherence values in the shaded rectangle of panel at right. The lacunosum-moleculare (LM) exhibits a significantly larger coupling strength compared with the other layers. Both total (aggregate) and strictly theta-gamma coupling strength show significant variability as a function of rat speed and hippocampal layer. Note that the y-axis differs between nonlinearity measures to optimize for display of the theta-gamma-gamma nonlinearity. Red line is the mean, dark blue or yellow is 1.96 of the SE, and light blue denotes the boundaries of 1 SD. Right: region used for estimating the strength of theta-gamma coupling is a rectangle covering the intervals [6 Hz, 32 Hz] for theta and [50 Hz, 120 Hz] for gamma.

When the quantification of nonlinearity was restricted to the theta (6–32 Hz) and gamma (50–120 Hz) frequency ranges (Fig. 7), there was also a strong effect of speed on nonlinearity [F_(1,16) = 38.53, P = 0.0001; repeated measures]. Within the theta and gamma frequency ranges there was also a significant effect of layer on nonlinearity [F_(3,16) = 19.87, P = 0.001] that did not significantly interact with speed [F_(3,16) = 0.48, P = 0.70]. Interestingly, the theta-gamma bicoherence values in the LM were significantly greater than in the other three laminae (P < 0.001 for all comparisons; Tukey’s HSD). The nonlinearity between the Or, CA1.Pyr, and CA1.Rad was not significantly different, however (P > 0.32 for all comparisons; Tukey’s HSD).

DISCUSSION

The current article reports the novel finding of power-power, phase-power, and phase-phase coupling between theta and gamma oscillations that is dependent on speed and varies across the different lamina of CA1. Macroscopically, bouts of input at theta frequency provide the excitation/inhibition to organize synaptic activity rhythmically. Neurons within the entorhinal-hippocampal circuit are tuned to resonate at theta frequencies, evident in the ability of the hippocampus to locally generate theta when provided sufficient input (Bland et al. 1988; Fraser and MacVicar 1991; Kamondi et al. 1998; Kocsis et al. 1999; Konopacki et al. 1987). When the energy into the network increases, the endogenous timing of the local circuits finds a temporally stable interaction, as evidenced by an increase in power in higher frequency bands. For example, the theta-paced drive could conceivably cause basket cells to fire gamma frequency bursts at theta frequency (Bragin et al. 1995; Ylinen et al. 1995b). The consequence of this organization is that neuronal activity of both pyramidal cells and interneurons are organized to both the relatively slow theta oscillation and the faster gamma oscillation (Buzsáki and Chrobak 1995).

Because synaptic drive is the critical parameter that organizes LFP dynamics across the spectrum, it may not be surprising that oscillatory power and theta-gamma interactions differ across CA1 lamina. Although the oriens and radiatum layers receive a larger proportion of excitatory input relative to the LM, the LM exhibits the highest sources and sinks both during perforant pathway stimulation and in relation to theta (Bragin et al. 1995; Buzsaki et al. 1986). The LM also exhibits a larger proportion of perforated synapses, which are associated with plasticity and tend to have a greater density of AMPA receptors. Furthermore, dendrites in the LM have a higher inhibitory-to-excitatory synaptic ratio (Megías et al. 2001), which may give rise to increased oscillatory power. Finally, the LM is the major input from the entorhinal cortex, which theoretically carries some portion of velocity modulated input (Kropff et al. 2015). Given these distinctions between LM and other CA1 lamina, it stands to reason that the LM would have the greatest cross-frequency interaction as a function of running speed. The laminar differences in LFP dynamics observed in the current experiments highlight a critical issue regarding interpreting oscillatory data. Specifically, not functionally defining the specific lamina from which recordings are obtained may obfuscate the detection of neural-behavioral relationships and the ability to quantify cross-frequency interactions. Moreover, a number of studies examining theta and gamma have restricted the recording site to the stratum pyramidale. Although this layer is optimal for recoding spikes, it has relatively fewer excitatory synapses, lower oscillatory power, and a reduced modulation of the LFP spectrum by running velocity. These caveats need to be considered when attempting to extrapolate LFP data obtained from the stratum pyramidale to the entire CA1 network.

Increasing the total amount of activity into a network will have multiple consequences, including more coincident synaptic events (reflected as increases in local field potential power). There is a dramatic increase in firing rates across hippocampal neurons with speed (Hirase et al. 1999; Maurer et al. 2005; McNaughton et al. 1983). Moreover, running speed alters sequence compression of place cell spikes (Maurer et al. 2012). Because the single units change their dynamics and the LFP is generated by membrane events, it stands to reason that there must be associated changes in LFP power and gamma frequency (Ahmed and Mehta 2012; Chen et al. 2011; Kemere et al. 2013; Zheng et al. 2015). It is worth noting that there is a low fraction of observed gamma locking between CA3 or entorhinal LFP and CA1 pyramidal neurons (Schomburg et al. 2014). These observations support the idea that gamma can provide a measure of upstream temporal dynamics but fails to entrain the individual units (Buzsáki and Schomburg 2015). Rather, because the distal dendrites operate as a low-pass filter (Golding et al. 2005), theta-gamma-paced synaptic input in the LM or CA1 radiatum are reverted to just theta at the soma (Vaidya and Johnston 2013). Nevertheless, the LM exhibited the highest theta-gamma coupling as a function of speed, suggesting that theta-modulated gamma inputs are conveyed from the entorhinal cortex (Fernández-Ruiz et al. 2017), which exhibits a high amount of sensitivity to path integration and self-motion (Kropff et al. 2015; Moser and Moser 2008; Sargolini et al. 2006).

The interplay between theta and gamma rhythms as a function of speed is not to suggest that theta is a required prerequisite for gamma. There are two considerations with respect to this point. First, the power spectra density of the LFP demonstrates an ~1/f^α slope, indicating that any frequency has the potential of being isolated. Power will exist across all frequencies, with low frequencies exhibiting the highest amplitude. Therefore, although there may not be a large peak in theta power, there still may be enough activity in the network that leads to local circuit entrainment at gamma frequency. Experimentally, this has been observed in situations in which severing the fimbria fornix or lesioning the entorhinal cortex severely diminished theta power but yielded increases in gamma power (Bragin et al. 1995; Buzsáki et al. 1987). This highlights the second consideration, that it is the characteristics of neurons and the local network that defines the ability to capture the incoming activity. In the absence of entorhinal input, it is tenable that the network undergoes reorganization to compensate for the loss of input. This compensation results in an easier entrainment of local circuits (gamma) that occurs with weak, low-frequency input across the population. Other aspects theoretically modulate the ability of local circuits to capture the global input including age-related synaptic changes and pharmacological manipulation.

The current article links prior findings of theta-gamma interaction in the service of cognition (e.g., Jensen and Colgin 2007; Lisman and Jensen 2013; Montgomery et al. 2008; Tort et al. 2008, 2009) to other studies that have observed layer-dependent theta-gamma effects during exploration (Belluscio et al. 2012; Lasztóczi and Klausberger 2016; or use of data sets with and without a mnemonic requirement Schomburg et al. 2014). The current data, however, point to a new perspective. In partial agreement with the idea that gamma and theta couple only under certain mnemonic conditions, we propose that coupling is enhanced in situations in which there is increased input into the network. These instances of increased energy to the network would encompass faster running speeds or instances of high mnemonic load. Broadly, afferent input into the hippocampus allows the network to move further away from equilibrium with the dynamic interaction between smaller groups of neurons self-organizing their activity as local “pacemakers” (for examples in which energy into the system is a parameter in governing spatiotemporal organization, see Bertram et al. 2002; Cross and Hohenberg 1993; Gutierrez et al. 2013; Halatek et al. 2018; Halatek and Frey 2018; James et al. 2018). Specifically, theta and gamma are interdependent, coupled by the cascade of energy across spatial and temporal (frequency) scales (Buzsaki, 2006); this energy may come in the form of self-motion or speed information, or as the consequence of higher cognitive processes.

This perspective, however, runs counter to the recent theory of oscillatory multiplexing in the brain, where individual frequencies carry different components of information (e.g., Akam and Kullmann 2014; McLelland and VanRullen 2016). For example, it has been suggested that communication across brain regions may occur in a frequency-specific manner and that aspects of cognition can be determined through calculation of cross-regional coherence, with different bands conveying different psychological components (Knight and Eichenbaum 2013; Siegel et al. 2012; Watrous et al. 2013). In this model, a neuronal population would theoretically have heterogeneity in terms of its preferred burst frequency. Should rhythmic bursting at one specific frequency emerge within a brain region, presumably it would organize the spike firing times of multiple, distant cell assemblies at the same frequency (Canolty et al. 2010).

However, this communication through oscillatory entrainment may be an oversimplification. For example, the dendrites of hippocampal pyramidal neurons operate as a low-pass filter, with gamma-paced inputs being reverted to a depolarization that resembles theta near the soma (Golding et al. 2005; Vaidya and Johnston 2013). The direct consequence of this is that gamma frequency activity within the LM (the afferent input layer of the entorhinal cortex) has little consequence on the gamma frequency activity within the pyramidal layer. This is evident in the relatively low coherence between gamma frequencies between the medial entorhinal cortex and pyramidal layer compared with theta between the same two regions (~0.3 and ~0.85, respectively, Colgin et al. 2009). Therefore, rather than operate as a mechanism of entrainment, external inputs organizing their activity at gamma frequency may instead provide the necessary input to coordinate the phase of theta within a network (Lopez-Madrona et al. 2018). Tersely, entorhinal input at gamma frequency most likely supports theta-paced dynamics. This interpretation favors the cascade hypothesis in which energy into the network is responsible for theta-gamma interactions.

There are few major derivations that come with the energy cascade theory, but perhaps the most outstanding relative to the contemporary literature and the multiplexing theory of neural communication is that, in the energy cascade model, it is improvident to assign a particular psychological process to a specific frequency. Nonlinear dynamics and iterative processing in the nervous system (e.g., Buzsaki 2006) make it implausible to assign a cause and effect relationship between a cognitive process and a narrow oscillatory band. Instead, the gamma rhythm is organized spatiotemporally by the larger, theta-paced afferent input, making the two oscillations inherently entangled in the awake behaving animal. As such, cognition occurs across multiple frequency bands simultaneously with organization occurring as a function of the amount of energy iteratively propagated through the brain (for a broad synthesis, see Nadel and Maurer 2018). This suggests that the LFP, rather than being indicative of psychological processes, is diagnostic of the underlying interactions, providing information to the experimenter with respect to how the network is predisposed to organize. This point is emphasized by the fact that synaptic events, contributing the ionic flux that shapes the LFP, have no knowledge with respect to whether they are supporting “gamma” or “theta.” Parsing oscillatory frequencies to specific biophysical mechanisms, circuits, or behavioral correlations for the purposes of higher cognition loses relevance if the nervous system does not make the distinction (unless it is implemented for the purposed of diagnostics).

The next major derivation of the energy cascade hypothesis is that it can offer insight into the shape of the power spectral density. As an example, although assigning certain frequency oscillations may be gratifying to the experimentalist, Fourier decomposition is an analytical tool, far removed from synaptic or circuit dynamics. Nevertheless, it is often tempting to construct a power spectrum and ask a question regarding deviations away from the 1/f^α slope (e.g., after whitening). In the current article, we demonstrate that the spectral slope α is not constant throughout the entire frequency range, revealing a methodological flaw to standard whitening techniques. Moreover, our spectral decomposition revealed harmonics of theta at 16, 24, 32, 40 Hz and higher (Sheremet et al. 2016). Although the decomposition “uncovers” these oscillations, the harmonics are the consequence of a single aggregate process in which theta changes from a sinusoid into a sawtooth with high asymmetry and skewness. Furthermore, there is an associated loss of power between ~1 and 6 Hz as running speed increases (Fig. 3). Interestingly, the loss of lower frequency power along with the development of the harmonics suggests that as the amount of input increases, the initial effect will not necessarily be the entrainment of local circuits at gamma frequency but increasing the network activity in the theta band. This hypothesis is supported by the observation of inhibition-dependent theta resonance (Stark et al. 2013). When there is little to no input, interneurons that resonant at theta frequency will express incoherent entrainment between 1 and 6 Hz. As input increases, these neuron begin to resonate, with power redistributing into theta. Finally, as hippocampal activity increases with speed, the oscillatory energy begins to extend beyond the theta resonance and begins to entrain local circuits at gamma frequency. As energy cascades down from theta, into the gamma range, the power spectra in the range of 50–120 Hz develops a “front” that moves to the right at increasing running speeds. This front is indicative of an increase in both frequency and power, maintaining congruence with the idea that hippocampal neurons must increase their interactions at higher running speeds (Geisler et al. 2007; Maurer et al. 2012).

This theory of energy cascade is not novel. In fact, it shares similarity with the concepts of self-organized criticality (Bak et al. 1987). Self-organized criticality was broadly used to describe any system in which there is an inverse correlation between oscillatory power and oscillatory frequency. This concept later found an analogous home in neuroscience, describing both the shape of the power spectra as well as neuronal avalanches (Beggs and Plenz 2003; Beggs and Timme 2012; Plenz and Thiagarajan 2007). With these insights, it is possible to consider the mechanisms by which the brain gives rise to cognition by relating activity through neural circuits.

GRANTS

This work was supported by the McKnight Brain Research Foundation, National Institute of Mental Health (NIHM) Grant R01MH109548, and a Diversity Supplement to NIHM Grant R01MH109548 (to J. P. Kennedy).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.P.K. and S.D.L. performed experiments; A.S., J.P.K., Y.Q., Y.Z., and A.P.M. analyzed data; A.S., Y.Z., S.N.B., and A.P.M. interpreted results of experiments; A.S., Y.Z., and A.P.M. prepared figures; A.S. and A.P.M. drafted manuscript; A.S., Y.Z., S.N.B., and A.P.M. edited and revised manuscript; A.S., J.P.K., Y.Q., Y.Z., S.D.L., S.N.B., and A.P.M. approved final version of manuscript.