Nonlinear dynamics underlying sensory processing dysfunction in schizophrenia

Significance

One of the fundamental challenges of neuroscience is to understand the seamless orchestration of many interconnected brain regions, which is needed to produce the integrated experience of cognition. This paper describes a method based on dynamical systems theory to identify important nonlinear features underlying brain signals. We show that this method can indeed detect unique dynamical states underlying normal and altered auditory information processing in large cohorts of healthy subjects and schizophrenia patients. These dynamical states correspond to network changes preceding well-known auditory–neurophysiological responses. Results indicate that brain signals can be analyzed using a rather unconventional method to extract important large-scale dynamical information that is not apparent from conventional methods commonly used in the study of neuropsychiatric disorders.

Abstract

Natural systems, including the brain, often seem chaotic, since they are typically driven by complex nonlinear dynamical processes. Disruption in the fluid coordination of multiple brain regions contributes to impairments in information processing and the constellation of symptoms observed in neuropsychiatric disorders. Schizophrenia (SZ), one of the most debilitating mental illnesses, is thought to arise, in part, from such a network dysfunction, leading to impaired auditory information processing as well as cognitive and psychosocial deficits. Current approaches to neurophysiologic biomarker analyses predominantly rely on linear methods and may, therefore, fail to capture the wealth of information contained in whole EEG signals, including nonlinear dynamics. In this study, delay differential analysis (DDA), a nonlinear method based on embedding theory from theoretical physics, was applied to EEG recordings from 877 SZ patients and 753 nonpsychiatric comparison subjects (NCSs) who underwent mismatch negativity (MMN) testing via their participation in the Consortium on the Genetics of Schizophrenia (COGS-2) study. DDA revealed significant nonlinear dynamical architecture related to auditory information processing in both groups. Importantly, significant DDA changes preceded those observed with traditional linear methods. Marked abnormalities in both linear and nonlinear features were detected in SZ patients. These results illustrate the benefits of nonlinear analysis of brain signals and underscore the need for future studies to investigate the relationship between DDA features and pathophysiology of information processing.

In neuropsychiatric disorders, subtle abnormalities in low-level processes contribute to the complex constellation of symptoms. Schizophrenia (SZ) is among the most intractable and disabling illnesses, with impairments in multiple domains of cognitive and psychosocial functioning (1). In this study, a nonlinear analysis technique for characterizing large-scale systems from a theoretical physics perspective was applied to leading candidate biomarkers in healthy nonpsychiatric subjects and SZ patients.

Among many domains of clinically relevant dysfunctions, altered early auditory information processing (EAIP), as measured by event-related potentials (ERPs), is a fundamental feature of SZ (2, 3). Mismatch negativity (MMN) is an ERP biomarker of EAIP with promise for improving our understanding and treatment of SZ. MMN has been shown to reliably correlate with cognition and psychosocial functioning (1, 4). MMN can be used for predicting the development of psychosis among individuals at high clinical risk and is sensitive to interventions that target cognition (5, 6). MMN is automatically elicited via a passive auditory oddball paradigm in response to infrequent deviant sounds randomly interspersed in a sequence of frequently presented standard sounds. MMN is followed by a positive component also reflective of EAIP that peaks at 250–300 ms called P3a. Although less studied, the P3a is followed by a negative wave called the reorienting negativity (RON) (7). This MMN–P3a–RON response has been referred to as the auditory deviance response (ADR) complex (8). Many studies have found significant ADR component reductions in SZ that correlate with impairments across multiple domains of higher-order cognitive and psychosocial functioning (9, 10). Recently, Thomas et al. (1) proposed and validated a hierarchical information processing cascade model, where impairments in these early auditory sensory processing measures propagate and substantially contribute to deficits in cognition, clinical symptoms, and real-world functional disability in SZ. Thus, small changes in early auditory processing measures contribute to deficits in higher-order functions and macroscopic manifestations of SZ.

The vast majority of ERP studies in neuropsychiatry have used linear analysis of EEG signals. These linear methods include ERP peaks and latencies (11, 12), frequency (13) or time frequency analyses (14, 15), and cross-frequency coupling (16, 17). Such conventional linear methods, while highly informative, focus on a priori determined time-locked events or frequency ranges (i.e., delta, theta, gamma bands) and therefore, fail to capture important underlying nonlinear system dynamics. Thus, characterizing general dynamical components of broadband data without such restrictions may reveal information about altered systems-level states associated with SZ.

To characterize the large-scale, neural system-level dynamics present in brain electrical activity in patients with SZ, computational models based on nonlinear dynamics and systems theory recently emerged as a promising tool in neuroscience (18, 19). In contrast to our prevailing focus on microscale neuronal activity, methods that characterize large-scale, system-level dynamics may help us understand emergent phenomena of behavior and cognition (18, 20). This perspective also underlies past work linking nonlinear analysis of the EEG to the “disconnection hypothesis” of SZ (21, 22). Breakspear and Terry (23) used a technique for estimating the nonlinear dynamical interdependence of several EEG channels across and within both hemispheres and found significant differences in the topography of dynamical interdependence across the scalp between SZ patients and matched healthy comparison subjects (24). Here, we apply a distinct but related technique to probe the nonlinear dynamics of a single EEG channel, which allows us to investigate the nonlinear properties of a broader range of data. Delay differential analysis (DDA) is designed to capture large-scale dynamics present in nonlinear time series signals (25–28). DDA operates in the time domain and maps unprocessed data onto a functional embedding basis. Embeddings are used in nonlinear dynamics to reveal invariant dynamical properties underlying a more extensive, largely unknown dynamical system (i.e., the brain) when only a single time series (e.g., EEG data) is available. Previous studies have shown that DDA can be used to extract disease-specific dynamical features: Parkinson’s movement data (29, 30), ECG recordings (27, 31), sleep EEG (26), classification of Parkinson’s disease EEG data (32, 33), and electrocorticography data for epileptic seizure characterization (34).

In this study, DDA was applied to the unprocessed EEG recordings from SZ patients and nonpsychiatric comparison subjects (NCSs) who participated in the Consortium on the Genetics of Schizophrenia (COGS-2), a multicenter case-control study of SZ and related endophenotypes (10). In contrast to our prior focus on linear ERP features (MMN and P3a amplitudes) (1, 10), this study aimed to determine (i) whether nonlinear dynamics can be detected in raw EEG recordings and if so, (ii) if they can be used to differentiate SZ patients from NCSs; by mapping the trial information onto the DDA feature space, we also aimed to determine (iii) whether the MMN, P3a, and RON responses reflect nonlinear processes even after controlling for SZ–NCS amplitude differences, which would provide an important perspective on EAIP deficits in SZ. Such information may be important for guiding future studies of the genomic and neural substrates of SZ and may provide targets for treatment developments.

DDA

We developed and applied a signal processing technique, DDA, based on embedding theory in nonlinear dynamics. DDA combines two types of embeddings via a delay differential equation: delay embedding and derivative embedding. The general nonlinear DDA model can be formulated as

$$\dot{x}=\sum _{i=1}^I{a}_i\prod _{n=1}^N{x}_{{\tau }_n}^{m_{n,i}},$$ [1]

where ${\tau }_n$, $m_{n,i}\in {\mathbb{N}}_0$ with $x=x\left(t\right)$, $x_{{\tau }_n}=x\left(t-{\tau }_n\right)$, relating the signal derivative $\dot{x}\left(t\right)$ to delayed versions of the signal. Most of the terms in this template are set to zero depending on the data type. The following DDA model has been shown to capture important dynamical information from EEG signals (26, 33–35):

$$\dot{x}=a_1{x}_1+a_2{x}_2+a_3{x}_1^2.$$ [2]

This model was chosen through a structure selection procedure, repeated random subsampling cross-validation (36) (SI Appendix), using separate EEG and intracranial EEG datasets (26, 33–35). The coefficients $a_{\mathrm{1,2,3}}$ were used as features to distinguish dynamical differences in time series data. Together with these coefficients, the least squares error $\rho$ was also considered. Therefore, the full DDA feature set was composed of $\left\{a_1,a_2,a_3,\rho \right\}$. These previous studies have shown that the four DDA parameters of Eq. 2 reflect both linear and nonlinear features underlying nonlinear signals (25). Since previous results converged on $a_3$ as most informative (25), this parameter was carried forward for detailed characterization in this dataset.

Results

ADR Complex.

Consistent with established methods (10), individual subject deviant minus standard waveform averages derived from the preprocessed ERP signals showed significantly reduced MMN and P3a positivity components for the SZ patients (Fig. 1A, Upper). The group-averaged signals (Fig. 1A, Lower) also revealed significantly diminished ADR complex composed of MMN, P3a positivity, and RON for the SZ group.

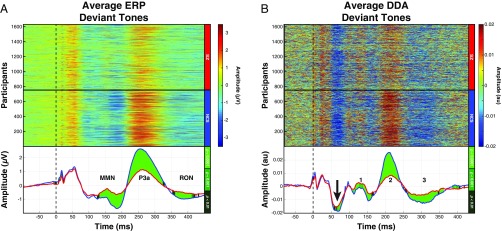
Fig. 1.

DDA identified dynamical state changes preceding each of the ADR complex components. (A) NCSs demonstrated robust MMN, P3a, and RON components as shown in the heat map of the individual subject difference (deviant tone ERP − standard tone ERP) average signals (Upper). All three components of the ADR (MMN, P3a, and RON) can be appreciated in the group-level average signals (Lower). (B) DDA $a_3$ coefficient values averaged within each subject revealed significantly decreased $a_3$ in the SZ patients (Upper). As with the ERP results, the DDA group averages displayed three components with homologous waveform morphology and severity of deficits in SZ, but the DDA components (numbered 1–3 in Lower) preceded their corresponding ERP peaks identified in A by 71, 54, and 82 ms, respectively. The shaded regions in the group average signals represent group differences that are statistically significant after adjusting for multiple comparisons (false discovery rate). Cohen’s d, t values, and degrees of freedom are shown in SI Appendix, Fig. S9.

Performing the DDA on the difference waveforms and computing individual subject $a_3$ averages showed significantly lower $a_3$ values across the SZ patients in the 180- to 240-ms time window (Fig. 1B, Upper) (mean t value = 10.8, mean Cohen’s d = 0.55). The group-averaged $a_3$ signals revealed three distinct areas corresponding to the ADR components (numbered areas in Fig. 1B, Lower). Interestingly, the timing of the three DDA peaks occurred before their corresponding ADR components identified in the group-averaged ERP signals. For instance, the peak group difference in area 1 in Fig. 1B occurred 70 ms before the peak group difference in the ERP MMN window in Fig. 1A. This suggests that DDA reflects dynamical state changes (as estimated by the amplitude changes in $a_3$) occurring immediately before each of the ERP ADR components. Thus, DDA not only captures the group differences but also, identifies the underlying dynamical state changes that contribute to the linear ERP changes of the ADR complex components.

Responses to Constituent Deviant and Standard Tones.

To determine whether findings in the deviant minus standard difference waves were driven by effects to constituent tones, responses to deviant and standard tones were also examined separately. Consistent with the results presented above, similar waveform morphology and magnitude of SZ impairment were observed in both ERP and DDA results. Also consistent with the previous section, peaks observed with DDA, including those related to SZ deficits, occurred earlier than those observed in the ERP analysis.

Responses to deviant tones.

Averaging the ERP signals corresponding to only deviant tones revealed three ERP components (Fig. 2A) that were reduced for the SZ group, consistent with other studies (10). DDA identified dynamical changes unique to each group occurring before each of the ERP components (Fig. 2B). In addition, the dynamical states of the NCS group were significantly different from those of the SZ patients during the 50- to 100-ms time window (black arrow in Fig. 2B) (mean t value = −2.6, mean Cohen’s d = −0.13). Notably, this window corresponds to the earliest time window during which a stimulus can be identified as deviant, since the deviant auditory tones were 100 ms in duration (vs. 50 ms for the standard tones). No such difference was observed in the grand average ERP signals (Fig. 2A).

Fig. 2.

ADR components were evident from both ERP analysis and DDA of waveforms elicited by deviant auditory tones. (A) Individual subject average signals from deviant tones revealed pronounced MMN and P3a components in the NCSs (Upper). The grand average signals from the two groups showed significantly different ADR component signals (Lower). (B) DDA $a_3$ amplitude changes were observed before each of the ADR components (numbered 1–3 in Lower). Furthermore, statistically significant differences in $a_3$ amplitude between groups were detected during the earliest time window (50–100 which ms) in an auditory tone could be processed as deviant (black arrow; mean t value = −2.6, mean Cohen’s d = −0.13).

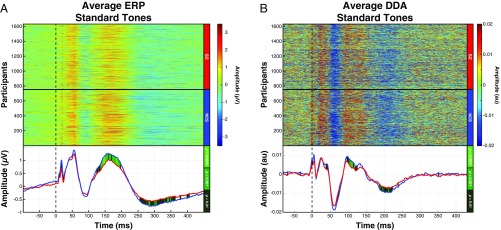
Responses to standard tones.

Unlike the robust group differences observed in the ERP responses to the deviant tones, the group differences in the standard tone ERP responses were much more modest as shown in Fig. 3A. DDA identified a similar group difference occurring between 90 and 130 ms (Fig. 3B). Consistent with ERP analysis of the standard tones, no significant dynamical changes were detected in the 50- to 100-ms time window.

Fig. 3.

DDA of standard tones detected significant dynamical state alterations preceding the P150 window. (A) ERP signals corresponding to the standard tones revealed a reduced P150 component in the SZ grand average signal (Lower). (B) Dynamic changes preceding the P150 ERP changes were observed in the 90- to 130-ms window (Lower; mean t value = 3.3, mean Cohen’s d = 0.17). The $a_3$ changes were reduced for the SZ group during this time window.

Discussion

In this study, DDA, a technique based on dynamical systems theory, was used to determine whether nonlinear features significantly contribute to leading neurophysiologic biomarker candidates of EAIP. The concept that nonlinear, chaos theory-based perturbations occur early in information processing in SZ patients has been hypothesized for some time (36). In this context, these early dynamical state changes precede commonly studied ERP features in both groups. SZ-related impairments in DDA metrics may contribute to impairments in higher-order neurocognitive and psychosocial functioning. A challenge has been with the identification and quantification of these early nonlinear abnormalities in the information processing cascade of function (1). DDA may provide a solution to this longstanding challenge.

DDA was used on large cohorts of 877 SZ patients and 753 NCSs using a well-validated paradigm from the COGS-2 multicenter study. DDA revealed nonlinear dynamical state changes, which preceded well-established ADR components of the ERP.

Importantly, the dynamical information extracted from EEG may also provide additional information about the underlying nature of the MMN, P3a, and RON components of the ADR. Interestingly, nonlinear features are evident nearly instantaneously in response to standard and deviant auditory stimulus onset as well as in the deviant minus standard comparison that is commonly used for measuring the ADR components. DDA detected nonlinear activity $>50$ ms before conventional ERP peaks. Since this early DDA effect does not seem to be an artifact of the analysis method, questions remain as to the functional significance of these early nonlinear effects. It is possible that the nonlinear features captured via DDA provide a more proximal and direct readout of the neurophysiological substrate of ERP measures and the earliest detectable changes in the brain representing deviance detection.

DDA utilizes embeddings to reveal the underlying dynamical patterns of brain activity in the feature space. These patterns, which are otherwise not observable in the EEG using conventional linear ERP methods, are sensitive to even small perturbations in brain network dynamics—including those on a small regional scale. The extracted features also provide a natural measure of the magnitude of dynamical changes, which may correspond to the severity of dysfunction in neuropsychiatric illness. In addition to revealing important information about nonlinear dynamics hidden in the EEG signals, DDA offers a number of important technical advantages over commonly used ERP measures: it is computationally fast, provides fine temporal resolution (10-ms data windows), and requires only minimal preprocessing (i.e., demeaning of the data) to avoid discarding meaningful contextual information. Since time-consuming preprocessing steps (e.g., blink correction and filtering) are not required for DDA, even very large datasets can be analyzed in minutes rather than days, weeks, or even months.

Although DDA has great promise, several caveats should be noted. As a measure, DDA findings do not neatly map onto the vast existing literature, which has nearly exclusively relied on linear methods; DDA findings, therefore, may be challenging to interpret. Likewise, the DDA methods have not undergone the same degree of validation for use in clinical studies (e.g., reliability, suitability for use as a repeated measure, sensitivity to therapeutic interventions). As with the original papers describing the underlying data used in this report, another caveat is that medications in the SZ patients were not experimentally controlled. It is possible that some of the observed deficits in the DDA features of the SZ patients could be attributable to differences in their medication status. Likewise, other clinical factors could also influence DDA findings. It is noteworthy that the large COGS-2 dataset allows for additional tests to verify that the observed SZ-related effects are not driven by group differences in age or sex (SI Appendix, Figs. S10 and S11). Future studies are required to disentangle medication effects and interacting clinical variables from the current DDA findings in SZ (1, 10). However, if DDA is sensitive to medication or clinical changes, this rapid approach may be useful for biomarker-guided clinical trial approaches.

Despite the caveats of this study, these results represent a clear and powerful demonstration of the potential benefits of using nonlinear techniques to study important nonlinear aspects of natural phenomena, including neural function. By applying DDA to this large, rich dataset, we were able to obtain linear and nonlinear features related to auditory information processing in healthy subjects and corresponding deficits observed in SZ patients. Elucidating the links among DDA features and brain network dynamics can lead to a better understanding of pathophysiology of cognitive impairment in SZ and neuropsychiatric disorders as well as contribute to biomarker-guided strategies to accelerate the development of treatments for CNS disorders.

Materials and Methods

The COGS-2 Data Collection.

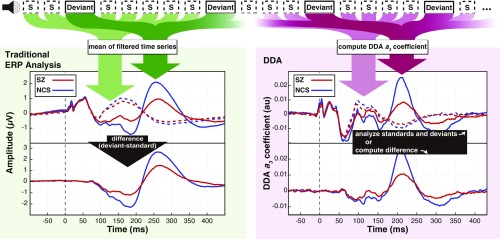
Data were collected at five centers across the United States: the University of California, San Diego; the University of California, Los Angeles; the University of Washington; the University of Pennsylvania; and Mount Sinai School of Medicine. Written consent was obtained from all of the participants, and the study was approved by the local human research protection committees at each site. Samples from a total of 1,630 COGS-2 subjects were analyzed: 877 SZ patients and 753 NCSs. Trains of auditory stimuli presented to each subject consisted of 50-ms standard tones (90% of stimuli) and 100-ms deviant tones (10% of stimuli) as shown in Fig. 4. There were a minimum of 1 standard tone and a maximum of 18 standard tones between deviants. EEG recordings were conducted at a sampling rate of 1 kHz from a single electrode at the CZ (central zero) position.

Fig. 4.

Subjects in both SZ and NCS groups were presented with auditory stimuli consisting of 50-ms standard tones with randomly interspersed 100-ms deviant tones. Data were analyzed according to a traditional ERP paradigm (Left) and using DDA to assess nonlinear dynamics (Right). In the standard ERP approach, EEG time series from standard (dashed lines) and deviant trials (solid lines) were averaged after preprocessing, and the difference waveform was computed from these averages. With DDA, a three-term delay differential equation was applied to the data, and the nonlinear coefficient $a_3$ was computed for both standard and deviant trials. Both ERP difference waveforms and the DDA $a_3$ coefficient time courses are aligned to tone onset, which is marked with vertical dashed lines at 0 ms.

ERP Analysis.

The COGS-2 data for each subject were segmented into trials with duration of 550 ms. Each trial contained 100-ms pretone and 450-ms posttone ERP signals. Trials corresponding to deviant tones ($n$ = 150) and standard tones ($n$ = 150) were extracted from each subject. Eye movement artifact was removed using a second-order blind identification algorithm, and trials containing residual artifact (signal activity >$\pm$50 $\mathrm{\mu }$V) were discarded. Finally, the average standard tone responses were subtracted from the average deviant tone responses.

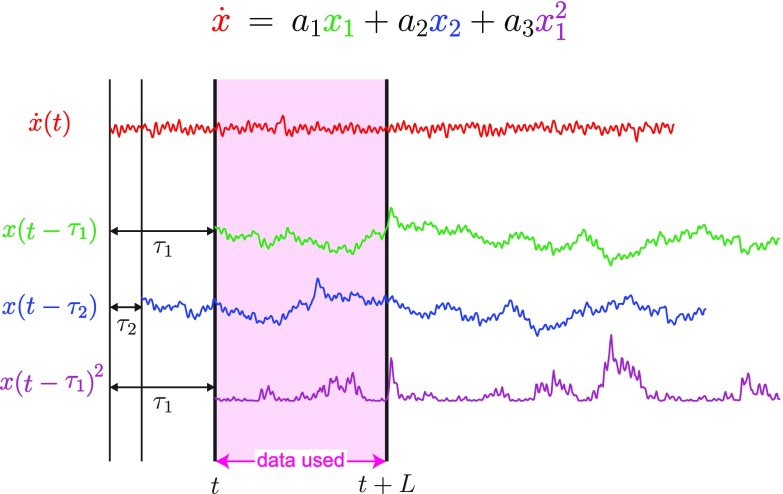
DDA of EEG Data.

DDA features are usually estimated from a data window of length $L$ as shown in Fig. 5. The data for each such window are normalized to zero mean and unit variance to remove amplitude information. Sliding overlapping windows are then applied to the data. For the COGS-2 data, windows of 10 ms were used, and the corresponding points are plotted at the beginning of each time window for all of the figures. Fig. 5 shows the single-trial version of DDA. The feature set $\left\{a_{\mathrm{1,2,3}},\rho \right\}$ is estimated from each trial, and then, the mean over several trials is taken as the nonlinear counterpart to traditional ERP, where the mean of the data (after preprocessing) is used. The difference is that, for DDA, the raw data are processed for each data window separately. To improve the performance and to reduce the number of trials needed, cross-trial DDA was used (SI Appendix, Fig. S3). Using the ergodic hypothesis (37), data windows of multiple trials were combined, and features were computed across trials. The DDA coefficients were estimated simultaneously from 150 trial windows (SI Appendix, Figs. S1–S11). Supervised structure selection was used to identify the delays that led to optimal group classification ($A\prime$) (32). Note that these delays have no frequency correspondence due to the nonlinear nature of the DDA model (25). Results from $a_3$, the most salient feature, are presented. As a measure of classification performance, the area $A\prime$ under the receiver operating characteristic was used (38). An unpaired Student’s t test was used to assess the significance of differences between the SZ and NCS groups as observed in both traditional trial mean difference waveforms and the DDA $a_3$ coefficient. The false discovery rate was adjusted using the Benjamini–Hochberg procedure. The optimal delays for the COGS-2 dataset were $\mathbf{\tau }=\left(\mathrm{3,8}\right)\hspace{0.17em}\text{time points}$, corresponding to (3, 8) ms.

Fig. 5.

Estimation of the features $a_{\mathrm{1,2,3}}$ for a data window of length $L$ for Eq. 2.