Significance
The integration of visual information over space is critical to human pattern vision. For either luminance detection or object recognition, the position of the target in the visual field governs the size of a window within which visual information is integrated. Here we analyze the relationship between the topographic distribution of ganglion cell density and the nonuniform spatial integration across the visual field. We find that the variation in the retinal ganglion cell (RGC) density across the human retina is closely matched to the variation in the extent of spatial integration. Our study suggests that a fixed number of RGCs subserves spatial integration of visual input, independent of the visual-field location.
Keywords: retinal ganglion cell density, spatial integration, Ricco’s area, crowding zone, Bouma’s law
Abstract
The ability to integrate visual information over space is a fundamental component of human pattern vision. Regardless of whether it is for detecting luminance contrast or for recognizing objects in a cluttered scene, the position of the target in the visual field governs the size of a window within which visual information is integrated. Here we analyze the relationship between the topographic distribution of ganglion cell density and the nonuniform spatial integration across the visual field. The extent of spatial integration for luminance detection (Ricco’s area) and object recognition (crowding zone) are measured at various target locations. The number of retinal ganglion cells (RGCs) underlying Ricco’s area or crowding zone is estimated by computing the product of Ricco’s area (or crowding zone) and RGC density for a given target location. We find a quantitative agreement between the behavioral data and the RGC density: The variation in the sampling density of RGCs across the human retina is closely matched to the variation in the extent of spatial integration required for either luminance detection or object recognition. Our empirical data combined with the simulation results of computational models suggest that a fixed number of RGCs subserves spatial integration of visual input, independent of the visual-field location.
The integration of visual information over space is a critical step in human pattern recognition. While the exact mechanism underlying the integration process remains elusive, the key property of the integration process—the extent over which spatial integration occurs—has been well characterized. For instance, the extent of spatial integration in luminance detection has been well described by Ricco’s area (1). Ricco’s area represents the extent of “complete spatial summation” under which the reciprocal relationship between detection threshold and stimulus area remains constant (i.e., Ricco’s law) (1). On the other hand, for object recognition, the extent of spatial integration is often described by critical spacing (i.e., the minimum distance between target and nearby items that yields reliable target recognition). Due to a perceptual phenomenon called “crowding,” objects that are easily identifiable on their own become unrecognizable when presented close together (2, 3). Interestingly, the extent of spatial integration, either Ricco’s area or crowding zone, depends on the position of the target in the visual field, such as eccentricity or quadrant. Ricco’s area (4, 5) and crowding zone both grow with eccentricity (3, 6, 7) and exhibit visual-field asymmetry (8–11): On average, there is a noticeably larger integration zone in the upper visual field compared with the others. As feature segmentation and integration are core processes of human pattern recognition, it is undoubtedly important to understand what determines the extent of spatial integration. Differing accounts have been offered to explain different types of spatial integration zones (e.g., Ricco’s area vs. crowding zone) and different characteristics of visual-field dependency (e.g., eccentricity vs. quadrant). For example, Ricco’s area has been predominantly explained by relatively low-level mechanisms such as spatial pooling of retinal ganglion cells (RGCs) (4, 12) and/or V1 cortical neurons (13). On the other hand, crowding zone has been explained by relatively higher-level mechanisms, including cortical (14–17), attentional (11, 18), and perceptual (19) constraints. While we acknowledge significant contributions made by these aforementioned accounts, we set out to examine the role of RGCs in spatial integration as the front-end sensory mechanism.
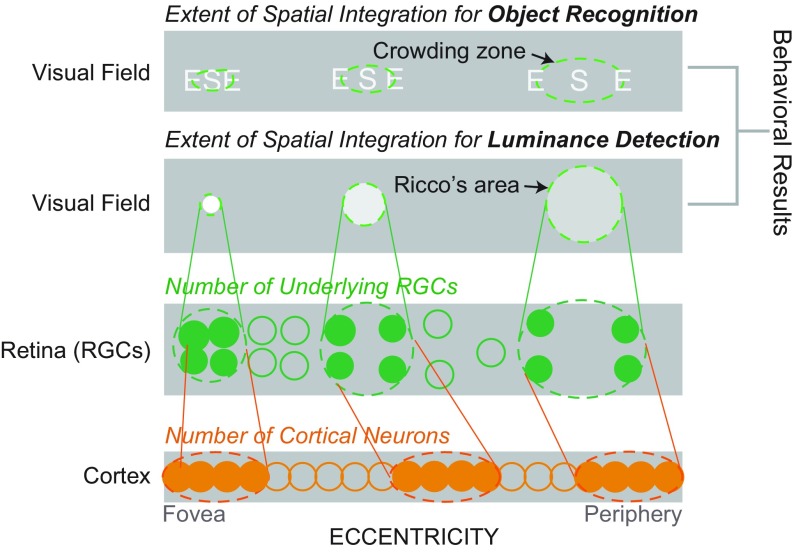
The RGCs are the output neurons of the retina and the first stage where visual sensory information is encoded as spikes (20). Furthermore, as illustrated in Fig. 1, to a large extent (although not completely) the topographic distribution of the RGC mosaic accounts for cortical representation of the visual field, the known cortical magnification (21–24) (premise 1). On the other hand, the variation of the spatial extent of crowding across the visual field has been attributed to the cortical magnification factor in V1 (i.e., a fixed cortical distance of 6 mm) (14, 25) (premise 2). Putting these two premises together allows us to infer that the sampling density of RGCs, which underpins said magnification, may set a limit on the extent of spatial integration. Thus, here we investigate whether some of the properties of spatial integration may be inherited from the sampling array of RGCs. We test this idea with a working hypothesis that if the variation in the extent of spatial integration across the visual field would represent the variation in the RGC density across the human retina, we are likely to see a fixed number of RGCs being involved in the process of visual detection or recognition (Fig. 1). Using a quantitative approach, we examine to what extent (if any) the RGC density would account for the variation in the extent of spatial integration of both human luminance detection and object recognition. Note that throughout the paper the phrases “is accounted for by,” “is explained by,” or “contribute to” are used in a purely statistical sense by which the variance of one variable is explained by another variable while other factors are held constant; this does not necessarily suggest any causal relationship between the two variables as the current study is correlational by nature.
Fig. 1.
Schematic diagram of linking the RGC density to psychophysically defined areas of spatial integration. The extent of spatial integration for visual recognition increases with retinal eccentricity. Like acuity thresholds (52), this eccentricity-dependent increase in the extent of spatial integration has been explained by cortical magnification (i.e., millimeter of cortex per degree of visual field decreases as a function of eccentricity) (14, 33). However, the topographic distribution of the RGC density to a large extent may govern cortical representation of the visual field as cortical projections of RGCs become uniformly distributed throughout the early visual cortical area V1 (99). Here we relate the variation in the RGC density directly to the variation in the extent of spatial integration across the visual field.
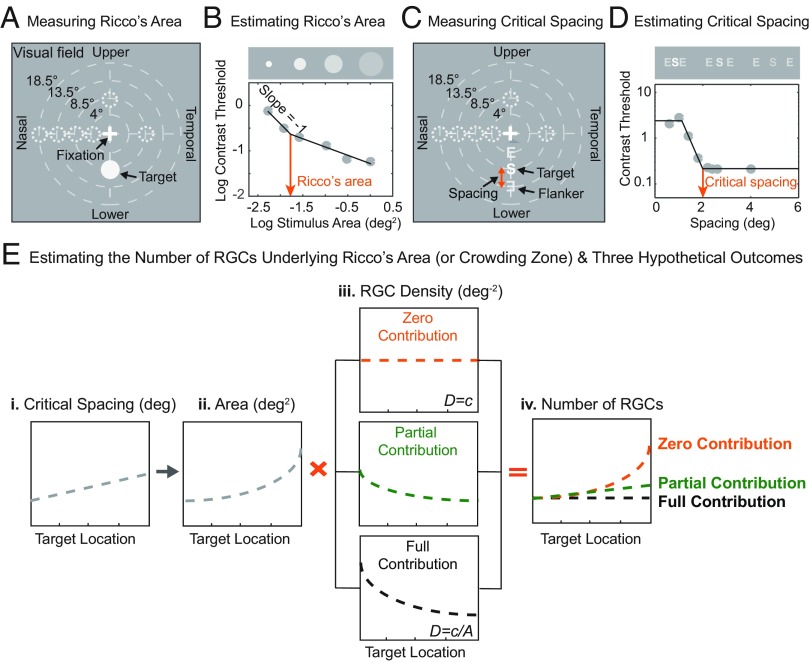
To address this question, we measured the extent of spatial integration for luminance detection (Ricco’s area) and object recognition (crowding zone) in young, normally sighted individuals [mean age ± standard deviation (SD) = 22.62 ± 3.81 y; mean visual acuity = −0.09 ± 0.09 logMAR; mean log contrast sensitivity = 1.82 ± 0.15 for the tested eye]. The sample size (n) for each experimental condition is provided in SI Appendix, Table S1. To obtain the RGC density of the human retina, we used Drasdo et al.’s equation (26) based on previous histological studies (27, 28) of the adult human retina [note that we also replicated our results using Watson’s equation (29); see SI Appendix, Figs. S1 and S2]. In the current study, the RGC density refers to the RGC density of a mix of different ganglion cell types (e.g., midget and parasol cells) unless otherwise stated. Ricco’s area was defined as the extent of stimulus area within which the product of stimulus area and contrast detection threshold remains constant. A subject’s contrast detection threshold was measured with luminance discs of varying sizes (Fig. 2A) and Ricco’s area was estimated from the two-limbed fit to the data of log detection threshold vs. log stimulus area (Fig. 2B). Crowding zone represents the spatial extent of the feature integration zone that allows for reliable object recognition in the presence of nearby distractors (3, 6). A subject’s contrast recognition threshold was measured using a flanked letter with varying spacings between the target and flankers (Fig. 2C). Critical spacing was estimated from the clipped-lines fit to the data of log recognition threshold vs. spacing between target and flankers (6) (Fig. 2D). For each subject, both Ricco’s area and critical spacing were measured at seven different visual-field locations: four eccentricities (4°, 8.5°, 13.5° and 18.5° on the horizontal meridian) in the nasal visual field and three additional locations at the eccentricity of 8.5°. Each location can be denoted as (ρ, θ) in the polar coordinates: (4°, 180°), (8.5°, 180°), (13.5°, 180°), (18.5°, 180°), (8.5°, 0°), (8.5°, 90°), and (8.5°, 270°) if the subject’s test eye is the right eye. The data in the current study are all expressed in visual field coordinates (i.e., Uvf, Lvf, Nvf, and Tvf for the upper, lower, nasal, and temporal visual fields, respectively) rather than retinal coordinates. See the details of stimuli and task procedures in SI Appendix, Supplemental Methods.
Fig. 2.
Schematic diagram summarizing task stimuli, analysis methods, and three hypothetical outcomes. (A) Measuring Ricco’s area. The stimulus was an achromatic luminance disk displayed on a uniform gray background. A subject’s contrast detection threshold was measured with a staircase procedure, yielding 79.4% correct criterion (100). Thresholds were obtained for six different disk sizes. Ricco’s area was measured at seven different visual field locations: four eccentricities (4°, 8.5°, 13.5°, and 18.5° on the horizontal meridian) in the nasal visual field and three additional locations at the eccentricity of 8.5°. Each location can be denoted as (ρ, θ) in the polar coordinates: (4°, 180°), (8.5°, 180°), (13.5°, 180°), (18.5°, 180°), (8.5°, 0°), (8.5°, 90°), and (8.5°, 270°) if the subject’s test eye is the right eye. Note that the data in the current study are all expressed in visual-field coordinates (i.e., Uvf, Lvf, Nvf, and Tvf) rather than retinal coordinates. Therefore, the data from the nasal visual field contain the subject’s left or right visual-field data depending on the subject’s tested eye. The same applies to the data from the temporal visual field. (B) Estimating Ricco’s area. The spatial summation curve, a plot of log contrast detection thresholds as a function of log stimulus area (degrees2), was fitted with two lines. To estimate Ricco’s area, the slope of the first line was constrained to a value of −1 in accordance with Ricco’s law, whereas the slope of the second line was allowed to vary. Ricco’s area was defined as the breakpoint of the two-limbed function. (C) Measuring critical spacing. The stimuli consisted of a target letter flanked by two tumbling Es appearing on both sides of the target along the radial axis (connecting the target to the fovea). The target letter was randomly drawn from a set of 10 Sloan letters: CDHKNORSVZ. The subject’s task was to identify the target letter and the subject’s letter-recognition contrast threshold was measured with the staircase procedure described earlier. Critical spacing was measured at the same locations as Ricco’s area. (D) Estimating critical spacing. Thresholds were obtained for eight different spacings (i.e., the center-to-center distance between the target letter and flankers). Clipped lines were fitted to the data of log recognition threshold vs. spacing. Critical spacing was defined as the minimum spacing (degrees) that yields no threshold elevation in the fit (6). (E) Estimating the number of RGCs underlying Ricco’s area (or crowding zone) and three hypothetical outcomes. To compute the number of RGCs, the following steps were taken. Step 1: Each subject’s critical spacing in a unit of length (E, i) was converted into a corresponding unit of area (degrees2) for each target location (E, ii). Considering the radial–tangential anisotropy of crowding zone (7–10, 37), an elliptical shape was used for the area conversion (SI Appendix, Supplemental Methods). Here we illustrate an example of crowding zone because Ricco’s area is already measured by a unit of area and thus there is no need for this unit conversion. Step 2: The RGC density (E, iii) corresponding to each target location in the visual field was derived from the equation (26). Step 3: The product of Ricco’s area (degrees2) (or crowding zone) and the RGC density (degrees−2) was computed for each target location. To be more precise, we calculated the integral of products of ∆Ricco’s area or ∆crowding zone and the corresponding RGC density over the entire integration zone. This yields a plot of the number of RGCs as a function of target location (E, iv). Depending on the patterns of underlying RGC density (E, iii), three hypothetical outcomes (E, iv) are expected: zero contribution, partial contribution, and full contribution.
To see if the sampling density of RGCs mirrors the visual-field dependence of the extent of spatial integration, we estimated the number of RGCs underlying Ricco’s area and the area corresponding to critical spacing (we hereafter refer to this area as crowding zone to distinguish it from critical spacing) (Fig. 2 E, ii) for each target location. This was achieved by computing the product of Ricco’s area (degrees2) (or crowding zone) and the RGC density (degrees−2) at each target location (Fig. 2 E, iii). To be more precise, we calculated the integral of products of ∆Ricco’s area or ∆crowding zone and the corresponding RGC density over the entire integration zone. This was done to take into account that the RGC density varies continuously over the extent of spatial integration. A resulting plot of the number of RGCs as a function of target location (Fig. 2 E, iv) was used to test our hypothesis. Consider how the shape of the resulting plot of the product may differ depending on the contribution of the underlying RGC density. (i) “Zero contribution” is a case in which the RGC density plays no role in the extent of spatial integration. Here we assume the hypothetical RGC density is a constant function (D = c) across target locations, as illustrated in Fig. 2 E, iii (orange dashed line). In this case, the shape of the resulting curve would look more like the plot of the psychophysically defined integration zone, as illustrated by the orange dotted line in Fig. 2 E, iv. (ii) “Partial contribution” is a case in which the RGC density may explain the variance to some degree. The effect would result in the relative flattening of the slope of the resulting curve depicted by the green dotted line in Fig. 2 E, iv. (iii) “Full contribution” is a case in which the RGC density fully accounts for the variation in the extent of spatial integration, indicating that a fixed number of RGCs is employed to represent sensory inputs for reliable visual detection or recognition, independent of the target location. In this case, the number of RGCs would remain constant across the visual field. Thus, this hypothetical curve can be derived from fitting the linear function whose slope is zero to the resulting data of the number of RGCs vs. target location shown by the black dotted line in Fig. 2 E, iv. Finally, we quantified the contribution of the RGC density by computing the amount of the variance that can be explained by the underlying RGC density with respect to the total variance (SI Appendix, Supplemental Methods): A value of 0% means zero contribution whereas a value of 100% indicates full contribution.
Results
Relating the Variation in the RGC Density to the Variation in Ricco’s Area.
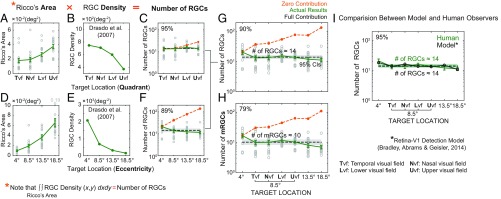
Consistent with previous findings (4, 5), Ricco’s area (i.e., the spatial summation area required for luminance detection) increases with increasing eccentricity (Fig. 3D) [F(3,38) = 57.62, P < 0.001] and is noticeably larger in the upper visual field compared with the other visual fields (Fig. 3A) [t(16) = 7.05, P < 0.001]. The plot of the RGC density as a function of target location appears to be the mirror reversal of behavioral data (Fig. 3 B and E). The number of RGCs (i.e., the product of Ricco’s area and the underlying RGC density) is plotted as a function of visual-field quadrant (Fig. 3C) and eccentricity (Fig. 3F), respectively. As mentioned earlier, there are three hypothetical outcomes describing the relationship between Ricco’s area and the RGC density: full, partial, and zero contributions. In Fig. 3C and Fig. 3F, it becomes apparent that the number of RGCs underlying Ricco’s area remains more or less constant across target locations. Our analysis further reveals that the RGC density explains nearly 95% of the variance in Ricco’s area across different quadrants (Fig. 3C) and 89% of the variance across the eccentricities (Fig. 3F), ranging from 4° to 18.5°. Altogether, nearly 90% of the variance in Ricco’s area across the visual field is explained by the underlying RGC density (Fig. 3G). It is apparent that the data point at 4° eccentricity deviates from the rest of the data. Although speculative, this departure at 4° eccentricity might be the result of overestimation of the RGC density at lower eccentricities. In fact, Liu et al. (30) reported that peak RGC densities at lower retinal eccentricities measured by their adaptive optics optical coherence tomography (AO-OCT) are significantly lower than previous histologic estimates (27) (P = 0.01), consistent with our conjecture. In addition to the contribution of the overall RGC density, we also estimated the number of midget retinal ganglion cells (mRGCs) underlying Ricco’s area (Fig. 3H). We find that a fewer number of mRGCs is involved in Ricco’s area and its statistical accountability is not as good as using the overall RGCs (90% vs. 79%). This result is well-aligned with the view that parasol ganglion cells projected to the magnocellular pathway are more responsible for detecting changes in luminance (31).
Fig. 3.
Number of RGCs underlying Ricco’s area. (A) Ricco’s area is plotted as a function of visual-field quadrant. Gray open dots represent individual subjects’ data points. The green solid line indicates the average Ricco’s area across subjects for a given target location. Error bars represent ±1 SEM. (B) The RGC density (green solid line) estimated from the equation (26) is plotted against visual-field quadrant. (C) The number of RGCs (i.e., actual results indicated by green line) underlying Ricco’s area, that is, the product of Ricco’s area (degrees2) and the RGC density (degrees−2), is plotted against visual-field quadrant in comparison with zero contribution (orange dotted line) and full contribution (black dotted line) curves. Shaded gray areas indicate 95% CIs of full contribution. (D) Ricco’s area vs. visual-field eccentricity. (E) The RGC density vs. eccentricity. (F) The number of RGCs (i.e., actual results) underlying Ricco’s area vs. eccentricity. (G) The number of RGCs underlying Ricco’s area in comparison with zero contribution and full contribution curves. (H) The number of midget RGCs (mRGCs) underlying Ricco’s area is plotted against target location in comparison with zero contribution and full contribution curves. (I) Comparison between model and human observers. We implemented the retina-V1 detection model shown to provide an excellent account for human detection performance against various backgrounds (32). This model is based on a small set of the known optical, retinal, and V1 properties of the human/primate visual system combined with optimal response pooling in V1 and a decision rule. Ricco’s area was obtained from the model using the same stimuli and criterion level of detection performance (79.4% accuracy) as used for our human observers. The number of RGCs underlying Ricco’s area obtained from the model (black open dots and lines) is plotted against eccentricity in comparison with our empirical data (green bars and lines). Shaded gray areas indicate 95% CIs of the mean.
Taken together, our analysis allowed us to infer that independent of the visual-field location, ∼14 RGCs are involved in the process of the complete summation underlying human luminance detection (Fig. 3G). We, then, attempted to validate this result using a computational model based on a small set of the known optical, retinal, and V1 properties of the human/primate visual system (32). We chose this model because this simple retina-V1 detection model has been shown to provide an excellent account for human detection performance against various backgrounds (32). For the detailed information about the model see Bradley et al. (32). Briefly, the retina-V1 detection model consists of (i) the optical point spread function of the human eye, (ii) local luminance gain control, (iii) the sampling array of human RGCs (26) and their receptive field (RF) response function (i.e., on-and off-center responses), (iv) V1 masking (i.e., orientation and spatial frequency filter and contrast gain control) and optimal response pooling, and (v) a decision rule (i.e., translating the V1 pooled response into human detection performance). Ricco’s area was obtained from the model by employing the same stimuli (i.e., a circular disk embedded in the uniform background) and criterion level of detection performance (79.4% accuracy) as those used for our human observers. Ricco’s area obtained from the model simulation was then converted into the number of RGCs using Drasdo et al.’s (26) density data. As shown in Fig. 3I, the results of the model simulation (black lines) are in an excellent agreement with our empirical data (green lines) without any statistically significant difference between the two estimates (P > 0.5), that is, a total of 14 RGCs underlie Ricco’s area, independent of target location. We find that the parameter values (SI Appendix, Table S2) of the model are comparable to the values reported by Bradley et al. (32). Therefore, both our empirical data and the simulation results of the model provide a consistent picture of the number of RGCs subserving human detection performance.
Relating the Variation in the RGC Density to the Variation in Crowding Zone.
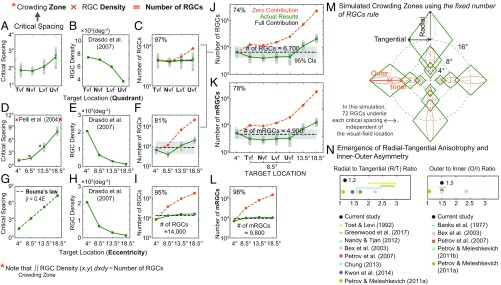
Similar to Ricco’s area, critical spacing (i.e., the extent of spatial integration for object recognition) also increases with eccentricity (Fig. 4D) [F(3,36) = 919, P < 0.001] and becomes significantly larger in the upper visual field compared with the other visual fields (Fig. 4A) [t(16) = 7.39, P < 0.001]. Our behavioral results are well-aligned with previous findings demonstrating the dependence of critical spacing on visual-field eccentricity (3, 7) and quadrant (8–11).
Fig. 4.
Number of RGCs underlying crowding zone or Bouma’s law of crowding. (A) Critical spacing (degrees) is plotted as a function of visual-field quadrant. Gray open dots represent individual subjects’ data points. The green solid line indicates the average critical spacing across subjects for a given target location. Error bars represent ±1 SEM. (B) The RGC density (green solid line) estimated from the equation (26) is plotted against visual-field quadrant. (C) The number of RGCs (i.e., actual results depicted by green line) underlying crowding zone, the product of crowding zone (degrees2) and the RGC density (degrees−2), is plotted against visual-field quadrant in comparison with zero contribution (orange dotted line) and full contribution (black dotted line) curves. Shaded gray areas indicate 95% CIs of full contribution. (D) Critical spacing vs. eccentricity data from our study (gray symbols) compared with the data (red crosses) from Pelli et al. (6). (E) The RGC density vs. eccentricity. (F) The number of RGCs (i.e., actual results) underlying crowding zone vs. eccentricity. (G) Critical spacing predicted by Bouma’s law (b = 0.4) as a function of eccentricity. (H) The RGC density vs. eccentricity. (I) The number of RGCs underlying crowding zone predicted by Bouma’s law, in comparison with zero contribution and full contribution curves. (J) The number of RGCs underlying crowding zone as a function of target location in comparison with zero contribution and full contribution curves. (K) The number of midget RGCs (mRGCs) underlying crowding zone as a function of target location. (L) The number of mRGCs underlying crowding zone predicted by Bouma’s law as a function of target location. (M) The simulated critical spacings based on the human RGC mosaic and the fixed number of RGCs rule are plotted in polar coordinates. (N) The mean ratio of radial to tangential directions (R/T ratio) and the ratio of outer to inner directions (O/I ratio) obtained from our simulated results (black dots) are plotted in comparison with the ratio values shown in previous human studies. The mean ratio from our simulation represents the average ratio value across 20 different target locations: 4°, 8°, 12°, 16°, and 20° eccentricities on the meridian of 0°, 90°, 180°, and 270°.
Eccentricity-dependent crowding zone has been considered a hallmark of crowding. It is approximated by Bouma’s law (3), which postulates that target and flankers must be spatially separated by at least half the eccentricity of the target (i.e., critical spacing = 0.5 eccentricity) in order for the observer to reliably recognize the target object. A proportionality constant of 0.4 (b = 0.4) was chosen for the current study because it allowed us to relate our results to previously published data. Eccentricity-dependent crowding zone has been explained by cortical constraints such as cortical separation in V1 (14, 33) or the size of RFs in higher cortical areas (15, 34). On the other hand, the visual-field asymmetry in crowding zone has been explained by the asymmetries in attentional resolution (11, 35) or space perception (19) between the upper and lower visual fields. While these accounts have made valuable contributions to our understanding of the mechanism underlying the perceptual process of crowding, it is also possible that we might have overlooked a much simpler explanation that could unify the two phenomena: Perhaps both eccentricity and quadrant-dependent crowding zones may be in part related to the nonuniform topographic distribution of the RGCs across the human retina. Our quantitative analysis allows us to test this very idea.
Fig. 4 shows the number of RGCs underlying crowding zone as a function of visual-field quadrant (Fig. 4C) and eccentricity (Fig. 4F), respectively. It is evident that once the RGC density is taken into account, the number of RGCs underlying crowding zone becomes less variable across the visual field compared with zero contribution. Our analysis further shows that the number of RGCs remains constant [F(3,48) = 0.74, P = 0.53] and the RGC density accounts for nearly 97% of the variance in crowding zone across visual-field quadrants (Fig. 4C). On the other hand, the variation across eccentricities cannot be fully explained by the variation in the RGC density (P < 0.001). Nevertheless, the RGC density still explains 81% of the variance in crowding zone across eccentricities (Fig. 4F). Altogether, nearly 74% of the variance in crowding zone is explained by the underlying RGC density (Fig. 4J). It is noteworthy that relative to Ricco’s area the contribution of the RGC density to the variation in crowding zone is much less (90% vs. 74%). Perhaps it is largely because higher cognitive and/or cortical factors play an increasing role in the perceptual process of crowding, consistent with previous research (11, 35). As mRGCs are known to be more responsible for the processing of object recognition (36), we performed the same analysis using the density of mRGCs (Fig. 4K). As expected, the contribution of the mRGC density was noticeably greater than that of the overall RGC density (74% vs. 78%).
Importantly, we also find that the Bouma’s law of crowding (Fig. 4G) can be nearly fully explained by the total RGC density (95% in Fig. 4I) and by the mRGCs (98% in Fig. 4L), respectively. The number of RGCs curve is in line with full contribution despite a noticeable departure at 4° eccentricity. In other words, Bouma’s law appears to formulate the important guiding principle of human pattern vision: A fixed number of RGCs is being employed to encode a target object into a neural representation, independent of eccentricity.
Simulated Crowding Zones Across the Visual Field Using the RGC Density.
In addition to the eccentricity and quadrant dependency of crowding, the spatial extent of crowding has been found to be dependent on the position (or configuration) of flankers with respect to the target. For example, radially arranged flankers (along the axis connecting the target and the fixation) induce more crowding than tangentially arranged ones (orthogonal to the target–fixation axis). This anisotropy results in radially elongated crowding zone (i.e., the radial–tangential anisotropy of crowding) (7–9, 17, 37–41). Furthermore, a flanker outside the target (outer flanker) often exerts stronger crowding than a flanker inside the target (inner flankers) (i.e., the inner–outer asymmetry of crowding) (3, 9, 38, 39, 42, 43). Due to their robustness, both the radial–tangential anisotropy and the inner–outer asymmetry are considered significant features of crowding (44, 45).
Here we further examined whether the sampling density of RGCs is implicated in various defining features of crowding, that is, its dependence on retinal eccentricity, quadrant, radial vs. tangential directions, and inner vs. outer directions. To this end, we simulated critical spacing solely based on the sampling array of RGCs for radial or tangential direction and inner or outer direction at different eccentricities and quadrants. More specifically, expected critical spacing at each target location (e.g., inner direction with respect to the target position at 16° eccentricity in the upper visual field) was estimated using the fixed number of RGCs rule in which a fixed number of 72 mRGCs corresponding to a 6-mm cortical distance (see the following section for this derivation) is employed, independent of target location. Fig. 4M shows the results of our simulation in polar coordinates. Fig. 4N shows a plot of the mean ratio of the radial to tangential conditions (R/T ratio) and the mean ratio of the outer to inner conditions (O/I ratio) that emerged from our simulation in comparison with the ratio values shown in previous human studies (7–10, 37–40, 42, 43). The mean ratio from our simulation represents the average ratio value across 20 different target locations: 4°, 8°, 12°, 16°, and 20° eccentricities on the meridian of 0°, 90°, 180°, and 270°.
As expected, the dependency of crowding on eccentricity and quadrant arises from the simulation, mirroring the empirical data found in human observers (Fig. 4M). We also find the inner–outer asymmetry of crowding of which ratio value (on average 1.5 for O/I ratio) is in a good agreement with published values (1.1∼2.4). The emergence of the inner–outer asymmetry further confirms the eccentricity-dependent crowding zone given the fact that outer direction is always farther away from the fovea compared with inner direction. However, the radial–tangential anisotropy of crowding (on average 1.2 for R/T ratio) that emerged from our simulation is noticeably weaker than published values ranging from 1.1 to 3.0. We also notice that the magnitude of the anisotropy that emerged from the RGC density varies across the visual field: It is much more pronounced in the upper visual field and at the far periphery, as shown in Fig. 4M. Despite its variability, the overall weak anisotropy observed in the simulation results may also indicate a critical role of higher cortical areas in the anisotropy of crowding. Indeed, Zhou et al. (46) reported that while there is a large anisotropy of crowding distance mapped to the surface of V1, no anisotropy of crowding distance is shown at the surface of V4, suggesting that the anisotropy might be largely cortical, changing dramatically from V1 to V4.
Linking the Retina to the Cortex.
We started off with the two premises. First, the topographic distribution of the RGC density largely underlies the cortical magnification factor (21). Second, the critical spacing expected from Bouma’s law (b = 0.4) in the visual field results in a fixed cortical distance (i.e., 6 mm at V1), independent of eccentricity (14). Now, let’s see how the fixed number of RGCs rule fits into this picture. Using published anatomical, physiological, and psychophysical data, we performed some calculations and arrived at these following conclusions:
-
i)
We find that the number of mRGCs underlying a 1-mm cortical distance is ∼12, independent of eccentricity (Fig. 5A). This is derived by the following equation:
| [1] |
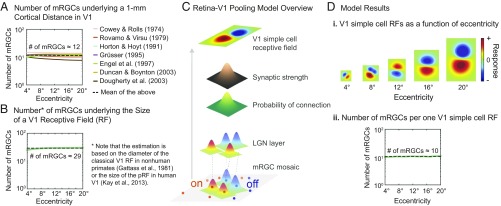
where is the mRGC density (in degrees−2), is the V1 cortical magnification factor (in millimeters per degree). For this estimation, we used a number of data reported in previous human studies (47–53) (SI Appendix, Table S3). In Fig. 5A, the estimated number of mRGCs underlying a 1-mm V1 cortical distance is plotted as a function of eccentricity ranging from 4° to 20°. Each solid line represents estimated values from each study. We find that the number of mRGCs remains fairly constant, independent of eccentricity, and ∼12 mRGCs underlie a 1-mm V1 cortical distance, as shown by the black dashed line in Fig. 5A. This result is consistent with a previous report that an approximately fixed number of parvocellular cells in the lateral geniculate nucleus (LGN), which receives input directly from mRGCs, underlies 1-mm2 cortical area in macaque (54). A similar relationship has also been found in macaque visual areas V1 and V4: The size of V4 RFs corresponds to a fixed cortical surface area in V1 (34).
-
ii)
From i, we derive that the number of mRGCs underlying a 6-mm cortical spacing shown to correspond to the Bouma’s law (b = 0.4) of eccentricity-dependent critical spacing is estimated to be about 72 mRGCs (6 mm × 12 mRGCs per millimeter), independent of eccentricity. This leads to 8,100 mRGCs per an ellipsoid-shaped crowding zone, comparable to our estimation of 9,800 mRGCs (Fig. 4L).
-
iii)
We find that the number of mRGCs corresponding to the size of a neuron’s classical RF or population RF (pRF) in V1 is estimated to be about 29, independent of eccentricity (Fig. 5B). This is derived from the following equation:
| [2] |
where is the RF size in V1 (i.e., diameter in degrees for classical RF or standard deviation of the Gaussian profile for pRF) and is the mRGC density (in degrees−2). Both the size of V1 RF in nonhuman primates (55) and the size of human pRF in V1 (56) are known to increase linearly with increasing eccentricity, while the increment of the RF size for a unit eccentricity (i.e., a slope of the function) varies across studies. For our analysis given in Fig. 5B, we used a slope of 0.16 shown in both Gattass et al.’s study (55) on macaques and Kay et al.’s fMRI study (57) on humans. Note that the use of a different slope value only shifts the curve vertically without any change to its shape.
Fig. 5.
Linking the retina to the cortex. (A) The number of mRGCs underlying a 1-mm cortical distance is estimated using the human V1 cortical magnification factor data reported in previous studies. The number of mRGCs estimated from each study (solid lines) is plotted as a function of eccentricity. The dashed black line represents the average value across different studies. (B) The number of RGCs underlying the size of a neuron’s classical RF or pRF in V1 is plotted against eccentricity. The estimation is based on the data from Gattass et al.’s study (55) on macaques and Kay et al.’s fMRI study (57) on humans. (C) Overview of the retina-V1 pooling model (see details of the model in Methods). (D) Model results. (D, i) Resulting V1 simple-cell RFs are shown for five different eccentricities. Color maps indicate the magnitude of V1 simple-cell responses. (D, ii) The number of mRGCs (green line) connecting to each V1 RF is plotted as a function of eccentricity.
Our empirical data combined with the foregoing derivation work suggest that the fixed number of RGCs rule might be one of the organizational principles of the human visual system. We, thus, implemented a simple retina-V1 pooling model as a potential mechanism that may help us understand the linkage between the retina to V1. This model consists of three basic layers: RGC, LGN, and V1 layers, and is based on statistical sampling of the RGC mosaic and probabilistic connections between layers. A similar yet more sophisticated model was originally proposed by Soodak (58) and Ringach (59) to show how the RGC mosaic accounts for the emergence of orientation columns in striate cortex of the cat. Our goal here is to demonstrate how the potential property of V1 RFs, the fixed number of RGCs rule, could arise from a simple pooling model rather than to describe or propose a biologically realistic model. The details of model implementation are provided in Methods, but in brief: (i) RGC layer was represented by a hexagonal lattice of human on- and off-center mRGC mosaics (26, 32). As shown at the bottom of Fig. 5C, mRGC RFs were modeled as 2D isotropic Gaussian functions of which SD was the spacing between cells at a given location in the mRGC mosaic. (ii) The LGN layer acted as a relay station between the retina and V1 without substantial modifications (60–62), where each LGN neuron received input directly from one RGC. (iii) The probability of connection between an LGN neuron and a cortical neuron varied as a function of the distance between their RF centers, which was modeled as a 2D isotropic Gaussian function of the distance for each cortical neuron. (iv) The strength of connection (synaptic weights) between an LGN neuron and a cortical neuron varied as a function of the distance between their RF centers, which was modeled as a 2D isotropic Gaussian function of the distance for each cortical neuron. (v) Each cortical neuron linearly summated its inputs from the LGN layer and its output represented V1 simple-cell responses as shown at the top of Fig. 5C. (vi) We ran the simulation over 1,000 times for each retinal location, 4°, 8°, 12°, 16°, and 20° eccentricities on the meridian of 0°, 90°, 180°, and 270°, and counted the number of RGCs connecting to each V1 simple-cell RF, as summarized in Fig. 5D.
As shown in Fig. 5D, the simulation results show that the size of V1 RFs increases with increasing eccentricity and on average 10 mRGCs are connected to one V1 simple-cell RF, independent of eccentricity. This approximates to the number of mRGCs obtained from our Ricco’s area experiment (∼10 mRGC) shown in Fig. 3H.
It has been shown that the RF of RGCs is elongated radially with average major-to-minor axis ratios of 1.2 to 1.3 in cats (63, 64). A similar pattern has also been observed in nonhuman primates (65, 66), especially for midget ganglion cells (67) with an average major-to-minor axis ratio of 1.72. In the current study, we, however, did not incorporate this anisotropy property or the nonlinearity of V1 simple-cell RFs (68) because they have inconsequential impacts on the primary goal of our modeling: estimating the number of RGCs connected to each V1 simple cell across different eccentricities.
Discussion
In the current study we analyze the relationship between the topographic distribution of ganglion cell density and the nonuniform spatial integration across the visual field. By directly relating the variation in the extent of spatial integration across the visual field to the variation in the RGC density across the human retina, we quantify the spatial integration with respect to the number of RGCs. The data from our empirical work combined with computational modeling and a set of derivations allow us to arrive at the following conclusions.
First, once the sampling density of RGCs is taken into account, the variation in the extent of spatial integration across the visual field becomes less pronounced for both Ricco’s area and crowding zone. The contribution of the underlying RGC density to the variation in the spatial integration is found to range from 74 to 98% when other factors are held constant. Second, some of the known properties of crowding arise when crowding zone is simulated across the visual field following the fixed number of RGCs rule. Third, the number of RGCs underlying either a fixed cortical distance or the size of a V1 RF (classical RF or pRF) remains constant, independent of retinal eccentricity. Fourth, a simple retina-V1 pooling model based on statistical sampling of the human RGC mosaic and probabilistic connections between layers shows that each V1 simple-cell neuron may receive a fixed number of mRGCs, independent of eccentricity.
We have shown that the number of RGCs underlying Ricco’s area remains more or less constant (∼14 RGCs) across the visual field (Fig. 3G). This result suggests that a fixed number of RGCs may be recruited by the visual system to achieve complete spatial summation for luminance detection. Of course, the absolute value (e.g., ∼14 RGCs) for the number of RGCs underlying Ricco’s area is subject to change depending on experimental conditions, such as the luminance of the background or the wavelength of target stimulus (69, 70). However, what matters here is that when other factors are held constant the variation in the RGC density largely accounts for the variation in Ricco’s area across the visual field. We further validated our findings using a published retina-V1 detection model (32). Bradley et al. (32) have shown that human detection performance is well captured by this detection model based on a small set of the known optical, retinal, and V1 properties of the human/primate visual system. Consistent with our empirical findings, the results of the model also show that ∼14 RGCs are involved in the process of luminance detection, independent of target location in the visual space. The impact of the RGC density on the spatial pooling mechanism has already been suggested in clinical studies. For example, a significant loss of RGCs, due to pathological conditions such as glaucoma (71, 72), has been shown to bring about an enlargement in Ricco’s area (12, 73). Enlarged RFs have also been observed in the adult rat brain following experimentally induced glaucoma (i.e., loss of RGCs) (74). Our study, together with the findings from previous studies, supports the view that Ricco’s area is closely related to the RFs (4) and/or the density of RGCs (12).
Then, what about the relationship between the RGC density and the spatial integration involved in complex object recognition? Although the contribution of the RGC density to the variation in crowding zone becomes noticeably less compared with Ricco’s area (74% vs. 90%), we find that the number of RGCs underlying crowding zone stays fairly constant [F(3,48) = 0.74, P = 0.53] across different quadrants (Fig. 4C). Interestingly, we also find that Bouma’s law (b = 0.4) describing eccentricity-dependent increase in crowding zone can be expressed in units of underlying RGCs (∼14,000 RGCs or 9,800 mRGCs) (Fig. 4 I and L). The spatial extent of crowding approximated by Bouma’s law has been predominantly explained by cortical constraints, that is, a target and flankers need to be separated by a fixed number of cortical neurons (a fixed cortical distance) for the visual system to achieve reliable object recognition (14). By quantifying Bouma’s law with respect to the number of RGCs, we illuminate the relationship between the topographic distribution of the RGC density and the spatial integration underpinning human object recognition. Again, the absolute value for the number of RGCs underlying crowding zone will differ depending on the coefficient value of Bouma’s law, whether it is 0.4 (75) or 0.5 (3) of the eccentricity of the target object. However, it should be noted that using a different coefficient value only leads to a vertical shift of the resulting curve (i.e., a plot of the number of RGCs vs. eccentricity) without changing the shape of the curve. Therefore, the coefficient value per se does not make any difference as to our main point, whether the number of RGCs underlying eccentricity-dependent increase in critical spacing remains constant across eccentricities or not.
Various accounts (14, 15, 33, 37, 76–81) have been proposed to explain what might govern the spatial extent of crowding. However, it is still unresolved whether the integration zone is predominantly mediated by bottom-up computations, such as hardwired integration fields (14, 15, 33, 34), and/or top-down cognitive factors, such as a spotlight of attention (11) or perceptual bias (19). However, the involvement of low- and higher-level cortical areas has been evidenced by both behavioral and brain imaging studies (33, 45, 82, 83), including our own (8). For example, a number of studies (33, 82, 84) demonstrated that crowding occurs under dichoptic viewing conditions in which a target and flankers are presented to two different eyes. It has been also shown that crowding effect can be alleviated if a target and flankers are dissimilar in color, shape, size, or holistic configuration [e.g., Kooi et al. (85)]. Also, cueing of a target location (86) or suppression of flankers from visual awareness (87) has been shown to reduce the crowding effect, suggesting top-down feedback influences on the perceptual process of crowding (see reviews in refs. 44, 45, and 88). Consistent with behavioral evidence, crowding effect has also been observed at various stages of visual processing, from as early as V1 and V2 (8, 14–17) or V4 and beyond (89–91). Among a great deal of literature on crowding, one of the unique contributions of our study is to reveal a close link between some of the defining features of crowding and the properties of the human RGC mosaic. This is indeed consistent with the findings by Greenwood et al. (10) showing that the common pattern of variations in various visual tasks such as crowding, saccadic eye movements, and spatial localization are present across the visual field. Greenwood et al. (10) attributed the common variations to the shared topology of spatial vision in the early visual pathway such as the RGCs.
Then, what may explain the linkage between the topographic distribution of RGC density and the extent of spatial integration? Although the exact mechanism linking the two remains elusive, we can speculate that the RF mosaics of RGCs may give rise to some intrinsic properties of the RFs of visual cortical neurons. For instance, cortical magnification, that is the fundamental organizational property of the visual cortex, has been largely attributed to the RF mosaics of RGCs (21), thereby affecting the way visual information is integrated in the cortex. It has been even argued that the RGC mosaic defines signals of visual pattern to V1 (58, 59, 92). Regardless of the mechanism involved, our derivation work elucidates that ∼29 RGCs correspond to the size of a V1 RF, independent of eccentricity and ∼72 RGCs underlies a 6-mm cortical spacing (i.e., critical spacing expected from Bouma’s law), independent of eccentricity. Our results from the retina-V1 pooling model (Fig. 5C) further suggest that a fixed number of retinal neurons could be recruited for a cortical processing unit (e.g., V1 simple cells). These results collectively lead us to expect that a significant loss of RGCs due to either normal aging or some pathological conditions such as glaucoma may impact the extent of spatial integration, which has been indeed reported in published research (12, 73, 93).
We acknowledge limitations of the current study. Despite recent advancements in imaging techniques such as AO-OCT (30), direct counting of RGCs in the living human eye is still challenging. For this reason, we relied on indirect measurements of the RGC density: deriving RGC densities from the empirical formula based on average densities of RGCs of the adult human retina (26). In addition, most of the results reported in the current study are based on the overall RGC density of a mix of different ganglion cell types and also based on psychophysical measurements made in eccentricities between 4° and 20°. Therefore, it remains to be addressed in a future study whether the pattern of results will hold true for experimental conditions beyond what we have tested in the current study, especially for the macular region of the retina. For instance, Wässle et al. (22) showed that RGC density can fully account for the cortical magnification factor and there is no need to postulate a selective amplification of the foveal representation. Other studies, however, have shown that the cortical representation of the macula (corresponding to the central 4° of the visual field) is found to be amplified more than expected from RGC density in both human and nonhuman primates (94–96). Nonetheless, given limitations such as the sizable individual variability across subjects (27) and functional variability across cell types (e.g., midget, parasol, or bistratified cells) (97) (see ref. 98 for review), the close match between the estimated RGC density and the psychophysical results is rather remarkable. Importantly, we also replicated our findings using Watson’s density equation (29), which helps us believe that the pattern of our results is not likely due to a particular formula employed in the current study (see details in SI Appendix, Figs. S1 and S2).
In summary, our results show a quantitative agreement between the topographic distribution of the RGC density and the nonuniform spatial integration across the visual field: The variation in the sampling density of RGCs across the human retina is closely matched to the variation in the extent of spatial integration required for either luminance detection or object recognition. Our findings suggest that a fixed number of RGCs subserves spatial integration of visual input, independent of the visual-field location.
Methods
Participants.
A total of 21 young, normally sighted individuals (age range 19 to 34 y, mean 22.62 ± 3.81 y, six males) took part in this study. The sample size for each experimental condition is summarized in SI Appendix, Table S1. The study participants were recruited from the University of Alabama at Birmingham campus. All participants were native English speakers without known cognitive or neurological impairments. The mean visual acuity (ETDRS charts) was −0.09 ± 0.09 logMAR (or 20/16 Snellen equivalent) and the mean log contrast sensitivity (Pelli–Robson charts) was 1.82 ± 0.15 for the tested eye. The experimental protocols followed the tenets of the Declaration of Helsinki and were approved by the Internal Review Board of the University of Alabama at Birmingham. Written informed consents were obtained from all subjects before the experiment and after explanation of the nature and possible consequences of the study. Only dominant eye (determined by the Miles test) was tested while the other eye was covered with an eye patch. Proper refractive correction for the viewing distance was used for each participant.
Stimuli and Task Procedures.
The details of stimuli and task procedures are provided in SI Appendix, Supplemental Methods.
Data Analyses.
The details of data analyses are provided in SI Appendix, Supplemental Methods.
Model Overview and Implementation.
We implemented a simple retina-V1 pooling model as a potential mechanism linking the retina to V1. A similar yet more sophisticated model was originally proposed by Ringach (59), Paik and Ringach (92), and Soodak (58) to show how the properties of the RGC mosaic accounts for the emergence of orientation columns in striate cortex of cats and rodents. The goal of modeling in our study is to demonstrate how the RFs of V1 simple cells increase with retinal eccentricity while maintaining their connection with a fixed number of RGCs. As shown in Fig. 5C, the model includes three major processing stages: the RGC, LGN, and V1 layers. We adopted the known properties of the mRGC mosaic and the connection between the RGC and LGN layers based on human or nonhuman primate studies. We, however, used the same probabilistic connection and synaptic strength values between a geniculate RF and a cortical neuron as those from Ringach’s study (59) because no human data are currently available on these components. First, the RGC layer was represented by a hexagonal lattice of human mRGC mosaics. Two RGC mosaics representing the center points of on- and off-center mRGC cells were generated from Bradley et al.’s model (32) based on Drasdo’s human RGC data (26). Both on-center or off-center mRGC RFs were modeled as 2D isotropic Gaussian functions of which SD was the spacing between cells in the mRGC mosaic:
| [3] |
where is the SD of the RF of a mRGC and is the spacing between mRGCs for a target retinal location (i, j) derived from the spacing function provided in Bradley’ study (32). Second, the LGN layer acted as a relay station between the retina and V1 without substantial modifications (60–62), where each LGN neuron received input directly from one RGC. Thus, the total number of cells at the LGN layer was equal to the sum of on- and off- center mRGCs. The RF mosaic of LGN neurons remained the same as the RGC layer as shown in Fig. 5C. Third, the probability of connection between an LGN neuron and a cortical neuron varied as a function of the distance between their RF centers, which was modeled as a 2D isotropic Gaussian function of the distance for each cortical neuron:
| [4] |
where is the probability of connection between a geniculate RF centered at (i.e., the RF center of a geniculate neuron) and a cortical cell centered at (i.e., the RF center of a cortical neuron), is the SD of the Gaussian function , and c is the maximum probability value (c = 0.85). An LGN neuron was considered being connected to a cortical neuron if it had (i.e., a threshold connection value). [Note that the absolute number of connected LGN neurons depends on the threshold connection value. However, using a different threshold value only results in a vertical shift of the resulting curve (Fig. 5 D, ii) without any change to its shape.] Fourth, once an LGN neuron made its connection to a cortical neuron, the strength of connection (synaptic strength) was modeled as a Gaussian function of the distance between their RF centers:
| [5] |
where is the synaptic strength between a geniculate RF centered at and a cortical cell centered at when the two are connected. is the SD of the Gaussian function for synaptic strength . Fifth, each cortical neuron linearly summated its inputs from the LGN layer and its output represented V1 simple-cell responses :
| [6] |
where and are on-center and off-center LGN RFs and the same as and , respectively. is the index of LGN neurons connecting to one V1 cortical neuron. and are the weights for the kth on- and off-center LGN neuron, respectively. We ran the simulation for 20 different retinal locations: 4°, 8°, 12°, 16°, and 20° eccentricities on the meridian of 0°, 90°, 180°, and 270°. For each location, we ran the simulation over 1,000 times and each time we randomly varied the center position of a cortical neuron within a circular region of radius r = 0.4° centered at the target retinal location. We then obtained the number of mRGCs connecting to one cortical neuron for each eccentricity by averaging over 1,000 simulation results and over the four meridian locations (Fig. 5 D, ii).
Supplementary Material
Acknowledgments
We thank the editor and two anonymous reviewers for their helpful comments and suggestions; and Lillian Chien, Victoria L. Chen, and Lindsay Washington for proofreading the manuscript. This work was supported by the NIH/National Eye Institute Grant R01 EY027857 (to M.K.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1817076116/-/DCSupplemental.
References
- 1.Riccò A. Relazione fra il minimo angolo visuale e l’intensità luminosa. Mem R Accad Sci Lett Arti Modena. 1877;17:47–160. [Google Scholar]
- 2.Pelli DG, Tillman KA. The uncrowded window of object recognition. Nat Neurosci. 2008;11:1129–1135. doi: 10.1038/nn.2187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bouma H. Interaction effects in parafoveal letter recognition. Nature. 1970;226:177–178. doi: 10.1038/226177a0. [DOI] [PubMed] [Google Scholar]
- 4.Wilson ME. Invariant features of spatial summation with changing locus in the visual field. J Physiol. 1970;207:611–622. doi: 10.1113/jphysiol.1970.sp009083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Inui T, Mimura O, Kani K. Retinal sensitivity and spatial summation in the foveal and parafoveal regions. J Opt Soc Am. 1981;71:151–163. doi: 10.1364/josa.71.000151. [DOI] [PubMed] [Google Scholar]
- 6.Pelli DG, Palomares M, Majaj NJ. Crowding is unlike ordinary masking: Distinguishing feature integration from detection. J Vis. 2004;4:1136–1169. doi: 10.1167/4.12.12. [DOI] [PubMed] [Google Scholar]
- 7.Toet A, Levi DM. The two-dimensional shape of spatial interaction zones in the parafovea. Vision Res. 1992;32:1349–1357. doi: 10.1016/0042-6989(92)90227-a. [DOI] [PubMed] [Google Scholar]
- 8.Kwon M, Bao P, Millin R, Tjan BS. Radial-tangential anisotropy of crowding in the early visual areas. J Neurophysiol. 2014;112:2413–2422. doi: 10.1152/jn.00476.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Petrov Y, Meleshkevich O. Asymmetries and idiosyncratic hot spots in crowding. Vision Res. 2011a;51:1117–1123. doi: 10.1016/j.visres.2011.03.001. [DOI] [PubMed] [Google Scholar]
- 10.Greenwood JA, Szinte M, Sayim B, Cavanagh P. Variations in crowding, saccadic precision, and spatial localization reveal the shared topology of spatial vision. Proc Natl Acad Sci USA. 2017;114:E3573–E3582. doi: 10.1073/pnas.1615504114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.He S, Cavanagh P, Intriligator J. Attentional resolution and the locus of visual awareness. Nature. 1996;383:334–337. doi: 10.1038/383334a0. [DOI] [PubMed] [Google Scholar]
- 12.Redmond T, Garway-Heath DF, Zlatkova MB, Anderson RS. Sensitivity loss in early glaucoma can be mapped to an enlargement of the area of complete spatial summation. Invest Ophthalmol Vis Sci. 2010;51:6540–6548. doi: 10.1167/iovs.10-5718. [DOI] [PubMed] [Google Scholar]
- 13.Pan F, Swanson WH. A cortical pooling model of spatial summation for perimetric stimuli. J Vis. 2006;6:1159–1171. doi: 10.1167/6.11.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pelli DG. Crowding: A cortical constraint on object recognition. Curr Opin Neurobiol. 2008;18:445–451. doi: 10.1016/j.conb.2008.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Freeman J, Simoncelli EP. Metamers of the ventral stream. Nat Neurosci. 2011;14:1195–1201. doi: 10.1038/nn.2889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Millin R, Arman AC, Chung ST, Tjan BS. Visual crowding in V1. Cereb Cortex. 2014;24:3107–3115. doi: 10.1093/cercor/bht159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Anderson EJ, Dakin SC, Schwarzkopf DS, Rees G, Greenwood JA. The neural correlates of crowding-induced changes in appearance. Curr Biol. 2012;22:1199–1206. doi: 10.1016/j.cub.2012.04.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fang F, He S. Crowding alters the spatial distribution of attention modulation in human primary visual cortex. J Vis. 2008;8:6.1–6.9. doi: 10.1167/8.9.6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fortenbaugh FC, Silver MA, Robertson LC. Individual differences in visual field shape modulate the effects of attention on the lower visual field advantage in crowding. J Vis. 2015;15:19. doi: 10.1167/15.2.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jing W, Liu W-Z, Gong X-W, Gong H-Q, Liang P-J. Visual pattern recognition based on spatio-temporal patterns of retinal ganglion cells’ activities. Cogn Neurodyn. 2010;4:179–188. doi: 10.1007/s11571-010-9119-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wässle H, Grünert U, Röhrenbeck J, Boycott BB. Cortical magnification factor and the ganglion cell density of the primate retina. Nature. 1989;341:643–646. doi: 10.1038/341643a0. [DOI] [PubMed] [Google Scholar]
- 22.Wässle H, Grünert U, Röhrenbeck J, Boycott BB. Retinal ganglion cell density and cortical magnification factor in the primate. Vision Res. 1990;30:1897–1911. doi: 10.1016/0042-6989(90)90166-i. [DOI] [PubMed] [Google Scholar]
- 23.Hubel DH, Wiesel TN. Uniformity of monkey striate cortex: A parallel relationship between field size, scatter, and magnification factor. J Comp Neurol. 1974;158:295–305. doi: 10.1002/cne.901580305. [DOI] [PubMed] [Google Scholar]
- 24.Drasdo N. The neural representation of visual space. Nature. 1977;266:554–556. doi: 10.1038/266554a0. [DOI] [PubMed] [Google Scholar]
- 25.Motter BC, Simoni DA. The roles of cortical image separation and size in active visual search performance. J Vis. 2007;7:6.1–15. doi: 10.1167/7.2.6. [DOI] [PubMed] [Google Scholar]
- 26.Drasdo N, Millican CL, Katholi CR, Curcio CA. The length of Henle fibers in the human retina and a model of ganglion receptive field density in the visual field. Vision Res. 2007;47:2901–2911. doi: 10.1016/j.visres.2007.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Curcio CA, Allen KA. Topography of ganglion cells in human retina. J Comp Neurol. 1990;300:5–25. doi: 10.1002/cne.903000103. [DOI] [PubMed] [Google Scholar]
- 28.Curcio CA, Drucker DN. Retinal ganglion cells in Alzheimer’s disease and aging. Ann Neurol. 1993;33:248–257. doi: 10.1002/ana.410330305. [DOI] [PubMed] [Google Scholar]
- 29.Watson AB. A formula for human retinal ganglion cell receptive field density as a function of visual field location. J Vis. 2014;14:15. doi: 10.1167/14.7.15. [DOI] [PubMed] [Google Scholar]
- 30.Liu Z, Kurokawa K, Zhang F, Lee JJ, Miller DT. Imaging and quantifying ganglion cells and other transparent neurons in the living human retina. Proc Natl Acad Sci USA. 2017;114:12803–12808. doi: 10.1073/pnas.1711734114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pokorny J. Review: Steady and pulsed pedestals, the how and why of post-receptoral pathway separation. J Vis. 2011;11:1–23. doi: 10.1167/11.5.7. [DOI] [PubMed] [Google Scholar]
- 32.Bradley C, Abrams J, Geisler WS. Retina-V1 model of detectability across the visual field. J Vis. 2014;14:22. doi: 10.1167/14.12.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Levi DM, Klein SA, Aitsebaomo AP. Vernier acuity, crowding and cortical magnification. Vision Res. 1985;25:963–977. doi: 10.1016/0042-6989(85)90207-x. [DOI] [PubMed] [Google Scholar]
- 34.Motter BC. Central V4 receptive fields are scaled by the V1 cortical magnification and correspond to a constant-sized sampling of the V1 surface. J Neurosci. 2009;29:5749–5757. doi: 10.1523/JNEUROSCI.4496-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Intriligator J, Cavanagh P. The spatial resolution of visual attention. Cognit Psychol. 2001;43:171–216. doi: 10.1006/cogp.2001.0755. [DOI] [PubMed] [Google Scholar]
- 36.Livingstone M, Hubel D. Segregation of form, color, movement, and depth: Anatomy, physiology, and perception. Science. 1988;240:740–749. doi: 10.1126/science.3283936. [DOI] [PubMed] [Google Scholar]
- 37.Nandy AS, Tjan BS. Saccade-confounded image statistics explain visual crowding. Nat Neurosci. 2012;15:463–469. doi: 10.1038/nn.3021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bex PJ, Dakin SC, Simmers AJ. The shape and size of crowding for moving targets. Vision Res. 2003;43:2895–2904. doi: 10.1016/s0042-6989(03)00460-7. [DOI] [PubMed] [Google Scholar]
- 39.Petrov Y, Popple AV, McKee SP. Crowding and surround suppression: Not to be confused. J Vis. 2007;7:12.11–12.19. doi: 10.1167/7.2.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chung ST. Cortical reorganization after long-term adaptation to retinal lesions in humans. J Neurosci. 2013;33:18080–18086. doi: 10.1523/JNEUROSCI.2764-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.van den Berg R, Roerdink JBTM, Cornelissen FW. A neurophysiologically plausible population code model for feature integration explains visual crowding. PLoS Comput Biol. 2010;6:e1000646. doi: 10.1371/journal.pcbi.1000646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Petrov Y, Meleshkevich O. Locus of spatial attention determines inward-outward anisotropy in crowding. J Vis. 2011b;11:1. doi: 10.1167/11.4.1. [DOI] [PubMed] [Google Scholar]
- 43.Banks WP, Bachrach KM, Larson DW. The asymmetry of lateral interference in visual letter identification. Percept Psychophys. 1977;22:232–240. [Google Scholar]
- 44.Levi DM. Crowding–An essential bottleneck for object recognition: A mini-review. Vision Res. 2008;48:635–654. doi: 10.1016/j.visres.2007.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Whitney D, Levi DM. Visual crowding: A fundamental limit on conscious perception and object recognition. Trends Cogn Sci. 2011;15:160–168. doi: 10.1016/j.tics.2011.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhou J, Benso N, Winawer J, Pelli D. Conservation of crowding distance in human V4. J Vis. 2018;18:856. [Google Scholar]
- 47.Grüsser O-J. Migraine phosphenes and the retino-cortical magnification factor. Vision Res. 1995;35:1125–1134. doi: 10.1016/0042-6989(94)00187-q. [DOI] [PubMed] [Google Scholar]
- 48.Cowey A, Rolls ET. Human cortical magnification factor and its relation to visual acuity. Exp Brain Res. 1974;21:447–454. doi: 10.1007/BF00237163. [DOI] [PubMed] [Google Scholar]
- 49.Rovamo J, Virsu V. An estimation and application of the human cortical magnification factor. Exp Brain Res. 1979;37:495–510. doi: 10.1007/BF00236819. [DOI] [PubMed] [Google Scholar]
- 50.Horton JC, Hoyt WF. The representation of the visual field in human striate cortex. A revision of the classic Holmes map. Arch Ophthalmol. 1991;109:816–824. doi: 10.1001/archopht.1991.01080060080030. [DOI] [PubMed] [Google Scholar]
- 51.Engel SA, Glover GH, Wandell BA. Retinotopic organization in human visual cortex and the spatial precision of functional MRI. Cereb Cortex. 1997;7:181–192. doi: 10.1093/cercor/7.2.181. [DOI] [PubMed] [Google Scholar]
- 52.Duncan RO, Boynton GM. Cortical magnification within human primary visual cortex correlates with acuity thresholds. Neuron. 2003;38:659–671. doi: 10.1016/s0896-6273(03)00265-4. [DOI] [PubMed] [Google Scholar]
- 53.Dougherty RF, et al. Visual field representations and locations of visual areas V1/2/3 in human visual cortex. J Vis. 2003;3:586–598. doi: 10.1167/3.10.1. [DOI] [PubMed] [Google Scholar]
- 54.Schein SJ, de Monasterio FM. Mapping of retinal and geniculate neurons onto striate cortex of macaque. J Neurosci. 1987;7:996–1009. doi: 10.1523/JNEUROSCI.07-04-00996.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gattass R, Gross CG, Sandell JH. Visual topography of V2 in the macaque. J Comp Neurol. 1981;201:519–539. doi: 10.1002/cne.902010405. [DOI] [PubMed] [Google Scholar]
- 56.Dumoulin SO, Wandell BA. Population receptive field estimates in human visual cortex. Neuroimage. 2008;39:647–660. doi: 10.1016/j.neuroimage.2007.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kay KN, Winawer J, Mezer A, Wandell BA. Compressive spatial summation in human visual cortex. J Neurophysiol. 2013;110:481–494. doi: 10.1152/jn.00105.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Soodak RE. The retinal ganglion cell mosaic defines orientation columns in striate cortex. Proc Natl Acad Sci USA. 1987;84:3936–3940. doi: 10.1073/pnas.84.11.3936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ringach DL. Haphazard wiring of simple receptive fields and orientation columns in visual cortex. J Neurophysiol. 2004;92:468–476. doi: 10.1152/jn.01202.2003. [DOI] [PubMed] [Google Scholar]
- 60.So YT, Shapley R. Spatial tuning of cells in and around lateral geniculate nucleus of the cat: X and Y relay cells and perigeniculate interneurons. J Neurophysiol. 1981;45:107–120. doi: 10.1152/jn.1981.45.1.107. [DOI] [PubMed] [Google Scholar]
- 61.Smith EL, 3rd, Chino YM, Ridder WH, 3rd, Kitagawa K, Langston A. Orientation bias of neurons in the lateral geniculate nucleus of macaque monkeys. Vis Neurosci. 1990;5:525–545. doi: 10.1017/s0952523800000699. [DOI] [PubMed] [Google Scholar]
- 62.Sincich LC, Adams DL, Economides JR, Horton JC. Transmission of spike trains at the retinogeniculate synapse. J Neurosci. 2007;27:2683–2692. doi: 10.1523/JNEUROSCI.5077-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hammond P. Cat retinal ganglion cells: Size and shape of receptive field centres. J Physiol. 1974;242:99–118. doi: 10.1113/jphysiol.1974.sp010696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Levick WR, Thibos LN. Analysis of orientation bias in cat retina. J Physiol. 1982;329:243–261. doi: 10.1113/jphysiol.1982.sp014301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Watanabe M, Rodieck RW. Parasol and midget ganglion cells of the primate retina. J Comp Neurol. 1989;289:434–454. doi: 10.1002/cne.902890308. [DOI] [PubMed] [Google Scholar]
- 66.Schall JD, Perry VH, Leventhal AG. Retinal ganglion cell dendritic fields in old-world monkeys are oriented radially. Brain Res. 1986;368:18–23. doi: 10.1016/0006-8993(86)91037-1. [DOI] [PubMed] [Google Scholar]
- 67.Passaglia CL, Troy JB, Rüttiger L, Lee BB. Orientation sensitivity of ganglion cells in primate retina. Vision Res. 2002;42:683–694. doi: 10.1016/s0042-6989(01)00312-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Movshon JA, Thompson ID, Tolhurst DJ. Spatial summation in the receptive fields of simple cells in the cat’s striate cortex. J Physiol. 1978;283:53–77. doi: 10.1113/jphysiol.1978.sp012488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Barlow HB. Temporal and spatial summation in human vision at different background intensities. J Physiol. 1958;141:337–350. doi: 10.1113/jphysiol.1958.sp005978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Redmond T, Zlatkova MB, Vassilev A, Garway-Heath DF, Anderson RS. Changes in Ricco’s area with background luminance in the S-cone pathway. Optom Vis Sci. 2013;90:66–74. doi: 10.1097/OPX.0b013e318278fc2b. [DOI] [PubMed] [Google Scholar]
- 71.Medeiros FA, et al. Retinal ganglion cell count estimates associated with early development of visual field defects in glaucoma. Ophthalmology. 2013;120:736–744. doi: 10.1016/j.ophtha.2012.09.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Kerrigan-Baumrind LA, Quigley HA, Pease ME, Kerrigan DF, Mitchell RS. Number of ganglion cells in glaucoma eyes compared with threshold visual field tests in the same persons. Invest Ophthalmol Vis Sci. 2000;41:741–748. [PubMed] [Google Scholar]
- 73.Mulholland PJ, Redmond T, Garway-Heath DF, Zlatkova MB, Anderson RS. Spatiotemporal summation of perimetric stimuli in early glaucoma. Invest Ophthalmol Vis Sci. 2015;56:6473–6482. doi: 10.1167/iovs.15-16921. [DOI] [PubMed] [Google Scholar]
- 74.King WM, et al. Expansion of visual receptive fields in experimental glaucoma. Vis Neurosci. 2006;23:137–142. doi: 10.1017/S0952523806231122. [DOI] [PubMed] [Google Scholar]
- 75.Andriessen JJ, Bouma H. Eccentric vision: Adverse interactions between line segments. Vision Res. 1976;16:71–78. doi: 10.1016/0042-6989(76)90078-x. [DOI] [PubMed] [Google Scholar]
- 76.Parkes L, Lund J, Angelucci A, Solomon JA, Morgan M. Compulsory averaging of crowded orientation signals in human vision. Nat Neurosci. 2001;4:739–744. doi: 10.1038/89532. [DOI] [PubMed] [Google Scholar]
- 77.Balas B, Nakano L, Rosenholtz R. A summary-statistic representation in peripheral vision explains visual crowding. J Vis. 2009;9:1–18. doi: 10.1167/9.12.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Levi DM, Hariharan S, Klein SA. Suppressive and facilitatory spatial interactions in peripheral vision: Peripheral crowding is neither size invariant nor simple contrast masking. J Vis. 2002;2:167–177. doi: 10.1167/2.2.3. [DOI] [PubMed] [Google Scholar]
- 79.Greenwood JA, Bex PJ, Dakin SC. Positional averaging explains crowding with letter-like stimuli. Proc Natl Acad Sci USA. 2009;106:13130–13135. doi: 10.1073/pnas.0901352106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Strasburger H, Malania M. Source confusion is a major cause of crowding. J Vis. 2013;13:24. doi: 10.1167/13.1.24. [DOI] [PubMed] [Google Scholar]
- 81.Harrison WJ, Bex PJ. A unifying model of orientation crowding in peripheral vision. Curr Biol. 2015;25:3213–3219. doi: 10.1016/j.cub.2015.10.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Westheimer G, Hauske G. Temporal and spatial interference with vernier acuity. Vision Res. 1975;15:1137–1141. doi: 10.1016/0042-6989(75)90012-7. [DOI] [PubMed] [Google Scholar]
- 83.Flom MC, Weymouth FW, Kahneman D. Visual resolution and contour interaction. J Opt Soc Am. 1963;53:1026–1032. doi: 10.1364/josa.53.001026. [DOI] [PubMed] [Google Scholar]
- 84.Flom MC, Heath GG, Takahashi E. Contour interaction and visual resolution: Contralateral effects. Science. 1963;142:979–980. doi: 10.1126/science.142.3594.979. [DOI] [PubMed] [Google Scholar]
- 85.Kooi FL, Toet A, Tripathy SP, Levi DM. The effect of similarity and duration on spatial interaction in peripheral vision. Spat Vis. 1994;8:255–279. doi: 10.1163/156856894x00350. [DOI] [PubMed] [Google Scholar]
- 86.Yeshurun Y, Rashal E. Precueing attention to the target location diminishes crowding and reduces the critical distance. J Vis. 2010;10:16. doi: 10.1167/10.10.16. [DOI] [PubMed] [Google Scholar]
- 87.Wallis TS, Bex PJ. Visual crowding is correlated with awareness. Curr Biol. 2011;21:254–258. doi: 10.1016/j.cub.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Manassi M, Whitney D. Multi-level crowding and the paradox of object recognition in clutter. Curr Biol. 2018;28:R127–R133. doi: 10.1016/j.cub.2017.12.051. [DOI] [PubMed] [Google Scholar]
- 89.Chicherov V, Plomp G, Herzog MH. Neural correlates of visual crowding. Neuroimage. 2014;93:23–31. doi: 10.1016/j.neuroimage.2014.02.021. [DOI] [PubMed] [Google Scholar]
- 90.Farzin F, Rivera SM, Whitney D. Holistic crowding of Mooney faces. J Vis. 2009;9:18. doi: 10.1167/9.6.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Motter BC. Modulation of transient and sustained response components of V4 neurons by temporal crowding in flashed stimulus sequences. J Neurosci. 2006;26:9683–9694. doi: 10.1523/JNEUROSCI.5495-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Paik SB, Ringach DL. Retinal origin of orientation maps in visual cortex. Nat Neurosci. 2011;14:919–925. doi: 10.1038/nn.2824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Liu R, Patel BN, Kwon M. Age-related changes in crowding and reading speed. Sci Rep. 2017;7:8271. doi: 10.1038/s41598-017-08652-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Adams DL, Horton JC. A precise retinotopic map of primate striate cortex generated from the representation of angioscotomas. J Neurosci. 2003;23:3771–3789. doi: 10.1523/JNEUROSCI.23-09-03771.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Popovic Z, Sjöstrand J. Resolution, separation of retinal ganglion cells, and cortical magnification in humans. Vision Res. 2001;41:1313–1319. doi: 10.1016/s0042-6989(00)00290-x. [DOI] [PubMed] [Google Scholar]
- 96.Perry VH, Cowey A. The ganglion cell and cone distributions in the monkey’s retina: Implications for central magnification factors. Vision Res. 1985;25:1795–1810. doi: 10.1016/0042-6989(85)90004-5. [DOI] [PubMed] [Google Scholar]
- 97.Dacey DM. Physiology, morphology and spatial densities of identified ganglion cell types in primate retina. Ciba Found Symp. 1994;184:12–28; discussion 28–34, 63–70. doi: 10.1002/9780470514610.ch2. [DOI] [PubMed] [Google Scholar]
- 98.Callaway EM. Structure and function of parallel pathways in the primate early visual system. J Physiol. 2005;566:13–19. doi: 10.1113/jphysiol.2005.088047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Carlo CN, Stevens CF. Structural uniformity of neocortex, revisited. Proc Natl Acad Sci USA. 2013;110:1488–1493. doi: 10.1073/pnas.1221398110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Wetherill GB, Levitt H. Sequential estimation of points on a psychometric function. Br J Math Stat Psychol. 1965;18:1–10. doi: 10.1111/j.2044-8317.1965.tb00689.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.