Infiltration of CD8⁺ T cells into tumor cell clusters in triple-negative breast cancer

Significance

The infiltration of cytotoxic T cells into tumors is a critical factor in immunotherapy efficacy. We developed an algorithm to quantify infiltration level using whole-section immunohistofluorescence images from different patients. We observed consistent infiltration patterns of cytotoxic T cells (on the tumor cell cluster level) at the core and margin of each tumor. These spatial distributions enabled us to generate several hypotheses for mechanisms underlying the various infiltration levels. We used mathematical models to test which hypothetical mechanisms could recapitulate these patterns. One hypothesis, that of a fibrotic barrier, was shown to be unlikely. The other, involving a T cell chemorepellent, agrees with the data and can be tested in future experiments that directly measure the chemokine spatial patterns.

Abstract

Infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T lymphocytes into solid tumors is associated with good prognosis in various types of cancer, including triple-negative breast cancer (TNBC). However, the mechanisms underlying different infiltration levels are largely unknown. Here, we have characterized the spatial profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells around tumor cell clusters (tightly connected tumor cells) in the core and margin regions in TNBC patient samples. We found that in some patients, the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell density first decreases when moving in from the boundary of the tumor cell clusters and then rises again when approaching the center. To explain various infiltration profiles, we modeled the dynamics of T cell density via partial differential equations. We spatially modulated the diffusion/chemotactic coefficients of T cells (to mimic physical barriers) or introduced the localized secretion of a diffusing T cell chemorepellent. Combining the spatial-profile analysis and the modeling led to support for the second idea; i.e., there exists a possible chemorepellent inside tumor cell clusters, which prevents ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells from infiltrating into tumor cell clusters. This conclusion was consistent with an investigation into the properties of collagen fibers which suggested that variations in desmoplastic elements does not limit infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T lymphocytes, as we did not observe significant correlations between the level of T cell infiltration and fiber properties. Our work provides evidence that ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells can cross typical fibrotic barriers and thus their infiltration into tumor clusters is governed by other mechanisms possibly involving a local repellent.

Activated ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T lymphocytes have been demonstrated to be able to kill cancer cells via various mechanisms (1). Not surprisingly, stronger infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells into tumors generally associates with better prognosis; this has been demonstrated in various cancer types such as melanoma (2, 3), ovarian (4), colorectal (5), bladder (6), breast (7), and pancreatic (8) cancers. Furthermore, stronger infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells can predict patient response to standard of care chemotherapy (9–11) and to immune checkpoint blockade therapy such as anti–CTLA-4 (12) or anti–PD-1 (13, 14). Therefore, it is important to characterize the infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells in solid tumors and mechanisms that regulate this.

Several efforts have been launched to quantify the distribution of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells at the whole-tumor level. For example, the “immunoscore” was developed to evaluate the differences between the density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells at the core (CT) vs. the invasive margin (IM) of a tumor (15, 16). Promisingly, higher immunoscore, essentially the ratio of T cell density in CT over IM, is indicative of a good prognosis for patients with colorectal cancer and melanoma (15, 17).

On the other hand, solid tumors usually consist of tumor cell clusters interdigitated with nontumoral (stromal) cells, which include T cells among other cell types. Within the tumor core, T cells can be constrained to lie within stromal regions in various types of cancer (18–22). The limited infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells into individual tumor cell clusters is an indicator of worse prognosis (4, 23, 24) and lack of response to immune-blockade therapy (21, 25). Therefore, it is also important to quantify a complete spatial profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells at the tumor cell clusters level and investigate possible mechanisms underlying differences in the spatial-infiltration patterns in different patients.

At least two mechanisms have previously been proposed to qualitatively explain the limited infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells into tumor cell clusters: (i) the physical-barrier hypothesis (26–29) and (ii) the biochemical-barrier hypothesis (30, 31). In support of the physical-barrier hypothesis, ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells were mostly observed to move back and forth along extracellular matrix (ECM) fibers that are parallel to the surface of tumor cell clusters (29). Therefore, it might be difficult for ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells to move across the fibers toward tumor cell clusters. For the biochemical-barrier hypothesis, treating tumor spheroids (composed of both tumor cells and fibroblasts) with CXCL12 antibody can increase the number of infiltrating T lymphocytes (31).

In this paper, we focused on the infiltration profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells in samples from patients with triple-negative breast cancer (TNBC). TNBC represents 15–20% of all diagnosed breast cancers and lacks markers amenable to targeted therapies. Importantly, TNBC harbors heterogeneity in the level of immune infiltration and activation and furthermore the presence of tumor-infiltrated ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells inside of tumor cell clusters significantly reduces the relative risk of death from disease (24). Therefore, it is valuable to investigate mechanisms underlying different infiltration patterns in TNBC.

To evaluate whether a physical barrier or an alternative explanation such as a repellent-barrier hypothesis could better explain the infiltration pattern of the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells, we developed a method to quantify the spatial profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell density based on images containing immunohistochemical labeling of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells and cancer cells in whole-tumor samples from patients with TNBC. We quantified the infiltration pattern across both the tumor IM and the boundary of tumor cell clusters. By combining these spatial profile determinations with mathematical modeling studies and measurements of tissue fiber properties (such as length, density, thickness, alignment), our results strongly suggest that a physical barrier around tumor cell clusters is not responsible for limiting the infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells into either the tumor as a whole or the tumor cell clusters within. Instead, our results favor the hypothesis whereby a biochemical factor such as the balance between chemoattractant and chemorepellent concentrations is the most likely mechanism underlying the observed ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell location profile. Our findings imply that different ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell profiles are a consequence of the different signaling properties of cancer cells in different patients.

Results

Spatial Distribution of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T Cells in Primary Tumors of TNBC.

To gain an understanding of the factors impacting ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell distribution patterns, the localization of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells was investigated and quantified following immunostaining with anti-CD8 (to label ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells) and anti–pan-cytokeratin (to label epithelial tumor cells) in 28 whole-tumor TNBC specimens.

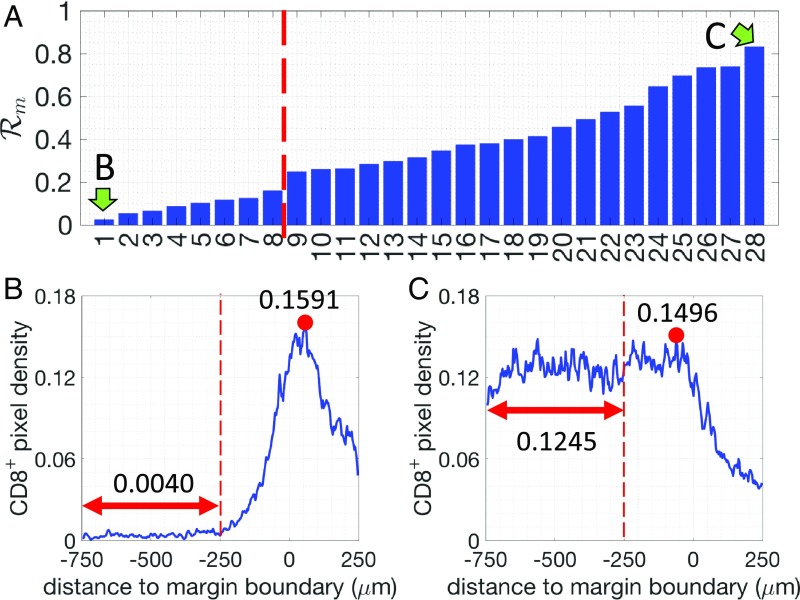
First, we assessed and quantified the infiltration patterns of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells across the tumor margin boundary (Fig. 1). For each specimen, we calculated the density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels with respect to their distance from the tumor margin boundary (Fig. 1). A 500-$\mathrm{\mu }$m-wide region centered on the margin boundary was defined as the “margin area” of a tumor (region I, Fig. 1A). Another 500-$\mathrm{\mu }$m-wide region (250–750 $\mathrm{\mu }$m inside the margin boundary) was defined as the tumor core region proximal to the tumor margin boundary (region II, Fig. 1A). For each specimen, we determined the infiltration level of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells as follows. The average density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels in region II ($<{\rho }_{II}>$) is compared with the maximum density in region I (${\rho }_I^{max}$) (Materials and Methods and Fig. 2). A ratio ${\mathcal{R}}_m$ is defined as $<{\rho }_{II}>/{\rho }_I^{max}$. ${\mathcal{R}}_m$ for all 28 patients and representative examples of profiles are presented in Fig. 2. Profiles of the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels are shown in SI Appendix, Fig. S1. Based on their value of ${\mathcal{R}}_m$, the tumors are divided into two groups: tumors where more ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells accumulate in the margin area (called “margin restricted”) vs. tumors that have more ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells infiltrated across the margin area (called “margin infiltrated”). Representative examples for each group are shown in Fig. 2. Note that the cutoff values for separating different groups are used just for illustrative purposes. The effect of ECM on the infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells, which is shown in later sections, is evaluated by the correlation analysis and does not depend on the assumed cutoffs.

Fig. 1.

(A) Illustration of different regions defined in the image analysis. (B) Illustration of the selected regions of tumor margin and tumor core. For the tumor margin, parts of the margins were excluded whenever the juxtatumoral tissue did not exist. For the tumor core, whenever possible three regions ($1.95\hspace{0.17em}\mathrm{m}\mathrm{m}\times 1.95$ mm) were selected for each tumor. (C) Illustration of the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$–T cell profile calculation for two levels: margin-boundary level and tumor cell cluster level (Materials and Methods). (D) Based on the spatial profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells at the tumor margin and the tumor core, 28 patients were grouped into two groups (margin-boundary level) and three groups (tumor cell cluster level), respectively.

Fig. 2.

(A) The density ratio of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels for all 28 patients analyzed (margin-boundary–level analysis). Two patients, indicated by green arrows, are selected to illustrate the corresponding ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$-pixel profiles. (B and C) Examples of the density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels (blue lines) for one margin-restricted tumor and one infiltrated tumor, respectively. The average densities in region II (Fig. 1A, between $-750\hspace{0.17em}\mathrm{\mu }$m and $-250\hspace{0.17em}\mathrm{\mu }$m, red double-arrowed lines) are as indicated. The maximal densities (red circles) in the margin area (region I) (between $-250\hspace{0.17em}\mathrm{\mu }$m and $250\hspace{0.17em}\mathrm{\mu }$m) are as indicated.

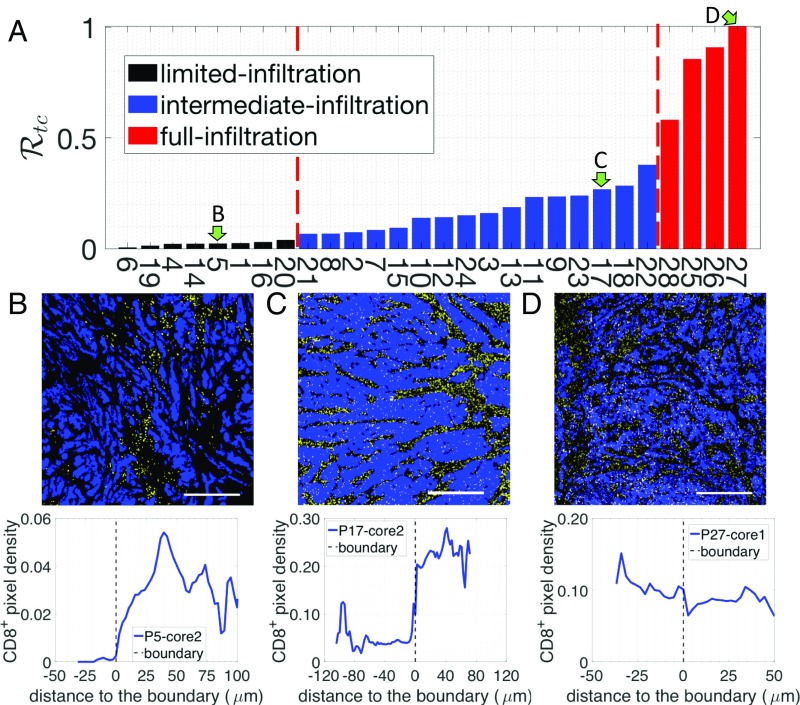
We next performed a more detailed assessment of the tumor cell clusters. For each sample, we selected three distinct regions within the tumor core (Fig. 1 A and B) and quantified the density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels with respect to their distance to the boundary of tumor cell clusters (Fig. 1C). The tumor core is defined as at least 250 $\mathrm{\mu }$m within the margin and the tumor cell clusters are the tumor islands within the tumor core, separated by stroma (Fig. 1A). To estimate the infiltration level of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ cells into tumor cell clusters, we compare the average density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixel inside tumor cell clusters ($<{\rho }_{in}>$) to the maximum density in the stroma (${\rho }_{out}^{max}$) (Materials and Methods and Fig. 1C). Based on a ratio ${\mathcal{R}}_{tc}$ defined as $<{\rho }_{in}>/{\rho }_{out}^{max}$, we further divided these tumors into three subgroups (Materials and Methods and Fig. 3A). The tumors in the first subgroup (6 patients) have ${\mathcal{R}}_{tc}$ values (averaged by three different regions of the tumor core) below 0.05 and are termed “limited-infiltration” cases (for a representative example, see Fig. 3B). Tumors in the second subgroup (18 patients) with ${\mathcal{R}}_{tc}$ values between 0.05 and 0.5 are termed “intermediate-infiltration” cases (for a representative example see Fig. 3C), while tumors in the third subgroup (4 patients) with ${\mathcal{R}}_{tc}$ values above 0.5 are termed “full-infiltration” cases (for a representative example, see Fig. 3D). The spatial profiles of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells for all patients are depicted in SI Appendix, Fig. S2. Note again that the cutoff values for separating different groups are used just for illustrative purposes. In addition, it is important to note that in most tumors of the intermediate-infiltration subgroup, the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell density profile inside the tumor cell clusters displays a specific feature: The density first decreases when moving from the boundary to the center of the tumor cell clusters and then rises again when approaching the center (Fig. 3D).

Fig. 3.

(A) The density ratio of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels ${\mathcal{R}}_{tc}$ for all 28 patients. Three patients, indicated by green arrows, are selected to illustrate the corresponding ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$-pixel profiles on the tumor cell cluster level. (B) Representative image with limited ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration inside of tumor cell clusters (Top) and the corresponding ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell distribution quantification (Bottom). (C) Representative image with intermediate ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration inside of tumor cell clusters (Top) and the corresponding ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell distribution quantification (Bottom). (D) Representative image with full ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration inside of tumor cell clusters (Top) and the corresponding ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell distribution quantification (Bottom). In the representative images, tumor epithelial cells are in blue (pan-cytokeratin) and ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells in yellow (CD8). (Scale bar, 500 $\mathrm{\mu }$m.)

Mathematical Models Considering only Reduced T Cell Motility Around Tumor Cell Clusters Predict T Cell Profiles That Are Inconsistent with Experimental Observations.

Next, we tested whether a mechanism-based model of T cell infiltration dynamics could explain the observed ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell localization patterns. We have limited this attempt to the tumor cluster-level data, as there are clear consistent structural elements in these findings (for example, we observed a consistent accumulation of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells outside of tumor cell clusters for all tumors with limited and intermediate ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration; SI Appendix, Fig. S2) as opposed to the ones related to the margin (for example, the peak of the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$-pixel density was not consistently located outside of the tumor margin; SI Appendix, Fig. S1). We believe that this difference arises because the overall geometry of the tumor is highly patient specific and this has a large effect on the ability to cross the margin.

It has been shown that the motility of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells can be reduced by ECM in human lung and ovarian tumors (19, 29), and this has been hypothesized to be responsible for the limited infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells into a solid tumor (27). Therefore, we used a mathematical modeling approach to test the effects of reduced T cell motility on the spatial distribution of T cells. An overview of our mathematical models is given in Table 1.

Table 1.

Summary of mathematical models in this work

Main hypothesis of the model	Detailed variations	Common features
Physical barrier	i)T cell motility toward tumor cell clusters is totally lost ii)T cell motility toward tumor cell clusters continuously decreases toward the center iii.a)T cell diffusion toward tumor cell clusters continuously decreases, approaching the edge of tumor cell clusters, but regains once T cells get inside iii.b)T cell chemotaxis ability is lost once T cells get inside iv)T cell motility toward tumor cell clusters continuously decreases, approaching the edge of tumor cell clusters, but regains once T cells get inside	Diffusion and chemotaxis coefficients are spatially modulated
Chemorepellent barrier	i)T cell chemotaxis ability is lost once T cells gets inside of tumor cell clusters ii)No additional assumptions on motility coefficients	T cell repellent is secreted by tumor cells

In all of our models, we assume that ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells follow the gradient of a chemoattractant and hence migrate toward a tumor cell cluster. Stochasticity in the migration of a T cell is modeled by an effective Brownian diffusion. The possible reduced motility of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells in the matrix of collagen fibers is modeled by reduced effective diffusion and chemotaxis coefficients (Materials and Methods).

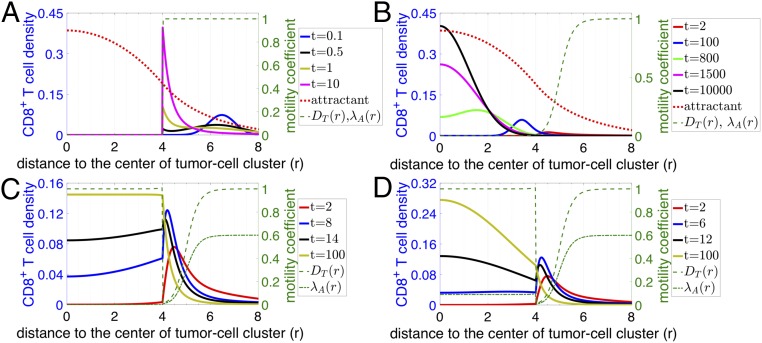
Initially, we tested an “abrogated T cell motility” scenario, in which dense collagen fibers would directly limit T cell migration as soon as a T cell contacts such fibers outside the tumor cell cluster. In this scenario, the density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells would reach its maximum exactly at the boundary of the dense fiber region and decay to lower values as we move through the stroma toward the tumor cluster (Fig. 4A). In the samples examined, ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells were not found inside the dense fiber region. Thus, this predicted profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells does not match the experimental observations as shown in Fig. 3. Based on this analysis, an abrogated T cell motility scenario is not a likely mechanism for the observed T cell infiltration patterns.

Fig. 4.

Time evolution of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell profiles predicted by various scenarios of models based on the physical-barrier hypothesis. For all graphs, the right y axis represents the diffusion ($D_T$) and/or chemotaxis coefficient (${\lambda }_A$) of T cells as indicated in the key. The left y axis represents the attractant concentration and the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell distribution at different time points (in model units) as indicated in the key. The distribution of attractant is the same for all models. (A) Abrogated T cell motility scenario where dense fibers prevent T cell infiltration. (B) Reduced T cell motility scenario within regions of dense fibers and tumor cell clusters. Note that ${\lambda }_A\left(r\right)$ is scaled by a factor of 1/30 in A and B. (C) Reduced followed by regained T cell motility scenario where diffusion of T cells ($D_T$) gradually decreases in the region with dense fibers but goes back to a normal level once T cells reach the region with tumor cells (dashed green line). ${\lambda }_A\left(r\right)$ is scaled by a factor of 1/50 in the plot and is assumed to be zero once T cells move into tumor cell clusters (dashed-dotted green line). (D) Reduced followed by regained T cell motility and chemotaxis scenario. Scenario is similar to that in C with the exception that T cells retain their chemotaxis ability inside of tumor cell clusters. ${\lambda }_A\left(r\right)$ is scaled by a factor of 1/50 in the plot (dashed-dotted green line).

Next, we tested a “reduced T cell motility” scenario in which the motility of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells is reduced, but not completely abrogated, in the region with dense collagen fibers (Materials and Methods). In this model, T cells are still able to migrate toward the center of the tumor cell cluster (Fig. 4B). Over time, the model predicts that the peak of T cell density gradually moves into the tumor core and eventually most ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells would occupy the center of the tumor cell cluster instead of accumulating at the boundary. Therefore, this hypothesis would lead us to expect that in different patients the density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell peaks would be located at various infiltration depths inside tumor cell clusters. However, this scenario was not observed in the samples investigated, rendering it unlikely as well that this simplified reduced T cell motility scenario represents the main driver of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration patterns.

In the aforementioned reduced T cell motility scenario, ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells maintain their reduced T cell motility as they infiltrate the tumor epithelium and thus display very limited movement inside the tumor cell cluster (Fig. 4B). We next modified this model by testing the role of a potential regaining of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell motility in the tumor cell clusters as a consequence of a decreased fiber network density (“reduced followed by regained T cell motility” scenario) (Fig. 4C; spatial pattern of the diffusion coefficient is represented as a dashed line). For example, T cell movement could be impeded by the dense collagen fibers in stroma, but would be regained as they progress within the tumor epithelium and move away from the dense fibers. In this scenario, ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells will be attracted to tumor cell clusters and transiently accumulate in the region with dense collagen fibers. Furthermore, if we assume that ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells are no longer attracted to the center of the tumor cell clusters once inside the clusters, in the intermediate time, ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells will then diffuse within the tumor cell cluster and their profile will monotonically decrease from the cluster boundary into the center of the cluster. In the long-time limit, ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells would be distributed homogeneously inside tumor cell clusters (Fig. 4C). At an early time in this reduced followed by regained T cell motility model, the modeled ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell profile (solid red line in Fig. 4C) is qualitatively similar to the observed limited-infiltration profiles (Fig. 3A and SI Appendix, Fig. S2). However, for the intermediate- and full-infiltration groups, only one-third (12 of 35) of the observed profiles (SI Appendix, Fig. S2, intermediate infiltration) are qualitatively similar to these predicted ones (solid blue, solid black, and solid light-green lines in Fig. 4C). Indeed, in the other samples with an intermediate level of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration, the observed profile is not monotonic inside tumor cell clusters but rather displays an accumulation of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells in the center of tumor cell clusters (Fig. 3B and SI Appendix, Fig. S2). In conclusion, this reduced followed by regained T cell motility scenario can explain only a limited range of the observed ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration profiles and only by assuming that these patterns are in a transient phase.

We further investigated other parameters and assumptions that could augment this reduced followed by regained T cell motility scenario. For example, we can allow the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells to also regain their chemotactic ability inside tumor cell clusters (Fig. 4D). This scenario permits an accumulation of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells inside tumor cell clusters but the steady-state shapes of the T cell profiles again do not fully recapitulate the experimental ones shown in Fig. 3B. Specifically, in the long-time steady-state limit of this model, instead of reaching a homogeneous distribution, the modeled density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells inside tumor cell clusters decreases from the center to the boundary (Fig. 4D, solid light-green line). This distribution of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells is similar to that in most of the fully infiltrated tumors but not to that in the others (Fig. 3C and SI Appendix, Fig. S2). In addition, similar to the modeling results in Fig. 4C, at an early time, the modeled profile (solid red line in Fig. 4D) is also qualitatively similar to the observed limited-infiltration profiles (Fig. 3A and SI Appendix, Fig. S2). In conclusion, a scenario with “reduced followed by regained T cell motility and chemotaxis” could explain the observed ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration profile in limited and fully infiltrated TNBC tumors.

Therefore, using mathematical models including a physical-barrier term giving rise to both a reduced followed by regained T cell motility and chemotaxis, we are able to explain the observed infiltration profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells in patients with limited or full infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells (SI Appendix, Fig. S2). However, this hypothesis cannot robustly explain the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell profiles for many patients with an intermediate infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells. Furthermore, we need to appeal to transient profiles in this type of model, which means that eventually we should expect the full infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells in the long-time limit for all patients. Based on the measurement of the motility coefficient of T cells in a tumor nest by Salmon et al. (19), one T cell can cover the length of 100 $\mathrm{\mu }$m (the typical size of tumor cell clusters observed in our samples) in 6 h with a diffusion coefficient of 5 $\mathrm{\mu }$m²/min. Therefore, T cells should be able to fully infiltrate the tumor cell clusters through diffusion within days, which is a very much shorter time scale than that of the clinical course of disease. However, patients with a full infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells are uncommon (only 4 of 28). These observations thus lead us to consider alternative mechanisms.

Mathematical Models with a Hypothetical Repellent Predict T Cell Profiles That Resemble Profiles Observed in Patient Data.

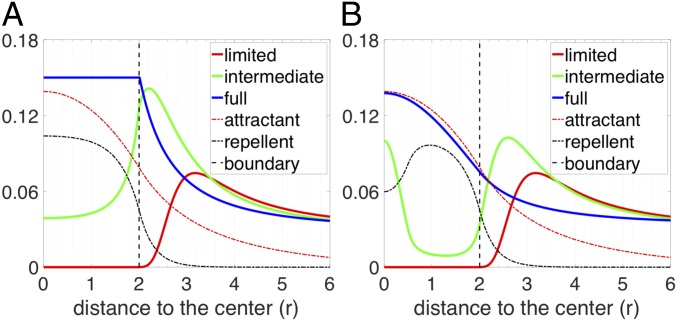
It is clear that biochemical signaling processes can play a role beyond purely biophysical ones in determining T cell infiltration. For example, Lyford-Pike et al. (32) explicitly showed that PD-L1 is enriched at the boundary of tumor cell clusters, which may create a biochemical immunoprotective “barrier” for tumor cell clusters. More recently, the role of cytokine signaling by tumor cells has been shown to be critical for infiltration in a genetically engineered mouse pancreatic cancer system (33). We therefore tested a simple scenario involving a repulsive interaction between ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells and cancer cells. Specifically, we hypothesized that (i) there is a repellent, secreted by cancer cells that are close to the boundary of tumor cell clusters; (ii) this repellent drives exclusion of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells from the region with high repellent concentration; and (iii) all cancer cells secrete a T cell attractant. In our model, if ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells strongly respond to the repellent, T cells would barely infiltrate into the tumor cell clusters (red solid lines in Fig. 5). In the same model, if the effect of the repellent is moderate, ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells can infiltrate into the tumor cell clusters (light-green solid lines in Fig. 5). In addition, depending on the profile of the repellent (determined by the source locations and the repellent diffusion coefficient) and the chemotactic ability of T cells, the modeled T cell profile can be monotonic (Fig. 5A) or nonmonotonic (Fig. 5B) inside tumor cell clusters. Finally, if the effect of the repellent is very weak, T cells will infiltrate extensively into the tumor cell clusters (blue solid lines in Fig. 5). In this case, T cells distribute homogeneously inside the tumor cell cluster (Fig. 5A) or accumulate in the center (Fig. 5B), depending on the profile of the repellent and the chemotactic ability of T cells in following the gradient of attractant. Notably, the profiles shown in Fig. 5 are all steady-state distributions of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells. To further demonstrate that the repellent-barrier model can capture features of the spatial profiles of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells, we used patient-specific parameters to successfully fit the model to the profiles derived from the samples. The corresponding results are shown in SI Appendix, Fig. S5. In conclusion, a scenario with both a repellent and an attractant of T cells could robustly explain all observed ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration patterns in TNBC tumors.

Fig. 5.

${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell profiles predicted by various scenarios of models based on the repellent-barrier hypothesis. For both graphs, the y axis represents the long-term distribution of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells and attractant and repellent (scaled) concentration as indicated in the key. (A) The chemotactic ability of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells in following the gradient of the attractant is assumed to be zero once T cells are inside of the tumor cell cluster ($r\le 2$). The region of the source of the repellent is assumed to be between $r=0$ and $r=2$. Depending on how strongly the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells react to the repellent, the infiltration level can be limited (${\lambda }_R=20$, ${\lambda }_A=30$), intermediate (${\lambda }_R=2$, ${\lambda }_A=30$), or full (${\lambda }_R=0$, ${\lambda }_A=10$). (B) The chemotaxis ability of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells following the gradient of the attractant is assumed to be spatially uniform. The region of the source of the repellent is assumed to be between $r=1$ and $r=2$. Depending on how strongly the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells react to the gradient of the repellent, the infiltration level can be limited (${\lambda }_R=40$, ${\lambda }_A=60$), intermediate (${\lambda }_R=10$, ${\lambda }_A=30$), or full (${\lambda }_R=0$, ${\lambda }_A=10$). The diffusion coefficient of repellent ($D_R=60$) is assumed to six times larger than that in A ($D_R=10$). Note that in A and B, the spatial profile of chemorepellent is scaled by a factor of 0.1 and 0.2, respectively.

Desmoplastic Elements Are Not Limiting Lymphocytic Infiltration in TNBC.

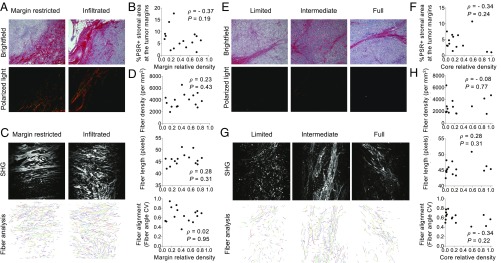
Our modeling results strongly suggest that a purely physical motility barrier cannot fully account for the variety of T cell infiltration patterns seen in our patients with TNBC. We therefore studied in detail whether this prediction applied to fibrosis (19, 34). Fibrosis is elevated in TNBC tumors relative to other breast cancer subtypes (35) as assessed through increased collagen cross-linking and thickening. We first assessed whether the stroma at the margin of tumors, where the infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells decreases, demonstrates increased collagen deposition and cross-linking as visualized by polarized-light imaging of Picrosirius Red-stained sections. We did detect thick collagen fibers at the tumor margin compared with the tumor core, consistent with previous observations (35). However, no significant correlations were observed between the thickness of collagen fibers and the level of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ cell margin infiltration (Fig. 6 A and B). To further characterize ECM status, we performed second harmonic generation (SHG) imaging using two-photon microscopy (Fig. 6C) that allowed us to quantify fiber density, fiber length, and fiber alignment. The fiber alignment is defined by the coefficient of variation (CV) of the angle for all fibers per tumor. The smaller the CV is, the more aligned the fibers are. This analysis revealed that the fiber density, fiber length, and fiber alignment at the margin of the TNBC tumor samples do not correlate with the level of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ cell margin infiltration (Fig. 6D).

Fig. 6.

Desmoplastic elements are not limiting lymphocytic infiltration in TNBC. (A) Representative images of Picrosirius Red staining at the tumor margins. Bright-field images (Upper) and matched polarized-light images (Lower) are presented. (B) Quantification of Picrosirius Red polarized-light signal in tumor margin areas. (C) SHG images (Upper) and representation of fiber individualization (Lower) using the CT Fire software (tumor margins). (D) Quantification of tumor margin fiber parameters as described. (E) Representative images of Picrosirius Red staining at the tumor core. Bright-field images (Upper) and matched polarized-light images (Lower) are presented. (F) Quantification of Picrosirius Red polarized-light signal in tumor core areas. (G) SHG images (Upper) and representation of fiber individualization (Lower) using the CT Fire software (tumor margins). (H) Quantification of tumor margin fiber parameters as described. Spearman correlation is shown.

To test the presence of a purely physical motility barrier at the tumor cell cluster level, we also performed the same type of measurements on collagen fibers in the tumor core (Fig. 6 E–H). Again, no significant differences in the properties of collagen fibers were observed among tumors with various infiltration levels into the tumor clusters (Fig. 6 E–H).

In conclusion, our data on the ECM structure in TNBC thus support our theoretical modeling results that disfavor the hypothesis of a stromal physical barrier preventing ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell infiltration. As has previously been suggested in pancreatic ductal adenocarcinoma (PDAC) (8), desmoplastic elements do not appear to be the critical factor limiting lymphocytic infiltration in TNBC either at the core or at the margin level.

Discussion

In this paper, we quantified the spatial distribution of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells with respect to their distance to both the tumor margin and the boundary of individual tumor cell clusters. Generally, we observed that (i) patients differ both in the infiltration across the margin and in the infiltration at the cluster level; (ii) for most samples, T cells mainly accumulate outside the tumor cell clusters; (iii) for some samples, T cells can effectively infiltrate the tumor cell clusters; and (iv) for other samples, the T cell profile is intermediate. This last possibility reveals a nonmonotonic distribution of T cells, i.e., a drop of T cell density at the boundary coupled with a second accumulation of T cells at the center of tumor cell clusters.

Based on the quantified ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell profiles on the tumor cluster level, we constructed various mathematical models to test two hypothesized contributors affecting the spatial distribution of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells: a physical motility barrier set up by the ECM fibers in the stroma and a biochemical inhibitor ultimately due to the cancer cells inside the tumor cell clusters. Mathematical models that include only physical-barrier effects can qualitatively capture many (but not all) spatial features of the T cell profiles. However, there is one significant shortcoming: The physical-barrier scenario predicts that the profiles observed should be transient and hence eventually T cells should infiltrate all tumors. This appears inconsistent with simple time-scale estimates. Also, our data show no correlation between cluster-level infiltration patterns and measures of typical ECM properties that could alter motility (Fig. 6). Furthermore, when observing the position of the dense-fiber region and the region where lymphocytes accumulate at the tumor margin, many lymphocytes can be found in the region close to the tumor cell clusters whereas the dense-fiber region is farther outside (SI Appendix, Fig. S3). Our interpretation of this observation is that the dense-fiber region might not be able to shield tumor cells from lymphocytes.

A biochemical model focusing on T cell repulsion can give rise to the observed spatial profiles as steady-state solutions; the different patterns correspond to different properties of cancer cells in different patients. We therefore favor this modeling framework. Of course, a definitive test would require experiments which would enable us to study the infiltration of T cells in a time-dependent manner or alternatively perturb possible mechanisms with drugs to directly test their effects on the infiltration pattern of T cells. For example, intravital imaging of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells inside mouse tumors might tell us whether there is an increased infiltration of T cells inside tumor cell clusters as the tumor progresses or vice versa. Increased infiltration would support the physical-barrier hypothesis whereas a more or less steady profile (or even a decreasing level of infiltration) would be more consistent with the chemorepellent hypothesis. Also, gene-expression analysis of tumor cells for infiltrated vs. noninfiltrated tumors might shed light on possible candidates of the chemorepellent and immunohistochemistry staining of the repellent as well as ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells on the same sample could confirm the model-predicted patterns of chemorepellent. Furthermore, ablation of a putative chemorepellent, using an antibody or gene knockdown in mouse models, for cases of limited infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells together with evidence of enhanced levels in infiltrated tumors, could confirm the role of the repellent in driving ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells out of tumor cell clusters.

We also investigated whether it is the stroma at the margin of the whole tumor that prevents the infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells on the whole-tumor level. To do so we manually determined the outer boundary of tumors and quantified the spatial profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells with respect to this manually curated boundary. Although an accumulation of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells is still observed around the manually curated tumor boundary for most patient samples, compared with the profiles quantified on the tumor cell cluster level for the same region, the peak of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell density profile is not always outside of the outer boundary. From the actual images, this difference can be partially explained by the existence of T cells in the stroma between tumor cell clusters but inside the tumor margin. This observation implies that (i) T cells can manage to get across the physical barrier if there is one and (ii) additional factors prevent T cells from further infiltrating the tumor. We have not tried to create an analogous mathematical model for these margin-related profiles, as one would clearly need to take into account the complex patient-specific geometry of the tumor and stroma. Nevertheless, our current repellent model offers a qualitative picture to understand why ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells do not fully infiltrate the whole tumor: ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells may have a difficult time infiltrating tumor cell clusters but still can move into the tumor core by following complex paths within the stroma.

For the biochemical barrier set up by the cancer cells, our current mathematical model uses an explicit diffusing repellent. In addition, in the model, the sources of the potential repellent are taken to lie at least partially inside of tumor cell clusters instead of being located exclusively at the boundary. This prediction could be verified once we have a good candidate for the repellent. Essentially, chemokines are the most likely candidates. For example, CXCL12, one of the chemokines that couples to ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T lymphocytes, has recently been shown to hinder the infiltration of T cells into spheroids formed by cancer cells and fibroblasts (31). Consistently, the gene-expression amplification of a chemokine cluster on chromosome 17 inversely correlates with the frequency of activated ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells (36). A different possibility relies on the recent demonstration that TGF-$\beta$ secreted by fibroblasts can contribute to exclusion of T cells at the margin (37); this might also happen on the tumor cell cluster level. In addition, another recent analysis using gene-expression data from The Cancer Genome Atlas database suggested that MAPK pathways are linked to reduced infiltration of cancer-fighting immune cells (38). Further investigation of the downstream secreted proteins of these MAPK pathways may reveal additional possible candidates for the predicted repellent.

In a preliminary investigation along these lines, we investigated the gene-expression data of the bulk tumors of patients studied. The data are published in ref. 39 (GSE58644) and we focused on the gene-expression data of the 28 patients analyzed in this work. However, according to our analysis described in SI Appendix, there were no specific chemokines that were statistically enriched in tumors with limited infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells. Perhaps we need to await gene-expression data from samples that were more specifically gathered from tumor islands; eventually the gold standard would be spatially registered single-cell measurements. Nevertheless, the results to date indicate that CCL28 might be worth investigating.

On the other hand, the interactions between other types of immune cells and ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells can also be important for the final distribution of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells. For example, the exclusion of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells from tumors can be at least partially caused by the suppressed recruitment of one specific type of dendritic cell (${\mathrm{C}\mathrm{D}\mathrm{103}}^{+}$) (40). Similarly the exclusion of T cells in a recent pancreatic cancer model could depend on myeloid suppressor cells (33). Therefore, investigating the spatial correlation of other types of immune cells with the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells may provide additional clues regarding the infiltration profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells.

In the current model, we did not consider the proliferation and death of T cells. There exists a possibility that those processes can contribute quantitatively to the spatial profiles of T cells. However, to explain the nonmonotonic distribution of T cells inside the tumor cell cluster, a complex spatially dependent hypothesis on the cell birth/death rates would be required. We checked the expression of Ki67 in patient specimens using immunohistochemistry (IHC). In the corresponding images, lymphocytes are identified as cells with smaller and round nuclei. Examples are summarized in SI Appendix, Fig. S4. Qualitatively, most lymphocytes in the lymphocyte cluster in stroma are not ki${\mathrm{67}}^{+}$, which suggests that the accumulation of lymphocytes outside of tumor cell clusters is mainly determined by the transport of lymphocytes. On the other hand, for patients belonging to the full-infiltration group, many lymphocytes inside tumor cell clusters are also not ki${\mathrm{67}}^{+}$, which suggests that those lymphocytes infiltrate into tumor cell clusters via transport. Therefore, based on the current experimental observations and modeling analysis, we argue that the spatially dependent motility should be the major factor contributing to the observed ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell profiles.

In summary, we studied the spatial profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells around tumor cell clusters and around the tumor as a whole, in patients with TNBC. Combining data analysis and mathematical modeling, we provide evidence against the hypothesis that a physical barrier created by dense collagen fibers prevents the infiltration of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells into tumors and tumor cell clusters. Instead, we propose that there could be a type of chemorepellent inside tumor cell clusters that prevents the infiltration. Further experiments on characterizing the level and patterns of chemokines inside tumor cell clusters will be needed to verify the hypothesis in differing patient groups.

Materials and Methods

Calculation of the Density Profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T Cells with Respect to Their Distance to the Tumor Margin Boundary.

We developed an algorithm to extract the spatial information of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells from section images. For a given tissue section image, we manually draw the tumor margins. Next, a binary image of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels is generated by manually selecting a cutoff for the fluorescence intensity of CD8. With the spatial information of tumor margins and each ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixel, the distance ($d$) between each ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixel and its nearest pixel on the tumor-margin boundary is calculated. The distance is binned and the size of the bin is 3 pixels (0.325 $\mathrm{\mu }$m ×3). In addition, for all pixels, the nearest distance between each pixel and its nearest pixel on the boundaries is also calculated. Therefore, for each bin of the distance, the number of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels ($N_{\mathrm{C}\mathrm{D}\mathrm{8}}\left(d\right)$) can be normalized by the total number of pixels ($N_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\left(d\right)$), which gives the density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels ($\rho \left(d\right)$) as a function of the distance to their nearest boundary pixels.

A ratio ${\mathcal{R}}_m$ is defined to divide patients into two groups. The definition of ${\mathcal{R}}_m$ is given by the spatial average of $\rho$ between $d=-750\hspace{0.17em}\mathrm{\mu }$m and $d=-250\hspace{0.17em}\mathrm{\mu }$m divided by the maximum of $\rho$ between $d=-250\hspace{0.17em}\mathrm{\mu }$m and $d=250\hspace{0.17em}\mathrm{\mu }$m. Here negative distance means the pixel is inside the tumor-margin boundary and vice versa.

Calculation of the Density Profile of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T Cells with Respect to Their Distance to the Boundary of Tumor Cell Clusters.

For a given tissue section image, regions of tumor cell clusters are identified by manually selecting a cutoff for the fluorescence intensity of pan-cytokeratin. Second, the boundary of tumor cell clusters is identified using ImageJ based on the binary image of tumor cell clusters. Next, a binary image of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels is generated by manually selecting a cutoff for the fluorescence intensity of CD8. With the spatial information of tumor cell clusters and each ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixel, we then separate ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels into two sets based on whether they overlap with tumor cell clusters or not. For ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels in each set, the distance ($d_{\mathrm{i}\mathrm{n}}$ and $d_{\mathrm{o}\mathrm{u}\mathrm{t}}$) between each ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixel and its nearest pixel on the boundaries is calculated. The distance is binned and the size of the bin is one pixel. At the same time, for all pixels, the nearest distance between each pixel and its nearest pixel on the boundaries is also calculated. Therefore, for each bin of the distance, the number of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels [$N_{\mathrm{i}\mathrm{n}}^{\mathrm{C}\mathrm{D}\mathrm{8}}\left(d_{\mathrm{i}\mathrm{n}}\right)$ and $N_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{C}\mathrm{D}\mathrm{8}}\left(d_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$] can be normalized by the total number of pixels [$N_{\mathrm{i}\mathrm{n}}^{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\left(d_{\mathrm{i}\mathrm{n}}\right)$ and $N_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\left(d_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$], which gives the density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ pixels [$\rho \left(d_{\mathrm{i}\mathrm{n}}\right)$ and $\rho \left(d_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$] as a function of the distance to their nearest boundary pixels.

A ratio $\mathcal{R}$ is defined to divide patients into three groups. The definition of $\mathcal{R}$ is given by the spatial average of $\rho \left(d_{\mathrm{i}\mathrm{n}}\right)$ divided by the maximum of $\rho \left(d_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$; i.e., $\mathcal{R}=<\rho \left(d_{\mathrm{i}\mathrm{n}}\right)>/max\left(\rho \left(d_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)\right)$.

Mathematical Modeling of the Reduced T Cell Motility by Collagen Fibers.

In this type of model, we assume that ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells follow the gradient of a chemokine (attractant) and migrate toward a tumor cell cluster. The stochasticity of the migration of a T cell is modeled by an effective Brownian diffusion. The corresponding mathematical equations are

$$\begin{array}{cc}\hfill \frac{\partial A}{\partial t}& =\frac{D_A}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial A}{\partial r}\right)+{\alpha }_A\cdot C-{\beta }_A\cdot A\hfill \\ \hfill \frac{\partial T}{\partial t}& =\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2{D}_T\cdot \frac{\partial T}{\partial r}\right)-\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2{\lambda }_A\cdot T\cdot \frac{\partial A}{\partial r}\right),\hfill \end{array}$$ [1]

where $A$ is the concentration of the chemotaxis attractant; $T$ is the density of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells; $D_A$ and $D_T$ are the diffusion coefficients of the chemotaxis attractant and ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells, respectively; ${\lambda }_A$ is the chemotaxis coefficient of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells; ${\alpha }_A$ is the secretion rate of the chemotaxis attractant by tumor cells; and ${\beta }_A$ is the degradation rate of the attractant.

In our model, $D_A$ is set to be 10. $D_T$ and ${\lambda }_A$ are a function of $r$ (the distance from the center of a tumor cell cluster). In Fig. 4A, $D_T$ = 0 and $D_T^0$ ($=1$) inside and outside of the tumor cell cluster, respectively. In Fig. 4B, $D_T=D_T^0\left[r^n/\left(r^n+R_0^n\right)+\delta \right]$ and ${\lambda }_A={\lambda }_A^0\left[r^n/\left(r^n+R_0^n\right)+\delta \right]\hspace{0.17em}$. $R_0=5$, $\delta =0.001$, and ${\lambda }_A^0=30$. In Fig. 4C, $D_T$ = $D_T^0$ ($=1$) inside of the tumor cell cluster. Outside of the tumor cell cluster, $D_T=D_T^0{r}^n/\left(r^n+R_0^n\right)\hspace{0.17em}$. ${\lambda }_A$ = 0 and ${\lambda }_A={\lambda }_A^0{r}^n/\left(r^n+R_0^n\right)$ inside and outside of the tumor cell cluster, respectively. In Fig. 4D, $D_T$ is the same as that in Fig. 4C, whereas ${\lambda }_A$ = $0.15\times {\lambda }_A^0$ and ${\lambda }_A={\lambda }_A^0{r}^n/\left(r^n+R_0^n\right)$ inside and outside of the tumor cell cluster, respectively. ${\alpha }_A=1$ and ${\beta }_A=0.8$ in Fig. 4. The density of tumor cells $C$ is equal to 1 and 0 for $r\le 4$ and $r>4$, respectively. The boundary condition to solve Eq. 1 is ${\left.\left(\partial A/\partial r\right)\right|}_{r=0}$, ${\left.\left(\partial T/\partial r\right)\right|}_{r=0}=0$, ${\left.A\right|}_{r=10}=0$, and ${\left.\left(\partial T/\partial r\right)\right|}_{r=10}=0$.

Mathematical Modeling of the Effects of a Hypothesized Repellent.

In this type of model, the basic assumptions are the same as above: ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells follow the gradient of a chemokine (attractant) and migrate toward a tumor cell cluster and the stochasticity of the migration of a T cell is modeled by an effective Brownian diffusion. Furthermore, there exists a region inside a tumor cell cluster where the ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cell repellent is secreted. The corresponding mathematical equations are

$$\begin{array}{cc}\hfill \frac{\partial A}{\partial t}& =\frac{D_A}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial A}{\partial r}\right)+{\alpha }_A\cdot C-{\beta }_A\cdot A\hfill \\ \hfill \frac{\partial R}{\partial t}& =\frac{D_R}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial R}{\partial r}\right)+{\alpha }_R\cdot C-{\beta }_R\cdot R\hfill \\ \hfill \frac{\partial T}{\partial t}& =\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2{D}_T\cdot \frac{\partial T}{\partial r}\right)-\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2{\lambda }_A\cdot T\cdot \frac{\partial A}{\partial r}\right)\hfill \\ \hfill & \hspace{1em}+\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2{\lambda }_R\cdot T\cdot \frac{\partial R}{\partial r}\right),\hfill \end{array}$$ [2]

where $R$ is the concentration of the chemotaxis repellent; $D_R$ is the diffusion coefficient of the chemotaxis repellent; ${\lambda }_R$ is the chemotaxis coefficient of ${\mathrm{C}\mathrm{D}\mathrm{8}}^{+}$ T cells with respect to the repellent $R$; and ${\alpha }_R$ and ${\beta }_R$ are the secretion and degradation rates of the chemotaxis repellent, respectively.

Here, $D_R$ ($=10$) and $D_T$ ($=1$) are constants. For different T cell profiles in Fig. 5, the values of ${\lambda }_R$ and ${\lambda }_A$ are described in the Fig. 4 legend. ${\alpha }_R=85$, ${\beta }_R=80$. The density of tumor cells $C$ is equal to 1 and 0 for $r\le 2$ and $r>2$, respectively. The boundary condition to solve Eq. 2 is ${\left.\left(\partial A/\partial r\right)\right|}_{r=0}$, $\left(\partial R/\partial r\right){|}_{r=0}$, ${\left.\left(\partial T/\partial r\right)\right|}_{r=0}=0$, $A{|}_{r=10}=0$, ${\left.R\right|}_{r=10}=0$, and ${\left.\left(\partial T/\partial r\right)\right|}_{r=10}=0$.

Sample Collection and Selection.

Samples were collected from patients undergoing breast surgeries at the McGill University Health Center (MUHC) between 1999 and 2012. All patients provided appropriate prior informed consent. Human tissue samples and patient information used in this study were collected under protocols approved by the McGill University Health Centre Research Ethics Board (studies SDR-99-780 and SDR-00-966). All tissues were snap-frozen in O.C.T. Tissue-Teck Compound within 30 min of removal. For the purposes of this study, samples were selected according to the following criteria: therapy-naive at time of surgical excision; clinically documented lack of expression/amplification of ER, PR, and HER2; a histological subtype assignment of invasive ductal carcinoma (not otherwise specified) [IDC (NOS)]; and availability of matched formalin-fixed paraffin-embedded (FFPE) tumor blocks. Information regarding clinical variables and disease course (follow-up) was obtained through review of medical records at the MUHC. Five-micrometer sections from frozen tissue were prepared for each sample, subjected to routine hematoxylin and eosin (H&E) staining, and evaluated by an attending clinical pathologist with expertise in breast tissue to identify invasive, in situ, and normal components.

Primary Antibodies for IHC and Immunohistofluorescence (Table 2).

Table 2.

Primary antibodies

Ab	Target clone	Reference	Company	Dilution	Application	Antigen retrieval
Ki67	30-9	790-4286	Roche	1, prediluted	IHC	EDTA
CD8a	C8/144B	M710301-2	DAKO	1/50	IHF	Citrate
Pan-cytokeratin	AE1/AE3 and PCK26	760-2135	Ventana	1/2	IHF	Citrate

IHF, immunohistofluorescence.

IHC protocol.

Sections were deparaffinized and conditioned and antigens were retrieved using proprietary buffers (pH 6 or pH 9). Slides were blocked for 5 min with Power Block reagent. Primary antibodies were applied at optimized concentrations overnight at $\mathrm{4}\hspace{0.17em}°$C, followed by 30 min of incubation with SignalStain Boost (Cell Signaling). Detection was performed with a DAB substrate kit (Cell Signaling). Slides were counterstained with Harris Hematoxylin.

IHF protocol.

Sections were deparaffinized and conditioned and antigens were retrieved using proprietary buffers (pH 6 or pH 9). Slides were blocked for 5 min with Power Block reagent. Primary antibodies were applied at optimized concentrations overnight at $\mathrm{4}\hspace{0.17em}°$C, followed by 30 min of incubation with SignalStain Boost (Cell Signaling). Detection was performed with Tyramide Signal Amplification (TSA) kits (Thermo Fisher Scientific). Slides were counterstained with DAPI.

Picrosirius Red microscopy and imaging.

FFPE tumor tissue tissues were sectioned and stained using 0.1% Picrosirius Red (PSR) (Direct Red 80; Sigma) and counterstained with Weigert’s Hematoxylin, as per Valerie Weaver’s lab protocol described in (35). PSR-polarized imaging was performed on an inverted Axio Observer Z1 microscope (Carl Zeiss Canada), using a 10×objective (PLAN NEOFLUAR, N.A. 0.30, Ph 1) with linear polarizers and a quarter-wave plate. Halogen lamp intensity was kept constant for both image types, and an exposure time that optimized the signal-to-noise ratio was chosen and kept constant within each image type. All images were digitally captured using Luminara’s INFINITY3 color CCD camera (no. INFINITY3-6URC). Ten images were taken for each tumor (5 at tumor margins and 5 within tumor core). Images were quantified using ImageJ. Briefly, a minimal intensity threshold was used to eliminate the background and then the fiber density was measured as percentage of stromal area covered by fibers in each image. This was performed on the whole image for margin images; for intratumoral stroma, stromal areas were manually identified from matched bright-field images and delineated before quantification.

SHG microscopy and imaging.

H&E sections were imaged using a Zeiss Axioexaminer upright microscope (Carl Zeiss Canada). SHG signal was generated using 830-nm excitation light from a Chameleon (Coherent) laser using a 20×objective (PLAN APOCHROMAT, N.A. 0.8, DIC). All images were acquired with photomultiplier tube detectors and using ZEN black software with consistent parameters. The measurement was performed as per Valerie Weaver’s lab protocol described in (35). Six images were taken for each tumor (three at the tumor margins and three within the tumor core). Fiber individualization and quantitation of fiber parameters were performed using CT Fire software (freely available at loci.wisc.edu/software/ctfire).