Modeling groundwater nitrate concentrations in private wells in Iowa

Abstract

Contamination of drinking water by nitrate is a growing problem in many agricultural areas of the country. Ingested nitrate can lead to the endogenous formation of N-nitroso compounds, potent carcinogens. We developed a predictive model for nitrate concentrations in private wells in Iowa. Using 34,084 measurements of nitrate in private wells, we trained and tested random forest models to predict log nitrate levels by systematically assessing the predictive performance of 179 variables in 36 thematic groups (well depth, distance to sinkholes, location, land use, soil characteristics, nitrogen inputs, meteorology, and other factors). The final model contained 66 variables in 17 groups. Some of the most important variables were well depth, slope length within 1 km of the well, year of sample, and distance to nearest animal feeding operation. The correlation between observed and estimated nitrate concentrations was excellent in the training set (r-square = 0.77) and was acceptable in the testing set (r-square = 0.38). The random forest model had substantially better predictive performance than a traditional linear regression model or a regression tree. Our model will be used to investigate the association between nitrate levels in drinking water and cancer risk in the Iowa participants of the Agricultural Health Study cohort.

Graphical Abstract

INTRODUCTION

Nitrate is one of the most common anthropogenic contaminants of groundwater.¹ Nitrate ingestion has been linked to methemoglobinemia, adverse reproductive outcomes, and specific cancers.² The U.S. Environmental Protection Agency has set the maximum contaminant level (MCL) for nitrate in municipal drinking water supplies at 10 mg/L as nitrate-nitrogen (~44 mg/L as nitrate) and the World Health Organization guideline is 50 mg/L as nitrate. The MCL was set to protect against the development of methemoglobinemia in infants; however, long-term exposures and risks of chronic diseases were not considered.² Nitrate in drinking water is a health concern because under certain conditions ingestion results in the endogenous formation of carcinogenic N-nitroso compounds (NOC).³ Endogenous formation of NOCs can occur in the gastrointestinal tract of humans when nitrate-derived nitrosating agents react with amines and amides in the absence of inhibitors such as vitamin C. Dietary sources of amines and amides include meats and fish. The International Agency for Research on Cancer determined that nitrate and nitrite ingestion under such conditions is “probably carcinogenic to humans”.⁴

The contamination of water sources by nitrogen (N) is of increasing concern because the amount of anthropogenic nitrogen produced and entering the environment, largely via fertilizer, has dramatically increased over recent decades and currently exceeds biological nitrogen fixation in terrestrial systems.^5–7 Fertilizer N use increased 10-fold between 1950 and the early 1980s.⁸ Nitrogen at the land surface and in soils can readily leach to groundwater. Public water supplies are regularly monitored and usually meet the nitrate MCL even in agricultural areas; however, private wells are typically tested when constructed or when a property is sold but are not routinely monitored, and a recent national summary of nutrients in water resources reported that 22% of private wells in agricultural areas exceeded the nitrate MCL.⁸ Due to the lack of regulation, measurement data for nitrate and other water contaminants is sparse. Therefore, various modeling approaches have been used to estimate nitrate concentration in groundwater, including regression (linear, nonlinear, logistic)^9–14 and, more recently, classification and regression trees¹⁵ and random forest.^16–18 In general, the models represent N sources applied to the land surface and transport and attenuation of nitrate in soils and groundwater.

Groundwater nitrate levels at a well depend on many factors, including nitrogen sources, climate, soils, geology, groundwater geochemistry, the land surface area contributing to the well, and travel time in the aquifer. Here we consider these factors to develop a random forest regression model to predict nitrate levels in private drinking water wells in Iowa with the goal of accurately describing nitrate exposures from private well drinking water sources in Iowa. The model will be used to predict nitrate concentrations in drinking water for Iowa private well users in the Agricultural Health Study (AHS), a cohort of about 90,000 licensed pesticide applicators and their spouses in Iowa and North Carolina who primarily use private wells for their drinking water.¹⁹ We modeled nitrate levels in Iowa because the majority (65%) of the cohort resided there at enrollment and the U.S. Geological Survey has characterized aquifer properties in the glaciated U.S., which generated additional data for Iowa. The AHS represents a unique population for prospectively investigating the association between drinking water nitrate exposure and risk of adverse health outcomes, focusing on chronic diseases that have been studied in limited fashion previously. Given the higher expected exposures among users of private wells compared to public water supplies, studying the population using private wells may provide new insights into disease risk.

The objectives of the study were (1) to assemble a comprehensive data set of nitrate measurement data for private wells and predictor variables representing the sources, transport, and fate of nitrogen in soils and groundwater, and (2) to use the data to develop and test a random forest model for estimating past groundwater nitrate exposure in private wells. The exposure timeframe (early 1990s) for our model corresponds to the enrollment period for the cohort (1993–1997).

The modeling approach has several unique aspects. First, statistical water quality models at large spatial scales typically are snapshots in time that are intended for aquifer vulnerability mapping. In contrast, our model includes an explicit temporal component to accommodate historical N input and three decades of nitrate measurements in order to predict past exposures. Second, the model includes aquifer intrinsic susceptibility variables representing the entire thickness of glacial deposits, which ranges up to 157 m for the data set. Prior groundwater quality models relied on soil variables that have a maximum depth of 2 m.^10,11,13,20 Third, our modeling approach of random forests considers many potentially correlated explanatory variables and models interactions between variables when estimating nitrate concentrations at individual wells.^16,17 Fourth, random forest is an ensemble method based on bootstrap aggregation of regression trees, which typically outperforms traditional models such as logistic regression in prediction.^21,22

MATERIALS AND METHODS

Study Area and Nitrate Measurement Data

We compiled 34,084 nitrate measurements from private wells sampled in 1980 through 2011 by the following programs: the Iowa Grants to Counties Water Well Program, the Iowa Private Well Tracking System, the Iowa Statewide Rural Well Water Survey, the Iowa Community Private Well Study, and the U.S. Geological Survey (USGS) (Table S1, Supporting Information). We used only those wells with the most accurate locations as determined by global positioning system (GPS) measurements, topographic quadrangle maps, and geocoded street addresses. Seventy-five percent of the well locations were based on geocoded residential street addresses.

The private wells were completed in both Quaternary unconsolidated deposits and bedrock aquifers. The unconsolidated deposits form the glacial aquifer system¹³ and comprise alluvium, loess, and glacial till,²³ collectively referred to herein as “glacial deposits.” Whereas loess and coarse-grained alluvium can readily transmit water and nitrate, fine-grained glacial till commonly restricts their movement. Glacial deposits blanket Iowa except for bedrock outcrops in the northeastern part of the state. The deposits overly multiple stacked bedrock aquifers consisting chiefly of limestone, dolomite, and sandstone that range in age from the Cretaceous to the Cambrian. The bedrock aquifers are separated by confining units comprising shale, siltstone, and other rocks.

Nitrate data were reported either as nitrate-nitrogen or nitrite-plus-nitrate as NO₃⁻, and the latter were converted to nitrate-nitrogen (hereafter referred to as “nitrate”). Values below the detection limit were imputed from a log-normal distribution of uncensored data.²⁴ Same-day samples at the same well location and depth were excluded if their standard deviation was 5 mg/L nitrate-N or more, otherwise the average of such samples was used. Nitrate data were natural log transformed prior to modeling and separated into training (n = 11,931) and testing (n = 22,153) data subsets. The training data were obtained by randomly selecting approximately half of the wells sampled in the 1980s and 1990s and one-third of wells sampled in the 2000s, maintaining the overall ratio of wells within and above bedrock (approximately 2:1, respectively). Sampling dates in the training data subset ranged from May 1984 to November 2011, and those in the testing data set were from June 1980 to August 2011.

Predictor Variables

Using a geographic information system (GIS), we constructed a set of nearly 300 variables to be used as model inputs. Variables tested in the model describe the sources, transport, and attenuation of N in soils and groundwater and included agricultural land use, nitrogen input to the land surface (fertilizers and animal waste), soils, geology, climate, irrigation, aquifer characteristics, and other factors. As mentioned above, a unique aspect of the study was development of a suite of aquifer variables representing the intrinsic susceptibility of aquifer materials near the well. These variables included the total thickness of fine-grained glacial materials above the well screen, average and minimum thickness of such materials near sampled wells, and horizontal and vertical hydraulic conductivities of all glacial deposits near the well (see Table S2, Supporting Information for descriptions of select variables). Although aquifer properties were not available for bedrock aquifers, recharging groundwater moves through the overlying unconsolidated deposits into the bedrock, and therefore the surficial aquifer properties influence the quality of deeper groundwater. Data on the depth to the top of the well screen were unavailable so we calculated the value as screen depth = well depth – 3, where 3 ft is a typical screen depth for private wells in the region. Additional details on the variables and data sources are provided in the Supporting Information.

We evaluated buffer sizes of 500 m and 1 km for compiling land use and other predictor variables. Buffers of 1 km yielded better prediction of log nitrate and were used in the final model. Prior researchers concluded that “circular area surrogates” are appropriate when it is impractical to use a physically based approach such as a numerical flow model to determine the contributing land surface area to a well.²⁵ Such models do not exist in Iowa at the state scale.

Because sampling dates encompassed three decades, we compiled time-sensitive predictor variables in a manner consistent with the residence time of water and contaminants in soils and aquifers (i.e., “lag time”). To create a consistent measure of agricultural intensity over the decades, we aggregated several agricultural land-use categories, including cropland, pasture, pasture/hay, alfalfa/hay, and others as described in the Supporting Information. Aggregating crop categories is appropriate because the groundwater sampled by a well is a mixture of ages rather than a single year or even a single decade, and crops commonly are rotated over time. Long-term crop rotations in Iowa include corn, soybeans, oats, and alfalfa hay.²⁶ The agricultural intensity variable also reflects additional N sources such as mineralization and fixation by legumes, which can exceed inorganic fertilizer N in Iowa soils.²⁷

Appropriate years of land use were determined empirically by testing all of the above land cover years that occurred before the sampling date of a well, which introduces lag time into the model. Numerical groundwater flow models have shown that groundwater travel time increases with increasing distance up-gradient of a well.²⁸ Inclusion of multiple well buffer radii and land-use years represented the interaction of contributing area and groundwater travel time. For example, if 1990 agricultural land cover within a 1-km radius well buffer was important in the model, it would suggest a 10-yr travel time within 1 km of a well sampled in 2000, and previous years would suggest longer travel times. A 10-yr travel time is reasonable for areas with well-drained soils and flat topography.⁸ Travel time typically is much longer for deeper wells in bedrock aquifers. For this reason, well depth and a variable indicating whether the aquifer was unconfined or confined were tested in the models. Land use near deep bedrock wells is potentially relevant despite uncertainties of the contributing areas and apparent long travel times. Prior researchers noted that wells, boreholes, and natural preferential flow paths allowed contaminants to reach public supply wells or aquifer depths more quickly than expected.²⁹ In Iowa, some deeper rural wells have defects in the upper parts of iron casing that permit entry of shallow groundwater and nitrate.³⁰ Time-sensitive variables representing fertilizer and animal manure use were handled in similar fashion, and these details are in the Supporting Information.

Statistical Analysis

We used tree-based methods for building the prediction model for log nitrate concentration because classification and regression trees are able to handle interactions, non-linearity, and missing values.^22,31–33 Tree-based approaches predict decisions based on a sequential splitting pattern that resembles an inverted tree, with the root at the top and nodes that divide observations into branches below. At the bottom are leaves that provide the predicted value. The nodes are selected iteratively with the most predictive variable at each node used to split the observations into two branches according to that variable. The regression tree algorithm recursively partitions the training data set into smaller and smaller subsets of increasing homogeneity in the outcome variable.²² Within each branch, the splitting continues until the model meets specified stopping criteria, such as a minimum number of observations per leaf or a complexity parameter set to control the growth of the tree.

With the random forest method, a large number of randomized regression trees are grown from bootstrap samples and combined to form an aggregated predictor, named the random forest.²¹ The process of combining many trees built from bootstrap samples of the learning data sets is known as bootstrap aggregation, or bagging, and is a form of ensemble learning. In addition to bootstrapping, another source of randomness in a random forest is the use of a subset of predictor variables for splitting nodes to build each tree. The best predictor to split each node is selected from a subset of predictors chosen randomly at that node, in contrast to a standard regression tree, which splits each node using the best predictor among the entire input set.²² An advantage of random variable sampling is that it can help to de-correlate variables, as not all variables are evaluated when selecting a splitting variable.

Bagging can improve the predictive performance (i.e., lower mean squared error (MSE)) of individual regression trees through averaging a group of predictors, which produces a predictor with variance less than or equal to that of any of the individual predictors.³⁴ An estimate of the prediction error based on the training data is obtained in a random forest using the data not in the bootstrap sample, called the out-of-bag (OOB) data. At each bootstrap iteration, predictions are made for the OOB sample using the tree grown with the bootstrap sample. The predictions for each data point are aggregated over all the OOB samples to calculate the OOB-based MSE. On average, each data point will be in 36% of the OOB samples.³⁵ The percent variance explained by the random forest is also calculated using the OOB MSE.

We used three different strategies to build random forest models to predict log nitrate levels in the training set. Two approaches were based on the variable importance (according to the percent increase in mean squared error in the OOB samples) in the random forest model given all possible input variables. The first approach added variables individually in descending order of the variable importance and retained variables that lowered the prediction error in the OOB sample. The second approach removed variables individually in ascending order of the variable importance and made the removal permanent if the prediction error decreased in the OOB sample. The last approach grouped the variables according to 36 thematic groups (soil characteristics, land use, nitrogen inputs, meteorology, and other factors), and incrementally added a group to the model and retained it if the OOB prediction error decreased. We found that the thematic grouping of variables yielded the lowest prediction error, and used this approach for the final random forest model, which consisted of 66 predictor variables (Table S2, Supporting Information).

Random forests require the setting of several parameters, including the number of trees in the ensemble, the number of variables to consider for splitting at a node, and the terminal node size. For ensemble size, we used 500 trees. We used p/3 for the number of variables to consider for splitting, where p is the number of input predictor variables. We evaluated a range of terminal node sizes and found 11 to yield the lowest OOB prediction error, and hence used this value for the final model.

For comparative purposes, we fitted several other statistical models including a regression tree and a linear regression model with main effects for all the covariates available in the final random forest model, ordinary kriging, and universal kriging³⁶ and a generalized additive model (GAM)^37,38 adjusted for well depth. While regression trees generally do not predict as well as random forests, they are easier to interpret.³³ Linear regression models are commonly used to estimate environmental concentrations of contaminants.^39–42 The kriging models and GAM explicitly model a spatial process in log nitrate. We used a thin plate regression spline³⁸ for modeling the residual spatial pattern in the GAM after adjusting for the important variable well depth. We estimated the best single regression tree by selecting the complexity parameter that minimized the cross-validation error according to the 1-standard error rule.²² We fitted all models in the R computing environment,⁴³ and used the randomForest package³⁵ for the random forest and the rpart package⁴⁴ for the regression tree. We used the library mgcv³⁸ for the GAM and gstat⁴⁵ for the kriging models. We predicted log nitrate for observations in the testing set with the three random forest models and compared the MSE and correlation between observed and predicted values.

RESULTS AND DISCUSSION

Summary Statistics for Sampled Wells

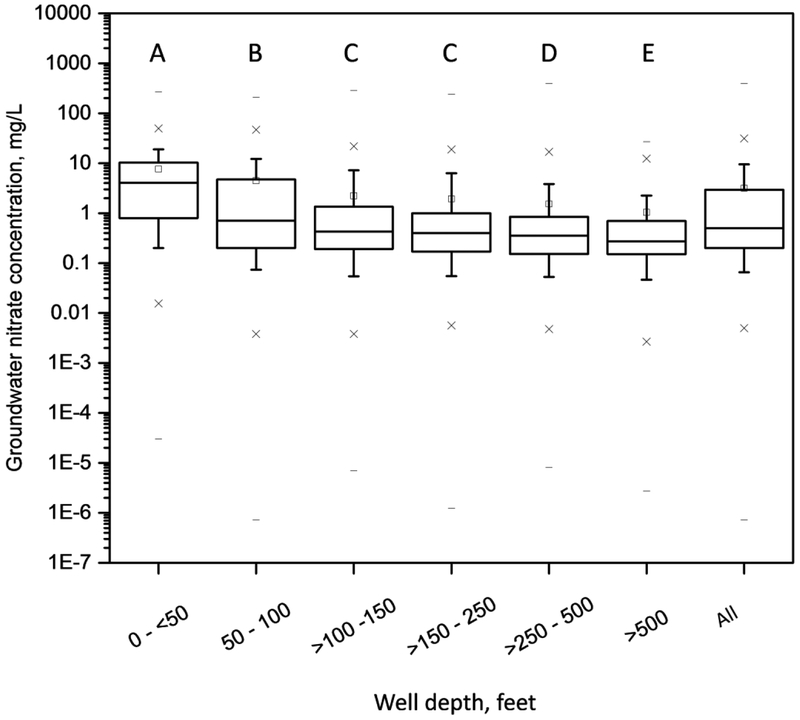
The distribution of nitrate concentration in the training and testing data subsets combined (N=34,084) by well depth is shown in Figure 1. Overall, mean nitrate concentration was 3.2 mg/L, the standard deviation was 8.0 mg/L, the median concentration was 0.5 mg/L, the 25^th percentile concentration was 0.20 mg/L, and the 75^th percentile concentration was 2.9 mg/L. The quartile nitrate concentrations for the training and testing data sets were the same as for the overall data set, except that the 75th percentile for the training data set was 3.0 mg/L. Nitrate concentrations decreased with increasing well depth with the greatest decrease in concentration between well depth categories of <50 ft and 50–100 ft.

Figure 1.

Box plots of groundwater nitrate concentration by well-depth category, and for all well depths, for training and testing data subsets combined; whiskers indicate the 10^th and 90^th percentiles, “–” is minimum or maximum nitrate concentration, “x” is the 1^st or 99^th percentile concentration, and “□” is the mean concentration. Boxes with the same letter are not significantly different according to the Tukey HSD (honest significant difference) test applied to ranked data.

Modeling Results

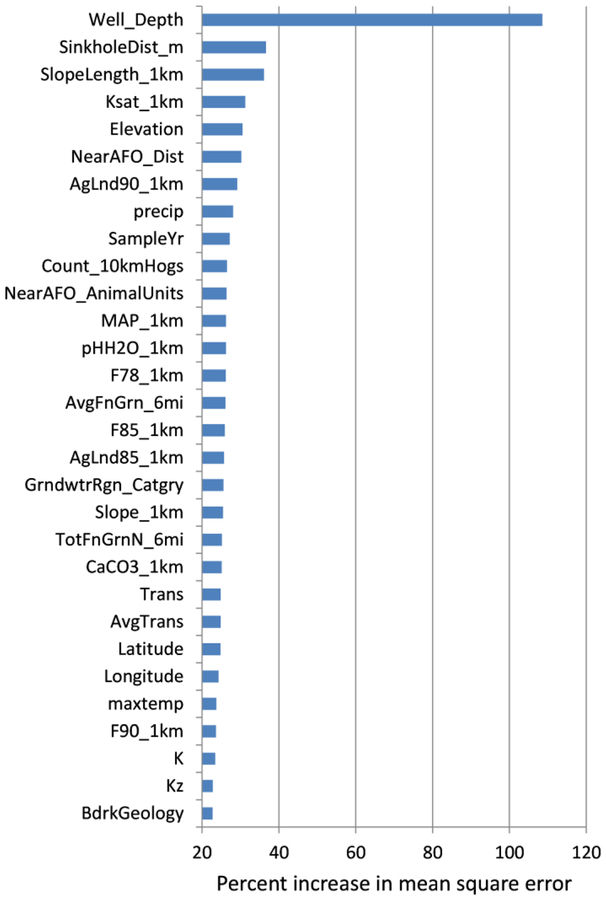
The final random forest model included variables for well depth, agricultural land, fertilizer use, and variable groups for slope, space, time, population density, aquifer and soil characteristics, geology, and animal feeding operation (AFO) counts and distance (Table S2, Supporting Information). The relative importance of the top 30 variables (out of 66 total) in the final random forest model is plotted in Figure 2. The three most important variables in the model were well depth, sinkhole distance, and slope length within 1km. The partial dependence plot in Figure S1 gives a graphical depiction of the marginal effect of well depth on log nitrate concentration in the random forest. It is clear that shallower wells are associated with higher predicted values of log nitrate. This same relation was seen for observed nitrate concentration (Figure 1) and was highly significant (Kruskal-Wallis p < 0.0001). Mean nitrate concentration decreased from 7.7 mg/L for 0 – <50 ft well depths to 1.0 mg/L for depths > 500 ft. The inverse relation between depth and nitrate concentration is consistent with previous groundwater studies that considered well depth or depth of the screened interval.^{8,10,11,13,17} Deeper groundwater typically is older and may predate periods of intensive fertilizer application (1950 – present), and there is enhanced opportunity for denitrification because groundwater requires more time to travel to deeper aquifers. Additionally, the deeper the well, the more likely that the sampled groundwater is a mixture of different ages and land uses.⁸

Figure 2.

Variable importance according to the percent increase in MSE without the variable in the random forest for the top 30 predictor variables. Variables are defined in Table S2, Supporting Information.

The partial dependence plot for sample year (Figure S1) shows that predicted log nitrate increased substantially in the early 1990s, which may relate to increases in numbers of animal feeding operations (AFOs) in Iowa. The average number of hogs per farm has increased substantially since the 1970s as the number of farms with hogs declined, resulting in increased concentration of waste in fewer, larger units.⁴⁶ Injection of liquid swine manure into soils became more common with the increase in AFOs. The practice can result in significantly greater nitrate loss from soils compared with application of urea ammonium nitrate fertilizer.^47–49 The lagged increase in groundwater nitrate concentration relative to increasing AFOs suggests groundwater travel times of years or decades, and travel time itself depends on well depth as noted above. The effect of travel time is also suggested by the ranking of important time-sensitive N input variables in the model. In order of importance in Figure 2, these are AgLnd90_1km (proportion of agricultural land in 1990 within a 1-km radius well buffer), F78_1km (1978 county nitrogen fertilizer (kg of N/yr) apportioned to 1978 agricultural lands within a 1km well buffer), F85_1km, AgLnd85_1km, and F90_1km. Therefore, 1978 – 1990 N inputs were more important in the model than later N inputs (1992 – 2006). The range of suggested travel times (up to decades for the most recent samples) may reflect both bedrock aquifers and unconsolidated deposits. A 10-yr travel time is reasonable for the latter in areas with well-drained soils and flat topography.⁸ Models calibrated to sulfur hexafluoride and tritium tracer data indicated that the mean groundwater age of a well in stratified unconsolidated glacial deposits was 5 – 6 years, and that 99% of contaminant mass applied near the well was flushed within 8 – 14 years.⁵⁰

The random forest model indicates interactions among the amount and timing of nitrogen input and the intrinsic susceptibility of the aquifer to contamination. The model preferentially selected variables from aquifer thematic groups over bulk physical soil characteristics such as texture, organic matter, bulk density, etc., which indicates the importance of deeper aquifer variables to the predictions. This differs from previous regression models that did not model aquifer hydraulic and texture variables and relied instead on shallow soils data.^10,11,13 Aquifer group variables among the 30 most important variables in the model included: the average and total thickness of fine-grained sediments within 6 mi (10 km) of the well (AvgFnGrn_6mi and TotFnGrn_6mi, respectively), the transmissivity of glacial deposits at the well point (Trans), the average transmissivity of glacial deposits near the well (AvgTrans), and the average horizontal and vertical hydraulic conductivities near the well (K and Kz, respectively). For the single regression tree (see Figure S2), log nitrate concentration in groundwater demonstrated a positive association with K on one branch and a negative association with AvgFnGrn_4mi on another branch. Increasing K means that groundwater moves to the well at a faster rate, and decreasing AvgFnGrn_4mi indicates that there is less fine-grained material to inhibit groundwater flow to the well. The most important soil property in the final random forest model is saturated hydraulic conductivity (Ksat_1km in Figure 2), which was treated as a separate thematic group from the physical properties.

Some of the important variables in the random forest model are more difficult to interpret. For example, the average length of sloping land within 1,000 m of a well (SlopeLength_1km) was positively related to groundwater nitrate concentration (see Figure S2). Slope length in this context is the distance from where overland flow originates to the point where it enters a well-defined channel. Nutrient losses from agricultural land have been shown to increase with increasing slope length, which reflects the land area receiving rainfall.⁵¹ In the present study, longer distances may provide more opportunity for nitrate in runoff water to infiltrate the soil and percolate to groundwater. The average percent slope within 1,000 m of a well also was positively related to groundwater nitrate (Figure S2), which contrasts with a prior national model that showed a negative relation.¹¹ In that study, reduced vertical permeability and increased runoff were thought to transport nitrate away from sampled wells. In the present study in Iowa, the positive relation (i.e., average slope < 3%, lower nitrate concentration) suggests saturated soils in poorly drained areas, which promote denitrification. Slope values < 3% may also represent tile-drained lands, which are extensive in Iowa and which short-circuit the natural leaching process. Diversion of nitrate in tile drainage and subsequent discharge to streams has been cited as the major fate of N applied to the land surface in portions of the Corn Belt.⁵

The prediction errors for the final random forest model and the comparison models are listed in Table 1 for both the training and testing data sets. For the random forest, both the prediction error for the entire training set and the OOB samples in the training data are listed. For the other methods, the MSEs reported are for the entire data set. The random forest had the best prediction performance in the training and testing data sets, explaining nearly 77% of the variation in log nitrate in the entire training set (Table 1; see Figure S3, Supporting Information, for a plot of predicted versus observed values). In comparison, the regression tree explained only 38.1%, the linear regression model explained only 23.8%, and the GAM explained only 18.5% of the variation in log nitrate in the training set. Performance measures for the kriging models for the training data are not listed because a property of kriging models is that they perfectly fit observed measurements in the data used for fitting the model. In the testing set, the random forest explained 38.3% of the variation in log nitrate, which was only slightly less than the variation explained in log nitrate in the OOB samples in the training set (39.6%). The spatially explicit models did not predict as well as models that considered all 66 variables used in the random forest as inputs. The random forest had better predictive performance in the OOB samples than all other models had when using all the data for estimating nitrate concentrations in the training set.

Table 1.

Predictive performance of random forest, regression tree, linear regression, kriging models, and generalized additive model (GAM) for training and testing data sets. The random forest, regression tree, and linear regression model had the same set of 66 variables as inputs. The universal kriging and GAM adjusted for well depths.

	Training Data		Testing Data
Model	MSE	% Variation Explained	MSE	% Variation Explained
Random forest	0.97	76.86	2.39	38.27
OOB	2.52	39.64	-	-
Regression tree	2.58	38.08	2.86	26.10
Linear regression	3.18	23.84	3.03	21.85
Generalized additive model	3.40	18.46	3.20	17.45
Ordinary kriging	-	-	3.17	18.20
Universal kriging	-	-	3.06	20.99

MSE, mean squared error; OOB, Out-of-bag data

By specifying sampling date and time-sensitive N input variables, we plan to use the random forest prediction model to predict past nitrate concentrations in private drinking wells in the AHS cohort for evaluation of nitrate exposure and cancer risk. Therefore, we assessed the predictive performance of the model in terms of categorical levels of exposure that are typically used in epidemiologic studies. We computed the predicted nitrate values as $\exp \left(\widehat{y}+0.5*s^2\right)$, where $\widehat{y}$ is the model prediction and s² is an estimate of the variance of the model error.⁵² The agreement between quartiles of observed and predicted nitrate concentrations was generally good in the training set (Table 2). The overall agreement was 65% (7744/11931 predicted correctly). For the extreme categories, 67% of the nitrate measurements in the lowest level were correctly classified and 85% of the measurements in the highest category were correctly classified. The Somers’ d measure of agreement for ordinal variables was 0.76. Somers’ d is an asymmetric measure of association, computed as the difference between the proportions of pairs of observations that are concordant and those that are discordant in the observed and predicted scores (among the observations that are not tied in the observed scores).⁵³ It can be interpreted similarly to other correlation measures with a scale ranging from −1 to 1. The agreement in the testing set was not as good, with a correct prediction for 44% of the observations and a Somers’ d of 0.47. However, the model did correctly predict the true class as the majority class for all four categories of nitrate (Table 2). In the extreme categories, 40% of the lowest level measurements and 66% of the highest level measurement were correctly predicted.

Table 2.

Agreement counts and percentages between quartiles for predicted and observed nitrate concentrations in the training and testing sets.

	Training Set
		Observed
		1	2	3	4
Predicted	1	2434 (67.2%)	432 (17.9%)	117 (4.0%)	0 (0.0%)
	2	927 (25.6%)	1216 (50.4%)	834 (28.6%)	6 (0.2%)
	3	258 (7.1%)	755 (31.3%)	1543 (53.0%)	426 (14.3%)
	4	2 (0.1%)	11 (0.1%)	419 (14.4%)	2551 (85.5%)
	Testing Set
		Observed
		1	2	3	4
Predicted	1	2694 (40.2%)	1520 (32.7%)	1192 (22.5%)	133 (2.4%)
	2	2335 (34.8%)	1642 (35.4%)	1209 (22.9%)	352 (6.4%)
	3	1370 (20.4%)	1110 (23.9%)	1678 (31.7%)	1380 (25.0%)
	4	307 (4.6%)	373 (8.0%)	1210 (22.9%)	3648 (66.2%)

In addition to quartiles of nitrate concentration, we compared the agreement between binary indicators of nitrate exposure, where 5 mg/L was used as the cut-point between high and low exposure. Agreement was excellent in the training set (Table 3), with 92% of observations classified correctly. Sensitivity and specificity in the training set were 0.75 and 0.96, respectively. Agreement in the testing set was very good, with 82.5% percent of observations predicted correctly. Sensitivity and specificity were 0.67 and 0.86, respectively.

Table 3.

Agreement counts and percentages between binary indicators of observed and predicted nitrate exposure (using 5 mg/L as the threshold for high exposure) in the training and testing sets.

	Training Set
		Observed
		0	1
Predicted	0	9317 (96.1%)	564 (25.2%)
	1	376 (3.9%)	1674 (74.8%)
	Testing Set
		Observed
		0	1
Predicted	0	15660 (85.8%)	1280 (32.9%)
	1	2598 (14.2%)	2615 (67.1%)

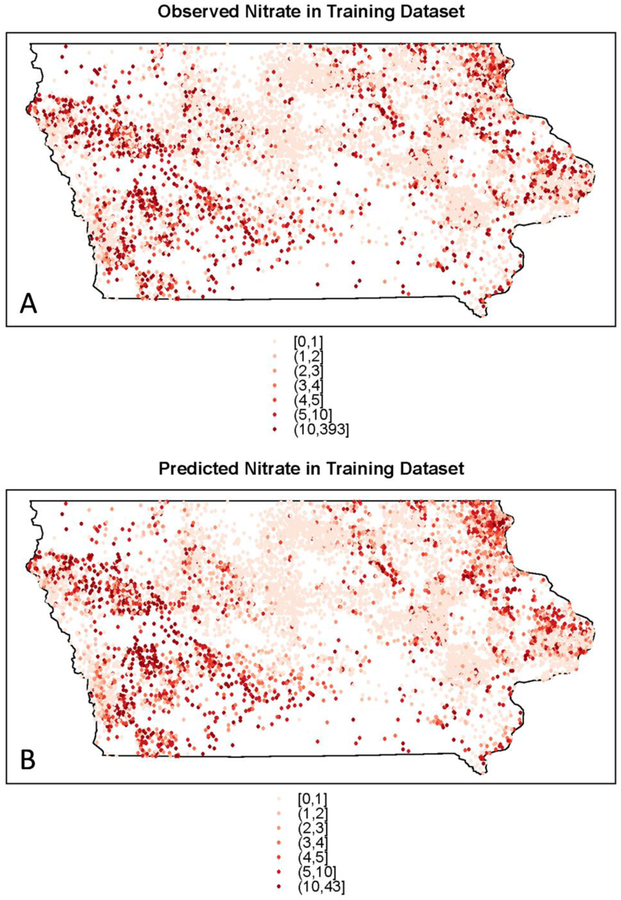
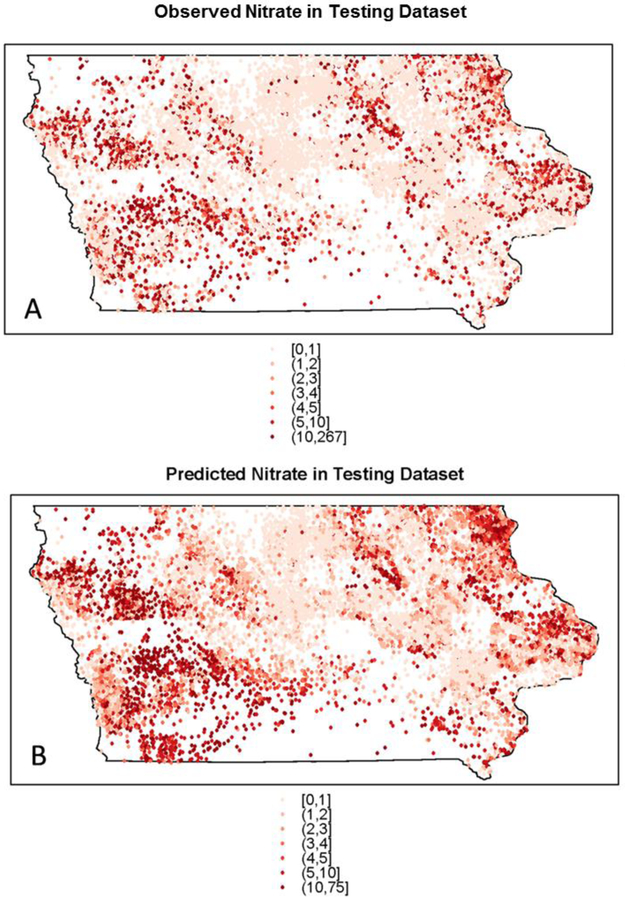
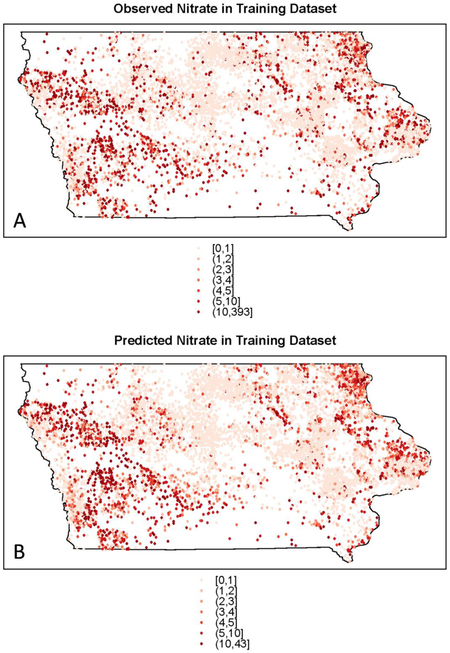
Observed groundwater nitrate concentrations varied spatially at a fine scale, but some overall patterns were evident (Figure 3A). Concentrations were generally higher in northeastern and western Iowa and lower in central Iowa. Predicted nitrate concentrations in the training set (Figure 3B) had a similar pattern to the observed values, with low concentrations in central Iowa, a cluster of higher values in northeastern Iowa, and two clusters of high values in western Iowa. The swath of low nitrate concentration coincides with the Des Moines Lobe, an area characterized by till plains and lacustrine deposits created as Wisconsin-aged glaciers receded.⁵⁴ The glacial till ranges in texture from silty or clayey to partly stratified sand layers,⁵⁵ and generally has low permeability.⁵⁴ Fine-grained sediments in this area can restrict groundwater flow, and tile drainage is extensive. Conversely, northeastern Iowa has a high potential for karst geology, which can rapidly transmit water and contaminants through solution cavities and sinkholes. Maps of the observed (Figure 4A) and predicted nitrate concentrations (Figure 4B) in the testing set demonstrate that the random forest model was effective in predicting the spatial pattern of observed nitrate concentrations. The same areas of lowered and elevated nitrate concentrations identified in the training set maps are evident in the testing set maps. Maps of observed nitrate concentrations by well depth status (<150ft, >=150ft) in the training set (Figure S4, Supporting Information) show that nitrate concentrations were generally higher for shallower wells.

Figure 3.

(A) Observed and (B) predicted groundwater nitrate concentrations for private wells in the training set in Iowa.

Figure 4.

(A) Observed and (B) predicted groundwater nitrate concentrations for private wells in the testing set in Iowa.

Conclusions

Contamination of drinking water by nitrate is a growing problem in many agricultural areas of the country. Ingested nitrate can lead to the endogenous formation of N-nitroso compounds, which are potent carcinogens. In this research, we assembled a comprehensive data set of nitrate measurement data for private wells and predictor variables representing the sources, transport, and fate of nitrogen in soils and groundwater, and then used the data to develop and test a random forest model for predicting past groundwater nitrate exposure in private wells in Iowa. The random forest model had substantially better predictive performance than a linear regression model, a regression tree, a generalized additive model, and two kriging models. In future work, our random forest model will be used to predict nitrate levels in private wells for Iowa participants of the Agricultural Health Study cohort in order to evaluate nitrate ingestion and risk of cancer and other health outcomes.

Highlights.

• We developed a prediction model for nitrate concentrations in private wells in Iowa.

• Our model had substantially better predictive performance than competing models.

• Model sensitivity and specificity in a testing data set were acceptable.

• Important predictor variables were well depth, sinkhole distance, and slope length.

• Nitrate decreased with increasing well depth.

ABBREVIATIONS

AFO

animal feeding operation

AHS

Agricultural Health Study

GIS

geographic information system

GPS

global positioning system

MCL

maximum contaminant level

MSE

mean squared error

N

nitrogen

NOC

N-nitroso compounds

OOB

out-of-bag

USGS

U.S. Geological Survey