Convolutional Neural Networks with Template-Based Data Augmentation for Functional Lung Image Quantification

Abstract

Rationale and Objectives:

We propose an automated segmentation pipeline based on deep learning for proton lung MRI segmentation and ventilation-based quantification which improves on our previously reported methodologies in terms of computational efficiency while demonstrating accuracy and robustness. The large data requirement for the proposed framework is made possible by a novel template-based data augmentation strategy. Supporting this work is the open-source ANTsRNet— a growing repository of well-known deep learning architectures first introduced here.

Materials and Methods:

Deep convolutional neural network (CNN) models were constructed and trained using a custom multilabel Dice metric loss function and a novel template-based data augmentation strategy. Training (including template generation and data augmentation) employed 205 proton MR images and 73 functional lung MRI. Evaluation was performed using data sets of size 63 and 40 images, respectively.

Results:

Accuracy for CNN-based proton lung MRI segmentation (in terms of Dice overlap) was left lung: 0.93 ± 0.03, right lung: 0.94 ± 0.02, and whole lung: 0.94 ± 0.02. Although slightly less accurate than our previously reported joint label fusion approach (left lung: 0.95 ± 0.02, right lung: 0.96 ± 0.01, and whole lung: 0.96 ± 0.01), processing time is <1 second per subject for the proposed approach versus ~30 minutes per subject using joint label fusion. Accuracy for quantifying ventilation defects was determined based on a consensus labeling where average accuracy (Dice multilabel overlap of ventilation defect regions plus normal region) was 0.94 for the CNN method; 0.92 for our previously reported method; and 0.90, 0.92, and 0.94 for expert readers.

Conclusion:

The proposed framework yields accurate automated quantification in near real time. CNNs drastically reduce processing time after offline model construction and demonstrate significant future potential for facilitating quantitative analysis of functional lung MRI.

INTRODUCTION

Probing lung function under a variety of conditions and/or pathologies has been significantly facilitated by the use of hyperpolarized gas imaging and corresponding quantitative image analysis methodologies. Such developments have provided direction and opportunity for current and future research trends (1). Computational techniques targeting these imaging technologies permit spatial quantification of localized ventilation with potential for increased reproducibility, resolution, and robustness over traditional spirometry and radiological readings (2, 3).

One of the most frequently used image-based biomarkers for the study of pulmonary development and disease is based on the quantification of regions of limited ventilation, also known as ventilation defects (4). These features have been shown to be particularly salient in a clinical context. For example, ventilation defect volume to total lung volume ratio has been shown to outperform other image-based features in discriminating asthmatics versus nonasthmatics (5). Ventilation defects have also demonstrated discriminative capabilities in chronic obstructive pulmonary disease (6) and asthma (7). These findings, along with related research, have motivated the development of multiple automated and semiautomated segmentation algorithms which have been proposed in the literature (eg, (8—11, 12)) and are currently used in a variety of clinical research investigations (eg, (13)).

Despite the enormous methodological progress with existing quantification strategies, recent developments in machine learning (specifically “deep learning” (14)) have generated new possibilities for quantification with improved capabilities in terms of accuracy, robustness, and computational efficiency. Deep learning, a term denoting neural network architectures with multiple hidden layers, has seen recent renewed research development and application. In the field of image analysis and computer vision, deep learning with convolution neural networks (CNNs) has been particularly prominent in recent years due, in large part, to the annual ImageNet Large Scale Visual Recognition Challenge (15). Specifically, one of the participating groups in the 2012 ImageNet challenge was the earliest adopter of CNNs. The resulting architecture, colloquially known as “AlexNet” (16), surpassed any approach that had been proposed previously and laid the groundwork for future CNN-based architectures for image classification such as VGG (17) and GoogLeNet (18). The recent successes of CNNs are historically rooted in the pioneering work of LeCun et al. (19) and Fukushima (20) and others which drew inspiration from earlier work on the complex arrangement of cells within the feline visual cortex (21). CNNs are characterized by common components (ie, convolution, pooling, and activation functions) which can be put together in various arrangements to perform such tasks as image classification and voxel-wise segmentation. The outgrowth ofresearch, in conjunction with advances in computational hardware, has resulted in significant developments in various image research areas including classification, segmentation, and object localization and has led to co-optation by the medical imaging analysis community (22).

In this work, we develop and evaluate a convolutional neural network segmentation framework, based on the U-net architecture (23), for functional lung imaging using hyperpolarized gas. As part of this framework, we include a deep learning analog to earlier work from our group targeting segmentation of proton lung MRI (24). This is motivated by common use case scenarios in which proton images are used to identify regions of interest in corresponding ventilation images (8, 9, 10), which typically contain no discernible boundaries for anatomic structures.

One of the practical constraints to adopting deep learning techniques is the large data requirement for the training process oftentimes necessitating ad hoc strategies for simulating additional data from available data—a process termed data augmentation (25). While common approaches to data augmentation include the application of randomized simulated linear (eg, translation, rotation, and affine) or elastic transformations and intensity adjustments (eg, brightness and contrast), we advocate a tailored paradigm to commonly encountered medical imaging scenarios in which data are limited but are assumed to be characterized by a populationwide spatial correspondence. In the proposed approach, an optimal shape-based template is constructed from a subset of the available data. Subsequent pairwise image registration between all training data and the resulting template permits a “pseudo-geodesic” transformation (26) of each image to every other image thus potentially converting a data set of size N to an augmented data set of size N². In this way, transformations are constrained to the shape space representing the population of interest.

To enhance relevance to the research community, we showcase this work in conjunction with the introduction of ANTsRNet—a growing open-source repository of well-known deep learning architectures which interfaces with the Advanced Normalization Tools (ANTs) package (27) and its R package, ANTsR (28). This permits the public distribution of all code, data, and models for external reproducibility which can be found on the GitHub repository corresponding to this manuscript (29). This allows other researchers to apply the developed models and software to their data and/or use the models to initialize their own model development tailored to specific studies.

In the work described below, we first provide the acquisition protocols for both the proton and ventilation MR images followed by a discussion of the analysis methodologies for the proposed segmentation framework. This is contextualized with a brief overview of existing quantification methods (including that previously proposed by our group and used for the evaluative comparison). We also summarize the key contributions of this work viz., the template-based data augmentation and the current feature set of ANTsRNet.

MATERIALS AND METHODS

Image Acquisition

Both proton and ventilation images used for this study were taken from current and previous studies from our group. Ventilation images comprised both helium-3 and xenon-129 acquisitions, as our current segmentation processing does not distinguish between ventilation gas acquisition protocols, and we expected similar agnosticism for the proposed approach.

Hyperpolarized MR image acquisition was performed under an Institutional Review Board-approved protocol with written informed consent obtained from each subject. In addition, all imaging studies were performed under Food and Drug Administration-approved physician’s Investigational New Drug applications for hyperpolarized gas (either helium-3 or xenon-129). MRI data were acquired on a 1.5 T whole-body MRI scanner (Siemens Sonata, Siemens Medical Solutions, Malvern, PA) with broadband capabilities and corresponding hyperpolarized gas chest radiofrequency coils (Rapid Biomedical, Rimpar, Germany; IGC Medical Advances, Milwaukee, WI; or Clinical MR Solutions, Brookfield, WI).

Two imaging protocols were used to acquire the MR images. Both of them are combined hyperpolarized gas (helium-3 or xenon-129) and proton imaging acquisitions. Protocol 1 uses 3-D balanced steady-state free-precession or spoiled gradient echo pulse sequences with isotropic resolution = 3.9 mm, TR= 1.75–1.85 ms, TE = 0.78–0.82 ms, flip angle = 9—10°, bandwidth per pixel =1050–1100 Hz/Pixel, total duration = 10—20 seconds. Protocol 2 uses a contiguous, coronal, 2-D gradient echo pulse sequence with interleaved spiral sampling scheme, in-plane resolution = 2—4 mm, slice thickness = 15 mm, TR = 8—8.5 ms, TE = 0.8—1.0 ms, flip angle = 20° interleaves = 12—20 (plus 2 for field map), total duration = 3—8 seconds. All subjects provided written informed consent and the data were de-identified prior to analysis.

Image Processing and Analysis

We first review our previous contributions to the segmentation of proton and hyperpolarized gas MR images (8, 24), as we use these previously described techniques for evaluative comparison. We then describe the deep learning analogs (including preprocessing) extending earlier work and discuss the proposed contributions which include:

• CNNs for structural/functional lung segmentation,

• template-based data augmentation, and

• open-source availability.

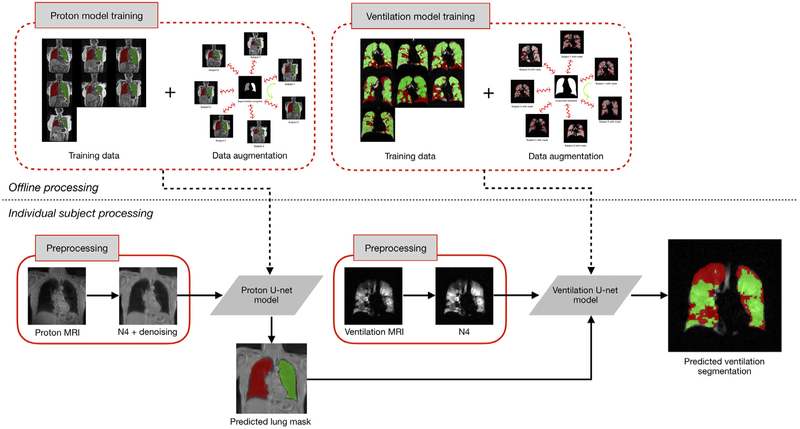
An overview of the resulting framework is provided in Figure 1. The most computationally intensive portion is the offline processing for model training for both structural and functional imaging. However, once that is complete, individual processing consists of a couple of preprocessing steps followed by application of the models which has minimal computational requirements.

Figure 1.

Illustration of the proposed workflow. Training the U-net models for both proton and ventilation imaging includes template-based data augmentation. This offline training is computationally intensive but is only performed once. Subsequent individual subject preprocessing includes MR denoising and bias correction. The proton mask determined from the proton U-net model is included as a separate channel (in deep learning software parlance) for ventilation image processing.

Previous Approaches From Our Group for Lung and Ventilation-Based Segmentation

The automated ventilation-based segmentation, described in (8), employs a Gaussian mixture model with a Markov random field (MRF) spatial prior optimized via the Expectation-Maximization algorithm. The resulting software, called Atropos, has been used in a number of clinical studies (eg, (7, 30)). Briefly, the intensity histogram profile of the ventilation image is modeled using Gaussian functions with optimizable parameters (ie, mean, standard deviation, and normalization factor) designed to model the intensities of the individual ventilation classes. At each iteration, the resulting estimated voxel-wise labels are refined based on MRF spatial regularization. The parameters of the class-specific Gaussians are then re-estimated. This iterative process continues until convergence. We augment this segmentation step by iterating the results with application of N4 bias correction (31). Unlike other methods that rely solely on intensity distributions, thereby discarding spatial information (eg, K-means variants (9), (11) and histogram rescaling and thresholding (10), our previous MRF-based technique (8) employs both spatial and intensity information for probabilistic classification.

Because of our dual structural/functional acquisition protocol (32), we also previously formulated a joint label fusion (JLF)-based framework (33) for segmenting the left and right lungs in proton MRI as well as estimating the lobar volumes (24). This permits us to first identify the lung mask in the proton MRI. This information is transferred to the space of the corresponding ventilation MR image via image registration. The JLF method relies on a set of atlases (proton MRI plus lung labels) which is spatially normalized to an unlabeled image where a weighted consensus of the normalized images and labels is used to determine each voxel label. Although the method yields high-quality results which are fully automated, one of the drawbacks is the time and computational resources required to perform the image registration for each member of the atlas set and the subsequent voxel-wise label consensus estimation.

Note that we have provided self-contained examples for both of these segmentation algorithms using ANTs tools: lung and lobe estimation (34) and lung ventilation (35). However, given the previously outlined benefits of deep learning approaches to these same applications, we expect that adoption by other groups will be greatly facilitated by the proposed algorithms described below.

Preprocessing

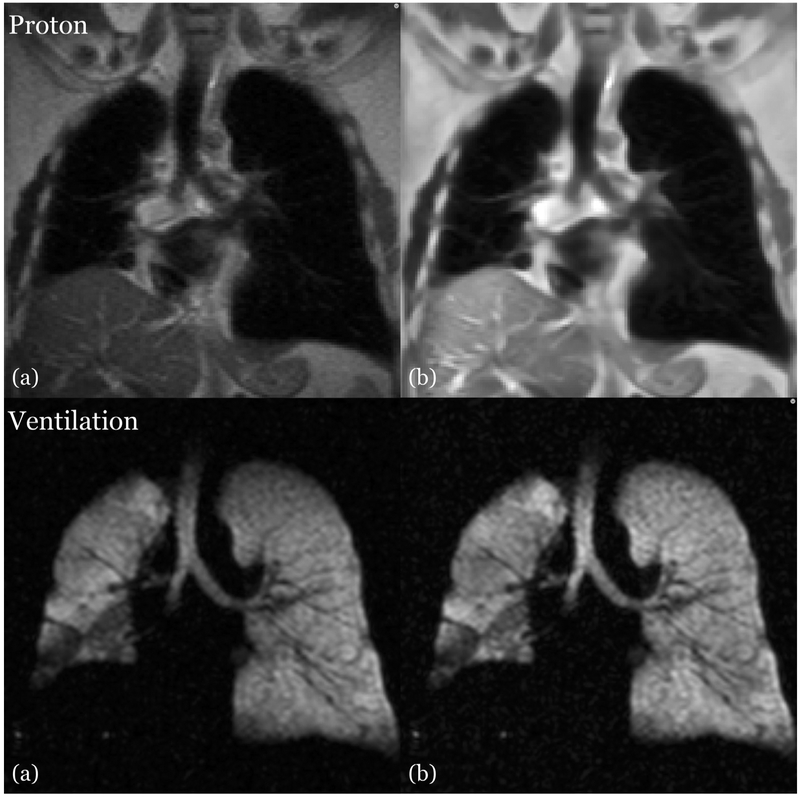
Because of the low-frequency imaging artifacts introduced by confounds such as radiofrequency coil inhomogeneity, we perform a retrospective bias correction on both proton and ventilation images using the N4 algorithm (36). These are included in our previously proposed ventilation (8) and structural (24) segmentation frameworks. Since the initial release of these pipelines, we have also adopted an adaptive, patch-based denoising algorithm specific to MR (36) which we have reimplemented in the ANTs toolkit. The effects of these data cleaning techniques on both the proton images and ventilation images are shown in Figure 2.

Figure 2.

Side-by-side image comparison showing the effects of preprocessing on the proton (top) and ventilation (bottom) MRI. (a) Uncorrected image showing MR field inhomogeneity and noise. (b) Corresponding corrected image in which the bias effects have been ameliorated.

U-Net Architecture for Structural/Functional Lung Segmentation

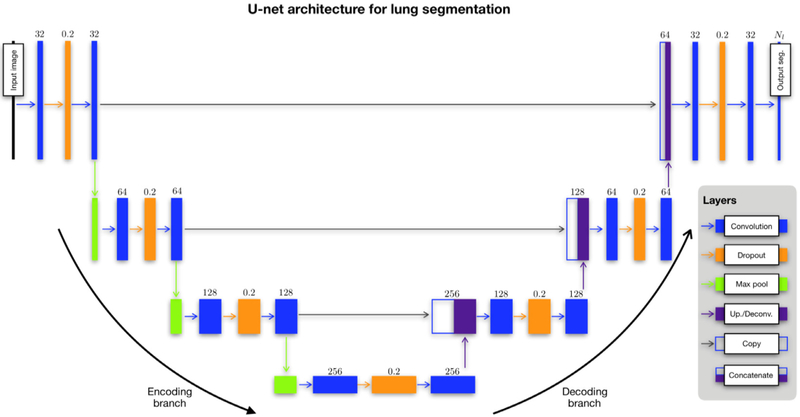
The U-net architecture was introduced in (23) which extended the fully convolutional neural network approach introduced by Long, Shelhamer, and Darrel (37). U-net augments the “encoding path” (see left side of Fig 3) common to such architectures as VGG and fully convolutional neural network with a symmetric decoding path, where the corresponding encoding/decoding layers are linked via skip paths for enhanced feature detection. The nomenclature reflects the descending/ascending aspect of its architecture. Each series in both encoding and decoding branches is characterized by an optional dropout layer in between two convolutional layers. This latter modification from the original is meant to provide additional regularization for overfitting prevention (38). Output consists of a segmentation probability image for each label from which a segmentation map can be generated.

Figure 3.

The modified U-net architecture for both structural and functional lung segmentation (although certain parameters, specifically the number of filters per convolution layer, are specific to the functional case). Network layers are represented as boxes with arrows designating connections between layers. The main parameter value for each layer is provided above the corresponding box. Each layer of the descending (or “encoding”) branch of the network is characterized by two convolutional layers. Modification of the original architecture includes an intermediate dropout layer for regularization (dropout rate = 0.2). A max pooling operation produces the feature map for the next series. The ascending (or “decoding”) branch is similarly characterized. A convolutional transpose operation is used to upsample the feature map following a convolution→ dropout→ convolution layer series until the final convolutional operation which yields the segmentation probability maps.

We used the U-net architecture to build separate models for segmenting both structural and functional lung images. For cases where dual acquisition provides both images, we use the structural images to provide a mask for segmentation of the ventilation image. We used an open-source implementation written by our group and provided with the ANTsRNet R package (39) which is described in greater detail below. We also implemented a multilabel Dice coefficient loss function along with specific batch generators for generating augmented image data on the fly.

Template-Based Data Augmentation

The need for large training data sets is a well-known limitation of deep learning algorithms. Whereas the architectures developed for such tasks as the ImageNet competition have access to millions of annotated images for training, such data availability is atypical in medical imaging. In order to achieve data set sizes necessary for learning functional models, various data augmentation strategies have been employed (25). These include application of intensity transformations, such as brightening and enhanced contrast. They might also include spatial transformations such as arbitrary rotations, translations, and even simulated elastic deformations. Such transformations might not be ideal if they do not represent shape variation within the typical range exhibited by the population under study.

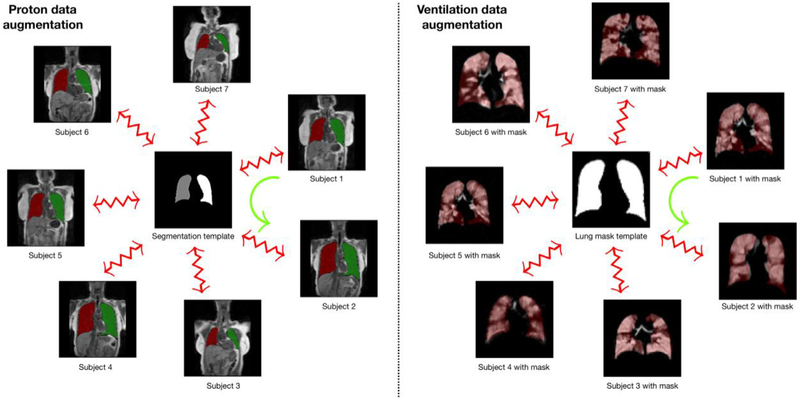
We propose a template-based data augmentation approach whereby image data sampled from the population are used to construct a representative template that is optimal in terms of shape and/or intensity (40). In addition to the representative template, this template-building process yields the transformations to/from each individual image to the template space. This permits a propagation of individual training data to the space of every other training data as illustrated in Figure 4. Specifically, the template-building process produces an invertible, deformable mapping for each subject. For the k^th subject, S_k, and template, T, this mapping is denoted as φ^k with inverse given by ${\phi }_k^{-1}$. During model training, each new augmented data instance, S_new, is produced by randomly selecting a source subject and target subject, and mapping S_source to the space of S_target according to

$$S_{new}=S_{source}\left({\phi }_{target}^{-1}({\phi }_{source})\right)$$ (1)

Figure 4.

Template-based data augmentation for the proton (left) and ventilation (right) U-net model generation. For both cases, a template is created, or selected, to generate the transforms to and from the template. The derived deformable, invertible transform for the k^th subject, S_k to the template, T, is denoted by φ_k: S_k↔T. These subject-specific mappings are used during model training (but not the template itself). Data augmentation occurs by randomly choosing a reference subject and a target subject during batch processing. In the illustration above, the sample mapping of Subject 1 to the space of Subject 2, represented by the green curved arrow, is defined as ${\phi }_2^{-1}({\phi }_1)$.

Note that each S comprises all channel images and corresponding segmentation images. In the simplest case, the training data are used to construct the template and then each individual training image and corresponding labels are propagated to the space of every other image. In this way, a training data set of size N can be expanded to a data set of size N². A slight variation to this would be to build a template from M data sets (where M > N). Transformations between the training data and the template are then used to propagate the training data to the spaces of the individual members of the template-generating data for an augmented data set size of M × N.

Since U-net model generation is completely separate for the proton and ventilation data, template-based data augmentation is also isolated between the two protocols. The proton template is created from the right/left segmentation images of the training data denoted by the red/green labels which have voxel values of “1” and “2,” respectively, in Figure 4. The resulting template located in the center of the left panel is an average of all the transformed label images. This whole lung approach avoids the possible lack of internal correspondence while generating plausible global shape variations when mapping between individual training data. We used 60 proton MR images thus permitting 60² = 3600 possible deformable shapes which can be further augmented by more conventional strategies (eg, brightness transformations, translations, etc.). Similarly, the ventilation template is created from the training ventilation images resulting in the grayscale template in the center of the right panel of Figure 4.

ANTsRNet

In addition to the contributions previously described, we also introduce ANTsRNet (39) to the research community which not only contains the software to perform the operations specific to structural and functional lung image segmentation but also performs a host of other deep learning tasks wrapped in a thoroughly documented and well-written R package. The recent interest in deep learning techniques and the associated successes with respect to a variety of applications have motivated adoption of such techniques. Basic image operations such as classification, object identification, segmentation, as well as more focused techniques, such as predictive image registration (41), have significant potential for facilitating basic medical research. ANTsRNet is built using the Keras neural network library (available through R) and is highly integrated with the ANTsR package, the R interface of the ANTs toolkit. Consistent with our other software offerings, ongoing development is currently carried out on GitHub using a well-commented coding style, thorough documentation, and self-contained working examples (39).

Several architectures have been implemented for both 2-D and 3-D images spanning the broad application areas of image classification, object detection, and image segmentation (cf. Table 1). It should be noted that most reporting in the literature has dealt exclusively with 2-D implementations. This is understandable due to memory and computational speed constraints limiting practical 3-D applications on current hardware. However, given the importance that 3-D data have for medical imaging and the rapid progress in hardware, we feel it worth the investment in implementing corresponding 3-D architectures. Each architecture is accompanied by one or more self-contained examples for testing and illustrative purposes. In addition, we have made novel data augmentation strategies available to the user and illustrated them with Keras-specific batch generators.

TABLE 1.

Current ANTsRNet Capabilities Comprising Architectures for Applications in Image Segmentation, Image Classification, Object Localization, and Image Super-Resolution. Self-Contained Examples with Data are also Provided to Demonstrate Usage for Each of the Architectures. Although the Majority of Neural Network Architectures are Originally Described for 2-D Images, we Generalized the Work to 3-D Implementations Where Possible

		ANTsRNet
Image Segmentation
U-net [23]	(2-D)	Extends fully convolutional neural networks by including an upsampling decoding path with skip connections linking corresponding encoding/decoding layers.
V-net [47]	(3-D)	3-D extension of U-net which incorporates a customized Dice loss function.
Image Classification
AlexNet [16]	(2-D, 3-D)	Convolutional neural network that precipitated renewed interest in neural networks.
VGG16/VGG19 [17]	(2-D, 3-D)	Also known as “OxfordNet.” VGG architectures are much deeper than AlexNet. Two popular styles are implemented.
GoogLeNet [18]	(2-D)	A 22-layer network formed from inception blocks meant to reduce the number of parameters relative to other architectures.
ResNet [48]	(2-D, 3-D)	Characterized by specialized residualized blocks (and skip connections.
ResNeXt [49]	(2-D, 3-D)	A variant of ResNet distinguished by a hyperparameter called cardinality defining the number of independent paths.
DenseNet [50]	(2-D, 3-D)	Based on the observation that performance is typically enhanced with shorter connections between the layers and the input.
Object Localization
SSD [51]	(2-D, 3-D)	The Multibox Single-Shot Detection (SSD) algorithm for determining bounding boxes around objects of interest.
SSD7 [52]	(2-D, 3-D)	Lightweight SSD variant which increases speed by slightly sacrificing accuracy. Training size requirements are smaller.
Image super-resolution
SRCNN [53]	(2-D, 3-D)	Image super-resolution using CNNs.

Processing Specifics

Two hundred five proton MR images each with left/right lung segmentations and 73 ventilation MR images with masks were used for the separate U-net model training. These images were denoised and bias corrected offline (as previously described) and required <1 minute for both steps per image using single threading although both preprocessing steps are multithreading capable. An R script was used to read in the images and segmentations (available in our GitHub repository (29)), create the model, designate model parameters, and initialize the batch generator.

For the proton data, we built a 3-D U-net model to take advantage of the characteristic 3-D shape of the lungs. This limited the possible batch size as our GPU (Titan Xp) is limited to 12 GB although this can be revisited in the future with additional computational resources. Transforms derived from the template-building process described previously were passed to the batch generator where reference and source subjects were randomly assigned. During each iteration, these random pairings were used to create the augmented data according to Equation (1). These data are publicly available for download at (42).

The U-net ventilation model was generated from 73 ventilation MRI. The smaller data set size was a result of data pruning to ensure class balance. Even though the functional images are processed as 3-D volumes and a 3-D ventilation template is created for the template-based data augmentation, the generated U-net model is 2-D. Limiting functional modeling to 2-D was motivated by a couple considerations. In addition to decreased training and prediction time for 2-D models over 3-D models, previous work (43) has shown that 2-D CNNs can achieve comparable performance as their 2-D analogs in certain problem domains. We find 2-D to be sufficient for functional lung imaging as current state-of-the-art methods listed in the Introduction (which are capable of outperforming human raters), lack sophisticated shape priors (including 3-D shape modeling). More practically, though, Protocol 2 acquisition has low through-plane resolution (15 mm slice thickness) and 2-D modeling permits compatibility across both sets of data.

The basic processing strategy is that any ventilation image to be segmented will be processed on a slice-by-slice basis where each slice is segmented using the 2-D model. For data augmentation, the full 3-D transforms are supplied to the batch generator. At each iteration, a set of generated 3-D augmented images are created on the fly based on Equation (1) and then a subset of slices are randomly selected for each image until the batch set is complete. For this work, we randomly sampled slices in the coronal direction using a specified sampling rate (= 0.5). It should be noted that a whole lung mask is assumed to exist and supplied as an additional channel for processing. Prediction on the evaluation data is performed slice-by-slice and then collated into probability volumetric images.

The 3-D U-net structural model and 2-D U-net functional model that were created, as previously described and included with the GitHub repository, can then be used for future processing. Using these models, the basic deep learning workflow is as follows:

• Assume simultaneous structural and functional image acquisition.

• Generate left/right lung mask from the structural image using the corresponding 3-D U-net structural model.

• Convert left/right lung mask to a single label.

• Process ventilation image slice-by-slice using the 2-D U-net functional model using the ventilation image and single-label structural lung mask as input.

Note that this workflow is not absolutely necessary. For example, one could use the 2-D functional model if one provides the input lung masks.

Image size was not identical across both image cohorts so we settled on a common resampled image size of 128 × 128 × 64 for the proton images and 128 × 128 for the ventilation images. Resampling of each image and segmentation were handled internally by the batch generator after transformation to the reference image using ANTsR functions (28). Additionally, during data augmentation for proton model optimization, a digital “coin flip” was used to randomly vary the intensity profile of the warped proton images between their original profiles and the intensity profile of the randomly selected reference image. The latter intensity transformation is the histogram matching algorithm of Nyul et al. (42) implemented in the Insight Toolkit. Specific parameters for the U-net architecture for both models are as follows (3-D parameters are included in parentheses):

• Adam optimization:

  - proton model learning rate = 0.00001

  - ventilation model learning rate = 0.0001

• Number of epochs: 150

• Training/validation data split: 80/20

• Convolution layers

  - kernel size: 5 × 5(× 5)

  - activation: rectified linear units (ReLU) (44)

  - number of filters: doubled at every layer starting with N =16 (proton) and N =32 (ventilation)

• Dropout layers

  - rate: 0.2

• Max pooling layers

  - size: 2 × 2(× 2)

  - stride length: 2 × 2(× 2)

• Upsampling/transposed convolution (ie, deconvolution) layers

  - kernel size: 5 × 5(× 5)

  - stride length: 2 × 2(× 2)

  - activation: rectified linear units (ReLU) (44)

Training took approximately 10 hours for both models. After model construction, prediction per image (after preprocessing) takes < 1 second per image. Both model construction and prediction utilized a NVIDIA Titan Xp GPU.

RESULTS

Proton MRI Lung Segmentation

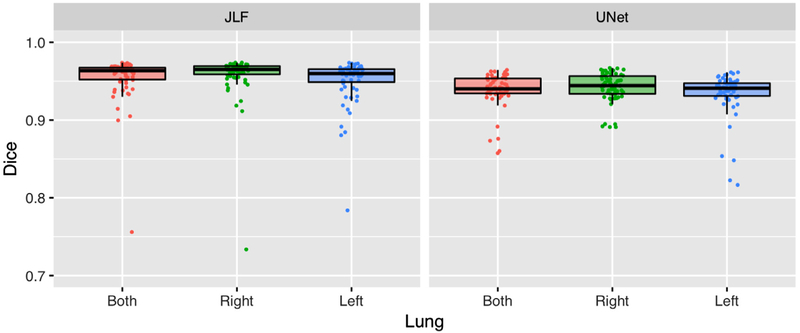
After constructing the U-net structural model using template-based data augmentation,¹ we applied it to the evaluation data consisting of the same 62 proton MRI used in (8). We performed a direct comparison with the JLF method of (8) with an adopted modification that we currently use in our studies. Instead of using the entire atlas set (which would require a large number of pairwise image registrations), we align the center of the image to be segmented with each atlas image and compute a neighborhood cross-correlation similarity metric (27). We then select the 10 atlas images that are most similar for use in the JLF scheme. The resulting performance numbers (in terms of Dice overlap) are similar to what we obtained previously and are given in Figure 5 along with the Dice overlap numbers from the CNN-based approach.

Figure 5.

The Dice overlap coefficient for the left and right lungs (and their combination) between the updated latter requires significantly less computation time.

Accuracy for the latter was left lung: 0.93 ± 0.03, right lung: 0.94 ± 0.02, and whole lung: 0.94 ± 0.02. The analogous JLF numbers were slightly more accurate (left lung: 0.95 ± 0.02, right lung: 0.96 ± 0.01, and whole lung: 0.96 ± 0.01), although the processing time is significantly greater—less than 1 second per subject for the proposed approach versus ~25 minutes per subject using JLF using four CPU threads running eight parallel pairwise registrations per evaluation image.

Ventilation MRI Lung Segmentation

We applied the deep learning approach described in the previous section to the evaluation data used in (8). The resulting probability images were converted into a single segmentation image, which were then compared to the manual segmentation results and Atropos results from our previous work (8). Note that the Otsu thresholding and K-means thresholding were omitted as they were the poorest performers and, as mentioned previously, discard spatial information in contrast to both computational methods and the human readers.

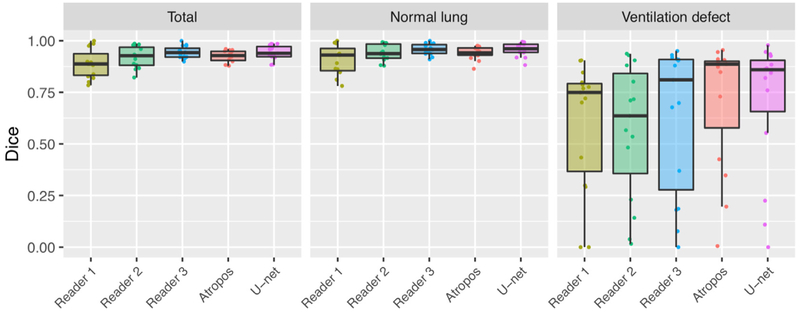
In the absence of ground truth, the STAPLE algorithm (45) was used to create a consensus labeling. The Dice overlap coefficient was used to quantify agreement between each of the segmentation raters and the consensus labeling as an indicator performance. The results are shown in Figure 6. Mean values (± standard deviation) were as follows (total, normal lung, ventilation defect): Reader 1: 0.89 ± 0.07, 0.91 ± 0.06, 0.6 ± 0.3; Reader 2: 0.92 ± 0.05, 0.94 ± 0.04, 0.57 ± 0.3; Reader 3: 0.94 ± 0.03, 0.96 ± 0.03, 0.63 ± 0.3; Atropos: 0.92 ± 0.03, 0.94 ± 0.03, 0.71 ± 0.3; and U-net: 0.94 ± 0.03, 0.96 ± 0.03, 0.70 ± 0.3. Computational time for processing was slightly less than a minute per subject for Atropos, between 30 and 45 for the human readers, and less than a second for the U-net model.

Figure 6.

The Dice overlap coefficient for total, normal lung, and ventilation defect regions for segmentation of the functional evaluation data set.

DISCUSSION

Significant progress has been made from earlier quantification approaches in which human labelers manually identified areas of poor ventilation or applied simple thresholding techniques. More sophisticated automated and semiautomated techniques have advanced our ability to investigate the use of hyperpolarized gas imaging as quantitative image-based biomarkers. Deep learning techniques can further enhance these methodologies by potentially increasing accuracy, generalizability, and computational efficiency. In this work, we provided a deep learning framework for segmentation of structural and functional lung MRI for quantification of ventilation. This framework is based on the U-net architecture and implemented using the Keras API available through the R statistical project.

There are several limitations to the proposed framework. The most obvious is that it only leverages the full 3-D nature of the image data collected for the proton segmentation. The trained models for ventilation image segmentation were based on 2-D coronal slices and therefore subsequent prediction is limited to those views. Even though good results were achieved in this study, even better results might be achieved by training 3-D models for the latter. Also, evaluative comparison was made using manually refined segmentations which is certainly useful but additional evaluations using various clinical measures would also be helpful in determining the relative utility of various segmentation approaches. For example, how does the performance of the various methods translate into utility as an imaging biomarker for lung function?

The template-based data augmentation strategy follows the generic observation in (46) where constrained augmentation to plausible data instances enhances performance over generic data augmentation. Although we find the presented framework to be generally useful for model training, further enhancements could increase utility. A template-based approach for continuous sampling of the population shape distribution could provide additional data for training beyond that provided by the discrete sampling approach proposed. Also, further evaluation needs to be conducted to determine the performance bounds of these augmentation strategies (not just template-based) for a variety of medical imaging applications.

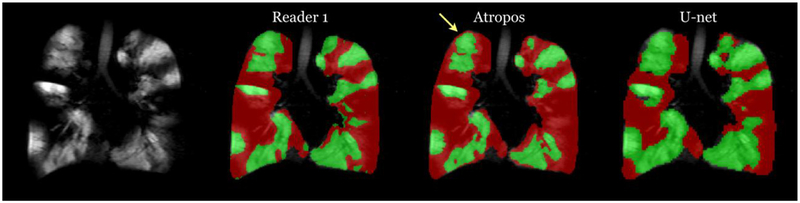
Despite these limitations of the proposed framework, there are also limitations of previously reported methods. For example, in addition to the significant time requirements for JLF of lung images, shown in Figure 7, is an example where difficult pairwise image registration scenarios can cause algorithmic failures. In contrast, the trained U-net model is capable of learning features which can potentially circumvent registration failures. Similarly, the online feature capabilities of deep learning can overcome some of the drawbacks to more conventional segmentation approaches of ventilation lung images. A well-known artifact for these approaches is partial voluming effects which can confound certain intensity-based segmentation approaches (see Fig 8).

Figure 7.

Problematic case showing potential issues with the JLF approach (left) for proton lung segmentation where a difficult pairwise image registration caused segmentation failure. In contrast, by learning features directly, the U-net approach (right) avoids possible registration difficulties.

Figure 8.

Ventilation segmentation comparison between a human reader and the two computational approaches. Notice the effects of the partial voluming at the apex of the lungs, indicated by the yellow arrow, which are labeled as ventilation defect by the Atropos approach whereas U-net and the human reader correctly label this region. (Color version of figure is available online.)

Future research will certainly look into these issues as potential improvements to the existing framework. As a surrogate for full 3-D models, we are looking into developing additional 2-D U-net models for the axial and sagittal views. Since slice-by-slice processing is computationally efficient in the deep learning paradigm, we can process 3-D images along the three canonical axes and combined the results for increased accuracy. More broadly, it would be of potential interest to investigate the use of image classification techniques (eg, VGG (17)) for classifying lung disease phenotype directly from the images. More immediate benefits could result from augmenting the limited, single-site data set used in this work to include data contributed from other groups which could translate into more robust models. Additionally, as the U-net architecture is application-agnostic, investigators can apply the contributions discussed in this work to their own data, such as lung CT.