An automated, machine learning–based detection algorithm for spike‐wave discharges (SWDs) in a mouse model of absence epilepsy

Summary

Objective

Manual detection of spike‐wave discharges (SWDs) from electroencephalography (EEG) records is time intensive, costly, and subject to inconsistencies/biases. In addition, manual scoring often omits information on SWD confidence/intensity, which may be important for the investigation of mechanistic‐based research questions. Our objective is to develop an automated method for the detection of SWDs in a mouse model of absence epilepsy that is focused on the characteristics of human scoring of preselected events to establish a confidence‐based, continuous‐valued scoring.

Methods

We develop a support vector machine (SVM)–based algorithm for the automated detection of SWDs in the γ2R43Q mouse model of absence epilepsy. The algorithm first identifies putative SWD events using frequency‐ and amplitude‐based peak detection. Four humans scored a set of 2500 putative events identified by the algorithm. Then, using predictors calculated from the wavelet transform of each event and the labels from human scoring, we trained an SVM to classify (SWD/nonSWD) and assign confidence scores to each event identified from 60, 24‐hour EEG records. We provide a detailed assessment of intra‐ and interrater scoring that demonstrates advantages of automated scoring.

Results

The algorithm scored SWDs along a continuum that is highly correlated with human confidence and that allows us to more effectively characterize ambiguous events. We demonstrate that events along our scoring continuum are temporally and proportionately correlated with abrupt changes in spectral power bands relevant to normal behavioral states including sleep.

Significance

Although there are automated and semi‐automated methods for the detection of SWDs in humans and rats, we contribute to the need for continued development of SWD detection in mice. Our results demonstrate the value of viewing detection of SWDs as a continuous classification problem to better understand “ground truth” in SWD detection (ie, the most reliable features agreed upon by humans that also correlate with objective physiologic measures).

1.

Key Points.

• Clinicians and researchers may benefit from an automated method of SWD detection that provides a framework for the quantitative description of SWDs and how they relate to other electrographic events

• We present an algorithm for the automated, consistent, and rapid scoring of SWDs that assigns a confidence to detected events that is highly correlated with human scoring confidence

• We characterize the human inter‐ and intrarater consistency in the scoring of potential SWD events and compare them with the algorithm

• Events along the scoring continuum generated by the algorithm are temporally and proportionately correlated with changes in spectral power bands relevant to behavioral states including sleep

2. INTRODUCTION

Spike‐wave discharges (SWDs) are the signature electrographic (ie, electroencephalography [EEG]) feature associated with absence epilepsy.1, 2 These oscillations are thought to be associated with reverberations in thalamocortical networks and in rodents have a characteristic ~6 Hz oscillation.3, 4, 5 Identification of SWDs from EEG records is extremely important both in the clinic as a tool for the diagnosis of absence epilepsy6 and in research. In the clinic, identifying the presence of seizure‐related events in a patient's EEG may be sufficient to identify appropriate treatments. However, detailed scoring of epilepsy‐related events may be required for better patient care7 and to identify potential mechanisms of disease or to investigate the efficacy of drug treatments in research laboratories.

Manual scoring of SWDs is time‐consuming and costly.8 In our experience, a person skilled in manual scoring of SWDs may require 2‐3 hours to score a 24‐hour record. In both clinical and research settings there may be many hundreds of hours of EEG from humans or experimental animals that must be scored. As a result of the significant burden of scoring numerous long EEG records, research labs may use only snippets of EEG recordings that are presumed to be representative of the full dataset. Selective cherry‐picking of data could introduce unanticipated bias.

In addition to the time and cost associated with manual scoring of SWDs, inconsistencies between multiple scorers may be abundant.3 Such inconsistencies are not well characterized for SWD detection (we present a detailed example here); however, inconsistencies have been described in the scoring of other nonconvulsive epileptiform events (eg, interictal spikes).9 Indeed, nonconvulsive epileptiform events are difficult to identify and classify for numerous reasons. First, the definition of “epileptiform” is often vague10, 11, 12 and is subject to disagreement. Clinicians and researchers typically use subjective criteria, such as that an event “stands out of the background,”13 to force events into binary categories. In addition, many electrographic features appear hidden in the time domain14 and thus may be difficult to detect via visual inspection of EEG records. As we show, events can appear ambiguous to the same expert scorer such that, on repeated presentations, a scorer changes their mind about an event's categorization. Such ambiguity is reminiscent of human perception of optical illusions such as the Necker Cube15 and suggests that “ground truth” (What do humans define as SWDs and how do those events relate to, or arise from, ongoing nonepileptic brain activity?) in identifying electrographic events may need to be considered in terms of confidence measures rather than certainty.

Thus, there is a need for the development of robust, automated methods for the detection of SWDs that allow for confidence‐based scoring of events along a continuum that mirrors physiologically relevant EEG features and that matches human scoring characteristics. Although algorithms have been developed for detection of SWDs,16, 17, 18, 19 there has been little development of algorithms for the detection or quantification of SWDs in mice.16 This is an important gap because rodent models are currently the main research tools for understanding the basic mechanisms of epilepsy.

We present a support vector machine (SVM)–based algorithm for the detection of SWDs in mice expressing a γ‐aminobutyric acid A (GABA_A) receptor mutation (γ2R43Q) that causes absence epilepsy.5, 20 This algorithm is much faster than manual scoring; it scores a 24‐hour record in ~3 minutes. It is important to note that this algorithm agrees well with human scoring and captures the statistical characteristics of human uncertainty. In addition, and unlike human experts, it is 100% self‐consistent. Finally, we show that events along the scoring continuum generated by the algorithm are temporally and proportionately correlated with changes in spectral power bands relevant to behavioral states including sleep.

3. METHODS

All use of animals in this manuscript conformed to the Guide for the Care and Use of Laboratory Animals 21 and was approved by the University of Wisconsin‐Madison Institutional Animal Care and Use Committee.

3.1. Animal colonies

Animals were bred from a colony maintained at the University of Wisconsin‐Madison. In a paired breeding scheme, female wild‐type (RR) mice of a C57BL/6J‐OlaHsD background (Harlan, Madison, WI) were bred with male heterozygous mice expressing the γ2R43Q knock‐in mutation in the same background. Heterozygous knock‐in mice (RQ) experience SWDs concurrent with behavioral arrests5 whereas homozygous mutants are rare. The γ2R43Q strain was provided by Dr. Steven Petrou (The University of Melbourne, Parkville, Australia).

3.2. Computer programing and code accessibility

All analyses, data processing, and event classification was done in MATLAB (MathWorks, Natick, MA). The final version of this algorithm was executed with MATLAB 2017b and code is available at the GitHub repository: https://github.com/jessePfammatter/detectSWDs.

3.3. EEG implantations, recording, and data

EEG electrodes were implanted as described by Nelson et al. 22 Briefly, male heterozygous knock‐in (RQ) and wild‐type (RR) mice were implanted at postnatal day 24 under isoflurane anesthesia (1%‐2% in 100% O₂). Each animal was implanted with gold‐plated miniature‐screw electrodes over the right and left frontal and parietal cortices, and one over the cerebellum as reference. Two vinyl‐coated braided stainless‐steel wire electrodes were placed in the nuchal muscle for electromyography (EMG) recording. The EEG and EMG leads were wired to a head cap, which was affixed to the skull with dental acrylic.

After recovery from surgery (2‐3 days), animals were connected to a multichannel neurophysiology recording system (Tucker‐Davis Technologies, TDT, Alachua, FL) to continually sample EEG and EMG signals at 256 Hz (digitally bandpass filtered between 0.1 and 100 Hz) for up to 14 days. Offline, data were notch filtered at 60 Hz using a Chebyshev Type II digital filter and high‐pass (>2 Hz) filtered with a Chebyshev Type I digital filter. We selected these infinite impulse response (IIR) filters because of their highly specific frequency attenuation without ripple in unintended frequencies, acceptable phase shift given our largely time‐frequency–based algorithm, and computational efficiency (see Figure S1 for frequency and phase responses of these filters). EEG signals were then normalized using the following variation of a z‐score normalization: First, we fit a Gaussian distribution to the all‐points histogram (calculated using the histfit() function with bins equal to the floor of the square‐root of the number of data points in each EEG signal) of each 24‐hour record using least‐squares minimization via Nelder‐Mead simplex optimization23 as implemented by the fminsearch() function in Matlab using the mean and standard deviation of the 24‐hour EEG as starting guess for the optimization. We then normalized the 24‐hour record by subtracting the mean from each data point and dividing by the standard deviation of the model fit. The resultant normalization is different from the standard z‐score normalization in that the mean and standard deviation are calculated from estimating the Gaussian portion of the signal via the best‐fit Gaussian model (using sum of squared errors) rather than being empirically calculated. We employed this normalization technique to comparatively normalize the EEG from healthy and epileptic animals alike. High‐amplitude EEG signal such as convulsive seizures or high‐amplitude spikes produce EEG data with non‐Gaussian all‐points histograms and thus poor results from the maximum likelihood estimates of the mean and standard deviation. In addition, more simplistic methods such as a median normalization did not perform as well and fundamentally do not attempt to normalize the data to the “normal” component of the EEG signal in the same way as our method. All analyses used a frontal EEG channel.

3.4. Automated event detection

We used a 2‐stage algorithm for the detection and classification of SWDs. In Stage 1, we automatically detected putative SWDs using a frequency and amplitude threshold‐based approach. First, we detected all peaks that were (a) above 3 standard deviations from the mean of the normalized EEG signal and (b) that had a peak greater 3 three standard deviations from the mean of the derivative signal (the negative of the first derivative of the normalized signal calculated with the gradient() function and normalized again with the same procedure as the original signal) that preceded (within 60 msec) the peaks identified in the normalized EEG. Then, sets of peaks were grouped into “possible SWD events” if their frequency was between 3 and 11 Hz. The parameters for event selection were selected heuristically rather than optimized. We choose these parameters with the aim to minimize the number of false negatives at the cost of false positives (filtered in Stage 2) as compared with unaided human scoring (described in the next section and results presented in the top confusion matrix of Figure 4H) while also remaining within previously published guidelines for the characteristics of SWDs in mice5, 24 and rats.3, 4

Figure 4.

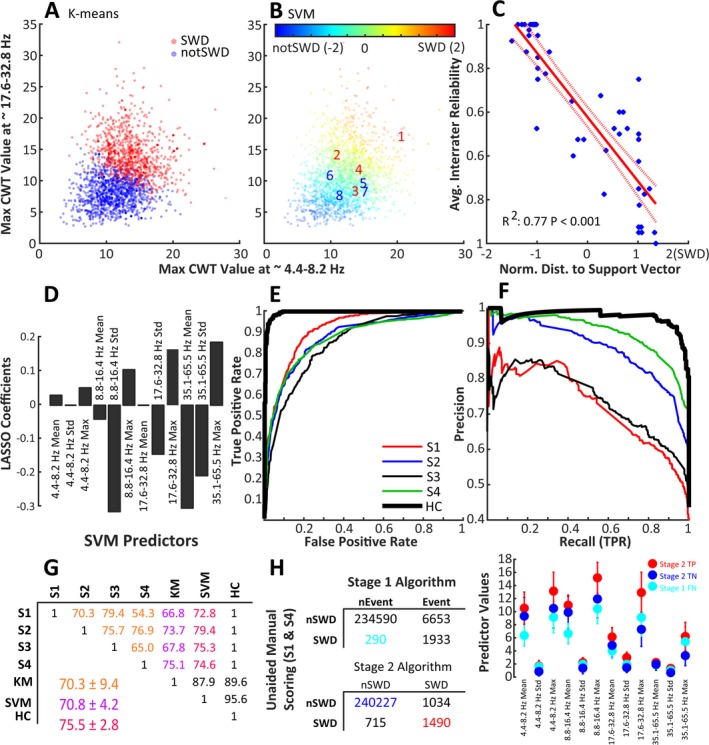
Support vector machine (SVM)–based approach to SWD classification. A, B, each of the 2500 potential SWD events displayed by the maximum value of the wavelet transform from ~4.4‐8.2 Hz vs the maximum value of the wavelet transform from ~17.6‐32.8 Hz. A, Shows events as clustered by K‐means clustering using the 12 wavelet transform predictor variables. B, Events labeled by an SVM trained with the human scoring labels and fit with a Gaussian kernel. The numbers 1‐8 are overlaid to show the SVMs classification of the 8 example events from Figure 2. C, The relationship between the distance to nearest support vector (x axis, 2 is more likely SWD) and the average intrarater reliability (from Figure 2C) for the 50 repeated events. D, The coefficients from a LASSO regression, which highlights the relative importance (absolute value of coefficients) and relative magnitude (sign of coefficients) of the variables as compared to the SVM scores. E, Receiver‐operating characteristic and F, precision‐recall curves showing the performance of each human scorer and the human consensus labels (HC) as compared to the SVM scores. G, The agreement matrix for classification of 2500 potential SWD events as classified by 4 human scorers (S1‐S4), an SVM trained with the KM labels, and the human consensus data (HC, the events on which all human scorers agreed). Note that the agreement between all of the humans (orange) was comparable to that between the SVM classification and the humans (red), although the agreement between the SVM and the humans shows much lower variability than the agreement between the humans alone. H, Confusion matrices comparing the epoch‐by‐epoch scoring of events identified by Stage 1 of the algorithm (top matrix) and events classified as SWD by the Stage 2 SVM (bottom matrix) and S1/S4 scoring of 5, 24‐h EEG records representing 2 RQ and 2 WT animals. The Youden's J statistic (sensitivity + specificity −1) between S1 and S4 equals 0.80. S1 and S4 scored these files without the any information from the algorithm regarding putative SWD events. Events within epochs identified as Stage 2 TP (red), Stage 1 FN (cyan), and Stage 2 TN (blue) have significantly different multivariate means for the 12 predictor variables used by the SVM for event classification (lower‐right plot)

3.5. Manual event classification

Completely unaided from our computer algorithms, scorers (S1 and S4: R.K.M. and J.A.P.) each manually scored 5, 24‐hour EEG records (n = 4 RQ, n = 1 RR) for the presence of SWDs. Scorers marked epochs (4 s) containing SWDs using Svarog v1.0.10 (Braintech, Ltd., UK). We use these manual scores to help validate the performance of both our Stage 1 and Stage 2 algorithms.

We also presented 2500 putative SWD events identified by the Stage 1 detection method to each of 4 human scorers (S1‐S4: R.K.M., E.P.W., M.V.J., and J.A.P.) including an epileptologist with over 20 years of experience (R.K.M.) for manual classification. Of these, 2050 were randomly selected unique events from 10, 24‐hour EEG records from 5 animals (3 RQ and 2 RR). From these we selected 50 events to be repeated 10 times each. Each of the resultant 2500 events were shown to the human scorers in random order. Each event was presented as an 8‐second length of normalized single‐channel EEG with the putative event highlighted in yellow. Scorers classified events as either SWD or nonSWD and were given as much time as they needed to view/review/reclassify events. All human scorers were skilled in the identification of SWDs but were blinded to the genotypes, and 2 were blinded to the presence of repeated events. None of the scorers were aware of which events were repeated because the order of events was random.

EEG/EMG signals were also manually scored for sleep stages (wake, non‐rapid eye movement [nREM], or rapid eye movement [REM]) (see Figure 3) in epochs (4 s) with Serenia Sleep Pro software (Pinnacle Technology, Lawrence, KS) following criteria similar to Nelson et al (2013).22 Stretches ≥8 seconds (2 epochs) were required for valid transitions.

Figure 3.

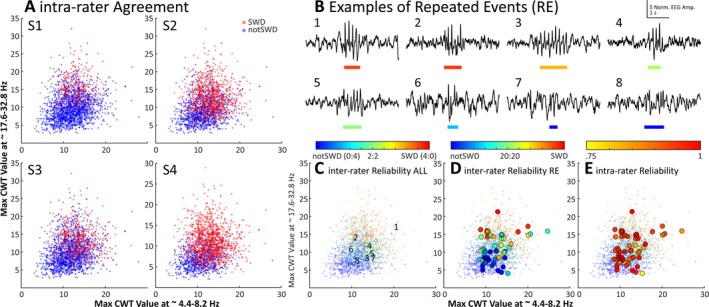
A characterization of the variability of human classification of SWD events. A, Each of the 2500 events as labeled by human scorers 1‐3. Note the dramatic variability in labeling between each of the scorers. B, Examples of 8 events identified as “putative” SWD events by the first stage of the algorithm. The colored bar below each trace represents the start and end of each event, where color shows the degree of agreement between human scorers. This color scale matches that above Panel C. C, Each of the 2500 putative SWD events presented to each human scorer, plotted by the maximum value of the wavelet transform from ~ 4.4‐8.2 Hz vs the maximum value of the wavelet transform from ~ 17.6‐32.8 Hz. The numbers mark locations of the 8 example events from panel B. D, The average interrater agreement for each of the 50 repeated events (REs, large circles) plotted over the same data. Note that the agreement between raters approaches a coin flip (green) near the intersection of the strong SWD and nonSWD events. E, The average intrarater reliability for the same 50 REs as shown in panel D. Note the shifting scale associated with the color bars above panels C, D, and E

3.6. Event predictor variables

From the putative events detected by Stage 1, we extracted 12 predictor variables for use in Stage 2 of the automated algorithm: event classification with an SVM. These variables were calculated from 4 scale ranges from the wavelet transform (using the cwt() function specifying “amor” for the Morlet wavelet) of each event. These ranges were chosen to target the characteristic ~6 Hz frequency of SWDs in mice and several of its harmonic components.3, 4, 5 For each of the 4 frequency bands (4.4‐8.2 Hz, 8.8‐16.4 Hz, 17.6‐32.8 Hz, and 35.1‐65.5 Hz) we summed the absolute value in each bin (9 bins per band) across the duration of each event (including 10 data points before the first peak and after the last peak identified for each event) and calculated the mean, standard deviation, and maximum values for each event (4 frequency bands * 3 statistics = 12 predictors).

3.7. Automated event classification

For Stage 2 of the algorithm we developed an SVM‐based automated method to classify SWD events identified in Stage 1 using the 12 predictors. In brief, an SVM is a machine learning–based classification method that aims to separate groups of events after being trained with set of “known” labels. The boundaries of the classification space are defined by events assigned as support vectors. The location of each event relative to the nearest support vectors can be used for classification of events, and the distance from each event to its nearest support vector can be used as a proxy for confidence in the assigned classification of each events. Readers unfamiliar with SVM may find a suitable introduction in25.24 We trained the SVM (fitcsvm() function) using the labels provided by the human scorers (10 000 labels, 2500 per scorer for 2050 unique events) where the algorithm created a weighted response for each unique event based on the average human label across all 4 scorers. In our preliminary testing of the algorithm and upon visual inspection of the predictor variables for these events, we choose a Gaussian kernel for the SVM.24 To choose the proper hyperparameters for the SVM (kernel scale, box constraint, and cost matrix used in fitcsvm()), we employed a grid‐search based optimization process. We trained the SVM under each unique combination of the following parameters; kernel scale = [1, 5, 10, 15, 20], box constraint = [5, 10, 15, 20, 25], and a cost matrix of [0, 1; x, 0] where x = [1, 1.5, 2, 2.5, 3]. We then chose hyperparameters with the following guidelines: (a) We aimed to minimize the standard deviation of the agreement among the human scorers and the SVM in order to minimize individual scorer bias. We chose this method as opposed to maximizing the average agreement between the human scorers and the SVM because that quantity can be maximized to a significantly higher value than the agreement within human scorers, resulting in model overfitting and poor performance on novel data. (b) To avoid overfitting, we calculated the fivefold cross validation, which partitions the data into multiple subsets and tests model fit on each subset,24 between the SVM and the training labels. Because Matlab uses a stochastic fitting process for the generation of the SVM, we repeated SVM fitting and calculation of the fivefold cross validation 10 times and took the standard deviation of fivefold cross validations.26 Minimizing this quantity allowed us to select a model that performs similarly on numerous randomly chosen subsets of data. (c) The model should match human uncertainty in order to generate accurate confidence‐based model scores (distance from each event to the nearest support vector). We aimed to maximize the R ² between the model scores and the weighted human responses for each of the 50 repeated events (not the entire 2500 events) within the data set (ie, intrarater reliability), which produces a model with high fit to the human uncertainty (the 50 repeated events are our predictors of human uncertainty in SWD scoring). Although these parameters are important, their optimal set point is unclear given that variability between human scorers suggests that ground truth labels may not exist for these data. Here, we used the following hyperparameters: kernel scale = 10, box constraint = 10, cost matrix x = 1.5. We present graphical results for the optimization of our tunable SVM parameters in Figure S2.

To better understand the relationship of the 12 predictor variables calculated from the wavelet transform of each event with the classification scores produced by the SVM, we performed a least absolute shrinkage and selection operator (LASSO) regression.27 Although this analysis does not allow direct understanding of the classification space of the SVM, such direct understanding is difficult to achieve and therefore methods that allow some intuition as to the relative importance of predictor variables in the system are useful. We allowed the LASSO regression 100 iterations with cross validated (10‐fold) fits and selected the final coefficients from the model with a lambda value (indicating lowest cross validation error) that was one standard deviation larger than the model with the lowest lambda value.

To highlight the differences between the human and SVM scoring of the 2500 events identified by Stage 1, we calculated receiver‐operating characteristic (ROC) and precision‐recall curves between each scorer and the algorithm. In addition we provide a table showing pairwise agreement between the human scorers, the SVM trained with K‐means28 labels (generated using the kmeans() function from the 12 predictor variables for each event), the final SVM, and the human consensus labels. In addition, we calculated the sensitivity, specificity, and precision between the human consensus labels and the final SVM (for the 2500 events identified by Stage 1). To demonstrate the performance of the algorithm in comparison to human scoring (2 scorers) of an unannotated (no information from Stage 1) and out‐of‐training data set (5, 24‐hour EEG recordings), we calculated confusion matrices from the epoch‐by‐epoch scoring of SWDs identified by humans (S1 and S2) and the Stage 1 events, and SWDs identified by humans (S1 and S2) and the Stage 2 (final SVM) scores. From these confusion matrices we calculated the 12 event predictor variable values for each event within 3 categories: Stage 2 true positives (TP, events within epochs classified by Stage 2 the humans as SWDs), Stage 1 false negatives (FN, events within epochs classified by humans as SWDs but missed by Stage 1), and Stage 2 true negatives (TN, events within epochs classified by Stage 2 and the humans as nonSWDs). We then calculated a multivariate analysis of variance (MANOVA; using the manova1() function) to demonstrate if the means of the 12 predictor variables collectively varied between the three test groups (Stage 2 TP, Stage 1 FN, and Stage 2 FN).

3.8. Application of the algorithm and preliminary testing of the SWD output scores

We applied the algorithm to classify SWDs in 60, 24‐hour EEG records from 8 RQ and 3 RR animals including 45 records that were not used for algorithm development (ie, out‐of‐sample data). Using the output of the algorithm, we calculated the event‐triggered average: (ie, the average of all segments of one signal aligned to the time of events in another signal) of 50 random examples of strong SWDs (distance to support vector of >1 to 2), moderate SWDs (>0.5 to 1), weak SWDs (>0 to 0.5), weak nonSWDs (<0 to −0.5), moderate nonSWDs (<−0.5 to −1), and strong nonSWDs (<−1 to −2), and 50 random locations not identified by our algorithm to delta (0.5‐4 Hz), theta (6‐9 Hz), sigma (10‐14 Hz), and gamma (25‐100 Hz) power surrounding each event during lights‐on and lights‐off periods.

4. RESULTS

We found that events identified by our algorithm as SWDs in γ2R43Q animals have a characteristically strong and continuous power in the ~6 Hz frequency range during the entire discharge event (Figure 1), consistent with previous descriptions of SWDs in these animals.5 In addition, these events have a reliable “fingerprint” in the time‐frequency decomposition (Figure 1).

Figure 1.

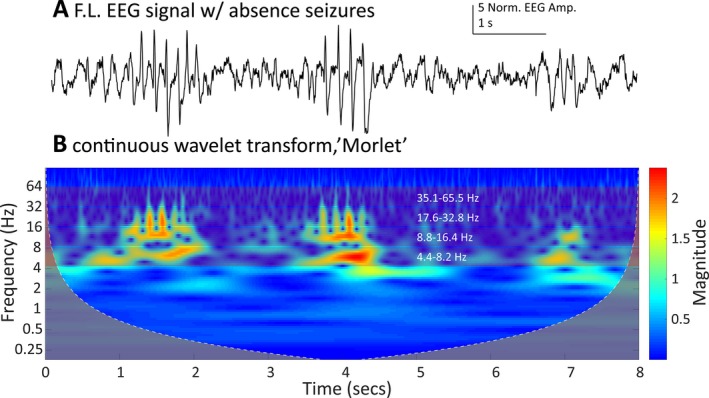
A, An EEG trace from the frontal left channel of a mutant γ2R43Q mouse showing three putative SWD events detected by Phase 1. B, The wavelet transform scalogram of the trace in A. We use the maximum, average and standard deviation of the scalogram amplitude from four bands (~4.4‐8.2 Hz, ~8.8‐16.4 Hz, ~17.6‐32.8 Hz, and, ~35.1‐65.5 Hz shown as bands with white frequency labels) to generate 12 predictors to train the SVM‐based classification algorithm.

4.1. Manual scoring and inter‐ and intrarater reliability of preselected events

Overall, human scorers were variable in their scoring. Of the 2050 unique events, the 4 human scorers were in complete agreement (ie, consensus labels) for 57% of the events (1159 events, 940 nonSWDs, and 219 SWDs). Figure 2 shows a characterization of human scoring of the 2500 events presented as 2‐dimensional cross‐sections in predictor space for 6 of the predictor variables used in the SVM. Further characterization of the inter‐ and intrarater reliability is shown in Figure 3, which demonstrates the difference in rating trends of the human scorers. Figure 3B shows 8 example events pulled from the 50 events presented to each human scorer 10 times. For each of the 2500 events presented to human scorers, agreed‐upon SWD events have high values for both the maximum values in 4.4‐8.2 Hz and 17.6‐32.8 Hz ranges, whereas agreed‐upon nonSWD events have a low maximum value for these bands (Figure 3B). Intra‐ and interrater reliability data are shown in Figure 3C‐E. Interrater reliability on the 50 repeated events (REs) data (Figure 3D) agreed with the trend in distribution of human agreement for all of the 2500 events presented (low‐resolution data). Average intrarater reliability across all scorers was 100% for 13 of 50 REs (Figure 3E). Thirteen of the 50 REs had an average intrarater agreement of 90% or less across all scorers. For individual scorers, intrarater agreement was as low as 50% for the most ambiguous events. Average Intrarater reliability was 94% across all scorers and all 50 repeated events.

Figure 2.

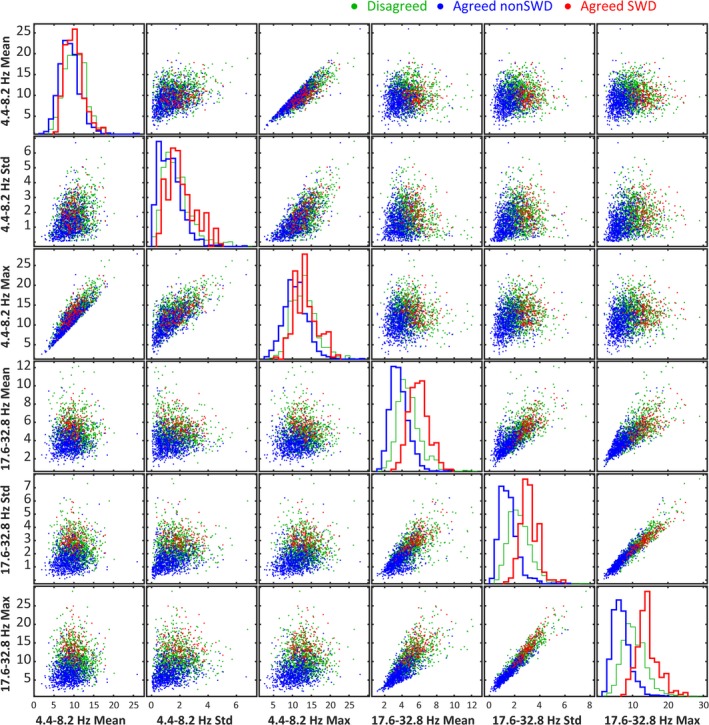
Each of the 2500 human‐scored events labeled by agreed SWD (red), consensus agreed nonSWD (blue), and consensus disagreed (green) shown as a 2‐dimensional cross‐section in predictor space for 6 of the 12 predictor variables used to characterize an SWD event. The diagonal shows the histograms for each category of label for each of the 6 predictor variables. Notice how disagreed‐upon events tend to align with SWD rather than nonSWD events.

4.2. Comparing automated and manual scoring of preselected events

Although only one of many possible clustering methods, K‐means, a more traditional clustering method, failed to partition the data similarly to the human scorers (notice the “fuzziness” in SWD/nonSWD scoring in Figure 3A) but rather drew a hard line between SWD/nonSWD events (Figure 4A). The output of the SVM trained with human labels demonstrates a similar “fuzziness” in scoring as human scorers (Figure 4B). In fact, the SVM classification associated with events (eg, distance to the nearest support vector) is strongly correlated with human interrater reliability (Figure 4C). In comparing labels from our final SVM algorithm and the human consensus labels, the sensitivity (equal to the number of true positives, the SWD events agreed upon between SVM and the human consensus labels, divided by the total number of SWD events from the human consensus labels) was 0.98. The specificity (equal to the number of true negatives, the nonSWD events agreed upon between SVM and the human consensus labels, divided by the total number of nonSWD events from the human consensus labels) was 0.95. The precision (equal to the true positives divided by the sum of the true positives and false positives, the number of events classified as SWD by the SVM but nonSWD by the human consensus labels) was 0.83. The values for sensitivity, specificity, and precision presented here were calculated using events identified by Stage 1 of the algorithm, and although these are useful metrics they should not be interpreted as the sensitivity and specificity of the algorithm as compared to unaided human scoring of SWDs (see next section). Figure 4D shows the coefficients for the LASSO regression. The absolute value of these coefficients indicates the relative importance of each variable, whereas the sign indicates whether a large versus small value of that variable was most predictive of the SVM classification scores. Negative coefficients do not indicate that the magnitude for those variables was lower for SWDs than nonSWDs on average. Figure 4E‐F shows the ROC and precision‐recall curves between the 2500 events scored by each of the human scorers and the SVM scores. The average agreement between humans was similar to that between humans and K‐means but lower than the average agreement between the SVM and the humans. The standard deviation of the agreement between the SVM and the human scorers is lower than between the human scorers themselves, indicating that the SVM agrees with the humans better than they agree with themselves (Figure 4G).

4.3. Comparing automated scoring with unaided manual scoring

Figure 4H shows a comparison between performance of the scoring of 5 unannotated (without computer assistance) 24‐hour EEG records by humans (S1 and S4) with the Stage 1 events and the Stage 2 SVM results. Stage 1 of the algorithm compared with the unaided human scoring had a precision of 0.22 and a recall (equal to the true positives divided by the sum of the true positives and false negatives) of 0.87. Stage 2 of the algorithm compared with the unaided human scoring had a precision of 0.59 and a recall of 0.68. Epochs containing SWD events identified by humans but missed by Stage 1 of the algorithm (Stage 1 FN, 290 collective epochs containing 244 unique events) events within those epochs have significantly different characteristics (values for predictor variables used in the SVM) than those events within epochs identified as Stage 2 TP (1490 collective epochs containing 1150 unique events) or Stage 2 TN (240227 collective epochs containing 3143 unique events) (MANOVA dimension = 2, P‐values < 0.001, Figure 4H).

4.4. Application of the algorithm

We applied the algorithm to analyze SWDs in a set of 60, 24‐hour EEG recordings from RR and RQ animals, 50 of which were not used for SVM development. The algorithm analyzed these records in ~3 minutes per 24‐hour record. Figure 5 shows the application of our algorithm on a representative 24‐hour record from an RQ animal. In addition, using the output of the algorithm on an RQ animal, we demonstrated the relatedness of SWD and nonSWD events (as labeled by the SVM) to sleep staging. We found strong and abrupt relationships between SWDs and each power band that sometimes preceded the SWD by several minutes (Figure 5D‐K).

Figure 5.

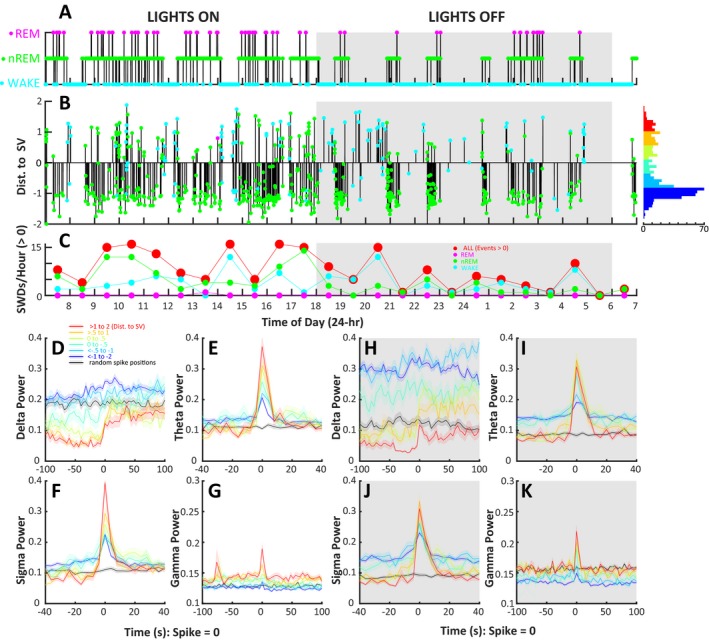
Implementation of the SWD detection algorithm on a 24‐h EEG recording from a mutant γ2R43Q mouse with absence epilepsy and a demonstration of the high‐resolution data provided the “distance to support vector (SV)” measure associated with each identified event. A, A hypnogram showing WAKE (blue), nREM (green), and REM (magenta) epochs (4 s) manually scored by R.M. B, A visual representation of the events identified by the SVM‐based algorithm. The vertical height of each bar represents the distance to nearest support vector. Values >0 are likely to be SWDs, whereas events <0 are likely nonSWD events. The color at the end of each vertical bar shows the sleep stage associated with the identified event. The histogram on the right of Panel C shows the distribution of event scores, and colors are representative of the categories of events used in panels D‐K. C, Shows the average number of SWDs (score >0) per hour for all sleep stages (red, larger circles), WAKE, nREM, and REM sleep stages. Notice the pattern of increased SWD events during lights‐on periods (07:00‐18:00, normal sleep time for mice) as compared to the lights‐off period. The event‐triggered average of delta (D, H), theta (E, I), sigma (F, J), and γ (G, K) power (calculated in 4 s epochs) for events at several sets of distances from the nearest support vector where redder colors are more likely to be SWDs (red: >1 to 2, yellow: >0.5 to 1, lime: 0 to 0.5, green: 0 to −0.5, cyan: <−0.5 to −1, blue: <−1 to −2). Note that the color scale in this figure matches the color scale in Panel B of Figure 3. The black trace in each of these panels shows the null‐hypothesis: the event‐triggered average of each power value for 100 randomly selected epochs in the EEG record. Events with the largest positive distance to SV (red) show a strong relationship to all power bands during lights‐on (white panels) and lights‐off (gray panels) and this relationship deteriorates as event distances decrease. Note that all events identified by the algorithm show some sort of temporal relationship with theta and sigma power as compared to randomly selected EEG locations. Further investigation is needed to identify the relationship of each group of these events to absence epilepsy

We found an average of 737.51 ± 482.28 events per 24‐hour RQ record (n = 8 animals, 45, 24‐hour records), of which 194.09 ± 169.37 of were classified as SWDs (>0 SVM score). In RR animals (n = 3 animals, 14, 24‐hour records), we found 409.64 ± 207.28 possible events per 24‐hour record, of which 26.79 ± 21.18 were classified as SWD events. The events identified as SWDs had a significantly lower SVM score in RR animals (0.797 ± 0.445) than in RQ animals (0.519 ± 0.376, t = 24.39, df = 17410, P‐value <0.001). Despite having a lower average SVM score, SWDs identified in RR animals show strong visual SWD characteristics (Figure 6A) and show similar temporal relationships with delta, theta, sigma, and gamma power bands as events from RQ animals (data not shown). Despite being very similar, compared to RQ animals, events from RR animals do have a significantly different multivariate profile for the 12 continuous wavelet transform cwt‐based predictor variables (MANOVA df_chi‐square = 12, chi‐square value = 984.27, P‐value < 0.001, Figure 6B). However, these differences appear to be relatively small compared to those differences observed between TPs and TN/FNs presented in Figure 4H.

Figure 6.

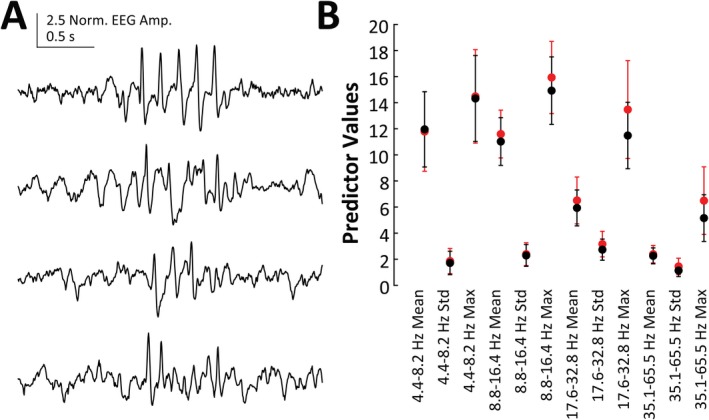
A, Four SWD‐like events from a 24‐h record of a wild‐type (RR) animal as identified by the SWD‐detection algorithm. B, Means and standard deviations for the 12 predictor variables calculated for SWD events found by our algorithm in RR (black circles, n = 3 animals, 14 24‐h records) and RQ (red circles, n = 8 animals, 45 24‐h records) animals

5. DISCUSSION

We have developed an automated, SVM‐based algorithm for the detection of SWDs that leverages human agreement in the scoring of machine‐preselected events to develop a continuous, confidence‐based score in addition to a binary classification (SWD/nonSWD). The algorithm was trained using a dataset with 2500 putative events and labels (SWD or nonSWD) from 4 expert human scorers, using fivefold internal cross validation, and tested against the performance of 2 human scorers (S1 and S4) on multiple, unannotated (no computer information), and out‐of‐training data records. The resultant SVM agreed with humans as well as they agreed with each other when scoring machine‐preselected events (~70%), but unlike the other classification technique that we investigated (K‐means, Figure 4A), the SVM did not draw sharp boundaries in predictor space between regions containing SWDs vs nonSWDs. Instead, it drew fuzzy, tightly interleaved boundaries similar to those of human scorers. The algorithm also correlated well with the uncertainty of individual humans when presented with repetitions of the same waveforms, thus capturing ~77% of the ambiguity in human perception of SWD waveforms (Figure 4C). Although other groups have developed algorithms for the detection of SWDs,16, 17, 18, 19 to the best of our knowledge, no other group has designed an algorithm to mirror human confidence in scoring.

Of course, there are a few limitations and concerns to address about our algorithm. Most notable is the fact that the primary focus of our attention in this article is on highlighting the performance of the SVM with the human scoring of machine‐preselected events rather than on the performance between the SVM and unaided human scoring of raw EEG. As stated earlier, our thorough description of the intra‐ and interrater variability in the scoring of events is perhaps the most important contribution of this study to the current state of event detection in absence epilepsy. Given that we show how variably humans perform on the scoring events presented in such a controlled setting, it is not surprising that performance metrics comparing unaided human scoring of SWDs to our algorithm are suboptimal. Regardless, the performance metrics comparing the SVM with unaided human scoring are very important and are not to be ignored. Indeed, our method may have produced better results if we had performed a rigorous optimization in order to set the Stage 1 parameters—a potential weakness of this work. However, optimization of parameters to data scoring in such an uncontrolled fashion (eg, humans often view EEG records at different time and amplitude scales when scoring) may not necessarily lead to a better understanding of ground truth in SWD detection. Rather, the true definition of SWDs should arise from comparison of rigorously definable events (eg, events defined as having a particular set of predictor variables) with other known EEG features (such as we have demonstrated in Figure 5) or treatments (eg, ethosuximide) known to alter SWDs. We believe that our work sets a framework for investigating a rigorously selected and definable set of SWDs and we plan to follow this line of research in future work.

Although we believe that this method performs well on data from the γ2R43Q model of absence epilepsy, we have yet to fully test it in other models of absence epilepsy. Continued development will include testing and expansion to other animal models as well as to human EEG. We anticipate that Stage 1 (event detection) should work well for most types of absence seizures exhibiting a ~6 Hz character (as occurs in rodents). The frequency range of interest can be easily adjusted for different data sets. However, for Stage 2 (the SVM classification), some retraining of the algorithm may be necessary, using human scoring on a very small subset of data that are representative of the different types of subjects/treatments being analyzed. In this current version, we selected a set of optimization parameters and SVM kernel that best fit the characteristics of human scoring. In general, modification of the hyperparameters or kernel can make an SVM more generalizable.25 Continued development of this algorithm may also include components shown to be important for other SWD detection algorithms such as using phase information from the wavelet transform such as was done by Richard et al.16 In addition, some concern may exist about the nonstandard normalization procedure used in this algorithm. Although we are confident in this normalization and are not removing or cleaning the data through this procedure (besides the stated filters), the matter certainly deserves more attention and is one focus of our ongoing research.

Despite its limitations, we have used this algorithm to highlight a few important aspects of SWDs that would have been difficult to identify solely with human classification. Our data show that events along the spectrum of the SVM score (and thus SWD confidence) show temporal and proportional correlations with abrupt changes in EEG power bands. Although these correlations are most prominent in SWDs with the highest SVM scores, events with lower scores (and even those below threshold) continue to show correlations, albeit with smaller effects. Qualitatively similar temporal patterns were observed in all of the γ2R43Q animals analyzed in this study (data not shown). Thus, the SVM reveals physiologically relevant changes in brain activity that are commonly used in the scoring of sleep and shows that these changes are temporally linked to, and could potentially be used to predict, the occurrence of SWDs. It is notable that our findings align with previous work showing shifts in phase‐amplitude coupling up to a minute prior to SWDs,29 and that SWDs are related to sleep timing.30 Furthermore, our algorithm includes SWDs and SWD‐like activity of short duration, which are discarded by most studies.16 We also identified SWD‐like events in wild‐type mice, consistent with the hypothesis that SWD events represent a corruption of otherwise normal brain processes.31 Given this hypothesis, finding examples of SWDs in wild‐type mice with low intensity (ie, smaller distance to nearest SV) is to be expected. In addition,32 found that 8 of 27 strains of wild‐type mice had SWDs including several from the C57‐related backgrounds. Although low‐intensity events show temporal relationships with several EEG power bands that coincide with confident SWD events (data not shown), further research is needed to understand if the SWDs observed in RR animals are related to the same processes as those that generate SWDs in absence epilepsy or if they are representative of other normal physiologic processes.

DISCLOSURE

The authors report no conflicts of interest. We confirm that we have read the Journal's position on issues involved in ethical publication and affirm that this report is consistent with those guidelines.

Supporting information

 

 

Pfammatter JA, Maganti RK, Jones MV. An automated, machine learning–based detection algorithm for spike‐wave discharges (SWDs) in a mouse model of absence epilepsy. Epilepsia Open. 2019;4:110–122. 10.1002/epi4.12303