A Phylogenetic Approach Finds Abundant Interlocus Gene Conversion in Yeast

Abstract

Interlocus gene conversion (IGC) homogenizes repeats. While genomes can be repeat-rich, the evolutionary importance of IGC is poorly understood. Additional statistical tools for characterizing it are needed. We propose a composite likelihood strategy for incorporating IGC into widely-used probabilistic models for sequence changes that originate with point mutation. We estimated the percentage of nucleotide substitutions that originate with an IGC event rather than a point mutation in 14 groups of yeast ribosomal protein-coding genes, and found values ranging from 20% to 38%. We designed and applied a procedure to determine whether these percentages are inflated due to artifacts arising from model misspecification. The results of this procedure are consistent with IGC having had an important role in the evolution of each of these 14 gene families. We further investigate the properties of our IGC approach via simulation. In contrast to usual practice, our findings suggest that the IGC should and can be considered when multigene family evolution is investigated.

Introduction

A variety of mutational mechanisms generate repeated sequences. Following their formation, the evolutionary fates of individual repeated elements are intertwined. One source of this mutual dependence is interlocus gene conversion (IGC). IGC homogenizes repeats by copying sequence stretches from one repeat into the equivalent region of another. This means that the evidence for nucleotide substitution in one paralog can be erased when IGC copies over the sequence that experienced it. In addition, IGC can make it appear as if separate nucleotide substitutions arose in two different paralogs. Failure to consider IGC can therefore obscure the process of nucleotide substitution and thereby potentially impact inferences of phylogenies, divergence times, and diversifying positive selection.

However, the consequences of ignoring IGC depend on its frequency. Although repeats often constitute a large fraction of an organism’s DNA, the evolutionary importance of IGC on a genomic scale is unclear. There have been substantial advances toward disentangling the duplications, deletions, and speciation events that shape multigene families (reviewed by Szöllősi et al. 2015 ), but less progress has been made toward separating IGC events from the nucleotide or codon substitutions that arise from point mutations. There are available tools for detecting IGC and illuminating evolutionary investigations of IGC have been performed (e.g., Sawyer, 1989 ; Jackson et al. 2005 ; Dumont and Eichler, 2013 ; Dumont, 2015 ), but the overall paucity of information about IGC is largely attributable to a shortage of appropriate statistical techniques. Simulations suggest that previously proposed tests for detecting IGC can have low power ( Mansai and Innan, 2010 ).

Here, we employ a composite likelihood-based approach with models that consider the possibility that corresponding sequence positions in two paralogs can be homogenized due to IGC. We do this with a phylogenetic framework that can be added to any existing probabilistic model of sequence evolution where sequence variation arises via point mutation. We will refer to these existing conventional models as point-mutation models. The basis of our IGC-extension is to: (1) jointly consider corresponding nucleotide or codon sites in paralogs within a genome; (2) have point-mutation models independently affect different paralogs; and (3) have rates at which nucleotide or codon states are homogenized in two different paralogs be the sums of rates from the point-mutation models plus the IGC rates. For changes that do not homogenize paralogs, rates are determined exclusively by the point-mutation models.

We illustrate our approach by applying it to quantify the amount of IGC that occurred in 14 groups of protein-coding genes subsequent to a genome-wide duplication in yeast. Simulations are conducted to characterize the properties of our approach and to examine how robust it is to violations of its assumptions. We conclude by discussing the weaknesses of the approach and future potential improvements.

New Approaches

We have been pursuing extensions of simple codon substitution models ( Goldman and Yang, 1994 ; Muse and Gaut, 1994 ) because their ability to differentiate between synonymous and nonsynonymous change is appealing. Consider a simple 61-state codon model that has the Muse-Gaut treatment of codon frequencies together with a distinction between transition and transversion substitutions. Using the notation of the codeml software ( Yang, 2007 ), we specifically consider a model that would be denoted $F1\times 4MG+\kappa +\omega$ . However, we will refer to this as the independently-evolving paralog model (IND) in order to contrast it with our approach that adds dependence among paralogs due to IGC. The IND model has the instantaneous rate $Q_{i,j}$ from codon triplet i to j be 0 if i and j differ in more than one of their three positions or if j encodes a stop codon. If i and j differ in exactly one nucleotide that has type h ( $h\in \{A,G,C,T\}$ ) in codon j , the IND model has rates:

$$Q_{i,j}=\{\begin{array}{ll}u{\pi }_h& \text{\hspace{0.17em} for \hspace{0.17em} a \hspace{0.17em} synonymous \hspace{0.17em} transversion \hspace{0.17em}}\\ & \\ u{\pi }_h\kappa & \text{\hspace{0.17em} for \hspace{0.17em} a \hspace{0.17em} synonymous \hspace{0.17em} transition \hspace{0.17em}}\\ & \\ u{\pi }_h\omega & \text{\hspace{0.17em} for \hspace{0.17em} a \hspace{0.17em} nonsynonymous \hspace{0.17em} transversion \hspace{0.17em}}\\ & \\ u{\pi }_h\kappa \omega & \text{\hspace{0.17em} for \hspace{0.17em} a \hspace{0.17em} nonsynonymous \hspace{0.17em} transition}.\end{array}$$ (1)

To incorporate IGC when there are two paralogs, the corresponding codon triplets in the two paralogs are jointly considered. This transforms a 61-state codon substitution model into a ${61}^2=3721$ -state joint codon substitution model. We define $Q_{(i,i\prime ),(j,j\prime )}$ to be the instantaneous rate at which i changes to j in one paralog and the corresponding codon $i\prime$ in the other paralog changes to $j\prime$ . Codon substitutions originating by point mutation are assumed to occur independently for the two paralogs with rates that are determined by the above IND model for each paralog and, when $j=j\prime$ , homogenization due to IGC is reflected by adding τ to synonymous rates and $\omega \tau$ to nonsynonymous rates. While other parameterizations can be explored in the future, we reason that ω reflects natural selection that operates on nonsynonymous changes and so the IGC contribution to a nonsynonymous rate can be modified by a factor ω just as the point mutation contribution to codon substitution is modified by ω . The joint codon substitution model has rates

$$Q_{(i,i\prime ),(j,j\prime )}=\{\begin{array}{ll}0& i\ne j,i\prime \ne j\prime \\ & \\ Q_{i,j}& i\ne j,i\prime =j\prime ,j\ne j\prime \\ & \\ Q_{i\prime ,j\prime }& i=j,i\prime \ne j\prime ,j\ne j\prime \\ & \\ Q_{i,j}+\nu & i\ne j,i\prime =j\prime ,j=j\prime \\ & \\ Q_{i\prime ,j\prime }+\nu & i=j,i\prime \ne j\prime ,j=j\prime ,\end{array}$$ (2)

where $\nu =\tau$ if the change is synonymous and where $\nu =\omega \tau$ if the change is nonsynonymous. While point mutation leads to codon substitutions that can change only one of the three codon substitutions, IGC events can simultaneously affect multiple positions in a codon and this is reflected in the above set of joint codon substitution rates.

For the rates in equation 2 , the joint stationary distribution of the two paralogs when $\tau >0$ is different from the joint stationary distribution when the paralogs are evolving independently according to the IND model (i.e., when τ  = 0). Most obviously, when $\tau >0$ , the joint stationary distribution has higher probabilities of identical codon states at the two paralogs than does the joint stationary distribution for τ  = 0. Although the IND model happens to be time reversible, the joint process of the rates in equation 2 is not. For instance, corresponding codons in two paralogs can change in an instant from having two or more nucleotide differences to being identical, but cannot instantly change from being identical to having two or more differences. Interestingly, the marginal stationary distribution of one paralog in the joint process is unaffected by the value of τ . Also, if two paralogs initially have identical codon states at some position, the marginal transition probability of the codon state in one paralog at some later time is unaffected by the value of τ .

As described in more detail in Materials and Methods, the rates of equation 2 can be used in conjunction with numerical optimization and Felsenstein’s pruning algorithm ( Felsenstein, 1981 ) to obtain maximum likelihood estimates of branch lengths, τ , and other rate parameters. The 3721-state joint codon model has a larger state space than is usually considered for models of sequence change. Our implementation of Felsenstein’s pruning algorithm ( Felsenstein, 1981 ) makes likelihood-based inference on a phylogeny computationally tractable by using the procedure of Al-Mohy and Higham (2011) to compute products of exponentiated rate matrices and vectors of conditional likelihoods.

While this treatment uses the phylogeny, reflects dependence between paralogs due to IGC, and allows IGC events to simultaneously affect multiple positions within a codon, it does not account for the fact that single IGC events can simultaneously affect contiguous codons. Because it has IGC independently affecting codon positions, our strategy can be classified as a composite likelihood approach. Although we have not yet explored the possibility, uncertainty in parameter estimates could therefore be approximated via the inverse of the Godambe information matrix (e.g., see Kent, 1982 ; Varin et al. 2011 ).

The impact of ignoring dependence between consecutive codons is partially influenced by the length distribution of IGC tracts and how often single IGC events simultaneously homogenize multiple codons that would otherwise differ between paralogs. Mansai et al. (2011) summarize and analyze evidence regarding the tract length distribution of IGC mutations. They report estimates for average IGC tract length that range from substantially less than 100 nucleotides to several hundred nucleotides. These estimates depend on which paralogs are examined and also on the species in which the paralogs are found.

However, the impact of ignoring dependence between consecutive codons when analyzing fixed IGC-induced changes in interspecific data will be less than the amount of dependence between codons when new IGC mutations are considered. The impact is also shaped by how homologous recombination rates affect the covariance in fixation probabilities among sequence positions that are homogenized by a single IGC event. If a chromosome with an IGC tract that is different from the wild type enters the population, then the amount of that tract, if any, that eventually becomes fixed in the population will be influenced by subsequent homologous recombinations that interrupt the tract. In summary, our IGC treatment can be viewed as a composite likelihood approach that should be most realistic when there are high homologous recombination rates, or short IGC mutation tracts, or point mutation rates that are low relative to IGC mutation rates.

Results

Analysis of Yeast Data

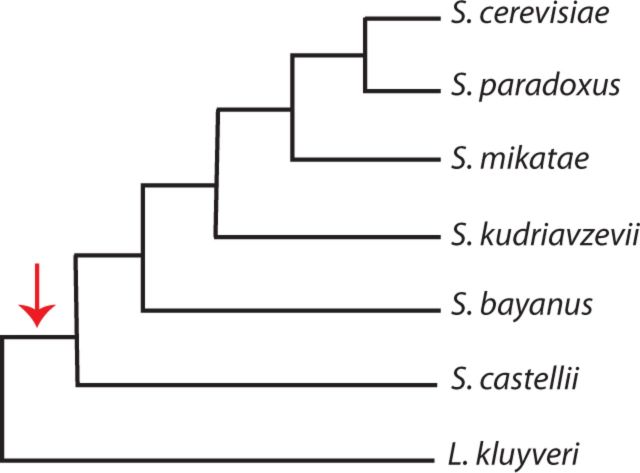
The 14 data sets that we analyzed all consist of protein-coding genes from yeast. As described in the Materials and Methods, these data represent all genes that remained after applying filters designed to reduce concerns about sequence alignment and paralogy status. All 14 data sets happen to represent yeast ribosomal proteins. In every data set, six yeast species are each represented by two paralogs that stem from an ancient genome-wide duplication ( Wolfe et al. 1997 ; Philippsen et al. 1997 ; Kellis et al. 2004 ; Dietrich et al. 2004 ; Dujon et al. 2004 ). Each data set also includes a sequence from a species ( L. kluyveri ) that diverged from the other six prior to the genome-wide duplication. Our analyses relied on the well-established phylogenetic tree topology of Figure 1 .

Fig. 1.

The tree topology used for evolutionary analyses. The arrow indicates the branch on which the genome-wide duplication occurred.

IGC is detected for all 14 data sets. To estimate the proportion of sequence changes due to IGC rather than point mutation for each data set, we conditioned upon the maximum likelihood parameter estimates from our IGC-extension and adapted the “integral of matrix exponentials” approach of Tataru and Hobolth (2011) to determine the expected number of postduplication changes from IGC on the tree and the expected number of postduplication substitutions on the tree that originated with point mutations. For each of the 14 data sets, these proportions are substantial (see Table 1 ).

Table 1.

Results of Analyzing 14 Paralogous Gene Pairs.

Paralog	Len	%	LnL	Diff	Diff	τ	IGC
Pair		ID		( τ = 0)	(IND)		Prop
YLR406C,YDL075W*	112	91	−1178.10	16.98	−4.18	1.65 (0.51)	0.20 (0.05)
YER131W,YGL189C	118	92	−1205.19	15.69	−5.21	1.36 (0.45)	0.20 (0.05)
YML026C,YDR450W	140	95	−1377.25	67.07	62.80	3.64 (0.94)	0.34 (0.04)
YNL301C,YOL120C*	185	95	−2139.31	75.76	30.76	2.48 (0.53)	0.26 (0.03)
YNL069C,YIL133C	197	87	−2322.83	58.61	48.48	1.46 (0.31)	0.22 (0.03)
YMR143W,YDL083C*	134	94	−1209.75	37.23	34.16	3.16 (0.70)	0.29 (0.03)
YJL177W,YKL180W*	183	92	−1837.06	36.62	28.68	1.76 (0.43)	0.21 (0.03)
YBR191W,YPL079W***	159	94	−1467.29	66.10	62.44	3.83 (1.04)	0.32 (0.03)
YER074W,YIL069C	133	97	−1251.96	109.59	103.63	7.47 (1.66)	0.37 (0.03)
YDR418W,YEL054C**	163	92	−1739.18	32.04	24.69	1.41 (0.42)	0.21 (0.04)
YBL087C,YER117W	136	94	−1367.68	47.61	43.71	2.81 (0.58)	0.29 (0.03)
YLR333C,YGR027C*	107	92	−1262.00	83.65	69.24	3.28 (0.96)	0.29 (0.04)
YMR142C,YDL082W***	197	93	−2054.05	142.98	136.02	5.71 (1.00)	0.38 (0.03)
YER102W,YBL072C**	198	98	−2058.96	137.70	130.18	4.87 (0.87)	0.36 (0.02)

Each row begins with the systematic names of two S. cerevisiae paralogous open reading frames. The GENECONV software ( Sawyer, 1989 ) was used to examine the null hypothesis of no gene conversion (see Materials and Methods) and the symbols ***, **,* are respectively used to indicate gene pairs yielding P -Values < 0.001, between 0.001 and 0.01, and between 0.01 and 0.05. The “Len” column shows the length in codons of each aligned data set. The “% ID” column has the percentage identity at the nucleotide level of the two S. cerevisiae paralogs in each data set. The “LnL” column contains the maximum log-likelihood of the IGC-extension analysis for paralog pairs. The “Diff ( τ  = 0)” column specifies the number of log-likelihood units by which the IGC-extension value exceeds the maximum log-likelihood value when τ is constrained to 0. The “Diff (IND)” column shows the difference when the IND value is subtracted from the IGC-extension value. Estimated τ values are in the column labeled “ τ ”. The τ parameter and other rate parameters are scaled such that branch lengths are expected numbers of substitutions arising from point mutations per codon site per paralog. Estimated proportions of sequence changes attributable to IGC are in the “IGC Prop” column. Estimated standard deviations are in parentheses. These estimates are based upon 100 pseudoreplicates of nonparametric bootstrapping where corresponding triplets of columns representing codon sites are sampled with replacement from the two paralogs and where codons within a paralog are assumed to independently evolve.

The IGC-extension jointly considers evolution of the paralogs and thereby constrains each postduplication branch of the species tree to have the same length for the two paralogs. These constraints are absent when the data sets are analyzed via the conventional IND implementation where each branch of the species tree is free to have its own length for each paralog. While the IGC-extension adds the parameter τ , the branch length constraints mean that the IGC-extension actually has 10 fewer free parameters than the conventional IND analyses. Despite having fewer free parameters, the IGC-extension produces a higher maximum log-likelihood for 12 out of 14 data sets (see Table 1 ) and, subject to the caveat that independent evolution among codons within a paralog is assumed, the IGC-extension is preferred for all data sets according to model selection criteria such as AIC ( Akaike, 1974 ). If maximum log-likelihoods of the IGC-extension are compared to the ones obtained for the special case where τ is constrained to be 0, AIC prefers the unconstrained IGC-extension for all 14 data sets (see Table 1 ).

Sometimes statistical fits of models improve by adding parameters, but not due to the phenomena that the parameters are meant to represent. Here, we intend τ to capture the tendency for paralogs within the same genome to be homogenized. However, numerous other biological phenomena are not included in our evolutionary model. For example, variation of preferred amino acid residues among protein sites is incorporated into the CAT model of amino acid replacement ( Lartillot and Philippe, 2004 ) but is not yet included in our IGC-extension.

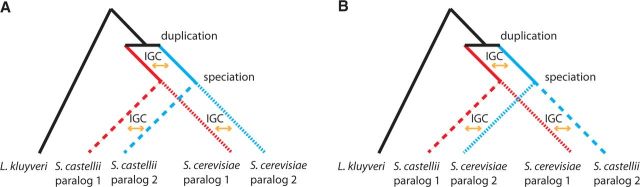
To investigate whether the improvements in model fit with our IGC-extension are actually attributable to a statistical artifact possibly arising from some non-IGC phenomenon, we designed a two-scenario experiment using gene copies from L. kluyveri , S. castellii , and S. cerevisiae (see Figure 2 ). Figure 2A depicts the biologically correct scenario where IGC events homogenize paralogs within the same genome. Figure 2B depicts a biologically incorrect scenario where IGC events homogenize paralogs from different species. If the IGC-extension is improving the model fit because of some phenomenon that does not homogenize paralogs within the same genome, we expect τ estimates and maximum log-likelihood values to be similar for the two scenarios.

Fig. 2.

A paralog-swapping experiment addressing whether improvement to model fit can be attributed to IGC or to artifacts. Both Scenarios A and B specify the correct rooted phylogeny between L. kluyveri and the paralogs of S. castellii and S. cerevisiae . Scenario A shows the biologically correct situation that has IGC between paralogs in the same genome. In Scenario B , IGC homogenization events involve one paralog from S. castellii and one from S. cerevisiae . Because Scenario A corresponds to how observed data are generated, Scenario A should fit better than Scenario B if IGC is actually being detected. Note that this paralog-swapping experiment would not be possible if only 1 postduplication species was used and would not be effective with more than two postduplication species.

We analyzed both the Figure 2A and B scenarios for all 14 genes using our IGC-extension. We report τ estimates and log-likelihood differences for the paralog-swapping experiment of Figure 2 where a strict molecular clock is assumed, but qualitatively similar results were obtained without the clock constraints. For all 14 data sets, the τ estimate is larger for the biologically correct scenario ( Figure 2A ) than for the incorrect one ( Figure 2B ). For the correct scenario, τ estimates ranged from 1.22 to 10.52 with a median of 3.58. For the incorrect scenario, τ estimates ranged from 0 to 0.76 with a median of 0.10. The maximum log-likelihood values were higher for the correct scenario for all 14 data sets with differences ranging from 2.82 to 118.89 log-likelihood units and with a median difference of 34.63. When we examined the null hypothesis of no gene conversion with the GENECONV software ( Sawyer, 1989 ), 9 of the 14 data sets yielded P -Values < 0.05 (see Table 1 ). These findings are all consistent with the conclusion that our approach is finding and quantifying IGC.

Simulations

As detailed in Materials and Methods, we performed simulations to characterize our IGC procedure. For the simulations, rates are normalized so that the expected rate per paralog per codon is 1 for substitutions that originated with a point mutation. The parameter τ can be viewed as the expected rate at which homogenization due to IGC occurs for corresponding codon sites in the two paralogs that happen to differ prior to the IGC event. In the simulations, a codon site might experience IGC because an IGC tract began at that site or because a tract initiated elsewhere and continued through the site.

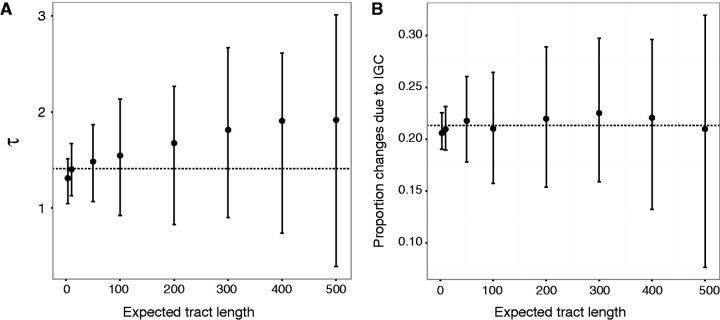
When the inference model is violated because expected tract lengths exceed 1 codon in the simulations, the average estimated values of τ are relatively close to the true value ( Figure 3A ). The variability of estimated τ values increases as tract length increases, presumably because the actual numbers of IGC events experienced per codon will vary more among simulated data sets when tracts are long but the expected number of tracts per simulation are few. Similarly, the expected tract lengths have little influence on the averages of the estimated proportions of sequence changes attributable to IGC but the standard deviations of these proportions grow as average tract lengths increase ( Figure 3B ).

Fig. 3.

Effect on parameter estimates of expected tract length. A . The mean estimate of τ among 100 simulated data sets is plotted versus the expected length in nucleotides of IGC tracts. Vertical line segments depict interquartile ranges of the estimates. The horizontal line shows the true value $\tau =1.40948$ . B . The average among 100 simulated data sets of the estimated proportion of nucleotide changes originating with IGC rather than point mutation is plotted versus the expected length in nucleotides of IGC tracts. Vertical line segments depict interquartile ranges of the estimates. The horizontal line at 0.2131 represents the estimate of the proportion of changes due to IGC in the actual data.

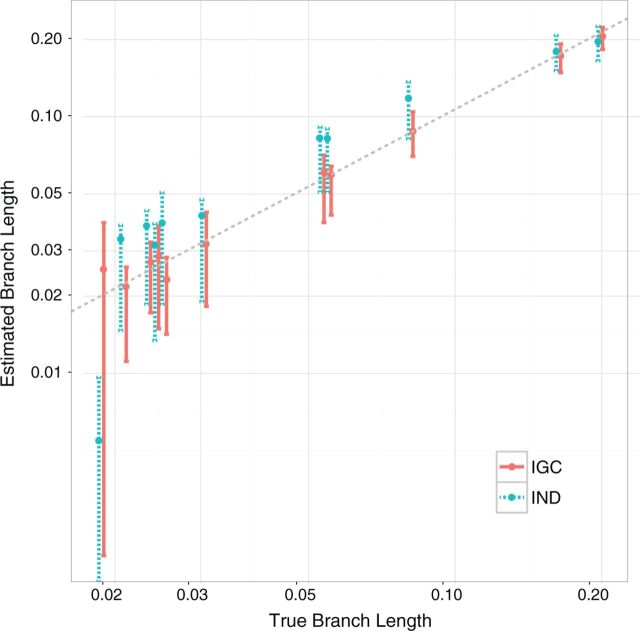
With the IGC model, average branch length estimates are close to the true values. Figure 4 shows the branch length estimates for an expected tract length of 100 nucleotides from both the IGC model and the IND model as implemented in the PAML software ( Yang, 2007 ). We depict the expected tract length of 100 because it is relatively representative of previously obtained estimates of tract lengths for IGC mutations ( Mansai et al. 2011 ). Similar plots to Figure 4 are observed for other tract lengths with the exception that variation of branch length estimates grows as tract length grows for both IGC and IND estimates (data not shown).

Fig. 4.

Branch lengths from IGC and IND models for expected IGC tract lengths of 100 nucleotides. The Y-axis shows average estimated values and interquartile ranges while the X-axis shows true values. All postduplication branches are depicted. The logarithmic scale on both axes as well as slight offsets of the IGC and IND model values are used to enhance visibility. The dashed diagonal line shows where estimated values equal true values.

The comparison between the branch length estimates from our IGC-extension and the IND model is especially interesting for the branch of the yeast tree that separates the genome duplication from the first postduplication speciation event. This branch happens to have the shortest true length among the branches represented in Figure 4 . For all tract lengths, the IND analyses consistently underestimated this branch length. With the IGC-extension, estimates of this branch length were quite variable but we did not observe the consistent underestimation of the IND analyses.

This variability is observed even though the IGC-extension uses information from both paralogs to estimate a shared branch length whereas the IND analyses separately estimate this branch length for each paralog. The bias of the IND analyses for this branch presumably stems from the fact that IGC-events on one branch can mimic the pattern that would be observed from nucleotide substitutions that originate with a point mutation on other branches. We believe that the variability of the branch length estimates from the IGC model is due to the two paralogs beginning this branch with identical sequences. For other postduplication branches on the yeast species tree, the sequence differences between paralogs at the beginning of a branch facilitate identification of IGC events that occur in the branch. The lack of sequence differences at the beginning of the initial postduplication branch means that disentangling nucleotide substitutions that arise from a point mutation versus IGC is difficult and is overly dependent on values of model parameters.

Discussion

Whether the high level of IGC affecting these yeast genes is characteristic of other multigene families in yeast or other lineages remains unclear and needs further examination. Dumont (2015) estimates that at least 2.7% of single nucleotide polymorphisms in duplicated human regions are attributable to IGC. When we estimate the percentage of nucleotide substitutions that originate with an IGC event rather than a point mutation, our 14 yeast data sets yield values ranging from 20% to 38%. Considering that point mutation can affect sequences at any time whereas IGC can change codons only when paralogs differ, the 20% to 38% range is especially striking. While our simulations suggest that these percentages are difficult to accurately estimate for individual data sets, they do not exhibit a strong bias in these percentages and all 14 data sets yielded relatively high estimates for these percentages.

However, our 14 yeast data sets may be unusually prone to IGC. As noted in the Results, the 14 data sets all encode ribosomal proteins even though ribosomal protein-coding genes were not explicitly sought. Yeast ribosomal proteins have previously been connected to IGC ( Evangelisti and Conant, 2010 ). As described in the Materials and Methods, we only analyzed yeast data sets that satisfied criteria that were instituted to reduce the possibility of artifacts associated with alignment errors and long phylogenetic branches. Homogenization between paralogs due to IGC would reduce alignment uncertainty and therefore our criteria would inadvertently favor genes that are especially prone to IGC. The ancient date of the yeast whole genome duplication works against being able to draw general conclusions about IGC levels following whole genome duplication. To assess how representative the inferred IGC levels from our 14 data sets are for genes that experience a whole genome duplication, future studies could apply our IGC models to cases of more recent whole genome duplications in other evolutionary lineages. It may also be worthwhile to examine other yeast data that do not meet the stringent criteria that we adopted here.

While evidence is consistent with these 14 yeast data sets having experienced IGC, this study does not shed light on the physical mechanism by which IGC affects repeats created via whole genome duplication. This IGC approach can also be applied to paralogs that are the result of tandem duplications or retrotranspositions. In light of hypothesized IGC mechanisms ( Chen et al. 2007 ), it seems plausible that repeats that are scattered throughout the genome due to retrotransposition might experience less IGC than those that arise via tandem duplication.

Extensive effort has been devoted to studying the fates of duplicated genes and how duplicated regions influence the evolution of gene function ( Conant and Wolfe, 2008 ). However, the role of IGC homogenization in these fates is understudied. Tools for quantifying IGC levels are needed and the approach described here can be refined. For example, it could be employed to quantify how IGC levels change as paralogs diverge. Previous studies suggest that IGC decreases as paralogs diverge ( Mansai et al. 2011 ). Also, there is substantial evidence that some paralogs tend to be the donors and other paralogs tend to be the recipients when IGC occurs ( Chen et al. 2007 ). The model that we have explored here does not include a possibility for such asymmetry, but minor model modifications could.

Other future directions for this line of research include extending IGC analysis to multigene families with more members. This would facilitate investigation of how IGC levels change as the number of paralogs in the multigene family changes. One possibility is that paralogs in big multigene families tend to be the recipients of more IGC events than paralogs in small ones. To accommodate more than two paralogs with codon-based models, the high number of possible joint states will presumably mean that another inference strategy is necessary. While 4-state nucleotide substitution models are less appealing than codon-based models in many regards, they would be amenable to joint consideration of multigene families with more than two paralogs. By employing the Al-Mohy and Higham (2011) algorithm, we anticipate that IGC-extensions of 4-state models with up to six paralogs will be computationally tractable.

Materials and Methods

Data Set Collection

We started with 475 previously identified paralogous S. cerevisiae gene pairs ( Byrne and Wolfe, 2005 ; Casola et al. 2012 ). Corresponding genes of S. kudriavzevii , S. bayanus , S. paradoxus and S. mikatae were determined via the orthology mapping of Scannell et al. (2011) . The Fungal Orthogroups Repository ( Wapinski et al. 2007 ) was employed to include S. castellii and L. kluyveri genes. Genes were not included unless there was exactly one L. kluyveri copy and exactly two paralogous copies in each of the other six species. After this step, 105 data sets remained. Sequence data were obtained from the Saccharomyces Genome Database ( Cherry et al. 2012 ). As an additional filter aimed at avoiding alignment uncertainty, data sets were excluded unless the shortest sequence length was at least 90% of the longest. After this filter, there were 37 data sets. One data set was removed because of ambiguity in the reported sequence data.

Sequences in the 36 remaining data sets were aligned at the amino acid level with the MAFFT software ( Katoh and Standley, 2013 ). The results were then converted to alignments at the codon level and codons in the same columns as gaps were removed. Next, we did maximum likelihood analyses of the aligned data sets using the known gene tree topology and the IND model. As a final filter designed to lessen paralogy and/or alignment uncertainty, we summed the estimated number of changes per codon over all branches in the gene tree and eliminated the data sets where the sum from the IND model exceeded 3.0.

Analyses of Yeast Data

To test the null hypothesis of no IGC, analyses with the GENECONV software ( Sawyer, 1989 ) were performed with default settings.

Inferences with our IGC-extension were obtained by the software that we wrote. IGC analyses were done by assuming that the IND model operated and was at stationarity on the lineage to the outgroup L. kluyveri and also prior to the duplication (see Figure 1 ).

Simulations

The simulations were designed to resemble the YDR418W_YEL054C data set. This dataset was selected because the τ estimate obtained from it was neither unusually high nor unusually low relative to the other 13 yeast data sets. Also, this data set consists of genes with only one exon in S. cerevisiae and, with only one exon, the complications of IGC tracts that partially or completely span introns can be avoided.

For each simulation condition, 100 data sets were generated. Each simulated data set had sequences of the same length as our actual YDR418W_YEL054C data (i.e., 163 codons) and each was generated according to the species tree and duplication placement of Figure 1 . To simulate, we used values of κ and π _h ( $h\in \left\{A,C,G,T\right\}$ ) that were estimated from the YDR418W_YEL054C data set. The branch lengths that were inferred from the YDR418W_YEL054C data were used as the true values for the simulations. While the value of ω estimated from the YDR418W_YEL054C data was about 0.076, data sets were simulated using ω  = 1 because we wanted to examine our model when IGC events affected more than one consecutive codon in simulated data and we did not want to complicate the simulations by having to deal with natural selection when IGC tracts introduce multiple nonsynonymous changes.

In the situation where all IGC events are forced to affect exactly 1 codon, multiple nonsynonymous changes per tract cannot occur and therefore the ω  = 1 constraint can be avoided. In addition to the simulation results that are presented, we performed simulations for the case where all tracts affect exactly 1 codon and where the true value of ω is its maximum likelihood estimate from the actual data. We do not report these results because they follow similar patterns to the ones that are reported where ω  = 1.

Our inference model has each IGC event potentially affect all three nucleotides of a single codon. One way in which the inference model is unrealistic is that there is no reason to believe that all IGC events respect codon boundaries. In other words, IGC events need not initiate at the first position of a codon and end at the third position of a codon. Another way in which the inference model is unrealistic is that multiple consecutive codons can be affected by an IGC tract. In addition to simulating according to our model (3 nucleotide positions affected by each IGC event with codon boundaries respected), we explored simulation scenarios where codon boundaries were respected but IGC tracts can exceed 1 codon in length. We also explored simulation scenarios with the same average tract lengths but where codon boundaries are not necessarily respected. For the simulations that did not respect codon boundaries, the number of consecutive nucleotides affected was geometrically distributed with means that were selected to correspond to the means used for the simulations that respected codon boundaries. The simulations that did not necessarily respect codon boundaries had IGC tract lengths with means 3, 10, 50, 100, 200, 300, 400, or 500 nucleotides. We only report results here from the simulations that did not respect codon boundaries, but results from the simulations that respected codon boundaries tend to be quite similar.

The parameter τ in our inference model represents the rate at which IGC events homogenize codons that differ among paralogs. This rate can be interpreted as the rate at which IGC events initiate multiplied by the average number of consecutive codons affected per IGC event. For each simulation scenario that we explored, we set the product of the IGC initiation rate and the average number of consecutive codons affected to 1.40948 because that was the value of τ estimated from the YDR418W_YEL054C data. To be consistent with our inference model when ω  = 1, IGC tract initiation events were independent of the sequences affected by the IGC event. Furthermore, we wanted each sequence position to experience the same expected number of IGC events. To accomplish this, we accounted for IGC tracts that initiate 5’ of the first sequence position and continue into the simulated sequence. We also accounted for tracts that continue in the 3’ direction past the last simulated sequence position. Data sets were simulated on the phylogenies by using the Gillespie algorithm ( Gillespie, 1976 ) to randomly intersperse times at which IGC tracts occurred with times at which sequence changes arose due to point mutation.

To investigate the impact of ignoring IGC when it actually occurred, we analyzed all simulated data sets with IGC-extension and with the IND model as implemented in Version 4.8a of the PAML software ( Yang, 2007 ). To make the comparisons sensible, both kinds of branch length estimates are in units of expected numbers of codon substitutions originating by point mutation per paralog per codon site. We note that our IGC model implementation constrains both paralogs to have the same branch length for each postduplication branch of the species tree whereas the PAML analyses are set up to separately estimate the branch lengths for each paralog.

For the simulated data sets, we noticed that PAML sometimes had numerical optimization failure. The failure seemed to usually involve the two branches that separate the duplication event from the first postduplication speciation event. We found that numerical optimization could be facilitated by having PAML analyze four topologies (the species tree and duplication placement of Figure 1 and the three multifurcating trees that result when one or both of the two earliest postduplication branches in Figure 1 are constrained to have length 0) and then choosing the analysis that yielded the highest likelihood among the 4 topologies.

Acknowledgments

We thank Paula Cohen, Jonathan Pritchard, Ed Susko, Eric Stone, Jeffrey Townsend, and two anonymous reviewers for help. This work was supported by the National Institute of General Medical Sciences at the National Institutes of Health (grant numbers GM070806 and GM118508). X.J. was also supported by a graduate fellowship from the Statistical and Applied Mathematical Sciences Institute. Data sets are available at https://github.com/xji3/JGT_MBE_2016 . Software for inferring IGC is available at https://github.com/xji3/JGT_MBE_2016 and http://jsonctmctree.readthedocs.org/en/latest/ .