Evolution of Stratospheric Chemistry in the Saturn Storm Beacon Region

Abstract

The giant northern-hemisphere storm that erupted on Saturn in December 2010 triggered significant changes in stratospheric temperatures and species abundances that persisted for more than a year after the original outburst. The stratospheric regions affected by the storm have been nicknamed “beacons” due to their prominent infrared-emission signatures (Fletcher, L.N. et al. [2011]. Science 332, 1413). The two beacon regions that were present initially merged in April 2011 to form a single, large, anticyclonic vortex (Fletcher, L.N. et al. [2012]. Icarus 221, 560). We model the expected photochemical evolution of the stratospheric constituents in the beacons from the initial storm onset through the merger and on out to March 2012. The results are compared with longitudinally resolved Cassini/CIRS spectra from May 2011. If we ignore potential changes due to vertical winds within the beacon, we find that C₂H₂, C₂H₆, and C₃H₈ remain unaffected by the increased stratospheric temperatures in the beacon, the abundance of the shorter-lived CH₃C₂H decreases, and the abundance of C₂H₄ increases significantly due to the elevated temperatures, the latter most notably in a secondary mixing-ratio peak located near mbar pressures. The C₄H₂ abundance in the model decreases by a factor of a few in the 0.01–10 mbar region but has a significant increase in the 10–30 mbar region due to evaporation of the previously condensed phase. The column abundances of C₆H₆ and H₂O above ~30 mbar also increase due to aerosol evaporation. Model-data comparisons show that models that consider temperature changes alone underpredict the abundance of C₂H_x species by a factor of 2–7 in the beacon core in May 2011, suggesting that other processes not considered by the models, such as downwelling winds in the vortex, are affecting the species profiles. Additional calculations indicate that downwelling winds of order −10 cm s⁻¹ near ~0.1 mbar need to be included in the photochemical models in order to explain the inferred C₂H_x abundances in the beacon core, indicating that both strong subsiding winds and chemistry at elevated temperatures are affecting the vertical profiles of atmospheric constituents in the beacon. We (i) discuss the general chemical behavior of stratospheric species in the beacon region, (ii) demonstrate how the evolving beacon environment affects the species vertical profiles and emission characteristics (both with and without the presence of vertical winds), (iii) make predictions with respect to compositional changes that can be tested against Cassini and Herschel data, and higher-spectral-resolution ground-based observations of the beacon region, and (iv) discuss future measurements and modeling that could further our understanding of the dynamical origin, evolution, and chemical processing within these unexpected stratospheric vortices that were generated after the 2010 convective event.

1. Introduction

The pristine, hazy appearance of Saturn, with its muted atmospheric banding, is known to be disturbed on rare occasions by enormous convective storms dubbed “Great White Spots” (e.g., Sanchez Lavega, 1982; Sanchez Lavega and Battaner, 1987). In December 2010, one such gigantic storm system erupted at northern mid-latitudes on Saturn (Sánchez-Lavega et al., 2011; Fischer et al., 2011; Fletcher et al., 2011). The “head” of the storm drifted westward with the prevailing zonal winds, leaving a turbulent wake of fresh cloud particles. Within a couple of months of the storm onset, the storm head had caught up with its wake “tail” to form a distinct planet-encircling band of clouds that persisted for more than a year after the storm’s initial appearance (e.g., Sánchez-Lavega et al., 2012; Sayanagi et al., 2013). Although the convective disturbance originated in the troposphere and had a notable effect on the cloud structure, lightning activity, atmospheric dynamics, thermal structure, and distribution of molecular species within the troposphere (Fischer et al., 2011; Sánchez-Lavega et al., 2011, 2012; Fletcher et al., 2011, 2012; Hurley et al., 2012; Sanz-Requena et al., 2012; Janssen et al., 2013; Laraia et al., 2013; Sayanagi et al., 2013; Dyudina et al., 2013; Sromovsky et al., 2013; Achterberg et al., 2014; Trammell et al., 2014), the storm also had some profound and unexpected consequences for higher-altitude regions. In particular, temperatures in the stratosphere were found to be greatly elevated in latitude regions associated with the storm, perhaps as a result of momentum and energy redistribution from vertically-propagating atmospheric waves generated from tropospheric convective plume activity and/or from dynamical compression within the resulting vortex region (Sayanagi and Showman, 2007; Fletcher et al., 2011, 2012). In addition, the gas-phase abundances of ethylene and water were inferred to have increased by roughly two orders of magnitude in these high-temperature stratospheric regions in the months after the storm onset (Hesman et al., 2012; Cavalié et al., 2012).

The strong stratospheric temperature increase was initially confined to two broad air masses nicknamed “beacons” due to their distinctive bright signatures at infrared wavelengths (Fletcher et al., 2011). These two initial air masses, centered at different longitudes/latitudes and associated with zonal winds of different relative velocities, encountered each other in April 2011, at which point the two beacons merged into a single, enormous, anticyclonic vortex (Fletcher et al., 2012). Temperatures within the initial two beacons rose rapidly in the months before the merger, intensified and reached a maximum in the combined beacon vortex after the merger, and then cooled slowly but steadily from May 2011 onward (Fletcher et al. 2012; see also Fletcher et al. 2011; Hesman et al. 2012).

The Cassini spacecraft was in a prime position to track the evolution of the storm and its associated beacon features. Figure 1 shows the vertical temperature profiles derived by Fletcher et al. (2012) from spectra acquired with the Composite Infrared Spectrometer (CIRS) instrument aboard Cassini. These temperature retrievals were obtained from spectra coadded over broad areas of the beacons (i.e., within ±10° longitude, ±5° latitude of the beacon center) — temperatures within the hottest regions at the beacon centers were even higher. For example, on May 4, 2011, after the merger, 2-mbar temperatures at the central “core” of the beacon reached ~220 K, about 80 K greater than the pre-storm temperature (Fletcher et al. 2012; see also Hesman et al. 2012), whereas the broader-scale averages indicated temperatures of ~210 K at 2 mbar.

Figure 1:

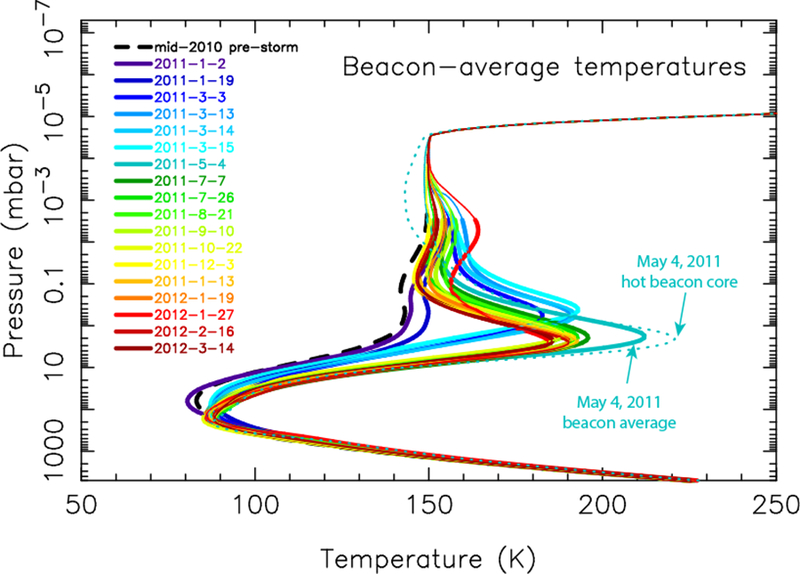
Evolution of the vertical temperature profiles within one of the initial beacons (‘B1’) and the merged beacon (‘B0’) as a function of time after the storm onset, as retrieved by Fletcher et al. (2012) from Cassini CIRS spectra coadded from regions within ± 5° latitude and ± 10° longitude of the beacon centers. Dates of the observations are color-coded, as labeled. The actual retrievals are shown by the thicker lines, while the thinner lines at high altitude show model profiles artificially expanded beyond the pressure range of CIRS sensitivity (i.e., the actual published CIRS retrievals extend to ~10⁻³ mbar, although note that the nadir temperature retrievals lose their sensitivity beyond the ~0.5–230 mbar range). Although our photochemical models require extensions to higher altitudes, no simultaneous temperature data exist for the beacon regions at such high altitudes. The dotted line represents the retrieved thermal profile from the hottest region of the beacon on May 4, 2011. Figure is adapted from Fletcher et al. (2012).

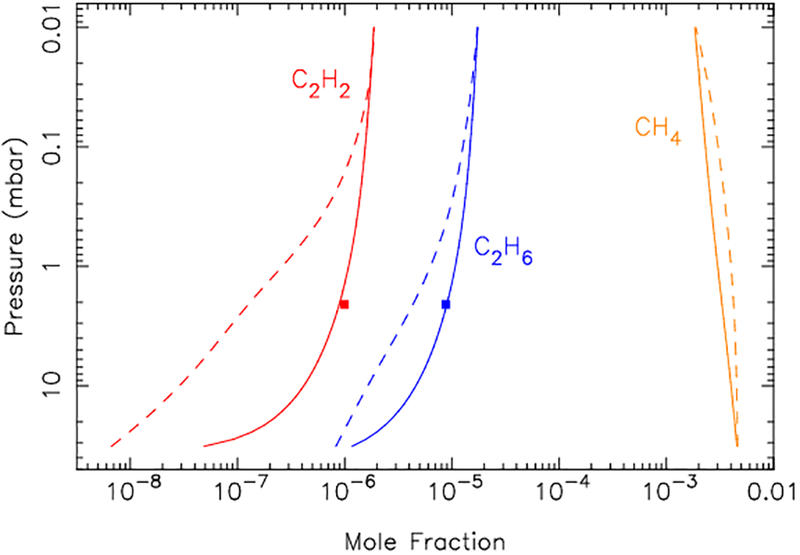
The higher temperatures resulted in increased infrared emission, making molecular bands from trace stratospheric constituents easier to identify. One such example is ethylene (C₂H₄), which was not identified in CIRS spectra before the storm at northern mid-latitudes, but which was detected by Hesman et al. (2012) in the post-storm beacon region in May 2011, from both Cassini CIRS data and ground-based infrared observations. Hesman et al. (2012) derived stratospheric temperatures at ~0.5–5 mbar using the v₄ band of methane (CH₄) in the 1250–1311 cm⁻¹ wavenumber region, which then allowed them to retrieve the C₂H₄ abundance from the observed ethylene emission band near 950 cm⁻¹. The retrievals of the ethylene abundance profile are complicated by the possibility that the C₂H₄ emission may not originate from the 0.5–5-mbar pressure levels where the temperatures are best constrained; however, the Hesman et al. (2012) analysis clearly indicates that the ethylene abundance in May 2011 was significantly increased in the beacon region at ~10–10⁻² mbar in comparison with pre-storm observations and expectations (Fig. 2). In fact, Hesman et al. (2012) found that their pre-storm photochemical-model profile for C₂H₄ would need to be increased uniformly by almost two orders of magnitude in order to reproduce the observed ethylene emission from the beacon, whereas their photochemical models predicted only a factor of ~2 increase in the C₂H₄ mixing ratio due to the elevated temperatures in the beacon. Hesman et al. (2012) explored several ideas as to the mechanisms that could be the cause of the C₂H₄ enhancement, but they did not come up with a definitive conclusion. Figure 2 shows their predicted pre-storm ethylene profile, in comparison with their post-storm beacon retrievals from May 2011. Note the large post-storm “peak” in C₂H₄ in the mbar region.

Figure 2:

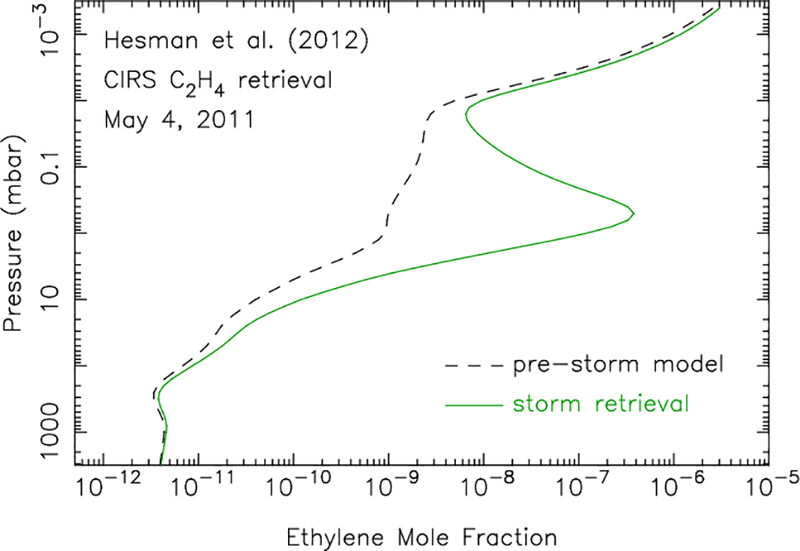
The ethylene mole fraction predicted from the photochemical model presented in Hesman et al. (2012) (dashed line), compared with the Hesman et al. (2012) retrieval from 2.5 cm⁻¹-resolution CIRS beacon spectra from May 2011 (green solid line). Note the strongly peaked behavior between 0.1–1 mbar and the very large increase in the retrieved C₂H₄ mole fraction compared with pre-storm predictions. Figure is adapted from Hesman et al. (2012).

Acetylene was also observed to increase in the beacon region after the merger (Fletcher et al., 2012; Hesman et al., 2014), albeit less dramatically than ethylene. In contrast, a preliminary analysis by Hesman et al. (2014) indicates that CH₃C₂H, C₃H₈, and C₄H₂ exhibit little or no enhancement in the beacon, and Fletcher et al. (2012) find that the beacon enhancement of C₂H₆ was at the level of retrieval uncertainty and therefore inferred to be smaller than that of C₂H₂.

In an attempt to explain these observations, Cavalié et al. (2015) used a photochemical model to track the expected evolution of hydrocarbon chemistry in the beacon region. Their models predicted a small factor of ~3 increase in the C₂H₄ abundance at mbar pressures due to the elevated beacon temperatures — an amount that is insufficient to explain the observed ethylene emission reported by Hesman et al. (2012). The Cavalié et al. (2015) model also predicted very little change in the acetylene (C₂H₂) and ethane (C₂H₆) abundances at mbar pressures due to the elevated beacon temperatures, in contrast to the post-merger beacon observations of Fletcher et al. (2012) and Hesman et al. (2014).

In this paper, we further explore the theoretical chemical evolution of stratospheric hydrocarbon and oxygen species in the storm beacon region in an attempt to reconcile models and observations and to better understand the physical and chemical conditions within this unusual stratospheric anti-cyclonic vortex on Saturn.

2. Photochemical Model

To calculate the vertical distribution of stratospheric species in the beacon region on Saturn, we use the Caltech/JPL KINETICS code developed by Yuk L. Yung and Mark Allen (Allen et al., 1981; Yung et al., 1984) to solve the coupled one-dimensional (1-D) continuity equations for each species i in the model:

$$\frac{\partial n_i}{\partial t}+\frac{\partial {\Phi }_i}{\partial z}=P_i-L_i$$ (1)

where n_i is the number density (cm⁻³), Φ_i is the vertical flux (cm⁻² s⁻¹), and P_i and L_i are, respectively, the chemical production and loss rates (cm⁻³ s⁻¹) of the i-th species, all of which are explicit functions of time t and altitude z. The flux term is calculated for the vertical direction only and includes transport by molecular diffusion, eddy diffusion, and potential vertical winds:

$${\Phi }_i=-n_i{D}_i\left(\frac{1}{n_i}\frac{d{n}_i}{dz}+\frac{1}{H_i}+\frac{\left(1+{\alpha }_i\right)}{T}\frac{dT}{dz}\right)-n_i{K}_{zz}\left(\frac{1}{n_i}\frac{d{n}_i}{dz}+\frac{1}{H_a}+\frac{1}{T}\frac{dT}{dz}\right)+n_{i}w$$ (2)

where D_i is the molecular diffusion coefficient (cm² s⁻¹), H_i is the pressure scale height (cm) of the i-th constituent, H_a is the pressure scale height (cm) of the background atmosphere, T is the temperature (K), α_i is the thermal diffusion factor (e.g. Chamberlain and Hunten, 1987), K_zz is the vertical eddy diffusion coefficient (cm² s⁻¹), and w is the vertical wind velocity (cm s⁻¹). Vertical winds are typically neglected in 1-D models, given that such models are most often intended to describe global, steady-state averages; however, we include vertical winds in some specific test cases to better describe the behavior in the beacon vortex.

The hydrocarbon chemical reaction mechanism in our model is taken from Model C of Moses et al. (2005), with updates to several association reactions (including radiative association) based on the recommendations of Vuitton et al. (2012), and updates to several reactions involving C₃H_x species based on recommendations of Hébrard et al. (2013). The rate coefficients for reactions involving oxygen species are taken from Moses et al. (2000b). The model contains 70 hydrocarbon and oxygen species that interact via ~500 chemical reactions. Condensation and evaporation of water (H₂O), diacetylene (C₄H₂), and benzene (C₆H₆) are considered in a manner described in Moses et al. (2000b). The expressions for the vapor pressures of H₂O, C₄H₂, and C₆H₆ over their respective ices are taken from Marti and Mauersberger (1993), Orton et al. (2014), and Reid and Prausnitz (1987); see also Fray and Schmitt (2009). Model calculations are performed for 34° planetocentric latitude (~40° planetographic latitude), relevant to the beacon center after the merger, and we consider diurnally averaged fluxes, fixed seasonal parameters near equinox, and a low-to-average solar ultraviolet flux (see Moses et al., 2000a, for details). These choices are appropriate for the beacon situation in 2010–2011, and none have much influence on the time-variable results over the short time period of the beacon model.

The model atmospheric grid contains 198 pressure levels, ranging from 5.1 bar to 10⁻⁸ mbar. At the lower boundary, the helium and methane mole fractions are fixed at, respectively, 0.119 (Conrath and Gautier, 2000) and 4.7 × 10⁻³ (Fletcher et al., 2009), and the carbon monoxide mole fraction is fixed at 1.0 × 10⁻⁹, which is the upper limit for tropospheric CO derived by Cavalié et al. (2009). All other trace species are assumed to have a concentration gradient of zero at the lower boundary, which causes these species to flow through the lower boundary at a maximum possible velocity. The lower boundary is far removed from the stratospheric region of interest in this problem, and our choice of the lower boundary condition for the photochemically produced species has no effect on our results. Atomic H, some of which is produced photochemically in the high-altitude thermosphere and ionosphere above the top of our model, is assumed to have a downward flux of 1.0 × 10⁸ cm² s⁻¹ at the upper boundary of our model, whereas all other species are given zero flux boundary condition at the top of the model (cf. Moses et al., 2000a, 2005). Water, CO, and CO₂ are assumed to be introduced to the atmosphere from external sources (Feuchtgruber et al., 1997, 1999; de Graauw et al., 1997; Moses et al., 2000b; Bergin et al., 2000; Cavalié et al., 2009, 2010). The ultimate origin of the external oxygen compounds is uncertain. Guerlet et al. (2010) demonstrate from back-of-the-envelope calculations that Enceladus could be the dominant source (see also Jurac and Richardson, 2007; Cassidy and Johnson, 2010; Hartogh et al., 2011; Fleshman et al., 2012), while Cavalié et al. (2010) favor a relatively recent cometary impact within the past ~200–250 years. For simplicity, we assume that the external oxygen species are introduced to the atmosphere through ablation of small icy grains, with assumed influx rates of 8.5 × 10⁵ H₂O molecules cm⁻² s⁻¹, 4.1 × 10⁵ CO molecules cm⁻² s⁻¹, and 1.2 × 10⁵ CO₂ molecules cm⁻² s⁻¹ (cf. Moses et al., 2000b). These fluxes, in combination with our inferred pre-storm K_zz profile, thermal structure, and chemical reaction mechanism, reproduce the observed global-average stratospheric abundances of H₂O and CO₂ from observations from the Infrared Space Observatory (ISO) (de Graauw et al., 1997; Feuchtgruber et al., 1997, 1999; Moses et al., 2000b).

The temperature-pressure profiles adopted in the model are shown in Fig. 1. The pre-storm temperature profile is taken from CIRS temperature retrievals averaged over 36–44° planetographic latitude from spectra acquired in May-August 2010 (see Section 3). The profiles adopted after the storm onset (hereafter called “post-storm”) are the Fletcher et al. (2012) retrievals from coadded CIRS spectra acquired from within a 10° latitude and 20° longitude region centered over the initial ‘B1’ and merged ‘B0’ beacons from 18 separate dates ranging from January 2, 2011 (~1 month after storm onset) to March 14, 2012 (last available data from the Fletcher et al. 2012 study; see Fig. 1). The May 4, 2011 CIRS observations are of particularly high quality (i.e., high signal-to-noise ratio), and we adopt the retrieved temperatures from the hottest longitude region at the beacon core (see the dotted line in Fig. 1) for some models. Although the CIRS temperature retrievals are most sensitive to the ~0.5–230 mbar pressure region, Fletcher et al. (2012) present retrieved temperatures over a broader range from 10 bar to 10⁻³ mbar, and we adopt these values over that entire pressure range. At higher altitudes, we smoothly (and arbitrarily) connect the Fletcher et al. (2012) profiles to a thermospheric temperature profile derived from Voyager Ultraviolet Spectrometer (UVS) occultation observations (Vervack and Moses, 2015). Note that the full 198-level pressure range was used in the retrievals from the hot beacon core shown by the dotted line in Fig. 1, which is why the high-altitude profile for that curve differs from the others. We will show results assuming both of these May 4, 2011 profiles, with the hot-beacon core profile referred to as the “hot” nominal model, and the beacon-average profile as the “beacon-average” nominal model. We then determine the complete background atmospheric grid for these temperature profiles by assuming hydrostatic equilibrium. That is, the pressure grid is kept constant for the different dates, and the altitude and density profiles are calculated from the temperature-pressure profiles via solution of the hydrostatic-equilibrium equation.

Our modeling procedure is to first run the photochemical model for the fixed-season, pre-storm conditions at 40° planetographic latitude, allowing the solution to converge and reach a steady state. The eddy K_zz profile, which is a free parameter in the model, is adjusted in this pre-storm model (see Fig. 3) until the C₂H₆ and C₂H₂ mixing ratios are consistent with the CIRS pre-storm emission at the relevant 40° latitude. The scaling factors — i.e., the uniform-with-altitude multiplicative factors — that the model mixing-ratio profiles need to be scaled by to reproduce the pre-storm (May-August 2010) CIRS zonal-mean nadir spectra are shown in Fig. 4 (see also the discussion of these observations in Section 3). The pre-storm model underestimates the acetylene abundance slightly, such that the C₂H₂ profile needs to be scaled by 1.07 to fit the CIRS spectra at 40° planetographic latitude, whereas the pre-storm model overestimates ethane slightly, such that the model C₂H₆ mixing ratios need to be scaled by ~0.91 to explain the pre-storm ethane emission at that latitude. In fact, although the reaction mechanism used in this study provides a good representation of the global-average hydrocarbon abundances on Saturn (e.g., Moses et al., 2005), existing 1-D photochemical models for Saturn do not reproduce the CIRS observations for the meridional distribution — and in some cases the vertical distribution — of all observed hydrocarbon species at all locations on Saturn (Moses and Greathouse, 2005; Guerlet et al., 2009, 2010; Sinclair et al., 2013; Hue et al., 2015). Some of the model-data mismatch likely results from the lack of atmospheric circulation in the photochemical models, but the chemistry itself may also be incomplete or inaccurate. It is precisely for this reason that the elevated temperatures within the beacon region provide a useful “laboratory” test case to evaluate the viability of the chemical mechanism, or at least to provide insight into the key temperature-sensitive reactions involved in stratospheric chemistry on Saturn.

Figure 3:

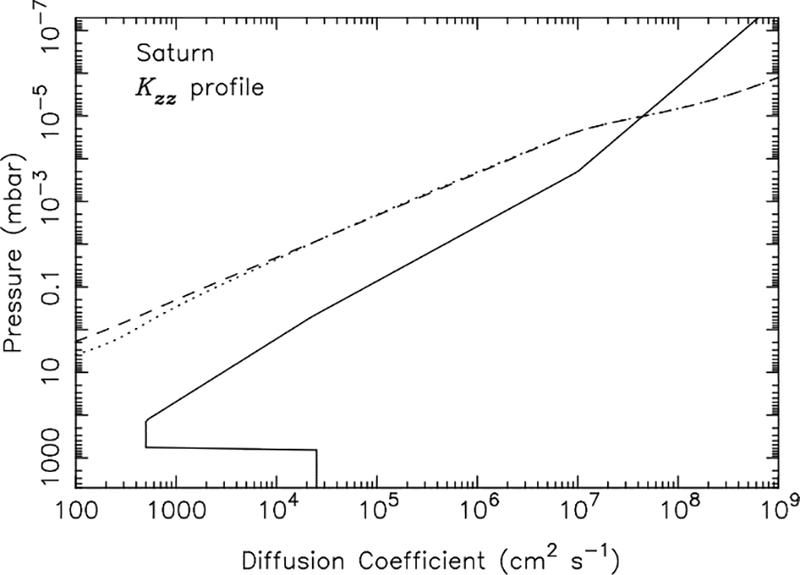
The eddy diffusion coefficient (K_zz) profile adopted in our models (solid line), along with the CH₄ molecular diffusion coefficient profile for the pre-storm thermal profile (dashed line) and the post-storm “hot” beacon core thermal profile from May 4, 2011 (dotted line). Note that because the K_zz profile is defined as a function of pressure and because the temperature profiles are similar at high altitudes, the methane homopause pressure level (i.e., where K_zz equals the CH₄ molecular diffusion coefficient) does not change between the pre-storm and post-storm models.

Figure 4:

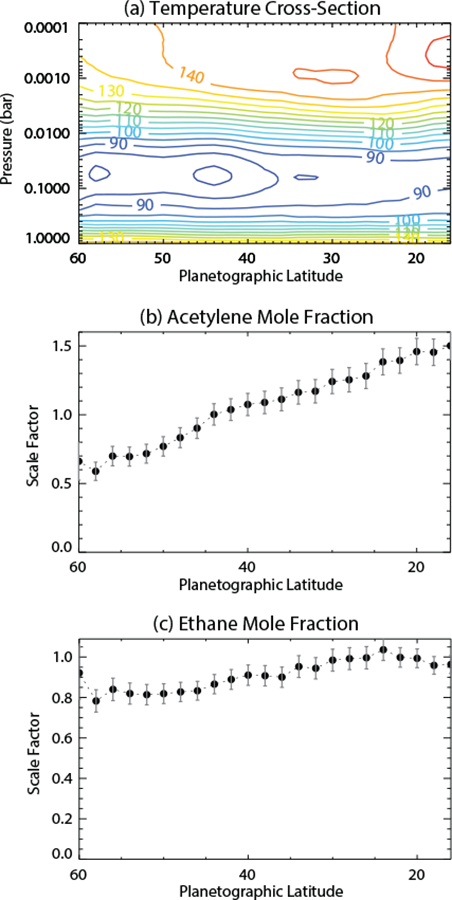
Zonal mean retrievals of pre-storm conditions derived from CIRS nadir data from May-August 2010 as a function of planetographic latitude: temperatures (a), and scaling factors for acetylene (b), ethane (c). The scaling factors are uniform-with-height multiplicative factors that have been applied to the mixing-ratio profiles predicted by our pre-storm photochemical model, with several model iterations conducted to ensure that these scaling factors are close to unity at the location of the beacon core (approximately 40°N). Note that ethylene is not detected in these pre-storm observations, as is consistent with the predictions from the pre-storm model.

Once a pre-storm K_zz profile has been established, we use the converged pre-storm photochemical-model solution as our initial condition and run the time-variable model for 40° planetographic latitude, starting at December 5, 2010 with the pre-storm temperatures, and then let the temperature profiles (and atmospheric grid) vary as a function of time for the 15 months for which CIRS beacon data have been reported. The observational data are spaced unevenly in time, and we simply update the model temperature profiles at the halfway point between each of the observations. This choice of when to update the thermal structure is arbitrary and can affect the results for the shortest-lived molecules (including C₂H₄), but modifications to this assumption result in only small differences in the quantitative conclusions. The ending mole-fraction profiles for the results from one time segment at one temperature are passed on to the next run as initial conditions for the new temperature sequence. The stratospheric gas abundances thus evolve with time as the temperatures in the beacon regions change. For our initial set of models, we ignore any dynamical or eddy-diffusion changes within the beacon region, keeping K_zz fixed at pre-storm values, but we later explore how vertical winds affect the results.

3. Observations and Spectral Modeling

The observations discussed in this paper were obtained from the Cassini CIRS Fourier transform spectrometer (Flasar et al., 2004), using the mid-infrared focal planes (FP3, covering 600–1000 cm⁻¹; FP4, covering 1100–1500 cm⁻¹). We adopt without modification the Fletcher et al. (2012) retrievals of the average thermal structure within the beacons from CIRS observations acquired in 2010–2012 with a variety of observing strategies and spectral resolutions (see Table 1 of Fletcher et al., 2012, and associated discussion). We also present new analyses of CIRS spectra at 2.5 cm⁻¹ spectral resolution acquired during two epochs: (i) previously unpublished pre-storm observations obtained in mid-2010 covering the 25–55°N latitude range (130SA MIRMAP001 on May 5, 2010; 134SA MIRMAP001 on July 10, 2010; 135SA MIRMAP001 on July 19, 2010; and 137SA MIRMAP001 on August 28, 2010); and (ii) a re-analysis of previously published post-storm observations acquired on May 4, 2011, shortly after the beacon merger event (148SA MIRMAP001) that have been shown to exhibit enhanced acetylene (Fletcher et al., 2012) and ethylene (Hesman et al., 2012) emission within the beacon. The May 2011 observations have been averaged in 10°-wide bins on a 5° longitude grid. All spectra use 4000 calibration reference spectra to improve the signal-to-noise ratio in the observed emission features. We simultaneously retrieve atmospheric temperatures and hydrocarbon scale factors, exploiting methane emission between 1250–1350 cm⁻¹, H₂-He collision induced absorption from 600–700 cm⁻¹, and emission from acetylene (~730 cm⁻¹), ethane (~820 cm⁻¹) and ethylene (~950 cm⁻¹), using all available data from 700–1000 cm⁻¹.

Inversions of spectral data can be prone to extreme degeneracy, where a wide variety of potential solutions can reproduce the data equally well. This situation is particularly true at mid-infrared wavelengths, where the magnitude of hydrocarbon emission features is governed by both their mixing ratio profiles and the atmospheric temperature structure in the line-forming region. Spectral retrieval algorithms, such as the NEMESIS model employed here (Irwin et al., 2008), use a priori profiles to constrain solutions, but the resulting retrieved thermal and chemical distributions can sometimes be biased towards this prior information. In this study, we combine the photo-chemical modeling with spectral inversion, taking advantage of the synergistic nature of the forward and reverse modeling, to better assess how well the CIRS spectra can constrain the photochemical model. Throughout the analysis, we adopt the spectral inversion techniques described by Fletcher et al. (2011) and Fletcher et al. (2012), using identical sources of spectroscopic line data. In each case, we use the predicted mixing ratio profiles for all hydrocarbon species in the photochemical model as prior information, and scale these profiles simultaneously with a temperature retrieval to reproduce the CIRS measurements. Our goal is to find a set of theoretically derived mixing-ratio profiles, based on chemistry and vertical motions, that require minimal scaling in order to reproduce the CIRS emission features.

Several iterations between the photochemical model priors and the spectral fitting were required to (a) converge on a pre-storm model that reproduced the emission at 40°N planetographic latitude (Section 2); (b) determine that photochemistry at elevated temperatures alone is insufficient to explain the enhanced emissions (Section 4; see also Hesman et al., 2012; Cavalié et al., 2015); and (c) converge on a solution with subsiding winds that required minimal scaling of the model hydrocarbon profiles (Section 4.5). Examples of the spectral fits are shown in Section 5.

Throughout the paper, the errors in the retrieved species mixing ratios that we quote are the formal uncertainties from the optimal estimation procedure used by NEMESIS. These formal errors take into account measurement uncertainties, temperature uncertainties due to the degeneracy between abundance and temperature when fitting the observed emission, and a fractional error accounting for uncertainties in the spectral line database and other spectral modeling assumptions. The quoted uncertainties do not account for systematic errors. More importantly, they do not account for errors due to the uncertain shape of the species vertical profiles used to define the priors — the vertical model profiles are simply scaled uniformly at all altitudes until a best fit is obtained. As such, the formal errors will underestimate the true uncertainties, especially for pressure regions far removed from the peak of the contribution functions.

4. Results and Discussion

For our nominal beacon model, we keep the K_zz profile fixed at pre-storm values (Fig. 3), and we neglect vertical winds. Because time-variable dynamics are not being considered in the nominal model, changes in the mixing-ratio profiles of the hydrocarbons are caused solely by temperature-dependent reactions. Figure 5 shows the predicted time variation for several important species from January 2, 2011 through March 14, 2012 from our “beacon-average” nominal model that assumes the beacon-average temperature profiles for all dates, including May 4, 2011. Note that C₂H₄ experiences a strong increase at mbar pressures due to the increased temperatures, while the C₃H₄ isomer methylacetylene (CH₃C₂H) and diacetylene (C₄H₂) decrease in the ~10–10⁻² mbar region, and C₂H₂, C₂H₆, and C₃H₈ (propane) are unaffected by the temperature increase. Species that condense under pre-storm stratospheric conditions on Saturn, such as H₂O, C₄H₂, and C₆H₆, exhibit strong increases in abundance in the lower-stratosphere due to evaporation of the aerosols at the elevated temperatures in the beacon.

Figure 5:

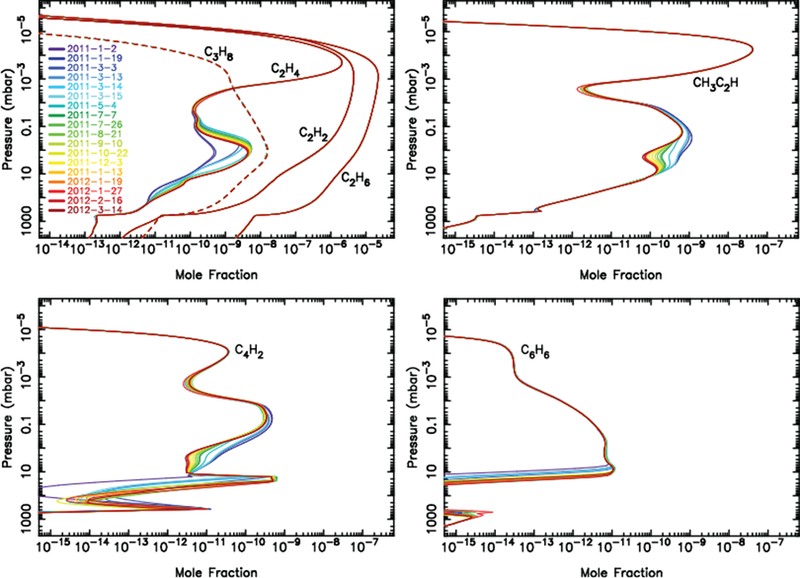
The vertical profiles of several hydrocarbons (as labeled) as they evolve with time in the beacon for our “beacon-average” nominal photochemical model that uses the beacon-average thermal profiles (see Fig. 1). The color coding corresponds to the dates listed in the top left figure. The shorter-lived species C₂H₄, CH₃C₂H, and C₄H₂ are affected by the changing temperatures, while the longer-lived species C₂H₆, C₂H₂, and C₃H₈ are not.

In Fig. 6, the pre-storm and post-storm (for May 4, 2011) C₂H_x model profiles are compared with derived abundances from various global and local observations. The lighter green squares in Fig. 6 show the C₂H₂ and C₂H₆ mole fractions from our analysis of the May-August 2010 pre-storm CIRS nadir spectra, the darker green circles show the 2005–2006 pre-storm mole fractions from the CIRS limb data analysis of Guerlet et al. (2009, 2010) for 40° planetographic latitude, and the red squares show our retrieved mole fractions from the hot beacon-core region on May 4, 2011. Note that the C₂H₂ and C₂H₆ mole fractions are actually observed to increase in the hot beacon-core region in comparison with the pre-storm retrievals, whereas our models predict virtually no change in these species in the beacon over that time period. These nominal models without a temporally variable dynamical component underpredict the C₂H_x abundances in the beacon by factors of ~2–7. If the observed beacon increases in C₂H_x abundance were caused by temperature-dependent chemistry alone, the additional carbon would have to come from methane, as methane is the only sufficiently large source of local carbon. We are unable to identify any temperature-sensitive chemical reactions that efficiently convert methane to C₂H_x species at mbar levels on Saturn on the short time scales involved, suggesting that dynamics may be contributing to the observed increase in C₂H_x species in the beacon. Figure 6 also illustrates that the “hot” nominal model that uses the beacon-core temperatures from May 4, 2011 produces slightly more C₂H₄ at mbar pressures than the “beacon-average” nominal model that uses beacon-average temperatures from that date. In particular, the ~10-K temperature difference between the “hot” and “beacon-average” model at ~2 mbar leads to 16% higher C₂H₄ mole fraction in the hot model.

Figure 6:

The mole-fraction profiles for CH₄, C₂H₂, C₂H₄, and C₂H₆ from our pre-storm model (green solid lines) and our post-storm “hot” beacon-core (red solid lines) and “beacon-average” (blue dashed lines) models, in comparison with the Moses and Greathouse (2005) seasonally variable model results (black dotted lines) for 40°N plane-tocentric latitude at L_s = 20°, the closest available model latitude and season to the May 2011 beacon observations. The data points with error bars represent various observations: the dark green circles are from the Guerlet et al. (2009, 2010) CIRS limb analysis at 40° planetographic latitude from 2005–2006, the lighter green squares are from our analysis of the CIRS nadir data for 40°planetographic latitude from May-August 2010, and the red squares represent our retrieved abundances from the beacon core (294.8° System III longitude, 36.6°planetographic latitude) on May 4, 2011. The formal error bars from our retrievals (see section 3) are smaller than the width of the square data points. The other observational data points are described in Fouchet et al. (2009).

Figure 7 shows the scaling factors that need to be applied to our hot nominal beacon-core model profiles in order to fit the molecular emission from the longitudinally resolved spectra across the beacon. The resulting retrieved mole fractions at 1.8 mbar at the beacon central core at 294.8° System III longitude on May 4, 2011 are 1.08 (± 0.02) × 10⁻⁶ for C₂H₂, 2.0 (± 0.3) × 10⁻⁸ for C₂H₄, and 9.4 (± 0.1) × 10⁻⁶ for C₂H₆, with the formal error bars neglecting both systematic uncertainties and uncertainties in the hydrocarbon vertical profiles (see Section 3). From Fig. 7, it is obvious that the beacon photochemical model underpredicts the C₂H_x hydrocarbon abundances in the beacon vortex by factors of ≳ 2–7. These scale factors are in relation to the hot beacon-core model only, and are not necessarily directly comparable to the pre-storm model scaling factors shown in Fig. 4. However, recall that the C₂H₂ and C₂H₆ vertical profiles in the hot beacon-core model have not changed much in comparison with the pre-storm model. Figure 7 therefore indicates that the C₂H₂ abundance has experienced a general factor of ~2 increase outside of the beacon vortex across the entire beacon latitude region observed on the May 4, 2011 date, with larger increases found within with the beacon vortex itself, and especially in the central core region at 294.8° System III longitude and a secondary peak at C₂H₂ peak at 273.3°longitude (the latter associated with a local high-altitude increase in temperature). Ethane also exhibits longitudinal structure, with the largest abundances located within the vortex itself, again at 273.3° and 294.8° longitude. At longitudes away from the vortex itself, the C₂H₆ scaling factors trend back to the pre-storm case on the east side, but the “hot” nominal model profile apparently overestimates the C₂H₆ abundance on the west side of the vortex, where temperatures are not as large. Note from Fig. 7a that the stratospheric temperatures themselves have also increased compared to the pre-storm case (cf. Fig. 4a) throughout the observed region, but especially within the vortex itself.

Figure 7:

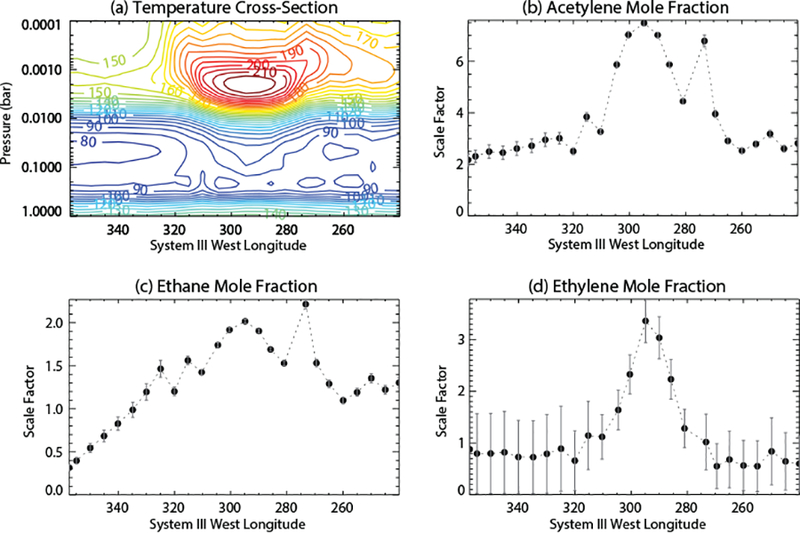
Retrievals of temperatures and hydrocarbon distributions as a function of longitude through the beacon core on May 4, 2011. Spectra were averaged over the 36 – 43°N latitude range, and model-predicted mixing-ratio profiles from our nominal hot beacon-core photochemical model were uniformly scaled to reproduce the emission observed by CIRS. In all cases, the required scaling factors still exceed unity within the beacon, implying that the distributions must be affected by processes in addition to photochemistry.

The large-scale longitudinal perturbations in temperatures and abundances throughout the storm latitude are not too surprising, as neither the tropospheric storm head nor the stratospheric beacon vortex were stationary with respect to System III longitude. The storm head drifted westward and encountered the southern branch of its wake tail within about 50 days of the storm’s appearance, forming a planet encircling band of active tropospheric clouds that continued to be influenced by each ~120-day circumnavigational pass of the storm head through the region (Sánchez-Lavega et al., 2011, 2012; Sayanagi et al., 2013). Similarly, the beacon vortices also drifted longitudinally at their own rates, with the final merged beacon vortex circling the planet once every 130 days or so (Fletcher et al., 2012). The fact that stratospheric warming was observed throughout the entire latitude band in which the beacon resides (Fletcher et al., 2012, see also Fig. 7) indicates that large regions of the stratosphere were perturbed by the storm, rather than the effects just being limited to the merged vortex itself. That is especially true at higher altitudes (see Fig. 11a of Fletcher et al. 2012), where a large swath of the northern hemisphere was observed to have enhanced temperatures in comparison with pre-storm values. If the tropospheric convective plumes provided a source of upward-propagating planetary and gravity waves that transported energy and momentum to the stratosphere (e.g., Fletcher et al., 2011, 2012), both stratospheric dynamics and temperatures could have been affected over broad regions, leading to different thermal and vertical abundance profiles across the latitude band. Indeed, the different zonal profiles for the different species suggest different chemical-dynamical-thermal coupling as a function of longitude across the beacon. Ethylene is more sensitive to the thermal structure than either acetylene or ethane, but the difference in morphology of all the C₂H_x scaling factors as a function of longitude across the beacon suggests complicated longitudinally and vertically variable wind fields and a different chemical/dynamical response of the different species to the winds and temperatures at different altitudes.

Figure 11:

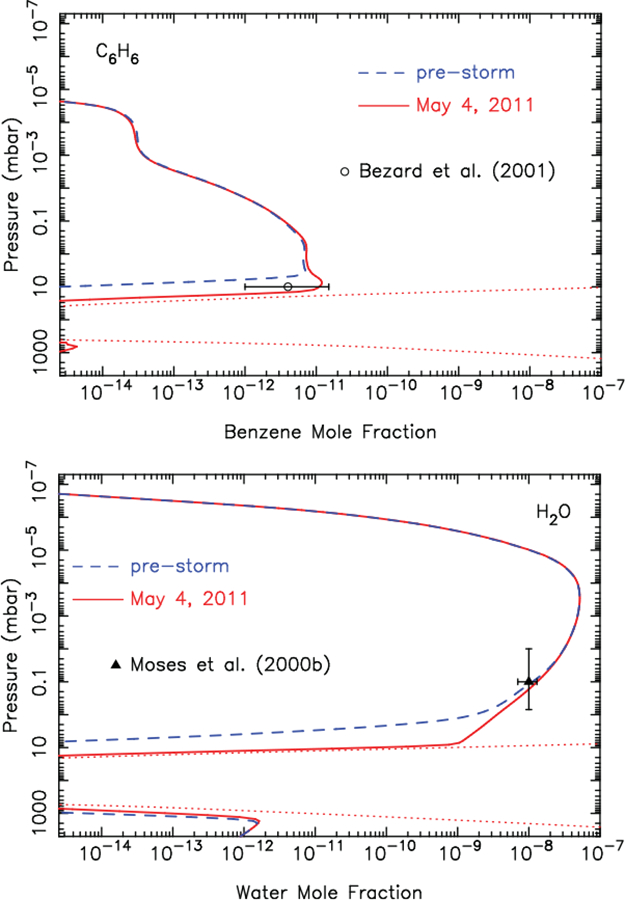
The mole-fraction profile for benzene (top) and water (bottom) in our pre-storm model (blue dashed line) and in the hot beacon-core model for May 4, 2011 (red solid line). The red dotted lines represents the saturation vapor density curve for temperatures relevant to the May 4, 2011 CIRS observations. The data points with error bars are from ISO observations: C₆H₆ from Bézard et al. (2001) and H₂O from Moses et al. (2000b).

The results regarding the chemical response of the individual species to the elevated beacon temperatures are discussed in detail below, while the potential effects of vertical winds are discussed in Section 4.5.

4.1. Nominal Model Results: Ethane, Acetylene, and Propane

The lack of significant temporal evolution of C₂H₆, C₂H₂, and C₃H₈ in our nominal beacon model (Fig. 5) is due to the long chemical lifetime of these species, even at the higher temperatures experienced in the beacon. If we define the net chemical lifetime τ_chem of a species i as n_i/|P_i − L_i|, where n_i is the concentration (cm⁻³) and P_i and L_i are the chemical production and loss rates (cm⁻³ s⁻¹) at any particular altitude, we find that τ_chem at the temperature maximum at ~2 mbar in the hot beacon core is 580 (Earth) yrs for C₂H₆, 1.4 yrs for C₂H₂, and 6.9 yrs for C₃H₈. In contrast, the highest beacon temperatures were observed in May of 2011, only 5 months after the storm onset. The C₂H₆, C₂H₂, and C₃H₈ abundances in the model have not had enough time to respond chemically to the elevated temperatures in a notable way by the May 2011 observations. Considering the fact that the beacon has been cooling slowly but steadily since May 2011, we do not expect continued evolution of C₂H₆ and C₃H₈ due to chemistry alone, but Fig. 5 does illustrate some slight expected changes in the C₂H₂ abundance over the ~1.3-year span of the published CIRS observations.

Chemical loss exceeds production of C₂H₂ over much of the pressure region in which temperatures are elevated within the beacon. The rate coefficient for the reaction number R130 in our list (H + C₂H₂ + M → C₂H₃ + M, with M representing any third-body molecule or atom) becomes much larger at the higher beacon temperatures, but the background density and H mole fraction drop in the elevated-temperature region (the latter largely due to reaction R130), leading to an overall ~60% increase in the loss rate of C₂H₂ at 2 mbar in the beacon on May 4, 2011; however, there is sufficient C₂H₂ at these pressures that the perturbation to the C₂H₂ abundance is minor over the relatively short time period involved. On the other hand, this increased loss of C₂H₂ in the beacon contributes to the increased production rate of less-abundant species such as C₂H₃ and ultimately C₂H₄.

The small loss of C₂H₂ in the beacon contributes to a ~70% increase in the production rate of C₂H₆ at 2 mbar in the hot beacon core on May 4, 2011, through the dominant pathway H + C₂H₂ + M → C₂H₃ + M, C₂H₃ + H₂ → C₂H₄ + H, and H + C₂H₄ + M → C₂H₅ + M, followed by reaction of atomic H with C₂H₅ to either form C₂H₆ directly, or to form two CH₃ radicals, which recombine to form C₂H₆. Given the already large C₂H₆ mole fraction at the relevant pressure levels, this increased production has an insignificant effect on the C₂H₆ mole fraction in the beacon over the time scales involved, however.

Like ethane, the production rate of propane exceeds its loss rate over much of the elevated temperature region of the beacon. The increased acetylene loss rate in the beacon leads to increased amounts of C₂H₅ and therefore C₃H₈ through the reaction R232: CH₃ + C₂H₅ + M → C₃H₈ + M. Again, however, the perturbation in the net production rate has little effect on the C₃H₈ mole fraction in the beacon over the relevant time scales.

We therefore do not expect much change in the abundance of ethane, acetylene, and propane in the beacon due to chemistry alone. Any observed changes in these species (e.g., Figs. 6 & 7) are likely caused by changes in dynamics within the beacon region. Cavalié et al. (2015) arrived at a similar conclusion for these species, although Cavalié et al. did predict small changes to the abundances of C₂H₂ and C₂H₆ at high stratospheric altitudes within the beacon. The differences at high altitudes between our model and that of Cavalié et al. (2015) are caused by transport and the prescription of high-altitude temperatures, which are not constrained by CIRS. In the Cavalié et al. (2015) model, the high-altitude temperatures are assumed to remain isothermal above 10⁻³ mbar; the different dates then have different high-altitude temperatures, which leads to different high-altitude density structures and different pressure levels for the methane homopause at the different dates within the Cavalié et al. (2015) model. As is shown in Figs. 1 and 3, we assume in our models here that the upper-atmospheric temperatures are unperturbed by the beacon, so the thermal profiles from all dates converge at high altitudes, and the methane homopause pressure level does not change significantly with time in our model. High-altitude diffusion therefore does not have much effect on the evolution of the profiles in our nominal models. The elevated temperatures within the beacon region do expand the atmosphere in terms of the altitude scaling at the relevant pressures within the beacon, but the diffusion time scales at these pressures are longer than the total observational period after the storm, so changes due to diffusion are minor in our nominal model.

4.2. Nominal Model Results: Ethylene

Because ethylene has one of the shortest chemical time scales of all the stable species (e.g., 40 days at the 2-mbar temperature maximum in the hot beacon-core model), it has one of the most pronounced responses to the elevated temperatures in the beacon (Fig. 5). From a column-integrated standpoint, the dominant reactions producing C₂H₄ in Saturn’s unperturbed (pre-storm) stratosphere are reaction R184 (CH + CH₄ → C₂H₄ + H), reaction R132 (H + C₂H₃ + M → C₂H₄ + M), and reaction R267 (C₂H₃ +H₂ → C₂H₄ + H), with lesser contributions from C₂H₆ photolysis and from R136 (H + C₂H₅ → C₂H₄ + H₂) (see also Moses et al., 2000a, 2005). The dominant loss processes are reaction R134 (H + C₂H₄ + M → C₂H₅ + M) and photolysis. The reaction C₂H₃ + H₂ → C₂H₄ + H (R267) contributes only 21% to the stratospheric column-integrated production rate of C₂H₄ in the pre-storm model. However, when temperatures in the beacon increase dramatically over pre-storm values, the highly temperature-sensitive reaction R267 overwhelmingly dominates the production of ethylene (see also Cavalié et al., 2015) and is correspondingly responsible for the major increase in the C₂H₄ abundance at ~mbar pressures in our nominal beacon model (see Fig. 5). Although the rate coefficient for R267 is relatively modest at room temperature and below (Callear and Smith, 1986; Tsang and Hampson, 1986; Weissman and Benson, 1988; Fahr et al., 1995; Mebel et al., 1995; Litwinowicz et al., 1995; Knyazev et al., 1996; Li et al., 2004; Laufer and Fahr, 2004; Tautermann et al., 2006; Agarwal et al., 2011), Saturn’s atmosphere contains enough background H₂ to make this reaction important.

The rate coefficient for this temperature-sensitive abstraction reaction R267 at low temperatures is poorly known, and extrapolations of the various published literature expressions to the lower temperatures relevant to Saturn can differ by many orders of magnitude (see Fig. 8). For our nominal model, we adopt one of the largest available published rate coefficients at low temperatures (i.e., the expression of Weissman and Benson, 1988), which results in a large predicted post-storm spike in the C₂H₄ abundance. Note, however, that the transition-state theory estimation method used by Weissman and Benson (1988) to derive the rate-coefficient expression of k₂₆₇ = 5.25 × 10⁻¹⁵ T^0.7 exp (−2574 K/T) cm³ s⁻¹ for this reaction is outdated in comparison to more modern techniques. Many recent theoretical calculations suggest smaller rate coefficients at low temperatures. For example, from a combined experimental and ab initio theoretical study, Knyazev et al. (1996) recommend a rate-coefficient of k₂₆₇ = 1.57 × 10⁻²⁰ T^2.56 exp (−2529 K/T) cm³ s⁻¹ for this reaction, while Tautermann et al. (2006) use quantum-scattering theory on a 2D reduced dimensionality potential-energy surface to derive even smaller values at low temperature: k₂₆₇ = 1.0738 × 10⁻¹⁹ T^2.3689exp (−3145.4 K/T) cm³ s⁻¹ (see Fig. 8). Mebel et al. (1995) and Li et al. (2004) use various ab initio theoretical techniques to predict the rate coefficients for this reaction; Li et al.’s calculations that use improved canonical variational transition-state theory with small-curvature tunneling corrections result in rate constants as large as those derived by Weissman and Benson (1988) (see dotted purple line in Fig. 8), while most other methods result in much slower rates at low temperature. Moreover, most of the theoretical expressions were developed for high-temperature combustion studies and were not designed to be extrapolated to the ~100–220 K temperatures relevant to Saturn’s stratosphere. The sparse available experimental data do not help resolve the situation, with Fahr et al. (1995) deriving rate coefficients at room temperature that are significantly smaller than those favored by Callear and Smith (1986) and Knyazev et al. (1996). The most recent study of the reaction energetics of C₂H₃ + H₂ → C₂H₄ + H by Agarwal et al. (2011) provides further evidence that the rate coefficient for this abstraction reaction has yet to be well resolved.

Figure 8:

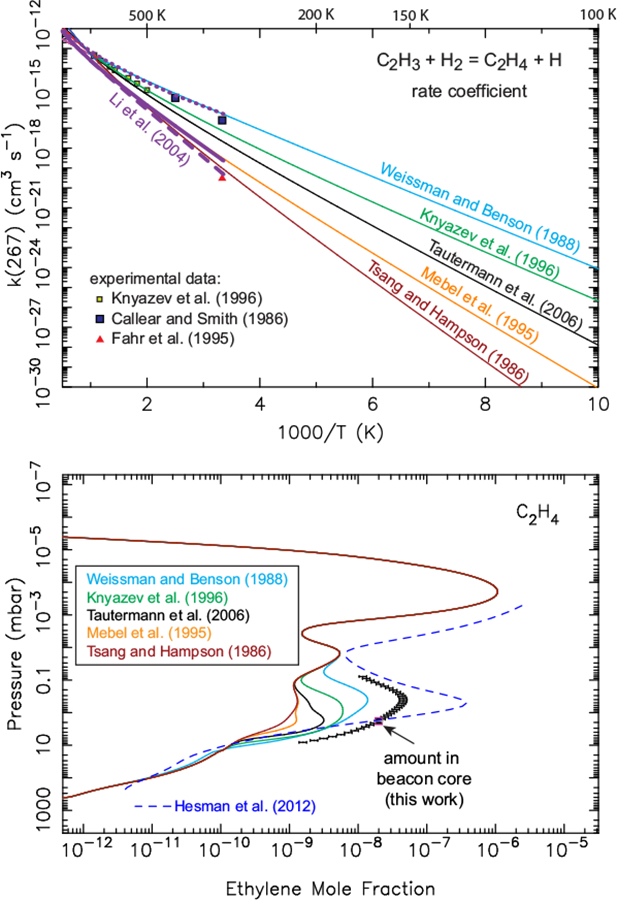
(Top) The rate coefficient for the reaction C₂H₃ + H₂ → C₂H₄ + H as a function of inverse temperature, from various literature sources (as labeled). (Bottom) The predicted C₂H₄ mole-fraction profile in the hot core of the beacon on May 4, 2011 for different assumptions about the rate coefficient for the aforementioned reaction, in comparison with the CIRS-derived C₂H₄ beacon-core abundance from that date as derived from Hesman et al. (2012) (blue dashed curve) and from our analysis (black square with pink outline, see text, and black data points with error bars).

The fact that the C₂H₄ abundance was observed to increase so significantly with increasing temperatures in the beacon region on Saturn (Hesman et al., 2012) makes it tempting to rule out the lowest estimates or determinations of the rate coefficient for this reaction (such as that of Tsang and Hampson 1986 or Fahr et al. 1995), because such low rate coefficients prevent the C₂H₃ + H₂ → C₂H₄ + H reaction from being significant for ethylene production on Saturn, even at the elevated 220-K beacon-core maximum temperature. The observed beacon behavior itself suggests that some reaction with a strong temperature dependence dominates ethylene production in the beacon, and the C₂H₃ + H₂ → C₂H₄ + H reaction fills that role nicely. However, the modeled behavior of C₂H₄ depends on a complex coupling of many reactions, not all of which are well constrained from experimental or theoretical data, so it is possible that other yet-to-be-identified reactions are contributing to the observed ethylene increase, or that dynamical changes in the beacon are responsible for the observed increase.

In any case, Fig. 8 shows the sensitivity of the model results to the adopted expression for the rate coefficient for C₂H₃ + H₂ → C₂H₄ + H. A distinct peak in the C₂H₄ is formed at ~mbar pressures for most of the cases, with the larger rate-coefficient assumptions for this reaction leading to larger predicted C₂H₄ abundances in the beacon. However, even with the adoption of the comparatively fast Weissman and Benson (1988) reaction rate coefficient, our “hot” nominal model underpredicts the emission in the C₂H₄ bands in the beacon core on May 4, 2011 by a factor of ~3.4 (see Fig. 7); that is, the photochemical model profile for C₂H₄ using the Weissman and Benson (1988) rate coefficient for reaction R267 would need to be multiplied uniformly by a factor of ~3.4 in order to reproduce the observed CIRS emission.

Figure 8 also shows that our derived vertical profile for C₂H₄ at the beacon center differs from that of Hesman et al. (2012), despite the fact that both analyses use the NEMESIS retrieval program and both consider the same beacon-center CIRS data set from May 4, 2011. This difference is due to different analysis strategies with NEMESIS. The thermal structure and C₂H₄ vertical profile in the beacon region are not known a priori. Hesman et al. (2012) proceeded by first determining the thermal structure from the CIRS data over a broad wavelength range, using the constrained linear inversion algorithm described in Conrath et al. (1998) and Achterberg et al. (2008). Then, Hesman et al. kept that temperature structure fixed and allowed NEMESIS to freely adjust the C₂H₄ vertical profile within a certain pressure range to provide a best fit to the C₂H₄ emission. We, on the other hand, simultaneously fit both the thermal structure and the scale factor for the hydrocarbon vertical profiles with NEMESIS, letting the temperature be adjusted freely but retaining the overall shape of the hydrocarbon vertical profiles from the photochemical models and requiring NEMESIS to scale these profiles uniformly to provide the best fit to the emission from all the hydrocarbons (see Section 3). Both procedures have their strengths and weaknesses. The photochemical model profiles provide a welcome connection to physical reality, but when the models do not adequately reproduce the observations — as is the case with these beacon models where vertical winds are not included — those constraints may not be meaningful. At the 2.5 cm⁻¹ spectral resolution of these nadir observations, the CIRS data provide little concrete information about the vertical profile of C₂H₄. Instead, the retrievals provide C₂H₄ abundance information that is most reliable in the pressure region where the emission contribution function peaks, which is near the ~2 mbar region for the C₂H₄ emission bands observed here (see the black square with the pink outline in Fig. 8). Therefore, it is interesting to note that the vertical profiles retrieved from both our technique and that of Hesman et al. (2012) converge on a similar C₂H₄ abundance in this ~2 mbar region. Although the two techniques lead to vastly different C₂H₄ abundances at pressures less than 1 mbar, those high-altitude regions have less influence on the C₂H₄ emission seen by CIRS than the deeper ~2 mbar region. Hereafter, we plot a single observational data point at the peak of the contribution function for C₂H₄ and the other hydrocarbons rather than the full retrieved vertical profile, but we also note that the location at which the contribution function peaks depends on the vertical profiles of both the temperature and the hydrocarbon in question, so that data point will be located at different pressures for different prior model profiles.

Although uncertainties in the C₂H₃ + H₂ → C₂H₄ + H production reaction cause the most dramatic changes in the C₂H₄ profile in the photochemical model, uncertainties in the dominant loss reaction R134, H + C₂H₄ + M → C₂H₅ + M, can also affect the predicted ethylene abundance. This reaction is important as an intermediate in the conversion of C₂H₂ to C₂H₆ on the giant planets (e.g., Allen et al., 1992; Romani, 1996; Moses et al., 2000a, 2005) — a slow rate will short-circuit this conversion, leading not only to more C₂H₄ but to increased abundances of C₂H₂ and most other hydrocarbon photochemical products, as a result of C₂H₂ being a key “parent” molecule for many species. As discussed in the review of Baulch et al. (2005), the high-pressure limiting rate coefficient for the H + C₂H₄ + M → C₂H₅ + M reaction has been measured in the ~200–600-K temperature range (e.g., Lee et al., 1978; Sugawara et al., 1981; Lightfoot and Pilling, 1987; Michael et al., 2005) and is fairly well established. Experimental measurements at low pressures and in the intermediate fall-o pressure regime are also available, but only at room temperature and higher (e.g., Braun and Lenzi, 1967; Kurylo et al., 1970; Brouard et al., 1986; Lightfoot and Pilling, 1987; Hanning-Lee et al., 1993; Sillesen et al., 1993; Clarke et al., 2000). The low-pressure limiting rate coefficient at the low temperatures relevant to Saturn’s atmosphere is not well established, nor is the influence of tunneling on the high-pressure rate coefficient at low temperatures.

Theoretical calculations could potentially help bridge the gap, but such studies seldom extend to the low pressures and temperatures required for Saturn (e.g., Miller and Klippenstein, 2004; Michael et al., 2005). The recent ab initio transition-state theory based master-equation calculations presented by Vuitton et al. (2012) are an exception, as expressions are provided that are valid at low pressures in the 50–300-K range. The Vuitton et al. (2012) expressions, which result in very efficient C₂H₅ adduct formation under Saturn stratospheric conditions, are adopted in our nominal model. In contrast, Li et al. (2014) suggest that the underestimation of the C₂H₄ abundance in many photochemical models of the giant planets and Titan could be the result of an overestimation of the rate coefficient of R134 at low temperatures, and they suggest adopting an expression that leads to rate coefficients much smaller than our adopted ones under the relevant conditions. Such low rate coefficients would imply that tunneling is very inefficient for this reaction, in conflict with existing theoretical calculations (Miller and Klippenstein, 2004; Michael et al., 2005; Vuitton et al., 2012), but the use of this expression does provide a better fit to Titan observations (Li et al., 2014).

Figure 9 shows how the models results are affected by variations in the rate coefficient for R134 (H + C₂H₄ + M → C₂H₅ + M). Our adoption of the relatively efficient Vuitton et al. (2012) expression for R134 results in a notably smaller C₂H₄ abundance at mbar levels than is predicted from using the Li et al. (2014) expression. Our nominal model profiles using the Vuitton et al. (2012) expression for R134 are consistent with the non-detection of C₂H₄ before the storm, but the model underpredicts the beacon-core C₂H₄ abundance after the storm. On the other hand, the Li et al. (2014) expression leads to a better fit to the post-storm C₂H₄ abundance, but results in too much C₂H₄ pre-storm, as well as excessive amounts of C₂H₂, CH₃C₂H, C₃H₈, C₄H₂, C₄H₁₀, C₆H₆, and most other hydrocarbons in comparison with pre-storm observations. We therefore favor the Vuitton et al. (2012) expression for R134, which has a strong theoretical basis, and we seek other non-chemical explanations for the underestimation of the beacon C₂H_x abundances from our nominal model (see Section 4.5).

Figure 9:

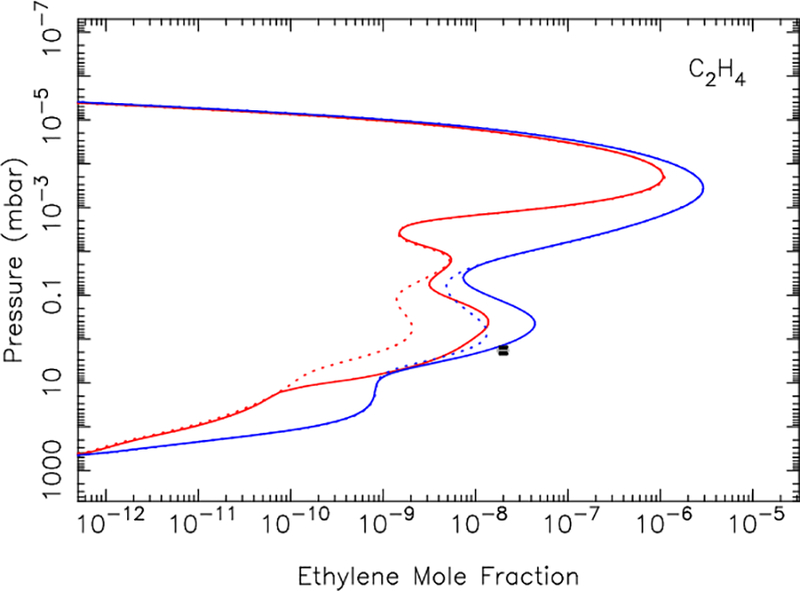
The sensitivity of the C₂H₄ profile to the rate coefficient for reaction R134 (H + C₂H₄ + M →C₂H₅ + M) for pre-storm conditions (dotted lines) and the hot beacon core on May 4, 2011 (solid lines), for our nominal model (red) and a model in which the rate coefficient for R134 is taken from the recommendation of Li et al. (2014) (blue). The black square is our CIRS-derived C₂H₄ beacon-core abundance from May 4, 2011.

More information about the rate coefficients for the reaction C₂H₃ + H₂ → C₂H₄ + H at low temperatures (50 ≲ T ≲ 250 K) and experimental confirmation of the theoretical reaction rate coefficients for H + C₂H₄ + M → C₂H₅ + M at low pressures and temperatures (P ≲ 1 mbar, T ≲ 200 K) are needed before we can feel confident about the quantitative predictions for the C₂H₄ abundance in photochemical models of the giant planets and Titan. However, the highly temperature-sensitive reaction C₂H₃ + H₂ → C₂H₄ + H is the most likely culprit of the enormous observed increase in the abundance of C₂H₄ detected by Hesman et al. (2012) in Saturn’s beacon region.

4.3. Nominal Model Results: Methylacetylene and Diacetylene

Both CH₃C₂H and C₄H₂ have relatively short chemical lifetimes at mbar regions in the beacon models — just 26 days for CH₃C₂H and 28 days for C₄H₂ at the 2-mbar temperature maximum in the beacon. Figure 5 demonstrates that the stratospheric mole fraction of CH₃C₂H is expected to decrease with time in the beacon region. As discussed by Cavalié et al. (2015), the depletion is due in large part to the increased loss rate of CH₃C₂H due to the reaction H + CH₃C₂H + M → C₃H₅ + M, which has a moderately large energy barrier and is more effective at elevated temperatures.

The results for C₄H₂ are more complicated and interesting. Figure 10 shows the model results for the hot beacon-core model on May 4, 2011, in comparison with the unperturbed, pre-storm model profile. In the ~10–10⁻² mbar pressure region, C₄H₂ becomes depleted due to the elevated temperatures in the beacon. As discussed by Cavalié et al. (2015), the decrease of C₄H₂ at these pressures in the beacon is due to the decrease in C₂H₂ photolysis and, more importantly, to the increase in the rate coefficient for the temperature-sensitive reaction R252, C₂H + H₂ → C₂H₂ + H, which both result in a decreased concentration of C₂H at these pressures. The reduction in C₂H reduces the effectiveness of the primary non-recycling C₄H₂ production mechanism, C₂H + C₂H₂ → C₄H₂ + H, resulting in less C₄H₂ in the beacon at these pressures. Although the chemical mechanism we are adopting underestimates the pre-storm C₄H₂ abundance (see Fig. 10), the rate coefficients for the reactions C₂H + H₂ → C₂H₂ + H and C₂H + C₂H₂ → C₄H₂ + H have been well studied experimentally (see the review of Laufer and Fahr, 2004), and the prediction regarding the more rapid depletion of C₄H₂ at increased temperatures is robust.

Figure 10:

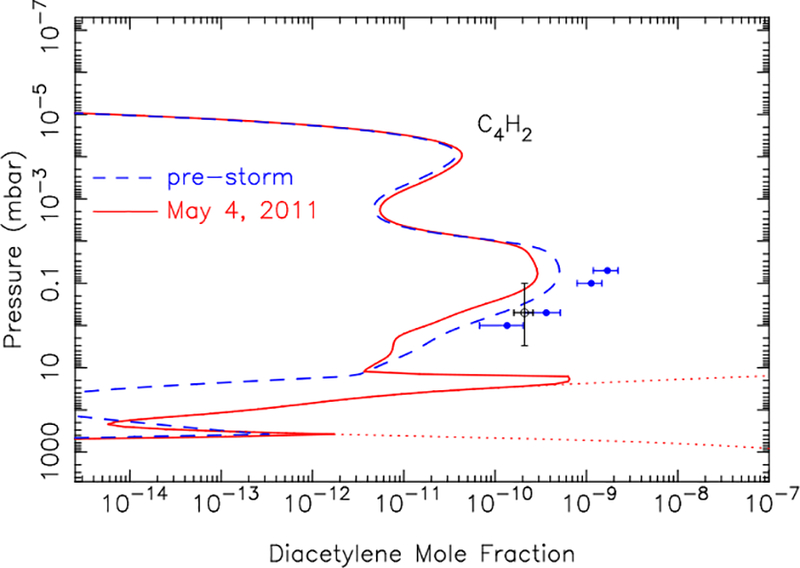
The mole-fraction profile for diacetylene in our pre-storm model (blue dashed line) and in the hot beacon-core model for May 4, 2011 (red solid line). The large spike in the abundance in the 10–40 mbar region is due to evaporation of icy C₄H₂ aerosols. The red dotted line represents the saturation vapor density curve for temperatures relevant to the May 4, 2011 CIRS observations, the blue circles represent the pre-storm CIRS limb retrievals of Guerlet et al. (2010) for 40° planetographic latitude, and the open black circle represents the global-average C₄H₂ abundance derived from ISO (Moses et al., 2000a).

Condensation is a major loss process for C₄H₂ in Saturn’s lower stratosphere over much of the planet, and as the beacon temperatures increase, our models predict a large increase in the C₄H₂ vapor abundance at pressures greater than ~10 mbar due to evaporation of solid C₄H₂ aerosols. The very large magnitude of the post-storm spike in the C₄H₂ abundance shown in Fig. 10 is partially an artifact of our model in that we only include condensation and evaporation and neglect other aerosol-microphysical processes like gravitational settling; in particular, we allow the condensates to diffuse through the atmosphere as a just another heavy gas, which enables more of the condensed phase to persist in the lower stratosphere than it would in the real atmosphere. However, some sort of large evaporation “spike” is expected in the beacon, even in the real atmosphere, because in situ production of C₄H₂ occurs readily within the C₄H₂ condensation region as a result of C₂H₂ photolysis, followed by C₂H + C₂H₂ → C₄H₂ + H, and because gravitational settling times for the aerosols are relatively long (e.g., Roman et al., 2013). The condensation of C₄H₂ shuts o the local recycling back to C₂H₂, so acetylene photolysis continues to produce a steady, irreversible leak of carbon into condensed C₄H₂, which then can become a major aerosol component in Saturn’s stratosphere (see also Moses et al., 2000a,b). This evaporation spike in the beacon is too deep to be detectable by infrared instruments like CIRS, but it would be worthwhile to search for increased C₄H₂ absorption signatures at ultraviolet wavelengths or for signatures of stratospheric aerosol thinning or clearing within the beacon in high-phase-angle images at ultraviolet/visible/near-IR wavelengths. It is worth noting that Fletcher et al. (2012) did not see any effects of the beacon in their preliminary check of images from the Cassini Visual Infrared Mapping Spectrometer (VIMS). Because the stratospheric haze is optically thin in the vertical direction (e.g., Karkoschka and Tomasko, 2005), effects due to thinning of the haze would be most apparent with the beacon feature(s) at the limb of the planet.

4.4. Nominal Model Results: Benzene and Water

Benzene and water can also condense in Saturn’s lower stratosphere, but because there is less in situ production of these species within their condensation regions, the models do not predict that same kind of evaporation spike as was predicted for C₄H₂. Instead, the condensable vapor flows into the condensation region from higher altitudes. Evaporation of the aerosols then causes a smoother local increase in the vapor abundance (see Fig. 11) and an increase in the overall stratospheric column abundance of H₂O and C₆H₆. Again, this increased vapor abundance in the beacon is at deep-enough pressures that it might be difficult to detect, but we note that Cavalié et al. (2012) reported a factor of 30–100 increase in the column abundance of H₂O in the beacon with the PACS instrument on the Herschel Space Observatory. Our hot beacon-core model for May 4, 2011, predicts a similar factor of 30–100 increase in the water mole fraction in the ~2–3 mbar region compared to prestorm values, but only a factor of 3 increase in the integrated water column abundance in the beacon compared to pre-storm levels. Direct comparison of synthetic model spectra with the Herschel/PACS observations would be needed before we can determine whether our predictions from the beacon models are consistent with the observations. In any case, we know of no chemical mechanisms that would increase the water abundance so severely in the beacon, so the Herschel/PACS observations most likely result from evaporation of water ice, with the water originating from outside the planet, and/or an increase due to vertical winds in the beacon (see Section 4.5). The benzene column abundance in our May 4, 2011, model increases by a factor of 4 in comparison with the pre-storm model as a result of evaporation.

4.5. The Potential Influence of Transport in the Beacon

As discussed in Section 4, the fact that our beacon models (and those of Cavalié et al. 2015) underpredict the abundances of all the C₂H_x hydrocarbons in the hot beacon core on May 4, 2011 suggests that dynamics may play a large role in controlling the observed abundance increases within the beacon region. The beacon vortex is inherently a 3-D atmospheric structure that is difficult to capture accurately in a 1-D model, even if the 1-D model equations were appropriately solved. However, if horizontal advection of species is small in comparison to vertical advection, then some useful estimates can still be made, so we proceed with the examination of the 1-D behavior in the presence of vertical winds. For the situation with winds included, it is convenient to reformulate Eq. (1) in terms of mixing ratios rather than number densities. In the well mixed region of the atmosphere below the homopause, assuming hydrostatic equilibrium is maintained, and accounting for the continuity of the total atmospheric density n_a, Eq. (1) can be rewritten as

$$\frac{\partial q_i}{\partial t}+w\frac{\partial q_i}{\partial z}-\frac{1}{n_a}\frac{\partial }{\partial z}\left(K_{zz}{n}_a\frac{\partial q_i}{\partial z}\right)=\frac{Q_i}{n_a}$$ (3)

where q_i is the mole fraction of species i, w is the vertical wind velocity, z is the altitude, K_zz is the vertical eddy diffusion coefficient, and Q_i is the net chemical source/sink term for species i.

If we further assume that chemistry and turbulent eddy transport have a minor influence in comparison with large-scale vertical winds, then Eq. (3) reduces to

$$\frac{\partial q_i}{\partial t}=-w\frac{\partial q_i}{\partial z}.$$ (4)

Equation (4) demonstrates that for subsidence (i.e., a downward wind, w < 0), the local mixing ratio will increase with time if the mixing-ratio gradient of the species is positive (dq_i/dz > 0), and it will decrease with time if the mixing-ratio gradient of the species is negative (dq_i/dz < 0). Both C₂H₂ and C₂H₆ have mixing-ratio gradients that are positive throughout the stratospheric beacon region, implying that subsidence is needed to increase the mixing ratios of these species locally within the beacon (see also the discussion of subsidence on the mixing ratios in the unperturbed atmosphere; Flasar et al., 2005; Fletcher et al., 2008, 2015; Fouchet et al., 2009; Guerlet et al., 2009, 2010; Sinclair et al., 2013, 2014). The C₂H₄ profile is more complicated, and chemical production and loss of C₂H₄ cannot be ignored, so we focus on C₂H₂ and C₂H₆ for the moment. The CH₄ mixing ratio actually decreases with height, especially in the upper stratosphere, and a downwelling wind would reduce the CH₄ mixing ratio locally in the beacon, which may in turn affect derived temperatures in the spectral analyses.

Subsidence within the beacon is also consistent with the increased beacon temperatures (i.e., due to adiabatic compression of the atmosphere resulting from the subsidence). Although energy deposition from atmospheric waves may have contributed to the stratospheric heating (Fletcher et al., 2011, 2012), especially initially or outside of the vortices themselves (i.e., to the extent of 10–20 K), we can make a first-order estimate of the magnitude of the subsiding winds in the final merged beacon by assuming that the observed temperature increase in the beacon is entirely due to adiabatic heating, and then by solving for the wind speeds needed to produce this temperature increase. In other words, we assume that the adiabatic heating (e.g., Holton, 1979, p. 52) is balanced by radiative relaxation:

$$w\left(\frac{dT}{dz}+\frac{g}{c_p}\right)=\frac{T-T_b}{{\tau }_{rad}}$$ (5)

where w is the vertical velocity, T is the unperturbed atmospheric temperature, g is the gravitational acceleration, c_p is the specific heat at constant pressure, T_b is the beacon temperature, and ˝_rad is the radiative time constant, all which are functions of altitude z. Given the observed T_b and T, we can solve for w.

The only difficult term to handle in Eq. (5) is τ_rad. Conrath et al. (1990) determine that the globally and annually averaged τ_rad is approximately 3 × 10⁸ seconds (almost 10 yrs) in the mbar region of Saturn. However, actual temperature-evolution observations and more recent models (Fletcher et al., 2007, 2010; Fouchet et al., 2008; Greathouse et al., 2008; Guerlet et al., 2009, 2010, 2014; Friedson and Moses, 2012; Sinclair et al., 2013, 2014) suggest that stratospheric cooling times may be shorter than this value, and τ_rad likely decreases more rapidly with height than is described in Fig. 2 of Conrath et al. (1990) because the mixing ratios of major coolants like C₂H₂ and C₂H₆ are increasing with height, whereas Conrath et al. (1990) assumed profiles that are constant with height. From the Friedson and Moses (2012) general circulation model (GCM), we note that a roughly −0.027 cm s⁻¹ wind at 1 mbar at 25° N latitude (Fig. 9 of Friedson and Moses 2012) results in a temperature increase from ~137 K to ~142 K (Fig. 5 of Friedson and Moses 2012). Plugging this information back into Eq. (5) and solving for τ_rad gives us ~3 × 10⁷ seconds. However, τ_rad will strongly depend on the emission temperature: τ_rad = T/ (dT/dt), and dT/dt ∝ T⁴, so τ_rad ∝ 1/T³. Using the results from the Friedson and Moses (2012) GCM situation described above, we can estimate τ_rad = 3 × 10⁷ (142 K/T_b)³ seconds. At the elevated temperatures of the beacon, τ_rad is considerably shorter than the nominal radiative time constant of the unperturbed atmosphere. For example, at the beacon maximum temperature of ~220 K, the radiative time constant is just 3 months.

When we solve Eq. (5) for w, using the CIRS-derived thermal structure and the temperature- and altitude-dependent τ_rad, we derive the vertical wind profile shown in Fig. 12. The resulting winds exhibit upwelling in the troposphere (see also Fletcher et al., 2011) and strong, but narrowly focused, downwelling in the stratosphere, with a peak magnitude of roughly −1 cm s⁻¹ centered at ~2 mbar. While a −1 cm s⁻¹ vertical wind in the stratosphere is very strong by terrestrial standards, we will show that such a wind velocity is not sufficient to transport the necessary amount of C₂H₂ and C₂H₆ from higher altitudes (p ≲ 0.1 mbar) to the mbar region, where these species are observed to be enhanced in the beacon on May 4, 2011. Moreover, the overall profile is not consistent with the steady 1-D continuity equation for the total atmospheric density, d/dz(n_a w) = 0, which would require the vertical wind to be proportional to 1/n_a, such that the magnitude of the downwelling wind exponentially increases with height. The stratospheric region below the wind peak in Fig. 12 roughly exhibits this behavior, while the implied winds above the ~2 mbar peak do not, indicating that horizontal winds are important in conserving mass in the beacon at higher altitudes. Although the relatively short radiative time scale τ_rad ≈ 3 months at the maximum 2-mbar beacon temperature in May 2011 (five months after the storm onset, less than 1 month after the merger) could be contributing to the situation such that some of the excess energy from potentially higher temperatures at high altitudes could have radiated away before the May observations, the overall shape of the derived wind profile in Fig. 12 suggests that the vertical winds do not extend indefinitely in altitude. Instead, horizontal winds could be converging toward the beacon center at high altitudes, followed by vertical descent through the mbar region, with diverging winds being present at lower altitudes.

Figure 12:

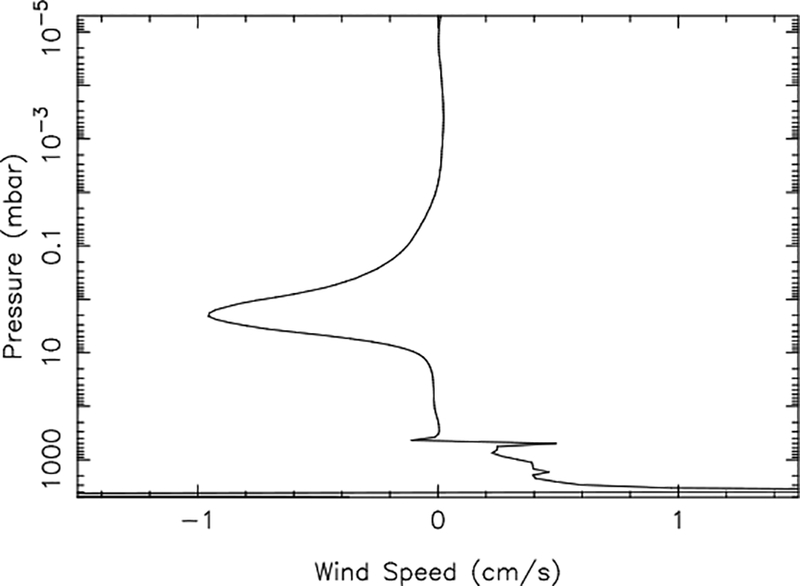
The wind profile derived from the assumption that the adiabatic heating in the beacon is balanced by radiative cooling (e.g., Eq. 5; solid line), using the CIRS-retrieved temperatures to define the radiative relaxation term.

In any case, we can use the above concepts to help us explore the possible effects of strong downwelling winds on the species abundances in the beacon. The inclusion of vertical winds that are proportional to 1/n_a, which is required for the continuity of the total density in 1-D, causes major instability problems with KINETICS. We therefore solve Eq. (4) for chemically long-lived species outside of KINETICS, using finite-difference techniques with the Lax method (e.g., Press et al., 1986). Fig. 13 shows the solution for a wind profile that varies as w(z) = w(0)n_a(0)/n_a(z), where w(0) = −1.0 cm s⁻¹, n_a(0) = 6.8 × 10¹⁶ cm⁻³ at p(0) = 2 mbar. The wind is assumed to be constant with time and is applied for 25 days (for consistency with the KINETICS beacon model for the May 4, 2011 date), with boundary conditions of dq_i/dz = 0 (i.e., constant flux in this 1-D description, allowing the species to flow through the boundaries) and initial species profiles given by the pre-storm KINETICS results shown in Fig. 6. Although the results are sensitive to the boundary conditions, the assumed vertical extent of the atmosphere, and the time scale over which the winds are applied, Fig. 13 shows that a subsiding wind acts to redistribute the species from high altitudes to lower altitudes. Because the mixing-ratio profiles for C₂H₂ and C₂H₆ are positive in this region, the mixing ratios of C₂H₂ and C₂H₆ increase at mbar pressures within the beacon, while the CH₄ mixing ratio decreases. From exploring various wind profiles that are proportional to 1/n_a, we find that the beacon-core observations from May 4, 2011 are best reproduced when winds are of order −10 cm s⁻¹ in the 0.1–0.3 mbar region.

Figure 13:

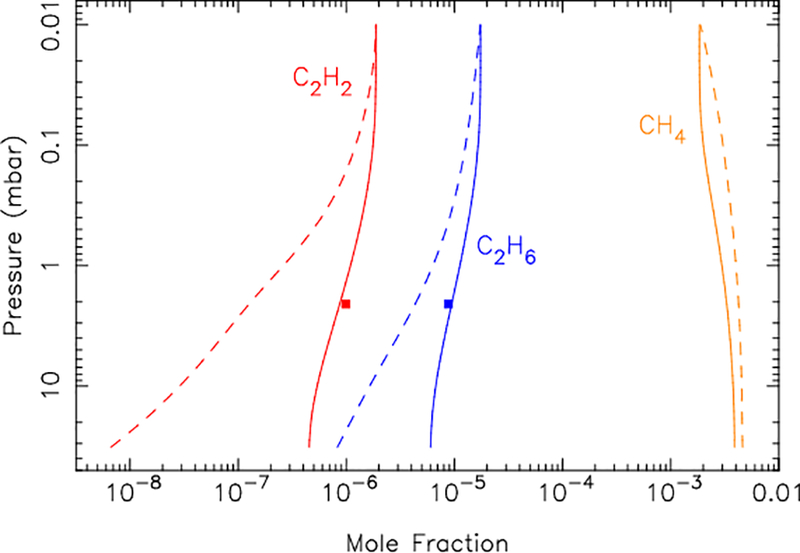
The vertical profiles of the chemically long-lived species CH₄ (orange), C₂H₂ (red), and C₂H₆ (blue) in the hot beacon core on May 4, 2011 determined from our photochemical model without winds (dashed lines) and determined from solving Eq. (4) outside of KINETICS, for an assumed downwelling wind that increases exponentially with height: w(z) = −6.84 × 10¹⁶ cm⁻³/n_a(z), where n_a(z) is the atmospheric density at altitude z (solid lines). Note that the wind approaches −10 cm/s at ~0.15 mbar. The colored squares are our retrieved abundances for C₂H₂ (red) and C₂H₆ (blue) from the CIRS spectra acquired on that date.

However, the wind profile inferred from the adiabatic heating (e.g., Fig. 12) implies that the downwelling wind speeds do not increase exponentially with height indefinitely within the upper stratosphere. There is a limit to the vertical extent of the beacon, and horizontal winds must dominate at some point in the upper stratosphere. Fig. 14 shows the results for C₂H₂ and C₂H₆ when we include a Gaussian-shaped downward wind in log(P) space with a peak magnitude of −10 cm s⁻¹ centered at log₁₀(P mbar) = −0.5, with a standard deviation of log₁₀(P mbar) = 0.8. Our assumptions for the finite-difference model are the same as the previous case, with one exception — because the vertical winds do not extend to higher and lower altitudes, we assume that the species mixing ratios remain fixed at their initial values at the boundaries. Again, the downwelling winds transport the species from higher to lower altitudes, and the C₂H₂ and C₂H₆ mixing ratios thus increase in the beacon in the presence of these winds, whereas the CH₄ mixing ratio decreases. Downwelling winds of order −10 cm s⁻¹ at ~0.1–0.3 mbar are again required to transport sufficient C₂H₂ and C₂H₆ to the ~2 mbar region to explain the elevated beacon-core abundances from May 4, 2011; that is, other wind profiles that fulfill this criterion provide similar results. The main advantage of the Gaussian wind profile is that it mitigates the severe instability problems that plague the inverse-density wind profile within the KINETICS code, so we can use KINETICS to study how the downwelling winds affect all species, including those with short chemical lifetimes. The main disadvantage is that the Gaussian profile violates the 1-D continuity equations for total density, and horizontal winds must be present to maintain mass conservation. The only way we can justify the use of the Gaussian vertical wind profile in the 1-D photochemical model is to demonstrate that the vertical advection term dominates over the horizontal advection term in the continuity equation.

Figure 14:

The vertical profiles of the chemically long-lived species CH₄ (orange), C₂H₂ (red), and C₂H₆ (blue) in in the hot beacon core on May 4, 2011 determined from our photochemical model without winds (dashed lines) and determined from solving Eq. (4) outside of KINETICS, for an assumed Gaussian downwelling wind with a peak wind speed of −10 cm s⁻¹ at 10^−0.5 mbar (see text). The colored squares are our retrieved abundances for C₂H₂ (red) and C₂H₆ (blue) from the CIRS spectra acquired on that date.

To pursue this justification, we examine the density continuity equation assuming the beacon exhibits cylindrical symmetry, such that the continuity equation for the total atmospheric density becomes:

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r{v}_r\right)+\frac{\partial w}{\partial z}+\frac{w}{n_a}\frac{\partial n_a}{\partial z}=0,$$ (6)

where r is the radial distance, v_r is the velocity in the radial direction, w is the vertical velocity, n_a is the total atmospheric density, and z is the altitude. Right at the Gaussian wind maximum, ∂w/∂z = 0, so v_r ~ w_max r/2H_d, where H_d is the density scale height and w_max is the maximum wind speed. If we go back to Eq. (3) in the cylindrical coordinate system now and assume eddy diffusion and chemistry have a negligible influence, then Eq. (3) becomes

$$\frac{\partial q_i}{\partial t}+v_r\frac{\partial q_i}{\partial r}+w\frac{\partial q_i}{\partial z}=0.$$ (7)

We can compare the magnitude of the radial horizontal advection term | v_r ∂q_i/∂r| with the vertical advection term |w ∂q_i/∂z|. Using the longitudinally resolved species scaling factors to determine ∂q_i/∂r near the beacon center, considering a distance r as the average of the nearest longitude points from the beacon center for which we have retrievals (e.g., see Fig. 7), and considering the pressure at which the Gaussian wind has its maximum, we find that the vertical advection term is indeed much stronger than the horizontal advection term at the beacon center:

$$\left|v_r\frac{\partial q_i}{\partial r}\right|=\left|\left(\frac{w_{max}r}{2H_d}\right)\frac{\partial q_i}{\partial r}\right|\ll \left|w_{max}\frac{\partial q_i}{\partial z}\right|$$ (8)

for both C₂H₂ and C₂H₆ near the beacon center, so the vertical advection dominates. In fact, using Eq. (7) to define v_r at any altitude near the beacon center, we can show that |w ∂q_i/∂z| dominates over horizontal advection up to 0.01 mbar and beyond for our assumed Gaussian profile, so we are justified in considering this vertical wind profile in our 1-D calculations.

We therefore proceed with considering Gaussian wind profiles within our 1-D photochemical model. We continue to solve the continuity equations from Eq. (1) with KINETICS, but we now include the vertical wind term in the flux equation (Eq. 2). The vertical winds are introduced only at the point when the model switches to the thermal structure for the May 4, 2011 date, which happens on April 9, 2011, roughly coincident with the beacon merger. When we include the weaker, roughly Gaussian, wind profile calculated from the adiabatic heating (see Fig. 12 and Eq. 5), the resulting C₂H₂ and C₂H₆ mole fractions are only slightly increased in the mbar region, suggesting, as expected, that winds that are about an order of magnitude stronger are needed to explain the chemical abundances in the beacon.

Figure 15 shows the results for the C₂H_x species when we include the stronger Gaussian winds considered in the finite-difference calculations described earlier; i.e., a Gaussian downward wind in log(P) space with a peak magnitude of −10 cm s⁻¹ centered at log₁₀(P mbar) = −0.5, with a standard deviation of log₁₀(P mbar) = 0.8. The eddy diffusion coefficient is not changed from the nominal model, but the transport time scale due to these stronger winds is much shorter than the diffusion time scale in the mbar region, so the downwelling winds very effectively transport the C₂H_x from high altitudes to lower altitudes, increasing the local mole fractions in the mbar region. Note that because the unperturbed C₂H₂ mixing-ratio gradient in the mbar region is greater than that for C₂H₆ (see Fig. 15), the local C₂H₂ abundance increases more significantly than that of C₂H₆ when the subsiding winds are included (recall Eq. 4). In contrast, the main effect of the winds on C₂H₄ is to “push” the local mixing-ratio peak downward, making it deeper but narrower. Note that because CH₄ has a negative mixing-ratio gradient, the subsiding winds actually deplete the local CH₄ mixing ratio in the mbar region, which in turn affects the retrieved temperatures. The results shown in Fig. 15 have been through one additional iteration in which we re-retrieved the thermal structure in the hot-beacon core using the initial wind-model species profiles as priors, and then we adopted the resulting retrieved thermal structure for a final beacon model with the winds imposed. Additional tests indicated that further iterations were unnecessary because the retrieved temperatures and hydrocarbon abundances converged on the same solution. The new retrieved “wind-derived” thermal structure for the hot beacon core is cooler by ~7 K at 1 mbar and warmer by ~ 7 K at 5 mbar; in essence, the winds shown in Fig. 15 caused the peak temperatures to migrate downward in altitude.

Figure 15:

(Top) The vertical wind profile from Fig. 12 (solid line), compared to an assumed Gaussian wind profile with a peak magnitude of −10 cm s⁻¹ (dotted line). (Bot tom) Same as Fig. 6, except the green curves represent the nominal pre-storm model, the red curves represent the nominal post-storm model for the hot beacon core on May 4, 2011, and the dotted black curves represent this same beacon-core model, but now with the dotted-line Gaussian vertical winds from the top panel included in the calculations. Note that the model with downwelling winds produces a much better fit to the retrieved post-storm species abundances (red squares).

The multiplicative factors by which the wind-model species vertical profiles need to be scaled in order to reproduce the emission in the hot beacon core on May 4, 2011 are shown in Fig. 16. In comparison with our nominal hot-core model without winds, the wind model does a much better job of reproducing the amount of C₂H₂, C₂H₄, and C₂H₆ that is needed to explain the observed CIRS emission — scaling factors at the beacon core at 294.8° System III longitude are all 1.0 ± 0.3 now for these species (cf. Figs. 7 & 16).

Figure 16:

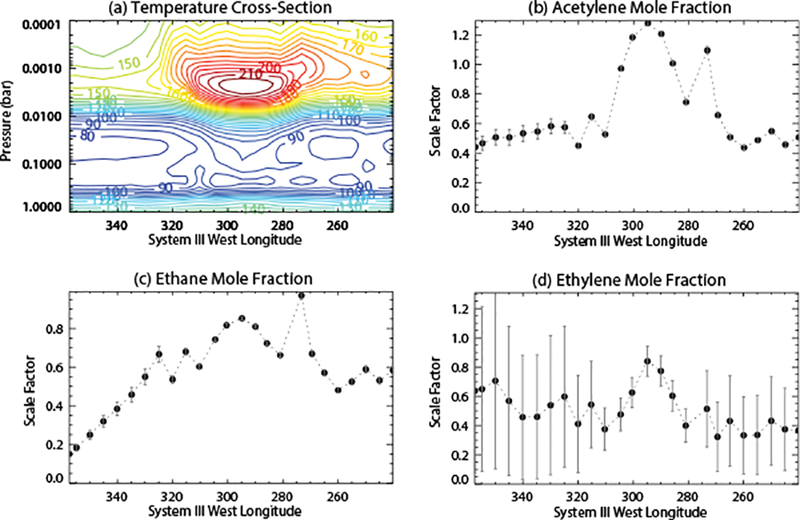
Retrievals of temperatures and hydrocarbon distributions as a function of longitude through the beacon core on May 4, 2011, following the technique used for Figure 7. However, vertically subsiding winds were added to the photochemical model to produce the predicted mixing ratio profiles that were scaled here to fit the CIRS observations. Several model iterations with different assumed wind profiles were needed before we obtained mixing ratio profiles that reproduced the CIRS emissions with only minimal (±30%) scalings in the retrieval model.

The resulting beacon-center volume mixing ratios from the CIRS spectral retrievals using the wind model profiles as priors are (9.17 ± 0.11) × 10⁻⁷ for C₂H₂, (1.86 ± 0.23) × 10⁻⁸ for C₂H₄, and (8.19 ± 0.08) × 10⁻⁶ for C₂H₆ at 2.4 mbar. The wind model actually predicts slightly too much C₂H₄ at the beacon core, and slightly too much C₂H₆, but not quite enough C₂H₂.

Although not shown in Fig. 15, the middle-stratospheric mixing-ratio peaks for CH₃C₂H and C₃H₈ are simply pushed downward in the wind model, with the overall column abundance above 10 mbar increasing only slightly. For C₄H₂, the middle-stratospheric peak also migrates downward, but given that the mixing-ratio gradient in the mbar region is large for C₄H₂ in the un- perturbed model, the downwelling winds cause a comparatively large factor of 4.5 increase in the C₄H₂ column abundance above 10 mbar in comparison with the nominal hot-beacon model without winds (or an overall increase of a factor of 2.2 in comparison with the cooler pre-storm column abundance). The subsiding winds also have an interesting effect on the oxygen species, whose source is external material deposited at high altitudes. In comparison with the pre-storm column abundances, the post-storm column abundance above 30 mbar has increased by a factor of 3.2 for CO₂ and a factor of 8.5 for H₂O (which includes the contribution from evaporation).

Judging from Fig. 16, however, it appears that the strong downwelling winds are not uniform across the beacon vortex, as the scale factors have apparent structure as a function of longitude (see also Fig. 7). Our wind model tends to notably overestimate the species’ abundances at longitudes away from the beacon center, except for an additional strong enhancement in C₂H₆ and C₂H₂ at 273° System III longitude. This feature at 273° longitude appears to be associated with a higher-altitude temperature increase (see Fig. 16a), suggesting that the strongest vertical winds were located both at 273° and at the core 295° longitude at the time of the observations, but that the winds at 273° longitude may have been confined to higher altitudes than at the beacon core. Interestingly, the C₂H₄ longitudinal cross section across the beacon does not show this same 273° feature, perhaps because the C₂H₄ abundance is not predicted to increase much due to subsiding winds in the ~0.1 mbar region, whereas C₂H₂ and C₂H₆ are (see Fig. 15). The narrower C₂H₄ central enhancement as a function of longitude better tracks the temperature structure across the beacon at ~1–5 mbar.

In fact, further analysis of the retrievals of temperature profiles and species abundances a function of latitude and longitude across the beacon could potentially illuminate the details of the 3-D dynamics within the beacon vortex, which may in turn reveal the complex dynamical coupling that was responsible for the stratospheric response in the first place. The prevailing theory for the stratospheric beacon formation is that the tropospheric convective plumes in the storm served as a source of upward-propagating planetary waves and/or gravity waves that deposited energy and momentum in the stratosphere (Fletcher et al., 2012); upwelling and divergence of air on a rotating planet will naturally cause an anticyclonic vorticity, although these waves may also have interacted with the mean flow in the stratosphere to form the observed anticyclonic beacon vortices. Because we expect C₂H₆ (and to a lesser extent C₂H₂) to be chemically stable in the beacon region, even at elevated temperatures, C₂H₆ and potentially C₂H₂ could serve as tracers of atmospheric vertical motions within the beacon(s), whereas C₂H₄ is also strongly sensitive to temperatures. Assuming chemical stability, the whole system could be potentially modeled with a 3-D mesoscale circulation model, which could provide insights into the wind fields before and after the storm event. Very little is currently known about stratospheric dynamics on Saturn, and the response to the storm could be a fertile source of information for the burgeoning stratospheric GCMs that are now being developed (e.g., Friedson and Moses, 2012; Guerlet et al., 2014).

An astute reader may notice that the original tendency of the model to overestimate the pre-storm ethane mole fraction and to underestimate the pre-storm acetylene mole fraction in comparison with the Cassini CIRS pre-storm data (see Figs. 4 & 6) is also still present (and even magnified) in the post-storm models that include vertical winds, in comparison with the post-storm CIRS data (see Figs. 13, 14, 15, & 16). Uncertainties in the chemical mechanism are likely at fault for some part of this model-data discrepancy, because the overall C₂H₂/C₂H₆ ratio is controlled in large part by chemistry (Moses et al., 2005). The effect of seasonal variations in solar insolation and/or dynamics due to large-scale stratospheric circulation may also play a role (e.g., Moses and Greathouse, 2005; Hue et al., 2015; Friedson and Moses, 2012) — neither of these effects were considered in the model presented here. The fact that the Cassini CIRS limb observations of Guerlet et al. (2009, 2010) indicate that our pre-storm model underestimates the C₂H₆ abundance at high altitudes suggests that we may be underestimating the vertical winds needed to carry sufficient amounts of C₂H₆ down to the ~mbar region to explain the May 2011 beacon observations. However, given the likely complicated 3-D nature of the problem and uncertainties in the time scales over which the winds are operating, we do not further pursue 1-D models to attempt to narrow down the necessary vertical wind magnitudes for an assumed initial C₂H₆ vertical profile that follows the Guerlet et al. (2009, 2010) retrieved profile.

5. Comparison with CIRS Spectra

In Fig. 17, we demonstrate how synthetic spectra generated from the photochemical model results compare with the CIRS beacon observations from May 4, 2011. The green curves show the results from the pre-storm photochemical model. Although this model compares well with CIRS spectra acquired 4–5 months before the 2010 storm event, the predicted molecular emission features clearly fall far short of the observed intensities in the beacon — illustrating why the high-temperature air masses were nicknamed “beacons” in the first place. The purple curves show the synthetic emission assuming that the molecular abundances remain at these pre-storm model values, but assuming that the temperature profile follows that from the CIRS retrievals from the May 4, 2011 beacon core. From a comparison of the purple-curve emission intensity with that of the observations, one can see that the increased temperatures alone cannot explain the observed emission intensities in the C₂H_x molecular bands. The beacon is clearly characterized by both increased temperatures and increased C₂H_x abundances. The red curve shows the predicted emission from our hot-beacon core model with no vertical winds (e.g., see Fig. 6). The temperature-dependent chemistry in the beacon region has led to an increase in the C₂H₄ abundance in this model, but the emission in the C₂H₄ band near 950 cm⁻¹ is still clearly underpredicted. Similarly, because the photochemical model predicts little change in the C₂H₂ and C₂H₆ abundances due to high-temperature chemistry in the beacon, there is little difference between the red and purple synthetic emission curves for these species.

Figure 17:

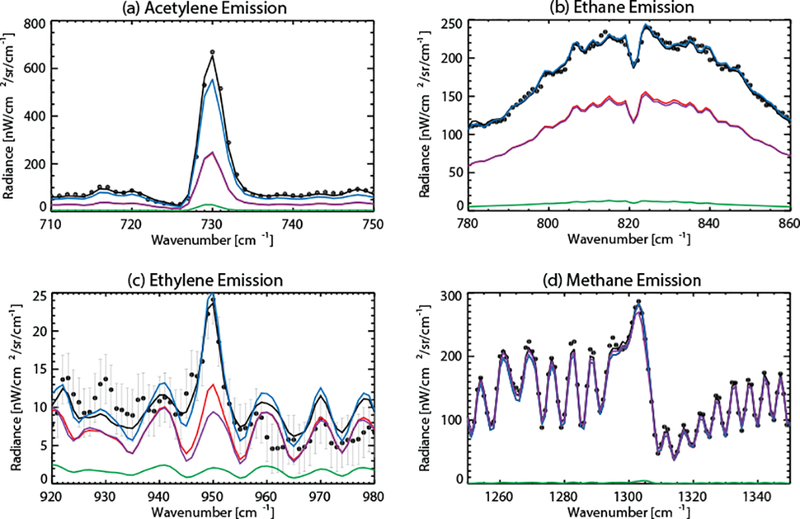
CIRS spectra (dots with error bars) from May 4, 2011, averaged over ±5° longitude surrounding the beacon core at 294.8°W, and between 36 – 43°N latitude, compared to a series of synthetic spectra. The red line shows emission based on our nominal hot beacon-core model with no winds, and with no scaling of hydrocarbon profiles (see Fig. 6). The black line is our best-fitting model for the beacon core (in this case from scaling the hydrocarbon profiles with the beacon-center scaling factors shown in Fig. 16, associated with the predictions of the photochemical model that considers the Gaussian downwelling wind profile from Fig. 15); the blue line shows emission based on this same wind model, but with no scaling of hydrocarbon profiles. The green line is the best fitting pre-storm model for latitude 40°N. The purple line shows emission based on this same pre-storm model, but with temperatures matching those retrieved from the beacon, to demonstrate that (i) temperature variations alone cannot provide a good fit the hydrocarbon emission features and that (ii) ethylene experiences the largest differences in emission based on temperature-dependent chemistry alone (i.e., difference between the red and purple lines).

The blue curves in Fig. 17 represent the synthetic spectra predicted from our hot-beacon core model with the Gaussian-profile downwelling winds described in Fig. 15. This wind-aided model clearly provides a much better fit to the data, although the model slightly underpredicts the C₂H₂ emission and slightly overpredicts the C₂H₄ and C₂H₆ emission. The best fit (black curves) occurs when we allow NEMESIS to scale the hydrocarbon profiles by the scale factors at the beacon-center longitude, shown in Fig. 16. Note that our favored wind profile is by no means unique; other wind profiles that consider winds of roughly −10 cm s⁻¹ in the ~0.1–0.3 mbar region produce similar results. However, from a comparison of the red and blue curves with the observational data it is clear here that both high-temperature chemistry and strong downwelling winds are needed to reproduce the C₂H_x emission features observed in the beacon in May 2011.

6. Conclusions

Although Saturn’s gigantic northern-hemisphere storm of 2010–2011 generated obvious changes in tropospheric cloud structure and dynamics in the weeks and months following the outburst (Sánchez-Lavega et al., 2011, 2012; Sayanagi et al., 2013), the more unexpected consequence has been a radical and long-lived change in the dynamics, energetics, and chemistry of the stratosphere. Detailed analyses of these stratospheric changes can shed new light on the complex coupling of physical and chemical processes throughout the atmosphere.

We have used a photochemical model to track the expected evolution of the stratospheric hydrocarbon and oxygen species in the anticyclonic vortex “beacons” that formed in Saturn’s northern-hemisphere stratosphere after the eruption of this massive storm system. We start from a fully converged 1-D stratospheric photochemical model for the appropriate northern mid-latitude region, and then allow the temperature and density structure in the model to change with time as described by the Fletcher et al. (2012) Cassini/CIRS observational retrievals of the thermal structure within the

initial beacon “B1” and the final single beacon “B0” after the two initial beacons merged sometime in April 2011. From our photochemical models that consider the increased temperatures in the beacon but no corresponding changes in the dynamics of the region, we obtain the following results:

• The beacon models predict a large factor of 7 increase in the C2H4 mole fraction in a localized middle-stratospheric peak centered at ~0.4 mbar within 5 months of the storm onset, resulting solely from the increased temperatures within the beacon regions (see Fig. 6).

• The large predicted increase in C2H4 in our models is caused by the strong temperature dependence of the reaction C2H3 + H2 → C2H4 +H. Although laboratory measurements of the rate coefficient for this reaction are challenging at room temperature and below, more definitive information at low temperatures is needed before we can make quantitative predictions regarding the expected C2H4 abundance in the beacon, and before we can fully understand C2H4 chemistry both within Saturn’s beacon regions and at ambient conditions on all the giant planets.

• In contrast to C2H4, our photochemical models predict little or no change in the stratospheric mixing ratios of the longer-lived hydrocarbons C2H2, C2H6, and C3H8 due to the beacon-temperature increase alone, whereas the mixing ratios of the less chemically stable species CH3C2H and C4H2 decrease with time in the ~10–10−2 mbar region as a result of the elevated temperatures (see also Cavalié et al., 2015).

• Constituents that condense in Saturn’s lower stratosphere, such as C4H2, C6H6, and H2O (the latter from external sources) exhibit strong increases in abundance in the beacons at pressures greater than a few mbar due to the evaporation of icy aerosols.

• The evaporation of C4H2-bearing ices is a particularly interesting result and could lead to a large local “spike” in the gas-phase C4H2 abundance at depth because the in situ production of C4H2 has made condensed C4H2 a major local sink of carbon in the pre-storm model, and conversion back to C2H2 and other hydrocarbons once the C4H2 evaporates is not instantaneous. The predicted clearing of the lower-stratospheric hazes (which are optically thin under normal undisturbed conditions) may be observable when the beacon features are near the planetary limb.

• The increased temperatures alone in the beacon cannot explain the C2Hx band emission intensities observed by Cassini CIRS in May 2011, just after the beacon merger. Our beacon model with the temperature increase alone (and no winds) underestimates the C2H4 abundance in the hot central core of the beacon on May 4, 2011 by a factor of ~3.5, and underestimates the abundance of C2H2 and C2H6 by factors of ~ 7.5 and ~2, respectively (see Fig. 7).

• If the inferred beacon increases in the abundance of C2H2, C2H4, and C2H6 (see also Hesman et al., 2012, 2014) were due to chemistry alone, the carbon would have had to have originated in CH4, as methane is the only local source of carbon large enough to explain the observed increases (e.g., Figs. 6 & 7). We could identify no temperature-dependent loss reaction for CH4 in the middle stratosphere that is effective enough on the time scales involved to produce the observed increase in C2Hx hydrocarbon abundances. We therefore conclude that vertical winds are contributing to the observed hydrocarbon increases in Saturn’s beacon regions.

Our results considering the effects of temperature changes alone are qualitatively consistent with those of Cavalié et al. (2015), except that we predict a larger increase in the C₂H₄ abundance (our factor of 7 versus their factor of ~3), and Cavalié et al. do not mention effects due to evaporation of lower-stratospheric aerosols.

In Section 4.5, we demonstrate that the observed increase in C₂H₂, C₂H₄, and C₂H₆ in the beacon is best explained both by altered chemistry due to the increased beacon temperatures and by strong descent of air in the middle stratosphere within the beacon. We also discuss the magnitude of the subsiding winds that are implied by the observations. The main results from our photochemical models that include vertical winds in the merged beacon are the following:

• Downwelling winds of order −10 cm s⁻¹ in the ~0.1–0.3 mbar region are needed to carry the necessary amounts of C₂H₂ and C₂H₆ from higher altitudes, where the primary chemical production regions reside and where the C₂H₂ and C₂H₆ mixing ratios are larger, to the ~1–5 mbar pressure region, where the C₂H_x mixing ratios were observed to increase.

• When we include downwelling winds of the appropriate magnitude in our 1-D photochemical model, the resulting C₂H₂, C₂H₄, and C₂H₆ profiles are within 30% of the abundances needed to reproduce the observed CIRS emission within the core of the merged beacon on May 4, 2011 (see Figs. 15 & 16).

• The resulting volume mixing ratios derived from CIRS spectral retrievals from the observations of the beacon center on May 4, 2011 are (9.17 ± 0.11) × 10⁻⁷ for C₂H₂, (1.86 ± 0.23) × 10⁻⁸ for C₂H₄, and (8.19 ± 0.08) × 10⁻⁶ for C₂H₆ at 2.4 mbar.

• The corresponding inferred abundance increases above pre-storm values are a factor of 7.6 for C₂H₂ and 2.2 for C₂H₆ based on CIRS observations alone, and a factor of ~25 for C₂H₄ based on the pre-storm photochemical model in comparison with CIRS beacon observations (i.e, C₂H₄ was not detected in the CIRS observations before the storm).

• Because the unperturbed CH₄ mixing-ratio gradient decreases with height due to molecular diffusion in the upper stratosphere, the down-welling winds cause a depletion of CH₄ within the beacon model (see Fig. 15). This tendency complicates retrievals of the thermal structure within the beacon, given that using the observed emission within the v₄ band of methane is a typical way of deriving the stratospheric temperatures — one can no longer assume that the CH₄ mixing-ratio profile is well known within the beacon, and model-data iterations are needed to ensure a consistent solution in terms of both the temperature and hydrocarbon profiles.

• The subsiding wind can also affect oxygen species like CO₂ and H₂O, whose source is presumed to be external to the planet (Feuchtgruber et al., 1997, 1999; Moses et al., 2000b; Bergin et al., 2000; Hartogh et al., 2011; Fleshman et al., 2012). Our model that includes down-welling winds predicts a factor 3.2 and 8.5 increase, respectively, in the column abundance of CO₂ and H₂O above 30 mbar in comparison with the pre-storm model abundances. These predictions are testable with further analysis of CIRS observations of hydrocarbons and CO₂ within the beacon region (e.g., Hesman et al., 2014) and of H₂O in the beacon from longer wavelength Herschel and Cassini observations (e.g., Cavalié et al., 2012; Bjoraker et al., 2014).

• Our photochemical model with winds included also predicts a factor of 2.2 increase in the column abundance of C₄H₂ above 10 mbar, but only a minor increase in the column abundances of C₃H₈ and CH₃C₂H.

• As with the photochemical model without winds, our wind model predicts that evaporation of icy C₄H₂, H₂O, and C₆H₆ aerosols in the lower stratosphere at the elevated beacon temperatures should cause a localized clearing or thinning of the stratospheric haze. The predicted increased gas-phase abundances in the lower stratosphere due to evaporation of these aerosols are likely too deep to affect the CIRS emission spectra, but the clearing of the stratospheric aerosol layer may affect the scattering behavior in Cassini visible and ultraviolet images (and at near-infrared wavelengths in regions where methane strongly absorbs), particularly at high phase angles, and the increased C₄H₂ abundance at depth may affect the ultraviolet spectra within the beacon region, in comparison with regions outside the beacon. These potential effects are worth further investigation.

Our model results were compared only with the Cassini CIRS observations. Our resulting inferred vertical profile for C₂H₄ from our wind-aided model differs from that derived by Hesman et al. (2012) for the May 2011 beacon from observations both from Cassini/CIRS (see Fig. 8) and from ground-based observations with the Celeste instrument. However, both analyses predict a similar C₂H₄ mole fraction at the ~2 mbar region, where the contribution function for the C₂H₄ emission band has a maximum. The C₂H₄ emission from the 2.5 cm⁻¹ resolution CIRS data are less sensitive to the higher-altitude ~0.5 mbar region where Hesman et al. (2012) derive a large localized maximum in the C₂H₄ mixing-ratio. Our solution does not require such a large peak; however, it remains to be seen whether our preferred C₂H₄ profile is consistent with the higher-spectral-resolution Celeste observations of Hesman et al. (2012). Future investigations comparing our model predictions with the Celeste data and with other ground-based high-spectral-resolution observations, such as those obtained with the TEXES instrument (e.g., Fouchet et al., 2013), would provide useful tests of the models. Note that the very large peak abundance (volume mixing ratio of nearly 10⁻⁵) at ~0.1 mbar from the Hesman et al. (2012) Celeste retrieval (see their Fig. 5) would be particularly difficult to explain photochemically, as C₂H₄ photo-chemical production in that pressure region is not very strong, and subsiding winds cannot explain such an abundance because the high-altitude C₂H₄ mixing ratios never reach such large values.

Our model provides a solution consistent with known physical and chemical principles, within the limitations of model parameter uncertainties. Our conclusion that the air within the beacon is subsiding is reasonable for anticyclonic vortices, but the magnitude of the necessary downwelling is larger than is expected based on the observed increased temperatures if adiabatic compression were responsible for the heating (see Section 4.5 and Eq. 7). A −10 cm s⁻¹ downwelling wind is also much larger than typical stratospheric subsiding winds on Earth or those predicted for the giant planets due to residual (diabatic) circulation (e.g., Andrews et al., 1987; Conrath et al., 1990; Friedson and Moses, 2012). However, some apparently similar extreme downwellings do occur in the middle atmospheres of terrestrial planets. For example, from temperature measurements from solar and stellar occultations with the SPICAV/SOIR spectrometers on Venus Express, Bertaux et al. (2007) inferred a downwelling wind of −43 cm s⁻¹ on the night side of Venus at 90–100 km as a result of the subsolar-to-antisolar flow in the Venus upper atmosphere. Another example is the so-called “stratospheric sudden warming” (SSW) events on Earth (e.g., Matsuno, 1971; Andrews et al., 1987), where descent rates as large as −1 to −5 cm s⁻¹ have been inferred in the middle atmosphere (e.g., Holt et al., 2013; Bailey et al., 2014). These SSW events are marked by very rapid temperature increases in the high-latitude winter hemisphere caused by enhanced downwelling. The downwelling in turn is triggered by the dissipation of large-amplitude, planetary-scale waves that are generated in the troposphere and propagate upwards to the stratosphere, where they interact with the mean zonal flow, causing deceleration and even reversal of the polar-night jet that surrounds the polar vortex. Although the Saturn beacons are not high-latitude features, they too may have been caused by upward-propagating storm-generated waves interacting with the mean stratospheric circulation (e.g., Fletcher et al., 2012).

Future work should include 3-D dynamical modeling of the beacon systems. The Saturn storm beacons are inherently 3-D dynamical phenomena that would be best studied with mesoscale circulation models, particularly in terms of investigating how the anticyclonic stratospheric vortices formed and evolved in the months following the 2010 tropospheric convective outburst. Given the chemical stability of C₂H₆, and to a lesser extent C₂H₂, these species could act as useful tracers to diagnose winds within the beacon — their chemistry over the lifetime of the beacon can be ignored to first order.

The stratospheric beacons were an intriguing and unexpected consequence of the gigantic 2010–2011 convective outburst on Saturn. Studying the underlying factors controlling the evolution of the beacon temperatures and chemical-constituent abundances can further our knowledge of dynamical coupling between the troposphere and stratosphere, the mean wind fields within the unperturbed and perturbed stratosphere, the energetics and long-term energy balance of the atmosphere, and the dominant chemical processes both within the unperturbed and beacon stratospheric environments.