Dust Ablation on the Giant Planets: Consequences for Stratospheric Photochemistry

Abstract

Ablation of interplanetary dust supplies oxygen to the upper atmospheres of Jupiter, Saturn, Uranus, and Neptune. Using recent dynamical model predictions for the dust influx rates to the giant planets (Poppe, A.R. et al. [2016], Icarus 264, 369), we calculate the ablation profiles and investigate the subsequent coupled oxygen-hydrocarbon neutral photochemistry in the stratospheres of these planets. We find that dust grains from the Edgeworth-Kuiper Belt, Jupiter-family comets, and Oort-cloud comets supply an effective oxygen influx rate of ${1.0}_{-0.7}^{+2.2}\times {10}^7$ O atoms cm⁻² s⁻¹ to Jupiter, ${7.4}_{-5.1}^{+16}\times {10}^4$ cm⁻² s⁻¹ to Saturn, ${8.9}_{-6.1}^{+19}\times {10}^4$ cm⁻² s⁻¹ to Uranus, and ${7.5}_{-5.1}^{+16}\times {10}^5$ cm⁻² s⁻¹ to Neptune. The fate of the ablated oxygen depends in part on the molecular/atomic form of the initially delivered products, and on the altitude at which it was deposited. The dominant stratospheric products are CO, H₂O, and CO₂, which are relatively stable photochemically. Model-data comparisons suggest that interplanetary dust grains deliver an important component of the external oxygen to Jupiter and Uranus but fall far short of the amount needed to explain the CO abundance currently seen in the middle stratospheres of Saturn and Neptune. Our results are consistent with the theory that all of the giant planets have experienced large cometary impacts within the last few hundred years. Our results also suggest that the low background H₂O abundance in Jupiter’s stratosphere is indicative of effective conversion of meteoric oxygen to CO during or immediately after the ablation process — photochemistry alone cannot efficiently convert the H₂O into CO on the giant planets.

1. Introduction

Small interplanetary dust grains are continually showering down into the atmospheres of solar-system planets. This dust originates from the disruption and outgassing of comets, from impacts and collisions between objects of various sizes (particularly from mutual collisions within the asteroid belt and Edgeworth-Kuiper belt), from particles ejected from active plumes on satellites such as Io, Enceladus, and Triton, and from interstellar dust particles streaming into the solar system. Beyond Jupiter’s orbit, the main progenitors are the Edgeworth-Kuiper belt, long-period Oort-cloud comets, and short-period Jupiter-family and Halley-type comets (e.g., Stern, 1996; Yamamoto and Mukai, 1998; Landgraf et al., 2002; Poppe, 2015, 2016), and the particles likely contain ices, along with silicate and organic material. As the dust grains spiral in through the outer solar system, they are affected by gravity from the Sun and planets, solar wind and Poynting-Robertson drag, stellar radiation pressure, and collisions (e.g., Burns et al., 1979; Gustafson, 1994; Horanyi, 1996; Liou and Zook, 1997).

Poppe (2016) recently developed a comprehensive model for the dynamical evolution and density distribution of dust grains in the outer solar system. The model considers the dominant interplanetary dust sources for the outer solar system described above, and includes the relevant physics for the dynamical and collisional evolution of the grains. In situ spacecraft measurements from the New Horizons Student Dust Counter, the Galileo Dust Detection System, and the Pioneer 10 meteoroid detector are used to constrain the model. One important byproduct of the Poppe (2016) model is a prediction of the total mass influx rate of dust grains to the giant planets.

Gravitational focusing by the planets will cause the incoming dust particles to enter the upper atmospheres of Jupiter, Saturn, Uranus, and Neptune at high velocities (Poppe, 2016), leading to full or partial ablation of the grains (Moses, 1992, 1997, 2001; Pryor et al., 1994; Moses et al., 2000b; Kim et al., 2001). This ablation introduces gas-phase metals and water to the thermospheres and stratospheres of these planets; such species would otherwise not be present in the upper atmosphere because of condensation and sequestering of the intrinsic water and metals in the deeper troposphere. The unablated or recondensed refractory component provides a source of high-altitude haze and condensation nuclei that can facilitate condensation of stratospheric hydrocarbons (Moses et al., 1992) and can alter atmospheric radiative and scattering properties (e.g., Rizk and Hunten, 1990; Pryor et al., 1994; Moses et al., 1995). The ablated metals and water can affect the chemistry and structure of the ionosphere (e.g., Connerney and Waite, 1984; Connerney, 1986; Majeed and McConnell, 1991; Cravens, 1994; Lyons, 1995; Moses and Bass, 2000; Kim et al., 2001; Grebowsky et al., 2002; Moore et al., 2004; Molina-Cuberos et al., 2008), while water and the other oxygen species can affect the neutral photochemistry and aerosol structure in the stratosphere (e.g., Moses, 1992; Moses et al., 2000b, 2005; Ollivier et al., 2000).

Sublimation from H₂O, CO, and CO₂ ices in the grains as they are heated during atmospheric entry releases these molecules directly into the atmosphere, while thermochemical reactions within the meteor trail, energetic collisions with atmospheric molecules, or subsequent photochemical interactions within the stratosphere can further process the oxygen-bearing component. For example, the ablated water can be photolyzed by ultraviolet radiation from the Sun to produce hydroxyl radicals (OH), which can react with methane photochemical products to produce CO (e.g., Prather et al., 1978; Strobel and Yung, 1979; Moses et al., 2000b, 2005; Ollivier et al., 2000), potentially diminishing the abundance of unsaturated hydrocarbon molecules such as C₂H₂ and C₂H₄ in the process (e.g., Moses et al., 2000b). The H₂O introduced from the icy component of the grains will condense at relatively high altitudes on all the giant planets, affecting the stratospheric aerosol structure and properties, while the CO₂ will condense on colder Uranus and Neptune.

Although CO has been observed in giant-planet stratospheres and is a major end product of the chemistry of the ablated vapor (see sections 3.2–3.6), it is the most volatile of the major oxygen-bearing species on the giant planets and is not expected to condense. Stratospheric CO has additional potential sources, both external and internal to the giant planets, such as large cometary impacts and/or thermochemical quenching and convective transport from the deep troposphere (Prinn and Barshay, 1977; Fegley and Lodders, 1994; Lodders and Fegley, 2002; Bézard et al., 2002; Lellouch et al., 2002, 2005, 2006, 2010; Visscher and Fegley, 2005; Visscher et al., 2010b; Hesman et al., 2007; Cavalié et al., 2008b, 2009, 2010, 2013, 2014, 2017; Luszcz-Cook and de Pater, 2013; Wang et al., 2015, 2016); water and carbon dioxide can also be delivered from cometary impacts (e.g., Lellouch, 1996; Lellouch et al., 2002). Accurately predicting the fate of the oxygen from interplanetary dust sources therefore has important implications for the bulk elemental oxygen abundance on the giant planets, the strength of convective mixing from the deep atmosphere, and the impact rates of large comets in the outer solar system. These implications, combined with the recent improved predictions for the incoming dust fluxes to Jupiter, Saturn, Uranus, and Neptune (Poppe, 2016) and new constraints on the abundance of stratospheric oxygen species from Spitzer and Herschel observations (Meadows et al., 2008; Lellouch et al., 2010; Fletcher et al., 2012; Cavalié et al., 2013, 2014; Orton et al., 2014a,b), motivate us to theoretically track the fate of the volatiles released from the ablation of interplanetary dust on the giant planets.

To determine how the dust-delivered oxygen affects stratospheric photo-chemistry on the outer planets, we first run an ablation code (see Moses, 1992, 1997) with the interplanetary dust fluxes, mass distributions, and velocity distributions from the Poppe (2016) dynamical model as input. After making assumptions about the bulk composition of the grains based on cometary dust and nucleus compositions (Greenberg and Li, 1999; Lisse et al., 2006, 2007), we then use the ablation model to calculate the mass loss and vapor release as a function of altitude from the incoming grains (see section 3.1). The resulting gas production rate profiles from the ablation process are then included as a source of oxygen species to stratospheric photochemical models (e.g., Moses et al., 2000b, 2005, 2015) that consider coupled hydrocarbon-oxygen chemistry (see sections 3.2–3.5). In sections 3.2–3.5, we compare the photochemical model results with observations and discuss the implications with respect to the origin of the observed oxygen species on each planet, and in section 4 we discuss the likely importance of thermochemistry and high-energy collisions during the meteor phase in securing the high inferred CO/H₂O ratio in the stratospheres of these planets.

2. Theoretical model description

Two main theoretical models are used for these calculations. The first is the meteoroid ablation code described in Moses (1992), with updates from Moses (1997). The second is the Caltech/JPL one-dimensional (1D) KINETICS photochemical model developed by Yuk Yung and Mark Allen (e.g., Allen et al., 1981; Yung et al., 1984), most recently updated for the giant planets by Moses et al. (2015).

The physics of meteoroid ablation has been understood for decades, at least in an idealized sense (e.g., Öpik, 1958). The interplanetary dust grains being considered here are typically much smaller than the mean free path of the atmosphere in the region in which they ablate, which puts the physics in the free-molecular-flow regime. Under such conditions, the incoming grains collide directly with individual air molecules, leading to deceleration and heating of the grains. The heating is o set by radiative and evaporative cooling and by the change in internal energy of the grains. As in Moses (1992) and Moses (1997), we assume the incoming grains are solid compact spheres (and remain spherical throughout their flight), have a uniform composition, are heated uniformly throughout their volume, and are not affected by sputtering, fragmentation, or thermal diffusion within the solid. For more sophisticated treatments, see Vondrak et al. (2008).

The physics in this case is reduced to a set of four coupled differential equations that track the evolution of an incoming dust grain’s mass, velocity, temperature, and position within the atmosphere (see equations (1)–(4) in Moses, 1992). We assume that the entry angle is 45°and remains constant throughout the particle’s flight. The grains are assumed to be composed of either pure water ice, “silicates”, or “organics”, with the incoming dust mass flux being divided such that 26% of the grains are silicate, 32% are refractory organic, and 42% are ices, based roughly on their corresponding mass fractions within cometary nuclei and dust (Greenberg and Li, 1999). The water ice and silicate material properties are taken from Moses (1992) (and references therein), except for the vapor pressures, which follow the recommendations of Moses (1997). For the organic grains, which were not considered by Moses (1992, 1997), we take the material properties somewhat arbitrarily from benzo(a)pyrene (C₂₀H₁₂), as a refractory organic that has a vaporization temperature in the appropriate 400–600 K range. The vapor pressure of the representative organic material is log₁₀ p(atm) = 9.110 − 7100/T (K) (Murray et al., 1974), with an assumed bulk density of 1.24 g cm⁻³, an assumed latent heat of sublimation of 118 kJ/mol, and an assumed specific heat of 254.8 J mol⁻¹ K⁻¹ (Roux et al., 2008). For the purposes of converting mass loss into the amount of organic vapor “molecules” injected into the atmosphere, we assume a mean molecular mass of 77 amu for the organic vapor (e.g., a single C₆H₅ organic ring), although the exact choice is unimportant, as the organic vapor is ignored in the subsequent photochemical calculations because the carbon released is a small fraction of the carbon already in the atmosphere.

Grains smaller than the wavelength of the peak emission in the Planck blackbody function do not radiate their heat efficiently (i.e., they have emissivities less than 1). If the grain materials are relatively transparent at infrared wavelengths, with a low imaginary refractive index, emissivities can drop much lower than unity, increasing the overall ablation rate (e.g., Rizk et al., 1991). We therefore calculate the emissivity from the absorption efficiency determined from Mie theory at the wavelength of maximum emission (Wien’s law) for the particle’s temperature and size at each time step in the calculations. The optical properties for the representative silicate material are taken from the “olivine with iron” case of Rizk et al. (1991), the water-ice values are from Warren (1984), and the “organic” values are from Li and Greenberg (1997).

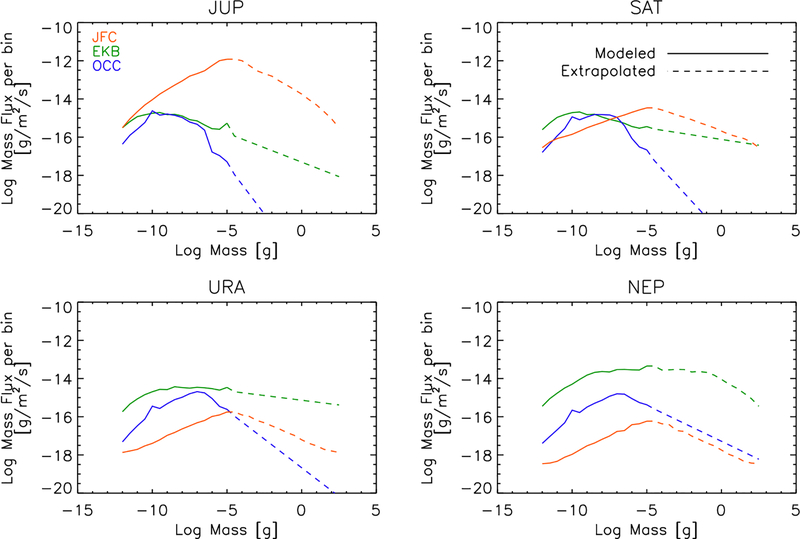
The initial mass and velocity distributions of the incoming grains are taken from Poppe (2016). The velocities vary with the particle size, source population, and the planet in question. Gravitational focusing of the interplanetary dust velocity distribution was appropriately taken into account by dynamically tracing the dust-grain trajectories from the Hill radius to the planetary exobase and recomputing the dust velocity distribution immediately before entry into the planetary atmosphere. The particle mass flux distributions for the different dominant populations — Edgeworth-Kuiper belt grains, Jupiter-family comet grains, and Oort-cloud comet grains — encountering the different planets are shown in Figs. 1, 2, & 3, as well as are provided in tables in the Supplementary Material. The contribution from Halley-type cometary grains was determined by Poppe (2016) to be a much less significant source of dust in the outer solar system and is not considered here. Due to the computational constraints associated with modeling the dynamics of large grains (which have progressively larger lifetimes), Poppe (2016) considers grain masses only up to 10⁻⁵ g (or ~100 μm radius for an assumed particle density of 2.5 g cm⁻³). Larger particles will also be present in the outer solar system, and the mass flux from these particles could constitute an important fraction of the incoming total mass flux to the planets. We therefore crudely estimate the flux from these larger particles in the following manner. First, if the mass-flux-versus-mass curve for a given population/planet possesses a well-defined peak in the 10⁻¹² to 10⁻⁵ g range, then we simply extrapolate linearly in log-space to higher masses (see, for example, the Oort cloud distributions in Fig. 1 for any of the planets). Secondly, if the mass-flux-versus-mass curve does not have a well-defined peak in the lower-mass range, we make the assumption that the peak of the mass function occurs right at 10⁻⁵ g, and we “reflect” the mass curve about 10⁻⁵ g to make a symmetric mass curve versus mass (see, for example, the Jupiter-family comet grain curves at any planet, or the Edgeworth-Kuiper belt grains at Neptune in Fig. 1). This assumption, which must remain crude as a result of the lack of constraints from actual data, is nevertheless motivated by the fact that the mass flux of interplanetary grains at 1 AU is observed to peak at ~10⁻⁵ g (e.g., Grün et al., 1985). For the velocity distribution of the extrapolated large grains, we simply adopt the velocity distribution from the 10⁻⁵ g grains from the Poppe (2016) model. Note that the velocity distributions vary only moderately with particle size, so this assumption should not be too problematic. One can see from Fig. 1 that different source populations dominate the total incoming mass flux at different planets, with Edgeworth-Kuiper belt grains strongly dominating at Neptune, Jupiter-family comet grains strongly dominating at Jupiter, and multiple sources contributing at Saturn and Uranus. Figs. 2 & 3 further show how the mass flux varies with incoming particle velocity.

Figure 1:

Total particle mass flux (g m⁻² s⁻¹) in each mass bin encountering Jupiter (Top left), Saturn (Top right), Uranus (Bottom left), and Neptune (Bottom right) at the planet’s exobase, for dust populations from Jupiter-family comets (orange), the Edgeworth-Kuiper belt (green), and Oort-Cloud comets (blue). Particles were grouped into bins based on mass, with 2 bins per decade of mass. The solid curves are from Poppe (2016), and the dashed curves were extrapolated as described in the text. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

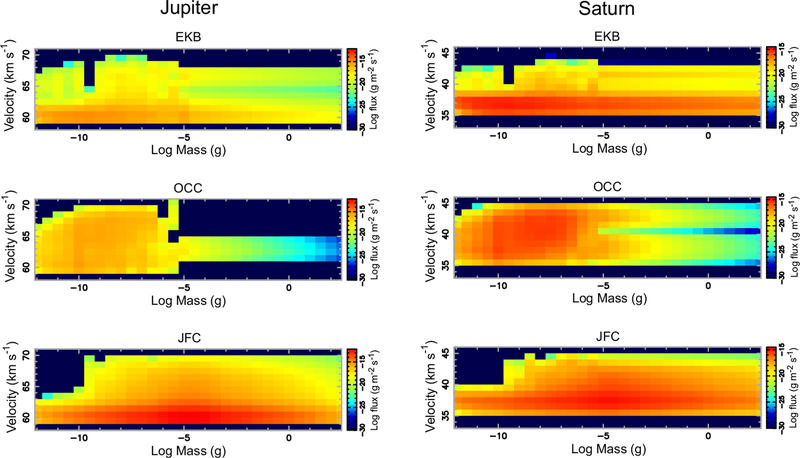
Figure 2:

Differential particle mass flux (g m⁻² s⁻¹) as a function of mass and velocity encountering the top of the atmosphere (exobase) for Jupiter (Left) and Saturn (Right), for dust populations from the Edgeworth-Kuiper belt (EKB, Top), Oort-Cloud comets (OCC, Middle), and Jupiter-family comets (JFC, Bottom). Particle fluxes of zero were assigned to 10⁻³⁰ g m⁻² s⁻¹ (dark blue) for plotting purposes on this logarithmic scale. Gravitational focusing is considered in these calculations, such that the lower limit to the particle entry velocity is the escape velocity of the planet at the exobase. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

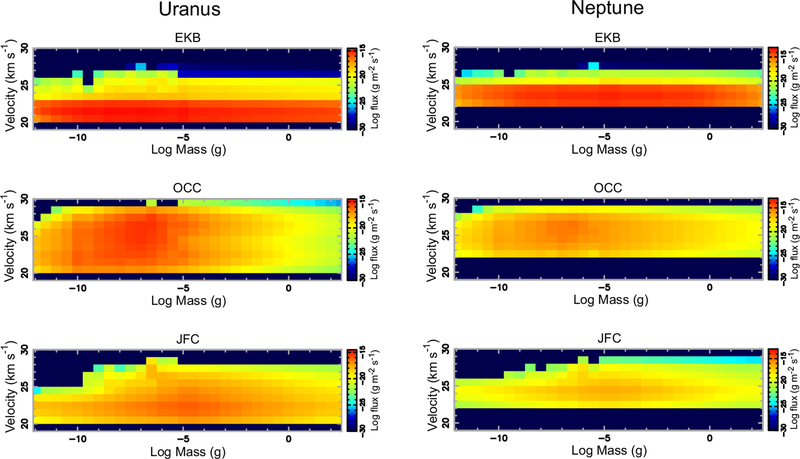
Figure 3:

Same as Fig. 2, except for Uranus (Left) and Neptune (Right).

The coupled ablation equations are solved using a fourth-order Runge Kutta technique (Press et al., 1992). The background atmospheric structure is taken from Moses et al. (2005) for Jupiter and Neptune, Moses et al. (2015) for Saturn, and Orton et al. (2014a) for Uranus; the same background structure is also used in the photochemical models.

The vapor released from the ablation process described above is then added as a source term to a steady-state, diurnally averaged, one-dimensional (1D) photochemical model for the outer planets. The photochemical model, which is based on the Caltech/JPL KINETICS code (Allen et al., 1981; Yung et al., 1984), solves the continuity equations for over 60 hydrocarbon and oxygen species as they interact via ~500 chemical reactions and are transported vertically via molecular and eddy diffusion. The use of a 1D model is justified by the fact that, to first order, the incoming dust has no preferred latitude distribution, and transport over longitudes within the atmosphere is very rapid compared with vertical settling time scales. The chemical reaction list and photolysis cross sections are taken largely from Moses et al. (2015); the rate coefficients for the non-photolysis reactions are included in the Supplementary Material. The cross sections for the photolysis reactions are discussed more fully in Moses et al. (2000a, 2005) and references therein, along with some additional recent updates (e.g., Sander et al., 2011; Hébrard et al., 2013). The photochemical models consider neutral chemistry only (no ion chemistry) and are designed to represent global-average conditions. Tropospheric nitrogen and phosphorus photochemistry is also omitted, as our main goal is to better understand the stratospheric chemistry.

The eddy diffusion coefficient profiles and other details of the models can be found in Moses et al. (2005) for Jupiter and Neptune, and Moses et al. (2015) for Saturn, as well as in the full model output in the Supplementary Material. For Uranus, we started with the eddy diffusion coefficient profile from the nominal model of Orton et al. (2014b), but the chemical reaction rate coefficients for that Orton et al. model were chosen in such a way as to optimize the high C₂H₂/C₂H₆ ratio observed for Uranus. Those rate-coefficient choices did not provide as good a fit to the C₂H₂ and C₂H₆ abundances on the other giant planets. The reaction mechanism adopted in this paper provides a better compromise for all the giant planets, although the fit to the Uranus Spitzer data is not as good as with the Orton et al. (2014b) nominal model. Our resulting adopted eddy diffusion coefficient for Uranus is 5000 cm² s⁻¹, independent of altitude, for a tropopause CH₄ mixing ratio of 1 × 10⁻⁵. The choice of the eddy diffusion coefficient profile has a minor effect on the shape of the vertical profiles for the oxygen species, the vertical diffusion time scales, and (potentially, but not necessarily) the inferred influx rates needed to fit the oxygen-species observations, but the choice does not affect any of our conclusions regarding the chemistry of the oxygen species.

Carbon monoxide is the only oxygen-bearing constituent that is assumed to have a non-negligible source from below our 5–7 bar lower model boundaries. In our nominal models, we assume a fixed CO lower-boundary mole fraction (volume mixing ratio) of 1 × 10⁻⁹ for Jupiter (Bézard et al., 2002), 1 × 10⁻⁹ for Saturn (Noll and Larson, 1990; Cavalié et al., 2009), 5 × 10⁻¹⁰ for Uranus (below the upper limit of Teanby and Irwin, 2013), and 8 × 10⁻⁸ for Neptune (Luszcz-Cook and de Pater, 2013). If the external source of oxygen were ignored, the upward flux of CO from the interior would supply some oxygen to the stratospheres of the giant planets, but in amounts insufficient to explain the observed abundances of H₂O, CO₂, and CO in the stratosphere (cf. Beer, 1975; Beer and Taylor, 1975; Larson et al., 1978; Bjoraker et al., 1986; Noll et al., 1986a, 1988, 1997; Rosenqvist et al., 1992; Marten et al., 1993, 2005; Guilloteau et al., 1993; Encrenaz et al., 1996, 2004; Courtin et al., 1996; Feuchtgruber et al., 1997, 1999; de Graauw et al., 1997; Moses et al., 2000b, 2005; Bergin et al., 2000; Bézard et al., 2002; Lellouch et al., 2002, 2005, 2006, 2010; Moreno et al., 2003; Burgdorf et al., 2006; Hesman et al., 2007; Meadows et al., 2008; Cavalié et al., 2008a, 2009, 2010, 2012, 2013, 2014; Fletcher et al., 2010b, 2012; Abbas et al., 2013; Luszcz-Cook and de Pater, 2013; Orton et al., 2014b; Irwin et al., 2014). The tropospheric CO mixing ratio has only been firmly established for Jupiter (Bézard et al., 2002), and the vertical profile has not been uniquely determined for any of the planets. However, recent observations have made it clear that the distribution of CO is not vertically uniform on any of the giant planets — the CO mixing ratio increases from the troposphere to the stratosphere, indicating an external source of CO to these planets (e.g., Bézard et al., 2002; Encrenaz et al., 2004; Lellouch et al., 2005; Cavalié et al., 2009, and more recent observations listed above).

A source of external oxygen is introduced to the stratosphere using the ablation profiles from the “ice” component of the incoming interplanetary dust grains. Although the “silicate” portion of the grains also contains a non-trivial amount of oxygen, we assume that the oxygen from silicate ablation eventually ends up back in condensed silicates once it is released in the atmosphere (e.g., the oxygen is ablated via vapor species such as SiO, which are more likely to recondense than be photolyzed to release the O). If this sequestering back into silicates does not occur or is only partially occurring, there could be an additional deeper release of oxygen that is not being considered in the models. Once the ablated oxygen-bearing vapor is released from the grain, it can be photolyzed by ultraviolet radiation from the Sun and by solar Lyman alpha photons scattered from atomic hydrogen in the interplanetary medium — the latter source (assumed isotropic in the model) becomes more important to the overall methane photochemistry the farther the planet is from the Sun (e.g., Strobel et al., 1990; Bishop et al., 1992). The oxygen species can also react with hydrocarbons produced from methane photochemistry. Water vapor is recycled fairly efficiently in giant-planet stratospheres, but coupled water-methane photochemistry can also lead to the production of CO and CO₂ (Moses et al., 2000b, 2005). Initially, we assume the ablated vapor is 100% water. However, because that assumption provides a poor fit to the stratospheric H₂O, CO₂, and CO observations for all of the giant planets, we also scale the overall influx rate and/or adjust the speciation of the ablated vapor in later models to produce a better fit. These model-data comparisons provide insight into the possible chemical processing of the oxygen that might be occurring in the meteor phase before the further processing that occurs from photochemistry.

The external oxygen species diffuse down from their high-altitude ablation source region, where they eventually encounter lower-stratospheric regions that are cold enough to cause the H₂O (all planets) and CO₂ (Uranus and Neptune) to condense. Condensation is included in the photochemical model in the manner described in (Moses et al., 2000a,b). Note that we neglect methane condensation in the photochemical models because it tends to cause annoying numerical instabilities. Because CH₄ does actually condense on Uranus and Neptune, we simply adopt the observed stratospheric mixing ratios at the lower boundary of these models in order to have appropriate stratospheric CH₄ abundances. This assumption will lead to inaccurate chemical abundances within the methane condensation region and below (particularly for CH₄ in the troposphere), so we only focus on the stratosphere when showing results for Uranus and Neptune. However, because CH₄ is not photochemically active in the tropopause region or below, this assumption has little effect on the hydrocarbon and oxygen photochemistry itself.

3. Results and Discussion

3.1. Ablation profiles

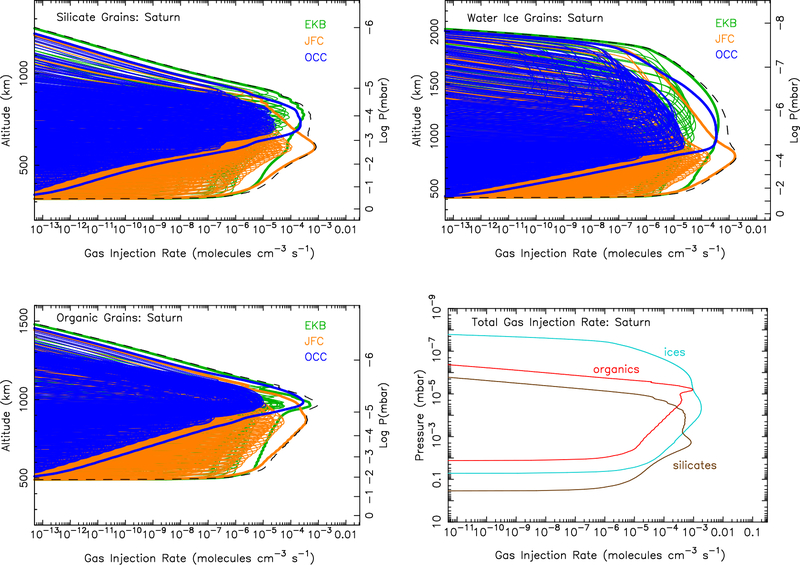
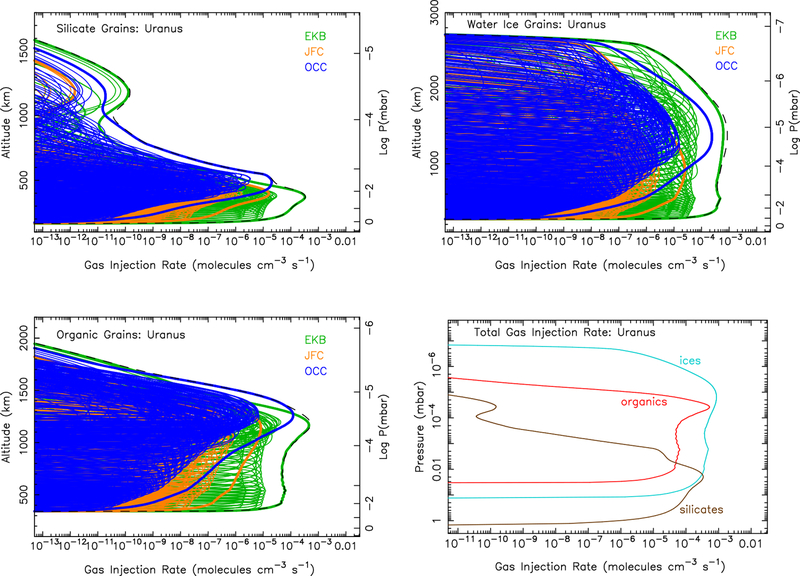
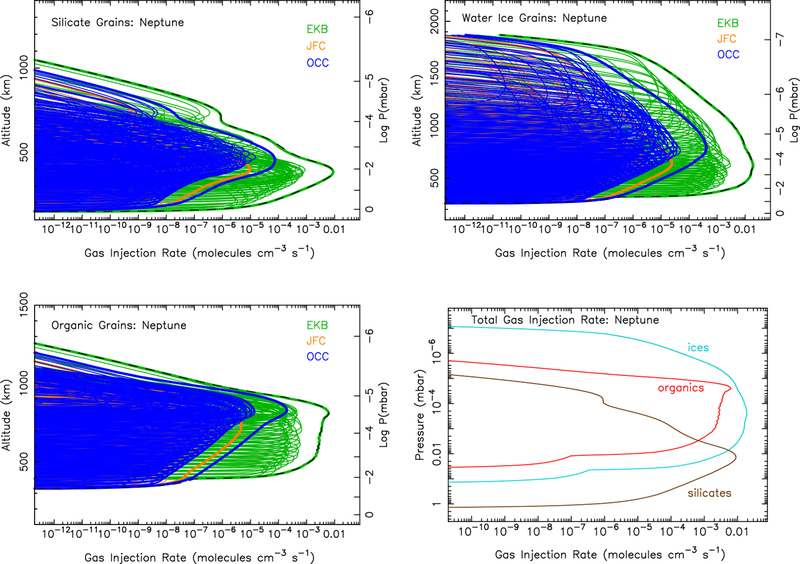
The calculated ablation profiles for each giant planet are shown in Figs. 4 (Jupiter), 5 (Saturn), 6 (Uranus), & 7 (Neptune). Jupiter-family comet grains clearly dominate the dust ablation source of external material at Jupiter, while Edgeworth-Kuiper belt grains clearly dominate at Uranus and Neptune. This result is largely a reflection of the incoming mass flux for the different populations from the Poppe (2016) model, as shown in Fig. 1. The incoming mass fluxes for the different populations are more balanced at Saturn, so all three populations contribute notably to the ablation profile in Fig. 5, with the Jupiter-family comet grain population dominating at the lower altitudes and Edgeworth-Kuiper belt grains at higher altitudes. The larger grains in the Jupiter-family comet population are not decelerated as efficiently as the smaller grains in the Edgeworth-Kuiper belt population and so tend to penetrate deeper before being ablated.

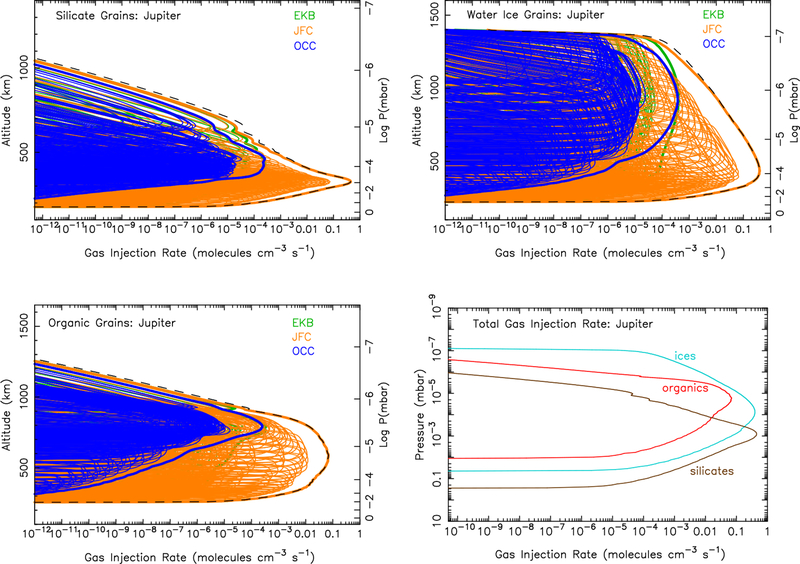
Figure 4:

Ablation rate profiles at Jupiter for silicate grains (Top left), water-ice grains (Top right), organic grains (Bottom left), and the total ablation rate from each component (Bottom right). The colored lines in the first three panels show the ablation profiles from each individual entry velocity and mass bin for the Edgeworth-Kuiper belt grains (green), Jupiter-family comet grains (orange), and Oort-cloud comet grains (blue). The thicker colored lines show the sum of all grains within each of these three populations, and the black dashed lines show the sum of all grains from all populations. These totals from all populations are shown as a function of pressure instead of altitude in the bottom right panel. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Figure 5:

Same as Fig. 4, except for Saturn.

Figure 6:

Same as Fig. 4, except for Uranus.

Figure 7:

Same as Fig. 4, except for Neptune.

In general, larger grains penetrate deeper than smaller grains for any given incoming velocity and material properties. In addition, because the larger grains experience a greater number of collisions with air molecules, they are heated to higher temperatures and ablate more fully than smaller particles. Entry velocity also has an effect. Grains entering the atmosphere at higher velocities heat up faster than those at lower velocities because of the larger kinetic energy being converted into heating the grain. Faster particles therefore tend to ablate at higher altitudes and reach higher maximum temperatures, allowing them to ablate more efficiently.

Because of gravitational focusing by the planet, entry velocities at Jupiter are larger than those for the other planets (see Figs. 2 & 3). For the case of the relatively refractory silicate grains, the greater incoming velocities on Jupiter and Saturn lead to greater maximum temperatures during atmospheric entry, allowing all of the grains to completely ablate before they are decelerated. The slower entry velocities at Uranus and Neptune lead to smaller maximum temperatures, such that some of the silicate grains do not completely ablate before they are decelerated and cool through radiative and evaporative cooling (see Moses, 1992). The residual grains continue to fall through the atmosphere at the terminal settling velocity and contribute to the overall aerosol burden of the atmosphere. For Neptune, only 53% of the incoming silicate grain mass flux is ablated, releasing silicon and metal vapor into the atmosphere. Entry velocities at Uranus are even lower, and only 22% of the silicate mass flux ends up being released as vapor. In fact, even some of the slowest and smallest organic particles will not fully ablate, leading to a 95% ablation efficiency of the organic grains on Uranus. The organic grains fully ablate on the other three planets, and the ice grains ablate fully on all four planets. Tables of the total ablation rate profile for each composition at each planet as a function of pressure are provided in the Supplementary Material.

The difference in material properties also affects the ablation profile. The ablation peak for silicate grains is deeper in the atmosphere than that of the water-ice or organic grains because of the much higher vaporization temperature of the silicates, whereas the water-ice grains begin to ablate at very high altitudes because of their low vaporization temperatures. Organic grains fall in between. The latent heat of vaporization and the emissivity of the material also affect the overall shape of the ablation profile. If the latent heat is low for any given material vapor pressure, the particles do not cool as efficiently during entry, so they heat up faster, ablate at higher altitudes, and have an overall narrower profile with a greater maximum ablation rate at the peak. Water (both ice and liquid) has a higher latent heat of vaporization than that of the organics assumed here, which explains why the water-ice ablation profile is so much broader in altitude than that of the organic grains. The water begins to sublimate from the grains at low temperatures high up in the atmosphere, and the relatively large latent heat causes evaporative cooling to be effective at keeping the grains at low temperatures throughout their flight through the atmosphere. For organic grains, on the other hand, the latent heat cooling term is less efficient, so although the organics begin to ablate at lower altitudes than the water ice, the ablation is complete before that of the water-ice grains. Similarly, if we had assumed the grain emissivity were constant at 1.0, the grains would have radiated the heat away more efficiently, so they would have survived to deeper altitudes, but would have had narrower ablation peaks with greater maximum peak ablation rates because of the increased heating in the higher-density deeper atmosphere.

Given that real particles consist of a mixture of materials, are not spherical, and are subject to other physical processes like sputtering and fragmentation during entry, our ablation calculations are simple approximations of the real situation. Observations of metals in the Earth’s atmosphere and in residual micrometeoroids suggest that “differential ablation” does occur in real atmospheres, such that the more volatile components can ablate at higher altitudes and more completely than less volatile components (e.g., McNeil et al., 1998; von Zahn et al., 1999; Vondrak et al., 2008; Janches et al., 2009); however, fragmentation and simple ablation also occur. The overall shape of the ablation profiles for the different vapors being released is complicated and cannot be entirely captured with simplified models and their assumptions (Malhotra and Mathews, 2011). Fortunately, the chemical consequences of the oxygen vapor being released have little sensitivity to the actual shape of the ablation profile, and a much greater dependency on the overall integrated flux of the oxygen-bearing vapor being released (Moses et al., 2000b; Moses and Bass, 2000) and the molecular/atomic form of the released vapor (section 4). That lack of sensitivity to the details of the ablation profile results from the fact that most of the interesting (i.e., non-recycling) oxygen chemistry occurs in the ~10−10⁻² mbar region, which is below the peak ablation region for the icy component, as well as to the fact that diffusion time scales in the upper atmosphere are shorter than the chemical lifetimes for the oxygen species, and the overall total available amount of chemically active oxygen is an important factor affecting the resulting chemistry.

Given the various uncertainties in the modeling of both the dust dynamics and the ablation process, as well as uncertainties in the dust composition, we estimate that our predicted oxygen influx rates from ablation are uncertain by about an order of magnitude.

3.2. Jupiter results and comparisons with observations

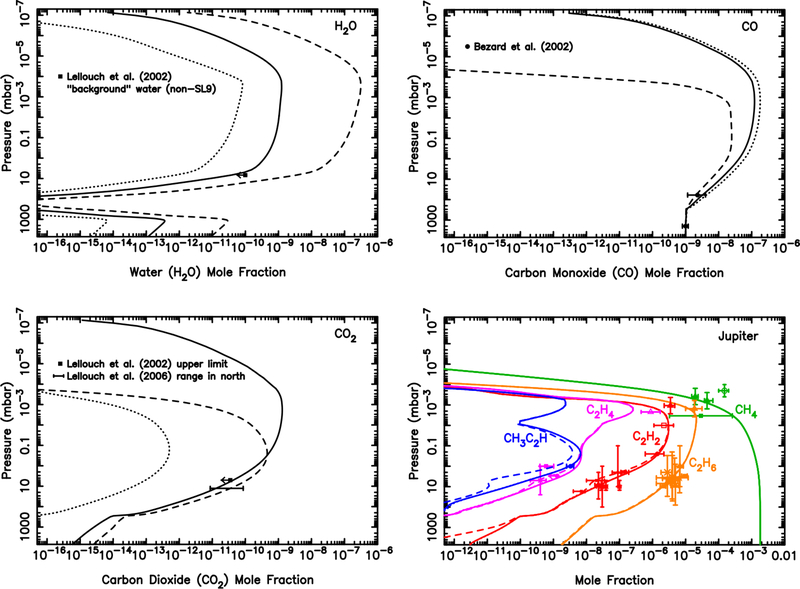
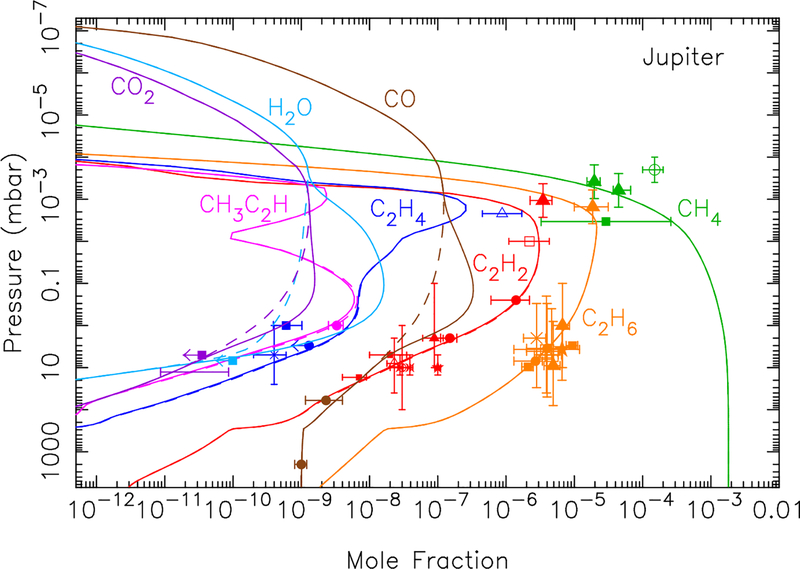
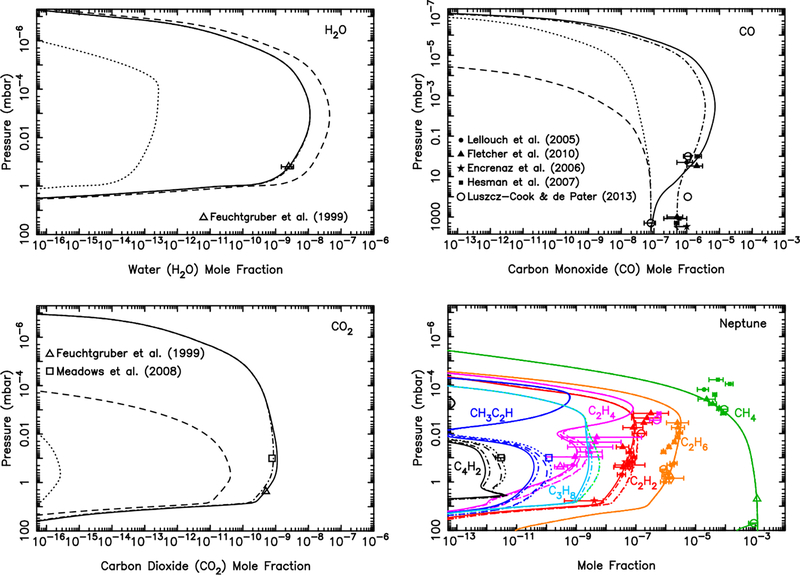
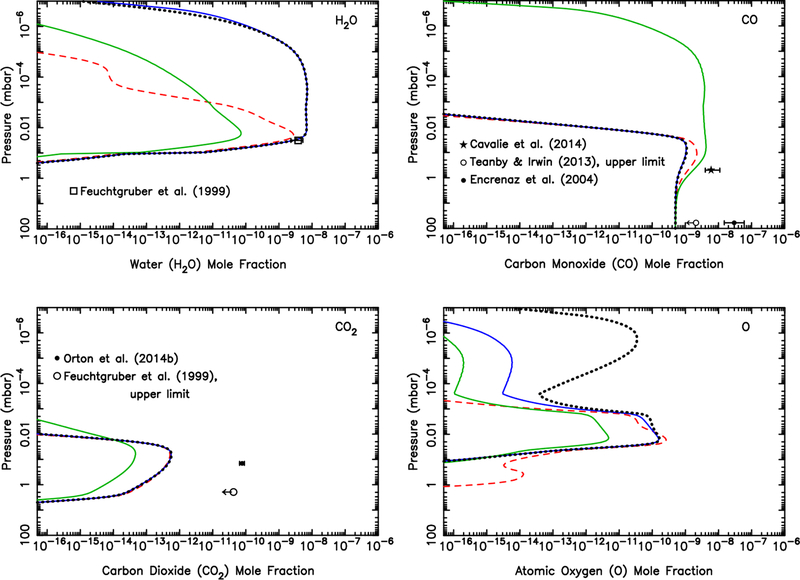
The effect of the ablated oxygen vapor on the composition of the Jovian atmosphere is shown in Fig. 8. The ablation of the icy grains, as calculated in section 3.1, peaks near 8 × 10⁻⁵ mbar, which is just above the methane homopause. The full ice ablation profile extends decades in pressure in both directions away from this peak, with a total integrated column influx of oxygen of ${1.0}_{-0.7}^{+2.2}\times {10}^7$ O atoms cm⁻² s⁻¹. If we assume that the gas released from the icy grains is all in the form of water, then the photochemical model produces the results shown by the dashed lines in Fig. 8. The total stratospheric water column abundance in this model is 1.9 × 10¹⁶ cm⁻². This H₂O column abundance is ~5–20 times greater than the observed global-average water abundance on Jupiter (Feuchtgruber et al., 1999; Bergin et al., 2000; Cavalié et al., 2008a, 2012), the bulk of which actually derives from the 1994 impact of Comet Shoemaker-Levy 9 (SL9) with Jupiter (e.g., Lellouch et al., 2002, 2006; Cavalié et al., 2013). The “background” water influx rate from interplanetary dust is observationally constrained by Lellouch et al. (2002) to be less than 8 × 10⁴ H₂O molecules cm⁻² s⁻¹, and probably as low as 4 × 10⁴ H₂O molecules cm⁻² s⁻¹.

Figure 8:

Mixing ratio profiles for H₂O (Top left), CO (Top right), CO₂ (Bottom left), and several hydrocarbons (Bottom right), as labeled, in Jupiter’s atmosphere as a result of the ablation of oxygen-rich icy grains. The dashed lines represent a model in which all the ablated icy component is released as water (integrated flux of 1.0 × 10⁷ H₂O molecules cm⁻² s⁻¹), the dotted lines represent a model in which all the ablated icy component is released as carbon monoxide (integrated flux of 1.0 × 10⁷ CO molecules cm⁻² s⁻¹), and the solid lines represent a model in which the relative influx rates (4.0 × 10⁴ H₂O molecules cm⁻² s⁻¹, 7.0 × 10⁶ CO molecules cm⁻² s⁻¹, 1.0 × 10⁵ CO₂ molecules cm⁻² s⁻¹) are scaled to fit the H₂O, CO, and CO₂ observations of Lellouch et al. (2002, 2006) and Bézard et al. (2002) for the regions the least influenced by the Shoemaker-Levy 9 impacts. The data points with error bars represent various observational constraints (see text). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Thus, as first discussed by Poppe (2016), we have an interesting situation in which the dust dynamical model delivers seemingly too much water to Jupiter. Photochemistry cannot resolve this problem. While some of the water is photochemically converted to CO and CO₂, the conversion is simply too in effective to remove enough water to explain the observations — kinetic recycling of H₂O is efficient in Jupiter’s hydrogen-dominated atmosphere (see also Moses et al. 2000b, 2005 and section 3.6). It seems unlikely that the incoming dust, which is dominated by Jupiter-family comet grains, is two orders of magnitude less oxygen-rich than we have assumed, so oxygen-depleted dust is also unsatisfactory as a possible explanation (see Bockelée-Morvan 2011 and Dello Russo et al. 2016 for reviews of cometary composition). Although Jupiter-family comet grains do spend more time at smaller heliocentric distances than their Edgeworth-Kuiper Belt counterparts, such that the ice components within the grains have a greater chance of being sublimated before atmospheric entry, other sources of oxygen and H₂O in the grains should remain intact, such as hydrated silicates.

The overall large CO/H₂O ratio in Jupiter’s atmosphere has led Bézard et al. (2002) to conclude that small comets are responsible for supplying Jupiter’s external oxygen, and this explanation has been reinforced by recent observations and modeling e orts (Lellouch et al., 2002, 2006; Cavalié et al., 2008a, 2012, 2013). The prevailing theory is that oxygen from cometary impacts is thermochemically converted to CO during the energetic impact and plume splashback phases (e.g., Zahnle, 1996), whereas it is unclear whether this conversion to CO can happen during dust ablation. However, it seems unlikely that the Poppe (2016) dust flux predictions are over two orders of magnitude too high, especially given the in situ observational constraints provided by the Galileo Dust Detection System, the Pioneer 10 meteoroid detector, and the New Horizons Student Dust Detector. Instead, we suggest that H₂O can be kinetically or thermochemically converted to CO during the meteoric entry phase, a topic that will be discussed further in section 4.

Therefore, we also show in Fig. 8 what happens if CO rather than H₂O were the only oxygen-bearing product released from the icy grain ablation (see dotted model curves). Carbon monoxide, like water, is relatively stable photochemically in Jupiter’s atmosphere because it is shielded from short-wavelength UV radiation by other atmospheric gases, and its strong carbon-oxygen bond makes it kinetically unreactive at Jovian atmospheric temperatures once the CO is thermalized. A small amount of the CO is photochemically converted to H₂O and CO₂ (see Fig. 8 and section 3.6), but most remains as CO. This model scenario fits the data better, with a predicted CO column abundance consistent with the observations of Bézard et al. (2002) and a predicted H₂O column abundance well within the upper limit for the background (non-SL9) water abundance (Lellouch et al., 2002). This model, however, predicts too little carbon dioxide to explain the CO₂ abundance in the northern hemisphere of Jupiter, which is believed to have been relatively unaffected by the SL9 impacts at the time of the observations (Lellouch et al., 2006).

We therefore freely adjust the relative influx rates of CO, H₂O, and CO₂ to better match all the oxygen species observations, keeping the shape of the ablation profile the same, but adjusting the magnitude of the different gases released. The solid lines in Fig 8 show model results that assume a column-integrated influx rate of 7 × 10⁶ CO molecules cm⁻² s⁻¹, 1 × 10⁵ CO₂ molecules cm⁻² s⁻¹, and 4 × 10⁴ H₂O molecules cm⁻² s⁻¹ (i.e., a relative influx rate of 98% CO, 1.4% CO₂, and 0.6% H₂O). This low water value is the favored “background” water influx rate from interplanetary dust as derived by Lellouch et al. (2002) (see also Lellouch et al. 2006, Cavalié et al. 2008a, 2012, 2013), and the CO influx rate is within the (1.5–10) × 10⁶ molecules cm⁻² s⁻¹ range determined by Bézard et al. (2002) for the external source on Jupiter. The influx rates for all three species in this model produce CO and CO₂ column abundances consistent with the Bézard et al. (2002) high-resolution ground-based infrared observations of CO, and the Lellouch et al. (2006) northern-hemisphere Cassini Composite Infrared Spectrometer (CIRS) observations of CO₂. The total oxygen influx rate from this model, 7.2 × 10⁶ O atoms cm⁻² s⁻¹, is ~30% smaller than that predicted from our dust ablation model, which is well within our estimated order of magnitude uncertainty due to the Poppe (2016) dynamical modeling, our extrapolation to larger grain sizes, and our assumptions about the grain composition and ablation process.

From these model-data comparisons, we conclude that dust grains supply a major component of the external oxygen on Jupiter, in addition to what is being supplied by large comets such as SL9 or smaller, more frequent cometary impacts (e.g., Bézard et al., 2002). In fact, interplanetary dust grains could be the dominant source of external oxygen on Jupiter when averaged over long time scales, provided that the ablated oxygen is released predominantly in the form of CO, or if the oxygen is converted to CO during the meteor phase (i.e., to explain the low H₂O abundance in Jupiter’s stratosphere). We explore this topic further in section 4.

The bottom right panel in Fig. 8 shows how the external oxygen species affect the mixing ratios of several hydrocarbons. The observational data for the hydrocarbons are from Gladstone and Yung (1983), Wagener et al. (1985), Noll et al. (1986b), Kostiuk et al. (1987), Morrissey et al. (1995), Yelle et al. (1996, 2001), Sada et al. (1998), Fouchet et al. (2000), Bézard et al. (2001), Moses et al. (2005), Romani et al. (2008), Greathouse et al. (2010), Nixon et al. (2010), and Kim et al. (2014). For the model with a water influx rate of 1 × 10⁷ H₂O molecules cm⁻² s⁻¹ (dashed line), the coupled water-hydrocarbon photochemistry causes a notable reduction in the abundance of unsaturated hydrocarbons such as C₂H₂, C₂H₄, CH₃C₂H, and (not shown) C₄H₂. Much of the carbon removed from these species ends up in CO, and to a much lesser extent CO₂ (see Moses et al., 2000b, 2005, and section 3.6). However, for the more realistic water influx rate of 4 × 10⁴ H₂O molecules cm⁻² s⁻¹ (solid model curves), the oxygen photochemistry has little effect on the hydrocarbon abundances because the resulting H₂O mixing ratio is much less than that of C₂H₂, the main hydrocarbon with which the OH reacts, and because the dominant oxygen species in that model — CO — is less photochemically active.

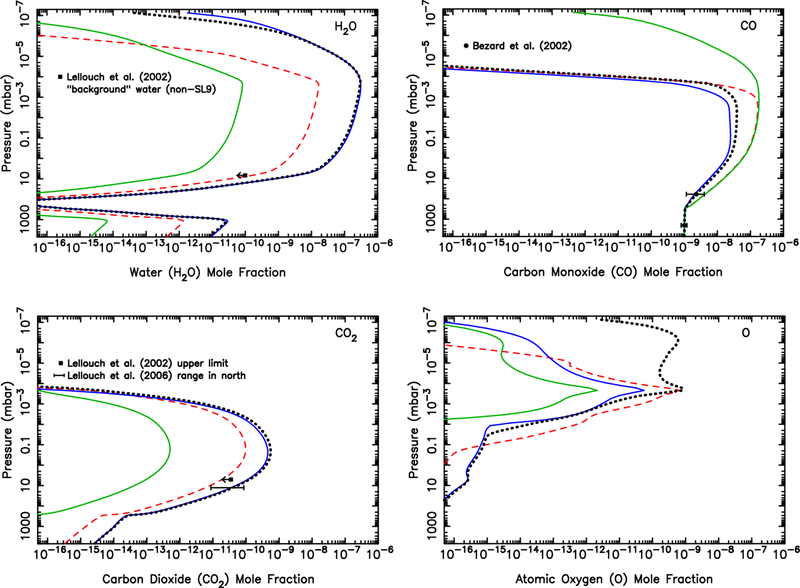
On top of the steady background dust influx described above and in Fig. 8, the Shoemaker-Levy 9 impacts delivered a large amount of oxygen to Jupiter’s middle stratosphere in 1994 (see the review of Lellouch, 1996), much of which is still concentrated in the southern hemisphere (e.g., Moreno et al., 2003; Lellouch et al., 2002, 2006; Cavalié et al., 2013). To illustrate what the H₂O, CO, and CO₂ profiles might look like today from this recent cometary source, we ran an additional time-variable model using observed comet-derived profiles as initial conditions, along with the steady background dust influx from our best-fit model (solid line) shown in Fig. 8. This model that includes the cometary source is more representative of conditions in the southern hemisphere at the present time. Although we cannot capture the full 3D atmospheric behavior with this simple 1D model, much of the horizontal spreading of the comet debris occurred in the first few years after the impacts (Lellouch et al., 2002; Moreno et al., 2003), so we use observations a couple years or more after the impacts to set our initial conditions. Based on the analysis of Lellouch et al. (2002), we assume that the initial mixing ratios of H₂O and CO₂ are a constant 4 × 10⁻⁸ and 7 × 10⁻⁹, respectively, above 0.5 mbar. Based on Moreno et al. (2003), we assume that the initial CO mixing ratio is 9 × 10⁻⁷ above 0.3 mbar. The resulting abundances after 23 years (representing the time since the 1994 impacts) are shown in Fig. 9 and can be directly compared with Fig. 8. The middle-stratospheric bulges in all three oxygen-bearing molecules are readily apparent in the 10−10⁻² mbar region more than 20 years after the impacts. However, more recent observations by Cavalié et al. (2012) suggest that the rate of diffusion or spreading of H₂O may be greater than is indicated by these models, leading to some overpredictions of the oxygen species abundances in the ~0.1–1 mbar region in our model. In any case, the SL9 impacts strongly perturbed the background oxygen-bearing species abundances in the middle stratosphere; however, as can be seen from a comparison of Figs. 8 & 9, these comet-delivered species today have little effect on the profiles below ~5 mbar (because the cometary oxygen species have not yet been transported to the lower stratosphere) or above 1 microbar (where dust delivery of oxygen dominates the source, and molecular diffusion time scales are short).

Figure 9:

Mixing ratio profiles for several species (as labelled) in Jupiter’s atmosphere for a model (solid line) that includes a source of oxygen from the Comet Shoemaker-Levy 9 impacts, along with the background steady dust influx rate. This model is more representative of the Jovian southern hemisphere today than the pure dust ablation model (dashed line in the figure here, solid line in Fig. 8).

Another interesting consequence of the predicted large dust influx rate to Jupiter is the relatively large resulting CO mixing ratio in the upper atmosphere. The CO will influence ionospheric chemistry by reacting with H₃⁺ (which dominates below the main electron-density peak) to produce HCO⁺, and the HCO⁺ will rapidly recombine with an electron to produce CO + H (see Moses and Bass, 2000), potentially causing a reduction in the local electron density in the process. Ablated metal vapor could also affect the lower ionospheric chemistry and structure (e.g., Moses, 1992; Moses and Bass, 2000; Lyons, 1995), as could unablated dust or recondensed ablation products. Future Jovian ionospheric models should therefore consider the potential effects of CO, metals, and other debris resulting from meteoric input.

3.3. Saturn results and comparisons with observations

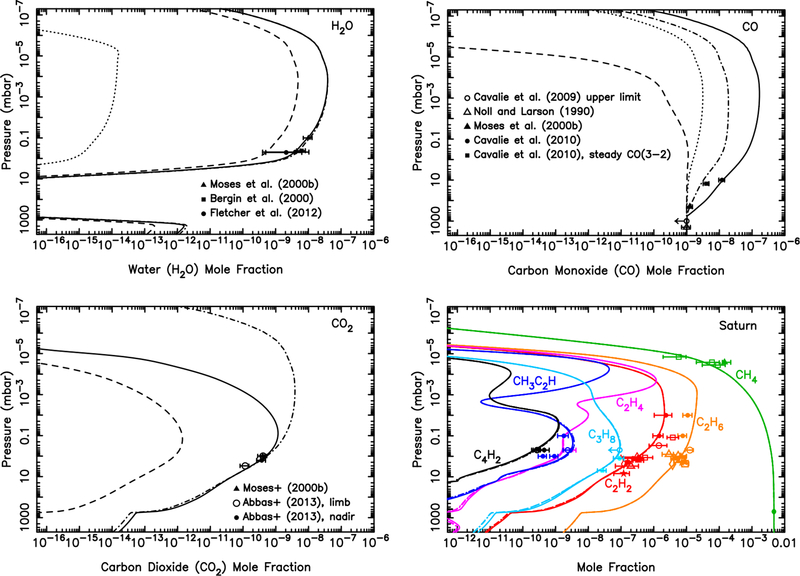
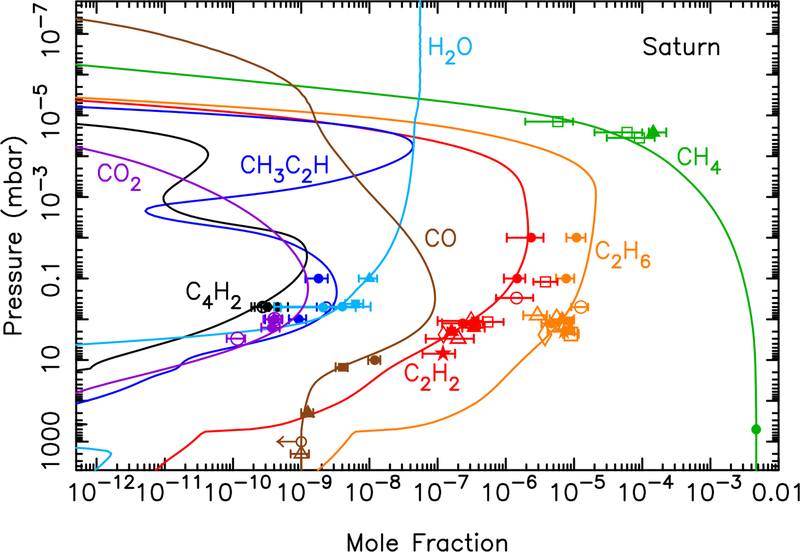
Our models predict that volatile oxygen is released from icy-grain ablation in Saturn’s atmosphere with a column-integrated influx rate of ${7.4}_{-5.1}^{+16}\times {10}^4$ atoms cm⁻² s⁻¹. As discussed in Poppe (2016), this flux is more than an order of magnitude too small to explain the stratospheric H₂O, CO, and CO₂ observed on Saturn (Feuchtgruber et al., 1997, 1999; Moses et al., 2000b; Bergin et al., 2000; Cavalié et al., 2009, 2010; Fletcher et al., 2012; Abbas et al., 2013). Cassini’s discovery of plumes on Enceladus (Dougherty et al., 2006; Porco et al., 2006) that are spewing water molecules into the Saturnian system has helped reveal the likely source of the large stratospheric water abundance on Saturn (e.g., Cassidy and Johnson, 2010; Hartogh et al., 2011; Fleshman et al., 2012), but Saturn’s rings (Connerney and Waite, 1984; Tseng et al., 2010; Moore et al., 2015) and large cometary impacts (Cavalié et al., 2010) could also be major contributors.

Figure 10 shows the vertical mixing ratio profiles of the major oxygen and hydrocarbon species on Saturn for different assumptions about the oxygen influx rate. If we assume that the gas released from the ablated icy grains is all in the form of H₂O (or CO) with an integrated influx rate of 7.4 × 10⁴ molecules cm⁻² s⁻¹, as indicated by our modeling, then the photochemical model produces the results shown by the dashed (or dotted) lines in Fig. 10. Both models fall grossly short in explaining the observed stratospheric abundance of H₂O and CO₂ from the Infrared Space Observatory (ISO), the Submillimeter Wave Astronomy Satellite (SWAS), the Herschel SPIRE, and the Cassini CIRS limb and nadir observations (see Feuchtgruber et al., 1997; Moses et al., 2000b; Bergin et al., 2000; Fletcher et al., 2012; Abbas et al., 2013). A model in which the ablation profile is scaled such that the column-integrated influx rates of H₂O, CO, and CO₂ are 6.2 × 10⁵, 4.2 × 10⁵, and 1.2 × 10⁵ cm⁻² s⁻¹, respectively, fits the H₂O and CO₂ observations well (dot-dashed line in Fig. 10), and produces a CO column abundance above 400 mbar that is consistent with the ground-based infrared CO observations of Noll and Larson (1990) (see Moses et al. 2000b for further details). The relative influx rates in this model are 53% H₂O, 36% CO, and 10% CO₂. This model, however, has insufficient middle-stratospheric carbon monoxide to explain the large CO mixing ratios derived from ground-based limb observations of the emission core of the CO(6–5) rotational line at submillimeter wavelengths (Cavalié et al., 2010), and falls slightly short of the CO mixing ratio inferred from analysis of the CO(3–2) rotational line, using model profiles that assume a steady background influx of CO (Cavalié et al., 2010).

Figure 10:

Same as Fig. 8, but for Saturn. The dashed lines represent a model in which all the ablated icy component is released as water (integrated flux of 7.4 × 10⁴ H₂O molecules cm⁻² s⁻¹); the dotted lines represent a model in which all the ablated icy component is released as carbon monoxide (integrated flux of 7.4 × 10⁴ CO molecules cm⁻² s⁻¹); the dot-dashed lines represent a model in which the relative influx rates are scaled to 6.2 × 10⁵ H₂O molecules cm⁻² s⁻¹, 4.2 × 10⁵ CO molecules cm⁻² s⁻¹, and 1.2 × 10⁵ CO₂ molecules cm⁻² s⁻¹; and the solid lines represent a model in which the relative influx rates are scaled to 6.2 × 10⁵ H₂O molecules cm⁻² s⁻¹ and 4.1 × 10⁶ CO molecules cm⁻² s⁻¹, with no direct CO₂ injection. The data points with error bars represent various observational constraints (see text). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We therefore also test a model in which the integrated CO influx rate is 4.1 × 10⁶ molecules cm⁻² s⁻¹ (favored by Cavalié et al. 2010 for the assumption of a steady background influx from their analysis of the CO(6–5) line), the H₂O influx rate is 6.2 × 10⁵ molecules cm⁻² s⁻¹, and the CO₂ influx rate is zero (i.e., CO₂ is not released as a separate component but is formed by coupled H₂O-CO photochemistry only). The relative influx rates in this model are 87% CO, 13% H₂O, and 0% CO₂. Figure 10 demonstrates that this model (solid lines) fits the H₂O and CO₂ observations well, and the results are also consistent with the CO mixing ratios needed to explain the CO(6–5) line, but the CO column abundance in the lower stratosphere and upper troposphere is too high to explain the Noll and Larson (1990) infrared observations (Moses et al., 2000b) or the Cavalié et al. (2010) CO(3–2) sub-millimeter observations. In fact, Cavalié et al. (2010) find that they can only fit both the CO(3–2) and CO(6–5) lines if the CO is concentrated at relatively high altitudes, and so they favor a scenario in which a large cometary impact 220 ± 30 years ago deposited (2.1 ± 0.4) × 10¹⁵ g of CO above 0.1 mbar on Saturn. Although it remains to be seen whether such a scenario can be consistent with the infrared observations of Noll and Larson (1990) — and note that such cometary models would be more consistent with the infrared observations if the internal tropospheric CO source were smaller than we have assumed at our lower boundary — we concur that a relatively recent cometary impact is the most reasonable explanation for the submillimeter CO observations.

The bottom right panel in Fig. 10 shows that for the fluxes considered here, the external oxygen species have little effect on the hydrocarbon mixing ratios. In this plot, the observational data for the hydrocarbons derive from Festou and Atreya (1982), Smith et al. (1983), Courtin et al. (1984), Noll et al. (1986b), Chen et al. (1991), Sada et al. (1996, 2005), Moses et al. (2000a, 2015), Bézard et al. (2001), Greathouse et al. (2005, 2006), Fletcher et al. (2009), Guerlet et al. (2009, 2010), and Sinclair et al. (2013).

Based on the Cavalié et al. (2010) scenario, the CO in Saturn’s stratosphere most likely derives from a large cometary impact that occurred a couple hundred years ago. This putative impact may also have been responsible for some fraction of the currently observed water on Saturn. The diffusion time scale from an assumed 0.1 mbar plume-splashback deposition region to the ~3 mbar H₂O condensation region in our model is about 150 years, so cometary water would be removed from the stratosphere faster than its corresponding cometary CO counterpart (note that this time scale is an order of magnitude longer than a previous quote from Moses et al. (2000b) due to an apparent typographical or calculation error in the previous paper). However, if the shocked cometary material maintains the same CO/H₂O influx ratio of ≳ 100 as the SL9 impacts on Jupiter (see Zahnle, 1996; Lellouch, 1996; Bézard et al., 2002, and section 3.2 above), then the bulk of the water currently in Saturn’s stratosphere must derive from an additional external source, such as Enceladus plume vapor (Guerlet et al., 2010; Cassidy and Johnson, 2010; Hartogh et al., 2011; Fleshman et al., 2012). In that situation, the vertical profiles for the oxygen species shown in Fig. 10 could be quite different. The comet-derived CO would be more concentrated in the middle stratosphere and less abundant elsewhere, while the H₂O could be more prevalent in the thermosphere than is shown in Fig. 10.

We therefore consider an additional model in which H₂O vapor flows in from the top of the atmosphere, as with the possible Enceladus source, and the CO derives from an historical cometary impact (see Fig. 11), along with our predicted oxygen influx rate due to the ablation of icy grains. The H₂O flux at the top of the atmosphere due to the “Enceladus” source is set to 6.2 × 10⁵ cm⁻² s⁻¹ to remain roughly consistent with the ISO, SWAS, and Herschel/SPIRE observations (Moses et al., 2000b; Bergin et al., 2000; Fletcher et al., 2012) and with model predictions (e.g., Cassidy and Johnson, 2010; Hartogh et al., 2011). The dust ablation source is assumed to supply an integrated 6.7 × 10⁴ CO molecules cm⁻² s⁻¹ and 7.2 × 10³ H₂O molecules cm⁻² s⁻¹, with no separate CO₂ source. The cometary source of CO is assumed to have an initial mixing ratio of 3 × 10⁻⁶ confined to pressures less than 0.1 mbar, based on Cavalié et al. (2010). Because our eddy diffusion coefficient in the relevant middle stratospheric region is smaller than that adopted by Cavalié et al. (2010), we find that the model has to evolve for a longer time than the 220 ± 30 years derived by Cavalié et al. (2010) to bring sufficient CO down to the altitude regions in which the (sub)-millimeter observations are most sensitive — the model results shown in Fig. 11 are for 400 years after the impact. This model provides a reasonable fit to all the available observations of the oxygen species, but it is not unique. Other combinations of the amount of cometary CO deposited, the height at which it was deposited, the time elapsed since the impact, and the eddy diffusion coefficient profile could provide similar results.

Figure 11:

Mixing ratio profiles for several species (as labelled) in Saturn’s atmosphere for a model that includes a source of H₂O flowing in at the top of the atmosphere from a local source such as Enceladus, and a cometary source from an impact that occurred 400 years ago, along with a background injection rate of 6.7 × 10⁴ CO molecules cm⁻² s⁻¹ and 7.2 × 10³ H₂O molecules cm⁻² s⁻¹ from the ablation of icy grains.

In any case, we conclude that the ablation of interplanetary dust plays a very minor role in delivering oxygen to Saturn, based on the observed abundances of CO and H₂O in comparison with our relatively low predicted dust influx rates. Better observational determinations of the CO and H₂O vertical profile will be critical for determining the relative roles of various external and internal sources in supplying oxygen to Saturn’s stratosphere. High-spectral-resolution observations in the near- and far-infrared, in particular (see the Jupiter observations of Bézard et al., 2002; Feuchtgruber et al., 1999), would be useful to have in hand before the planning stage of any future entry probe mission such as is described in Atkinson et al. (2012) or Mousis et al. (2014, 2016).

3.4. Uranus results and comparisons with observations

Sluggish atmospheric mixing on Uranus prevents methane from being carried to high altitudes, resulting in a unique situation in which much of the ablation occurs above the CH₄ homopause. In fact, water delivered by interplanetary dust particles will largely condense before it can photochemically interact with hydrocarbons, leading to less photochemical production of CO and CO₂ from coupled H₂O-CH₄ photochemistry. Therefore, the relative abundance of H₂O, CO, and CO₂ on Uranus could provide a “cleaner” representation of the source itself and could help us to better understand the initial chemical form of the ablated vapor.

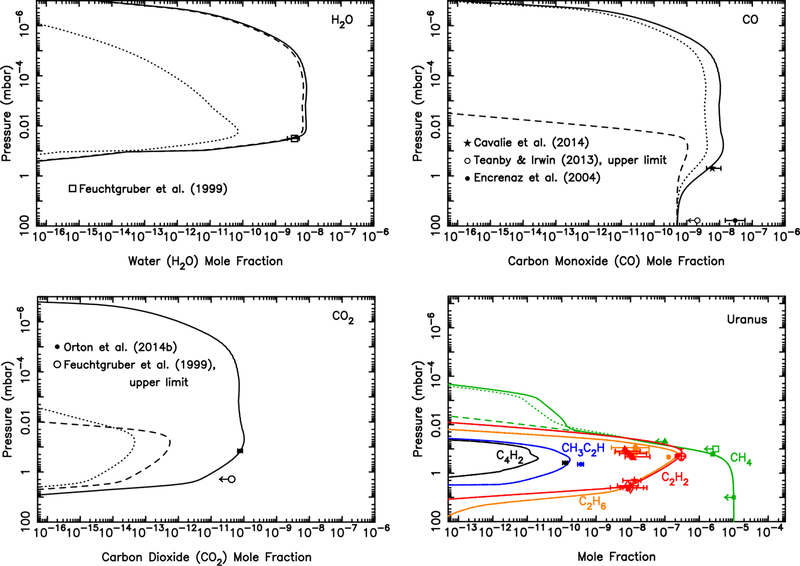
Our dust-ablation model predicts an integrated influx of ${8.9}_{-6.1}^{+19}\times {10}^4$ oxygen atoms cm⁻² s⁻¹ to Uranus from the ablation of icy grains. Fig. 12 demonstrates that while the external delivery of this amount of H₂O could explain the infrared water observations of Feuchtgruber et al. (1997, 1999), that scenario (i.e., dashed curves in Fig. 12) cannot explain the relatively large amount of CO and CO₂ observed in the Uranian stratosphere (Cavalié et al., 2014; Orton et al., 2014b). On the other hand, if all that oxygen were introduced as CO (dotted curves in Fig. 12), our models predict much less H₂O and CO₂ than is observed on Uranus. We therefore freely scale the relative influx rates of these three species, keeping the shape of the ablation profile the same, but adjusting the magnitude in order to provide a better fit to the observations. Our best-fit model has an integrated influx rate of 1.2 × 10⁵ H₂O molecules cm⁻² s⁻¹ (which is fully consistent with the range determined by Feuchtgruber et al., 1999, from ISO observations and modeling), 2.7 × 10⁵ CO molecules cm⁻² s⁻¹ (the same CO influx rate derived by Cavalié et al. 2014 when considering the case of a steady background influx for the same Orton et al. 2014b thermal structure), and 3 × 10³ CO₂ molecules cm⁻² s⁻¹ (the same influx rate derived by Orton et al. 2014b from their Spitzer spectral analysis). The corresponding relative influx rates for this best-fit model are 31% H₂O, 69% CO, and 0.8% CO₂.

Figure 12:

Mixing ratio profiles for H₂O (Top left), CO (Top right), CO₂ (Bottom left), and several hydrocarbons (Bottom right), as labeled, in Uranus’ atmosphere as a result of the ablation of oxygen-rich icy grains. The dashed lines represent a model in which all the ablated icy component is released as water (integrated flux of ~9 × 10⁴ H₂O molecules cm⁻² s⁻¹), the dotted lines represent a model in which all the ablated icy component is released as carbon monoxide (integrated flux of 9.0 × 10⁴ CO molecules cm⁻² s⁻¹), and the solid lines represent a model in which the relative influx rates (1.2 × 10⁵ H₂O molecules cm⁻² s⁻¹, 2.7 × 10⁵ CO molecules cm⁻² s⁻¹, 3.0 × 10³ CO₂ molecules cm⁻² s⁻¹) are scaled to fit the H₂O, CO, and CO₂ observations of Feuchtgruber et al. (1999), Cavalié et al. (2014), Teanby and Irwin (2013), and Orton et al. (2014b). The data points with error bars represent various observational constraints (see text). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The total oxygen influx rate in this best-fit model is 4 × 10⁵ oxygen atoms cm⁻² s⁻¹, which is roughly a factor of 4 greater than our original predictions from the ablation of icy grains. This model-data mismatch could simply represent uncertainties in our modeling procedure, such as the extrapolation of the mass flux to larger grains, or it could indicate an additional external source of oxygen to Uranus, such as satellite/ring debris or cometary impacts. One possible source is the interaction of the extended Uranian exosphere with the inner ring system (Esposito and Colwell, 1989). Based on the observed or inferred cometary impact source of CO on Jupiter, Saturn, and Neptune (Lellouch, 1996; Lellouch et al., 2005; Cavalié et al., 2010), a cometary source of CO is not an unexpected possibility for Uranus, as well. In fact, based on the outer solar system impact-rate calculations of Levison and Duncan (1997) and Zahnle et al. (2003), comets might supply an external amount of oxygen that is of the same magnitude as the dust influx (Poppe, 2016). Note, however, that our inferred CO/H₂O influx ratio of ~2 on Uranus is much less than that inferred for Jupiter. It is unclear at this point whether this difference is due to (1) the slower entry velocity at Uranus leading to different relative chemical processing of CO vs H₂O during cometary impacts and/or meteor entry, (2) whether there is a fundamental difference in chemical composition of Edgeworth-Kuiper belt dust, which dominates at Uranus, in comparison with Jupiter-family comet dust, which dominates at Jupiter, or (3) whether there is an additional local source of H₂O on Uranus, as with Enceladus on Saturn.

It should also be kept in mind that the eddy diffusion coefficient (K_zz) profile is not well constrained on Uranus due to uncertainties in the thermal structure, stratospheric methane profile, and related degeneracies in the modeling of infrared emission features (Orton et al., 2014a,b). We have not explored the sensitivity of the results to different eddy diffusion coefficient profiles in this paper. Orton et al. (2014b) performed numerous such sensitivity tests, including sloped K_zz profiles and different combinations of tropopause CH₄ mixing ratio and K_zz values. Although not discussed in their paper, the Orton et al. sensitivity tests suggest that changes in the eddy diffusion coefficient profile have only a minor effect on the profiles of H₂O and CO₂, which both condense in the middle-to-upper stratosphere of Uranus, while the mixing ratio of CO could be affected by a factor of a few in the ~0.03–3 mbar region.

Figure 12 demonstrates that CO and H₂O are the dominant molecules (other than H₂) at pressures less than ~10 μbar on Uranus. As such, molecular ions such as HCO⁺ and H₃O⁺ will dominate over hydrocarbon ions in the lower portion of the extended Uranian ionosphere. The effect of H₂O leading to reduced peak electron densities in giant-planet ionospheres has been well studied (e.g., Connerney and Waite, 1984; Nagy et al., 2009), and CO could play a similar role in the lower ionosphere. It remains to be seen whether our relatively moderate predicted oxygen influx rate of ≲4 × 10⁵ cm⁻² s⁻¹ can provide sufficient CO and H₂O (and/or solid particles) in the thermosphere to help explain the very low electron densities observed on Uranus (Lindal et al., 1987), but earlier modeling of the process suggests not (Waite and Cravens, 1987; Shinagawa and Waite, 1989). We note that our predicted dust-derived oxygen influx rate of 9 × 10⁴ cm⁻² s⁻¹ and the observationally inspired 4 × 10⁵ cm⁻² s⁻¹ influx rate discussed above are both comfortably below the upper limit of 1 × 10⁶ H₂O molecules cm⁻² s⁻¹ required to explain the lack of H₂O absorption in the Voyager 2 Ultraviolet Spectrometer occultation observations (Herbert et al., 1987; Shinagawa and Waite, 1989).

3.5. Neptune results and comparisons with observations

The integrated influx rate from the ablation of icy grains supplies ${7.5}_{-5.1}^{+16}\times {10}^5$ O atoms cm⁻² s⁻¹ to Neptune, according to our ablation models. This flux is consistent with the ISO observational analysis of Feuchtgruber et al. (1999), who conclude that an H₂O flux of (1.2–150) × 10⁵ molecules cm⁻² s⁻¹ and a CO₂ flux of (6–7) × 10⁴ molecules cm⁻² s⁻¹ are needed to reproduce the infrared observations of these species on Neptune. However, the observed CO abundance on Neptune is enormous in comparison to that on the other giant planets (see Marten et al., 1993, 2005; Rosenqvist et al., 1992; Guilloteau et al., 1993; Naylor et al., 1994; Encrenaz et al., 1996; Courtin et al., 1996; Lellouch et al., 2005, 2010; Hesman et al., 2007; Fletcher et al., 2010b; Luszcz-Cook and de Pater, 2013; Irwin et al., 2014). A deep-tropospheric source from Neptune’s heavy-element-rich interior could potentially explain the large observed CO abundance (e.g. Lodders and Fegley, 1994; Luszcz-Cook and de Pater, 2013; Cavalié et al., 2017), but the most recent series of observations listed above confirm that the CO mixing ratio is at least a factor or 2 larger in the stratosphere than the troposphere, unambiguously pointing to the existence of an external source of CO for Neptune that dominates over the internal source. The required external flux, which is ~1 × 10⁸ CO molecules cm⁻² s⁻¹ (e.g., Lellouch et al., 2005), is well outside our estimated uncertainty for the interplanetary dust delivery, but is consistent with what might be expected from cometary impacts (Luszcz-Cook and de Pater, 2013). In fact, the large abundance of CO, its vertical profile, the large observed CO/H₂O ratio, and the additional presence of HCN in Neptune’s stratosphere (Marten et al., 1993, 2005; Rosenqvist et al., 1992; Lellouch et al., 1994; Rezac et al., 2014) originally prompted Lellouch et al. (2005) to suggest a cometary impact within the last couple hundred years as the source of the observed CO. High-resolution submillimeter and millimeter observations of CO (Hesman et al., 2007; Luszcz-Cook and de Pater, 2013) on Neptune continue to support this possibility. The fact that the Poppe (2016) dust dynamical models fall many orders of magnitude short in explaining the observed amount of CO on Neptune also makes this comet impact hypothesis very likely.

Figure 13 shows the results of the photochemical modeling for Neptune. If we assume that all the vapor from the ablation of icy dust grains is released in the form of H₂O only (dashed curves, with an integrated H₂O influx rate of ~7.5 × 10⁵ molecules cm⁻² s⁻¹), then this model overestimates the stratospheric abundance of H₂O (Feuchtgruber et al., 1999), but underestimates the stratospheric abundances of CO₂ (Feuchtgruber et al., 1999; Meadows et al., 2008) and CO (Lellouch et al., 2005, 2010; Hesman et al., 2007; Fletcher et al., 2010b; Luszcz-Cook and de Pater, 2013). If we assume that all the vapor from icy grains is released in the form of CO only (dotted curves, with an integrated CO influx rate of 7.5 × 10⁵ molecules cm⁻² s⁻¹), then this model underestimates the stratospheric abundance of all the observed oxygen species. If we keep the vertical ablation profile the same but scale the relative magnitude of the influx rates such that we have 2 × 10⁵ H₂O molecules cm⁻² s⁻¹, 2 × 10⁸ CO molecules cm⁻² s⁻¹, and 2 × 10⁴ CO₂ molecules cm⁻² s⁻¹ (solid curves in Fig. 13), then this model reproduces the observed H₂O and CO₂ abundances, the relatively small tropospheric CO mixing ratio determined by Luszcz-Cook and de Pater (2013) (see also Irwin et al. 2014), and the relatively large stratospheric mixing ratio determined by Hesman et al. (2007) and Fletcher et al. (2010b). However, some of the CO observations favor larger tropospheric CO mixing ratios and/or smaller stratospheric CO mixing ratios, so we also ran a model (dot-dashed curves in Fig. 13) with a lower-boundary CO mixing ratio of 5 × 10⁻⁷ (cf. Lellouch et al., 2005, 2010; Hesman et al., 2007; Fletcher et al., 2010a) and a CO influx rate of 1 × 10⁸ CO molecules cm⁻² s⁻¹, with the fluxes of H₂O and CO₂ remaining the same as the solid-curve model. This model also fits the observed stratospheric H₂O and CO₂ abundances (Feuchtgruber et al., 1999; Meadows et al., 2008).

Figure 13:

Mixing ratio profiles for H₂O (Top left), CO (Top right), CO₂ (Bottom left), and several hydrocarbons (Bottom right), as labeled, in Neptune’s atmosphere as a result of the ablation of oxygen-rich icy grains. The dashed lines represent a model in which all the ablated icy component is released as water (integrated flux of 7.5 × 10⁵ H₂O molecules cm⁻² s⁻¹), the dotted lines represent a model in which all the ablated icy component is released as carbon monoxide (integrated flux of 7.5 × 10⁵ CO molecules cm⁻² s⁻¹), and the solid lines represent a model in which the relative influx rates are scaled to 2 × 10⁵ H₂O molecules cm⁻² s⁻¹, 2 × 10⁸ CO molecules cm⁻² s⁻¹, and 2 × 10⁴ CO₂ molecules cm⁻² s⁻¹ to fit the low tropospheric CO mixing ratio determined by Luszcz-Cook and de Pater (2013) and the large stratospheric mixing ratio determined by Hesman et al. (2007) and Fletcher et al. (2010b). For the dot-dashed model, we increased the CO mixing ratio at the lower boundary of the model and scaled the dust influx rates to 2 × 10⁵ H₂O molecules cm⁻² s⁻¹, 1 × 10⁸ CO molecules cm⁻² s⁻¹, and 2 × 10⁴ CO₂ molecules cm⁻² s⁻¹ to compare better with the observations of Lellouch et al. (2005, 2010). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Both the vertical profile and absolute stratospheric abundance of CO have not been firmly established to date, in part because of uncertainties in the atmospheric thermal structure, so we do not favor either of these “best-fit” models over the other. Both, however, have the same inferred influx rate for CO₂ and H₂O, and both have very large inferred influx rates for CO. In fact, the stratospheric CO mixing ratio in both these models exceeds that of C₂H₆, the dominant methane photochemical product. Such a large CO abundance has consequences for the hydrocarbon photochemistry, with larger CO mixing ratios leading to smaller abundances of C₂H₂ and several other higher-order hydrocarbons. However, as is discussed in section 3.6, the sensitivity of the hydrocarbons to the CO abundance could be largely an artifact of the low-resolution ultraviolet cross sections used in the model. When the CO abundance becomes large enough, it shields C₂H₆ from photolysis in the model, whereas that is unlikely to happen as effectively in the real atmosphere. The hydrocarbon observational data points in Fig. 13 derive from numerous ultraviolet, infrared, and sub-millimeter observations (Caldwell et al., 1988; Bézard et al., 1991; Bishop et al., 1992; Orton et al., 1992; Kostiuk et al., 1992; Yelle et al., 1993; Schulz et al., 1999; Burgdorf et al., 2006; Meadows et al., 2008; Fletcher et al., 2010b; Greathouse et al., 2011; Lellouch et al., 2015).

Note that if the observed CO on Neptune derives from a large cometary impact that occurred roughly 200 years ago, as was suggested originally by Lellouch et al. (2005), then the steady-state CO mixing-ratio profile shown in Fig. 13 contains too much CO at the highest thermospheric altitudes. The plume splashback phase of a large cometary impact can deposit shock-produced CO predominantly in the middle stratosphere (Zahnle, 1996; Lellouch, 1996; Lellouch et al., 1997), and this CO will slowly settle through the atmosphere over time, causing the peak CO abundance to migrate downward and lessen in magnitude with time (see Bézard et al., 2002; Lellouch et al., 2002, 2006; Moreno et al., 2003; Cavalié et al., 2009, 2012).

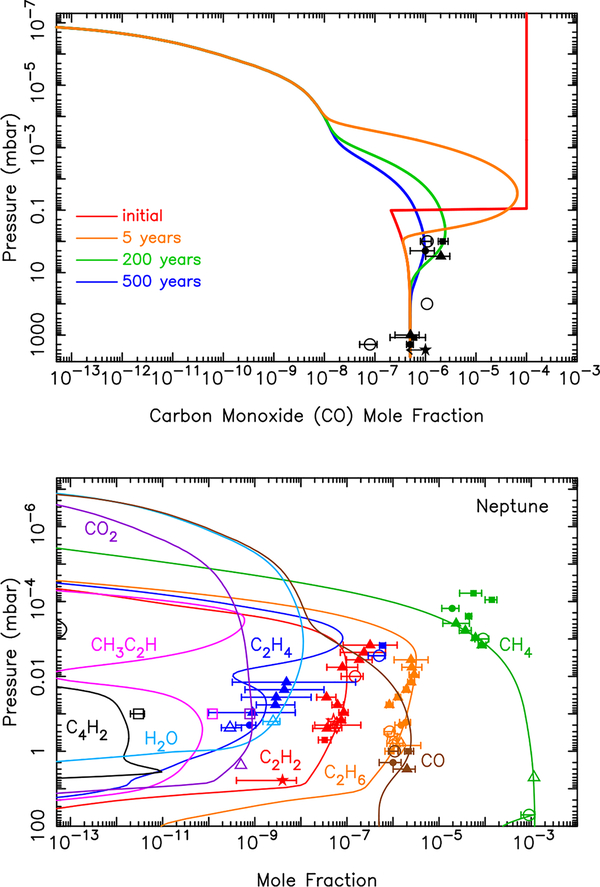
We therefore investigate a separate case to illustrate what the CO profile would look like now from this scenario of a large cometary impact that occurred 200 years ago (Fig. 14). For this model, we assume that the ablation of interplanetary dust supplies a steady background influx rate of 2 × 10⁵ H₂O molecules cm⁻² s⁻¹, 5 × 10⁵ CO molecules cm⁻² s⁻¹, and 2.3 × 10⁴ CO₂ molecules cm⁻² s⁻¹ (consistent with our predicted overall oxygen influx rate); however, in addition to that background influx is a sudden comet-supplied CO amount with a initial mixing ratio of 1 × 10⁻⁴ above 0.1 mbar that then evolves within the confines of the photochemical model. Figure 14 illustrates how the CO profile evolves with time, being lost quickly in the upper stratosphere and thermosphere due to molecular diffusion, and diffusing more slowly into the lower stratosphere due to eddy diffusion. This model is presented purely for illustrative purposes — the exact shape of the CO profile will depend on how much CO was originally deposited, the altitude at which it was deposited, the date at which it was deposited, and the eddy diffusion coefficient profile or other details about stratospheric circulation, none of which are well known. The main point here is that although the comet-derived CO mixing ratio is very large in the middle and lower stratosphere, it is likely smaller in the upper stratosphere and thermosphere than is shown in Fig. 13 for our simple dust-scaled case. Because the presence of large amounts of CO would affect ionospheric chemistry, future investigations into aeronomical consequences of oxygen influx on the giant planets should keep the possible cometary source of this CO in mind.

Figure 14:

(Top) Time evolution of CO delivered from a large cometary impact, in combination with a smaller steady influx due to the ablation of icy grains (see text for details). (Bottom) Mixing ratio profiles for important hydrocarbon and oxygen species 200 years after the cometary impact described in the top panel.

Note also that the observed H₂O column abundance on Neptune is a couple orders of magnitude smaller than that of CO above a few millibar. Although the very large amount of CO in Neptune’s stratosphere, along with a vertical profile that increases with height, strongly suggests that the CO was supplied by a large cometary impact at some point in the recent past, the amount of H₂O delivered by that putative cometary impact must have either been much smaller than that of the CO, or any comet-delivered H₂O must have already diffused down from its deposition region to pressure levels where it would condense and be removed from the vapor phase. In relation to this last point, the diffusion time scale from a potential deposition region near 0.1 mbar to the condensation region near 1 mbar in our model is roughly 60 years. Cometary water would have already been removed from the stratosphere for any large impact that occurred much more than 60 years ago.

3.6. Dominant oxygen reactions

The dominant chemical reactions influencing the oxygen species in giant-planet atmospheres are discussed in the Saturn study of Moses et al. (2000b). The key reactions are initiated by coupled water-methane photochemistry, i.e., the kinetics resulting from the photolysis of water and methane — carbon monoxide is too kinetically stable to play a dominant role, and CO₂ is less abundant. Jupiter, Saturn, and Neptune have very similar oxygen chemistry, whereas Uranus differs because of its low-altitude methane homopause.

On all the planets, water is lost primarily by photolysis throughout the middle and upper stratosphere and by condensation in the lower stratosphere. In the background H₂-rich atmosphere, however, the OH released from water photolysis is efficiently recycled through the following dominant scheme:

$$\begin{gathered} {\text{H}}_2\text{O}+\text{h}v\to \text{ H}+\text{OH } \\ \underset{\_}{\text{OH}+{\text{H}}_2\to {\text{H}}_2\text{O}+\text{H}} \\ \text{Net : }{\text{H}}_2\to 2\text{H}, \end{gathered}$$ (1)

where hν represents an ultraviolet photon. Despite the relatively small rate coefficient for the reaction OH + H₂ → H₂O + H (Baulch et al., 2005) at the low atmospheric temperatures characteristic of the giant planets, the large background H₂ abundance ensures that this scheme dominates the OH loss.

The OH that does not get recycled back to water ends up predominantly in CO, with a lesser amount in CO₂. On Jupiter, Saturn, and Neptune, the main chemical schemes for photochemically converting the H₂O to CO involve the addition of OH radicals with unsaturated hydrocarbons such as C₂H₂ and C₂H₄ (e.g., see schemes (7), (8), (14), & (15) of Moses et al., 2000b), with the resulting C₂H₂OH and C₂H₄OH molecules reacting with H and CH₃ to produce species that are eventually photolyzed or react with H or hydrocarbon radicals to form CO. The most efficient of these schemes from a column-integrated standpoint in the stratosphere is

$$\begin{gathered} {\text{H}}_2\text{O}+hv\to \text{H}+\text{OH} \\ \text{OH}+{\text{C}}_2{\text{H}}_2+\text{M}\to {\text{C}}_2{\text{H}}_2\text{OH}+\text{M} \\ {\text{C}}_2{\text{H}}_2\text{OH}+\text{H}\to \text{HCO}+{\text{CH}}_3 \\ \text{HCO}+\text{H}\to \text{CO}+{\text{H}}_2 \\ \text{H}+{\text{CH}}_3+\text{M}\to {\text{CH}}_4+\text{M} \\ \overline{\text{Net}:{\text{H}}_2\text{O}+{\text{C}}_2{\text{H}}_2+2\text{H}\to \text{CO}+{\text{CH}}_4+{\text{H}}_2,} \end{gathered}$$ (2)

with M representing any third atmospheric molecule or atom. However, these schemes represent a small percentage of the overall loss of H₂O and OH, with reactions that recycle the water dominating by more than an order of magnitude.

Other schemes that convert H₂O to CO and that involve the CH₃ radical (e.g., via the reactions O + CH₃ → H₂CO + H and OH + CH₃ → H₂CO + H₂) also occur and can be especially important in the upper stratospheres of Jupiter, Saturn, and Neptune. On Uranus, where the column abundance of C₂H_x species is small, schemes such as (2) above are relatively unimportant, and the dominant process converting the H₂O to CO from a column-integrated standpoint is

$$\begin{gathered} {\text{H}}_2\text{O}+hv\to 2\text{H}+\text{O} \\ {\text{CH}}_4+hv\to {\text{CH}}_3+\text{H} \\ \text{O}+{\text{CH}}_3\to {\text{H}}_2\text{CO}+\text{H} \\ {\text{H}}_2\text{CO}+hv\to {\text{H}}_2+\text{CO } \\ \overline{\text{Net}:{\text{CH}}_4+{\text{H}}_2\text{O}\to \text{CO}+{\text{H}}_2+4\text{H}.} \end{gathered}$$ (3)

Another important loss process for the water on all the giant planets is photolysis to produce OH, followed by reaction of the resulting OH with CO to form CO₂:

$$\begin{gathered} {\text{H}}_2\text{O}+hv\to \text{ H}+\text{OH} \\ \text{OH}+\text{CO }\to {\text{CO}}_2+\text{H } \\ \overline{\text{Net}:{\text{H}}_2\text{O}+\text{CO }\to {\text{CO}}_2+2\text{H}.} \end{gathered}$$ (4)

This scheme is an important loss process for both CO and H₂O, and provides the dominant mechanism for producing CO₂ in these atmospheres. Note that this scheme provides a photochemical source of carbon dioxide for the giant-planet stratospheres even if CO₂ is not directly released from the ablating grains or thermochemically produced during cometary impacts.

Carbon dioxide is lost by photolysis, with CO and oxygen atoms (either excited O(¹D) or ground state) as the products. The bulk of the O(¹D) reacts with background H₂ to produce OH and eventually water, while the bulk of the ground-state O atoms can react with CH₃ radicals to produce H₂CO and eventually lead back to CO. On Uranus and Neptune, the CO₂ is also lost through condensation in the lower stratosphere.

Carbon monoxide can be destroyed by photolysis, but only at very high altitudes, as it is shielded to a large extent by the more abundant H₂ and CH₄. The dominant loss reaction for carbon monoxide is H + CO + M → HCO + M, but the bulk of the HCO produced this way ends up back as CO through reaction of HCO with atomic H or through photolysis. Given the efficiency of CO recycling and the lack of permanent effective loss processes, carbon monoxide is very long lived in the giant-planet stratospheres.

Other oxygen species, such as methanol, formaldehyde, ketene, and acetaldehyde are produced from the coupled oxygen-hydrocarbon photochemistry, but in amounts that are currently unobservable. See Moses et al. (2000b) for their dominant production and loss reactions.

Scheme (1) above and others involving C₂H₄ and OH (see Moses et al., 2000b) can cause a slight reduction in the abundance of C₂H₂, C₂H₄, and other unsaturated hydrocarbons whose abundance depends on C₂H₂ and/or C₂H₄. However, for the water influx rates we derive for the giant planets, this reduction is negligible for all planets, even Saturn, with its relatively large inferred H₂O influx rate (see Fig. 10). The large CO abundance on Neptune, on the other hand, appears to affect the hydrocarbon photochemical products (see Fig. 13), reducing the abundance of C₂H₂, C₂H₄, and higher-order hydrocarbons whose production depends on C₂H₂ and C₂H₄. This reduction in hydrocarbon mixing ratios is caused by shielding of C₂H₆ from ultraviolet radiation in the ~1450–1550 Å range by the fourth positive band system of CO, leading to a reduced photolysis rate for C₂H₆ in the middle and lower stratosphere. However, this result is largely an artifact of the low spectral resolution of our UV cross sections and solar flux (i.e., 5-nm resolution in the relevant wavelength region). The fourth positive system of CO has a lot of fine structure not captured in our model (see Myer and Samson, 1970), with a fairly low continuum cross section between strong peaks that will not be as effective in shielding the ethane. Future models should test the effect of higher-resolution cross sections.

On Uranus, the methane homopause is so deep within the atmosphere that the bulk of the ablation of icy grains occurs above the region where methane resides. The coupled oxygen-carbon chemistry then occurs through CO and H₂O, or through CO alone, not through H₂O and CH₄. In fact, the photolysis of CO actually provides a source of CH₄ in the thermosphere, which shows up as the extra bulge in the 10⁻⁴−10⁻² mbar region in Fig. 12. The dominant mechanism for producing the CH₄ in this region is

$$\begin{gathered} \text{CO}+hv\to \text{C}+\text{O} \\ \text{C}+{\text{H}}_2+\text{M}{\to }^3{\text{CH}}_2+\text{M} \\ \text{H}{+}^3{\text{CH}}_2\to \text{CH}+{\text{H}}_2 \\ \text{CH}+{\text{H}}_2+\text{M}\to {\text{CH}}_3+\text{M} \\ \text{H}+{\text{CH}}_3+\text{M}\to {\text{CH}}_4+\text{M } \\ \overline{\text{Net}:\text{CO}+{\text{H}}_2+2\text{H}\to {\text{CH}}_4+\text{O}.} \end{gathered}$$ (5)

4. Other potential chemical processing of the ablated vapor

The observations described in sections 3.2–3.5 indicate that CO is more abundant than H₂O in the stratospheres of the giant planets. Large cometary impacts may explain the high CO/H₂O ratios on Neptune (Lellouch et al., 2005), Saturn (Cavalié et al., 2010), and in the southern hemisphere (at least) of Jupiter (Lellouch et al., 1997, 2002), with the oxygen from the comet being thermochemically converted to CO in high-temperature shocks during a plume-splashback phase of the impact (Zahnle, 1996). However, our predicted magnitude of the “background” oxygen influx to Jupiter and Uranus from the ablation of ice-rich dust grains is consistent with the amount needed to explain the CO in lower stratospheres of these planets. In fact, on Jupiter, our predicted oxygen ablation rate from icy grains is a factor of ~250 larger than is needed to explain the low background amount of water not related to the recent Comet Shoemaker-Levy 9 impacts (Lellouch et al., 2002). Why, then, is the background water abundance on Jupiter so low? We demonstrate in section 3.6 that photochemistry cannot efficiently convert ablated water vapor to CO in giant-planet stratospheres. Does some other chemical processing occur during the meteoroid entry phase or immediately after that can explain the relatively large CO/H₂O ratios in the stratospheres of Jupiter and Uranus?

One potential source of the CO is reaction of the oxygen in ices with the carbon from within the grains themselves. From a thermochemical equilibrium standpoint, O and CO are the favored forms of the oxygen at the high temperatures and low pressures relevant to the silicate ablation process, with H₂O being a very minor component. If reactions between vapor species within the grain itself occur as the grain heats up, or if reactions occur within the meteor trail, the tendency of these kinetic reactions could be to drive the oxygen toward O and CO if there is sufficient time for these reactions to occur (and note that the grains typically remain at the relevant high temperatures for tens of seconds or less). Thus, if differential ablation is not very effective during meteoroid entry and the silicate phases dominate the grain heating behavior, then water would be a minor species being released from the grains. For example, Fig. 15 shows the oxygen vapor partitioning in thermochemical equilibrium at pressure and temperature conditions relative to the peak of the silicate ablation profile for grain material of the same composition as the coma of Comet Hale Bopp (Lisse et al., 2007). Here, we assume a solar ratio for elements not considered by Lisse et al. (2007), with P/C and N/C remaining in solar proportions, and other elements remaining in solar proportions relative to Si, and thermochemical equilibrium is calculated as described in Moses et al. (2013). Note from Fig. 15 that O, CO, and SiO dominate the oxygen vapor under these conditions, with H₂O coming in at ≪ 1%.

Figure 15:

Partitioning of the oxygen-bearing vapor species in thermochemical equilibrium for a cometary composition grain (Lisse et al., 2007, see text) at the temperatures and pressures corresponding to the peak of the silicate ablation profile for Jupiter (Top left), Saturn (Top right), Uranus (Bottom left), Neptune (Bottom right).

Another possibility is dissociation of any molecular vapor phases following ablation, simply resulting from the high velocities of entry. According to the dust dynamical modeling results of Poppe (2016), grain velocities at atmospheric entry are in the range 59.5–70.5 km s⁻¹ for Jupiter, 35.5–44.5 km s⁻¹ for Saturn, 20.5–29.5 km s⁻¹ for Uranus, and 22.5–28.5 km s⁻¹ for Neptune. From the point of view of the just-ablated oxygen-bearing molecules, they are experiencing collisions with H₂ molecules that have incoming energies of 37–52 eV for Jupiter, 13–21 eV for Saturn, 4.4–9.1 eV for Uranus, and 5.3–8.5 eV for Neptune. The ionization energy for H₂O is 12.62 eV (Reutt et al., 1986), so the ablated water molecules can be ionized on Jupiter and Saturn, but not Uranus and Neptune. The ionization energies for O, CO, and SiO are 13.6, 14.0, and 11.6 eV (Linstrom and Mallard, 2017; Hildenbrand and Murad, 1969), so these species can also be potentially ionized on Jupiter and Saturn, but not Uranus and Neptune. The H–OH bond energy is 5.1 eV, and that of O–H is 4.4 eV (Okabe, 1978), so dissociation of the H₂O and OH can occur on all the planets while the water is still being decelerated. The bond energies of C–O and Si–O are 11.09 and 7.93 eV, respectively (Okabe, 1978; Hildenbrand and Murad, 1969), so while collisions with H₂ may have su cient energy to dissociate CO and SiO on Jupiter and Saturn, that is not necessarily the case on Uranus and Neptune. The final ionization and energy states of the oxygen products will be important in determining the ultimate fate of the oxygen from further chemical reactions; unfortunately, we could not find experimental or theoretical data on collisions of H₂ with H₂O, CO, SiO at relevant energies.

If these collisions lead to the formation of OH, O⁺, or excited oxygen atoms such as O(¹D), the main final product will be water, due to the effectiveness of reactions of these species with H₂. If the collisions primarily produce atomic O, which seems likely based on the above arguments, then the oxygen can end up in either CO or H₂O, depending on whether the ablation is occurring above or below the methane homopause. Below the CH₄ homopause, atomic oxygen will largely end up in CO through the reactions O + CH₃ → H₂CO + H (followed by photolysis and subsequent reactions to form CO) and O + CH₃ → CO + H₂ + H. Above the homopause, the atomic O is longer lived and reacts relatively slowly with H₂ to form OH and eventually H₂O, but the vapor diffuses downward sufficiently slowly on all the giant planets that any atomic O ablated above the methane homopause will largely end up as H₂O.

Figure 16 demonstrates the fate of the volatile oxygen in the incoming grains on Jupiter if it were all quickly converted to atomic O once released from the grains. Two different cases are shown. The first case (black dotted curves) assumes that differential ablation dominates, such that the oxygen from the icy component of the grains is released first, at high altitudes, and the second case (red dashed curves) assumes that simple ablation dominates, such that the oxygen from icy grains is released only when the silicate phases ablate at lower altitudes (see Fig. 4). Because a significant fraction of the silicate ablation occurs below the methane homopause, a significant fraction of the O released in the latter case ends up in CO, while the O in the first case overwhelmingly ends up as H₂O. Note that the first case results in too much H₂O in Jupiter’s atmosphere compared with the observationally inferred “background” water abundance (i.e., the H₂O not related to the SL9 impacts, Lellouch et al. 2002), while the second case provides a decent fit to the H₂O, CO, and CO₂ observations for the background abundances not related to SL9.

Figure 16:

Mixing ratio profiles for H₂O (Top left), CO (Top right), CO₂ (Bottom left), and O (Bottom right) on Jupiter under the assumption that all the oxygen in the ices arrives in the atmosphere as (1) CO, with the icy grain ablation profile shown in Fig. 4 (green curves); (2) H₂O, with the icy grain ablation profile shown in Fig. 4 (blue curves); (3) O, with the icy grain ablation profile shown in Fig. 4 (dotted black curves); (4) O, with the silicate grain ablation profile shown in Fig. 4 (dashed red curves). Above the methane homopause, chemical reactions largely convert the atomic O to H₂O, while below the homopause, the O is converted to CO. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

This better fit from the low-altitude ablation case could be used as an argument in favor of the simple ablation process for Jupiter. Alternatively, it is possible that the available oxygen in the incoming grains is tied up in silicates and/or hydrated silicates in the first place, rather than in ices. Jupiter-family comet grains spend more of their lifetime at smaller heliocentric distances than their Oort-cloud or Edgeworth-Kuiper belt counterparts (Poppe, 2016), and it is possible that sublimation of the ice phases has occurred before the Jupiter-family comet grains enter the Jovian atmosphere. However, studies subjecting carbonaceous chondrite samples to stepped pyrolysis (Court and Sephton, 2014) find that H₂O is released at a variety of temperatures, ranging from less than 600 K (perhaps due to desorption of terrestrial water contamination) to 700–900 K (dehydration of hydrated minerals) to > 1100 K (mineral decomposition), so it might be expected that the ablation of hydrated-mineral phases would release water at temperatures intermediate between our assumed organic and silicate cases, rather than requiring much higher magnesium-silicate vaporization temperatures. In any event, more sophisticated ablation models that consider realistic particle compositions and structures, as well as the immediate fate of the ablated vapor, will be needed to shed more light on the interesting puzzle of the low background water abundance in the Jovian stratosphere.

Fig. 17 illustrates the same cases for Uranus. Because the methane homopause is so deep in the atmosphere on Uranus (due to weak atmospheric mixing), the dust grains ablate largely in the methane-free thermosphere, particularly for the differential-ablation case where the ice ablates high in the atmosphere (black dotted curves). Therefore, the O is converted to H₂O in that case, and the results are not too different from the assumption of the oxygen arriving purely as H₂O from icy grain ablation. On the other hand, a portion of the silicate ablation curve for Uranus (see Fig. 6) falls within and below the methane homopause in the 0.01–0.1 mbar region, so more of the O is converted to CO under the assumption of simple ablation, for which the silicate phases dominate the gas release. Even in that case, however, there is insufficient CO and CO₂ being produced to explain the observations of Cavalié et al. (2014) and Orton et al. (2014b). As discussed in section 3.4, uncertainties in our meteoroid influx and ablation calculations could potentially be the cause of the model-data mismatch, combined with the possibility of any CO being released during the ablation process remaining as CO due to the lower entry energies at Uranus. However, the fact that CO₂ is grossly underpredicted in the models suggests that either CO₂ is also being released from the grains and survives the ablation process and collisional aftermath (CO–O bond energy is 5.453 eV Okabe 1978; see the solid line model shown in Fig. 12), or that Uranus has also experienced a large cometary impact within the last few hundred years that deposited both CO and CO₂. Note that because H₂O condenses at such high altitudes on Uranus, it is possible that a non-trivial fraction of oxygen from any putative cometary impact could be tied up in water-ice hazes in the stratosphere.

Figure 17:

Mixing ratio profiles for H₂O (Top left), CO (Top right), CO₂ (Bottom left), and O (Bottom right) on Uranus under the assumption that all the oxygen in the ices arrives in the atmosphere as (1) CO, with the icy grain ablation profile shown in Fig. 6 (green curves); (2) H₂O, with the icy grain ablation profile shown in Fig. 6 (blue curves); (3) O, with the icy grain ablation profile shown in Fig. 6 (dotted black curves); (4) O, with the silicate grain ablation profile shown in Fig. 6 (dashed red curves). Above the methane homopause, chemical reactions largely convert the atomic O to H₂O, while below the homopause, the O is converted to CO. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

5. Conclusions

Small interplanetary dust grains are continually bombarding the upper atmospheres of Jupiter, Saturn, Uranus, and Neptune. Ablation of these grains during high-velocity atmospheric entry can deliver oxygen, silicates, metals, and other material to the thermospheres and stratospheres of these planets — material that is otherwise not intrinsically present at such altitudes. Using the Poppe (2016) dynamical model predictions for the dust populations in the outer solar system, we have modeled the meteoroid ablation process on the giant planets, along with the subsequent oxygen-hydrocarbon neutral stratospheric photochemistry that results from meteoroid ablation.

We find that dust ablation occurs over a broad altitude range within the upper atmospheres of the giant planets. Under the assumption that differential ablation dominates (McNeil et al., 1998), whereby different materials within the grain ablate at different points as the grain heats up, our models predict that the volatile icy components within the grains will ablate at the highest altitudes, beginning well above the methane homopause but extending down into the upper stratosphere where methane is present. The more refractory components take longer to reach temperatures high enough to vaporize the material, so the ablation of these components (i.e., silicates, metals) extends well below the methane homopause and into the middle stratospheres of the planets. Organic components will ablate at altitudes intermediate between those of the ice and silicate components. The larger impact velocities at Jupiter and Saturn lead to higher grain temperatures during atmospheric entry for any particular particle size and material properties, leading to more efficient ablation than on Uranus and Neptune. In fact, impact velocities at Uranus and Neptune are low enough that not all the silicates within the grains will completely ablate before the grains are decelerated and cool. The lower the initial mass of a grain coming into Uranus and Neptune, the smaller the mass fraction that is lost during the ablation process.

We tracked the fate of the ablated oxygen-bearing species with a 1D photochemical model. The molecular and/or atomic makeup of the ablated vapor is not obvious from first principles, so we tested the sensitivity of the photochemical results to the form of the ablated vapor. Nominal best-fit models were created by adjusting the relative fraction of ablated molecules such as H₂O, CO, and CO₂ to produce the best fits to observations of these species on the giant planets.

The following main results are obtained from the theoretical calculations and model-data comparisons:

• The effective oxygen influx rate to Jupiter from the ablation of the icy components within the grains is ${1.0}_{-0.7}^{+2.2}\times {10}^7$ O atoms cm⁻² s⁻¹. Dust from Jupiter-family comets dominates this influx rate, and the magnitude is consistent with what is needed to explain the large “background” CO abundance in the Jovian lower stratosphere and upper troposphere that is unrelated to the recent Comet Shoemaker-Levy 9 impacts (Bézard et al., 2002). However, because the background (non-SL9) H₂O abundance is inferred to be quite small in Jupiter’s stratosphere (Lellouch et al., 2002), we conclude that the oxygen ablating from the incoming grains must be released directly in the form of CO, must be thermochemically converted to CO soon after ablation, or must be released as atomic O below the methane homopause, with subsequent photochemistry involving reactions of atomic O with CH₃ converting the oxygen to CO. If the ablated oxygen were released as H₂O or OH, or as O or O⁺ above the methane homopause, with only photochemical reactions shaping the speciation, then the predicted background water abundance in the Jovian stratosphere would be much larger than is observed.

• Given the large expected oxygen influx rates to Jupiter from the ablation of interplanetary dust, and the requirement that the ablated oxygen predominantly end up as CO rather than H₂O, we conclude that dust ablation plays a major role in delivering external oxygen to Jupiter. The delivery of oxygen by small comets, invoked by Bézard et al. (2002), may still be important on Jupiter but is not required to explain the observations.

• The effective oxygen influx rate to Saturn from the ablation of the ices within the incoming interplanetary dust particles is ${7.4}_{-5.1}^{+16}\times {10}^4$ O atoms cm⁻² s⁻¹. The interplanetary dust at Saturn derives from a mix of Jupiter-family comet, Oort-cloud comet, and Edgeworth-Kuiper belt dust populations. Our predicted oxygen influx rate from interplanetary dust is more than an order of magnitude too small to explain the observed stratospheric H₂O, CO, and CO₂ abundances on Saturn (Feuchtgruber et al., 1997; Moses et al., 2000b; Bergin et al., 2000; Cavalié et al., 2009, 2010; Abbas et al., 2013), so we conclude that interplanetary dust plays a minor role in delivering external oxygen to Saturn. Instead, Saturn likely gets its external oxygen from water ejected from Enceladus (e.g., Jurac and Richardson, 2007; Cassidy and Johnson, 2010; Hartogh et al., 2011; Fleshman et al., 2012), from water and other oxygen from the rings (e.g., Connerney and Waite, 1984; Luhmann et al., 2006; Tseng et al., 2010; Moore et al., 2015), and/or from CO deposited from a large cometary impact that occurred a couple hundred years ago (e.g., Cavalié et al., 2010).

• Because of the Enceladus and ring sources of H₂O, Saturn likely has a larger thermospheric H₂O/CO ratio than all the other giant planets (cf. Figs. 9, 11, 12, 14). The incoming water will affect ionospheric chemistry and structure (see Connerney and Waite, 1984; Moses and Bass, 2000; Moore et al., 2015), but our models demonstrate that at the H₂O influx rate needed from these sources to explain the observed stratospheric water abundance on Saturn, coupled oxygen-hydrocarbon photochemistry does not have a notable affect on the abundances of neutral hydrocarbon photochemical products (see also Moses et al., 2000b).

• The effective oxygen influx rate to Uranus from the ablation of the icy grain components is ${8.9}_{-6.1}^{+19}\times {10}^4$ O atoms cm⁻² s⁻¹. Edgeworth-Kuiper belt grains supply the largest fraction at Uranus, but Oort-cloud comet dust and Jupiter-family comet dust populations also contribute. Our predicted oxygen influx rate here is somewhat smaller than is needed to explain the observed amount of H₂O, CO, and CO₂ in the stratosphere of Uranus (Feuchtgruber et al., 1999; Cavalié et al., 2014; Orton et al., 2014b), which our best-fit models indicate is of the order ~4 × 10⁵ O atoms cm⁻² s⁻¹. This underprediction could simply be a consequence of uncertainties in our dust population or ablation calculations/assumptions, or it could suggest an additional source of external oxygen to Uranus, such as from cometary impacts. Impact rate studies for the outer solar system (Levison and Duncan, 1997; Zahnle et al., 2003) suggest that kilometer and sub-kilometer size comets may deliver an oxygen amount similar to what we derive from interplanetary dust (Poppe, 2016). This result, along with the fact that photochemical models that just consider ablated vapor in the form of CO or H₂O fail to reproduce the CO₂ abundance, and the fact that most of the ablation occurs above the methane homopause and so favors H₂O over CO as a final photochemical product from the ablated oxygen, combine to suggest that a cometary impact within the past few hundred years may contribute notably to the stratospheric CO and CO₂ currently seen on Uranus.

• The comparatively high inferred H₂O/CO influx-rate ratio on Uranus in comparison to Jupiter and Neptune may be a consequence of the weak Uranian atmospheric mixing and resulting low-altitude methane homopause. Most of the dust ablation takes place at altitudes where atmospheric methane is not present, so the photochemistry that occurs after the oxygen is ablated favors H₂O production over CO production. Alternatively, the high H₂O/CO ratio may indicate a local source of water from the Uranian rings or satellites.

• The effective oxygen influx rate to Neptune from the ablation of the ices within the incoming interplanetary dust particles is ${7.5}_{-5.1}^{+16}\times {10}^5$ O atoms cm⁻² s⁻¹, with the bulk of the dust deriving from the Edgeworth-Kuiper belt. Although this dust influx rate can support the observed amount of H₂O in Neptune’s atmosphere (Feuchtgruber et al., 1997, 1999), it is more than an order of magnitude too small to explain the huge amount of CO seen in Neptune’s middle stratosphere (e.g., Lellouch et al., 2005; Hesman et al., 2007; Fletcher et al., 2010a; Luszcz-Cook and de Pater, 2013). This model-data mismatch, along with the CO vertical profile that requires an external source and the fact that HCN was also discovered in Neptune’s stratosphere (e.g., Marten et al., 1993), strongly suggests that Neptune experienced a large cometary impact within the past few hundred years (see Lellouch et al., 2005). Based on our dust ablation calculations, the bulk of the stratospheric oxygen on Neptune at the present time derives from that cometary impact, and not from interplanetary dust.

• Coupled oxygen-hydrocarbon photochemistry is not very effective in the stratospheres of the giant planets. Although H₂O is lost readily by UV photolysis, the main product, OH, reacts with H₂ to reform the water, so the water is quickly recycled and remains stable. A small fraction of oxygen originally in water can be converted to CO through addition reactions of OH with C₂H₂ and C₂H₄, followed by further reactions that eventually produce CO (see section 3.6). At the inferred H₂O influx rates for the giant planets, these reactions have very little effect on hydrocarbon abundances. By the same token, CO is shielded to some extent from photolysis below the methane homopause, and any atomic oxygen thus formed ends up largely reacting with CH₃ to eventually reform the CO. At the inferred CO influx rates for the giant planets, we only see CO affecting hydrocarbon abundances on Neptune — through the shielding of C₂H₆ from photolysis — and that result is probably an artifact of the low-resolution UV cross sections in our model. Coupled CO-H₂O photochemistry produces CO₂, through the reaction CO + OH → CO₂ + H.

• Cometary impacts naturally deliver a much greater amount of CO than H₂O to giant-planet stratospheres (e.g., Zahnle, 1996; Lellouch, 1996), but the high observed CO/H₂O ratio on the giant planets could also be a consequence of CO and O being the favored forms of volatile oxygen in thermochemical equilibrium at the high temperatures and low pressures encountered during the ablation of cometary-composition grains. If simple ablation dominates over differential ablation, such that the volatile oxygen in the grains is released by ablation below the homopause, and if subsequent collisions with ambient H₂ molecules dissociate molecular species to produce atomic O, then further photo-chemical reactions will strongly favor CO over H₂O in giant-planet atmospheres. Note that the CO abundance in giant-planet stratospheres rivals that of the major hydrocarbon photochemical products, a fact that is not widely appreciated (see Figs. 9, 11, 12, 14).

• The apparently large external source of CO on the giant planets from both comets and the ablation of interplanetary dust complicates the determination of the deep oxygen abundance on the giant planets (e.g. Prinn and Barshay, 1977; Lewis and Fegley, 1984; Fegley and Prinn, 1985, 1986; Fegley and Lodders, 1994; Lodders and Fegley, 2002; Visscher and Fegley, 2005; Visscher et al., 2010b; Visscher and Moses, 2011; Wang et al., 2015, 2016; Cavalié et al., 2017). The externally supplied CO is transported downward into the troposphere, adding to the quenched component upwelling from the interior. Therefore, it may be difficult to uniquely separate the CO mixing ratio resulting from the interior source, which then makes it difficult to indirectly determine the deep H₂O abundance on the giant planets from this method.

The inferred influx rates from our photochemical models that provide the best overall fits to the available H₂O, CO, and CO₂ observations are shown in Table 1. Note that these solutions are not unique, so the influx values should be considered as representative only. The “effective” oxygen influx rates — independent of the form in which the oxygen was introduced — given by Poppe (2016) provide a robust measure of the amount of total oxygen delivered to the giant planets from interplanetary dust impacts, independent of any photochemical modeling uncertainties.

Table 1:

Dust-Supplied Oxygen Influx Rates (cm⁻² s⁻¹) From Our Best-Fit Photochemical Models

	CO	H2O	CO2	extra source of H2O needed?	extra source of CO needed?
Jupiter	7 × 106	4 × 104	1 × 105	Yes (from SL9)	Yes (from SL9)
Saturn*	6.7 × 104	7.2 × 103	< 1 × 103	Yes (Enceladus)	Yes (comet?)
Uranus	2.7 × 105	1.2 × 105	3 × 103	No?	No?
Neptune*	5 × 105	2 × 105	2.3 × 104	No	Yes (comet)

^*Using the cometary models shown in Figs. 11 & 14.

The ablation of interplanetary dust will have other interesting consequences for giant-planet atmospheres. The addition of oxygen to the thermosphere — potentially in the form of both CO, which has typically been ignored to date, as well as H₂O — will affect ionospheric chemistry and structure through reactions with the main ions H⁺ (for H₂O) and H₃⁺ (for CO), with both H₃O⁺ and HCO⁺ becoming important components in the lower ionosphere. Other vapor phases released from ablation could also affect ionospheric chemistry and structure, with long-lived atomic metal ions being particularly important in the lower ionosphere. Residual unablated grains or tiny recondensed meteoric debris particles could also affect ionospheric structure by becoming a sink for electrons and could provide a source of condensation nuclei that aids nucleation and condensation of other gas-phase species in the lower stratosphere. Water introduced to the stratosphere from meteoroid ablation will condense in the lower stratosphere of all the giant planets, and CO₂ will condense on Uranus and Neptune. The additional aerosols provided from the ablation of interplanetary dust can potentially affect hydrocarbon condensation at lower altitudes, as well as atmospheric temperatures, atmospheric transmission in the UV, and heterogeneous chemistry on grain surfaces.

The ablation models presented here contain a lot of simplifying assumptions, such as uniform composition, uniform heating throughout the grain, and spherical particles. More sophisticated future models could consider mixed compositions, diffusion of gases through the grain, sputtering, fragmentation, thermochemical reactions within the heated grain, and other more realistic treatments of the meteor stage. Future models should also more realistically track the immediate fate of the energetic gases released during ablation, in terms of the consequences of further energetic collisions with atmospheric gases before the ablated vapor becomes thermalized. We have focused here on the consequences to neutral atmospheric chemistry, but as mentioned above, the consequences of the ablation of interplanetary dust for ionospheric chemistry and the electron density profiles on the giant planets could be quite interesting. It would also be worthwhile to investigate how the aerosols that result from the ablation process influence other physical and chemical processes in the atmosphere as the particles rain down through the atmosphere (e.g., Frankland et al., 2016).

Although interplanetary dust particles represent only a tiny incremental mass addition to the giant planets, the consequences of the continual dust bombardment can have important observable consequences for the upper atmospheres of these planets.