Exploring the Role of the Third Active Site Metal Ion in DNA Polymerase η with QM/MM Free Energy Simulations

Abstract

The enzyme human DNA polymerase η (Pol η) is critical for bypassing lesions during DNA replication. In addition to the two Mg²⁺ ions aligning the active site, experiments suggest that a third Mg²⁺ ion could play an essential catalytic role. Herein the role of this third metal ion is investigated with quantum mechanical/molecular mechanical (QM/MM) free energy simulations of the phosphoryl transfer reaction and a proposed self-activating proton transfer from the incoming nucleotide to the pyrophosphate leaving group. The simulations with only two metal ions in the active site support a sequential mechanism, with phosphoryl transfer followed by relatively fast proton transfer. The simulations with three metal ions in the active site suggest that the third metal ion may play a catalytic role through electrostatic interactions with the leaving group. These electrostatic interactions stabilize the product, making the phosphoryl transfer reaction more thermodynamically favorable with a lower free energy barrier relative to the activated state corresponding to the deprotonated 3’OH nucleophile, and also inhibit the subsequent proton transfer.

Graphical Abstract

Introduction

DNA polymerase η (Pol η) is an essential enzyme for the replication of DNA and is capable of repairing damage caused by exposure to solar radiation. In particular, ultraviolet (UV) radiation causes the formation of covalent bonds between adjacent thymine nucleotides in the DNA, forming thymine-thymine dimers that lead to stalls during replication. Pol η rescues the stalled replication forks at thymine-thymine dimers by extending the primer with the correct complementary bases and hence bypassing the lesion.^1–2 The lack of fully functional Pol η leads to Xeroderma pigmentosum, a disease that is associated with UV-induced skin damage and skin cancer.³ Furthermore, Pol η has been shown to interfere with Pt-based anticancer agents, enabling cancer cells to proliferate during chemotherapy treatment.⁴ As a result, Pol η is a target for the development of skin cancer drugs and strategies to overcome cancer chemotherapy resistance.

Given the biomedical importance of Pol η, numerous experimental and computational studies have been conducted to examine its mechanism.^{2, 5–19} Recently, evidence of a possible catalytic role for a third metal ion in the active site of Pol η was revealed through time-resolved X-ray crystallography, where the electron densities associated with the third metal ion and the catalytically formed new phosphodiester bond appear simultaneously at ~60 s and continue to grow concurrently until ~600 s.⁸ However, these data do not definitively show whether the third metal ion is required for catalysis or is a result of catalysis. A third metal ion has also been observed in the active site of other polymerases and ribozymes, but the catalytic role of this third metal ion in these systems is also not fully resolved, although several proposals have been examined.^{18, 20–27}

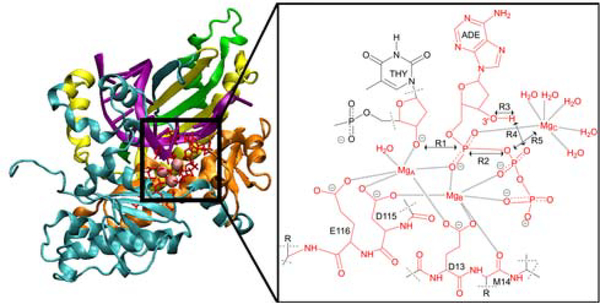
The objective of this paper is to investigate the role of the third divalent metal ion in the active site of Pol η, as depicted in Figure 1. Specifically, we examine the possibility that this third metal ion may play a catalytic role in the phosphoryl transfer mechanism. Previous quantum mechanical/molecular mechanical (QM/MM) simulations of Pol η focused on the proton transfer steps relevant to the proposed self-activated mechanism involving proton transfer from the nucleophilic 3’OH to the pyrophosphate leaving group and did not simulate the phosphodiester bond cleavage part of the mechanism.¹⁶ Moreover, these previous QM/MM simulations included only two metal ions in the active site and considered the third metal ion to be transiently bound only in the product state, with the predominant roles of assisting the exit of the pyrophosphate leaving group and preventing the reverse reaction. Another recent computational study using the empirical valence bond method suggested that the main role of the third metal ion is to lower the barrier for product release, but this study used a small number of specific reaction coordinates that did not enable the simulation of the entire catalytic reaction, also noting that investigation of catalysis would require QM/MM simulations with more extensive sampling.¹⁸

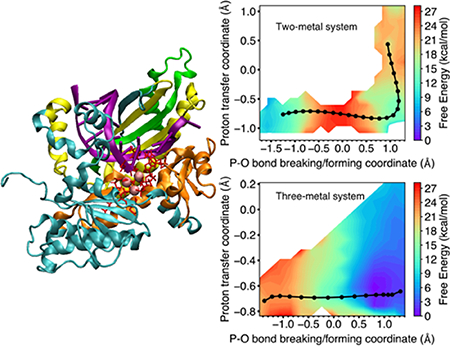
Figure 1.

Left: Structure of Pol η (PDB ID: 4ECV) with domains colored as follows: palm (cyan), finger (orange), thumb (yellow), and polymerase-associated domain (green). Right: The active site of Pol η containing three Mg²⁺ ions in the reactant state. For the QM/MM simulations presented herein, the atoms in red are in the QM region, and the dashed lines indicate the QM/MM boundaries. The key reaction coordinates are labeled R1 through R5, and the ten other reaction coordinates used in the simulations are depicted in Figure S1 of the Supporting Information (SI).

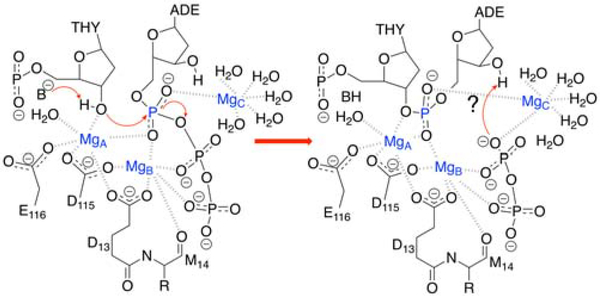
To investigate the possible catalytic role of the third metal ion, we utilized a finite temperature string method with umbrella sampling in conjunction with a QM/MM treatment^28–29 to generate the minimum free energy path and explore the relevant regions of the multidimensional free energy surface. In addition to the phosphoryl transfer reaction, we also examined the possibility of proton transfer from 3’OH to O2B, thereby protonating the pyrophosphate leaving group (Figure 2), as proposed in the previous theoretical studies that included only two metal ions in the active site.¹⁶ Our simulations considered the possibility of both sequential and concerted mechanisms for the phosphoryl transfer and proton transfer steps. A comparison of the minimum free energy paths and free energy surfaces for the reaction with two and three metal ions in the active site elucidates the role of the third metal ion.

Figure 2.

The proposed mechanism of Pol η. An undetermined base B deprotonates the O3’ of thymine, preparing it for the phosphoryl transfer reaction shown in this figure, followed by the possibility of a self-activating deprotonation of the incoming nucleotide (adenine) to protonate the leaving group, as indicated by a question mark.

Methods

Our simulations were based on the crystal structures corresponding to PDB ID: 3MR2 and PDB ID: 4ECS for the reactant and product, respectively, with two metal ions in the active site and PDB ID: 4ECV for the reactant and product with three metal ions in the active site.^7–8 The QM region was composed of 124 and 140 atoms for the two-metal and three-metal systems, respectively, including the active site metal ions, the metal-coordinated ligands, the incoming nucleobase, and the active site water molecules within 3 Å of the active site metal ions (Figure 1). The remainder of the system was treated with the AMBER ff14SB force field^30–34 within the QM/MM framework with the QM region at the DFT/B3LYP/6–31G** level.^35–36 The triphosphate of dATP, which has three oxygen atoms coordinated to Mg_B in the reactant state and an oxygen coordinated to Mg_C in the product state of the three-metal system, is assumed to be fully deprotonated based on the experimentally measured pK_a of 4.6 for Mg²⁺-bound dATP³⁷ (Table S1). The free energy surface was computed as a function of eleven and fifteen reaction coordinates for the two-metal and three-metal systems, respectively (Figure S1). These reaction coordinates were chosen to describe the structural changes occurring during the phosphoryl transfer and proton transfer reactions. The QM/MM free energy simulations were performed with a QChem³⁸/CHARMM³⁹ interface, and the computational details are given in the SI.

For each system, two independent finite temperature string simulations starting from different initial strings were performed. The two initial strings corresponded to the sequential mechanism, in which the phosphoryl transfer reaction results in a stable intermediate prior to the proton transfer, and the concerted mechanism, in which both reactions occur in the absence of a stable intermediate (i.e., a single barrier connects the reactant and product associated with both phosphoryl transfer and proton transfer). Previous simulations of the HDV ribozyme indicated that this simulation approach is robust enough to produce the same final mechanism from mechanistically distinct initial strings.²⁹ Similarly, our simulations on Pol η indicate that the two mechanistically distinct initial strings lead to the same mechanism in the converged string, although quantitative differences in the reaction free energies and free energy barriers were observed due to limitations in sampling (Figures S2 and S3). For each system, we present the results from the string that was better converged due to a greater number of images, but we provide the results from the other independent string in the SI to illustrate that the final mechanism is independent of the initial string.

Results/Discussion

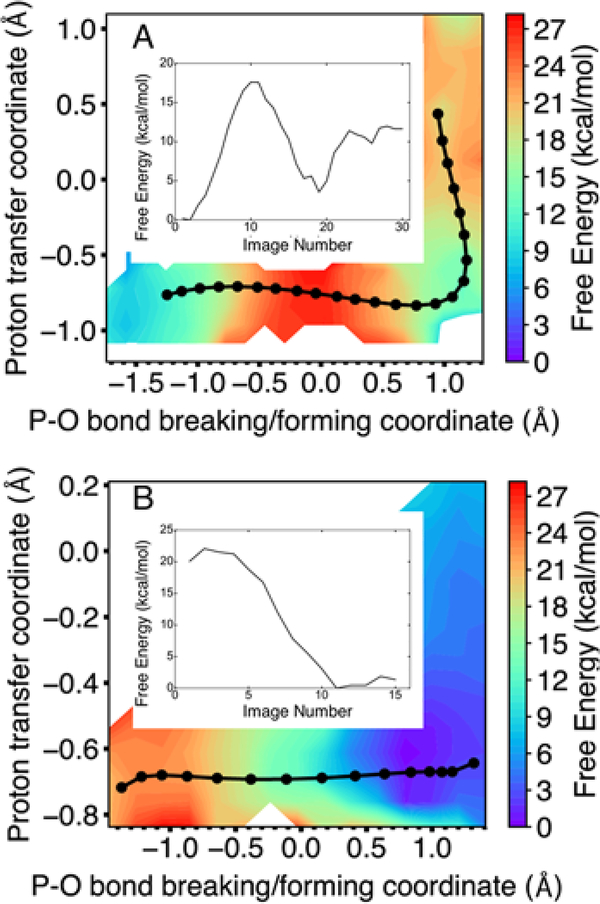
We calculated the multidimensional free energy surface as a function of the eleven and fifteen reaction coordinates for the two-metal and three-metal systems, respectively. Figure 3 depicts the multidimensional free energy surfaces projected onto the two-dimensional space defined by the proton transfer coordinate (R1 – R2) and the coordinate associated with phosphorous-oxygen bond breaking and forming (R3 – R4) for the two-metal and three-metal systems, where R1 through R4 are defined in Figure 1. For each system, the minimum free energy path (MFEP) is depicted in black on the two-dimensional free energy surface, and the free energy along the MFEP is provided in a one-dimensional plot shown as an insert. Figure 4 depicts the values of key reaction coordinates along the MFEP, where the reaction coordinates are defined in Figure 1. Analysis illustrating the convergence of the strings is provided in Figures S5 and S6.

Figure 3.

Two-dimensional free energy surface as a function of the proton transfer coordinate (R1 – R2) and the P–O bond breaking/forming coordinate (R3 – R4) for the Pol η system with (A) two metal ions and (B) three metal ions in the active site. For each system, the MFEP is shown in black, with the images along the string depicted as black circles, and the free energy along the MFEP is shown in the inset as a function of evenly spaced images. The two-metal system follows a sequential mechanism, with phosphoryl transfer preceding proton transfer, while the three-metal system exhibits only phosphoryl transfer with no subsequent proton transfer. The results from two independent string simulations corresponding to two different initial mechanisms, along with statistical error bars, are given in Figures S2 and S3 for the systems with two metal ions and three metal ions, respectively.

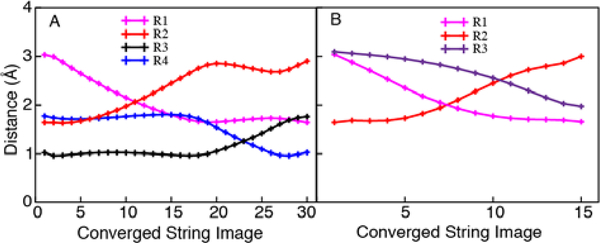
Figure 4.

Plots of select reaction coordinates (defined in Figure 1) along the MFEPs shown in Figure 3 for Pol η with (A) two metal ions and (B) three metal ions in the active site. The reaction coordinates correspond to the following distances: R1 (O3’-P, magenta); R2 (P-O3’, red); R3 (HO3’-O2B, black); R4 (O2B-HO3’, blue); and R5 (Mg_C-O3A, purple).

For the two-metal system, the MFEP corresponds to a sequential mechanism, in which the phosphoryl transfer reaction precedes the proton transfer reaction (Figure 3A). The intermediate is ~4 kcal/mol higher than the reactant with a barrier of ~18 kcal/mol for the first step. The product is ~10 kcal/mol higher than the reactant with a barrier of ~5 kcal/mol for the second step. For this system, the reactant is defined to be the structure on the left side of Figure 2 after the initial proton abstraction, the intermediate is defined to be the structure on the right side of Figure 2, and the product is the result of the proton transfer indicated on the right side, all in the absence of the third metal. The sequential mechanism for the two-metal system is also illustrated by Figure 4A, which depicts the four key reaction coordinates R1 through R4 along the MFEP, clearly indicating that the P–O bond breaking/forming (red/magenta curves in Figure 4A) occurs prior to the proton transfer (blue/black curves in Figure 4A). The proton transfer barrier in this sequential mechanism is qualitatively consistent with previous metadynamics simulations of the two-metal system, which produced a free energy barrier of ~2 kcal/mol.¹⁶ This previous work did not investigate the three-metal system.

For the three-metal system, the MFEP corresponds to only the phosphoryl transfer reaction without a subsequent proton transfer reaction, and the reaction is thermodynamically downhill with no observable barrier (Figure 3B). Our simulations suggest that the proton transfer reaction does not occur in the three-metal system because of electrostatic effects. Thus, for this system, the reactant is defined to be the structure on the left side of Figure 2 after the initial proton abstraction, and the product is defined to be the structure on the right side of Figure 2. According to the X-ray crystal structures (PDB ID: 4ECV)⁸ of the reactant and product states, the third divalent metal ion in the active site loses a water ligand and coordinates to the highly negatively charged leaving group of pyrophosphate in the product (Figure 2). The presence of the positively charged metal ion partially neutralizes the negatively charged leaving group and thereby disfavors protonation. The coordination of the third metal ion to the O3A oxygen of the pyrophosphate leaving group (R5 in Figure 1) is illustrated by the shortening of this distance during the phosphoryl transfer reaction (Figure 4B, purple curve, decreasing as the red/magenta curves indicate phosphoryl transfer).

In the reactant state for these free energy simulations, the 3’OH nucleophile is already activated by deprotonation, and all free energies are computed relative to this activated state. Analogous to previous studies on the HDV ribozyme,²⁹ if the 3’OH deprotonation were in rapid equilibrium, the observed rate constant could be expressed as the product of an equilibrium constant associated with O3’ activation and the rate constant associated with phosphoryl transfer. This equilibrium constant is determined by the pK_a difference between 3’OH and the deprotonating base, which is expected to be similar for the two-metal and three-metal systems. Assuming the pre-equilibrium constant is similar for these two systems, the free energies relative to the activated state can be compared. Moreover, the low barrier for the three-metal system should be viewed in the context of the high free energy of the activated state relative to the ground state prior to proton abstraction, leading to a small preequilibrium constant.

The base that deprotonates 3’OH prior to attacking the phosphate group is unknown, but various possibilities for Pol η and other polymerases have been discussed in the literature. The pK_a of 3’OH in Pol η has not been quantified, but comparisons to the measured pK_a of RNA 2’OH in solution (13.9)⁴⁰ and DNA 3’OH in RNA polymerase with Mn²⁺ (8.2),⁴¹ as well as computed values of 8 – 9.5 in Pol β,⁴² suggest that it is at least 8, even when coordinated to Mg²⁺, as shown in Figure 2. Thus, the proposals^43,44 of Asp, Glu, or bulk water as the base (pK_a’s of 3.71, 4.15, and −1.74, respectively) are problematic unless the pK_a values are increased significantly in the protein environment. In addition, both Asp115 and Glu116 in Pol η are coordinated to Mg_A, further decreasing their pK_a values. Another possibility is the water-mediated and substrate-assisted mechanism, where the 3’OH is deprotonated by the α-phosphate through a bridging water molecule, followed by additional water-mediated proton transfers to the γ- and β-phosphates.⁴⁵

We performed additional calculations to investigate the possibilities for the activating base. First we performed a hydrogenbonding analysis of 150 ns classical MD trajectories with the 3’OH protonated for the two- and three-metal systems (Tables S2 and S3). The predominant hydrogen-bonding partners of 3’OH for the two-metal and three-metal systems were the α-phosphate of dATP (83% and 54%) and bulk water (9% and 13%). These observations are consistent with the transient water molecule observed in the crystal structure⁸ and the watermediated deprotonation mechanism proposed previously.⁴⁵

We propose another water-mediated deprotonation involving Mg²⁺-bound hydroxide, whose pK_a of ~11.2 is high enough to deprotonate 3’OH when it is also coordinated to Mg²⁺ (Figure 2). Thus, we investigated the possibility of a hydroxide ion coordinated to Mg_A acting as the base. In this case, the Mg_A²⁺bound water is assumed to be deprotonated by a buffer molecule or other base whose pK_a would determine the pre-equilibrium constant, and this water would mediate the proton abstraction from 3’OH. To test this hypothesis, we propagated additional QM/MM MD trajectories, where the starting structures were configurations in the reactant region of the converged string, subsequently adding a proton to O3’ and deprotonating the Mg²⁺-bound water, allowing a hydrogen bond to form. For the two-metal system, we found that the Mg²⁺-bound hydroxide deprotonated the 3’OH for configurations corresponding to 3’OH starting to attack the phosphate, which decreases its pK_a. For the three-metal system, this hydroxide deprotonated a water molecule coordinated to Mg_C. These simulations suggest that a hydroxide ion bound to Mg_A could potentially deprotonate 3’OH prior to the arrival of Mg_C. Computational details and a movie are provided in the SI.

The mechanism by which the pyrophosphate leaving group is protonated is another open question. For the two-metal system, the previously proposed¹⁶ proton transfer from the nucleophilic 3’OH is possible. For the three-metal system, three of the oxygen atoms are coordinate to Mg²⁺ following phosphoryl transfer (Figure 2), and the pK_a is most likely ~4.6. This protonation could occur in bulk solution as the pyrophosphate group is shuttled from the active site, possibly via a Mg²⁺-bound water molecule.

A previous study²⁵ of Pol β found that the energy barrier in the forward direction was similar with two or three metal ions in the active site. This finding is consistent with experiments in which a non-bridging oxygen of the α-phosphate of the incoming nucleotide was substituted with sulfur, appearing to prevent binding of the third divalent metal ion but only decreasing the rate of nucleotide insertion by three-fold. Although compelling, the crystallographic experiments were performed with Mn²⁺ rather than Mg²⁺, weakly bound ions could dissociate during crystallization, and small amounts of unsubstituted nucleotide could dominate the kinetics. Moreover, analogous experiments have not been performed for Pol η. Additionally, the previous calculations did not include conformational sampling or entropic contributions and consisted of geometry optimizations of a 100atom QM region along a single reaction coordinate, the O3’-P distance, in a frozen MM environment. These previous calculations also assumed that the triphosphate was protonated and that the base deprotonating the O3’H was an Asp. These methodological differences, in conjunction with the inherent differences between Pol η and Pol β, prevent a direct comparison between the two studies. However, the proposal²⁵ that a possible role of the third metal in Pol β is to inhibit the reverse pyrophosphorolysis reaction may also apply to Pol η.

Conclusions

The simulations presented in this paper provide evidence that the third metal ion in the active site of Pol η may play a catalytic role through electrostatic interactions with the pyrophosphate leaving group, thereby stabilizing the product. These electrostatic interactions make the phosphoryl transfer reaction more thermodynamically favorable with a lower free energy barrier relative to the activated state corresponding to the deprotonated 3’OH nucleophile. In addition, these electrostatic interactions may prevent proton transfer from the nucleophilic 3’OH and therefore disfavor the previously proposed self-activated mechanism.¹⁶ However, several mechanistic questions remain unresolved, including the timing of the sequence of events. If the third metal ion enters the active site after the phosphoryl transfer reaction, it would not be able to effectively facilitate catalysis through these electrostatic interactions.

Another unresolved issue is the identity of the base that abstracts the proton from the O3’ oxygen prior to attacking the phosphate group. Our calculations support the possibility of a water mediated mechanism with Mg²⁺-bound hydroxide acting as the base that deprotonates O3’H. The mechanism by which the pyrophosphate group might be protonated when the third metal ion is present is another open question that could also involve Mg²⁺-bound water. The previously proposed role of the third metal ion in guiding the pyrophosphate leaving group out of the active site^{16, 18, 23, 25} and reducing the barrier for product release¹⁸ may be a crucial part of the overall mechanism. Additional experimental and computational studies will be necessary to further elucidate the mechanism of this complex yet biomedically important enzyme.