Peripapillary Sclera Architecture Revisited: A Tangential Fiber Model and its Biomechanical Implications

Abstract

The collagen fiber architecture of the peripapillary sclera (PPS), which surrounds the scleral canal, is a critical factor in determining the mechanical response of the optic nerve head (ONH) to variations in intraocular pressure (IOP). Experimental and clinical evidence point to IOP-induced deformations within the scleral canal as important contributing factors of glaucomatous neural tissue damage and consequent vision loss. Hence, it is imperative to understand PPS architecture and biomechanics. Current consensus is that the fibers of the PPS form a closed ring around the canal to support the delicate neural tissues within. We propose an alternative fiber architecture for the PPS, in which the scleral canal is supported primarily by long-running fibers oriented tangentially to the canal. We present evidence that this tangential model is consistent with histological observations in multiple species, and with quantitative measurements of fiber orientation obtained from small angle light scattering and wide-angle X-ray scattering. Using finite element models, we investigated the biomechanical implications of a tangential fiber PPS architecture. We found that the tangential arrangement of fibers afforded better mechanical support to the tissues within the scleral canal as compared to a simple circumferential ring of fibers or a combination of fibers oriented radially and circumferentially. We also found that subtle variations from a tangential orientation could reproduce clinically observed ONH behavior which has yet to be explained using current theories of PPS architecture and simulation, namely, the contraction of the scleral canal under elevated IOP.

Graphical Abstract

1. Introduction

In order for visual stimuli to be transmitted from the retina to the brain, there exists a hole in the back of eye through which the retinal ganglion cell axons exit to form the optic nerve (Fig. 1 A, B). This hole, termed the scleral canal, is often regarded as a mechanical weak spot in the relatively stiff scleral shell of the eye. The organization and properties of the collagen microstructure of the peripapillary sclera (PPS) which surrounds the canal has been a topic of intense study for well over a century [1–8] as the fibers of the PPS must reinforce the canal so as to prevent excessive deformation within the neural tissues of the optic nerve head (ONH) due to changes in intraocular pressure (IOP) and extraocular forces. Much of the recent interest in the PPS stems from substantial clinical evidence suggesting that the initial neural damage in glaucoma occurs within the neural tissues inside the scleral canal, and in particular, the lamina cribrosa (LC) region of the ONH. [9–12]

Fig. 1.

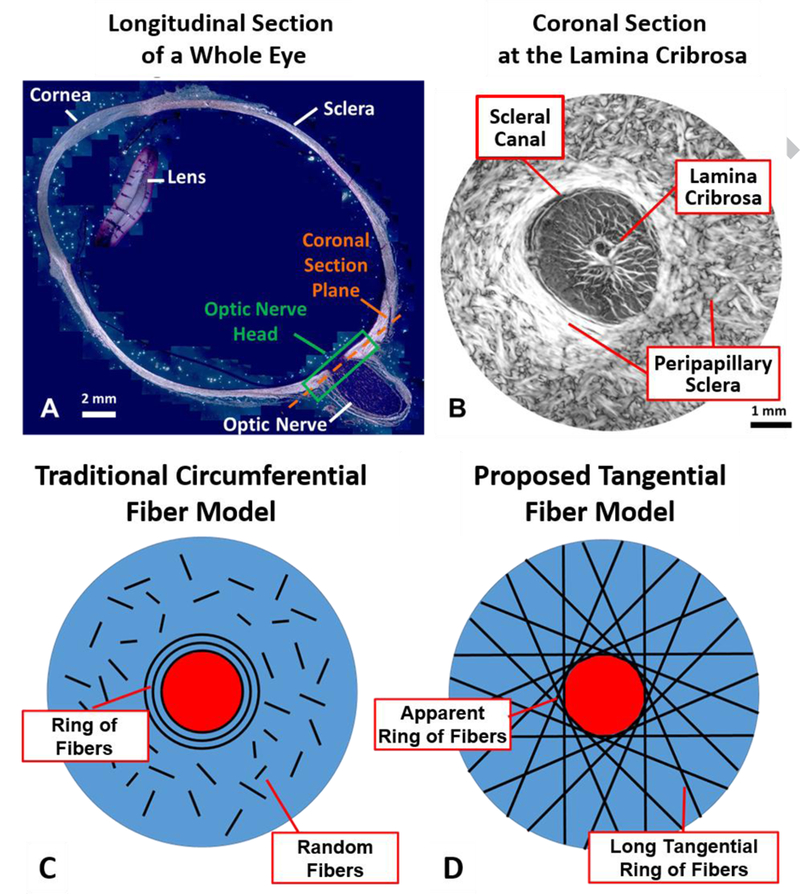
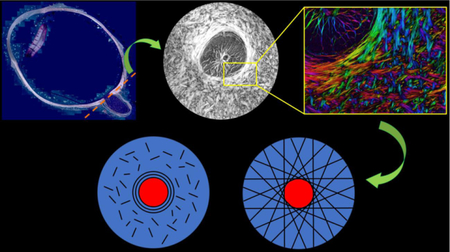
The anatomy of the eye and models of fiber orientation. A) A longitudinal cross-section of a whole eye, with the location of the optic nerve head (ONH) shown. B) A coronal section of the ONH showing the peripapillary sclera (PPS) and lamina cribrosa located within the scleral canal. C) The current consensus opinion as to the organization of collagen fibers in the PPS is a closed ring of fibers surrounded by short randomly oriented fibers. D) Our proposed organization of fibers is a collection of long fibers oriented tangentially to the canal edge, giving the appearance of a closed ring of fibers around the canal. A&B Adapted from Voorhees et al, 2017.

The current consensus in the ophthalmology community appears to be that the fibers of the PPS form a circumferential ring around the canal (Fig. 1C). [5, 7, 13–17] Since collagen fibers stiffen when stretched, this ring would serve to restrict the opening of the canal that would be expected under elevated IOP. However, this current consensus is largely based on low-resolution, light scattering imaging techniques including small angle light scattering (SALS) and wide angle x-ray scattering (WAXS) [5, 7, 15, 16, 18, 19] or high resolution techniques such as second harmonic generation [17, 20] or electron microscopy [20–22] with excellent resolution but modest field of view. SALS and WAXS methods have been adopted in part due to their abilities to provide quantitative data that can be easily incorporated into mechanical models, however the resolution of these methods is on the order of 100–300 μm [5, 23], far below the resolution needed to observe individual collagen fibers or even bundles, on the order of 10–50 μm in width. These low-resolution techniques have not been able to describe the collagen fiber orientation outside the circumferential ring of fibers other than to suggest a somewhat random distribution of fibers [7], and perhaps more importantly have not offered insight as to how this circumferential ring is integrated into the rest of the sclera.

We propose that the PPS is supported not just by a circumferential ring of fibers, but is instead primarily supported by long-running fibers oriented tangentially to the canal (Fig 1D). This arrangement creates the appearance of a strong circular ring when observed using low-resolution imaging techniques. We hypothesize that this tangential arrangement affords multiple biomechanical advantages to the ONH which a simple ring of fibers cannot. Further, we anticipate that this tangential arrangement will explain some of the outstanding disagreements between experimental data and modeling such as the occasional contracture of the scleral canal under elevated IOP. [24–26]

The goals of this paper are three-fold: 1) To provide evidence to support the claim that the scleral canal is reinforced not simply by a closed ring of collagen fibers, but by the convergence of long-running fibers oriented tangentially to the canal; 2) To establish the compatibility of this arrangement with previous characterizations of PPS architecture made using SALS and WAXS; and 3) To examine the biomechanical implications this fiber arrangement would have for the tissues of the ONH using mechanical modeling.

2. Methods

2.1. Histology and polarized light microscopy

All new experimental evidence used to support our tangential fiber model was obtained via polarized light microscopy of histological sections from multiple species. Sheep and pig samples were obtained from a local abattoir. The monkey sample was obtained from the laboratory of Dr. Pamela Moalli at the University of Pittsburgh. The human sample was obtained from an ostensibly healthy donor through the Center for Organ Recovery and Education of Pennsylvania. The study was conducted in accordance with the tenets of the Declaration of Helsinki, the guidelines of the Association for Research in Vision and Ophthalmology, and the Health Insurance Portability and Accountability Act. Eyes were fixed in formalin and cryosectioned with slice thickness ranging from 16 to 30 μm. Histological processing and polarized light microscopy (PLM) methods have been previously described. [6, 27] Sheep sections were imaged with an Olympus BX60 microscope (Olympus, Tokyo, Japan) with a SPOT camera (SPOT imaging Solutions, Sterling Heights, MI) with a 10x objective. Pig sections were imaged with an Olympus IX83 microscope with an Olympus DP27 camera with a 10x objective. Human and monkey sections were imaged with an Olympus IX83 microscope with a 10x resolution and an Olympus DP74 camera. Elsewhere we have shown that the fiber orientation analyses are independent of the microscope and camera system. [6, 27]

2.2. SALS and WAXS simulation

In order to demonstrate that our tangential fiber theory is consistent with previous reports of PPS fiber architecture, we simulated the distributions of fibers that SALS and WAXS techniques would find for an ONH with collagen fibers in the PPS oriented tangentially to the canal. For these simulations, we modeled a planar section through the ONH centered on the scleral canal at a depth corresponding to the mid-sclera. The scleral canal was assumed to be a circle with a radius of 1 mm, while the radius of the entire section was assumed to be 3 mm. The fibers within the canal were assumed to be randomly oriented. To model the tangential fibers in the PPS, two families of fibers were created, with one family radiating tangentially from the canal in a clockwise direction and the other radiating from the canal in a counter clockwise direction. From our observations, not all tangential fibers directly intersect the edge of the canal, instead many fibers have their closest point of approach to the canal further outside. To capture this, we modeled a distribution of fibers such that the minimum distance to the canal followed a half-normal distribution that peaked at the canal edge and had a standard deviation of 600 μm. In preliminary work, we also simulated the case where all fibers were oriented tangentially to the canal edge, similar to the model shown in Fig. 1. This case produced similar trends to the simulations we report herein, however we found that including fibers with a distribution of minimum distances to the canal matched better the spatial patterns observed both in our histology and in experimental SALS and WAXS data. The connective tissue volume fraction of the LC is lower than that of the sclera, and therefore we assumed that the scattering signal from this tissue would be 25% that of the sclera.

Both SALS and WAXS use a collimated light beam to measure the light scattering properties of a material. The intensity profile of these beams follows a Gaussian distribution, so that the material near the center of the beam contributes more to the distribution than material further from the center. The variance of this distribution is dependent on the diameter of the beam, with a commonly used measure being that the diameter is that which contains 1–1/e^2 of the total beam power, or roughly 86.5%. [28] Thus, for a given location within the simulated ONH, the distribution of fibers was calculated by a Gaussian weighting of the simulated fiber orientations based on the distance to the center of the laser and a weighting of the scattering signal due to the connective tissue density as described above. To simulate SALS data, we chose a beam diameter of 300 μm and calculated the distribution at grid points with a spacing of 100 μm. [23] For WAXS data, we chose a beam diameter of 200 μm and calculated the distribution at grid points with a spacing of 500 μm [8]. To compare our simulated data to previous reports, SALS data is presented as a quiver plot showing the mode of the angular distribution on top of a blue-white-red colormap of the angular fiber concentration, calculated as the inverse of the circular variance, with high concentrations representing high degrees of anisotropy. For WAXS data, the angular fiber distribution is plotted at each sample point and colored to represent the angular fiber concentration. All imaging simulation was done using Matlab v2015b (Mathworks, Natick, MA).

2.3. Mechanical modeling

In order to examine the biomechanical implications of having a PPS composed of long tangential fibers, we used finite element modeling to compare the mechanics of four different PPS fiber arrangements, including the standard circular model. Following the approaches used elsewhere to study the mechanical effects of PPS collagen fiber architecture [23, 29, 30], we modeled the ONH as a disk (Fig. 2). The geometry was created and meshed using Preview v1.16.3 software (Musculoskeletal Research Laboratory, University of Utah). The ratio of the radius of the LC to the radius of the entire domain was 5.13. The ratio of the disk radius to thickness was 20.5. In total, the mesh consisted of 13,824 linear hexahedral elements with 3,584 for the LC and 10,240 for the sclera. The non-fibrous components of the disk were modeled as isotropic elastic solids with Young’s modulus of 500 kPa, matching the stiffness of the LC used in our previous studies, and Poisson’s ratio of 0.49. [31–33] We chose this value to represent a homogenous mixture of randomly oriented collagen and ground substance. Individual scleral collagen fibers were then added to the model to represent the anisotropic reinforcement provided by each of the four models. These fibers were modeled as discrete spring elements with a linear stiffness when in tension and zero stiffness in compression.

Fig. 2.

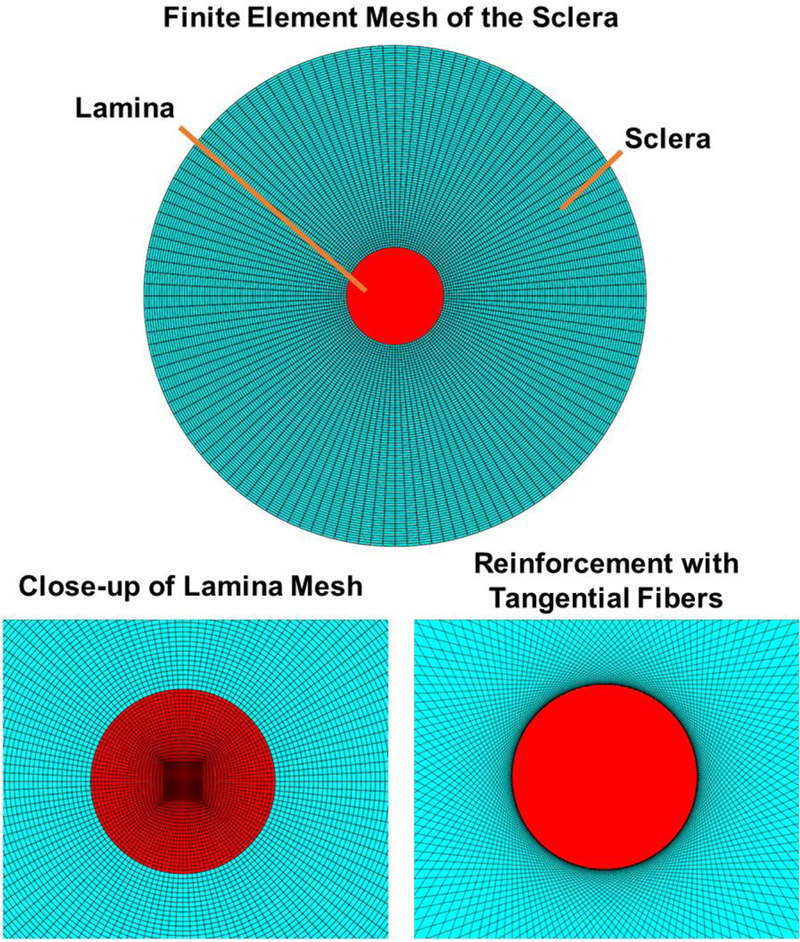
Finite element mesh used to model the ONH. (Top) The model geometry shown en face. (Bottom Left) A close-up view highlighting the mesh in the lamina cribrosa region. (Bottom Right) A close up-view of the model near the canal showing the discrete spring elements used to model the collagen fibers in the tangential fibers model.

For the circumferential fibers model, each node on the scleral – LC boundary was connected to its neighboring nodes using a spring element. This was done for nodes on both the top and bottom surfaces of the disk. For the radial fibers model, spring elements were used to connect each node at the exterior of the disk to the corresponding node on the sclera - LC boundary. The combination model included both sets of radial and circumferential springs. For the tangential model, each node at the sclera - LC boundary was connected to nodes on the exterior surface of the disk such that the lines connecting the exterior nodes to the canal nodes was tangential to the scleral canal, within 0.004°. For both the circumferential and radial fiber models, a total of 256 springs were used and the Young’s modulus for these springs was chosen to be 5 MPa, corresponding to the stiffness of the sclera used in our previous studies.[31, 33] The combination model and tangential models each consisted of 512 springs as the nodes on the sclera – LC interface were doubly connected. To ensure that our results were not simply due to the addition of extra fibers in these two models, the stiffness of each spring was set to 2.5 MPa. This strategy effectively kept the fiber volume fraction the same across each model. In preliminary studies, we compared models with all fibers having a modulus of 5 MPa and found that this did little to change our overall conclusions. An outward boundary pressure of 250 mmHg was applied to the outer boundary of the sclera to mimic an IOP increase of 25 mmHg. This pressure was calculated based on the law of Laplace for a thin walled-sphere, with a hoop stress multiplier (one half the ratio of the sphere radius to the wall thickness) equal to 10 as in our previous studies. [29, 30] This loading created a state of in-plane biaxial tensile stress in the ONH. Readers interested in more details on the usage, assumptions, and limitations of the law of Laplace are directed to our previous work. [34] All finite element simulation was done using FEBio v2.3.0 [35] and strain analysis was done using custom scripts for Matlab. We note that in preliminary studies we tested models using different geometries and different numbers of springs and found similar results to those shown below. [36]

We conducted a parametric sensitivity analysis in which the stiffness of the springs in each model was decreased and increased by an order of magnitude, to determine the influence of spring stiffness on sclera and LC strains across the four models. We also tested two variants on the tangential model, where the springs were oriented either positive or negative 3° from tangential, to test how the deformations varied with small deviations in the alignment of the tangential fibers. To test the robustness of the circumferential and tangential models, we removed a small region of fibers from each model representing a loss of 2.5% of the total number of fibers.

3. Results

3.1. High-resolution polarized light microscopy shows long-running fibers oriented tangentially to the scleral canal

We have recently developed high-resolution PLM techniques that allow for quantitative analysis of ONH microstructure from histological sections. [6, 27] In our past and ongoing work, we have used PLM to examine PPS microstructure in more than a hundred eyes across ten different species. In every eye, we observe what appear to be long collagen fibers oriented tangentially to the canal. We present here only representative images for human, pig, sheep and monkey (Fig. 3). We noted a great deal of fiber intertwining and splitting; however, individual fiber bundles of the sclera appeared to primarily follow straight paths with little curvature. A small population of fibers adjacent to the canal did appear to curve following the canal edge. In large part, we observed that the appearance of the circumferential ring of fibers in the PPS was the result of the intersection, and interweaving of predominately straight fibers running tangential to the canal. In the regions of the sclera more distal from the canal, fibers were also seen following paths oriented tangentially to the canal or to larger rings concentric with the canal. As our PLM images are of 2D histological sections, many fibers, particularly those further from the canal appear somewhat randomly oriented, probably, in part, due to their significant out of plane orientations.

Fig. 3.

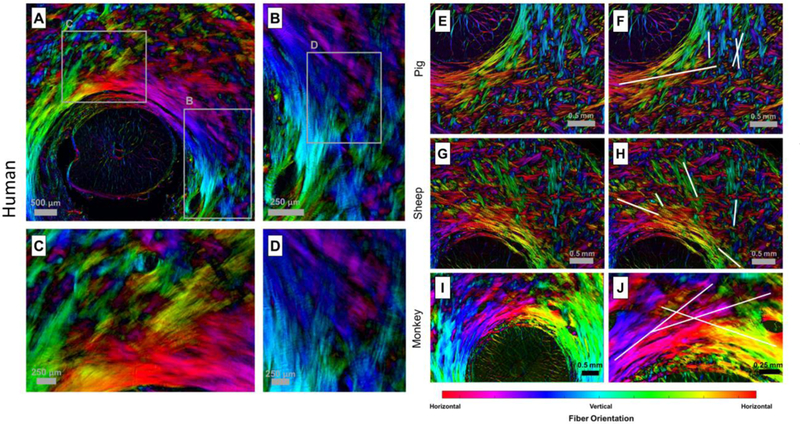
Examples of tangential fibers obtained from polarized light microscopy in four species. The color in the images represents the orientation of the fibers, while the brightness represents the density of the collagen fibers. A–D) Images from a human eye. A) Large field of view showing long running fibers. B–D) Close-up views showing the crossing of fibers near the canal. E–J) Examples of tangential fibers obtained from polarized light microscopy for pig, sheep and monkey. F,H,J) Show the same regions as E,G,I but have lines indicating example fiber paths.

3.2. A tangential model of PPS architecture agrees with results from lower-resolution studies

To test if our proposed arrangement of tangential fibers agrees with previous experimental data, we simulated the distributions of fibers that SALS and WAXS techniques would find for an ONH with collagen fibers in the PPS oriented tangentially to the canal. We chose to simulate SALS and WAXS as they are two of the most common methods for quantitatively studying the fiber anisotropy of PPS tissues. [5, 7, 15, 16, 18, 19]

Our simulated SALS data was compared to experimental data from Zhang et al and Jones et al (Fig. 4). [14, 23] The simulated SALS data replicated many of the features present in experimental SALS data for human eyes, including the highly aligned ring of circumferential fibers surrounding the canal. The simulations also demonstrated how the highly scattering scleral fibers produce artefactual fiber orientations within the scleral canal (Supplementary material). Within the canal the preferred fiber angle still appears circumferential albeit with a diminished fiber concentration factor, due to the influence of the highly scattering scleral fibers outside the canal partially within the beam. We suspect, this beam averaging effect is also partly the cause of the ring of highest anisotropy in experimental data, being located not at the identified canal boundary. This effect is also observed in our simulated data, as peak anisotropy was identified at a distance of about 300 μm from the canal.

Fig. 4.

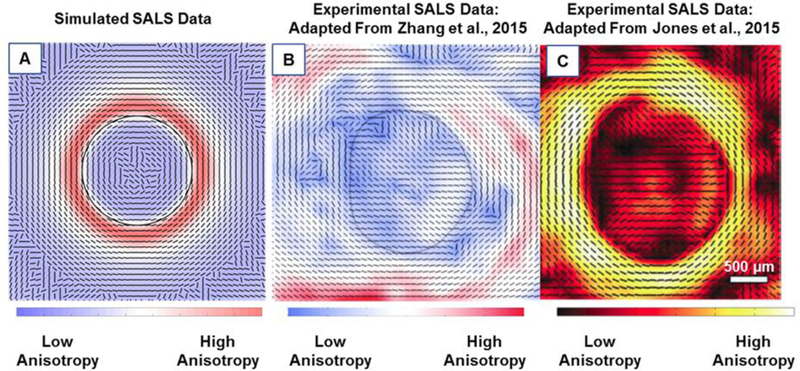
A comparison of the simulated (A) and experimental (B and C) SALS data from human eyes [14, 23]. The lines represent the mean fiber orientation and the color represents the strength of alignment. The black line in A and B represents the canal boundary. Both simulated and experimental SALS data show that fibers are highly aligned around the canal with a mean orientation that appears circumferential. Fibers oriented tangentially to the canal are seen between 12 and 3 o’clock matching simulated data.

The simulated WAXS data (Fig. 5) again replicates several features observed in experimental WAXS data from human eyes. [8] Here, the collagen fibers appear to form a highly aligned circular ring around the canal. In this particular image, there also appears to be two clearly identifiable families of tangential fibers, one running from the top of the image to the right side and the other from the bottom to the right side. Our simulated WAXS data was not similar to the actual WAXS data away from the canal.

Fig. 5.

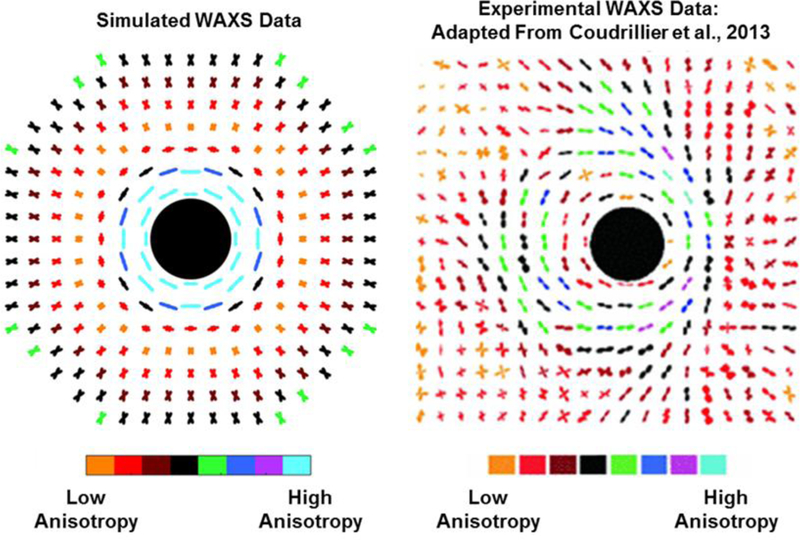
A comparison of the simulated (left) and experimental (right) WAXS data from human eyes [8]. The angular distribution of fibers at each sampling point is shown, and the degree of alignment is represented by the color. The black circle represents the canal. In simulated data, the fibers near the canal appear circumferentially aligned. Moving away from the canal the fibers first appear weakly aligned then appear as two distinct families of fibers. In actual WAXS data, a similar circumferential ring of fibers appears, which is surrounded in most locations by one or two families of fibers oriented tangentially to the canal.

3.3. Mechanical modeling predicts that a PPS architecture consisting of long-running tangential fibers provides robust support to ONH

Since the biomechanical response of the ONH to elevated IOP is predominately determined by the collagen architecture of the PPS, we used computational modeling to study how the mechanical behavior of a PPS constructed from long-running fibers oriented tangentially to the canal would compare to previous models of PPS architecture. In total, we considered four different models of collagen fiber organization: 1) The current consensus model consisting of a circumferential arrangement of fibers around the scleral canal [5, 7, 13–17]; 2) An organization we described in a recent study using PLM consisting of a combination of radially oriented fibers and circumferentially oriented fibers [6]; 3) For completeness, a simplified version consisting only of radial fibers; and 4) A tangential arrangement of fibers.

The circumferential and radial strain maps are shown for all four models in Fig. 6A, and the volume-averaged mean radial and circumferential strains in the lamina and sclera are shown in Fig. 6B. In the circumferential fiber model, representing the current consensus, the ring of fibers maintained low strains in the LC on the order of 1–1.5%. However, the circumferential fibers provided little support to the scleral tissue with radial strains peaking at around 5% in the PPS. Conversely, radial fibers lessened the strains in the sclera at the expense of the LC with mean radial and circumferential strains above 8%. In this model, the radial fibers essentially pulled outwards on the sclera – LC boundary. The addition of circumferential fibers to the radial fibers reduced the strains on the LC while maintaining relatively low scleral strains however this effect was small as the mean LC strains were still around 6%. The strains in the tangential model were near zero, 0.005% in the LC and 0.004% in the sclera, much lower than any of the other models.

Fig. 6.

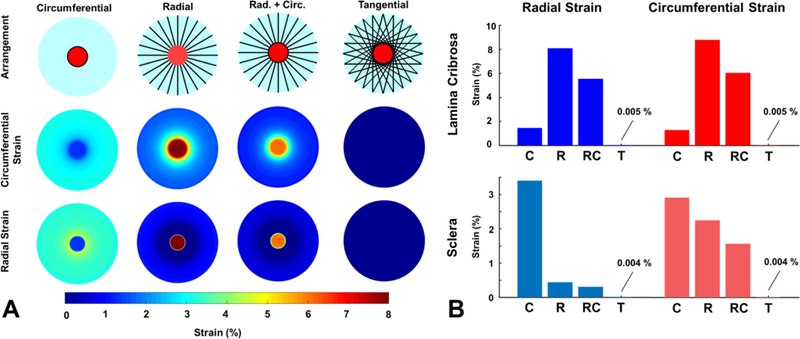
The mechanical behavior of a scleral canal reinforced by four different arrangements of collagen fibers. A) A simple reinforcement of the canal with circumferential fibers limited the strain in the lamina due to IOP but did provide support the sclera. Conversely, a radial arrangement of fibers reduced the strain in the sclera, but lead to high strains within the lamina. The combination of radial and circumferential fibers still caused high strains in the lamina. A tangential arrangement of fibers provided the best reinforcement for the sclera and the lamina, reducing the strains to near zero-levels for this perfectly symmetrical idealized test model. B) The mean strains in the sclera and lamina for the four different PPS fiber arrangements. C – circumferential, R – radial, RC – radial and circumferential, T – tangential.

Since the mechanical behavior of the ONH is determined both by the organization and the stiffness of the collagen fibers in the PPS we conducted a parametric analysis to determine the dependence of our modeling results on the fiber stiffness. For each of the four models, we tested the effects of a one order of magnitude increase and a one order of magnitude decrease in fiber stiffness. The results for the parametric analysis of collagen fiber stiffness are shown in Fig. 7. Both LC and sclera strains were still lower in the tangential model with Young’s modulus of 0.250 MPa than in the any other model, even compared to the circumferential fiber model with 50 MPa fibers. The LC strains were highly dependent on the stiffness of the fibers in the circumferential model, the combination model and the tangential model. In the radial model, both LC strains and scleral strains were almost unaffected by the stiffness of the fibers.

Fig. 7.

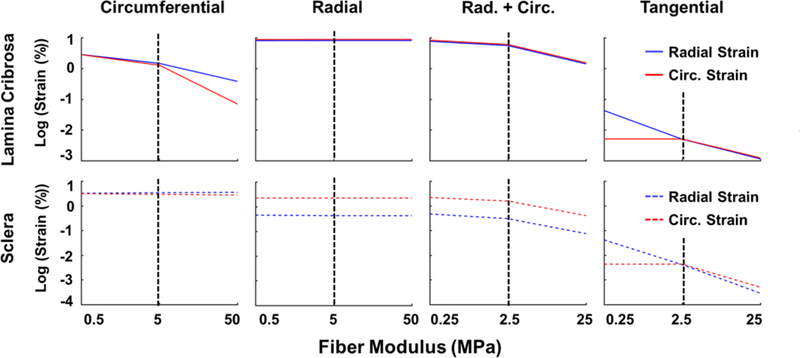
Sensitivity of lamina and sclera strains to the stiffness of the collagen fibers. Note that strains and modulus are both plotted using non-linear scales. The stiffness of the collagen fibers was varied over two orders of magnitude. The black dotted lines denote the baseline conditions. A line with zero slope indicates that the strain was insensitive to the stiffness of the fibers. Increasing the fiber stiffness in the model with circumferential fibers reduced the strains in the lamina but not the sclera. Increasing the fiber stiffness in the model with radial fibers did little to change the strains in the lamina and sclera. In the case of a combination of radial and circumferential fibers, increasing fiber stiffness resulted in small reductions in both lamina and scleral strains, although these changes were not in direct 1 to 1 proportion to the increase in stiffness. For the tangential fibers, lamina and scleral strains were reduced almost in direct proportion to the increase in stiffness. Note that both the sclera and lamina strains in the tangential fiber model with a modulus of 0.25 MPa were an order of magnitude smaller than the strains in the circumferential models with 50 MPa fibers.

When we changed the orientation of the fibers in the tangential model so that they were initially arced concavely around the scleral canal, the fibers straighten and pull the canal open when IOP is elevated (Fig. 8). Alternatively, when the fibers were arced convexly around the canal, the straightening of the fibers contracted the canal, compressing the LC. We note still, that for these two models, the ONH strains were still small compared to the other three models. To test if the consensus circumferential fiber model and our tangential fiber model were robust to a loss of collagen fibers, we made a model where a small region of collagen fibers, representing 2.5% of the total collagen content, was removed (Fig. 9). The loss circumferential fibers created a strain concentration at the site of the defect, whereas the tangential fiber model was relatively robust to the loss of fibers, maintaining low levels of strain in the LC and sclera.

Fig. 8.

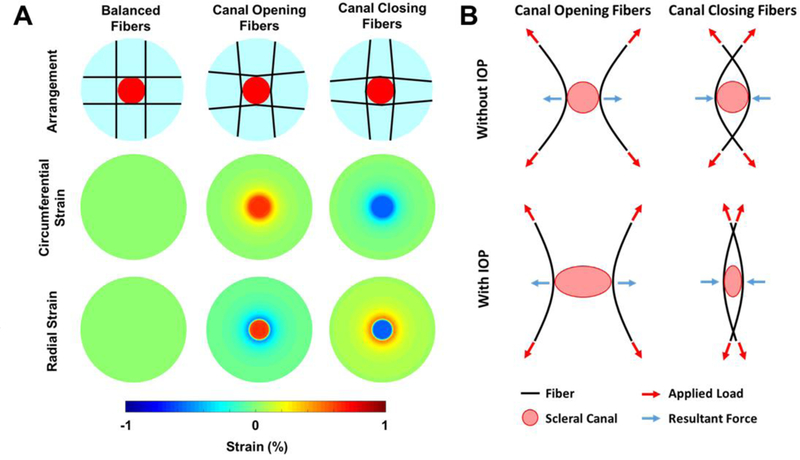
Small changes in the orientation of the fibers determined whether the canal opened or closed due to IOP-induced hoop stress. A) Strain maps for the different fiber arrangements. When the fibers were oriented convexly to the canal (Canal Opening Fibers) the strains in the lamina were positive. When the fibers were oriented concavely around the canal (Canal Closing Fibers) the strains in the lamina were negative. B) Diagram depicting the mechanism of action. For fibers oriented concavely around the canal, the applied load results in an outward tensile force at the canal boundary as the fiber straightens. For fibers oriented convexly around the canal, the applied load results in an inward compressive force at the canal boundary as the fibers straighten. Note only two fibers for each case are shown here for simplicity.

Fig. 9.

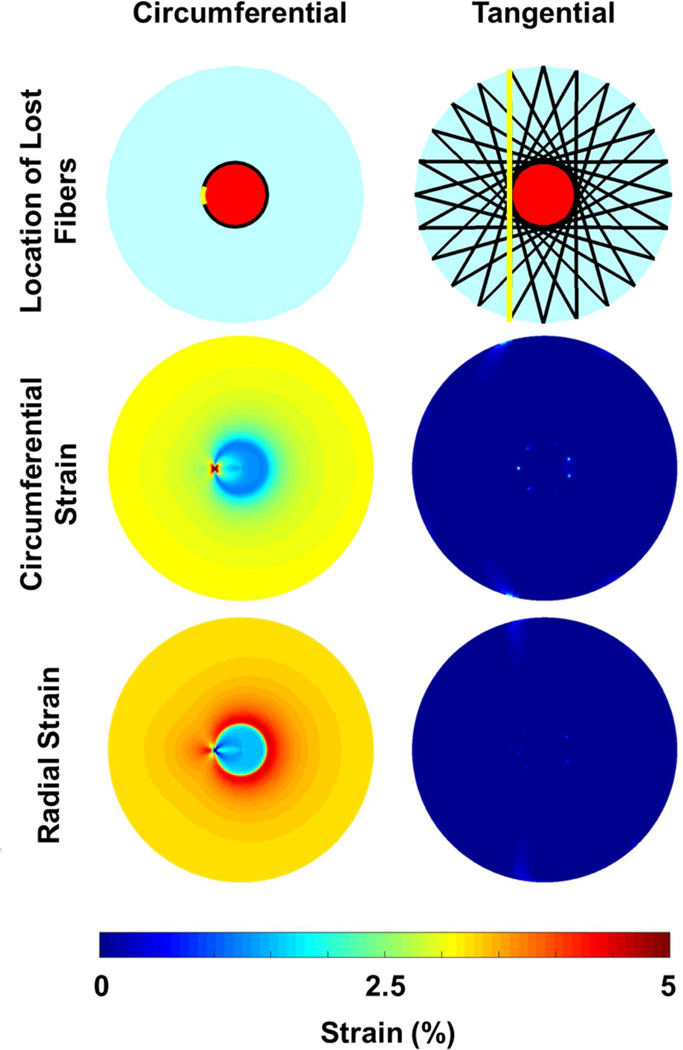
Robustness of the ONH to the loss of scleral fibers. The loss of a small region of circumferential fibers (~2.5% of the total number of fibers; location indicated in top row) created a region of elevated circumferential strain in the lamina and reduced radial strain. The tangential fiber model was robust to the loss of fibers, maintaining near-zero strains.

4. Discussion

We have presented a model for the organization of collagen fibers in the PPS wherein the ONH is reinforced primarily by long fibers oriented tangentially to the scleral canal. We have shown histological evidence across multiple species supporting the model, and demonstrated that the model is compatible with previous low resolution experimental studies and observations. The tangential arrangement of long fibers we propose provides robust mechanical support to both the sclera and neural tissues in the canal. This arrangement is tremendously flexible as subtle alterations in collagen alignment can result in a contraction of the scleral canal under elevated IOP, consistent with experimental findings which could not be explained by traditional models of the ONH. [24–26]

A primary motivation for this study was our observation that the collagen of the sclera forms long fibers, a feature that has been largely overlooked by recent studies of scleral collagen architecture and biomechanics. As stated in the introduction, investigations into the organization of the scleral microstructure have been ongoing for more than a century with some of the best insight into scleral microstructure coming from the studies from the 1930’s. [2–4] In particular, the microdissection work of Becher in 1932 [2] and Fischer in 1933 [3] describe the fibers of the bovine sclera as long and continuous fibers, splitting and interweaving with each other. Fischer, via observations made with a stereo dissection microscope, even described the fibers of the PPS as not running circularly around the canal, but instead forming two bowed arcs running along the canal with fibers intersecting above and below the nerve [3], somewhat similar to our proposed model of tangential fibers.

Current opinion on the biomechanics of the sclera seems to be influenced by the widespread adoption of discretized computational modeling techniques such as finite element analysis. [37, 38] Instead of considering the sclera as a structure formed from long interwoven collagen fiber bundles, the sclera has become a continuous material composed of short (finite-element sized) freely rotating collagen fibrils, which fit nicely within the size of a finite element. [23, 39, 40] While the mechanical models we presented here may seem like simplifications of the ONH we chose to use this approach using discrete spring elements precisely because it allowed us to model the mechanics of the sclera as a fibrous structure. In fact, it is only through the use of this structural analysis approach that we can begin to predict mechanical behaviors such as the closing of the scleral canal under elevated IOP.

All previous models of the ONH predict that the scleral canal will expand under elevated IOP. [8, 23, 39–41] Experimental data shows that there is a great diversity in the response of the canal opening to IOP, with some eyes experiencing almost no expansion of the canal and others even experiencing a contraction of the canal [24–26, 42]. For example, Strouthidis et al, reported in monkeys that the area of the scleral canal opening was reduced by around 1 to 3% in 5 out of 10 eyes after an acute IOP elevation from 10 to 45 mmHg. [24] Our tangential fiber model offers an explanation for these phenomena. Collagen fibers straighten as they are stretched. The straightening of the fibers requires very little force, however, once straightened, the fibers become very stiff and require large forces to stretch. In a model with perfectly straight fibers, any increase in loading requires not just the stretching of one fiber, but every fiber in the model. When the fibers are initially curved, as in the canal opening and canal closing models (Fig. 8) the fiber straightening allows the tissues to deform. When the fibers are arced convexly around the canal they bend inwards towards the canal as they are straightened, whereas fibers that arc concavely to the canal bend outwards away from the canal thereby pulling it open. Our sensitivity study backs up these conclusions, showing that the deformation of the LC is due more to the organization of the fibers around it than to the stiffness of the fibers. Mechanically, the distinction between canal opening and closing is important as an opening of the canal would cause a flattening and lateral stretching of the lamina, and a canal contraction would induce deepening and lateral compression of the lamina. [41, 43] From a mechanobiological standpoint, we would expect that these distinct forms of deformation would have different effects on the axons and glial cells within the canal, with compression of the axons perhaps being more likely to disrupt axoplasmic transport.

Experiments have also shown that the aspect ratio of the canal does not change, or even elongates with elevated IOP. [26, 44] This is in contradiction with mechanical models based on the conventional PPS architecture, which uniformly predict that an elliptical canal will become more circular with an increase in IOP. We speculate that this behavior, perhaps counterintuitive yet observed experimentally, could be explained by combinations of convex and concavely arced fibers working in concert.

Inverse modeling techniques are currently being used to derive tissue PPS mechanical properties through a combination of experimental inflation testing and either the standard circumferential ring model of collagen orientation or low-resolution measurements such as SALS or WAXS. [7, 8, 45, 46] Without the correct model of fiber architecture, inverse modeling may reach artefactual conclusions.

It is important to consider that we made the simplifications of modeling the PPS and LC as flat, without considering the direct effects of IOP on the PPS and LC. We did this without the intent to imply that these features are not important, as we have argued previously that they are. [41, 43] Our intention was simply to explore the potential role that the long tangentially oriented fibers we observe in our histology play in supporting the ONH in the plane of maximum IOP induced tensile stress. A 3D model is necessary to fully account for the complex behavior of curved fibers and tissues. It is possible that when considering the bending of the LC caused by IOP, that combinations of the various fiber arrangements afford the best support to the LC. We also chose to model the ground substance and collagen fibers of the ONH as linear elastic materials, which may fail to capture the stress strain behavior of the ONH at low IOP. However, we do not expect that including collagen non-linearity would drastically alter the mechanism of action of the tangential fibers. Nonetheless, as we continue our studies of ONH fiber architecture and mechanics, we will look to incorporate non-linear fiber mechanics, with experimentally derived material properties into our models.

While our goal here was to present a new model of PPS architecture, we note that the actual microstructure of the PPS is far from simple and we do not propose that tangential fibers are the only fibers forming the sclera. The PPS has distinct features at different depths through the tissue including radial and circumferentially aligned fibers in various locations, at least in our microscopic observations. On the inner portion of the sclera is a thin layer of collagen fibers aligned predominately in the meridional direction of the globe, or radially from the canal, as we and others have described elsewhere. [2, 5, 6] Further, our model describes the fibers of the sclera as following the plane of the scleral surface, omitting the fact that the fibers of the sclera interweave with one another in three-dimensions. We suspect that each of these features is important to the mechanical behavior of the ONH, and we are continuing to develop techniques to quantitatively analyze and model these features. [47] Despite the inherent complexity of the ONH microstructure, our simulated SALS and WAXS data reproduces several features found in experimental results, including the circumferential ring around the canal, multiple families of fibers within the distal PPS, and fibers that become meridionally oriented moving towards the equator. [5, 7, 15, 48] Of course, when comparing our idealized data to experimental data, our simulations are highly homogeneous and do not account for a great deal of variability and complexity in actual eyes. Future work should include studies of how well the proposed model with tangential fibers can account for displacements and deformations measured experimentally. [7, 8, 26, 46]

In conclusion, we propose that the scleral canal is not simply reinforced by a closed circuit of circumferentially oriented collagen fibers, but is supported by long-running scleral fibers oriented tangentially to the canal which converge to give the appearance of a circumferential ring. Although, these two arrangements appear similar in low resolution imaging, there is a significant mechanical distinction between the two, with the tangential arrangement of fibers providing a more robust system of mechanical support for both the lamina and sclera. In addition, the tangential arrangement may explain experimental observations that more traditional models have not been able to account for.

Statement of Significance.

It is hypothesized that vision loss in glaucoma is due to excessive mechanical deformation within the neural tissue inside the scleral canal. This study proposes a new model for how the collagen of the peripapillary sclera surrounding the canal is organized to support the delicate neural tissue inside. Previous low-resolution studies of the peripapillary sclera suggested that the collagen fibers are arranged in a ring around the canal. Instead, we provide microscopic evidence suggesting that the canal is also supported by long-running interwoven fibers oriented tangentially to the canal. We demonstrate that this arrangement has multiple biomechanical advantages over a circular collagen arrangement and can explain previously unexplained experimental findings including contraction of the scleral canal under elevated intraocular pressure.