On the accuracy of classifying hospitals on their performance measures

Abstract

The evaluation, comparison, and public report of health care provider performance is essential to improving the quality of health care. Hospitals, as one type of provider, are often classified into quality tiers (e.g., top or suboptimal) based on their performance data for various purposes. However, potential misclassification might lead to detrimental effects for both consumers and payers. Although such risk has been highlighted by applied health services researchers, a systematic investigation of statistical approaches has been lacking. We assess and compare the expected accuracy of several commonly used classification methods: unadjusted hospital-level averages, shrinkage estimators under a random-effects model accommodating between-hospital variation, and two others based on posterior probabilities. Assuming that performance data follow a classic one-way random-effects model with unequal sample size per hospital, we derive accuracy formulae for these classification approaches and gain insight into how the misclassification might be affected by various factors such as reliability of the data, hospital-level sample size distribution, and cutoff values between quality tiers. The case of binary performance data is also explored using Monte Carlo simulation strategies. We apply the methods to real data and discuss the practical implications..

1. Introduction

The assessment and report of hospital quality is increasingly important in quality improvement efforts as the US health care system undergoes major reform. Because quality of care is an abstract and multidimensional construct that cannot be measured directly, measurable indicators are used to characterize three dimensions of quality of care: structure, process, and outcome [1]. Structural measures are ‘hardware’ type of characteristics such as presence of residence programs in hospitals. Outcome measures refer to responses that characterize patient health status following care received, such as the 30-day hospital mortality rate after surgery. Process measures are meant to reflect the extent to which a provider complies with evidence-based guidelines. For example, we use the compliance rate of hospitals on providing influenza vaccination for patients diagnosed with pneumonia to illustrate the proposed methods (Section 5). In contrast to outcome measures, profiling hospitals on their process measures does not require risk-adjustment [2] when restricted to sample of patients eligible for the given procedure. This enables us to build the analytical framework on a simple two-stage Gaussian model (Section 2.1), and extensions of our methods can be applied to outcome measures (Section 6).

Hospital profiling involves a comparison of a hospital’s performance data to a normative or community standard [3]. A major profiling interest is to classify hospitals into quality tiers (e.g., top or suboptimal) on the basis of their performance data [4]. This has several important policy implications. First, such information could be used by patients, employers, and insurance plans to make better choices of hospitals from which they would buy services, thus improving hospital performance indirectly through the market. Second, a hospital’s quality tier has been used as the basis for pay-for-performance initiatives, which in theory improves the quality of providers using direct economic incentives [5]. These initiatives use retrospectively collected information on performance measures to provide financial rewards to hospitals that show high quality based on these data. For example, the Center for Medicare and Medicaid Services (CMS) initiated in 2005 the Premier Hospital Quality Incentive Demonstration project that paid bonuses totaling $8.69m to 115 superior (those in the upper decile) performing institutions that voluntarily participated in the project [6]. In such projects, hospital-specific compliance rates for some standard treatments were used as performance indicators. For example, a high tier can be defined as hospitals having compliance rate higher than an objective threshold (e.g., 0.9) or a relative threshold (e.g., 90%-tile of the sample).

There are two main analytical approaches to quantifying hospital quality on the basis of performance data collected over patient samples. One popular approach is to use the sample average of the chosen quality indicator across patients (or procedures) at hospital level. We refer to it as a direct estimator because it is based only on the hospital-specific sample data and does not involve data from other hospitals. We borrow this term from the literature of small area estimation in surveys [7], treating a hospital as a ‘small area’ (cluster or unit). On the other hand, justified by the multilevel structure of hospital performance data, an alternative estimation approach uses a shrinkage estimator obtained under a random-effects (hierarchical or multilevel) model, which assumes that there exist hospital-specific ‘random effects’ drawn from some common distributions. Such models are particularly appealing because they have a full account of variation (within-hospital sampling variation and between-hospital variation). Past literature has well documented the benefit of using shrinkage estimators over direct estimators. See Section 2.1 for more details.

Given predetermined thresholds (cutoff points), hospital classification can be conducted using either direct or shrinkage estimators. Related to the use of shrinkage estimators, another advanced approach with a more Bayesian flavor uses posterior probabilities for classification [8]. However, the risk of misclassification exists for these approaches because hospital quality is an unknown quantity under statistical models, and the uncertainty associated with its estimate would lead to misclassification. Such risk is often ignored in practice, yet it would have important implications to consumers’ decisions and targeting quality improvement efforts [9]. For example, misclassifying hospitals with suboptimal care into the tier meant for high quality might lead to detrimental effects to patients who seek best care or result in economic loss for those pay-for-performance programs. Although this issue has been identified in applied health services research [10], there is little statistical literature on systematically studying the classification accuracy of profiling methods.

Recently, Adams et al. [11] pointed out the connection between the reliability of provider performance data and risk of misclassification, showing that classifying data with lower reliability would be more error-prone. However, several unanswered methodological questions remain. One is whether using advanced methods (e.g., shrinkage estimators or posterior probabilities) rather than direct estimators might lead to improved accuracy. Given the increasing popularity of using hierarchical Bayesian models for provider profiling [12], the answer to this question is critical to both practitioners and methodologists. In addition, the impact of several key factors including the reliability of data, the distribution of hospital-level sample size, and the cutoff point between quality tiers have not been well characterized. Elucidating these patterns might also have important practical implications. For example, patient volume often varies across hospitals, and in practice, those with small sample size are often excluded to obtain reliable profiling estimates. Yet, the decision rule for the sample size cutoff is often ad hoc (e.g., fewer than 30) and does not depend on the actual data. Therefore, it is preferable to have a more rigorous and data-driven procedure. Several of these issues have been raised in the discussion of [11] ([13, 14])

These concerns therefore call for more methodological studies on the issue of misclassification in hospital profiling. Monte Carlo simulation assessments have been conducted in limited cases [15, 16]; yet, there is the lack of systematic studies for identifying general patterns. We assess and compare the classification accuracy of conventional and advanced approaches both analytically and numerically. The remainder of the paper is organized as follows. In Section 2, we introduce a one-way unbalanced random-effects model for hospital performance data and present the classification methods. In Section 3, we derive the formulae of accuracy measures for these methods under the model and investigate some of the properties. In Section 4, we provide numerical illustrations using both real examples and simulations, and include some recommendations for practitioners. In Section 5, we briefly study the case for binary performance data using simulation-based strategies. Finally, in Section 6, we discuss limitations of our approach and propose a basis for future work.

2. Statistical background

2.1. One-way normal random-effects model for hospital performance data

For hospital i = 1, …, M, we consider a two-level normal random-effects model:

$$\begin{gathered} y_{ij}|{\mu }_i,{\sigma }^2~N\left({\mu }_i,{\sigma }^2\right), \\ {\mu }_i|\mu ,{\tau }^2~N\left(\mu ,{\tau }^2\right), \end{gathered}$$ (1)

where y_ij denotes the performance measurement of patient j at hospital i, j = 1; …, n_i, n_i is the sample size for hospital i, μ_i is the unknown quality for hospital i, σ² is the within-hospital variation, and τ² is the between-hospital variation. When n_i’s are different, this is also often referred to as an unbalanced one-way analysis of variance model. An example of continuous performance measure y_ij might be door-to-balloon time for patients having a heart attack who require percutaneous coronary intervention or patient waiting time in hospital emergency departments (EDs) (Section 4).

Despite its simplicity, model (1) can be viewed as a basic characterization of hospital performance and frequently used as a statistical framework for research on profiling [17]. Without covariates, it is particularly suitable for process measures. Its extensions and generalizations include generalized mixed-effects models for categorical outcomes, risk-adjustment models including patient-level confounders for outcome measures [2], and multivariate generalized mixed-effects models for multiple performance measures [18]. A survey of profiling models can be found in [12] and reference therein.

We focus on the expected accuracy of classification methods under model (1). For better illustration, we use an alternative form of model (1):

$$\begin{gathered} {\overline{Y}}_i.|{\mu }_i,{\sigma }^2,n_i~N\left({\mu }_i,{\sigma }^2/n_i\right), \\ {\mu }_i|\mu ,{\tau }^2~N\left(\mu ,{\tau }^2\right), \end{gathered}$$ (2)

where ${\overline{Y}}_{i\cdot }={\sum }_{ij}{y}_{ij}/n_i$ Without a loss of generality, we assume that a hospital with larger μ_i has better quality under model (2). We view the collection of sample size over hospitals {n_i} as fixed quantities for a particular dataset. For the ease of derivation, we assume that μ, τ², and σ² are known in model (2), although these parameters are unknown and require estimation from model (1) with actual data. Therefore, we further assume that the estimators, under either classic or Bayesian estimation strategies, are consistent under some regularity conditions. We also consider a Bayesian version of model (1) where μ, τ², and σ² are treated as random variables. See Section 3 for more details.

Under model (2), the direct estimator for μ_i is ${\overline{Y}}_{i\cdot }$, and the shrinkage estimator is $B_i{\overline{Y}}_{i\cdot }+\left(1-B_i\right)\mu$, where B_i = τ²/(τ² + σ²/n_i) is the shrinkage factor [19], also the reliability measure (Section 2.3). Theoretical arguments [20] and empirical studies [21] have demonstrated the improved average point predictive ability of shrinkage estimators over direct estimators. In addition, the shrinkage of the direct estimator toward the overall average implies that the shrinkage prediction adjusts for regression-to-the-mean [22,23]. The weighting scheme of the shrinkage estimator also allows increased precision for units with small n_i (i.e., ‘stabilizing’). However, from our limited experience, there is less research on demonstrating the advantages, if any, of using shrinkage estimators (and posterior probabilities) for the purpose of classifying clusters/units. We investigate this topic in the context of hospital classification.

2.2. Classification methods

For simplicity, we consider only two tiers (‘high’ and ‘suboptimal’), although the methods can be readily extended to more than two tiers. In a straightforward manner, we compare the point estimate for the quality ${\widehat{\mu }}_i$ against some threshold to decide which tier hospital i belongs to: it would be included in the high tier if ${\widehat{\mu }}_i$ is greater than the threshold and included in the other tier otherwise. The cutoff value can be either absolute or relative. We focus on using the relative threshold for classification. That is, for a given c ∊ (0, 1) (e.g., c = 0.9), the goal is to select 100(1 − c)% of M hospitals into the top tier. The primary reason for using a relative threshold is that all methods would identify an identical proportion of top-tier hospitals so that the comparison among methods has a common ground. Practically, this also aligns with ‘pay-for-performance’ initiatives, which award hospitals whose performance estimates place them in top 100(1 − c)% of the sample. We include a brief study for classification using an external threshold in Appendix.

The following are two classification methods corresponding to using the direct and shrinkage estimators:

• Direct method (DIR): Hospital i is included in the high tier if ${\overline{Y}}_{i\cdot }>{\left\{{\overline{Y}}_{i\cdot }\right\}}_{100c}$, where ${\left\{{\overline{Y}}_{i\cdot }\right\}}_{100c}$ denotes the 100c%-tile of the collection of ${\overline{Y}}_{i\cdot }’\text{s},i=1,\dots ,M$.

• Shrinkage method (SHR): Hospital i is included in the high tier if $B_i{\overline{Y}}_{i\cdot }+\left(1-B_i\right)\mu >\{B_i{\overline{Y}}_{i\cdot }+(1-B_i)\mu {\}}_{100c}$ [13].

As both DIR and SHR are solely based on point estimates of μ_i’s, there exist some proposals for incorporating the uncertainty of point estimates. From a Bayesian perspective, Christiansen and Morris [8] proposed to make a decision using the posterior probability that μ_i exceeds some threshold, that is, Pr(μ_i > C_prob|Y) > P_prob, where C_prob is a threshold value at performance level and P_prob is the cutoff for the posterior probability. Austin and Brunner [24] provided justifications of this approach from the perspective of Bayesian decision theory. However, there exist two subtly different methods depending on whether C_prob or P_prob is given:

• Posterior probability method I (PROB1): P_prob is given, and this requires that all selected top-tier hospitals have at least P_prob (posterior) chance of being greater than the threshold C_prob. For hospital i, the probability for μ_i being greater than the 100(1 − P_prob)%-tile of the posterior distribution of μ_i is P_prob. If we choose C_prob as the 100c%-tile of the collection of these percentiles from all hospitals, then we can guarantee that exactly 100(1 − c)% of the M hospitals would be selected into the top tier [18]. Typical choices of P_prob are generally greater than 0.5 (e.g., 0.9).

• Posterior probability method II (PROB2): C_prob is given, and P_prob = {Pr(μ_i > C_prob|Y)}_100c. Under model (2), an apparent choice is to set $C_{\text{prob}}={\left\{{\mu }_i\right\}}_{100c}=\mu +\tau {\mathrm{\Phi }}^{-1}(c)$ [25]. Practical choices of C_prob can be based on expert opinions [8].

For all methods, we use sensitivity (the probability of assigning a true top-tier hospital into the top tier) and specificity (the probability of assigning a true suboptimal-tier hospital into the suboptimal tier) as the accuracy measure. This corresponds to a null hypothesis stating that the hospital of interest belongs to a suboptimal tier. These two measures suffice for our purpose because the typical measures for misclassification, the false positive rate and false negative rate are one minus sensitivity and one minus specificity, respectively.

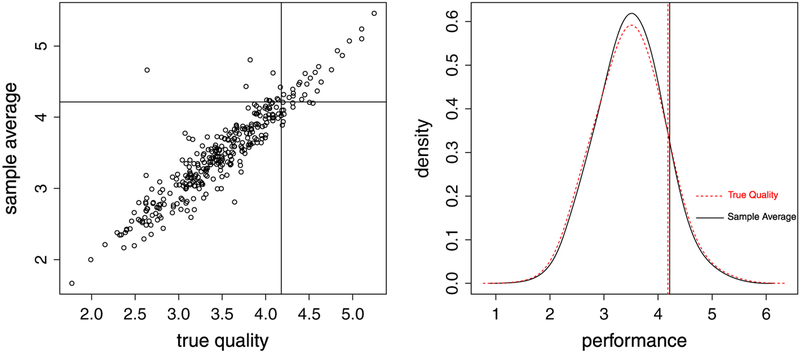
Misclassification can be readily illustrated by simulation. For example, we set μ = 3.48, τ² = 0.29, and σ² = 2.31 (all are estimates from the real data in Section 4) and use sample size {n_i} of the data to generate random numbers of {μ_i} and $\left\{{\overline{Y}}_{i\cdot }\right\}$ using model (2). Suppose our aim is to identify the top 10% from these 329 hospitals in the data. From one simulation, the true top-tier hospitals are those for which ${\mu }_i>\mu +\tau {\mathrm{\Phi }}^{-1}(0.9)=4.181$, yet the identified top performers using DIR are those for which ${\overline{Y}}_{i\cdot }>\{{\overline{Y}}_{i\cdot }{\}}_{90}=4.281$. The sensitivity is therefore $Pr\left({\overline{Y}}_{i\cdot }>4.281|{\mu }_i>4.181\right)=0.608$. Figure 1 demonstrates the misclassification using the simulated data. The left panel is a scatter plot of {μ_i} versus $\left\{{\overline{Y}}_{i\cdot }\right\}$, divided into four regions by {μ_i}₉₀ and ${\left\{{\overline{Y}}_{i\cdot }\right\}}_{90}$. The sensitivity is the relative frequency of the sample from the top right region over that from the right region. The right panel shows the smoothed marginal density plots of {μ_i} and $\left\{{\overline{Y}}_{i\cdot }\right\}$ and their respective 90%-tiles, which are purposefully overlapped to show the distinction between the two distributions and cutoff values.

Figure 1.

Left panel: scatter plot of {μ_i} versus $\left\{{\overline{Y}}_{i\cdot }\right\}$, and the sample space is divided into four regions by {μ_i}₉₀ and ${\left\{{\overline{Y}}_{i\cdot }\right\}}_{90}$. Right panel: smoothed density plots of {μ_i} and $\left\{{\overline{Y}}_{i\cdot }\right\}$ and their respective 90%-tiles. Dashed line: true quality {μ_i}; Concrete line: sample average $\left\{{\overline{Y}}_{i\cdot }\right\}$.

2.3. Past literature on reliability and misclassification

In the context of physician cost profiling, Adams et al. [11] suggested using the measure of reliability, the between-provider variance divided by the sum of between-provider and within-provider variance, to gauge the risk of misclassification. Performance data with higher reliability are expected to have better classification accuracy.

A technical argument is sketched here. For hospital i, model (2) implies that

$${\overline{Y}}_{i\cdot }|\mu ,{\tau }^2,{\sigma }^2,n_i~N\left(\mu ,{\tau }^2+{\sigma }^2/n_i\right),$$ (3)

$${\overline{Y}}_{i\cdot },{\mu }_i|\mu ,{\tau }^2,{\sigma }^2,n_i~BVN\left(\left(\begin{array}{c}\mu \\ \mu \end{array}\right),\left(\begin{array}{cc}{\tau }^2+{\sigma }^2/n_i& {\tau }^2\\ {\tau }^2& {\tau }^2\end{array}\right)\right),$$ (4)

where BVN (μ, μ, τ² + σ²/n_i, τ², ρ_i)denotes a bivariate normal distribution with identical mean μ, marginal variance τ² + σ²/n_i and τ², and correlation coefficient ${\rho }_i=\sqrt{\frac{{\tau }^2}{{\tau }^2+{\sigma }^2/n_i}}=\sqrt{B_i}$, the square root of reliability measure. Note that $cov\left({\overline{Y}}_{i\cdot },{\mu }_i\right)=E\left({\overline{Y}}_{i\cdot }{\mu }_i\right)-E\left({\overline{Y}}_i\right)E\left({\mu }_i\right)=E\left({\overline{Y}}_{i\cdot }{\mu }_i\right)-\mu E\left({\mu }_i\right)=E\left({\overline{Y}}_{i\cdot }{\mu }_i\right)-{\mu }^2$. But $E\left({\overline{Y}}_{i\cdot }{\mu }_i\right)=E{E}_{{\mu }_i}{\overline{Y}}_{i\cdot }{\mu }_i=E\left({\mu }_i{E}_{{\mu }_i}{\overline{Y}}_i\right)=E{\mu }_i^2={\mu }^2+{\tau }^2$, and therefore $cov\left({\overline{Y}}_{i\cdot },{\mu }_i\right)={\mu }^2+{\tau }^2-{\mu }^2={\tau }^2$.

By using DIR, the expected sensitivity of identifying top 100(1 − c)% of hospitals is $Pr\left({\overline{Y}}_{i\cdot }>{\overline{Y}}_{i\cdot ,100c}|{\mu }_i>{\mu }_{i,100c},\mu ,{\tau }^2,{\sigma }^2,n_i\right)={\mathrm{\Phi }}_2\left(Z_1>{\mathrm{\Phi }}^{-1}(c),Z_2>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(1-c)$, and the specificity is ${\mathrm{\Phi }}_2\left(Z_1<{\mathrm{\Phi }}^{-1}(c),Z_2<{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/c$. In both formulae, Φ() denotes the cumulative distribution function of a standard univariate normal, and Φ₂() denotes the cumulative distribution function of a standard bivariate normal (Z₁ and Z₂) with correlation coefficient ρ_i. Given a fixed c, Φ₂ is a monotonic function of ρ_i [26], hence both sensitivity and specificity increase with higher reliability.

However, an implicit assumption behind the aforementioned reasoning is equal sample size per hospital, that is, n_i = n for i = 1, … M. Less is known for the accuracy of all considered methods in the case of unequal sample size across hospitals routinely encountered in practice. Section 3 provides our answers to these questions.

3. Accuracy of classification approaches

3.1. Linear classifiers

Under model (2), the sensitivity from DIR is

$$Pr\left({\overline{Y}}_{i\cdot }>{\left\{{\overline{Y}}_{i\cdot }\right\}}_{100c}|{\mu }_i>{\left\{{\mu }_i\right\}}_{100c},\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=\frac{Pr\left({\overline{Y}}_{i\cdot }>{\left\{{\overline{Y}}_{i\cdot }\right\}}_{100c},{\mu }_i>{\left\{{\mu }_i\right\}}_{100c}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)}{Pr\left({\mu }_i>{\left\{{\mu }_i\right\}}_{100c}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)}.$$

The denominator is 1 − c. For the numerator, we treat $\left\{{\overline{Y}}_{i\cdot }\right\}$ as independent realizations of a univariate random variable, denoted by ${\widehat{\mu }}_{i,DIR}$. The key is to obtain its marginal distribution $f\left({\widehat{\mu }}_{i,DIR}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)$ (the smoothed marginal density plot of $\left\{{\overline{Y}}_{i\cdot }\right\}$ in right panel of Figure 1) and its joint distribution with μ_i, $f\left({\widehat{\mu }}_{i,DIR},{\mu }_i|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)$. Because $f\left({\overline{Y}}_{i\cdot }|\mu ,{\tau }^2,{\sigma }^2,n_i\right)=N\left(\mu ,{\tau }^2+{\sigma }^2/n_i\right)$ by Eq. (3), and noting that hospital i has an independent 1/M probability being in the sample, $f\left({\widehat{\mu }}_{i,DIR}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)$ is a mixture of normals, denoted as $\frac{1}{M}\sum {}_{i}N\left(\mu ,{\tau }^2+{\sigma }^2/n_i\right)$. Similarly, $f\left({\widehat{\mu }}_{i,DIR},{\mu }_i|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=\frac{1}{M}\sum {}_{i}BVN\left(\mu ,\mu ,{\tau }^2+{\sigma }^2/n_i,{\tau }^2,{\rho }_i\right)$, a mixture bivariate normals.

The aforementioned reasoning can be generalized to a class of linear classifiers $a_i{\overline{Y}}_{i\cdot }+b_i$, where a_i and b_i are functions of μ, τ², σ², and n_i. This is motivated by the fact that both DIR and SHR can be considered as a linear combination of ${\overline{Y}}_{i\cdot }$ and μ. Later, the four classification methods are shown to be special cases of this linear classifier. Viewing $\left\{a_i{\overline{Y}}_{i\cdot }+b_i\right\}$ as independent realizations of a univariate random variable ${\widehat{\mu }}_i,LIN$, then under model (2)

$$f\left(\left\{a_i{\overline{Y}}_{i\cdot }+b_i\right\}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=\frac{1}{M}\sum _{i}N\left(a_i\mu +b_i,a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)\right),$$ (5)

$$f\left(\left\{a_i{\overline{Y}}_{i\cdot }+b_i\right\},{\mu }_i|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=\frac{1}{M}\sum _{i}BVN\left(a_i\mu +b_i,\mu ,a_i^2\left({\tau }^2+{\sigma }^2/n_i\right),{\tau }^2,{\rho }_i\right),$$ (6)

both of which are mixture of normals.

The sensitivity of using the linear classifier is $Pr\left({\widehat{\mu }}_{i,LIN}>{\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c}|{\mu }_i>{\left\{{\mu }_i\right\}}_{100c},\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=\frac{Pr\left({\widehat{\mu }}_{i,LIN}>{\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c},{\mu }_i>{\left\{{\mu }_i\right\}}_{100c}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)}{Pr\left({\mu }_i>{\left\{{\mu }_i\right\}}_{100c}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)}.$ The denominator is 1 − c. Let $c_{LIN}={\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c}$, then c_LIN has to satisfy $\sum {}_i\mathrm{\Phi }\left(\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}}\right)=Mc$. The numerator is an average of cumulative distribution functions of bivariate normals. After some simplification (Appendix), we obtain

$$SE{N}_{LIN}=\frac{1}{M(1-c)}\sum _i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right),$$ (7)

$$SP{E}_{LIN}=\frac{1}{Mc}\sum _i{\mathrm{\Phi }}_2\left(Z_{1i}<\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}},Z_{2i}<{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right),$$ (8)

where SEN and SPE denote sensitivity and specificity, respectively. For simplicity, we omit the conditioning statements in equations hereafter.

For DIR, a_i = 1 and b_i = 0. For SHR, a_i = B_i and b_i = (1 − B_i)μ. For PROB1 and PROB2, because $f\left({\mu }_i|Y,\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=N\left(B_i{\overline{Y}}_{i\cdot }+\left(1-B_i\right)\mu ,B_i{\sigma }^2/n_i\right),Pr\left({\mu }_i>C_{\text{prob}}|Y\right)>P_{\text{prob}}$ (after further conditioning on μ, τ², and σ²) implies that

$$B_i{\overline{Y}}_{i\cdot }+\left(1-B_i\right)\mu -{\mathrm{\Phi }}^{-1}\left(P_{\text{prob}}\right)\sqrt{B_i{\sigma }^2/n_i}>C_{\text{prob}}.$$ (9)

For PROB1 in which P_prob is given, a_i = B_i and $b_i=\left(1-B_i\right)\mu -{\mathrm{\Phi }}^{-1}\left(P_{\text{prob}}\right)\sqrt{B_i{\sigma }^2/n_i}$. In addition, let $h_i=B_i{\overline{Y}}_{i\cdot }+\left(1-B_i\right)\mu -{\mathrm{\Phi }}^{-1}\left(P_{\text{prob}}\right)\sqrt{B_i{\sigma }^2/n_i}$, which is the 100(1 − P_prob)%-tile of the posterior distribution of μ_i. From Eq. (9), we obtain that C_prob is {h_i}_100c (Section 2.2). However, for PROB2 is which C_prob prefixed, Eq. (9) implies that

$$\sqrt{\frac{B_i}{{\sigma }^2/n_i}}{\overline{Y}}_{i\cdot }+\frac{1-B_i}{\sqrt{B_i{\sigma }^2/n_i}}\mu -\frac{C_{\text{ prob }}}{\sqrt{B_i{\sigma }^2/n_i}}>{\mathrm{\Phi }}^{-1}\left(P_{\text{ prob }}\right).$$ (10)

Therefore, $a_i=\sqrt{\frac{B_i}{{\sigma }^2/n_i}},b_i=\frac{1-B_i}{\sqrt{B_i{\sigma }^2/n_i}}\mu -\frac{C_{\text{prob}}}{\sqrt{B_i{\sigma }^2/n_i}}$. Let $s_i=\sqrt{\frac{B_i}{{\sigma }^2/n_i}}{\overline{Y}}_{i\cdot }+\frac{1-B_i}{\sqrt{B_i{\sigma }^2/n_i}}\mu -\frac{C_{\text{prob}}}{\sqrt{B_i{\sigma }^2/n_i}}$, then Φ⁻¹(P_prob) is {s_i}_100c based on Eq. (10). Plugging these a_i’s and b_i’s into Eqs. (7) and (8), we obtain the sensitivity and specificity functions for all methods (Table I).

Table I.

Sensitivity and specificity functions for classifying top 100(1 − c)% of hospitals.

Method	Accuracy measures
DIR	Cutoff equation: ${\sum }_i\mathrm{\Phi }\left(\frac{C_{\text{DIR}}^{*}-\mu }{\tau /{\rho }_i}\right)=Mc$
	Sensitivity: ${\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{C_{\text{DIR}}^{*}-\mu }{\tau /{\rho }_i},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(M(1-c))$
	Specificity: ${\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}<\frac{C_{\text{DIR}}^{*}-\mu }{\tau /{\rho }_i},Z_{2i}<{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(Mc)$
SHR	Cutoff equation: ${\sum }_i\mathrm{\Phi }\left(\frac{C_{\text{SHR}}^{*}-\mu }{\tau {\rho }_i}\right)=Mc$
	Sensitivity: ${\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{C_{\text{SHR}}^{*}-\mu }{\tau {\rho }_i},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(M(1-c))$
	Specificity: ${\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}<\frac{C_{\text{SHR}}^{*}-\mu }{\tau {\rho }_i},Z_{2i}<{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(Mc)$
PROB1	Cutoff equation: ${\sum }_i\mathrm{\Phi }\left(\frac{C_{\text{prob}}^{*}-\left(\mu -{\mathrm{\Phi }}^{-1}\left(P_{\text{prob}}\right){\rho }_i\sqrt{\frac{{\sigma }^2}{n_i}}\right)}{\tau {\rho }_i}\right)=Mc$
	Sensitivity: ${\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{C_{\text{prob}}^{*}-\left(\mu -{\mathrm{\Phi }}^{-1}\left(P_{\text{prob}}\right){\rho }_i\sqrt{\frac{{\sigma }^2}{n_i}}\right)}{\tau {\rho }_i},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(M(1-c))$
	Specificity: ${\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}<\frac{C_{\text{prob}}^{*}-\left(\mu -{\mathrm{\Phi }}^{-1}\left(P_{\text{prob}}\right){\rho }_i\sqrt{\frac{{\sigma }^2}{n_i}}\right)}{\tau {\rho }_i},Z_{2i}<{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(Mc)$
PROB2	Cutoff equation: ${\sum }_i\mathrm{\Phi }\left(\frac{C_{\text{prob}}-\left(\mu -{\mathrm{\Phi }}^{-1}{\left(P_{\text{prob}}\right)}^{*}{\rho }_i\sqrt{\frac{{\sigma }^2}{n_i}}\right)}{\tau {\rho }_i}\right)=Mc$
	Sensitivity: ${\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{C_{\text{prob}}-\left(\mu -{\mathrm{\Phi }}^{-1}{\left(P_{\text{prob}}\right)}^{*}{\rho }_i\sqrt{\frac{{\sigma }^2}{n_i}}\right)}{\tau {\rho }_i},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(M(1-c))$
	Specificity: ${\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}<\frac{C_{\text{prob}}-\left(\mu -{\mathrm{\Phi }}^{-1}{\left(P_{\text{prob}}\right)}^{*}{\rho }_i\sqrt{\frac{{\sigma }^2}{n_i}}\right)}{\tau {\rho }_i},Z_{2i}<{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(Mc)$

Note: ${\rho }_i=\sqrt{\frac{{\tau }^2}{{\tau }^2+{\sigma }^2/n_i}}$, $C_{\text{DIR}}^{*}$, $C_{\text{SHR}}^{*}$, $C_{\text{prob}}^{*}$ and ${\mathrm{\Phi }}^{-1}{\left(P_{\text{prob}}\right)}^{*}$ are the cutoff points.

DIR, direct method; SHR, shrinkage method.

With actual data, μ, τ², and σ² are unknown and require estimation. We can plug the corresponding estimates into these formulae to estimate the accuracy. However, the associated uncertainty due to estimation is unknown. Because there generally exists no closed-form solution to c_LIN, the (asymptotic) variance formulae of the accuracy functions are intractable. On the other hand, this problem might be better approached if we adopt a Bayesian version of model (1) in which μ, τ², and σ² are treated as random variables. For each posterior draw of the parameters under the Bayesian model, we calculate the accuracy measures using formulae to construct the corresponding posterior distribution, f (SEN_LIN|Y) and f (SPE_LIN|Y), and then use the credible intervals to summarize the uncertainty.

3.2. Optimal approach

When all n_i’s are equal, the sensitivity/specificity from all methods are identical. For PROB1, set P_prob = 0.5 makes it identical to SHR. In addition, as all n_i’s → ∞ or K = τ/σ → ∞, both sensitivity and specificity → 1 for all methods. When n_i’s are different, there is generally no closed-form solution to c_LIN. Thus, it might be difficult to compare these methods algebraically. Section 4.3 provides some numerical comparisons.

To see which method is the optimal one in terms of yielding the highest sensitivity/specificity, we note that Eqs. (7) and (8), including their special cases in Table I, can be framed as an optimization problem subject to a constraint. example Take the of sensitivity, the goal is to maximize the objective function $\frac{1}{M}\sum {}_i{\mathrm{\Phi }}_2\left(Z_{1i}>x_i,Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)$, subject to $\sum {}_i\mathrm{\Phi }\left(x_i\right)=Mc$, where $x_i=\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}}\in R$. This optimization problem can be solved by the Lagrange multiplier, $L(X,\lambda )=\sum {}_i{\mathrm{\Phi }}_2\left(Z_{1i}>x_i,Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)-\lambda \left(\sum {}_i\mathrm{\Phi }\left(x_i\right)-Mc\right)$. After some algebra (Appendix), the solution $x_i^{*}=\frac{{\mathrm{\Phi }}^{-1}(c)-{\mathrm{\Phi }}^{-1}\left({\lambda }^{*}+1\right)\sqrt{1-{\rho }_i^2}}{{\rho }_i}$, where λ* is the solution to λ. From Table I, we observe that the cutoff values from DIR and SHR are not the solutions because the functional form of $x_i^{*}$ does not involve μ yet only involves τ² and σ². For PROB2, set C_prob = μ + τΦ⁻¹ (c), the cutoff as $\frac{{\mathrm{\Phi }}^{-1}(c)+{\mathrm{\Phi }}^{-1}{\left(P_{\text{prob}}\right)}^{*}\sqrt{1-{\rho }_i^2}}{{\rho }_i}$, and ${\lambda }^{*}=\mathrm{\Phi }\left(-{\mathrm{\Phi }}^{-1}{\left(P_{\text{prob}}\right)}^{*}\right)-1$ then we obtain the solutions to the Lagrange multiplier. in addition, the second derivative test [27] shows that these solutions (critical points) are strictly local maxima (Appendix). These arguments suggest that PROB2 with C_prob = μ + τΦ⁻¹ (c) is the optimal approach among the linear classifiers.

3.3. Reliability

We derive the reliability measure for direct and shrinkage estimators as a generalization from [11] to hospitals with unequal sample size. We follow the definition that reliability is the squared correlation between a measurement and true value. For the linear function $a_i{\overline{Y}}_{i\cdot }+b_i$, its correlation with μ_i is $\frac{cov\left(a_i{\overline{Y}}_{i\cdot }+b_i,{\mu }_i\right)}{\sqrt{var\left({\mu }_i\right)}\sqrt{var\left(a_i{\overline{Y}}_{i\cdot }+b_i\right)}}$, conditional on μ, τ², σ², and {n_i}. Under models (5) and (6),

$$R{E}_{LIN}=\frac{{\sum }_i{a}_i{\tau }^2}{\tau \sqrt{\frac{1}{M}{\sum }_i{\left(a_i\mu +b_i\right)}^2-{\left(\frac{1}{M}{\sum }_i{a}_i\mu +b_i\right)}^2+\frac{1}{M}{\sum }_i{a}_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}}$$ (11)

For the direct estimator, set a_i = 1 and b_i = 0, then $R{E}_{\text{DIR}}=\frac{{\tau }^2}{{\tau }^2+\frac{1}{M}\sum {}_i{\sigma }^2/n_i}=M/\sum {}_{i}1/B_i$. For the shrinkage estimator, set a_i = B_i and b_i = (1 − B_i)μ, then $R{E}_{\text{SHR}}=\frac{{\left(\sum {}_i{B}_i\right)}^2{\tau }^2}{M\sum {}_i{B}_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}=\sum {}_i{B}_i/M$.

By Cauchy–Schwartz inequality, $\frac{1}{M}\sum {}_i{B}_i⩾M/\sum {}_{i}1/B_i$, and the equality holds if and only if n_i = n for each i. Therefore, RE_SHR ⩾ RE_DIR, showing that shrinkage estimators generally have larger correlation with true quality values than direct estimators, consistent with the literature that the former approach produces smaller prediction error.

4. Numerical illustration

4.1. Data background and setup

Our data come from the 2008 ED component of the National Hospital Ambulatory Care Survey (NHAMCS) (http://www.cdc.gov/nchs/ahcd.htm). This annual survey is conducted by the Centers for Disease Control and Preventions National Center for Health Statistics. The NHAMCS collects data on a nationally representative sample of visits to EDs and outpatient departments of non-Federal, short-stay general, or childrens general hospitals and uses a multistage probability sample design [28]. The data include multiple visit-related and patient-related characteristics. For example, visit-level characteristics include what type of provider was seen; what type and number of medications were prescribed; and the times at which the patient arrived, was seen by a provider, and was granted a final disposition (either discharged or admitted to the hospital).

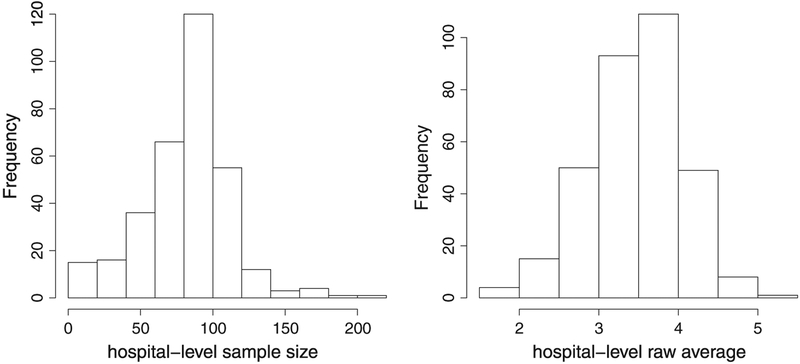
We focus on the continuous time interval between a patients arrival and the time when they are seen by a doctor (provider). Waiting time to see a provider in the ED has been proposed as a quality metric by the National Quality Forum and is expected to be reported without any adjustment [29]. Our analytic sample consists of 27,151 ED visit-level wait times recorded from 329 hospitals and was obtained from the public-use file of NHAMCS. The left panel of Figure 2 shows the distribution of sample size {n_i} (the number of visits from each ED). We apply a log transformation to the wait time before the analysis to make the normality assumption of y_ij in model (1) more plausible. We also exclude the missing cases and obtain a weighted average $\left\{{\overline{Y}}_{i\cdot }\right\}$ at ED level, incorporating the survey design. The right panel of Figure 2 shows the distribution $\left\{{\overline{Y}}_{i\cdot }\right\}$. Although we estimate the classification accuracy for this dataset using developed methods (Section 4.2), we focus on numerically illustrating some general patterns of accuracy functions (Sections 4.3–4.5), using elicited parameter values from this dataset.

Figure 2.

Left panel: the distribution of emergency department-level sample size {n_i}. Right panel: the distribution of direct estimates ${\overline{Y}}_i$..

We consider a Bayesian version of model (1) [30], assuming vague priors for the parameters: p(μ) ~ N(0, 1000), p(τ) ~ Unif (10⁻³, 100), and p(σ) ~ Unif (10⁻³, 100), where Unif denotes uniform distribution. We diagnose the convergence of the Gibbs sampling chain in the model fitting using statistics developed by [31] and conclude that the Gibbs chain achieves the convergence after 1000 iterations (the $\widehat{R}$ statistics is below 1.1). The posterior median estimates are $\widehat{\mu }=3.48$, ${\widehat{\tau }}^2=0.29$ and ${\widehat{\sigma }}^2=2.31$ based on 1000 posterior samples after discarding the first 1000 iterations.

4.2. Estimating the accuracy

We use R (www.r-project.org) library ‘nor1mix’ to obtain the cutoff points for normal mixtures and library ‘mvtnorm’ to obtain the cumulative distribution functions of bivariate normals (sample code attached in Appendix). Although hospitals with shorter wait time are considered as having better quality, it is unnecessary to reverse the signs in formulae of Table I because of the symmetry of the normal distribution function. That is, the accuracy of identifying top and bottom (1 − c)100% of hospitals are identical, and the formulae can therefore be directly applied. For identifying top 10% of the hospitals, Table II shows the estimates by plugging in $\widehat{\mu }$, ${\widehat{\tau }}^2$, ${\widehat{\sigma }}^2$ from the formulae as well as Bayesian estimates from 1000 posterior draws. The plug-in estimates are rather close to the posterior medians. Using PROB2 yields the highest accuracy, and around a half more hospital would be correctly identified compared with using DIR(329×0.1×(0.778 − 0.765) = 0.423). Of additional note is that the Bayesian method provides credible intervals to quantify the uncertainty of the estimates.

Table II.

Bayesian estimates of expected accuracy for identifying top 10% of hospitals.

	Sensitivity			Specificity
Method	Direct	Posterior median	95%CI	Direct	Posterior median	95% CI
DIR	0.760	0.765	(0.546, 0.874)	0.974	0.974	(0.950, 0.986)
SHR	0.773	0.778	(0.573, 0.878)	0.975	0.975	(0.953, 0.986)
PR0B1	0.765	0.771	(0.566, 0.871)	0.974	0.975	(0.952, 0.986)
PROB2	0.773	0.778	(0.574, 0.878)	0.975	0.975	(0.953, 0.986)

Note: CI: credible interval. In PROB1 method (P_prob = 0:9). In PROB2 method $\left(C_{prob}=\mu +\tau {\mathrm{\Phi }}^{-1}(0.9)\right)$.

Direct: plug-in estimates.

DIR, direct method; SHR, shrinkage method.

4.3. Comparison among methods

For practitioners without sophisticated statistical background, DIR versus SHR might be of interest because it compares between the naïve method and an advanced approach. This directly answers the question from [13] on how well shrinkage estimators perform for classification. For methodologists, SHR versus PROB1 and PROB2 might be of interest because they all have shrinkage properties, yet there is the lack of comparison among them in past literature. In the latter approaches, however, the thresholds in classification can vary. Therefore, we choose multiple C_prob’s and P_prob’s in the assessment.

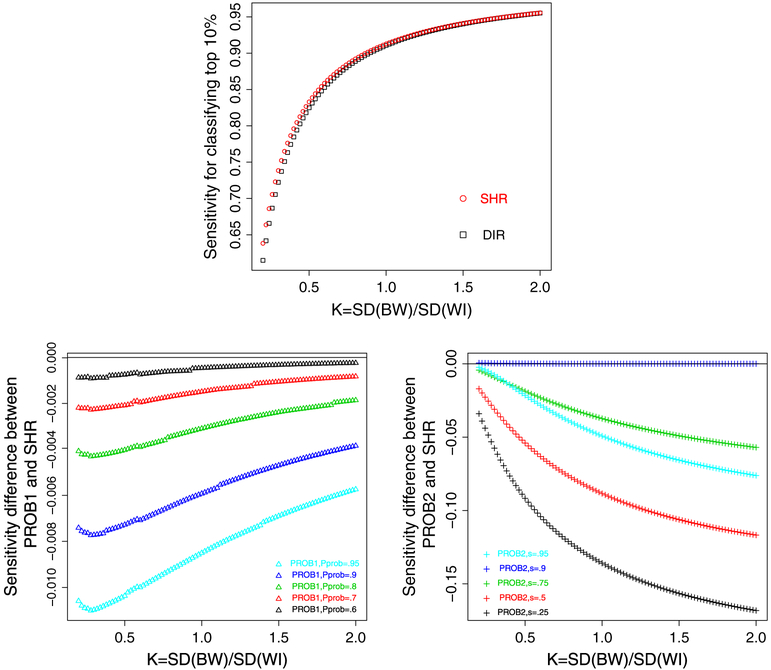
Let K = τ/σ characterize the between/within-hospital standard deviation ratio, a measure of reliability. We fix μ = 3:48 and τ² = 0.29 but change σ² so that K increases from 0.2 to 2 with a consecutive increment of 0.02. In each scenario, we calculate the sensitivity and specificity of identifying top 10% of hospitals using each method. For PROB1, we set P_prob = {0.6, 0.7, 0.8, 0.9, 0.95}. For PROB2, we choose C_prob = μ + τΦ⁻¹ (s), where s = {0.25, 0.5, 0.75, 0.9, 0.95}. Note that the option with s = 0.9 corresponds to the optimal method by our theoretical argument (Section 3.2).

Figure 3 shows the comparative patterns. The top panel plots the sensitivity from DIR and SHR. When K increases, both sensitivities increase and approach 1. The sensitivity from SHR is consistently higher than that from DIR, and the advantage of the former is more prominent with smaller K. In addition, because we assess PROB1 using multiple C_prob’s, the bottom left panel plots the difference of the sensitivity between PROB1 and SHR, and the horizonal line at 0 is the benchmark. It suggests that the sensitivity from PROB1 is consistently lower than that from SHR regardless of P_prob chosen. The bottom right panel plots the difference of sensitivity between PROB2 and SHR. When s = 0.9, which corresponds to the optimal classification, the sensitivity from PROB2 is slightly higher than SHR with smaller K yet indistinguishable as K increases, consistent with the theoretical argument. But for s ≠ 0.9, the sensitivity from PROB2 is apparently lower, corresponding to the curves below the benchmark line. The comparative pattern for specificity is similar (results not shown). These results suggest that PROB2 (with appropriately chosen C_prob = μ + τΦ⁻¹ (c)) and SHR are the preferred methods to DIR and PROB1.

Figure 3.

Top panel: sensitivity from direct method (DIR) and shrinkage method (SHR) (square: DIR and circle: SHR). Bottom left panel: the difference of sensitivity between PROB1 and SHR (triangle: PROB1, P_prob takes 0.6, 0.7, 0.8, 0.9, and 0.95 for the five curves from top to bottom). Bottom right panel: the difference of sensitivity between PROB2 and SHR (plus: PROB2, s = 0:95 for the curve above 0, and s takes 0.25, 0.5, 0.75, and 0.9 for the 4 curves below). The classification goal is to identify top 10% of hospitals.

4.4. The impact of hospital-level sample size on accuracy

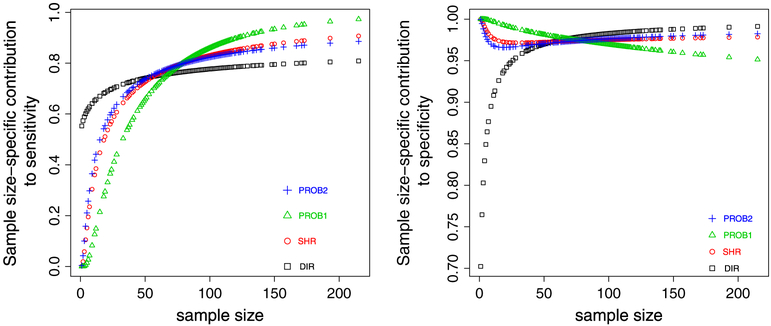
Equations (7) and (8) show that the accuracy function is an average of contributions from each hospital. For sensitivity, the hospital-level contribution is $S\left(n_i\right)={\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/\text{( 1}\text{-}c\text{ )}$. Showing S(n_i) as a function of n_i while fixing other parameters reveals the impact of the distribution of hospital-level sample size on accuracy. Figure 4 plots S(n_i) against n_i in the example data (P_prob = 0.9 in PROB1 and C_prob = μ + τΦ⁻¹ (0.9) in PROB2). For each method, the accuracy can be viewed as the area under the curve, however weighted by the frequency of the distinct sample size, as some hospitals have identical sample size. Clearly, these plots show the complicated impact of n_i on S_ni.

Figure 4.

Left panel: hospital size-specific contribution to overall sensitivity. Right panel: hospital size-specific contribution to overall specificity. square: direct method (DIR), circle: shrinkage method (SHR), triangle: PROB1 with P_prob = 0.9, plus: PROB2 with $C_{\text{prob}}=\mu +\tau {\mathrm{\Phi }}^{-1}(0.9)$. The classification goal is to identify top 10% of hospitals.

To gain better insight, Table III shows S(n_i) evaluated at a few selected sample size. For DIR, S(n_i) is smaller with a larger hospital (e.g., n_i > 50), yet larger with a smaller hospital (e.g., n_i < 15) compared with other methods, all of which have the shrinkage property. We give an intuitive explanation. In general, the accuracy of a classifier improves if the estimator has a smaller bias or variance. For a small hospital whose true quality is in the top tier, its shrinkage estimate is pulled toward the population average, yet the direct estimate is unbiased. Although the variance of the shrinkage estimate might be smaller, the effect of bias dominates, and therefore, DIR is a better classifier. This hospital is less likely to be classified as the top performer using methods other than DIR, leading to a smaller contribution from this small hospital to sensitivity. But for a large hospital whose true quality is in the top tier, the shrinkage effect is little, yet its smaller variance makes it a more reliable classifier than the direct estimate. Therefore, using shrinkage-based methods other than DIR tend to lead to a larger contribution from this large hospital to the sensitivity.

Table III.

Individual hospital-level contribution to the overall sensitivity for identifying top 10% of hospitals.

	Method
Sample size ni	DIR	SHR	PROB1	PROB2
1	0.553	0.001	5.63 ×10−6	0.004
15	0.670	0.447	0.214	0.498
50	0.741	0.727	0.658	0.738
100	0.777	0.831	0.860	0.823
150	0.795	0.876	0.934	0.860

DIR, direct method; SHR, shrinkage method.

4.5. The impact of cutoff on accuracy

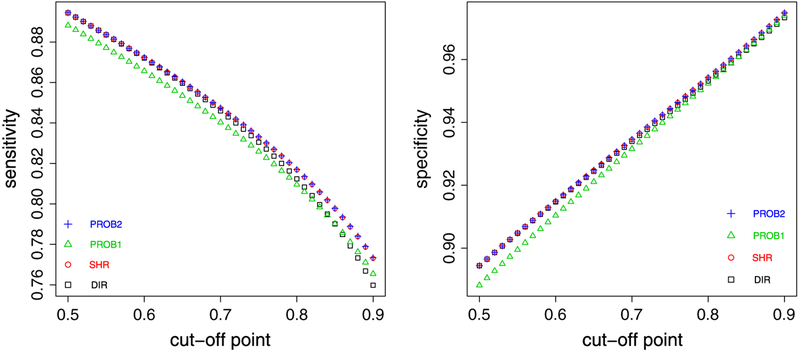
In previous illustrations, c is fixed at 0.9. We now assess the impact of changing c on the accuracy of these methods, motivated by the fact that c determines the distribution of quality tiers. For example, if identifying top performers is associated with monetary award, for which the total amount might be fixed in certain cases, then program evaluators might vary c for different options of awarding mechanisms, such as rewarding fewer hospitals with paying each more or rewarding more hospitals with paying each less. Figure 5 shows the sensitivity and specificity, fixing μ = 3.48, τ² = 0.29, σ² = 2.31 and changing c from 0.5 to 0.9 with a consecutive increment of 0.01. Sensitivity estimates from all methods decrease as c increases, as it would be more difficult to distinguish among hospitals on the tail of the distribution. PROB1 (P_prob = 0:9) generally has the lowest sensitivity. PROB2 (C_probe = μ + τΦ⁻¹ (c)) and SHR are nearly indistinguishable, and they have better performance than the other two methods. As c increases, the advantages from SHR and PROB2 over DIR is more prominent, corresponding to the tail of the distribution. The pattern of specificity function overall mirrors that from the sensitivity.

Figure 5.

Left panel: sensitivity versus cutoff c. Right panel: specificity versus cutoff c. square: direct method (DIR), circle: shrinkage method (SHR), triangle: PROB1 with P_prob = 0.9, plus: PROB2 with C_prob = μ + τΦ⁻¹(c). The classification goal is to identify top 100(1 − c)% of hospitals.

4.6. Simulation validation

We conduct a brief simulation study to assess the validity of the developed formulae. We fix μ = 3:48, τ² = 0.29 but change σ² so that K = 0.2, 0.6, 1.0. For each of the three scenarios, we generate random samples of {μ_i} and $\left\{{\overline{Y}}_{i\cdot }\right\}$ under model (2) for 100 simulations, using sample size {n_i} from the example data. For each simulation, we implement two strategies to estimate the sensitivity of classifying top 10% of hospitals. One is to plug posterior medians of parameters (based on 1000 draws) into the formulae, as the proposed strategy in Section 3.1. We denote the results as the ‘estimated’ sensitivity. The other is to calculate the proportion of hospitals identified in the top tier among true top performers, because we know the true tier status of each hospital from the data generating process. This Monte Carlo simulation procedure has been used in literature [15, 16] where the closed-form formulae have not been developed. We denote the results as the ‘empirica’ sensitivity. We average both ‘estimated’ and ‘empirical’ sensitivity over 100 simulations and compare them with the one calculated from the formulae by plugging in true data generating parameters. We refer to the latter quantity as the ‘true’ sensitivity. Table IV shows the results, and the closeness between three sensitivity estimates suggest the validity of the formulae. The validation results for specificity are similar (not shown).

Table IV.

Simulation validation: sensitivity estimates for identifying top 10% of hospitals.

τ/σ = 0.2
Method	True	Estimated	Empirical
DIR	0.615	0.613	0.612
SHR	0.638	0.635	0.643
PROB1	0.631	0.628	0.636
PROB2	0.639	0.635	0.641
τ/σ = 0.6
DIR	0.853	0.849	0.849
SHR	0.859	0.856	0.850
PROB1	0.852	0.850	0.845
PROB2	0.859	0.856	0.855
τ/σ = 1.0
DIR	0.911	0.904	0.901
SHR	0.913	0.907	0.900
PROB1	0.907	0.901	0.897
PROB2	0.913	0.907	0.903

Note: The data generating parameter μ = 3.48 and τ² = 0.29. ‘True’ is based on the formulae using the population generating parameters. ‘Estimated’ is based on the formulae using posterior medians of parameters. ‘Empirical’ is the relative frequency of correctly identified top performers from the Monte Carlo procedure. Both ‘estimated’ and ‘empirical’ are averages over 100 simulations.

DIR, direct method; SHR, shrinkage method.

4.7. Practical implications

We discuss some of the practical implications from the methodological development. First, the developed formulae provide an accessible tool for practitioners to quantify the accuracy from different classification methods. Rather than merely identifying hospitals in quality tiers, we recommend practitioners also reporting estimated accuracy associated with the classification, analogous to providing variance of point estimate in statistical analysis. Such information might be helpful for the decision making, as apparently the classification with suboptimal accuracy might be less preferable. In addition, the preferred classification methods are SHR and PROB2 (with C_prob = μ + τΦ⁻¹ (c)) based on our evaluation results.

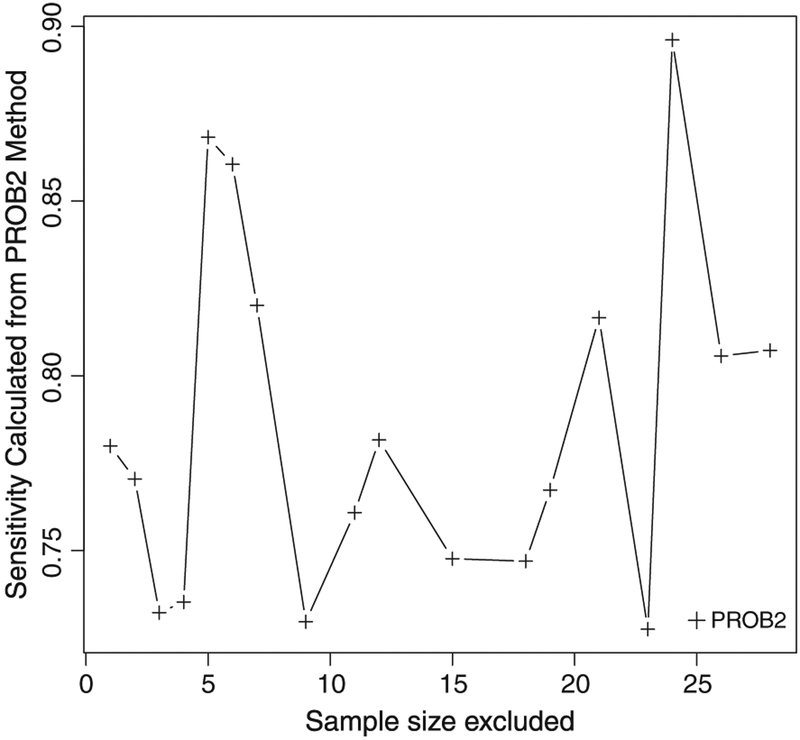
The estimates of accuracy can also be used to refine classification. One conventional practice in hospital profiling is to exclude those with small samples to obtain more reliable hospital-level performance estimates. However, there exists no formal rule on how small a hospital would need to be for exclusion. If the primary goal is to tier hospitals, we can remove small hospitals sequentially with increasing sample size, estimate the classification accuracy for those remain in the data, and identify the appropriate cutoff based on the desired level of accuracy. For example, Figure 6 shows the sensitivity estimates from PROB2 in classifying top 10% of hospitals when small hospitals (n_i ranges from 1 to fewer than 30) are excluded sequentially from the example data. The sensitivity overall increases as small hospitals are excluded. However, we see some fluctuation because the estimates of μ, τ², and σ² vary with different hospitals excluded. Suppose, we would like to achieve at least 75% for the sensitivity, then hospitals with fewer than 10 patients might need to be excluded. Compared with some ad hoc rules (e.g., exclude hospitals with n_i < 20 regardless of the data structure), this data-based procedure would prevent one from excluding too many (or too few) small hospitals.

Figure 6.

The sensitivity for classifying top 10% of hospitals when small-size hospitals are sequentially excluded. Plus: PROB2 C_prob = μ + τΦ⁻¹(0.9).

The developed formulae might also be useful for designing profiling studies. For example, to estimate the required sample size for achieving the desired accuracy in classification, we can solve n_i’s from the accuracy functions in Table I when either sensitivity or specificity is predetermined. A simple solution is to assume equal sample size per hospital. But it might be impractical because hospital volume often varies. For example, it is unlikely that many patients can be recruited for some rural hospitals within a limited study period. We can stratify the distribution {n_i} (e.g., using historical data) and solve for the required n_i’s from each strata. For instance, we might divide hospitals into three groups (large, medium, and small) based on their volume and assume that the average sample size in the small-volume hospitals is n_S and that in the medium-volume and large-volume hospitals are n_M = K₁n and n_L = K₂n, respectively. On the basis of some empirical estimates of K₁ and K₂, we could solve for n_S, n_M, and n_L from the formulae.

5. Binary outcome

We next consider the extension to a binary performance measure. The example dataset is a subset of the hospital compare database (www.hospitalcompare.hhs.gov), which is collected by CMS and includes process performance measures from 4000 plus US hospitals for care delivered to patients eligible for Medicare. We use one measure designated for assessing the compliance rate of ‘Influenza vaccination’ for patients diagnosed with pneumonia from October 2005 to September 2006. For each hospital, the data contain the number of patients who were admitted and were eligible for the therapy (denominator) and the number of eligible patients who received the treatment (numerator). The guidelines for defining the eligibility for a patient and sample selection criteria are given by the specifications from CMS. The dataset includes 3304 hospitals with nonmissing values for both numerator and denominator.

Because of the binary nature of the outcome, we consider a logistic-normal model [32]:

$$\begin{gathered} y_i|n_i,p_i~Binomial\left(n_i,p_i\right), \\ log\left(\frac{p_i}{1-p_i}\right)|{\mu }_B,{\tau }_B^2~N\left({\mu }_B,{\tau }_B^2\right), \end{gathered}$$ (12)

where y_i is the number of patients receiving the vaccination at hospital i (numerator), n_i is the hospital-level patient size (denominator), p_i is the hospital-level compliance rate, and μ_B and ${\tau }_B^2$ are the mean and variance of the random effects on the logit scale of p_i. A larger p_i might indicate a higher compliance rate for hospital i for the vaccination procedure, implying a better quality.

Similar to the case of continuous measures (Section 2), we consider four classification methods:

• DIR: Hospital i is included in the high tier if ${\widehat{p}}_{i,DIR}=y_i/n_i>{\left\{{\widehat{p}}_{i,DIR}\right\}}_{100c}$.

• SHR: Hospital i is classified the high tier if ${\widehat{p}}_{i,SHR}>{\left\{{\widehat{p}}_{i,SHR}\right\}}_{100c}$, where ${\widehat{p}}_{i,SHR}$ is the shrinkage estimator for p_i under model (12).

• PROB1: Hospital i is included in the high tier if $Pr\left(p_i>C_{\text{prob}}|Y\right)>P_{\text{prob}}$, where P_prob is given.

• PROB2: Hospital i is included in the high tier if $Pr\left(p_i>C_{\text{prob}}|Y\right)>P_{\text{prob}}$, where C_prob is given.

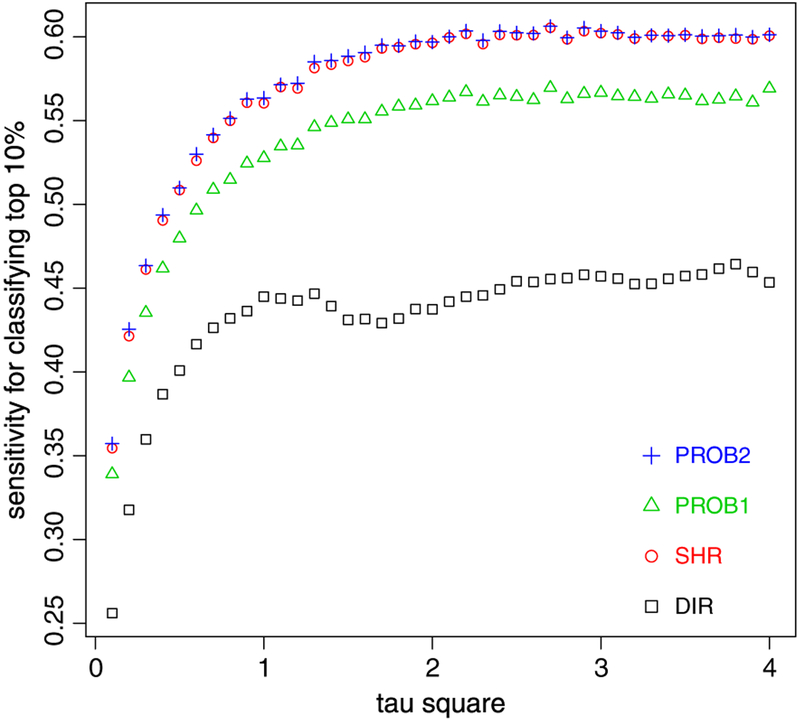
However, unlike model (2), closed-form formulae for accuracy measures under model (12) are intractable. We use a simulation-based strategy to assess and compare among different methods. We first fit model (12) to the dataset using a Bayesian scheme assuming vague priors: p(μ_B) ~ N(0, 1000), p(τ) ~ Unif (10⁻³, 100). The posterior medians for parameters are ${\widehat{\mu }}_B=1.1$ and ${\widehat{\tau }}_B^2=1.4$ based on 1000 draws. In the simulation, μ_B is fixed at 1.1, and we increase ${\tau }_B^2$ from 0.1 to 4.0 with a consecutive increment of 0.1 to reflect an increasing between-hospital variation. For each combination of μ_B and ${\tau }_B^2$, we use the actual sample size {n_i} to generate data {y_i} under model (12) for 100 replicates. We apply the four methods to each replicate to identify top 10% of hospitals (PROB1: P_prob = 0.9; PROB2: logit.(C_prob) = μ_B + τ_BΦ⁻¹ (0.9)). We calculate the average ‘empirical’ sensitivity and specificity over 100 simulations.

Figure 7 shows the sensitivity estimates within the range of ${\tau }_B^2$. The results seem to suggest that with an increasing ${\tau }_B^2$, the sensitivity from all methods overall increase. DIR has the lowest sensitivity. Both SHR and PROB2 have some advantages over the other two methods, and they are nearly indistinguishable over the range of ${\tau }_B^2$ tested. Results for the specificity function reflect similar patterns (not shown). Overall, the comparative pattern is similar to that for continuous measures under normal random-effects models (Section 4).

Figure 7.

Sensitivity estimates for binary performance data. square: direct method (DIR), circle: shrinkage method (SHR), triangle: PROB1, plus: PROB2. The classification goal is to identify top 10% of hospitals.

In addition, we might use a double simulation strategy to yield the variation of the estimate of accuracy measures. First, we obtain posterior draws of μ_B and ${\tau }_B^2$ from $p\left({\mu }_B,{\tau }_B^2|Y\right)$. Then, for each draw of parameters, we treat them as true values of parameters to generate random samples of {y_i}and obtain the average accuracy estimates across simulations as described earlier. Ignoring the Monte Carlo error, this constitutes a posterior sample of the accuracy function, from which the 95% credible interval can be constructed. However, this strategy might be computationally intensive.

An alternative strategy is to apply the arcsine square root transformation to the proportion data by considering the model [33]

$$\begin{gathered} y_i|n_i,p_i~Binomial\left(n_i,p_i\right), \\ {\widehat{\theta }}_i=arcsin\left(\sqrt{y_i/n_i}\right)|n_i,{\theta }_i\dot{~}N\left({\theta }_i,1/4n_i\right), \\ {\theta }_i|{\mu }_{\theta },{\tau }_{\theta }^2~N\left({\mu }_{\theta },{\tau }_{\theta }^2\right), \end{gathered}$$ (13)

where ${\theta }_i=arcsin\left(\sqrt{p_i}\right)$. On the transformed scale θ_i, model (13) is reduced to model (2) with σ² set to 1/4. Because θ_i is a monotonic transformation of p_i, the accuracy of classifying hospitals on p_i can be readily calculated on θ_i using formulae in Table I.

However, the simulation-based strategy might be a more viable strategy for models with more complicated features such as with risk adjustment or non-normal random effects (Section 6) when closed-form formulae are lacking. Using software familiar to practitioners (e.g., R and WinBUGS), this approach can be largely automatic with well-specified input such as hospital-level sample size, population mean of the underlying quality, and between/within hospital variation. For model (12), the simulation programming code is available upon request.

6. Discussion

Profiling hospitals using performance data is an important activity in both research and practice. The purpose of this study is to assess and compare the accuracy of several commonly used approaches to classifying hospitals into quality tiers. We derive the function of expected accuracy for these methods under the classic unbalanced one-way random-effects model (2), the basic form of profiling models. Our study shows that the optimal approach is to use posterior probabilities for classification (PROB2) and set C_prob = {μ_i}_100c. Our numerical evaluations show that the classification using SHR might have comparable performance. Therefore, we suggest that practitioners use these two methods rather than other alternatives. However, for data with high reliability (larger between than within-provider variance), there is little difference among these methods. We advocate practitioners calculating and reporting the expected accuracy of the classification using the developed formulae or simulation strategies.

Actual hospital performance data often have complicated structure and therefore require more sophisticated statistical models. Our study is based on the one-way random-effects model, a largely simplified analytical framework. Our research is therefore a building block, and there exist several limitations, which deserve future research. For example, our simulation results for the binary performance data also suggest that PROB2 has the highest classification accuracy. This prompts us to ponder the generality of this pattern. If we view competing classification approaches as alternative decisions, then the goal of identifying top 100(1 − c)% of hospitals with the largest μ_i’s has the utility function U(d, μ_i) = I(μ_i >{μ_i}_100c) and the expected utility $E(d)=\int U\left(d,{\mu }_i\right)f\left({\mu }_i|Y\right)d{\mu }_i$. Arguments from [16, 24], which stem from the Bayesian decision theory [34], suggest that the optimal decision should maximize $E(d)=Pr\left({\mu }_i>{\left\{{\mu }_i\right\}}_{100c}|Y\right)$. Therefore, choosing top 100(1−c)% of hospitals with the largest posterior probability of being greater than {μ_i}_100c would minimize the expected misclassification. This argument might hold regardless of model assumptions on the distribution of {μ_i} and data features (e.g., unbalance data). Verification of our conjecture, however, requires further research.

Also note from Figure 7, the ‘wiggle’ of the curves suggests that the accuracy functions over τ² for binary performance measures might have more complicated forms than those for continuous case, which is apparently more smooth (Figure 3). One future research topic, with a more technical flavor, is to obtain approximation formulae for accuracy measures under model (12). This problem might be related to the well-known problem of constructing approximate confidence intervals for binomial proportions [35]. Approximation formulae can be used as off-the-shelf tools for exploratory analysis and might guard against possible programming errors in simulation studies.

In addition, we will consider models with risk adjustment that are suitable for outcome performance measures, controlling for patient-level confounders. An example is

$$\begin{gathered} y_{ij}={\beta }_{0i}+{\beta }_1{x}_{ij}+{ϵ}_{ij},{ϵ}_{ij}~N\left(0,{\sigma }^2\right) \\ {\beta }_{0i}~N\left({\beta }_0,{\tau }^2\right), \end{gathered}$$ (14)

where the risk is adjusted through covariates x_ij. The random effects β_0i, unexplained by risk-adjustment, quantifies the quality of hospital i. For an estimator of β_0i, ${\widehat{\beta }}_{0i}$, the sensitivity of using ${\widehat{\beta }}_{0i}$ to classify top 100(1−c)% hospitals is $Pr\left({\widehat{\beta }}_{0i}>{\left\{{\widehat{\beta }}_{0i}\right\}}_{100c}|{\beta }_{0i}>{\left\{{\beta }_{0i}\right\}}_{100c},{\beta }_0,{\beta }_1,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right).$

When the normality assumption of the random-effects models (1, 12, and 14) is violated, as often happen for actual data, the problem of classification might be considerably harder. We foresee two future research directions. One is to conduct simulation-based comparative studies, assessing the performance of the classification approaches on data generated from models with non-normal random effects. However, when applying these methods, we still assume normal random-effects for estimation approaches because the software assuming non-normal random effects is not readily available. Similar studies can be found in [36–38], where they studied the behavior of the estimates for fixed effects and variance components under mis-specified linear or generalized linear mixed effects models. Another research topic is to estimate the classification accuracy using semiparametric Bayesian approach, such as using Dirichlet process prior to model non-normal random effects [39, 40].

The methods development for a single outcome can be extended to the case in which hospital programs collect and report multiple yet related performance indicators. A commonly used strategy is to summarize these measures into a unidimensional composite score and to classify the programs using the summary score. The composite score can be constructed using a simple average or estimated via Bayesian hierarchical latent models [18, 41–43]. Because a latent variable in general can also be treated as random-effects [44], the developed formulae under model (2) might be extended to the summary scoring approach.

A related technique in profiling is to rank hospitals, and there exist a large body of related literature. For example, [45] pointed out that ranking based on the posterior distribution of ranks is more optimal than ranking based on the posterior means under a two-stage model as in Eq. (2). Lockwood et al. [46] performed a simulation-based investigation on the performance of optimal ranking procedures and related percentile methods, showing their considerable variations within a normal range of reliability. Lin et al. [47] presented a theoretical study of optimal ranking procedures under various loss functions. For the loss function on identifying top 100(1−c)% of the units using ranks, they have shown that the optimal ranking is asymptotically equivalent to the ‘exceeding probability’ procedure, which is better than ranking using observed means or posterior means. This is consistent with our finding that PROB2 achieves better accuracy than DIR or SHR for classification under model (1). Therefore, additional research might be conducted to elucidate the connection between ranking and classification.

Finally, although our research is motivated from hospital classification, the methods might also be applied and extended to other settings involve program classification, most notably for the performance indicators in education [48–50].

Appendix

Classification using an external threshold (Section 2.2)

We develop the functions for accuracy measures if an absolute threshold c₁ is used. The sensitivity from using the linear classifier is

$$Pr\left({\widehat{\mu }}_{i,LIN}>c_1|{\mu }_i>c_1,\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=\frac{1}{M\mathrm{\Phi }\left(\frac{\mu -c_1}{\tau }\right)}\sum _i{\mathrm{\Phi }}_2\times \left(Z_{1i}>\frac{c_1-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}},Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right),$$

and the specificity is

$$Pr\left({\widehat{\mu }}_{i,LIN}<c_1|{\mu }_i<c_1,\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=\frac{1}{M\mathrm{\Phi }\left(\frac{c_1-\mu }{\tau }\right)}\sum _i{\mathrm{\Phi }}_2\times \left(Z_{1i}<\frac{c_1-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}},Z_{2i}<\frac{c_1-\mu }{\tau },{\rho }_i\right).$$

In the following, we gauge the behavior of the classifier using the direct and shrinkage estimators. For brevity, we do not consider the classifier using posterior probabilities because it require an additional cutoff on probability scale. We consider the sensitivity, specificity, and probability of correct classification (PCC) as a summary measure of sensitivity and specificity [51]. After some algebra, the corresponding formulae are derived and listed in Table A1.

We focuses on the comparison between the two classifiers. Without a loss of generality, suppose c₁ > μ, then

$$\begin{gathered} \frac{c_1-\mu }{\tau /{\rho }_i}<\frac{c_1-\mu }{\tau {\rho }_i}\Rightarrow \\ {\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_1-\mu }{\tau /{\rho }_i},Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)>{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_1-\mu }{\tau {\rho }_i},Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)\Rightarrow \\ \frac{1}{M\mathrm{\Phi }\left(\frac{\mu -{\text{c}}_1}{\tau }\right)}\sum _i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_1-\mu }{\tau /{\rho }_i},Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)>\frac{1}{M\mathrm{\Phi }\left(\frac{\mu -c_1}{\tau }\right)}\sum _i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_1-\mu }{\tau {\rho }_i},Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)\Rightarrow \\ SE{N}_{\text{DIR}}>SE{N}_{\text{SHR}}. \end{gathered}$$ (A1)

An intuitive explanation for Eq. (A1) is that compared with the true quality μ_i, the direct estimator ${\widehat{\mu }}_{i,DIR}$ tend to be over-dispersed yet the shrinkage estimator ${\widehat{\mu }}_{i,DIR}$ shrunk to the center. If the goal is to identify the hospitals on the right tail (top performers), then SHR is more likely to miss them because of the shrinkage and therefore has a lower sensitivity than DIR. It can also be shown that SPEC_DIR < SPEC_SHR. When c₁ < μ, the inequality switches. When c₁ = μ, SEN_DIR = SEN_SHR, and SPEC_DIR = SPEC_SHR.

Table A1.

Sensitivity, specificity, and probability of correct classification for classifying hospitals using the external threshold c1.

Method	Accuracy measures
DIR	Sensitivity: $\frac{1}{M\mathrm{\Phi }\left(\frac{\mu -c_1}{\tau }\right)}{\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_1-\mu }{\tau /{\rho }_i},Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)$
	Specificity: $\frac{1}{M\mathrm{\Phi }\left(\frac{\mu -c_1}{\tau }\right)}{\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}<\frac{c_1-\mu }{\tau /{\rho }_i},Z_{2i}<\frac{c_1-\mu }{\tau },{\rho }_i\right)$
	PCC: $\frac{1}{M}\sum _i{\text{Φ}}_2\left(Z_{1i}>\frac{c_1-\mu }{\tau /{\rho }_i},Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)+{\text{Φ}}_2\left(Z_{1i}<\frac{c_1-\mu }{\tau /{\rho }_i},Z_{2i}<\frac{c_1-\mu }{\tau },{\rho }_i\right)$
SHR	Sensitivity: $\frac{1}{M\mathrm{\Phi }\left(\frac{\mu -c_1}{\tau }\right)}{\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_1-\mu }{\tau /{\rho }_i},Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)$
	Specificity: $\frac{1}{M\mathrm{\Phi }\left(\frac{\mu -c_1}{\tau }\right)}{\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}<\frac{c_1-\mu }{\tau /{\rho }_i},Z_{2i}<\frac{c_1-\mu }{\tau },{\rho }_i\right)$
	PCC: $\frac{1}{M}{\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_1-\mu }{\tau /{\rho }_i},Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)+{\mathrm{\Phi }}_2\left(Z_{1i}<\frac{c_1-\mu }{\tau /{\mathcal{l}}_i},Z_{2i}<\frac{c_1-\mu }{\tau },{\rho }_i\right)$

DIR, direct method; SHR, shrinkage method; PCC, probability of correct classification.

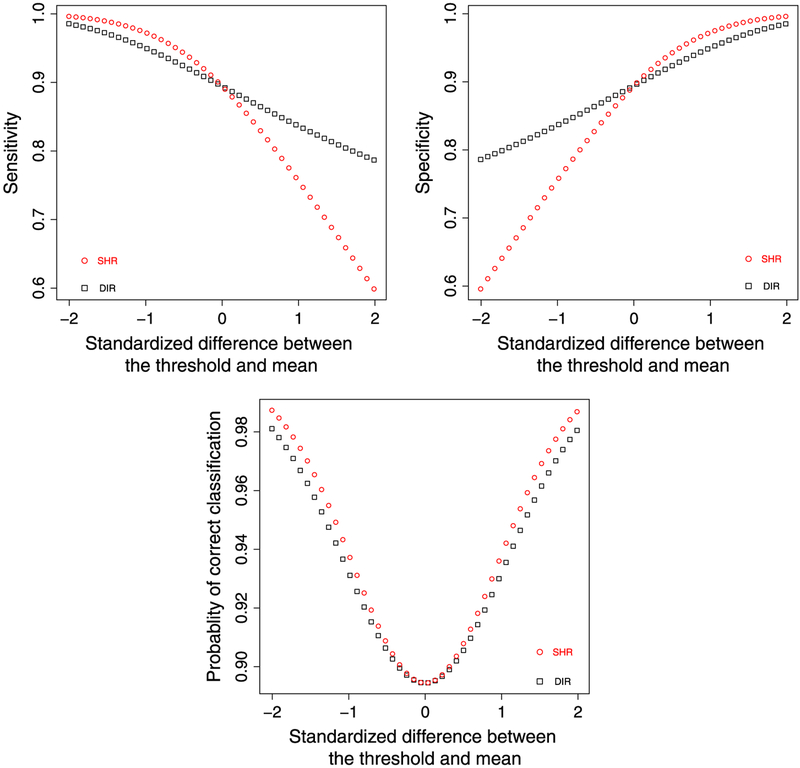
Despite the trade-off between sensitivity and specificity of the two methods, one might wonder which method yields higher PCC. Note that PCC for both methods is an average of ${\mathrm{\Phi }}_2\left(Z_{1i}>x_i,Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)+{\mathrm{\Phi }}_2\left(Z_{1i}<x_i,Z_{2i}<\frac{c_1-\mu }{\tau },{\rho }_i\right)$, where $x_i=\frac{c_1-\mu }{\tau /{\rho }_i}$ for DIR and $x_i=\frac{c_1-\mu }{\tau {\rho }_i}$ for SHR. Let $L_i={\mathrm{\Phi }}_2\left(Z_{1i}>x_i,Z_{2i}>\frac{c_1-\mu }{\tau },{\rho }_i\right)+{\mathrm{\Phi }}_2\left(Z_{1i}<x_i,Z_{2i}<\frac{c_1-\mu }{\tau },{\rho }_i\right)$ we seek to find the maxima of L_i as a function of x_i. After some algebra, we obtain $\partial L_i/\partial x_i=\varphi \left(x_i\right)\left(2\mathrm{\Phi }\left(\frac{\frac{c_1-\mu }{\tau }-{\rho }_i{x}_i}{\sqrt{1-{\rho }_i^2}}\right)-1\right)$. Set it as 0 leads to $x_i=\frac{c_1-\mu }{\tau {\rho }_i}$. In addition ${\partial }^2{L}_i/\partial x_i{}^2{|}_{x_i=\frac{c_1-\mu }{\tau {\rho }_i}}=\varphi \left(\frac{c_1-\mu }{\tau {\rho }_i}\right)\frac{2}{\sqrt{2\pi }}\frac{-{\rho }_i}{\sqrt{1-{\rho }_i^2}}<0$. therefore L_i achieves the local maxima for $x_i=\frac{c_1-\mu }{\tau {\rho }_i}$, corresponds to SHR. Sum it over i and take the average, then PCC_SHR > PCC_DIR. More generally, SHR yields the highest PCC among all linear classifiers when an external threshold is used.

We use the example data in Section 4 to illustrate the comparative pattern. We set c₁ = sτ, where s varies from −2 to 2 with a consecutive increment of 0.01, and calculate the sensitivity, specificity, and PCC of DIR and SHR using various c₁’s. Figure A1 plots the results, showing the trade-off of sensitivity and specificity between two methods, and the superiority of SHR over DIR for PCC across all c₁’s.

Derivations of Eqs. (7) and (8) (Section 3.1)

Figure A1.

Top left panel: sensitivity from direct method (DIR) and shrinkage method (SHR) (square: DIR, circle: SHR). Top right panel: specificity from DIR and SHR. Bottom panel: probability of correct classification from DIR and SHR. X-axis: $\frac{c_1-\mu }{\tau }$.

The sensitivity of using the linear classifier is

$$Pr\left({\widehat{\mu }}_{i,LIN}>{\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c}|{\mu }_i>{\left\{{\mu }_i\right\}}_{100c},\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=\frac{Pr\left({\widehat{\mu }}_{i,LIN}>{\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c},{\mu }_i>{\left\{{\mu }_i\right\}}_{100c}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)}{Pr\left({\mu }_i>{\left\{{\mu }_i\right\}}_{100c}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)},$$

where μ_i > {μ_i}_100c means that hospital i belongs to the top-tier, and ${\widehat{\mu }}_{i,LIN}>{\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c}$ means that hospital i is classified as in the top-tier using the linear classifier ${\widehat{\mu }}_{i,LIN}$. The denominator Pr(μ_i > {μ_i}_100c is 1 − c because we use the relative threshold to identify top 100(1−c)% of the hospitals, where ${\left\{{\mu }_i\right\}}_{100c}=\mu +\tau {\mathrm{\Phi }}^{-1}c$ under model (2).

To work out the numerator $Pr\left({\widehat{\mu }}_{i,LIN}>{\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c},{\mu }_i>{\left\{{\mu }_i\right\}}_{100c}\right)$, first let $c_{LIN}\text{=}{\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c}$, the 100c%-tile of ${\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c}$, this implies that $Pr\left({\widehat{\mu }}_{i,LIN}>c_{LIN}\right)=1-c$. On The basis of Eq. (5), ${\widehat{\mu }}_{i,LIN}$ has a marginal distribution of normal mixtures. Therefore, $Pr\left({\widehat{\mu }}_{i,LIN}>c_{LIN}\right)=\frac{1}{M}\mathrm{\Phi }\left(\frac{a_i\mu +b_i-c_{LIN}}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}}\right)=1-c$ On basis of Eq. (6), ${\widehat{\mu }}_{i,LIN}$ and μ_i jointly have a marginal distribution bivariate normal mixtures. Therefore, $Pr\left({\widehat{\mu }}_{i,LIN}>c_{LIN},{\mu }_i>{\left\{{\mu }_i\right\}}_{100c}\right)=\frac{1}{M}{\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)$.

Similarly, for specificity

$$Pr\left({\widehat{\mu }}_{i,LIN}<{\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c}|{\mu }_i<{\left\{{\mu }_i\right\}}_{100c},\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)=\frac{Pr\left({\widehat{\mu }}_{i,LIN}<{\left\{{\widehat{\mu }}_{i,LIN}\right\}}_{100c},{\mu }_i<{\left\{{\mu }_i\right\}}_{100c}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)}{Pr\left({\mu }_i<{\left\{{\mu }_i\right\}}_{100c}|\mu ,{\tau }^2,{\sigma }^2,\left\{n_i\right\}\right)}.$$

The denominator $Pr\left({\mu }_i<{\left\{{\mu }_i\right\}}_{100c}\right)$ is c, as 100c% of the M hospitals in the sub-optimal tier. For the numerator, the cutoff point c_LIN remains the same as that of the sensitivity, whereas $Pr\left({\widehat{\mu }}_{i,LIN}<c_{LIN},{\mu }_i<{\left\{{\mu }_i\right\}}_{100c}\right)=\frac{1}{M}{\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}<\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}},Z_{2i}<{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)$ can still be calculated from the bivariate normal mixture, yet with reversed signs from the numerator of the sensitivity. Also note that in general ${\mathrm{\Phi }}_2\left(Z_{1i}<\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}},Z_{2i}<{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)+{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)<=1$ The equality only holds in some limiting cases (e.g., both c_LIN → ∞ and c → 1 or ρ_i → 1). This leads to Equations (7) and (8).

Identifying the optimal linear classifier (Section 3.2)

The optimal classifier is expected to maximize sensitivity or specificity. For sensitivity, the goal is to maximize objective function $\frac{1}{M}{\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>x_i,Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)$, subject to ${\sum }_i\mathrm{\Phi }\left(x_i\right)=Mc$, where $x_i=\frac{c_{LIN}-\left(a_i\mu +b_i\right)}{\sqrt{a_i^2\left({\tau }^2+{\sigma }^2/n_i\right)}}\in R$. This optimization problem can be solved by the Lagrange multiplier. Let $L(X,\lambda )={\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>x_i,Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)-\lambda \left({\sum }_i\mathrm{\Phi }\left(x_i\right)-Mc\right)$, then $\partial L/\partial \lambda =-\left({\sum }_i\mathrm{\Phi }\left(x_i\right)-Mc\right)$, and $\partial L/\partial x_i=\partial {\mathrm{\Phi }}_2/\partial x_i-\lambda \varphi \left(x_i\right)$ where Φ₂ abbreviates ${\mathrm{\Phi }}_2\left(Z_{1i}>x_i,Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)$ and ϕ() denotes the probability density function of the univariate standard normal. Also

$$\begin{gathered} {\mathrm{\Phi }}_2={\int }_{x_i}^{\infty }{\int }_{{\mathrm{\Phi }}^{-1}(c)}^{\infty }\frac{1}{2\pi \sqrt{1-{\rho }_i^2}}\exp \left(-\frac{1}{2}\frac{z_{1i}^2-2{\rho }_i{z}_{1i}{z}_{2i}+z_{2i}^2}{1-{\rho }_i^2}\right)d{z}_{1i}d{z}_{2i} \\ ={\int }_{x_i}^{\infty }\varphi \left(z_{1i}\right)d{z}_{1i}{\int }_{{\mathrm{\Phi }}^{-1}(c)}^{\infty }\frac{1}{\sqrt{2\pi }\sqrt{1-{\rho }_i^2}}\exp \left(-\frac{1}{2}\frac{{\left(z_{2i}-{\rho }_i{z}_{1i}\right)}^2}{1-{\rho }_i^2}\right)d{z}_{2i} \\ ={\int }_{x_i}^{\infty }\varphi \left(z_{1i}\right)d{z}_{1i}{\int }_{\frac{{\mathrm{\Phi }}^{-1}(c)-{\rho }_i{z}_{1i}}{\sqrt{1-{\rho }_i^2}}}^{\frac{\infty -{\rho }_i{z}_{1i}}{\sqrt{1-{\rho }_i^2}}}\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{1}{2}\frac{{\left(z_{2i}-{\rho }_i{z}_{1i}\right)}^2}{1-{\rho }_i^2}\right)d\left(\frac{z_{2i}-{\rho }_i{z}_{1i}}{\sqrt{1-{\rho }_i^2}}\right) \\ ={\int }_{x_i}^{\infty }\varphi \left(z_{1i}\right)\left(1-\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(c)-{\rho }_i\left(z_{1i}\right)}{\sqrt{1-{\rho }_i^2}}\right)\right)d{z}_{1i}. \end{gathered}$$ (A2)

Therefore, $\partial {\mathrm{\Phi }}_2/\partial x_i=-\varphi \left(x_i\right)\left(1-\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(c)-{\rho }_i\left(x_i\right)}{\sqrt{1-{\rho }_i^2}}\right)\right)$, and $\partial L/\partial x_i=\varphi \left(x_i\right)(\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(c)-{\rho }_i{x}_i}{\sqrt{1-{\rho }_i^2}}\right)-(\lambda +1)),i=1,\dots ,n$.

Set the derivatives to 0, that is, $-\left({\sum }_i\mathrm{\Phi }\left(x_i\right)-Mc\right)=0$ and $\varphi \left(x_i\right)\left(\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(c)-{\rho }_i{x}_i}{\sqrt{1-{\rho }_i^2}}\right)-(\lambda +1)\right)=0$, Because ϕ(x_i) > 0 for x_i ∊ R, then $\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(c)-{\rho }_i{x}_i}{\sqrt{1-{\rho }_i^2}}\right)-(\lambda +1)=0$, suggesting that the solution to x_i, $x_i^{*}=\frac{{\mathrm{\Phi }}^{-1}(c)-{\mathrm{\Phi }}^{-1}\left({\lambda }^{*}+1\right)\sqrt{1-{\rho }_i^2}}{{\rho }_i}$ where λ* is the solution to λ.

For the Hessian matrix, $H=\left\{{\partial }^{2}L/\partial x_i\partial x_j\right\}$, the off-diagonal element is zero because $\partial L/\partial x_i$ does not involve x_j for j ≠ i. The i-th diagonal element ${\partial }^{2}L/\partial x_i^2=\frac{\partial \varphi \left(x_i\right)}{\partial x_i}\left(\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(c)-{\rho }_i{x}_i}{\sqrt{1-{\rho }_i^2}}\right)-(\lambda +1)\right)+\varphi \left(x_i\right)\varphi \left(\frac{{\mathrm{\Phi }}^{-1}(c)-{\rho }_i{x}_i}{\sqrt{1-{\rho }_i^2}}\right)\frac{-{\rho }_i}{\sqrt{1-{\rho }_i^2}}$. Plugging in $x_i=x_i^{*}$, the first term drops, and after simplification for the second term, we obtain $\frac{{\partial }^{2}L}{\partial x_i^2}{|}_{x_i=x_i^{*}}=-\varphi \left(x_i^{*}\right)\varphi \left({\mathrm{\Phi }}^{-1}\left({\lambda }^{*}+1\right)\right){\rho }_i/\sqrt{1-{\rho }_i^2}$. For any nonzero vector A = (a₁,a₂, …, a_n)^t, the quadratic term $A^{t}HA={\sum }_i-\varphi \left(x_i^{*}\right)\varphi \left({\mathrm{\Phi }}^{-1}\left({\lambda }^{*}\right)+1\right)a_i^2{\rho }_i/\sqrt{1-{\rho }_i^2}<0$ Similar derivations apply for specificity, and we omit the details.

Sample R code for calculating expected classification accuracy

rm(list=ls());

# library(mvtnorm) is used to calculate cumulative distribution function of bivariate normals; library(nor1mix) is used to calculate the quantiles of the normal mixtures;

library(mvtnorm);

library(nor1mix);

# functions sens.formula.vec and spec.formula.vec calculate the cumulative distribution functions for bivariate normals on the vector form;

# The parameter q is the cutoff point;

# The parameter x is a 2×1 vector. The first element x[1] is the cutoff point for Z_1i in Table I; the 2nd element x[2] is the correlation coefficient ρ_i;

sens.formula.vec=function(q,x)pmvnorm(lower=c(x[1],qnorm(q)),upper=Inf,corr=matrix(c(1,x[2],x[2],1),2,2))/(1-q);

spec.formula.vec=function(q,x)pmvnorm(lower=-Inf,upper=c(x[1],qnorm(q)),corr=matrix(c(1,x[2],x[2],1),2,2))/q;

# assign parameter values: true.mean is μ; sigma.square is σ²; tau.square is τ²;

# we assign them as values solicted from Example data in Section 4.

# But they can be changed depending on the any actual data analysts have. true.mean=3.48;

sigma.square=2.31;

tau.square=0.29;

# K is τ/σ, the ratio of between/within variability.

# K ≈ 0.4;

K=sqrt(tau.square)/sqrt(sigma.square);

# sample.size is {n_i}, the vector containing sample size for each hospital;

# we attach the example dataset in Section 4 with the manuscript;

# The users can input the sample size from their own data;

sample.size=scan(file=“ed08_sample_size.dat”, na.strings=“.”);

# N is the number of hospitals, equal to 329.

N=length(sample.size);

# q is the cutoff point, q=0.9 is for classifying top 10% of the hospitals;

# The users can change it to other values they want.

q=0.9;

# prob.class is the probability threshold in prob1 method;

# The users can change it to other values they want.

prob.class=0.9;

# cut.prob is the cutoff value for the prob2 method;

# set it to the upper 90

# The users can change it to other possibel values.

cut.prob=true.mean+qnorm(q)*sqrt(tau.square);

# true.rho.vec is the vector containing correlation coefficient {ρ_i} true.rho.vec=sqrt(K**2/(K**2+1/sample.size));

# In the following code, the label “dir” is for DIR method; the label “shr” is for SHR method; the label “prob1” is for PROB1 method; the label “prob2” is for PROB2 method;

# marginal.var.dir is the marginal variance of the DIR classifier, corresponding to the variance of normal mixturs in Eq. (6)

marginal.var.dir=tau.square+sigma.square/sample.size;

marginal.var.shr=tau.square**2/marginal.var.dir;

marginal.var.prob1=marginal.var.prob2=marginal.var.shr;

# dir.mixture is the normal mixture for the DIR method, stated in Eq. (6) dir.mixture=norMix(rep(true.mean, N), sig2=marginal.var.dir);

# quantile.dir.mixture is the cutoff values for the dir method, stated as $c_{\text{DIR}}^{*}$ in Table I.

quantile.dir.mixture=qnorMix(p=q, obj=dir.mixture);

shr.mixture=norMix(rep(true.mean, N), sig2=marginal.var.shr);

quantile.shr.mixture=qnorMix(p=q, obj=shr.mixture);

prob1.mixture=norMix(true.mean-qnorm(prob.class)*sqrt(K**2/(K**2+1/sample.size)*sigma. square/sample.size), sig2=marginal.var.prob1);

quantile.prob1.mixture=qnorMix(p=q, obj=prob1.mixture);

prob2.mixture=norMix((true.mean-cut.prob)/sqrt(K**2/(K**2+1/sample.size)*sigma.square/sample. size), sig2=sample.size*K**2);

quantile.prob2.mixture=qnorMix(p=q, obj=prob2.mixture);

# cut.off.dir is the cutoff for Z_1i in the bivariate normal cdf function from DIR method, stated in Table I.

cut.off.dir=(quantile.dir.mixture-true.mean)/sqrt(marginal.var.dir);

cut.off.shr=(quantile.shr.mixture-true.mean)/sqrt(marginal.var.shr);

cut.off.prob1=(quantile.prob1.mixture-true.mean+qnorm(prob.class)

*sqrt (K**2/(K**2+1/sample.size)*sigma.square/sample.size)/sqrt(marginal.var.prob1);

cut.off.prob2=(quantile.prob2.mixture*sqrt(K**2/(K**2+1/sample.size)*sigma.square/sample.size)-true.mean+cut.prob)/sqrt(marginal.var.prob2);

# dir.mat combines cut.off.dir and true.rho.vec from DIR method for the purpose of vector computation;

dir.mat=cbind(cut.off.dir, true.rho.vec);

shr.mat=cbind(cut.off.shr, true.rho.vec);

prob1.mat=cbind(cut.off.prob1, true.rho.vec);

prob2.mat=cbind(cut.off.prob2, true.rho.vec);

# sens.mixture.dir.vec is the sensitivity vector function from DIR method, calculate ${\mathrm{\Phi }}_2(Z_{1i}>\frac{C_{\text{DIR}}^{*}-\mu }{\tau /{\rho }_i},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i)/(1-c)$ for each i

sens.mixture.dir.vec=apply(dir.mat, 1, sens.formula.vec, q=q);

sens.mixture.shr.vec=apply(shr.mat, 1, sens.formula.vec, q=q);

sens.mixture.prob1.vec=apply(prob1.mat, 1, sens.formula.vec, q=q);

sens.mixture.prob2.vec=apply(prob2.mat, 1, sens.formula.vec, q=q);

# spec.mixture.dir.vec is the specificity vector function from DIR method; spec.mixture.dir.vec=apply(dir.mat, 1, spec.formula.vec, q=q);

spec.mixture.shr.vec=apply(shr.mat, 1, spec.formula.vec, q=q);

spec.mixture.prob1.vec=apply(prob1.mat, 1, spec.formula.vec, q=q);

spec.mixture.prob2.vec=apply(prob2.mat, 1, spec.formula.vec, q=q);

# average over all hospitals for the overall sensitivity of DIR method;

# calculate ${\sum }_i{\mathrm{\Phi }}_2\left(Z_{1i}>\frac{C_{\text{DR}}^{*}-\mu }{\tau /{\rho }_i},Z_{2i}>{\mathrm{\Phi }}^{-1}(c),{\rho }_i\right)/(M(1-c))$ mean(sens.mixture.dir.vec);

mean(sens.mixture.shr.vec);

mean(sens.mixture.prob1.vec);

mean(sens.mixture.prob2.vec);

# average over all hospitals for the overall specificity of DIR method; mean(spec.mixture.dir.vec);

mean(spec.mixture.shr.vec);

mean(spec.mixture.prob1.vec);

mean(spec.mixture.prob2.vec);

# The previous estimates should be corresponding to those in the table ‘DIRECT’ under Table II.