Will the Real Cryptic Pocket Please Stand Out?

Main Text

A mysterious and intriguing aspect of proteins is their ability to harbor “cryptic” pockets or never-before-seen areas hidden within them or on their surface that are capable of binding ligands. Such hidden sites can be extensions of an already known binding pocket or entirely new pockets that are distant from the known binding or active site (Fig. 1). From a drug-targeting perspective, developing small molecules that bind to allosteric cryptic sites is an attractive strategy that offers numerous advantages, including the possibility of designing compounds that have reduced off-target effects and absolute subtype specificity (1). Yet, techniques to capture and characterize these hidden sites have seen limited success (2) because of the relatively limited set of experimental methods that enable direct, detailed structural characterization of the highly dynamic regions from which these cryptic sites arise.

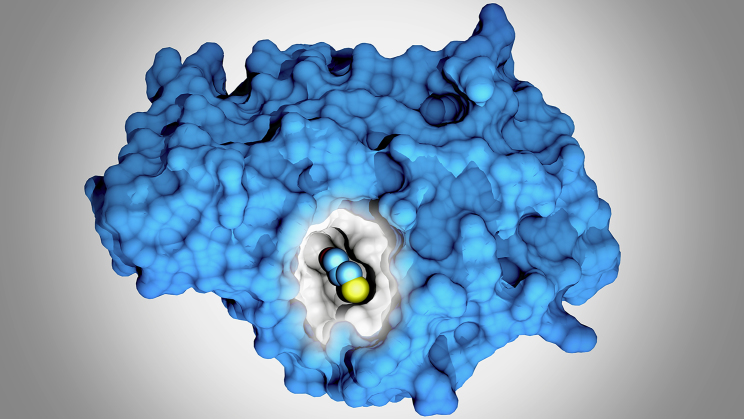
Figure 1.

A novel cryptic pocket identified in CTX-M-9 beta lactamase by G. Bowman and colleagues (11).

Computational approaches, on the other hand, and molecular-dynamics-based methods in particular, have been steadily increasing their repertoire of success in terms of characterizing and exploiting cryptic sites for small-molecule binding for a number of otherwise challenging drug targets (3, 4, 5, 6). Precisely because molecular-dynamics-based methods explore and enumerate the diverse dynamical ensembles of proteins with atomic resolution, they are well-suited to the discovery and characterization of such sites (7, 8, 9). Yet, these simulations generate huge amounts of data, and in the end, it is an enormous challenge to identify, from the vast amounts of data being generated, which of these new pockets, if targeted with ligands, would affect or modulate protein function. Moreover, cryptic sites that are allosteric in nature (i.e., not direct extensions of the protein active site but sites that instead appear far from known active sites) introduce yet another level of complexity and, correspondingly, opportunities for control by small molecules (10). Discovering allosteric cryptic sites becomes like trying to find a very much prized needle in a haystack.

The work by Bowman and colleagues (11) presents a new approach to this challenge that couples an elegant statistical method, Markov state modeling, for trajectory analysis (12, 13), with an efficient graph network method known as affinity propagation (14) to identify novel areas on the surface of proteins that become exposed to solvent during the course of the simulations (Fig. 1). The Markov state modeling states are developed in terms of residue solvent exposure, and subsequently, mutual information between residue pairs is computed and used to assign clusters with the affinity propagation method. This method essentially coarse grains the protein structure and dynamics into a network in which the nodes are groups of solvent-exposed residues and the edges are weighted by the mutual information or communication between the nodes and returns a prioritized list of network hubs that exhibit cooperative changes in solvent exposure over time. They call these hubs or groups of residues “exposons” for their abilities both to reveal themselves to solvent during the dynamical trajectories and to be predicted to be functionally important. Retrospective tests of this new method on two classic β-lactamase systems confirm the ability of the method to identify known cryptic pockets. At the same time, they computationally discover and experimentally verify a novel allosteric cryptic site on a long-studied protein, TEM-1 β-lactamase. In doing so, they set the stage for the application of this new method to novel drug targets of interest and provide a promising new data-centric approach to the design and discovery of allosterically modulating small molecules.

Editor: Nathan Baker.