Weighting Non-probability and Probability Sample Surveys in Describing Cancer Catchment Areas

Abstract

Background:

The Population Health Assessment initiative by National Cancer Institute (NCI) sought to enhance cancer centers’ capacity to acquire, aggregate and integrate data from multiple sources, as well as to plan, coordinate, and enhance catchment area analysis activities.

Methods:

Key objectives of this initiative are pooling data and comparing local data with national data. A novel aspect of analyzing data from this initiative is the methodology used to weight datasets from sites that collected both probability and non-probability samples. This article describes the methods developed to weight data which cancer centers collected with combinations of probability and non-probability sampling designs.

Results:

We compare alternative weighting methods in particular for the hybrid probability and non-probability sampling designs employed by different cancer centers. We also include comparisons of local center data with national survey data from large probability samples.

Conclusions:

This hybrid approach to calculating statistical weights can be implemented both within cancer centers that collect both probability and non-probability samples with common measures. Aggregation can also apply to cancer centers that share common data elements, and target similar populations, but differ in survey sampling designs.

Impact:

Researchers interested in local versus national comparisons for cancer surveillance and control outcomes should consider various weighting approaches, including hybrid approaches, when analyzing their data.

Introduction

In May 2016, the National Cancer Institute’s (NCI) Division of Cancer Control and Population Sciences (DCCPS) announced a new administrative grant supplement, the Population Health Assessment in Cancer Center Catchment Areas, to support catchment area research related to cancer communications and cancer surveillance at selected NCI-designated cancer centers. Fifteen centers received awards under this initiative. The supplements sought to enhance cancer centers’ capacity to acquire, aggregate and integrate data from multiple sources, as well as plan, coordinate, and enhance catchment area analysis activities. Pooling data is a key objective of this initiative as it provides the opportunity for NCI and cancer centers to enhance and share learnings, foster cross-site and local to national comparisons, and investigate new methods for integrating data.

With an overarching goal of conducting pooled analyses, achieving data uniformity across cancer centers, is a key step. Each of the 15 funded cancer centers has unique population characteristics, scientific focus, common and distinct cancer challenges, and varying levels of expertise in the lifecycle of population health assessments. Moreover, the study designs implemented by each cancer center included differences in data collection, populations of interest, and study mode. Standardized approaches are needed to create consistency across cancer centers given variations in study design. This process involved selecting a common set of demographic and behavioral measures in advance of field work, incorporating data standardization and harmonization procedures to improve data quality, and refining the sample weighting strategies to incorporate traditional methods and hybrid approaches to support the design differences between funded cancer centers.

This paper discusses approaches used to prepare weighted datasets across different survey designs. It highlights issues unique to combining and weighting data from probability and non-probability samples (i.e., a hybrid approach). Many cancer centers adopted hybrid designs for cost effectiveness, to capture special sub-populations in sufficient numbers, and to capitalize on existing surveys. The paper describes alternative methodologies for weighting non-probability sample and hybrid design data. We also discuss our approaches for comparing the methodologies so as to choose the strategy most suitable for each cancer center. These approaches balance variance reduction with the minimization of potential biases. Similar approaches were also developed for combining data across cancer centers. The paper discusses challenges and lessons learned from preparing these weighted datasets as well as implications for future cancer surveillance and control studies.

Materials and Methods

Program Infrastructure

Prior to weighting data, program infrastructure and common data elements had to be established, without which pooled analyses and/or statistical weighting would prove difficult. NCI and funded cancer centers received technical and statistical expertise from ICF Inc. for construct and measure selection, geographic analyses, data standardization and harmonization, pooled data analyses, and statistical weighting. An important goal of this initiative is fostering a collaborative environment with the goal of achieving pooled analyses. To support this goal, two workgroups were established with representatives from NCI, the cancer centers and ICF. The first workgroup selected key demographic variables and behavioral measures to be used by all funded cancer centers. A second workgroup was established to focus on rural health, with the goal of understanding the beliefs and needs of rural populations as compared to their urban counterparts.

Data sharing agreements were established between NCI, the cancer centers, and ICF. Cancer centers submitted data to ICF, using a secure file transfer protocol, after the completion of their fielding period. ICF and each respective cancer center negotiated file formats, codebook structures, data review and re-submission procedures, and timing of data transfer to ensure files were transferred after agreements were signed and to eliminate the possibility of receiving datasets with personally identifiable data.

For eight cancer centers, ICF computed sample weights. This effort required careful analysis of each study design and study mode to develop center-specific weighting strategies. This ensured that studies are aligned to support pooled analyses. Weighting methods incorporated traditional methods of post stratification to population control totals, using a combination of raking and propensity scores, as well as, application of a novel hybrid approach.

Data Standardization, Harmonization, and Imputation

“Data standardization is the critical process of bringing data into a common format that allows for collaborative research” (1). Data harmonization is the process of combining data from different sources to a common structure to enable pooled analyses. Harmonization must take into account the idiosyncratic nature of the source data (2,3). By using common measures across the various studies, data comparisons across cancer centers and to national estimates are more meaningful (4).

To foster data standardization, the measures workgroup met over six months to discuss and reach agreement on the selection of behavioral and demographic variables. The working group included researchers from NCI, the cancer centers, and ICF. The workgroup first identified a range of demographic measures and health topics of interest to all researchers, ranging from health information seeking to cancer beliefs. The group then selected survey questions from various national health surveys which reflected these topics and measures. Once candidate common measures were identified, key stakeholders discussed and voted on which specific question would best meet their future analytical goals.

A measure required a majority of the working group votes to be included. Of the 43 demographic and 27 behavioral measures considered, 13 and 23 variables were selected, respectively. Source surveys for variables include the Health Information National Trends Survey (HINTS), the Behavioral Risk Factor Surveillance System (BRFSS), Gallup Surveys, and the National Health Interview Survey (NHIS). A principal challenge with using these measures is that cancer centers would implement with differing survey modes. Thus, the common measures were constructed to accommodate self-administered and interviewer-administered modes.

The standardized demographic measures ranged from age and gender to economic metrics such as household income and home ownership. The behavioral measures included questions on tobacco use; health information seeking; access to healthcare; preventive screening behaviors, and beliefs, knowledge; and awareness of cancer risk were included. Cancer centers were encouraged to incorporate all the core measures into their surveys without modification. While cancer centers largely used the core measures, at times they adapted the question skip patterns, response options/scales, and variable names to align with their analytical goals, study population, or survey application or mode.

After the studies completed data collection, each cancer center’s dataset was reviewed to determine compliance with the common measures and the format and amount of data missing for those variables used to compute weights. Key demographic variables were selected from raw survey responses, and imputation was used for missing demographic and behavioral variable data used in the weighting process. Race/ethnicity, age categories, and binary gender, were calculated in slightly different but consistent ways across sites to reflect the cancer center’s sample, questionnaire design, and analytical goals.

Race/ethnicity was classified into the five HINTS categories, namely, Hispanic, Non-Hispanic White, Non-Hispanic Black or African American, Non-Hispanic Asian, and Non-Hispanic Other. Survey respondents who selected Hispanic or a Hispanic origin to the single-select ethnicity question were considered Hispanic. Non-Hispanic respondents were then classified by race as White, Black or African American, or Asian. If the race question had a different selection or more than one selection, then the respondent was considered as Other. This variable was further collapsed in different ways to support weighting so as to provide sufficient numbers of respondents in each category. The most common collapsing included a four-level variable: Hispanic, Non-Hispanic White, Non-Hispanic Black, and Other. An alternate collapsing was Hispanic, Non-Hispanic Black, Non-Hispanic Asian, and Other. We also considered a two-level variable: Non-Hispanic White versus Non-White.

Age categories were derived from a continuous age variable and ensured an adequate number of respondents in each category to support weighting adjustments. A binary gender variable was used. For cancer centers with additional response categories (e.g., transgender male to female) or who included a sex at birth question, binary gender was derived solely from the gender identity question and responses of refusal, genderqueer or other non-binary gender categories were treated as missing prior to imputation.

Imputation was limited to variables required for the calculation of weight adjustments and were specific to each cancer center’s dataset. Where possible, variables were imputed logically or using external data. For example, cancer centers using address-based samples had access to data derived from the sampling frame (e.g., the number of adult household members). Otherwise, a probabilistic imputation method was used following the variable distribution for the cases with non-missing data within each imputation cell. This imputation method has been found effective for a range of weighting variables (5). Note that multiple imputation methods were used for analysis variables which are central for the pooled analyses conducted for a few grantees’ data. In other words, we distinguish imputation methods which are effective for weighting variables from those methods which lead to more rigorous inferences for analysis purposes.

The process was stepwise using variables previously imputed for defining imputation cells. Imputation cells were based on variables suggested by the bivariate analysis (chi square tests). Generally, demographic variables with less than five percent missing were imputed first without the use of imputation cells. Next, the fully imputed demographic variables were used to define imputation cells for demographics with missing data above 5 percent and behavioral measures. When necessary, imputation was performed separately along the different sample types or strata (e.g., urbanicity classification) within a given dataset. In defining imputation cells, the initial univariate and bivariate distribution of non-missing data was retained within 0.5 percentage points. This paper provides analyses of several key variable estimates for two grantees using hybrid weighting. The weighting in part is based on key demographic variables such as gender, age, education, and race/ethnicity when available. The amount of missing data was relatively small for the weighting variables, age, gender, education and race/ethnicity, ranging from no missing (0%) to 5% for the probability samples and non-probability samples which were weighted for the cancer centers. For the two cancer centers using hybrid sample designs discussed in the next sections, the percentage missing was 4.35% for age and education.

Weighting Approaches

Weighting methods for the different study samples

Weighting adjustments help ensure that the weighted sample distributions are similar to the target population distribution along key demographic dimensions. Table 1 shows the diverse sampling designs used by the cancer centers and can be classified into three general designs: probability, non-probability, and hybrid (both probability and non-probability samples). The table also describes the target catchment areas from the surveys.

Table 1.

Cancer centers sampling design summaries.

Cancer Institute Center	Probability Sample Design	Non-probability Sample Design	Catchment Area
Albert Einstein College of Medicine	Patient records	Community recruitment sample	Bronx County
Dana-Farber Cancer Institute	Online sample	Web panel and Community-based	State of Massachusetts
Dartmouth-Hitchcock Norris Cotton Cancer Center	Random digit dial	Web panel	States of NH and VT
Duke Cancer Institute	N/A	Community recruitment sample	6 counties in North Carolina
Indiana University Melvin & Bren Simon Cancer Center	Patient records	N/A	State of Indiana
Memorial Sloan Kettering Cancer Center	N/A	Community recruitment sample	8 neighborhoods in New York City
Ohio State University Cancer Center	Web panel	Community recruitment sample	State of Ohio
Roswell Park Cancer Institute	N/A	Web panel and In-person interview	8 counties in western New York
Temple University Fox Chase Cancer Center	N/A	In-person recruitment from existing cohort study	6 counties in Pennsylvania and 9 in New Jersey
University of California at San Francisco – Helen Diller Family Comprehensive Cancer Center	N/A	Web panel	San Francisco (city/county).
University of Hawaii Cancer Center	N/A	Venue-based Initiation of Respondent Driven Sample	Hawaii, Guam
University of Kentucky – Markey Cancer Center	Address-based sample	Community recruitment sample	54 counties in eastern KY designated as Appalachian
University of Pennsylvania Abramson Cancer Center	Random digit dial	N/A	4 counties in eastern Pennsylvania
University of Pittsburgh Hillman Cancer Institute	Random digit dial	N/A	29 counties in western Pennsylvania
University of Texas MD Anderson Cancer Center	Address based sample	Web panel	State of Texas

While weighting methods for probability and non-probability samples are relatively well established, weighting for hybrid samples are a novel aspect of this research. For probability samples, survey weights are calculated by adjusting sampling weights for nonresponse, followed by either a simple post-stratification method or iterative post-stratification method (known as raking). Post-stratification adjustments ensure that sample weighted totals match known population control totals for key demographic variables. The choice between simple post-stratification and raking methods depends on the availability of population total data for various demographic categories for the target area.

For non-probability samples, there has been extensive discussions in the relative advantages of assigning weights, as well as, the issues associated with their use. A comprehensive review is provided in an AAPOR Task Force Report (6). This research has included alternative weighting approaches for non-probability samples ranging from simple post-stratification adjustments and raking methods (7) to more complex propensity model-based methods (8,9,10). Propensity methods can be applied when a parallel probability sample is available, sharing a core of survey variables, to benchmark and calibrate the non-probability sample.

For hybrid samples, probability sample’s weights are first calculated through simple post-stratification or raking, then several methods can be explored for the non-probability sample: a) simple post-stratification or raking only; b) propensity score matching (PSM) only; c) PSM plus simple post-stratification or raking. The selection of methods for non-probability sample depends on the bias and variability of the adjusted weights.

Population Control Totals

Post-stratification adjustments rely on population control totals which are known, or can be compiled, for key demographics. To support post-stratification, population control totals were based on the needs of the individual weighting task for a cancer center. This was done programmatically, by distilling the 2015 5-year American Community Survey (ACS) results down to the area of interest and then creating the necessary age and sex categories. Race and ethnicity totals were adjusted to ensure they were in line with the adult population 18 and older. Where requested, education totals were compiled using the American FactFinder tool provided for use by the U.S. Census Bureau.

In general, cancer centers sampled adults 18 and over, though one center defined an adult as 21 – 74 years, so a modification was necessary to post-stratify to the correct representative group. Complex sampling designs at some institutions required totals within race categories, since some sites targeted specific races and therefore were not able to be weighted to the total across the catchment area of interest.

Raking and Propensity Modeling Strategies

To account for differential sampling designs, raking and propensity matching methods were explored for weighting. These two methods can be used separately, but they can also be combined for hybrid designs including both a probability and a non-probability sample. This section describes these approaches, and the weighting steps for both probability sample and non-probability sampling designs.

Raking is an iterative post-stratification method for adjusting the sampling weights of the sample data based on population totals. Using a base or initial weight, a factor (f_w) was created by dividing the known population total (N_i) by the sum of the weights (Σw₁) from the sample within that dimension; i.e., by age, gender, or race/ethnicity, one dimension at a time:

$$f_w=N_i∕\mathrm{\Sigma }{w}_1$$

This factor is then used to create the next weight (w2).

$$w_2=f_w\times w_1$$

This process of creating a factor and then using the factor to adjust the initial weight is done within each dimension iteratively until the sum of the adjusted weight is equal to the population control total being compared for a given category.

The propensity score matching method uses a logistic regression model to predict the probability of a respondent being a member of the non-probability sample, using a set of variables of interest as predictors. (Ideal predictors are correlated with the key survey outcomes as well as with response propensity.) In the final step, the inverse of calculated predicted probabilities, known as propensity scores, are computed as the propensity weights. The propensity score weights adjust the non-probability sample to match the characteristics of a probability sample. Conditional on the propensity score, the distribution of some covariates of interest will be similar between the probability and non-probability sample.

The propensity matching and post-raking methods can be combined to use for a non-probability sample, when key demographics still need adjustment to align with population totals after propensity matching method. With this combined approach, the first step is performing the propensity matching, and the second step is raking the propensity score matched weights on the dimensions of key demographics.

Results

We developed weighted data sets for seven cancer centers following the data cataloging and preparation, and weighting procedures previously discussed. Two weighted datasets were a result of probability sample designs, three from non-probability sample designs, and two from hybrid samples. While sites using solely probability or non-probability sample designs required some specialization in weighting procedures to account for unique designs, the two sites with hybrid samples provided an opportunity to explore combining sample types.

For both sites using a hybrid sample design, we explored the utility of each sample independently as well as combined. We considered factors such as the representativeness and number of respondents in each sample type and the mode of data collection. For example, a non-probability sample of respondents that skewed female and which was obtained via intercept at community events in one of fifty-four targeted counties may harm the accuracy of any estimates if combined with a more rigorous probability sample. For one site, we decided that the probability and non-probability sample could be combined for analytical purposes (combined hybrid site), and for the other we decided to keep the two samples separate due to the possibility of introducing bias into estimates from the more rigorous probability sample (separate hybrid site).

Tables 2 and 3, respectively, presents the predictors included in the propensity models, both potentially and actually used in the models, for the University of Kentucky and for Dartmouth. The tables also show the significance of these potential predictors in the bivariate analyses and multivariate models

Table 2.

Propensity models used in the University of Kentucky non-probability samples

Predictors	Bivariate Analysis Chi-square Test Results		Logistic Regression Propensity Model Results
	Chi- Square	P Value	Wald Chi-Square	P Value
Age 18-34, 35-54, 55+.	41.73	<0.0001	5.44	0.0659
Sex Male, Female	14.15	0.0002	42.21	<0.0001
Education High school or less, Some college, College graduate	12.22	0.0022	4.70	0.0955
Health Insurance Plana Yes, No	3.40	0.0651
Rent/Own Own, Rent, Occupied without paying monetary rent	2.78	0.2488
Household Income Less than 50,000, 50,000+.	3.91	0.0480	0.65	0.4195
Confident Can Get Cancer Infob Completely confident, Very confident, Somewhat confident, A little confident, Not confident at all	20.88	0.0003	13.10	0.0108
Smoke 100 Cigarettes in Lifetimeb Yes, No	1.19	0.2749
Cost Barrier to Carea Yes, No, No need to see a doctor in the past 12 months	1.94	0.3787
Rather Not Know Chance of Cancerb Strongly agree, Somewhat agree, Somewhat disagree, Strongly disagree	2.93	0.4027
Rurality Strata Slightly rural, Rural, Completely rural	69.39	<0.0001	11.92	0.0026

^a.These measures are from the HINTS 4 Cycle 4 instrument. https://hints.cancer.gov/docs/Instruments/HINTS_4_Cycle_4_English_Annotated_Form.pdf

^b.These measures are from the BRFSS 2016 instrument. https://www.cdc.gov/brfss/questionnaires/pdf-ques/2016_BRFSS_Questionnaire_FINAL.pdf

Table 3.

Propensity models used in the Duke non-probability samples

Predictors	Bivariate Analysis Chi- square Test Results		Logistic Regression Propensity Model Results
	Chi-Square	P Value	Wald Chi-Square	P Value
Age 18-34, 35-54, 55+.	156.2628	<.0001	28.0854	<.0001
Sex Male, Female	58.8048	<.0001	40.3171	<.0001
Education High school or less, Some college, College graduate	22.9597	<.0001	12.1582	0.0023
Health Insurance Plana Yes, No	6.8474	0.0089
Household Income Less than 50,000, 50,000+.	85.2096	<.0001	53.6291	<.0001
Confident Can Get Cancer Infob More confident, less confident	36.1589	<.0001	26.4981	<.0001
Cost Barrier to Carea Yes, No Yes, No, No need to see a doctor in the past 12 months	64.9169	<.0001	7.9916	0.0047
Ever Look at Cancer Infob Yes, No	13.0708	0.0003	7.2273	0.0072
Race and Ethnicity Non-Hispanic white, Non-Hispanic black, Hispanic, Other/Multiple races	1.8449	0.6052

^a.These measures are from the HINTS 4 Cycle 4 instrument. https://hints.cancer.gov/docs/Instruments/HINTS_4_Cycle_4_English_Annotated_Form.pdf

^b.These measures are from the BRFSS 2016 instrument. https://www.cdc.gov/brfss/questionnaires/pdf-ques/2016_BRFSS_Questionnaire_FINAL.pdf

For the purpose of selecting the final non-probability weights among the hybrid sample sites, we reviewed the coefficients of variation (CV) of the three sets of non-probability weights (i.e., raking only, propensity score matching only, and propensity score matching followed by raking). These statistics are provided in Table 4 for each hybrid site. This table shows that the CVs of the raked only weights were substantially smaller than the other two sets of weights. We also considered weighted estimates of several core behavioral measures as derived from the three versions of weights.

Table 4.

Coefficient of Variation for Non-Probability Weighting Methods among Hybrid Sample Sites

Weights	Coefficient of Variation	Sum	Mean	Median	Maximum
Combined Hybrid Site
Raking Only	58.5	3,433,370	1,999.6	1,830.9	7,263.0
Propensity Score Matching Only	83.0	3,445,048	2,006.4	1,504.5	16,355.1
Propensity Score Matching and Raking	83.5	3,433,370	1,999.6	1,506.6	16,015.1
Separate Hybrid Site
Raking Only	67.7	1,429,887	4,454.5	3,070.2	13,002.8
Propensity Score Matching Only	82.6	1,403,237	4,371.5	3,091.9	27,924.4
Propensity Score Matching and Raking	86.6	1,429,887	4,454.5	2,965.4	28,736.7

In both hybrid samples, estimates and variances were very close across the sets of weights. Therefore, we selected the raked-only weights as the final weights for both cancer centers’ non-probability samples, since it had the smallest coefficients of variation (CVs). The variability due to unequal weighting effects can be quantified by the design effect due to weighting, DEFF (wts), which can be computed in terms of the CV of the weights as 1 + CV**2. Note that the CV is expressed as a percentage in Table 4.

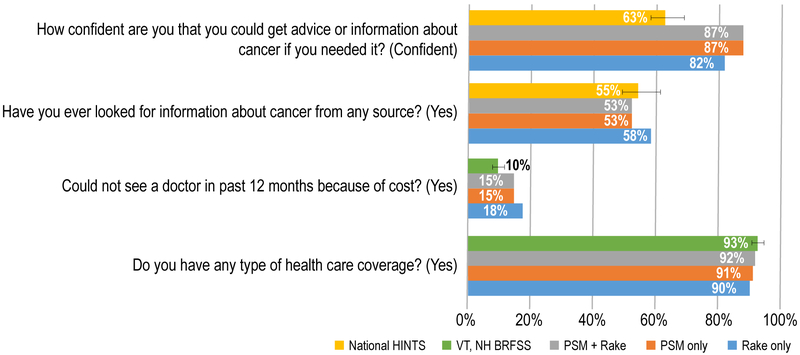
Figure 1 presents results for Dartmouth-Hitchcock Norris Cotton Cancer Center which supported combining sample data for both probability and non-probability components of the hybrid sample. For two measures, it shows results for two variables selected from the HINTS survey, which support comparisons with HINTS national data. The other two measures present results for variables selected from the BRFSS survey, which support comparisons with the BRFSS state data.

Figure 1. Dartmouth-Hitchcock Norris Cotton Cancer Center comparisons of weighting methods and national or state level data.

Description: Figure 1 presents weighted results for Dartmouth-Hitchcock Norris Cotton Cancer Center which supported combining sample data for both probability and non-probability components of the hybrid sample. For two estimates, the figure shows results for two variables from the Dartmouth instrument that were selected from the Health Information National Trends Survey (HINTS) thus supporting comparisons with HINTS national data. The other two estimates present results for variables in the Dartmouth instrument selected from the Behavioral Risk Factor Surveillance System (BRFSS), which support comparisons with the BRFSS state data.

RBG Colors Used in Figure 1:

• National HINTS: Gold: 255/192/0
• PSM+ Rake: Gray: 165/165/165
• PSM Only: Orange: 237/125/49
• Rake Only: Light Blue: 91/155/213
• VT, NH BRFSS: Green: 112/173/71

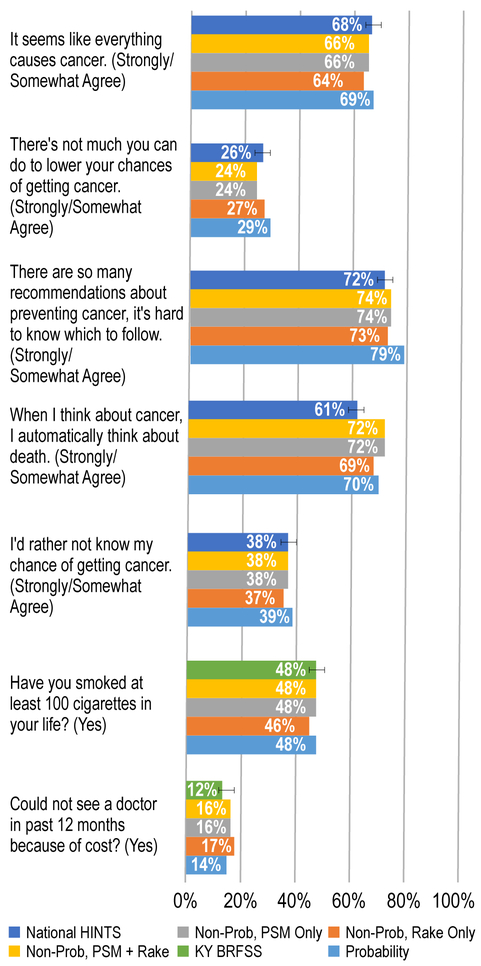
Figure 2 presents results for University of Kentucky – Markey Cancer Center which required the probability and non-probability samples to be weighted separately. The first four measures in the figure present results for two variables selected from the HINTS survey, which support comparisons with HINTS national data. The last two measures present results for two variables selected from the BRFSS survey, which support comparisons with the BRFSS state data.

Figure 2. University of Kentucky – Markey Cancer Center comparisons of weighting methods and national or state level data.

Description: Figure 2 presents results for University of Kentucky – Markey Cancer Center which required the probability and non-probability samples to be weighted separately. The first four measures in the figure present results for two variables selected from the HINTS survey, which support comparisons with HINTS national data. The last two measures present results for two variables selected from the BRFSS survey, which support comparisons with the BRFSS state data.

RBG Colors Used in Figure 2:

• National HINTS: Dark Blue: 68/114/196
• NonProb, PSM + Rake: Gold: 255/192/0
• NonProb, PSM Only: Gray: 165/165/165
• NonProb, Rake Only: Orange: 237/125/49
• Probability: Light Blue: 91/155/213
• KY BRFSS: Green: 112/173/71

These figures illustrate the range of additional, bias-related information used in combination with Table 4 to decide on the most suitable weighting method for these two cancer centers. Generally, the use of propensity models, possibly in combination with raking, did not tend to reduce substantially the differences from the national nor state estimates. These comparisons need to be qualified, of course, by the differences that may be expected between local and national data. Due to the smaller variability associated with raking alone, this method was adopted for the cancer centers using hybrid designs.

The figures also display the array of comparisons that can be made between local catchment area estimates with state (BRFSS) and national (HINTS) survey data, keeping in mind the same caveats about these comparisons; i.e., that differences between local and national (or state) are to be expected. To allow statistical statements about the closeness of the local cancer center data with the national and state data based on probability samples, the latter survey estimates charted from HINTS and the BRFSS also include 95% confidence bars. Both surveys have substantial levels of non-response which may lead to non-response bias even though bias often does not go hand in hand with high non-response rates (11). These confidence bars allow us to see if the local estimates fall within the 95% confidence intervals for each measure being compared.

Discussion

This NCI Population Health Assessment initiative to define and describe cancer center catchment areas presented challenges, opportunities, and lessons for future cohorts and for similar multi-site research initiative interested in weighting data. Each funded cancer center adopted a study design suited to their unique research needs and the population of interest in the catchment area. By using a common core of key measures derived from national and state surveys, the surveys generally supported local community estimates that can be compared to national estimates. A novel aspect of analyzing data from this initiative is managing datasets from sites that collected both probability and non-probability samples.

The cancer centers used an array of non-probability and probability sampling designs, as well as, combinations of probability and non-probability sampling (i.e., hybrid designs). Many cancer centers adopted hybrid designs for cost effectiveness, to capture special sub-populations in sufficient numbers, and to capitalize on existing surveys. These hybrid designs, used by several cancer centers, can make effective use of the probability sample to calibrate the non-probability sample weights. While these designs have varying degrees of statistical rigor and representativeness, we were able to generate survey weights to support population estimates and population-level inferences for each respective cancer center, or to guide the cancer center in the computation of valid weights. The weights can also support pooled analyses using data aggregated over multiple cancer center studies.

We examined three sets of non-probability weights (i.e., raking only, propensity score matching only, and propensity score matching followed by raking) for hybrid designs and found that “raking only” estimates had the smallest coefficients of variation. While propensity methods may reduce the bias, this reduction is harder to quantify. Comparisons to state and national survey estimates have a number of caveats that limit the scope of bias conclusions. Therefore, we used the simplest raking method for these hybrid samples as well as the non-probability samples. Propensity methods may become more attractive depending on the probability sample size and the number of variables that are common to both sample components which can be used in the propensity models. This consideration will be important for all centers considering hybrid designs in current and future studies.

It must be noted that for some cancer centers using a hybrid sampling approach, the differences in target populations made it inappropriate to combine the two disparate samples for analysis. These sites may use unweighted data for combined analysis.

Several challenges arose in the process of preparing data from the various cancer centers for statistical weighting. These included some centers not including common measures, some centers adapting common measures to meet their needs (creating measure variability), differences in survey modes, and variability in defining the respective catchment areas. However, these challenges are common to pooled analyses in general. When considering weighting data, challenges included defining the target populations to reflect the populations of interests of the catchment area while at the same time allowing the use of general population control totals. This balance allowed the sample results to be generalized to the catchment area population.

Limitations of the weighting approaches examined for non-probability samples are inherent to this type of sampling design and extend to hybrid samples which include both probability and non-probability samples. Depending on the non-probability sampling designs used by cancer centers, the sample may not be truly representative of the target population even when weighted to minimize any potential biases. In addition, non-probability sampling designs make it difficult to assess variability of the survey estimates without reliance on established statistical theory available for probability sampling designs.

Overall, this paper illustrates a novel approach to combine and analyze probability and non-probability samples. It also lays out the foundation for analyses combining data from different cancer centers. Future research initiatives that involve multiple sites with different sampling designs, either within one site or between different sites, should take into consideration the benefits of including a probability sample either by itself or in conjunction with a non-probability sample.