Model-based network discovery of developmental and performance-related differences during risky decision-making

Abstract

Theories of adolescent neurodevelopment have largely focused on group-level descriptions of neural changes that help explain increases in risk behavior that are stereotypical of the teen years. However, because these models are concerned with describing the “average” individual, they can fail to account for important individual or within-group variability. New methodological developments now offer the possibility of accounting for both group trends and individual differences within the same modeling framework. Here we apply GIMME, a model-based approach which uses both group and individual-level information to construct functional connectivity maps, to investigate risky behavior and neural changes across development. Adolescents (N=30, M_age=13.22), young adults (N=23, M_age=19.19), and adults (N=31, M_age=43.93) completed a risky decision-making task during an fMRI scan, and functional networks were constructed for each individual. We took two subgrouping approaches: 1) a confirmatory approach where we searched for functional connections that distinguished between our a priori age categories, and 2) an exploratory approach where we allowed an unsupervised algorithm to sort individuals freely. Contrary to expectations, we show that age is not the most influence contributing to network configurations. The implications for developmental theories and methodologies are discussed.

1. Introduction

A large focus of developmental neuroscience research has been on characterizing what features of adolescent neurodevelopment help explain behavioral patterns (e.g., risk taking) which can arise during this period. Several influential theories of adolescent neurodevelopment (e.g., Steinberg et al., 2008; Casey et al., 2008) have proposed models where differences in frontal and subcortical developmental trajectories help explain increases in risky behavior seen during the teen years (Kann et al., 2015). These models have enjoyed widespread influence, and research across a variety of contexts and tasks have lent support to the idea that adolescent neurodevelopment pre-disposes teens to risky or impulsive behavior (McCormick & Telzer, 2017a; McCormick et al., 2018; see Shulman et al., 2016 for a review). However, these models can face challenges as they are, by necessity, overly simplistic (e.g., Pfeifer & Allen, 2012) and are primarily concerned with describing trends in developmental processes that generalize to the population at large. This contrasts with the growing theoretical (e.g., Crone & Dahl, 2012; Bjork & Pardini, 2015; Casey 2015) and empirical (e.g., Qu et al., 2015; Telzer et al., 2013; Braams et al., 2015; Telzer, 2016; McCormick & Telzer, 2017b; Blankenstein et al., 2018) work which has shown that there are significant individual differences in adolescents’ neural processing and risk behavior (see Foulkes & Blakemore, 2018; Sherman, Steinberg, & Chein, 2017). Even studies which show group or continuous age-related differences in risk behavior or subcortical reactivity almost always show significant within-group variability (e.g., Hare et al., 2008; Somerville et al., 2011; Chein et al., 2011; Qu et al., 2015). Thus, one of the key challenges of developmental theory and methodology rests in adopting models that can describe group-level effects found for this population, as well as the individual-level nuances which underlie them (Foulkes & Blakemore, 2018). Incorporating individual differences in population models of adolescent neurodevelopment is an exciting new direction for the field and may help to not only create more predictive models of adolescent behavior, but also reconcile results across disparate samples.

Perhaps the most relevant methodological approach that has prevented this advancement is the reliance of developmental neuroimaging analyses on the “average” person (e.g., grouping teens to compare to a group of adults; Smith, 2012; Ramsey et al., 2010) where the sample mean is assumed to be representative of members within the sample (an implicitly the population at large). At a descriptive and statistical level, the average (assuming no outliers are present) is an attractive and intuitive metric. For instance, it works well for investigations of regional activity. The idea that, on average, brain regions are more or less active across task conditions or age is the bedrock of inference in the neuroimaging literature. While averages can sometimes be a meaningful construct for drawing conclusions, this concept is not well-suited for capturing all characteristics of brain processes. This is particularly true when attempting to arrive at an “average” pattern of functional connectivity for a sample. Individuals likely differ in the patterns and strengths of their brain connectivity (Finn et al., 2015; Lamout et al., 2015). When individuals have this heterogeneity in their brain processes, the connectivity patterns obtained from averaging across individuals may not even apply to one individual within the sample (Molenaar, 2004). Further complicating the analysis of brain processes is that focusing only on between-group differences can mask important within-group variability that may be more relevant to the behavior overall than group assignment. This can often be relevant when a priori groups (e.g., age groups; clinical versus controls) show significant within-group heterogeneity (e.g., Gates et al., 2014). In cases where groups show significant within-group variability, the averaging approach can mask important differences in connectivity patterns which might distinguish between relevant groups in a more data driven analysis.

Fortunately, exciting methodological advances are now available which can address these limitations by combining individual and group-level information in the construction of models. Several recent papers (Braams et al., 2015; Peters et al., 2017; see Telzer et al. 2018 for discussion) have utilized mixed effects models to characterize developmental trends in univariate activation across childhood, adolescence, and young adulthood. For functional connectivity approaches, new tools such as Group Iterative Multiple Model Estimation (GIMME; Gates & Molenaar, 2012) provide promising approaches for producing individual and group-level connectivity models from task-based fMRI. The GIMME approach can be used to construct directed functional networks by relying on path selection by means of improvement to overall model fit, utilizing individual-level information to detect signal from noise across the group (i.e., sample), and controlling for autoregressive paths (i.e., how activity in a region of interest [ROI] at one time-point predicts that ROI’s activity at the next time-point) for each ROI. Furthermore, in conjunction with clustering algorithms, GIMME modeling approaches can successfully characterize connectivity features which distinguish between subgroups of individuals (e.g., Gates et al., 2014; Gates et al., 2017; Price et al., 2017). Extending these tools to the field of developmental neuroscience provides the exciting opportunity for researchers to better account for individual variability when constructing representative connectivity maps across the lifespan.

We explored age-related changes in functional network maps during a risky decision-making task in adolescents, young adults, and adults. During an fMRI scan, participants completed the Balloon Analogue Risk Task (BART), a sequential risk-taking task which measures participants’ willingness to engage in risk behavior to earn rewards. A model-based approach (i.e., GIMME) was used to characterize both individual and group level directed graphs during risky decisions. We took two subgrouping approaches to assess differences in functional network organization during the BART. First, we categorized individuals based on their age (i.e., adolescents, young adults, and adults), in order to assess what network maps differ between stages of development. Data-driven connectivity maps are optimized using GIMME to identify connections that best discriminate between age groups. However, this a priori classification might not be the best way to partition variance in the sample. As such, we ran a second, unsupervised clustering, which was free to select features which best subgrouped individuals without any constraints. Two competing hypotheses were plausible based on the current literature. First, in line with theories of adolescence as a time of unique sensitivity to risk (e.g., Casey et al., 2008; Steinberg et al., 2008), the unsupervised clustering could recover the age groups with some margin for error. This would suggest that adolescent neural configurations are significantly distinct from older age groups. Alternatively, there might be a more general phenotype that characterizes risky behavior, and thus, the amount of risky behavior that participants engage in might be a stronger predictor of functional organization. If the unsupervised clustering recovered groups based on risk engagement rather than age, this would highlight the importance of considering within age variability (i.e., individual differences) when examining the neural processes of risk taking. While this approach does not investigate individual differences directly, it allows us to account for these differences when investigating developmental effects and investigate whether age is the best variable on which to partition the variation in neural connectivity during risk taking.

2. Methods

2.1. Participants

Eighty-four participants (ages 12.44-54.33 years) completed an fMRI scan. Participants were grouped into 3 age categories: adolescents (N=30, 15 male; M_age=13.22, SD=.64, range=12.44-14.83 years), young adults (N=23, 11 male; M_age=19.19, SD=.35, range=18.64-19.85 years), and adults (N=31, 11 male; M_age=43.93, SD=3.80, range=35.92-54.33 years). Participants provided written consent and assent in accordance with the University of Illinois’ Institutional Review Board.

2.2. Risky Decision-Making Task

Participants completed a version of the Balloon Analogue Risk Task (BART), a well-validated experimental paradigm (Lejuez et al., 2002; Wallsten et al., 2005) that has been adapted for fMRI in developmental populations (Telzer et al., 2014; McCormick & Telzer, 2017a). The BART measures participants’ willingness to engage in risky behavior in order to earn rewards and is associated with real-life risk taking in adolescents (Qu et al., 2015; McCormick & Telzer, 2017b) and adults (Lejuez et al., 2002; Wallsten et al., 2005). During the scan session, participants were presented with a sequence of 24 balloons that they could pump up to earn points. Each pump decision was associated with earning one point but increased the risk that a balloon would explode. If participants pumped too many times on a balloon, the balloon would explode and participants would lose all the points they had earned for that balloon. However, if participants chose to cash out before the balloon exploded, the points they earned would be added to the running total of points, which was presented on the screen as a points meter. Participants were instructed that their goal was to earn as many points as possible during the task. Each event (e.g., larger balloon following a pump, new balloon following cashed or explosion outcomes) was separated with a random jitter (500-4000 ms). Balloons exploded between 4 and 10 pumps, and the order of balloons was presented in a fixed order (after being pseudo-randomly ordered prior to data collection), although none of this information was made available to participants. The BART was self-paced and would not advance unless the participant made the choice to either pump or cash out. Participants were told that they could win a $10 gift card at the end of the neuroimaging session if they earned enough points during the task. The point threshold for winning this prize was intentionally left ambiguous so that participants were motivated to continue earning points throughout the task. In reality, all participants were given a $10 gift card after completing the scan session.

2.2.1. Behavioral Modeling.

We explored three standard behavioral metrics in order to assess participant performance on the BART. First, participants’ willingness to take risks was indexed by the average number of pumps each individual committed on balloons that they eventually cash-out out. Based on previous research (Lejuez et al., 2002; McCormick & Telzer, 2017a), pumps on balloons that ended in an explosion were not included in this metric, as an explosion artificially constrains the individual’s planned risky behavior. Secondly, participants’ exposure to negative outcomes was indexed by the number of explosions that occurred as a result of their risky behavior. Finally, adaptive outcomes were indexed by the total number of points individuals earned on the task.

2.3. fMRI Data Acquisition and Processing

2.3.1. fMRI data acquisition.

Imaging data were collected utilizing a 3 Tesla Trio MRI scanner. The BART included collection of T2*-weighted echoplanar images (EPI; slice thickness=3mm; 38 slices; TR=2sec; TE=25ms; matrix=92×92; FOV=230 mm; voxel size=2.5×2.5×3mm³). Additionally, structural scans were acquired, including a T1* magnetization-prepared rapid-acquisition gradient echo (MPRAGE; slice thickness=0.9mm; 192 slices; TR=1.9sec; TE=2.32ms; matrix=256×256; FOV=230mm; voxel size=0.9×0.9×0.9mm³; sagittal plane) and a T2*-weighted, matched-bandwidth (MBW), high resolution, anatomical scan (slice thickness=3mm; 192 slices; TR=4sec; TE=64ms; matrix=192×192; FOV=230mm; voxel size=1.2×1.2×3mm³). EPI and MBW scans were obtained at an oblique axial orientation in order to maximize brain coverage and minimize dropout in orbital regions.

2.3.2. fMRI data preprocessing and analysis.

Preprocessing utilized FSL FMRIBs Software Library (FSL v6.0; https://fsl.fmrib.ox.ac.uk/fsl/). Steps taken during preprocessing included correction for slice-timing using MCFLIRT; spatial smoothing using a 6mm Guassian kernel, full-width-at-half maximum; high-pass temporal filtering with a 128s cutoff to remove low frequency drift across the time-series; and skull stripping of all images with BET. Functional images were re-sampled to a 2×2×2 mm space and co-registered in a two-step sequence to the MBW and the MPRAGE images using FLIRT in order to warp them into the standard stereotactic space defined by the Montreal Neurological Institute (MNI) and the International Consortium for Brain Mapping. Preprocessing was completed utilizing individual-level independent component analysis (ICA) with MELODIC combined with an automated component classifier (Tohka et al., 2008; Neyman-Pearson threshold=0.3), which was applied to filter signal origination from noise sources (e.g., motion, physiological rhythms).

2.3.3. Time-series processing.

Timeseries were extracted from each voxel within each a priori ROI using FSL’s fslmeants, and averaged to create an ROI time-series. Prior to modeling time-series associations, we took several steps to reduce the influence of motion, which has been shown to be especially problematic for functional connectivity measures (e.g., Power et al., 2012; Van Dijk et al., 2012). First, as mentioned previously, we subjected each participants’ data to individual-level ICA in order to remove motion-related signal from the time-series. We also regressed out 8 nuisance regressors from the original time-series: 6 motion parameters generated during realignment and the average signal from both the white matter and cerebrospinal fluid masks. Finally, slices with greater than 2mm of motion were scrubbed from the time-series to remove the effects of large, sudden movements on the functional data. No participant exceeded 2.5% of slices being censored (range: 0-2.5%). Previous work (see Ciric et al., 2017) has shown that these strategies reduce the influence of motion on functional connectivity analyses.

2.4. Time-series Analysis

2.4.1. Regions of Interest.

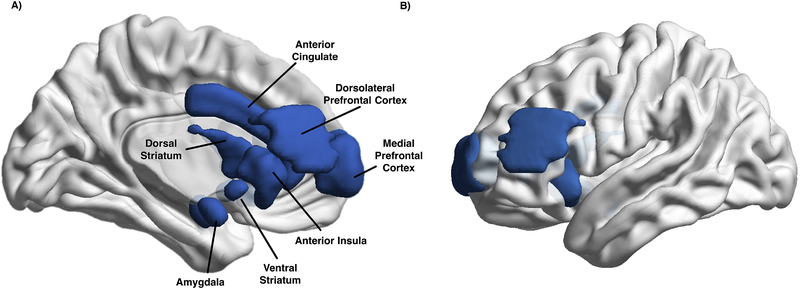
To assess a neural network of risky decision-making, we selected 12 a priori regions of interest (ROIs) based on previous neuroimaging work with the BART and other risk-taking tasks. These ROIs included subcortical, salience, and prefrontal regions. Subcortical regions included the bilateral ventral striatum (VS) and dorsal striatum (DS), as well as bilateral amygdala (Ernst et al., 2005; van Duijvenvoorde et al., 2014; Sesscouse et al., 2013; McCormick & Telzer, 2017a, 2017b). Salience regions included those most often found in decision making tasks, the anterior cingulate cortex (ACC) and bilateral anterior insula (AI; Schonberg et al., 2012; Qu et al., 2015; McCormick & Telzer, 2017a). Finally, we included two prefrontal regions, the medial prefrontal cortex (mPFC), which has been implicated in feedback processing (van Duijvenvoorde et al., 2014; McCormick & Telzer, 2017a,b, c), and the dorsolateral prefrontal cortex (dlPFC), a region involved in goal maintenance and cognitive control (Ridderinkoff et al., 2004; McCormick & Telzer, 2017a). Masks were defined from a number of sources, including the Harvard-Oxford (ACC, AI, amygdala; Harvard Center for Morphometric Analysis), Neurosynth (VS; Yarkoni et al., 2011), and the WFU PickAtlas (DS, DLPFC, mPFC; Maldjian et al., 2003). We utilized multiple sources for ROIs because of the lack of a single template which contained well-specified masks of the functional regions commonly involved in risk-taking behavior. Ventral striatum masks were constructed by searching “ventral striatum” on Neurosynth and thresholding the resulting meta-analytic image at Z=14. The dorsal striatum was defined as the caudate head and caudate tail in the AAL using the WFU pickatlas. The DLPFC was defined as BA 9, and the mPFC as the medial portion of BA 10 using the WFU pickatlas. Masks were evaluated using the Marsbar toolbox in SPM (Brett et al., 2002) and FSL to ensure that ROIs did not contain any voxels that overlapped with another mask or exceeded the boundaries of the whole-brain mask (see Figure 1). A 3D, navigable image containing all masks superimposed onto a single brain map is available on NeuroVault (https://neurovault.org/collections/QYLSPBSV/; Gorgolewski et al., 2015).

Figure 1:

ROIs Used for Network Analyses. A) We constructed 12 ROIs of regions previously implicated in risky decision-making including the anterior cingulate and medial PFC, as well as bilateral dorsal and ventral striatum, anterior insula, amygdala, and dorsolateral prefrontal cortex. B) A 3D video showing the ROIs embedded in the brain surface as well as free in space.

2.4.2. Group Iterative Multiple Model Estimation (GIMME).

GIMME is a data-driven search algorithm which utilizes both individual and group-level information to derive directed functional connectivity maps (Gates & Molenaar, 2012). GIMME estimates connectivity graphs using both unified SEM (uSEM; Gates et al., 2010, Kim et al., 2007) and extended unified SEM (euSEM; Gates et al., 2011) to assess whether the presence of a path between ROIs significantly improves the overall model fit to the time-series data. GIMME estimates both contemporaneous (e.g., ROI₁ at t predicts ROI₂ at t) and lagged (e.g., ROI₁ at t-1 predicts ROI₂ at t) effects between ROIs, as well as the autoregressive (e.g., ROI₁ at t-1 predicts ROI₁ at t) for each ROI time-series. GIMME assesses directional paths by testing whether a given ROI can predict another, controlling for the predicted ROI’s autoregressive effect (i.e., establishing Granger Causality) and other potential contemporaneous effects (e.g., ROI₃ predicts ROI₂) that may be present. Simultaneously the reciprocal path (ROI₂ predicting ROI₁) is also tested. GIMME has been developed for both block (Gates et al., 2010) and event-related (Gates et al., 2011) fMRI data, and is freely available through the open-source R platform (Lane et al., 2016; https://cran.r-project.org/web/packages/gimme/index.html; version 0.4-1; R version 3.4.4; https://www.r-project.org/). For a fully explicated model definition, including a representative path diagram, see Gates and colleagues (2017; figure 1 and supplemental).

In contrast with many other functional connectivity approaches (e.g., graph theoretical approaches), GIMME constructs functional maps through a data-driven, multi-step processing of model building and pruning. First, information across all participants is used to derive a common functional network map that is representative of the majority of the sample. Group paths are only kept if they are significant for 75% of all individuals. In the current sample results remain unchanged if this threshold is varied from 50-75% of the total sample suggesting that important effects are not being masked by an overly restrictive threshold. Note that this offers an improvement over simply averaging across individuals (as is commonly done when using correlation matrices) since results cannot be swayed here by individuals who deviate greatly from the sample. Simulations studies have demonstrated that using this threshold appropriately detects signal from noise (Gates & Molenaar, 2012) to recover true relations in the generated data at rates higher than many competing approaches. Importantly, false positives are rarely obtained (Gates & Molenaar, 2012). All autoregressive paths are automatically estimated in order to accurately assess directionality in the between-ROI paths (Lane et al., 2017). Once a group map has been obtained, unnecessary paths are pruned at the group level, and additional paths at the individual level are evaluated based on improvements to model fit for that individual. Individual-level paths are then pruned if they do not significantly improve the fit of the final model. The addition of paths is determined by Lagrange multiplier test equivalents (i.e., modification indices; Sörbom, 1989. Non-significant paths are removed at the individual level, and removed for group and subgroup levels if they no longer meet criterion (Gates & Molenaar, 2012). As such, GIMME offers the unique advantage of being able to derive a group-level map that should be applicable to the majority of the sample, while still allowing for individual-level paths to emerge.

Our task provided two main challenges when measuring neural connectivity. First, our goal was to analyze connectivity patterns during risky decisions; however, the BART also contains feedback trials (i.e., cash-out decisions, explosions). Secondly, our task was self-paced and as such, we needed a modeling approach that would allow for individuals to possess different amounts of data. To arrive at the time series used in connectivity analysis we extracted the measurement occasions (i.e., MR volume acquisitions) wherein the participant was engaged only during “risky decisions”. Fortunately, GIMME is capable of handling unequal amounts of data between participants, as well as the inclusion of missing data (Gates et al., 2014). Missing values are replaced with placeholder NaN values to maintain the temporal ordering of scans, and neither contemporaneous nor lagged effects are estimated based on missing values. These features make GIMME especially well-suited to estimating connectivity graphs for the BART, allowing for the self-paced nature of the task, as well as specifically examining connectivity during risk decisions, without considering connectivity during outcomes. However, as an additional check, we ensured that effects were not driven by differences in the amount of data available across participants because of variable reaction times through post-hoc tests. The number of TRs was unrelated to subgroup assignment across confirmatory (${\chi }_{(2,N=84)}^2=3.50$, p=.174) and exploratory analyses (U=677, Z=−1.43, p=.153) using non-parametric tests of mean differences.

2.4.3. Subgroup GIMME.

GIMME can also search for subgroup-specific connectivity paths. Subgroup-level analysis can be used in two ways. The first approach, confirmatory subgroup GIMME (CS-GIMME), utilizes a researcher-provided vector of subgroup assignments. In this case, after the group-level search CS-GIMME identifies which additional paths emerge for the pre-determined subgroups using the same procedures as were used for the group-level model building. A second approach, subgrouping GIMME (S-GIMME) arrives at subgroup assignments in an unsupervised manner by using features of individuals’ connectivity maps. In this option, S-GIMME generates a similarity matrix using the individual-level estimates of group-level connections, as well as anticipated estimates for candidate connections (Gates et al., 2017). In this way the subgroups are based on connectivity characteristics such as the presence/absence, strength, sign (positive/negative), temporal pattern (contemporaneous/lagged) and directionality (ROI₁ → ROI₂ versus ROI₂ ← ROI₁) of paths. This similarity matrix is then subjected to the community detection approach Walktrap (Pons and Latapy, 2006; see Gates, Henry, Steinley, & Fair, 2016 for a discussion of clustering in the context of fMRI). In short, Walktrap arrives at clusters using an entirely data-driven random walk approach to maximize modularity within the sample. Walktrap has been shown to be robust to common issues in community detection (e.g., unequal sample sizes; Orman and Labatut, 2009; Gates et al., 2016), and can return a single “subgroup” solution, avoiding spurious partitions of the data (Gates et al., 2016). Walktrap provides a powerful method for partitioning data into representative subgroups without relying on significance testing (see Gates et al., 2016), which is notoriously difficult in network contexts. We ran both options: CS-GIMME where a vector of age group assignment (i.e., adolescent, young adult, adult) was provided, and S-GIMME where Walktrap was allowed to freely arrive at an optimal subgroup solution based on the available data. The first method reveals which connections best explain differences in the neural representation of risk decisions that are dependent on age, while the second approach shows which paths are the most important for characterizing variability within the sample. Importantly, this second approach is free to cluster individuals on whatever feature is most important for discrimination between subgroups, which might be age, engagement in risky behavior, or some unknown alternative.

3. Results

3.1. Group-Level Connectivity Graph during Risk Taking

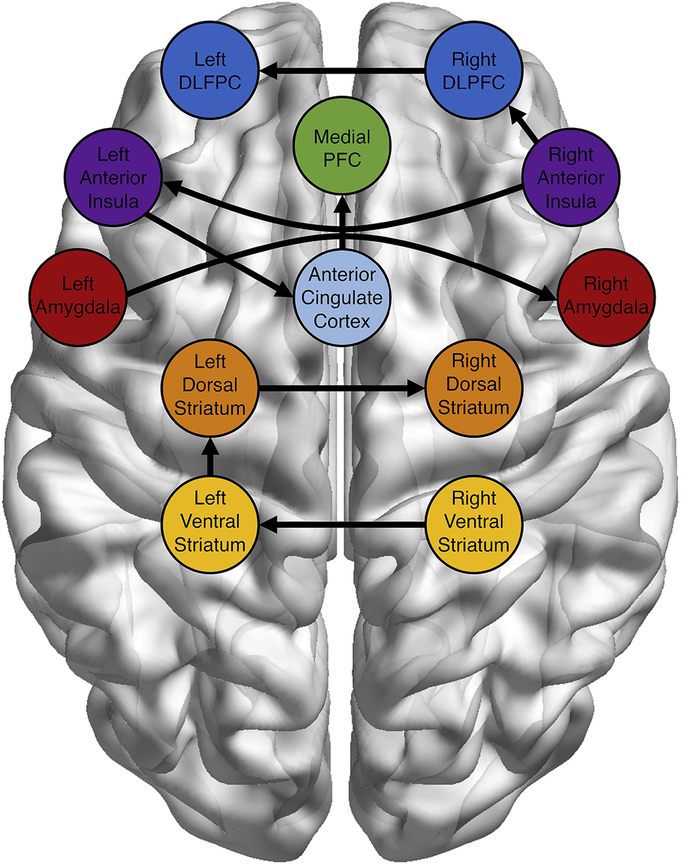
We first assessed the group level connectivity graph that consistently represented connectivity patterns interactions during risky decisions across the sample. As shown in Figure 2, group paths included paths between bilateral counterparts (e.g., left and right VS), as well as cross-region connections, including ACC-mPFC, AI-ACC, AI-DLPFC, and VS-DS paths. Interesting, at the group level, no regions evidenced paths with the amygdala (although the L/R amygdala path was present). For descriptive purposes, we have made the univariate main effects available on NeuroVault (https://neurovault.org/collections/QYLSPBSV/).

Figure 2:

Group-level Connectivity Map. GIMME estimated a group-level, directed network map. All paths were significant for at least 75% of subjects. Autoregressive paths (ROI at t predicted by ROI at t-1) are not shown, but were estimated for all regions within the network. All between-region paths included in the group-level connectivity maps were contemporaneous relationships.

3.2. Age-related Behavioral and Connectivity Differences during Risk Taking

3.2.1. Age-Related Behavioral Differences.

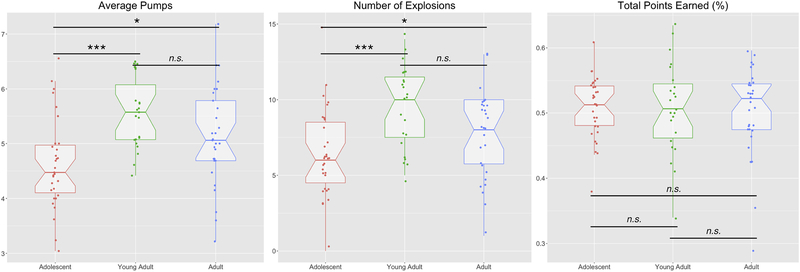
We first tested for age-related subgroup differences in task behavior (for group means, see Table 1). There was a significant difference across age groups in both average number of risk decisions (i.e., pumps; ${\chi }_{(2,N=84)}^2=17.00$, p<.001) and the number of explosions ${\chi }_{(2,N=84)}^2=14.49$, p=.001), but not for total points earned ${\chi }_{(2,N=84)}^2=0.02$, p=.992; Figure 3). Post-hoc contrasts showed that adolescents showed lower average risk decisions (i.e., pumps) than both young adults (U=125.5, Z=−4.04, p<.001) and adults (U=287.5, Z=−2.56, p=.010), and that adolescents experienced fewer explosions than young adults (U=143.5, Z=−3.76, p=.001), or adults (U=310, Z=−2.25, p=.024). Young adults and adults showed no differences in either average number of risk decisions (U=255.5, Z=−1.61, p=.108) or number of explosions (U=254, Z=−1.64, p=.101). These results show that while young adults and adults engage in greater risky behavior, this exposes them to more explosions (where they fail to earn points), resulting in equivalent outcomes.

Table 1.

Group Descriptions in Task Behavior on the BART

Group	Variable	M	SD	Range
Age Groups
Adolescents
	Risk Behavior	4.63	0.83	3.04-6.56
	# Explosions	6.39	2.97	0-15
	Total Points %	0.51	0.05	0.38-0.61
Young Adults
	Risk Behavior	5.56	0.64	4.42-6.50
	# Explosions	9.57	2.64	5-15
	Total Points %	0.51	0.07	0.34-0.63
Adults
	Risk Behavior	5.22	1.01	3.31-7.86
	# Explosions	8.37	3.69	1-17
	Total Points %	0.50	0.07	0.29-0.60
Data-Driven Groups
High Risk
	Risk Behavior	5.59	0.87	4.15-7.86
	# Explosions	9.53	3.40	3-17
	Total Points %	0.50	0.07	0.29-0.63
Low Risk
	Risk Behavior	4.79	0.83	3.04-7.18
	# Explosions	7.00	3.04	0-15
	Total Points %	0.51	0.06	0.34-0.62

Figure 3:

Age-related Behavioral Differences. Adolescents showed reduced Average Pumps and Number of Explosion compared with young adults and adults. No age group showed an advantage in terms of the number of points earned during the task. Median values are marked by the thick horizontal line, and box boundaries represent the range from the first to third quartiles. Whisker lines extend to 1.5 times the inter-quartile range. * p<.05, **p<.005, ***p<.001

3.2.2. Confirmatory Age-Related Subgroups Connectivity Patterns during Risk Taking.

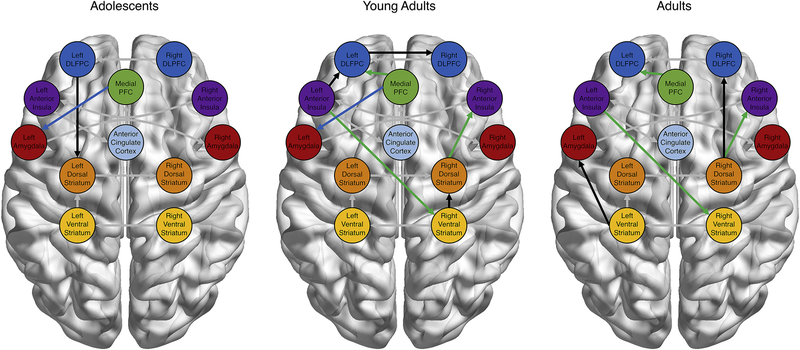
Next, we examined age group differences in the connectivity graphs of adolescents, young adults, and adults. In addition to the group-level paths which are shared among all participants, adolescents showed additional paths connecting PFC and subcortical regions (Figure 4a). Young adults showed a relatively large number of subgroup-specific paths, including PFC and insular connections with subcortical regions, insular-PFC pathways, and cortical-cortical connections (Figure 4b). Finally, adults showed several connections between subcortical regions and both the insula and PFC, as well as a striatal-amygdala path (Figure 4c). Importantly, young adults show paths which overlap with adolescents (i.e., mPFC to left amygdala; see blue paths in Figure 4b) and with adults (i.e., mPFC to left DLPFC, left AI to right VS, and right DS to right AI; see green paths in Figure 4c), which did not overlap between adolescents and adults. Furthermore, young adults showed an increased number of subgroup paths compared to the other age groups. Post-hoc analyses using the person-specific graphs generated for each participant showed that this increase was not driven by young adults showing a greater number of paths at the individual level (as compared with adolescents and adults; F_(2,81)=0.46, p=.636), suggesting that young adults showed more consistency across individuals in the paths which were estimated as significant at the individual level. These features suggest a transition from teen to adult network states through a hyper-connected young adult configuration.

3.3. Unsupervised Recovery of Subgroups Based on Network Connectivity

3.3.1. Recovery of High- and Low-Risk Subgroups.

Next, we conducted S-GIMME to perform an unsupervised search for meaningful subgroups. The algorithm returned two subgroups from the data. Subgroup 1 was smaller (N=32) and was largely composed of young adults and adults (adolescents=4; young adults=14; adults=13), while Subgroup 2 was larger (N=52), and composed of a mix of age groups (adolescents=26, young adults=9; adults=17). Age group and exploratory subgroup assignment were related ${\chi }_{(2,N=84)}^2=11.75$, p<.003) such that older age groups were overrepresented in Subgroup 1 relative to teens, but there were no differences in terms of gender between the two subgroups ${\chi }_{(2,N=84)}^2=.25$, p=.620). To investigate the alternative hypothesis outlined above, we used the generated subgroup assignments to test for differences in risky behavior on the task (for group means, see Table 1). Subgroup 1 engaged in higher rates of risk decisions (U=418.5, Z=−3.81, p<.001) and exploded more balloons (U=472.5, Z=−3.33, p=.001) than subgroup 2. Similar to the age-related results, this pattern of overly risky behavior resulted in no differences in the total number of points earned between the two groups (U=824.5, Z=−.069, p=.945). Given that age group was also related to the data-driven subgroups, follow-up multiple binary logistic regression analyses were conducted to investigate which relations remained when including both age and risk taking variables. These results showed that while age-group (coded as 1-3) was a significant predictor of group membership when entered as a single predictor (B=−.601, SE=.276, p=.030), this effect was not significant when controlling for risk behavior (B=−.414, SE=.310, p=.182). In contrast, risk behavior (i.e., number of risk decisions) was a significant predictor even when controlling for age group (B=−1.064, SE=.327, p=.001). Given this pattern of results, we subsequently refer to Subgroup 1 as the high-risk group, and Subgroup 2 as the low-risk group.

3.3.2. Exploratory Subgroups Connectivity Patterns during Risk Taking.

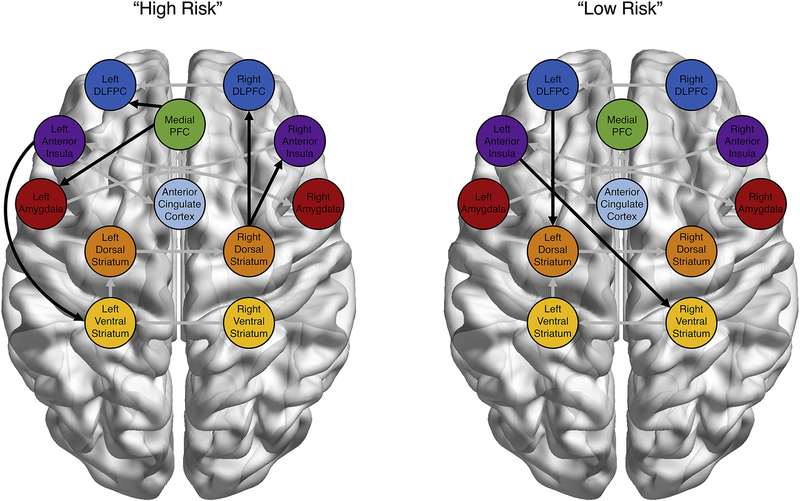
S-GIMME also generated connectivity maps relating to these high- and low-risk subgroups. Paths that characterized the high-risk group included paths from the mPFC to the DLPFC and amygdala, the right DS to the right DLPFC and AI, as well as the right VS to the right AI (Figure 5a). In contrast, the only paths which characterized the low-risk group were those from the left DLPFC to the left DS and the left AI to the R VS (Figure 5b). Interestingly, most of the paths used by the Walktrap algorithm to freely group participants were also relevant to distinguishing between age groups, with the lone exception of the path between right VS and AI (see Figures 4 and 5 for comparison). However, rather than simply replicating the age-group connectivity results, the subgroup paths which predicted high- versus low-risk individuals were a combination of adolescent-typical and adult-typical paths. For instance, even though adolescents as a group were the lowest risk age-group, the mPFC-amygdala paths that characterizes adolescent connectivity is present in the high-risk exploratory subgroup. In the same vein, the path between left AI and right VS, which characterizes the two higher-risk age-groups (i.e., young adults and adults) is a characteristic of the low-risk exploratory subgroup. These results clearly show that age is not the sole source of variance in network configurations during risky decision making, but that variability in neural network connectivity that cuts across age can be related more-powerfully to behavior indicators of interest. Indeed, our results suggest that within-group variability was more powerful than between-group differences in our data, as unsupervised subgrouping failed to recover age-categories.

Figure 4:

Neural Connectivity as a Function of Age. Confirmatory subgrouping of neural networks revealed age-specific paths in addition to the group-level functional connections. Adolescents (blue) and adults (green) showed path overlap with young adults but not with each other, suggesting a transition from the youngest to the oldest brain state through a hyper-connected transition state. All between-region paths included in the group-level connectivity maps were contemporaneous relationships. Unique subgroup paths are in black, while group-level paths are in grey.

Figure 5:

Recovery of High- and Low-Risk Subgroups. An exploratory subgrouping revealed two groups distinguished by their neural connectivity patterns. Rather than recovering age-related groups, the Walktrap algorithm appears to select subgroup membership more on risky behavior in the task. All between-region paths included in the group-level connectivity maps were contemporaneous relationships. Unique subgroup paths are in black, while group-level paths are in grey.

4. Discussion

The field of developmental neuroscience has dedicated significant attention to questions related to what characterizes adolescent risky decision-making at the neural level, and how adolescents differ from other age groups in these decisions (e.g., Casey, 2015; Shulman et al., 2016). However, one of the limitations of current methodologies is that they largely rely on characterizing the “average” individual within a given group. However, these approaches have significant drawbacks since they fail to consider within-group variability, and may mask important differences between adolescents (or other age group). Fortunately, the development of new methodologies such as multi-level (or mixed-effects; e.g., Braams et al., 2015; Peters et al., 2017 and GIMME (Gates et al., 2017) models offer an exciting opportunity to begin to characterize both within- and between-age variability in behavior and in neural networks. Data-driven connectivity approaches, such as the GIMME set of models, have the advantage over other techniques in that they fit a group-level model, but then allow individuals’ to be specified uniquely to maximize model fit for each participant. Additionally, while clustering results in groups, the exploratory method of S-GIMME allows the researcher to investigate whether a priori categorizations (e.g., age, diagnostic category) are the only source of variability, or whether important differences in network connectivity occur across different axes (e.g., individual differences in behavior).

In contrast with previous work (e.g., Shulman et al., 2016), our results show that adolescents in the sample actually make the fewest risk decisions, with both young adults and adults showing comparatively heightened risk-taking behavior. Furthermore, despite previous suggestions that young adults (ages 18-20) should more-closely resemble adolescents (Cohen et al., 2017), we found that young adults were significantly more risky than adolescents and showed no significant differences from adults. Interestingly, these age-related increases in risk behavior did not translate into increases in adaptive outcomes (i.e., total points earned), as this elevated risk behavior resulted in an increased rate of explosions. Taken together, these behavioral results counter prevailing models which suggest that adolescents should be hyper-risky compared with older counterparts (Casey et al., 2008; Steinberg et al., 2008). The increase from adolescence to early adulthood is consistent with more-recent cross-cultural data on risk-taking propensity (Duell et al., 2018). This may be that since the BART (and similar tasks like the Iowa Gambling Task) tend to be more predictive of real-world risky behavior (Schonberg et al., 2011), they are necessarily more complex and cognitively demanding for participants. However, that adults also take more risks than adolescents in this sample is difficult to reconcile with past work. One potential difficulty in comparing these results is that we utilized narrow age-ranges, whereas previous studies have primarily recruited groups across a wider range of actual ages (see van Duijvenvoorde et al., 2016). As such, we interpret these results not as a challenge to these oft-replicated trends, but rather as evidence that models of adolescent neurodevelopment should be expanded upon to account for those adolescents who (either individually or as a subgroup) do not engage in enhanced risk taking.

On the neural level, adolescents and adults both shared age group-specific paths with young adults, but did not share any between them. Furthermore, young adults showed the greatest number of age-specific paths, although follow-up analyses suggest this is due to a greater consistency across subjects in the young adult age group rather than a greater absolute number of paths at the individual level. These results suggest a transition in neural configuration between adolescents, young adults, and adults. Given that our hypotheses were related to age-related changes in network-level configurations of connectivity, and the relative scarcity of network findings in adolescent neurodevelopmental research, we avoid speculating about each of the specific paths which differed between age- and behaviorally-related subgroups. As such, the current work should foster more regionally-specific hypotheses, which are a clear necessity for furthering our understanding of how neural networks vary across individuals and development.

Even more striking than the differences in risk behavior and neural networks as a function of age were the results of the exploratory subgrouping approach. Rather than recovering our defined age categories with any appreciable fidelity, the unsupervised algorithm instead categorized individuals in the sample by their task behavior, namely their engagement in risk behavior (i.e., high versus low). These results suggest that rather than age, the most powerful factors that discriminated between neural connectivity patterns in the current study are related to task behavior. These results emerged despite the fact that we utilized narrow and well-separated age ranges for our three age groups in order to avoid some of the issues related to inconsistent age-group definitions of adolescence and (young) adulthood across samples (e.g., van Duijvenvoorde et al., 2016). In principle, this approach should reduce within-group heterogeneity and maximize the ability to detect developmental differences. Given these features of sampling, the fact that the data-driven clustering failed to recover age groups is even more remarkable, and suggests that individuals differences in behavior can reflect greater variability in network configurations than age alone.

These findings have clear implications for the importance of considering within-group variability even when looking across development (e.g., Foulkes & Blakemore, 2018). If some adolescents can more-closely resemble young adults and adults at the neural level than do their same-age peers, models of adolescent neurodevelopment may need to expand in order to address the very real variability that exists in the population. Follow-up work on the antecedents and consequences of within-age variability in risk behavior and functional network configurations is an exciting new frontier in the field, and can be aided through the adoption of methodological techniques which allow us to uncover and characterize both within- and between-age differences and the neural states which underlie those differences. These methods offer several advantages over traditional techniques, including being robust to assumption violations, partitioning variance appropriately to avoid inference fallacies (e.g., Curran & Bauer, 2011), and allowing comparisons of variance between samples that can help reconcile findings across different populations. With the advent of large-scale longitudinal designs becoming available (e.g., the Adolescent Brain and Cognitive Development Study; Jernigan et al., 2018), methods that account for multiple sources of variable will be crucial for drawing appropriate conclusions about developmental trajectories. GIMME could also be implemented on data gathered longitudinally. For instance, using the data-driven subgrouping approach, GIMME would identify if individuals tend to subgroup with themselves across time or with other individuals measured at the same time.

Taken together, the findings of the current study raise several interesting questions for future research, as well as introducing a methodological approach which can be used to leverage insights on questions central to developmental neuroscience. Utilizing a model-based network approach, we investigated age-related differences in functional connectivity between a set of task-relevant regions, including subcortical, salience, and prefrontal areas. Furthermore, we investigated whether age was in fact the most important factor in categorizing individuals based on their network configurations. In contrast with previous work, we found that adolescents were the least risky individuals as a group in our sample, and that task behavior was a more powerful organizer for neural networks than age. Understanding how these, and other results highlighting within-adolescence variability (e.g., Braams et al., 2015; Telzer, 2016; McCormick & Telzer, 2017b; Blankenstein et al., 2018) fit into the broader literature on adolescent neurodevelopment, especially as it is relevant to risk behavior, requires a broadening of our understanding what characterizes changes during adolescent. Specifically, moving away from characterizing what is “average” for adolescents, and instead acknowledging and building our developmental models around the rich variation that exists between individuals.