Abstract
Analysis of fluorescence fluctuation experiments by the mean-segmented Q (MSQ) method was recently used to successfully characterize the oligomeric state and mobility of proteins within the nuclear envelope (NE) of living cells. However, two significant shortcomings of MSQ were recognized. Non-ideal detector behavior due to dead-time and afterpulsing as well as the lack of error analysis currently limit the potential of MSQ. This paper presents time-shifted MSQ (tsMSQ), a new formulation of MSQ that is robust with respect to dead-time and afterpulsing. In addition, a protocol for performing error analysis on tsMSQ data is introduced to assess the quality of fit models and estimate the uncertainties of fit parameters. Together, these developments significantly simplify and improve the analysis of fluorescence fluctuation data taken within the NE. To demonstrate these new developments, tsMSQ was used to characterize the oligomeric state and mobility of the luminal domains of two inner nuclear membrane SUN proteins. The results for the luminal domain of SUN2 obtained through tsMSQ without correction for non-ideal detector effects agree with a recent study that was conducted using the original MSQ formulation. Finally, tsMSQ was applied to characterize the oligomeric state and mobility of the luminal domain of the germline-restricted SUN3.
1. Introduction
The contents of the nucleoplasm are physically separated from the cytoplasm by the nuclear envelope (NE) [1]. This specialized domain of the endoplasmic reticulum (ER) consists of the inner nuclear membrane (INM), the outer nuclear membrane (ONM), nuclear pore complexes (NPCs), and the nuclear lamina [1]. The ribosome-studded ONM is an extension of the ER, while the INM interacts with chromatin and the nuclear lamina [2]. While the INM and ONM are separated by the ~40–50 nm wide perinuclear space that is contiguous with the ER lumen, they are fused together at thousands of specific sites resulting in the formation of aqueous channels occupied by NPCs [1]. Besides the transmembrane domain containing NPC proteins, there are numerous other NE-associated proteins that are critically important for a wide-variety of fundamental cellular processes, including cell cycle progression, DNA repair, gene expression, genome organization, lipid synthesis, and mechanotransduction [3–8]. The importance of these NE-associated proteins is further highlighted by the fact that they are mutated in a growing list of human diseases collectively referred to as “nuclear envelopathies”, such as cardiomyopathy, muscular dystrophy, and premature aging [9]. Unfortunately, the dynamics and the assembly of NE proteins within living cells are difficult to assess with currently available methods. To begin addressing this deficiency we recently demonstrated that fluorescence fluctuation spectroscopy (FFS) has the potential to quantify the association and mobility of NE proteins within their native environment [10].
The double membrane system of the NE proved to be a challenging environment for traditional FFS techniques and prompted us to use the recently developed mean-segmented Q (MSQ) method for analysis [11]. Nanometer-sized undulations of the INM and ONM introduce fluctuations in the local thickness of the NE that are superimposed on the fluorescence intensity fluctuations caused by NE proteins passing through the observation volume (OV) of the microscope. MSQ proved to be essential for separating these different noise sources and characterizing the oligomeric state of proteins in the NE [10]. Unfortunately, the application of MSQ is not straightforward as it requires compensation for non-ideal detector effects to remove significant biases from the collected data [12]. While methods to account for these effects exist [12,13], they necessitate the difficult task of properly calibrating each detector. Moreover, the correction procedure becomes unreliable once the amplitude of the bias correction approaches the amplitude of the signal. In addition, the original formulation of MSQ lacks error analysis [11], which is a significant shortcoming that prevents the statistical testing of models and the determination of uncertainties in fit parameters. This paper addresses these challenges by introducing time-shifted MSQ (tsMSQ) together with a simple procedure for proper error analysis. Experimental verification of the theory demonstrates that tsMSQ is inherently robust with respect to non-ideal detector effects, which significantly simplifies the analysis of FFS data obtained within the NE, and is suitable for model analysis with error estimates.
To demonstrate the utility of tsMSQ for analyzing FFS data collected within the NE, we used it to quantify the assembly and dynamics of the EGFP-tagged luminal domain of the Sad1/UNC-84 (SUN) protein SUN2, which is an INM protein and a key component of the linker of nucleoskeleton and cytoskeleton (LINC) complex [3]. The decision to initially analyze the luminal domain of SUN2 provided an important test case for tsMSQ, since we previously reported that this protein homo-trimerizes within the NE as determined by MSQ analysis of FFS data [14]. We then used tsMSQ to determine the assembly state of the luminal domain of the germline-restricted SUN protein, SUN3 [15], which is currently unknown. Taken together, these results establish tsMSQ as a simple, yet powerful method for analyzing FFS data taken within the NE, which eliminates the need for an in-depth knowledge of detector effects.
2. Material and Methods
2.1. Experimental Setup
Brightness measurements were performed on a custom two-photon microscope with a 63x C-Apochromat water-immersion objective with numerical aperture (NA) = 1.2 (Zeiss, Oberkochen, Germany) as described previously [16] using a wavelength of 1000 nm and an average power after the objective in the range of 0.3 to 0.4 mW. Photon counts were detected using avalanche photodiodes (SPCM-AQ-141 APD; Perkin-Elmer, Dumberry, Quebec, Canada), recorded with a Flex04–12D card (correlator.com, Bridgewater, NJ) sampled at 20 kHz and analyzed using programs written in IDL 8.7 (Research Systems, Boulder, CO). Z-scans were performed using an arbitrary waveform generator (model No. 33522A; Agilent Technologies, Santa Clara, CA) to move a PZ2000 piezo stage (ASI, Eugene, OR) axially. The selected waveform of the generator was a linear ramp function with peak-to-peak amplitude of 1.6 V, corresponding to 24.1 μm of axial travel, and period of 10 s for a speed of 4.82 μm/s.
2.2. Measurement Procedure
Calibration measurements were performed on cells transiently transfected with EGFP. Transfected cells were identified using brief epifluorescence illumination. The selected cell was centered and the two-photon laser spot was focused into the cytoplasm of the cell. Fluorescence intensity fluctuation data was acquired for ~60 s followed by z-scans. These data were used to determine the molecular brightness, which is also referred to simply as brightness, λEGFG as previously described [13,17]. In cells expressing NE localized proteins, z-scans were used to identify cells with NE intensity fractions >90% for FFS measurements [10]. The point spread function (PSF) was focused on the ventral NE and fluorescence intensity fluctuations data were acquired for ~60 s to ~300 s; the same procedure was repeated at the dorsal NE. A detailed description of the measurement protocol is found in Hennen et al.[18]. The FFS data was analyzed as described in the results section of this paper.
2.3. Sample Preparation
Experiments were performed using transiently transfected U2OS cells (ATCC, Manassas, VA), which were maintained in DMEM with 10% FBS (Hyclone Laboratories, Logan, UT) before being sub-cultured into 24-well glass bottom plates (In Vitro Scientific, Sunnyvale, CA) 24 hours prior to transfection. Transfections were performed using GenJet (SignaGen Laboratories, Rockville, MD) 12–24 hours prior to measurement according to the protocol provided by the manufacturer. Growth medium was replaced immediately before measuring with DPBS containing calcium and magnesium (BioWhittaker, Walkerville, MD).
2.4. DNA Constructs
The SS-EGFP and SS-EGFP-SUN2261−731 constructs were described previously [10]. The SS-EGFP-SUN330–320construct was generated as follows. First, the cDNA encoding full length (FL) SUN3 was PCR amplified using the SUN3FL-F and SUN3FL-R primer pair (Table 1) from a prep of cDNA isolated from the testes of post-embryonic day 21 male mice, which was a gift from Drs. Vivian Bardwell and David Zarkower (University of Minnesota, Minneapolis, MN). The PCR product was purified and digested beside pEGFP-C1 with EcoRI and XhoI. Following gel purification, the digested PCR product and plasmid were ligated together to create EGFP-SUN3FL. To create SS-EGFP-SUN330–320, the sequence encoding amino acids 30–320 was PCR-amplified from EGFP-SUN3FL using the primers SS-EGFP-SUN330−320-F and SS-EGFP-SUN330–320-R (Table 1). SS-EGFP-SUN330−320-F also encodes a 10-amino acid linker (GHGTGSTGSG) following the BsrGI site. The resulting PCR product was purified and digested beside SS-EGFP with BsrGI and XhoI. Following gel purification, the digested PCR product and plasmid were ligated together to create SS-EGFP-SUN330–320. The cytoplasmic EGFP-tagged SUN330−320 construct was generated via a T4 polynucleotide kinase (PNK), T4 DNA ligase, DpnI reaction after EGFP-SUN330−320 was PCR amplified using the primers SSΔ-F and SSΔ-R (Table 1). All of the constructs used in this work were sequence-validated by the University of Minnesota Genomics Center. Phusion DNA polymerase, T4 DNA ligase, and T4 PNK were purchased from New England Biolabs (NEB, Ipswich, MA). Restriction enzymes were either purchased from NEB or Promega (Madison, WI). Wizard SV Gel and PCR Clean-Up System was purchased from Promega. GeneJet Plasmid Midiprep Kit was purchased from ThermoFisher Scientific (Waltham, MA). All other chemicals were purchased from Sigma-Aldrich (St. Louis, MI) unless otherwise specified.
Table 1:
Primers used to generate the constructs used in this paper. The F or R in the primer name refers to forward or reverse, respectively. Restriction enzyme (RE) cut sites are underlined. The sequence encoding the linker is bolded.
| Primer Name | DNA Sequence | 5’ RE Site |
|---|---|---|
| SUN3FL-F | TTTTCTCGAGATGTTAACTCGATCATGGAAGATTATCC | XhoI |
| SUN3FL-R | AAAAAGAATTCCTAAGTGTAATCACTGGGGATGCCG | EcoRI |
| SS-EGFP-SUN330−320-F | GCTGTACAAGGGGCACGGGACCGGGTCTACAGGGAGCGGGAAAGAAACAGAGTTTCCTCA | BsrGI |
| SS-EGFP-SUN330−320-R | AAAACTCGAGCTAAGTGTAATCACTGGGGATGC | XhoI |
| SSΔ-F | GTGGCTAGCGTGAGCAAGGG | - |
| SSΔ-R | CATGGATCCGAGCTCGGTACC | - |
3. Background
3.1. Brightness experiments in the cytoplasm
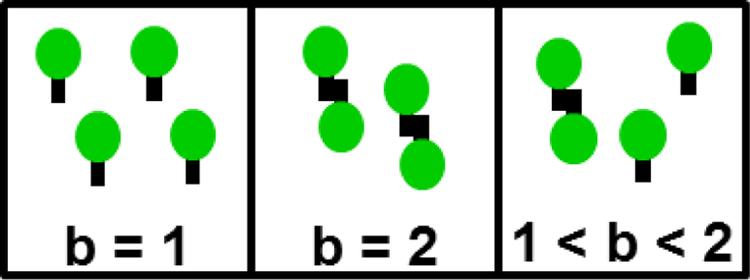
We start by reviewing a few central concepts of FFS. First and foremost, the analysis of intensity fluctuations determines the molecular brightness λ, which specifies the fluorescence intensity associated with a single fluorescent protein (FP). If the brightness of monomeric EGFP is λEGFP, then the brightness of the tandem dimer EGFP2 is increased by a factor of two, . Thus, brightness is a measure of the average oligomeric state of an EGFP-tagged protein complex as illustrated in Fig. 1. The normalized brightness b is defined by the ratio of the measured brightness λ to that of EGFP, b = λ/λEGFP, and provides a direct numerical readout of the average oligomeric state of an EGFP-tagged protein complex [19]. For example, a monomer corresponds to b = 1, while a dimer equals b = 2. Note that not all FPs behave as simply as described here. Thus, it is important to always perform control experiments to check the brightness of the monomeric label and its tandem dimer as previously described [16,17].
Fig. 1. Brightness b identifies the average oligomeric state of a fluorescently labeled protein complex.
Monomers and dimers are characterized by b of 1 and 2, respectively. The brightness of a mixture of monomers and dimers is between 1 and 2 depending on the composition of the mixture.
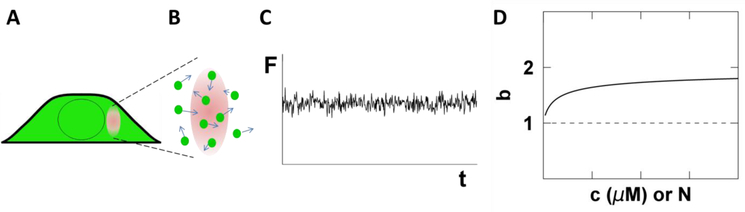
Central to FFS is the OV, which in our case is given by the overlap between the two-photon excitation PSF and the sample volume. Fig. 2A illustrates the PSF completely embedded in a thick cytoplasmic section of the cell. In this case, the cytoplasmic FP has access to the entire volume of the PSF and therefore the OV and PSF are equivalent (Fig. 2B). The fluorescence signal, F, emanating from the OV fluctuates with time as a consequence of FPs entering and exciting the OV (Fig. 2C). The sampling, or binning, time TS specifies the time period over which the signal is integrated. The data acquisition electronics record the photon counts k for each sampling period. There are two important parameters that are directly measured from the record of photon counts k, the average intensity <F> and Mandel’s Q-parameter Q, which we also refer to as the Q-factor [20]. A description and definition of the Q-factor is found in section 4.1.
Fig. 2. Illustration of FFS in the cytoplasm.
A) The PSF (red oval) is completely embedded within the cytoplasm. B) The entire volume of the PSF is accessible to the fluorescent proteins. Therefore the OV is equivalent to the PSF volume. C) The fluorescence signal fluctuates in time reflecting the passage of proteins through the OV. D) The brightness titration curve of a FP-labeled monomer is independent of concentration (dashed line). A labeled protein that forms dimers leads to a concentration-dependent brightness titration curve (solid line) that increases from 1 to 2. The x-axis depicts either molar concentration c or the occupation number N.
Further interpretation of the FFS parameters depends on a mathematical model of the PSF, which for our instrument is well approximated by a modified Gaussian-Lorentzian (mGL) PSF [17]. This function, combined with the geometry of the sample, determines the volume VOV, gamma-factor γ2, and binning function B2 (TS)of the OV, which enable proper interpretation of the measured FFS parameters[16,17,21]. The brightness λ is identified from the asymptotic Q-factor, which is discussed in further detail in section 4.1, by [13]
| (1) |
Due to its direct relation to brightness, the determination of the asymptotic Q-factor is essential for the characterization of oligomeric state through FFS. The average occupation number N of FPs within the OV is determined from the average intensity by <F> = λEGFPN. The molar concentration c is calculated from N with the help of Avogadro’s number NA and the OV by N = cVOVNA. For each cell measured, the brightness b and concentration c are identified. The concentration-dependent oligomerization of an FP-labeled protein is identified by measuring many cells with different expression levels and plotting their brightness versus concentration, which we refer to as a brightness titration curve [16]. A monomeric protein is distinguished from a protein undergoing a monomer / dimer transition by the brightness titration curves depicted in Fig. 2D. Finally, the diffusion time τD of an FP-labeled protein is determined from the autocorrelation function of the intensity fluctuations [22,23]. Association of a soluble molecule with a large complex or a membrane significantly reduces its mobility, which is identified by an increase in τD [24].
3.2. Brightness experiments within the NE
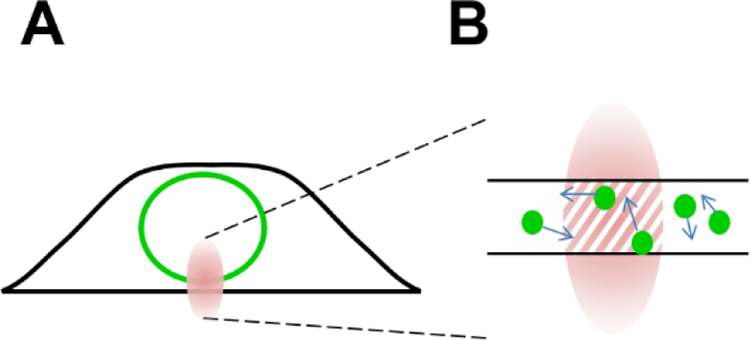
Performing FFS within the NE requires a few changes to the measurement protocol and analysis. First, the two-photon beam is focused onto the ventral or dorsal NE prior to data collection (Fig. 3A). We will assume throughout the remainder of this work that the FP-tagged protein is localized properly to the NE and its concentration in the cytoplasm and nucleus is negligible. Experimental tests for proper localization have been described recently [10]. Second, because the thickness of the NE is on the order of 40 nm, only a small section of the PSF is accessible to labeled NE proteins. To account for this change the OV is no longer equivalent to the PSF, but instead defined as the intersection between the PSF and the NE (Fig. 3B). The resulting VOV is the product of the cross-sectional area A of the PSF and the thickness tNE of the NE, VOV = A tNE. Similarly, the parameters γ2 and B2(TS) depend on the intersection between the PSF and the NE [17,21], which is modeled by a two-dimensional Gaussian distribution [10,14]. While N is still determined by <F> = λEGFPN, it reflects the number of labeled proteins within a much smaller volume (Fig. 3B). Because tNE cannot be directly measured, the molar concentration can only be estimated by assuming the thickness of the NE layer. We therefore prefer to use N rather than c when reporting FFS results [10,14].
Fig. 3. FFS within the NE.
A) The PSF (red oval) is not fully embedded within the NE. B) The OV (hatched area) reflects the overlap between the PSF and the NE.
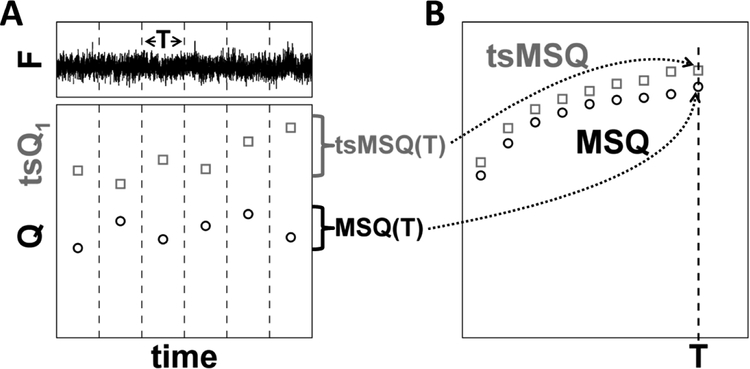
We recently showed that conventional FFS analysis of NE proteins can introduce severe distortions in the recovered brightness values and confound data interpretation as a result of NE membrane undulations [10]. Analysis methods which ignore the temporal information of fluctuations, such as cumulant analysis, PCH, and FIDA are unable to distinguish the diffusion and membrane undulation processes and therefore are unsuited to recover brightness in the NE [25]. Methods that include temporal information, such as FCS, TIFCA, and FIMDA [25], do not account for the finite data segment length incorporated in the analysis algorithm, which has the potential to introduce biases when applied to slow processes as was observed recently due to the NE membrane undulations [10]. To remedy this issue, we introduced MSQ analysis to obtain brightness values that accurately reflect the oligomeric state of FP-tagged proteins within the NE [11]. The MSQ curve is determined by dividing the recorded photon counts into segments with period T (Fig. 4A). Q is calculated for each segment and subsequently averaged to yield the data point MSQ(T). By repeating this process for different values of T, the MSQ curve is constructed (Fig. 4B). Fitting of the MSQ curve is used to recover both the brightness and the diffusion time of the labeled protein. Using this method we demonstrated that the luminal domain of SUN2 undergoes a monomer / trimer transition, whereas the luminal domain of the related protein SUN1 forms higher-order oligomers within the NE [14].
Fig. 4. Construction of MSQ and tsMSQ curves.
A) The recorded fluorescence intensity signal is divided into segments of period T (top panel). Q or tsQ1 is calculated for each of these segments (bottom panel). B) The Q-values for the segment time T are converted by an algorithm into an MSQ(T) value. Similarly, the tsQ1 values are converted into a tsMSQ(T) value. Repeating this procedure for a range of segment times identifies the experimental MSQ or tsMSQ curve.
4. Theory
This section describes derivations of functions that are important for tsMSQ. Interpretation and usage of the derived equations is found in section 5.
4.1. Sampling time dependence of the Q-parameter
The Q-parameter of FFS data sampled with a time resolution TS is calculated by [20]
| (2) |
The raw data ki represents the photon counts detected at time i×TS, while <> symbolizes the population mean. The deviation or fluctuation of ki from the mean <ki> is given by δki ≡ ki − <ki>. For an arbitrary sampling time, the Q-parameter of a single diffusing species with brightness λ and diffusion time τD is determined by [13,21]
| (3) |
where accounts for the decrease in Q(TS) relative to the asymptotic Q-factor Q0 and, in the case of a two-dimensional Gaussian OV, is given by [26]. This decrease in Q(TS) is significant when TS ≥ τD, which is referred to as undersampling [27]. In the case of oversampling (TS ≪ τD), converges to 1 and the Q-value Q(TS) reduces to the limiting value of Q0, which is directly related to λ by Eq. (1). Since FFS data obtained in cells are typically oversampled, Eq. (1) is usually quoted in the literature. In this paper we use Eq. (3), which is correct for all sampling times, as it facilitates comparison with the time-shifted FFS theory described in section 4.3.
4.2. Eliminating the shot noise term from MSQ
The MSQ value of FFS data sampled with a time resolution TS is calculated by dividing the data into segments of duration T and determining the expectation value of the Q-estimator QT across all data segments (Fig. 4) as previously described [11]. Here, we introduce an updated definition of MSQ by adding the term TS/T,
| (4) |
This redefinition removes the bias caused by the shot-noise of the detector, which provides no relevant information about the sample. Moreover, it simplifies the expression of the MSQ curve to
| (5) |
The first term represents the sampling-time correction of the asymptotic Q-parameter. The second term characterizes the remaining degree of correlation within a segment of length T and depends on the second-order binning function B2(T, τD) for FP-tagged proteins with diffusion time τD [21,26]. For simplicity, we omit the parameter τD in the derivations below. The MSQ curves with and without the shot-noise bias term are provided in Sup. Fig. S1.
4.3. tsMSQ for a diffusing species
tsMSQ and MSQ are conceptually very similar algorithms that are applied to the same FFS data sampled with frequency 1/TS (Fig. 4). However, while MSQ calculates Mandel’s Q-parameter using (Eq. 2), tsMSQ is based on a generalized form of the Q-factor [13],
| (6) |
which we refer to as time-shifted Q-value. In the oversampling limit, where TS ≪ τD, the time-shifted covariance is given by [21]. G2 (TS) is the second-order normalized autocorrelation function of a single diffusing species and accounts for the correlation between successive data points. Thus, the oversampled, time-shifted Q-factor is written as
| (7) |
A generalization of Eq. (7) valid for all sampling times,
| (8) |
is derived in section 4.4. The factor describes the reduction of tsQ1 from Q0 due to diffusion, where tsB2 represents the time-shifted binning function of second order defined in section 4.4.
While Eq. (8) specifies the population value, experimental data are always finite and require a statistical estimator. Because estimators frequently introduce biases, their expectation value must be critically assessed. We begin by assuming a segment with M data points, which corresponds to a segment time period of T = M×TS, and define the following estimator of tsQ1,
| (9) |
which we express as a function of T to emphasize the estimator’s dependence on the segment time. is the estimator of the mean and
| (10) |
is the estimator of the time-shifted covariance <δkiδki+1> with and .
To evaluate the expectation value of the estimator of tsQ1 we rewrite the fluctuation estimators in terms of δki,
| (11) |
Inserting these expressions into Eq. (9) results in
| (12) |
Since the ensemble average of a ratio is equal to the ratio of the respective ensemble averages, we obtain
| (13) |
where the first term is equal to the ideal tsQ1-factor given by Eq. (6) and the second term reflects the bias introduced by using the estimator of the mean instead of the population mean. Because the second term becomes negligible as M increases, the estimator is asymptotically unbiased. Evaluating Eq. (13) (see section 4.4) leads to
| (14) |
For convenience we defined a new function,
| (15) |
in the third term of Eq. (14), which describes the influence of the correlation of the data due to diffusion. The shot noise for i = j+1 gives rise to the second term. Finally, to eliminate the shot noise term we define tsMSQ by
| (16) |
which leads to an analytical expression for tsMSQ of a diffusing species,
| (17) |
The above equation applies to a single species, but a straightforward generalization of tsMSQ to account for a mixture of S species is provided by,
| (18) |
where tsMSQi is the time-shifted MSQ of the i-th species and fi is its intensity fraction.
4.4. Derivation of tsQ1
This section derives an analytical expression for tsQ1 given by Eq. (8) based on concepts introduced in earlier work [21,26]. To model the mean <ki> and time-shifted covariance <δkiδki+1> of photon counts, consider a system of Ntot non-interacting fluorescent molecules diffusing in the sample volume V. The fluorescent intensity for a single molecule depends on the position of the molecule relative to the PSF during the sampling time TS. The integrated intensity Wi of a single molecule with trajectory over the time interval from iTs to (i+1)TS is [21]
| (19) |
The molecule is equally likely to occupy any location in the sample volume, which is expressed by the probability density . This leads to the expectation value <W>(1) = λTSVOV/V, where is the volume of the overlap between the sample and the PSF, or the OV [21]. The superscript (1) denotes that the expectation value refers to a single molecule. Because independent molecules contribute equally to the signal, the mean photon count is
| (20) |
where N = NtotVOV/V is the mean number of molecules within the OV.
The time-shifted covariance <δkiδki+1> for independent fluorescent molecules is related to the correlation <WiWi+1>(1) of the time-integrated intensity of a single molecule by [13],
| (21) |
By defining to simplify notation, the expectation value of the time-shifted correlation <WiWi+1>(1) is given by [13]
| (22) |
with probability density . The propagator Pro is given by
| (23) |
where d is the spatial dimension and D is the diffusion coefficient [21]. For a stationary signal the correlation only depends on the time difference . Since ,
| (24) |
where G2 is the second-order normalized correlation function [21],
| (25) |
With these definitions Eq. (22) is rewritten as
| (26) |
We define the time-shifted binning function tsB2 as
| (27) |
which describes the under-sampling corrected correlation due to time-shifting by TS. This equation is simplified by the variable substitution τ=t2−t1, resulting in
| (28) |
which is suitable for deriving the expression of tsB2(TS) for specific correlation functions G2.
For the three-dimensional Gaussian (3DG) PSF, tsB2(TS) is given by
| (29) |
where , , and tS = TS/τD. For the two-dimensional Gaussian (2DG) PSF, the formula for tsB2(TS) is [13]
| (30) |
Note that tsB2 is related to the regular binning function,
| (31) |
as can be verified by direct substitution of the integral expression defining B2 [21]. Utilizing Eqs. (21), (26), and (27) yields a formula for the time-shifted covariance of the photon counts,
| (32) |
Finally, by combining Eqs (6) and (32) we arrive at the general expression for the time-shifted Q-parameter of Eq. (8).
4.5. Estimator mean of tsMSQ
In general, the covariance of photon counts ki and kj with i < j is expressed by [21]
| (33) |
The double sum is broken into three parts. First, for i = j+1 there are M-2 terms, so we obtain
| (34) |
where we used and <ki> = λNTS [21,26]. Second, for i > j + 1, the substitution variable k = i − j − 1 runs from 1 to M-3, and for each k there are M-k-2 terms. Summation of these terms leads to
| (35) |
Finally, for i < j + 1, k = j + 1 − i runs from 1 to M – 1, and for each k there are M – k terms. The partial sum evaluates to
| (36) |
The double sum is determined by adding the partial sums for each of the three conditions,
| (37) |
where the first term comes from the shot-noise contributions in Eq. (34), while the second term describes the effect of correlations between data points within a segment. The mean of the estimator is determined by inserting Eq. (37) into Eq. (13) and using the relation T =MTS.
4.6. tsMSQ for an exponential correlation process
An exponential correlation with T0 as the characteristic time is needed to account for the additional intensity fluctuation process experienced by proteins residing within the lumen of the NE. This correlation process is caused by undulations in the gap size separating the INM and ONM [10]. The oversampled, time-shifted Q-factor, is given in accordance with Eq. (7) by
| (38) |
where we used A0 instead of Q0 for the amplitude to emphasize the difference in the physical origin of the fluctuation process. Thus, following the same steps as presented in sections 4.3 and 4.4,
| (39) |
is the general form of the time-shifted Q-factor for an exponential correlation process that is valid for all sampling times with tsB2,exp denoting the time-shifted binning function of second order for an exponential correlation, which is derived below.
The undulation process is slow enough to introduce estimator bias into MSQ [10]. Here we derive the corresponding expression for the time-shifted estimator for the exponential correlation process,
| (40) |
The time-shifted covariance <δkiδkj>exp for j > 1 is equal to in the oversampling limit and to in general. The time-shifted binning function for the exponential correlation is according to Eq. (27)
| (41) |
which reduces to the analytical expression
| (42) |
For the special case of j – i = 1 we obtain .
The evaluation of the double sum in Eq. (40) closely follows the steps in section 4.4 and yields a bias term due to the exponential correlation of
| (43) |
where . The binning function for the exponential correlation is given by [10]
| (44) |
These results provide an analytical expression for of Eq. (40), which is converted by Eq. (16) into an expression for tsMSQ of an exponential correlation process,
| (45) |
The FFS signal of diffusing proteins in the lumen of the NE is comprised of two independent sources of correlated fluctuations: the correlations due to diffusion and an exponential correlation process caused by membrane undulations. Since both processes are present, the time-shifted covariance for oversampling is given by sum of the individual contributions, <δkiδki+1>d+exp = Q0 <ki> G2,d (TS) + A0 <ki> G2,exp (TS), where we used the subscript d to identify diffusion. Following the same derivation steps described above we arrive at an analytical expression for tsMSQ,
| (46) |
where the first and second term account for the diffusion and the exponential correlation process, respectively.
4.7. Dead-time and afterpulsing effects on MSQ and tsMSQ
For the sake of simplicity, we treat the case of oversampled data with negligible estimator bias (T → ∞). In this limit, the ideal MSQ and tsMSQ approach the asymptotic Q-value, MSQ = Q0 and tsMSQ = Q0. Here we consider the first-order or leading correction term due to dead-time and afterpulsing. Quantities biased by afterpulsing and dead-time are denoted by an asterisk and a prime, respectively. Further details on dead-time and afterpulsing effects on FFS can be found elsewhere [12,13,28].
Afterpulsing leads to an increased number of observed counts <ki>* = <ki>(1+P), where P is the probability of the detector to generate a spurious count following a real event [12,13,28]. The second-order factorial cumulant, , is changed to in the presence of afterpulsing [28], where the factor 2P<k> is due to the shot noise. Thus, the afterpulsing affected MSQ is given by
| (47) |
where we used P ≪ 1 (P is typically on the order of 0.01). In the case of tsMSQ, the correlation of afterpulsing between the two consecutive counts is negligible because the characteristic time of afterpulsing is a few microseconds which is much smaller than the sampling time TS used in FFS [13]. Thus, we treat the consecutive counts ki and ki+1 as independent events with the same P, which leads to <δkiδki+1>* = <δkiδki+1>(1+P)2 [13,28], and an afterpulsing affected tsMSQ of
| (48) |
Dead-time causes the detector to miss photon counts for the dead-time period τ† after a detection event [12,13,28]. The dead-time affected MSQ amplitude relevant for FFS experiments in cells is given by [12,13]
| (49) |
with the parameter δ = τ†/TS.
We now consider the effect of dead-time on tsMSQ. Two consecutive photon count measurements can be treated as independent experiments since the characteristic dead-time is much smaller than the sampling time. Therefore, the time-shifted covariance in the presence of dead-time is [13]
| (50) |
which is approximated by
| (51) |
In addition, for a typical FFS experiment the effect of dead-time on the mean count is negligible, <ki>‘ ≈ <ki> [13]. Thus, the dead-time affected tsMSQ is given by
| (52) |
Finally, to account for the combined effect of dead-time and afterpulsing, the correction terms for each effect are summed [12]. For MSQ and tsMSQ we obtain
| (53) |
and
| (54) |
to first order in δ and P. The difference between Eqs. (53) and (54) is striking as illustrated in Sup. Fig. S2 using typical dead-time and afterpulsing values for our detectors. Note that the predicted influence of the two non-ideal detector effects on tsMSQ is negligible, while its influence on MSQ is significant.
5. Results
5.1. MSQ in the presence of dead-time and afterpulsing
Our original definition of MSQ includes a term due to shot noise [11], which alters the amplitude of the curve (Sup. Fig. S1), but carries no information about the sample. Since this term is identical for all MSQ curves, we introduce here an alternative definition of MSQ given by Eq. (4) that removes the shot noise term and simplifies the direct comparison between MSQ curves from different samples.
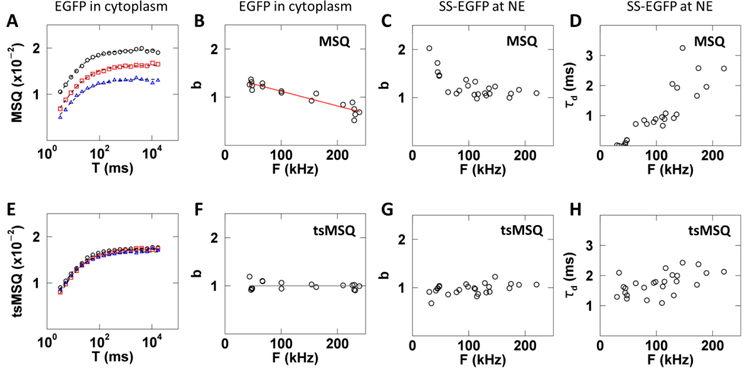
However, even with this improved definition the application of MSQ to cellular FFS data has to be done cautiously as illustrated by a simple control experiment. MSQ curves were calculated from FFS experiments performed in the cytoplasm of U2OS cells expressing varying levels of EGFP (Fig. 5A). Theory ((Eq. 5)) dictates that the MSQ curves only depend on the brightness and diffusion time of EGFP. Thus, the experimental MSQ curves are expected to be independent of the EGFP expression level. However, this prediction is not supported by the data, as they differ in both amplitude and shape (Fig. 5A). The brightness value determined from fits to the MSQ curve taken from ~15 cells shows a strong dependence on the fluorescence intensity (Fig. 5B). The explanation for this discrepancy between experiment and theory is found in non-ideal detector effects, i.e. afterpulsing and dead-time [12,13]. Because the determination of Q is biased by non-ideal detector effects [13], the MSQ curve is affected as well ((Eq. 53)).
Fig. 5. Results of MSQ and tsMSQ analysis of FFS data collected for EGFP and SS-EGFP within the cytoplasm and NE, respectively.
A – D) Results based on MSQ analysis include biases. E – H) Results based on reanalysis by tsMSQ removes bias. A) MSQ curves from EGFP expressing cells with low (black circles), medium (red squares), and high (blue triangles) intensities with fits (dashed lines). B) Biased b from MSQ vs. intensity for EGFP expressing cells (n = 17) with a linear fit (red line) representing first-order non-ideal detector effects (Eq. (53)). C) Biased brightness from MSQ vs. intensity for SS-EGFP expressing cells (n = 13). D) Biased diffusion time from MSQ for SS-EGFP vs. intensity. E) tsMSQ curves from EGFP expressing cells with low (black circles), medium (red squares) and high (blue triangles) intensities with fits (dashed lines). F) b from tsMSQ for EGFP vs. intensity and the average brightness (grey line). G) Brightness from tsMSQ for SS-EGFP vs. intensity. H) Diffusion time from tsMSQ for SS-EGFP vs. intensity.
The presence of an exponential correlation process due to membrane undulations at the NE [10] complicates the situation further as it changes the bias. This effect is demonstrated by FFS data with EGFP targeted to the lumen of the NE by a signal sequence (SS-EGFP), which was analyzed by MSQ fitting without accounting for non-ideal detector effects. Since EGFP is a monomer throughout the concentration range measured, a constant brightness of b = 1 was expected. However, we observed an unexpected increase in brightness at low intensities (Fig. 5C), erroneously implying the presence of EGFP dimers (b = 2) at low intensities. Unlike our observation in the cytoplasm, the biased brightness in the NE is not fully captured by the simple model of (Eq. 53) (Figs. 5B and C). This deviation from the model is most likely due to the presence of an additional fit term to account for the NE membrane undulations. At low intensities the effect of the membrane undulations on the fluorescence signal is minimal and the diffusion and extra fit term combine to result in an increased b and low τD (Figs. 5C and D). As the intensity increases, the diffusion and undulation process grow more distinct, allowing the fitter to resolve both processes which leads to b values in the NE that approach the behavior observed in the cytoplasm (Sup. Fig. S3). We also expected that the diffusion time of SS-EGFP in the lumen would be independent of concentration, yet we observed an apparent increase in the diffusion time with intensity (Fig. 5D), which is caused by subtle shape changes in the MSQ curve as a result of non-ideal detector effects.
5.2. tsMSQ in the presence of dead-time and afterpulsing
The potential for erroneous interpretations, as shown in section 5.1, emphasizes the importance of including non-ideal detector effects in the MSQ analysis of cellular FFS data. While algorithms for modeling the influence of detector afterpulsing and dead-time exist [13], they are cumbersome, require detailed calibration measurements, and become unreliable once the correction amplitude approaches the amplitude of the signal. Furthermore, proper use of these algorithms is nontrivial and represents a significant barrier for quantifying protein-protein association and mobility within the NE by FFS.
In section4.3–4.4, we derived a modified and improved form of MSQ that overcomes these complications by using the time-shifted Q-value () instead of Mandel’s Q factor. It has been previously noted that is far less susceptible to non-ideal detector effects than Q [13], making it a superior choice for application in cells. The value is calculated by splitting the photon count record into segments of length T and then applying (Eq. 9) to each segment (Fig. 4A). Next, the average is calculated and the time-shifted MSQ (tsMSQ) value is calculated from (Eq. 16). This is repeated for a range of segment times T (Fig. 4B).
The same FFS data that revealed biased behavior with MSQ were reevaluated using tsMSQ. Unlike the MSQ curves (Fig. 5A), the tsMSQ curves determined from cells expressing varying levels of EGFP now coincide (Fig. 5E). The brightness recovered by fitting tsMSQ curves taken from cells expressing a range of EGFP levels was independent of fluorescence intensity (Fig. 5F). tsMSQ analysis of FFS data collected for SS-EGFP within the NE included an exponential correlation process ((Eq. 46)). This analysis demonstrated that both brightness and diffusion time are independent of intensity (Figs. 5G and H). No bias was detected in any of the results obtained by tsMSQ, which agrees with the theoretical prediction described in section 4.7 and demonstrates that tsMSQ is an effective tool for removing bias due to non-ideal detector effects.
5.3. Determining goodness-of-fit for tsMSQ
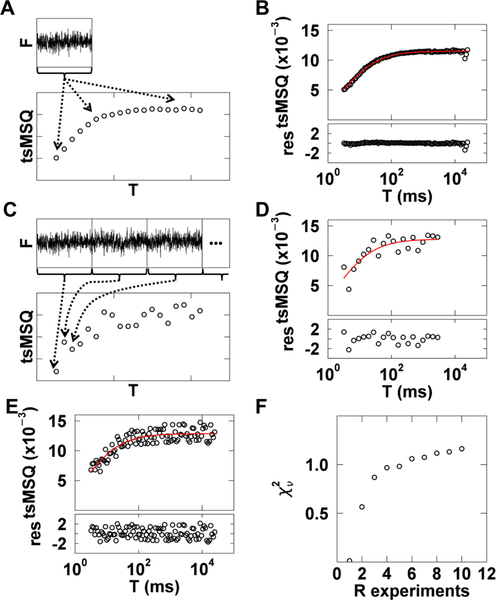
Because the tsMSQ curve is constructed by repeatedly resegmenting the same data set (Fig. 6A), the individual data points of the curve are not statistically independent but self-correlated, which confounds traditional goodness-of-fit tests. This problem is immediately evident when fitting a typical tsMSQ curve for data from cytoplasmic EGFP. The computed residuals are significantly smaller in magnitude than expected (Fig. 6B) and result in an abnormally low of 0.04. These unusual values arise from the self-correlation of the tsMSQ curve, which invalidates the χ2 test. However, goodness-of-fit tests are crucial for cellular applications of tsMSQ in order to accept and reject fit models as well as to identify uncertainties in the fitted parameters.
Fig. 6. χ2curve fitting of tsMSQ data.
A) Illustration of tsMSQ curve construction using the same experimental data set to determine each tsMSQ point along the curve. B) Experimental tsMSQ curve from cytoplasmic EGFP with fit to Eq. (17) (red line) and residuals (bottom panel). C) Illustration of the construction of a decorrelated tsMSQ curve, where a long photon count record is split into separate experiments (top) and each point on the tsMSQ curve is calculated from a unique experiment (bottom). D) Experimental decorrelated tsMSQ curve for cytoplasmic EGFP, constructed as described in the previous panel, with fit (red) and residuals. E) Experimental decorrelated tsMSQ curve for cytoplasmic EGFP, constructed by randomly selecting from 10 experiments for each data point, with fit (red) and residuals. F) The dependence of on the number of experiments used to construct the decorrelated tsMSQ. Four cells expressing cytoplasmic EGFP were used and the average over the four cells was calculated (black circles).
The most straightforward way to avoid self-correlation is to calculate each data point in the tsMSQ curve from an independently measured data set. This is achieved by performing a longer FFS measurement and dividing the data record into distinct data sets, each of which represents an individual experiment (Fig. 6C). The tsMSQ curve can now be constructed with each data point calculated using a unique experimental realization. To do this, we assign each tsMSQ data point to a different experiment, eliminating any self-correlations (Fig. 6C). A tsMSQ curve for cytoplasmic EGFP constructed in this way shows an increase in scatter between neighboring data points, indicating the absence of self-correlation (Fig. 6D). Moreover, a fit of the curve to a model of a single diffusing species ((Eq. 17)) resulted in residuals that were distributed as expected with a value of 0.95 (Fig. 6D).
In practice, we have found that not every data point has to originate from a unique experimental realization. For example, we assigned each point of the tsMSQ curve randomly to one out of ten data sets. Because each tsMSQ curve typically has more than 20 data points, some of the points are calculated from the same experiment. Nevertheless, a fit of the tsMSQ curve determined from R = 10 experiments to the single species model resulted in a of 1.2 with reasonable residuals (Fig. 6E). By changing the random assignment for each tsMSQ data point, we constructed 100 tsMSQ curves from R unique experiments, and the curves were fitted to a single species model. We repeated this process for FFS data taken from four cells expressing EGFP. The values of all fits were averaged to identify the trend of as a function of the number R of experiments (Fig. 6F). We observed that the averaged plateaus for R ≥ 5 with a reduced chi-square value close to one. For R < 5, the averaged drops steeply with a value near zero for R = 1, which confirms the presence of self-correlations in tsMSQ, resulting in a reduction of as observed in Fig. 6B. This result provides important guidelines for the experimental construction of tsMSQ curves suitable for goodness-of-fit testing. Since plateauing is observed for R ≥ 5, the tsMSQ curve should be constructed by randomly selecting data points from five or more experiments to ensure sufficient decorrelation for meaningful error analysis. We have found that 30 to 60 seconds of data is sufficient for a single FFS experiment performed in cells. Thus, the data acquisition time should be at least five times longer, and we suggest a total measurement time between 3 and 5 minutes.
5.4. Applying tsMSQ to the luminal domain of SUN2
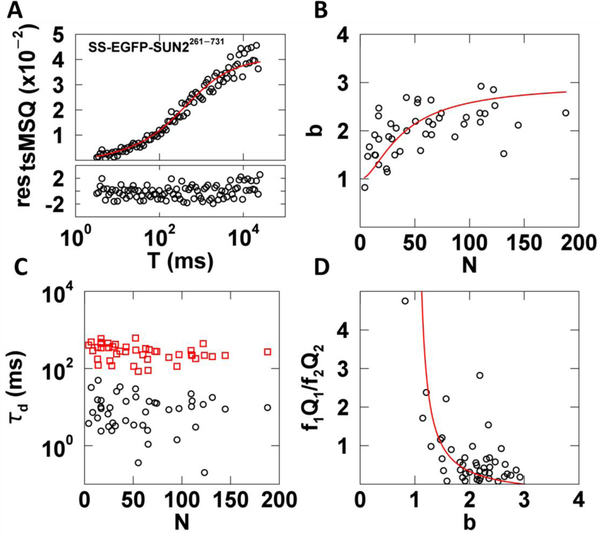
We applied decorrelated tsMSQ to SS-EGFP-SUN2261−731 to provide a point of comparison with our recent FFS studies of the same protein using the original MSQ, which included corrections for dead-time and afterpulsing [10,14]. FFS data were taken in U2OS cells expressing SS-EGFP-SUN2261−731 as previously described [14]. No corrections for non-ideal detector effects were applied to the tsMSQ data in this study. The decorrelated tsMSQ curves were in good agreement with our previously proposed model of two diffusing species ((Eq. 18)), as exemplified by the data presented in Fig. 7A. The uncertainty in tsMSQ was determined from the experimental variance of tsQ1 over all segments. We obtained reasonable residuals and a χ2 value of 1.0 for the fit to a two-species model (Fig. 7A), which supports the chosen fit model. The fitted brightness values of SS-EGFP-SUN2261−731 collected from a large number of measured cells followed the same trend as previously reported [14]. The b increased with increasing N before reaching a saturating value in the vicinity of b = 3 (Fig. 7B). This data was fit to a monomer / trimer transition model as previously described with a dissociation coefficient K = 70 ± 40, in agreement with our previously reported value [14] (Fig. 7B red line).
Fig. 7. tsMSQ analysis of SS-EGFP-SUN2261−731 within the NE.
A) Decorrelated tsMSQ curve with a fit to a two species diffusion model (Eq. (18)) with residuals calculated from experimental uncertainty. B) Plot of b vs. N of SS-EGFP-SUN2261−731 in the NE (n = 23 cells) with a fit to a monomer / trimer binding model (red curve). C) Diffusion times from tsMSQ fits identify a fast (black circles) and a slow (red squares) diffusing species. D) Plot of relative amplitude of the fast species to the slow species vs. b with a model of a transition from fast monomers to slow trimers (red line).
The fit of the tsMSQ curves identified a fast and a slow species with average diffusion times of ~10 and 300 ms, respectively. The diffusion times remain approximately constant as a function of the protein concentration (Fig. 7C), which is consistent with our previous results [10]. We hypothesized that these two distinct species represent a fast population of freely diffusing luminal proteins and a slow population associated with the nuclear membrane. While we cannot directly identify the oligomeric state of these two populations, tsMSQ provides information about their relative contributions to the total Q value using Eqs. (17) and (18). Specifically, the ratio of the relative amplitudes fiQi identified by the tsMSQ is instructive. High values of the ratio f1Q1/f2Q2 indicate that the fast species (subscript 1) has a larger amplitude and low values indicate the slow species (subscript 2) dominates. Plotting this ratio vs. the total brightness shows that the fast species dominates at low brightness values while the slow species dominates at high brightness values. This observation is consistent with a model of fast diffusing monomers and slow diffusing trimers (Fig. 7D) and is consistent with our previous results [10]. Indeed, a monomer / trimer transition model is in good agreement with the FFS data (Fig. 7D). This analysis is completely analogous to the earlier analysis performed with MSQ [10] and confirms that tsMSQ provides the same information content as MSQ. All the results obtained with tsMSQ without corrections for detector artifacts are in agreement with our previous study.
5.5. Application of tsMSQ to the luminal domain of SUN3
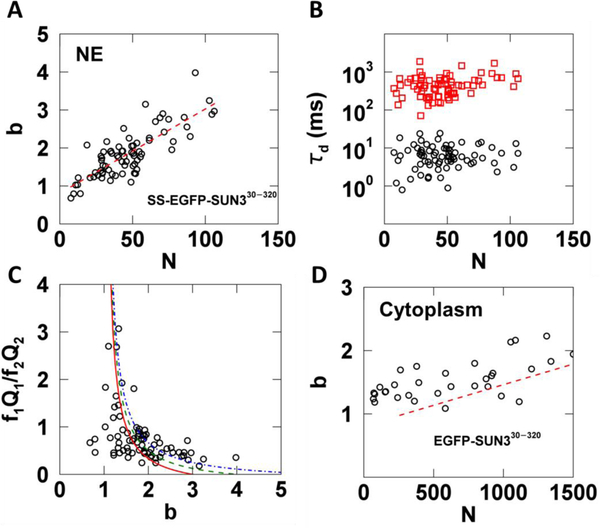
In addition to SUN1 and SUN2, mammals express three testes-specific SUN proteins: SUN3, SUN4, and SUN5 [29]. Based on sequence homology to SUN1 and SUN2, these SUN proteins are also thought to be able to form homo-trimers within the NE [30]. To test this hypothesis experimentally in living cells, we applied the same measurement and analysis protocol used for SS-EGFP-SUN2261−731 to the SS-EGFP-tagged luminal domain of SUN3 (SS-EGFP-SUN330−320) expressed within the NE. We decided to focus on the SUN3 luminal domain, since full-length NE proteins are frequently too immobile for the type of FFS experiments described here [31]. This same strategy was previously used to characterize the oligomeric states of SUN1 and SUN2 in the NE [14]. We found that the brightness of SS-EGFP-SUN330−320 increased with increasing N to a brightness of at least 3 without a decrease in slope (Fig. 8A). A binding curve with a limiting stoichiometry of 3 would exhibit a clear decrease in slope for b > 2. Thus, the lack of an observed decrease in slope in Fig. 8A indicates that like SUN1, the oligomerization of SUN3 may not be limited to a trimer [14].
Fig. 8. tsMSQ analysis of EGFP tagged SUN330−320 within the NE and cytoplasm.
A-C) Results from fitting tsMSQ data from SS-EGFP-SUN330−320 within the NE to a two species diffusion model. A) Plot of b vs. N for SS-EGFP-SUN330−320 measured within the NE (n = 41 cells) together with a linear fit to data (red dashed line). B) Diffusion times from two species fits of MSQ curves showing both a fast (black circles) and slow (red squares) component. C) Relative amplitude of the fast component to the slow component vs. brightness. The lines represent a monomer / trimer (solid red), monomer / tetramer (dashed green), and monomer / hexamer (dashed-dotted blue) transition. D) Plot of b vs. N for EGFP-SUN330−320 within the cytoplasm (n = 32 cells) with best fit line from NE (red dashed line) after converting N from the NE to its equivalent cytoplasmic value.
The tsMSQ curves for SS-EGFP-SUN330−320 revealed the presence of a fast and a slow species with average diffusion times of ~7 and 500 ms, respectively (Fig. 8B). These values are similar to the diffusion times observed for SS-EGFP-SUN2261−731 (Fig. 7C). The ratio f1Q1/f2Q2 of the relative amplitudes of the fast and slow species behaved similar to what was observed for SS-EGFP-SUN2261–731. Specifically, the fast species dominates at low b values, while the slow species dominates at high b values (Fig. 8C). However, unlike SS-EGFP-SUN2261−731, the data cannot be modeled as a simple transition from a fast diffusing monomer to a slow diffusing trimer (Fig. 8C, solid red line). While models of a fast diffusing monomer assembling into a slow diffusing tetramer or hexamer (Fig. 8C, dashed green or dashed-dotted blue lines respectively) were unable to describe all of the data, these models approached the experimental data at high brightness values, in agreement with our earlier inference that SS-EGFP-SUN330−320 oligomeric states in excess of a trimer exist.
Finally, we performed brightness measurements on the same construct without a signal sequence (EGFP-SUN330−320). This construct is found in the cytoplasm and was measured by FFS as previously described [17]. We observed an increase of b with N, which indicates the presence of oligomerization in the cytoplasm (Fig. 8D). Because the OV in the cytoplasm and at the NE are different, a direct comparison of N is not meaningful. However, by assuming a NE thickness of 40 nm, the OV in the NE can be estimated and compared to that of the cytoplasm. We have used this approach in the past to convert the occupation number from the NE to the cytoplasm for direct comparison of brightness binding curves [14]. Using this method we plotted the best fit line from the NE data (Fig. 8A) after conversion together with the brightness data obtained in the cytoplasm (Fig. 8D). While the brightness in the cytoplasm appears to be slightly higher than in the NE at equivalent protein concentrations (Fig. 8D, red dashed line), converting N in the NE to its cytoplasmic equivalent is only an approximation based on the assumption of a mean thickness of 40 nm for the NE. Increasing this value by only 10 nm would shift the red dashed line resulting in significant overlap with the cytoplasmic data. Because the thickness of the NE is not precisely known, we have to conclude that given current experimental uncertainties no significant difference between the cytoplasmic and NE brightness at equivalent concentrations was found. This conclusion implies that the binding affinity of the SUN3 luminal domain is approximately the same in the NE and the cytoplasmic environment of U2OS cells. In contrast, the binding affinity of the luminal domains of SUN1 and SUN2 was significantly higher in the cytoplasm than in the NE [14]. We previously ruled out competition from endogenous SUN1 and SUN2 with their respective EGFP-tagged counterparts as the cause for this change between the behavior in the NE and cytoplasm. Thus, the results of our earlier study suggest the existence of potential regulators in the NE that affect SUN1 and SUN2 oligomerization. Unlike the luminal domains of SUN1 and SUN2, we found that the binding affinities of the SUN3 luminal domain for itself in the cytoplasmic and NE environments were approximately similar. We can rule out the effect of competition from endogenous SUN3 in our experiments, as the expression of SUN3 is limited to the testes in mice [15]. While SUN3 can associate with another SUN protein, SUN4 [32], it too is expressed solely within the mammalian male germline [33,34]. It is currently unknown whether or not SUN3 is capable of interacting with SUN1 or SUN2; however, our results described above do not support the existence of these interactions within the NE of U2OS cells. Therefore, we propose that either the potential regulators of SUN3 oligomerization are only expressed within the NE of male germline cells or that the homo-oligomerization of SUN3 is not subject to regulation.
6. Discussion
While the theory underlying tsMSQ presented in this paper is complex, the application of tsMSQ is relatively straightforward and can be broken down into a few easy steps. FFS data is collected for ~5 minutes in the NE as described in detail in Hennen et al. [18]. This photon count record is divided into five data sets, each representing an independent measurement. For a given segment time T of the tsMSQ curve, one of these five data sets is chosen at random, segmented into intervals of time T, and (Eq. 9) is used to calculate on each segment. The average of over all segments is changed into the tsMSQ value by applying (Eq. 16) as shown in Fig. 4. This procedure is repeated for a range of segment times to construct the decorrelated tsMSQ curve as required for χ2 curve fitting. Fitting of decorrelated tsMSQ curves to model functions that describe diffusing molecules in the absence (Eqs. (17), (18)) as well as in the presence of an exponential correlation process ((Eq. 46)) should be evaluated using well-established goodness-of-fit criteria to accept or reject each model. We have successfully applied these models to soluble luminal proteins ((Eq. 46)), simple membrane bound proteins ((Eq. 17)), and proteins which transition from luminal to membrane-associated proteins ((Eq. 18)) [10]. Evaluation of fit models should be performed on a representative sample of cells covering the range of expression levels to be measured in order to ensure that a model accurately describes the behavior of a given protein. Upon determining the proper model, fits are used to obtain values for the asymptotic Q-factor, Q0, and diffusion time, τD. Using b = Q0/(γ2λEGFP) and N = <F>/λEGFP, plots of b vs. N can be constructed and analyzed to determine the extent of oligomerization, if any, as in Figs. 7B and8A. Further information may be obtained from the tsMSQ fit results, as described here and in Hennen et al [10].
The membrane undulations at the NE pose a special challenge for conventional FFS analysis methods. To illustrate the problem let us divide commonly used point FFS techniques into two groups. The first group, which includes PCH and moment analysis, exploits the amplitude of fluctuations, but ignores their temporal correlation [25]. Because temporal information is discarded, it is impossible to differentiate fluorescence fluctuations caused by the NE membrane undulations from those caused by molecular diffusion, which precludes identification of molecular brightness. The second group, which includes FCS and TIFCA, utilizes temporal correlations [25]. However, these analysis methods use algorithms that segment the data using a predetermined length, which significantly improves the robustness of FFS analysis of cellular data [16]. We found that the finite and fixed segment length leads to biased results in the presence of slow processes such as the NE membrane undulations [10]. This was a key observation that prompted us to use MSQ instead of FCS for the analysis of fluorescence fluctuation data from NE proteins. MSQ and tsMSQ overcome these challenges by providing dynamic information while accounting for and visualizing the effect of data segment length on the analysis.
The application of MSQ to the NE of living cells has proven to be a powerful tool, revealing insights into the dynamics and oligomerization of proteins within the NE as well as the NE itself [10,14]. tsMSQ produces the same results as the original MSQ method and is considerably easier to apply, as it avoids the background work of characterizing detectors. Incorrect application of non-ideal detector corrections is a potential source of error in interpreting FFS results, which is avoided by using tsMSQ. Because of these advantages, we recommend the use of tsMSQ over MSQ. Furthermore, the procedure for producing decorrelated tsMSQ curves provides a strong foundation for future investigations of NE proteins by FFS. These developments serve to strengthen the results and simplify the analysis of FFS data obtained within the NE of living cells.
While it is possible to apply tsMSQ in other cellular compartments, the NE of mammalian cells is the only environment where we have found it to be particularly advantageous over more established techniques [10]. The standard analysis techniques have proven to be successful when applied to measurements performed in the nucleoplasm, cytoplasm, and at the plasma membrane [16,17,35]. It is in the presence of a slow fluctuation process not caused by the motion of single molecules, as is the case for the NE membrane undulations, where tsMSQ becomes necessary.
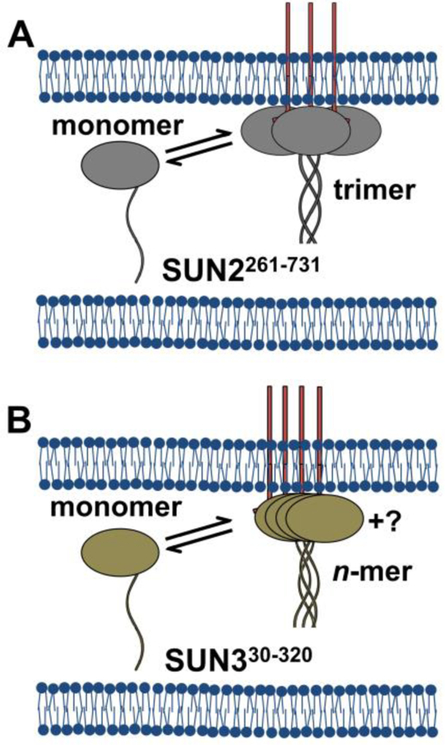
Our observation that both SS-EGFP-SUN2261−731 and SS-EGFP-SUN330−320 exist as two distinct diffusing species suggests the presence of a luminal and a membrane-associated population. The data obtained for SS-EGFP-SUN2261−731 can be modeled as a simple transition of free monomers to membrane-associated trimers (Fig. 9A). While the data from SS-EGFP-SUN330−320 do not follow a monomer / n-mer transition model, it is clear that there is a transition from low to high oligomeric states as the membrane-associated population increases. These results may indicate the transition of the SUN3 luminal domain from soluble monomers to membrane-associated oligomers with different assembly states, with a strong indication of the presence of oligomers larger than a trimer (Fig. 9B).
Fig. 9. Working models for the observed behavior of the luminal domains of SUN2 and SUN3.
A) SS-EGFP-SUN2261−731 (grey) exists as either freely diffusing, luminal monomers or membrane-associated trimers, potentially due to interactions with endogenous nesprins (red lines) at the ONM. B) SS-EGFP-SUN330−320 (tan) exists as either freely diffusing, luminal monomers or membrane-associated oligomers. The size of these membrane associated oligomers has yet to be determined.
While the developments described in this paper represent a significant improvement to the application of FFS within the NE, there is substantial need for further advances. For example, the current use of truncated luminal domains of nuclear membrane proteins is not optimal, as they might not accurately represent the oligomerization behavior and dynamics of the FL proteins. Future developments in combining tsMSQ with an imaging-based approach [36–38] would potentially allow for measurement of relatively immobile proteins, including FL SUN proteins. In addition, SUN proteins only represent one part of the proposed LINC complexes with nesprins being a necessary binding partner. Although we performed FFS on the soluble KASH peptide of nesprin-2 within the perinuclear space [10], it is the interaction of the KASH peptides of nesprins with the SUN domains of SUN proteins which is required for forming functional LINC complexes [39,40]. Investigating the SUN-KASH interaction and its regulation within the NE of living cells requires the use of two differently colored FPs to label each protein species in order to identify their association by dual-color FFS [41]. In addition, quantifying the interaction between different SUN proteins via dual-color FFS is of considerable interest, as it will enable testing of previously proposed models of SUN protein hetero-oligomerization [42,43]. Thus, the development of dual-color tsMSQ will be essential for addressing these questions in future studies.
Supplementary Material
Acknowledgement
We thank Ang Li and Patrick Willey for excellent technical assistance. This work was supported by the National Institutes of Health (R01 GM064589).
Footnotes
Declarations of interest: none
References
- [1].Watson ML, THE NUCLEAR ENVELOPE J Biophys Biochem Cytol. 1 (1955) 257–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Güttinger S, Laurell E, Kutay U, Orchestrating nuclear envelope disassembly and reassembly during mitosis, Nat. Rev. Mol. Cell Biol. 10 (2009) 178–191. doi: 10.1038/nrm2641. [DOI] [PubMed] [Google Scholar]
- [3].Crisp M, Liu Q, Roux K, Rattner JB, Shanahan C, Burke B, Stahl PD, Hodzic D, Coupling of the nucleus and cytoplasm: role of the LINC complex, J. Cell Biol. 172 (2006) 41–53. doi: 10.1083/jcb.200509124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Liu J, Rolef Ben-Shahar T, Riemer D, Treinin M, Spann P, Weber K, Fire A, Gruenbaum Y, Essential roles for Caenorhabditis elegans lamin gene in nuclear organization, cell cycle progression, and spatial organization of nuclear pore complexes, Mol. Biol. Cell 11 (2000) 3937–3947. doi: 10.1091/mbc.11.11.3937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Lei K, Zhu X, Xu R, Shao C, Xu T, Zhuang Y, Han M, Inner nuclear envelope proteins SUN1 and SUN2 play a prominent role in the DNA damage response, Curr. Biol 22 (2012) 1609–1615. doi: 10.1016/j.cub.2012.06.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Schmit F, Korenjak M, Mannefeld M, Schmitt K, Franke C, von Eyss B, Gagrica S, Hänel F, Brehm A, Gaubatz S, LINC, a human complex that is related to pRB-containing complexes in invertebrates regulates the expression of G2/M genes, Cell Cycle. 6 (2007) 1903–1913. doi: 10.4161/cc.6.15.4512. [DOI] [PubMed] [Google Scholar]
- [7].Mekhail K, Moazed D, The nuclear envelope in genome organization, expression and stability, Nat. Rev. Mol. Cell Biol. 11 (2010) 317–328. doi: 10.1038/nrm2894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Barbosa AD, Sembongi H, Su W-M, Abreu S, Reggiori F, Carman GM, Siniossoglou S, Parton RG, Lipid partitioning at the nuclear envelope controls membrane biogenesis, MBoC. 26 (2015) 3641–3657. doi: 10.1091/mbc.e15-03-0173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Worman HJ, Östlund C, Wang Y, Diseases of the Nuclear Envelope, Cold Spring Harb Perspect Biol. 2 (2010). doi: 10.1101/cshperspect.a000760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Hennen J, Hur K-H, Saunders CA, Luxton GWG, Mueller JD, Quantitative Brightness Analysis of Protein Oligomerization in the Nuclear Envelope, Biophys. J 113 (2017) 138–147. doi: 10.1016/j.bpj.2017.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Hur K-H, Mueller JD, Quantitative Brightness Analysis of Fluorescence Intensity Fluctuations in E. Coli, PLoS One. 10 (2015). doi: 10.1371/journal.pone.0130063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Hillesheim LN, Müller JD, The photon counting histogram in fluorescence fluctuation spectroscopy with non-ideal photodetectors, Biophys. J 85 (2003) 1948–1958. doi: 10.1016/S0006-3495(03)74622-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Sanchez-Andres A, Chen Y, Müller JD, Molecular brightness determined from a generalized form of Mandel’s Q-parameter, Biophys. J 89 (2005) 3531–3547. doi: 10.1529/biophysj.105.067082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Hennen J, Saunders CA, Mueller JD, Luxton GWG, Fluorescence Fluctuation Spectroscopy Reveals Differential SUN Protein Oligomerization In Living Cells, Mol. Biol. Cell (2018). doi: 10.1091/mbc.E17-04-0233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Kracklauer MP, Link J, Alsheimer M, LINCing the nuclear envelope to gametogenesis, Curr. Top. Dev. Biol 102 (2013) 127–157. doi: 10.1016/B978-0-12-416024-8.00005-2. [DOI] [PubMed] [Google Scholar]
- [16].Chen Y, Wei L-N, Müller JD, Probing protein oligomerization in living cells with fluorescence fluctuation spectroscopy, Proc Natl Acad Sci U S A. 100 (2003) 15492–15497. doi: 10.1073/pnas.2533045100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Macdonald PJ, Chen Y, Wang X, Chen Y, Mueller JD, Brightness Analysis by Z-Scan Fluorescence Fluctuation Spectroscopy for the Study of Protein Interactions within Living Cells, Biophys J. 99 (2010) 979–988. doi: 10.1016/j.bpj.2010.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Hennen J, Angert I, Hur K-H, Gant Luxton GW, Mueller JD, Investigating LINC Complex Protein Homo-oligomerization in the Nuclear Envelopes of Living Cells Using Fluorescence Fluctuation Spectroscopy, in: Gundersen GG, Worman HJ (Eds.), The LINC Complex: Methods and Protocols, Springer; New York, New York, NY, 2018: pp. 121–135. doi: 10.1007/978-1-4939-8691-0_11. [DOI] [PubMed] [Google Scholar]
- [19].Chen Y, Müller JD, Determining the stoichiometry of protein heterocomplexes in living cells with fluorescence fluctuation spectroscopy, Proc Natl Acad Sci U S A. 104 (2007) 3147–3152. doi: 10.1073/pnas.0606557104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Mandel L, Sub-Poissonian photon statistics in resonance fluorescence, Opt Lett. 4 (1979) 205–207. [DOI] [PubMed] [Google Scholar]
- [21].Wu B, Müller JD, Time-Integrated Fluorescence Cumulant Analysis in Fluorescence Fluctuation Spectroscopy, Biophys J. 89 (2005) 2721–2735. doi: 10.1529/biophysj.105.063685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Berland KM, So PT, Gratton E, Two-photon fluorescence correlation spectroscopy: method and application to the intracellular environment, Biophys. J 68 (1995) 694–701. doi: 10.1016/S0006-3495(95)80230-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Müller JD, Chen Y, Gratton E, Fluorescence correlation spectroscopy, Meth. Enzymol 361 (2003) 69–92. [DOI] [PubMed] [Google Scholar]
- [24].Lippincott-Schwartz J, Snapp E, Kenworthy A, Studying protein dynamics in living cells, Nature Reviews Molecular Cell Biology. 2 (2001) 444–456. doi: 10.1038/35073068. [DOI] [PubMed] [Google Scholar]
- [25].Bag N, Wohland T, Imaging fluorescence fluctuation spectroscopy: new tools for quantitative bioimaging, Annu Rev Phys Chem. 65 (2014) 225–248. doi: 10.1146/annurev-physchem-040513-103641. [DOI] [PubMed] [Google Scholar]
- [26].Müller JD, Cumulant Analysis in Fluorescence Fluctuation Spectroscopy, Biophys J. 86 (2004) 3981–3992. doi: 10.1529/biophysj.103.037887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Chen Y, Tekmen M, Hillesheim L, Skinner J, Wu B, Müller JD, Dual-Color Photon-Counting Histogram, Biophys J. 88 (2005) 2177–2192. doi: 10.1529/biophysj.104.048413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Wu B, Chen Y, Müller JD, Dual-Color Time-Integrated Fluorescence Cumulant Analysis, Biophys J. 91 (2006) 2687–2698. doi: 10.1529/biophysj.106.086181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Göb E, Schmitt J, Benavente R, Alsheimer M, Mammalian Sperm Head Formation Involves Different Polarization of Two Novel LINC Complexes, PLoS One. 5 (2010). doi: 10.1371/journal.pone.0012072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Sosa BA, Kutay U, Schwartz TU, Structural insights into LINC complexes, Curr. Opin. Struct. Biol 23 (2013) 285–291. doi: 10.1016/j.sbi.2013.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Hur K-H, Macdonald PJ, Berk S, Angert CI, Chen Y, Mueller JD, Quantitative measurement of brightness from living cells in the presence of photodepletion, PLoS ONE. 9 (2014) e97440. doi: 10.1371/journal.pone.0097440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Calvi A, Wong ASW, Wright G, Wong ESM, Loo TH, Stewart CL, Burke B, SUN4 is essential for nuclear remodeling during mammalian spermiogenesis, Dev. Biol 407 (2015) 321–330. doi: 10.1016/j.ydbio.2015.09.010. [DOI] [PubMed] [Google Scholar]
- [33].Shao X, Tarnasky HA, Lee JP, Oko R, van der Hoorn FA, Spag4, a novel sperm protein, binds outer dense-fiber protein Odf1 and localizes to microtubules of manchette and axoneme, Dev. Biol 211 (1999) 109–123. doi: 10.1006/dbio.1999.9297. [DOI] [PubMed] [Google Scholar]
- [34].Tarnasky H, Gill D, Murthy S, Shao X, Demetrick DJ, van der Hoorn FA, A novel testis-specific gene, SPAG4, whose product interacts specifically with outer dense fiber protein ODF27, maps to human chromosome 20q11.2, Cytogenet. Cell Genet. 81 (1998) 65–67. doi: 10.1159/000014990. [DOI] [PubMed] [Google Scholar]
- [35].Smith EM, Macdonald PJ, Chen Y, Mueller JD, Quantifying Protein-Protein Interactions of Peripheral Membrane Proteins by Fluorescence Brightness Analysis, Biophys J. 107 (2014) 66–75. doi: 10.1016/j.bpj.2014.04.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Digman MA, Dalal R, Horwitz AF, Gratton E, Mapping the Number of Molecules and Brightness in the Laser Scanning Microscope, Biophys J. 94 (2008) 2320–2332. doi: 10.1529/biophysj.107.114645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Wiseman PW, Squier JA, Ellisman MH, Wilson KR, Two-photon image correlation spectroscopy and image cross-correlation spectroscopy, J Microsc. 200 (2000) 14–25. [DOI] [PubMed] [Google Scholar]
- [38].Sankaran J, Manna M, Guo L, Kraut R, Wohland T, Diffusion, Transport, and Cell Membrane Organization Investigated by Imaging Fluorescence Cross-Correlation Spectroscopy, Biophysical Journal. 97 (2009) 2630–2639. doi: 10.1016/j.bpj.2009.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Meinke P, Schirmer EC, LINC’ing form and function at the nuclear envelope, FEBS Lett. 589 (2015) 2514–2521. doi: 10.1016/j.febslet.2015.06.011. [DOI] [PubMed] [Google Scholar]
- [40].Kim DI, Birendra KC, Roux KJ, Making the LINC: SUN and KASH protein interactions, Biol. Chem 396 (2015) 295–310. doi: 10.1515/hsz-2014-0267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Slaughter BD, Li R, Toward Quantitative “In Vivo Biochemistry” with Fluorescence Fluctuation Spectroscopy, Mol Biol Cell. 21 (2010) 4306–4311. doi: 10.1091/mbc.E10-05-0451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Wang Q, Du X, Cai Z, Greene MI, Characterization of the structures involved in localization of the SUN proteins to the nuclear envelope and the centrosome, DNA Cell Biol. 25 (2006) 554–562. doi: 10.1089/dna.2006.25.554. [DOI] [PubMed] [Google Scholar]
- [43].Lu W, Gotzmann J, Sironi L, Jaeger V-M, Schneider M, Lüke Y, Uhlén M, Szigyarto CA-K, Brachner A, Ellenberg J, Foisner R, Noegel AA, Karakesisoglou I, Sun1 forms immobile macromolecular assemblies at the nuclear envelope, Biochim. Biophys. Acta 1783 (2008) 2415–2426. doi: 10.1016/j.bbamcr.2008.09.001. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.