Efficacy of different dynamic functional connectivity methods to capture cognitively relevant information

Abstract

Given the dynamic nature of the human brain, there has been an increasing interest in investigating short-term temporal changes in functional connectivity, also known as dynamic functional connectivity (dFC), i.e., the time-varying inter-regional statistical dependence of blood oxygenation level-dependent (BOLD) signal within the constraints of a single scan. Numerous methodologies have been proposed to characterize dFC during rest and task, but few studies have compared them in terms of their efficacy to capture behavioral and clinically relevant dynamics. This is mostly due to lack of a well-defined ground truth, especially for rest scans. In this study, with a multitask dataset (rest, memory, video, and math) serving as ground truth, we investigated the efficacy of several dFC estimation techniques at capturing cognitively relevant dFC modulation induced by external tasks. We evaluated two framewise methods (dFC estimates for a single time point): dynamic conditional correlation (DCC) and jackknife correlation (JC); and five window-based methods: sliding window correlation (SWC), sliding window correlation with L1-regularization (SWC_L1), a combination of DCC and SWC called moving average DCC (DCC_MA), multiplication of temporal derivatives (MTD), and a variant of jackknife correlation called delete-d jackknife correlation (dJC). The efficacy is defined as each dFC metric’s ability to successfully subdivide multitask scans into cognitively homogenous segments (even if those segments are not temporally continuous). We found that all window-based dFC methods performed well for commonly used window lengths (WL ≥ 30sec), with sliding window methods (SWC, SWC_L1) as well as the hybrid DCC_MA approach performing slightly better. For shorter window lengths (WL ≤ 15sec), DCC_MA and dJC produced the best results. Neither framewise method (i.e., DCC and JC) led to dFC estimates with high accuracy.

1. Introduction

Functional connectivity (FC), defined as the inter-regional relationship between fMRI traces from spatially segregated brain regions, provides valuable information about the brain’s functional architecture during both rest and task (Cole et al., 2014; Gonzalez-Castillo and Bandettini, 2018). Traditionally, FC studies have focused on average FC patterns computed using entire scans (5–10 min or longer), yet it is also common to explore how FC patterns evolve within the constraints of individual scans (Chang and Glover, 2010; Sakoğlu et al., 2010). Many techniques have been proposed to characterize the dynamic aspects of FC (dFC), including: sliding window correlation (SWC; Allen et al., 2014; Sakoğlu et al., 2010), dynamic conditional correlation (DCC; Lindquist et al., 2014), wavelet coherence analysis (Chang and Glover, 2010; Yaesoubi et al., 2015), state-space models (Eavani et al., 2013; Taghia et al., 2017; Yaesoubi et al., 2018), and dynamic phase synchronization analysis (Glerean et al., 2012; Ponce-Alvarez et al., 2015). The different mathematical frameworks and assumptions underlying these methods, make comparing and interpreting the results from different dFC studies difficult. Despite some recent efforts to bring dFC methods to a common theoretical framework (Thompson and Fransson, 2018), it remains to be elucidated which dFC techniques, if any, provide an accurate estimation of neurally-linked dFC changes with clinical and behavioral value. Previous comparisons based on resting scans have reached somehow divergent conclusions. For example, Choe et al. (2017) recently determined that DCC produces more reliable dFC estimations than SWC, yet Damaraju et al. (2018) concluded DCC provides less predictive accuracy to track wakefulness states. We believe such discrepant conclusions may arise partly due to lack of clear gold standards for measuring “success” when using resting scans (e.g., test-retest reliability or wakefulness), as there is currently a lack of clear behavioral correlates to use as anchors for comparison. For example, a recent paper evaluating various motion correction techniques found an inefficient motion correction strategy may yield high test-retest reliability given the trait-like motion patterns being reproducible across sessions (Parkes et al., 2018). Moreover, resting data can succumb to substantial contributions from artifactual sources (Allen et al., 2014; Haimovici et al., 2017; Handwerker et al., 2012; Laumann et al., 2016; Power et al., 2012), making interpretations of cognitive/emotional/attentional correlates of dFC metrics derived from resting data more challenging. To address some of these challenges, we use multitask scans as the framework for evaluation of dFC metrics because they permit clear quantitative evaluations of how well each method captures behaviorally relevant dFC patterns. We hypothesize that if a dFC method cannot effectively distinguish robust task-induced changes, its chances of detecting what are potentially more subtle fluctuations occurring during rest are very low. As such, we believe our results here provide a first filter for the evaluation of a method’s potential to capture cognitively meaningful dFC during rest.

Here we rely on a previously acquired multitask dataset (Gonzalez-Castillo et al., 2015) for our evaluations. Each scan in the dataset was acquired as subjects engaged and transitioned between 4 different mental states dictated by tasks—namely rest, mathematical computations, working memory (2-back), and visual attention. Subjects were asked to perform each task for two non-consecutive three-minute segments, resulting in approximately 25-min long scans. Using this data, we evaluated the efficacy of seven time-domain dFC methods to achieve successful temporal segmentation of the scans into cognitively homogenous segments using an approach previously described by Gonzalez-Castillo et al. (2015). The methods under evaluation are: 1) those being widely used (e.g., SWC and its L1-regularization variant), 2) those based on statistical models (DCC), and 3) recently proposed methods showing improvement compared to SWC, such as jackknife correlation (JC; Thompson et al., 2017) and multiplication of temporal derivatives (MTD; Shine et al., 2015).

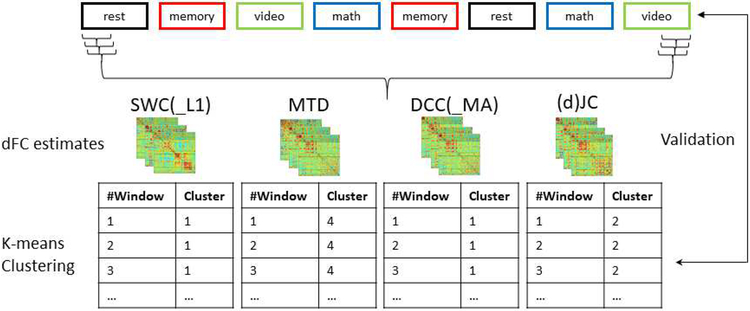
Following preprocessing, whole-brain dFC patterns were computed using different methods (Figure 1). Subsequently, those estimates were input to k-means clustering (k = 4) to group all dFC patterns from a given method into 4 groups. Success is then measured in terms of how well k-means clusters agree with the ground truth imposed by the experimental design, and the level of similarity between within-task and across-task dFC estimates (see methods for additional details). In other words, under the assumption that task modulation is the dominant contributing factor to dFC differentiation in the dataset on the subject level, a good dFC method should yield whole-brain dFC patterns that are more consistent within a given condition (e.g., task) versus across mental states, allowing for tracking ongoing cognition more effectively.

Figure 1.

Schematic of multitask experimental design and evaluation pipeline. The multitask paradigm consisted of four conditions, i.e., resting-state, working memory, visual search and math calculation. We evaluated two framewise dFC methods that can resolve dFC of a single time point, including dynamic conditional correlation (DCC; Lindquist et al., 2014) and jackknife correlation (JC; Richter et al., 2015) as well as five window-based approaches, i.e., sliding window correlation (SWC; Sakoğlu et al., 2010), sliding window correlation with L1 regularization (SWC_L1; Allen et al., 2014), multiplication of temporal derivatives (MTD; Shine et al., 2015), moving average DCC (DCC_MA), and delete-d jackknife correlation (dJC).

2. Materials and methods

2.1. Data acquisition & experimental design

The multitask dataset used in this study consisted of eighteen publicly available subjects (https://central.xnat.org, project ID: FCStateClassif) from the original study by Gonzalez-Castillo et al. (2015). After giving informed consent in compliance with a protocol approved by the Institutional Review Board of the National Institute of Mental Health in Bethesda, MD, subjects were scanned for approximately 25 minutes as they engaged and transitioned between four different conditions (math, memory, video and rest). The imaging data were acquired on a Siemens 7T MRI scanner with a 32-element receive coil (Nova Medical) using a gradient recalled, single shot, echo planar imaging (gre-EPI) sequence. The scanning parameters are the following: repetition time TR = 1.5sec; echo time TE = 25msec; flip angle FA = 50°; field of view FOV = 192 mm; in-plane resolution = 2 × 2 mm; slice thickness = 2 mm; and forty interleaved slices.

Each of the four task blocks (180sec) was repeated twice resulting in a total of eight task blocks, and instructions between two task blocks lasted for 12sec. During the resting-state scan, subjects were asked to passively fixate the crosshair in the center of the screen. During the memory task, subjects were shown a continuous sequence of five different geometric shapes which appeared in the center of the screen every 3sec (shapes appeared on the screen for 2.6sec, followed by a blank screen for 0.4sec). Subjects were asked to press the button when the current shape matched that of two shapes before. There was a total number of 60 memory trials per task block. For the video (visual search) task, a short video clip of fish swimming in a fish tank was presented, and subjects were asked to identify whether the fish highlighted by a red crosshair is a clown fish by pressing the left button (or right button if the target fish is not a clown fish). Each cue (i.e., the red crosshair) lasted for 200msec and there was a total number of 16 trials per task block. During the math task, the subjects were instructed to choose one correct answer among two choices for a math operation involving subtraction and addition of three numbers between 1 and 10. The operation remained on the screen for 4sec followed by a blank screen for 1sec. There were a total number of 36 math trials per task block.

2.2. Data preprocessing

AFNI was used for data preprocessing, and the following preprocessing steps were performed for each subject: a) despiking (3dDespike); b) slice time correction (3dTshift); c) head motion correction (3dvolreg); d) detrending (3dDetrend up to a 7^th order polynomial); e) nuisance signal regression including physiological noise regressors, mean signal from white matter and ventricles, and 12 motion parameters; f) conversion to percent signal change and bandpass filtering (0.006 – 0.18 Hz); g) spatial smoothing with FWHM = 4mm (3dBlurInMask); and h) spatial normalization to Montreal Neurological Institute (MNI) space using align_epi_anat.py.

The Craddock atlas (Craddock et al., 2012) was used for brain parcellation, using 200 ROIs, which is the minimum number of ROIs needed to separate underlying cognitive states using whole-brain dFC patterns (Gonzalez-Castillo et al., 2015). Forty-three ROIs with less than 10 voxels within the field of view for all subjects were removed. These removed ROIs were located primarily in cerebellar, inferior temporal, and orbitofrontal regions. Additionally, principal component analysis (PCA) was performed to reduce the dimensionality of the connectivity matrices and ease computational constraints. Principal components (PCs) accounting for 97.5% variance were kept. On average, this reduced the dimensionality of dFC patterns from 157×157 connections between ROIs to 72×72 connections between components, which were then used as the input for dFC estimation.

2.3. Whole-brain dFC estimation

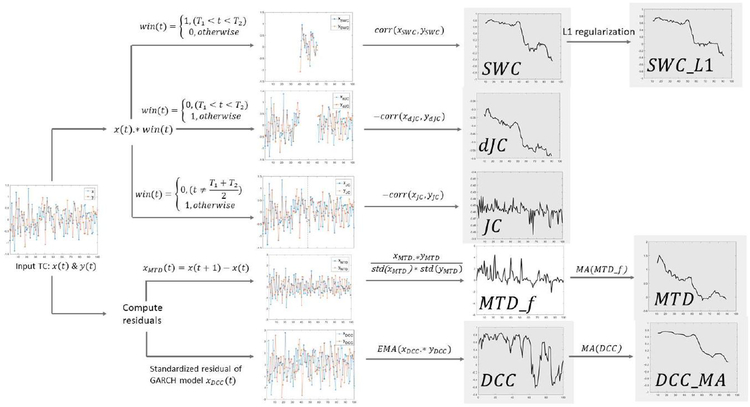
Seven dFC methods were evaluated in this study, i.e., sliding window correlation (SWC), sliding window correlation with L1 regularization (SWC_L1), multiplication of temporal derivatives (MTD), dynamic conditional correlation (DCC), and moving average dynamic conditional correlation (DCC_MA), jackknife correlation (JC) and delete-d jackknife correlation (dJC). Figure 2 provides a conceptual overview of the key steps involved in each method.

Figure 2.

Seven dFC methods under evaluation. Final dFC output is shown with grey background. Computing bivariate connectivity given two timeseries x and y. Sliding window correlation (SWC) characterizes dFC as correlation between two windowed/segmented time courses (x_swc, y_swc). Sliding window correlation with L1 regularization (SWC_L1) also penalizes the inverse covariance matrix. Delete-d jackknife correlation (dJC) excludes d consecutive observations and computes correlation using the remaining time points (x_dJC, y_dJc) and multiplies by negative one. Jackknife correlation (JC) is a special case of dJC, while only one sample is excluded each time. Multiplication of temporal derivates (MTD) first computes the first-order temporal derivatives (x_MTD, y_MTD) and then computes frame-wise MTD estimation (MTD_f), which is later smoothed using simple moving average (MA). Dynamic conditional correlation (DCC) first fits the timeseries using a GARCH (generalized autoregressive conditional heteroskedasticity) model to compute standardized residuals (x_DCC, y_DCC). Exponentially weighted moving average (EMA) is applied on element-wise product of two standardized residual timeseries resulting framewise DCC estimation. Moving average DCC (DCC_MA) is computed by applying simple moving average (MA) on DCC estimations, with the window length matching other window-based dFC methods.

2.3.1. Sliding window correlation (SWC)

Sliding window correlation (SWC) is perhaps the most commonly applied method to characterize dFC in fMRI studies (Hutchison et al., 2013; Preti et al., 2017). Given two windowed timecourses x_i(t) and X_j(t), the T^th SWC estimation is:

$$SWC\left(x_i,x_j,T\right)=\frac{{\sum }_{T-\lfloor WL/2\rfloor }^{T+\lfloor (WL-1)/2\rfloor }\left(x_i(t)-\overline{x_l}\right)\left(x_j(t)-\overline{x_J}\right)}{\sqrt{{\sum }_{T-\lfloor WL/2\rfloor }^{T+\lfloor (WL-1)/2\rfloor }{\left(x_i(t)-{\overline{x}}_l\right)}^2}\sqrt{{\sum }_{T-\lfloor WL/2\rfloor }^{T+\lfloor (WL-1)/2\rfloor }{\left(x_j(t)-\overline{x_j}\right)}^2}},$$ (1)

where $\overline{x_l}$ and $\overline{x_J}$ are the sample mean of windowed timeseries, and WL denotes the window length. $\lfloor X\rfloor$ denotes the greatest integer less than or equal to X. Then the window is shifted across time until all timepoints are used.

Here, we used a Gaussian tapered window by convolving a rectangle with a Gaussian kernel with o = 1 TR, and iteratively sliding each window by 1 TR = 1.5sec. In a tapered window, the data at the beginning and end of the window are downweighed. It should be noted that the window function in Equation 1, as well as in Figure 2, corresponds to a rectangular window instead of Gaussian tapered window. The window length is also a parameter in all equations for window-based methods. Five different window lengths: 6, 9, 15, 30, 45sec were evaluated. We evaluated SWC as well as other dFC metrics with window lengths as short as 6sec to test the limit of different dFC techniques (how few sample points are needed to produce plausible dFC estimation). Moreover, given the claim that multiplication of temporal derivatives (MTD) has higher sensitivity than SWC (Shine et al., 2015), we would also like to test if this statement is true with a small window length. High-pass filtering was performed before windowing with cut-off frequency equal to 1/WL to remove spurious dFC fluctuations (Leonardi and Van De Ville, 2015). For the shortest windows (i.e., WL <15s), this leads to the removal of signals within the bands commonly explored in resting-state connectivity (<0.1Hz); as such, it is our expectation that classification under these conditions will fail. The resulting SWC timeseries were Fisher Z-transformed.

2.3.2. Sliding window correlation with L1 regularization (SWC_L1)

When estimating dFC patterns, the number of samples per window is usually smaller than the number of ROIs (which is the case even for studies focusing on average FC). Not only is the estimated covariance/correlation matrix singular, but the estimation accuracy can be lower as well due to the large number of free parameters to estimate (Fan et al., 2016). One way to deal with this instability is to apply regularization, e.g., graphical LASSO (Allen et al., 2014; Friedman et al., 2008), so that the estimation of the covariance matrix can be better conditioned.

A key assumption in graphical LASSO is that the target matrix of interest is sparse, i.e., it contains many zero or near-zero entries. In terms of estimating (d)FC patterns for fMRI data, it may be impractical to assume that most ROIs’ timeseries are marginally independent. Hence, instead of assuming correlation matrices being sparse, graphical LASSO assumes the inverse covariance matrix Θ to be sparse, Θ(i,j) = 0 indicating conditional independence between the i^th and j^th ROI. Conditional independence means the marginal correlation observed between ROIs’ timeseries is driven by some latent nodes. This is similar to the concept of partial correlation which is inferred after removing the effects of all other nodes. However, graphical LASSO also encourages a sparse solution of the inverse covariance matrix Θ by maximizing the following log-likelihood function:

$$L_1=logdet\Theta -tr(s\Theta )-\lambda \Vert \Theta {\Vert }_1,$$ (2)

where det denotes the determinant; tr denotes the trace which is the sum of all elements on the main diagonal; s is the empirical covariance matrix; λ is the regularization parameter and ||Θ||₁ denotes the L1 penalty on Θ (i.e., the sum of the absolute values of the elements of the positive definite matrix Θ).

The regularization parameter λ enables a trade-off between the sparsity of the resulting inverse covariance matrix Θ and goodness of fit. An increasing λ shrinks the entries in Θ towards zero as shown in Figure 3(c). Graphical LASSO produces same results as partial correlation when λ = 0, or entries could be shrunk to zero given a large λ. As a result, the L1 penalty imposed by graphical LASSO encourages only the presence of edges which are best supported by the data (Monti et al., 2014), potentially yielding more robust estimation.

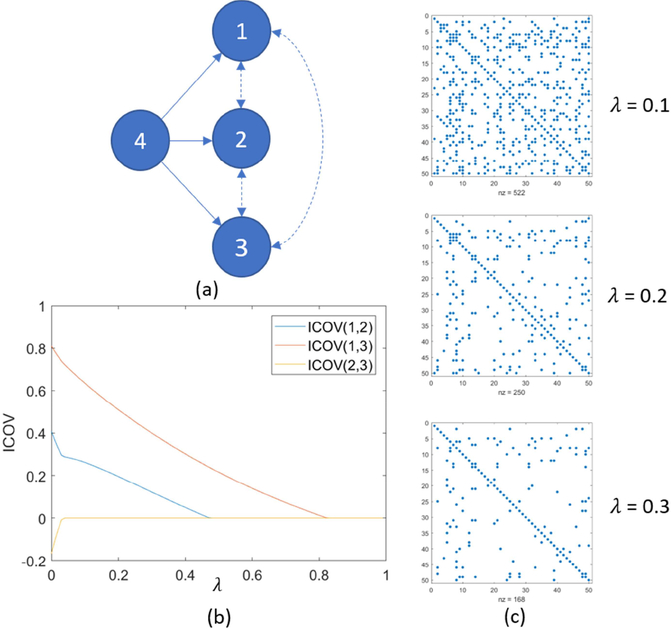
Figure 3.

(a) Nodes 1, 2, and 3 are marginally correlated and they are driven by a common source (node 4). Nodes 1, 2 and 3 are conditionally independent to each other after factoring out the common source. (b) Graphical LASSO promotes the sparsity of inverse covariance matrix (ICOV) and shrinks small entries to zero first. X-axis: regularization parameter λ, y-axis: regularized inverse covariance estimation. (c) Another example of regularized ICOV estimation using graphical LASSO and larger regularization parameter λ produces sparser Θ estimation (i.e., fewer non-zero entries).

Usually, graphical LASSO is performed along a path of regularization parameters, and then the optimal λ is selected. One way to achieve this is through cross-validation (Allen et al., 2014; Wang et al., 2016; Xie et al., 2017), which estimates the optimal λ for each subject by evaluating how well the inverse covariance matrix of a training set estimated with a given λ describes a test set from the same subject. For this purpose, after applying a window function and high-pass filtering (as described in SWC estimation), each subject’s resulting time series were assigned to two groups: 90% for training and 10% for testing. The following log-likelihood was used to compare matrices in the testing and training sets:

$$L_2(\lambda )=logdet\Theta -tr(s\Theta ),$$ (3)

where s is the sample covariance of the test set and Θ is the inverse covariance matrix estimated from the training data. We then chose the λ that maximizes the log-likelihood L₂(λ). Performance of the regularized correlation matrix and the regularized inverse covariance matrix were both evaluated.

2.3.3. Multiplication of temporal derivatives (MTD)

A slightly different window-based method is multiplication of temporal derivatives (MTD; Shine et al., 2015). MTD (Equation 4) first computes the entry-wise products of first-order temporal derivatives of the signal, and then normalizes the result using the standard deviation of whole timeseries.

$$MT{D}_{-}f\left(x_i,x_j,t\right)=\frac{d{x}_i(t)\times d{x}_j(t)}{{\sigma }_i\times {\sigma }_j},$$ (4)

where MTD_f(x_i, x_j, t) denotes the t^th framewise MTD estimation between node i and node j; dx_i and dx_j are the first-order temporal derivative of node i and j respectively, and σ_i and σ_j is the global standard deviation of dx_i or dx_j respectively (note neither σ_i nor σ_j is the standard deviation of dx_t or dxj within the window).

Then, a moving average window with window length WL is applied to the frame-wise estimation, which is taken as the dFC pattern for MTD (Equation 5).

$$MTD(T)=\frac{1}{WL}{\sum }_{T-\lfloor WL/2\rfloor }^{T+\lfloor (WL-1)/2\rfloor }MT{D}_{-}f(t)=\frac{1}{WL}{\sum }_{T-\lfloor WL/2\rfloor }^{T+\lfloor (WL-1)/2\rfloor }\frac{d{x}_i(t)\times d{x}_J(t)}{{\sigma }_i\times {\sigma }_j}.$$ (5)

By taking the first-order temporal derivative, MTD is effectively convolving the timeseries with a [−0.5 0.5] differentiation operator, which can be viewed as a high-pass filter (Figure S1) with a cut-off frequency equal to 0.25/TR (0.167Hz for TR = 1.5sec), hence no further filtering was performed for MTD. This step also makes MTD more sensitive to fast changes than SWC, assuming a fixed window size, and less sensitive to slower changes. It is also worth noting that if the denominator of equation (5) becomes the L2 norm of the windowed samples (instead of global standard deviation), then MTD would become cosine similarity between the time series as shown in equation (6):

$$cos\left(d{x}_i,d{x}_j,T\right)=\frac{{\sum }_{T-\lfloor WL/2\rfloor }^{T+\lfloor (WL-1)/2\rfloor }d{x}_i(t)\times d{x}_J(t)}{\sqrt{{\sum }_{T-\lfloor WL/2\rfloor }^{T+\lfloor (WL-1)/2\rfloor }d{x}_i{(t)}^2}\sqrt{{\sum }_{T-\lfloor WL/2\rfloor }^{T+\lfloor (WL-1)/2\rfloor }d{x}_i{(t)}^2}}.$$ (6)

2.3.4. Dynamic conditional correlation (DCC) and moving average DCC (DCC_MA)

Dynamic conditional correlation (DCC) was originally proposed to investigate time-varying correlation between asset returns (Engle, 2002), and was then introduced to characterize time-varying FC by Lindquist et al. (2014). DCC mainly consists of two steps. In the first step, it fits a generalized autoregressive conditional heteroskedasticity (GARCH) model to each time series. Then, the time-varying correlation is estimated from the standardized residuals. This is similar to the use of autoregressive (AR) and autoregressive moving-average (ARMA) models during more conventional fMRI analysis (Woolrich et al., 2001).

Given a univariate process y_t:

$$y_t={\sigma }_t{ϵ}_t,$$ (7)

where ϵ_t is the standard residuals used to compute DCC, and ${\sigma }_t^2$ is the conditional variance that we want to model.

A GARCH(1,1) model describes the conditional variance ${\sigma }_t^2$ at time t in terms of the previous conditional variance ${\sigma }_{t-1}^2$ and squared form of the previous observation $y_{t-1}^2$

$${\sigma }_t^2=\omega +\alpha y_{t-1}^2+\beta {\sigma }_{t-1}^2,$$ (8)

where ω > 0 and α, β ≥ 0 and α + β <1. Here, α controls the contribution of the intensity of the previous timepoint to the variance, and β controls the influence of past conditional variance on the present condition variance.

Fitting a GARCH model enables us to estimate the time-varying conditional variance ${\sigma }_t^2$ as well as standardized residuals ϵ_t. The standardized residual is a scaling factor describing the difference between the observed BOLD signal and the model estimation, which is then used to compute the constant conditional correlation $\overline{Q}$ and a non-normalized version of dynamic conditional correlation termed as Q_t.

$$\begin{array}{c}{ϵ}_t={\sigma }_t^{-1}{y}_t\\ \overline{Q}=\frac{1}{T}{\sum }_{t=1}^T{ϵ}_t{ϵ}_t^{\text{'}}\\ Q_t=\left(1-{\theta }_1-{\theta }_2\right)\overline{Q}+{\theta }_1{ϵ}_t{ϵ}_t^{\prime }+{\theta }_2{Q}_{t-1}\end{array},$$ (9)

where (θ₁, θ₂) are non-negative scalars and satisfy 0 < θ₁ + θ₂ < 1, and ϵ_t is a matrix consisting of standardized residuals of two nodes.

The normalized version of DCC is given as:

$$\begin{array}{c}{\text{Σ}}_t=D_t{R}_t{D}_t\\ R_t=diag{\left\{Q_t\right\}}^{-1/2}{Q}_{t}diag{\left\{Q_t\right\}}^{-1/2}\end{array},$$ (10)

where D_t = diag{σ_i,t,σ_j,t}, which represents the conditional variance estimated from the timeseries of nodes i and j.

The key difference between DCC and other window-based dFC methods lies in the fact that DCC first uses all the samples to fit a GARCH model and takes the residuals to estimate dFC, which is also known as whitening (fitting a model and removing the predictable component). This is quite common in activation-based analysis which uses AR or ARMA models to account for the temporal autocorrelation in the timeseries (Woolrich et al., 2001). The code used for DCC estimation is available at https://github.com/canlab/Lindquist_Dynamic_Correlation.

Since DCC yields frame-wise estimation of dFC matrices, we also applied moving average to smooth the DCC estimation to match the window length of other window-based methods as adopted by MTD.

$$DC{C}_{-}MA(T)=\frac{1}{WL}{\sum }_{T-\lfloor WL/2\rfloor }^{T+\lfloor (WL-1)/2\rfloor }DCC(t),$$ (11)

where DCC(t) is the frame-wise estimation of DCC and DCC_MA(T) is moving average DCC with window length WL.

2.3.5. Jackknife correlation (JC) and delete-d jackknife correlation (dJC)

Jackknife correlation (JC) offers an alternative way to quantify frame-wise dFC (Richter et al., 2015; Thompson and Fransson, 2018). In this case, to estimate the frame-wise dFC at a given time point T, JC computes the Pearson’s correlation between all the data except for that particular time point and then multiplies by −1.

$$\begin{array}{ll}JC\left(x_i,x_j,T\right)=-\frac{{\sum }_1^N\left(x_i(t)-{\overline{x}}_l\right)\left(x_j(t)-\overline{x_J}\right)}{\sqrt{{\sum }_1^N{\left(x_i(t)-{\overline{x}}_l\right)}^2}\sqrt{{\sum }_1^N{\left(x_j(t)-\overline{x_j}\right)}^2}}\hfill & t\ne T\hfill \end{array},$$ (12)

where $\overline{x_l}$ and $\overline{x_J}$ are the expected values of x_i and x_j excluding the data at that time point. The inverse is taken to correct for the leave-one-out process.

JCcorrelation can be seen as a special case of delete-d jackknife correlation (dJC; also known as leave-d-out correlation), where d consecutive samples are excluded, and dFC is estimated using the remaining samples. Simulation results have suggested correspondence between dFC traces generated from dJC and SWC with window length equal to d, except for the window length that is either close to zero or length of the whole timeseries (Thompson et al., 2017), as the correlation estimation becomes unstable with few samples. As Thompson et al. explain, the JC leads to compression of variance depending on the length of timeseries, and it is recommended to scale or standardize the JC estimation before further analysis. Here, we evaluated the performance of JC and delete-d JC (dJC) with the d matching the window length of SWC.

2.4. dFC metrics evaluation

To gain some intuition about how dFC metrics related to each other, we first computed the pairwise similarity in terms of Pearson’s correlation between dFC traces, e.g., corr(SWC(PC1, PC2), MTD(PC1, PC2)). Following that, and to further evaluate the efficacy of the different dFC methods at tracking mental states, two metrics were employed, i.e., adjusted Rand index (ARI; Hubert and Arabie, 1985) and silhouette index (SI; Rousseeuw, 1987). A high efficacy method would yield homogenous within-condition dFC matrices and while distinct across different conditions, leading to a high ARI and positive SI.

2.4.1. Adjusted Rand Index

We performed k-means clustering on dFC matrices for each subject and window length with the number of clusters equal to four (i.e., the number of different mental states subjects engage as imposed by task demands), Pearson’s correlation as the distance measure, the maximum number of iterations equal to 10000, and number of repetitions equal to 100. Note, this is a different initialization strategy than that proposed by Allen et al. (2014), in which a two-step initialization approach is adopted. Moreover, given the temporal lag of the hemodynamic response we dropped the first five and the last five dFC matrices near the beginning and end of each task block.

Since the k-means algorithm provides unlabeled results, we evaluated the clustering performance using the ARI (Hubert and Arabie, 1985). ARI is a cluster validation technique that measures the agreement between unlabeled clustering results (k-means partitions) and an external criterion obtained from prior knowledge of the data (i.e., the ground truth timing of task blocks). Here, given a set of N observations grouped into r ground truth (GT) partitions, we want to evaluate the performance of k-means at reproducing such r clusters. The contingency table as shown in Table 1 summarizes all the possible ways of correspondence between unlabeled clustering results and ground truth partition (e.g., cluster 1 -> task 1, cluster 2-> task 2; and cluster 1 -> task 2, cluster 2-> task 1).

Table 1.

A contingency table. Each entry in the cell is an occurrence count.

GT╲Cluster	Y1	Y2	…	Ys	Sum
X1	n11	n12	…	n1s	a1
X2	n21	n22	…	n2s	a2
…	…	…	…	…	…
Xr	nr1	…	…	nrs	ar
Sum	b1	b2	…	bs	N

Based on this contingency table, the ARI is defined as follows:

$$ARI=\frac{{\sum }_{ij}\left(\begin{array}{c}{n}_{ij}\\ 2\end{array}\right)-\left[{\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right){\sum }_j\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)\right]/\left(\begin{array}{l}N\hfill \\ 2\hfill \end{array}\right)}{\frac{1}{2}\left[{\sum }_i\left(\begin{array}{l}{a}_i\hfill \\ 2\hfill \end{array}\right)+{\sum }_j\left(\begin{array}{l}{b}_j\hfill \\ 2\hfill \end{array}\right)\right]-\left[{\sum }_i\left(\begin{array}{l}{a}_i\hfill \\ 2\hfill \end{array}\right){\sum }_j\left(\begin{array}{l}{b}_j\hfill \\ 2\hfill \end{array}\right)\right]/\left(\begin{array}{l}N\hfill \\ 2\hfill \end{array}\right)},$$ (13)

where n_ij is the entry in the contingency table at the i^th row and j^th column, and $\left(\begin{array}{l}N\hfill \\ 2\hfill \end{array}\right)=N(N-1)/2$. ARI was computed for each subject and window length. An ARI smaller than 0.65 signals poor agreement between clustering results and ground truth; 0.65 < ARI < 0.8 indicates moderate agreement; 0.8 < ARI < 0.9 indicates good agreement; and 0.9 < ARI < 1.0 indicates excellent agreement (Steinley, 2004).

2.4.2. Silhouette Index

Another metric used for evaluating dFC efficacy is the silhouette index (SI), which compares the differentiability of the dFC metrics, under the assumption that dFC patterns would be more similar to each other within a task, than across different tasks. Let a(i) be the average dissimilarity of the i^th dFC pattern to all other dFC patterns that belong to the same cluster (a measure of compactness); and b(i) be the lowest average dissimilarity between the i^th dFC pattern and the dFC patterns belonging to any other cluster (a measure of separation). Here, we used correlation distance between dFC estimates as the dissimilarity measure to be consistent with our clustering analysis. Using the notation defined above, SI can be computed as follows:

$$SI(i)=\frac{b(i)-a(i)}{\text{max}\{a(i),b(i)\}}.$$ (14)

SI ranges from −1 to 1. A positive SI suggests that a given dFC pattern is more similar to its own cluster and different from dFC patterns from other clusters. This would highlight a well performing dFC method.

To avoid the potential bias introduced by using maximally overlapping sliding windows, i.e., the significant overlap in the data contained in consecutive windows biasing SI_ for longer WL, we made some modifications to original SI definition by limiting a(i) to only the between-block dissimilarity, as pointed by the arrow in Figure 4. Therefore, the modified SI can be seen as a metric of across-block within-condition reliability.

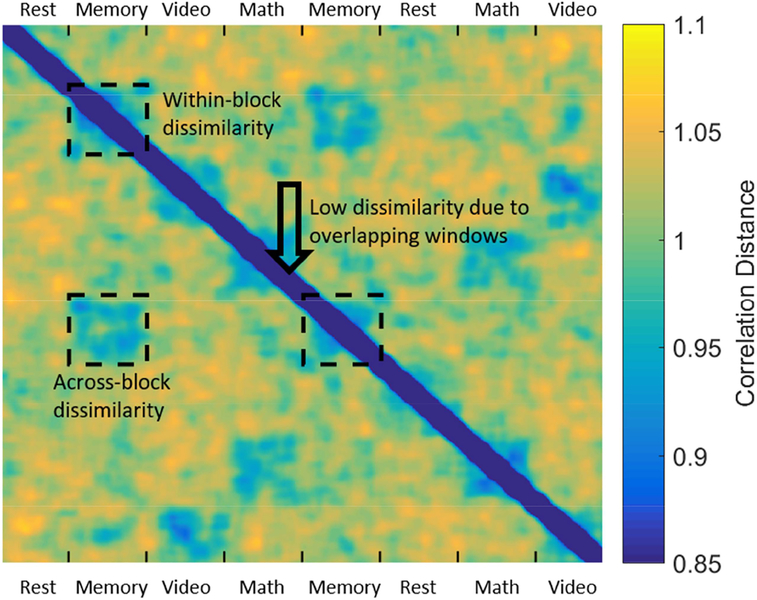
Figure 4.

Whole-brain dFC patterns (SWC, WL = 45sec) were vectorized and correlated with each other to compute a correlation dissimilarity matrix (1 - correlation). A spuriously low within-cluster dissimilarity, may arise due to the maximally overlapping sliding windows (high similarity of neighboring dFC patterns), noted by the black arrow. To account for this potential bias, we only used the dissimilarity values across two task blocks of the same task to compute a(i).

3. Results

3.1. dFC traces and similarity

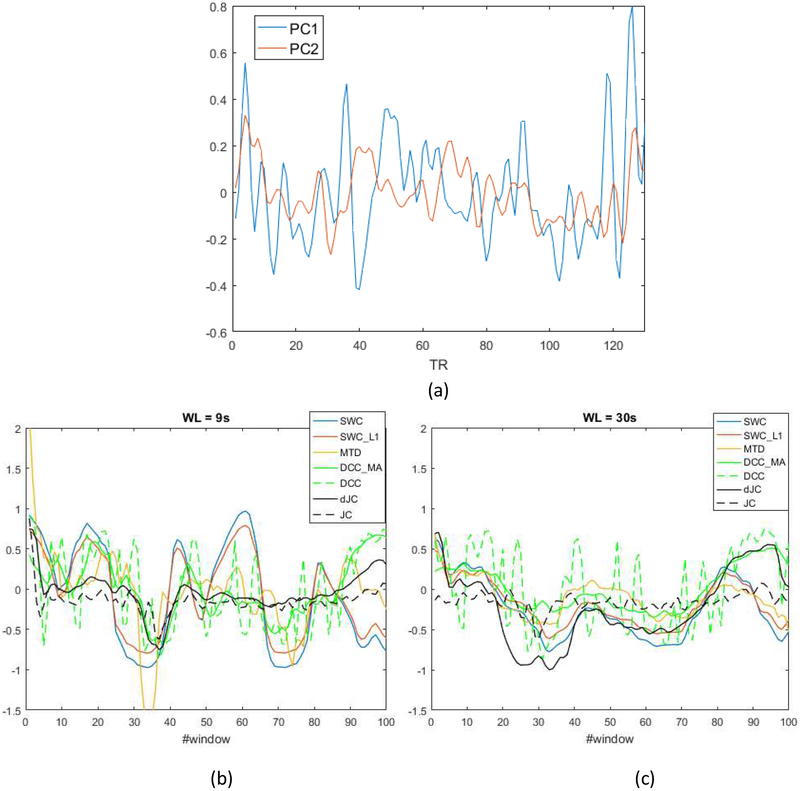
To gain some intuition about how similar dFC methods are to each other, we generated plots of dFC traces derived from each dFC method (Figure 5). Upon inspection of these plots, we made a few observations: 1) framewise DCC estimation was highly variable; 2) MTD was the only method leading to estimates outside the [−1,1] range; 3) SWC_L1 resembled a shrunk version of SWC traces due to the shrinkage effect; 4) MTD showed more resemblance to SWC/SWC_L1 than other metrics; 5) dJC and DCC_MA followed a similar pattern; 6) dFC traces became more similar as the window length increased.

Figure 5.

(a) Time courses of the first two principal components of subject 1. Visualization of dFC traces between first two principal components of subject 1 with window length = 9sec (b) and 30sec (c). SWC: tapered sliding window correlation; SWC_L1: tapered sliding window correlation with L1 penalty; MTD: multiplication of temporal derivatives; DCC_MA: moving average dynamic conditional correlation; DCC: dynamic conditional correlation; dJC: delete-d jackknife correlation; JC: jackknife correlation. Note, the frame-wise estimation (DCC and JC) was shifted based on the window length. JC and dJC are scaled between −1 and 1 for visualization purpose.

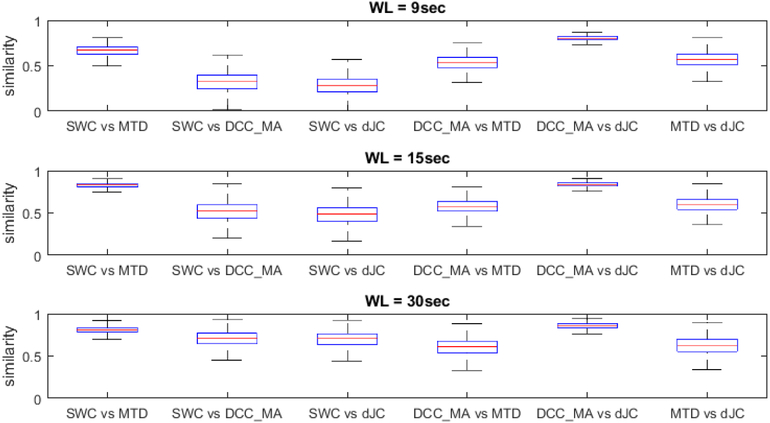
Our initial observations were confirmed at the group level. For this purpose, we computed the overall similarity between all five window-based dFC metrics by correlating corresponding dFC traces for each subject according to the window length, the result of which is depicted in Figure 6. Since SWC and SWC_L1 produced highly similar dFC traces (lowest average similarity between the two is greater than 0.97), we did not include SWC_L1 in the plot. The five window-based dFC metrics appear to be subdivided into two groups: SWC, MTD and SWC_L1 (not shown here); DCC_MA and dJC, and the dFC metrics within each group shared a higher degree of similarity across all window lengths. Besides, the overall similarity between all dFC methods increased as window length increased.

Figure 6.

Boxplot of similarity between dFC traces of different methods with window length equal to 9, 15 and 30 seconds.

3.2. Efficacy of dFC metrics to track cognition

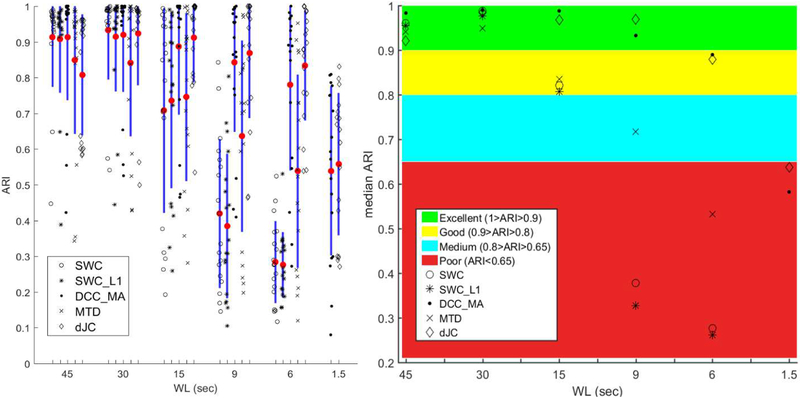
Figure 7 provides a graphical summary of ARI computed using different methods across different WLs. We observed that longer window length generally led to higher ARI (except for dJC with WL = 45sec), and all dFC methods produced reasonably good accuracy for window length longer than or equal to 30sec. We then performed the non-parametric Kruskal-Wallis ANOVA test on the ARI for unequal medians using Matlab function kruskalwallis. After correcting for multiple comparison (i.e., 10 multiple comparisons per window length) using Matlab function multcompare, the groups with significantly different medians were reported in Table 2 (p < 0.1, Tukey Test). We found that DCC_MA produced the best ARI across all WLs, closely followed by dJC. Moreover, SWC_L1 did not lead to significant increase in ARI compared to SWC (all p-values > 0.95). There was trend-level significance for MTD to outperform SWC_L1 for the smallest WL (WL = 6sec; p < 0.1), while MTD performed worse for longer WL than SWC and its variant (but not statistically significantly). It is also worth noting that DCC and MTD produced more outliers than SWC and SWC_L1 with longer WL (WL ≥ 30sec), and so did dJC with WL = 45sec.

Figure 7.

Left: graphical summary of ARI of DCC_MA, SWC, SWC_L1, MTD and dJC (from left to right) of WL = 45, 30, 15, 9, 6 sec, and WL = 1.5sec corresponds to the framewise methods (DCC and JC). Different symbols represent the ARI achieved using a given method from a subject. Mean is denoted by a red dot and one standard deviation is shown as the blue bar. Right: Median ARI of each method across all subjects. Interpretation of ARI as a measure of clustering performance is also included. The rightmost column (WL = 1.5sec) corresponds to ARI of framewise DCC and JC. Note, both DCC and DCC_MA are represented by dots, and both dJC and JC are represented by diamonds.

Table 2.

Kruskal-Wallis ANOVA test results on ARI with p-values in parentheses. p-values smaller than 0.05 are highlighted in bold.

WL = 45sec	DCC_MA > MTD (0.007); DCC_MA > dJC (0.001)
WL = 15sec	DCC_MA > SWC (0.024); DCC_MA > SWC_L1 (0.031); DCC_MA > MTD (0.070); dJC > SWC (0.037); dJC > SWC_L1 (0.048)
WL = 9sec	DCC_MA > SWC (<0.001); DCC_MA > SWC_L1 (<0.001); dJC > SWC (< 0.001); dJC > SWC_L1 (< 0.001); dJC > MTD (0.040)
WL = 6sec	DCC_MA > SWC (<0.001); DCC_MA > SWC_L1 (<0.001); DCC_MA > MTD (0.099); MTD > SWC_L1 (0.089); dJC > SWC (< 0.001); dJC > SWC_L1 (< 0.001); dJC > MTD (0.031)

We further compared the framewise DCC and JC with three window-based dFC approaches (i.e., SWC, SWC_L1 and MTD), we found the framewise DCC (ARI: 0.539 ± 0.237) and JC (0.558 ± 0.199) were significantly worse than those methods with commonly used window length (WL ≥ 30sec) with the largest p-value equal to 0.002.

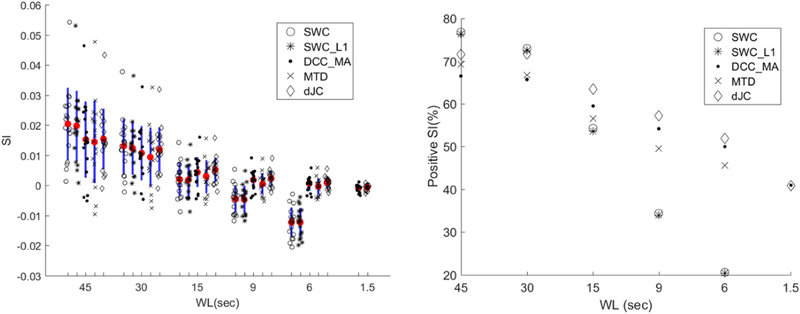
Since ARI for all dFC methods plateaued for relatively long WL (WL ≥ 30sec), we used SI as a complementary metric to describe the efficacy of each dFC method and get additional insights from scenarios where the ARI had a ceiling effect. Figure 8 shows SI results. A significant positive correlation between ARI and subject-average SI (p < 0.001) is observed. One-sample t-tests show that only two dFC metrics produced positive SI at WL = 6sec, i.e., DCC_MA (p = 0.016) and dJC (p = 0.001). As the WL increased, the mean SI as well as the percentage of positive SI increased. While DCC_MA, MTD, and dJC yielded higher/more positive SI than SWC and its variant for WL ≤ 15sec, such trend was reversed for longer WL. We performed a one-way ANOVA on subject-averaged SI and reported the Tukey’s test results in Table 3. We found DCC_MA, MTD, and dJC outperformed SWC and its variant for WL ≤ 9sec, while no significant difference was found for longer WL. Moreover, we applied one-way ANOVA on SI comparing framewise dFC methods (DCC and JC) with window-based dFC approaches (i.e., SWC, SWC_L1 and MTD). Post hoc tests again confirmed that framewise dFC estimation yielded lower SI than those window-based metrics with commonly used window length (WL ≥ 30sec; all p-values < 0.001).

Figure 8.

Left: Graphical summary of SI. Each shape represents the subject-average SI derived from a given dFC method. Mean is highlighted by the red dot and one standard deviation was shown in blue. The two columns to the right are the SI of both framewise methods (DCC and JC). Right: Percentage of positive SI of different dFC methods across different WLs.

Table 3.

One-way ANOVA test results on SI with p-values in parentheses. No significant differences in mean SI were found for WL = 45, 30 and 15sec.

WL = 9sec	DCC_MA > SWC (<0.001); DCC_MA > SWC_L1 (<0.001); MTD > SWC (0.001); MTD > SWC_L1 (0.001); dJC > SWC (<0.001); dJC > SWC_L1 (<0.001)
WL = 6sec	DCC_MA > SWC (<0.001); DCC_MA > SWC_L1 (<0.001); MTD > SWC (<0.001); MTD > SWC_L1 (<0.001); dJC > SWC (<0.001); dJC > SWC_L1 (<0.001)

In Table 4, we report the mean and standard deviation of ARI of all the dFC methods tested in this study. We also tested a few other dFC metrics including rectangular sliding window correlation (rSWC), DCC after whitening using an ARMA(1,1) model (DCC_MAw), inverse covariance matrix (ICOV), and sliding window cosine similarity after regressing out the task structure (SWCos_reg).

Table 4.

Mean and standard deviation of ARI of different dFC methods. Note, the rightmost column (1.5sec = 1TR) corresponds to the framewise dFC estimation. SWC_d: sliding window correlation on temporal derivative. SWCos_d: sliding window cosine similarity on temporal derivative. SWCos: sliding window cosine similarity. SWCos_reg: sliding window cosine similarity with task structure regressed. rSWC: rectangular sliding window correlation. DCC_MAw: moving average dynamic condition correlation after whitening with ARMA(1,1) model. ICOV: inverse covariance matrix with L1 regularization.

	45sec	30sec	15sec	9sec	6sec	1.5sec
DCC(_MA)	0.91 ± 0.18	0.94 ± 0.13	0.89 ± 0.19	0.85 ± 0.19	0.78 ± 0.24	0.54 ± 0.24
SWC	0.91 ± 0.14	0.93 ± 0.14	0.71 ± 0.29	0.42 ± 0.21	0.28 ± 0.11
SWC_L1	0.91 ± 0.15	0.91 ± 0.15	0.74 ± 0.25	0.38 ± 0.20	0.28 ± 0.09
MTD	0.85 ± 0.21	0.84 ± 0.21	0.75 ± 0.24	0.64 ± 0.27	0.54 ± 0.27
d(JC)	0.81 ± 0.17	0.92 ± 0.15	0.91 ± 0.13	0.87 ± 0.18	0.83 ± 0.15	0.56 ± 0.20
SWC_d	0.85 ± 0.19	0.87 ± 0.19	0.74 ± 0.25	0.53 ± 0.23	0.31 ± 0.15
SWCos_d	0.86 ± 0.19	0.88 ± 0.17	0.80 ± 0.23	0.66 ± 0.25	0.51 ± 0.23
SWCos	0.91 ± 0.10	0.95 ± 0.08	0.89 ± 0.17	0.83 ± 0.20	0.70 ± 0.23
SWCos_reg	0.87 ± 0.16	0.94 ± 0.15	0.91 ± 0.17	0.81 ± 0.22	0.69 ± 0.23
rSWC	0.91 ± 0.13	0.91 ± 0.14	0.74 ± 0.26	0.40 ± 0.20	0.27 ± 0.11
DCC__MAw	0.80 ± 0.23	0.82 ± 0.25	0.76 ± 0.27	0.70 ± 0.25	0.66 ± 0.29	0.60 ± 0.26
ICOV	0.88 ± 0.22	0.89 ± 0.17	0.66 ± 0.27	0.51 ± 0.28	0.31 ± 0.11

4. Discussion

There are multiple methodological options for those interested in exploring human brain dynamic functional connectivity (dFC) (Calhoun and Adali, 2016; Preti et al., 2017). This raises the question of how to choose and compare the outcomes of various approaches. Given differences in explicit and implicit assumptions underlying each method, direct comparison of dFC estimations is not straightforward. In addition, comparison of dFC methods with resting data can be challenging due to lack of a gold standard and information about subject’s behaviors inside the scanner. Here, we propose the use of multitask scans as a proxy for dFC evaluation. More specifically, four mental states were imposed by external stimuli which induced changes in whole-brain connectivity patterns (Gonzalez-Castillo et al., 2015). While neurally-driven connectivity changes during rest are subtler than those elicited by externally imposed tasks, we posit that, at a minimum, a useful dFC metric should be able to produce patterns that can be used to reliably distinguish externally imposed tasks, and such a metric would have a better chance to uncover the true dFC fluctuation during rest. Yet, the opposite might not hold true, meaning that metrics that perform well here, may still be insufficient to capture all behaviorally and clinically relevant resting-state dFC patterns given the introspectively oriented and self-referential nature of rest.

In this paper, we evaluated efficacy of seven different dFC methods: sliding window correlation (SWC), sliding window correlation with L1 regularization (SWC_L1), multiplication of temporal derivatives (MTD), dynamic conditional correlation (DCC), moving average DCC (DCC_MA), jackknife correlation (JC), and delete-d jackknife correlation (dJC). The dFC metrics in our study all characterize time-domain properties (so that the dFC traces can be efficiently compared and evaluated under our clustering scheme). We evaluated the dFC efficacy with varying window lengths (WL) ranging from 45sec (30 TRs) to 1.5sec (1TR). Results showed window-based dFC approaches performed better compared to the framewise DCC estimation (Lindquist et al., 2014) and jackknife correlation (Richter et al., 2015) with commonly used WLs (30sec and 45sec). Our proposed moving average DCC (DCC_MA) offered the most consistent performance across the entire range of short to long window lengths. MTD showed higher accuracy compared to SWC and its variant for small WL (WL ≤ 15sec). All dFC methods showed increasing similarity and accuracy with increasing WL, and such convergence at longer WL (WL ≥ 30sec) suggests they are all capturing more similar task-evoked whole-brain changes in the connectivity patterns, despite the difference in their underlying mathematical frameworks.

The choice of WL has always been critical for SWC (and other window-based dFC metrics), and the optimal WL is still a matter of debate (Hindriks et al., 2016; Sakoğlu et al., 2010; Shakil et al., 2016; Vergara et al., 2017). For example, to reliably detect pairwise dFC using SWC, it has been shown that if one assumes the underlying data are primarily oscillatory signals, the optimal WL should be around one third of the characteristic timescale of FC fluctuations or 50 seconds without prior knowledge (Hindriks et al., 2016). Here, we empirically show that even with WL = 15sec = 10TRs, window-based methods offered reasonable performance to separate underlying cognitive processes (see Table 4), while SWC worked poorly for WL smaller than 15sec. This is to be expected as correlation becomes unstable with too small of a window size and the adaptive high-pass filtering with the cut-off frequency equal to 1/WL has removed all signals with frequency <0.1Hz, namely those most strongly contributing to resting-state functional connectivity (Cordes et al., 2001). Here, we also compared Gaussian tapered sliding window correlation (SWC) with rectangular sliding window correlation (rSWC), and found no significant difference in median ARI between two methods using Wilcoxon rank sum test across all WLs. Tapered sliding windows are suggested to be less sensitive to sharp state transitions than rectangular window (Shakil et al., 2016), while we mainly investigated dFC patterns imposed by steady state tasks (block design), which prevented us from evaluating the dFC efficacy to capture transient connectivity changes.

For SWC_L1 (or any high-dimensional covariance estimation technique), the goal is to robustly infer population covariance matrix from samples of multivariate data. This can become difficult with very high-dimensional data and rather limited sample sizes, such as fMRI data. It should be noted that this problem is not unique to dFC estimation, as it is not uncommon that the number of ROIs is greater than the scan length when computing static or averaged whole-brain FC patterns. As one of many graphical models, graphical LASSO (Friedman et al., 2008) produces a sparse inverse covariance matrix Θ by imposing an L1 penalty on Θ, and the sparsity is enforced by shrinking the off-diagonal term of Θ towards zero. Graphical LASSO is widely used to construct sparse undirected graph models, and the sparsity of the resulting graph largely depends on the choice of regularization parameter. It has been shown to behave the same as thresholding when the regularization parameter is relatively large (Sojoudi, 2016). In our case, the regularization parameter was estimated for each subject to be 0.04 via ten-fold cross-validation, and with this small regularization parameter resulted in very similar SWC_L1 estimation as SWC. In lieu of cross-validation, model selection criteria such as Akaike information criterion (AIC) and Bayesian information criterion (BIC) can also be used to determine the optimal regularization parameter (Zhu and Cribben, 2017). It should be noted that the criterion to determine the regularization parameter used here is different from that used in Allen et al. (2014), and our criterion resulted in very similar dFC traces of SWC_L1 compared to SWC. Further investigation is needed to determine which criteria may lead to improved performance for SWC_L1.

Multiplication of temporal derivatives (MTD) takes a first-order temporal derivative of timeseries, which is equivalent to applying a high-pass filter with a cut-off frequency equal to 0.25/TR (Keilholz et al., 2017. However, this is not a typical high-pass filter that has a sharp transition band. Rather, differentiation attenuates the low-frequency component of the signal while keeping the high-frequency fluctuations. MTD then computes the dot product of two temporal derivative timeseries normalized by their standard deviation. If we replace the denominators in MTD (i.e., standard deviation of the whole temporal derivative timeseries) with the L2 norm of the two windowed timeseries, it would become the cosine similarity, which is a measure of the angle between two vectors. As an uncentered version of correlation, cosine similarity is invariant to change of scale but sensitive to baseline shift. To investigate which one of the two steps (or both) led to the improved performance of MTD for small WL (WL ≤ 9sec) as compared to SWC(_L1) in terms of SI (although none of these methods resulted in good ARI), we performed some additional analyses by computing sliding window correlation on the temporal derivatives (SWC_d), sliding window cosine similarity on the temporal derivatives (SWCos_d) and sliding window cosine similarity on the original timeseries (SWCos). As shown in Table 4, we conclude that taking derivatives (SWC_d) did not lead to improved performance of MTD, while choosing cosine distance (SWCos) over Pearson’s correlation did. We also performed simulations, which showed that with small window length, centering the windowed timeseries decreased the discriminative power of dFC, and the difference disappeared as the window length increased. Given timeseries with mean of zero (or very close to zero), centering the windowed timeseries with windowed mean might introduce greater estimation error in the correlation estimation compared to without centering (especially with only a handful of samples). As the number of observations increases, the two metrics would converge as windowed mean would become close to the mean of the entire time series—which is zero, due to centering.

Dynamic conditional correlation (DCC) utilizes multivariate volatility models which can resolve dFC of a single time point. As ARMA or AR models are used to remove the structured signal in the mean of the fMRI signal (i.e., autocorrelation; Woolrich et al., 2001), a GARCH(1,1) model is first fit to remove any predictable structure in covariance, and the residuals from the first step are used to estimate the time-varying correlation matrices. DCC has been shown to provide higher test-retest reliability compared to SWC (Choe et al., 2017), while both methods show low reliability when estimating brain states. In this study, we showed the efficacy of DCC (i.e., framewise DCC) in tracking cognitive states was lower than SWC with commonly used window length (WL ≥ 30sec). However, a modified approach which computes a moving average of framewise DCC (DCC_MA) improved the sensitivity of detecting brain states significantly, which suggested that framewise DCC estimates may be excessively sensitive to noise. This could be due to several reasons, namely improper model order, autocorrelation in the signal, or the presence of additional structured signal (such as residual structured noise). Despite the best overall efficacy of DCC_MA, it is important to notice that DCC_MA as well as MTD produced more outliers (low ARI with long window length) than SWC and SWC_L1 (3 vs. 2 outliers). The two common outliers identified by all dFC methods correspond to the bad performers in Gonzalez-Castillo et al. (2015), whereas the extra one identified by DCC_MA and MTD is not a bad performer, suggesting that given enough samples SWC and SWC_L1 could possibly produce more reliable whole-brain dFC estimation. Another remark concerning DCC is its much higher complexity and computational cost as compared to the other dFC methods under evaluation. For example, DCC estimation for subject 1 (1017TRs × 78PCs) took 158 min to finish, while the other methods took less than 2 minutes. The high computation load is mainly due to the fitting of a GARCH model using all data points of a given node (Equation 8), which makes whole-brain computation of DCC much more time consuming.

Jackknife correlation (JC) and delete-d JC (dJC) use the jackknife resampling strategy, originally proposed to evaluate bias and variance (Quenouille, 1949; Tukey, 1958), which has been recently introduced to characterize dFC (Thompson and Fransson, 2018). More specifically, dJC excludes d neighboring observations and computes the dFC with remaining samples, while JC leaves out one observation at a time, offering an alternative way to quantify framewise dFC. JC and dJC are very different from the conventional jackknife resampling, since (d)JC performs resampling to estimate moment-to-moment correlation fluctuations, while the conventional jackknife resampling is to derive robust estimates of standard errors and confidence intervals of a population statistic. A recent simulation study showed JC with better performance than SWC and MTD (Thompson et al., 2017), which is consistent with our results. Moreover, dJC showed remarkable similarity to DCC_MA across different WLs (Figure 7), despite very different mathematical frameworks behind the two methods. Another remark is that both DCC(_MA) and (d)JC use many more samples than the other three dFC methods, as they use all the time points (DCC and DCC_MA) or those outside the window (JC and dJC), whereas the other three methods do not. Unexpectedly, we found dJC with lower ARI and more outliers for WL = 45sec. It suggests that like other window-based approaches the performance of dJC is also subject to the choice of WL, which is confirmed in a study comparing different resampling strategies for bias reduction (Radovanov and Marcikic, 2014). Besides, even though it makes perfect sense to take the additive inverse to estimate node-to-node dFC traces (Equation 12), flipping the sign also means reversing the whole-brain dFC patterns completely. JC and dJC lead to variance compression which is proportional to the length of the data, and they also produce relative dFC values (Thompson et al., 2017), making the results difficult to compare across studies and hard to interpret. It is also worth noting that JC is conceptually very similar to some diagnostic metrics used to estimate the influence of a data point in a regression analysis, such as differences between the betas (DFBETAS) which describe how leaving out a sample affects regression parameter estimation, potentially leaving the framewise JC vulnerable to outliers. However, this could potentially help reveal any remaining noise such as motion artifacts.

Limitations and future directions

In this study, we focused on the efficacy of seven dFC methods by comparing their ability of extracting cognitively relevant information. Pearson’s correlation is the most common method in (d)FC research. However, from the perspective of pattern recognition and signal detection theory, Pearson’s correlation is just one of many pairwise similarity measures that are used to describe the temporal synchronization between brain regions (Smith et al., 2011); to name a few, cityblock, Mahalanobis, and mutual information. Despite some rules of thumb (e.g., Euclidean distance being suboptimal for highdimensional data), there has not been much work on optimal similarity measures that result in the most meaningful notion of proximity between two objects (Aggarwal et al., 2001), both in terms of similarity between two timeseries within a short period of time and similarity between two whole-brain dFC patterns, and in this paper we only discussed a few candidate connectivity metrics of the former, whereas the choice of the latter could also affect the k-means outcomes. Apart from those time-domain dFC methods, time-frequency methods such as wavelet coherence analysis (Chang and Glover, 2010; Yaesoubi et al., 2015) and dynamic phase synchronization analysis (Glerean et al., 2012; Ponce-Alvarez et al., 2015) also provide valuable insights into spatiotemporal synchronization patterns of human brains, which should be further evaluated.

Higher efficacy does not guarantee that one dFC metric is more accurate (or less biased) than another one. A given dFC method can perfectly predict mental states while being biased, as long as it produces consistent estimation (i.e., low variance). For example, the sample correlation is a biased estimator of the population correlation coefficient for normal populations. For small sample size of 10 or 20, the bias can be of the order of 0.01 or 0.02 when correlation is about 0.2 or 0.3 (Zimmerman et al., 2003). Another example would be computing SWC_L1 via graphical LASSO, as we traded in-sample estimation accuracy for out-of-sample estimation error by imposing L1 penalty. Should it work, graphical LASSO would provide more robust dFC estimation especially when the sample size is small (Smith et al., 2011). While we investigated the amplitude of dFC traces, variance of dFC traces can also provide valuable insights. For example, Elton and Gao showed decreased functional connectivity variability associated with improved task performance during a selective attention task (Elton and Gao, 2015). With that being said, since all methods tested here are descriptive rather than generative (Bolton et al., 2018; Eavani et al., 2013), we mainly focused on the discriminative power of whole-brain dFC estimation instead of how accurate the dFC estimation is. Hence, we should be careful when interpreting the value of dFC traces, as there would be no impact on ARI or SI if we multiply all dFC values by negative one like in JC estimation. In this work, we used ARI and SI to define which methods are better than others, but other evaluation metrics with different priorities may define “better” differently. More work is needed for a deeper understanding of the neural mechanisms of BOLD FC dynamics in order to truly answer which method is more accurate. Future work should place more emphasis on development of generative models as well as multimodal data fusion (Allen et al., 2017; Tagliazucchi and Laufs, 2015).

All dFC metrics are computed after the PCA dimensionality reduction to be consistent with the previous study (Gonzalez-Castillo et al., 2015), moreover, DCC(_MA) is too computationally expensive without the dimensionality reduction. Hence, further investigation is needed to determine how the PCA dimensionality reduction influences the outcome, as those PCs may indeed bear some neurobiological significance (Shine et al., 2018, also see Figure S2). Other analysis decisions, such as parcellation schemes, nuisance regression strategy, and bandpass filtering may also have an impact on the results, and should be the subject of further evaluations. For example, we bandpass filtered the timecourses with a high-end cutoff frequency equal to 0.18Hz. The rationale here was to avoid the influence of the periodic motor response during the math task (responses required every 5sec); yet future work should compare dFC efficacy for broader bandwidths or in a bandwidth-specific manner (Sala-Llonch et al., 2018. Also, it would be interesting to test if any other linear and non-linear dimensionality reduction methods (e.g., independent component analysis and kernel PCA) would further increase the efficacy. Future work is needed to determine the generalizability of our conclusions using a different set of tasks/experimental design and data acquired on more widely available 3T systems. For example, we found that even with as few as six TRs, we could well separate underlying cognitive processes with some dFC metrics, which is likely due to the tasks used here taxing very different cognitive domains. In this paper, we solely focused on the dynamic functional connectivity measures in terms of second-order statistic, however, brain dynamics can also be characterized as transient activity patterns as a first-order statistic (Karahanoglu and Van De Ville, 2015; Liu et al., 2018; Saggar et al., 2018). Future work could systematically compare the validity of those activity-based brain dynamics methods, which could help us better understand the relationship between the time-varying connectivity pattern and BOLD mean activity pattern as well as the BOLD variance pattern (Fu et al., 2017; Glomb et al., 2018).

Conclusions

In this study, we compared seven dynamic functional connectivity (dFC) metrics in terms of each method’s efficacy to reveal underlying cognitive processes with a multitask dataset serving as the ground truth (Gonzalez-Castillo et al., 2015). For commonly used window lengths (WL ≥ 30sec), all window-based methods had high efficacy and similar node-to-node dFC traces, suggesting all dFC methods capture similar and stable task-evoked whole-brain FC patterns over a longer period of time. Moving average dynamic conditional correlation (DCC_MA) and delete-d jackknife correlation (dJC) were able to uncover the ongoing cognitive processes at a shorter temporal scale (WL < 30sec), while the other three window-based methods showed reduced performance. We also reported low efficacy of framewise dFC methods (i.e., dynamic conditional correlation and jackknife correlation), potentially due to inherent limitations of signal-to-noise ratio with a single time point.