Automatic Lacunae Localization in Placental Ultrasound Images via Layer Aggregation

Abstract

Accurate localization of structural abnormalities is a precursor for image-based prenatal assessment of adverse conditions. For clinical screening and diagnosis of abnormally invasive placenta (AIP), a life-threatening obstetric condition, qualitative and quantitative analysis of ultrasonic patterns correlated to placental lesions such as placental lacunae (PL) is challenging and time-consuming to perform even for experienced sonographers. There is a need for automated placental lesion localization that does not rely on expensive human annotations such as detailed manual segmentation of anatomical structures. In this paper, we investigate PL localization in 2D placental ultrasound images. First, we demonstrate the effectiveness of generating confidence maps from weak dot annotations in localizing PL as an alternative to expensive manual segmentation. Then we propose a layer aggregation structure based on iterative deep aggregation (IDA) for PL localization. Models with this structure were evaluated with 10-fold cross-validations on an AIP database (containing 3,440 images with 9,618 labelled PL from 23 AIP and 11 non-AIP participants). Experimental results demonstrate that the model with the proposed structure yielded the highest mean average precision (mAP=35.7%), surpassing all other baseline models (32.6%, 32.2%, 29.7%). We argue that features from shallower stages can contribute to PL localization more effectively using the proposed structure. To our knowledge, this is the first successful application of machine learning to placental lesion analysis and has the potential to be adapted for other clinical scenarios in breast, liver, and prostate cancer imaging.

1. Introduction

Abnormally invasive placenta (AIP) refers to a life-threatening obstetric condition in which the placenta adheres to or invades into the uterine wall. Depending on the degree of adherence or invasion, any attempt to forcibly remove the embedded tissue may lead to catastrophic maternal hemorrhage during child-birth [1]. Ultrasonography is widely used to identify women at high risk of AIP. However, recent population studies have shown that the rate of successful prenatal diagnosis of AIP remains unsatisfactory: merely between half and two-thirds [2, 3]. In a recent review [1], Jauniaux et al. evaluated the pathophysiology of different ultrasound signs associated with AIP to better understand their relevance to prenatal screening and diagnosis, among which placental lacunae are of particular interest. Placental lacunae (PL) are sonolucent spaces within the placenta that appear to be randomly distributed with irregular shapes and have unpredictable size and number in a placental ultrasound image (Fig. 1(a)). PL occur in almost all pregnancy. However, as shown in Fig. 1, numerous, large, and irregular PL are more likely to occur in AIP cases than in non-AIP cases [4].

Fig. 1.

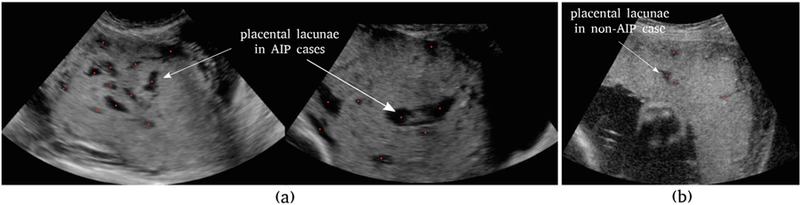
Placental lacunae (PL) in placental ultrasound images. Red dots refer to expert dot annotations. (a) two AIP cases containing numerous PL of irregular shapes and sizes, (b) a placenta (with normal pregnancy outcome) containing only a few PL.

The contributions of this paper are twofold. First, we introduce an automatic method that generates confidence maps from expert dot annotations for subsequent training, as an alternative to detailed yet expensive manual segmentation of PL. This method harnesses over-segmentation techniques to generate Gaussian-like confidence maps centered at PL by taking into account local information, such as size, shape, and texture of PL. Second, we compare three layer aggregation structures: deep supervision (DS), feature pyramid network (FPN) and iterative deep aggregation (IDA) and then propose an IDA-based fully convolutional network (FCN) for PL localization in 2D grayscale placental ultrasound images. We demonstrate its effectiveness in localizing PL by running experiments on an AIP database.

2. Methods

2.1. From Dot Annotation to Conftdence Map

Detailed human labelling, such as manual segmentation of anatomical structures, is sometimes too expensive to carry out in large-scale medical image analysis studies. In this work, we investigate a weak way of annotating images, which is referred to as dot annotation [5]. The annotation protocol requires that the centroid of the observed PL is pinpointed by the annotator and the spatial coordinates stored. As shown in Fig. 1, dot annotations pinpoint the most reasonable locations of PL in expert opinion. Learning these coordinates directly would generally require computational complexity proportional to the number of PL in the image. Instead, we present a bottom-up approach that dissociates runtime complexity from the number of PL by generating a confidence map for each image, encoding the belief that PL would occur at each pixel location. Intuitively, dot annotations correspond to peaks in confidence maps.

Previous map generation approaches tend to fit a standard, isotropic Gaussian function at each annotated dot [5,6]. Here we propose an alternative by considering the size, shape, and texture of PL in order to improve localization performance. For each labelled PL, a local patch is first cropped, centering at the dot annotation location P, as shown in Fig. 2(a). Then the simple linear iterative clustering (SLIC) algorithm is applied on the patch to cluster pixels that are close to each other in a 3-D space spanned by pixel intensity and spatial coordinates [7], as shown in Fig. 2(b). A simple cluster expansion is then performed by recursively grouping adjacent clusters of similar average pixel intensity. The resulting grouped clusters form a binary mask, as shown in Fig. 2(c). In the final step (Fig. 2(d)), a 2D Gaussian function is fit that centered at P, whose covariance matrix Σ is determined by the ellipse that has the same variance as the binary mask, such that the eigenvalues of Σ are the lengths of the major and minor axes of the ellipse, scaled by a factor $l=\frac{1}{3}$ in order to control its spread. We rescale the Gaussian function by a factor of 50 as suggested in [5], yielding the peak to be larger than 45 for most PL. By repeating this process for all PL within an ultrasound image, we generate a smoothed confidence map. Where two or more Gaussian functions spatially overlap with each other, we take the pixel-wise maximum of the overlapping regions.

Fig. 2.

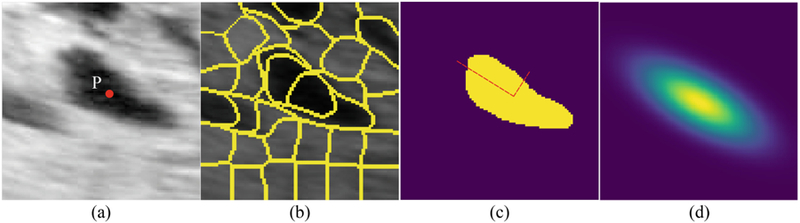
The analysis pipeline that generates a local confidence map around PL given only a dot annotation. (a) a cropped PL image with the dot annotation in the center, (b) the SLIC over-segmentation of the region, (c) a cluster expansion algorithm yielding a binary mask around the dot annotation, (d) a local confidence map is generated by fitting a Gaussian function at the labelled PL.

2.2. Lacunae Localization: Layer Aggregation Approaches

Layer Aggregation:

For convenience, we put layers that yield the same feature resolution into the same stage. FCN’s natural pyramidal feature hierarchy enables aggregations of both spatial (i.e. where) and semantic (i.e. what) information from shallower stages to deeper ones. To achieve more accurate spatial inference of PL, whose size is essentially much smaller than the placenta itself, we propose to build up non-linear pathways that explicitly aggregate multi-scale semantics and resolutions. Specifically, we investigate two generic FCN architectures that have been widely used in medical image analysis: (1) a downsampling network (DN) and (2) a U-shape network (UN). As shown in Fig. 3, DN sequentially down-samples stages, leading to semantically richer but spatially coarser features [8]. UN follows an encoder-decoder architecture, with the encoder part being a DN and the decoder part an up-sampling network that gradually restores resolution via 2×2 transposed convolution [9]. We consider three layer aggregation approaches: deep supervision (DS) [10], feature pyramid network (FPN) [11], and iterative deep aggregation (IDA) [12]. As shown in Fig. 3(a), DS concatenates intermediate side-outputs and makes the final prediction. Here a side-output is a prediction made by the output of a stage. FPN intends to enhance semantically stronger features (from deeper stages) with weaker ones (from shallower stages) via skip connection and linear pixel-wise addition. In FPN, the shallowest stage will be aggregated last. IDA, on the other hand, starts from the shallowest stage and iteratively merges deeper ones. All feature channel mismatches in Fig. 3 are resolved by 1×1 convolution and resolution mismatches by bilinear upsampling.

Fig. 3.

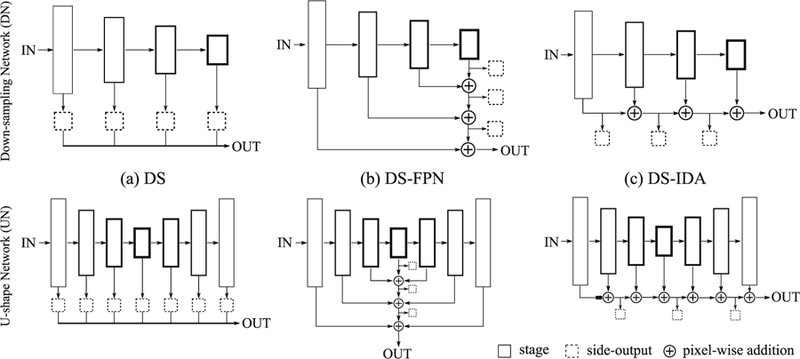
Two generic FCN architectures: DN and UN with three layer aggregation structures: (a) deep supervision (DS), (b) deeply supervised feature pyramid network (DS-FPN), and (c) deeply supervised iterative deep aggregation (DS-IDA). Intuitively, the box size is proportional to the spatial resolution and the box linewidth to the feature channel number.

To achieve accurate PL localization, we propose two layer aggregation structures, namely deeply supervised feature pyramid network (DS-FPN, Fig. 3(b)) and deeply supervised iterative deep aggregation (DS-IDA, Fig. 3(c)). We introduce a non-linear pixel-wise addition in both structures for input feature maps {x_i}. The output is σ(BN(Σ_i w_ix_i)), where σ is a non-linearity (e.g. ReLU), BN is a batch normalization layer, and w_i are convolutional weights to be learnt. Side-outputs are produced in both structures to cast additional supervision alongside the aggregation pathways. Intuitively, DS-FPN focuses more on semantically stronger features from deeper stages while DS-IDA progressively enhances spatially finer features from shallower stages. This comparison allows us to investigate the importance of features from shallower versus deeper stages in PL localization. The model output looks like a ‘heatmap’ that encodes PL localization confidence. PL centroid predictions are obtained by performing non-maximum suppression at a certain confidence level.

Loss Function:

The objective function of DS-FPN and DS-IDA are the same, which is given by $\mathcal{L}\left(\mathbf{W}\right)=\ell \left(S_{OUT},\widehat{S}\right)+\frac{1}{N}{\sum }_{i=1}^N\ell \left(S_i,\widehat{S}\right)$. Here $\widehat{S}$ is the reference confidence map, S_OUT is the final output of the model, and ${\left\{S_i\right\}}_{i=1}^N$ are N side-outputs. We cast supervision not only on the final output, but also on all the side-outputs to improve localization performance. W represents all the learnable parameters. ℓ(., .) denotes the L-2 loss between the inputs.

3. Experiments

Dataset:

34 placental ultrasound scans from 34 participants (23 AIP and 11 non-AIP) were collected as part of a large obstetrics research project [13]. Written consent was obtained with local research ethics approval. Static transabdominal 3D ultrasound volumes of the placental bed were obtained according to the predefined protocol with participants in semi-recumbent position and a full bladder using a 3D curved array abdominal transducer. Each 3D volume was sliced along the sagittal plane into 2D images and annotated by Huan Qi under the guidance of Dr. Sally Collins. The database contains 3,440 2D images with 9,618 labelled PL in total, from 60 to 140 slices per volume. A subject-level 10-fold cross-validation was performed for each model. In each fold, test data consisting of 2D image slices from 3–4 volumes were held out while images from the remaining volumes were used for training and validation.

Implementation Details:

All models were trained end-to-end using the Adam optimizer. Pre-trained models were loaded for DN as well as the encoder part of UN. The decoder part of UN was initialized by sampling from a Gaussian distribution $\mathcal{N}\left(0,\sqrt{2/n}\right)$, where n is the number of trainable parameters for each layer. The inputs were normalized to have zero mean and unit variance and resized to have the dimension of 384 × 384 × 3. Horizontal flip was used for data augmentation. The hyper-parameters were: mini-batch size 8; weight decay 0.0005; initial learning rate 0.0001. All models reached convergence after 20 epochs. All experiments were implemented in PyTorch. A 10-fold training took around 30 h on a 12 GB NVIDIA graphic card.

Evaluation Metrics:

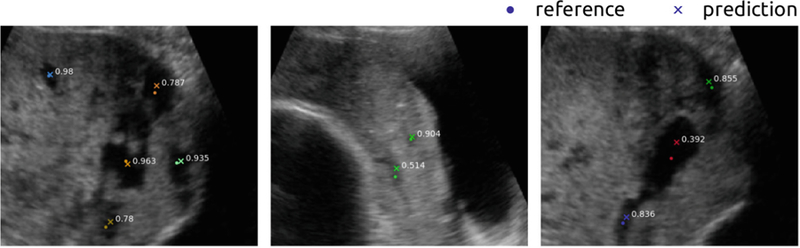
Our task requires simultaneous detection and localization. For each PL, we already have its dot annotation (x_i, y_i), i.e. coordinates of its centroid. Each PL also has a scale s_i which we define as the square root of its SLIC cluster area. Following the evaluation metrics of the COCO Keypoint Challenge, we define a Simplified Object Keypoint Similarity (SOKS) score for each prediction-reference pair indexed by $j:\text{SOKS}\left(j\right)=\exp \left(-d_j^2/2s_j^2{k}^2\right)$. d_j is the Euclidean distance between reference and prediction and k is a constant that controls the overall falloff, which is empirically set to 0.424¹. The intuition behind SOKS is that larger tolerance is given to PL of larger sizes. In practice, we found SOKS ≥ 0.3 generally yields a perceptually acceptable localization, as shown in Fig. 4. For evaluation, we compare AP_x, which denotes the average precision by thresholding SOKS at x. Specifically, any prediction with SOKS ≥ x would be marked as true positive (TP) and otherwise false positive (FP). Any undetected PL would be marked as false negative (FN). AP_x is the mean of precision over the recall interval at [0, 1]. To achieve a high score of AP_x, a model needs to have high precision at all levels of recall (or sensitivity), which is practically difficult in PL localization. We report four metrics: AP_0.3, AP_0.5, AP_0.75, and mAP. mAP is the mean of {AP_x} for x ∈ [0.3 : 0.05 : 0.95], measuring the overall localization performance at different SOKS levels. We use mAP as the primary metrics. Please refer to [6] for more details.

Fig. 4.

Example images illustrating the use of SOKS to score PL localization. In each image, a dot denotes the dot annotation (reference) and a cross denotes the prediction. The value next to a pair of dot and cross is the SOKS score between them.

Performance Evaluation:

As shown in Table 1, we chose ResNet18 and VGG16 as model backbones and ran tests for three layer aggregation structures: DS, DS-FCN, DS-IDA. We removed the first 7×7 convolutional layer and the max-pooling layer from ResNet18 such that all models contain three down-sampling operations. We also introduced skip connections in all UN models in the same way as U-Net [9]. Performances of different PL localizers are given in Table 1. The median, first, and third quartile of 10-fold results are presented. The proposed UN-DS-IDA surpasses all other PL localizers in all AP metrics. Two-tailed paired t-tests showed that mAP from UN-DS-IDA is significantly higher than those from the rest PL localizers (with p-value < 0.001).

Table 1.

The performance of different PL localizers on the test set via 10-fold cross validation. All results (%) are in the format of median [first, third quartile]. APx at three SOKS thresholds (x ∈ {0.3, 0.5, 0.75}) are reported. mAP is the primary metrics. Models are named in the format of A-B, where A is its generic architecture (DN or UN) and B its layer aggregation structure (DS or DS-FCN or DS-IDA)

Model	Backbone	mAP	AP0.3	AP0.5	AP0.75
DN-DS	ResNet18	22.8 [20.2, 26.5]	33.0 [30.3, 36.3]	29.6 [27.1, 33.8]	19.7 [16.9, 23.9]
DN-DS-FCN		28.7 [22.0, 30.0]	42.7 [34.5, 43.6]	37.5 [30.6, 39.3]	24.0 [16.9, 25.7]
DN-DS-IDA		29.7 [25.3, 34.8]	38.6 [33.8, 46.0]	36.3 [31.0, 43.9]	28.5 [24.1, 32.5]
UN-DS	VGG16	32.6 [24.1, 37.5]	41.4 [35.2, 47.2]	39.6 [31.4, 44.1]	31.3 [22.0, 36.5]
UN-DS-FCN		32.2 [28.4, 37.4]	42.3 [39.7, 46.0]	40.2 [35.7, 44.1]	31.0 [24.8, 36.8]
UN-DS-IDA		35.7 [28.4, 40.7]	44.7 [40.9, 50.1]	42.3 [36.5, 48.5]	35.3 [26.4, 37.8]

Generating Conftdence Maps:

In this paper, we proposed to use a SLIC-based approach to generate confidence maps that take into account the size, shape, and texture of PL, instead of fitting an isotropic Gaussian at each dot annotation with a fixed falloff σ. We compared these two approaches in experiments. For the latter, an isotropic Gaussian function was fit at each PL to generate confidence maps. Let p_i be the position of a dot annotation. The value at location x in the map was defined as: $C\left(\mathrm{x}\right)=A\exp \left(-{\Vert \mathrm{x}-{\mathrm{p}}_i\Vert }_2^2/{\sigma }^2\right)$, where A was set to 50 as before. With this method, the best localization was achieved by a UN-DS-IDA model at σ = 5 with mAP = 29.9%, being outperformed by the proposed SLIC-based approach. This is because the size and shape of PL are variable. There is no σ that would achieve good localization for all PL. Our proposed approach uses local information, which makes it well-suited to PL localization. Moreover, our approach leads to better visualization that learns the size and shape automatically, as shown in Fig. 5, which can be beneficial for clinical use.

Fig. 5.

Example results showing two model outputs, trained using isotropic Gaussian confidence map and the proposed SLIC-based confidence map respectively.

4. Discussion

We further investigated the effectiveness of DS-IDA by probing the localization performance of side-outputs ${\left\{S_i\right\}}_{i=1}^N$. Let the side-outputs (from left to right) in DN-DS and UN-DS be ${\left\{S_i\right\}}_{i=1}^4$ and ${\left\{{\tilde{S}}_i\right\}}_{i=1}^7$ respectively. In the 10-fold cross validation experiment, the mAP score (median) of S₁, S₂, ${\tilde{S}}_1$, and ${\tilde{S}}_2$ are 0. Starting from S₃ and ${\tilde{S}}_3$, mAP scores start to increase as expected. From this, we argue that features from shallower stages are not effectively aggregated via either concatenation (DS) or skip connection (FPN). For instance, features from the shallowest stage in DS-FPN are aggregated last, with little room for adaption and improvement. On the contrary, DS-IDA structure progressively aggregates features from shallower stages. Our experimental results indicate that features from shallower stages can indeed contribute to PL localization effectively with the proposed DS-IDA structure. One reasonable explanation is that down-sampling operation would lose certain PL-related spatial information. Aggregating shallower features compensate such loss to some extent. In addition to use in placenta assessment such as lesion detection, we believe the analysis approach could be adapted for other clinical scenarios in breast, liver, and prostate cancer imaging.