A parameterised mathematical model to elucidate osteoblast cell growth in a phosphate-glass microcarrier culture

Abstract

Tissue engineering has the potential to augment bone grafting. Employing microcarriers as cell-expansion vehicles is a promising bottom-up bone tissue engineering strategy. Here we propose a collaborative approach between experimental work and mathematical modelling to develop protocols for growing microcarrier-based engineered constructs of clinically relevant size. Experiments in 96-well plates characterise cell growth with the model human cell line MG-63 using four phosphate glass microcarrier materials. Three of the materials are doped with 5 mol% TiO₂ and contain 0%, 2% or 5% CoO, and the fourth material is doped only with 7% TiO₂ (0% CoO). A mathematical model of cell growth is parameterised by finding material-specific growth coefficients through data-fitting against these experiments. The parameterised mathematical model offers more insight into the material performance by comparing culture outcome against clinically relevant criteria: maximising final cell number starting with the lowest cell number in the shortest time frame. Based on this analysis, material 7% TiO₂ is identified as the most promising.

Introduction

Bone trauma requiring treatment with bone grafting is common and can range from reconstructive interventions after bone tumour recession, to spinal fusions and non-union fractures, which occur at a rate of 5% of all fractures. While autologous or allogeneic grafts are the current gold standard and some of the most common tissue transplants, they are associated with a high rate of surgical revisions: 17% for autologous grafting and above 30% for allografts.¹ Autografts are associated with an increased probability of fracture at the graft donor site, alongside chronic pain or neurovascular injuries, while allografts lack the benefit of cellular activity. Tissue engineered bone grafts, as a personalised therapy, have the potential to mitigate some of these risks and augment bone grafting.

Cellularised engineered grafts have been shown in preclinical trials to perform better than non-cellular constructs^2–4 in bridging critically sized defects.⁵ Osteoblasts are the cells that create mature bone tissue, via mineralisation of the pre-calcified matrix deposited by precursor cells. As the natural osteoblast precursors^6,7 and with an established status in cell therapies, mesenchymal stem cells (MSCs) are the preferred cell source.^8–10 MSCs are valued for their potential for self-renewal, multilineage differentiation¹¹ and immunosuppressing activity in vivo,¹² which can facilitate allogeneic transplantation.^13,14

In order to ensure the functionality of the graft, the cell number delivered needs to be sufficiently large to initiate healing.^10,13 This often necessitates the in vitro expansion of a sample of a patient’s cells.¹⁵

Traditionally, cell cultures are expanded as monolayers in tissue culture T-flasks, and the standard techniques such as manual culture passaging may be damaging to the cells. Shear stresses are experienced during centrifugation, pipetting and tapping used to physically detach the adherent cells from their culture substrate, while trypsinisation destroys essential extracellular matrix (ECM) ligands, and cell mass is lost during transfer.¹⁶

An alternative to monolayer cultures is the use of microcarriers as attachment vehicles for the cells, which can eliminate the need for cell culture passaging. Microcarriers have successfully been used to culture MSCs in dynamic bioreactor systems such as spinner flasks.¹⁷ Microcarriers are typically used to expand cells and they are subsequently removed from the final product. Microcarrier material properties such as stiffness and coating can help differentiation into the desired lineage, and new developments such as temperature and electro- or magnetic responsive materials are making cell detachment easier.¹⁸

However, for bottom-up tissue engineering, it is necessary to create microcarriers from an implantable material. An added benefit to using such microcarriers is provision of a three-dimensional (3D) growth environment which preserves cell-to-cell signalling. This encourages the formation of cellular clusters, prevents de-differentiation and loss of cell functions.¹⁹ Resorbable microcarriers are especially suitable for bottom-up tissue engineering as they allow natural, homogeneous tissue development with the gradual replacement of the carrier material with ECM and do not require cell mass removal at the end of the expansion. The success of the strategy depends on the cellular affinity for attachment to the carriers, which is determined by their topological properties and chemical composition.¹⁵

Phosphate-based glasses are suitable microcarrier materials as they are biocompatible, biodegradable and easy to manufacture. Their biocompatibility can be improved by impregnation with different oxides, for example, cobalt oxide (CoO) has been shown to increase the density of the apatite layer formed after culturing in foetal bovine serum (FBS) and to improve mechanical strength.²⁰ Titanium dioxide (TiO₂) upregulates genes responsible for bone formation and promotes bone tissue deposition after implantation in vivo.²¹

3D tissue-engineered constructs of sufficiently large volume to expand a clinically meaningful number of cells are susceptible to mass transfer limitations of nutrients and waste products in diffusion-dependent cultures.^22–24 Such constructs often have a proliferating periphery and a necrotic core due to gradients in oxygen levels from the construct boundaries inwards, resulting in oxygen deprivation in the construct centre.²³ For this reason, bioreactors that provide dynamic mixing of the culture medium via convection to augment diffusive transport are preferable as cell expansion vehicles. They are designed to be automated to provide the required controlled environment, crucial for developing reproducible protocols.^23,25 Apart from improving oxygenation in the culture, bioreactors provide flow-induced shear stress which stimulates the naturally mechanosensitive differentiation of bone tissues²⁵ and triggers deposition of mineralised ECM and the expression of bone-marker proteins.^26,27 Bioreactors, thus, recreate the in vivo environment more realistically than static cultures.^25,28 While using bioreactors has many inherent benefits, such as increased osteogenic differentiation, improved proliferation and higher seeding efficiency and homogeneity of cell spreading in the engineered constructs,²⁹ bioreactor-grown bone grafts have not performed significantly better after implantation in vivo. Tailoring the bioreactor culture settings to maximise cell-yield and produce clinical sized tissues is challenging.

Modelling is a natural tool to apply in this setting, as it provides a framework to investigate the effect of the different factors in the tissue culture. It can build on experimental data and simulate more setups, configurations and operating conditions. These simulations can predict the culture outcome under new circumstances and direct future experimentation, thus streamlining the discovery of favourable culture protocols and minimising the need for extensive time-consuming and costly experimentation. These capabilities of modelling offer the potential to optimise the tissue engineering strategy.

In order to build highly informative models, parameter values must be found which ensure that simulations match the cell and material-specific behaviour investigated. Finding the coefficients describing cellular behaviour (for instance, rate of proliferation, uptake of nutrients, or secretion of ECM) is a key step in the development of models which can be used to improve the culture conditions. While some hypotheses about tissue morphogenesis in vitro can be tested with non-parameterised models,^30,31 parameterisation is essential to make the quantitative predictions required to fine tune bioreactor settings and design tissue engineering protocols for clinical applications. Performing a robust parameterisation requires a thorough knowledge of the experimental procedure and the raw data obtained. That is why comparisons to previously published data are often only qualitative.³²

Even when the parameterisation is performed in-house, it might be possible to find only a limited number of coefficients.³³ It is especially challenging to find the parameters which describe the biological behaviour – for example, oxygen consumption rate and proliferation rate as done by Zhao et al.³⁴ A good strategy to find these biological coefficients is to perform a series of small-scale experiments, investigating the cellular response to the different conditions of interest. Parameterised models are even more robust when validated against separate experiments, showcasing the repeatability of the modelling approach.

Parameterised models are often data fitted to experimental setups to show the simulations match the measurements made,^34–36 but the model is only rarely then used to gain insight into the effect of culture conditions.^33,37–40 Operating settings for future in vitro experiments have hardly been provided from models parameterised to cell growth data in particular.

This study aims to demonstrate how modelling can be an invaluable tool aiding experimentation in developing and improving culture protocols for bone tissue engineering. We outline the development of a parameterised mathematical model describing the growth behaviour of a microcarrier culture under static conditions. A non-phenomenological model of cell growth and metabolism is presented first. The cell growth parameters in the model are then parameterised to cell number data from small-scale experiments which investigate the cell growth potential of four phosphate glass biomaterials. In this study, the MG-63 osteosarcoma cell line is used to model osteoblastic cells in culture.

The data-fitted growth parameters for each microcarrier biomaterial are used to simulate the cell yield (fold increase from the starting cell number) at different initial (seeding) cell densities and culture duration. The objective is to use the parameterised mathematical model to investigate how to reduce the culture duration and minimise the seeding cell number (with view of reducing the invasiveness of the clinical procurement of stem cells for engineered bone grafts) while still achieving the required cell yield to promote healing. In this way, the performance of the different biomaterials is compared, the material with the greatest potential is identified and more efficient combinations of biomaterial, cell seeding number and culture duration are proposed for future in vitro experiments.

Materials and methods

Experimental work

Experimental protocols are described in detail in Peticone et al.⁴¹ and De Silva Thompson et al.,⁴² and briefly overviewed here.

Glass preparation and microcarrier fabrication

Phosphate glasses with different concentrations of CoO and TiO₂ were prepared as described in Abou Neel et al.^21,43 The chemical composition of the glasses is shown in Table 1. A previous study by Guedes et al.¹⁶ found that 5 and 7 mol% TiO₂ conferred a stable degradation rate of the phosphate carriers, which motivated the use of these particular concentrations. Two non-cytotoxic CoO concentrations were also examined: 2 and 5 mol%,⁴¹ as CoO has been found to encourage in vitro angiogenesis. Spherical phosphate glass microcarriers were manufactured following the procedure set out in Guedes et al.¹⁶ and sieved down to spheres with diameters between 63 and 106 μm.

Table 1.

Composition of the four different bioactive phosphate glass materials.^41,42

Glass type	Compound concentration (mol%)
	P2O5	CaO	Na2O	TiO2	CoO
5% TiO2	50	30	15	5	0
7% TiO2	50	30	13	7	0
2% CoO	45	28	20	5	2
5% CoO	45	25	20	5	5

MG63 osteoblast culture: cell growth and metabolism assays

Cell culture experiments were conducted with the human osteosarcoma cell line MG-63. A monolayer of microcarriers (5 mg/well) was seeded in ultra-low attachment 96-well plates (Corning Costar^®) with 1.5 × 10⁴ MG-63 cells per well (seeding cell density of 4.66 × 10⁴ cells/cm²). The cells were cultured in 150 μL of Dulbecco’s Modified Eagle Medium (DMEM), low glucose (1 g/L), supplemented with GlutaMAX, 10% FBS and 1% antibiotic/antimyocitic (ThermoFisher Scientific). They were incubated in static conditions at 37°C and 5% CO₂ for up to 14 days, replacing the medium every 2 days.

Cell proliferation was measured with the Cell Counting Kit-8 (CCK-8, Sigma) on the basis of absorbance at 450 nm detected in a Safire2 plate reader (Tecan). Metabolite concentrations (dextrose and lactate) are measured in an YSI 2300 STAT Plus enzyme-reaction analyser (YSI). MG-63 cells seeded as a two-dimensional (2D) monolayer on 96-well tissue-grade culture plastic plates (ThermoScientific) (sample sets seeded with 0.5 or 1.5 × 10⁴ cells/well) and cultured under the same conditions were used as positive control. Readings were taken at the end of the first day in culture (day 1), and subsequently every 2 days until day 13.

Statistical methods

Samples were analysed in triplicates and data are presented as mean ± standard deviation (SD). One-way analysis of variance (ANOVA) tests using the software Minitab were performed to establish statistical significant difference between the different biomaterial data sets.

Mathematical model

A mathematical model tailored to the experimental setup was created to simulate the behaviour of the cell cultures, with the goal of identifying coefficients which describe cell growth for each biomaterial used in the experiments. The domain of the model was the media inside a single micro-well from the 96-well plates where the cells were cultured (Figure 1). Since quantitative data were collected for cell number, glucose and lactic acid concentrations, the model was built on a system of differential equations which examined the behaviour of these variables, plus oxygen concentration, in the well. Initial and boundary conditions were selected to describe the experimental setup, and dimensions for the geometry of the truncated conical well were informed by the manufacturers’ specifications (Table 2).

Figure 1.

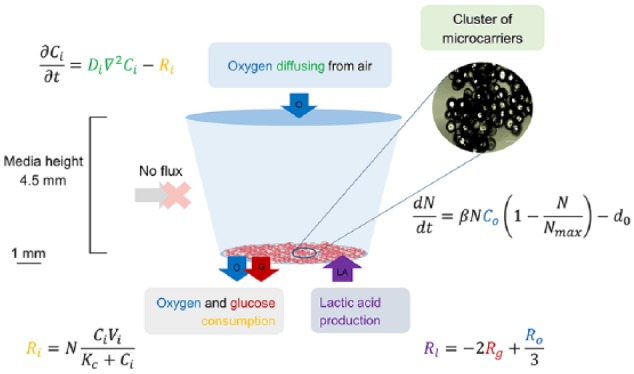
A graph illustrating the model setup and equations. Cells were seeded on microcarriers which sit on the bottom of a well in a 96-well plate. Enough carriers were used to cover the surface of the bottom of the well, which was assumed as the seeding area.

Table 2.

List of fixed model parameters, based on the experimental setup and geometry.

Parameter	Value	Units	Description
Rb	0.0032	m	Radius of the bottom of the well
Rtm	0.0033	m	Radius of the top of the media
Hm	0.0045	m	Height of the media
N 0	4.66 × 108	cells/m2	Initial cell density (15,000 cells)
Co(0)	0.218	mol/m3	Initial oxygen concentration
Cg(0)	5.55	mol/m3	Initial glucose concentration
Cl(0)	0	mol/m3	Initial lactic acid concentration

The cells were seeded on the microcarriers, which were assumed to cover the entire bottom surface of the well (Figure 1). Because the carriers were denser than water, they were not buoyant and rested on the bottom of the well. Therefore, the cells were not modelled explicitly but as an infinitely thin layer on the bottom of the well. Cell growth was described by an ordinary differential equation, whereby change in cell count was caused by cell proliferation and death as governed by the logistic growth law^44,45

$$\frac{dN}{dt}=\beta N{C}_o\left(1-\frac{N}{N_{max}}\right)-d_0,$$ (1)

where N is the cell density (cell/m²), β is the coefficient of proliferation (m³/(mol s)) and d₀ is a cell death constant (cell/(m² s)). The coefficients β and d₀ were found for each biomaterial by fitting to the experimental data. The death rate is treated as constant based on experimental observations (data not shown), and in order to adopt a simplest-first modelling approach (although we note that this could be readily adapted to incorporate further complexity in the future). If the cell density reaches zero, the death rate d₀ is set to zero. The proliferation term in equation (1) captures oxygen and cell-density-dependent growth. Osteoblast behaviour (proliferation and osteogenesis) has been shown to be sensitive to oxygen concentration, with normoxia (21% oxygen partial pressure (PO₂)) enhancing alkaline phosphatase activity and collagen synthesis, while severe hypoxia (less than 1% PO₂) suppresses proliferation.⁴⁶ Here, it was assumed the cell density N is linearly dependent on the local oxygen concentration, C_o (mol/m³), as oxygen concentration in the media did not fall under 10% PO₂. The saturation or maximum cell density parameter, N_max (cell/m²), is a cell type–specific constant and is defined by the maximum physical space the cells can occupy. It was empirically evident in the experiments as the density at which confluency was reached and cell growth slowed down, and we found this density for individual materials by parameterising the model against the experimental data on cell number. The initial cell density, N(0) = N₀ = 4.66 × 10⁸ cells/m², corresponded to seeding 15,000 cells on the well base. Table 2 lists all other experimentally fixed parameters.

Distribution of nutrients (oxygen and glucose) and waste products (lactic acid) were modelled by means of a system of diffusion equations

$$\frac{\partial C_i}{\partial t}=D_i{\nabla }^2{C}_i,$$ (2)

where C_i refers to the chemical concentration, and i is an index standing for oxygen (o), glucose (g) or lactic acid (l). The medium was assumed to have the same physical properties as water (density, viscosity), and diffusion coefficients in water for each solute were found in the literature and listed in Table 3. Due to the longer time scales of matrix secretion in comparison with cell proliferation (days vs hours), effects of matrix deposition on the diffusion coefficients were neglected in the initial analysis, which only considered the first week of culture.

Table 3.

List of non-fixed model parameters found in the literature.

Parameter	Estimated value	Units	Description	Reference
Nmax	3.5 × 1014	cells/m2	Max cell density	Unpublished work by R.J. Shipley
β	1.60 × 10−4	m3/(mol s)	Cell proliferation coeff.	Unpublished work by R.J. Shipley
d 0	1.40 × 104	cells/(m2 s)	Cell death coeff.	Unpublished work by R.J. Shipley
Vo	2.55 × 10−17	mol/(cell s)	Max consumption rate for oxygen	47, 48
Vg	3.08 × 10−15	mol/(cell s)	Max consumption rate for glucose	49–52
Ko	3.33 × 10−3	mol/m3	MMK constant for oxygen	47, 48
Kg	4.63	mol/m3	MMK constant for glucose	49–52
Do	1.91 × 10−9	m2/s	Oxygen diffusion coeff. in water	53–56
Dg	6.14 × 10−10	m2/s	Glucose diffusion coeff. in water	53, 56, 57
Dl	7.95 × 10−10	m2/s	Lactic acid diffusion coeff. in water	53, 56

MMK: Michaelis–Menten kinetics.

Initial and boundary conditions

Since the cell layer was assumed to be infinitely thin and was not modelled explicitly as a separate domain, the terms for the consumption or production of the metabolites (M_i) (equations (4) and (5)) were inputted in the model as flux (J (mol/m² s)) boundary conditions on the bottom of the well

$$M_i=-\mathit{n}\cdot \mathit{J},$$ (3)

where n is the unit normal vector pointing outward of the specified surface. Consumption of oxygen or glucose was set as an outward flux, while lactic acid production was represented by an inward flux.

Metabolic consumption of oxygen and glucose was modelled using Michaelis–Menten kinetics (MMK)

$$M_i=N\frac{V_i{C}_i}{C_i+K_i},$$ (4)

where V_i (mol/(cell s)) is the maximum rate of the reaction for the given chemical denoted by subscript i (oxygen or glucose), while K_i (mol/m³) is the Michaelis–Menten constant which is equal to the concentration at which the reaction rate is half the maximum, V_i. They are both empirical cell type–specific parameters, values for which were found in literature (Table 3). MMK is commonly the equation of choice for modelling consumption of these nutrients.^32,34,58 Buerk and Saidel⁵⁹ found that in comparison with zero and first-order kinetics, it is the one that most closely represents theoretically the consumption of oxygen in brain and liver tissues.

Production of lactic acid was coupled to the consumption of oxygen and glucose, using the relationship between glycolysis and aerobic respiration⁵³

$$R_l=-2R_g+\frac{R_o}{3},$$ (5)

A constant oxygen concentration (0.218 mol/m³) boundary condition was imposed on the top of the domain to account for oxygen diffusing from the air into the media. Oxygen, glucose and lactic acid were not subjected to any other boundary conditions apart from the flux at the bottom (equation 3) and the ‘no flux’ condition applied on all other boundaries

$$0=-\mathit{n}\cdot \mathit{J},$$ (6)

Representative of the culture media used in the experiments, oxygen concentration was initially set at C_o(0) = 0.218 mol/m³ throughout the domain (in equilibrium with 21% PO₂ in air). The initial glucose concentration was C_g(0) = 5.55 mol/m³ as indicated by the media (DMEM ThermoFisher Scientific) product specifications. Initial concentration of lactic acid in the media was set to nil (C_l(0) = 0 mol/m³). These initial conditions as well as experimentally imposed geometry parameters are listed in Table 2.

Model nondimensionalisation

A dimensionless version of the cell density equation was obtained in order to simplify the process of data fitting by identifying the dominant physical balances in the system and reducing the number of free parameters.

The rescaling procedure was done by introducing the following new rescaled variables: $\widehat{n}$, $\widehat{t}$, $\widehat{x}$, ${\widehat{c}}_i$ (where i is an index standing for oxygen (o), glucose (g) or lactic acid (l)), which are related to the original variables via the following rescalings

$$\begin{array}{l}N=\widehat{n}{N}_0,t=\widehat{t}T,x=\widehat{x}L,C_i={\widehat{c}}_i{C}_i(0)\\ \mathrm{and}{C}_l=\widehat{l}{C}_{la},\end{array}$$ (7)

where L = 1 m is the characteristic length, C_la = 1 mol/m³ is the characteristic lactic acid concentration and T is a parameter representing the proliferation time scale

$$T=\frac{1}{\beta C_o(0)},$$ (8)

Under this rescaling, the cell density equation (1) becomes

$$\frac{d\widehat{n}}{d\widehat{t}}={\widehat{c}}_o\widehat{n}\left(1-\frac{\widehat{n}}{N_{max}/N_0}\right)-P,$$ (9)

where P is defined by

$$P=\frac{d_0}{\beta N_0{C}_o(0)},$$ (10)

combining both original growth parameters, $\beta$ and $d_0$.

Rescaling the diffusion equation with the new variables led to the following nondimensional equation for oxygen, glucose and lactic acid

$$\frac{\partial {\widehat{c}}_i}{\partial \widehat{t}}={\chi }_i{\nabla }^2{\widehat{c}}_i,\mathrm{where}{\chi }_i=\frac{D_{i}T}{L^2},$$ (11)

After the rescaling, the boundary conditions imposed on the bottom of the well for the metabolic reactions of oxygen, glucose and lactic acid (equations (4) and (5)) become respectively

$${\widehat{R}}_i=\frac{-{\gamma }_i{\widehat{c}}_i\widehat{n}}{({\widehat{c}}_i+{\kappa }_i)}\mathrm{and}{\widehat{R}}_l=2{\widehat{R}}_g-\frac{{\widehat{R}}_o}{3},$$ (12)

where the dimensionless coefficients are known (functions of fixed and literature-found parameters listed in Tables 2 and 3) and are defined as follows

$${\gamma }_i=\frac{N_0{V}_{i}L}{C_i(0)D_i}\mathrm{and}{\kappa }_i=\frac{K_i}{C_i(0)},$$ (13)

The dimensionless initial conditions are as follows

$${\widehat{c}}_o(0)=1,{\widehat{c}}_g(0)=1,{\widehat{c}}_l(0)=0\mathrm{and}\widehat{n}(0)=1,$$ (14)

Adding a normal distribution function for the initial cell density

Cell number experimental data exhibited relative SDs in the order of 20% (see Figure 4 and section ‘Experimental data’). In order to introduce such level of variability in the model, we had to consider the reasons behind this.

Figure 4.

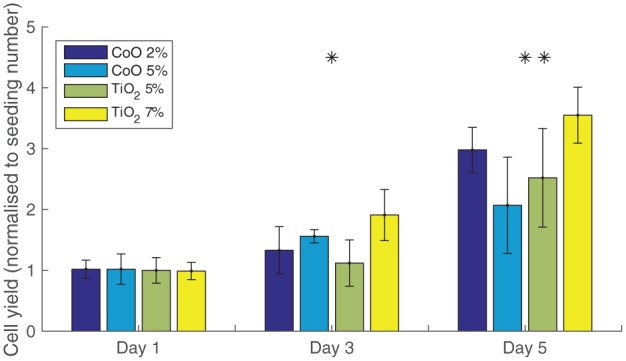
A graph of experimental cell yield (cell number normalised to seeding number) obtained with each of the four bioactive glass materials in static culture. Seeding number is 15,000 cells. The presented data are the average of three biological repeats each. The error bars are the standard deviations of each sample. One-way ANOVA test for statistical significance between material performance at each time point is performed. A 95% confidence interval is indicated by a *, while a 99% is denoted by **. Only the time points used for parameterisation are presented for clarity. The material factor has a significant effect on cell yield in the crucial period of highest proliferation (days 3, 5).

One possible explanation is that this was caused by a variation in the seeding cell number, because it is hard to precisely count and control the number of cells seeded in each experimental trial.

Sensitivity of final cell densities to changes in N₀ is substantial in the model. A 10% increase in initial cell density results in 64% increase in cell yield, while a 10% reduction in seeding density results in a 87% drop in cell yield. This shows that the model is very sensitive to the exact seeding density in the experiments, which is unknown.

To capture the inherent experimental variability in the seeding number, we introduced a normal distribution function to define N₀. The mean of the distribution was set to the intended seeding density (4.66 × 10⁸ cells/m²), while the SD was informed by the experimental data on day 1 (Figure 2). Fifty simulations were performed, each simulation run sampling from this normal distribution. Compiling the results from the 50 simulations, an approximately normal distribution of final cell densities was produced which was comparable with the experimentally reported cell data at the corresponding time point. The cell growth simulations also mimicked the experimental replacement of culture media by resetting metabolite concentrations to initial conditions at the appropriate time.

Figure 2.

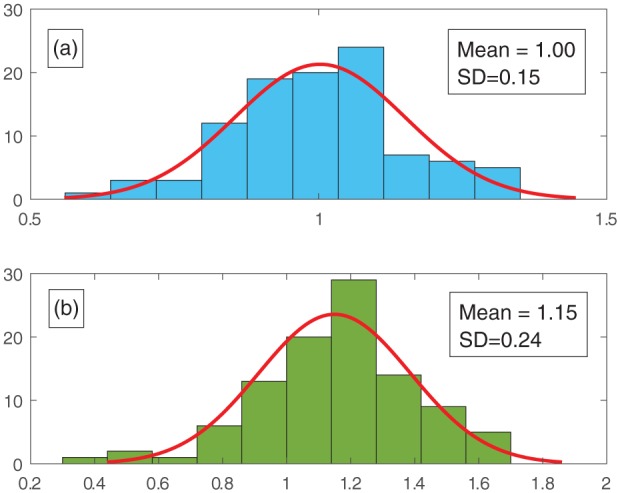
A graph demonstrating how the model mimics experimental variability as explained in section ‘Adding a normal distribution function for the initial cell density’. (a) An example normal distribution of initial cell density, used in the simulations for material 2% CoO, is plotted and (b) the resulting distribution of final cell densities is shown. All values are normalised to N₀ = 4.66 × 10⁸ cells/m² corresponding to seeding with 15,000 cells. The final cell density shown here is taken after 1 day of simulated culture. A Shapiro–Wilk test (p > 0.1) was performed to confirm a normal distribution in the final cell number distribution (n = 100).

Another explanation for the large deviations in the experimental data is that the cells can experience a range of growth behaviours in response to the culture conditions. In the context of the mathematical model, this can be represented by using probability density functions to describe the growth parameters. Analysis assessing which of the two proposed hypothesis is dominant revealed that the model was more sensitive to deviations in the starting cell density rather than in the growth parameters for values of β below 70 cm³/(mol s). Three out of four of the material-specific proliferation parameters found in the course of the model parameterisation fall below this value (Table 4). Supported by inaccuracies in cell counting methods of up to 30% and by reported static seeding efficiency of 60%,³⁰ it was decided to describe the starting cell density by a probability density function.

Table 4.

Values for the growth parameters specific to each bioactive glass composition used in the static cell culture in vitro experiments, found through data fitting.

Material type	β (m3/(mol s))	P	d0 (cells/(m2 s))	Floating	R 2
5% TiO2	5.5 × 10−5	0.58	3240	Day 3	0.93
7% TiO2	9 × 10−5	0.55	5030	Day 4	0.99
2% CoO	6 × 10−5	0.60	3660	Day 3	0.97
5% CoO	3.5 × 10−5	0.38	1350	N/A	0.95

Parameter values

A large number of the model parameters were initially found in literature and were used in the model with varying level of confidence in their accuracy. They are listed in Table 3 in the order of increasing confidence in the reported value.

For instance, we regard the coefficients of diffusion for oxygen, glucose and lactic acid found in literature as highly reliable. Both theoretical and experimentally measured values for the diffusion coefficients of each chemical species have been reported. These reported values are consistently in the same order of magnitude and an averaged value is used in our simulations.

The metabolism parameters have no (in the case of glucose and lactic acid) or a relatively low level of impact on the outcome of interest in our model: the cell growth in the culture. Therefore, we used an averaged value for the glucose and oxygen metabolism parameters from the reported values. The reported values for oxygen were all consistent in the order of magnitude and the values were quoted for chondrocytes and fibroblasts, which are relatively close to osteoblasts. As we do not have any experimental data on oxygen concentration in the culture under investigation, these values are satisfactory. It is possible to parameterise the glucose metabolism parameters to the experimental metabolite data, but this is not prioritised as this element is not modelled to impact cell growth.

In contrast, the cell growth parameters are scarcely reported in the literature, and no values for either were found for the same cell type or even species. These values are also inherently dependent on the experimental setup in addition to the cell type. As the most dominant determinants of culture growth, it was prioritised to determine the proliferation and death parameters through data fitting to the experimental results summarised in section ‘Experimental data’. The procedure for this is overviewed next.

Parameterisation

Parameterisation of the model was performed by varying the relevant growth parameters (β and P), examining their effect on the final cell number and comparing this to the cell numbers measured experimentally (Figure 4). The goal was to maximise the statistical R² value defined by

$$R^2=1-\frac{S{S}_{err}}{S{S}_{tot}}=1-\frac{{{\displaystyle \sum }}_i{\left(y_i-{\widehat{y}}_i\right)}^2}{{{\displaystyle \sum }}_i{\left(y_i-\overline{y}\right)}^2}$$ (15)

where SS_err is the sum of squared residuals, SS_tot is the total sum of squares, y_i is an experimental data point, ${\widehat{y}}_i$ is the equivalent simulation point and ${\widehat{y}}_i$ is the average of all experimental data points. The growth parameters which produced the highest R² value looking at data from days 1 to 5 were chosen as the data fits and used in the following simulations predicting cell growth under different culture conditions.

Model implementation and solution

The model equations were implemented and solved in COMSOL Multiphysics, Version 5.4 base system, where the ‘Transport of Chemical Species’ physics package was used for the diffusion of the metabolites – oxygen, glucose and lactic acid. The standard transport model (diffusion-only) was solved in 24 s, where the normal in-built mesh setting corresponding to 8505 mesh elements was used. Analysis of sensitivity to the mesh size found that for O₂ concentration at a single point, the error between results obtained with the normal mesh size and those obtained with the extremely fine mesh size (1,135,776 mesh elements) is less than 0.5%. The gain in accuracy of the results did not justify the increase in computational time to 40 min.

Results and discussion

Experimental data

Here, we provide a brief summary of the experimental data used to parameterise the model, which is presented in detail in Peticone et al.⁴¹ (for CoO-doped bioactive glasses) and in De Silva Thompson et al.⁴² (for TiO₂-doped bioactive glasses).

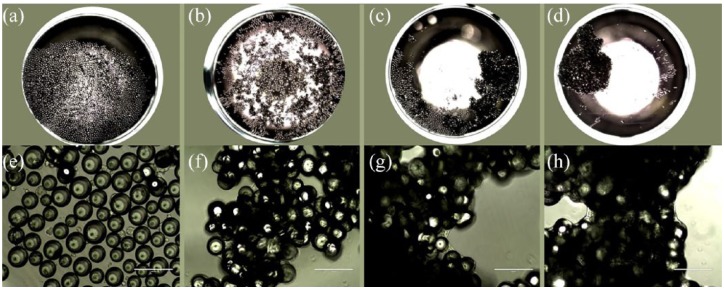
Figure 3, a phase contrast microscopic image, demonstrates the proliferation and self-assembly into clusters of the MG-63 cells seeded on glass microcarriers over 14 days. We present the cell growth data only for the first three time points, as they are used to parameterise the model (Figure 4). Upon initial inspection, the materials with 2% CoO and 7% TiO₂ stimulate the highest cell growth. The measured relative SD in the data ranges from 15% to 30%, averaging at 20%, which indicates a substantial level of variability in the culture outcome. Further investigation of the statistical significance of the effect of the material factor at each separate time point with a one-way ANOVA test reveals that the material composition has a significant impact on cell yield during the most intense cell growth phase (from days 3 to 7 (not shown)). At the final two experimental time points (not shown), a slowdown in cell growth across all materials is observed, rendering the effect of different material compositions less pronounced.

Figure 3.

A phase contrast microscopic image of osteoblast microcarrier (material 5% TiO₂) culture in 96-microwell plates. Seeding number is 15,000 cells. (a–d) are taken at 2× magnification, with a scale bar of 2000 µm and (e–h) at 20× magnification (scale bar of 200 µm). (a, e) represent the culture at day 1, (b, f) at day 2, (c, g) at day 9 and (d, h) at day 13.

These data provide means of calibrating the model to in vitro experiments to obtain specificity with regard to the culture setup and cell-type. They also motivate the choice to distinguish between the growth parameters of each biomaterial and to build a robust quantitative framework capable of predicting what cellular response they would elicit.

Modelling results

Determining the maximum cell density parameter

The maximum cell density parameter is found first. It is assumed that the same parameter value should apply to the tissue culture control samples as well as the microcarriers samples, as this parameter is cell-type specific and determined in part by the available space.

There is evidence of cell growth saturation at high cell densities in the control samples. This is an indicator that the maximum cell density, N_max, of this specific anchorage-dependent cell line (MG-63 carcinoma osteoblasts) can be determined using the model.

Experimental data show that the cell number at the final two time points exceeds the range which could be measured by the machine, so we focus on data up to day 7 only. This does not hinder the investigation into the slowdown in proliferation, as that still occurs even at this shorter time period.

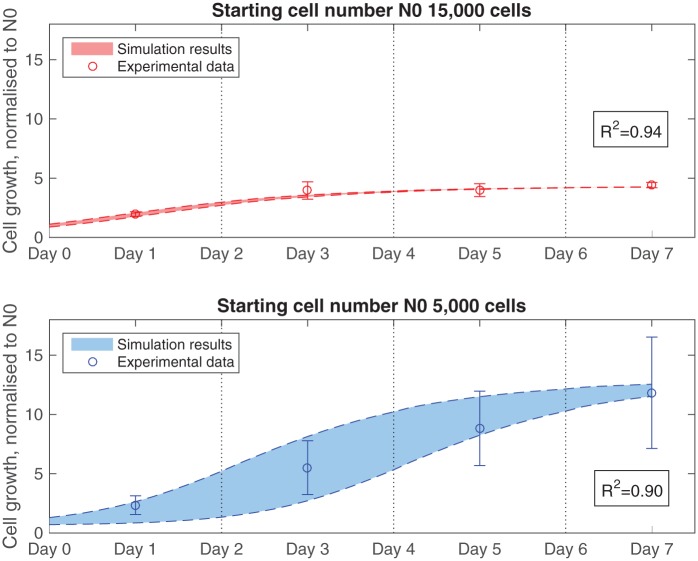
Two control data sets are used in the parameterisation procedure: one set seeded with 15,000 cells initially and one with 5,000 cells. The average relative SD measured in vitro for each control group, 12% for the 15,000 cells set and 30% for the 5,000 cells set, is used in the simulations in line with the methodology set out in section ‘Adding a normal distribution function for the initial cell density’.

The model assumes that the growth parameters are the same regardless of the cell number at the time for both data sets, while the effect of the population size is applied through the maximum cell density parameter. Accordingly, N_max is the value at which the same values for β and d₀ could make the model match simultaneously the two control data sets to satisfaction (R² above 0.85). Values for the proliferation coefficient, β = 8 × 10⁻⁵ m³/(mol s), and the death constant, d₀ = 1.7 × 10³ cells/(m² s), produced good fits for both sample sets at maximum cell density N_max = 2.4 × 10⁹ cells/m² (Figure 5).

Figure 5.

Model fit to experimental data for control groups with seeding numbers of 5,000 and 15,000 cells. Growth parameters are set as follows: β = 8 × 10⁻⁵ m³/(mol s), d₀ = 1.7 × 10³ cells/(m² s) and N_max = 2.4 × 10⁹ cells/m². The average relative standard deviations measured in vitro for each control group, 12% for the 15,000 cells group and 30% for the 5,000 cells group, are used in the simulations. The vertical dotted lines denote the points when model is reset to initial conditions to mimic replacement of the culture medium.

This value for N_max agrees well with a theoretically derived value of 1.4 × 10⁹ cells/m², which estimates the number of cells that can fit in a unit area, given the average osteoblast diameter is 20–30 μm and the cells cover the entire bottom surface of the well.

Determining the material-specific growth parameters

Parameterisation is done for paired values of β (proliferation parameter) and P (combined growth parameter) since the timescale of the reduced model is dependent on the value of β and each timescale is associated with a different optimal P value. The strategy used to fit the model parameters to the experimental cell growth results for the microcarrier cultures is outlined next.

Day 0 is considered a settling period due to the very slow growth observed experimentally during it (Figure 4). Simulations are started at day 1, using the experimentally reported mean and SD for cell density at day 1 to inform the initial cell density in the model. All paired values for β and P which are found to match growth at day 3 are then evaluated by their ability to predict growth at day 5 as described in section ‘Parameterisation’.

Hypothesis: floating of microcarriers and increase in surface area

It is observed that the growth between days 3 and 5 increases substantially for all but one of the microcarrier materials. In line with reports characterising these bioactive glass compositions,¹⁶ it is hypothesised that during microcarrier clustering, glass is dissolved and replaced by cells and cell-secreted ECM, resulting in increase in the buoyancy of the clusters and allowing them to float. This is observed experimentally as well, with some level of detachment of the microcarriers from the bottom detected. Since the carriers are 3D objects, this would free up more space for the cells to attach, effectively doubling the available area and increasing the rate of proliferation of the cells.

This hypothesis is implemented in the model by doubling the maximum cell density parameter, N_max, to recreate floating, instead of doubling the seeding area. Cell number simulations are run without floating and with two different time points when floating commences: days 3 and 4. The fit to experimental cell number data of all three conditions is compared for each material and evaluated for its suitability. For instance, in Figure 6, the results of these comparisons for material type 5% TiO₂ are presented. In this case, the closest match is achieved when floating begins on day 3. In contrast, for material 7% TiO₂, this is found to be day 4. These results further support the suitability of this hypothesis, because they match the relative rates of dissolution reported by Guedes et al.¹⁶ in their material characterisation study. There, the 5% TiO₂ microcarriers demonstrated a slightly greater rate of degradation and Ca²⁺ release than the 7% TiO₂ samples. Nevertheless, this hypothesis needs to be validated experimentally, taking into account the effect of the cells on the dissolution rate.

Figure 6.

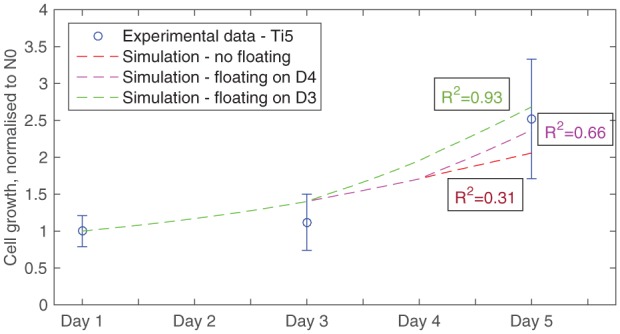
Model fits to experimental data for material 5% TiO₂, comparing scenarios (1) without introducing floating of microcarriers, and with floating starting at (2) day 4 or (3) day 3. Growth parameters are set as follows: β = 5.5 × 10⁻⁵ m³/(mol s), d₀ = 3.24 × 10³ cells/(m² s) and N_max = 2.4 × 10⁹ cells/m², while simulations were run with seeding cell number = 15,000 cells.

With this further development in the model, parameter fits for the growth parameters of each material are found. The values for the proliferation β, the combined growth P and death d₀ parameters are listed in Table 4 for all four materials, as well as the estimated point of ‘floating’ of the microcarriers and the achieved R² value indicative of the goodness of fit of the parameterisation.

Figure 7 demonstrates how well the model simulations fit the in vitro data after parameterisation for material 7% TiO₂. A value of R² = 0.99 is obtained for the statistical fit found with the corresponding parameters listed in Table 4.

Figure 7.

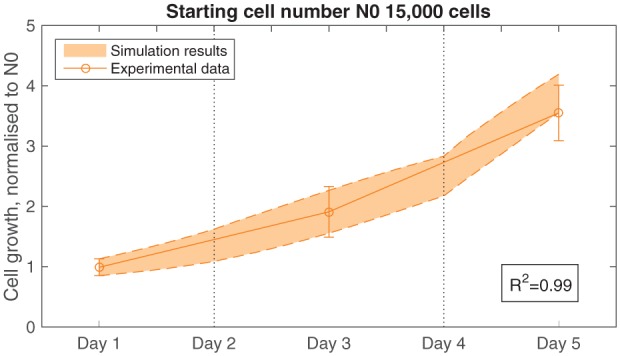
Model fit to experimental data for material 7% TiO₂, with floating starting at day 4. Growth parameters are set as follows: β = 9 × 10⁻⁵ m³/(mol s), d₀ = 5.03 × 10³ cells/(m² s) and N_max = 2.4 × 10⁹ cells/m². The initial standard deviation is 14%. The vertical dotted lines denote the point when the model is reset to initial conditions to mimic replacement of the culture medium.

In the following section, we demonstrate how the values of the growth parameters can be used to compare the growth performance of the materials when applied to particular clinically relevant culture scenarios.

Informing future in vitro experimental work

Here, we demonstrate how the model and the material-specific growth parameters can be employed to make suggestions for future in vitro experiments. Requirements for specific culture operating settings (seeding cell number and final cell number or culture duration and final cell number), motivated by the clinical application of bone grafting, can be applied in the model to inform the choice of the remaining condition (culture duration or seeding number) and the selection of the microcarrier biomaterial. We explain why these culture operating settings are of interest and show how they can be chosen with the help of the model based on particular desired in vitro results. It is important to point out that using the model to make these predictions is based on the assumption that the predicted performance is preserved at larger scales (the cells have not exhausted their growth potential).

A common strategy in the clinic to harvest patient stem cells for a bone graft would be to aspirate MSCs from the patient’s bone marrow. Typical MSCs concentrations in bone marrow aspirate are reported in the literature to range from 500⁶⁰ to 3000⁶¹ cells/mL. For older patients, the value is closer to the lower limit. The cell count per mL goes down with the number of aspirations taken in the procedure. The first 1 mL of aspirate usually has the highest cell concentration,¹⁰ as the removal of subsequent marrow causes the site to get filled with blood and dilutes consecutive extractions. For this reason, a material that minimises the seeding cell number required to set up a viable culture is preferable, as it would reduce the discomfort and trauma to the patient.

In addition, the main requirement for the success of cell-based engineered bone grafts in the clinic is the final number of cells delivered. Hernigou et al.¹⁰ found that a minimum of 50,000 osteogenic cells have to be implanted to be successful in inducing healing of non-unions, while both increasing the cell number and the cell density reduces the time to union and positively affects the outcome. Therefore, both minimising the seeding cell number and obtaining the desired final cell number are critical requirements in the clinic. Ensuring both are met depends on the choice of material and can be used to prescribe the duration of the cell culture.

Increasing the seeding cell number in our well from 5000 cells by 1000-cell increments to 14,000 cells and evaluating the presence of viable cell growth with the parameterised model revealed that 3.73 × 10⁴ cells/cm² (in our setup, equivalent to seeding with 12,000 cells) is the lowest seeding density supported by all biomaterials. With this new seeding number, we use the model to predict the length of culture required to reach 50,000 final cell number for each material, simulation results listed in Table 5. This allows experimentalists to first select a biomaterial (the material which requires the shortest culture time is preferable) based on these criteria and then to prescribe the duration of the culture for the desired outcome. The parameterised model predicts that material 7% TiO₂ achieves a final cell number of 50,000 cells in just 7 days, a day fewer than 2% CoO. Materials 5% CoO and 5% TiO₂ perform comparably, requiring a culture of 9 days. This analysis motivates the choice of 7% TiO₂ as a material capable of maximising cell yield at low seeding numbers.

Table 5.

Material performance predictions in terms of the time to reach 50,000 cells (required for a successful therapy) from the lowest common seeding cell number: 12,000 cells.

Seeding cell density	3.73 × 104 cells/cm2
Material	7% TiO2	2% CoO	5% CoO	5% TiO2
Time to reach 50,000 cells	7 days	8 days	9 days	9 days

Next, we use the model to inform the seeding density to achieve a desired final cell number when the culture duration is fixed (Table 6). Here, the culture duration is fixed at 6 days (7 days including an initial settling day), to minimise the time from obtaining a patient cell sample to expanding a sufficient cell number for treatment. We focus on two desired culture outcomes:

Table 6.

Seeding cell density for each material that (i) maximises the cell yield after 6 days in culture (as measured by the fold increase from starting cell number) and (ii) is the lowest required to reach 50,000 cells after 6 days of culture.

	Seeding density (×104 cells/cm2)
Material	Maximise cell yield	Expand culture to 50,000 cells
5% TiO2	4.35	4.97
7% TiO2	4.35	4.04
2% CoO	4.66	4.66
5% CoO	3.73	6.84

1. Maximising the cell yield efficiency. This might be desirable during scaling-up of the culture, for example, before it is moved to a bigger vessel.

2. Achieving final cell number of 50,000 cells, needed to promote healing.

The two outcomes are compared for each material for cell density equivalent to seeding in our setup with cell numbers ranging from 12,000 to 18,000 cells. The results reported in Table 6 are designed to act as a reference for experimentalists to help them choose appropriate seeding cell densities depending on the desired application and the choice of material.

In the case of delivering therapeutic cell numbers while minimising the culture duration to 1 week, the largest variation in seeding numbers reported in Tables 5 and 6 (part i) are observed for the materials to which the cells respond less favourably based on our previous analysis: 5% CoO and 5% TiO₂. Both require higher seeding numbers to ensure therapeutic functionality of the engineered tissue. For material 5% CoO, this is considerably more pronounced as the parameterised model does not indicate evidence of microcarrier floatation in this culture, and as a result it does not experience a boost in cell growth rate midway through the simulation. This analysis also identifies material 7% TiO₂ as the one requiring the lowest seeding numbers to achieve both desired outcomes, demonstrating its superior performance to the remaining materials in this context. This would make it the preferred material in the absence of any additional demands for the chemical composition of the biomaterial.

Conclusion

A strategy is proposed for in vitro expansion of bone cells (MG63 cell-line) on bioactive phosphate-glass microcarriers for the development of engineered bone grafts. The ability of four glass materials doped with either TiO₂ or CoO to promote cell culture expansion is tested experimentally. A mathematical model is derived to describe this experimental setup in static culture conditions and it is parameterised against the in vitro measurements to generate quantitative predictions. The parameterisation process enables the model to reproduce the in vitro behaviour observed and to examine how the choice of biomaterial determines culture outcome.

The interplay between biomaterial, seeding cell number and culture duration and their effect on the final cell number are studied in particular. The model is capable of simulating clinically relevant scenarios aiming to minimise the seeding number or culture duration while producing the target final cell number and examining how these differ based on the biomaterial. The model is flexible and a useful tool to investigate a range of different experimental features in future, for example, the influence of spatial heterogeneity in cell seeding on the well base, or the role of flow in stimulating the growing cell population. Among the bioactive glasses investigated, the material with 7% TiO₂ is predicted to perform best by meeting the required final cell number in the shortest time and starting from the lowest cell number. The ability of the model to predict the biomaterial performance in detail is used to inform future in vitro experiments by selecting the most promising materials and by proposing appropriate operating culture conditions to achieve better outcomes. The collaboration between modelling and experimentation can streamline the development of this culture expansion strategy by saving time and recourses.

Our work demonstrates how mathematical modelling can be used to generate a hypothesis about the behaviour of the tissue culture in vitro (floating microcarriers), which can then be tested in the laboratory. This is a good example of the collaborative potential between modellers and experimentalists. An alternative to our floating hypothesis might be that the sudden boost in proliferation is due to a complex growth behaviour in which the proliferation rate of the cells is non-constant but instead can be described by a complex function which can be dependent on multiple factors, including age of the cell culture, oxygen availability or rate of matrix synthesis. Growth could be bolstered midway through the culture by natural cell-driven processes such as fibronectin deposition (improving cell attachment affinity) and increase in growth factor concentration as a result of the higher number of cells present.

Currently, our simulations predict that a steady growth rate is maintained beyond the current time limit of 7 days in culture. This, however, is not what is observed experimentally. Growth during the second week of culture is irregular and does not surpass the peak cell yield at day 5. This behaviour can be explained by the culture maturing and entering an intensive state of matrix synthesis, but our model does not currently provide for this. Spatial heterogeneity of cell spreading also affects cell yield, its effect most prominent at early time points where cells proliferate into free spaces faster. This becomes less significant with time when confluency is reached and overcrowding leads to a drop in dividing cell number until a similar cell number is reached throughout (in 1–2 days).^62,63 Following this, the maintenance of a uniform nutrient field is instrumental in preserving uniform cell spreading. Supported by a homogeneous oxygen distribution across the base of the well, uniform cell spreading and growth are assumed in our model.

However, at later time points, lack of access to nutrients in densely cellularised parts of any culture become more common due to barriers formed by the newly deposited matrix. Thus, accounting for cell spreading is something we plan on including in the future to improve the flexibility and functionality of the model. To reconcile the model to experimental data for long-term cultures, we need to introduce an element of ECM production. An alternative explanation for the growth slowdown can be a lack of resources. This would be indicative of a need to transfer the culture to a bigger vessel, which also provides medium mixing. Current research undertaken by our group aims to address these questions by introducing medium mixing in the mathematical model and investigating its effect on the growth of the cell culture.