Mathematical modeling and computational prediction of cancer drug resistance

Abstract

Diverse forms of resistance to anticancer drugs can lead to the failure of chemotherapy. Drug resistance is one of the most intractable issues for successfully treating cancer in current clinical practice. Effective clinical approaches that could counter drug resistance by restoring the sensitivity of tumors to the targeted agents are urgently needed. As numerous experimental results on resistance mechanisms have been obtained and a mass of high-throughput data has been accumulated, mathematical modeling and computational predictions using systematic and quantitative approaches have become increasingly important, as they can potentially provide deeper insights into resistance mechanisms, generate novel hypotheses or suggest promising treatment strategies for future testing. In this review, we first briefly summarize the current progress of experimentally revealed resistance mechanisms of targeted therapy, including genetic mechanisms, epigenetic mechanisms, posttranslational mechanisms, cellular mechanisms, microenvironmental mechanisms and pharmacokinetic mechanisms. Subsequently, we list several currently available databases and Web-based tools related to drug sensitivity and resistance. Then, we focus primarily on introducing some state-of-the-art computational methods used in drug resistance studies, including mechanism-based mathematical modeling approaches (e.g. molecular dynamics simulation, kinetic model of molecular networks, ordinary differential equation model of cellular dynamics, stochastic model, partial differential equation model, agent-based model, pharmacokinetic–pharmacodynamic model, etc.) and data-driven prediction methods (e.g. omics data-based conventional screening approach for node biomarkers, static network approach for edge biomarkers and module biomarkers, dynamic network approach for dynamic network biomarkers and dynamic module network biomarkers, etc.). Finally, we discuss several further questions and future directions for the use of computational methods for studying drug resistance, including inferring drug-induced signaling networks, multiscale modeling, drug combinations and precision medicine.

Introduction

Cancer drug resistance is an important cause of the often inevitable failure of targeted drug therapeutics in clinical anticancer treatment [1]. In recent decades, targeted therapy has become one of the standard strategies for treating malignant tumors, as targeted therapy can significantly improve the survival rate of cancer patients [2]. However, resistance to targeted agents always emerges in various types of cancers, which eventually limits the long-term effectiveness of chemotherapy for cancer patients [3]. As such, drug resistance is currently one of the biggest obstacles for successfully treating cancers in clinical practice. Effective clinical approaches that could overcome or that could reduce drug resistance by restoring the sensitivity of tumors to the targeted agents are urgently required.

Drug resistance either preexists before drug treatment (i.e. intrinsic resistance) or develops after an early stage of initial drug response (acquired resistance) [4]. To better understand and to prevent cancer drug resistance, more and more attention has been paid to the underlying resistance mechanisms. Many experimental studies have been conducted that aim to reveal the various mechanisms of intrinsic or acquired drug resistance and to verify promising treatment strategies, such as combination therapy [5, 6], for reducing drug resistance. However, traditional hypothesis-driven experimental approaches are time-consuming and expensive because of the necessity for multiple experimental conditions, cell lines and time points. Moreover, cancer systems involve multiple scales and numerous interactive components, which are always dynamic and stochastic. Therefore, systems biology approaches are required to systematically and quantitatively investigate drug response and resistance and to generate new hypotheses for experimental validation.

In recent decades, various types of computational models have been developed in the area of cancer systems biology [7–15]. When combined with in vitro and/or in vivo experiments, as well as clinical data, the computational models that best use current knowledge of cancer mechanisms can be used to simulate molecular dynamics (MD), signaling kinetics, growth of the cellular population or tumor volume and the responses of cancers to therapeutic agents. Moreover, the rapid accumulation of high-throughput data in various cancers increasingly calls for powerful computational methods to unearth valuable information for the diagnosis, treatment, prognosis and prevention of cancers, particularly in the context of drug resistance. As such, the development of mathematical modeling and computational prediction methods is anticipated to advance our understanding of the underlying mechanisms of drug resistance and to facilitate the design of more effective treatment strategies to improve drug efficacy.

In this article, we first briefly review current knowledge of experimental data on cancer drug resistance mechanisms at various levels, including genetic, epigenetic, signaling networks, cellular, microenvironmental and pharmacokinetic scales. Then, we introduce some databases and Web servers that can be used for drug resistance studies. Next, we emphatically introduce two types of computational methods, i.e. mechanistic modeling approaches and data-driven prediction methods, for cancer drug resistance. Finally, we discuss several further questions and future directions for the use of computational methods for studying drug resistance, including inferring drug-induced signaling networks, multiscale modeling, drug combinations and precision medicine.

Experimentally revealed mechanisms of cancer drug resistance

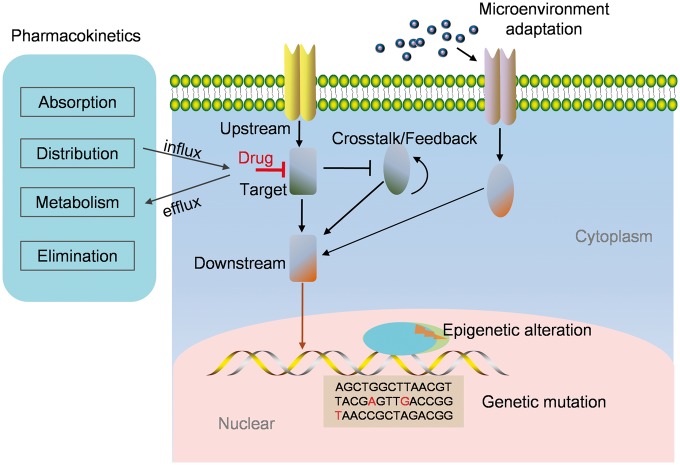
Some important progress on cancer drug resistance has been made because of the abundance of experimental studies that have been conducted to unravel resistance mechanisms at multiple levels, including at the molecular, cellular and microenvironmental scales [16–21]. The experimentally revealed mechanisms of cancer drug resistance involve at least the following mechanisms: genetic, epigenetic, posttranslational, cellular and microenvironmental (Figure 1).

Figure 1.

Various mechanisms of drug resistance. Cancer drug resistance can be caused by various mechanisms, including genetic mutation of the drug target or its upstream/downstream proteins, epigenetic alterations of proapoptotic gene expressions, signaling cross talk/feedback-mediated dynamic adaptive responses, microenvironment adaptation-induced signaling bypass or reactivation and pharmacokinetic mechanism.

Genetic mechanisms

Many experimental studies have demonstrated that a variety of newly acquired genetic modifications could render tumor cells insensitive to therapeutic agents [22], which is a well-studied paradigm for the mechanisms underlying drug resistance. The genetic mutation of the drug target can weaken the drug–target interaction, thus preventing the activation of the target and sustaining cell survival. For instance, epidermal growth factor receptor (EGFR) mutation can lead to the resistance of non-small cell lung cancer to Gefitinib by preventing this EGFR inhibitor from binding to its target [23]. Similarly, an acquired mutation at codon 2032 in the ROS1 kinase domain confers resistance to crizotinib during the treatment of metastatic lung adenocarcinoma through steric interference with drug binding [24].

Genomic modifications that regulate upstream or downstream signaling of a given target might also attenuate drug efficiency. For example, KRAS is an EGFR downstream signaling phosphoprotein, and the emergence of KRAS mutations is associated with acquired resistance to cetuximab, an inhibitor binding the extracellular domain of EGFR, in colorectal cancer (CRC) [25].

Epigenetic mechanisms

Epigenetic modifications in tumors can change gene expression patterns, which might adapt to the targeted therapy and cause acquired drug resistance [16]. For instance, an experimental study [26] suggested that histone deacetylase inhibitors (HDACis) could reduce the treatment effectiveness of some anticancer drugs (e.g. natural toxins to cyclic nucleotides) in acute myeloid leukemia cells. This study revealed an epigenetic mechanism by which HDACi could induce the hyperacetylation of histone proteins in the promoter regions of multiple ABC transporter genes, including MDR1, BCRP and MRP8, which modulated the expression patterns of these genes. Moreover, experimental evidence has indicated that epigenetic changes that silence proapoptotic genes (e.g. death-associated protein kinase 1) [27]. Apoptotic peptidase activating factor 1 [28] and regulating DNA-repair genes (e.g. MSH2, MLH1 and PMS2 [29]) also led to the acquisition of drug resistance [30]. These studies might have important clinical implications regarding epigenetic therapies and drugs that modify the corresponding epigenomes, as they could be designed to reverse the drug resistance responsiveness of anticancer drugs.

Posttranslational mechanisms

Various cancer studies involving targeted therapy have demonstrated that alteration of posttranslational signaling or rewiring can contribute to drug resistance. A typical paradigm is that subtle, posttranslational activations of signaling pathways that bypass therapeutic target stress can modulate the expression patterns of oncogenes and can thereby lead to acquired drug resistance. For instance, in many ‘oncogene-addicted’ cancer cells, a positive feedback loop of Stat3 induced by MEK inhibition can promote cell survival, which consequently limits overall drug response [19]. Another example of signaling feedback-mediated drug resistance is [31] the relief of ERK-dependent feedback inhibition on receptor tyrosine kinase (RTK) signaling by a RAF inhibitor, which could in turn attenuate the targeted effect in melanoma cells. Specifically, before treatment with the RAF inhibitor, strong ERK-dependent feedback can suppress RTK signaling and can maintain mutant BRAF in a drug-sensitive state. While using the RAF inhibitor, the inhibited feedback can then lead to the reestablishment of RTK signaling to Ras, which activates RAF dimers that are resistant to RAF inhibitors. Thus, the bypassed signaling pathway leads to the reactivation of ERK signaling and improves cell survival.

Cellular mechanisms

Intratumor cell populations are always heterogeneous. Cancer stem cells (CSCs) are a subpopulation of cancer cells with characteristics of normal stem cells in regard to their ability to self-renew and differentiate into multiple cell types [32]. The concept of CSCs has been proposed to explain tumor initiation, progression and, more importantly, drug resistance. Many biological processes and pathways have been found to be involved in the CSC-mediated cellular mechanisms that are responsible for drug resistance [33]. An experimental study [34] demonstrated that the acquisition of stem cell-like properties arose in some tumor cells along with the occurrence of drug resistance. These stem cell-like properties enabled the tumor cells to escape the drug assault. Moreover, in this study, the KRAS-RalB-NFκB pathway was identified to facilitate both cancer stemness and drug resistance to EGFR inhibition in lung cancer. The authors further indicated that α(v)β61 was a therapeutic target for sensitizing such resistant tumor cells to EGFR inhibition. Moreover, many resistance-associated characteristics, such as drug efflux [35], overexpression of antiapoptotic molecules [36, 37], activation of pro-survival signaling [38] and differentiation resistance [39], were found to be involved in CSC-mediated therapy resistance.

In addition, other cellular mechanisms, such as epithelial–mesenchymal transition [40, 41] and autophagy [42–44], were also found to contribute to drug resistance.

Microenvironmental mechanisms

Various cytokines or growth factors can be secreted from tumor cells or stromal cells into the microenvironment on drug treatment, which can promote the rapid emergence of acquired drug resistance [5, 45]. Therefore, microenvironmental adaptation [6] has been revealed as an important mechanism causing drug resistance. For instance, a recent study [5] demonstrated that, in response to targeted therapy with BRAF inhibition in melanoma, drug-sensitive cancer cells can secrete various cytokines (e.g. IGF, HGF, etc.) into the microenvironment. These secreted, soluble factors can in turn activate the survival signaling of drug-sensitive cells and can promote the proliferation, migration and metastasis of drug-resistant cancer cells.

Another preclinical study [46] revealed a microenvironment-dependent mechanism underlying the acquired resistance to CSF1R inhibition in gliomas. Without CSF1R inhibition, macrophages usually present a pro-tumorigenic M2 phenotype and promote glioma cell growth. While in the presence of CSF1R inhibition, macrophages switch to an antitumorigenic M1 phenotype that can promote tumor cell death. Following prolonged treatment of CSF1 inhibition, macrophages then secrete IGF1 into the microenvironment under the stimulation of accumulated IL4 from other cell types (e.g. T cells). The secreted IGF1 can sustain the survival and growth of glioma cells and thereby resist the CSF1 inhibition effect [46].

Pharmacokinetic mechanisms

Pharmacokinetic factors, including drug transportation, uptake, metabolism, elimination and efflux, determine the amount of drug delivered to tumor cells [47]. Zhang et al. [48] experimentally measured and quantitatively analyzed the cellular pharmacokinetics of adriamycin in human breast cancer cells MCF-7 and in adriamycin-resistant MCF-7 (MCF-7/Adr) cells. The differential distribution and accumulation of adriamycin in sensitive cells and resistant cells were found to influence drug-induced apoptosis. The resistant cells were found to express high levels of P-gp at cellular/subcellular membranes, which resulted in different cellular pharmacokinetic and pharmacological properties of adriamycin in resistant cells compared with sensitive cells. Furthermore, the authors found that inhibiting P-gp activity can attenuate adriamycin resistance.

Database and Web servers

Several Web-based tools, such as databases and Web servers, have been developed to collect and explore information related to drug resistance. For example, the National drug resistance database (http://www.portal.pmnch.org/hiv/topics/drugresistance/national_database/en/) [49] was developed to record and analyze HIV drug resistance data from WHO-recommended surveys. Another database, PIRSpred (http://protinfo.compbio.buffalo.edu/pirspred/) [50], was designed for the prediction of reliable HIV-1 protein inhibitor resistance/susceptibility. In particular, several databases and Web servers related to cancer drug sensitivity and resistance have been developed in recent years. Table 1 lists the current results (data deposited, potential applications, year developed, Web site and reference) of these databases and Web servers.

Table 1.

Databases and Web servers for cancer drug resistance

Databases	Data deposited	Potential applications	Year	Web site	Reference
CancerDR	Pharmacological profiling information of 148 anticancer drugs across 952 cancer cell lines	Identify genetic mutations in the drug targets and the associated residues responsible for drug resistance	2013	http://crdd.osdd.net/raghava/cancerdr/	[51]
HerceptinR	2500 Herceptin assays performed to test efficacy of Herceptin on various breast cell lines (∼30 unique cell lines) with and without supplementary drugs (∼100 unique drugs)	Assist to design Hercepting biomarkers to test whether Herceptin will work for a specific patient and examine whether Herceptin with supplementary drug can be used to treat this patient	2014	http://crdd.osdd.net/raghava/herceptinr/	[52]
MACE	Individual GI50 data of chemicals against NCI60 cell lines with DNA microarray data	Analyze mutation- or lineage-specific chemical response and expression signatures	2015	http://mace.sookmyung.ac.kr/	[53]
mutLBSgeneDB	Over 2300 genes with ∼12 000 somatic mutations at ∼10 000 ligand-binding sites across 16 cancer types; 744 drug-targetable genes	Search gene summary, mutated information, protein structure-related information, differential gene expression and gene–gene network, phenotype information, pharmacological information and conservation information	2017	http://zhaobioinfo.org/mutLBSgeneDB	[54]
GEAR	1781 associations between drugs and genomic elements (e.g. genes, miRNAs and SNPs)	Predict genomic elements that are responsible for drug resistance	2017	http://gear.comp-sysbio.org/	[55]

CancerDR

CancerDR (http://crdd.osdd.net/raghava/cancerdr/) [51] is a cancer drug resistance database based on the information of mutations in drug targets. CancerDR integrated several Web-based tools, such as COSMIC [56], CCLE [57], PubChem [58] and Therapeutic Target Database [59]. CancerDR collected pharmacological profiling information of 148 anticancer drugs (36 FDA-approved drugs, 48 drugs in clinical trials and 64 experimental drugs) across 952 cancer cell lines. The information about each drug target in this database includes the sequence of natural variants, mutations, tertiary structure and alignment profiles of mutants/variants. This database can be used to identify genetic mutations in the drug targets and the associated residues responsible for drug resistance.

HerceptinR

HerceptinR (http://crdd.osdd.net/raghava/herceptinr/) [52] is a database of assays performed to test sensitivity or resistance of Herceptin antibodies toward breast cancer cell lines. It can assist to design biomarkers to test whether Hercepting is effective for a specific patient and examine whether Herceptin with supplementary drug can be used to treat this patient.

MACE

MACE (http://mace.sookmyung.ac.kr/) [53] is a database with an interactive Web interface for a huge amount of chemical response and gene expression data on cancer cell lines. Individual GI50 data of chemicals against NCI60 cell lines were normalized and organized to statistically identify mutation- or lineage-specific chemical response. DNA microarray data on NCI60 cell lines were also processed to analyze mutation- or lineage-specific expression signatures.

mutLBSgeneDB

Kim et al. [54] built a mutated Ligand Binding Site gene database called mutLBSgeneDB (http://zhaobioinfo.org/mutLBSgeneDB). The authors collected and analyzed over 2300 genes with ∼12 000 somatic mutations at about 10 000 ligand-binding sites across 16 cancer types. From these, they selected 744 drug-targetable genes by integrating genetic, genomic, transcriptomic, proteomic, network and functional information. Pharmacological information, such as the binding affinities of selected genes with their drugs in wild-type and mutant forms, can be calculated from mutLBSgeneDB. Owing to the correlation between ligand-binding site mutation and drug resistance, mutLBSgeneDB provides a useful resource for researchers in the field of functional genomics, protein structure and, particularly, cancer drug resistance.

GEAR

GEAR (http://gear.comp-sysbio.org/) [55] contains 1631 associations between 201 human drugs and 758 genes, 106 associations between 29 human drugs and 66 microRNAs (miRNAs) and 44 associations between 17 human drugs and 22 single-nucleotide polymorphisms (SNPs). GEAR can be used to predict genomic elements that are responsible for drug resistance.

Mechanism-based mechanistic modeling approaches

Many computational methods have been developed to quantitatively model and simulate drug resistance based on biological mechanisms, such as signaling networks or cellular dynamics, or based on high-throughput data. Roughly speaking, there are two types of computational methods in drug resistance studies: (1) mechanism-based mechanistic modeling and (2) data-driven prediction methods. We first introduce mechanism-based mechanistic modeling approaches in this section, and review data-driven prediction methods in the following section. Figure 2 briefly summarizes various modeling approaches for cancer drug resistance based on different resistance mechanisms. The simulation tools, characteristics and typical references of these approaches are also listed.

Figure 2.

Summary on mechanism-based mathematical modeling approaches.

Molecular dynamics simulation

The interaction between the drug and the target is a dynamic process that involves numerous atoms. MD simulation is powerful in investigating drug resistance in silico because it can provide information on the dynamic changes of the drug and conformational changes of the target by analyzing the deviation or fluctuation of many atoms. Using MD simulation, one can examine how genetic mutation induces the occurrence of drug resistance by exploring the difference between the molecular bases of the wild-type target and mutated protein. In addition, we can use MD simulation to examine whether the selected potent inhibitors bind with a given target successfully and stably.

Giovanni et al. [60] used a GROMACS MD package [61] to perform MD simulation and analyzed the structural–dynamical behavior of the wild-type Thr729 and two mutants, Thr729Lys and Thr729Pro. Their analysis demonstrated the essential role of Thr729 in modulating the enzymatic function of human topoisomerase I, which was suggested to cause anticancer drug resistance by altering protein domain communications. In another example, Tang and Chen [62] used MD simulation to analyze the difference in the molecular character or structural variation between BRAF(V600E) and the wild-type BRAF protein, which might aid our understanding of the molecular mechanisms of drug resistance to BRAF inhibitors in cancers, such as advanced or metastatic melanoma.

Kinetic models of the signaling network

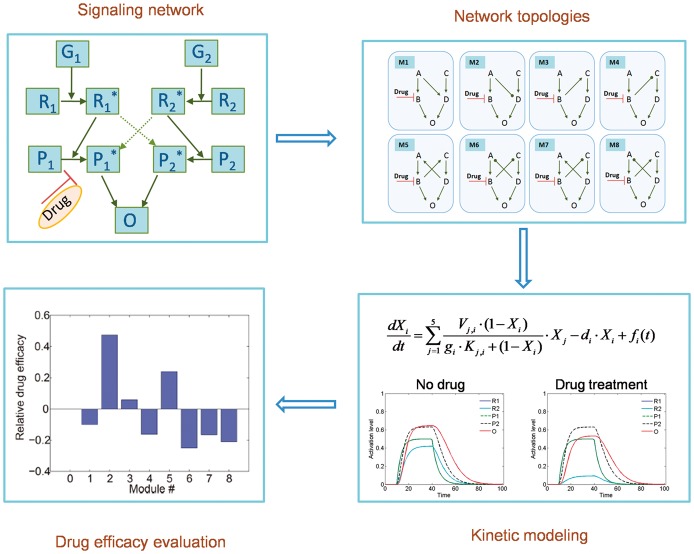
As described above, rewiring of posttranslational signaling is an important mechanism of acquired drug resistance. Therefore, using kinetic models to simulate the dynamic changes of the signaling network during drug treatment is a common method to quantitatively study drug resistance. The kinetics of the signaling network can be modeled using ordinary differential equations (ODEs) based on the law of mass action [63] or Michaelis–Menten kinetics [64] (Figure 3).

Figure 3.

A typical flowchart of signaling network-based kinetic modeling of drug resistance. According to the law of mass action or Michaelis–Menten kinetics, ODE models can be developed to describe the kinetics of signaling networks targeted by anticancer drugs. The drug efficacy can be evaluated based on quantitative model analysis. The model can be used to, for instance, investigate the effect of network structure on drug resistance.

Based on the law of mass action, Faratian et al. [65] used a kinetic model to simulate the temporal changes in the heregulin-induced HER2/3 signaling network, involving the MAPK and PI3K pathways. With this model, the authors studied the role of PIK3CA activation in RTK inhibitor resistance. They revealed that the ratio of PTEN to activated PIK3CA was correlated with the resistance of cancer cells to anti-HER2 therapies, which could therefore be used to predict the clinical response of patients to RTK inhibitor treatment based on clinical measurements of PTEN and PIK3CA levels. It also indicated that the combination of PIK3CA inhibition with RTK inhibitors would be beneficial to patients with tumors that had low PTEN levels.

Sun et al. [66] built an kinetic model of apoptosis regulation based on Michaelis–Menten kinetics to investigate the molecular mechanisms underlying stress-induced therapy resistance. Based on experimental studies of the epinephrine/beta2 adrenergic receptor/PKA/BAD pathway, which is critical in stress-mediated anti-apoptosis in prostate cancer cells, the authors could build and fit a network model of the signaling pathways that control BAD phosphorylation. Based on the experimentally validated model, they found that elevated epinephrine signaling could change the synergism pattern of the drug combination and decrease the efficacy of the therapy. By analyzing the network model of the signaling pathways affected by psychological stress, they explored the molecular mechanisms responsible for therapeutic resistance and the synergism pattern switch of drug combinations.

The pharmacological efficacy of signaling network-targeted drugs depends on the network topology. Therefore, it is important to investigate how variations in signaling network structure affect drug resistance. Sun et al. [67] built a Michaelis–Menten kinetics model for several small networks to investigate the contribution of the architecture of the signaling cross talk to induce drug resistance. Their results demonstrated that signaling cross talk affects the relative sensitivity of the targeted drugs and identified some typical cross talk modules that could yield resistance to the targeted drugs. In addition, the role of the strength of the cross talk in switching a module between drug sensitivity and drug resistance was analyzed. This study provided mechanistic insights into signaling cross talk-mediated drug resistance. Furthermore, their simulation results implied how to design synergistic drug combinations to reduce drug resistance.

Ordinary differential equation model of cellular population dynamics

As early as two decades ago, some theoretical and mathematical models of drug resistance in the context of tumor cell heterogeneity were developed based on population dynamics. The related literature has been reviewed by Michelson and Leith [68]. These models considered drug-sensitive cancer cells and drug-resistant cells as two different compartments. The growth dynamics of the cell populations, along with the effects of chemotherapy, were then modeled using a system of ODEs. The analysis of the model can determine the critical parameters and can help to design effective treatment strategies, such as combination chemotherapy [69].

Some other studies considered kinetic resistance based on the assumption that the cell division cycle could cause a reduction in the effectiveness of the drug, which is referred to as kinetic mutation. With this hypothesis, many drugs are assumed to be mainly effective during only one specific phase of the cell cycle. Therefore, the drug resistance is temporally changed. Some mathematical models of kinetic resistance have been developed [70–72] using ODEs. For example, Tomasetti and Levy [72] used a simple linear ODE model of kinetic resistance to obtain results comparable with those from much more complex mathematical techniques. The advantage of this simple deterministic approach lies in that it enables the possibility of determining analytic results for resistance to any number of drugs in such models. The authors further used this model to investigate the relationship among the amount of resistance, the turnover rate and the number of drugs used in the treatment.

Based on quantitative single-cell experimental measurements, mathematical modeling with ODEs and the Markov state transition model, Pisco et al. [73] investigated the contribution of growth rate and transition rate in a tumor cell population at steady state. Their model could explain the emergence of multidrug resistance in leukemia cells being treated with vincristine, which agreed with Lamarckian induction rather than Darwinian selection.

Recently, Mahasa et al. [74] developed a mathematical model of drug resistance because of the KRAS mutation in CRC. A system of ODEs was developed to model the dynamic interactions between various immune cell populations and tumor cell populations. The model illustrated the inevitable development of tumor cell immunoresistance and predicted natural killer (NK) cell-based immunotherapeutic approaches to enhance tumor immune surveillance.

Stochastic model

Stochastic models of drug resistance can be traced back to the studies by Goldie and Coldman [75–77], who used stochastic processes to describe the emergence and evolution of drug resistance because of point mutations. These models incorporated drug-resistant mutants and their impacts on eventual treatment outcome. They analyzed probabilities of the number of drug-sensitive and drug-resistant cells, as well as the optimal strategy of drug administration, by considering various treatment protocols to overcome drug resistance. Later, following these classical works, Komarova et al. [78–80] made further progress on the development of stochastic models of drug resistance because of point mutations. For example, in [78], Komarova developed a stochastic model with a nonzero death rate of cancer cells for multidrug resistance. This model investigated the dependence of treatment success on the initial tumor size, the turnover rate and the number of drugs used in combination therapy, where several drugs are administered concurrently.

Michor and her colleagues [81–84] also developed stochastic models describing the evolutionary dynamics of a tumor cell population during anticancer therapy to quantify the probability of resistance and to design optimal treatment strategies. For instance, Iwasa et al. [85] used continuous-time branching processes to calculate the probability of resistance at the time of cancer detection. Furthermore, Foo and Michor [86] developed a stochastic mathematical model to calculate the probability of drug resistance induced by a single (epi)genetic alteration. The model was further used to optimize drug-dosing schedules to minimize the risk of resistance emergence under the constrains of drug toxicity and side effects.

Stochastic differential equations (SDEs) have also been used to model the stochastic evolution of drug resistance. Taking into account microenvironment adaptations, Sun et al. [45] developed a stochastic model using a set of SDEs to describe the dynamics of drug-sensitive cells, drug-resistant cells and new metastatic cells. Their model was validated with clinical data and further predicted distinct patterns of dose-dependent synergy for two different sets of drug combinations in melanoma. This approach was anticipated to facilitate the study design of effective and robust cancer therapeutics. Furthermore, to investigate the functional role of noise in cancer drug response, Sun et al. [87] developed a Chemical Langevin Equation model for the signaling pathways involved in glioma differentiation therapy, which considered that stochastic noise inherently exists in signal transduction and phenotypic transition. The model simulation demonstrated that noise could induce a heterogeneous drug response in glioma differentiation therapy, thereby reducing the differentiation efficiency in drug-treated glioma cells.

Partial differential equation model

Considering the spatial heterogeneity of a tumor, partial differential equations (PDEs) are adequate tools to model the spatiotemporal dynamics of resistant tumor growth, along with drug treatment. Jackson and Byrne [12] developed a mathematical model using a system of PDEs that governs intratumoral drug concentration and cancer cell density to simulate the response of a vascular tumor to specific chemotherapeutic administration strategies. Two types of cancer cells with different drug sensitivities were considered. Using analytical and numerical techniques, the analysis of the model provided some insights into the response of the tumor to therapy. In addition, age-structured models in the form of PDEs were also used to model drug resistance [88].

Agent-based model

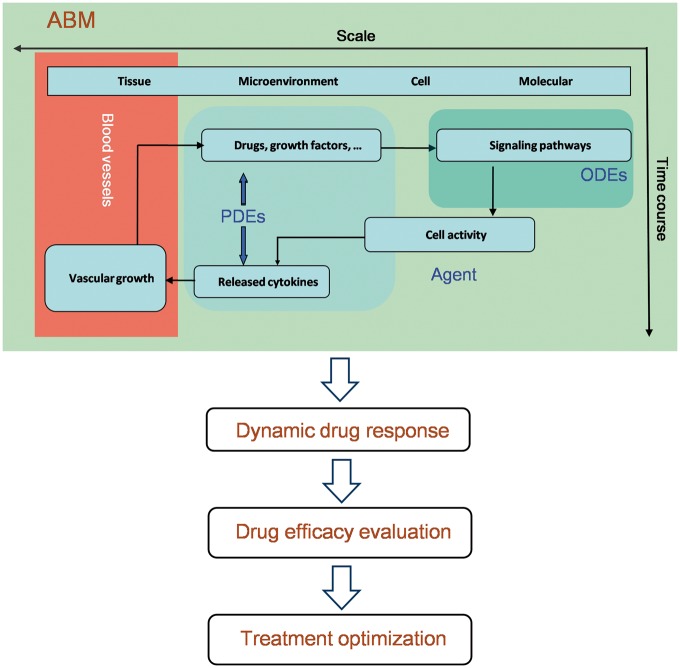
In recent years, the agent-based modeling (ABM) approach has been widely used to simulate various multiscale biological systems, such as cancer [9, 11, 89] and bone [90]. In ABMs, each cell is viewed as an intelligent individual that is equipped with an intracellular signaling network, which receives and responds to signals from the extracellular microenvironment. The dynamic changes of the signaling network can be modeled with ODEs, and the spatiotemporal dynamics of the concentrations of drugs or microenvironmental factors can be modeled using PDEs. Cell activity or phenotype switch is updated according to a series of rules on a two-dimensional or a three-dimensional lattice. The effect of the targeted drugs can be incorporated into the ODE model based on their mechanisms of action. ABMs can be used to simulate dynamic drug response and to evaluate drug efficacy (Figure 4).

Figure 4.

The flowchart of the ABM approach to predict and evaluate drug efficacy across multiple scales (e.g. molecular, cellular, microenvironment and tissue scales). ODEs describing intracellular signaling pathways, PDEs describing drug distribution and microenvironment changes and the rule-based simulation of angiogenesis can be integrated into an ABM. Collective behavior of the tumor cells and dynamic drug response can be simulated by the ABM. Based on a dynamic ABM model, drug efficacy can be evaluated, and optimal treatment strategies can be suggested.

Multiscale ABMs have been used to investigate drug resistance at multiple levels, as several different intracellular and microenvironmental factors are correlated with the emergence of drug resistance. For example, Gevertz et al. [91] developed a hybrid discrete-continuous ABM to examine the impact of the tumor microenvironment on drug resistance. In this model, cancer cells were simulated as individual agents through a particle-spring approach, while the microenvironmental oxygen and DNA-damaging drug concentrations were described using PDEs. They compared two kinds of resistance (i.e. preexisting and acquired resistance) and their influence on the spatial and temporal dynamics of tumor growth.

In addition, Sun et al. [92] developed a multiscale ABM that includes both angiogenesis and EGFR signaling networks to study the brain cancer response to tyrosine kinase inhibitor (TKI) treatment. Their simulations led to an interesting finding that angiogenesis may have a dual effect on TKI treatment. On the one hand, neovasculature can deliver TKIs to the tumor region and decrease tumor invasion. On the other hand, the neovasculature can transport nutrients such as glucose and oxygen to tumor cells to maintain their survival, which results in an increase in the cell survival rate in the late simulation stage. Therefore, these results indicated that angiogenesis might contribute to the resistance of tumor cells to drug treatment and thus induce tumor reoccurrence.

Pharmacokinetic–pharmacodynamic model

The intracellular and/or extracellular pharmacokinetics of anticancer drugs may play important roles in affecting drug efficacy. Pharmacokinetic–pharmacodynamic (PK-PD) models have been used to evaluate drug efficacy and to address the issues associated with drug resistance [93] based on in vitro or in vivo experimental data.

Zhang et al. [48] developed a cellular PK-PD model to investigate the impact of cellular pharmacokinetic properties of adriamycin resistance on MCF-7/Adr breast cancer cells. The parameters fitted from the quantitative experimental measurements revealed that the drug accumulated less and more slowly in resistant cells than in sensitive cells. The PK-PD model mathematically revealed the pharmacokinetic mechanisms of resistance of breast cancer cells to adriamycin treatment and indicated the potential action of 20(S)-Rh2 in improving drug efficacy.

Ji et al. [94] developed a PK-PD model by integrating the models for describing the phosphorylated EGFR (pEGFR) inhibitory effects and EGFR-TKI resistance to investigate the resistance behavior of TM208 in a mouse model of breast cancer. A one-compartment model with first-order absorption kinetics was used to describe the PK properties of TM208, and a logistic tumor growth/transit compartment model was fitted to characterize the relationship between tumor pEGFR levels and tumor growth inhibition. This integrated PK-PD model provides a better understanding of the preclinical pharmacokinetic properties of TM208 and can predict the possible occurrence of resistance in breast cancer.

Other methods

In addition to the above modeling approaches, other methods have also been used to theoretically study drug resistance. Evolutionary game theory [95] has been used to study optimal chemotherapy schedules for cancer patients. Using this theory, cancer treatment is viewed as a game in which the oncologists choose a therapy and the tumors ‘choose’ an adaptive strategy by evolving drug resistance. Orlando et al. [95] developed an eco-evolutionary model and formulated a control problem with the objective of minimizing tumor size at the end of the planning period. One conclusion is that both evolutionary trade-offs and drug interactions can affect cancer cell fitness in response to multiple drugs, which should be considered when designing optimal chemotherapy schedules for individual patients. In addition, landscape theory [96] is also used to quantify cell fate transition probabilities during the evolution of drug resistance [73, 97].

Data-driven prediction methods

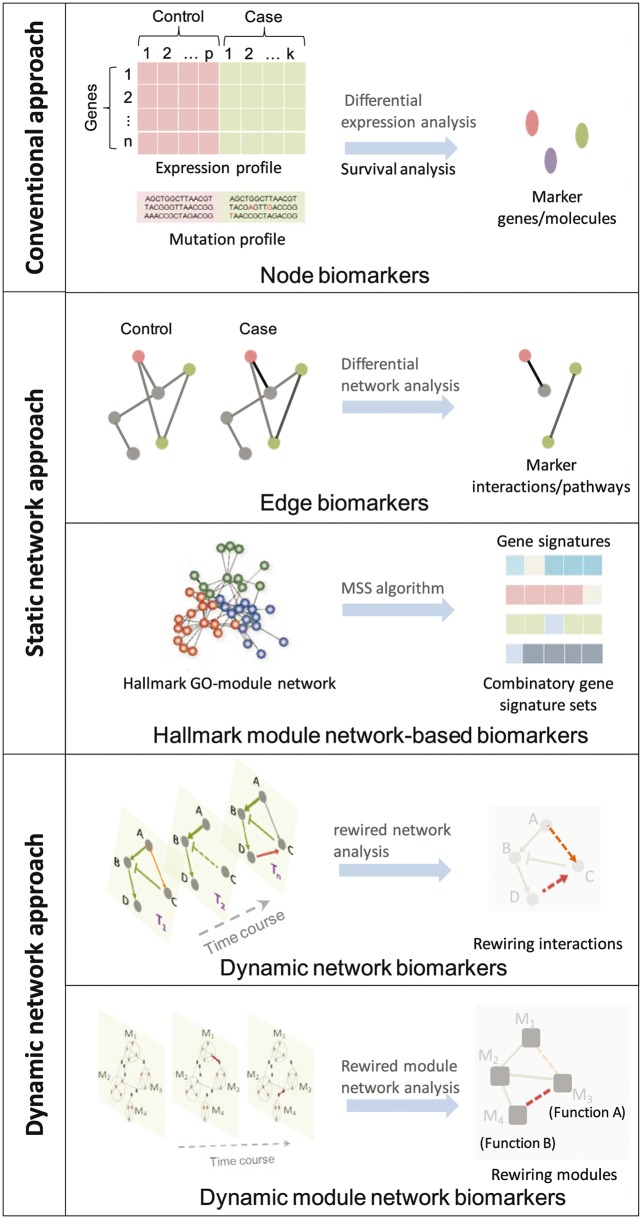
In this section, we introduce several typical data-driven prediction methods for identifying different types of biomarkers of cancer drug resistance. These methods include omics data-based conventional approach for screening node biomarker, static network approach for identifying edge biomarkers and module biomarkers and dynamic network approach for identifying dynamic network biomarkers and dynamic module network biomarkers. A comprehensive illustration of these methods is shown in Figure 5.

Figure 5.

A comprehensive illustration of various data-driven prediction methods for identifying biomarkers of cancer drug resistance. These methods include omics data-based conventional approach for screening node biomarkers, static network approach for identifying edge biomarkers and module biomarkers and dynamic network approach for identifying dynamic network biomarkers and dynamic module network biomarkers.

Omics data-based node biomarker screening

Fast generation and accumulation of a large amount of omics data provides a possible way to mine information regarding how pharmacological agents affect cancer systems at multiple bio-regulatory levels. Based on genomic [98], mutational [99], methylation [100], miRNA [101] and gene expression [102] data, many methods for screening biomarkers or signatures of drug resistance have been proposed. Conventional approach usually selects a set of single biomarkers that can be referred to as ‘node biomarkers’. A typical schematic illustration for selection and prediction of resistance signatures based on node biomarkers is shown in Figure 6. Based on gene microarray data and clinical information of a cancer patient cohort, the COX proportional hazard (COX PH) regression model can be used to screen candidate genes, and the optimal gene signature can be selected through model selection. A risk score can be defined to stratify patients into high-risk and low-risk groups, which can evaluate the long-term drug effect. In addition, further validation using independent and external data sets is indispensable in such an analysis. Below, we describe some examples to illustrate such methods based on various types of high-throughput data.

Figure 6.

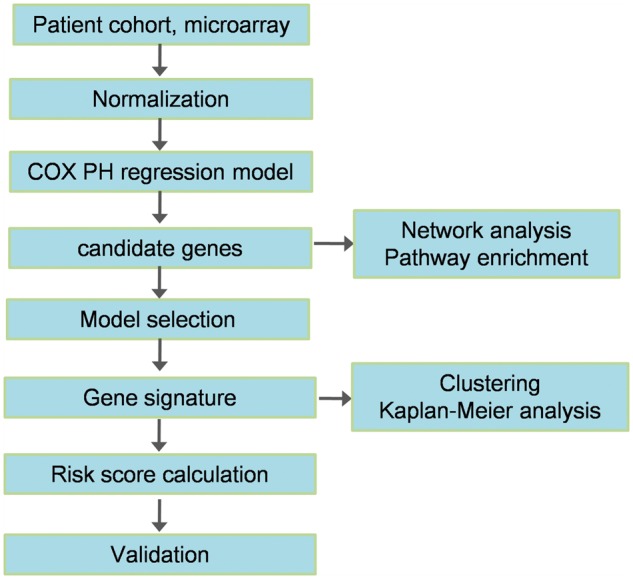
A typical flowchart of gene signature selection for drug resistance using survival analysis. Based on gene microarray data and the clinical information of cancer patient cohort, the COX PH regression model can be used to screen candidate genes, and the optimal gene signature can be selected through model selection. A risk score can be defined to stratify patients into a high-risk group and a low-risk group, which can evaluate long-term drug effects. In addition, further validation using independent and external data sets is indispensable in such an analysis.

Aksoy et al. [98] proposed a computational method to screen metabolic vulnerabilities in tumor samples from genomic profiles. The authors analyzed and identified candidate sample-specific metabolic vulnerabilities based on homozygous deletion for genomic data in 16 The Cancer Genome Atlas (TCGA) public cancer studies and 972 cancer cell lines. Furthermore, some candidate drugs were suggested to target these vulnerabilities.

Grasso et al. [103] proposed an exome-based method to profile the mutational landscape of castrate-resistant prostate cancers. The authors identified novel deregulation mechanisms of androgen receptor signaling in prostate cancer, which provided insights into the molecular mechanisms that have evolved in resistant tumors. In addition, this study identified several potential driving mutations and copy number alterations, such as FOXA1, which are candidates for future study. The genomics data set provided in this study is useful for the study of determinants of, and resistance mechanisms to, radiation and chemotherapy in lethal prostate cancer.

Based on high-resolution methylation microarrays, a global methylation profile of glioblastoma (GBM) samples was analyzed by Shukla et al. [100]. Survival analysis using a Cox regression model (Figure 6) was performed to identify methylation signatures. A nine-gene methylation signature was identified, and a methylation risk score was defined to predict survival in GBM patients. The activation of the NFκB pathway was shown to be associated with the high-risk group. Moreover, a risky methylated gene, neuronal pentraxin II (NPTX2), the transcripts of which were found to be low in the cells of glioma patients, was found to be responsible for glioma chemoresistance. Furthermore, it was revealed that targeting NFκB could prevent glioma chemoresistance.

Chan et al. [104] conducted miRNA microarray expression analysis and determined that miR-125b is involved in taxol resistance in breast cancer, which was verified by experimental procedures. Furthermore, the underlying mechanism of miR-125b-mediated drug resistance was illustrated by exploring its suppression regulation on proapoptotic Bcl-2 antagonist killer 1 (Bak1) expression.

Static network biomarker prediction

Biomolecules always achieve certain functions through extensive interactions with other molecules, rather than independently. Therefore, biomolecular networks, such as the signaling transduction network, metabolic network and gene regulatory networks, are important in biological systems. Reconstruction and analysis of biomolecular networks are thus anticipated to provide information in a more systematic manner at a higher level than single molecules. In recent years, network-based approaches [105–107] have been developed to study the mechanisms underlying various cancers and to predict therapy responses [108]. The construction of biomolecular networks together with analysis using signaling pathways databases have been used to uncover network mechanisms of drug resistance and to suggest more complex treatments schemes. For example, Basu et al. [109] created an interactive resource named the Cancer Therapeutics Response Portal (http://www.broadinstitute.org/ctrp) to correlate genetic features with sensitivity in individual lineages targeted by small molecules. They analyzed the β-catenin signaling network and associated its activating mutations with the sensitivity of cancer cells to navitoclax, an antagonist for the Bcl-2 family.

Network-based biomarkers for predicting cancer drug sensitivity and resistance can be identified based on network analysis. Typically, edge biomarkers in a form of molecule pairs in differential networks [110], and module biomarkers [111] based on functional module network construction can be obtained using static network analysis approach. Using a differential network analysis approach, Warsow et al. [112] developed a software tool ExprEssence to construct and analyze gene/protein interaction networks underlying breast cancer chemotherapy sensitivity and resistance. The authors integrated gene expression data into the interaction networks and used ExprEssence to determine the link score for each interaction. The most differentially regulated interactions were selected as edge biomarkers for predicting drug sensitivity.

Edwin Wang’s group [113] developed a novel cancer hallmark-based network analysis framework (Figure 5) to identify module network–based gene signatures, by constructing combinatory cancer hallmark-based gene expression signature sets (CSS sets) for accurately predicting the prognosis of patients with Stage II CRC. Cancer hallmark trait (tumor recurrence) was represented by a molecular interaction network that involves several biological processes according to gene ontology (GO) terms. Each GO term associates to a set of genes, and only a fraction of the associated genes are activated in a single tumor sample. Then, Multiple Survival Screening (MSS) algorithm [114] was used to identify a gene signature from a hallmark GO term, which only represents a fraction of the tumor samples. A combination of multiple such gene signatures would improve the prediction of the prognoses of most of the tumor samples. Using gene expression microarray data of about 1000 patients with Stage II CRC from 13 independent cohorts, the authors showed that CSS sets successfully predicted the recurrence and adjuvant therapeutic benefits in patients with Stage II CRC. Furthermore, the cancer hallmark-based network analysis was applied to investigate the network motifs in the PIK3CA-mutated luminal A tumors [115]. It was found that >70% of these tumors contain a positive regulatory loop (PDGF-D/FLT1/SHC1) that has a predictive power for the survival of the PIK3CA-mutated luminal A patients. In this sense, we can anticipate that specific network motifs [116] might serve as signatures for predicting cancer drug resistance.

Dynamic network biomarker prediction

In recent years, the concept of ‘dynamic network biomarkers’ [117] has been proposed to investigate the dynamic network-based mechanisms of complex disease and to identify biomarkers of the emergence or progression of these diseases. The dynamic network approach has also been used to investigate the underlying signaling mechanisms of cancer drug resistance. Recently, Eduati et al. [118] used cell line-specific data and a dynamic logic network model to identify biomarkers of drug response. The structure and dynamics of the signaling networks were determined by estimating parameters in a logic ODEs model using CellNOptR [119]. The authors investigated the association between cell-specific pathway dynamics represented by model parameters and drug sensitivity for a panel of 27 drugs. Specific parameters of signaling dynamics were identified as biomarkers of drug sensitivity for 14 of the drugs, 9 of which had no genomic biomarker. Based on one of these biomarkers, the authors predicted and validated a drug combination that could overcome resistance to MEK inhibitors by co-blockade of GSK3. Notably, this drug combination was not discovered based on associations with genomic data. This study suggested that signaling network dynamics that cannot be inferred from static genotypes might be used as novel biomarkers of cancer drug resistance for personalized medicine.

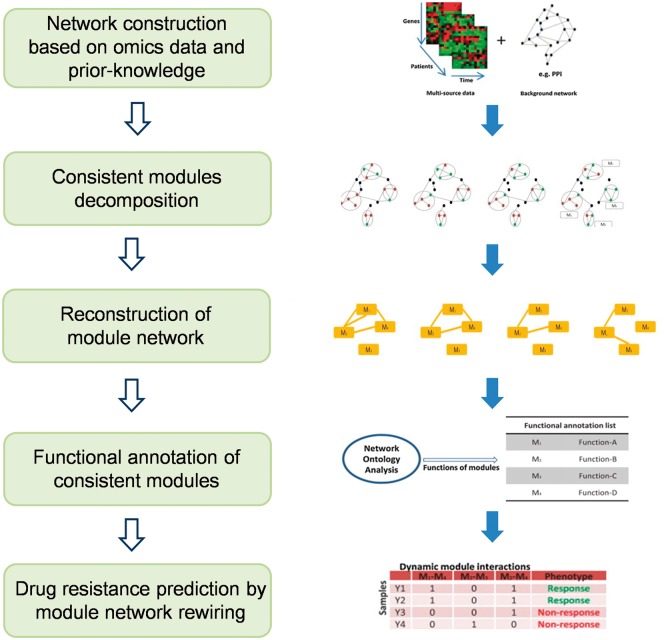
Zeng et al. [120] developed a module network rewiring-analysis method to identify ‘dynamic module network biomarker’ (Figure 7) of dynamic drug sensitivity and resistance based on transcriptional data. Each consistent module comprised interactive genes was viewed as a node, and the interaction between two such modules was viewed as an edge. Compared with a traditional static molecular network, such a dynamic module network can be viewed as a macro-network that represents a graphic model of higher-level molecular interactions. Within each consistent module, the interactions between genes are robust and invariant with respect to time evolution and external conditions, although the interaction strength might change during drug treatment. The connections between two modules might dynamically change along with the time course, drug schedules, dosages and delivery approaches. Therefore, a module network could be used to represent dynamic drug sensitivity and resistance.

Figure 7.

A typical flowchart of a dynamic module network biomarker identification method. Based on gene expression data and prior knowledge (such as protein-protein interaction (PPI) databases), gene co-expression networks can be constructed. Then, consistent modules can be decomposed from the constructed molecular network. Subsequently, a module network can be reconstructed where the node is each module. Functional annotation of consistent module and module network rewiring analysis can be performed to predict drug resistance. The right panel of this figure is partially reproduced from [120].

Discussion and conclusion

Increasing efforts in cancer research have been made to understand and to conquer drug resistance. Although tremendous experimental studies have been conducted, mathematical and computational approaches are indispensably important in studying drug resistance. However, to the best of our knowledge, there are few systematic reviews in the literature of mathematical modeling approaches and computational prediction methods for cancer drug resistance. In this article, we mainly introduced mechanisms-based modeling approaches and data-driven prediction methods, focusing on their applications for cancer drug resistance. As described above, multiple resistance mechanisms, including genetic, epigenetic, posttranslational, cellular mechanisms, microenvironmental adaptation mechanisms and pharmacokinetic mechanisms, have been unraveled using in vitro and in vivo experiments. Based on different mechanisms, appropriate modeling approaches can be applied to simulate the drug response of cancers at different levels. Modeling can help to provide mechanistic insights into drug resistance and to generate new hypotheses for experimental tests. On the other hand, data-driven computational methods, especially omics data-based screening and static/dynamic network-based prediction, have been developed to discover novel resistance mechanisms or to guide drug treatment design that can be further experimentally verified or potentially targeted.

Theoretical studies based on systems modeling have been used to study the dynamics of molecular pathways, networks and cellular populations in response to drug treatment. These mathematical and computational models can provide interesting insights into the biological mechanisms of drug response. Furthermore, it is possible to infer dynamic behaviors of the basic network building blocks such as network motifs in response to drugs or inhibitors [121]. Feedback loops are typical motifs of signaling network. Many theoretical studies have demonstrated that positive feedback loops can generate emergent properties, such as ultrasensitivity, bistability and switch-like behavior and noise amplification, while negative feedback loops can lead to adaptation, desensitization, homeostasis and noise reduction [116, 121]. For instance, a cyclin D1 feedback loop was shown to generate the bistable switch behavior during drug-induced glioma differentiation [122]. Furthermore, a stochastic modeling suggested that the cyclin D1 feedback could lead to the heterogeneous drug responses of glioma cells in the noisy environment, which could, therefore, induce the emergence of drug resistance [87]. In addition, it has been demonstrated that coherent feedforward transcriptional regulatory motifs could enhance drug resistance [123].

It should be emphasized that experimental evidence or validation is indispensable for testing hypotheses and verifying predictions of the mathematical models. For example, Deris et al. [124] built a growth-mediated feedback model that showed a bistable switch behavior and demonstrated a plateau-shaped fitness landscape for antibiotic-resistant bacteria. Importantly, their model prediction was consistent with experimental measurements in antibiotic-resistant bacteria. Therefore, a combined theoretical and experimental approach in this study well characterized antibiotic resistance growth. In future studies, more effort should be made to develop experimentally integrated models to investigate and predict drug resistance.

As Box [125] indicated, ‘all models are wrong, but some are useful’. Mathematical models of cancer drug resistance are by their very nature simplifications and as such are not perfectly accurate. Some models, for instance, PK-PD model, are simple, while other models (e.g. multiscale ABM) are relatively complicated. It is critical to consider the trade-off between simplicity and accuracy in choosing and creating a model. Therefore, modeling is not only a technical task but also an artistic work. Just as Albert Einstein said, ‘everything should be made as simple as possible, but not simpler’. For a specific scientific question we are trying to answer, the best model should be adequately simplified and specifically designed.

There are some limitations of mathematical models used for studying cancer drug resistance. (1) Mechanism-based mathematical models can quantitatively describe the cancer drug response based on known mechanisms but fall short in discovering novel molecules, biomarkers or targets for cancer drug resistance. (2) The most mathematical models used for cancer drug resistance, for instance, kinetic network model, are based on the experimental data generated from cell lines or animal models, rather than cancer patients. Furthermore, the clinical information of cancer patients is important for predicting drug resistance, but the existing modeling approaches rarely integrate such data. Therefore, this gap might limit the clinical effectiveness of model-based predictions. (3) A lot of mathematical models of cancer drug response involve many parameters that need to be estimated from experimental or clinical data. However, because of model complexity and data sparsity, only a fraction of parameters can be estimated from the available data, while the values of other parameters are always taken from previous literatures. A more comprehensive and consistent parameter estimation is absent sometimes. (4) The large-scale computation, for example, in MD simulation and mutiscale modeling, is of intensive computing burden, which might limit the speed of the prediction of cancer drug resistance.

The above limitations of mathematical models of drug resistance might be potentially resolved through the following strategies. (1) An integrative data-driven/mechanism-based modeling approach might facilitate both the identification of novel molecular mechanisms or drug targets and quantitative prediction. (2) The developed models integrating the clinical data might be more useful for predicting cancer drug resistance for the clinical purpose, which might be achieved through collaborations with clinicians. (3) The development of more rigorous parameter estimation procedures is expected to improve the prediction of cancer drug resistance. Alternatively, a convincing validation of the model prediction would also necessarily remedy the defect of parameter estimation. (4) The improved simulation algorithms and parallel computing as well as the utilization of high-performance computer might be helpful to improve the prediction efficiency.

Table 2 compares the characteristics (biomarker type, data type and typical computational methods), advantages and disadvantages of various data-driven prediction methods for identifying biomarkers of cancer drug resistance. The conventional node biomarker screening method using differential expression analysis and/or survival analysis is practical and easy for validation, but it does not take molecular interactions into account. The edge biomarker prediction method considers the functional interactions between pairs of molecules, but different edges are independent with each other. The hallmark-based network analysis framework constructs networks using information of hallmark-based functional interactions between genes and can identify a combination of multiple gene signatures that has more predictive power, but a large number of samples are usually required. Considering the dynamic nature of molecular networks, resistance development and disease progression, the dynamic network approach can identify dynamic (module) network biomarkers, but it requires time course data that are usually not available, particularly, in clinical situations.

Table 2.

Comparison among various data-driven prediction methods for studying cancer drug resistance

Approaches	Biomarkers	Data	Methods	Advantages	Disadvantages	References
Conventional approach	Node biomarkers	Various types of omics data (e.g. genomic, epigenomics, transcriptomics, proteomics, etc.)	Differential expression analysis, genomic analysis and survival analysis	Simple and easy for validation	The interactions between molecules are not considered	[98–104]
Static network approach	Edge biomarkers	Genomic, transcriptomics, etc.	Correlation approach, linear regression methods and differential network analysis	The functional associations between pairs of molecules are considered	Edges might be functionally independent and temporally stationary	[110, 112]
	Hallmark module network-based biomarkers	Genomic, transcriptomics, etc.	GO term enrichment, MSS algorithm and survival analysis	The hallmark-based functional interactions between genes are considered. A combination of multiple gene signatures has more predictive power	A large number of samples are required	[113–115]
Dynamic network approach	Dynamic network biomarkers	Time course data of proteomics or transcriptomics	Boolean network, fuzzy network, differential equations, dynamic Bayesian network, etc.	Dynamic properties of molecular network are considered	Time course data are required	[118]
	Dynamic module network biomarkers	Time course data or stage-varying data of transcriptomics	Correlation approach, module discovery methods and functional enrichment	Dynamic properties and modular interactions within molecular network are considered	Multiple samples of time course or stage-varying data are required	[120]

The most existing modeling studies of signaling pathways/networks for drug resistance are based on the prior knowledge of pathways that have been identified from experimental studies, which is sometimes referred to as a ‘bottom-up’ approach [126]. An alternative ‘top-down’ approach [127] to inferring drug-induced signaling network from high-throughput data, such as proteomic data, is extremely important in the study of drug resistance using a systems biology approach. Some data-driven methods [128–132] have been developed to construct biomolecular networks. For instance, Mitsos et al. [129] developed an integer linear program optimization method based on phosphoproteomic data to identify drug-induced topology alterations of the signaling pathways. In this study, diverse stimulations and numerous experimental conditions enabled the researchers to build a cell-type-specific signaling pathway. These methods are instructive for characterizing the signaling networks of drug sensitivity and resistance, provided that the data are of high quality, and the experimental procedure for data acquisition (e.g. experimental conditions, sample numbers and time points) is well designed.

As described above, genetic mutation of drug targets or their upstream or downstream proteins is one of the major mechanisms of drug resistance. A critical question is how to bridge the gap between mutation-induced structure changes in the protein and signaling network alteration, which ultimately leads to drug resistance evaluated at higher-level phenotypic markers or cellular populations. Therefore, a multiscale computational model linking molecular mutations to signaling networks and even to cellular populations is required to reconstruct this multilevel system, which would provide deeper insights into drug resistance mechanisms and drug treatment design. One feasible approach is to integrate structural-based mutation analysis and MD simulation of protein binding with ODE modeling of signaling network remodeling. Exemplary work using this approach has been done by Zhao et al. [133], who investigated mutation-induced apoptotic signaling dynamics. Through linking structural-based mutation analysis to protein-binding coefficients, which directly affect network-based dynamics, the authors mapped cancer-related gene mutations to network dynamics changes. In the future, multiscale modeling studies of drug resistance may address the issue of mapping target mutations or gene mutations to network dynamics changes and then to drug-sensitivity alterations. Such multiscale modeling might also be instructive for drug target design and structure-based drug screening.

Combination therapy has been proposed as a promising approach to reduce drug resistance. Computational models can not only provide insights into biological mechanisms of drug response but also provide quantitative guidance to the design of drug combinations [134]. Some computational prediction methods, such as network-based prediction methods [135, 136], similarity-based methods [137, 138] and machine-learning methods [139, 140], have been developed to predict effective or synergistic drug combinations. For example, Huang et al. [136] designed a computational tool that can be used to predict synergistic drug combinations based on network analysis of genomic profiles of both drugs and cancers. In addition, the scheduling of drug administration in terms of timing and dose in the temporal combination of drugs profoundly influences therapeutic efficacy [141, 142]. In the future, computational modeling is anticipated to facilitate the design of the temporal combination of drugs and to optimize the scheduling of drug administration for improving treatment efficacy.

The systems biology approach plays increasingly important roles in studying the underlying mechanisms of cancer drug resistance and in the optimal design of the treatment schedule, dosing and timing. In the era of precision medicine and big data, computational modeling that integrates bio-omics data and the clinical information of cancer patients will improve the identification of drug-sensitive or drug-resistant patients and guide the design of appropriate therapy by quantitative prediction of drug administration.

Key Points

• Many experimental studies have revealed various types of underlying mechanisms of cancer drug resistance, including genetic mechanisms, epigenetic mechanisms, posttranslational mechanisms, cellular mechanisms, microenvironmental mechanisms and pharmacokinetic mechanisms, etc. In addition, several databases and Web servers related to drug resistance have been developed.

• Computational methods for studying cancer drug resistance can be divided into two categories: mechanisms-based mathematical modeling approaches and data-driven prediction methods.

• Mechanisms-based modeling approaches include MD simulation, kinetic modeling of molecular networks, ODE models of cellular dynamics, stochastic models, PDE models, ABMs and PK-PD models.

• Data-driven prediction methods include omics data-based conventional screening approach for node biomarkers, static network approach for edge biomarkers and module biomarkers and dynamic network approach for dynamic network biomarkers and dynamic module network biomarkers.

• We discussed several further questions and future directions for the use of computational methods, including inferring drug-induced signaling networks, multiscale modeling, drug combinations and precision medicine for cancer drug resistance.

Funding

The National Natural Science Foundation of China (grant number 61503419), the Guangdong Nature Science Foundation (grant numbers 2014A030310355 and 2016A030313234), the National Basic Research Program of China (973 Program) (grant number 2014CB744600), the National Natural Science Foundation of China (grant numbers 61210010 and 61632014), the Program of International S&T Cooperation of MOST (grant number 2013DFA11140), and the Program of Beijing Municipal Science & Technology Commission (grant number Z171100000117005).

Biographies

Xiaoqiang Sun, PhD, is an assistant professor at the Zhong-shan School of Medicine, Sun Yat-Sen University. His research interests include computational biology, systems biology and bioinformatics.

Bin Hu, PhD, is a professor and Dean at the School of Information Science and Engineering, Lanzhou University. His research interests include computational biology and data modeling.