Fast Interpolation-based t-SNE for Improved Visualization of Single-Cell RNA-Seq Data

Abstract

t-distributed Stochastic Neighborhood Embedding (t-SNE) is widely used for visualizing single-cell RNA-sequencing (scRNA-seq) data, but it scales poorly to large datasets. We dramatically accelerate t-SNE, obviating the need for data downsampling, and hence allowing visualization of rare cell populations. Furthermore, we implement a heatmap-style visualization for scRNA-seq based on one-dimensional t-SNE for simultaneously visualizing the expression patterns of thousands of genes.

1. Main

scRNA-seq enables high-throughput transcriptome profiling at the individual cell level and is increasingly being used to study cell-to-cell heterogeneity in both physiologic and disease processes. Data visualization techniques have played a pivotal role in both analyzing the expression of different marker genes in known cell populations and in identifying new cell types. Over the last decade data visualization using t-SNE has become a cornerstone of scRNA-seq analysis. t-SNE is used to embed a scRNA-seq dataset into a low-dimensional space such that proximal pairs of single cells in the high-dimensional transcriptome space remain proximal in the low dimensional space. The embedding is often colored by the expression levels of a gene of interest, one gene at a time.

Several difficulties arise when applying t-SNE to scRNA-seq data. The number of cells profiled in scRNA-seq experiments has been growing exponentially,¹ with recent datasets measuring the expression of 30,000 genes in over 1,000,000 cells.² Profiling such large numbers of cells facilitates the characterization of rare and moderately-sized subpopulations not apparent in smaller samples. However, existing algorithms for constructing t-SNE embeddings are computationally expensive, often necessitating downsampling of the cells prior to running t-SNE, which can in turn result in rare cell populations being missed. Furthermore, removal of the few cells which may express a given marker gene can make even moderately sized populations difficult to identify.

An additional difficulty with applying t-SNE to scRNA-seq data is that overlaying the expression levels of marker genes on separate 2D t-SNE plots is cumbersome owing to the large number of marker genes for each dataset. Practically, only a modest number of such plots can be visually compared.

In this paper, we present two improvements for the application of t-SNE to scRNA-seq data visualization. First, we present FFT-accelerated Interpolation-based t-SNE (FIt-SNE), an algorithm for rapid computation of one- and two-dimensional t-SNE based on polynomial interpolation and further accelerated using the fast Fourier transform. We also present t-SNE heatmaps, a heatmap-style visualization method based on one-dimensional t-SNE, which simultaneously visualizes expression patterns of hundreds to thousands of genes.

FIt-SNE.

t-SNE is often run many times with different parameters and initializations, so that the embedding most consistent with prior knowledge can be chosen. FIt-SNE is a dramatically accelerated implementation of t-SNE, allowing practitioners to analyze entire datasets as opposed to first downsampling. By doing so, FIt-SNE allows practitioners to identify known populations using marker genes which may not be expressed in sufficiently many cells post-downsampling. For example, we used FIt-SNE to embed a dataset consisting of 1.3 million mouse brain cells² and identified two known cell types from the Allen Brain Atlas³ which cannot be identified using a random subset of 50,000 cells (Figure 1), as the latter does not have enough cells expressing both markers. Specifically, GABAergic neurons from the caudal ganglionic eminence which express marker genes Sncg and Slc18a8 and a population of vascular leptomeningeal cells (VLMC) expressing marker genes Spp1 and Col15a1 can both be identified using only the full embedding, as opposed to a random subset.

Figure 1.

FIt-SNE allows for embedding of the full 1.3 million mouse brain cell dataset (left), enabling the identification of known cell populations that cannot be identified when downsampling to a random 50,000 cells (right). (For the left figure, instead of plotting all 1.3 million embedded points, only 100,000 of the cells not expressing the marker genes are shown, whereas all the cells expressing the marker genes are shown.)

The t-SNE algorithm solves an optimization problem for embedding the cells (points) in a low-dimensional space based on their transcriptome similarities. Formally, this problem is equivalent to a physical system of particles (points) in which particles exert repulsive and attractive forces on each other. Naively implemented, computing the force each particle exerts on all the other particles is prohibitively slow; we devise approximation schemes for evaluating the repulsive and attractive forces that can scale to millions of points.

Computation of the repulsive forces between every pair of the N points is the most time-consuming step in t-SNE. Instead of calculating the interaction of each point with all the other points (which requires N² computations), Barnes-Hut (BH) t-SNE⁴ —the fastest published t-SNE implementation—uses a tree structure to compress the interaction between distant cells, hence requiring N log N computations. We take a different approach by defining a small number p of interpolation nodes, which “mediate” the interaction between the points. First, we calculate the interaction of each point with those nodes (p · N computations). Then we compute the interaction of those nodes with each other (p² naively, p log p using FFTs). Finally, we interpolate from the interpolation nodes to all of the original points (also p · N computations). Hence, we can approximate the repulsive force in ~ 2p · N computations, as opposed to N² or N log N (Table 1 and S1). We prove rigorous bounds on the approximation error in the Online Methods; in particular, we show that the number of interpolation nodes p required for a certain level of accuracy is independent of N. We set the default FIt-SNE parameters to give an approximation at least as accurate as BH t-SNE’s default setting (Figure S1 and Section §8.3.3).

Table 1.

Time taken for 1000 iterations of the gradient descent phase of 2D t-SNE using Barnes-Hut t-SNE (BH t-SNE) compared to our implementation (FIt-SNE), as compared on a 2017 Macbook Pro for a given number of points N. See section 8.3.5 for more details.

N	BH t-SNE	FIt-SNE
10,000	1 min.	< 1 min.
100,000	11 min.	< 1 min.
500,000	1 hr. 10 min.	3 min.
1,000,000	3 hr. 9 min.	15 min.

The attractive force between two points decays exponentially fast as a function of the distance between them, so that a point only exerts a significant attractive force on its nearest neighbors. In BH t-SNE, the k–nearest neighbors of each point are identified using vantage-point (VP) trees⁵ which tend to be prohibitively expensive for high-dimensional datasets. In FIt-SNE, there are two options for identifying nearest neighbors—multithreaded VP trees and approximate nearest neighbors using ANNOy⁶ (Tables 2 and S2). Multithreaded VP trees are exactly as accurate as the VP tree implementation of BH t-SNE, just substantially faster. The use of approximate nearest neighbors is even faster, but could theoretically obscure subtle detail. In practice, however, we find the resulting embedding quality to be essentially indistinguishable (Figures S2, S3, S4, and S5).

Table 2.

Time taken to compute input similarities in Barnes-Hut t-SNE (vptree) compared to FIt-SNE using either multithreaded vantage-point trees (vptreeMT) or a multi-threaded approximate nearest neighbor (annMT) approach on a 2017 Macbook Pro for a given number of points N.

	50 Dimensions			100 Dimensions
N	vptree	vptreeMT	annMT	vptree	vptreeMT	annMT
10,000	< 1 min.	< 1 min.	< 1 min.	< 1 min.	< 1 min.	< 1 min.
100,000	2 min.	< 1 min.	< 1 min.	3 min.	< 1 min.	< 1 min.
500,000	56 min.	15 min.	3 min.	1 hr. 30 min.	20 min.	4 min.
1,000,000	4 hr. 45 min.	1 hr. 15 min.	6 min.	7 hr. 9 min.	1 hr. 40 min.	8 min.

Although FIt-SNE makes it practical to run t-SNE on datasets with millions of points, the choice of parameters which lead to an ideal embedding is an active area of research. For example, when the number of points is large, the attractive forces must be exaggerated during the beginning stages of t-SNE in order to ensure optimal embedding of large numbers of points⁷ (Supplemental Figure S6). While this paper was in revision, a new paper by Belkina and colleagues (2018)⁸ proposed an approach for automatically determining the step size and the optimal number iterations to exaggerate the attractive forces, which they validate using CyTOF and scRNA-seq datasets. In another very recent work, Kobak and Berens (2018)⁹ proposed a protocol for exploratory analysis of scRNA-seq data using FIt-SNE (including suggested parameter choices), which leads to dramatically improved embedding quality, particularly with regard to preservation of multi-scale and global structure.

Heatmaps.

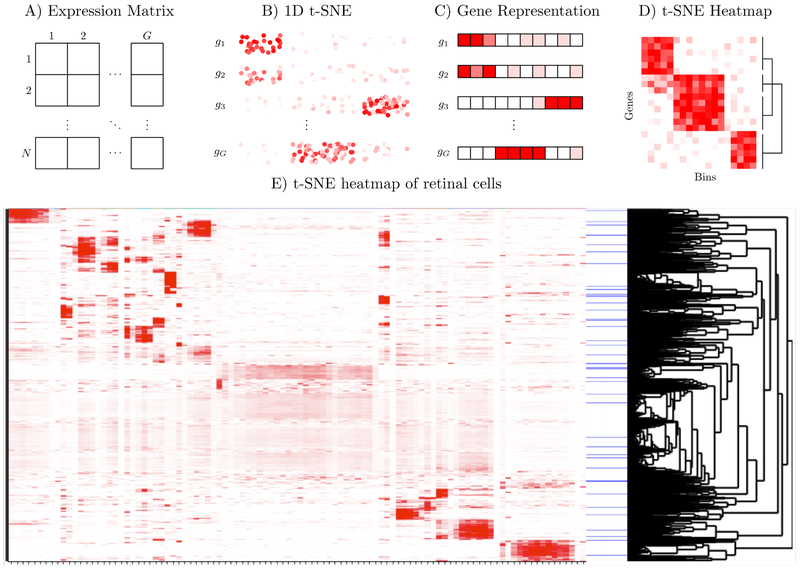
Exploration of scRNA-seq data using t-SNE consists of tiling two-dimensional t-SNE plots, each colored by the expression pattern of a different marker gene. Although this information is presented in two dimensions, users are most interested in which genes are associated with which clusters, not the shape or relative locations of the clusters. It has been shown that t-SNE preserved the cluster structure of well-clustered data regardless of the embedding dimension,⁷ and thus, one-dimensional t-SNEs usually contain the same information as two-dimensional t- SNEs. Furthermore, multiple one-dimensional t-SNEs, each using different groups of markers, have been previously used to visualize CyTOF data¹⁰ We develop a related approach which exploits the compactness of a single one-dimensional embedding to enable simultaneous exploration of expression patterns of hundreds to thousands of genes in heatmap form. This approach also allows us to discover new marker genes and organize the genes based on their smoothed expression patterns along the one-dimensional t-SNE representation of the cells.

In t-SNE Heatmaps, we first construct a one-dimensional t-SNE embedding of the cells. Next, we discretize the one-dimensional t-SNE embedding into b bins, where b is user specified, and represent each gene by the sum of its expression in the cells contained in each bin. We then visualize these vectors in heatmap format (i.e. each row is a gene and each column is a bin) using an interactive visualization tool called heatmaply.¹² Notably, unlike dotplots which present the average expression of genes in each cluster (e.g. Figure 2A of Shekhar et al. (2016)¹¹), it does not require pre-clustering, and hence can discover patterns in poorly clustered data that might be missed if averaging across clusters.

Figure 2.

Schematic and demo of t-SNE Heatmaps. Starting with the expression matrix (A) compute 1D t-SNE, which is plotted in (B) colored by the expression of each gene (with added jitter). We bin the 1D t-SNE, and represent each gene by its average expression in each bin (C), and then generate a heatmap of these vectors, so that genes with similar expression patterns in the t-SNE are grouped together (D). In (E), we demonstrate t-SNE heatmaps using retinal bipolar cells¹¹

Various strategies can be used to select the genes presented in the heatmap. If the user has prior knowledge as to genes of interest, these genes can be presented, along with genes whose onedimensional t-SNE binned representation are most similar, allowing for marker gene discovery. If the user wants to identify genes specific to clusters, a “metagene” can be constructed, which is 1 on cells in a cluster and 0 elsewhere. Then genes whose one-dimensional t-SNE binned representation are most similar to these “metagenes” (ie. specific to a cluster) can be presented in the heatmap. “Metagenes” for combinations of clusters can also be constructed.

Figure 2 demonstrates t-SNE heatmaps using retinal bipolar cells from Shekhar et al. (2016).¹¹ In this work, scRNA-seq was used to profile ~ 25,000 mouse retinal bipolar cells and classify them into 15 types. Using graph-based clustering techniques, cells were clustered, and marker genes corresponding to each of the putative subtypes of bipolar cells were subsequently identified. We embedded these bipolar cells using 1D t-SNE and found the 25 genes most associated with the marker genes listed in Table S2 of Shekhar et al. (2016). We also found the 25 genes most associated with “metagenes” for each cluster in the 2D t-SNE. The resulting t-SNE heatmap (Figure 2, Supplementary Figures S7, and S8) identified all 16 of the new bipolar cell markers listed in Figure 2A of Shekhar et al. (2016). The clustered structure of the dataset is evident in the heatmap, and the user can zoom in to identify the genes that characterize and distinguish different regions of the embedding. We note that the structure is substantially clearer than a heatmap of the same genes binned using standard hierarchical clustering, even when the rows are ordered as in the t-SNE heatmaps (Figure S9).

2. Methods

R, Python, and Matlab implementations of FIt-SNE and an R implementation of t-SNE heatmaps are available from https://github.com/KlugerLab/. Methods, including statements of data availability and any associated accession codes and references, are available in the online version of the paper. The Life Sciences Reporting Summary was also completed.

8. Online Methods

We first briefly review the t-SNE approach and then then present FIt-SNE’s method for optimizing the computation of the repulsive force in Section §8.3. Section §8.4 presents an implementation of out-of-core PCA for the analysis of datasets too large to fit in the memory. Finally, Section §8.5 provides details of the embedding of 1.3 million mouse brain cells (Figure 1), Section §8.6 describes the demonstration of t-SNE heatmaps (Figure 2), and Section §8.7 provides details about our comparison of VP trees to approximate nearest neighbors on three scRNA-seq datasets.

8.1. t-distributed Stochastic Neighborhood Embedding.

Given a d-dimensional dataset $X=\{x_1,x_2,\dots ,x_N\}\subset {\mathbb{R}}^d$, t-SNE aims to compute the low-dimensional embedding

$$Y=\{y_1,y_2,\dots ,y_N\}\subset {\mathbb{R}}^s,$$

where s ≪ d, such that if two points x_i and x_j are close in the input space, then their corresponding points y_i and y_j are also close. Affinities between points x_i and x_j in the input space, p_ij, are defined as

$$p_{i\mid j}=\frac{\text{exp}(-\Vert x_i-x_j{\Vert }^2∕2{\sigma }_i^2)}{{\sum }_{k\ne i}\text{exp}(-\Vert x_i-x_k{\Vert }^2∕2{\sigma }_i^2)}\text{and}{p}_{ij}=\frac{p_{i\mid j}+p_{j\mid i}}{2N}.$$

Here σ_i is the bandwidth of the Gaussian distribution is computed based on the user-specified perplexity P_i (the conditional distribution of all other points given x_i). Similarly, the affinity between points y_i and y_j in the embedding space is defined using the Cauchy kernel

$$q_{ij}=\frac{(1+\Vert y_i-y_j{\Vert }^2{)}^{-1}}{{\sum }_{k\ne l}(1+\Vert y_k-y_l{\Vert }^2{)}^{-1}}.$$

t-SNE finds the points {y₁, …, y_n} that minimize the Kullback-Leibler divergence between the joint distribution of points in the input space P and the joint distribution of the points in the embedding space Q,

$$C(\mathcal{Y})=KL(P\Vert Q)=\sum _{i\ne j}{p}_{ij}\log \frac{p_{ij}}{q_{ij}}.$$

Starting with a random initialization, the cost function $C(\mathcal{Y})$ is minimized by gradient descent, with the gradient¹³

$$\frac{\partial C}{\partial y_i}=4\sum _{j\ne i}(p_{ij}-q_{ij})q_{ij}Z(y_i-y_j),$$

where Z is a global normalization constant

$$Z=\sum _{k\ne l}(1+\Vert y_k-y_l{\Vert }^2){}^{-1}.$$

We split the gradient into two parts

$$\frac{1}{4}\frac{\partial C}{\partial y_i}=\sum _{j\ne i}{p}_{ij}{q}_{ij}Z(y_i-y_j)-\sum _{j\ne i}{q}_{ij}^{2}Z(y_i-y_j)$$

where the first sum F_attr,i corresponds to an attractive force between points and the second sum F_rep,i corresponds to a repulsive force

$$\frac{1}{4}\frac{\partial C}{\partial y_i}=F_{\text{attr},i}-F_{\text{rep},i}.$$

The computation of the gradient at each step is an N-body simulation, where the position of each point is determined by the forces exerted on it by all other points. Exact computation of N-body simulations scales as O(N²), making exact t-SNE computationally prohibitive for datasets with tens of thousands of points. It should be noted that since the input similarities do not change they can be precomputed and hence do not dominate the computational time.

8.2. Early Exaggeration.

In the expression for the gradient descent, the sum of attractive and repulsive forces,

$$\frac{1}{4}\frac{\partial C}{\partial y_i}=\alpha \sum _{j\ne i}{p}_{ij}{q}_{ij}Z(y_i-y_j)-\sum _{j\ne i}{q}_{ij}^{2}Z(y_i-y_j),$$

the numerical quantity α > 0 plays a substantial role as it determines the strength of attraction between points that are similar (in the sense of pairs x_i, x_j with p_ij large). In early exaggeration, first α =12 for the first several hundred iterations, after which it set¹³ to 1. One of the main results of Linderman and Steinerberger (2017)⁷ is that α plays a crucial role and that when it is set large enough, t-SNE is guaranteed to separate well-clustered data and also successfully embed various synthetic datasets (e.g. a swiss roll) that were previously thought to be poorly embedded by t-SNE.

8.3. Accelerating computation of repulsive forces in FIt-SNE.

In existing methods, the repulsive forces F_rep,i are approximated at each iteration using the Barnes-Hut Algorithm,¹⁷ a tree-based algorithm which scales as O(N log N), where N is the total number of data points. In this work, we present an interpolation-based fast Fourier transform accelerated algorithm for computing F_repul,i which scales as O(N). Moreover, empirical tests show a significant improvement over the Barnes-Hut approach for any sized system.

Recall that, {y₁, y₂, … , y_N} is the s-dimensional embedding of a collection of d-dimensional vectors {x₁, … , x_N}. At each step of gradient descent, the repulsive forces are given by

$$F_{\text{rep},k}(m)=\left(\sum _{\begin{array}{c}\hfill \ell =1\hfill \\ \hfill \ell \ne k\hfill \end{array}}^N\frac{y_{\ell }(m)-y_k(m)}{(1+\Vert y_{\ell }-y_k{\Vert }^2){}^{{}^2}}\right)/\left(\underset{\ell \ne j}{\sum _{j=1}^N\sum _{\ell =1}^N}\frac{1}{(1+\Vert y_{\ell }-y_j{\Vert }^2)}\right),$$ (1)

where k = 1, 2, … N, m = 1, 2 … s, and y_i(j) denotes the j^th component of y_i. Evidently, the repulsive force between the vectors {y₁, …, y_N} consists of N² pairwise interactions, and were it computed directly, would require CPU-time scaling as O(N²). Even for datasets consisting of a few thousand points, this cost becomes prohibitively expensive. Our approach enables the accurate computation of these pairwise interactions in O(N) time. Since the majority of applications of t-SNE are for at most two-dimensional embeddings, in the following we focus our attention on the cases where s = 1 or 2. However, we note that our algorithm extends naturally to arbitrary dimensions. In such cases, though the constants in the computational cost will vary, our approach will still yield an algorithm with a CPU-time which scales as O(N).

We begin by observing that the repulsive forces F_rep,k defined in eq. (1) can be expressed as s + 2 sums of the form

$$\varphi (y_i)=\sum _{j=1}^{N}K(y_i,y_j)q_j$$ (2)

where the kernel K(y, z) is either

$$K_1(y,z)=\frac{1}{(1+\Vert y-z{\Vert }^2)},\text{or}{K}_2(y,z)=\frac{1}{(1+\Vert y-z{\Vert }^2{)}^2},$$ (3)

for y, $z\in {\mathbb{R}}^s$. Note that both of the kernels K₁ and K₂ are smooth functions of y, z for all y, $z\in {\mathbb{R}}^s$. The key idea of our approach is to use polynomial interpolants of the kernel K in order to accelerate the evaluation of the N–body interactions defined in eq. (2).

8.3.1. Mathematical Preliminaries.

First, we demonstrate with a simple example how polynomial interpolation can be used to accelerate the computation of the N–body interactions with a smooth kernel. Suppose that y₁,…, y_M ∈ (y₀, y₀ + R) and z₁, … , z_N ∈ (z₀, z₀ + R). Let I_y0 and I_z0 denote the intervals (y₀, y₀ + R) and (z₀, z₀ + R), respectively. Note that no assumptions are made regarding the relative locations of y₀ and z₀; in particular, the case y₀ = z₀ is also permitted.

Now consider the sums

$$\varphi (y_i)=\sum _{j=1}^{N}K(y_i,z_j)q_j,i=1,2,\dots M.$$ (4)

Let p be a positive integer. Suppose that ${\tilde{z}}_1,\dots ,{\tilde{z}}_p$, are a collection of p points on the interval I_z0 and that ${\tilde{y}}_1,\dots ,{\tilde{y}}_p$, are a collection of p points on the interval I_y0. Let K_p(y, z) denote a bivariate polynomial interpolant of the kernel K(y, z) satisfying

$$K_p({\tilde{y}}_j,{\tilde{z}}_{\ell })=K({\tilde{y}}_j,{\tilde{z}}_{\ell }),j,\ell =1,2,\dots p.$$

A simple calculation shows that K_p(y, z) is given by

$$K_p(y,z)=\sum _{\ell =1}^p\sum _{j=1}^{p}K({\tilde{y}}_j,{\tilde{z}}_{\ell })L_{j,\tilde{y}}(y)L_{\ell ,\tilde{z}}(z),$$ (5)

where $L_{j,\tilde{y}}(y)$ and $L_{\ell ,\tilde{z}}(z)$ are the Lagrange polynomials

$$L_{\ell ,\tilde{y}}(y)=\prod _{\begin{array}{c}\hfill j=1\hfill \\ \hfill j\ne \ell \hfill \end{array}}^p(y-{\tilde{y}}_j)/\prod _{\begin{array}{c}\hfill j=1\hfill \\ \hfill j\ne \ell \hfill \end{array}}^p({\tilde{y}}_{\ell }-{\tilde{y}}_j),\text{and}{L}_{\ell ,\tilde{z}}(z)=\prod _{\begin{array}{c}\hfill j=1\hfill \\ \hfill j\ne \ell \hfill \end{array}}^p(z-{\tilde{z}}_j)/\prod _{\begin{array}{c}\hfill j=1\hfill \\ \hfill j\ne \ell \hfill \end{array}}^p({\tilde{z}}_{\ell }-{\tilde{z}}_j),$$

ℓ =1, 2 … p. In the following we will refer to the points ${\tilde{y}}_1,\dots ,{\tilde{y}}_p$, and ${\tilde{z}}_1,\dots ,{\tilde{z}}_p$ as interpolation points.

Let $\tilde{\varphi }(y_i)$ denote the approximation to φ(y_i) obtained by replacing the kernel K in eq. (4) by its polynomial interpolant K_p, i.e.

$$\tilde{\varphi }(y_i)=\sum _{j=1}^N{K}_p(y_i,z_j)q_j,$$

for i = 1, 2 … M. Clearly the error in approximating φ(y_i) via $\tilde{\varphi }(y_i)$ is bounded (up to a constant) by the error in approximating K(y, z) via K_p(y, z). In particular, if the polynomial interpolant satisfies the inequality

$$\underset{\begin{array}{c}\hfill y\in (y_0,y_0+R)\hfill \\ \hfill z\in (z_0,z_0+R)\hfill \end{array}}{\text{sup}}\mid K_p(y,z)-K(y,z)\mid \le \epsilon ,$$ (6)

then the error $\mid \tilde{\varphi }(y_i)-\varphi (y_i)\mid$ is given by

$$\begin{gathered} \mid \tilde{\varphi }(y_i)-\varphi (y_i)\mid =\mid \sum _{j=1}^N(K_p(y_i,z_j)-K(y_i,z_j))q_j\mid \\ \le \sum _{j=1}^N\mid K_p(y_i,z_j)-K(y_i,z_j)\mid \mid q_j\mid \\ \le \epsilon \sum _{j=1}^N\mid q_j\mid . \end{gathered}$$

A direct computation of φ(y₁), … , φ(y_M) requires O(M · N) operations. On the other hand, the values $\tilde{\varphi }(y_i)$, i =1, 2, … M, can be computed in O((M + N) · p + p²) operations as follows. Using eq. (5), $\tilde{\varphi }(y_i)$ can be rewritten as

$$\begin{gathered} \tilde{\varphi }(y_i)=\sum _{j=1}^N\sum _{\ell =1}^p\sum _{m=1}^{p}K({\tilde{y}}_{\ell },{\tilde{z}}_m)L_{\ell ,\tilde{y}}(y_i)L_{m,\tilde{z}}(z_j)q_j, \\ =\sum _{\ell =1}^p{L}_{\ell ,\tilde{y}}(y_i)\left(\sum _{m=1}^{p}K({\tilde{y}}_{\ell },{\tilde{z}}_m)\left(\sum _{j=1}^N{L}_{m,\tilde{z}}(z_j)q_j\right)\right), \end{gathered}$$

for i =1, 2, … M. The values $\tilde{\varphi }(y_1),\dots ,\tilde{\varphi }(y_M)$, are computed in three steps.

• Step 1: Compute the coefficients w_m defined by the formula

  $$w_m=\sum _{j=1}^N{L}_{m,\tilde{z}}(z_j)q_j,$$

  for each m = 1, 2, … p. This step requires O(N · p) operations.

• Step 2: Compute the values v_ℓ at the interpolation nodes ${\tilde{y}}_{\ell }$ defined by the formula

  $$v_{\ell }=\sum _{m=1}^{p}K({\tilde{y}}_{\ell },{\tilde{z}}_m)w_m$$

  for all ℓ = 1, 2, … p. This step requires O(p²) operations.

• Step 3: Evaluate the potential $\tilde{\varphi }(y_i)$ using the formula

  $$\tilde{\varphi }(y_i)=\sum _{\ell =1}^p{L}_{\ell ,\tilde{y}}(y_i)v_{\ell },$$

  for all i = 1, 2 … M. This step requires O(M · p) operations.

See Figure S10 for an illustrative figure of the above procedure.

8.3.2. Algorithm.

In this section, we present the main algorithm for the rapid evaluation of the repulsion forces eq. (2). The central strategy is to use piecewise polynomial interpolants of the kernel with equispaced points, and use the procedure described in Section §8.3.1.

Specifically, suppose that the points y_i, i = 1, 2, … N are all contained in the interval [y_min, y_max]. We subdivide the interval $[y_{\text{min}},y_{\text{max}}]={\bigcup }_{i=1}^{N_{\text{int}}}{I}_j$, into N_int intervals of equal length. Let ${\tilde{y}}_{j,\ell }$ denote p equispaced nodes on the interval I_l given by

$${\tilde{y}}_{j,\ell }=h∕2+((j-1)+(\ell -1)\cdot p)\cdot h,$$ (7)

where h = 1/(N_int · p), j = 1, 2 … p, and ℓ = 1, 2 …N_int.

Remark 1. The nodes ${\tilde{y}}_{j,\ell }$, j = 1, 2 … p, and ℓ =1, 2, … N_int, defined in eq. (7), are also equispaced on the whole interval [y_min, y_max].

The interaction between any two intervals I, J, i.e.

$$\sum _{y_j\in J}K(y_i,y_j)q_j,y_i\in I$$

can be accelerated via the algorithm discussed in section 8.3.1. This procedure amounts to using a piecewise polynomial interpolant of the kernel K(y, z) on the domain y, z ∈ [y_min, y_max] as opposed to using an interpolant on the whole interval. We summarize the procedure below.

• Step 1: For each interval I_ℓ, ℓ = 1, 2, … N_int, compute the coefficients w_m,ℓ defined by the formula

  $$w_{m,\ell }=\sum _{y_j\in I_{\ell }}{L}_{m,{\tilde{y}}^{\ell }}(y_j)q_j,$$

  for each m = 1, 2, … p. This step requires O(N · p) operations.

• Step 2: Compute the values v_m,n at the equispaced nodes ${\tilde{y}}_{m,n}$ defined by the formula

  $$v_{m,n}=\sum _{j=1}^{N_{\text{int}}}\sum _{\ell =1}^{p}K({\tilde{y}}_{m,n},{\tilde{y}}_{\ell ,j})w_{\ell ,j}$$ (8)

  for all m = 1, 2, … p, n = 1, 2 … N_int. This step requires O((N_int · p)²) operations.

• Step 3: For each interval I_ℓ, ℓ =1, 2, … N_int, compute the potential ^φ(y_i) via the formula

  $$\varphi (y_i)=\sum _{j=1}^p{L}_{j,{\tilde{y}}^{\ell }}(y_i)v_{j,\ell },$$

  for all points y_i ∈ I_ℓ. This step requires O(N · p) operations.

In this procedure, the functions $L_{j,{\tilde{y}}^{\ell }},j=1,2,\dots p$, are the Lagrange polynomials corresponding to the equispaced interpolation nodes on interval I_ℓ.

In Step 2 of the above procedure, we are evaluating N–body interactions on equispaced grid points. For notational convenience, we rewrite the sum eq. (8)

$$v_i=\sum _{j=1}^{N_{\text{int}}\cdot p}K({\tilde{y}}_i,{\tilde{y}}_j)w_j,$$ (9)

i = 1, 2, … N_int · p. The kernels of interest (K₁ and K₂ defined in eq. (3)) are translationally-invariant, i.e., the kernels satisfy K(y, z) = K(y + δ, z + δ) for any δ. The combination of using equispaced points, along with the translational-invariance of the kernel, implies that the matrix associated with the evaluation of the sums eq. (9) is Toeplitz. This computation can thus be accelerated via the fast-Fourier transform (FFT), which reduces the computational complexity of evaluating the sums eq. (9) from O((N_int · p)²) operations to O(N_int · p log (N_int · p)).

Algorithm 1 describes the fast algorithm for evaluating the repulsive forces eq. (2) in one dimension (s=1) which has computational complexity O(N · p + (N_int · p) log (N_int · p)).

Algorithm 1: FFT-accelerated Interpolation-based t-SNE (FIt-SNE)

$$\begin{array}{cc}\hfill & \mathbf{Input}:\text{Collection of points}\{y_i{\}}_{i=1}^N,\text{source strengths}\{q_i{\}}_{i=1}^N,\text{number of intervals}{N}_{\text{int}},\hfill \\ \hfill & \text{number of interpolation points per interval}p\hfill \\ \hfill & \mathbf{Output}:\varphi (y_i)=\sum \begin{array}{c}N\hfill \\ j=1\hfill \end{array}K(y_i,y_j)q_j\text{for}i=1,2,\dots N\hfill \\ \hfill & 1\text{For each interval}{I}_{\ell },\text{form the equispaced nodes}{\tilde{y}}_{j,\ell },j=1,2,\dots p\text{given by eq.}(7)\hfill \\ \hfill & 2\mathbf{for}I\leftarrow 1\mathbf{to}{N}_{int}\mathbf{do}\hfill \\ \hfill & \begin{array}{c}\hfill 3\hfill \\ \hfill \hfill \\ \hfill \hfill \end{array}\mid \begin{array}{c}\text{Compute the coefficients}{w}_{m,\ell }\text{given by}\hfill \\ w_{m,\ell }=\sum _{y_i\in I_{\ell }}{L}_{m,{\tilde{y}}^{\ell }}(y_i)q_i,\hfill \\ m=1,2,\dots p.\hfill \end{array}\phantom{\mid }\hfill \\ \hfill & 4\mathbf{end}\hfill \\ \hfill & 5\text{Use the fast-Fourier transform to compute the values of}{v}_{m,n}\text{given by}\hfill \\ \hfill & (10)\left[\begin{array}{c}\hfill v_{1,1}\hfill \\ \hfill v_{2,1}\hfill \\ \hfill ⋮\hfill \\ \hfill v_{p-1},N_{\text{int}}\hfill \\ \hfill v_p,N_{\text{int}}\hfill \end{array}\right]=\tilde{K}\cdot \left[\begin{array}{c}\hfill w_{1,1}\hfill \\ \hfill w_{2,1}\hfill \\ \hfill ⋮\hfill \\ \hfill w_{p-1},N_{\text{int}}\hfill \\ \hfill w_p,N_{\text{int}}\hfill \end{array}\right],\hfill \\ \hfill & \text{where}\tilde{K}\text{is the Toeplitz matrix given by}\hfill \\ \hfill & (11){\tilde{K}}_{i,j}=K({\tilde{y}}_i,{\tilde{y}}_j),\hfill \\ \hfill & i,j=1,2,\dots N_{\text{int}}\cdot p.\hfill \\ \hfill & 6\mathbf{for}I\leftarrow 1\mathbf{to}{N}_{int}\mathbf{do}\hfill \\ \hfill & \begin{array}{c}\hfill 7\hfill \\ \hfill \hfill \\ \hfill \hfill \end{array}\mid \begin{array}{c}\text{Compute}\varphi (y_i)\text{at all points}{y}_i\in I_{\ell }\text{via}\hfill \\ \varphi (y_i)=\sum _{j=1}^p{L}_{j,{\tilde{y}}^{\ell }}(y_i)v_{j,\ell }\hfill \\ \hfill \end{array}\phantom{\mid }\hfill \\ \hfill & 8\mathbf{end}\hfill \end{array}$$

8.3.3. Optimal choice of p and N_int.

Recall that the computational complexity of Algorithm 1 is O(N · p + N_int · p log (N_int · p)). We remark that the choice of the parameters N_int and p depends solely on the specified tolerance ε and is independent of the number of points N. Generally, increasing p will reduce the number of intervals N_int required to obtain the same accuracy in the computation. However, we observe that the reduction in N_int for an increased p is not advantageous from a computational perspective—since, as the number of points N increases, the computational cost is independent of N_int and is only a function of p. Moreover, for the t-SNE kernels K₁ and K₂ defined in eq. (3), it turns out that for a fixed accuracy the product N_int · p remains nearly constant for p ≥ 3. Thus, it is optimal to use p = 3 for all t-SNE calculations. In a more general environment, when higher accuracy is required and for other translationally invariant kernels K, the choice of the number of nodes per interval p and the total number of intervals N_int can be optimized based on the accuracy of computation required.

Remark 2. Special care must be taken when increasing p in order to achieve higher accuracy due to the Runge phenomenon associated with equispaced nodes. In fact, the kernels that arise in t-SNE are archetypical examples of this phenomenon. Since we use only low-order piecewise polynomial interpolation (p = 3), we encounter no such difficulties.

In our simulations, we set the values of p = 3 and N_int = max(50, ⌈y_max – y_min⌉). These values are chosen to ensure that the computation of F_rep,i is at least as accurate as the Barnes-Hut approximation at default setting (θ = 0.5). We test the accuracy of the two methods by comparing the repulsive forces computed using BH t-SNE and FIt-SNE to the exact repulsive forces computed using direct algorithm on a dataset with 4000 points. In Figure S1, we report the relative error of the BH t-SNE and FIt-SNE approximations at default values and note that the latter achieves the same (or better) accuracy. Since the approximation error is independent of the number of points (Section §8.3.6), this error analysis applies to datasets of any size.

8.3.4. Extension to two dimensions.

The above algorithm naturally extends to two-dimensional embeddings (s=2). In this case, we divide the computational square [y_min, y_max] × [y_min, y_max] into a collection of N_int × N_int squares with equal side length, and for polynomial interpolation, we use tensor product p × p equispaced nodes on each square. The matrix $\tilde{K}$ mapping the coefficients w to the coefficients v which is of size (N_int · p)² × (N_int · p)², is not a Toeplitz matrix, however, it can be embedded into a Toeplitz matrix of twice its size. The computational complexity of the algorithm analogous to Algorithm 1 for two-dimensional t-SNE is O(N · p² + (N_int · p)² log (N_int · p)).

8.3.5. Performance comparison.

The datasets for comparing the CPU-time performance of BH t-SNE and FIt-SNE in Tables 1, 2, S1, and S2 are generated in the following manner. For each N, we sample N/10 points from 10 gaussians in d–dimensions with mean $c_j\in {\mathbb{R}}^d$ and fixed variance σ = 0.0001. The experiments were performed on two systems—a 2017 Macbook Pro laptop with 2.9 GHz (Turbo up to 3.6GHz) Intel i7 CPU with 2 cores (each supporting 4 threads) and 16GB RAM; and a server with Intel Xeon CPUs with 24 cores clocked at 2.4 GHz and 500GB RAM. In FIt-SNE, the computation of nearest neighbors when computing input similarities, the summing of attractive forces at each iteration of gradient descent, and step 3 of the interpolation scheme outlined above are all multithreaded using C++11 threads, whereas the rest of the computation of the repulsive forces is done via single thread FFTs owing to the small size of FFTs involved. The poorer performance of both BH t-SNE and FIt-SNE on the server as compared to the Macbook can be attributed to the slower single processor clock speed.

8.3.6. Approximation error estimates.

In this section we prove error estimates related to interpolation by equispaced points on a subinterval of the computational domain. First we fix x₀ and suppose that K(x₀, y) is to be approximated on the interval [a, b] by the p-point Lagrange inter-polant w_p(y). For ease of exposition, let f (y) = K(x₀, y) where K(x, y) is either K₁ or K₂ given by eq. (3). Then, a classical theorem in approximation theory (see Dalquist and Björck (2008)¹⁸ for example) states that for all y ∈ (a, b) there exists a ζ_y ∈ (a, b) such that

$$E_p(y)=f(y)-w_p(y)=\frac{f^{(p)}({\zeta }_y)}{p!}{\pi }_p(y),$$

where f^(p) denotes the pth derivative of f, and

$${\pi }_p(y)=\prod _{k=1}^p(y-y_j).$$

Let h = (b – a)/p and the interpolation nodes on the interval (a, b) are y_j = a + (j – 1/2)h, j = 1, …, p.

We bound π_p(y) in the following way (see Trefethen (2013)¹⁹ for example). Suppose that y_j < y < y_j+1. Then

$$\begin{gathered} \mid {\pi }_p(y)\mid =\mid y-y_1\mid \cdot \mid y-y_2\mid \dots \mid y-y_p\mid \\ \le hj\cdots 2h(y-y_j)(y_{j+1}-y)2h\cdot 3h\cdots (p-j)h \\ =h^{p-2}j!(p-j)!(y-y_j)(y_{j+1}-y) \\ =\frac{h^{p}j!(p-j)!}{4}. \end{gathered}$$

Clearly this is bounded by $\frac{h^p(p-1)!}{4}$. Similarly, if y < y₁, or y > y_p then

$$\mid {\pi }_p(y)\mid \le \frac{h}{2}\frac{3h}{2}\dots \frac{2p-1}{2}=\frac{(2p)!}{2^{2p}p!}{h}^p.$$

In order to bound f^(p)(ζ_y) we first consider the case where f(y) = K₁(x₀, y). Then

$$f(y)=\frac{1}{1+\Vert y-x_0{\Vert }^2}=\frac{1∕2}{1+i(y-x_0)}+\frac{1∕2}{1-i(y-x_0)}.$$

Taking p derivatives we obtain

$$f^{(p)}(y)=\frac{1}{2}p!i^p\left[\frac{(-1{)}^p}{[1+i(y-x_0){]}^p}+\frac{1}{[1-i(y-x_0){]}^p}\right]$$

and hence

$$\mid f^{(p)}(y)\mid \le p!$$

Similarly, if f(y) = K₂(x₀, y) then

$$f(y)=\frac{1}{(1+\Vert y-z{\Vert }^2{)}^2}=\frac{1∕4}{[1+i(y-x_0){]}^2}+\frac{1∕4}{[1-i(y-x_0){]}^2}-\frac{1∕4}{1+i(y-x_0)}-\frac{1∕4}{1-i(y-x_0)},$$

from which it follows that

$$\mid f^{(p)}(y)\mid \le \frac{p+2}{2}p!.$$

Putting the above estimates together gives

$$\mid E_p(y)\mid \le \frac{(2p)!}{2^{2p}p!}{h}^p\frac{p+2}{2}=\frac{(2p)!}{2^{2p}p!}(b-a{)}^p\frac{1}{p^p}\frac{p+2}{2},$$

which holds for both K₁ and K₂. Using Stirling’s approximation (see Abramowitz and Stegun (1965),²⁰ for example) it follows that

$$\mid E_p(y)\mid \le \left(\frac{p+2}{\sqrt{2}}\right){\left(\frac{b-a}{e}\right)}^p{e}^{\frac{1}{24p}}.$$

We now use this estimate to construct an error bound of the form given in eq. (6). First, for fixed x ∈ [a, b] let K_r(x, y) denote the polynomial interpolant for y ∈ [c, d]. Then

$$\underset{x\in [a,b]}{\max }\underset{y\in [c,d]}{\max }\mid K(x,y)-K_r(x,y)\mid \le \left(\frac{p+2}{\sqrt{2}}\right){\left(\frac{d-c}{e}\right)}^p{e}^{\frac{1}{24p}}.$$

Similarly, for fixed y ∈ [c, d] let K_l(x, y) denote the polynomial interpolant for x ∈ [a, b], in which case

$$\underset{x\in [a,b]}{\max }\underset{y\in [c,d]}{\max }\mid K(x,y)-K_{\ell }(x,y)\mid \le \left(\frac{p+2}{\sqrt{2}}\right){\left(\frac{d-c}{e}\right)}^p{e}^{\frac{1}{24p}}.$$

Note that by construction,

$$K_r(x,y)=\sum _{j=1}^p{L}_{j,[c,d]}(y)K(x,y_j),$$

and

$$K_{\ell }(x,y)=\sum _{j=1}^p{L}_{j,[a,b]}(x)K(x_j,y),$$

where L_j,[c,d], j = 1, … , p are the Lagrange polynomials for the nodes y₁, … , y_p ∈ [c, d].

As above, let K_p(x, y) denote the polynomial interpolant of K(x, y) which is degree p in both x and y for x ∈ [a, b] and y ∈ [c, d]. Evidently,

$$K_p(x,y)=\sum _{j=1}^p\sum _{m=1}^p{L}_{j,[c,d]}(y)L_{m,[a,b]}(x)K(x_m,y_j).$$

Hence

$$\begin{gathered} \underset{x\in [a,b]}{\max }\underset{y\in [c,d]}{\max }\mid K_p(x,y)-K_r(x,y)\mid \le \underset{x\in [a,b]}{\max }\underset{y\in [c,d]}{\max }\sum _{j=1}^p\mid L_{j,[c,d]}(y)\mid \mid K(x,y_j)-\sum _{m=1}^p{L}_{m,[a,b]}(x)K(x_m,y_j)\mid \\ =\underset{x\in [a,b]}{\max }\underset{y\in [c,d]}{\max }\sum _{j=1}^p\mid L_{j,[c,d]}(y)\mid \mid K(x,y_j)-K_{\ell }(x,y_j)\mid \\ \le \left(\frac{p+2}{\sqrt{2}}\right){\left(\frac{b-a}{e}\right)}^p{e}^{\frac{1}{24p}}\sum _{j=1}^p\underset{y\in [c,d]}{\max }\mid L_{j,[c,d]}(y)\mid . \end{gathered}$$

A slight modification of the argument presented in Trefethen and Weideman (1991)²¹ yields the following bound,

$$\underset{y\in [c,d]}{\max }\mid L_{j,[c,d]}(y)\mid \le 8\frac{2^p}{p},$$

from which it follows that

$$\underset{x\in [a,b]}{\max }\underset{y\in [c,d]}{\max }\mid K_p(x,y)-K_r(x,y)\mid \le 8\left(\frac{p+2}{\sqrt{2}p}\right){\left(\frac{2(b-a)}{e}\right)}^p{e}^{\frac{1}{12p}}.$$

Then

$$\begin{gathered} \mid K(x_0,y_0)-K_p(x_0,y_0)\mid \le \mid K(x_0,y_0)-K_r(x_0,y_0)\mid +\mid K_r(x_0,y_0)-K_p(x_0,y_0)\mid \\ \le 8\left(\frac{p+2}{\sqrt{2}p}\right){\left(\frac{2(b-a)}{e}\right)}^p{e}^{\frac{1}{12p}}+\left(\frac{p+2}{\sqrt{2}}\right){\left(\frac{d-c}{e}\right)}^p{e}^{\frac{1}{24p}} \end{gathered}$$

which is the estimate we require. In particular, if L = b – a = d – c we obtain the bound

$$\mid K(x_0,y_0)-K_p(x_0,y_0)\mid \le 7\frac{(p+2)}{p}\frac{2^p{L}^p}{e^p}.$$

Note that if $L<\frac{e}{2}$ then the error will decay exponentially in p.

In two-dimensions an almost identical analysis shows that the error is bounded by

$$\mid K(x_0,y_0)-K_p(x_0,y_0)\mid \le {16}^3\frac{(p+2)}{\sqrt{8}{p}^3}\frac{8^p{L}^p}{e^p}.$$

In principle this guarantees convergence only when $L<\frac{e}{8}$. In practice, extensive numerical evidence suggests that the error decays exponentially in p provided that L < 1.4.

8.4. Out-of-Core PCA.

The methods for t-SNE presented above allows for the embedding of millions of points, but can only be used to reduce the dimensionality of datasets that can fit in the memory. For many large, high dimensional datasets, specialized servers must be used simply in order to load the data. In order to allow for visualization and analysis of such datasets on resource-limited machines, we present an out-of-core implementation of randomized PCA, which can be used to compute the top few (e.g. 50) principal components of a dataset to high accuracy, without ever loading it in its entirety.²² Note that out-of-core PCA was not used in the analysis above, but we include it as it can be useful for users interested in running t-SNE on large datasets using a resource-limited machine.

8.4.1. Randomized Methods for PCA.

The goal of PCA is to approximate the matrix being analyzed (after mean centering of its columns) with a low-rank matrix. PCA is primarily useful when such an approximation makes sense; that is, when the matrix being analyzed is approximately low-rank. If the input matrix is low-rank, then by definition, its range is low-dimensional. As such, when the input matrix is applied to a small number of random vectors, the resulting vectors nearly span its range. This observation is the core idea behind randomized algorithms for PCA: applying the input matrix to a small number of random vectors results in vectors that approximate the range of the matrix. Then, simple linear algebra techniques can be used to compute the principal components. Notably, the only operations involving the large input matrix are matrix-vector multiplications, which are easily parallelized, and for which highly optimized implementations exist. Randomized algorithms have been rigorously proven to be remarkably accurate with extremely high probability,^25,26 because for a rank-k matrix, as few as l = k + 2 random vectors are sufficient for the probability of missing a significant part of the range to be negligible. The algorithm and its underlying theory are covered in detail in Halko et al. (2011).²⁵ An easy-to-use “black box” implementation of randomized PCA is available and described in Li et al. (2017),²³ but it requires the entire matrix to be loaded in the memory. We present an out-of-core implementation of PCA in C++/R, oocPCA, allowing for decomposition of matrices which cannot fit in the memory.

Algorithm 2: Out-of-Core PCA (oocPCA)

$$\begin{array}{cc}\hfill & \mathbf{Input}:\text{Matrix}A\text{of size}m\times n\text{stored in slow memory},\text{non-negative integers}its,k,l,b,\hfill \\ \hfill & \text{where}0<k\le l<\text{min}(m,n),\text{and}l\text{defaults to}k+2\hfill \\ \hfill & \mathbf{Output}:\text{Orthonormal}U\text{of size}m\times k,\text{non-negative diagonal matrix}\Sigma \text{of size}k\times k,\hfill \\ \hfill & \text{orthonormal}V\text{of size}n\times k,\text{such that}A\approx U\Sigma V^{\ast }\hfill \\ \hfill & 1\text{Generate uniform random matrix}\Omega \text{of size}n\times l\hfill \\ \hfill & 2\text{Form}{Y}_0=A\Omega \text{block-wise},b\text{rows at a time}\hfill \\ \hfill & 3\text{Renormalize with LU factorization}{L}_0{U}_0=Y_0\hfill \\ \hfill & 4\mathbf{for}i\leftarrow 1\mathbf{to}its\mathbf{do}\hfill \\ \hfill & \begin{array}{c}\hfill 5\hfill \\ \hfill 6\hfill \\ \hfill 7\hfill \\ \hfill 8\hfill \end{array}\mid \begin{array}{c}\text{From}{Y}_i=A{A}^{\ast }{L}_{i-1}\text{block-wise},b\text{rows at a time}\hfill \\ \mathbf{if}i<\mathit{its}\mathbf{then}\hfill \\ \mid \text{Renormalize with LU factorization}{L}_i{U}_i=Y_i\hfill \\ \mathbf{end}\hfill \end{array}\phantom{\mid }\hfill \\ \hfill & 9\mathbf{end}\hfill \\ \hfill & 10\text{Renormalize with QR factorization}QR=Y_i\hfill \\ \hfill & 11\text{Compute SVD of small matrix}{U}^{\prime }\Sigma V^{\ast }=Q^{\ast }A\hfill \\ \hfill & 12\text{Set}U=Q{U}^{\prime }\hfill \end{array}$$

8.4.2. Implementation.

Our implementation is described in Algorithm 1. Given an m × n matrix of doubles A, stored in row-major format on the disk of a machine with M bytes of available memory, the number of rows that can fit in the memory is calculated as $b=\lfloor \frac{M}{8mn}\rfloor$. The only operations performed using A are matrix multiplications, which can be performed block-wise. Specifically, the matrix product AB, where B is an n × p matrix stored in the fast memory, can be computed by loading the first b rows of A, and forming the inner product of each row with the columns of B. The process can be continued with the remaining blocks of the matrix, essentially “filling in” the product AB with each new block. In this manner, left multiplication by A can be computed without ever loading the full matrix A.

By simply replacing the matrix multiplications in the implementation of Li et al. (2017)²³ with block-wise matrix multiplication, an out-of-core algorithm can be obtained. However, significant optimization is possible. The run-time of an out-of-core algorithm is almost entirely determined by disk access time; namely, the number of times the matrix must be loaded to the memory. As suggested in Li et al. (2017),²³ the renormalization step between the application of A and A* is not necessary in most cases, and in the out-of-core setting, doubles the number of times A must be loaded per power iterations. In our implementation, we remove this renormalization step, and apply AA* simultaneously, hence requiring the matrix only be loaded once per iteration.

Our implementation is in C++ with an R wrapper. For maximum optimization of linear algebra operations, we use the highly parallelized Intel MKL for all BLAS functions (e.g. matrix multiplications). The R wrapper provides functions for PCA of matrices in CSV and in binary format. Furthermore, basic preprocessing steps including log transformation and mean centering of rows and/or columns can also be performed prior to decomposition, so that the matrix need not ever be fully stored in the memory.

To demonstrate oocPCA’s performance, we generated a random 1,000,000 × 30,000 rank-50 matrix stored as doubles, which would require 240GB to simply store in the memory, far exceeding the memory capacity of a personal computer. Using oocPCA we can compute the top principal components of the matrix with much less memory. Using a 2017 Macbook Pro laptop with 16GB RAM, solid state drive, and a 2.9 GHz Intel i7 CPU, the rank-50 approximation was computed in 38 minutes.

8.5. FIt-SNE of 1.3 million mouse brain cells.

The scRNA-seq dataset consisting of 1.3 million cells from the cortex, hippocampus, and ventricular zones of embryonic day 18 mouse brains were downloaded from the 10X Genomics website and processed using the normalization and filtering steps of Zheng et al.,¹⁴ as implemented by the python package scanpy.¹⁵ Scanpy was also used to compute a neighborhood graph of the observations using a Gaussian kernel with adaptive widths, and then the points were clustered using the Louvain method. Subsequent analysis of this dataset was then performed in R. FIt-SNE of all 1,306,127 cells was computed with 4,000 iterations of gradient descent (2,000 of them being early exaggeration iterations) and other parameters set to defaults. FIt-SNE with the same parameters was also run on a random subset of 50,000 cells. We sought to identify known cell types from the Allen Brain Atlas (http://celltypes.brain-map.org/rnaseq/mouse) in the embedding, and gave two examples of cell populations (see Supplementary Table 9 of Tasic et al. (2018)³) that could be identified in the full dataset, but not in the downsampled embedding.

8.6. t-SNE heatmap of retinal cells.

The scRNA-seq retinal cells data of Shekhar et al. (2016)¹¹ was downloaded from GEO (GSE81905). The digital expression matrix was preprocessed using the code provided by the authors of the original publication (https://github.com/broadinstitute/BipolarCell2016). In short, libraries containing more than 10% mitochondrially derived transcripts were removed, cells with ≤ 500 genes were removed, as were genes with expression in ≤ 30 cells or having ≥ 60 transcripts, resulting in 13,166 genes and 27,499 cells. Finally, the data were median normalized, log-transformed, and the genes were Z-scored. The top 37 principal components were computed and used as input to 1D FIt-SNE with perplexity 30 and for 1000 iterations. Finally, the t-SNE heatmap (Figure 2) was computed as described in the main text, with the marker genes (Tacr3, Rcvrn, Syt2, Irx5, Irx6, Vsx1, Hcn4, Grik1, Gria1, Kcng4, Hcn1, Cabp5, Grm6, Isl1, Scgn, Otx2, Vsx2, Car8, Sebox, Prkca) from Shekhar et al. (2016)¹¹ listed in Supplemental Table 2. Each marker gene was enriched with the 25 genes with most similar expression patterns. Genes associated with each cluster in the 2D embedding were obtained by running dbscan on the 2D t-SNE with the settings ϵ = 2 and a minimum number of points of 40. For each cluster i, a “metagene” c_i of length 27,499 was generated, where c_i(k) = 1 if the kth cell is in the ith cluster and c_i(k) = 0 otherwise. These vectors were then treated as “genes” and enriched in the same fashion as the genes.

8.7. Comparing approximate nearest neighbors and VP trees on scRNA-seq data.

To evaluate the effect of approximate nearest neighbors on embedding quality of scRNA-seq data, we compared the resulting embeddings on several scRNA-seq datasets where labels are predetermined by other sources. For each dataset, we also compute the 1-nearest neighbor error (1N error), defined as the percentage of cells for which the cell closest to them in the embedding belongs to a different label. We did the comparison on the 1.3 million mouse brain cells from above, purified PBMC populations from Zheng et al. (2017),¹⁴ and mouse visual cortex cells from Hrvatin et al. (2018).¹⁶

Filtered expression matrices for FACS purified peripheral blood monocyte (PBMC) populations were downloaded from the 10X website¹⁴ and concatenated them to a single expression matrix. The matrix was filtered to include cells expressing more than 400 genes and gene expressed in more than 100 cells, resulting in a matrix with 83,992 cells and 12,776 genes. Purified CD4 helper T cells and cytotoxic T cells were removed, as they (by definition) are supersets of some of the other subtypes, leaving 64,664 cells. After library and log normalization, the top 25 principal components (PCs) were computed using randomized SVD.²⁴ FIt-SNE using VP trees and approximate nearest neighbors were was computed on the the PCs and qualitatively compared in Figure S4.

The scRNA-seq expression matrix of mouse visual cortex cells from Hrvatin et al.¹⁶ was obtained from GEO (GSE102827). Genes with mean expression less than 0.00003 and non-zero expression in less than 4 cells were excluded, resulting in a matrix with 65,539 cells and 19,155 genes. The cells were further subsetted to those assigned to subtypes, resulting in 48,266 cells. After library and log normalization, the top 25 principal components were computed using randomized SVD. FIt-SNE using VP trees and approximate nearest neighbors were then computed on the PCs and compared in Figure S5.

9. Code Availability

FIt-SNE is available at https://github.com/KlugerLab/FIt-SNE. The code for all experiments is available at request and will be publicly available at https://github.com/KlugerLab/FIt-SNE-paper on publication.

10. Data Availability

The 1.3 million mouse brain cells dataset and FACS purified PBMCs of Zheng et al.¹⁴ can be downloaded from 10X Genomics website (https://support.10xgenomics.com/single-cell-gene-expression/datasets/). Two other public scRNA-seq datasets from NCBI Gene Expression Omnibus (GEO) were used: Hrvatin et al. (GSE102827) and Shekhar et al. (GSE81905).