Eukaryotic Cell Dynamics from Crawlers to Swimmers

Abstract

Movement requires force transmission to the environment, and motile cells are robustly, though not elegantly, designed nanomachines that often can cope with a variety of environmental conditions by altering the mode of force transmission used¹. As with humans, the available modes range from momentary attachment to a substrate when crawling, to shape deformations when swimming, and at the cellular level this involves sensing the mechanical properties of the environment and altering the mode appropriately. While many types of cells can adapt their mode of movement to their microenvironment (ME)², our understanding of how they detect, transduce and process information from the ME to determine the optimal mode is still rudimentary. The shape and integrity of a cell is determined by its cytoskeleton (CSK), and thus the shape changes that may be required to move involve controlled remodeling of the CSK. Motion in vivo is often in response to extracellular signals, which requires the ability to detect such signals and transduce them into the shape changes and force generation needed for movement. Thus the nanomachine is complex, and while much is known about individual components involved in movement, an integrated understanding of motility in even simple cells such as bacteria is not at hand. In this review we discuss recent advances in our understanding of cell motility and some of the problems remaining to be solved.

Graphical abstract

1 Introduction

Locomotion of cells, both individually and collectively, plays an important role in morphogenesis during multicellular development, in the immune response, in wound healing, and in cancer metastasis(1). Single-cell organisms exhibit a variety of modes for translocation, including crawling, swimming, drifting with the surrounding flow, and others. Some prokaryotes such as bacteria use flagella to swim, while eukaryotes such as paramecia use cilia to swim, but both types can only use one mode. However other eukaryotes, such as tumor cells, are more flexible and can adopt the mode used to the environment in which they find themselves. For instance, whether a single-cell or collective mode of movement is used can depend on both the cell type and the mechanical properties of the the microenvironment in which they are moving(2; 3). This adaptability has significant implications for developing new treatment protocols for cancer and other diseases, for it implies that it is essential to understand the processes by which cells detect extracellular chemical and mechanical signals and transduce them into intracellular signals that lead to force generation, morphological changes and directed movement.

Controlled deformation by remodeling of the CSK, and control of force transmission to the ME involve multiple levels of control to produce the forces needed for movement. Much is known about the biochemical details of the constituent steps in signaling and force generation, and the focus is now shifting to understanding whole-cell movement. In view of the complexity of these processes, mathematical models are essential for synthesizing what is known to unify observations, and for making predictions that can guide further experimental work. Such models must link molecular-level behavior with macroscopic observations on forces exerted, cell shape, and cell speed, because the large-scale mechanical effects cannot be predicted from the molecular biology of individual steps alone. However, how to formulate a multiscale model that integrates the microscopic steps into a macroscopic model is poorly understood in this context.

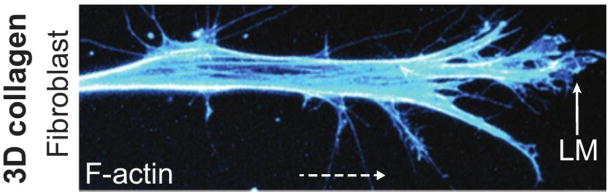
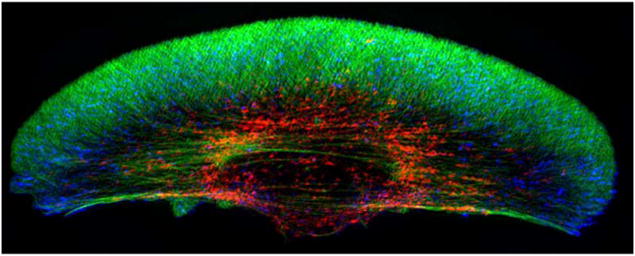
In eukaryotic cells, force transmission to the surroundings may involve one or more of different types of actin-driven protrusions, such as lamellipodia, filopodia, pseudpodia or invadapodia(5; 6), pressure-driven shape deformations such as blebs or lobopodia(7; 4), or movement using tension gradients in the membrane(8; 9). Movement is generally classified as either mesenchymal or amoeboid, the former characterized by strong adhesion to the ME, slow movement (~0.1 – 1μm/hr), and lamellipodial protrusions. The mesenchymal mode is used by fibroblasts, tumor cells of epithelial origin, and fish-scale keratocytes (cf. Figure 1), and may involve proteolytic modification of the ME.

Figure 1.

Two examples of mesenchymal motion. Top: A fibroblast in a 3D collagen matrix From Petrie et al(4). Bottom: A fish-scale keratocyte. Actin (green) myosin-II (red) and focal adhesions (blue). From www.hhmi.org/scientists/julie-theriot.

In contrast, the amoeboid mode utilizes a less-structured CSK that lacks stress fibers, involves lower adhesion to the substrate and leads to higher speeds. Proteolytic degradation of the ECM is not used, and cells adopt a more rounded cell shape, often with a highly contractile ‘tail’ called the uropod(10). The amoeboid mode can be far more effective and can lead to speeds up to forty times faster than those resulting from mesenchymal motion (11; 12). Cells such as leukocytes, which normally use the mesenchymal mode in the ECM, can migrate in vivo in the absence of integrins, using a ‘flowing and squeezing’ mechanism (10). The amoeboid mode is widely used, and when the environment is less favorable to mesenchymal movement, due eg.—, to changes in the adhesiveness of the substrate, cells compensate by undergoing a ‘mesenchymal-to-amoeboid’ transition (MAT) (13; 14; 15).

Several sub-types of amoeboid motion are known. Cells such as neutrophils and Dictyostelium discoideum (Dd) can move by extending actin-polymerization-driven pseudopodia and execute repeated cycles of extension, adhesion to the substrate, and retraction of the rear. Other cells, including Dd, can produce membrane ’blisters’ called blebs, in which the membrane detaches from the cortex locally and the internal pressure forces fluid into the bleb. Figure 2(a) shows a cell that blebs profusely, while not moving, whereas Figure 2(b) shows a motile, blebbing Dd cell. If bleb formation is restricted to the leading edge as in (b), forward motion is driven by contraction of the cortical network at the rear, but one also sees blebs that propagate around the surface of Dd cells (16).

Figure 2.

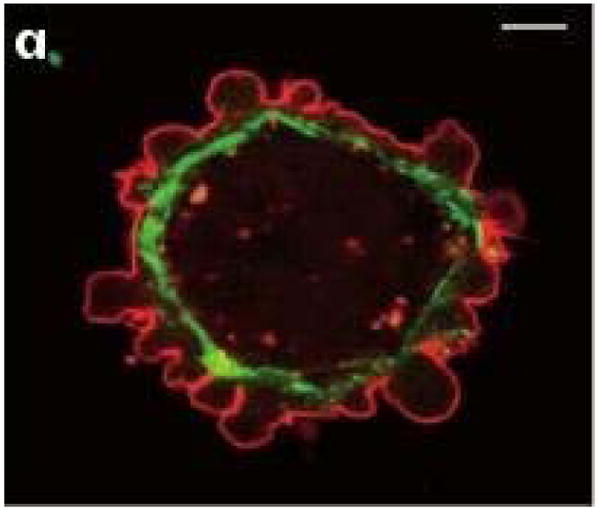
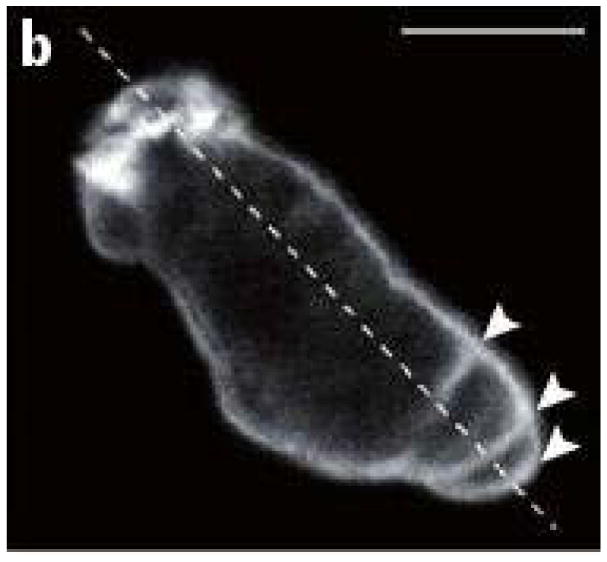
(a) Blebbing on a melanoma cell: myosin (green) localizes under the blebbing membrane (red) (b) The actin cortex of a Dd cell migrating to the lower right. Arrowheads indicate the successive blebs and arcs of the actin cortex. From Charras & Paluch(7).

In another amoeboid mode, cells move by generating a retrograde flow in the cortex, and the drag force created by the flow leads to a reactive tension gradient in the membrane that propels the cell forward. We call this the ’tension-’ or ’friction-driven’ mode. A third, less-studied mode of amoeboid movement is swimming in a fluid. Both Dd cells and neutrophils are able to do this(17), presumably to move through fluid-filled voids in their environment. Finally, some cells apparently can move using osmotic effects and pumps to move by fluid uptake at the leading edge and removal at the rear(18; 19).

Often the directed movement of cells is in response to signals in the ME, which requires mechanism for transducing the extracellular signals into intracellular signals that govern the cellular engine. Chemical, mechanical and other signals initiate signal transduction cascades that control movement, and at present, transduction of the chemical variety is understood better than other types. Cells such as macrophages or Dd detect differences across their body, and small signal differences over the cell can be amplified into large end-to-end intracellular differences that can control the spatial localization of the sites of force-generation needed to produce directed motion. Many eukaryotic cells, such as neutrophils and Dd, share common mechanisms for sensing and responding to chemoattractant gradients via G-protein-coupled receptors (GPCRs), and to adhesion gradients via integrins or their homologs.

Crawling and swimming are the extremes on a continuum of strategies, and the variety of modes used in different environments raises questions about how mechano-chemical sensing of the environment is used to control the evolution of the CSK (12). Protrusions and other shape changes require forces that must be correctly orchestrated in space and time to produce net motion, and to understand this orchestration one must couple the intracellular dynamics with the state of the ME. Tension in the membrane and cortex has emerged as an important determinant in the orchestration, whether in random cell movement, or movement in response to environmental cues. The complexity of the CSK poses significant problems for modeling it at a level that can give new insights and assist in experimental investigations, and added to this are the complexities of the biochemical networks involved in signal transduction and control of re-building the CSK. Together they pose enormous challenges.

2 Mesenchymal movement

2.1 The cytoskeleton

The forces needed for movement derive from the hydrolysis of ATP, which is used in the formation of actin networks and in myosin motor contraction. In vitro actin monomers (G-actin) assemble into two-stranded filaments (F-actin), bundles of filaments and gels. A helical F-actin filament is asymmetric, with a barbed (or plus) end and a pointed (or minus) end, which results in asymmetric reaction kinetics at the two ends. Once nucleated, actin filaments in solution reach a steady state phase of ’treadmilling’, in which G-ATP-actin is incorporated at the barbed end and G-ADP-actin is released at the pointed end. Nucleation of new filaments is very slow in solution, but in vivo there are two major modes of nucleation, one which utilizes a membrane-anchored protein from the formin family that can initiate and elongate filaments in a processive manner(21; 22), and the other that uses the Arp2/3 complex, which attaches to an existing filament and creates a new side branch(23).

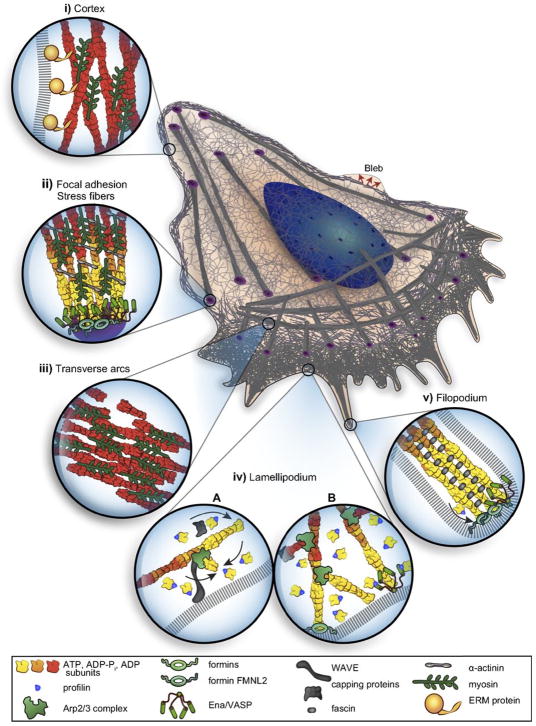
Formins are used in the formation of various thin, highly-localized cellular protrusions such as micro spikes and filopodia, the latter of which consist of 10–30 bundled parallel actin filaments that grow at the leading edge (cf. Figure 3) and may serve as ’sensors’ of the local ME. Side-branching controlled by Arp2/3 and mediated by various nucleation-promoting-factors, such as the WASP family of proteins, leads to a dense dendrite actin network that provides the mechanical force to drive various protrusions. These include lamellopdia, the flat, fan-shaped protrusions used in fibroblasts, keratocytes and other cell types, and pseudopodia used by Dd. It has been shown that mechanical loading of dendrite networks on micropatterned substrates increases the filament density and the power of the network(24), but it remains to be seen whether this occurs in all structures driven by actin polymerization.

Figure 3.

A schematic of a mesenchymal cell, showing the various sub-structures and protrusions. From Blanchoin et al.(20).

Stress fibers, another important actin structure, are bundles of actin filaments cross-linked by α-actinin(25; 26; 27). Bipolar filaments of myosin-II (myo-II), 15–20 molecules long(25), intercalated between the actin filaments, which leads to a muscle-like contractile force in stress fibers that are attached to focal adhesions or embedded in the actin network around the nucleus(28). In solution the stress-strain response of actin networks can be varied from that of a stiff gel to that of a liquid by controlled assembly, cross-linking, and disassembly of its components(29), and stresses generated by myo-II can increase the stiffness dramatically(30). Models of the network in which the stress tensor is decomposed into additive parts governing the passive and active stress components have been developed(31) (32), but a close connection between such models and whole-cell dynamics remains to be developed.

In vivo there are numerous actin-binding proteins used for the local control of network dynamics(33; 20). These include proteins such as thymosin-β4 that sequester actin monomers to prevent spontaneous nucleation, those that bind actin monomers to affect nucleotide exchange (profilin, cofilin, twinfilin), those such as α-actinin, which cross-link the actin filaments and can induce a sol-gel transition, and others that link the cortex to the plasma membrane. Some, such as the ADF/cofilin family and gelsolin, sever F-actin to generate more filament ends for assembly or disassembly. Finally, others function to cap filament ends to regulate addition or loss of actin subunits (capping protein, gelsolin, the Arp2/3 complex), to nucleate filament growth (the Arp2/3 complex, formin), or to enhance subunit dissociation (cofilin). Depending on the level and activity of these proteins, the rheological properties in vivo can be quite different from those of in vitro solutions and can vary significantly throughout the cell.

Recent experimental results illustrate the difficulties in modeling the CSK. Since cells are ~ 70% water it is to be expected that pressure variations propagate essentially instantaneously, because the speed of sound in water is ~ 1500 m/s and measurements of the speed in various cell types using scanning acoustic microscopy yield similar values (34; 35). However, recent experiments have measured relaxation times on the order of seconds for pressure variations, and it was concluded that the CSK is best described as a poro-elastic material(36; 37). This conclusion follows from an interpretation of the experimental results based on Darcy’s law, but this is questionable for the CSK, since the law is derived under the assumptions that the solid phase is fixed in space and that the inertial effects of the fluid are negligible. Since the CSK is highly deformable the first assumption is dubious, and the second assumption may not be applicable in some indentation experiments in which the deformation is large and the rise time short (~ 35ms)(37). A momentum-based approach to diffusion in a multi-component mixture shows that relaxation of perturbations is described by a wave equation on short time scales(38), and that may apply here. A number of multi-phase models of the CSK have been developed, but none to date incorporate detailed descriptions of the CSK and the numerous proteins that modulate it(39; 40; 41).

2.2 Force transmission

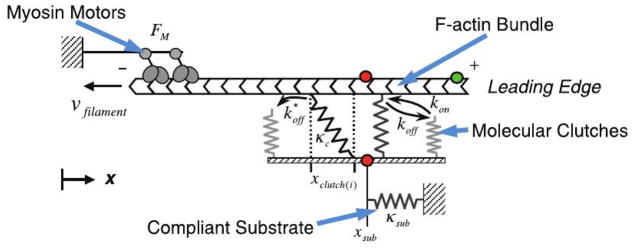
Four zones of actin networks are involved in mesenchymal movement: (i) the lamellipodium (LP), a region of rapid actin turnover which extends 3–5 μm from the leading edge of the cell, (ii) the lamellum (LM), a contractile network that extends from just behind the leading edge to the interior of the cell and contains stress fibers and transverse arcs, (iii) the convergence zone, in which the retrograde flow in the LP meets the anterograde flow in the cell body, and (iv) the actin network in the cell body, which contains the major organelles(42–45). To move the LP forward, the LP-LM network employs focal contacts and focal adhesions (FAs) that involve integrin binding to extracellular ligands, proteins such as talin and vinculin that link integrins to the actin network, and force-modulated receptor clustering(46–48). Growth of FAs involves positive feedback, since FA size is proportional to the force applied to it by the cell(49), and FAs grow in the direction of the applied force, even in the absence of stress fibers. In vivo these adhesions act as mechanotransducers that adjust their size in proportion to the stiffness of the ECM and the force applied to them. Force transmission between the actin network and integrins occurs via a ’molecular clutch’, which when engaged inhibits retrograde flow of the network and pushes the LP forward(50).

A model of the clutch based on Hookean springs for the actin-integrin connection (cf. Figure 4) showed how the ME could determine the mode of engagement(51). On a stiff substrate the attachments break independently under load, and the random nature of the process leads to a frictional slippage, low traction and rapid retrograde network flow. On a more flexible substrate the substrate compliance leads to more engaged connections, which in turn leads to higher traction force and slower retrograde flow.

Figure 4.

The molecular clutch model. From Chan & Odde(51).

The model predicts an increase in traction force at low substrate stiffness, followed by a monotone decreasing force at larger stiffness, but more recent experiments on the actin–talin–integrin–fibronectin clutch, using mouse embryonic fibroblasts, suggests that this biphasic dependence only arises in talin-deficient cells – otherwise the dependence is monotonic(52). In the framework of the multilayer model of the clutch connection(53; 54) this shows that slippage in either the cortex–talin connection or the talin–integrin connection is the source of the biphasic response. However, the picture is still unclear, since other experiments suggest that substrate elasticity is not the sole determinant of shape and spreading, but rather that it is whether or not the substrate exhibits stress relaxation(55). Their results show that cells cultured on viscoelastic substrates spread more than cells on elastic substrates of the same modulus, and the amount of spreading is similar to what is observed on stiffer elastic substrates. The role of pressure forces in driving the protrusion is also poorly understood, but it is known that the force due to cytosolic pressure is comparable to that due to actin polymerization in lamellipodia(56). A continuum model that incorporates actin flow, myosin contraction and adhesion dynamics can explain a number of observations(57), but incorporation of the molecular-level details into a continuum model remains to be done.

The adhesive properties of the ECM also play an important role in motility. It was first predicted theoretically that the levels of integrin ligands such as fibronectin, the amounts of integrin, and the integrin-ligand affinity could determine the maximum migration speed(58), and this has been confirmed experimentally(59–61). Cells exhibit a biphasic dependence of speed on adhesion strength, with optimal migration at intermediate levels of integrin ligands. Lower speeds result at low ligand concentrations because the cells cannot gain enough traction, whereas at high adhesion the cells become stuck(59). Other experimental and theoretical studies on the role of other factors such as motor activity show that the trade-offs that lead to maximal speeds are more complex than the early theoretical work predicts and a consistent picture has not yet emerged(62; 63). The latter authors show that migration in a 3D environment is determined by a complex interaction of adhesiveness, nuclear volume, contractility, and cell stiffness. Detailed models that capture some of these effects have been formulated and analyzed(64).

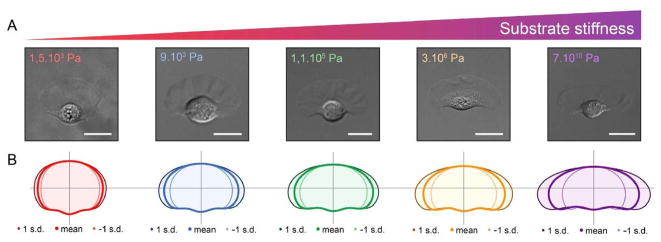
Thus far we have focused on extension of the ’front’ and adhesion to the substrate, but of course the rear must be brought along as well by relaxing the adhesion there. The integrated process of mesenchymal motion is understood best in keratocytes because of their simple shape and steady movement, and several 2D models of the cell have been developed(65). Substrate stiffness has a strong effect on the cell shape (cf. Figure 5) and on the initiation of movement(66). Detailed models of the dendrite network that predict the shape of keratocytes have been developed(67), but an open question is whether the membrane shape can be understood as the result of minimizing the membrane free energy. The time scales involved suggest that mechanical disturbances in the membrane relax quickly, and the shape of a 2D slice computed from the free energy closely approximates the observed shape(68). Whether similar reasoning applies to the more complex shapes observed in other cells remains to be determined.

Figure 5.

How the shape of a keratocyte depends on the subtrate stiffness. From Riaz et al.(69).

3 Amoeboid movement

3.1 Blebbing

The cell cortex, a 200–300 nm thick layer composed of an F-actin network cross-linked by filamin and tethered to the membrane, plays a major role in amoeboid motion. Embedded myo-II confers rigidity to the cortex, but it can also contract and exert tension in the cortex. Myo-I, a small motor protein that binds to both actin and the membrane(70) – or linker proteins such as ezrin, radixin, and moesin, tether the cortex to the membrane, but the connection is dynamic and the cortex can slide tangentially under the membrane (71; 72). Rheological studies in vitro have determined how the shear and storage moduli of actin networks depend on the concentrations of actin monomers, linking proteins and other factors (73–75). For example, the viscous element is strongly dependent on the presence of cross-linkers and myo-II – in the absence of cross-linkers the motors tend to fluidize the network (76). The time-scale for dissolution of the cortex following detachment from the membrane is ~ 10 sec (77), which is small compared to the viscous relaxation time of the cortex (78), and thus the initial response of the cortex to perturbations is elastic.

There is typically a positive pressure difference of a few hundred pascals from inside to outside in cells, and while the cortex is sufficiently porous (mesh size ~200 nm (79)) that cytosol can pass through it, it is not known what the pressure drop across the cortex is. If the pressure difference is primarily sustained by the membrane, a bleb may arise when it is detached from the cortex. The energy involved in the interaction between the membrane and cortex can be treated as an effective interfacial energy, and to separate them requires either physically or chemically breaking the attachments, e.g., by active contraction of the cortex and buckling of the membrane(80; 81). This energy has been measured as ~ 5 · 10⁻¹⁷J/μm² in zebrafish germ layer cells (82) and ~ 10⁻¹⁷J/μm² in Dd(83). Interestingly, the energy is about three-fold higher at the rear than in the front of an advancing Dd cell, which biases blebbing toward the front.

Blebs form by detachment of the membrane from the underlying cortex, which is triggered by rupture of the cortex or by local reduction of membrane—cortex adhesion(78). Blebs on Dd cells (cf. Figure 2(b)) expand in less than a second and they leave behind an F-actin ’scar’ that remains intact for a few seconds after the bleb forms, which suggests that detachment of the membrane from the cortex, rather than its rupture, is involved in their formation(84). Cells must produce sufficient fluid pressure due to cortical contraction to produce blebs, and there is a minimum tension below which blebs do not form(78). Above this threshold there is a smooth increase in the volume of the bleb as a function of cortical tension, which suggests that the transition involves a soft bifurcation, rather than a finite-amplitude one. Blebbing is abolished in myo-II mutants of Dd (85–87) or when cells are treated with blebbistatin to eliminate contraction(88). In intact cells local regions of high tension prevent blebbing in these regions(89), and thus it is important to understand the origin and role of spatially non-uniform cortical tension.

There are two major modes of blebbing, depending on whether or not the bleb is retracted. In the former blebs can undergo repeated cycles of nucleation, expansion and retraction(79), the characteristics of which depend on actin cross-linking proteins, the level of myo-II in the cell, and numerous other factors. When bleb formation is restricted to the leading edge, forward motion is driven by contraction of the cortical network at the posterior end of the cell (Figure 2(b)). The second mode occurs in suspended, microtubule-depleted fibroblast cells (90). Here a myosin-rich ring or collar forms where the cortex ruptures, and cortical contraction draws this over the cell body, thereby squeezing the cytoplasm into the bleb. This process may then occur cyclically, as is observed in fibroblasts(90), and this mode provides a mechanism for squeezing through tight spaces in the ECM, by a kind of ’push-me-pull-you’ mechanism described later for swimmers.

Though the conceptual model of blebbing is simple, there is currently little quantitative understanding of how the factors described above control the process. Equilibrium models based on a elastic description of the cortex have been developed(78), and simplified models of the various aspects of the dynamics exist(77; 91–93). However none describe both the membrane-cortex interaction and the intracellular fluid dynamics in detail, which is essential for understanding the dynamics of blebbing. Moreover there is as yet no mathematical model of a cell moving by blebbing in a confined environment.

3.2 Pseudopdia-driven movement

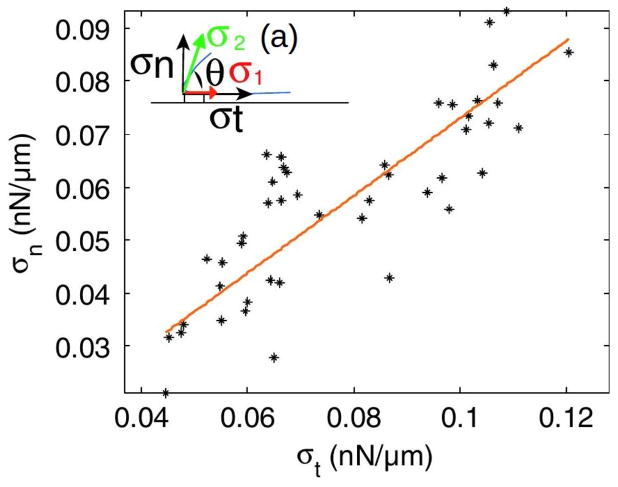
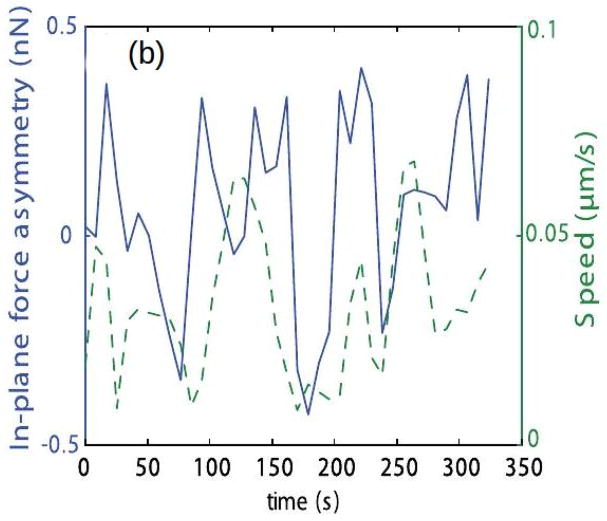
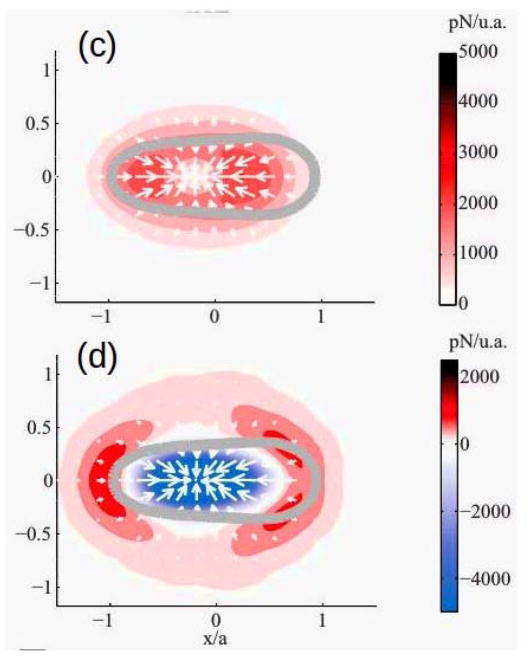
Because Dd can extend lamellipodia, pseudopodia or blebs, depending on the ME (94; 85; 84), it is widely used as a model biological system for amoeboid motion. Movement of wild-type cells is typically comprised of cycles of protrusion of pseudopodia or blebs at the front and retraction at the rear, with weak interactions with the surface and speeds ~ 10 – 20μm/min. Traction force maps typically only deal with the forces parallel to the substrate since they only reflect the tangential motion of marker beads in the substrate(95), and thus analysis of these maps may give an incorrect view of the forces exerted by the cell. A 3D map, in which the vertical motion of beads in the substrate is also measured, can give a more complete picture. Such 3D maps for pseudopod-driven movement of Dd cells on a soft gel show that the forces normal to the gel are comparable to the tangential forces (Figure 6(a))(96). The authors also measured the temporal variations of the forces to obtain the cycles of the speed (Figure 6(b)). More recent 3D force maps(97) show that the forces comprise two independent components – an in-plane, tangential component due to myosin contraction, and a normal component due to cortical tension. The vertical forces are upward along the edge of the cell and downward in the center of the contact area (cf. Figure 6(d)). A surprising result that reflects the strong interaction between the normal and tangential forces is that the velocity is positively correlated with their ratio, but not with either separately(97).

Figure 6.

(a) The normal vs the in-plane force in Dd. The inset shows the labeling. (b) The cyclic variation of the forces and the speed. (c) and (d) The tangential and normal forces in Dd. (a) and (b) taken from Delanoe-Ayari et al. (96), (c) and (d) taken from Alvarez-Gonzalez et al.(97).

However, the story is not complete, since these traction maps only give the force exerted on the substrate by a cell, but provide little information about the spatial distribution of forces within the cell. What is needed to replicate the movement is a 3D mechanical model that represents the composite membrane-cortex and its interaction with the CSK and the substrate. With this one can begin to understand the role of membrane tension and the nature of cell confinement in determining how and where on the membrane blebs are initiated, and whether blebbing or pseudopodia is used.

Dd ‘measures’ the compliance of its ME and switches from predominantly using pseudopods to using blebs when migrating under agarose overlays of increasing stiffness(84). The proportion of blebs compared with total cellular projections increases from 20 – 30% under buffer, to almost 100% in the same cells moving under overlays of more than 1% agarose. Furthermore, Dd blebbing cells are efficient in their chemotactic response to cAMP, extending most of their blebs up-gradient. The authors suggest that blebbing may be used to relieve membrane tension(84), but it may also be that more force is needed to move under agarose, and blebs could provide that. This raises the question of how the mode used depends on the mechanical properties of the medium and the magnitude of the cAMP gradient. Despite the fact that blebs and pseudopods involve very different actin dynamics, in that F-actin polymerization drives extension of a pseuopod while the cortex first detaches from the membrane in a bleb, blebs and F-actin–driven pseudopods can coexist at the leading edge(84). Moreover, blebs can transform into pseudopods by continued actin polymerization at the cortex, whereas pseudopods can spawn blebs at their periphery(84; 98). Uniform stimulation with cAMP can also induce blebbing, suggesting that blebs are under chemotactic control(86). The cAMP–induced blebbing can be induced independently of much of the known chemotactic signal transduction network, but for the PI3-kinase pathway described later.

4 Controllers of the actin networks

4.1 Pathway balances determine the mode

Since different types of protrusions are possible, the question arises as to how mechanical and chemical signals from the ME control the mode. In addition, since cells can be motile in the absence of extracellular signals, the autonomous dynamics of the actin network governing unstimulated movement have to be understood separately from the stimulated response. The fact that different modes can coexist in cells such as Dd suggests that the balance between factors or pathways that determine the modes may be delicate.

The pathways are those whose output determines whether dendrite network formation or myosin contraction dominates, the former leading to actin-driven protrusions and the latter to enhanced contraction and possible blebbing. The balance between them is largely controlled by Rho GTPases, which act as molecular switches, or more precisely, as adapting rheostats, for different pathways. In neutrophils three Rho GTPases – Cdc42, Rac and RhoA – control three pathways that determine whether filopodia (Cdc42)(99), lamellipodia (Rac) (100; 101), or the contraction of the F-actin network (Rho) dominate. Rac controls dendrite network formation by activation of scaffold proteins of the WASP family, which when activated facilitate actin polymerization by regulating Arp2/3(102), while activated RhoA facilitates formation of actin bundles and stress fibers by activating the contractile activity of myo-II.

The skeleton of the network downstream of Ras that controls the pathways in Dd is shown in Figure 7(C), and the primary steps in the Rac and Akt (RhoA in neutrophils) pathways are quite well-established(103–105). In Dd myo-II assembly is controlled by PAKa(106), and contraction is stimulated by inactivation of an inhibitor of myo-II contraction via the cGMP pathway(107)(cf. Figure 7(A)). Not all pathways are shown in Figure 7, and the feedback interactions shown in Figure 7(C) are a composite of known or postulated interactions in Dd and neutrophils (100, 108–112). The cross inhibition of these pathways may ensure that the mesenchymal and amoeboid modes are mutually exclusive in some cells, but it is not absolute since Dd uses a mixed-mode strategy that involves coexistence of pseudopodia and blebs(84). Phenomenological models of some of the interactions shown are reviewed elsewhere (113; 114).

Figure 7.

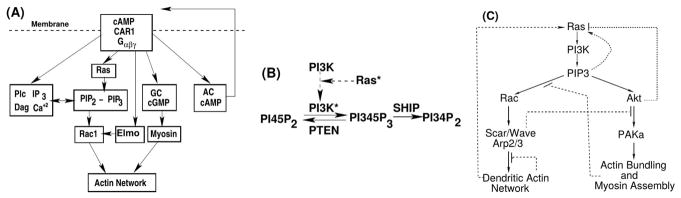
(A) Some of the major components of cAMP signal transduction in Dictyostelium discoideum. CAR1: the cAMP receptor, G_αβγ: a G-protein involved in the transduction of the extracellular signal, Ras: a small G-protein, PIP₂ and PIP₃; components of the membrane that can be interconverted via phosphorylation and de-phosphorylation, IP₃ and DAG: poducts that result from the degradation of PIP₂, Ca²: calcium, GC: guanylate cyclase – the enzyme that produces cyclic GMP (cGMP), AC: adenylate cyclase – the enzyme that produces cAMP, Rac1: a small G-rotein, Myosin: a motor protein involved in contraction of the actin network. (B) The PIP₂-PIP₃ trio. Activated Ras activates PI3K, which phosphorylates PIP₂. PIP₃ provides a binding site for cytosolic PI3K, thereby creating a positive feedback loop through PI3K. Similarly, PIP₂ provides a binding site for PTEN, which dephosphorylates PIP₃. PIP₃ levels are controlled in part by PTEN and SHIP, which dephosphorylate PIP₃ at different sites. (C) The skeletal network downstream of Ras that determines the balance between dendritic network formation and myo-II assembly in Dd.

4.2 Actin waves

Neutrophils and Dd extend pseudopods and migrate in the absence of directional signals(108; 115; 116), and while the motion may appear to be a random walk with persistence on a sufficiently long time scale, on a short time scale the extension of pseudopods is not random over the surface. In Dd a high percentage of new pseudopods forms by splitting off from existing ones(117), and thus the intracellular networks that control the CSK must be tuned to produce signals that generate this kind of movement. Since the balance between the Rac and Akt (RhoA) pathways determines whether dendrite network formation or bundling of F-actin dominates, it is thought that the complex patterns of traveling actin waves in the cortex that are observed in both cell types in the absence of directional signals are the result of competition between them. Vicker (120) was the first to suggest that the observed waves were the result of an excitable reaction-diffusion system involving actin dynamics, based on earlier observation of traveling waves in Dd(121). Since then such waves have been observed in Dd, neutrophils and other cell types(108,115,122–128). It is well known that properly-balanced positive feedback and slow inhibition can lead to a well-defined threshold and oscillations in the local dynamics, as well as waves in reaction-diffusion systems, and while experimental results suggest that the observed waves are governed by an excitable system, it has been difficult to identify a minimal set of components of the network shown in Figure 7 responsible for them. One proposed model involves only the PIP₂-PIP₃ components(124), but this fails to be excitable. Recent evidence from Dd(116) suggests a feedback loop from F-actin to Ras, as shown in Figure 7(C), but the feedback might also stem from components such as Scar/Wave/Arp2/3 further up the pathway.

Figure 7(A) shows the four main pathways in Dd involved in transducing an extracellular change in cAMP to a change in the actin network. The central pathway is via Ras, PIP₂, PIP₃, and Rac1, another pathway is through Plc and its products, the third is through guanylate cyclase, and the fourth is the cAMP production and secretion/relay pathway through adenylate cyclase. Despite the number of components shown, the diagram only contains representatives of the principal actors and pathways. For instance, there are a number of G_αs, and five different Ras proteins, two of which, RasG and RasC are principals in the chemotaxis pathways. We will only consider the Ras-PIP₂/PIP₃ pathway – a mechanistic description of the Plc, GC, and AC activation appears elsewhere(129; 104).

In the absence of an extracellular signal only the components in Figure 7(B) and (C) play a role, and the PIP₂ and PIP₃ dynamics are central. In Dd the actin waves arise during reconstruction of the actin network following treatment with latrunculin A (LatA), which sequesters G-actin monomers and leads to deconstruction of the network and rounding of the cells. The cells return to their pre-stimulus state after removal of the drug, but in the interim there are distinct domains in the portion of the membrane in contact with the surface in which different actin structures exist (cf. Figure 8(a)). In one PIP₃ is high and dendrite actin networks exist, whereas in the other PIP₃ is low, cortexillin is high, and F-actin is in bundles. The fact that there are two distinct domains separated by a propagating actin wave suggests that the underlying dynamics are bistable, with one state in which PIP₃ is high and PIP₂ is low, and the other with the roles reversed. The waves that arise at the boundary between domains of high and low PIP3 are typically closed and of varying shape, and they propagate by treadmilling, as shown by actin recovery after bleaching(118). These waves propagate by polymerization at the leading edge of the wave and in situ depolymerization at the trailing edge (130). Myosin-IB, which links the actin network to the membrane(70), is found at the front of a wave, and the Arp2/3 complex and a dense dendrite network are found throughout the wave. Coronin, which inhibits filament nucleation and indirectly regulates cofilin activity via dephosphorylation(131), and cortexillin, which organizes actin filaments into anti-parallel bundles, are found where PIP3 is low.

Figure 8.

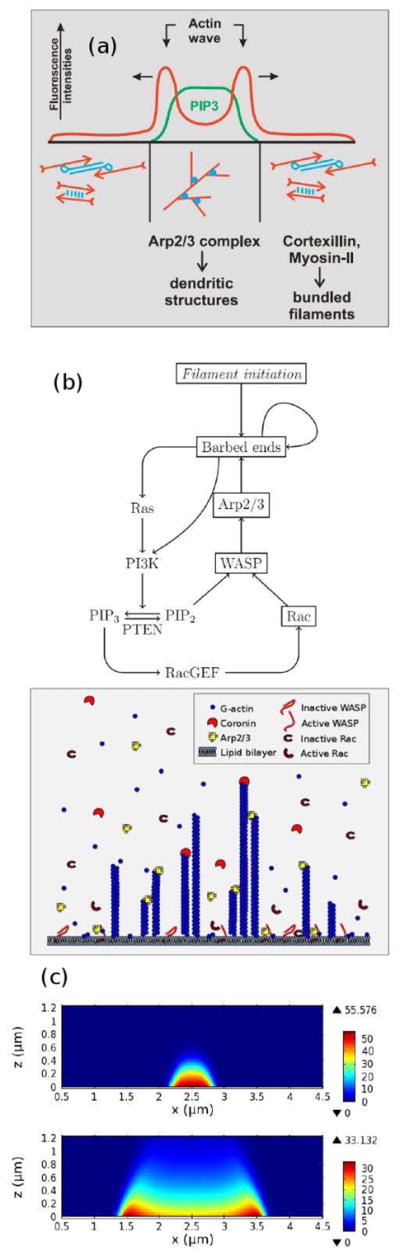
(a) A cross-section of the waves. From Gerisch(118). (b) A schematic of the network structure and molecular interactions in the model.(119) (c) Two snapshots in time of an actin wave initiated at x=2.5, showing the network density (color) as a function of space (x-axis) and network height (z-axis). From Khamviwath et al.(119) with permission.

A simple mathematical explanation of such propagation can be understood from the one-dimensional Fisher’s equation for a scalar variable u such as the concentration of PIP₃.

$$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}+u(1-u)$$ [1]

The zero state u ≡ 0 is unstable, and if given a local perturbation a propagating transition wave from u = 0 → u = 1 develops. However this equation cannot describe the reflection of waves sometimes observed when they reach a boundary. This can be understood qualitatively by considering the equation

$$\frac{\partial u}{\partial t}+(f_0+f_{1}u)\frac{\partial u}{\partial x}=\frac{{\partial }^{2}u}{\partial x^2}+g(u)$$ [2]

where the second term represents an active or convective transport process and g(u) is qualitatively a cubic nonlinearity with zeroes u₁ ≤ u₂ ≤ u₃. By adjusting the parameters f₁ and f₂ one can obtain a propagating transition wave from u₁ → u₃ or u₃ → u₁, or stationary transition waves(132). Thus if a second mechanism controls one of these parameters, one can make the waves stall(133) or reverse the waves at the boundary. However, this is only a cartoon description – the underlying mechanism is much more complicated.

Khamviwath et al. (119) have proposed a continuum mathematical model for actin waves based on a large number of molecular details of actin network dynamics and the PI3K pathway (Figure 8(b))³. Following initiation with a transient, sufficiently-large and spatially-localized increase in the nucleation rate of filaments, the subsequent evolution produces a single pulse, whose intensity grows over time while the pulse spreads in both the x- and z-directions, the latter representing the height of the actin network (Figure 8(c)). The existence of a threshold for initiation of a wave, which implies that the uniform rest state is stable, suggests that the model is excitable. Later the amplitude in the center decays, and the pulse splits into two symmetric pulses moving in opposite directions, which is consistent with experimental observations(122)(cf. Figure 8(a) & (c)). In addition, the concentration of Rac, which is treated as a proxy for PIP₃, does not display peaks, which is also consistent with the experimental observations(122). Another prediction of the simulation is that by artificially including PTEN the waves reverse, which agrees with the observations that the waves often propagate to the cell edge and then reverse direction. This reversal cannot be easily explained by standard reaction diffusion models of the type described by cf. Eqs. [1] and [2]) or by systems including these components. Mathematical models describing how actin networks and waves interact with deformable cell membranes and can result in protrusive behavior have been developed (134; 135) and other models are reviewed in (136; 137), but much remains to be done to understand whether the actin system is bistable or excitable, what role the surface contact plays, where the feedback originates in the system, and how many variations of the dynamics exist in different cell types. For example, it has been found in macrophages that PIP₂ is enriched in the wave center, rather than PIP₃, as in Dd(138).

4.3 Mechanotransduction and the role of tension

Additional feedback interactions between the membrane, the cortex, and signaling control the geometry, mechanics and movement of cells(139). In COS-1 cells the protein FBP17 senses membrane tension, localizes in regions of low tension, and activates WASP-dependent actin nucleation there(140). It is suggested that FBP17 is part of a feedback loop that senses the local curvature to stimulate actin polymerization where curvature is low, in a self-limiting process that is inhibited by the tension generated by this process. This is one aspect of the larger question that concerns the effect of membrane curvature on signaling and CSK dynamics(141; 142). A number of proteins containing a BAR domain can associate with curved membranes, either because they are sensitive to curvature or because they induce curvature, or both(143). High membrane tension may reduce the binding of such proteins by reducing the local curvature needed for their binding to the membrane(144). This effect could regulate the membrane binding of GEFs and GAPs, the proteins that regulate the GTPase switches, which in turn provides feedback between curvature and actin dynamics. A related aspect of membrane tension concerns the effect of myo-I, which plays a role in determining the cell morphology and movement by controlling the membrane-cortex linkage. Studies have shown that cortical tension, extension of pseudopodia, cell motility and chemotaxis are all altered in Dd with over- or under-expression of myo-I(145; 146).

Similar effects occur in neutrophils. Membrane tension doubles at the leading edge during actin-driven protrusion, and the resulting global increase in tension inhibits actin assembly and Rac activation over the remainder of the cell(147). It is suggested that the tension increase and the attendant increase in membrane curvature generate a negative feedback circuit that limits extension of the front and the formation of secondary fronts. Increased membrane tension acts to limit actin nucleation through phospholipase D2 (PLD2) and the mTORC2 pathway downstream of Akt, and blocking this pathway produces broader leading edges, higher membrane tension, and defective chemotaxis(148).

5 Directed motility

5.1 Direction sensing

In the presence of a chemotactic signal cells must orient properly, which means that the dynamical system controlling the actin network must respond to the bias. If the optimal strategy for movement of Dd in a noisy chemotactic field is to align with the local gradient, then a cell must determine the direction in which to move from a measurement of the local cAMP concentration at its surface. Choosing the direction precisely is not necessary — a mathematical model shows that Dd can aggregate as long as cells choose their direction within ± 135° of the correct direction, but they aggregate more slowly(150). It has also been shown, using a model for the G_βγ-AC-cAMP part of the network in Figure 7 (151), that a cell experiences a significant difference in the front-to-back ratio of cAMP when a neighboring cell begins to signal. One can infer from this that other components in the signal-transduction pathway may also show significant front-to-back differences in a gradient, and this has been demonstrated experimentally for PIP₃, PI3K, and PTEN. There are a number of theoretical models for how this can be achieved. Meinhardt (152) postulated an activator-inhibitor model with a third species that serves as a local inhibitor. Amplification of small external differences involves a Turing instability in the activator-inhibitor system, coupled to a slower inactivator that suppresses the primary activation. This model is an interesting high-level description of the process, but lacks a direct mapping onto the biochemistry. Most current models for direction sensing are based on an activator-inhibitor mechanism called LEGI – local excitation and global inhibition, similar to that proposed by Meinhardt, to explain both direction sensing and adaptation when the chemoattractant level is held constant (153). In existing LEGI models a fast-responding but slowly-diffusing activator and a slow-acting, rapidly-diffusing inhibitor set up an internal gradient of activity that locks onto the extracellular gradient. While these models provide a framework for thinking about direction sensing, their usefulness is limited due to the oversimplification of the signal transduction network and the necessity of a wide disparity in the diffusion coefficients of the activator and inhibitor to establish an intracellular gradient.

A more recent mathematical model for signal transduction and adaptation in Dd based on detailed descriptions of the underlying biochemistry can replicate a variety of experimental observations, including amplification at the level of Ras, a biphasic response to graded stimuli, the existence of a refractory period for repeated stimuli, and ’memory’ of the up-gradient direction in a wave, that are not addressed by other models(149). The model is built around a reaction-diffusion-translocation system that involves three main component processes: signal detection via CAR1, transduction based on activation of G_α2βγ, and an activation step of Ras (cf. Figure 9). The key components in the model are G_α2βγ 2, Ras, RasGEF and RasGAP, which control rapid excitation and slower adaptation of Ras, and Ric8, a GEF that activates G_α2 (154). Experimental data on LatA-treated cells was used to validate the model for a variety of stimulus protocols(155; 156).

Figure 9.

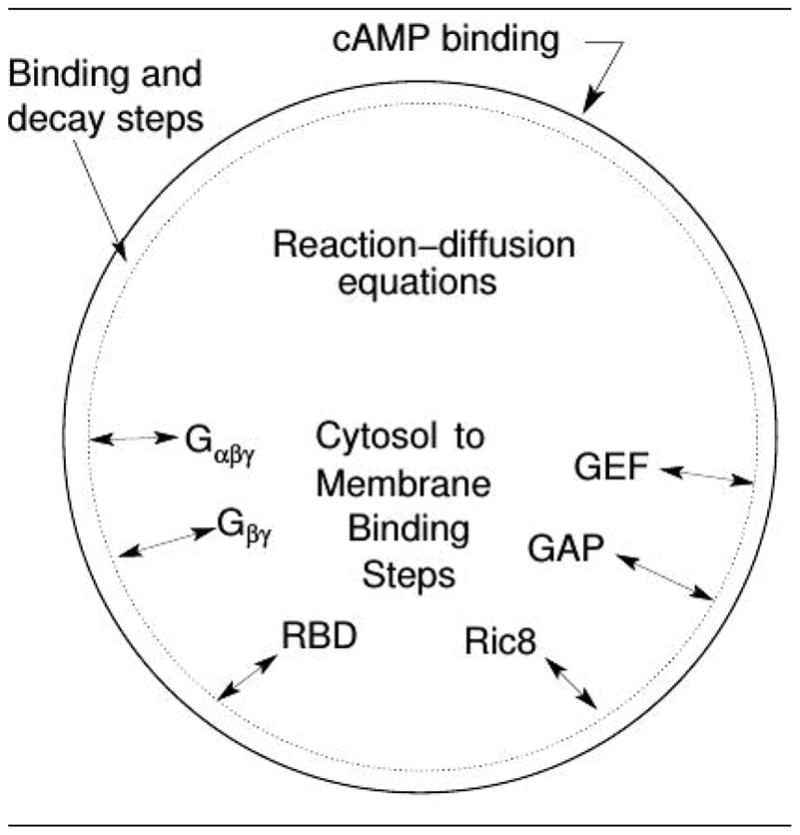
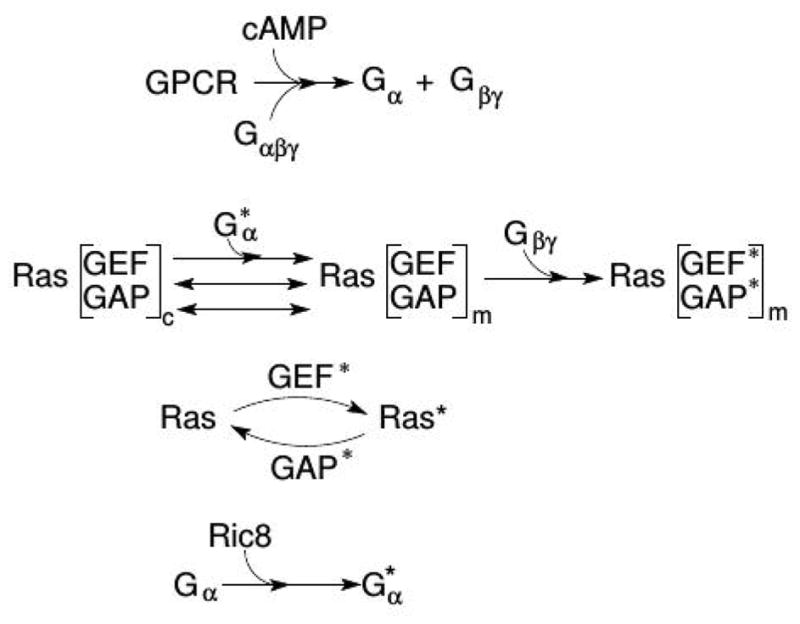
A schematic of the major processes in the model (top), and the major steps in the network (bottom). From Cheng & Othmer (149) with permission.

There are two sources of amplification of a cAMP gradient in the model network. Firstly, the higher concentration of $G_{\mathrm{\alpha }2}^{\ast }$ on the membrane at the front of the cell, where the cAMP concentration is highest, induces higher localization and activation of Ric8, which in turn reactivates G_α2 and further promotes RasGEF localization there. Secondly, faster G_α2βγ re-association at the rear due to lower Ric8 and higher $G_{\mathrm{\alpha }2}^{\ast }$ hydrolysis creates a gradient of G_α2βγ, high at the rear and low at the front, and thereby provides a flux of G_α2βγ toward the front.

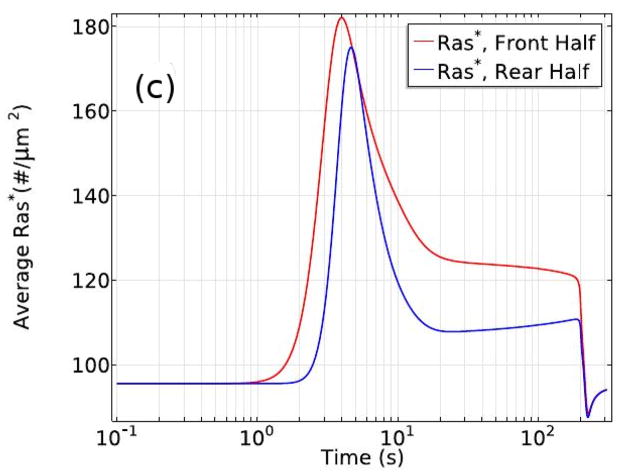
It was shown that G_βγ mediates adaptation of Ras activity in a uniform stimulus and transient activation in a gradient. In addition, $G_{\mathrm{\alpha }2}^{\ast }$ contributes to the imperfect adaptation in a uniform stimulus, and it is essential for front-to-back symmetry breaking in a gradient, highlighting the important roles of G_α2 and G_α2βγ 2 cycling between the bound and dissociated states. Furthermore, Ric8 contributes to the amplification of Ras activity by regulating G_α2 dynamics: the reactivation of G_α2 by Ric8 induces further asymmetry in G_α2βγ 2 dissociation, which in turn amplifies the Ras activity. Thus G_α2βγ 2 cycling modulated by Ric8 drives multiple phases of Ras activation and leads to direction sensing and signal amplification in cAMP gradients. Several results from the model are shown in Figure 10. One sees in (a) and (b) that the biphasic response – uniform around the cell at first followed by symmetry-breaking later – in a graded stimulus is captured. In a passing triangular wave of height 1000 nm and extent 1000 μm, Ras* at the front is always larger than at the rear (Figure 10(c)), which reflects a form of ’memory’ of the direction from which the cell first received the signal. A major conclusion of this investigation was that the symmetry-breaking at the level of Ras encodes sufficient ‘memory’ to maintain directional orientation during a passing wave and thus provides a solution to the ’back-of-the-wave’ problem. In contrast with classical LEGI models of symmetry-breaking, the results do not require a disparity between the diffusion coefficients of the Ras activator GEF and the Ras inhibitor GAP. Of course downstream components may amplify and imprint the broken symmetry.

Figure 10.

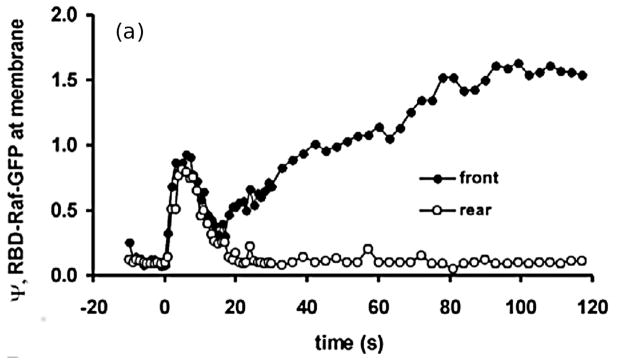
The levels of activated Ras* at the front and back in a static cAMP gradient as a function of time measured experimentally (a) From Kortholt et al(156) and the model prediction (b)(149) (c) The average Ras* in the front and rear halves in response to a passing triangle wave. From Cheng & Othmer(149) with permission.

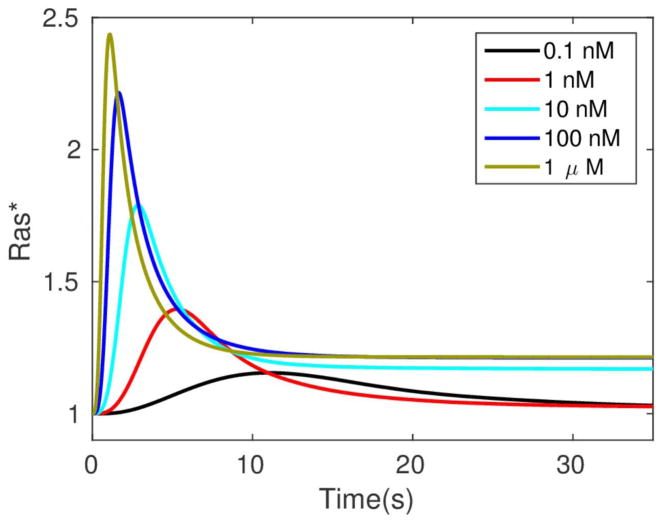
It has been proposed that an integrated model for direction sensing, adaptation, and signal-independent actin waves comprises two components – a signal transduction excitable network (STEN) coupled to a CSK oscillatory network (CON)(157). In the present context the STEN would correspond to the signal transduction network described above, while the CON network would correspond to that in Figure 7(c). Here the two are coupled at the level of Ras. The detailed STEN network exhibits a refractory period determined by the relaxation of the active GEF and GAP, but the network is not excitable – there is no threshold cAMP level below which the system does not respond, and the response increases monotonically with the stimulus level (cf. Figure 11). However, the definition of excitability is somewhat arbitrary — if the local dynamics has a stable rest point most stimuli will elicit some response, and it becomes a matter of whether there is a threshold stimulus that separates ’small’ responses from ’large’ ones.

Figure 11.

The ratio of Ras* under uniform stimulation to it’s basal level as a function of the stimulus level and time. From Cheng & Othmer (149) with permission.

An aspect of signaling that has not been widely studied concerns the role of noise at the receptor level in detection. Estimates of the signal noise show that it may be important at low signal levels (129), but detailed stochastic simulations of the full exterior reaction-diffusion system are needed to make this more precise.

5.2 Polarization

PTEN is a major regulator of migration during chemotaxis in both Dd and neutrophils (158; 159). Activated PI3K is increased at the site of signal reception, and PTEN localizes to the lateral and posterior regions of migrating cells. In the previous section we described a model for polarization at the level of Ras, and ipso facto, of PI3K and PIP₃. The latter has a pleckstrin homology domain that provides a docking site for cytoplasmic proteins such as PI3K, the kinase Akt and the GTPase Rac1. PTEN docks to PIP₂, and the reduction of PIP₂ due to conversion into PIP₃ reduces the membrane-bound PTEN, which produces a reverse gradient in bound PTEN and further increases PIP₃ at the leading edge. This leads to activation of Rac1 and stimulation of F-actin network formation there. The resulting spatial asymmetry in these components can lead to a more persistent polarization than at the level of Ras alone.

Myo-II, and hence contraction, is localized at the posterior end of migrating neutrophils and Dd (160). Whether PTEN controls myo-II localization is not known, but the foregoing shows how a gradient of PTEN can arise, and it is known that PTEN localizes at the side and rear prior to myo-II localization (161). It has been suggested that PTEN may be involved in a positive feedback loop in which contraction enhances accumulation of PTEN and myo-II (161). However, PTEN is not the sole controller of myo-II localization, for it still localizes in pten⁻ cells, and this may involve the cGMP pathway in Dd or the RhoA/Rock pathway in neutrophils(162; 163). In other cells myo-II preferentially binds to actin filaments in tension, and a reduction in the tension leads to release of myo-II(164). Localization of other factors may also play a role in polarized movement. For example, the suppression of cofilin expression, which binds to actin filaments and promotes their breakup, results in re-localization of Arp2/3 to one pole and protrusions from only that pole (165). An important question concerning polarization is whether the pressure-induced flow stemming from contraction – which would carry G-actin forward and PTEN and unbound myo-II to the rear – suffices, or whether other factors or mechanisms are needed.

The PIP₂/PIP₃ ratio is also a critical factor in the blebbing-pseudopod dichotomy. Depletion of PIP₂ increases blebbing, probably via its effect on membrane-cortex adhesion(166), whereas pi3k⁻ cells make only a fraction of the number of blebs made by wild-type cells(84; 98). Actin polymerization can also be stimulated by cAMP independently of PI3K(167), probably via the G_βγ-ELMO pathway. From Figure 7 one can see that another balance, this time between the Ras-independent and Ras-dependent pathways, may be an important factor in resolving the blebbing-pseudopod competition. A high-level mathematical model for polarization in which the balances between pathways is adjustable could be useful to gain insight into the dynamics and perhaps guide further experimental work.

6 Swimming via shape changes and tension gradients

6.1 Swimming by shape changes

In fluid mechanics the Reynolds number (Re) is defined as the ratio of inertial effects to viscous effects, and given a length scale L and a speed scale U, is defined as Re = ρLU/μ, where μ is the viscosity of the fluid. When Re ≪ 1 the inertial (i.e. acceleration) terms are negligible provided the shape of the swimmer is changed sufficiently slowly. The spatio-temporal scale of motion of small organisms in viscous fluids frequently leads to low Reynolds number (LRN) flows – a bacterium in water leads to Re ~ 10⁻⁵. As mentioned earlier, Dd and neutrophils both swim by time-dependent changes in the shape of the cell(17). Dd amoebae have a typical length L ~ 25μm and can swim at U ~ 3μm/min (16). Assuming the medium is water (ρ ~ 10³kg m⁻³, μ ~ 10⁻³ Pa ·s), and the deformation frequency ω ~ 1/s, Re ~ 𝒪(10⁻⁶). In fact the experiments done to prove that they can swim use oil that is significantly more viscous than water(17), and thus their movement generates an LRN flow.

Current interest in locomotion at LRN was stimulated by Purcell’s description of life at low Reynolds number (168). In particular, the observation that certain classes of shape changes produce no net motion in a viscous fluid led to studies on various types of discrete models of swimmers, with the goal of understanding how microorganisms swim at LRN. A LRN flow is governed by the Stokes equations

$$\mathrm{\mu }\mathrm{\Delta }\mathbf{u}-\nabla p=\mathbf{0},\nabla ·\mathbf{u}=0$$ [3]

where u is the velocity, p is the pressure, ∇ is the gradient, and Δ is the Laplace operator. To simplify the exposition we consider the propulsion problem in an infinite domain and impose the condition u |_x→∞ = 0 on the velocity.

In the LRN regime time does not appear explicitly, momentum is assumed to equilibrate instantaneously, and bodies move by exploiting the viscous resistance of the fluid. As a result, time-reversible deformations produce no motion, which is the content of the ’scallop theorem’ (168). Since there are no external forces (if the swimmer is not neutrally bouyant gravity can be subsumed in the pressure term), there is no net force or torque on a self-propelled swimmer in the Stokes regime. Therefore movement is a purely geometric process: the net displacement of a swimmer during a stroke is independent of the rate at which the stroke is executed, as long as the Reynolds number remains small enough. Thus the problem can be stated as: given a cyclic shape deformation of a swimmer specified by a prescribed velocity on the boundary, solve the Stokes equations subject to the force- and torque-free conditions.

One easy-to-understand example that is suggestive of motion by blebbing is called the push-me-pull-you (PMPY) model shown in Figure 12(169), in which two spheres that can expand or contract radially are connected by an extensible arm and submerged in a fluid. Suppose that the total volume of the sphere is fixed and the volume of the rod is negligible. A cycle of motion consists in moving volume to the rear, which moves the center of mass rearward, followed by extension of the rod, which moves the smaller leading sphere forward. The cycle is completed by moving the volume forward and retracting the rod. Analytical and numerical studies of the PMPY model has been done, and their efficiency of movement compared with alternate forms of discrete volume swimmers has been done. (170–172).

Figure 12.

The push-me-pull-you swimmer.

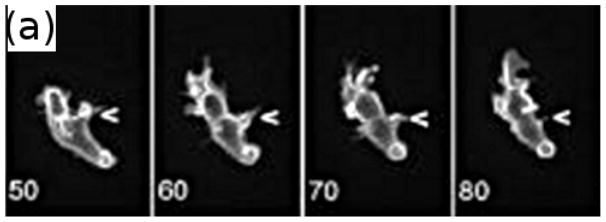
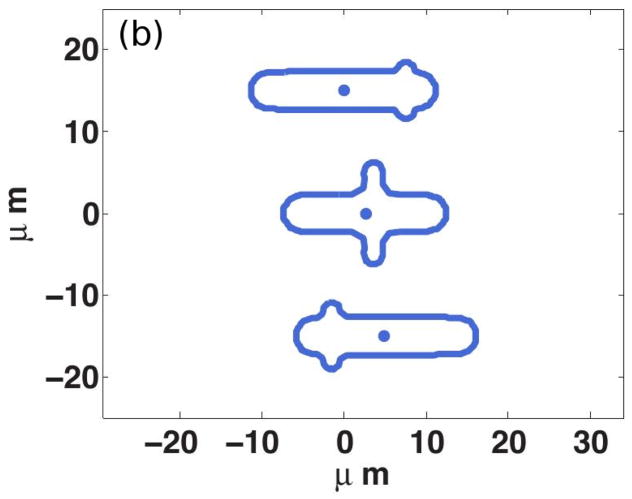
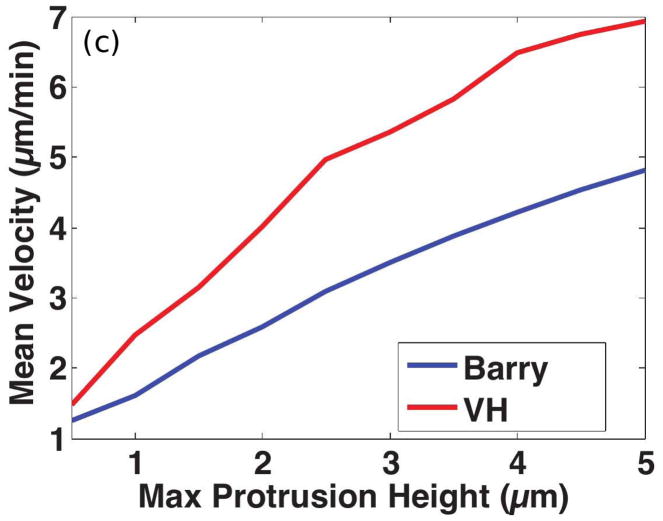
Of course shape changes require intracellular forces to generate them, but at present there is no realistic model for this interior problem. Therefore, in the following example we simply prescribe the shape changes and treat the exterior problem, which focuses on how the cell moves by interacting with the fluid. The shape of a Dd cell that swims by propagating a protrusion down its length is shown in Figure 13(a) (see also the movies in the supplemental information to Barry(17)). Computational results from a simulation of a 2D model, in which a cell swims using symmetric protrusions (cf. Figure 13(b)), are shown in Figure 13(c). There the speed of two strains of Dd, one used in Barry & Bretscher(17) –marked Barry – and one used by van Haastert(16) – marked VH — is shown as a function of the protrusion height. The VH cells are somewhat longer and thicker, and most importantly, the typical period of a VH cell stroke is 1 minute, vs. 1.5 minutes for the Barry cell. VH swims faster than Barry for all heights, but the speed of both increase significantly with the height of the protrusion, and the computed speeds are in the range of experimental observations. VH uses more power in the process and is less efficient by this measure, but excels by another measure of the performance(173). The experiments and analysis show that swimming by shape changes is feasible for cells, and analysis of how they do it may provide insights into both the design of nano-robots and possible interventions in tumor cell migration.

Figure 13.

(a)Four time points of a swimming Dd cell showing the axial propagation of protrusions along the length. From Barry & Bretscher(17). (b) Three time frames from a computational model of a 2D swimmer using symmetric protrusions. (c) The mean velocity of two swimmers as a function of the protrusion height. (b) and (c) from Wang & Othmer(173) with permission.

6.2 Tension-driven movement

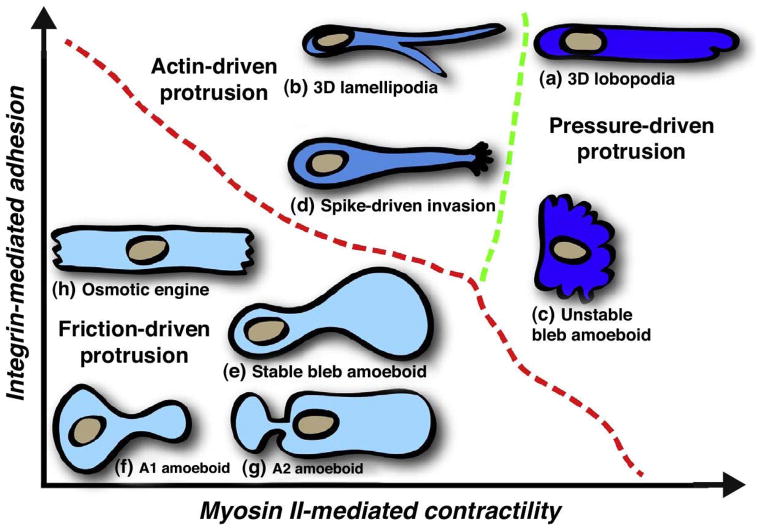
Swimming and movement in confined spaces are also possible without shape changes. Movement by blebbing is often thought of as using a ’push-pull’ mechanism as described earlier, but another variation is called ’stable-bleb’ or ’leader-bleb’ migration and is used by certain embryonic cells that form a balloon-like protrusion at their leading edge(174; 9; 175). Recent work has shown that movement driven by cortical flow in a fixed cell shape occurs in both human dermal fibroblast cells (8) and in zebrafish germ-layer cells(9). In the former the authors identify two morphologies, one type – A1 – has a rounded body and a small leading edge, and the other – A2 – has a more ellipsoidal body with a large uropod (Figure 14). Slow mesenchymal cells undergo the MAT when the adhesion is low and the cells are confined between plates, and this leads to one of the two shapes and two types of fast migration. The first (A1) involves low contractility of the cortex and a local protrusion, and the second (A2), is a stable-bleb type that involves high myo-II activity and involves a strong retrograde actin flow. Type A1 appears to require an external signal to polarize, whereas type A2 can appear spontaneously, as has been shown for other cell types(89; 176).

Figure 14.

A summary of the different modes of movement in different environments and under different substrate properties. From Petrie et al.(177).

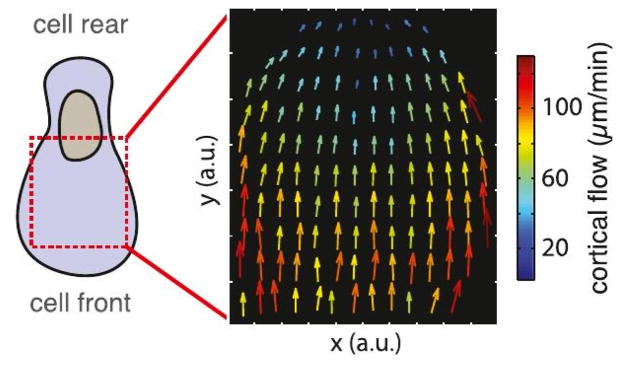
A stable bleb morphology with a more bulbous front (type (e) in Figure 14), arises as a transition from a stable non-polarized blebbing cell to a permanently polarized shape induced by increasing the contractility(9). In both zebrafish and A2 cells a (postulated) gradient of cortical density and myo-II generates a measurable cortical flow and an axial pressure gradient. Cortical flow rates of 10’s of microns/min are observed (cf. Figure 15(top)), which would certainly induce a posterior-to-anterior flow in the center, as shown in Figure 15(bottom). In both cases a high cortical growth rate at the front of a cell and a high disassembly rate of the cortex at the rear are assumed to generate the flow and polarization of the cell. The latter is supported by the fact that inhibition of myo-II contractility with blebbistan inhibits polarization, stretching actin filaments increases their affinity for myo-II(178), and the ADP release rate from myo-II increases 4-fold under tension(179). The postulated high disassembly rate at the rear is also consistent with what is found in keratocytes, where myo-II is involved in deconstruction of the actin network at the rear of the cell (180). In a model the transition has been attributed to an instability of a spherical shape to fluctuations in the membrane(181–183), but the desired pear shape requires a specific anisotropy of the cortical tension.

Figure 15.

Top: The type A1 morphology and the cortical flow rates observed in zebrafish progenitor cells. From Ruprecht et al. (9). Bottom: A schematic of the cortical and interior flow.

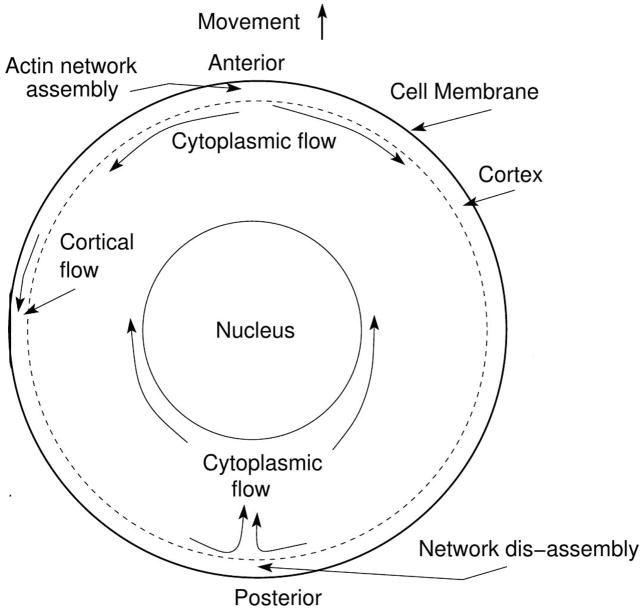
These observations raise a number of interesting questions. Firstly, can one predict the balance of forces within a cell needed to produce the various shapes shown in Figure 14, and to what extent are the shapes fixed by the mechanical feedback from interrogation of the ME? In particular, does the cortical flow in stable bleb cells arise in different environments, or is it specific to cells in a confined environment? Interestingly, some cells cannot move if they are only in contact with the substrate on the ventral side, but will move when confined in a micro-channel(176). This suggests that the circulating cortical flow shown in Figure 15(bottom) may not arise when the cell is in contact with a surface on only one side, and this has been shown experimentally in Dd (184). However, it is also observed that Dd cells can swim without shape changes for several body lengths(185), and one hypothesis is that they do so by maintaining an axial tension gradient in the membrane(68).

To see why swimming without shape changes is possible, consider the fact that the cortex slips past the membrane, and in a numerous cell types, including Dd(87) and leukocytes(186), the membrane does not flow in a cell-fixed coordinate frame – it merely translocates with the cell body. Thus the membrane functions more like an elastic than a viscous material, and the drag force due to cortical flow creates an opposed tension gradient in the membrane. Back-to-front tension gradients of the order of 5pN/μm² have been measured in axons and keratocytes(187), but only on the dorsal membrane of cells in surface contact on the ventral membrane. Whether the gradient contributes to or opposes motion under different combinations of contact with a surface can be studied with a computational model that integrates the cortical flow and the re-circulating flow described above(188; 189; 68).

Computational results from a model using a free-energy-based description of the membrane shows that cells can swim under various combinations of tension gradient in the membrane and heterogeneity of the bending rigidity(68). Moreover the direction of migration depends on the balance between the cortical tension gradient and the variation of the bending rigidity. This provides an explanation of the observation that some cells move using a small cap in the front, while other cells move with the large bleb in front (8). The model predicts a cell velocity of 6.0μm/min when the tension gradient is 10pN/μm², which is consistent with recent experiments. Furthermore, with a suitable spatial variation of the rigidity the cell can evolve to the asymmetric stable-bleb cell shape, and this also agrees with experimentally-determined values.

7 Conclusions

Improvements in analytical and imaging tools have led to enormous advances in our understanding of many aspects of cell motility. The challenge now is to integrate the knowledge of individual processes into a whole-cell description of cell motion subject to a variety of signals and microenvironments. Some may ask why this is necessary, and one compelling response is that we cannot claim to understand how the nanomachine works until we can assemble the pieces and make it run.

9 Appendix

In this appendix we give a brief description of the mathematical structure of the models discussed in Sections 4–6, and of the computational techniques used in the solution of the governing equations.

Actin waves

The pathway shown in Figure 8(b) is simplified further (119) so that a minimal number of the intermediate effectors are included. The simplified network involves Rac, WASP, and Arp2/3 in both activate and inactive forms, as well as the complex formation that leads to nucleation of actin branches. It is assumed that Rac is diffusible and has a low spontaneous activation rate in the cytosol, whereas the primary activation occurs via interaction with actin filaments at the membrane. WASP activity at the substrate-attached surface is regulated solely by activated Rac activity an activated WASP then recruits Arp2/3 to the membrane, forms a complex with G-actin, and nucleates a new branch on an existing filament.

The dynamics of cytosolic and membrane densities of molecular species are modeled by reaction-diffusion equations, with interactions between species are assumed to follow mass-action kinetics. Exchange between the cytosol and membrane follows a linear flux relation.

The entire system of equations is solved using the software package Comsol, which converts the equations to their weak form, discretizes the domain using finite elements, and solves the resulting system of nonlinear algebraic equations.

Direction sensing

The model for direction-sensing is built around a reaction-diffusion-translocation system that involves three main component processes: a signal detection step based on G-protein-coupled receptors for cyclic AMP, a transduction step based on a heterotrimetic G protein G_α2βγ, and an activation step of a monomeric G-protein Ras(149). The key components in the model are the G-protein G_α2βγ 2, RasGEF and RasGAP, which control rapid excitation and slower adaptation of Ras, and Ric8, a guanine nucleotide exchange factor that activates the G_α2-component of G_α2βγ 2. The model is developed for LatA-treated cells so as to remove the feedback effect from the actin cytoskeleton on Ras, and it can replicate many of the observed characteristics of Ras activation in Dictyostelium. Figure 9 summarizes the essential steps in the model. As in the actin-wave model, there are cytosolic and membrane-bound species. The former diffuse throughout the cytosol, but diffusion of membrane-bound species is ignored.

This model again leads to a large system of reaction-diffusion equations defined in a spherical cell, since cells round up when treated with LatA, which are solved using Comsol.

Swimming by shape changes

To investigate the swimming behavior of Dictyostelium amoebae, the velocity at the surface of the swimming cell is prescribed, and techniques of complex analysis are used to develop 2D models that enable one to study the fluid-cell interaction. In 2D one can introduce a stream function, which leads to a biharmonic equation, and the general solution of the LRN Stokes problem is expressed in terms of two analytic functions – the Goursat functions – that are determined by the motion of the boundary of the swimmer. This in turn leads to an integral equation for one of these functions, and the second function can then be expressed in terms of the first. Polygonal approximations to shape changes that represent the protrusions used by Dictyostelium are defined, and the Schwarz-Christoffel transformation, which maps the polygonal shape onto the unit disk, is used to reduce the problem to the solution of a linear system of equations for basis functions on the boundary of the unit disk. Realistic propagating shapes can produce propulsion at speeds in the range observed experimentally using realistic choices of the parameters.

Swimming by tension gradients

In this context swimming is driven by membrane tension gradients that arise from forces in the cortical layer underlying the membrane, and does not involve imposed cyclic shape changes. Such gradients can lead to a number of different characteristic cell shapes, and the objectives are to understand how different distributions of membrane tension influence the shape of cells, to analyze the effects of spatial variation in other membrane properties, and to study the effect of fluid-cell interactions and show how tension leads to cell movement(68). A detailed model of the cortex is not defined – rather an alternate high-level description of the cortical forces in the tangential and normal directions is used to investigate how cortical forces and heterogeneity of membrane properties determine the shape of cells in quiescent fluids, and how these factors determine the shape and speed of swimming cells.

In the absence of fluid-cell interactions, the shapes of cells are typically computed as minimizers of the free energy of the membrane, usually given by a Canham-Helfrich free energy, which has the following form

$${\mathcal{F}}_B={\int }_{S}2k_c{(H-C_0)}^{2}dS+{\int }_S{k}_G\mathit{KdS}.$$ [4]

Here H is the mean curvature, and K is the Gaussian curvature, C₀ is a phenomenological parameter called the spontaneous curvature, k_c the bending rigidity, and k_G the Gaussian rigidity.

To find the stationary shapes under prescribed forces, the first variation with respect to a deformation of the surface is computed to determine the membrane forces, and the cortical forces are added to these. The resulting partial differential equations are solved to determine the stationary shapes in various parameter regimes and under various combinations of applied forces. THe fluid-cell interaction problem that determines the velocity of a swimming cell is solved using a boundary integral method.